| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
5. Внешнее произведение знакопеременных форм.
Рассмотрим две знакопеременные формы:  и
и
В этом пункте мы введем основную операцию в теории знакопеременных форм — операцию внешнего умножения. Пусть

Рассмотрим следующую полилинейную форму 

Эта форма, вообще говоря, не является знакопеременной: при перестановке аргументов и где  форма (6.1.1) может не изменить знака. Этим обстоятельством и вызвана необходимость введения внешнего произведения.
форма (6.1.1) может не изменить знака. Этим обстоятельством и вызвана необходимость введения внешнего произведения.
Для того чтобы ввести внешнее произведение, нам понадобятся некоторые факты из теории перестановок. Напомним, что перестановкой чисел  называют функцию
называют функцию  определенную на этих числах и отображающую их взаимно однозначно на себя. Множество всех таких перестановок обозначается символом
определенную на этих числах и отображающую их взаимно однозначно на себя. Множество всех таких перестановок обозначается символом  . Очевидно, что содержит всего
. Очевидно, что содержит всего  различных перестановок. Для двух перестановок
различных перестановок. Для двух перестановок  естественным образом определяется суперпозиция
естественным образом определяется суперпозиция  . Перестановка
. Перестановка  называется обратной к а, если
называется обратной к а, если  , где
, где  тождественная перестановка (т. е.
тождественная перестановка (т. е. 
Перестановка о называется транспозицией, если она переставляет два числа, оставляя другие на своем месте. Иначе говоря, если существует пара чисел  такая, что
такая, что  для
для  Очевидно, если
Очевидно, если  — транспозиция, то
— транспозиция, то  .
.
Известно, что всякая перестановка о разлагается в суперпозицию транспозиций, переставляющих числа с соседними номерами, причем четность числа транспозиций в таком разложении не зависит от его выбора и называется четностью перестановки  .
.
Введем следующее обозначение:

Заметим, что форма  принадлежит
принадлежит  если для любой перестановки
если для любой перестановки 

Рассмотрим снова полилинейную форму (6.1.1). Для любой перестановки  положим
положим

Нетрудно убедиться в том, что если и  то
то 
Определение. Внешним произведением формы  и формы
и формы  называется форма
называется форма  определяемая равенством
определяемая равенством

где сумма берется по всем перестановкам  удовлетворяющим условию
удовлетворяющим условию

а величина  определяется равенствами (6.1.1) и (6.1.2).
определяется равенствами (6.1.1) и (6.1.2).
Внешнее произведение форм сор и  обозначается символом
обозначается символом

Проиллюстрируем на примере, как действует перестановка о, удовлетворяющая условию (6.1.4). Предположим, что по некоторой дороге параллельно движутся две колонны автомобилей, в первой из которых  , а во второй
, а во второй  машин. Через некоторое время дорога сужается и обе колонны на ходу перестраиваются в одну. При этом автомобили первой колонны занимают места где-то среди автомобилей второй, однако порядок следования автомобилей внутри каждой колонны сохраняется. В результате мы получаем перестановку, удовлетворяющую условию (6.1.4). Легко видеть, что и обратно всякая такая перестановка может быть реализована на нашей модели.
машин. Через некоторое время дорога сужается и обе колонны на ходу перестраиваются в одну. При этом автомобили первой колонны занимают места где-то среди автомобилей второй, однако порядок следования автомобилей внутри каждой колонны сохраняется. В результате мы получаем перестановку, удовлетворяющую условию (6.1.4). Легко видеть, что и обратно всякая такая перестановка может быть реализована на нашей модели.
Для того чтобы убедиться, что данное нами определение является корректным, необходимо доказать, что  . Очевидно, в доказательстве нуждается только знакопеременность формы
. Очевидно, в доказательстве нуждается только знакопеременность формы 
Покажем, что при перестановке двух аргументов и  форма
форма  меняет знак. Отсюда легко будет следовать, что
меняет знак. Отсюда легко будет следовать, что  . Пусть
. Пусть  является такой перестановкой. Убедимся в том, что
является такой перестановкой. Убедимся в том, что

Из равенства (6.1.3) получим

Разобьем эту сумму на две:

К первой сумме отнесем те перестановки о, для которых либо  либо
либо  Для каждой такой перестановки
Для каждой такой перестановки 
Для того чтобы сделать это утверждение более очевидным, обозначим  Форма ста представляет собой произведение форм сор и
Форма ста представляет собой произведение форм сор и  причем аргументами сор являются векторы
причем аргументами сор являются векторы  а аргументами
а аргументами  — векторы
— векторы  Если
Если  то
то  являются аргументами формы сор, которая по условию знакопеременна. Следовательно, при перестановке
являются аргументами формы сор, которая по условию знакопеременна. Следовательно, при перестановке  форма
форма  , а значит, и ста меняют знак. Аналогично рассматривается случай, когда
, а значит, и ста меняют знак. Аналогично рассматривается случай, когда 
Итак, для первой суммы выполняется равенство

Ко второй сумме отнесем те перестановки  для которых либо
для которых либо  либо
либо  . Покажем, что множество перестановок
. Покажем, что множество перестановок  удовлетворяющих этому условию (а также, разумеется, условию (6.1.4)), совпадает с множеством перестановок
удовлетворяющих этому условию (а также, разумеется, условию (6.1.4)), совпадает с множеством перестановок  где
где  Обратимся к нашей модели с двумя колоинами автомобилей. Утверждение примет следующий очевидный вид.
Обратимся к нашей модели с двумя колоинами автомобилей. Утверждение примет следующий очевидный вид.
Если при каком-либо перестроении автомобиль с номером  из первой колонны окажется непосредственно перед автомобилем с номером
из первой колонны окажется непосредственно перед автомобилем с номером  из второй колонны, то легко можно указать другое перестроение, в результате которого эти автомобили меняются местами, в то время как порядок движения остальных сохранится.
из второй колонны, то легко можно указать другое перестроение, в результате которого эти автомобили меняются местами, в то время как порядок движения остальных сохранится.
Таким образом, так как  то
то

Подставляя (6.1.7) и (6.1.8) в (6.1.6), получим (6.1.5).
Примеры. 1°. Рассмотрим две линейные формы  Внешним произведением этих форм является билинейная форма
Внешним произведением этих форм является билинейная форма

2°. Пусть  Внешним произведением
Внешним произведением  будет
будет  -форма, аргументы которой мы обозначим через
-форма, аргументы которой мы обозначим через 

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛОВЫЕ РЯДЫ
- § 1. ПОНЯТИЕ ЧИСЛОВОГО РЯДА
- 2. Критерий Коши сходимости ряда.
- § 2. РЯДЫ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сравнения.
- 3. Признаки Даламбера и Коши.
- 4. Интегральный признак Коши—Маклорена.
- 5. Признак Раабе.
- 6. Отсутствие универсального ряда сравнения.
- § 3. АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ
- 2. О перестановке членов условно сходящегося ряда.
- 3. О перестановке членов абсолютно сходящегося ряда.
- § 4. ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ
- § 5. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД СХОДЯЩИМИСЯ РЯДАМИ
- § 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
- 2. Связь между сходимостью бесконечных произведений и рядов.
- 3. Разложение функции sin x в бесконечное произведение.
- § 7. ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РАСХОДЯЩИХСЯ РЯДОВ
- 1. Метод Чезаро (метод средних арифметических).
- 2. Метод суммирования Пуассона—Абеля.
- § 8. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДВОЙНЫХ И ПОВТОРНЫХ РЯДОВ
- Глава 2. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
- § 1. ПОНЯТИЯ СХОДИМОСТИ В ТОЧКЕ и РАВНОМЕРНОЙ СХОДИМОСТИ НА МНОЖЕСТВЕ
- 2. Сходимость функциональной последовательности (функционального ряда) в точке и на множестве.
- 3. Равномерная сходимость на множестве.
- 4. Критерий Коши равномерной сходимости последовательности (ряда).
- § 2. ДОСТАТОЧНЫЕ ПРИЗНАКИ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 3. ПОЧЛЕННЫЙ ПЕРЕХОД К ПРЕДЕЛУ
- § 4. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- 2. Почленное дифференцирование.
- 3. Сходимость в среднем.
- § 5. РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИИ
- § 6. СТЕПЕННЫЕ РЯДЫ
- 2. Непрерывность суммы степенного ряда.
- 3. Почленное интегрирование и почленное дифференцирование степенного ряда.
- § 7. РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННЫЕ РЯДЫ
- 2. Разложение некоторых элементарных функций в ряд Тейлора.
- 3. Элементарные представления о функциях кемплексной переменной.
- 4. Теорема Вейерштрасса о равномерном приближении непрерывной функции многочленами.
- Глава 3. ДВОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ ДВОЙНОГО ИНТЕГРАЛА
- 2. Условия существования двойного интеграла для прямоугольника.
- 3. Определение и условия существования двойного интеграла для произвольной области.
- 4. Общее определение двойного интеграла.
- § 2. ОСНОВНЫЕ СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА
- § 3. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ ОДНОКРАТНОМУ
- 2. Случай произвольной области.
- § 4. ТРОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 5. ЗАМЕНА ПЕРЕМЕННЫХ В n-КРАТНОМ ИНТЕГРАЛЕ
- § 6. ВЫЧИСЛЕНИЕ ОБЪЕМОВ n-МЕРНЫХ ТЕЛ
- § 7. ТЕОРЕМА О ПОЧЛЕННОМ ИНТЕГРИРОВАНИИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 8. КРАТНЫЕ НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- 2. Два признака сходимости несобственных интегралов от неотрицательных функций.
- 3. Несобственные интегралы от знакопеременных функций.
- 4. Главное значение кратных несобственных интегралов.
- Глава 4. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ ПЕРВОГО И ВТОРОГО РОДА
- § 2. УСЛОВИЯ СУЩЕСТВОВАНИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
- Глава 5. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ ПОВЕРХНОСТИ И ЕЕ ПЛОЩАДИ
- 2. Вспомогательные леммы.
- 3. Площадь поверхности.
- § 2. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- Глава 6. ТЕОРИЯ ПОЛЯ. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- § 1. ОБОЗНАЧЕНИЯ. БИОРТОГОНАЛЬНЫЕ БАЗИСЫ. ИНВАРИАНТЫ ЛИНЕЙНОГО ОПЕРАТОРА
- 2. Биортогональные базисы в пространстве E^n.
- 3. Преобразования базисов. Ковариантные и контрвариантные координаты вектора.
- 4. Инварианты линейного оператора. Дивергенция и ротор.
- 5. Выражения для дивергенции и ротора линейного оператора в ортонормированном базисе.
- § 2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ ВЕКТОРНОГО АНАЛИЗА
- 2. Дивергенция, ротор и производная по направлению векторного поля.
- 3. Некоторые другие формулы векторного анализа.
- 4. Заключительные замечания.
- § 3. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- 2. Формула Остроградского—Гаусса.
- 3. Формула Стокса.
- § 4. УСЛОВИЯ НЕЗАВИСИМОСТИ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА НА ПЛОСКОСТИ ОТ ПУТИ ИНТЕГРИРОВАНИЯ
- § 5. НЕКОТОРЫЕ ПРИМЕРЫ ПРИЛОЖЕНИИ ТЕОРИИ ПОЛЯ
- 2. Выражение объема через поверхностный интеграл.
- ДОПОЛНЕНИЕ К ГЛАВЕ 6. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 1. ЗНАКОПЕРЕМЕННЫЕ ПОЛИЛИНЕЙНЫЕ ФОРМЫ
- 2. Билинейные формы.
- 3. Полилинейные формы.
- 4. Знакопеременные полилинейные формы.
- 5. Внешнее произведение знакопеременных форм.
- 6. Свойства внешнего произведения знакопеременных форм.
- 7. Базис в пространстве знакопеременных форм.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
- 2. Внешний дифференциал.
- § 3. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- 2. Свойства отображения.
- § 4. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
- 2. Дифференцируемые цепи.
- 3. Формула Стокса.
- 4. Примеры.
- Глава 7. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- § 1. РАВНОМЕРНОЕ ПО ОДНОЙ ПЕРЕМЕННОЙ СТРЕМЛЕНИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ К ПРЕДЕЛУ ПО ДРУГОЙ ПЕРЕМЕННОЙ
- 2. Критерий Коши равномерного стремления функции к предельной.
- 3. Применения понятия равномерного стремления к предельной функции.
- § 2. СОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Случай, когда пределы интегрирования зависят от параметра.
- § 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Несобственные интегралы второго рода, зависящие от параметра.
- § 4. ПРИМЕНЕНИЕ ТЕОРИИ ИНТЕГРАЛОВ, ЗАВИСЯЩИХ ОТ ПАРАМЕТРА, К ВЫЧИСЛЕНИЮ НЕКОТОРЫХ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
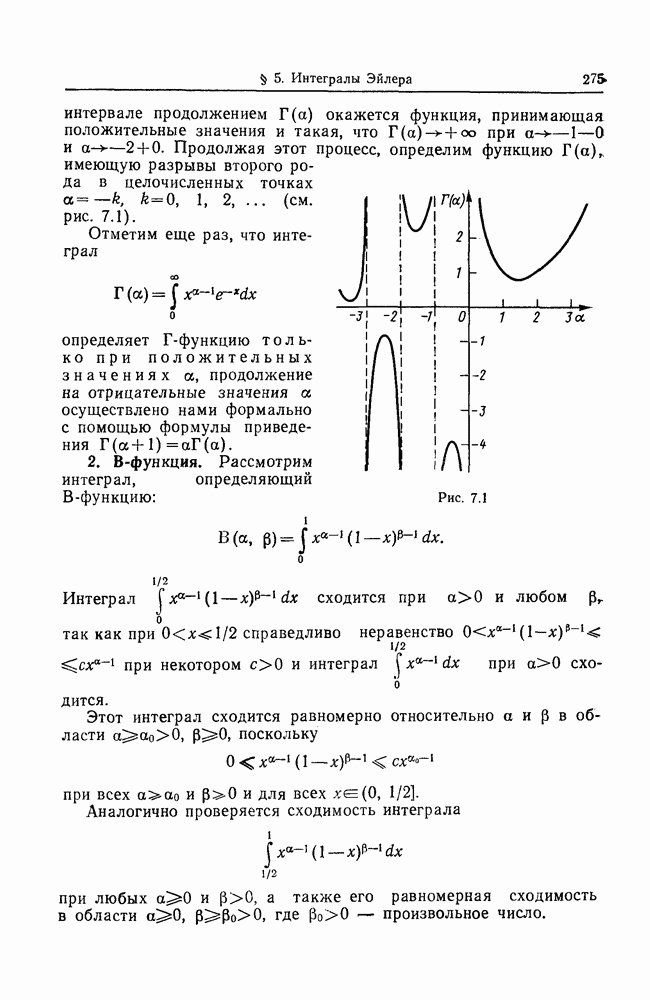
- § 5. ИНТЕГРАЛЫ ЭЙЛЕРА
- 2. В-функция.
- 3. Связь между эйлеровыми интегралами.
- 4. Примеры.
- § 6. ФОРМУЛА СТИРЛИНГА
- § 7. КРАТНЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- 2. Несобственные кратные интегралы, зависящие от параметра.
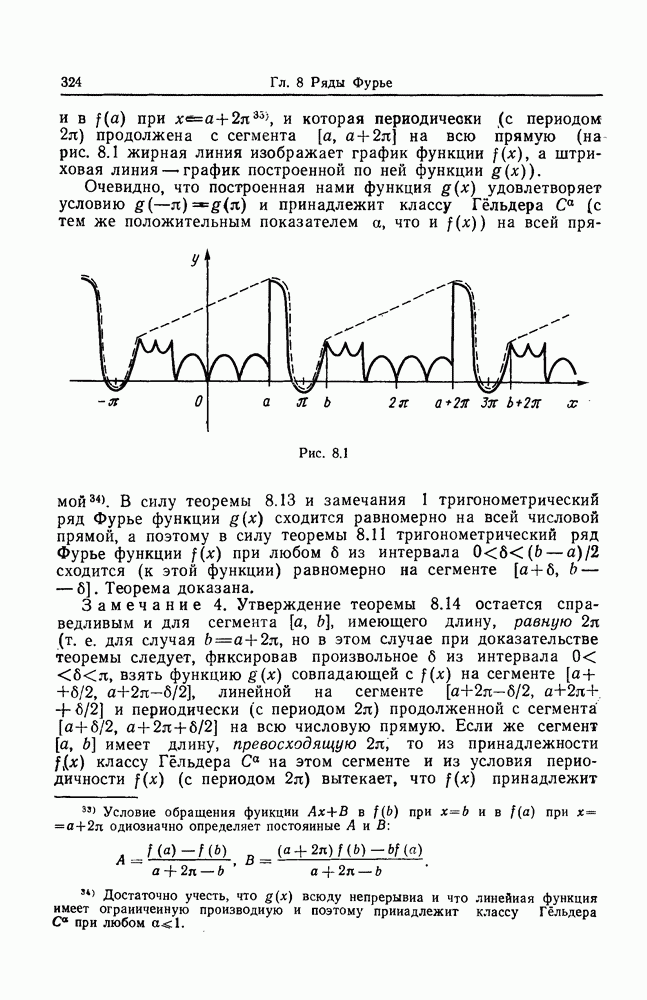
- Глава 8. РЯДЫ ФУРЬЕ
- § 1. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ И ОБЩИЕ РЯДЫ ФУРЬЕ
- 2. Понятие об общем ряде Фурье.
- § 2. ЗАМКНУТЫЕ И ПОЛНЫЕ ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
- § 3. ЗАМКНУТОСТЬ ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЫ И СЛЕДСТВИЯ ИЗ НЕЕ
- 2. Доказательство замкнутости тригонометрической системы.
- 3. Следствия замкнутости тригонометрической системы.
- § 4. ПРОСТЕЙШИЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И ПОЧЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ТРИГОНОМЕТРИЧЕСКОГО РЯДА ФУРЬЕ
- 2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
- 3. Простейшие условия почленного дифференцирования тригонометрического ряда Фурье.
- § 5. БОЛЕЕ ТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И УСЛОВИЯ СХОДИМОСТИ В ДАННОЙ ТОЧКЕ
- 2. Выражение для частичной суммы тригонометрического ряда Фурье.
- 3. Вспомогательные предложения.
- 4. Принцип локализации.
- 5. Равномерная сходимость тригонометрического ряда Фурье для функции из класса Гёльдера.
- 6. О сходимости тригонометрического ряда Фурье кусочно гёльдеровой функции.
- 7. Суммируемость тригонометрического ряда Фурье непрерывной функции методом средних арифметических.
- 8. Заключительные замечания.
- § 6. КРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ
- 2. Модуль непрерывности и классы Гёльдера для функции N переменных.
- 3. Условия абсолютной сходимости кратного тригонометрического ряда Фурье.
- Глава 9. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ
- 2. Основная теорема. Формула обращения.
- 3. Примеры.
- § 2. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- § 3. КРАТНЫЙ ИНТЕГРАЛ ФУРЬЕ