§ 4. ТРОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ

Изложенная нами теория двойного интеграла без каких-либо осложнений и новых идей переносится на случай тройного и вообще -кратного интеграла. Остановимся на основных моментах теории -кратного интеграла.

При определении класса квадрируемых множеств в и класса курируемых множеств в мы заимствовали из курса средней школы понятия площади многоугольной фигуры и объема многогранного тела, которые обладают свойствами аддитивности, инвариантности, монотонности (см. § 2, 3 гл. 10 ч. 1). В пространстве дело осложняется тем, что нам не известен объем множества (тела) в ограниченного гиперплоскостями. Для введения класса кубируемых тел в будем считать известным способ вычисления объема частного вида тел в — -мерного прямоугольного параллелепипеда.

Напомним (см. § 1 гл. 13 ч. 1), что множество всех точек для которых называется n-мерным координатным прямоугольным параллелепипедом. Если для всех то называют -мерным координатным кубом с ребром Точки где с; равны либо либо назовем вершинами а сегменты, соединяющие вершины типа — ребрами Все ребра параллельны координатным осям.

По аналогии с естественно определить объем -мерного прямоугольного параллелепипеда как число, равное произведению длин всех его ребер, выходящих из одной вершины, т. е. как число

Назовем элементарным телом множество точек представляющее собой объединение конечного числа -мерных прямоугольных параллелепипедов, не имеющих общих внутренних точек, ребра которых параллельны осям координат. Объем любого элементарного тела нам известен и равен сумме объемов составляющих его параллелепипедов.

Пусть теперь D — произвольная ограниченная область в Назовем нижним объемом области D точную верхнюю грань объемов всех содержащихся в D элементарных тел, а верхним объемом области D — точную нижнюю грань объемов всех элементарных тел, содержащих область D. Легко убедиться в том, что

Область D называется кубируемой, если При этом число называется -мерным объемом области D.

В полной аналогии со случаем плоской области доказывается следующее утверждение:

для того чтобы -мерная область D была кубируемой, необходимо и достаточно, чтобы для любого нашлись два элементарных тела, одно из которых содержит D, а другое содержится в D, разность объемов которых по модулю меньше числа е.

Поверхностью (или многообразием) -мерного объема нуль назовем замкнутое множество, все точки которого принадлежат элементарному телу как угодно малого -мерного объема.

Из приведенного утверждения получаем, что -мерная область D кубируема тогда и только тогда, когда граница этой области представляет собой многообразие -мерного объема нуль.

Определим n-кратный интеграл от функции переменных сначала в -мерном координатном прямоугольном параллелепипеде R. С этой целью производим разбиение Т параллелепипеда конечным числом гиперплоскостей, параллельных координатным осям, на конечное число частичных -мерных параллелепипедов.

Для указанного разбиения Т в полной аналогии со случаем определяем интегральную, верхнюю и нижнюю суммы любой ограниченной в функции Теперь определим ратный интеграл от функции по параллелепипеду как предел интегральных сумм при стремлении к нулю диаметра разбиения Т параллелепипеда

Как и для случая теория Дарбу устанавливает необходимое и достаточное условие интегрируемости в следующей форме:

Для интегрируемости функции в параллелепипеде необходимо и достаточно, чтобы для любого нашлось разбиение Т параллелепипеда для которого разность верхней и нижней сумм была меньше е.

Пусть теперь D — произвольная замкнутая ограниченная -мерная область, граница которой имеет -мерный объем нуль, -кратный интеграл от функции по области D определяется как интеграл по -мерному координатному прямоугольному параллелепипеду содержащему область D, от функции совпадающей с в D и равной нулю вне D.

Для обозначения n-кратного интеграла от функции о области D естественно использовать один из следующих символов:

Отметим, что произведение обычно называют элементом объема в пространстве

Точно так же, как и для случая доказывается интегрируемость по -мерной области D любой непрерывной функции, а

также функции обладающей в области -свойством (т. е. раниченной в D функции, множество точек разрыва которой имеет -мерный объем нуль). Вообще, изменение интегрируемой функции на множестве точек -мерного объема нуль не изменяет величину интеграла от этой функции.

Для определения -кратного интеграла можно использовать разбиение области D и при помощи конечного числа произвольных многообразий объема нуль на конечное число частичных областей произвольной формы. В полной аналогии с теоремой 3.5 доказывается, что такое общее определение -кратного интеграла эквивалентно указанному выше определению.

Для -кратного интеграла остаются справедливыми 8 основных свойств, сформулированные в § 2 для двойного интеграла.

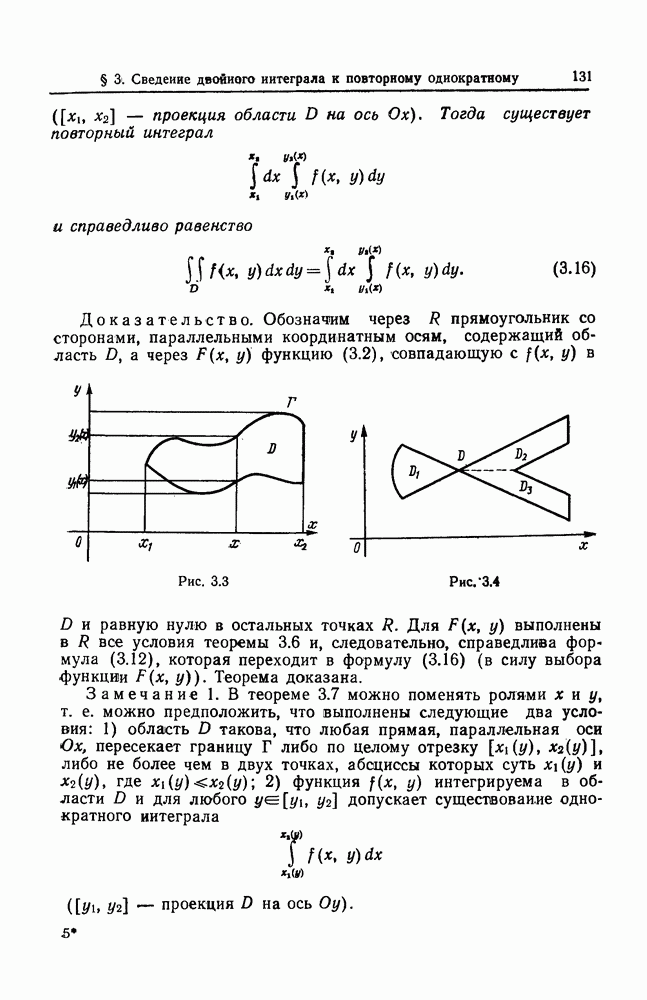
В полной аналогии с теоремами 3.6 и 3.7 устанавливается формула повторного интегрирования для интеграла (3.17).

Пусть -мерная область обладает тем свойством, что любая прямая, параллельная оси пересекает ее границу не более чем в двух точках (или по целому отрезку, ограниченному двумя точками), проекции которых на ось суть где

Пусть функция интегрируема в области и допускает существование для любых из -мерной области являющейся проекцией на координатную гиперплоскость однократного интеграла

Тогда существует -кратный интеграл

по области и справедлива формула повторного интегрирования

В сформулированном утверждении в роли может выступать любая из переменных

Договоримся называть область D простой, если для каждой из координатных осей любая прямая, параллельная этой оси, либо пересекает границу этой области не более чем в двух точках, либо имеет на этой границе целый отрезок. Примером простой области может служить -мерный прямоугольный параллелепипед (ребра которого не обязательно параллельны координатным осям). Для простой области формулу повторного интегрирования можно применять по любой из переменных

В заключение отметим, что, как и для случая справедливо следующее утверждение:

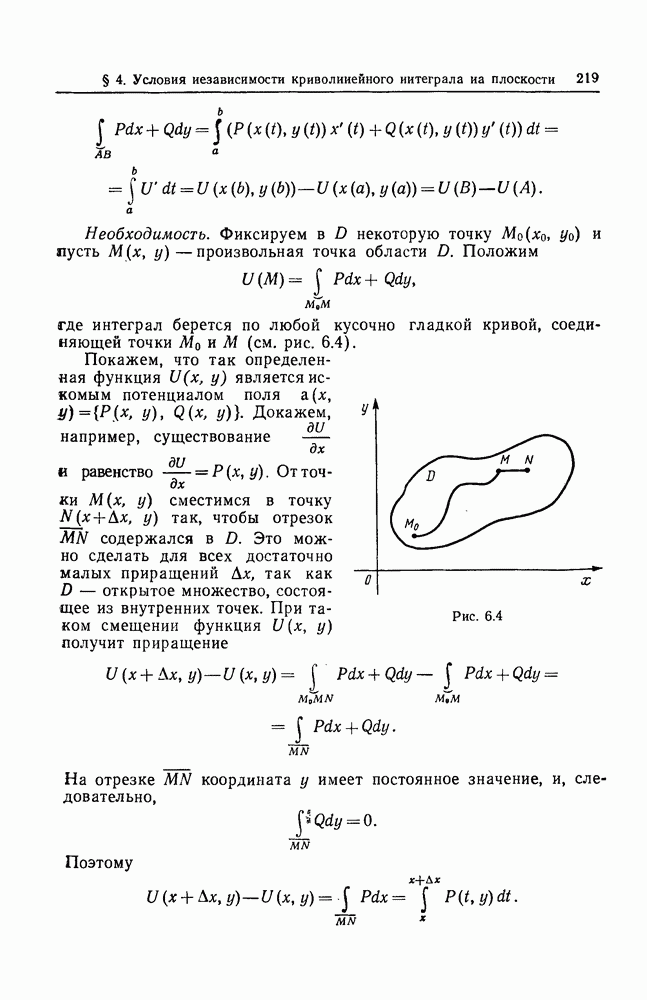
Пусть функция интегрируема в ограниченной кубируемой области D. Пусть пространство покрыто сеткой -мерных кубов с ребром — те кубы указанной сетки, которые целиком содержатся в произвольная точка куба Тогда каждая

имеет предел при равный -кратному интегралу (3.17) от функции по области D.

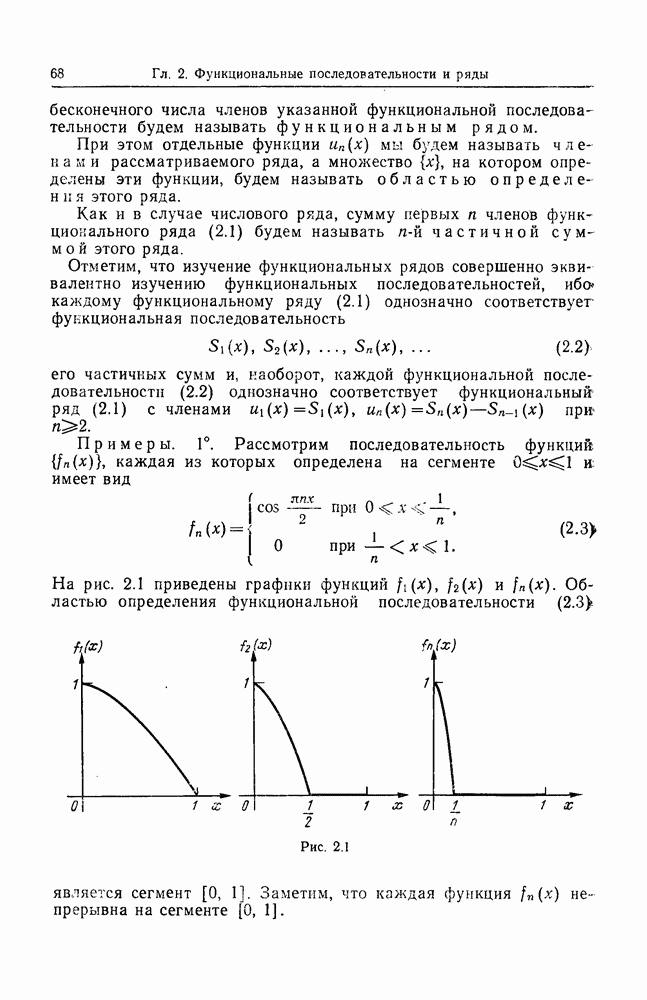
Примеры. 1°. Вычислить объем -мерного симплекса

Применяя формулу (3.18) последовательно по переменным , получим следующее выражение для объема:

Сделаем в каждом однократном интеграле в правой части (3.19) замену переменной Получим

Из (3.20) следует, что Для вычисления получаем следующую рекуррентную формулу:

Следовательно, и так как то

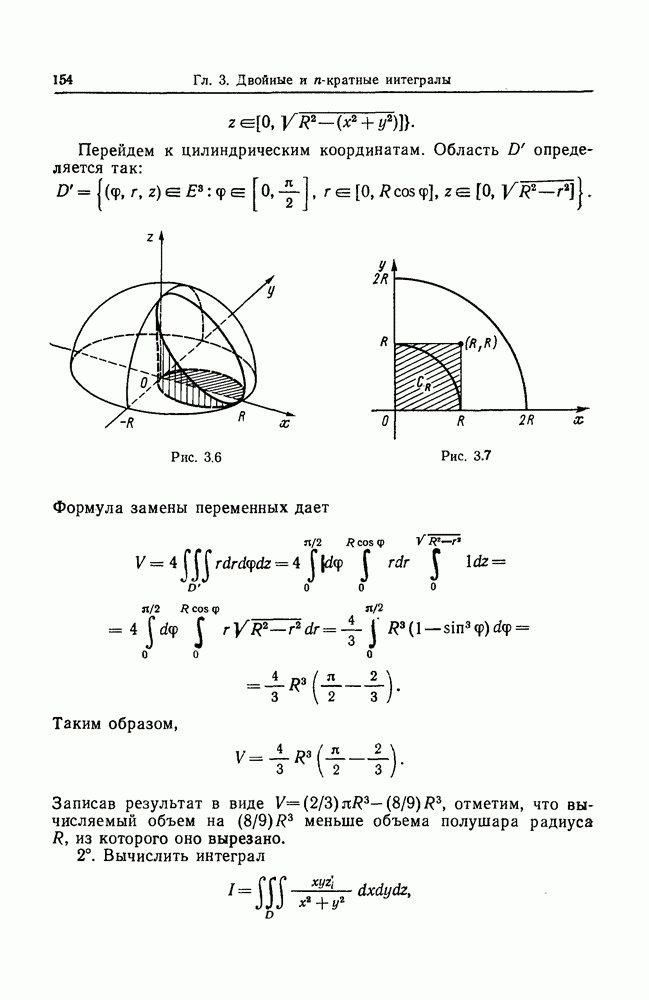
2°. Вычислить объем -мерного шара радиуса

Используя формулу (3.18), получаем

В однократном интеграле по переменной сделаем замену переменной и). Получим

Для вычисления как и в предыдущем примере, получаем рекуррентную формулу

Сделаем замену переменной в последнем интеграле, введем обозначение — и примем во внимание тот факт, что Тогда

Таким образом, объем -мерного шара радиуса выражается формулой

откуда, используя известные формулы для интегралов окончательно получаем