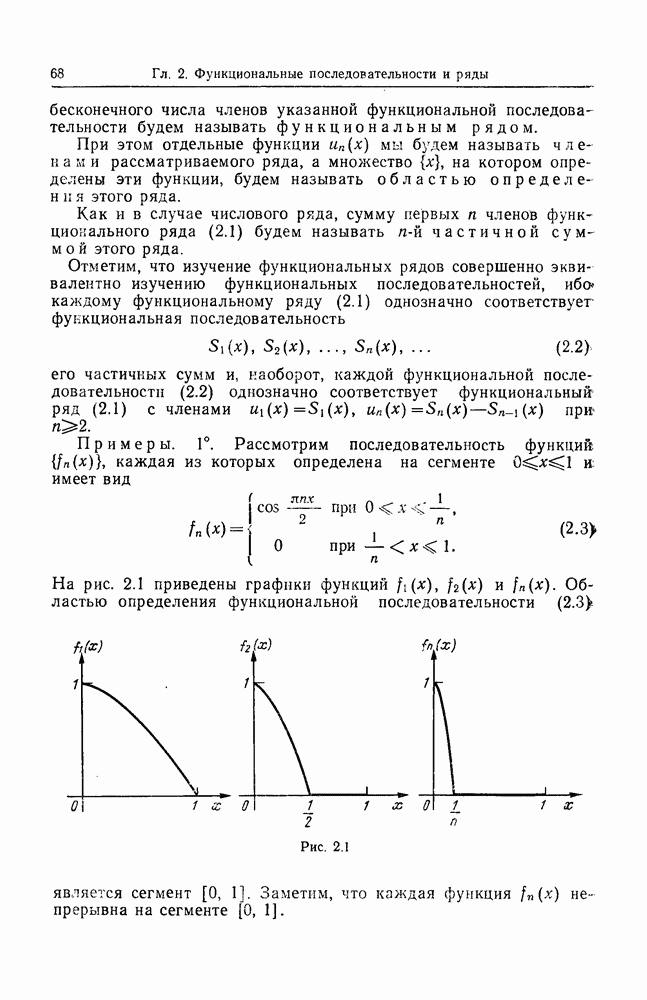
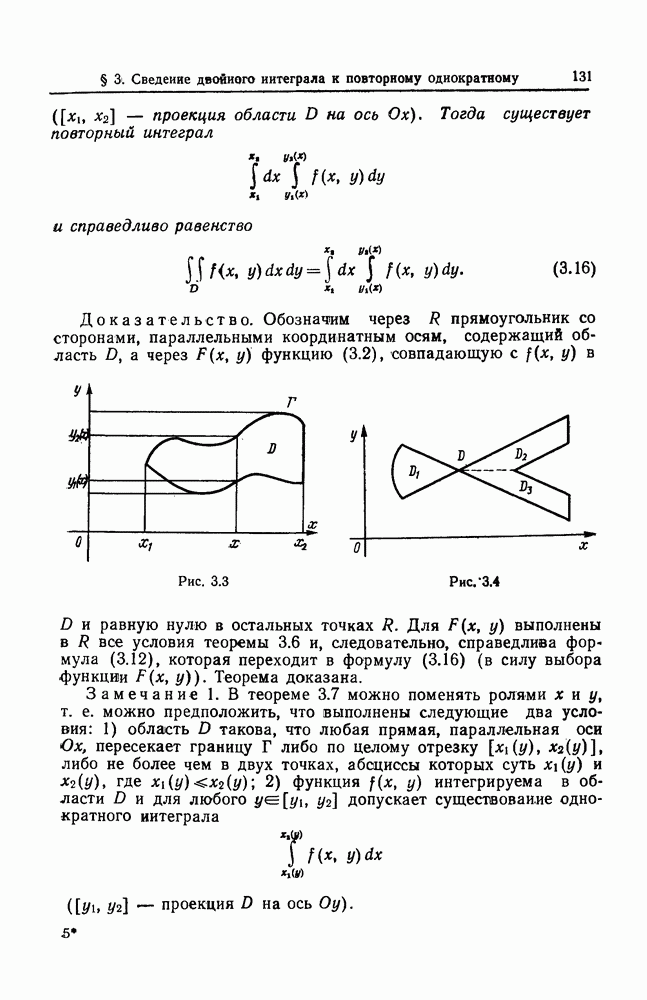
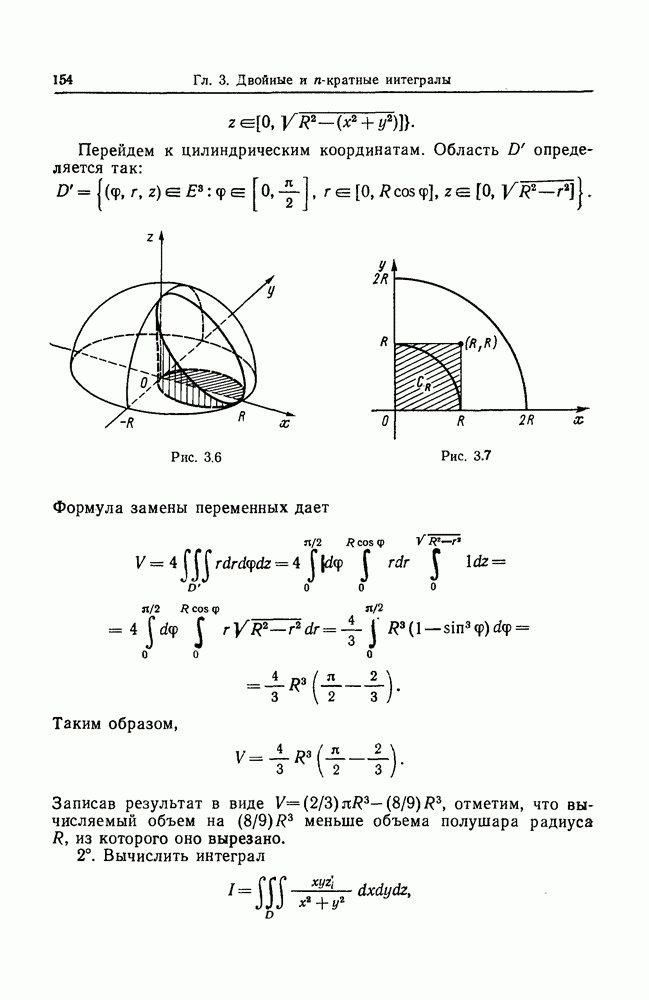
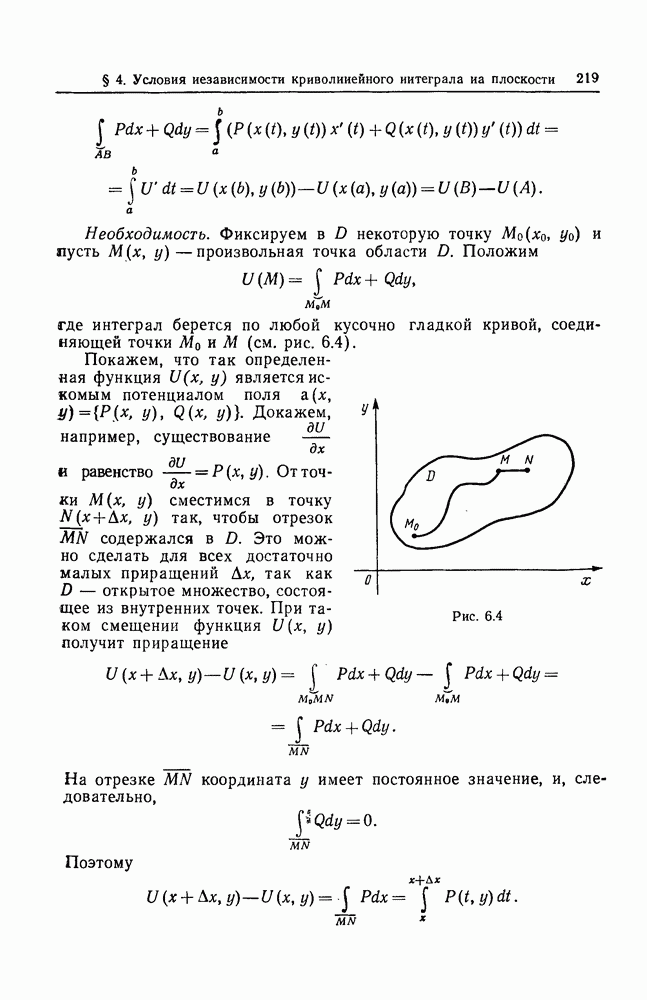
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ ВЕКТОРНОГО АНАЛИЗА
1. Скалярные и векторные поля.
В теории поля рассматриваются функции, которые каждой точке М фиксированной области
D сопоставляют некоторый специальный объект  называемый тензором. В этом случае говорят, что в области D задано тензорное поле. Мы будем изучать только два простейших частных случая тензорного поля, а именно скалярное и векторное поля
называемый тензором. В этом случае говорят, что в области D задано тензорное поле. Мы будем изучать только два простейших частных случая тензорного поля, а именно скалярное и векторное поля
Будем говорить, что в области D задано скалярное поле, если каждой точке М этой области сопоставлено по некоторому закону определенное число  Таким образом, понятия скалярного поля и скалярной функции, определенной в области D, совпадают.
Таким образом, понятия скалярного поля и скалярной функции, определенной в области D, совпадают.
Аналогично говорят, что в области D задано векторное  если каждой точке М этой области сопоставлен по некоторому закону вектор
если каждой точке М этой области сопоставлен по некоторому закону вектор  Таким образом, понятия векторного поля и векторной функции, определенной в области D, совпадают.
Таким образом, понятия векторного поля и векторной функции, определенной в области D, совпадают.
Пусть, например,  — напряженность электрического поля, созданного единичным отрицательным зарядом, помещенным в начало координат трехмерного пространства
— напряженность электрического поля, созданного единичным отрицательным зарядом, помещенным в начало координат трехмерного пространства  . Тогда в точке
. Тогда в точке  вектор
вектор  имеет, как известно, длину
имеет, как известно, длину  где
где  и направлен от точки М к началу координат. Получаем следующую формулу для задания данного векторного поля
и направлен от точки М к началу координат. Получаем следующую формулу для задания данного векторного поля 

Другими примерами скалярного и векторного полей могут быть скалярное поле температур внутри нагретого тела, векторное поле скоростей установившегося потока жидкости и т. д.
Приведем еще ряд примеров скалярных и векторных полей, играющих важную роль в анализе и физике. Для этого понадобится изучить понятие дифференцируемости скалярного и векторного полей.
Поскольку скалярное поле — это числовая функция, заданная в области D, то понятие дифференцируемости скалярного поля (этой числовой функции) мы уже знаем (см. определение п. 2 § 4 гл. 12 ч. 1).
Напомним это определение, заменяя слово «функция» на слова «скалярное поле». Пусть задано скалярное поле  в области D из
в области D из  .
.
Определение 1. Скалярное поле  называется дифференцируемым в точке
называется дифференцируемым в точке  области D, если его полное приращение
области D, если его полное приращение  в этой точке может быть представлено в виде
в этой точке может быть представлено в виде

где  — некоторые не зависящие от
— некоторые не зависящие от  числа, а
числа, а  — бесконечно малые при
— бесконечно малые при  функции, равные нулю при
функции, равные нулю при 
Условие дифференцируемости скалярного поля  (как показано в п. 2 § 4 гл. 12 ч. 1) может быть записано в виде
(как показано в п. 2 § 4 гл. 12 ч. 1) может быть записано в виде

где  причем это представление единственно.
причем это представление единственно.
Эту формулу можно переписать в более компактном виде:

где  — скалярное произведение векторов
— скалярное произведение векторов

Таким образом, можно дать следующее
Определение 1. Скалярное поле  дифференцируемо в точке М, если в этой точке для полного приращения справедливо соотношение (6.16). Скалярное поле
дифференцируемо в точке М, если в этой точке для полного приращения справедливо соотношение (6.16). Скалярное поле  дифференцируемо в области D, если оно дифференцируемо в каждой точке этой области.
дифференцируемо в области D, если оно дифференцируемо в каждой точке этой области.
Напомним (см. п. 8 § 4 гл. 12 ч. 1), что условие дифференцируемости (6.16) может быть переписано в виде

где вектор 
Формула (6.17) приводит нас еще к одному примеру векторного поля, а именно  полю градиента дифференцируемого в области D скалярного поля
полю градиента дифференцируемого в области D скалярного поля  Определение градиента не зависит от выбора системы координат, и поэтому он является инвариантом 6).
Определение градиента не зависит от выбора системы координат, и поэтому он является инвариантом 6).
Согласно рассмотрениям п. 8 § 4 гл. 12 ч. 1 в случае дифференцируемости поля  можно ввести производную
можно ввести производную  по направлению вектора
по направлению вектора 

Производная по направлению задает, очевидно, некоторое новое скалярное поле в области D.
Перейдем к изучению дифференцируемого векторного поля. Понятие дифференцируемости векторного поля дается в полной аналогии с понятием дифференцируемости скалярного поля, и это понятие было нами дано в дополнении 2 к гл. 12 ч. 1.
Пусть в области D пространства  задано векторное поле
задано векторное поле  (векторная функция
(векторная функция  точек М, принадлежащих
точек М, принадлежащих  Напомним, что
Напомним, что  каждой точке
каждой точке  ставит в соответствие вектор
ставит в соответствие вектор 
Определение 2. Векторное поле  называется дифференцируемым в точке М области D, если его полное приращение
называется дифференцируемым в точке М области D, если его полное приращение  представляется в виде
представляется в виде

где А — некоторый линейный оператор в 

 вектор, длина которого стремится к нулю при
вектор, длина которого стремится к нулю при 
Утверждение. Если векторное поле дифференцируемо, то представление (6.19) единственно.
Действительно (см. также дополнение 2 к гл. 12 ч. 1), если бы было два представления вида (6.19), т. е.

то

где 
Разделив на  обе части полученного равенства, получим
обе части полученного равенства, получим

где  - вектор единичной длины. Справа стоит бесконечно малый вектор (его длина стремится к нулю при
- вектор единичной длины. Справа стоит бесконечно малый вектор (его длина стремится к нулю при  следовательно, для любого единичного вектора
следовательно, для любого единичного вектора  величина слева равна нулю:
величина слева равна нулю:

Но если два линейных оператора А и В совпадают на единичной сфере, то они равны, очевидно, на любом векторе, т. е. совпадают всюду; Следовательно, 
Так же, как и в случае скалярного поля, векторное поле дифференцируемо в области D, если оно дифференцируемо в каждой точке области D.
Как и в случае скалярного поля, возникает вопрос об определении производной по направлению для векторного поля 
Пусть М — точка области  — единичный вектор с координатами
— единичный вектор с координатами  ,
,  определяющий некоторое направление. Пусть М — любая точка из D, отличная от М и такая, что вектор
определяющий некоторое направление. Пусть М — любая точка из D, отличная от М и такая, что вектор  коллинеарен вектору
коллинеарен вектору  . Обозначим расстояние между М и М через
. Обозначим расстояние между М и М через  .
.
Определение 3. Производной векторного поля а (М) в точке М по направлению  называется предел отношения
называется предел отношения

(в случае, если этот предел существует). Здесь  .
.
Утверждение. Пусть векторное поле  дифференцируемо, А — линейный оператор, определяемый из соотношения дифференцируемости (т. е. из соотношения
дифференцируемо, А — линейный оператор, определяемый из соотношения дифференцируемости (т. е. из соотношения  Тогда производная — поля в этой точке М по любому направлению
Тогда производная — поля в этой точке М по любому направлению  существует и определяется равенством
существует и определяется равенством

Интересно сравнить эту формулу с формулой (6.18). В формуле (6.18) справа также стоит результат действия оператора  на вектор е. Результат этого действия и есть скалярное произведение градиента поля и вектора е.
на вектор е. Результат этого действия и есть скалярное произведение градиента поля и вектора е.
Доказательство. Пусть  — фиксированный вектор. Выберем точку М так, чтобы
— фиксированный вектор. Выберем точку М так, чтобы  . Тогда согласно (6.19) получим
. Тогда согласно (6.19) получим

Поскольку  то
то

Переходя в этом соотношении к пределу при  получаем формулу (6.20), т. е. то, что и требовалось доказать.
получаем формулу (6.20), т. е. то, что и требовалось доказать.
Вернемся снова к рассмотрению формулы (6.19):

Здесь А — линейный оператор, действующий на вектор  из
из  Как мы знаем, в фиксированном базисе всякий линейный оператор
Как мы знаем, в фиксированном базисе всякий линейный оператор
тор определяется своей матрицей. Найдем матрицу линейного оператора А в ортонормированном базисе  , с которым связана декартова прямоугольная система координат
, с которым связана декартова прямоугольная система координат  Пусть в этом базисе вектор
Пусть в этом базисе вектор  имеет координаты
имеет координаты  Согласно формулам (6.20)
Согласно формулам (6.20)

По формулам (6.13) вычисляем элементы матрицы А оператора А:

| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- Глава 1. ЧИСЛОВЫЕ РЯДЫ
- § 1. ПОНЯТИЕ ЧИСЛОВОГО РЯДА
- 2. Критерий Коши сходимости ряда.
- § 2. РЯДЫ С НЕОТРИЦАТЕЛЬНЫМИ ЧЛЕНАМИ
- 2. Признаки сравнения.
- 3. Признаки Даламбера и Коши.
- 4. Интегральный признак Коши—Маклорена.
- 5. Признак Раабе.
- 6. Отсутствие универсального ряда сравнения.
- § 3. АБСОЛЮТНО И УСЛОВНО СХОДЯЩИЕСЯ РЯДЫ
- 2. О перестановке членов условно сходящегося ряда.
- 3. О перестановке членов абсолютно сходящегося ряда.
- § 4. ПРИЗНАКИ СХОДИМОСТИ ПРОИЗВОЛЬНЫХ РЯДОВ
- § 5. АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ НАД СХОДЯЩИМИСЯ РЯДАМИ
- § 6. БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
- 2. Связь между сходимостью бесконечных произведений и рядов.
- 3. Разложение функции sin x в бесконечное произведение.
- § 7. ОБОБЩЕННЫЕ МЕТОДЫ СУММИРОВАНИЯ РАСХОДЯЩИХСЯ РЯДОВ
- 1. Метод Чезаро (метод средних арифметических).
- 2. Метод суммирования Пуассона—Абеля.
- § 8. ЭЛЕМЕНТАРНАЯ ТЕОРИЯ ДВОЙНЫХ И ПОВТОРНЫХ РЯДОВ
- Глава 2. ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
- § 1. ПОНЯТИЯ СХОДИМОСТИ В ТОЧКЕ и РАВНОМЕРНОЙ СХОДИМОСТИ НА МНОЖЕСТВЕ
- 2. Сходимость функциональной последовательности (функционального ряда) в точке и на множестве.
- 3. Равномерная сходимость на множестве.
- 4. Критерий Коши равномерной сходимости последовательности (ряда).
- § 2. ДОСТАТОЧНЫЕ ПРИЗНАКИ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 3. ПОЧЛЕННЫЙ ПЕРЕХОД К ПРЕДЕЛУ
- § 4. ПОЧЛЕННОЕ ИНТЕГРИРОВАНИЕ И ПОЧЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- 2. Почленное дифференцирование.
- 3. Сходимость в среднем.
- § 5. РАВНОСТЕПЕННАЯ НЕПРЕРЫВНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИИ
- § 6. СТЕПЕННЫЕ РЯДЫ
- 2. Непрерывность суммы степенного ряда.
- 3. Почленное интегрирование и почленное дифференцирование степенного ряда.
- § 7. РАЗЛОЖЕНИЕ ФУНКЦИИ В СТЕПЕННЫЕ РЯДЫ
- 2. Разложение некоторых элементарных функций в ряд Тейлора.
- 3. Элементарные представления о функциях кемплексной переменной.
- 4. Теорема Вейерштрасса о равномерном приближении непрерывной функции многочленами.
- Глава 3. ДВОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 1. ОПРЕДЕЛЕНИЕ И УСЛОВИЯ СУЩЕСТВОВАНИЯ ДВОЙНОГО ИНТЕГРАЛА
- 2. Условия существования двойного интеграла для прямоугольника.
- 3. Определение и условия существования двойного интеграла для произвольной области.
- 4. Общее определение двойного интеграла.
- § 2. ОСНОВНЫЕ СВОЙСТВА ДВОЙНОГО ИНТЕГРАЛА
- § 3. СВЕДЕНИЕ ДВОЙНОГО ИНТЕГРАЛА К ПОВТОРНОМУ ОДНОКРАТНОМУ
- 2. Случай произвольной области.
- § 4. ТРОЙНЫЕ И n-КРАТНЫЕ ИНТЕГРАЛЫ
- § 5. ЗАМЕНА ПЕРЕМЕННЫХ В n-КРАТНОМ ИНТЕГРАЛЕ
- § 6. ВЫЧИСЛЕНИЕ ОБЪЕМОВ n-МЕРНЫХ ТЕЛ
- § 7. ТЕОРЕМА О ПОЧЛЕННОМ ИНТЕГРИРОВАНИИ ФУНКЦИОНАЛЬНЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И РЯДОВ
- § 8. КРАТНЫЕ НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
- 2. Два признака сходимости несобственных интегралов от неотрицательных функций.
- 3. Несобственные интегралы от знакопеременных функций.
- 4. Главное значение кратных несобственных интегралов.
- Глава 4. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ ПЕРВОГО И ВТОРОГО РОДА
- § 2. УСЛОВИЯ СУЩЕСТВОВАНИЯ КРИВОЛИНЕЙНЫХ ИНТЕГРАЛОВ
- Глава 5. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- § 1. ПОНЯТИЯ ПОВЕРХНОСТИ И ЕЕ ПЛОЩАДИ
- 2. Вспомогательные леммы.
- 3. Площадь поверхности.
- § 2. ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ
- Глава 6. ТЕОРИЯ ПОЛЯ. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- § 1. ОБОЗНАЧЕНИЯ. БИОРТОГОНАЛЬНЫЕ БАЗИСЫ. ИНВАРИАНТЫ ЛИНЕЙНОГО ОПЕРАТОРА
- 2. Биортогональные базисы в пространстве E^n.
- 3. Преобразования базисов. Ковариантные и контрвариантные координаты вектора.
- 4. Инварианты линейного оператора. Дивергенция и ротор.
- 5. Выражения для дивергенции и ротора линейного оператора в ортонормированном базисе.
- § 2. СКАЛЯРНЫЕ И ВЕКТОРНЫЕ ПОЛЯ. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ ВЕКТОРНОГО АНАЛИЗА
- 2. Дивергенция, ротор и производная по направлению векторного поля.
- 3. Некоторые другие формулы векторного анализа.
- 4. Заключительные замечания.
- § 3. ОСНОВНЫЕ ИНТЕГРАЛЬНЫЕ ФОРМУЛЫ АНАЛИЗА
- 2. Формула Остроградского—Гаусса.
- 3. Формула Стокса.
- § 4. УСЛОВИЯ НЕЗАВИСИМОСТИ КРИВОЛИНЕЙНОГО ИНТЕГРАЛА НА ПЛОСКОСТИ ОТ ПУТИ ИНТЕГРИРОВАНИЯ
- § 5. НЕКОТОРЫЕ ПРИМЕРЫ ПРИЛОЖЕНИИ ТЕОРИИ ПОЛЯ
- 2. Выражение объема через поверхностный интеграл.
- ДОПОЛНЕНИЕ К ГЛАВЕ 6. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
- § 1. ЗНАКОПЕРЕМЕННЫЕ ПОЛИЛИНЕЙНЫЕ ФОРМЫ
- 2. Билинейные формы.
- 3. Полилинейные формы.
- 4. Знакопеременные полилинейные формы.
- 5. Внешнее произведение знакопеременных форм.
- 6. Свойства внешнего произведения знакопеременных форм.
- 7. Базис в пространстве знакопеременных форм.
- § 2. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
- 2. Внешний дифференциал.
- § 3. ДИФФЕРЕНЦИРУЕМЫЕ ОТОБРАЖЕНИЯ
- 2. Свойства отображения.
- § 4. ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
- 2. Дифференцируемые цепи.
- 3. Формула Стокса.
- 4. Примеры.
- Глава 7. ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- § 1. РАВНОМЕРНОЕ ПО ОДНОЙ ПЕРЕМЕННОЙ СТРЕМЛЕНИЕ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ К ПРЕДЕЛУ ПО ДРУГОЙ ПЕРЕМЕННОЙ
- 2. Критерий Коши равномерного стремления функции к предельной.
- 3. Применения понятия равномерного стремления к предельной функции.
- § 2. СОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Случай, когда пределы интегрирования зависят от параметра.
- § 3. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
- 2. Несобственные интегралы второго рода, зависящие от параметра.
- § 4. ПРИМЕНЕНИЕ ТЕОРИИ ИНТЕГРАЛОВ, ЗАВИСЯЩИХ ОТ ПАРАМЕТРА, К ВЫЧИСЛЕНИЮ НЕКОТОРЫХ НЕСОБСТВЕННЫХ ИНТЕГРАЛОВ
- § 5. ИНТЕГРАЛЫ ЭЙЛЕРА
- 2. В-функция.
- 3. Связь между эйлеровыми интегралами.
- 4. Примеры.
- § 6. ФОРМУЛА СТИРЛИНГА
- § 7. КРАТНЫЕ ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРОВ
- 2. Несобственные кратные интегралы, зависящие от параметра.
- Глава 8. РЯДЫ ФУРЬЕ
- § 1. ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ И ОБЩИЕ РЯДЫ ФУРЬЕ
- 2. Понятие об общем ряде Фурье.
- § 2. ЗАМКНУТЫЕ И ПОЛНЫЕ ОРТОНОРМИРОВАННЫЕ СИСТЕМЫ
- § 3. ЗАМКНУТОСТЬ ТРИГОНОМЕТРИЧЕСКОЙ СИСТЕМЫ И СЛЕДСТВИЯ ИЗ НЕЕ
- 2. Доказательство замкнутости тригонометрической системы.
- 3. Следствия замкнутости тригонометрической системы.
- § 4. ПРОСТЕЙШИЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И ПОЧЛЕННОГО ДИФФЕРЕНЦИРОВАНИЯ ТРИГОНОМЕТРИЧЕСКОГО РЯДА ФУРЬЕ
- 2. Простейшие условия абсолютной и равномерной сходимости тригонометрического ряда Фурье.
- 3. Простейшие условия почленного дифференцирования тригонометрического ряда Фурье.
- § 5. БОЛЕЕ ТОЧНЫЕ УСЛОВИЯ РАВНОМЕРНОЙ СХОДИМОСТИ И УСЛОВИЯ СХОДИМОСТИ В ДАННОЙ ТОЧКЕ
- 2. Выражение для частичной суммы тригонометрического ряда Фурье.
- 3. Вспомогательные предложения.
- 4. Принцип локализации.
- 5. Равномерная сходимость тригонометрического ряда Фурье для функции из класса Гёльдера.
- 6. О сходимости тригонометрического ряда Фурье кусочно гёльдеровой функции.
- 7. Суммируемость тригонометрического ряда Фурье непрерывной функции методом средних арифметических.
- 8. Заключительные замечания.
- § 6. КРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ РЯДЫ ФУРЬЕ
- 2. Модуль непрерывности и классы Гёльдера для функции N переменных.
- 3. Условия абсолютной сходимости кратного тригонометрического ряда Фурье.
- Глава 9. ПРЕОБРАЗОВАНИЕ ФУРЬЕ
- § 1. ПРЕДСТАВЛЕНИЕ ФУНКЦИИ ИНТЕГРАЛОМ ФУРЬЕ
- 2. Основная теорема. Формула обращения.
- 3. Примеры.
- § 2. НЕКОТОРЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ФУРЬЕ
- § 3. КРАТНЫЙ ИНТЕГРАЛ ФУРЬЕ