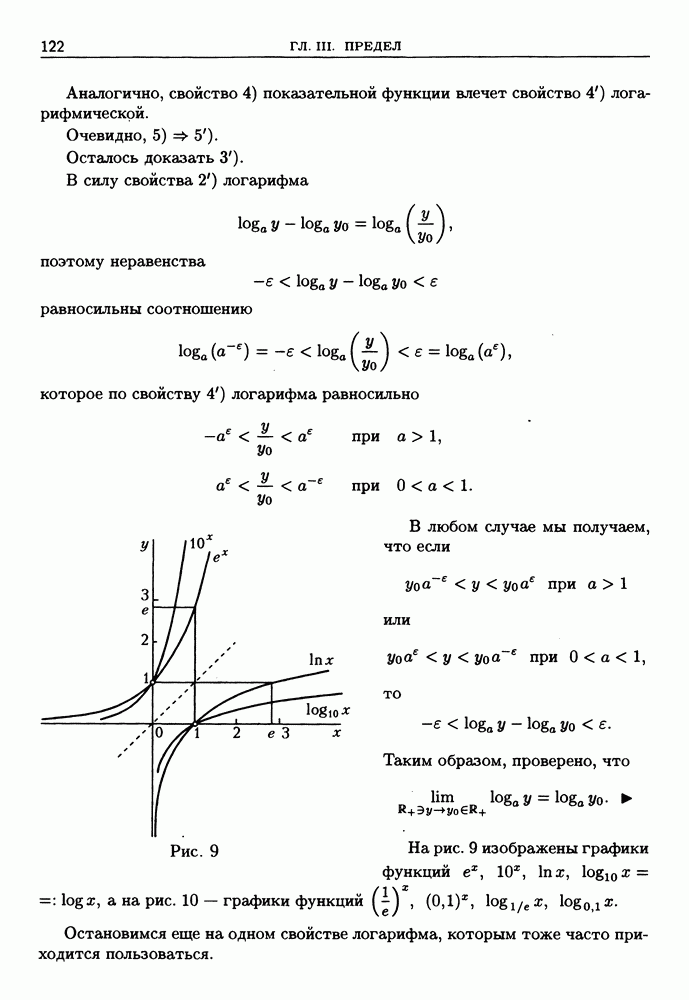
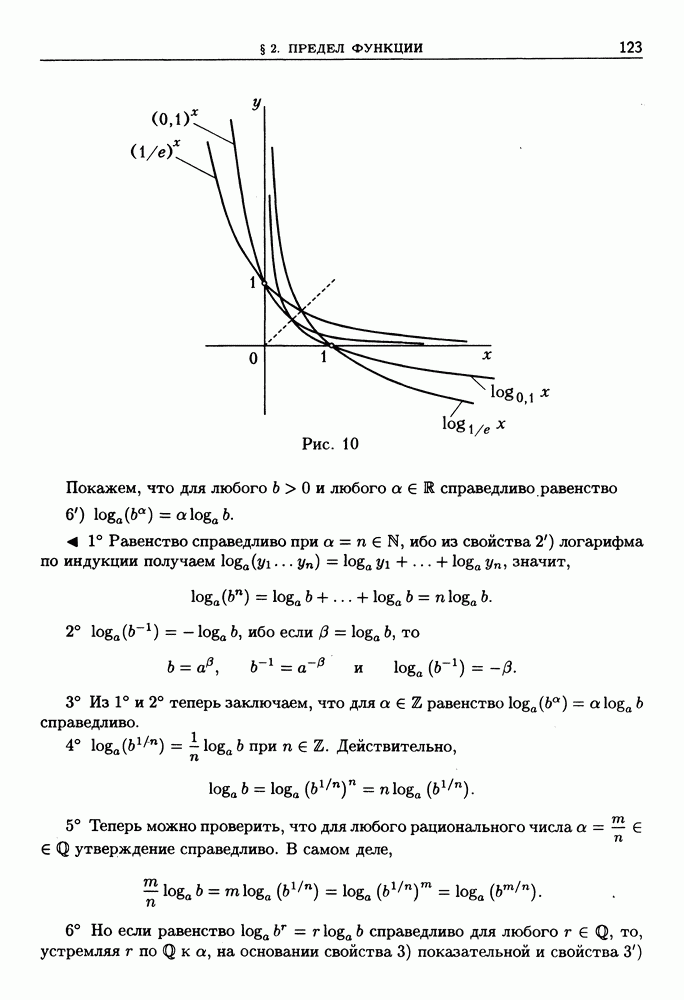
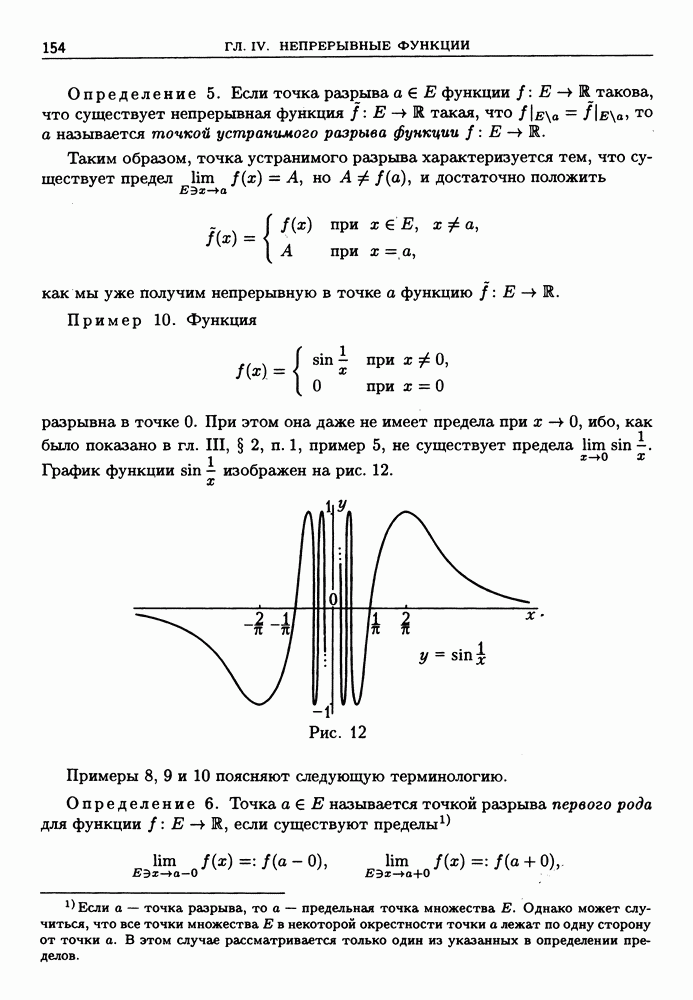
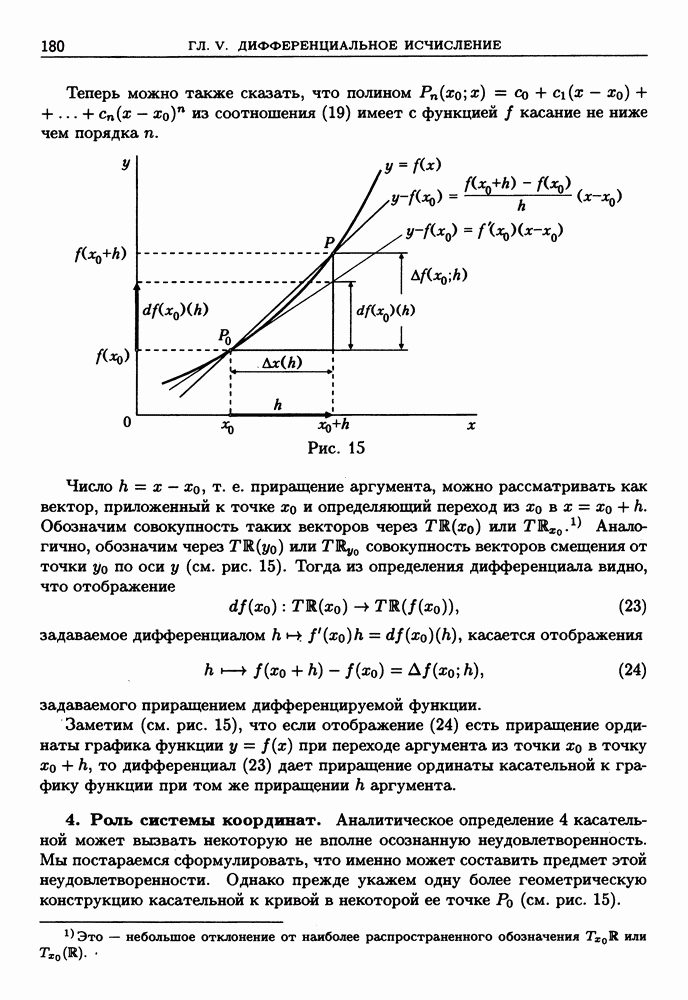
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Дифференцирование композиции отображений
а. Основная теорема
Теорема 3. Если отображение  множества
множества  . Если в множество Если дифференцируемо в точке
. Если в множество Если дифференцируемо в точке  отображение
отображение  дифференцируемо в точке
дифференцируемо в точке  , то композиция
, то композиция  этих отображений дифференцируема в точке х, причем дифференциал
этих отображений дифференцируема в точке х, причем дифференциал  композиции равен композиции
композиции равен композиции  дифференциалов
дифференциалов

Доказательство этой теоремы почти полностью повторяет доказательство теоремы 2 из § 2 гл. V. Чтобы обратить внимание на одну новую, появляющуюся теперь деталь, мы все же проведем еще раз это доказательство, не вдаваясь, однако, в уже разобранные технические подробности.
Используя дифференцируемость отображений  в точках
в точках  также линейность дифференциала
также линейность дифференциала  можно написать, что
можно написать, что

где  есть линейное отображение (как композиция линейных отображений), а
есть линейное отображение (как композиция линейных отображений), а

Но, как показывают соотношения (17), (18) из § 1,

и

Следовательно,

и теорема доказана.
Будучи переписана в координатной форме, теорема 3 означает, что если х — внутренняя точка множества X и

 — внутренняя точка множества
— внутренняя точка множества  и
и

то

В равенстве

справа имеется в виду суммирование по индексу  в пределах его изменения, т. е. от 1 до
в пределах его изменения, т. е. от 1 до 
В отличие от равенств (1), (2), (3), соотношение (4) нетривиально даже в смысле поэлементного равенства участвующих в нем матриц.
Рассмотрим некоторые важные частные случаи доказанной теоремы.
b. Дифференциал и частные производные сложной вещественнозначной функции.
Пусть  — вещественнозначная функция вещественных переменных
— вещественнозначная функция вещественных переменных  каждое из которых в свою очередь есть функция
каждое из которых в свою очередь есть функция  переменных
переменных  . В предположении дифференцируемости функций
. В предположении дифференцируемости функций  найдем частную производную
найдем частную производную  композиции отображений
композиции отображений 
По формуле (4), в которой при наших условиях  находим
находим

или, в более подробной записи,

c. Производная по вектору и градиент функции в точке.
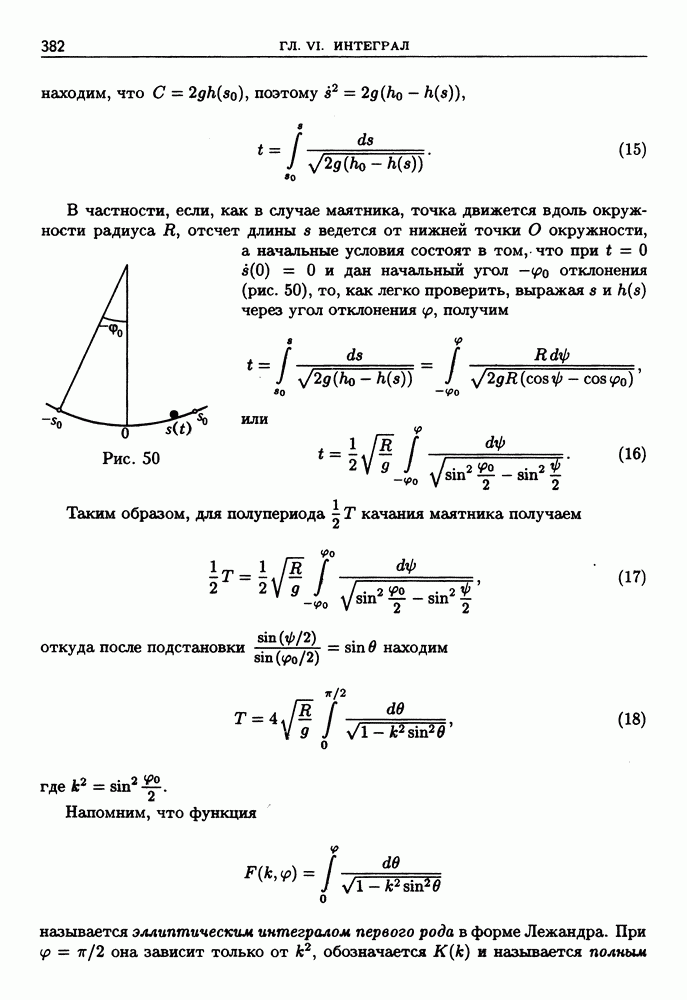
Рассмотрим установившийся поток жидкости или газа в некоторой области  пространства
пространства  Термин «установившийся» означает, что скорость потока в каждой точке области
Термин «установившийся» означает, что скорость потока в каждой точке области  не меняется со временем, хотя в различных точках области
не меняется со временем, хотя в различных точках области  она, разумеется, может быть различной. Пусть, например,
она, разумеется, может быть различной. Пусть, например,  — давление в потоке в точке
— давление в потоке в точке  Если мы будем перемещаться в потоке по закону
Если мы будем перемещаться в потоке по закону  где
где  — время, то в момент
— время, то в момент  мы будем регистрировать давление
мы будем регистрировать давление  Скорость изменения
Скорость изменения
давления со временем вдоль нашей траектории, очевидно, есть производная  по времени от функции
по времени от функции  Найдем ее в предположении, что
Найдем ее в предположении, что  — дифференцируемая в области
— дифференцируемая в области  функция. По закону дифференцирования композиции функций находим
функция. По закону дифференцирования композиции функций находим

где 
Поскольку  есть вектор скорости нашего перемещения в момент
есть вектор скорости нашего перемещения в момент  есть координатная запись дифференциала
есть координатная запись дифференциала  функции
функции  в точке
в точке  то равенство (6) можно переписать также в виде
то равенство (6) можно переписать также в виде

т. е. искомая величина есть значение дифференциала  функции
функции  в точке
в точке  на векторе
на векторе  скорости нашего движения.
скорости нашего движения.
В частности, если при  мы были в точке
мы были в точке  то
то

где  — вектор скорости в момент
— вектор скорости в момент 
Правая часть соотношения (8) зависит только от точки  и вектора
и вектора  скорости, которую мы имеем в этой точке, и не зависит от конкретного вида траектории
скорости, которую мы имеем в этой точке, и не зависит от конкретного вида траектории  лишь бы было выполнено условие
лишь бы было выполнено условие  Это означает, что на любой траектории вида
Это означает, что на любой траектории вида

где  при
при  , значение левой части равенства (8) будет одинаково, поскольку оно вполне определяется заданием точки
, значение левой части равенства (8) будет одинаково, поскольку оно вполне определяется заданием точки  и вектора
и вектора  приложенного к этой точке. В частности, если бы мы хотели непосредственно вычислить значение левой (а значит, и правой) части равенства (8), то можно было бы в качестве закона движения выбрать функцию
приложенного к этой точке. В частности, если бы мы хотели непосредственно вычислить значение левой (а значит, и правой) части равенства (8), то можно было бы в качестве закона движения выбрать функцию

отвечающую равномерному движению со скоростью  при котором в момент
при котором в момент  мы находимся в точке
мы находимся в точке 
Дадим теперь следующее
Определение 1. Если функция  определена в окрестности точки
определена в окрестности точки  — вектор, приложенный к точке
— вектор, приложенный к точке  то величина
то величина

(если указанный предел существует) называется производной функции  в точке
в точке  по вектору
по вектору 
Из проведенных рассмотрений следует, что если функция  дифференцируема в точке
дифференцируема в точке  то при любой функции
то при любой функции  вида (9) и, в частности, вида (10) имеет место равенство
вида (9) и, в частности, вида (10) имеет место равенство

что в координатном представлении означает

В частности, для базисных векторов  из этой формулы получаем
из этой формулы получаем

На основании равенства (12) в силу линейности дифференциала  заключаем, что если
заключаем, что если  — дифференцируемая в точке
— дифференцируемая в точке  функция, то для любых векторов
функция, то для любых векторов  и любых
и любых  функция имеет в точке
функция имеет в точке  производную по вектору
производную по вектору  и при этом
и при этом

Если пространство  рассматривать как евклидово пространство, т. е. как векторное пространство со скалярным произведением, то (см. § 1) любую линейную функцию
рассматривать как евклидово пространство, т. е. как векторное пространство со скалярным произведением, то (см. § 1) любую линейную функцию  можно будет записать в виде скалярного произведения
можно будет записать в виде скалярного произведения  фиксированного вектора
фиксированного вектора  и переменного вектора
и переменного вектора 
В частности, найдется, вектор  такой, что
такой, что

Определение 2. Вектор  отвечающий в смысле равенства (15) дифференциалу
отвечающий в смысле равенства (15) дифференциалу  функции
функции  в точке
в точке  называется градиентом функции в этой точке и обозначается символом
называется градиентом функции в этой точке и обозначается символом 
Итак, по определению

Если в  выбрана декартова система координат, то, сопоставляя соотношения (12), (13) и (16), заключаем, что в такой системе координат градиент имеет следующее координатное представление:
выбрана декартова система координат, то, сопоставляя соотношения (12), (13) и (16), заключаем, что в такой системе координат градиент имеет следующее координатное представление:

Выясним теперь геометрический смысл вектора  единичный вектор. Тогда в силу (16)
единичный вектор. Тогда в силу (16)

где  — угол между векторами
— угол между векторами 
Таким образом, если  то производная
то производная  принимает наибольшее значение. То есть скорость роста функции
принимает наибольшее значение. То есть скорость роста функции  (выраженная в единицах величины
(выраженная в единицах величины  отнесенных к единице длины в
отнесенных к единице длины в  при движении из точки
при движении из точки  максимальна и равна
максимальна и равна  когда мы смещаемся именно в направлении вектора
когда мы смещаемся именно в направлении вектора  При смещении в противоположном направлении значения функции наиболее резко уменьшаются, а при смещении в направлении, перпендикулярном вектору
При смещении в противоположном направлении значения функции наиболее резко уменьшаются, а при смещении в направлении, перпендикулярном вектору  скорость изменения значений функции равна нулю.
скорость изменения значений функции равна нулю.
Производную по единичному вектору данного направления обычно называют производной по данному направлению.
Поскольку единичный вектор в евклидовом пространстве задается направляющими косинусами:

где  — угол, который вектор
— угол, который вектор  образует с базисным вектором
образует с базисным вектором  декартовой системы координат, то
декартовой системы координат, то

Вектор  встречается очень часто и имеет многочисленные применения. Например, на отмеченном выше геометрическом свойстве градиента основаны так называемые градиентные методы численного (на
встречается очень часто и имеет многочисленные применения. Например, на отмеченном выше геометрическом свойстве градиента основаны так называемые градиентные методы численного (на  поиска экстремумов функций многих переменных. (См. в этой связи задачу 2 в конце параграфа.)
поиска экстремумов функций многих переменных. (См. в этой связи задачу 2 в конце параграфа.)
Многие важные векторные поля, как, например, ньютоновское поле сил тяготения или кулоновское поле заряда, являются градиентами некоторых скалярных функций — потенциалов этих полей (см. задачу 3).
Многие физические законы в самой своей формулировке используют вектор  Например, в механике сплошной среды эквивалентом основного закона Ньютона
Например, в механике сплошной среды эквивалентом основного закона Ньютона  динамики точки является соотношение
динамики точки является соотношение

связывающее ускорение  в потоке свободной от внешних сил идеальной жидкости или газа в точке х в момент
в потоке свободной от внешних сил идеальной жидкости или газа в точке х в момент  с плотностью среды
с плотностью среды  и градиентом давления
и градиентом давления  отнесенными к этой же точке и к этому же моменту времени (см. задачу 4).
отнесенными к этой же точке и к этому же моменту времени (см. задачу 4).
О векторе  мы еще будем говорить позже, при изучении векторного анализа и элементов теории поля.
мы еще будем говорить позже, при изучении векторного анализа и элементов теории поля.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
- § 1. Логическая символика
- § 2. Множество и элементарные операции над множествами
- 2. Отношение включения.
- 3. Простейшие операции над множествами.
- Упражнения
- § 3. Функция
- 2. Простейшая классификация отображений.
- 3. Композиция функций и взаимно обратные отображения.
- 4. Функция как отношение. График функции.
- § 4. Некоторые дополнения
- 2. Об аксиоматике теории множеств.
- 3. Замечания о структуре математических высказываний и записи их на языке теории множеств.
- Упражнения
- ГЛАВА II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
- § 1. Аксиоматика и некоторые общие свойства множества действительных чисел
- 2. Некоторые общие алгебраические свойства действительных чисел.
- 3. Аксиома полноты и существование верхней (нижней) грани числового множества
- § 2. Важнейшие классы действительных чисел и вычислительные аспекты операций с действительными числами
- 2. Рациональные и иррациональные числа
- 3. Принцип Архимеда.
- 4. Геометрическая интерпретация множества действительных чисел и вычислительные аспекты операций с действительными числами
- Задачи и упражнения
- § 3. Основные леммы, связанные с полнотой множества действительных чисел
- 2. Лемма о конечном покрытии (принцип Бореля — Лебега)
- 3. Лемма о предельной точке (принцип Больцано—Вейерштрасса).
- Задачи и упражнения
- § 4. Счетные и несчетные множества
- 2. Мощность континуума
- Задачи и упражнения
- ГЛАВА III. ПРЕДЕЛ
- 2. Свойства предела последовательности
- 3. Вопросы существования предела последовательности
- 4. Начальные сведения о рядах
- § 2. Предел функции
- 2. Свойства предела функции.
- 3. Общее определение предела функции (предел по базе).
- 4. Вопросы существования предела функции
- ГЛАВА IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 2. Точки разрыва.
- § 2. Свойства непрерывных функций
- 2. Глобальные свойства непрерывных функций.
- ГЛАВА V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- 2. Функция, дифференцируемая в точке.
- 3. Касательная; геометрический смысл производной и дифференциала.
- 4. Роль системы координат.
- 5. Некоторые примеры
- Задачи и упражнения
- § 2. Основные правила дифференцирования
- 2. Дифференцирование композиции функций
- 3. Дифференцирование обратной функции
- 4. Таблица производных основных элементарных функций.
- 5. Дифференцирование простейшей неявно заданной функции.
- 6. Производные высших порядков.
- § 3. Основные теоремы дифференциального исчисления
- 2. Теоремы Лагранжа и Коши о конечном приращении.
- 3. Формула Тейлора.
- § 4. Исследование функций методами дифференциального исчисления
- 2. Условия внутреннего экстремума функции.
- 3. Условия выпуклости функции
- 4. Правило Лопиталя.
- 5. Построение графика функции.
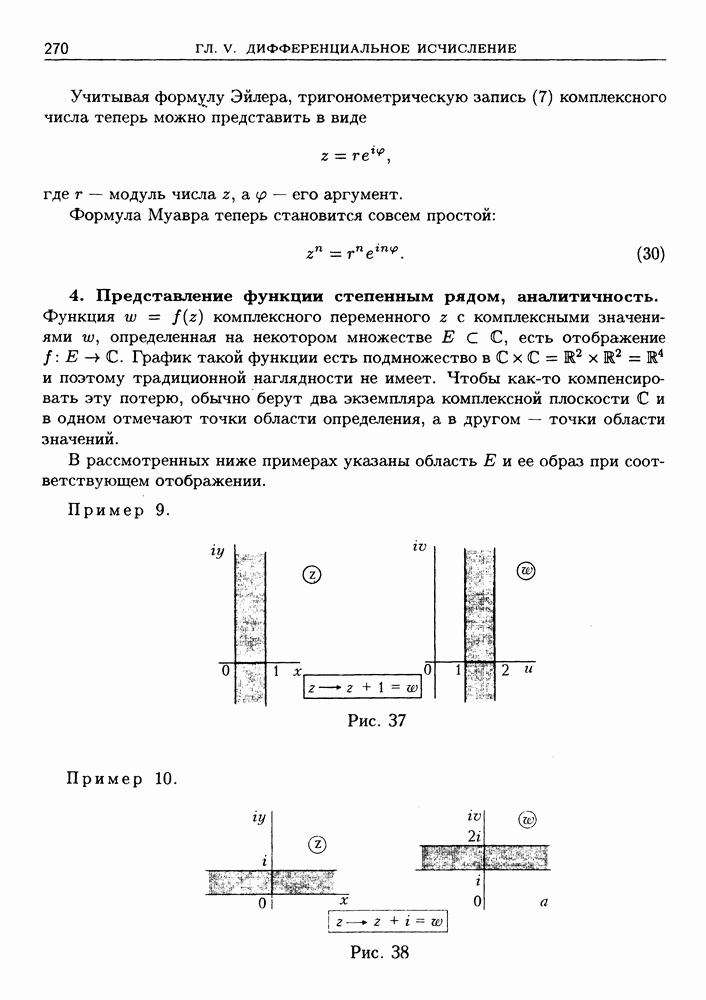
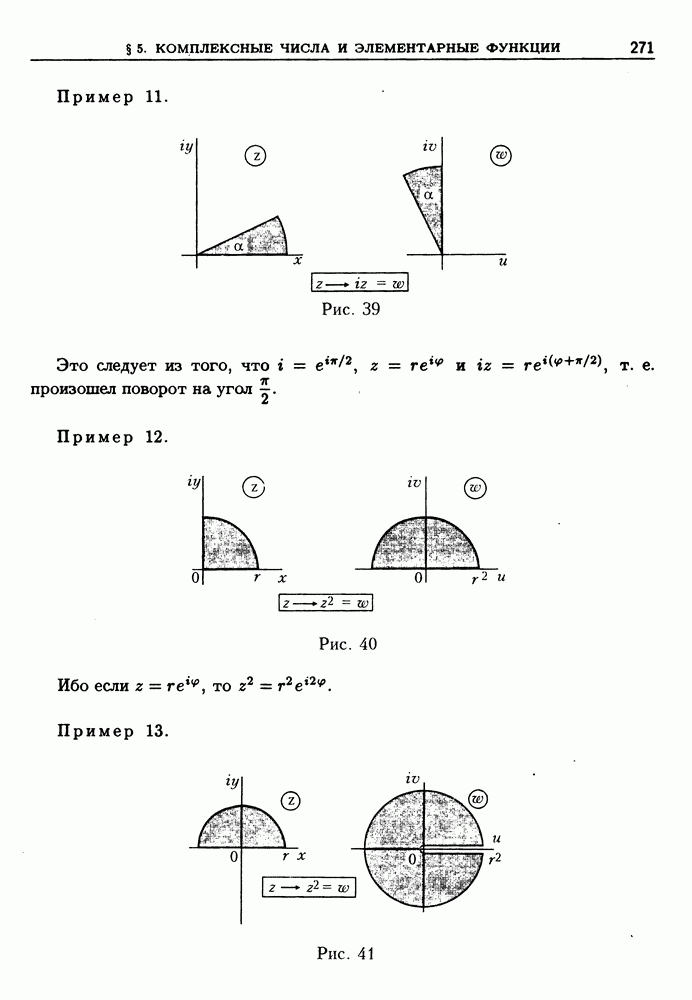
- § 5. Комплексные числа и взаимосвязь элементарных функций
- 2. Сходимость в С и ряды с комплексными членами.
- 3. Формула Эйлера и взаимосвязь элементарных функций.
- 4. Представление функции степенным рядом, аналитичность.
- 5. Алгебраическая замкнутость поля С комплексных чисел.
- § 6. Некоторые примеры использования дифференциального исчисления в задачах естествознания
- 2. Барометрическая формула.
- 3. Радиоактивный распад, цепная реакция и атомный котел.
- 4. Падение тел в атмосфере.
- 5. Еще раз о числе e и функции exp(x).
- 6. Колебания.
- § 7. Первообразная
- 2. Основные общие приемы отыскания первообразной.
- 3. Первообразные рациональных функций.
- 4. Первообразные вида …
- 5. Первообразные вида …
- ГЛАВА VI. ИНТЕГРАЛ
- § 1. Определение интеграла и описание множества интегрируемых функций
- 2. Определение интеграла Римана
- 3. Множество интегрируемых функций.
- § 2. Линейность, аддитивность и монотонность интеграла
- 2. Интеграл как аддитивная функция отрезка интегрирования.
- 3. Оценка интеграла, монотонность интеграла, теоремы о среднем
- § 3. Интеграл и производная
- 2. Формула Ньютона—Лейбница
- 3. Интегрирование по частям в определенном интеграле и формула Тейлора
- 4. Замена переменной в интеграле.
- 5. Некоторые примеры.
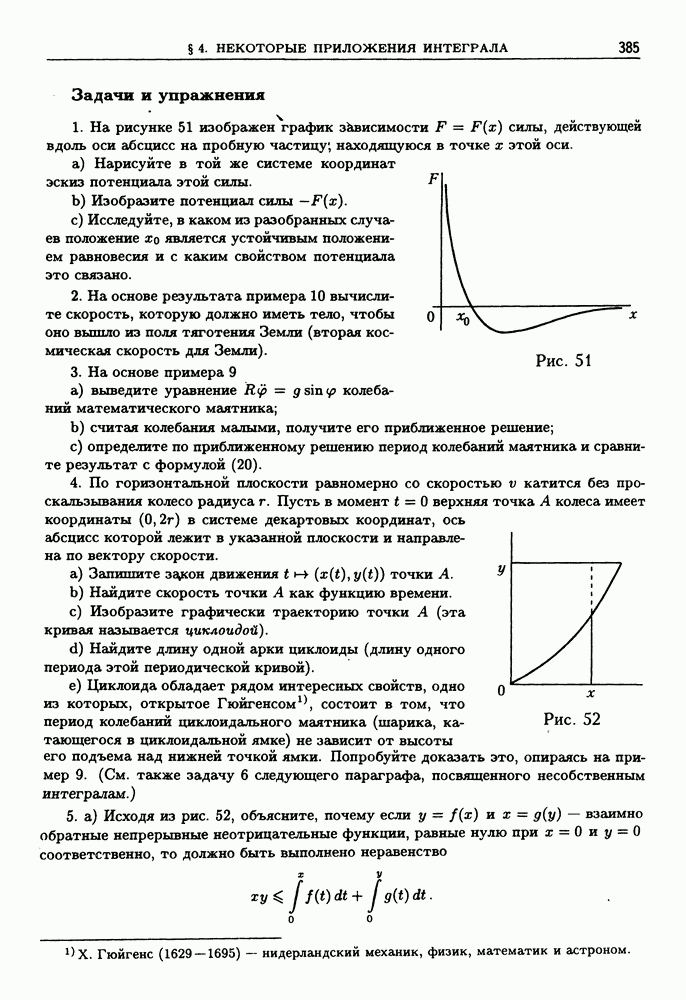
- § 4. Некоторые приложения интеграла
- 2. Длина пути.
- 3. Площадь криволинейной трапеции.
- 4. Объем тела вращения.
- 5. Работа и энергия.
- § 5. Несобственный интеграл
- 2. Исследование сходимости несобственного интеграла
- 3. Несобственные интегралы с несколькими особенностями.
- ГЛАВА VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ, ИХ ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
- 2. Открытые и замкнутые множества в R^m
- 3. Компакты в R^m
- § 2. Предел и непрерывность функции многих переменных
- 2. Непрерывность функции многих переменных и свойства непрерывных функций.
- ГЛАВА VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- 2. Линейные отображения L : R^m -> R^n.
- 3. Норма в R^m.
- 4. Евклидова структура в R^m.
- § 2. Дифференциал функции многих переменных
- 2. Дифференциал и частные производные вещественнозначной функции.
- 3. Координатное представление дифференциала отображения. Матрица Якоби.
- 4. Непрерывность, частные производные и дифференцируемость функции в точке.
- § 3. Основные законы дифференцирования
- 2. Дифференцирование композиции отображений
- 3. Дифференцирование обратного отображения
- § 4. Основные факты дифференциального исчисления вещественнозначных функций многих переменных
- 2. Достаточное условие дифференцируемости функции многих переменных
- 4. Формула Тейлора
- 5. Экстремумы функций многих переменных.
- 6. Некоторые геометрические образы, связанные с функциями многих переменных
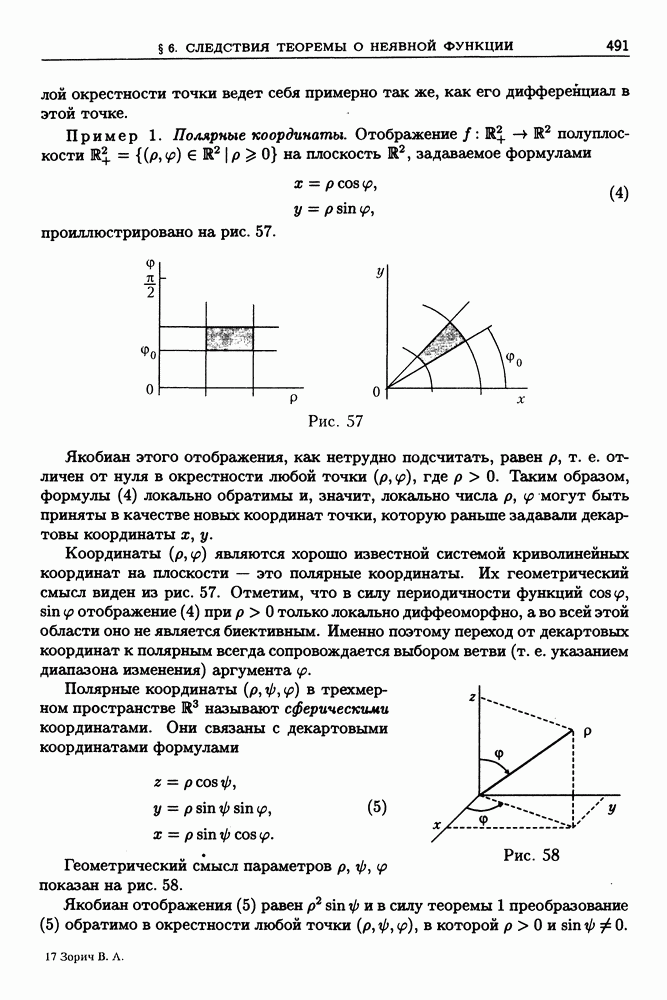
- § 5. Теорема о неявной функции
- 2. Простейший вариант теоремы о неявной функции.
- 3. Переход к случаю зависимости
- 4. Теорема о неявной функции.
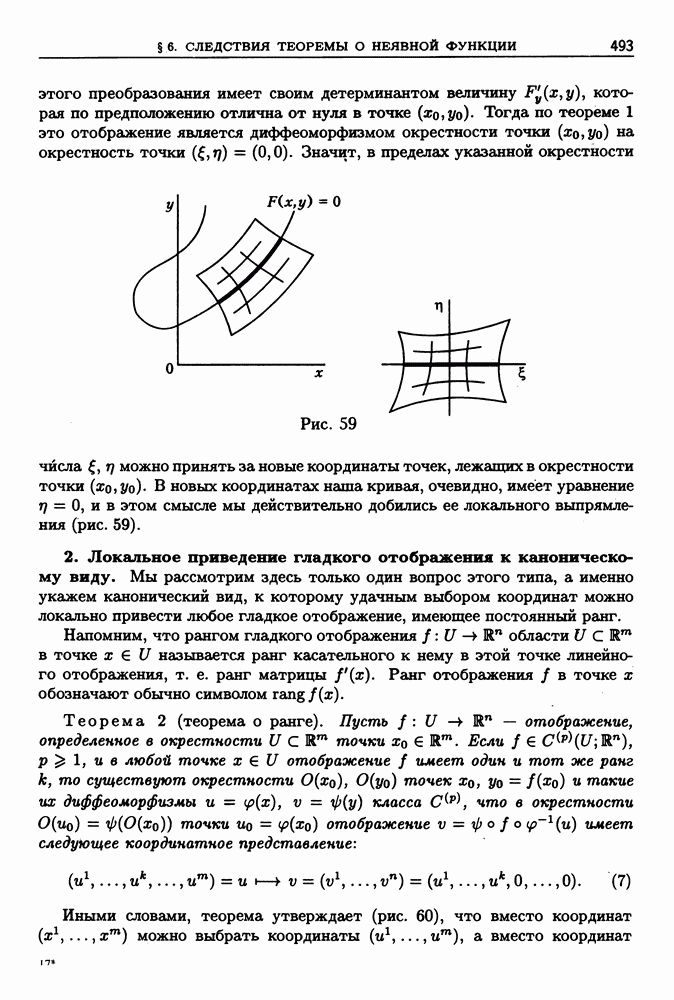
- § 6. Некоторые следствия теоремы о неявной функции
- 2. Локальное приведение гладкого отображения к каноническому виду.
- 3. Зависимость функций
- 4. Локальное разложение диффеоморфизма в композицию простейших.
- 5. Лемма Морса.
- § 7. Поверхность в R^n и теория условного экстремума
- 2. Касательное пространство.
- 3. Условный экстремум
- НЕКОТОРЫЕ ЗАДАЧИ КОЛЛОКВИУМОВ
- ВОПРОСЫ К ЭКЗАМЕНУ
- ЛИТЕРАТУРА