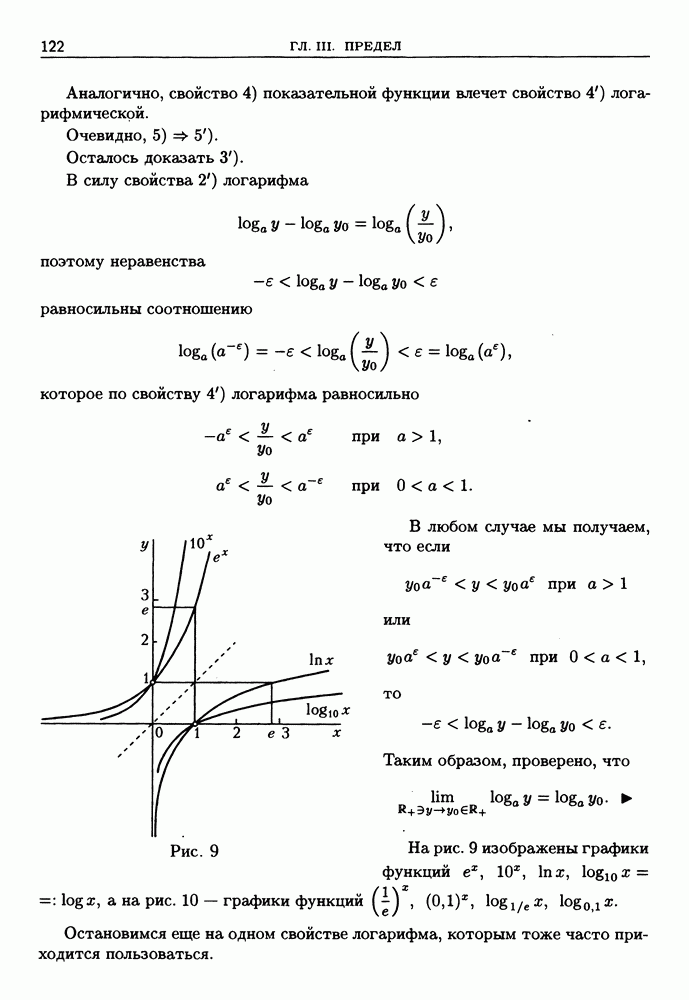
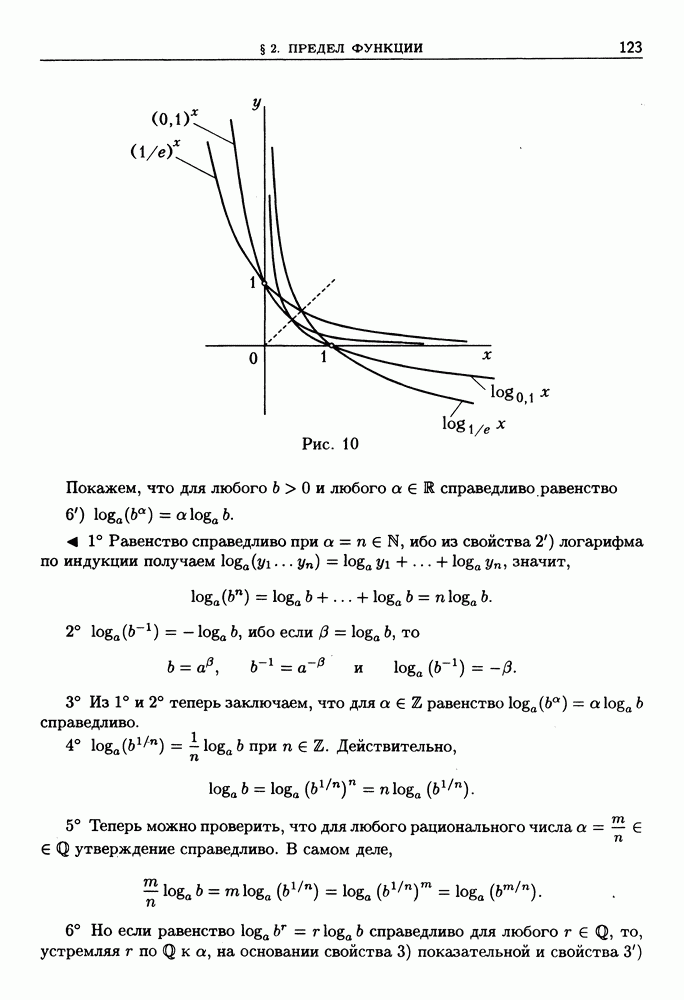
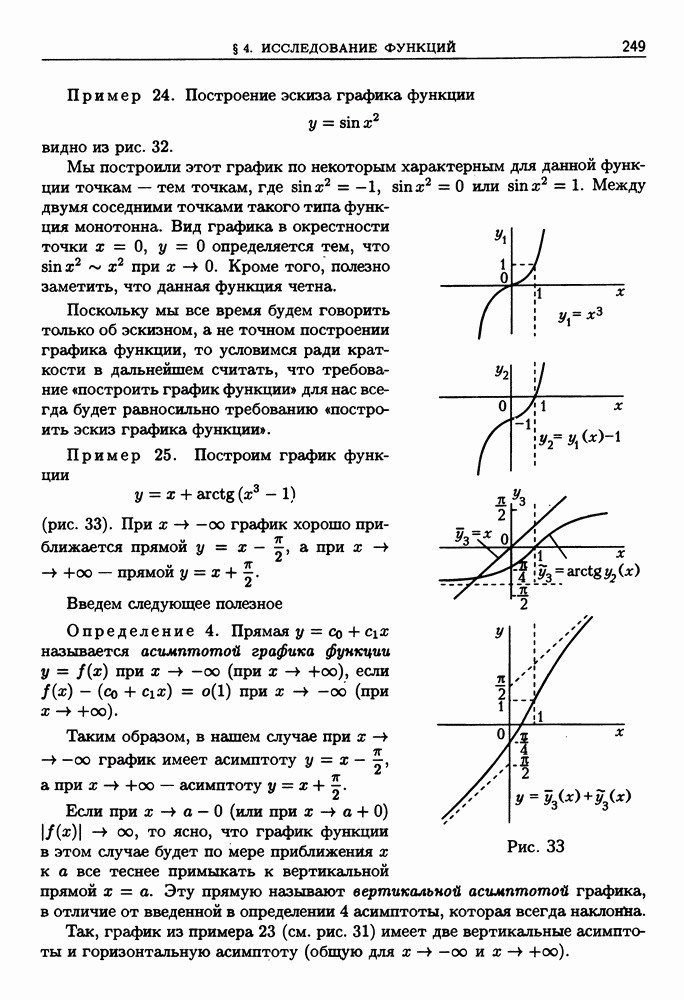
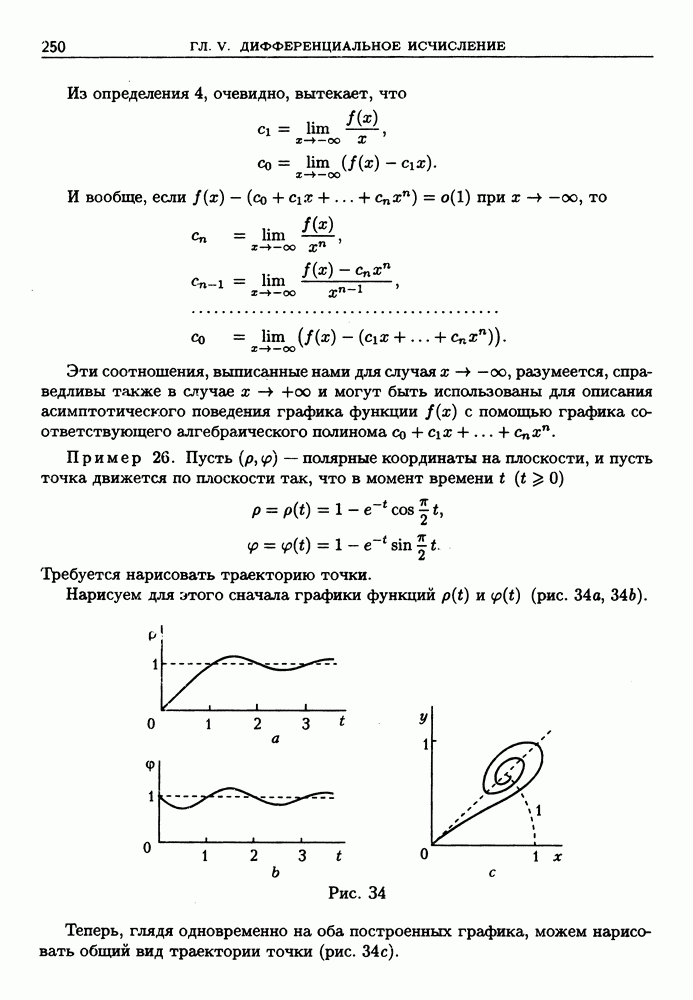
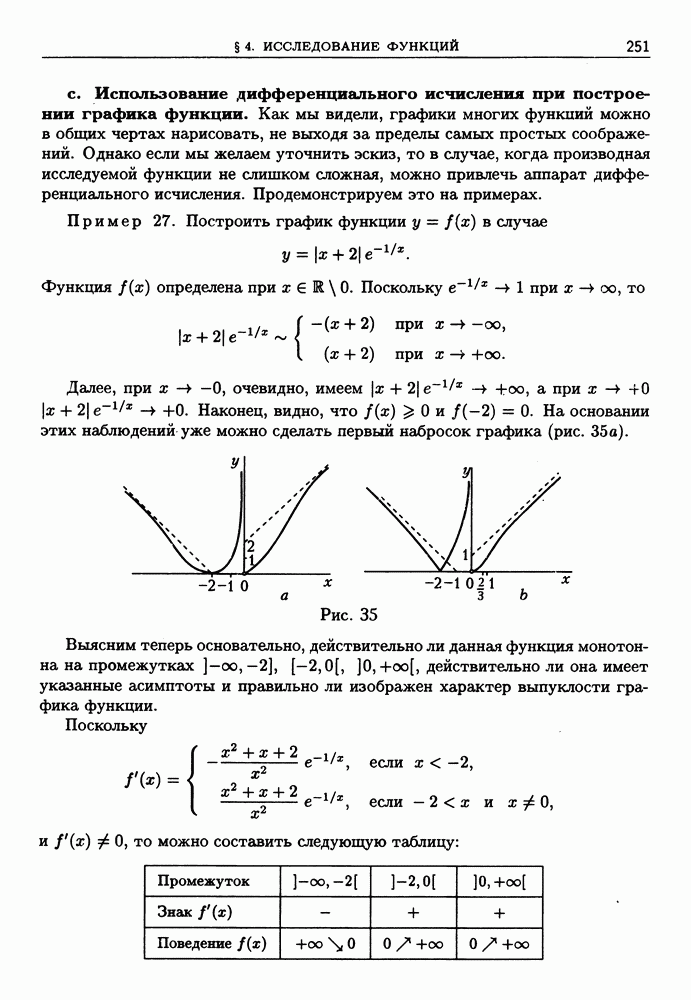
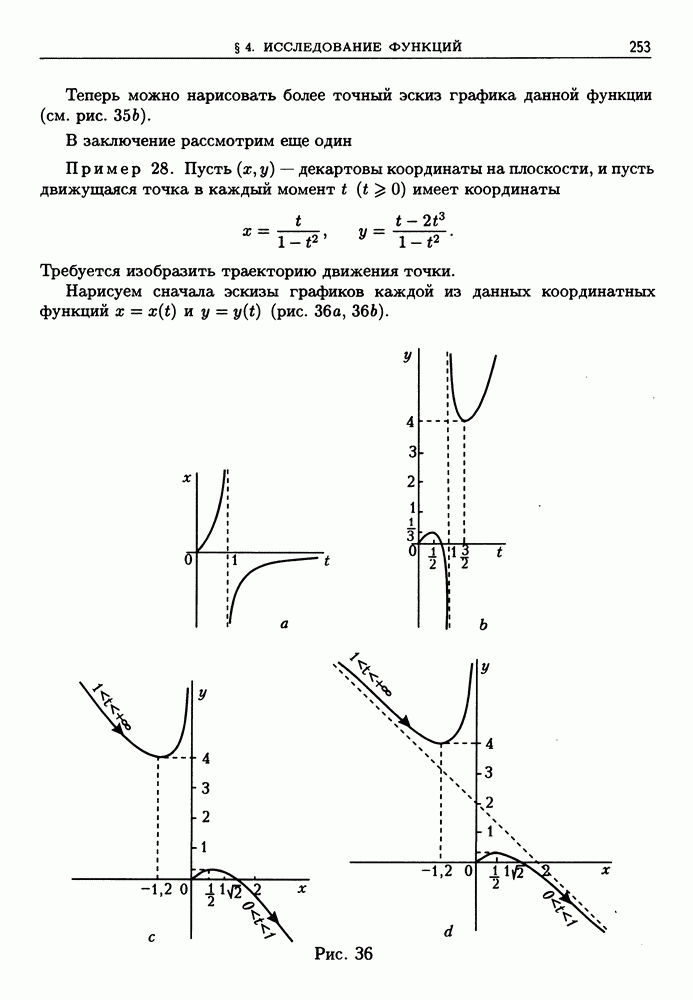
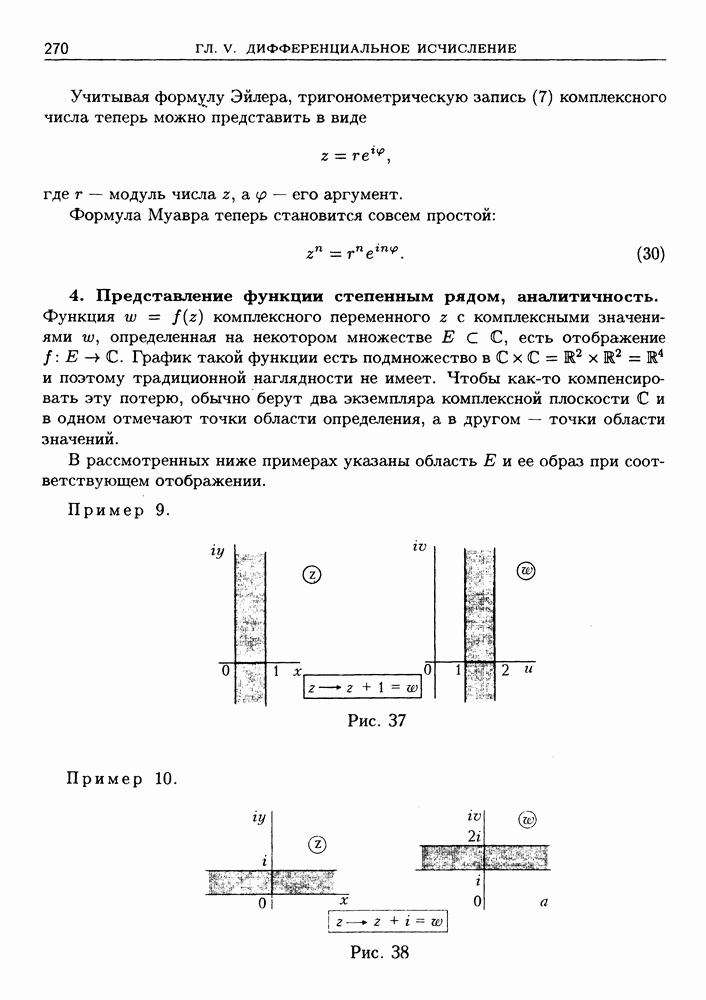
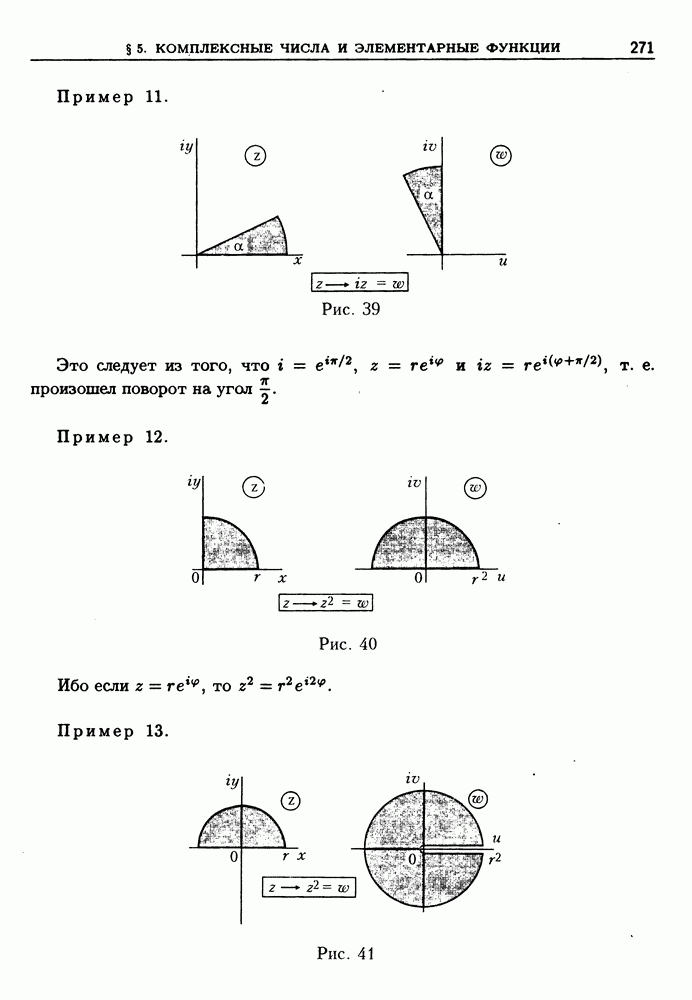
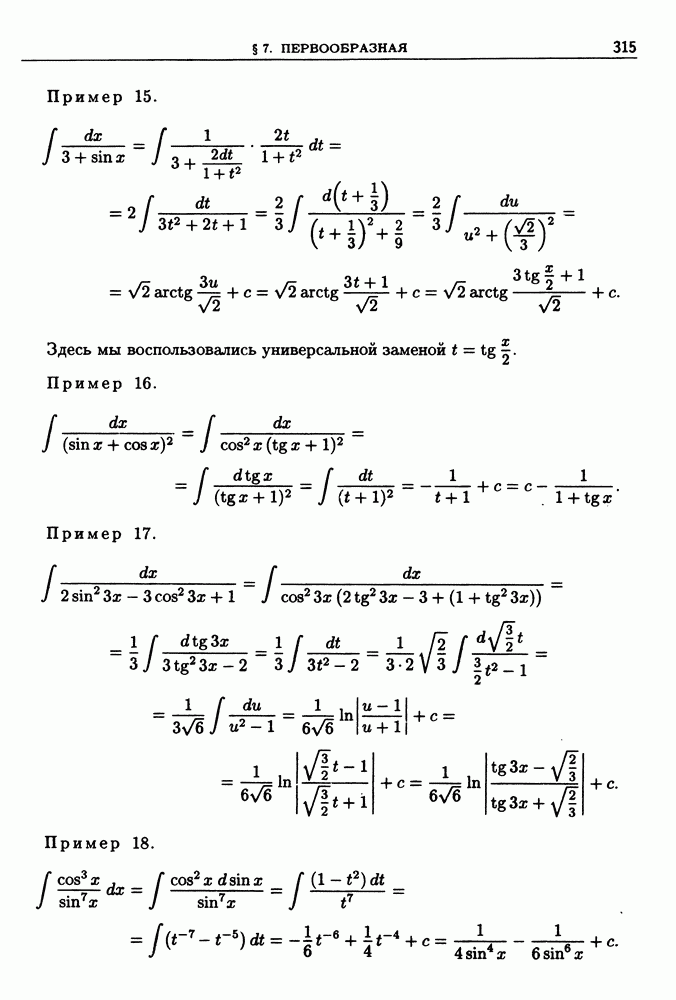| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Множество интегрируемых функций.
В силу определения интеграла (определение 4) и его переформулировок в виде (4) и (5), интеграл есть предел некоторой специальной функции  интегральной суммы, определенной на множестве V разбиений
интегральной суммы, определенной на множестве V разбиений  с отмеченными точками отрезка
с отмеченными точками отрезка  Предел этот берется по базе
Предел этот берется по базе  которую мы обозначили как
которую мы обозначили как 
Таким образом, интегрируемость функции  на
на  зависит от наличия указанного предела.
зависит от наличия указанного предела.
В силу критерия Коши этот предел существует тогда и только тогда, когда для любого числа  найдется элемент
найдется элемент  базы, в любых точках
базы, в любых точках  которого выполнено соотношение
которого выполнено соотношение

В более подробной записи сказанное означает, что для любого  найдется
найдется  такое, что для любых разбиений
такое, что для любых разбиений  с отмеченными точками отрезка
с отмеченными точками отрезка  для которых
для которых  выполнено неравенство
выполнено неравенство

 что то же самое, неравенство
что то же самое, неравенство

Мы воспользуемся сформулированным критерием Коши для того, чтобы получить сначала простое необходимое, а затем и достаточное условие интегрируемости функции по Риману.
а. Необходимое условие интегрируемости
Утверждение 1. Для того чтобы функция  определенная на отрезке
определенная на отрезке  была интегрируема на нем по Риману, необходимо, чтобы она была ограничена на этом отрезке.
была интегрируема на нем по Риману, необходимо, чтобы она была ограничена на этом отрезке.
Короче,

Если  не ограничена на
не ограничена на  то при любом разбиении Р отрезка
то при любом разбиении Р отрезка  функция
функция  окажется неограниченной по крайней мере на одном из отрезков
окажется неограниченной по крайней мере на одном из отрезков  разбиения Р. Это означает, что, выбирая различным образом точку
разбиения Р. Это означает, что, выбирая различным образом точку  можно сделать величину
можно сделать величину  сколь угодно большой. Но тогда и интегральную сумму
сколь угодно большой. Но тогда и интегральную сумму  можно сделать по модулю сколь угодно большой за счет изменений только точки
можно сделать по модулю сколь угодно большой за счет изменений только точки  в этом отрезке.
в этом отрезке.
Ясно, что в таком случае не может быть и речи о конечном пределе интегральных сумм, что, впрочем, видно и из критерия Коши, ибо соотношение
(6) в этом случае, очевидно, не имеет места даже для сколь угодно мелких разбиений.
Как мы увидим, полученное необходимое условие еще очень далеко от необходимого и достаточного условия интегрируемости, однако оно уже позволяет нам в дальнейшем исследовать только ограниченные функции.
b. Достаточное условие интегрируемости и важнейшие классы интегрируемых функций.
Начнем с нескольких обозначений и замечаний, которые используются в дальнейшем изложении.
Условимся, когда задано разбиение Р

отрезка  наряду с символом
наряду с символом  обозначающим разность
обозначающим разность  употреблять символ
употреблять символ  для обозначения отрезка
для обозначения отрезка 
Если разбиение Р отрезка  получено из разбиения Р только добавлением к Р некоторых новых точек, то условимся называть разбиение Р продолжением разбиения Р.
получено из разбиения Р только добавлением к Р некоторых новых точек, то условимся называть разбиение Р продолжением разбиения Р.
При построении продолжения Р разбиения Р некоторые (быть может, и все) отрезки  разбиения Р сами подвергаются разбиению
разбиения Р сами подвергаются разбиению  . В связи с этим нам будет удобно нумеровать точки разбиения Р двумя индексами. В записи
. В связи с этим нам будет удобно нумеровать точки разбиения Р двумя индексами. В записи  первый индекс означает, что
первый индекс означает, что  второй индекс есть порядковый номер точки на отрезке
второй индекс есть порядковый номер точки на отрезке  Теперь естественно положить
Теперь естественно положить  Таким образом,
Таким образом, 
Примером разбиения, являющегося продолжением как разбиения Р, так и разбиения  может служить разбиение
может служить разбиение  полученное объединением точек разбиений Р и
полученное объединением точек разбиений Р и 
Напомним, наконец, что, как и прежде, символ  будет обозначать колебание функции
будет обозначать колебание функции  на множестве Е, т. е.
на множестве Е, т. е.

В частности,  есть колебание функции
есть колебание функции  на отрезке
на отрезке  Это колебание заведомо конечно, если
Это колебание заведомо конечно, если  — ограниченная функция.
— ограниченная функция.
Теперь сформулируем и докажем следующее
Утверждение 2. Для того чтобы ограниченная на отрезке  функция
функция  была интегрируема на нем, достаточно, чтобы для любого числа
была интегрируема на нем, достаточно, чтобы для любого числа  нашлось число
нашлось число  такое, что при любом разбиении Р отрезка
такое, что при любом разбиении Р отрезка  с параметром
с параметром  выполнялось соотношение
выполнялось соотношение

Пусть Р — разбиение отрезка  — продолжение разбиения Р. Оценим разность интегральных сумм
— продолжение разбиения Р. Оценим разность интегральных сумм  Используя введенные выше обозначения, можем написать
Используя введенные выше обозначения, можем написать

В этих выкладках мы использовали то, что  также то, что
также то, что  поскольку
поскольку 
Из полученной оценки разности интегральных сумм следует, что если функция  удовлетворяет достаточному условию, сформулированному в утверждении 2, то по любому числу
удовлетворяет достаточному условию, сформулированному в утверждении 2, то по любому числу  можно найти
можно найти  так, что для любого разбиения Р отрезка
так, что для любого разбиения Р отрезка  с параметром
с параметром  и его продолжения
и его продолжения
Р при любом выборе отмеченных точек  будем иметь
будем иметь

Если теперь  — произвольные разбиения с отмеченными точками отрезка
— произвольные разбиения с отмеченными точками отрезка  параметры которых удовлетворяют условиям
параметры которых удовлетворяют условиям  то, рассмотрев разбиение
то, рассмотрев разбиение  являющееся продолжением обоих разбиений
являющееся продолжением обоих разбиений  по доказанному будем иметь
по доказанному будем иметь

Отсюда следует, что

как только  Таким образом, в силу критерия Коши существует предел
Таким образом, в силу критерия Коши существует предел

интегральных сумм, т. е. 
Следствие  т. е. любая непрерывная на отрезке функция интегрируема на этом отрезке.
т. е. любая непрерывная на отрезке функция интегрируема на этом отрезке.
Если функция непрерывна на отрезке, то она ограничена на нем, так что необходимое условие интегрируемости в этом случае, очевидно, выполнено. Однако непрерывная на отрезке функция еще и равномерно непрерывна на нем, поэтому для любого  можно найти
можно найти  так, что на любом отрезке
так, что на любом отрезке  длины меньше
длины меньше  будем иметь
будем иметь  Тогда для любого разбиения Р с параметром
Тогда для любого разбиения Р с параметром  будем иметь
будем иметь

В силу утверждения 2 теперь можно заключить, что 
Следствие 2. Если ограниченная на отрезке  функция
функция  непрерывна на этом отрезке всюду, кроме, быть может, конечного множества точек, то
непрерывна на этом отрезке всюду, кроме, быть может, конечного множества точек, то 
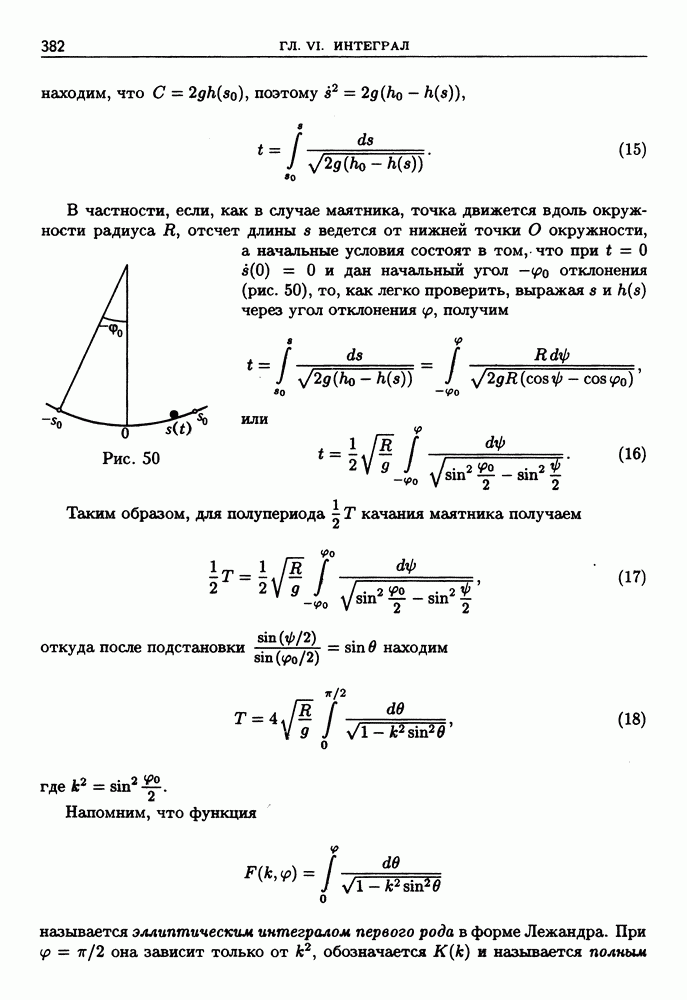
Пусть  имеет к точек разрыва на отрезке
имеет к точек разрыва на отрезке  Проверим выполнимость достаточного условия интегрируемости функции
Проверим выполнимость достаточного условия интегрируемости функции 
При заданном  возьмем число и построим
возьмем число и построим  -окрестности каждой из к точек разрыва функции
-окрестности каждой из к точек разрыва функции  на
на  Дополнительное к объединению этих окрестностей множество точек отрезка
Дополнительное к объединению этих окрестностей множество точек отрезка  состоит из конечного числа отрезков, на каждом из которых
состоит из конечного числа отрезков, на каждом из которых  непрерывна и, значит, равномерно непрерывна. Поскольку таких отрезков конечное число, по
непрерывна и, значит, равномерно непрерывна. Поскольку таких отрезков конечное число, по  можно указать
можно указать  так, что на любом отрезке
так, что на любом отрезке  длина которого меньше
длина которого меньше  и который полностью содержится в одном из указанных выше отрезков непрерывности
и который полностью содержится в одном из указанных выше отрезков непрерывности  будем иметь
будем иметь  . Возьмем теперь число
. Возьмем теперь число 
Пусть Р — произвольное разбиение отрезка  для которого
для которого 
Сумму  отвечающую разбиению Р, разобьем на две части:
отвечающую разбиению Р, разобьем на две части:

В сумму 2 включим те слагаемые, которые отвечают отрезкам  разбиения Р, не имеющим общих точек с построенными
разбиения Р, не имеющим общих точек с построенными  -окрестностями точек разрыва. Для таких отрезков имеем
-окрестностями точек разрыва. Для таких отрезков имеем  поэтому
поэтому

Сумма длин оставшихся отрезков разбиения Р, как легко видеть, меньше  поэтому
поэтому

Таким образом, мы получаем, что при 

т. е. выполнено достаточное условие интегрируемости и 
Следствие 3. Монотонная на отрезке функция интегрируема на этом отрезке.
Из монотонности функции  на отрезке
на отрезке  следует, что
следует, что 
Пусть задано  Положим
Положим  Мы считаем, что
Мы считаем, что  поскольку в противном случае
поскольку в противном случае  постоянна и интегрируемость
постоянна и интегрируемость  не вызывает сомнений. Пусть Р — произвольное разбиение отрезка
не вызывает сомнений. Пусть Р — произвольное разбиение отрезка  с параметром
с параметром 
Тогда для него с учетом монотонности  имеем
имеем

Таким образом,  удовлетворяет достаточному условию интегрируемости, т. е.
удовлетворяет достаточному условию интегрируемости, т. е. 
Монотонная функция может иметь уже бесконечно много точек разрыва на отрезке (счетное множество). Например, функция, определяемая соотношениями

на отрезке [0,1], не убывает и в каждой точке вида  имеет разрыв.
имеет разрыв.
Замечание. Отметим, что хотя мы сейчас имеем дело с вещественными функциями на отрезке, однако ни в определении интеграла, ни в доказанных выше утверждениях, за исключением следствия 3, мы по существу не использовали то, что рассматриваемые функции вещественнозначные, а не комплексно- или, например, векторнозначные функции точки отрезка 
Понятия верхней и нижней интегральной суммы, к которым мы переходим, напротив, специфичны только для функций с действительными значениями.
Определение 6. Пусть  — действительнозначная функция, определенная и ограниченная на отрезке
— действительнозначная функция, определенная и ограниченная на отрезке  — разбиение отрезка
— разбиение отрезка  — отрезки разбиения Р. Пусть
— отрезки разбиения Р. Пусть 
Суммы

и

называются соответственно нижней и верхней интегральной суммой функции  на отрезке
на отрезке  соответствующей разбиению Р этого отрезка. Суммы
соответствующей разбиению Р этого отрезка. Суммы  называют также нижней и верхней суммой Дарбу, соответствующей разбиению Р отрезка
называют также нижней и верхней суммой Дарбу, соответствующей разбиению Р отрезка 
Если  — произвольное разбиение с отмеченными точками отрезка
— произвольное разбиение с отмеченными точками отрезка  то, очевидно,
то, очевидно,

Лемма 1.

Проверим, например, что верхняя сумма Дарбу, отвечающая разбиению Р отрезка  является верхней гранью значений интегральных сумм, соответствующих разбиению с отмеченными точками
является верхней гранью значений интегральных сумм, соответствующих разбиению с отмеченными точками  отрезка
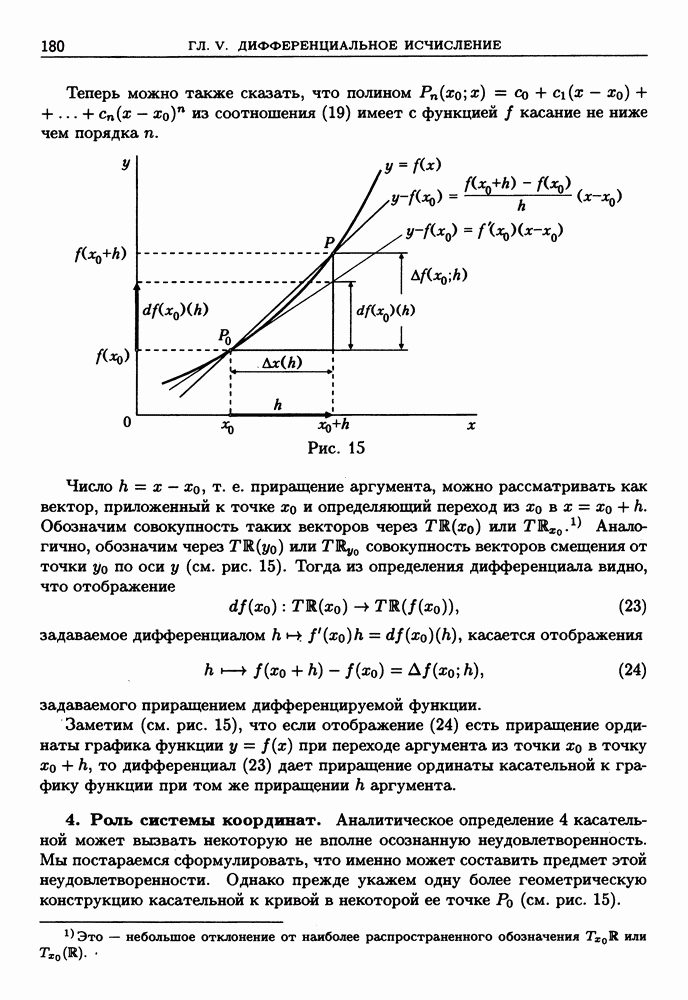
отрезка  причем верхняя грань берется по всевозможным наборам
причем верхняя грань берется по всевозможным наборам  отмеченных точек.
отмеченных точек.
Ввиду (7), для доказательства достаточно, чтобы при любом  нашелся такой набор
нашелся такой набор  отмеченных точек, что имеет место неравенство
отмеченных точек, что имеет место неравенство

По определению чисел М, при каждом  найдется точка
найдется точка  в которой
в которой  Пусть
Пусть  Тогда
Тогда

что и завершает доказательство второго утверждения леммы. Первое утверждение проверяется аналогично.
Из доказанной леммы и неравенства (7) с учетом определения интеграла Римана заключаем, что справедливо следующее
Утверждение 3. Ограниченная вещественнозначная функция  интегрируема по Риману на отрезке
интегрируема по Риману на отрезке  тогда и только тогда, когда существуют и равны между собой пределы
тогда и только тогда, когда существуют и равны между собой пределы

При этом их общее значение  совпадает с интегралом
совпадает с интегралом

Действительно, если пределы (9) существуют и равны между собой, то по свойствам предела из (7) заключаем о существовании предела интегральных сумм, причем

С другой стороны, если  т. е. существует предел
т. е. существует предел

то из (7) и (8) заключаем, что существует предел  причем
причем 
Аналогично проверяется, что 
В качестве следствия утверждения 3 получаем следующее уточнение утверждения 2.
Утверждение 2. Для того чтобы функция  заданная на отрезке
заданная на отрезке  была интегрируема по Риману, необходимо и достаточно выполнение соотношения
была интегрируема по Риману, необходимо и достаточно выполнение соотношения

Учитывая утверждение 2, нам остается лишь убедиться в необходимости соотношения (10) для интегрируемости 
Заметим, что  поэтому
поэтому

и теперь (10) следует из утверждения 3, коль скоро 
с. Векторное пространство R[a,b].
Над интегрируемыми функциями можно выполнять ряд операций, не выходя за пределы множества 
Утверждение 4. Если  то
то

Мы сейчас рассматриваем только вещественнозначные функции, но полезно отметить, что свойства а), Ь), с), d) окажутся справедливыми и для комплекснозначных и векторнозначных функций. Для векторнозначных функций, вообще говоря, не определено произведение  поэтому свойство
поэтому свойство  для них не рассматривается. Однако это свойство остается в силе для функций с комплексными значениями.
для них не рассматривается. Однако это свойство остается в силе для функций с комплексными значениями.
Перейдем теперь к доказательству утверждения 4.
Это утверждение очевидно, поскольку

Это утверждение очевидно, поскольку

Поскольку  то можно написать, что
то можно написать, что

и на основании утверждения 2 заключить, что 
Мы хотим проверить, что ограничение  интегрируемой на отрезке
интегрируемой на отрезке  функции на любой отрезок
функции на любой отрезок  является функцией, интегрируемой на
является функцией, интегрируемой на  Пусть
Пусть  — разбиение отрезка
— разбиение отрезка  Добавив к
Добавив к  некоторые точки, достроим
некоторые точки, достроим  до разбиения Р отрезка
до разбиения Р отрезка  но так, чтобы иметь
но так, чтобы иметь  . Ясно, что это всегда можно сделать.
. Ясно, что это всегда можно сделать.
Теперь можно написать, что

где  — сумма по всем отрезкам разбиения
— сумма по всем отрезкам разбиения  — сумма по всем отрезкам разбиения Р.
— сумма по всем отрезкам разбиения Р.
При  по построению также
по построению также  и на основании утверждения 2 из полученного неравенства заключаем, что
и на основании утверждения 2 из полученного неравенства заключаем, что  если
если 
 Проверим сначала, что если
Проверим сначала, что если  то
то 
Если  то
то  ограничена на
ограничена на  Пусть
Пусть  на
на  Тогда
Тогда

поэтому  если
если  Значит,
Значит,

откуда на основании утверждения 21 заключаем, что

Теперь перейдем к общему случаю. Запишем тождество

Из этого тождества с учетом только что доказанного утверждения и проверенных пунктов а) и  утверждения 4 заключаем, что
утверждения 4 заключаем, что

Из курса алгебры вам уже известно понятие векторного пространства. Вещественнозначные функции, определенные на некотором множестве, можно поточечно складывать и умножать на действительное число, получая при этом снова функцию с вещественными значениями на том же множестве. Если функции рассматривать как векторы, то можно проверить, что при этом выполнены все аксиомы векторного пространства над полем действительных чисел и указанное множество действительных функций является векторным пространством относительно операций поточечного сложения функций и умножения функций на действительные числа.
В пунктах а), b) утверждения 4 сказано, что сложение интегрируемых функций и умножение интегрируемой функции на число не выводит за пределы множества  интегрируемых функций. Таким образом,
интегрируемых функций. Таким образом,  само является линейным векторным пространством — подпространством векторного пространства вещественнозначных функций, определенных на отрезке
само является линейным векторным пространством — подпространством векторного пространства вещественнозначных функций, определенных на отрезке 
d. Критерий Лебега интегрируемости функции по Риману.
В заключение приведем пока без Доказательства теорему Лебега, дающую внутреннее описание интегрируемой по Риману функции.
Для этого введем следующее полезное само по себе понятие.
Определение 7. Говорят, что множество  имеет меру нуль или является множеством меры нуль (в смысле Лебега), если для любого числа
имеет меру нуль или является множеством меры нуль (в смысле Лебега), если для любого числа  существует такое покрытие множества Е не более чем счетной системой
существует такое покрытие множества Е не более чем счетной системой  интервалов, сумма
интервалов, сумма  длин которых не превышает
длин которых не превышает  .
.
Поскольку ряд  сходится абсолютно, порядок суммирования длин промежутков покрытия не влияет на сумму (см. утверждение 4 из гл. V, §
сходится абсолютно, порядок суммирования длин промежутков покрытия не влияет на сумму (см. утверждение 4 из гл. V, §  поэтому данное определение корректно.
поэтому данное определение корректно.
Лемма 2. а) Точка и конечное число точек суть множества меры нуль.
 Объединение конечного или счетного числа множеств меры нуль есть множество меры нуль.
Объединение конечного или счетного числа множеств меры нуль есть множество меры нуль.
 Подмножество множества меры нуль само есть множество меры нуль.
Подмножество множества меры нуль само есть множество меры нуль.
 Отрезок
Отрезок  при
при  не является множеством меры нуль.
не является множеством меры нуль.
М а) Точку можно покрыть одним интервалом длины меньшей, чем любое наперед заданное число  поэтому точка является множеством меры нуль. В остальном а) вытекает из
поэтому точка является множеством меры нуль. В остальном а) вытекает из 
Пусть  — не более чем счетное объединение множеств
— не более чем счетное объединение множеств  меры нуль. По
меры нуль. По  для каждого
для каждого  строим покрытие
строим покрытие  множества
множества  такое, что
такое, что 
Поскольку объединение не более чем счетного числа не более чем счетных множеств само не более чем счетно, промежутки  образуют не более чем счетное покрытие множества Е, причем
образуют не более чем счетное покрытие множества Е, причем

Порядок суммирования  по индексам пик безразличен, ибо ряд сходится к одной и той же сумме при любом порядке суммирования, если он сходится для какого-то порядка суммирования. Последнее в нашем случае имеет место, ибо любые частичные суммы нашего ряда ограничены сверху числом
по индексам пик безразличен, ибо ряд сходится к одной и той же сумме при любом порядке суммирования, если он сходится для какого-то порядка суммирования. Последнее в нашем случае имеет место, ибо любые частичные суммы нашего ряда ограничены сверху числом  .
.
Итак, Е есть множество меры нуль в смысле Лебега.
 Это утверждение, очевидно, непосредственно следует из определения множества меры нуль и определения покрытия.
Это утверждение, очевидно, непосредственно следует из определения множества меры нуль и определения покрытия.
 Поскольку для любого покрытия отрезка интервалами можно выделить конечное покрытие, сумма длин промежутков которого, очевидно, не превосходит суммы длин промежутков исходного покрытия, то нам достаточно
Поскольку для любого покрытия отрезка интервалами можно выделить конечное покрытие, сумма длин промежутков которого, очевидно, не превосходит суммы длин промежутков исходного покрытия, то нам достаточно
проверить, что сумма длин интервалов, образующих конечное покрытие отрезка  не меньше длины
не меньше длины  этого отрезка.
этого отрезка.
Проведем индукцию по количеству интервалов покрытия.
При  т. е. когда отрезок
т. е. когда отрезок  содержится в одном интервале
содержится в одном интервале  очевидно, имеем
очевидно, имеем 
Пусть утверждение доказано до индекса  включительно. Рассмотрим покрытие, состоящее из
включительно. Рассмотрим покрытие, состоящее из  интервалов. Возьмем интервал
интервалов. Возьмем интервал  покрывающий точку а. Бели
покрывающий точку а. Бели  то
то  и все доказано. Если же
и все доказано. Если же  то отрезок
то отрезок  покрыт системой, состоящей уже не более чем из к интервалов, сумма длин которых по предположению индукции не меньше чем
покрыт системой, состоящей уже не более чем из к интервалов, сумма длин которых по предположению индукции не меньше чем  Но
Но

и, таким образом, сумма длин интервалов исходного покрытия отрезка  больше, чем его длина
больше, чем его длина 
Интересно отметить, что в силу пунктов а) и  леммы 2 множество
леммы 2 множество  всех рациональных точек числовой прямой К является множеством меры нуль, что на первый взгляд выглядит несколько неожиданным при сопоставлении с пунктом
всех рациональных точек числовой прямой К является множеством меры нуль, что на первый взгляд выглядит несколько неожиданным при сопоставлении с пунктом  той же леммы.
той же леммы.
Определение 8. Если некоторое свойство выполнено в любой точке множества X, кроме, быть может, точек множества меры нуль, то говорят, что это свойство имеет место почти всюду на множестве X или почти во всех точках множества X.
Теперь сформулируем критерий Лебега.
Теорема. Функция, определенная на отрезке, интегрируема по Риману на этом отрезке в том и только в том случае, когда она ограничена на этом отрезке и непрерывна почти во всех его точках.
Итак,

Из критерия Лебега и свойств множеств меры нуль, изложенных в лемме 2, очевидно, легко можно получить как следствия 1, 2, 3 утверждения 2, так и утверждение 4.
Мы не станем сейчас доказывать критерий Лебега, поскольку при работе с достаточно регулярными функциями, с которыми нам предстоит иметь дело, он нам пока не нужен. Однако идейную сторону критерия Лебега вполне можно объяснить уже сейчас.
Утверждение 2 содержало критерий интегрируемости, выраженный соотношением (10). Сумма  может быть мала, прежде всего, за счет
может быть мала, прежде всего, за счет
множителей  , которые малы в малых окрестностях точек непрерывности функции. Если же некоторые из отрезков
, которые малы в малых окрестностях точек непрерывности функции. Если же некоторые из отрезков  содержат точки разрыва функции, то для них
содержат точки разрыва функции, то для них  не стремится к нулю, сколь мелким бы ни было разбиение Р отрезка
не стремится к нулю, сколь мелким бы ни было разбиение Р отрезка  Однако
Однако  в силу ограниченности
в силу ограниченности  на
на  поэтому сумма тех слагаемых, которые содержат точки разрыва, тоже может оказаться маленькой, если только мала сумма длин отрезков разбиения, покрывающих множество точек разрыва, или, точнее, если рост колебания функции на некоторых отрезках разбиения компенсируется малостью длин этих отрезков.
поэтому сумма тех слагаемых, которые содержат точки разрыва, тоже может оказаться маленькой, если только мала сумма длин отрезков разбиения, покрывающих множество точек разрыва, или, точнее, если рост колебания функции на некоторых отрезках разбиения компенсируется малостью длин этих отрезков.
Точной реализацией и формулировкой этого наблюдения и является критерий Лебега.
Приведем теперь два классических примера, поясняющих свойство функции быть интегрируемой по Риману.
Пример 1. Функция Дирихле

рассматриваемая на отрезке [0,1], не интегрируема на нем, поскольку для любого разбиения Р отрезка [0,1] в каждом отрезке  разбиения Р можно отметить как рациональную точку так и иррациональную точку Тогда
разбиения Р можно отметить как рациональную точку так и иррациональную точку Тогда

в то время как

Таким образом, интегральные суммы функции  не могут иметь предел при
не могут иметь предел при 
С точки зрения критерия Лебега неинтегрируемость функции Дирихле тоже очевидйа, поскольку функция  разрывна в каждой точке отрезка
разрывна в каждой точке отрезка  который, как было показано в лемме 2, не есть множество меры нуль.
который, как было показано в лемме 2, не есть множество меры нуль.
Пример 2. Рассмотрим функцию Римана

Мы уже рассматривали эту функцию в гл. IV, § 2, п. 2, и знаем, что функция  непрерывна во всех иррациональных точках и разрывна во всех рациональных точках. Таким образом, множество точек разрыва функции
непрерывна во всех иррациональных точках и разрывна во всех рациональных точках. Таким образом, множество точек разрыва функции  счетно и потому имеет меру нуль. В силу критерия Лебега можно заключить,
счетно и потому имеет меру нуль. В силу критерия Лебега можно заключить,
что функция  интегрируема на любом отрезке
интегрируема на любом отрезке  С
С  несмотря на то, что точки разрыва этой функции попадают в любой отрезок любого разбиения отрезка интегрирования.
несмотря на то, что точки разрыва этой функции попадают в любой отрезок любого разбиения отрезка интегрирования.
Пример 3. Рассмотрим теперь еще один, менее классический вопрос и пример.
Пусть  — интегрируемая на
— интегрируемая на  функция, принимающая значения на отрезке
функция, принимающая значения на отрезке  на котором непрерывна функция
на котором непрерывна функция  Тогда композиция
Тогда композиция  очевидно, определена и непрерывна во всех точках отрезка
очевидно, определена и непрерывна во всех точках отрезка  в которых непрерывна функция
в которых непрерывна функция  . В силу критерия Лебега отсюда следует, что
. В силу критерия Лебега отсюда следует, что 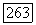
Покажем теперь на примере, что композиция произвольных интегрируемых функций — уже не всегда интегрируемая функция.
Рассмотрим функцию 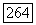 Эта функция равна единице при
Эта функция равна единице при 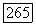 и нулю при
и нулю при 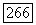 Непосредственной проверкой убеждаемся, что если, например, на отрезке [1,2] рассмотреть в качестве
Непосредственной проверкой убеждаемся, что если, например, на отрезке [1,2] рассмотреть в качестве 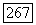 функцию Римана
функцию Римана 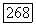 то на этом отрезке композиция
то на этом отрезке композиция 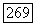 есть не что иное, как функция Дирихле
есть не что иное, как функция Дирихле 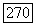 Таким образом, наличие даже одной точки разрыва
Таким образом, наличие даже одной точки разрыва  привело к неинтегрируемости композиции
привело к неинтегрируемости композиции 
Задачи и упражнения
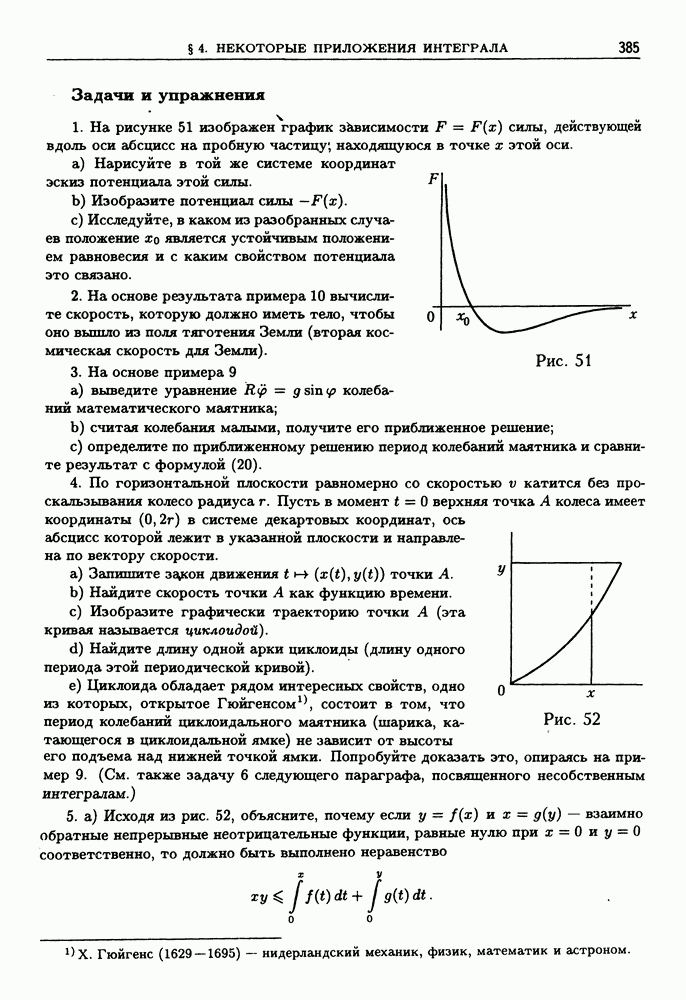
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
- § 1. Логическая символика
- § 2. Множество и элементарные операции над множествами
- 2. Отношение включения.
- 3. Простейшие операции над множествами.
- Упражнения
- § 3. Функция
- 2. Простейшая классификация отображений.
- 3. Композиция функций и взаимно обратные отображения.
- 4. Функция как отношение. График функции.
- § 4. Некоторые дополнения
- 2. Об аксиоматике теории множеств.
- 3. Замечания о структуре математических высказываний и записи их на языке теории множеств.
- Упражнения
- ГЛАВА II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
- § 1. Аксиоматика и некоторые общие свойства множества действительных чисел
- 2. Некоторые общие алгебраические свойства действительных чисел.
- 3. Аксиома полноты и существование верхней (нижней) грани числового множества
- § 2. Важнейшие классы действительных чисел и вычислительные аспекты операций с действительными числами
- 2. Рациональные и иррациональные числа
- 3. Принцип Архимеда.
- 4. Геометрическая интерпретация множества действительных чисел и вычислительные аспекты операций с действительными числами
- Задачи и упражнения
- § 3. Основные леммы, связанные с полнотой множества действительных чисел
- 2. Лемма о конечном покрытии (принцип Бореля — Лебега)
- 3. Лемма о предельной точке (принцип Больцано—Вейерштрасса).
- Задачи и упражнения
- § 4. Счетные и несчетные множества
- 2. Мощность континуума
- Задачи и упражнения
- ГЛАВА III. ПРЕДЕЛ
- 2. Свойства предела последовательности
- 3. Вопросы существования предела последовательности
- 4. Начальные сведения о рядах
- § 2. Предел функции
- 2. Свойства предела функции.
- 3. Общее определение предела функции (предел по базе).
- 4. Вопросы существования предела функции
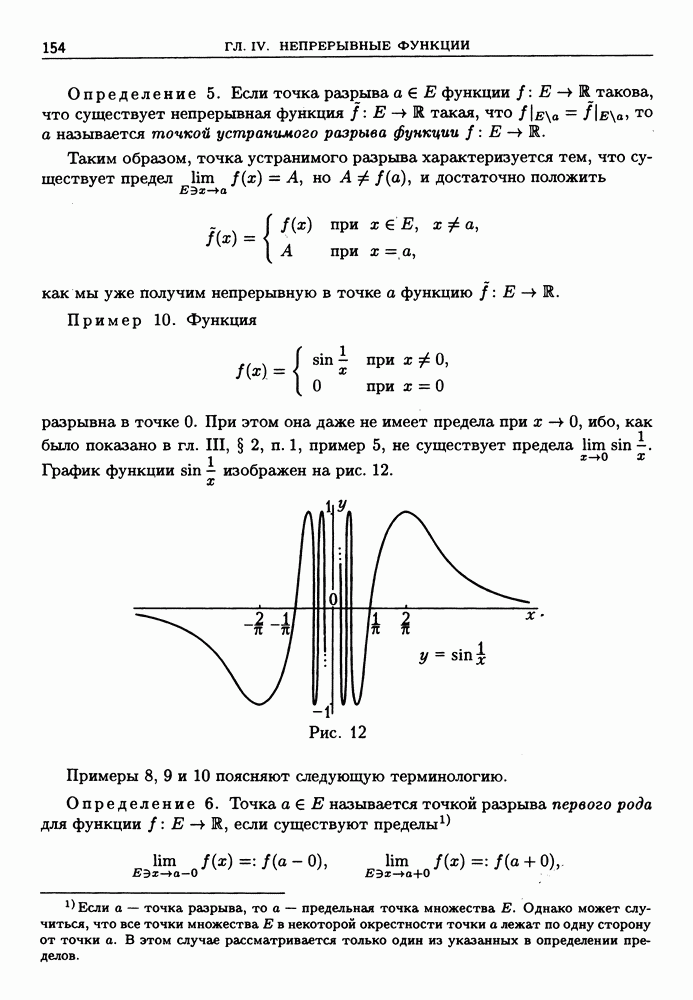
- ГЛАВА IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 2. Точки разрыва.
- § 2. Свойства непрерывных функций
- 2. Глобальные свойства непрерывных функций.
- ГЛАВА V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- 2. Функция, дифференцируемая в точке.
- 3. Касательная; геометрический смысл производной и дифференциала.
- 4. Роль системы координат.
- 5. Некоторые примеры
- Задачи и упражнения
- § 2. Основные правила дифференцирования
- 2. Дифференцирование композиции функций
- 3. Дифференцирование обратной функции
- 4. Таблица производных основных элементарных функций.
- 5. Дифференцирование простейшей неявно заданной функции.
- 6. Производные высших порядков.
- § 3. Основные теоремы дифференциального исчисления
- 2. Теоремы Лагранжа и Коши о конечном приращении.
- 3. Формула Тейлора.
- § 4. Исследование функций методами дифференциального исчисления
- 2. Условия внутреннего экстремума функции.
- 3. Условия выпуклости функции
- 4. Правило Лопиталя.
- 5. Построение графика функции.
- § 5. Комплексные числа и взаимосвязь элементарных функций
- 2. Сходимость в С и ряды с комплексными членами.
- 3. Формула Эйлера и взаимосвязь элементарных функций.
- 4. Представление функции степенным рядом, аналитичность.
- 5. Алгебраическая замкнутость поля С комплексных чисел.
- § 6. Некоторые примеры использования дифференциального исчисления в задачах естествознания
- 2. Барометрическая формула.
- 3. Радиоактивный распад, цепная реакция и атомный котел.
- 4. Падение тел в атмосфере.
- 5. Еще раз о числе e и функции exp(x).
- 6. Колебания.
- § 7. Первообразная
- 2. Основные общие приемы отыскания первообразной.
- 3. Первообразные рациональных функций.
- 4. Первообразные вида …
- 5. Первообразные вида …
- ГЛАВА VI. ИНТЕГРАЛ
- § 1. Определение интеграла и описание множества интегрируемых функций
- 2. Определение интеграла Римана
- 3. Множество интегрируемых функций.
- § 2. Линейность, аддитивность и монотонность интеграла
- 2. Интеграл как аддитивная функция отрезка интегрирования.
- 3. Оценка интеграла, монотонность интеграла, теоремы о среднем
- § 3. Интеграл и производная
- 2. Формула Ньютона—Лейбница
- 3. Интегрирование по частям в определенном интеграле и формула Тейлора
- 4. Замена переменной в интеграле.
- 5. Некоторые примеры.
- § 4. Некоторые приложения интеграла
- 2. Длина пути.
- 3. Площадь криволинейной трапеции.
- 4. Объем тела вращения.
- 5. Работа и энергия.
- § 5. Несобственный интеграл
- 2. Исследование сходимости несобственного интеграла
- 3. Несобственные интегралы с несколькими особенностями.
- ГЛАВА VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ, ИХ ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
- 2. Открытые и замкнутые множества в R^m
- 3. Компакты в R^m
- § 2. Предел и непрерывность функции многих переменных
- 2. Непрерывность функции многих переменных и свойства непрерывных функций.
- ГЛАВА VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- 2. Линейные отображения L : R^m -> R^n.
- 3. Норма в R^m.
- 4. Евклидова структура в R^m.
- § 2. Дифференциал функции многих переменных
- 2. Дифференциал и частные производные вещественнозначной функции.
- 3. Координатное представление дифференциала отображения. Матрица Якоби.
- 4. Непрерывность, частные производные и дифференцируемость функции в точке.
- § 3. Основные законы дифференцирования
- 2. Дифференцирование композиции отображений
- 3. Дифференцирование обратного отображения
- § 4. Основные факты дифференциального исчисления вещественнозначных функций многих переменных
- 2. Достаточное условие дифференцируемости функции многих переменных
- 4. Формула Тейлора
- 5. Экстремумы функций многих переменных.
- 6. Некоторые геометрические образы, связанные с функциями многих переменных
- § 5. Теорема о неявной функции
- 2. Простейший вариант теоремы о неявной функции.
- 3. Переход к случаю зависимости
- 4. Теорема о неявной функции.
- § 6. Некоторые следствия теоремы о неявной функции
- 2. Локальное приведение гладкого отображения к каноническому виду.
- 3. Зависимость функций
- 4. Локальное разложение диффеоморфизма в композицию простейших.
- 5. Лемма Морса.
- § 7. Поверхность в R^n и теория условного экстремума
- 2. Касательное пространство.
- 3. Условный экстремум
- НЕКОТОРЫЕ ЗАДАЧИ КОЛЛОКВИУМОВ
- ВОПРОСЫ К ЭКЗАМЕНУ
- ЛИТЕРАТУРА