| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
3. Дифференцирование обратной функции
Теорема 2 (теорема о производной обратной функции). Пусть функции  взаимно обратны и непрерывны в точках
взаимно обратны и непрерывны в точках  соответственно. Если функция
соответственно. Если функция  дифференцируема в точке
дифференцируема в точке  то функция
то функция  также дифференцируема в точке
также дифференцируема в точке  причем
причем

Поскольку функции  взаимно обратны, то величины
взаимно обратны, то величины  при
при  не обращаются в нуль, если
не обращаются в нуль, если  Из непрерывности
Из непрерывности  в
в  в у о можно, кроме того, заключить, что
в у о можно, кроме того, заключить, что  Используя теперь теорему о пределе композиции функций и арифметические свойства предела, находим
Используя теперь теорему о пределе композиции функций и арифметические свойства предела, находим

Таким образом, показано, что в точке  функция
функция  имеет производную и
имеет производную и

Замечание 1. Если бы нам заранее было известно, что функция дифференцируема в точке  то из тождества
то из тождества  по теореме о дифференцировании композиции функций мы сразу же нашли бы, что
по теореме о дифференцировании композиции функций мы сразу же нашли бы, что 
Замечание 2. Условие  очевидно, равносильно тому, что отображение
очевидно, равносильно тому, что отображение  осуществляемое дифференциалом
осуществляемое дифференциалом  , имеет обратное отображение
, имеет обратное отображение  задаваемое формулой
задаваемое формулой 
Значит, в терминах дифференциалов вторую фразу формулировки теоремы 3 можно было бы записать следующим образом:
Если функция  дифференцируема в точке
дифференцируема в точке  этой точке ее дифференциал
этой точке ее дифференциал  обратим, то дифференциал функции
обратим, то дифференциал функции  обратной к
обратной к  существует в точке
существует в точке  и является отображением
и является отображением

обратным к отображению  .
.
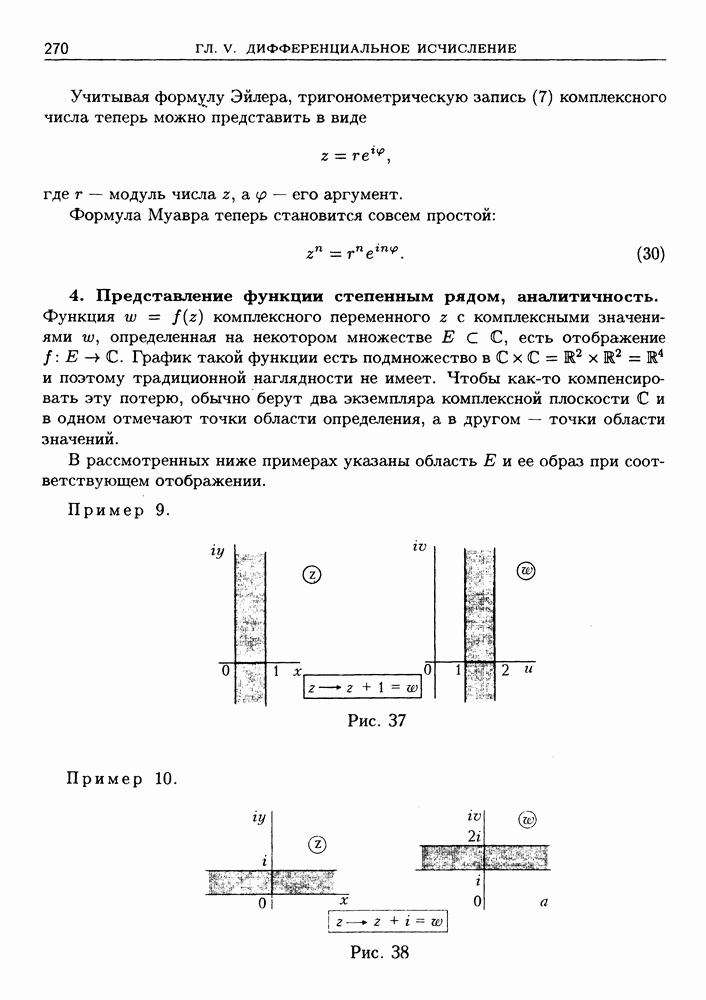
Пример 9. Покажем, что  при
при  Функции
Функции  взаимно обратны и непрерывны (см. гл. IV, § 2, пример 8), причем
взаимно обратны и непрерывны (см. гл. IV, § 2, пример 8), причем  , если
, если  При
При  для значений
для значений  имеем
имеем 
Таким образом, по теореме 3

Знак перед радикалом выбран с учетом того, что  при
при 
Пример 10. Рассуждая, как и в предыдущем примере, можно показать (с учетом примера 9 из § 2 гл. IV), что

Действительно,

Знак перед радикалом выбран с учетом того, что  если
если 
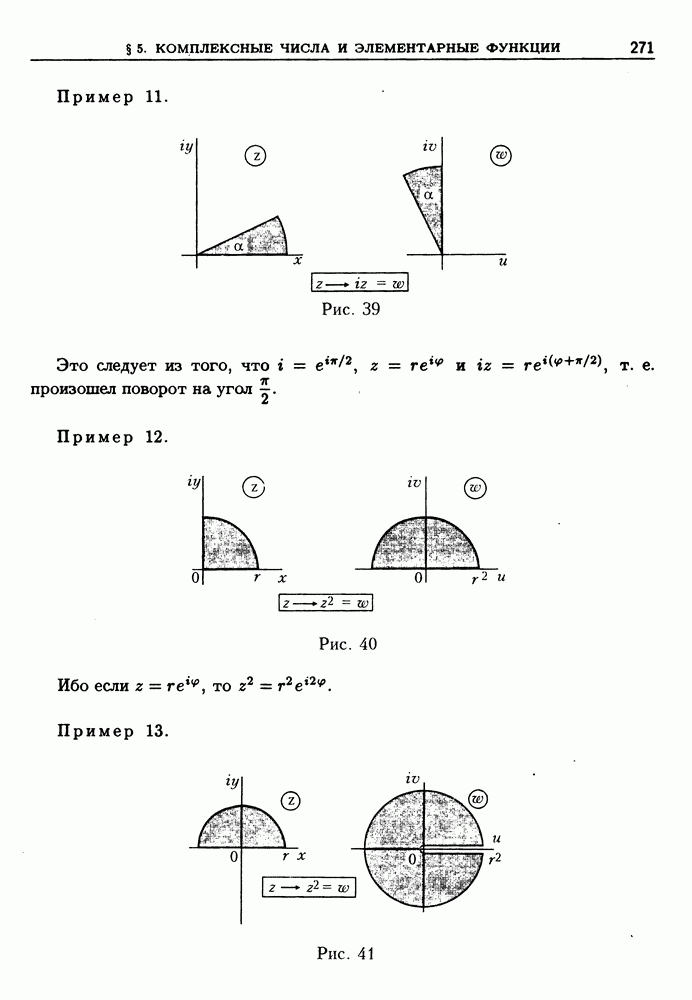
Пример 
Действительно,

Пример 
Действительно,

Пример 13. Мы уже знаем (см. примеры 10, 12 из § 1), что функции  имеют производные
имеют производные  и
и
Проверим, как это согласуется с теоремой 3:

Пример 14. Гиперболические, обратные гиперболические функции и их производные. Функции

называются соответственно гиперболическим синусом и гиперболическим косинусом 1 от х.
Эти в данный момент вводимые нами чисто формально функции, как выяснится, во многих вопросах появляются так же естественно, как появляются круговые функции 
Заметим, что

т. е. гиперболический синус — нечетная функция, а гиперболический косинус — функция четная.
Кроме того, очевидно следующее основное тождество:

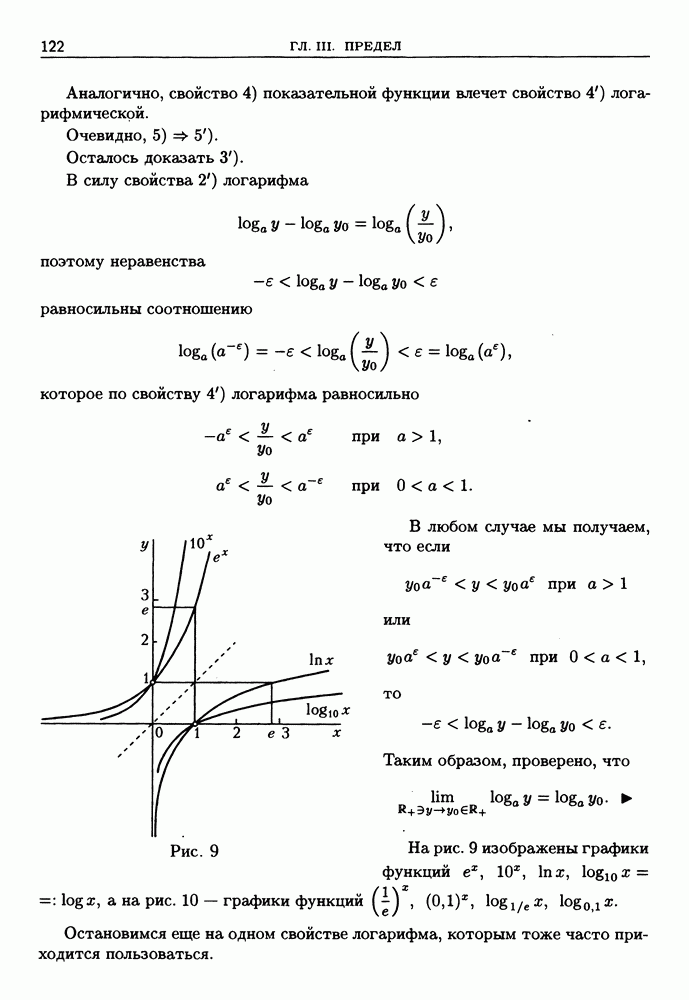
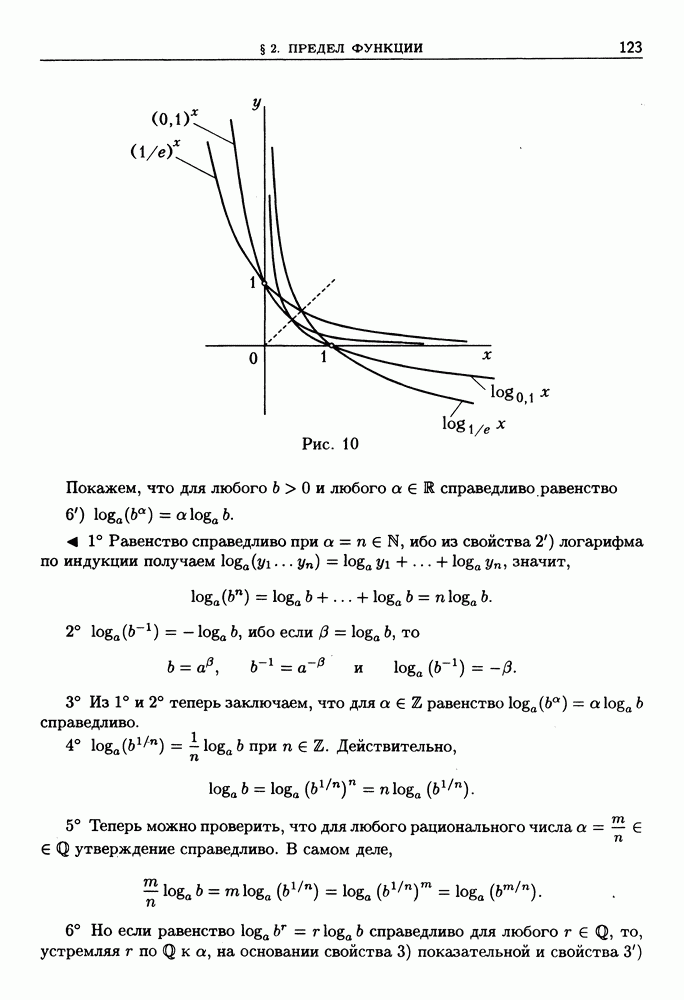
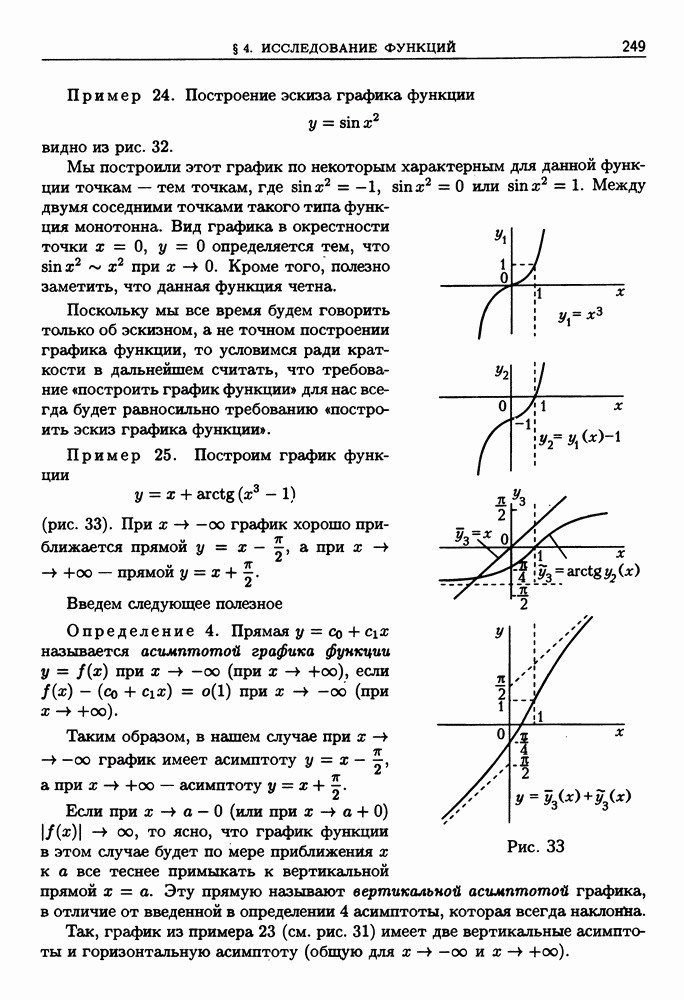
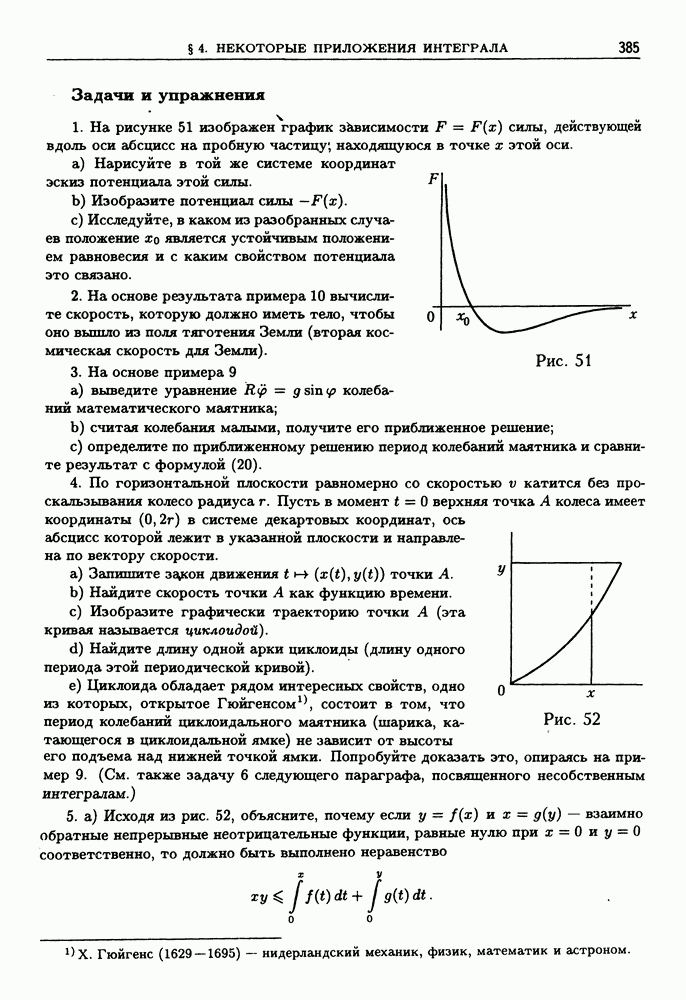
Графики функций  изображены на рис. 19.
изображены на рис. 19.

Рис. 19
Из определения функции  и свойств функции
и свойств функции  следует, что
следует, что  — непрерывная строго возрастающая функция, отображающая взаимно однозначно Е на К. Обратная функция к
— непрерывная строго возрастающая функция, отображающая взаимно однозначно Е на К. Обратная функция к  таким образом, существует, определена на
таким образом, существует, определена на  непрерывна и строго монотонно возрастает.
непрерывна и строго монотонно возрастает.
Ее обозначают символом

(читается ареа-синус от у»). Эту функцию легко выразить через уже известные. Решая уравнение

относительно х, найдем последовательно

и

Итак,

Аналогично, используя монотонность функции  на участках
на участках  можно построить функции
можно построить функции  определенные для
определенные для  и обратные к ограничению функции
и обратные к ограничению функции  на
на  соответственно.
соответственно.
Они задаются формулами

Из приведенных определений находим

а на основе теоремы о производной обратной функции получаем

Последние три соотношения можно проверить, используя явные выражения для обратных гиперболических функций  .
.
Например,

Подобно  можно рассмотреть функции
можно рассмотреть функции

называемые гиперболическим тангенсом и гиперболическим котангенсом соответственно, а также обратные им функции ареа-тангенс:

и ареа-котангенс:

Решения элементарных уравнений, приводящие к этим формулам, мы опускаем.
По правилам дифференцирования имеем

По теореме о производной обратной функции

Две последние формулы можно проверить и непосредственным дифференцированием явных формул для функций  .
.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
- § 1. Логическая символика
- § 2. Множество и элементарные операции над множествами
- 2. Отношение включения.
- 3. Простейшие операции над множествами.
- Упражнения
- § 3. Функция
- 2. Простейшая классификация отображений.
- 3. Композиция функций и взаимно обратные отображения.
- 4. Функция как отношение. График функции.
- § 4. Некоторые дополнения
- 2. Об аксиоматике теории множеств.
- 3. Замечания о структуре математических высказываний и записи их на языке теории множеств.
- Упражнения
- ГЛАВА II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
- § 1. Аксиоматика и некоторые общие свойства множества действительных чисел
- 2. Некоторые общие алгебраические свойства действительных чисел.
- 3. Аксиома полноты и существование верхней (нижней) грани числового множества
- § 2. Важнейшие классы действительных чисел и вычислительные аспекты операций с действительными числами
- 2. Рациональные и иррациональные числа
- 3. Принцип Архимеда.
- 4. Геометрическая интерпретация множества действительных чисел и вычислительные аспекты операций с действительными числами
- Задачи и упражнения
- § 3. Основные леммы, связанные с полнотой множества действительных чисел
- 2. Лемма о конечном покрытии (принцип Бореля — Лебега)
- 3. Лемма о предельной точке (принцип Больцано—Вейерштрасса).
- Задачи и упражнения
- § 4. Счетные и несчетные множества
- 2. Мощность континуума
- Задачи и упражнения
- ГЛАВА III. ПРЕДЕЛ
- 2. Свойства предела последовательности
- 3. Вопросы существования предела последовательности
- 4. Начальные сведения о рядах
- § 2. Предел функции
- 2. Свойства предела функции.
- 3. Общее определение предела функции (предел по базе).
- 4. Вопросы существования предела функции
- ГЛАВА IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
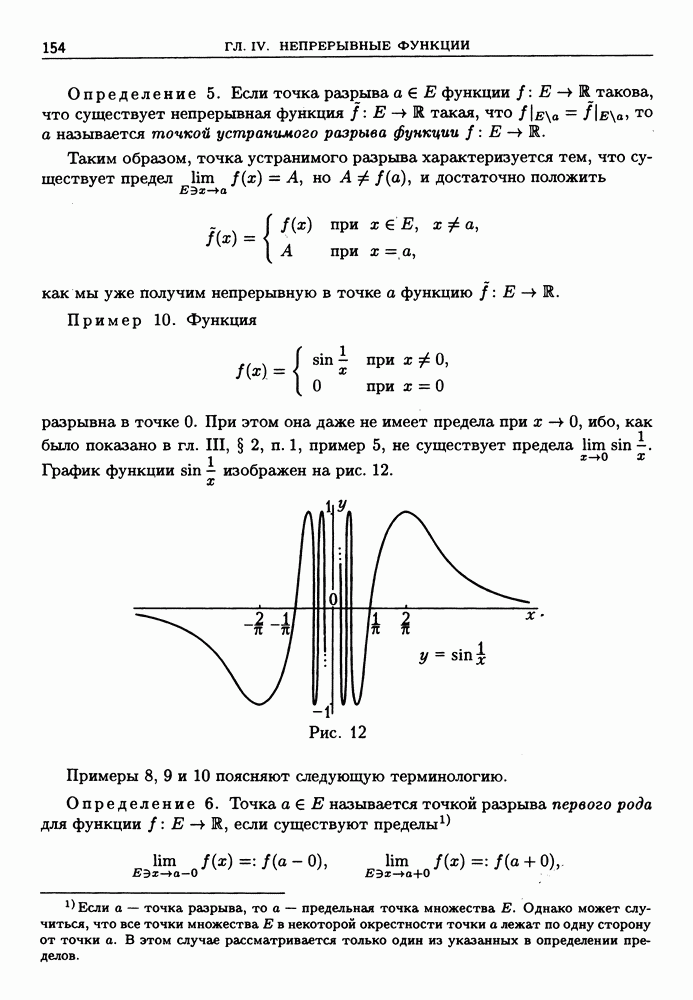
- 2. Точки разрыва.
- § 2. Свойства непрерывных функций
- 2. Глобальные свойства непрерывных функций.
- ГЛАВА V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- 2. Функция, дифференцируемая в точке.
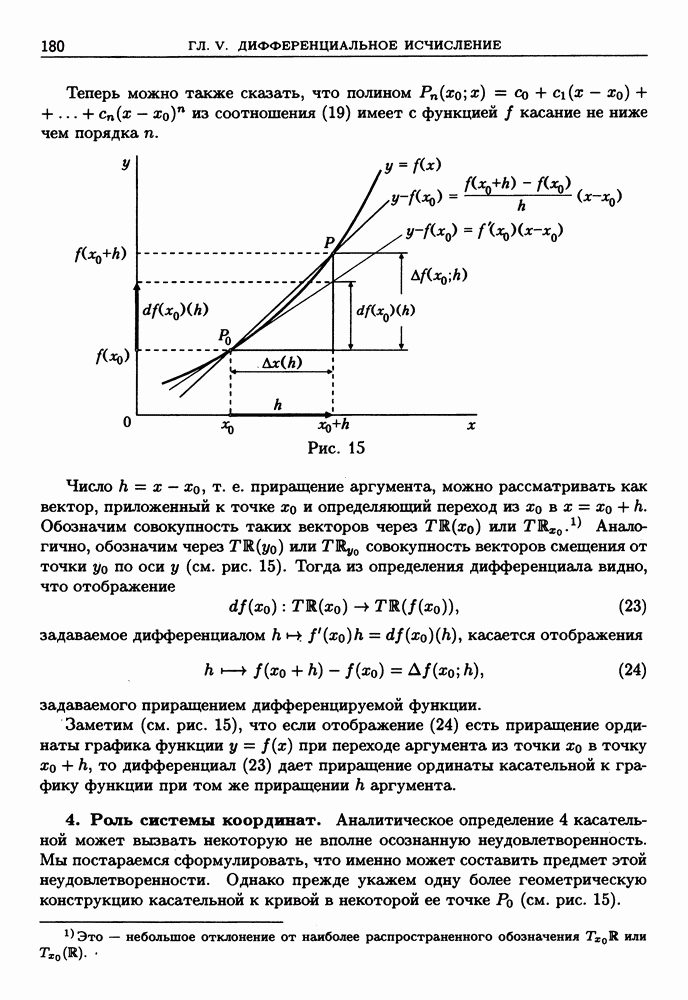
- 3. Касательная; геометрический смысл производной и дифференциала.
- 4. Роль системы координат.
- 5. Некоторые примеры
- Задачи и упражнения
- § 2. Основные правила дифференцирования
- 2. Дифференцирование композиции функций
- 3. Дифференцирование обратной функции
- 4. Таблица производных основных элементарных функций.
- 5. Дифференцирование простейшей неявно заданной функции.
- 6. Производные высших порядков.
- § 3. Основные теоремы дифференциального исчисления
- 2. Теоремы Лагранжа и Коши о конечном приращении.
- 3. Формула Тейлора.
- § 4. Исследование функций методами дифференциального исчисления
- 2. Условия внутреннего экстремума функции.
- 3. Условия выпуклости функции
- 4. Правило Лопиталя.
- 5. Построение графика функции.
- § 5. Комплексные числа и взаимосвязь элементарных функций
- 2. Сходимость в С и ряды с комплексными членами.
- 3. Формула Эйлера и взаимосвязь элементарных функций.
- 4. Представление функции степенным рядом, аналитичность.
- 5. Алгебраическая замкнутость поля С комплексных чисел.
- § 6. Некоторые примеры использования дифференциального исчисления в задачах естествознания
- 2. Барометрическая формула.
- 3. Радиоактивный распад, цепная реакция и атомный котел.
- 4. Падение тел в атмосфере.
- 5. Еще раз о числе e и функции exp(x).
- 6. Колебания.
- § 7. Первообразная
- 2. Основные общие приемы отыскания первообразной.
- 3. Первообразные рациональных функций.
- 4. Первообразные вида …
- 5. Первообразные вида …
- ГЛАВА VI. ИНТЕГРАЛ
- § 1. Определение интеграла и описание множества интегрируемых функций
- 2. Определение интеграла Римана
- 3. Множество интегрируемых функций.
- § 2. Линейность, аддитивность и монотонность интеграла
- 2. Интеграл как аддитивная функция отрезка интегрирования.
- 3. Оценка интеграла, монотонность интеграла, теоремы о среднем
- § 3. Интеграл и производная
- 2. Формула Ньютона—Лейбница
- 3. Интегрирование по частям в определенном интеграле и формула Тейлора
- 4. Замена переменной в интеграле.
- 5. Некоторые примеры.
- § 4. Некоторые приложения интеграла
- 2. Длина пути.
- 3. Площадь криволинейной трапеции.
- 4. Объем тела вращения.
- 5. Работа и энергия.
- § 5. Несобственный интеграл
- 2. Исследование сходимости несобственного интеграла
- 3. Несобственные интегралы с несколькими особенностями.
- ГЛАВА VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ, ИХ ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
- 2. Открытые и замкнутые множества в R^m
- 3. Компакты в R^m
- § 2. Предел и непрерывность функции многих переменных
- 2. Непрерывность функции многих переменных и свойства непрерывных функций.
- ГЛАВА VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- 2. Линейные отображения L : R^m -> R^n.
- 3. Норма в R^m.
- 4. Евклидова структура в R^m.
- § 2. Дифференциал функции многих переменных
- 2. Дифференциал и частные производные вещественнозначной функции.
- 3. Координатное представление дифференциала отображения. Матрица Якоби.
- 4. Непрерывность, частные производные и дифференцируемость функции в точке.
- § 3. Основные законы дифференцирования
- 2. Дифференцирование композиции отображений
- 3. Дифференцирование обратного отображения
- § 4. Основные факты дифференциального исчисления вещественнозначных функций многих переменных
- 2. Достаточное условие дифференцируемости функции многих переменных
- 4. Формула Тейлора
- 5. Экстремумы функций многих переменных.
- 6. Некоторые геометрические образы, связанные с функциями многих переменных
- § 5. Теорема о неявной функции
- 2. Простейший вариант теоремы о неявной функции.
- 3. Переход к случаю зависимости
- 4. Теорема о неявной функции.
- § 6. Некоторые следствия теоремы о неявной функции
- 2. Локальное приведение гладкого отображения к каноническому виду.
- 3. Зависимость функций
- 4. Локальное разложение диффеоморфизма в композицию простейших.
- 5. Лемма Морса.
- § 7. Поверхность в R^n и теория условного экстремума
- 2. Касательное пространство.
- 3. Условный экстремум
- НЕКОТОРЫЕ ЗАДАЧИ КОЛЛОКВИУМОВ
- ВОПРОСЫ К ЭКЗАМЕНУ
- ЛИТЕРАТУРА