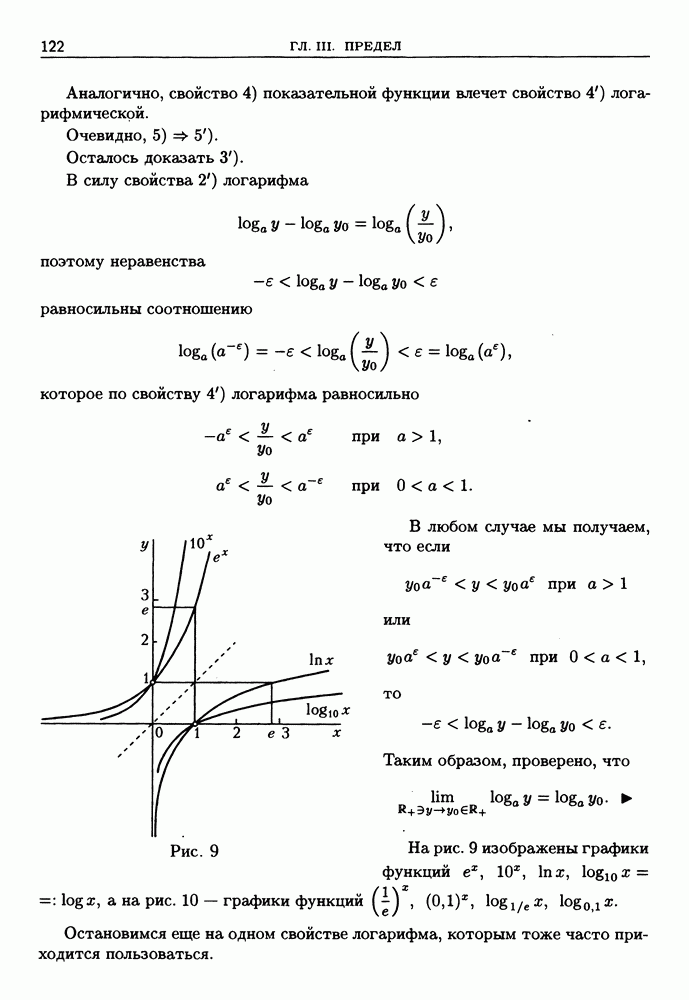
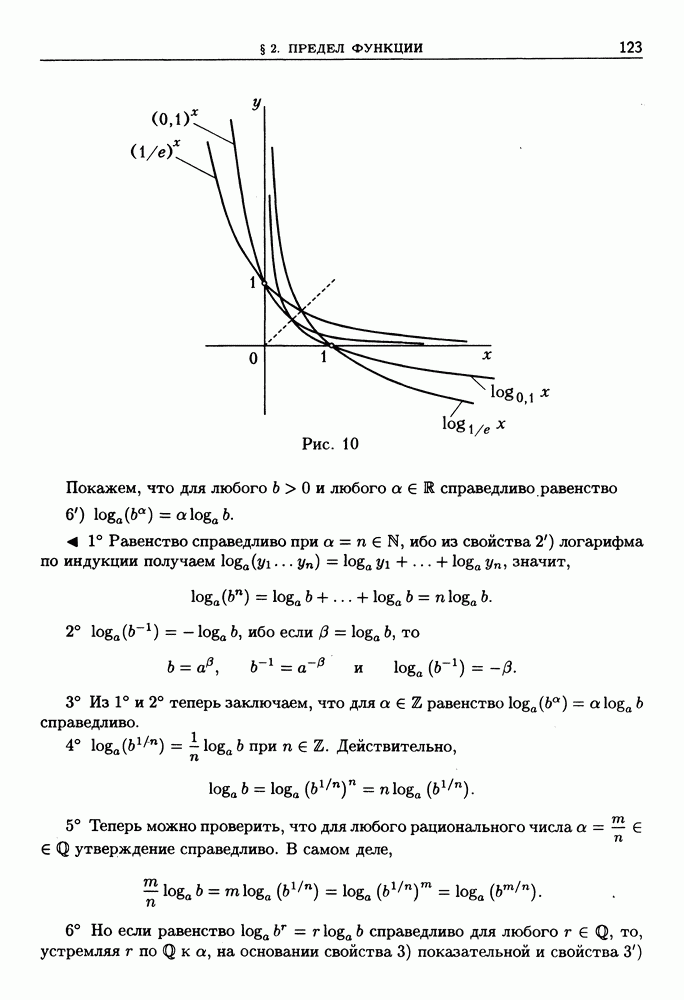
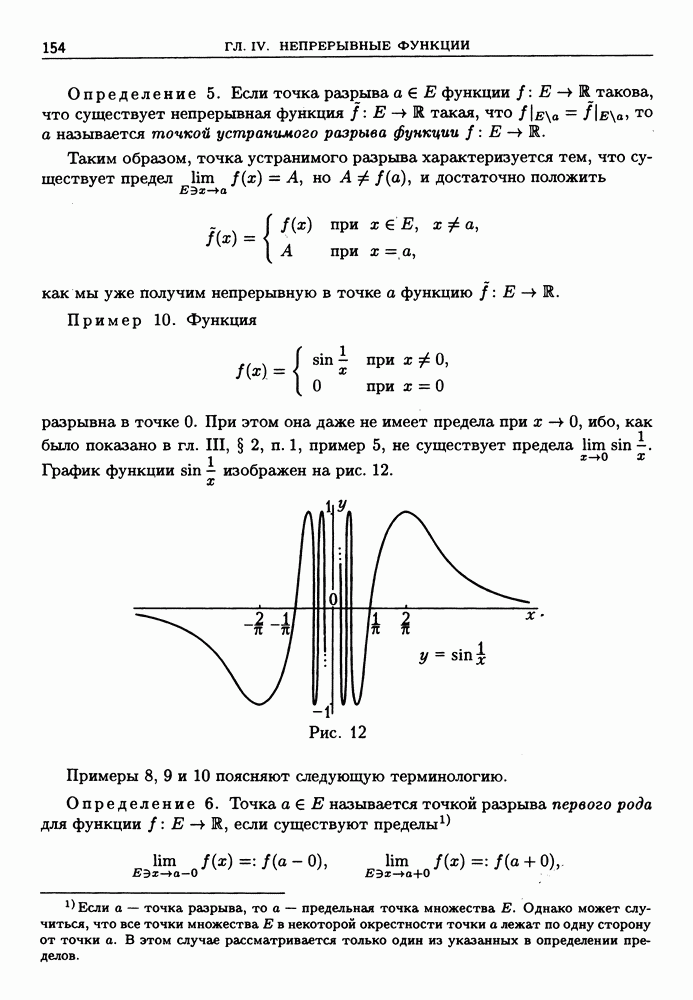
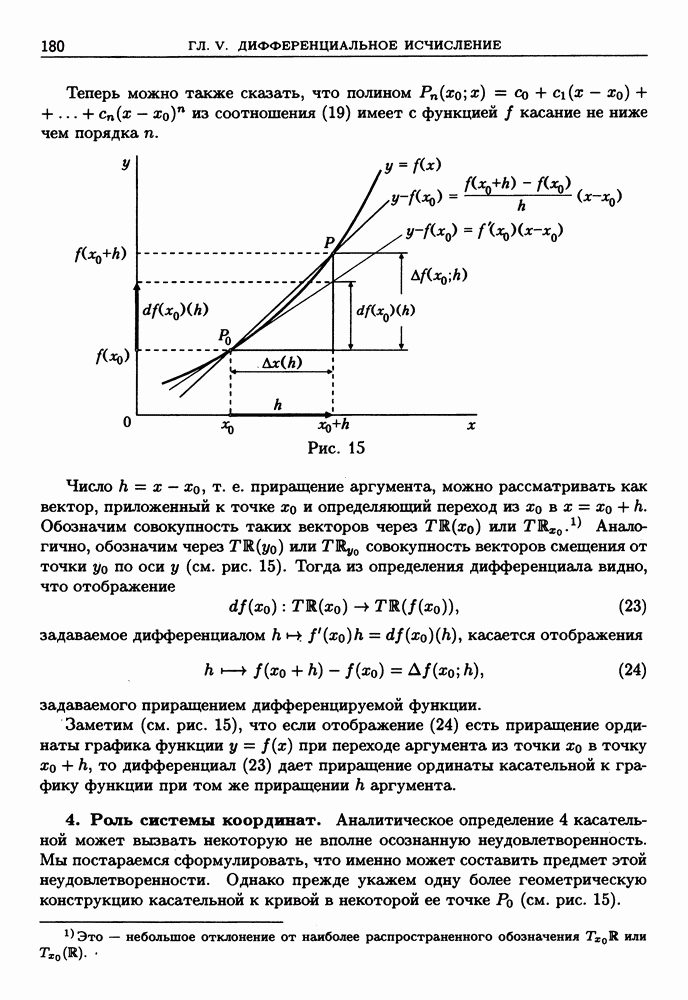
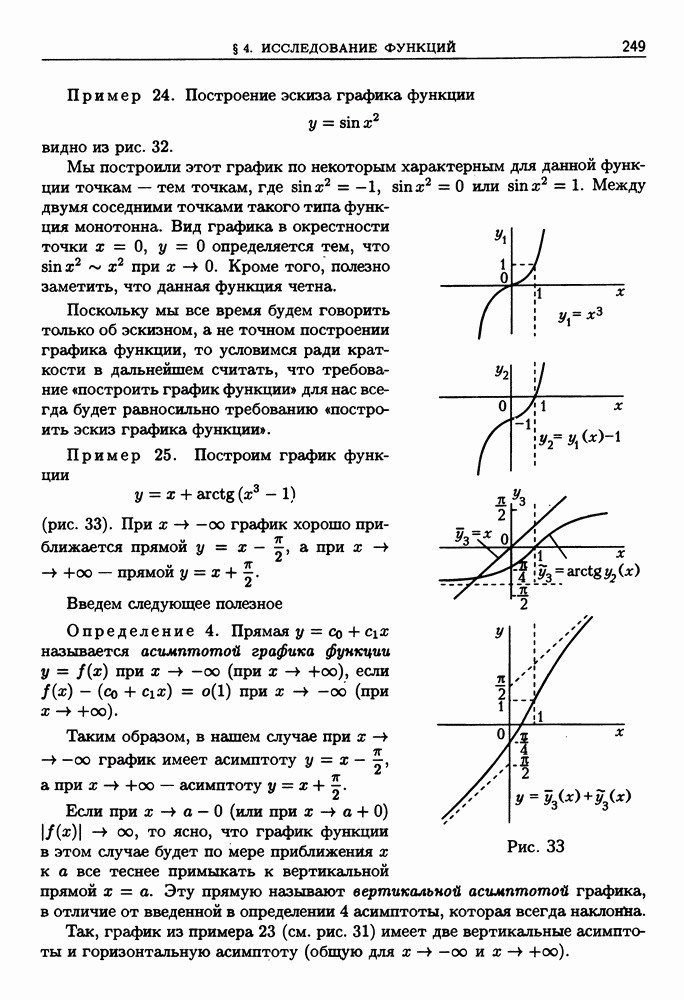
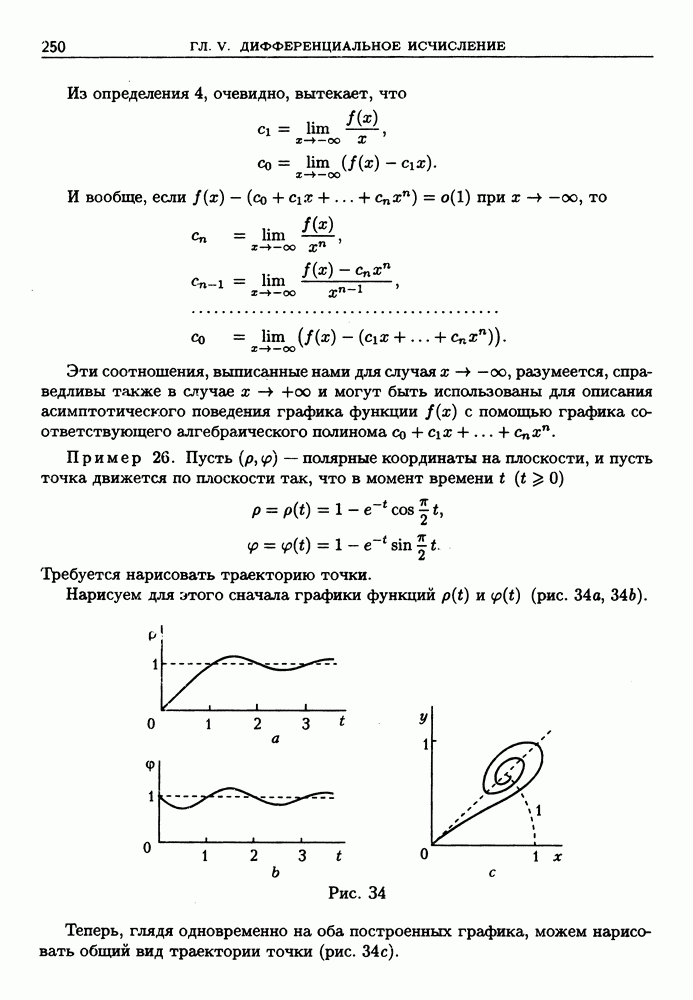
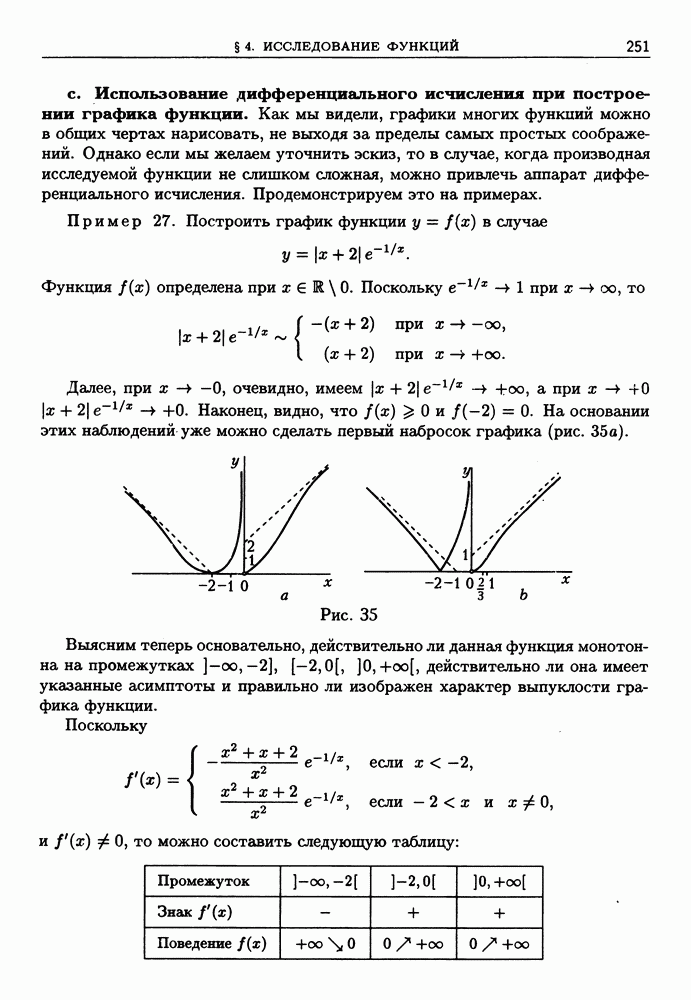
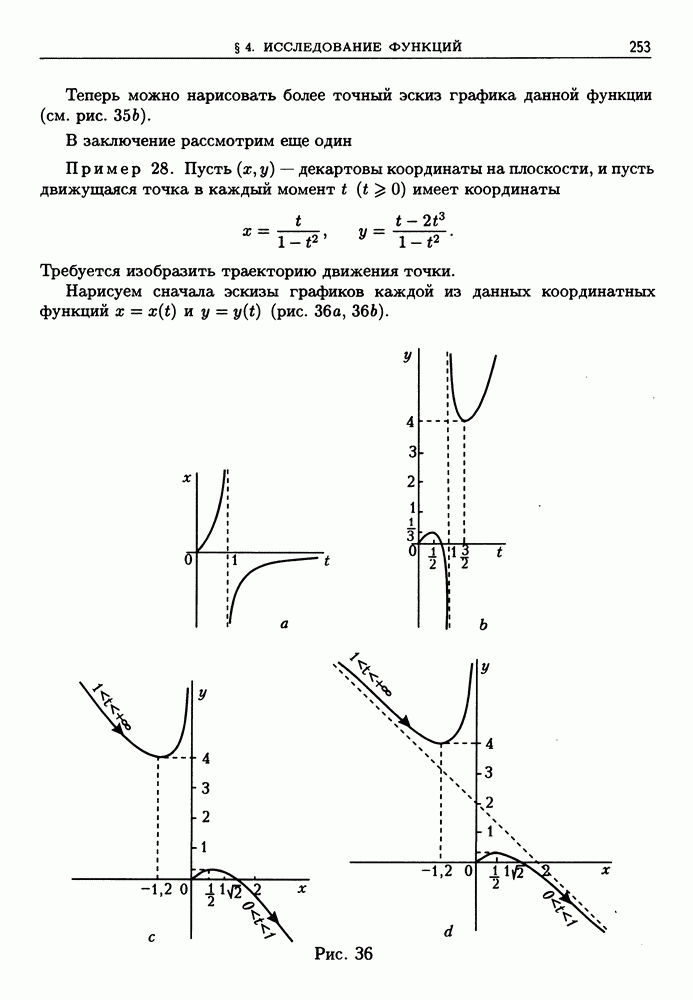
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Достаточное условие дифференцируемости функции многих переменных
Теорема 2. Пусть  — функция, определенная в окрестности
— функция, определенная в окрестности  точки
точки 
Если функция  имеет в каждой точке окрестности
имеет в каждой точке окрестности  все частные производные
все частные производные  непрерывности в точке х следует дифференцируемость функции
непрерывности в точке х следует дифференцируемость функции  в этой точке.
в этой точке.
Без ограничения общности будем считать, что  является шаром
является шаром  . Тогда вместе с точками
. Тогда вместе с точками  области
области  должны принадлежать также точки
должны принадлежать также точки  и соединяющие их отрезки. Воспользуемся этим, применяя в следующей выкладке теорему Лагранжа для функций одной переменной:
и соединяющие их отрезки. Воспользуемся этим, применяя в следующей выкладке теорему Лагранжа для функций одной переменной:

Пока мы воспользовались лишь наличием у функции  в области
в области  частных производных по каждой из переменных.
частных производных по каждой из переменных.
Теперь воспользуемся их непрерывностью в точке х. Продолжая предыдущую выкладку, получаем, что

где величины  в силу непрерывности частных производных в точке х стремятся к нулю при
в силу непрерывности частных производных в точке х стремятся к нулю при 
Но это означает, что

Из теоремы 2 следует, что если частные производные функции  непрерывны в области Если то функция дифференцируема в любой точке этой области.
непрерывны в области Если то функция дифференцируема в любой точке этой области.
Условимся в дальнейшем через  или, проще, через
или, проще, через  обозначать множество функций, имеющих в области
обозначать множество функций, имеющих в области  непрерывные частные производные.
непрерывные частные производные.
3. Частные производные высшего порядка. Если функция  , определенная в некоторой области Если имеет частную производную по одной из переменных
, определенная в некоторой области Если имеет частную производную по одной из переменных  то эта частная производная вновь является некоторой функцией
то эта частная производная вновь является некоторой функцией  , которая в свою очередь может иметь частную производную
, которая в свою очередь может иметь частную производную  по некоторой переменной
по некоторой переменной 
Функция  называется второй производной от функции
называется второй производной от функции  по переменным
по переменным  и обозначается одним из символов
и обозначается одним из символов

Порядок индексов указывает, в каком порядке производится дифференцирование по соответствующим переменным.
Мы определили частные производные второго порядка.
Если определена частная производная

порядка  то по индукции определяем частную производную порядка к
то по индукции определяем частную производную порядка к  соотношением
соотношением

Здесь возникает специфический для случая функций многих переменных вопрос о том, влияет ли порядок дифференцирований на вычисляемую частную производную.
Теорема 3. Если функция  имеет в области
имеет в области  частные производные
частные производные

то в любой точке  в которой обе эти производные непрерывны, их значения совпадают.
в которой обе эти производные непрерывны, их значения совпадают.
Пусть  — точка, в которой обе функции
— точка, в которой обе функции  непрерывны. Дальнейшие рассмотрения будем проводить в некотором шаре
непрерывны. Дальнейшие рассмотрения будем проводить в некотором шаре  являющемся выпуклой окрестностью точки
являющемся выпуклой окрестностью точки  Мы хотим проверить, что
Мы хотим проверить, что

Поскольку во всех дальнейших выкладках меняться будут только переменные  то мы для сокращения записи предположим, что
то мы для сокращения записи предположим, что  есть функция
есть функция
двух переменных  и нам надо проверить, что
и нам надо проверить, что

если в точке  обе указанные функции непрерывны.
обе указанные функции непрерывны.
Рассмотрим вспомогательную функцию

где смещение  предполагается достаточно малым, а именно таким, что
предполагается достаточно малым, а именно таким, что 
Если  рассмотреть как разность
рассмотреть как разность

где  то по теореме Лагранжа найдем, что
то по теореме Лагранжа найдем, что

Применяя к последней разности вновь теорему Лагранжа, найдем, что

Если теперь  представить в виде разности
представить в виде разности

где  то аналогично найдем, что
то аналогично найдем, что

Сравнивая равенства (2) и (3), заключаем, что

где  Воспользовавшись непрерывностью рассматриваемых частных производных в точке
Воспользовавшись непрерывностью рассматриваемых частных производных в точке  при
при  из (4) получаем нужное равенство
из (4) получаем нужное равенство

Заметим, что без каких-либо дополнительных предположений, вообще говоря, нельзя утверждать, что справедливо равенство  если обе указанные частные производные определены в точке
если обе указанные частные производные определены в точке  (см. задачу 2 в конце параграфа).
(см. задачу 2 в конце параграфа).
Договоримся в дальнейшем через  или
или  обозначать множество функций
обозначать множество функций  , все частные производные которых до порядка к включительно определены и непрерывны в области Если
, все частные производные которых до порядка к включительно определены и непрерывны в области Если
В качестве следствия теоремы 3 получаем
Утверждение 1. Если  то значение
то значение  частной производной не зависит от порядка
частной производной не зависит от порядка  дифференцирования, т. е. остается тем же при любой перестановке индексов
дифференцирования, т. е. остается тем же при любой перестановке индексов 
В случае  это утверждение содержится в теореме 3.
это утверждение содержится в теореме 3.
Предположим, что утверждение справедливо до порядка  включительно. Покажем, что тогда оно справедливо и для порядка
включительно. Покажем, что тогда оно справедливо и для порядка 
Но  Индексы
Индексы  по предположению индукции можно переставлять, не меняя функции
по предположению индукции можно переставлять, не меняя функции  следовательно, и функции
следовательно, и функции  Поэтому достаточно проверить, что можно переставлять также, например, индексы
Поэтому достаточно проверить, что можно переставлять также, например, индексы  не меняя значения производной
не меняя значения производной 
Поскольку

то возможность этой перестановки непосредственно вытекает из теоремы 3. В силу принципа индукции утверждение 1 доказано.
Пример 1. Пусть  — функция класса Пусть
— функция класса Пусть  таково, что отрезок
таково, что отрезок  содержится в области
содержится в области  Покажем, что функция
Покажем, что функция

определенная на отрезке [0,1], принадлежит классу  и найдем ее производную по
и найдем ее производную по  порядка к.
порядка к.
Имеем

Эти соотношения можно записать в форме действия оператора  на функцию:
на функцию:

По индукции получаем

(справа имеется в виду суммирование по всевозможным наборам  из А; индексов, каждый из которых принимает значения 1 или 2).
из А; индексов, каждый из которых принимает значения 1 или 2).
Пример 2. Если  то, в предположении, что Если для функции
то, в предположении, что Если для функции  определенной на отрезке [0,1], получаем
определенной на отрезке [0,1], получаем

где справа имеется в виду суммирование по всевозможным наборам индексов  каждый из которых может принимать любое значение от 1 до
каждый из которых может принимать любое значение от 1 до  включительно.
включительно.
Формулу (5) можно записать также в виде

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
- § 1. Логическая символика
- § 2. Множество и элементарные операции над множествами
- 2. Отношение включения.
- 3. Простейшие операции над множествами.
- Упражнения
- § 3. Функция
- 2. Простейшая классификация отображений.
- 3. Композиция функций и взаимно обратные отображения.
- 4. Функция как отношение. График функции.
- § 4. Некоторые дополнения
- 2. Об аксиоматике теории множеств.
- 3. Замечания о структуре математических высказываний и записи их на языке теории множеств.
- Упражнения
- ГЛАВА II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
- § 1. Аксиоматика и некоторые общие свойства множества действительных чисел
- 2. Некоторые общие алгебраические свойства действительных чисел.
- 3. Аксиома полноты и существование верхней (нижней) грани числового множества
- § 2. Важнейшие классы действительных чисел и вычислительные аспекты операций с действительными числами
- 2. Рациональные и иррациональные числа
- 3. Принцип Архимеда.
- 4. Геометрическая интерпретация множества действительных чисел и вычислительные аспекты операций с действительными числами
- Задачи и упражнения
- § 3. Основные леммы, связанные с полнотой множества действительных чисел
- 2. Лемма о конечном покрытии (принцип Бореля — Лебега)
- 3. Лемма о предельной точке (принцип Больцано—Вейерштрасса).
- Задачи и упражнения
- § 4. Счетные и несчетные множества
- 2. Мощность континуума
- Задачи и упражнения
- ГЛАВА III. ПРЕДЕЛ
- 2. Свойства предела последовательности
- 3. Вопросы существования предела последовательности
- 4. Начальные сведения о рядах
- § 2. Предел функции
- 2. Свойства предела функции.
- 3. Общее определение предела функции (предел по базе).
- 4. Вопросы существования предела функции
- ГЛАВА IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 2. Точки разрыва.
- § 2. Свойства непрерывных функций
- 2. Глобальные свойства непрерывных функций.
- ГЛАВА V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- 2. Функция, дифференцируемая в точке.
- 3. Касательная; геометрический смысл производной и дифференциала.
- 4. Роль системы координат.
- 5. Некоторые примеры
- Задачи и упражнения
- § 2. Основные правила дифференцирования
- 2. Дифференцирование композиции функций
- 3. Дифференцирование обратной функции
- 4. Таблица производных основных элементарных функций.
- 5. Дифференцирование простейшей неявно заданной функции.
- 6. Производные высших порядков.
- § 3. Основные теоремы дифференциального исчисления
- 2. Теоремы Лагранжа и Коши о конечном приращении.
- 3. Формула Тейлора.
- § 4. Исследование функций методами дифференциального исчисления
- 2. Условия внутреннего экстремума функции.
- 3. Условия выпуклости функции
- 4. Правило Лопиталя.
- 5. Построение графика функции.
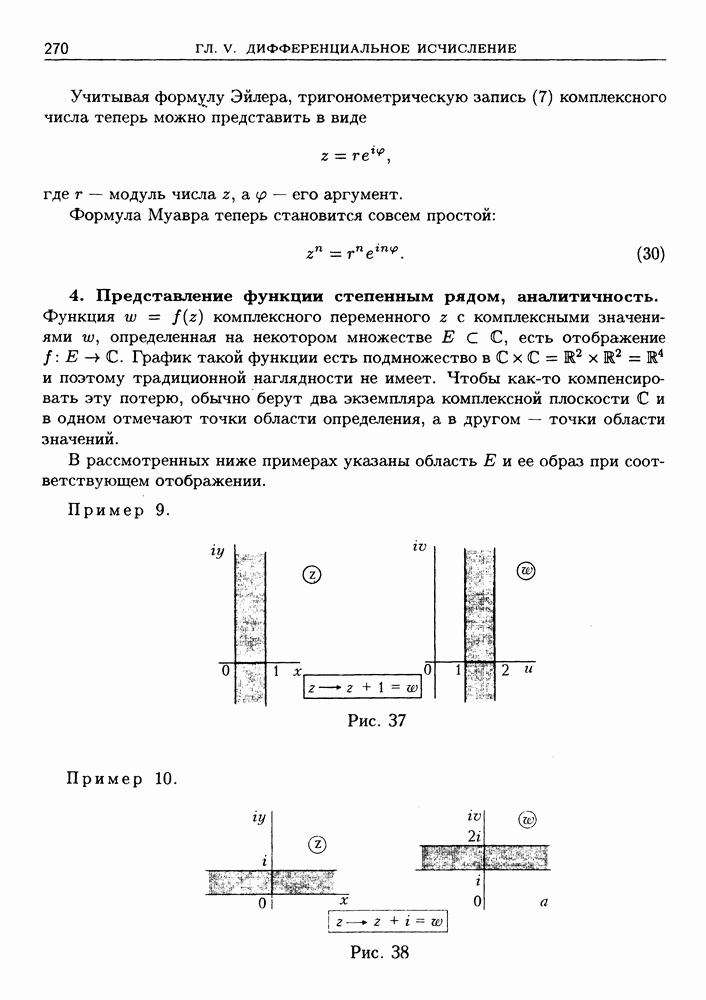
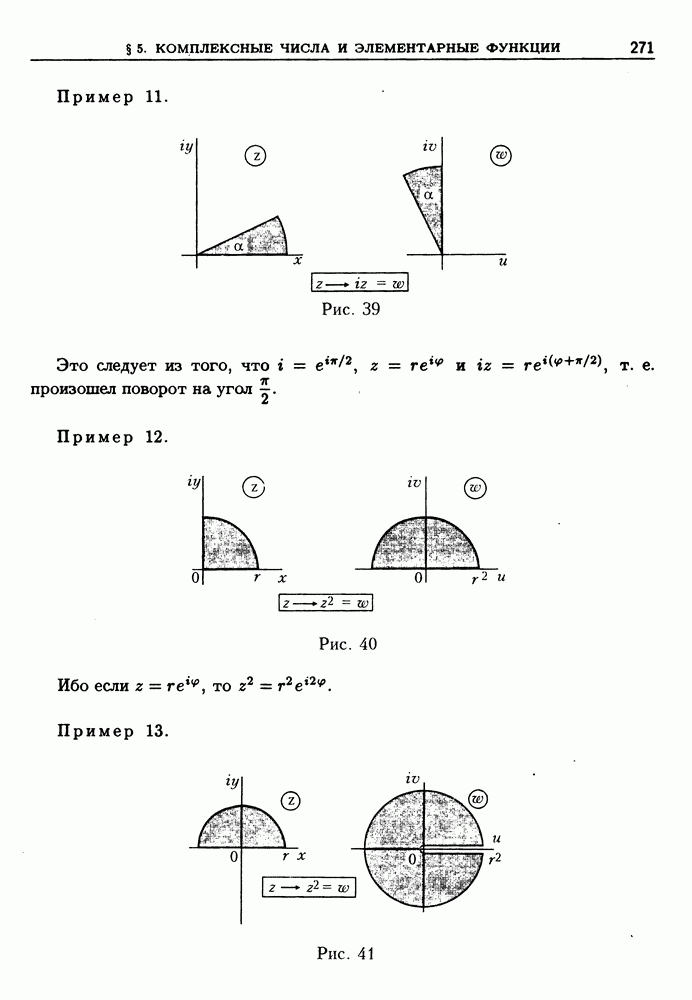
- § 5. Комплексные числа и взаимосвязь элементарных функций
- 2. Сходимость в С и ряды с комплексными членами.
- 3. Формула Эйлера и взаимосвязь элементарных функций.
- 4. Представление функции степенным рядом, аналитичность.
- 5. Алгебраическая замкнутость поля С комплексных чисел.
- § 6. Некоторые примеры использования дифференциального исчисления в задачах естествознания
- 2. Барометрическая формула.
- 3. Радиоактивный распад, цепная реакция и атомный котел.
- 4. Падение тел в атмосфере.
- 5. Еще раз о числе e и функции exp(x).
- 6. Колебания.
- § 7. Первообразная
- 2. Основные общие приемы отыскания первообразной.
- 3. Первообразные рациональных функций.
- 4. Первообразные вида …
- 5. Первообразные вида …
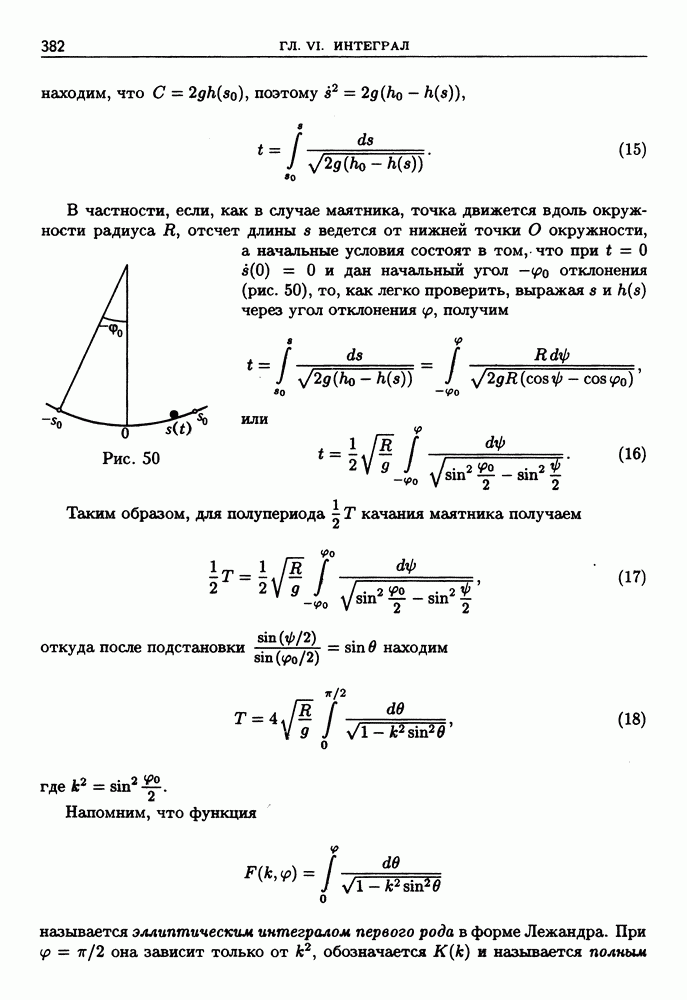
- ГЛАВА VI. ИНТЕГРАЛ
- § 1. Определение интеграла и описание множества интегрируемых функций
- 2. Определение интеграла Римана
- 3. Множество интегрируемых функций.
- § 2. Линейность, аддитивность и монотонность интеграла
- 2. Интеграл как аддитивная функция отрезка интегрирования.
- 3. Оценка интеграла, монотонность интеграла, теоремы о среднем
- § 3. Интеграл и производная
- 2. Формула Ньютона—Лейбница
- 3. Интегрирование по частям в определенном интеграле и формула Тейлора
- 4. Замена переменной в интеграле.
- 5. Некоторые примеры.
- § 4. Некоторые приложения интеграла
- 2. Длина пути.
- 3. Площадь криволинейной трапеции.
- 4. Объем тела вращения.
- 5. Работа и энергия.
- § 5. Несобственный интеграл
- 2. Исследование сходимости несобственного интеграла
- 3. Несобственные интегралы с несколькими особенностями.
- ГЛАВА VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ, ИХ ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
- 2. Открытые и замкнутые множества в R^m
- 3. Компакты в R^m
- § 2. Предел и непрерывность функции многих переменных
- 2. Непрерывность функции многих переменных и свойства непрерывных функций.
- ГЛАВА VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- 2. Линейные отображения L : R^m -> R^n.
- 3. Норма в R^m.
- 4. Евклидова структура в R^m.
- § 2. Дифференциал функции многих переменных
- 2. Дифференциал и частные производные вещественнозначной функции.
- 3. Координатное представление дифференциала отображения. Матрица Якоби.
- 4. Непрерывность, частные производные и дифференцируемость функции в точке.
- § 3. Основные законы дифференцирования
- 2. Дифференцирование композиции отображений
- 3. Дифференцирование обратного отображения
- § 4. Основные факты дифференциального исчисления вещественнозначных функций многих переменных
- 2. Достаточное условие дифференцируемости функции многих переменных
- 4. Формула Тейлора
- 5. Экстремумы функций многих переменных.
- 6. Некоторые геометрические образы, связанные с функциями многих переменных
- § 5. Теорема о неявной функции
- 2. Простейший вариант теоремы о неявной функции.
- 3. Переход к случаю зависимости
- 4. Теорема о неявной функции.
- § 6. Некоторые следствия теоремы о неявной функции
- 2. Локальное приведение гладкого отображения к каноническому виду.
- 3. Зависимость функций
- 4. Локальное разложение диффеоморфизма в композицию простейших.
- 5. Лемма Морса.
- § 7. Поверхность в R^n и теория условного экстремума
- 2. Касательное пространство.
- 3. Условный экстремум
- НЕКОТОРЫЕ ЗАДАЧИ КОЛЛОКВИУМОВ
- ВОПРОСЫ К ЭКЗАМЕНУ
- ЛИТЕРАТУРА