| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Рациональные и иррациональные числа
а. Целые числа
Определение 3. Объединение множества натуральных чисел, множества чисел, противоположных натуральным числам, и нуля называется множеством целых чисел и обозначается символом 
Поскольку, как уже было доказано, сложение и умножение натуральных чисел не выводят за пределы  то эти же операции над целыми числами не выводят за пределы множества
то эти же операции над целыми числами не выводят за пределы множества 
Действительно, если  то либо одно из этих чисел равно нулю и тогда сумма
то либо одно из этих чисел равно нулю и тогда сумма  равна другому числу, т. е.
равна другому числу, т. е.  произведение
произведение  либо оба числа отличны от нуля. В последнем случае либо
либо оба числа отличны от нуля. В последнем случае либо  и тогда
и тогда  либо
либо  и тогда
и тогда  либо
либо  и тогда
и тогда  либо, наконец,
либо, наконец,  и тогда
и тогда  и снова
и снова 
Таким образом,  есть абаяева группа по отношению к операции сложения. По отношению к операции умножения множество
есть абаяева группа по отношению к операции сложения. По отношению к операции умножения множество  и даже
и даже  не является группой, поскольку числа, обратные целым, не лежат в
не является группой, поскольку числа, обратные целым, не лежат в  (кроме числа, обратного единице и минус единице).
(кроме числа, обратного единице и минус единице).
Действительно, если  то, считал сначала
то, считал сначала  имеем
имеем  и, поскольку
и, поскольку  должно быть
должно быть  в предыдущем параграфе следствия аксиом порядка). Таким образом,
в предыдущем параграфе следствия аксиом порядка). Таким образом,  Случай, когда
Случай, когда  — отрицательное целое число, отличное от — 1, непосредственно сводится к уже разобранному.
— отрицательное целое число, отличное от — 1, непосредственно сводится к уже разобранному.
В том случае, когда для чисел  число
число  т. е. когда
т. е. когда  где
где  говорят, что целое число
говорят, что целое число  делится на целое число
делится на целое число  или кратно
или кратно  или что
или что  есть делитель
есть делитель 
Делимость целых чисел путем надлежащих изменений знаков, т. е. домножением на — 1, если в этом есть необходимость, немедленно приводится к делимости соответствующих натуральных чисел, в рамках которых она и изучается в арифметике.
Напомним без доказательства так называемую основную теорему арифметики, которой при рассмотрении некоторых примеров мы будем пользоваться.
Число  называется простым, если в
называется простым, если в  него нет делителей, отличных от 1 и
него нет делителей, отличных от 1 и  .
.
Основная теорема арифметики. Каждое натуральное число допускает и притом единственное (с точностью до порядка сомножителей) представление в виде произведения

где  — простые числа.
— простые числа.
Числа  называются взаимно простыми, если у них нет общих делителей, отличных от
называются взаимно простыми, если у них нет общих делителей, отличных от 
Из приведенной теоремы, в частности, видно, что если произведение  взаимно простых чисел
взаимно простых чисел  делится на простое число
делится на простое число  , то одно из чисел
, то одно из чисел  также делится на
также делится на  .
.
b. Рациональные числа
Определение 4. Числа вида  где
где  называются рациональными.
называются рациональными.
Множество рациональных чисел обозначается знаком 
Таким образом, упорядоченная пара  целых чисел определяет рациональное число
целых чисел определяет рациональное число  если
если 
Число  записывают также в виде отношения тип или так называемой рациональной дроби
записывают также в виде отношения тип или так называемой рациональной дроби 
Правила действий с рациональными числами, относящиеся к такой форме их представления дробями, изучавшиеся в школе, немедленно вытекают из
определения рационального числа и аксиом действительных чисел. В частности, «от умножения числителя и знаменателя дроби на одно и то же отличное от нуля целое число величина дроби не изменяется», т. е. дроби  и
и
— представляют одно и то же рациональное число. В самом деле, поскольку 
Таким образом, различные упорядоченные пары  задают одно и то же рациональное число. Следовательно, после соответствующих сокращений любое рациональное число можно задать упорядоченной парой взаимно простых целых чисел.
задают одно и то же рациональное число. Следовательно, после соответствующих сокращений любое рациональное число можно задать упорядоченной парой взаимно простых целых чисел.
С другой стороны, если пары (7711,721) и (7712,712) задают одно и то же рациональное число, т. е.  то
то  и если, например,
и если, например,  взаимно просты, то в силу упомянутого следствия основной теоремы арифметики
взаимно просты, то в силу упомянутого следствия основной теоремы арифметики 
Мы показали, таким образом, что две упорядоченные пары  задают одно и то же рациональное число тогда и только тогда, когда они пропорциональны, т. е. существует число к
задают одно и то же рациональное число тогда и только тогда, когда они пропорциональны, т. е. существует число к  такое, что, например,
такое, что, например, 
с. Иррациональные числа
Определение 5. Действительные числа, не являющиеся рациональными, называются иррациональными.
Классическим примером иррационального действительного числа является  , т. е. число
, т. е. число  такое, что
такое, что  Иррациональность
Иррациональность  в силу теоремы Пифагора эквивалентна утверждению о несоизмеримости диагонали и стороны квадрата.
в силу теоремы Пифагора эквивалентна утверждению о несоизмеримости диагонали и стороны квадрата.
Итак, проверим, во-первых, что существует положительное действительное число  , квадрат которого равен двум, и, во-вторых, что
, квадрат которого равен двум, и, во-вторых, что 
Пусть X и  — множества положительных действительных чисел такие, что
— множества положительных действительных чисел такие, что  Поскольку
Поскольку  то I и
то I и  - непустые множества.
- непустые множества.
Далее, поскольку для положительных  то любой элемент
то любой элемент  меньше любого элемента
меньше любого элемента  По аксиоме полноты существует число
По аксиоме полноты существует число  такое, что
такое, что  для
для 
Покажем, что 
Если бы было  то, например, квадрат числа
то, например, квадрат числа  большего чем
большего чем  , был бы меньше 2. Действительно, ведь
, был бы меньше 2. Действительно, ведь  поэтому
поэтому  Значит,
Значит,

Следовательно,  что несовместимо с неравенством
что несовместимо с неравенством  для любого элемента
для любого элемента 
Если бы было  то, например, квадрат числа
то, например, квадрат числа  , меньшего чем 5, был бы больше 2. Действительно, ведь
, меньшего чем 5, был бы больше 2. Действительно, ведь  , поэтому
, поэтому  или
или  Отсюда
Отсюда

и мы вступаем в противоречие с тем, что  ограничивает множество
ограничивает множество  снизу.
снизу.
Таким образом, реализуется только одна оставшаяся возможность: 
Покажем, наконец, что  Предположим, что
Предположим, что  и пусть
и пусть  несократимое представление
несократимое представление  Тогда
Тогда  следовательно,
следовательно,  значит, и
значит, и  делится на 2. Но если
делится на 2. Но если  то
то  и по той же причине
и по той же причине  должно делиться на 2, что противоречит несократимости дроби
должно делиться на 2, что противоречит несократимости дроби 
Сейчас мы трудились над тем, чтобы доказать существование иррациональных чисел. Вскоре мы увидим, что в некотором смысле почти все действительные числа иррациональны. Будет показано, что мощность множества иррациональных чисел больше мощности множества всех рациональных чисел и совпадает с мощностью множества всех действительных чисел.
Среди иррациональных чисел выделяют еще так называемые алгебраические иррациональности и трансцендентные числа.
Вещественное число называется алгебраическим, если оно является корнем некоторого алгебраического уравнения

с рациональными (или, что эквивалентно, с целыми) коэффициентами.
В противном случае число называется трансцендентным.
Мы увидим, что мощность множества алгебраических чисел такая же, как мощность множества рациональных чисел, а мощность множества трансцендентных чисел такая же, как мощность всех действительных чисел; поэтому на первый взгляд кажутся парадоксальными и неестественными трудности в предъявлении конкретного трансцендентного числа, точнее, в доказательстве его трансцендентности.
Так, например, только в 1882 г. было доказано, что классическое геометрическое число  является трансцендентным, а одна из знаменитых проблем
является трансцендентным, а одна из знаменитых проблем
Гильберта состояла в том, чтобы доказать трансцендентность числа а, где а — алгебраическое,  - алгебраическое иррациональное число (например,
- алгебраическое иррациональное число (например,  ).
).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
- § 1. Логическая символика
- § 2. Множество и элементарные операции над множествами
- 2. Отношение включения.
- 3. Простейшие операции над множествами.
- Упражнения
- § 3. Функция
- 2. Простейшая классификация отображений.
- 3. Композиция функций и взаимно обратные отображения.
- 4. Функция как отношение. График функции.
- § 4. Некоторые дополнения
- 2. Об аксиоматике теории множеств.
- 3. Замечания о структуре математических высказываний и записи их на языке теории множеств.
- Упражнения
- ГЛАВА II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
- § 1. Аксиоматика и некоторые общие свойства множества действительных чисел
- 2. Некоторые общие алгебраические свойства действительных чисел.
- 3. Аксиома полноты и существование верхней (нижней) грани числового множества
- § 2. Важнейшие классы действительных чисел и вычислительные аспекты операций с действительными числами
- 2. Рациональные и иррациональные числа
- 3. Принцип Архимеда.
- 4. Геометрическая интерпретация множества действительных чисел и вычислительные аспекты операций с действительными числами
- Задачи и упражнения
- § 3. Основные леммы, связанные с полнотой множества действительных чисел
- 2. Лемма о конечном покрытии (принцип Бореля — Лебега)
- 3. Лемма о предельной точке (принцип Больцано—Вейерштрасса).
- Задачи и упражнения
- § 4. Счетные и несчетные множества
- 2. Мощность континуума
- Задачи и упражнения
- ГЛАВА III. ПРЕДЕЛ
- 2. Свойства предела последовательности
- 3. Вопросы существования предела последовательности
- 4. Начальные сведения о рядах
- § 2. Предел функции
- 2. Свойства предела функции.
- 3. Общее определение предела функции (предел по базе).
- 4. Вопросы существования предела функции
- ГЛАВА IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 2. Точки разрыва.
- § 2. Свойства непрерывных функций
- 2. Глобальные свойства непрерывных функций.
- ГЛАВА V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- 2. Функция, дифференцируемая в точке.
- 3. Касательная; геометрический смысл производной и дифференциала.
- 4. Роль системы координат.
- 5. Некоторые примеры
- Задачи и упражнения
- § 2. Основные правила дифференцирования
- 2. Дифференцирование композиции функций
- 3. Дифференцирование обратной функции
- 4. Таблица производных основных элементарных функций.
- 5. Дифференцирование простейшей неявно заданной функции.
- 6. Производные высших порядков.
- § 3. Основные теоремы дифференциального исчисления
- 2. Теоремы Лагранжа и Коши о конечном приращении.
- 3. Формула Тейлора.
- § 4. Исследование функций методами дифференциального исчисления
- 2. Условия внутреннего экстремума функции.
- 3. Условия выпуклости функции
- 4. Правило Лопиталя.
- 5. Построение графика функции.
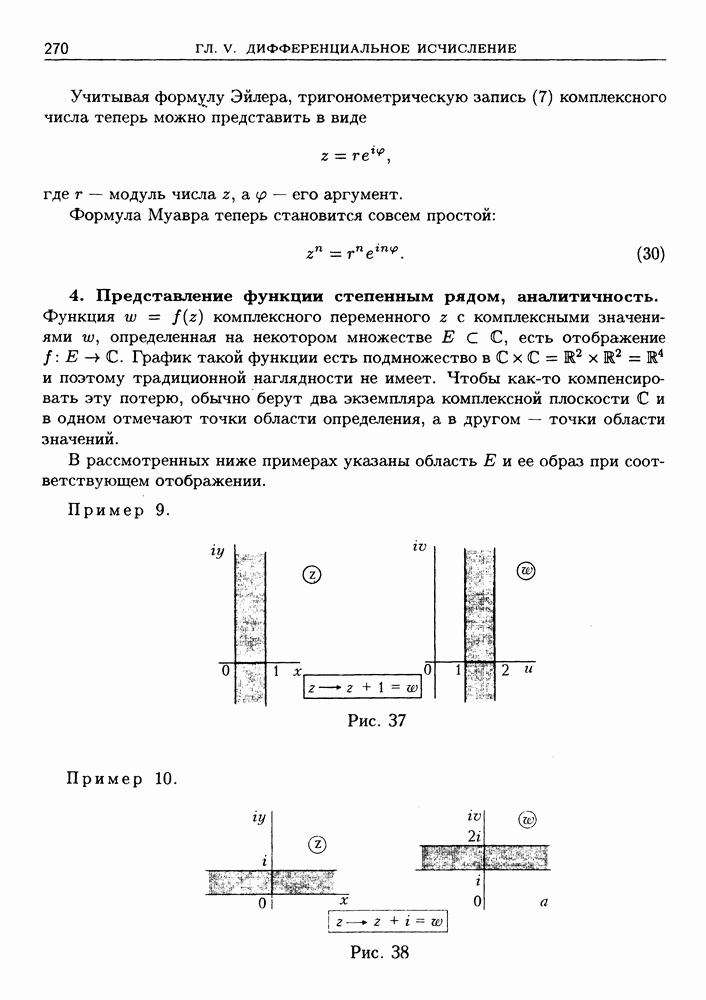
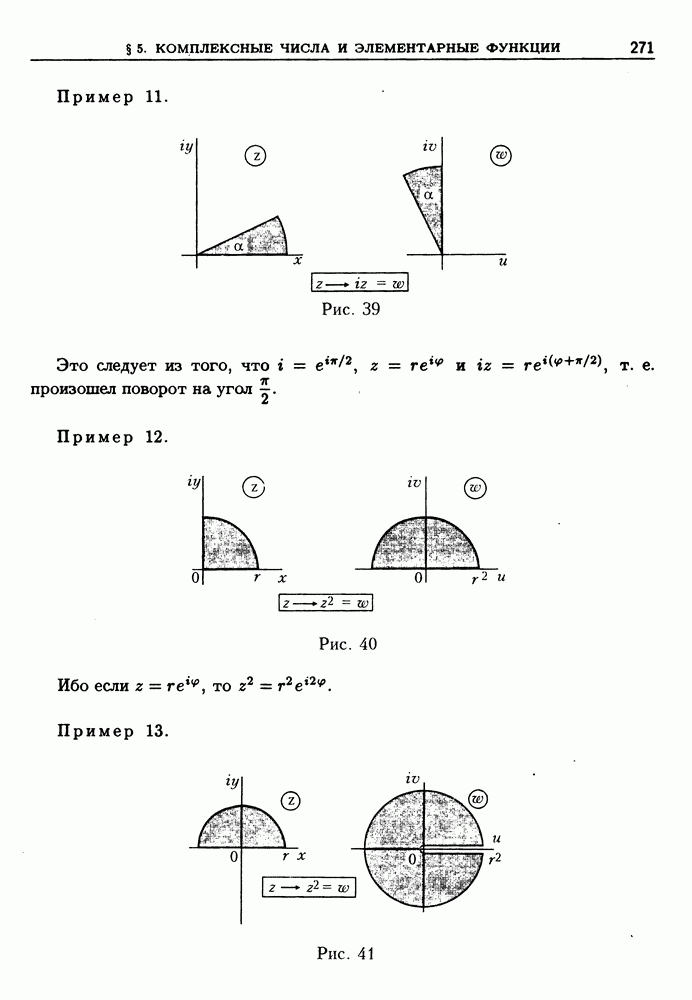
- § 5. Комплексные числа и взаимосвязь элементарных функций
- 2. Сходимость в С и ряды с комплексными членами.
- 3. Формула Эйлера и взаимосвязь элементарных функций.
- 4. Представление функции степенным рядом, аналитичность.
- 5. Алгебраическая замкнутость поля С комплексных чисел.
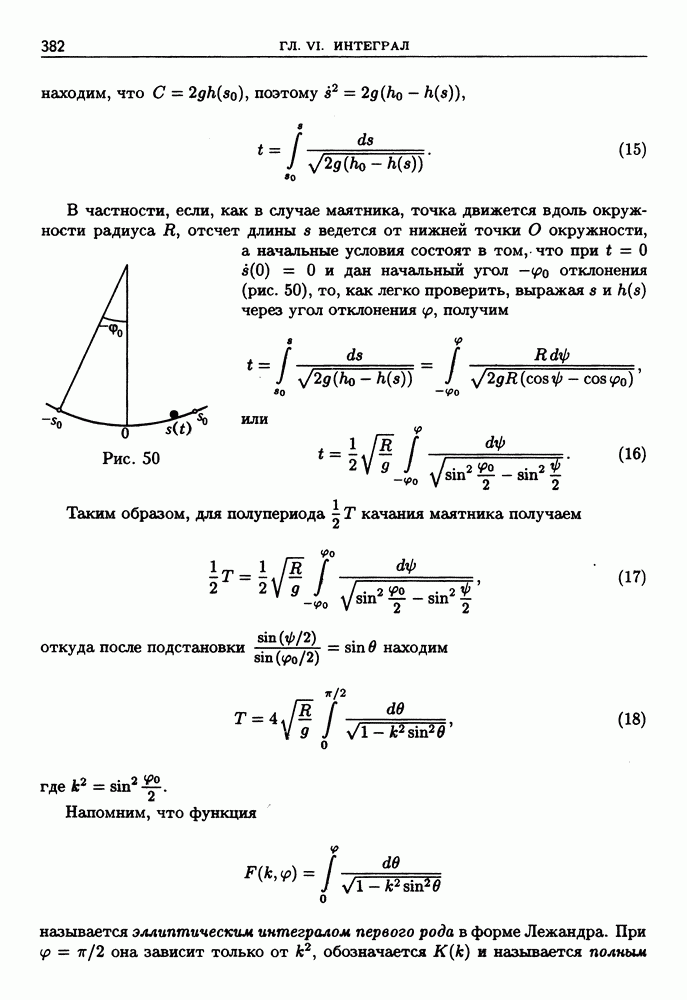
- § 6. Некоторые примеры использования дифференциального исчисления в задачах естествознания
- 2. Барометрическая формула.
- 3. Радиоактивный распад, цепная реакция и атомный котел.
- 4. Падение тел в атмосфере.
- 5. Еще раз о числе e и функции exp(x).
- 6. Колебания.
- § 7. Первообразная
- 2. Основные общие приемы отыскания первообразной.
- 3. Первообразные рациональных функций.
- 4. Первообразные вида …
- 5. Первообразные вида …
- ГЛАВА VI. ИНТЕГРАЛ
- § 1. Определение интеграла и описание множества интегрируемых функций
- 2. Определение интеграла Римана
- 3. Множество интегрируемых функций.
- § 2. Линейность, аддитивность и монотонность интеграла
- 2. Интеграл как аддитивная функция отрезка интегрирования.
- 3. Оценка интеграла, монотонность интеграла, теоремы о среднем
- § 3. Интеграл и производная
- 2. Формула Ньютона—Лейбница
- 3. Интегрирование по частям в определенном интеграле и формула Тейлора
- 4. Замена переменной в интеграле.
- 5. Некоторые примеры.
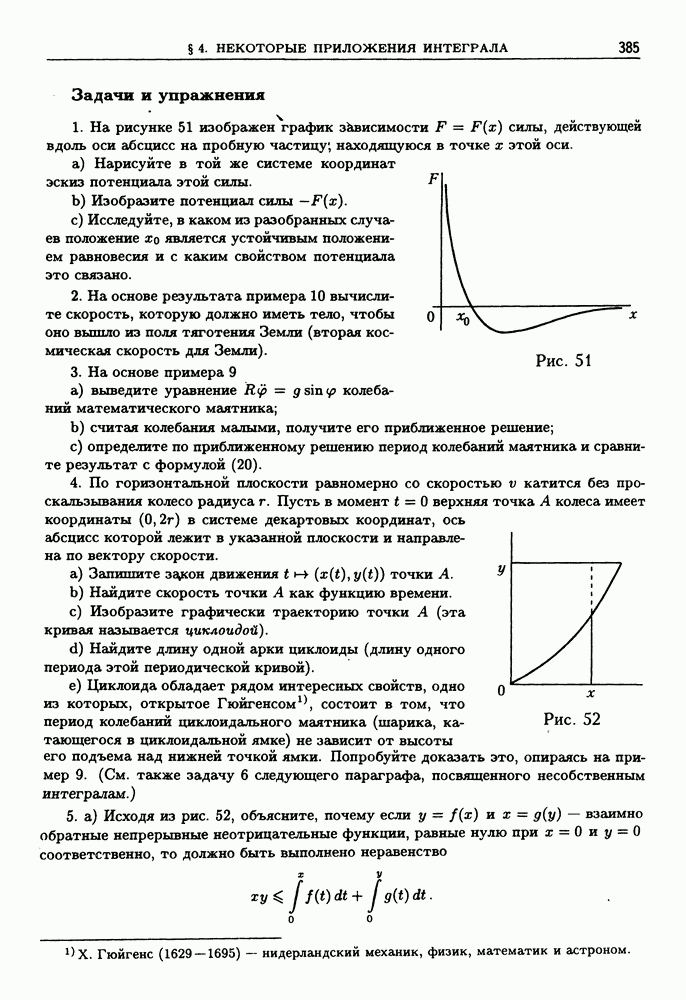
- § 4. Некоторые приложения интеграла
- 2. Длина пути.
- 3. Площадь криволинейной трапеции.
- 4. Объем тела вращения.
- 5. Работа и энергия.
- § 5. Несобственный интеграл
- 2. Исследование сходимости несобственного интеграла
- 3. Несобственные интегралы с несколькими особенностями.
- ГЛАВА VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ, ИХ ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
- 2. Открытые и замкнутые множества в R^m
- 3. Компакты в R^m
- § 2. Предел и непрерывность функции многих переменных
- 2. Непрерывность функции многих переменных и свойства непрерывных функций.
- ГЛАВА VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- 2. Линейные отображения L : R^m -> R^n.
- 3. Норма в R^m.
- 4. Евклидова структура в R^m.
- § 2. Дифференциал функции многих переменных
- 2. Дифференциал и частные производные вещественнозначной функции.
- 3. Координатное представление дифференциала отображения. Матрица Якоби.
- 4. Непрерывность, частные производные и дифференцируемость функции в точке.
- § 3. Основные законы дифференцирования
- 2. Дифференцирование композиции отображений
- 3. Дифференцирование обратного отображения
- § 4. Основные факты дифференциального исчисления вещественнозначных функций многих переменных
- 2. Достаточное условие дифференцируемости функции многих переменных
- 4. Формула Тейлора
- 5. Экстремумы функций многих переменных.
- 6. Некоторые геометрические образы, связанные с функциями многих переменных
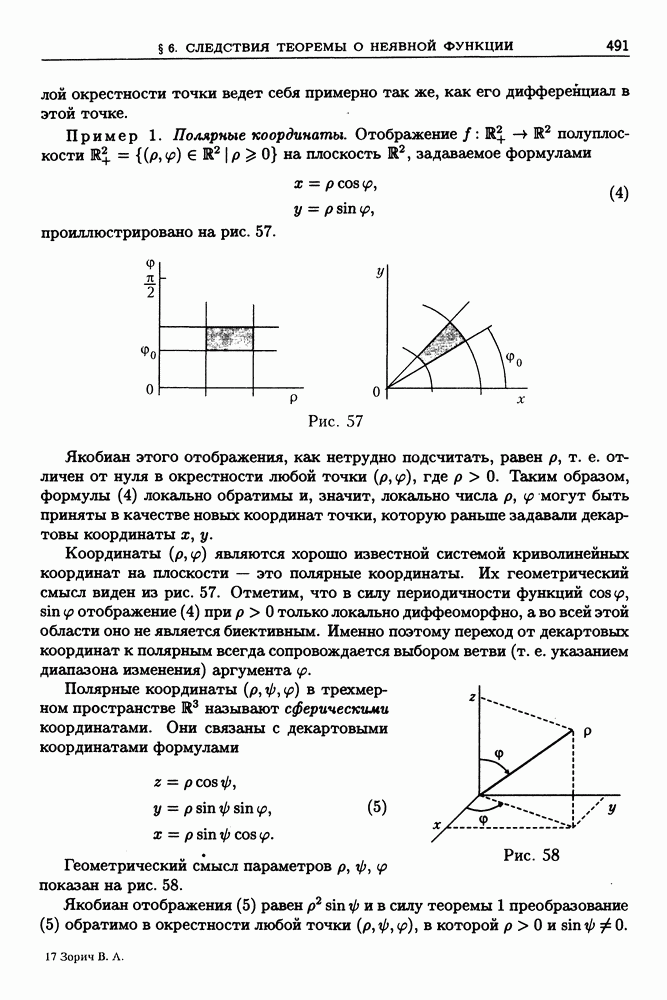
- § 5. Теорема о неявной функции
- 2. Простейший вариант теоремы о неявной функции.
- 3. Переход к случаю зависимости
- 4. Теорема о неявной функции.
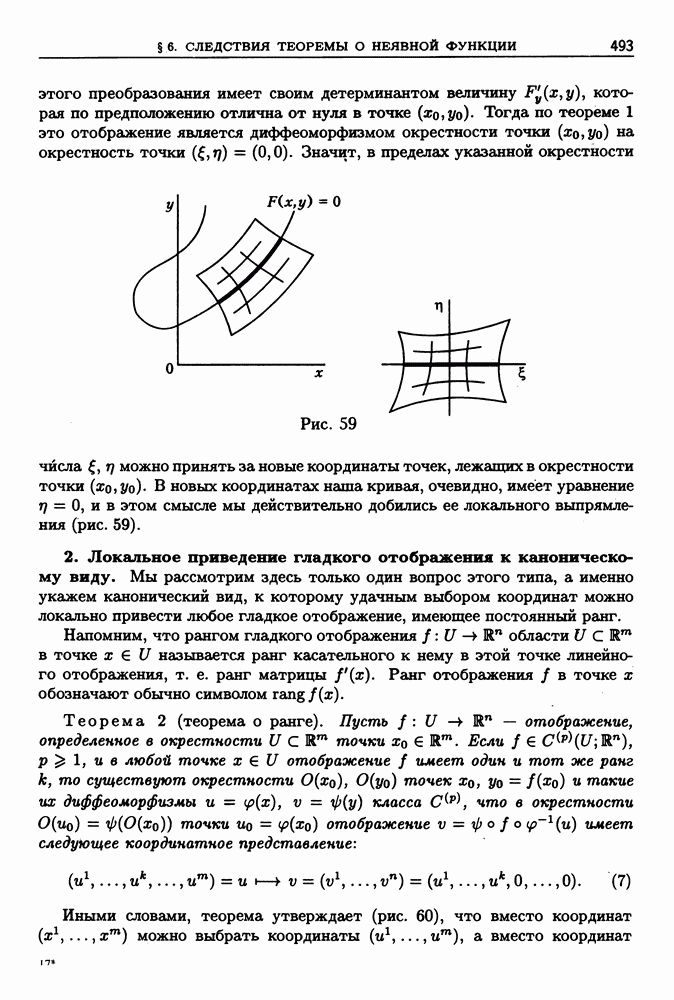
- § 6. Некоторые следствия теоремы о неявной функции
- 2. Локальное приведение гладкого отображения к каноническому виду.
- 3. Зависимость функций
- 4. Локальное разложение диффеоморфизма в композицию простейших.
- 5. Лемма Морса.
- § 7. Поверхность в R^n и теория условного экстремума
- 2. Касательное пространство.
- 3. Условный экстремум
- НЕКОТОРЫЕ ЗАДАЧИ КОЛЛОКВИУМОВ
- ВОПРОСЫ К ЭКЗАМЕНУ
- ЛИТЕРАТУРА