| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Проблема четырех красок.
Пример только что рассмотренной теоремы о кривой Жордана способен, пожалуй, навести на мысль, что топология занимается придумыванием строгих доказательств для таких истин, в которых не станет сомневаться ни один здравомыслящий человек. Но это совсем не так: существует много вопросов топологического характера, в числе которых иные формулируются чрезвычайно просто и на которые интуиция не дает удовлетворительных ответов. Примером может служить знаменитая «проблема четырех красок».

Рис. 129. Раскрашивание карты
Раскрашивая географическую карту, обыкновенно стараются распределить цвета между странами таким образом, чтобы две страны, имеющие общую границу, были окрашены по-разному. Было обнаружено на опыте, что любая карта, сколько бы ни было изображено на ней стран и как бы они ни были расположены, может быть раскрашена, с соблюдением указанного правила, не более чем четырьмя красками. Легко убедиться, что меньшее число достаточным для всех случаев не является. На рис. 129 изображен остров посреди моря, который никак нельзя раскрасить менее чем четырьмя красками, так как на нем имеется четыре страны, из которых каждая соприкасается с остальными тремя.
Тот факт, что до настоящего времени не было ни разу найдено такой карты, для раскрашивания которой потребовалось бы более четырех красок, приводит к мысли о справедливости такой теоремы: при любом данном разбиении плоскости на области, не покрывающие друг друга ни полностью, ни частично, всегда возможно пометить их цифрами 1, 2, 3, 4 таким образом, чтобы «прилежащие» области имели Разные цифры. Под «прилежащими» областями понимаются такие, которые имеют целый отрезок границы общим: две области, имеющие лишь
одну общую точку (или даже конечное число общих точек) — как, например, штаты Колорадо и Аризона — не будут называться «прилежащими», так как никакого смешения или неудобства не возникает, если их раскрасить одинаково.
Есть основания полагать, что впервые проблема четырех красок была поставлена Мебиусом в 1840 г.; позднее ее формулировали де Морган в 1850 г. и Кэли в 1878 г. «Доказательство» ее было опубликовано в 1879 г. Кемпе, но Хивуд (Heawood) в 1890 г. нашел ошибку в рассуждении Кемпе. Пересматривая доказательство Кемпе, Хивуд обнаружил, что пяти красок всегда достаточно. (Доказательство теоремы о пяти красках дано в приложении к этой главе.) Несмотря на усилия многих выдающихся математиков, положение вплоть до нашего времени остается в сущности неизменным. Было доказано, что пяти красок достаточно для всех карт, и имеется предположение, что достаточно также четырех. Но, как и в случае знаменитой теоремы Ферма (см. стр. 71), ни доказательства этого предположения, ни противоречащего ему примера приведено не было, и указанное предположение остается одной из нерешенных «больших» математических проблем. Заметим, между прочим, что проблема четырех красок была решена в положительном смысле для частных случаев, когда число областей не превышает тридцати восьми. Отсюда ясно, что если в общем случае теорема неверна, то опровергающий пример должен быть не особенно простым.
В рассматриваемой проблеме четырех красок предполагается, что карта нарисована или на плоскости, или на сфере. Эти два случая эквивалентны. В самом деле, каждая карта, заданная на сфере, может быть перенесена на плоскость, если проделаем дырочку внутри одной из областей А и затем расплющим оставшуюся часть сферы по плоскости, как мы это делали при доказательстве теоремы Эйлера. Полученная карта на плоскости покажет нам «остров», состоящий из всех нетронутых областей, и «море», состоящее из одной области А. С другой стороны, проделывая всю эту процедуру в обратном направлении, можно любую карту на плоскости превратить в карту на сфере. Итак, вместо карт на плоскости можно ограничиться рассмотрением карт на сфере. Больше того, так как деформации областей и их границ существенно не влияют на нашу проблему, то можно предположить, что граница каждой области есть простой замкнутый многоугольник, состоящий из дуг больших кругов. Но даже таким образом «регуляризированная» проблема не является решенной; трудности в данном случае (не в пример теореме Жордана) зависят не от общности понятия области и кривой.
В связи с проблемой четырех красок стоит отметить то замечательное обстоятельство, что для некоторых поверхностей более сложного типа, чем плоскость или сфера, соответствующие теоремы действительно были доказаны, так что, как это ни парадоксально, анализ более сложных (в геометрическом отношении) поверхностей в данном случае проводится легче, чем более простых. Например, было установлено для случая поверхности тора, имеющей вид «бублика» (см. рисунок 123), что всякая нарисованная на ней «карта» может быть раскрашена семью красками и что, с другой стороны, на ней мыслимы такие «карты», составленные из семи областей, что каждая область соприкасается с остальными шестью.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие ко второму русскому изданию
- Как пользоваться книгой
- Что такое математика?
- Глава I. Натуральные числа
- § 1. Операции над целыми числами
- 2. Представление целых чисел с помощью письменных знаков (нумерация).
- 3. Арифметические действия в недесятичных системах счисления.
- § 2. Бесконечность системы натуральных чисел. Математическая индукция
- 2. Арифметическая прогрессия.
- 3. Геометрическая прогрессия.
- 4. Сумма n первых квадратов.
- 5. Одно важное неравенство.
- 6. Биномиальная теорема.
- 7. Дальнейшие замечания по поводу метода математической индукции.
- Дополнение к главе I
- Теория чисел
- 2. Распределение простых чисел.
- § 2. Сравнения
- 2. Теорема Ферма.
- 3. Квадратические вычеты.
- § 3. Пифагоровы числа и большая теорема Ферма
- § 4. Алгоритм Евклида
- 2. Применение к основной теореме арифметики
- 3. Функция Эйлера. Еще раз о теореме Ферма.
- 4. Непрерывные дроби. Диофантовы уравнения
- Глава II. Математическая числовая система
- § 1. Рациональные числа
- 2. Возникновение надобности в рациональных числах внутри самой математики. Принцип обобщения.
- 3. Геометрическое представление рациональных чисел.
- § 2. Несоизмеримые отрезки. Иррациональные числа, пределы
- 2. Десятичные дроби: конечные и бесконечные.
- 3. Пределы. Бесконечные геометрические прогрессии.
- 4. Рациональные числа и периодические десятичные дроби.
- 5. Общее определение иррациональных чисел посредством стягивающихся отрезков.
- 6. Иные методы определения иррациональных чисел.Декиндовы сечения.
- § 3. Замечания из области аналитической геометрии
- 2. Уравнения прямых и кривых линий.
- § 4. Математический анализ бесконечного
- 2. Счетность множества рациональных чисел и несчетность континуума.
- 3. «Кардинальные числа» Кантора.
- 4. Косвенный метод доказательства.
- 5. Парадоксы бесконечного.
- 6. Основания математики.
- § 5. Комплексные числа
- 2. Геометрическое представление комплексных чисел.
- 3. Формула Муавра и корни из единицы.
- 4. Основная теорема алгебры.
- § 6. Алгебраические и трансцендентные числа
- 2. Теорема Лиувилля и конструирование трансцендентных чисел.
- Дополнение к главе II. Алгебра множеств
- 2. Применение к математической логике.
- 3. Одно из применений к теории вероятностей.
- Глава III. Геометрические построения. Алгебра числовых полей
- Часть 1. Доказательства невозможности и алгебра
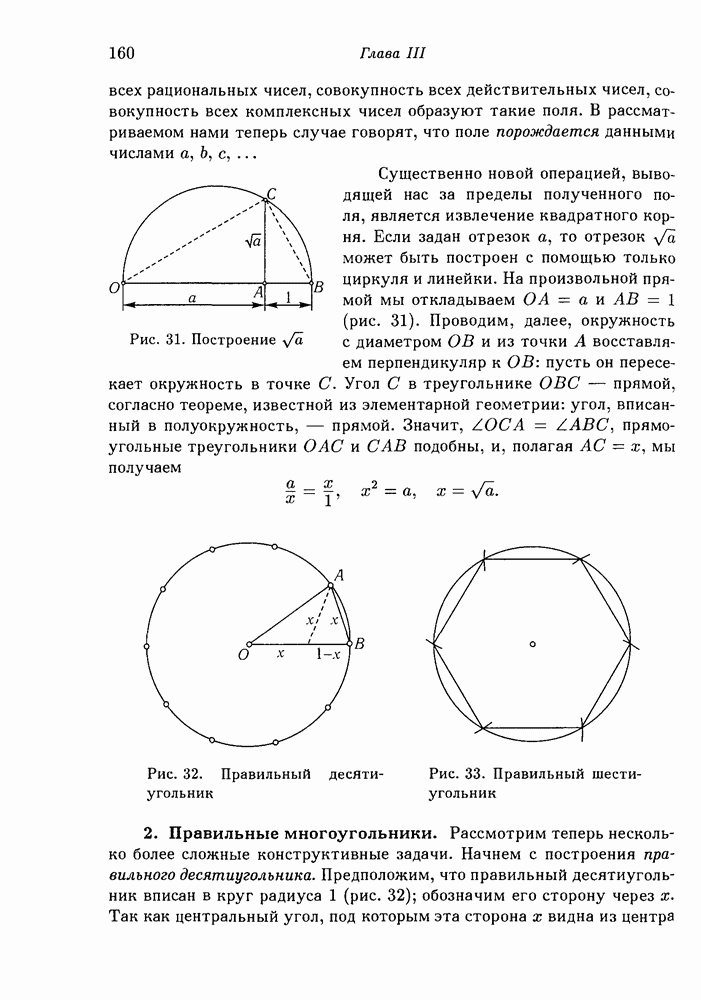
- 1. Построение полей и извлечение квадратных корней.
- 2. Правильные многоугольники.
- 3. Проблема Аполлония.
- § 2. Числа, допускающие построение, и числовые поля
- 2. Все числа, допускающие построение, — алгебраические.
- § 3. Неразрешимость трех классических проблем
- 2. Одна теорема о кубических уравнениях.
- 3. Трисекция угла.
- 4. Правильный семиугольник.
- 5. Замечания по поводу квадратуры круга.
- Часть 2. Различные методы выполнения построений
- § 4. Геометрические преобразования. Инверсия
- 2. Свойства инверсии.
- 3. Геометрическое построение обратных точек.
- 4. Как разделить отрезок пополам и как найти центр данного круга с помощью одного циркуля.
- § 5. Построения с помощью иных инструментов. Построения Маскерони с помощью одного циркуля
- 1. Классическая конструкция, служащая для удвоения куба.
- 2. Построения с помощью одного циркуля.
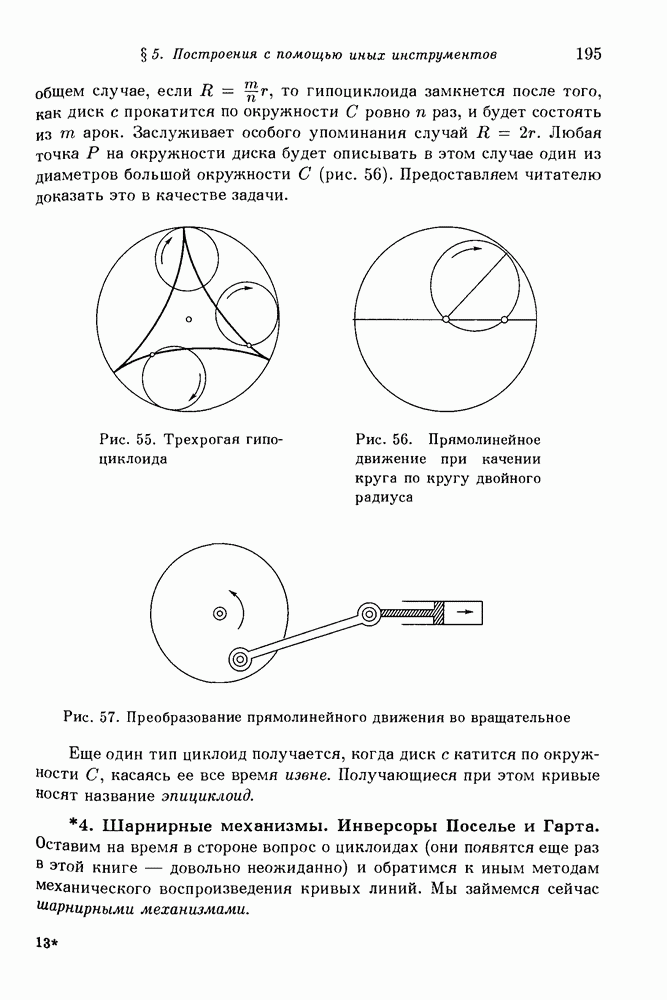
- 3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды.
- 4. Шарнирные механизмы. Инверсоры Поселье и Гарта.
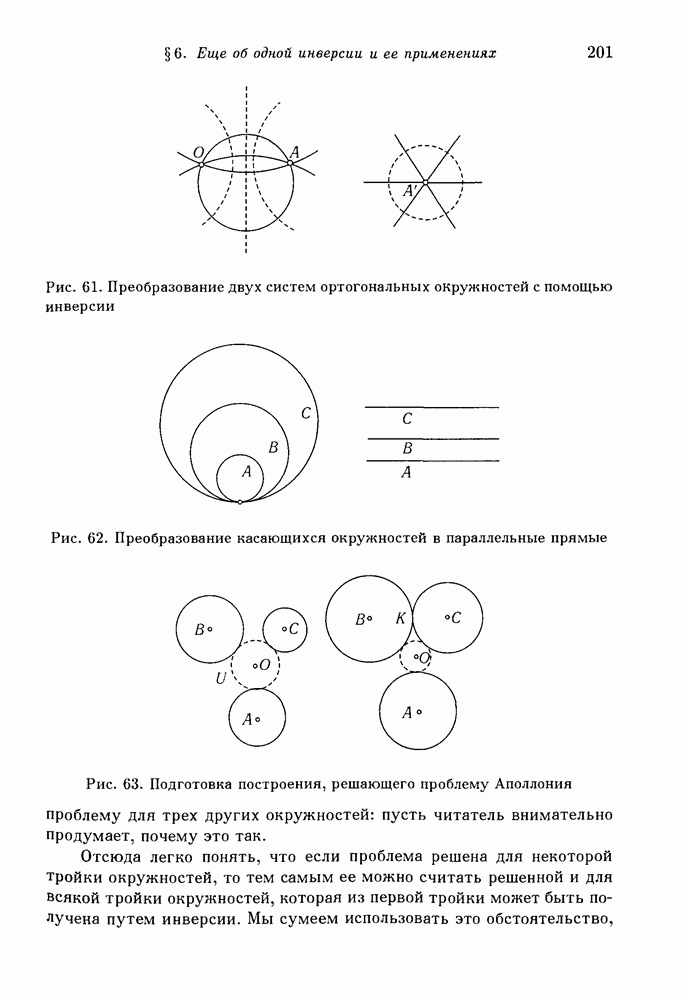
- § 6. Еще об одной инверсии и ее применениях
- 1. Инвариантность углов. Семейства окружностей.
- 2. Применение к проблеме Аполлония.
- 3. Повторные отражения.
- Глава IV. Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- 1. Классификация геометрических свойств. Инвариантность при преобразованиях.
- 2. Проективные преобразования.
- § 2. Основные понятия
- 1. Группа проективных преобразований.
- 2. Теорема Дезарга.
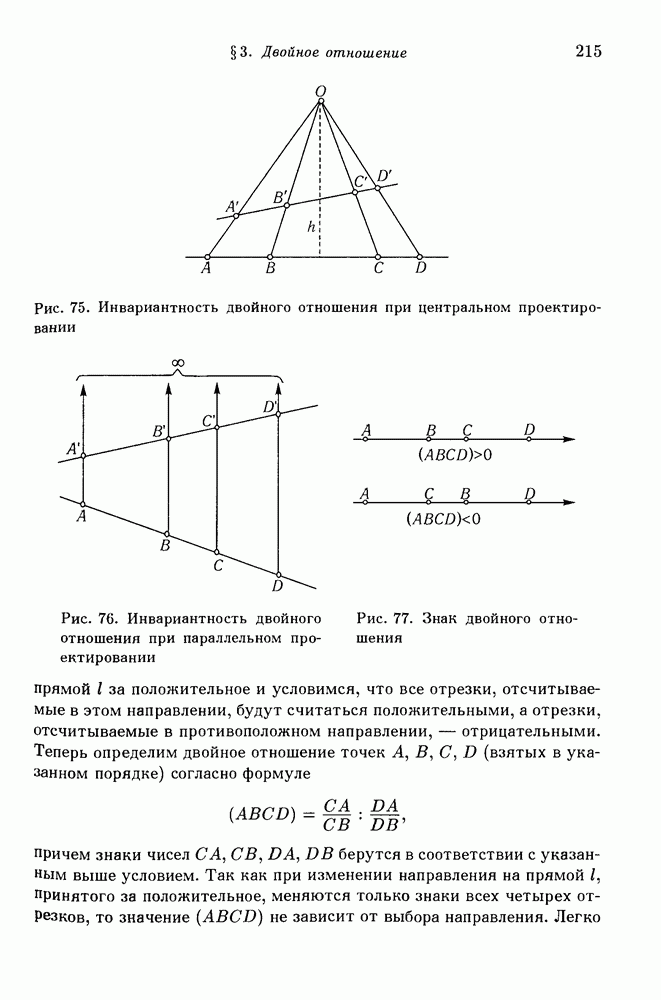
- § 3. Двойное отношение
- § 4. Параллельность и бесконечность
- 2. Идеальные элементы и проектирование.
- 3. Двойное отношение с бесконечно удаленными элементами.
- § 5. Применения
- 2. Двумерное доказательство теоремы Дезарга.
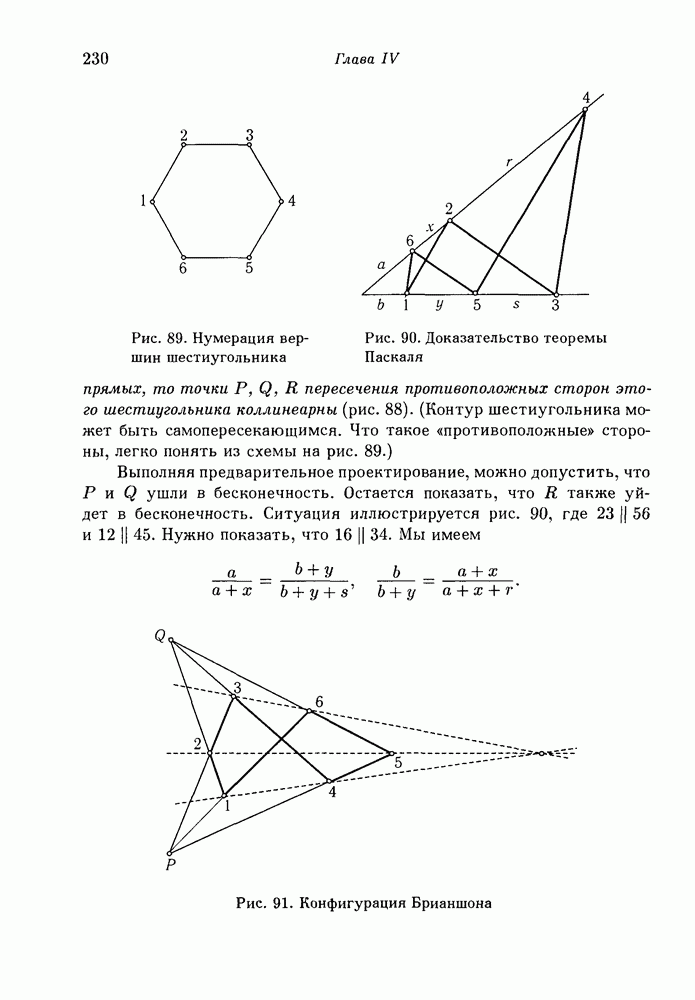
- 3. Теорема Паскаля.
- 4. Теорема Брианшона.
- 5. Замечание по поводу двойственности.
- § 6. Аналитическое представление
- 2. Однородные координаты. Алгебраические основы двойственности.
- § 7. Задачи на построения с помощью одной линейки
- § 8. Конические сечения и квадрики
- 2. Проективные свойства конических сечений.
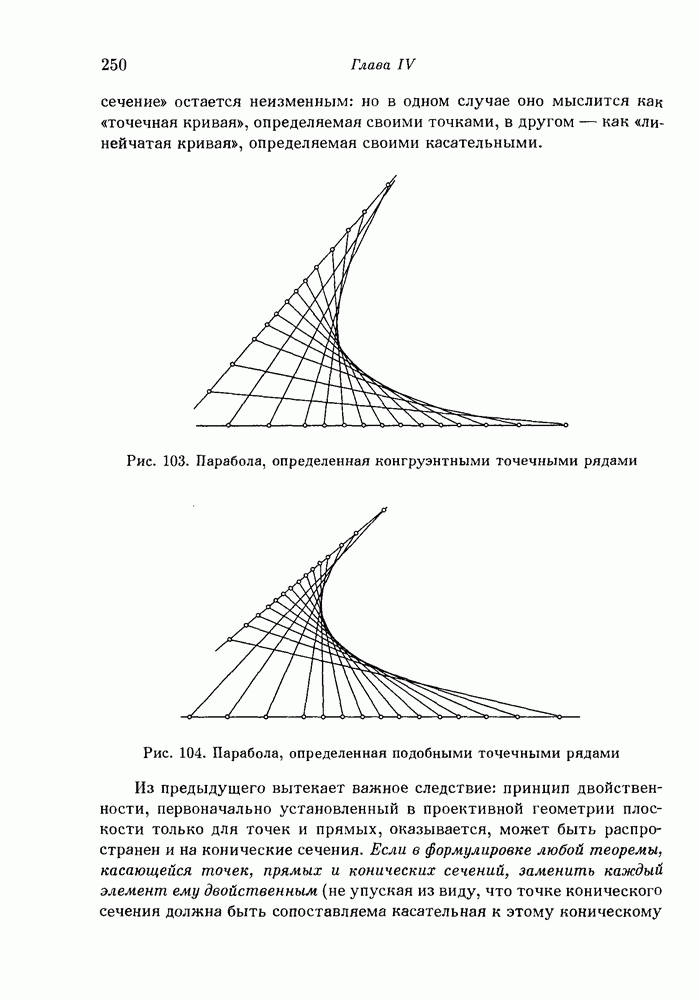
- 3. Конические сечения как «линейчатые кривые».
- 4. Теоремы Паскаля и Брианшона для общего случая произвольных конических сечений.
- 5. Гиперболоид.
- § 9. Аксиоматика и неевклидова геометрия
- 2. Гиперболическая неевклидова геометрия.
- 3. Геометрия и реальность.
- 4. Модель Пуанкаре.
- 5. Эллиптическая, или риманова, геометрия.
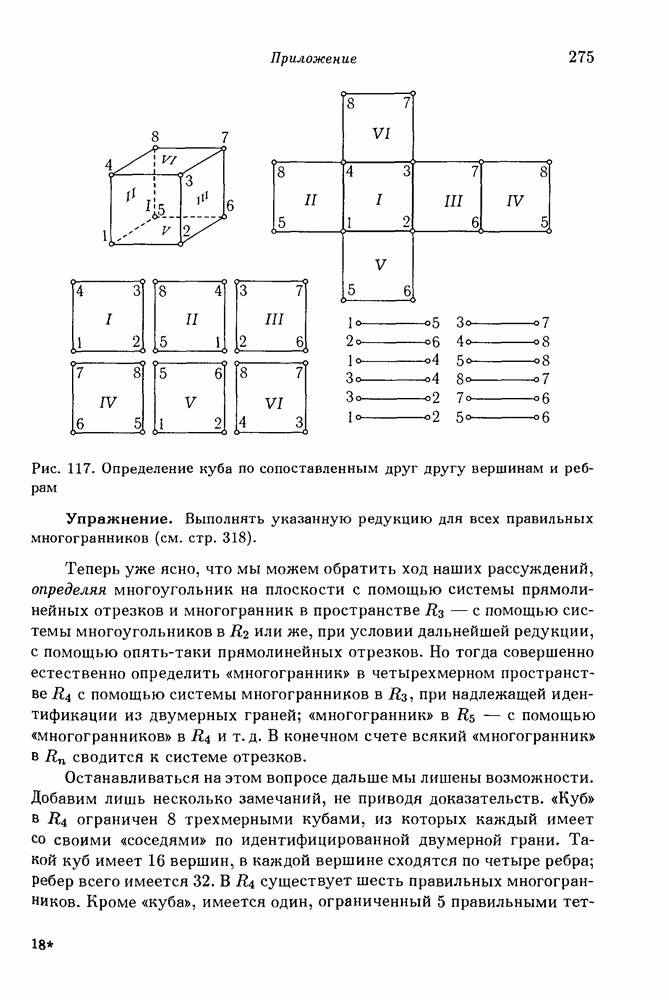
- Приложение. Геометрия в пространствах более чем трех измерений
- Глава V. Топология
- § 1. Формула Эйлера для многогранников
- § 2. Топологические свойства фигур
- 2. Свойства связности.
- § 3. Другие примеры топологических теорем
- 2. Проблема четырех красок.
- 3. Понятие размерности.
- 4. Теорема о неподвижной точке.
- 5. Узлы.
- § 4. Топологическая классификация поверхностей
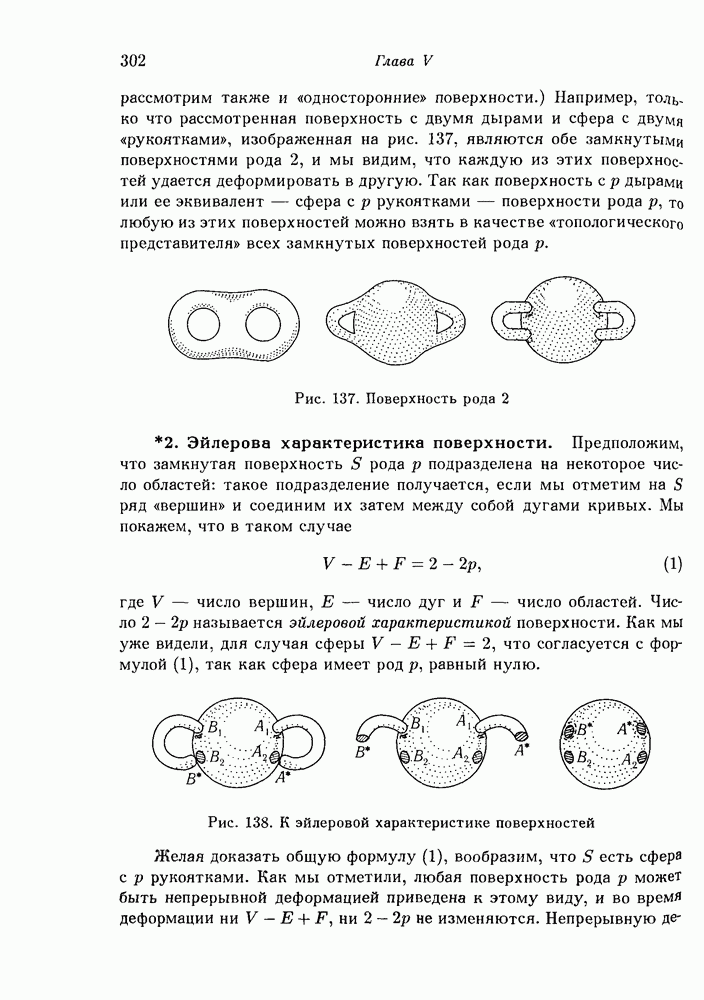
- 2. Эйлерова характеристика поверхности.
- 3. Односторонние поверхности.
- Приложение
- 2. Теорема Жордана для случая многоугольников.
- 3. Основная теорема алгебры.
- Глава VI. Функции и пределы
- § 1. Независимое переменное и функция
- 2. Радианная мера углов.
- 3. График функции. Обратные функции.
- 4. Сложные функции.
- 5. Непрерывность.
- 6. Функции нескольких переменных.
- 7. Функции и преобразования.
- § 2. Пределы
- 2. Монотонные последовательности.
- 3. Число Эйлера e.
- 4. Число «пи»
- 5. Непрерывные дроби.
- § 3. Пределы при непрерывном приближении
- 2. Замечания по поводу понятия предела
- 3. Предел sin x/x
- 4. Пределы при х -> оо.
- § 4. Точное определение непрерывности
- § 5. Две основные теоремы о непрерывных функциях
- 2. Доказательство теоремы Больцано.
- 3. Теорема Вейерштрасса об экстремальных значениях.
- 4. Теорема о последовательностях. Компактные множества.
- § 6. Некоторые применения теоремы Больцано
- 2. Применение к одной механической проблеме.
- Дополнение к главе VI. Дальнейшие примеры на пределы и непрерывность
- 4. Разрывные функции как предел непрерывных.
- 5. Пределы при итерации.
- § 2. Пример, относящийся к непрерывности
- Глава VII. Максимумы и минимумы
- § 1. Задачи из области элементарной геометрии
- 2. Теорема Герона. Экстремальное свойство световых лучей.
- 3. Применения к задачам о треугольниках.
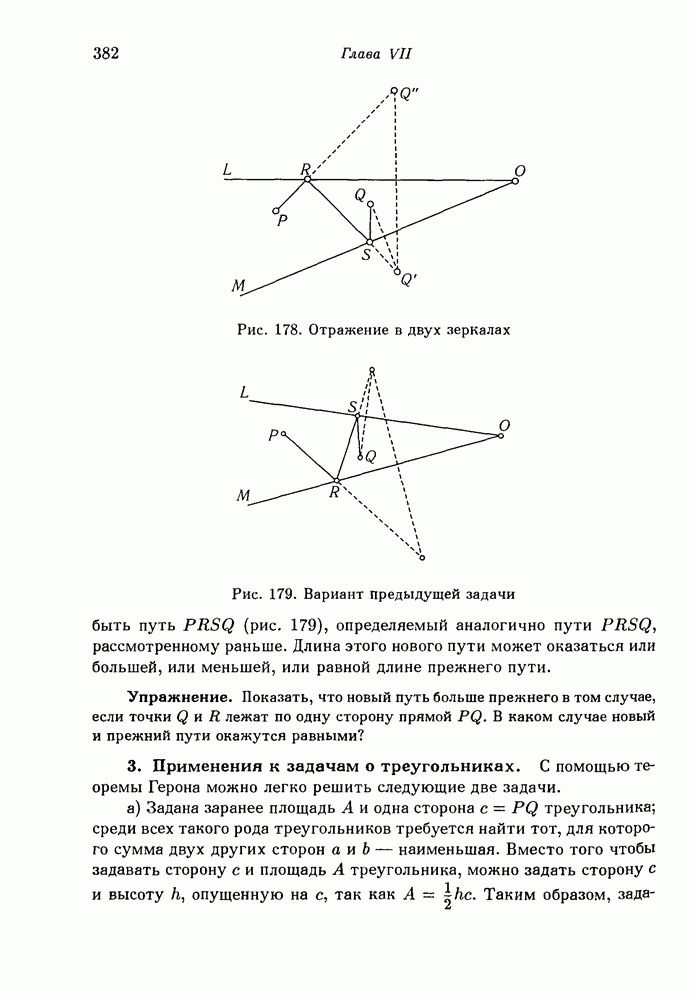
- 4. Свойства касательных к эллипсу и гиперболе. Соответствующие экстремальные свойства.
- 5. Экстремальные расстояния точки от данной кривой.
- § 2. Общий принцип, которому подчинены экстремальные задачи
- § 3. Стационарные точки и дифференциальное исчисление
- 2. Максимумы и минимумы функций нескольких переменных. Седловые точки.
- 3. Точки минимакса и топология.
- 4. Расстояние точки от поверхности.
- § 4. Треугольник Шварца
- 4. Треугольники, образованные световыми лучами.
- 5. Замечания, касающиеся задач на отражение и эргодическое движение.
- § 5. Проблема Штейнера
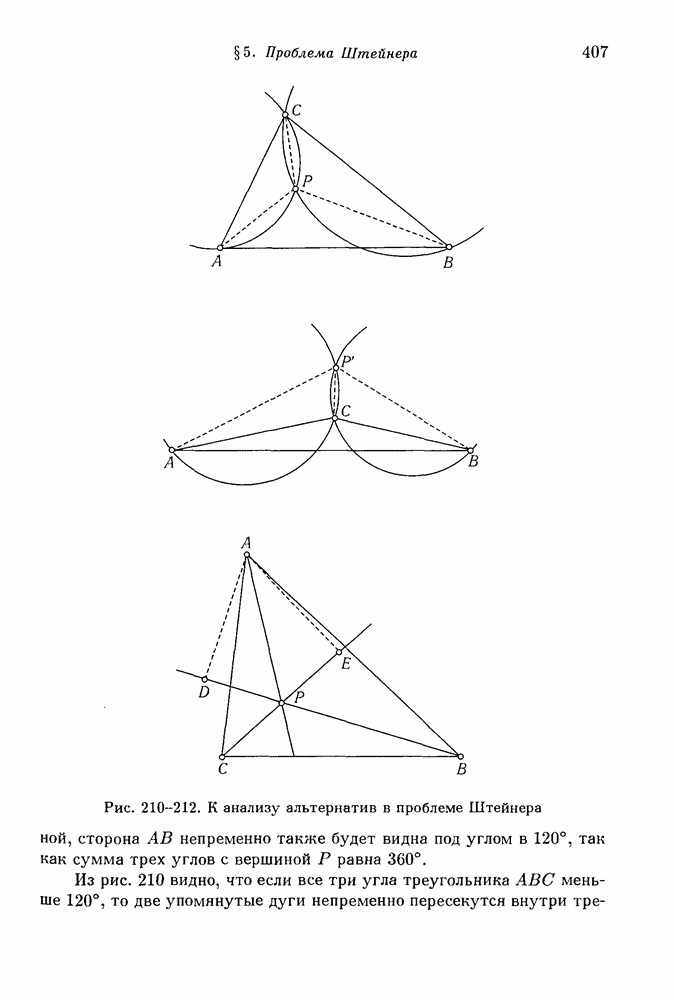
- 2. Анализ возникающих альтернатив.
- 3. Дополнительная проблема.
- 4. Замечания и упражнения.
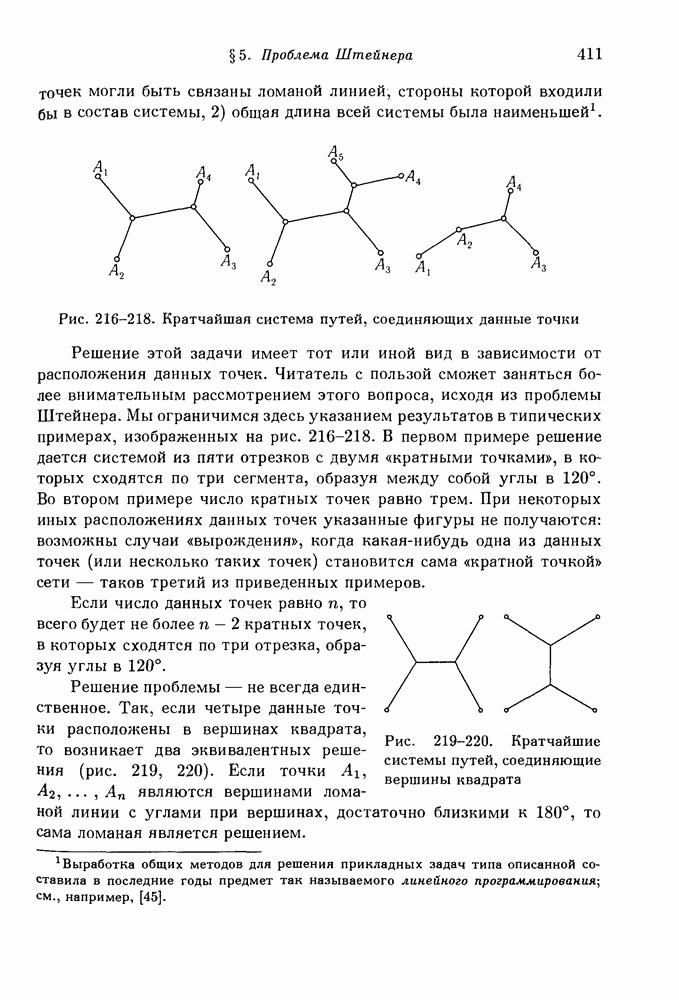
- 5. Обобщение: проблема уличной сети.
- § 6. Экстремумы и неравенства
- 1. Средние арифметическое и геометрическое двух положительных величин.
- 2. Обобщение на случай n переменных.
- 3. Метод наименьших квадратов.
- § 7. Существование экстремума. Принцип Дирихле
- 3. Экстремальные проблемы элементарного содержания.
- 4. Трудности, возникающие в более сложных случаях.
- § 8. Изопериметрическая проблема
- § 9. Экстремальные проблемы с граничными условиями. Связь между проблемой Штейнера и изопериметрической проблемой
- § 10. Вариационное исчисление
- 2. Вариационное исчисление. Принцип Ферма в оптике.
- 3. Решение задачи о брахистохроне, принадлежащее Якобу Бернулли.
- 4. Геодезические линии на сфере. Минимаксы.
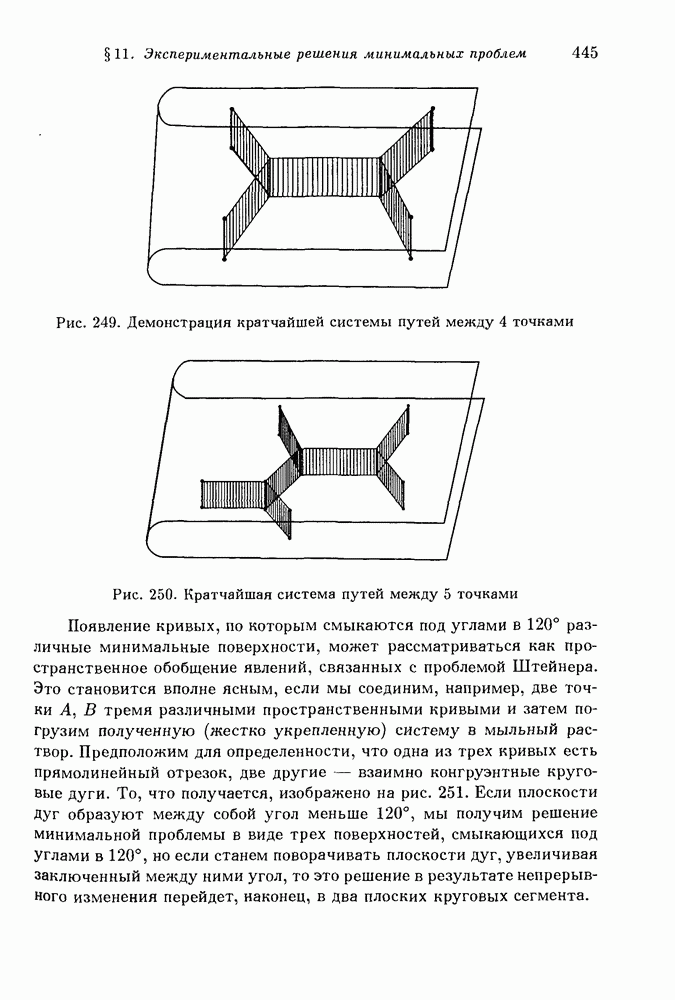
- § 11. Экспериментальные решения минимальных проблем. Опыты с мыльными пленками
- 2. Опыты с мыльными пленками.
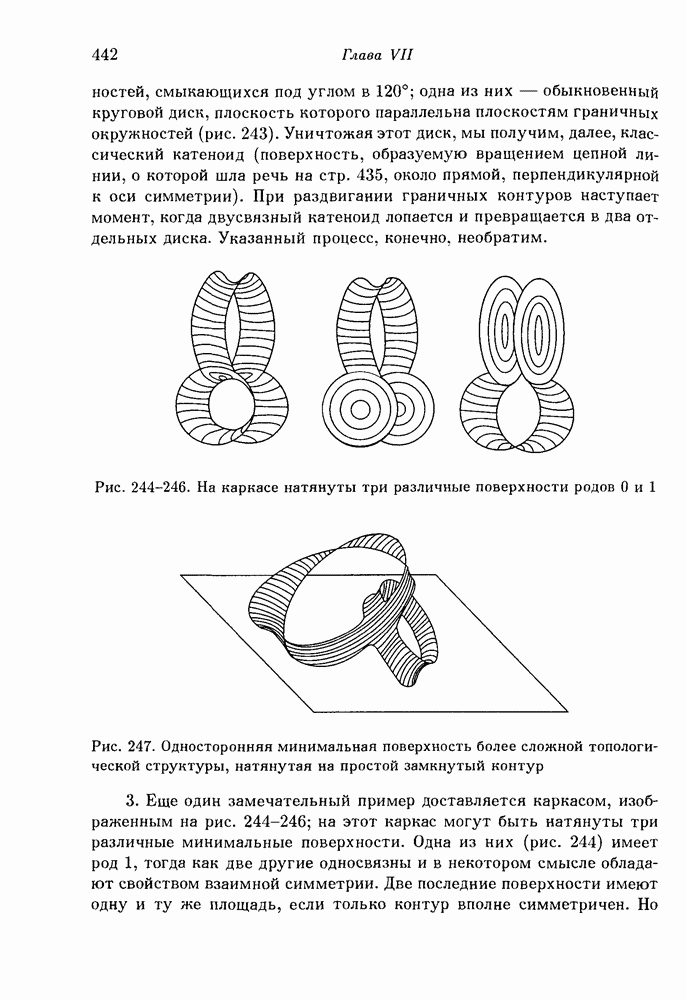
- 3. Новые опыты, относящиеся к проблеме Плато.
- 4. Экспериментальные решения других математических проблем.
- Глава VIII. Математический анализ
- § 1. Интеграл
- 2. Интеграл.
- 3. Общие замечания о понятии интеграла. Общее определение.
- 4. Примеры интегрирования. Интегрирование x^r.
- 5. Правила «интегрального исчисления».
- § 2. Производная
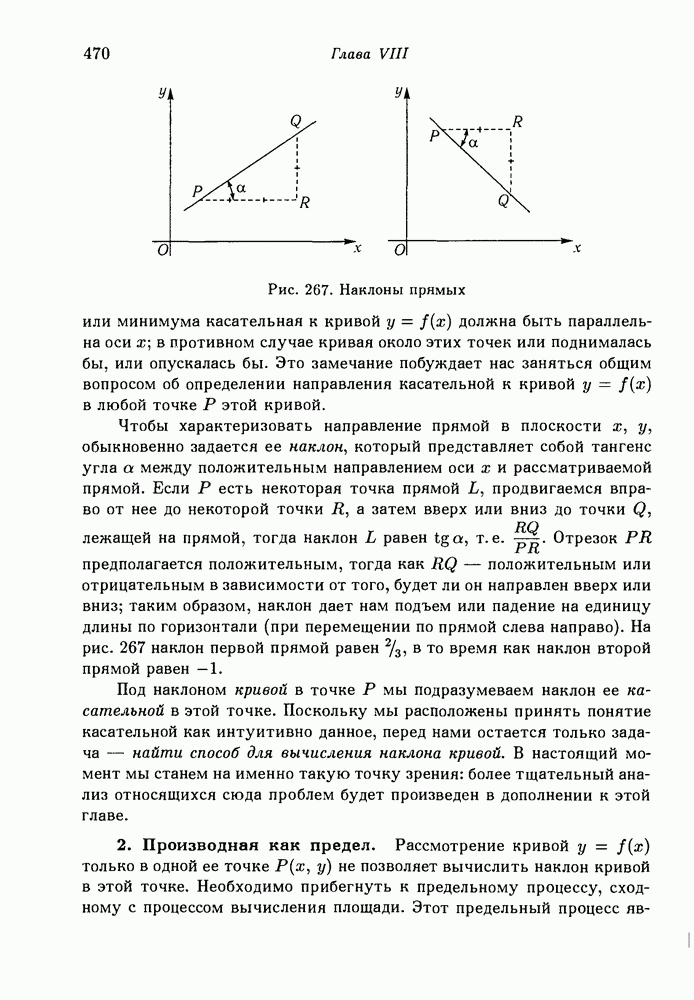
- 2. Производная как предел.
- 3. Примеры.
- 4. Производные от тригонометрических функций.
- 5. Дифференцируемость и непрерывность.
- 6. Производная и скорость. Вторая производная и ускорение.
- 7. Геометрический смысл второй производной.
- 8. Максимумы и минимумы.
- § 3. Техника дифференцирования
- § 4. Обозначения Лейбница и «бесконечно малые»
- § 5. Основная теорема анализа
- 2. Первые применения. Интегрирование функций x^r, cosx, sinx. Функция arctgx
- 3. Формула Лейбница для «пи»
- § 6. Показательная (экспоненциальная) функция и логарифм
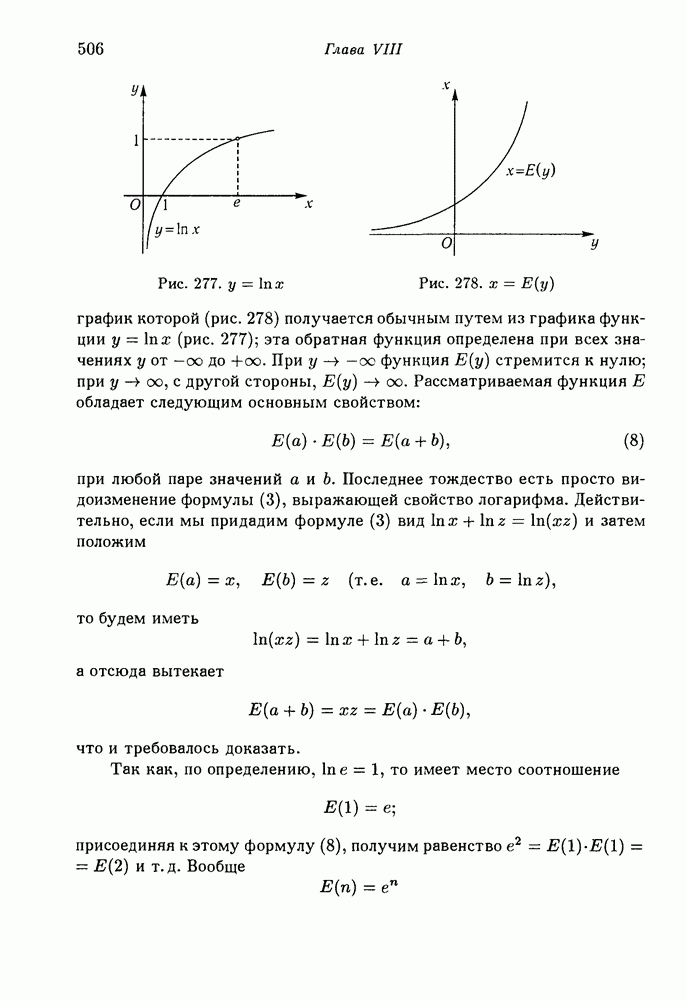
- 2. Показательная (экспоненциальная) функция.
- 3. Формулы дифференцирования функций е^х, а^х, x^s.
- 4. Явные выражения числа е^x и функций lnx в виде пределов.
- 5. Бесконечный ряд для логарифма. Вычисление логарифмов.
- § 7. Дифференциальные уравнения
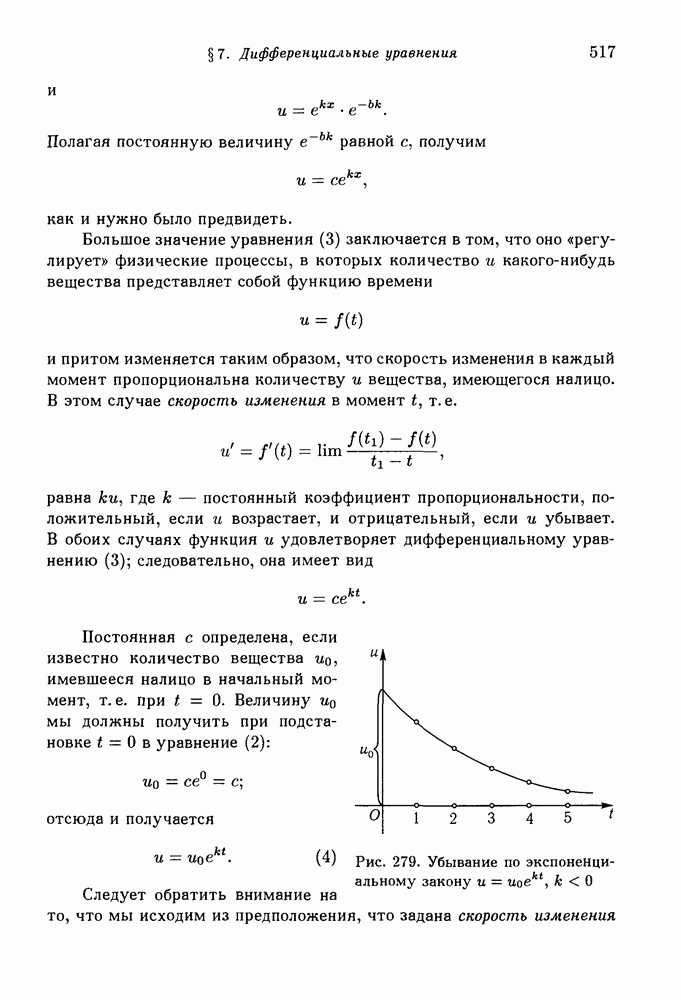
- 2. Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- 3. Другие примеры. Простейшие колебания.
- 4. Закон движения Ньютона.
- Дополнение к главе VIII
- § 1. Вопросы принципиального порядка
- 3. Другие приложения понятия интеграла. Работа. Длина кривой.
- § 2. Порядки возрастания
- 2. Порядок возрастания ln(n!)
- § 3. Бесконечные ряды и бесконечные произведения
- 2. Формула Эйлера cos x + i sin x = exp(ix).
- 3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin x в виде бесконечного произведения.
- § 4. Доказательство теоремы о простых числах на основе статистического метода
- Приложение. Дополнительные замечания, задачи и упражнения
- Аналитическая геометрия
- Геометрические построения
- Проективная и неевклидова геометрия
- Топология
- Функции, пределы, непрерывность
- Максимумы и минимумы
- Дифференциальное и интегральное исчисления
- Техника интегрирования
- Рекомендуемая литература