4. Экспериментальные решения других математических проблем.

Благодаря действию поверхностного натяжения жидкая пленка только при том условии может находиться в состоянии устойчивого равновесия, если площадь образуемой поверхности минимальна. Это обстоятельство является неистощимым источником экспериментов серьезной математической ценности. Если некоторые части границы пленки могут свободно перемещаться по заданным поверхностям (например, плоскостям), то на этих частях границы пленка будет стоять перпендикулярно к заданной поверхности.

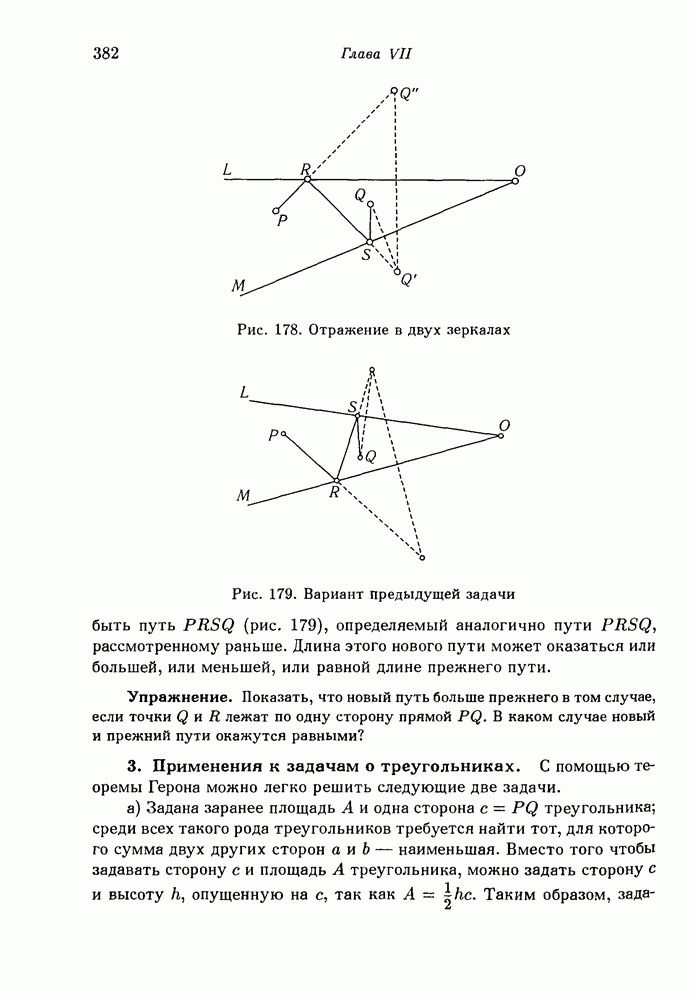
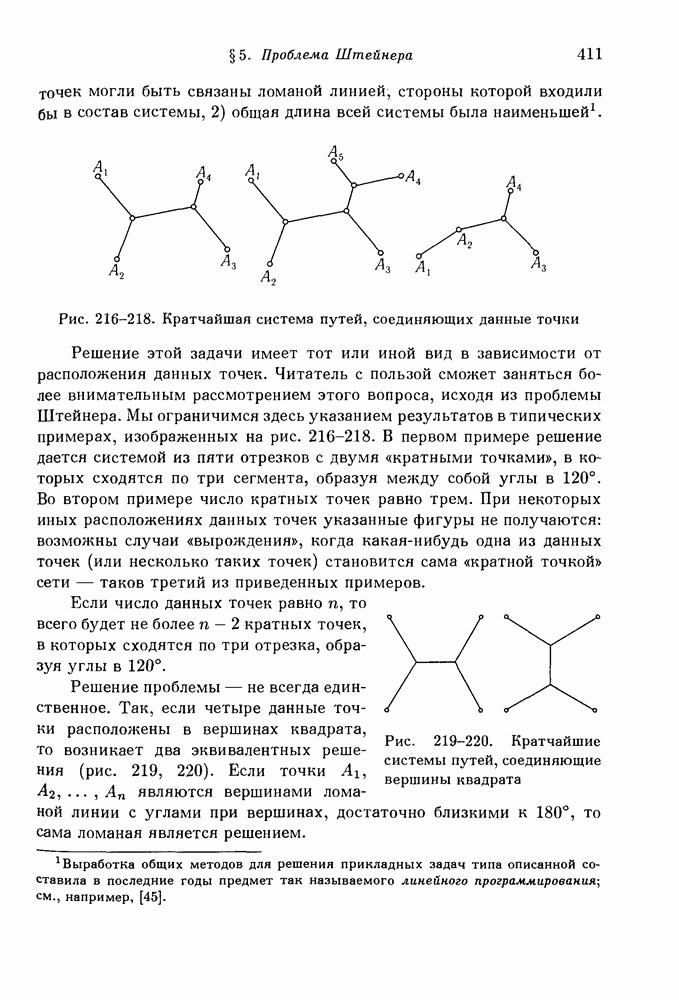
Мы можем использовать последнее отмеченное обстоятельство для наглядного решения проблемы Штейнера и ее обобщений (см. § 5). Пусть две параллельно расположенные стеклянные поверхности (или гладкие плитки) соединены тремя или большим числом перпендикулярно стоящих стержней. Если погрузить всю такого рода систему в мыльный раствор, затем вынуть, то пленка образует между плоскими поверхностями ряд вертикальных полос, связывающих между собой стержни. Проекция этих полос на горизонтальные плоскости есть не что иное, как решение проблемы Штейнера, рассмотренной на стр. 405.

Если две плоские поверхности не параллельны, или стержни к ним не перпендикулярны, или сами поверхности не являются плоскими, то кривые, по которым пленки пересекаются с поверхностями, не будучи прямыми линиями, смогут иллюстрировать решение новых вариационных проблем.

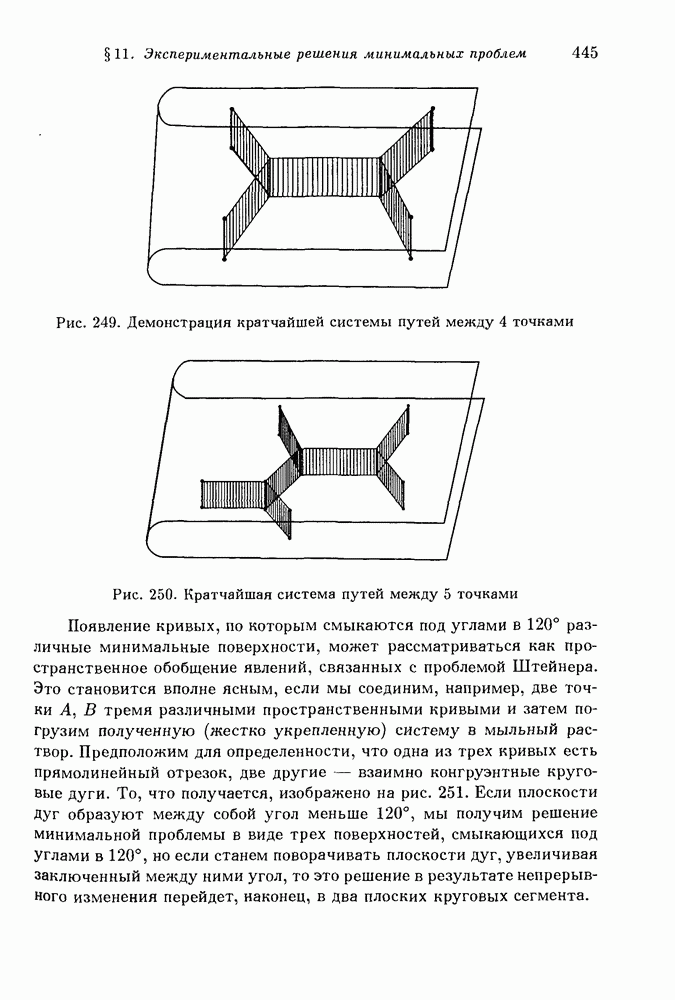
Рис. 249. Демонстрация кратчайшей системы путей между 4 точками

Рис. 250. Кратчайшая система путей между 5 точками

Появление кривых, по которым смыкаются под углами в 120° различные минимальные поверхности, может рассматриваться как пространственное обобщение явлений, связанных с проблемой Штейнера. Это становится вполне ясным, если мы соединим, например, две точки А, В тремя различными пространственными кривыми и затем погрузим полученную (жестко укрепленную) систему в мыльный раствор. Предположим для определенности, что одна из трех кривых есть прямолинейный отрезок, две другие — взаимно конгруэнтные круговые дуги. То, что получается, изображено на рис. 251. Если плоскости Дуг образуют между собой угол меньше 120°, мы получим решение минимальной проблемы в виде трех поверхностей, смыкающихся под Углами в 120°, но если станем поворачивать плоскости дуг, увеличивая заключенный между ними угол, то это решение в результате непрерывного изменения перейдет, наконец, в два плоских круговых сегмента.

Рис. 251. Три пересекающиеся под углом в 120° поверхности, натянутые на три проволоки, соединяющие две точки

Рис. 252. Три ломаные линии, соединяющие две точки

Рис. 253. Доказательство изопериметрического свойства круга

Допустим теперь, что точки соединены более сложными кривыми. В качестве примера возьмем три ломаные, состоящие каждая из трех ребер одного и того же куба и соединяющие диагонально противоположные вершины: тогда получатся три конгруэнтные минимальные поверхности, пересекающиеся по диагонали куба. (Мы получили бы ту же систему поверхностей из системы, изображенной на рис. 240, уничтожая пленки, прилежащие к трем надлежащим образом выбранным ребрам.) Если станем деформировать ломаные линии, соединяющие то линия взаимного смыкания поверхностей искривится, но углы неизменно останутся те же — в 120° (рис. 252).

Все явления, связанные со смыканием трех минимальных поверхностей по одной кривой, в основном одной и той же природы: они представляют собой обобщение плоской проблемы о соединении системы данных точек кратчайшей системой линий.

Наконец, добавим несколько слов о мыльных пузырях. Сферический мыльный пузырь показывает, что среди всех замкнутых поверхностей, охватывающих один и тот же объем (определенный запасом заключенного в нем воздуха), именно сфера имеет наименьшую поверхность. Если мы рассмотрим пузыри данного объема, стремящиеся сократить свою поверхность, но подчиненные некоторым дополнительным условиям, то убедимся, что получаться будут уже не обязательно сферы, а, вообще говоря, поверхности постоянной средней кривизны, частными примерами которых являются сферы и круговые цилиндры.

Предположим, например, что пузырь заключен между двумя параллельными стеклами или плитками, предварительно смоченными мыльным раствором. Прикоснувшись к одной из плоскостей, пузырь внезапно принимает форму полусферы, если же происходит соприкосновение также и с другой плоскостью, он сразу превращается в круговой цилиндр, тем самым чрезвычайно наглядно демонстрируя изопериметрическое свойство круга. Все дело, конечно, в том, что мыльная пленка располагается перпендикулярно к ограничивающим поверхностям. Помещая мыльные пузыри между двумя плоскостями, которые соединены между собой стержнями, мы имеем возможность проиллюстрировать проблемы, разобранные на стр. 411.

Рис. 254-255. Изопериметрические фигуры с граничными условиями

Можно еще рассмотреть, как изменяется решение изопериметрической проблемы при увеличении или уменьшении объема воздуха внутри пузыря. При этом следует воспользоваться тоненькой трубочкой или соломинкой. Однако, высасывая воздух, мы не получим тех

Рис. 256-257. Демонстрация изопериметрических свойств фигур с помощью мыльных пленок

фигур (см. стр. 429), которые состоят из касающихся друг друга круговых дуг. При уменьшении объема воздуха внутри пузыря углы в треугольнике из круговых дуг, однако, не станут (теоретически) меньшими, чем 120°: мы получим такие фигуры, какие изображены на рис. 254 и 255, причем при неограниченном уменьшении площади, заключенной внутри, в пределе получатся те же три сегмента, с которыми мы встретились и раньше (рис. 235). С математической точки зрения объяснение отмеченному различию заключается в том, что отрезок, связывающий пузырь с каким-нибудь стержнем, начиная с момента отделения пузыря от этого стержня, не должен считаться дважды. Соответствующие опыты иллюстрируются рис. 256 и 257.

Упражнение. Разобрать математическую проблему, отвечающую настоящим условиям: найти треугольник, составленный из круговых дуг и имеющий данную площадь, по условию, чтобы сумма его периметра и трех отрезков, соединяющих вершины с тремя данными точками, была минимальной.

Помещая мыльный пузырь внутрь кубического проволочного каркаса, в случае, если объем пузыря окажется больше, чем объем куба, мы получим поверхности постоянной средней кривизны с квадратными основаниями. Высасывая воздух из пузыря через соломинку, будем иметь целую цепь красивых структур, приводящих в конце концов к такой, какая изображена на рис. 258. Явления устойчивости и переход от одного состояния равновесия к другому порождают эксперименты, которые в математическом отношении нельзя не назвать весьма поучительными. Таким образом, возникает наглядная иллюстрация к теории стационарных значений; непрерывная цепь переходов от одного состояния равновесия к другому может быть выбрана таким образом, что в ее состав войдет состояние неустойчивого равновесия, все же являющееся «стационарным состоянием».

Рис. 258. Пленки на кубическом каркасе

Рассмотрим в качестве примера кубическую структуру на рис. 240. Мы видим здесь нарушение симметрии: в центре куба имеется вертикальная площадка, смыкающаяся с двенадцатью поверхностями, идущими от ребер куба. Но тогда, как нетрудно понять, должно существовать еще по меньшей мере два положения равновесия: одно с вертикальной (иначе расположенной) и другое с горизонтальной площадкой в центре. Чтобы на самом деле реализовать переход от одного положения равновесия к другому, нужно дуть через соломинку на ребра центральной площадки: таким образом удается эту центральную площадку превратить в точку — центр куба, но полученное таким образом состояние равновесия не будет устойчивым и немедленно же перейдет в иное устойчивое состояние, причем центральная площадка снова возникает, хотя и повернувшись на 90°.

Подобный же эксперимент можно произвести и с мыльной пленкой, демонстрирующей решение проблемы Штейнера для случая четырех точек, помещенных в вершинах квадрата (рис. 219, 220).

Если бы мы пожелали получить решение только что рассмотренных проблем как предельный случай цепи изопериметрических проблем, например, если бы мы хотели получить рис. 240 из рис. 258, нужно было бы понемногу высасывать воздух из центрального пузыря. Структура,

изображенная на рис. 258, строго симметрична, и в пределе, когда объем центрального «кубика» обращается в нуль, получается также строго симметричная структура из 12 плоских треугольников с общей вершиной в центре. Этого в самом деле можно добиться. Но возникающее предельное положение равновесия не является устойчивым: внезапно оно сменяется одним из трех положений, изображенных на рис. 240. Все явления можно наблюдать вполне отчетливо, если раствор сделать несколько более вязким, чем было указано в нашем рецепте. Перед нами возникает яркая картина, показывающая, что даже в проблемах из области физики решение не всегда находится в непрерывной зависимости от начальных данных: в самом деле, в предельном случае, когда объем воздуха, заключенного в «кубическом» пузыре, обращается в нуль, решение, изображенное на рис. 240, не является предельным для цепи решений, изображенных на рис. 258, возникающих для различных объемов когда стремится к нулю.