| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
3. Примеры.
Может показаться, что рассуждения, приведшие к определению (1), лишены всякого практического смысла. В самом деле, одна проблема подменена другой: вместо того чтобы искать наклон касательной к кривой  в некоторой точке, мы должны вычислять предел (1), что с первого взгляда кажется одинаково трудным. Но, как только мы откажемся от рассмотрении в общем виде и перейдем к отдельным функциям, мы получим весьма реальные результаты.
в некоторой точке, мы должны вычислять предел (1), что с первого взгляда кажется одинаково трудным. Но, как только мы откажемся от рассмотрении в общем виде и перейдем к отдельным функциям, мы получим весьма реальные результаты.
Простейшей из функций является функция  где с — постоянно. График этой функции
где с — постоянно. График этой функции  есть горизонтальная прямая,
есть горизонтальная прямая,
совпадающая со всеми своими касательными; очевидно, для всех значений х имеет место соотношение

Это вытекает также и из определения (1); в самом деле,

Таким образом, получаем тривиальный результат:

Вслед за этим рассмотрим простую функцию  графиком которой является биссектриса угла первого квадранта. Геометрически ясно, что для всех значений х
графиком которой является биссектриса угла первого квадранта. Геометрически ясно, что для всех значений х

а аналитическое определение (1) снова дает

Простейшим нетривиальным примером является дифференцирование функции

что в сущности является нахождением наклона параболы. Это — простейший случай, на котором мы можем учиться совершать переход к пределу, когда результат с первого взгляда не очевиден. Мы имеем

Если бы мы попытались перейти к пределу непосредственно в числителе и в знаменателе, то получили бы не имеющее смысла выражение  Но этого затруднения можно избежать, сократив дробь на мешающий
Но этого затруднения можно избежать, сократив дробь на мешающий
нам множитель  до перехода к пределу. (Такое сокращение законно, так как при вычислении предела разностного отношения мы считаем, что
до перехода к пределу. (Такое сокращение законно, так как при вычислении предела разностного отношения мы считаем, что  стр. 352.) Таким образом мы получаем результат
стр. 352.) Таким образом мы получаем результат

После сокращения нахождение предела при  не представляет уже никаких трудностей. Этот предел получается путем простой «подстановки», так как разностное отношение в своем новом виде
не представляет уже никаких трудностей. Этот предел получается путем простой «подстановки», так как разностное отношение в своем новом виде  непрерывно, а предел непрерывной функции при
непрерывно, а предел непрерывной функции при  есть просто значение этой функции при
есть просто значение этой функции при  в нашем примере мы получаем непосредственно
в нашем примере мы получаем непосредственно  и, следовательно, если
и, следовательно, если  то
то

Совершенно аналогично мы можем доказать, что в случае функции  мы будем иметь
мы будем иметь  . В самом деле, отношение
. В самом деле, отношение

может быть упрощено по формуле

знаменатель  сокращается, и мы получаем непрерывное выражение
сокращается, и мы получаем непрерывное выражение

При стремлении  это выражение стремится к сумме
это выражение стремится к сумме  в качестве предела получается выражение
в качестве предела получается выражение

И вообще, для функции

где  целое положительное, производная будет иметь вид
целое положительное, производная будет иметь вид

Упражнение. Доказать этот результат. (Примените алгебраическую формулу

В качестве следующего примера, позволяющего непосредственно определить производную, рассмотрим функцию

Мы имеем

Сократим опять дробь и тогда получим

— выражение, опять-таки непрерывное в точке  в качестве предела мы, следовательно, будем иметь
в качестве предела мы, следовательно, будем иметь

Само собой разумеется, что в данном случае ни производная, ни сама функция не определены в точке 
Упражнение. Доказать аналогичным способом, что функция  имеет производную
имеет производную  функция
функция  - имеет производную
- имеет производную  ; функция
; функция  имеет производную
имеет производную 
Продифференцируем теперь функцию

В качестве разностного отношения мы получаем:

Воспользовавшись формулой  можно сократить знаменатель с первым из множителей и получить выражение, непрерывное в точке
можно сократить знаменатель с первым из множителей и получить выражение, непрерывное в точке 

Переход к пределу дает

Упражнения. Доказать, что функция  имеет производную
имеет производную  Доказать далее:
Доказать далее:

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие ко второму русскому изданию
- Как пользоваться книгой
- Что такое математика?
- Глава I. Натуральные числа
- § 1. Операции над целыми числами
- 2. Представление целых чисел с помощью письменных знаков (нумерация).
- 3. Арифметические действия в недесятичных системах счисления.
- § 2. Бесконечность системы натуральных чисел. Математическая индукция
- 2. Арифметическая прогрессия.
- 3. Геометрическая прогрессия.
- 4. Сумма n первых квадратов.
- 5. Одно важное неравенство.
- 6. Биномиальная теорема.
- 7. Дальнейшие замечания по поводу метода математической индукции.
- Дополнение к главе I
- Теория чисел
- 2. Распределение простых чисел.
- § 2. Сравнения
- 2. Теорема Ферма.
- 3. Квадратические вычеты.
- § 3. Пифагоровы числа и большая теорема Ферма
- § 4. Алгоритм Евклида
- 2. Применение к основной теореме арифметики
- 3. Функция Эйлера. Еще раз о теореме Ферма.
- 4. Непрерывные дроби. Диофантовы уравнения
- Глава II. Математическая числовая система
- § 1. Рациональные числа
- 2. Возникновение надобности в рациональных числах внутри самой математики. Принцип обобщения.
- 3. Геометрическое представление рациональных чисел.
- § 2. Несоизмеримые отрезки. Иррациональные числа, пределы
- 2. Десятичные дроби: конечные и бесконечные.
- 3. Пределы. Бесконечные геометрические прогрессии.
- 4. Рациональные числа и периодические десятичные дроби.
- 5. Общее определение иррациональных чисел посредством стягивающихся отрезков.
- 6. Иные методы определения иррациональных чисел.Декиндовы сечения.
- § 3. Замечания из области аналитической геометрии
- 2. Уравнения прямых и кривых линий.
- § 4. Математический анализ бесконечного
- 2. Счетность множества рациональных чисел и несчетность континуума.
- 3. «Кардинальные числа» Кантора.
- 4. Косвенный метод доказательства.
- 5. Парадоксы бесконечного.
- 6. Основания математики.
- § 5. Комплексные числа
- 2. Геометрическое представление комплексных чисел.
- 3. Формула Муавра и корни из единицы.
- 4. Основная теорема алгебры.
- § 6. Алгебраические и трансцендентные числа
- 2. Теорема Лиувилля и конструирование трансцендентных чисел.
- Дополнение к главе II. Алгебра множеств
- 2. Применение к математической логике.
- 3. Одно из применений к теории вероятностей.
- Глава III. Геометрические построения. Алгебра числовых полей
- Часть 1. Доказательства невозможности и алгебра
- 1. Построение полей и извлечение квадратных корней.
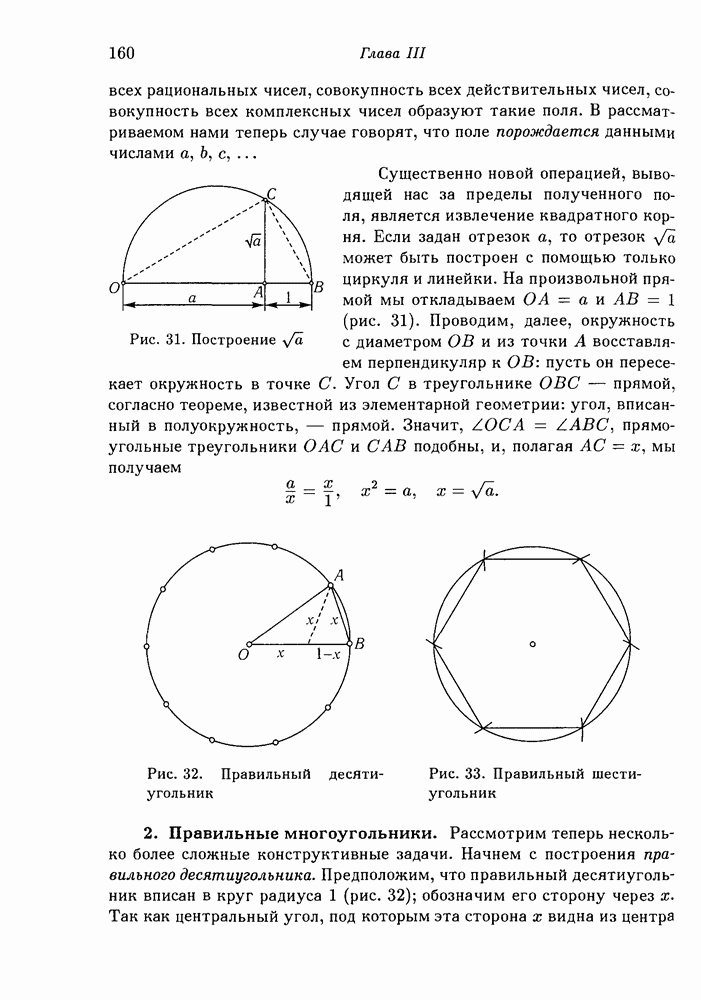
- 2. Правильные многоугольники.
- 3. Проблема Аполлония.
- § 2. Числа, допускающие построение, и числовые поля
- 2. Все числа, допускающие построение, — алгебраические.
- § 3. Неразрешимость трех классических проблем
- 2. Одна теорема о кубических уравнениях.
- 3. Трисекция угла.
- 4. Правильный семиугольник.
- 5. Замечания по поводу квадратуры круга.
- Часть 2. Различные методы выполнения построений
- § 4. Геометрические преобразования. Инверсия
- 2. Свойства инверсии.
- 3. Геометрическое построение обратных точек.
- 4. Как разделить отрезок пополам и как найти центр данного круга с помощью одного циркуля.
- § 5. Построения с помощью иных инструментов. Построения Маскерони с помощью одного циркуля
- 1. Классическая конструкция, служащая для удвоения куба.
- 2. Построения с помощью одного циркуля.
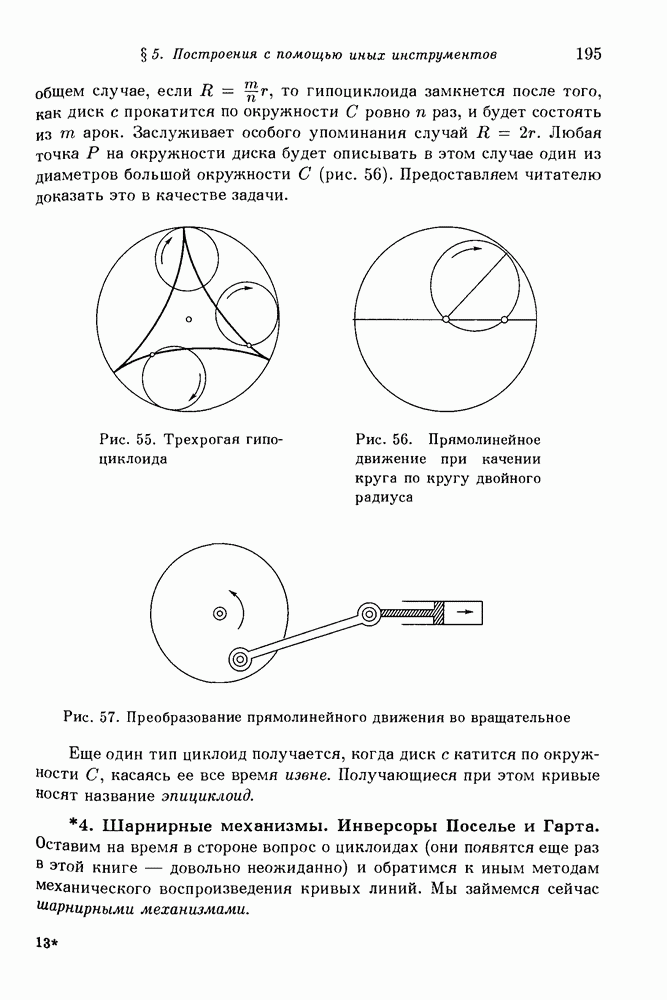
- 3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды.
- 4. Шарнирные механизмы. Инверсоры Поселье и Гарта.
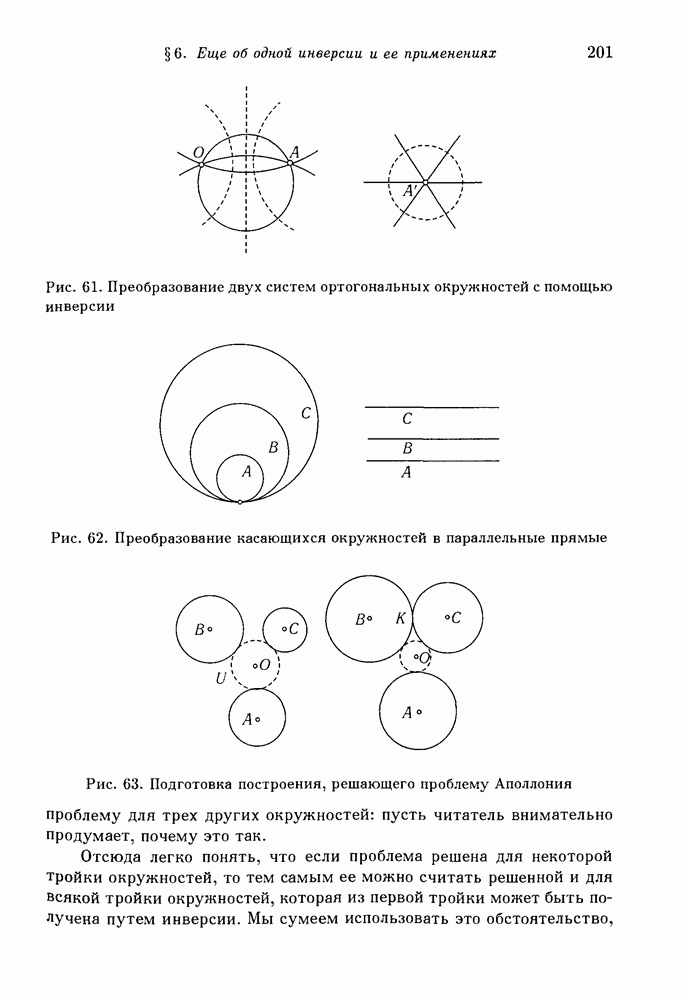
- § 6. Еще об одной инверсии и ее применениях
- 1. Инвариантность углов. Семейства окружностей.
- 2. Применение к проблеме Аполлония.
- 3. Повторные отражения.
- Глава IV. Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- 1. Классификация геометрических свойств. Инвариантность при преобразованиях.
- 2. Проективные преобразования.
- § 2. Основные понятия
- 1. Группа проективных преобразований.
- 2. Теорема Дезарга.
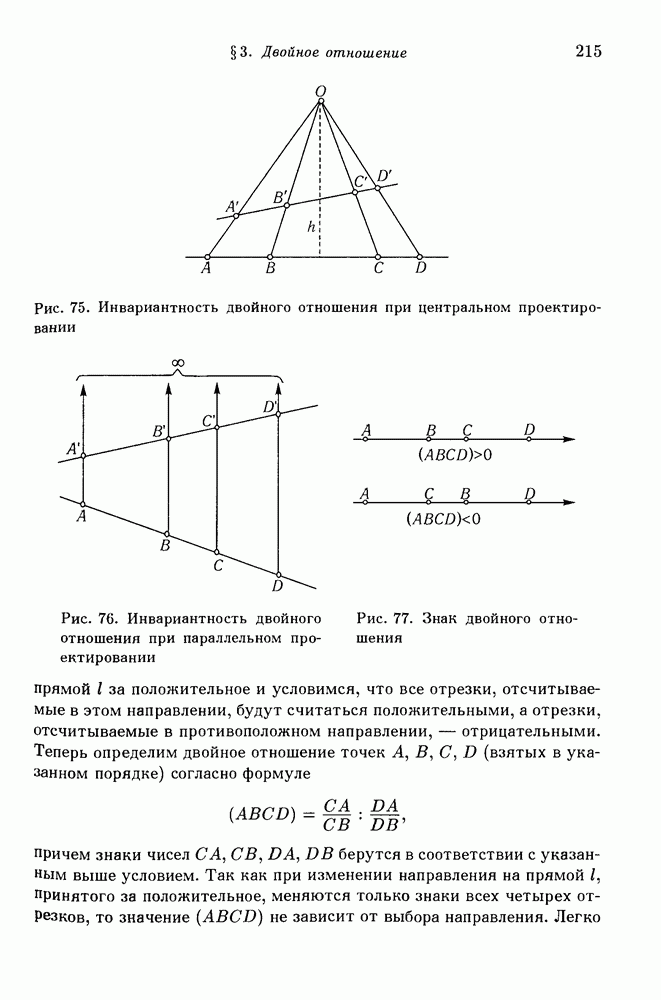
- § 3. Двойное отношение
- § 4. Параллельность и бесконечность
- 2. Идеальные элементы и проектирование.
- 3. Двойное отношение с бесконечно удаленными элементами.
- § 5. Применения
- 2. Двумерное доказательство теоремы Дезарга.
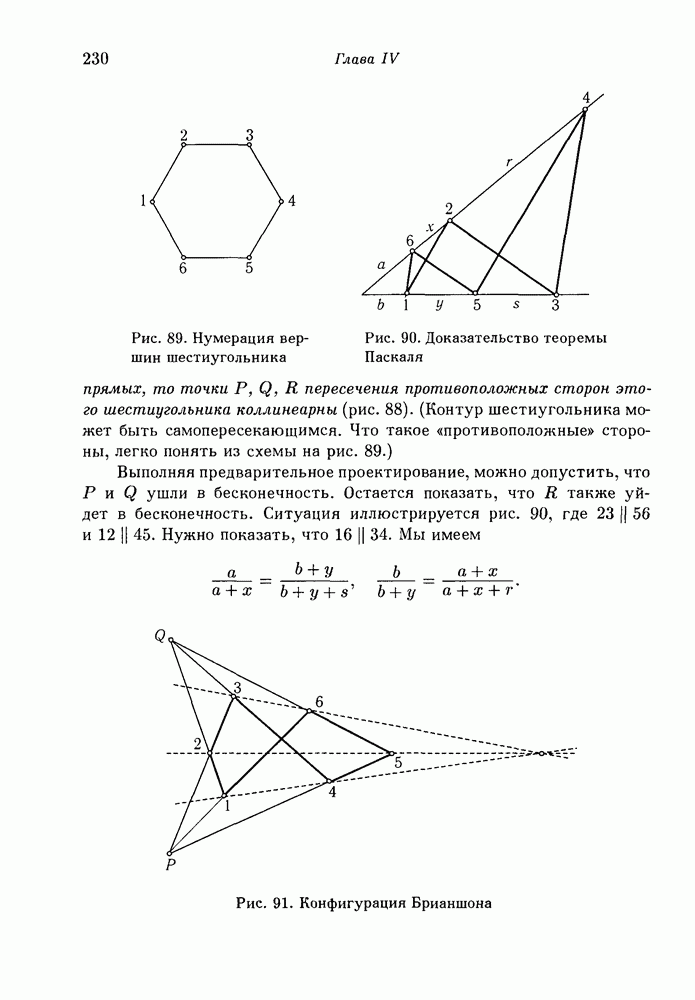
- 3. Теорема Паскаля.
- 4. Теорема Брианшона.
- 5. Замечание по поводу двойственности.
- § 6. Аналитическое представление
- 2. Однородные координаты. Алгебраические основы двойственности.
- § 7. Задачи на построения с помощью одной линейки
- § 8. Конические сечения и квадрики
- 2. Проективные свойства конических сечений.
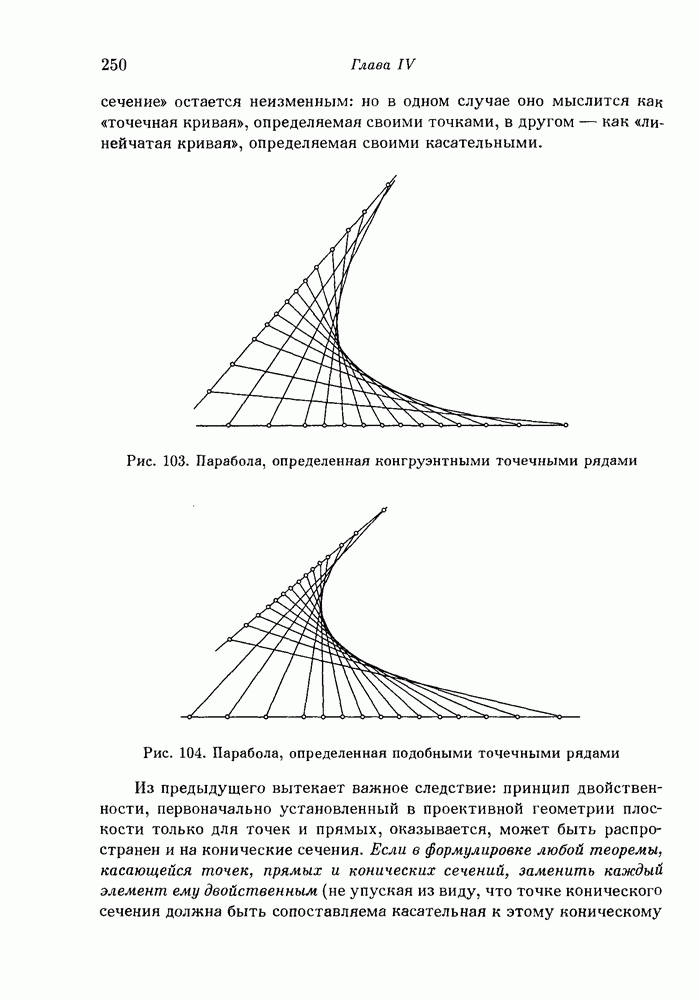
- 3. Конические сечения как «линейчатые кривые».
- 4. Теоремы Паскаля и Брианшона для общего случая произвольных конических сечений.
- 5. Гиперболоид.
- § 9. Аксиоматика и неевклидова геометрия
- 2. Гиперболическая неевклидова геометрия.
- 3. Геометрия и реальность.
- 4. Модель Пуанкаре.
- 5. Эллиптическая, или риманова, геометрия.
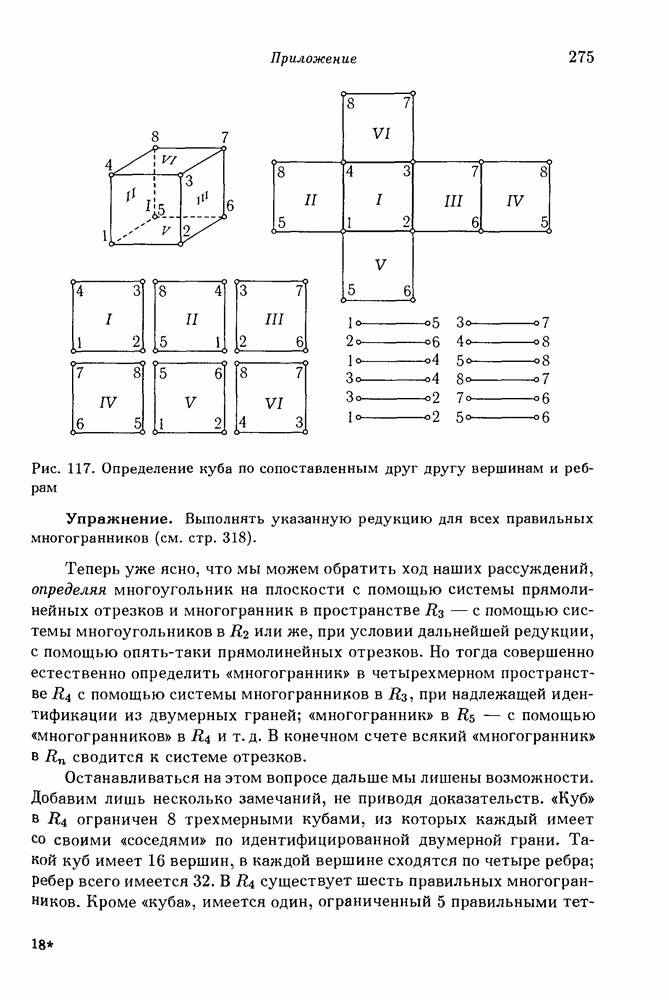
- Приложение. Геометрия в пространствах более чем трех измерений
- Глава V. Топология
- § 1. Формула Эйлера для многогранников
- § 2. Топологические свойства фигур
- 2. Свойства связности.
- § 3. Другие примеры топологических теорем
- 2. Проблема четырех красок.
- 3. Понятие размерности.
- 4. Теорема о неподвижной точке.
- 5. Узлы.
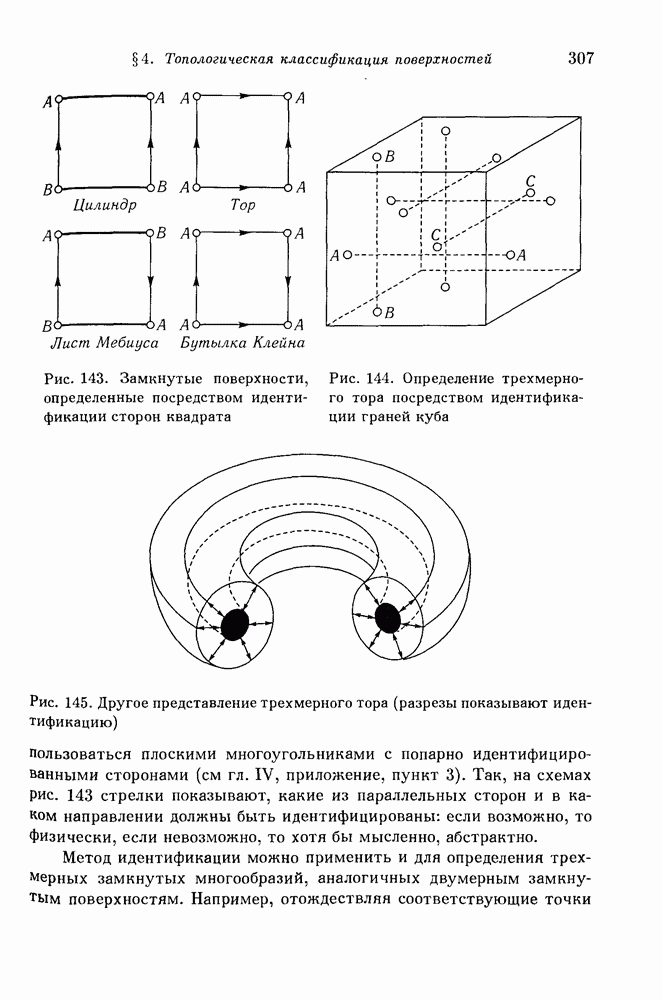
- § 4. Топологическая классификация поверхностей
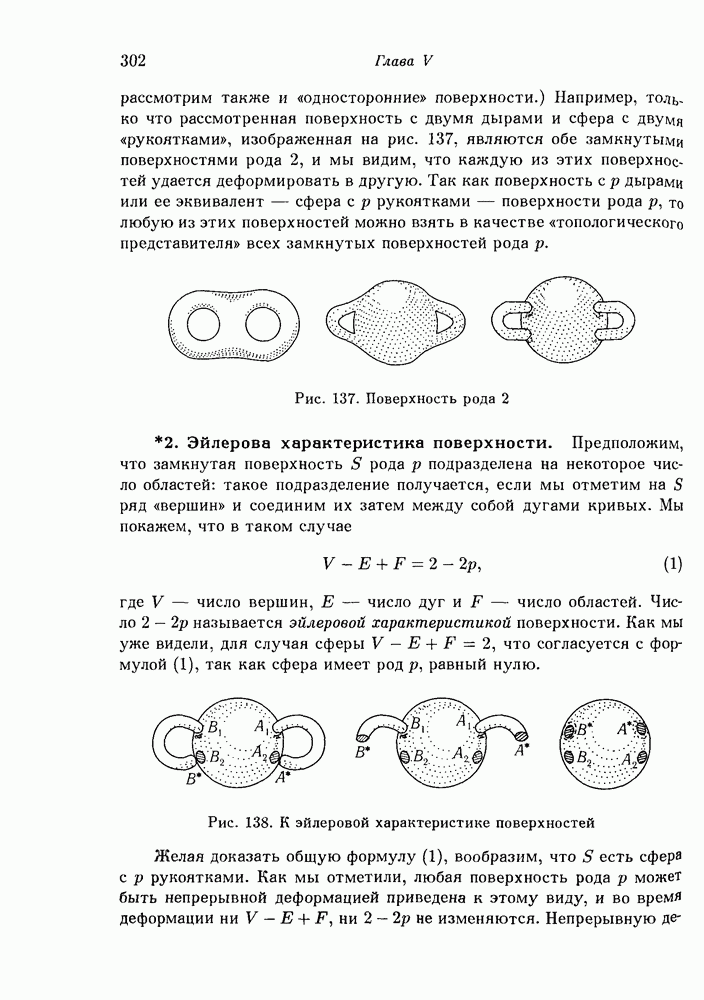
- 2. Эйлерова характеристика поверхности.
- 3. Односторонние поверхности.
- Приложение
- 2. Теорема Жордана для случая многоугольников.
- 3. Основная теорема алгебры.
- Глава VI. Функции и пределы
- § 1. Независимое переменное и функция
- 2. Радианная мера углов.
- 3. График функции. Обратные функции.
- 4. Сложные функции.
- 5. Непрерывность.
- 6. Функции нескольких переменных.
- 7. Функции и преобразования.
- § 2. Пределы
- 2. Монотонные последовательности.
- 3. Число Эйлера e.
- 4. Число «пи»
- 5. Непрерывные дроби.
- § 3. Пределы при непрерывном приближении
- 2. Замечания по поводу понятия предела
- 3. Предел sin x/x
- 4. Пределы при х -> оо.
- § 4. Точное определение непрерывности
- § 5. Две основные теоремы о непрерывных функциях
- 2. Доказательство теоремы Больцано.
- 3. Теорема Вейерштрасса об экстремальных значениях.
- 4. Теорема о последовательностях. Компактные множества.
- § 6. Некоторые применения теоремы Больцано
- 2. Применение к одной механической проблеме.
- Дополнение к главе VI. Дальнейшие примеры на пределы и непрерывность
- 4. Разрывные функции как предел непрерывных.
- 5. Пределы при итерации.
- § 2. Пример, относящийся к непрерывности
- Глава VII. Максимумы и минимумы
- § 1. Задачи из области элементарной геометрии
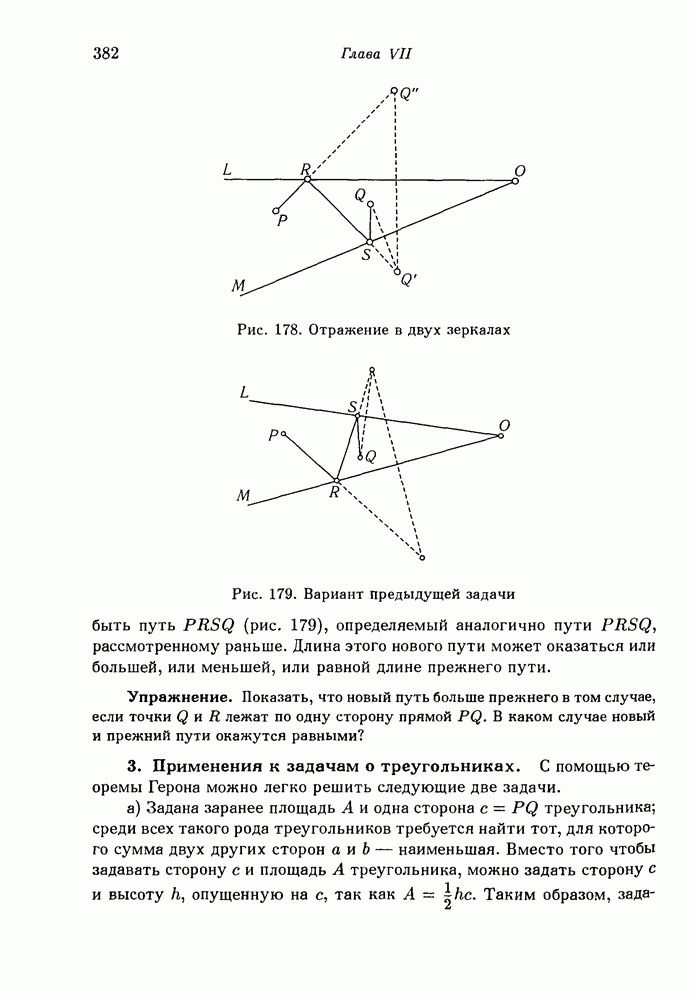
- 2. Теорема Герона. Экстремальное свойство световых лучей.
- 3. Применения к задачам о треугольниках.
- 4. Свойства касательных к эллипсу и гиперболе. Соответствующие экстремальные свойства.
- 5. Экстремальные расстояния точки от данной кривой.
- § 2. Общий принцип, которому подчинены экстремальные задачи
- § 3. Стационарные точки и дифференциальное исчисление
- 2. Максимумы и минимумы функций нескольких переменных. Седловые точки.
- 3. Точки минимакса и топология.
- 4. Расстояние точки от поверхности.
- § 4. Треугольник Шварца
- 4. Треугольники, образованные световыми лучами.
- 5. Замечания, касающиеся задач на отражение и эргодическое движение.
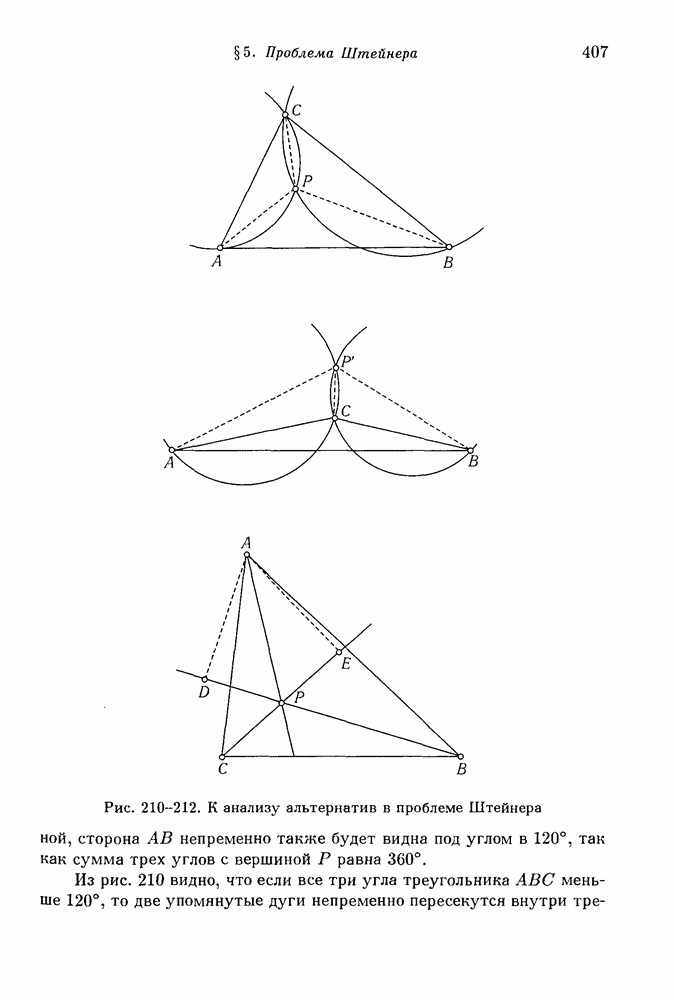
- § 5. Проблема Штейнера
- 2. Анализ возникающих альтернатив.
- 3. Дополнительная проблема.
- 4. Замечания и упражнения.
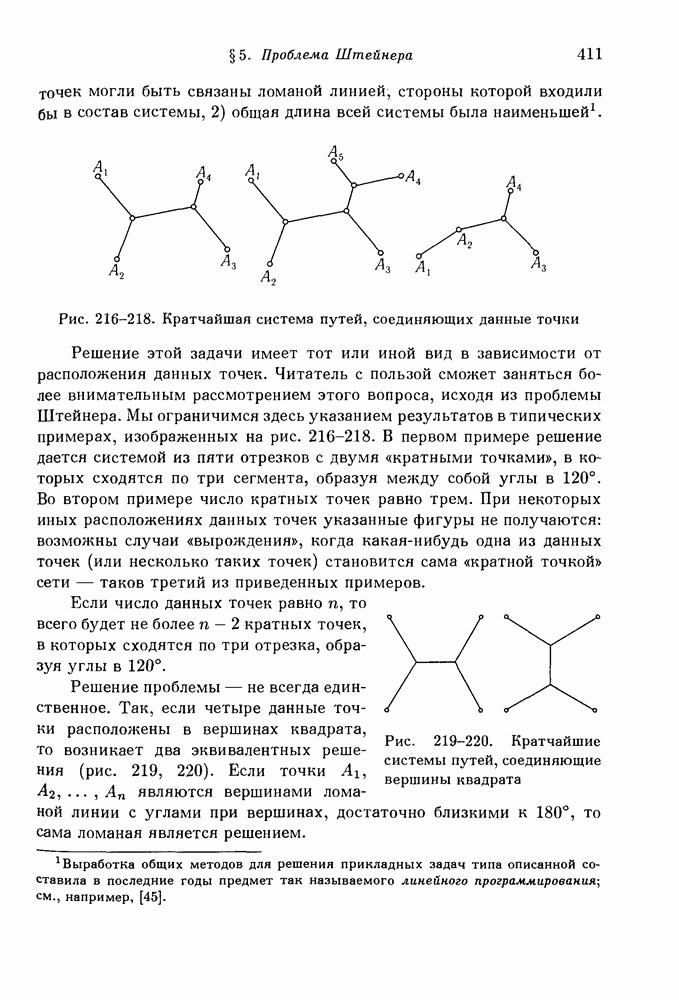
- 5. Обобщение: проблема уличной сети.
- § 6. Экстремумы и неравенства
- 1. Средние арифметическое и геометрическое двух положительных величин.
- 2. Обобщение на случай n переменных.
- 3. Метод наименьших квадратов.
- § 7. Существование экстремума. Принцип Дирихле
- 3. Экстремальные проблемы элементарного содержания.
- 4. Трудности, возникающие в более сложных случаях.
- § 8. Изопериметрическая проблема
- § 9. Экстремальные проблемы с граничными условиями. Связь между проблемой Штейнера и изопериметрической проблемой
- § 10. Вариационное исчисление
- 2. Вариационное исчисление. Принцип Ферма в оптике.
- 3. Решение задачи о брахистохроне, принадлежащее Якобу Бернулли.
- 4. Геодезические линии на сфере. Минимаксы.
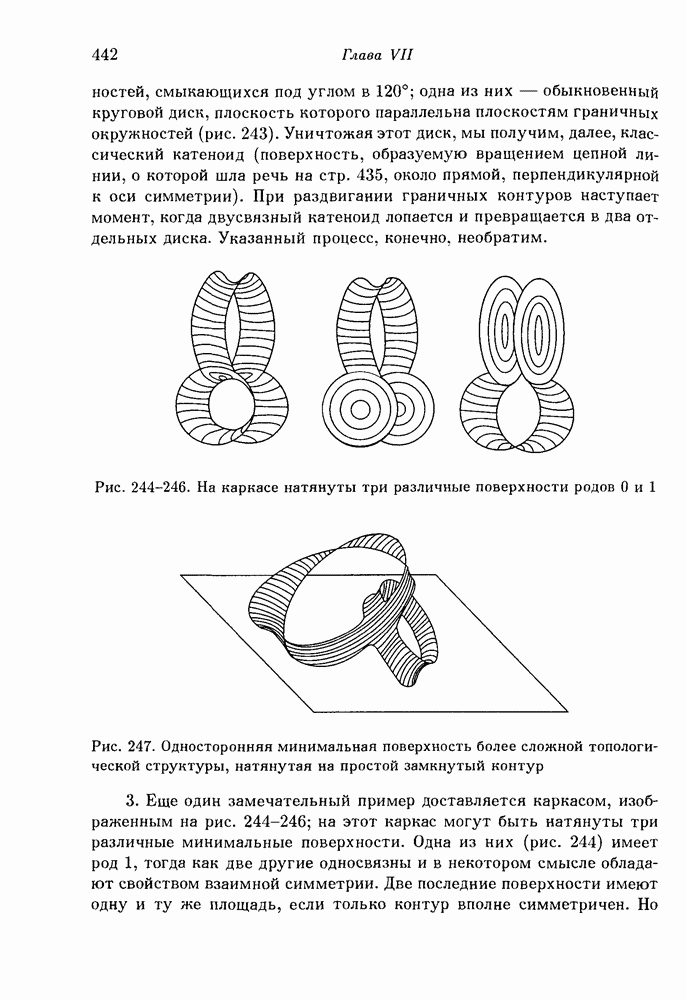
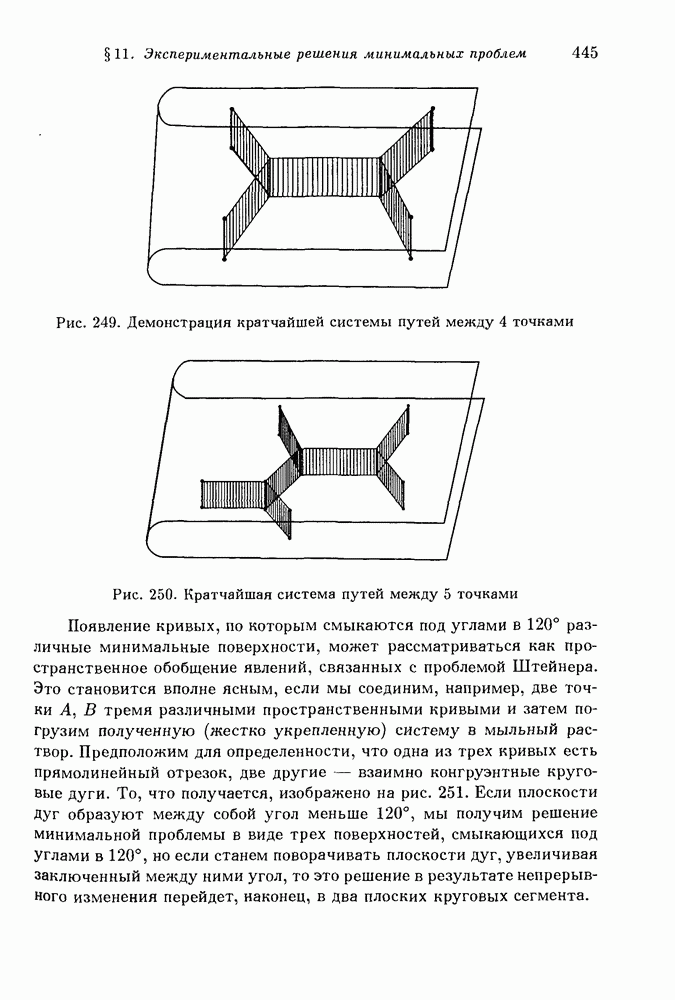
- § 11. Экспериментальные решения минимальных проблем. Опыты с мыльными пленками
- 2. Опыты с мыльными пленками.
- 3. Новые опыты, относящиеся к проблеме Плато.
- 4. Экспериментальные решения других математических проблем.
- Глава VIII. Математический анализ
- § 1. Интеграл
- 2. Интеграл.
- 3. Общие замечания о понятии интеграла. Общее определение.
- 4. Примеры интегрирования. Интегрирование x^r.
- 5. Правила «интегрального исчисления».
- § 2. Производная
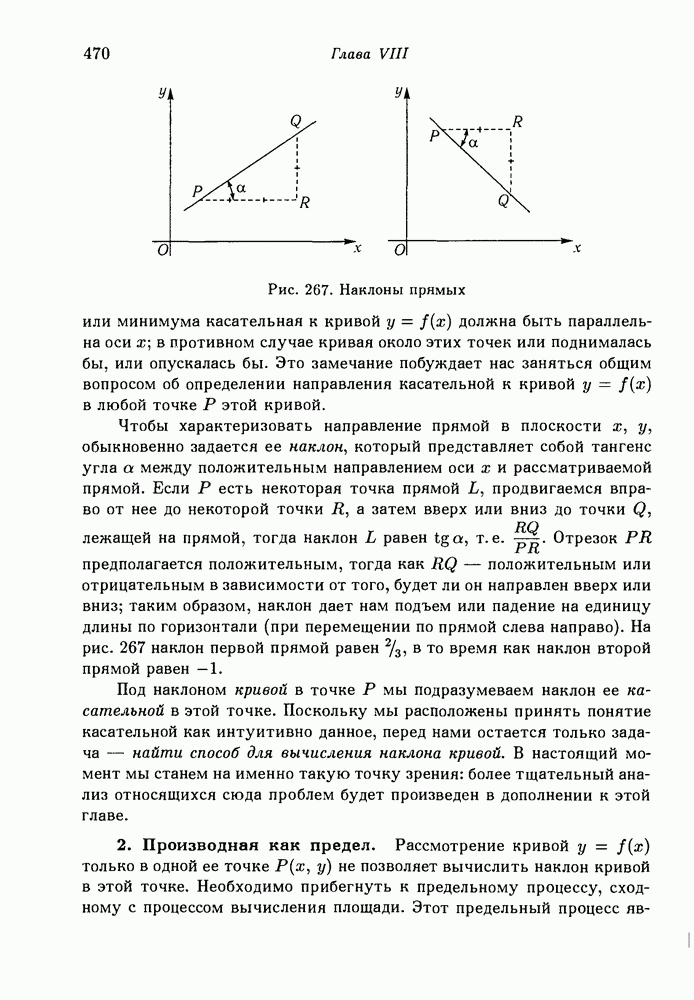
- 2. Производная как предел.
- 3. Примеры.
- 4. Производные от тригонометрических функций.
- 5. Дифференцируемость и непрерывность.
- 6. Производная и скорость. Вторая производная и ускорение.
- 7. Геометрический смысл второй производной.
- 8. Максимумы и минимумы.
- § 3. Техника дифференцирования
- § 4. Обозначения Лейбница и «бесконечно малые»
- § 5. Основная теорема анализа
- 2. Первые применения. Интегрирование функций x^r, cosx, sinx. Функция arctgx
- 3. Формула Лейбница для «пи»
- § 6. Показательная (экспоненциальная) функция и логарифм
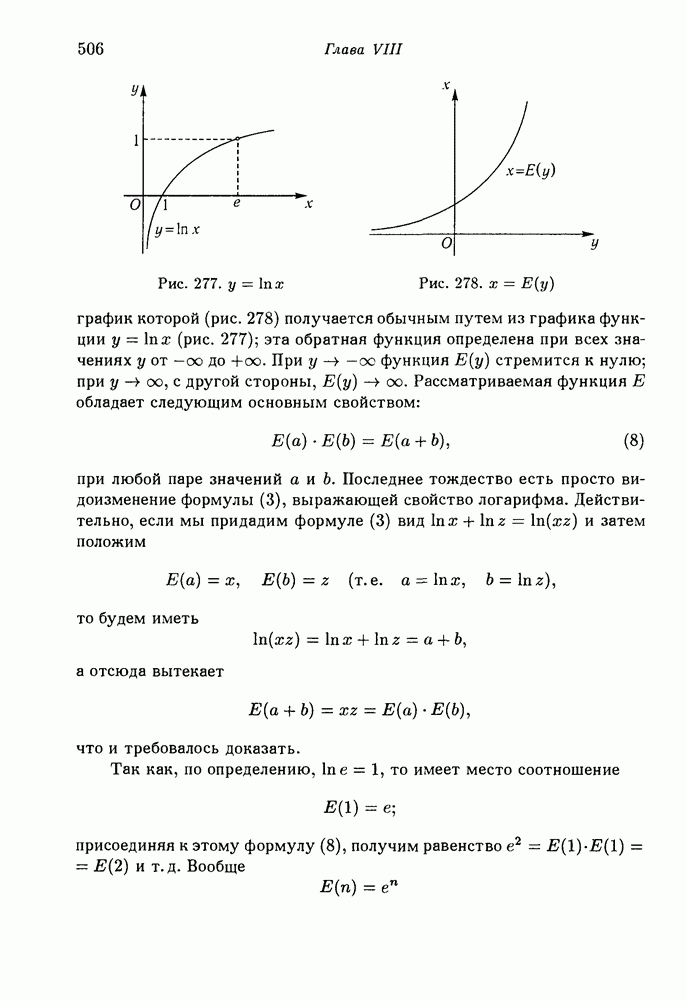
- 2. Показательная (экспоненциальная) функция.
- 3. Формулы дифференцирования функций е^х, а^х, x^s.
- 4. Явные выражения числа е^x и функций lnx в виде пределов.
- 5. Бесконечный ряд для логарифма. Вычисление логарифмов.
- § 7. Дифференциальные уравнения
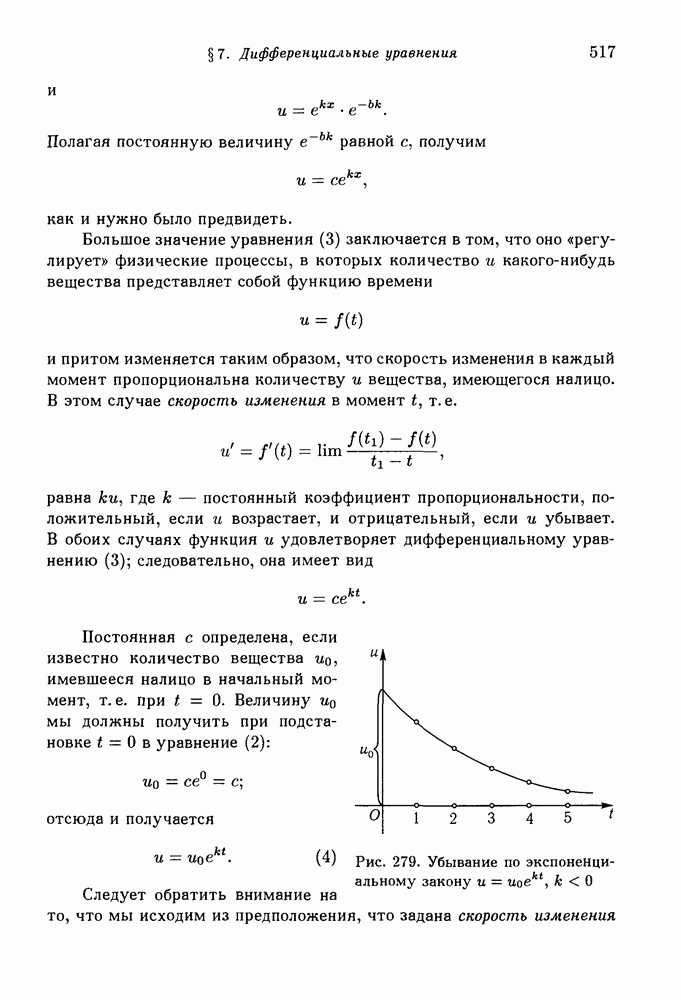
- 2. Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- 3. Другие примеры. Простейшие колебания.
- 4. Закон движения Ньютона.
- Дополнение к главе VIII
- § 1. Вопросы принципиального порядка
- 3. Другие приложения понятия интеграла. Работа. Длина кривой.
- § 2. Порядки возрастания
- 2. Порядок возрастания ln(n!)
- § 3. Бесконечные ряды и бесконечные произведения
- 2. Формула Эйлера cos x + i sin x = exp(ix).
- 3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin x в виде бесконечного произведения.
- § 4. Доказательство теоремы о простых числах на основе статистического метода
- Приложение. Дополнительные замечания, задачи и упражнения
- Аналитическая геометрия
- Геометрические построения
- Проективная и неевклидова геометрия
- Топология
- Функции, пределы, непрерывность
- Максимумы и минимумы
- Дифференциальное и интегральное исчисления
- Техника интегрирования
- Рекомендуемая литература