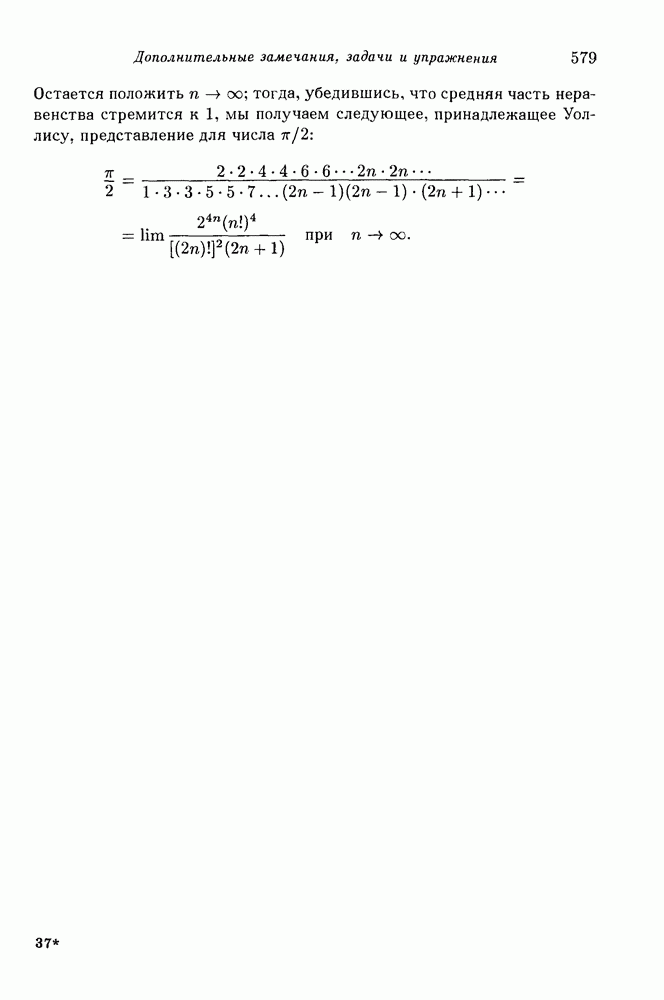| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. Теорема о неподвижной точке.
В приложениях топологии к другим отраслям математики играют важную роль теоремы о «неподвижной точке». Типическим примером является излагаемая ниже теорема Брауэра. Она гораздо менее «очевидна» в интуитивном смысле, чем другие топологические теоремы.
Рассмотрим круглый диск на плоскости. Под таковым мы понимаем внутренность некоторого круга вместе с его границей (окружностью). Предположим, что весь этот диск подвергается некоторому топологическому преобразованию (не обязательно взаимно однозначному), при котором всякая точка диска остается точкой диска, хотя и меняет свое положение. Например, представляя себе этот диск сделанным из тонкой резины, можно его сжимать, растягивать, вращать, изгибать — одним словом, деформировать как угодно, лишь бы его точки не вышли за пределы первоначального положения диска. Иначе еще можно представить себе, что жидкость, налитая в стакан, приведена в движение таким образом, что частицы, находившиеся на поверхности, остаются
на ней и во время движения; тогда в каждый определенный момент времени положение частиц на поверхности, определяет некоторое топологическое преобразование или трансформацию первоначального их распределения. Теорема Брауэра утверждает: каждое непрерывное преобразование такого рода оставляет неподвижной по крайней мере одну точку; другими словами, существует по меньшей мере одна точка, положение которой после преобразования совпадает с положением ее до преобразования. (В примере с жидкостью неподвижные точки зависят от избранного момента времени; в частности, если движение сводится к простому круговому вращению, то неподвижной точкой в любой момент является центр.) Излагаемое далее доказательство существования неподвижной точки — очень характерный пример рассуждений, применяемых в топологии.

Рис. 133. К доказательству теоремы Броуэра
Рассмотрим наш диск до и после трансформации и допустим, что, вопреки утверждению теоремы, ни одна точка не остается неподвижной, так что любая точка диска после трансформации превращается в некоторую другую точку диска. Каждой точке Р диска в его первоначальном положении сопоставим стрелку или «вектор трансформации»  причем Р есть та точка, в которую переходит Р после трансформации. Такая стрелка будет поставлена во всякой точке диска, так как всякая точка куда-то перемещается. Рассмотрим теперь все
причем Р есть та точка, в которую переходит Р после трансформации. Такая стрелка будет поставлена во всякой точке диска, так как всякая точка куда-то перемещается. Рассмотрим теперь все
точки граничной окружности вместе с соответствующими векторами трансформации. Все эти векторы направлены внутрь круга, так как, по предположению, ни одна точка не выходит за его пределы. Начнем с какой-нибудь точки Р, лежащей на граничной окружности, и пойдем по этой окружности в направлении, противоположном движению часовой стрелки. При этом направление вектора трансформации будет изменяться, так как различным точкам границы соответствуют различно направленные векторы. Все эти векторы можно также представить себе (подвергнувши их параллельному переносу) выходящими из некоторой одной и той же точки плоскости (рис. 133). Легко понять, что, когда мы обойдем один раз весь круг от точки  до точки
до точки  соответствующий вектор, после ряда поворотов, вернется в первоначальное положение. Число полных поворотов, сделанных при этом нашим вектором, мы назовем индексом рассматриваемой граничной окружности; точнее говоря, мы определим индекс как алгебраическую сумму различных изменений в угле векторов, условливаясь, что всякому частному повороту по часовой стрелке приписывается знак минус, против часовой стрелки — знак плюс. Индекс есть итоговый результат, который a priori равен одному из чисел
соответствующий вектор, после ряда поворотов, вернется в первоначальное положение. Число полных поворотов, сделанных при этом нашим вектором, мы назовем индексом рассматриваемой граничной окружности; точнее говоря, мы определим индекс как алгебраическую сумму различных изменений в угле векторов, условливаясь, что всякому частному повороту по часовой стрелке приписывается знак минус, против часовой стрелки — знак плюс. Индекс есть итоговый результат, который a priori равен одному из чисел  соответствующих итоговым поворотам на 0°, ±360°, ±720°,... Мы утверждаем теперь, что индекс граничной окружности равен единице, т. е. что итоговый поворот вектора трансформации составляет один полный поворот в положительном направлении. Прежде всего напомним еще раз, что вектор трансформации, имеющий начало в точке граничного круга, направлен непременно внутрь круга, а не по касательной. Если допустим, что итоговый поворот вектора трансформации отличается от итогового поворота касательного вектора (а этот последний поворот в точности равен 360°, так как касательный вектор, очевидно, делает один полный поворот), то разность между итоговыми поворотами касательного вектора и вектора трансформации будет равна кратному 360°, но никак не нулю. Отсюда следует, что вектор трансформации при обходе круга должен будет по крайней мере раз сделать полный поворот вокруг касательного вектора, а так как оба вектора изменяются непрерывно, то в некоторой точке окружности направления двух векторов совпадут. Но это, как мы видели, невозможно.
соответствующих итоговым поворотам на 0°, ±360°, ±720°,... Мы утверждаем теперь, что индекс граничной окружности равен единице, т. е. что итоговый поворот вектора трансформации составляет один полный поворот в положительном направлении. Прежде всего напомним еще раз, что вектор трансформации, имеющий начало в точке граничного круга, направлен непременно внутрь круга, а не по касательной. Если допустим, что итоговый поворот вектора трансформации отличается от итогового поворота касательного вектора (а этот последний поворот в точности равен 360°, так как касательный вектор, очевидно, делает один полный поворот), то разность между итоговыми поворотами касательного вектора и вектора трансформации будет равна кратному 360°, но никак не нулю. Отсюда следует, что вектор трансформации при обходе круга должен будет по крайней мере раз сделать полный поворот вокруг касательного вектора, а так как оба вектора изменяются непрерывно, то в некоторой точке окружности направления двух векторов совпадут. Но это, как мы видели, невозможно.
Рассмотрим теперь окружность, концентрическую границе диска, но с меньшим радиусом, а также соответствующие векторы трансформации. Для этой новой окружности индекс также непременно равен единице. В самом деле, при переходе от граничной окружности к новой окружности индекс должен меняться непрерывно, так как
направления самих векторов трансформации меняются непрерывно. Но индекс может принимать только целые значения и потому остается равным единице: действительно, переход от единицы к какому-нибудь другому целому числу обязательно был бы связан со скачком, т. е. нарушением непрерывности. (Очень характерное математическое рассуждение: величина меняется непрерывно, но может принимать только целые значения, значит, она постоянна.) Итак, мы можем найти окружность, концентрическую граничной, притом сколь угодно малую, для которой индекс будет равен единице. Но это невозможно, так как, в силу непрерывности преобразования, векторы трансформации в достаточно малом круге должны весьма мало отличаться от вектора в центре круга. И потому итоговый поворот такого вектора при обходе круга может быть сделан, скажем, меньше 10°, если только радиус круга будет достаточно мал. Но отсюда следует, что индекс такого круга (обязательно целое число) не может быть отличен от нуля. Полученное противоречие показывает, что сделанное нами допущение об отсутствии неподвижных точек преобразования должно быть отвергнуто. Таким образом, теорема доказана.

Рис. 132. Векторы преобразования
Теорема о неподвижных точках имеет место не только для кругового диска, но, конечно, и для треугольника, квадрата и всякой другой фигуры, в которую диск может быть переведен топологическим преобразованием. В самом деле, если бы некоторая фигура А, получающаяся из кругового диска посредством такого рода трансформации, могла быть преобразована сама в себя без неподвижных точек, то тем самым было бы определено и топологическое преобразование кругового диска самого в себя без неподвижных точек, а это, как мы видели, невозможно. Теорема обобщается также на случай трехмерных фигур — сфер или кубов, но доказательство не столь просто.
Хотя теорема Брауэра о неподвижных точках в случае круга не является вполне очевидной в интуитивном смысле, однако легко убедиться, что она является непосредственным следствием такой, достаточно очевидной теоремы: невозможно трансформировать непрерывно круговой диск в одну только его граничную окружность таким образом, чтобы каждая точка этой окружности оставалась неподвижной. Убедимся, что существование непрерывной
трансформации диска на себя без неподвижных точек противоречит этой последней теореме. Предположим, что указанного рода непрерывная трансформация  существует. Тогда для всякой точки Р нашего диска проведем вектор с началом в точке Р, проводя его через Р и заканчивая в точке
существует. Тогда для всякой точки Р нашего диска проведем вектор с началом в точке Р, проводя его через Р и заканчивая в точке  где он встретится с граничной окружностью. Тогда преобразование
где он встретится с граничной окружностью. Тогда преобразование  будет непрерывным преобразованием всего диска в граничную окружность, оставляющим неподвижными все точки этой окружности, возможность чего была отвергнута. Подобное рассуждение можно применить и при доказательстве теоремы Брауэра в трехмерном случае сферы или куба.
будет непрерывным преобразованием всего диска в граничную окружность, оставляющим неподвижными все точки этой окружности, возможность чего была отвергнута. Подобное рассуждение можно применить и при доказательстве теоремы Брауэра в трехмерном случае сферы или куба.
Легко убедиться, с другой стороны, что для некоторых фигур непрерывные преобразования в себя без неподвижных точек возможны.
Например, кольцеобразная область между двумя концентрическими кругами может быть подвергнута вращению около центра на угол, не являющийся кратным 360°, и это как раз будет непрерывным преобразованием области в себя без неподвижных точек. Такое же преобразование можно произвести над поверхностью сферы, сопоставляя всякой ее точке диаметрально противоположную. Но, применяя тот же метод, что и в случае диска, не представит труда доказать, что непрерывное преобразование сферической поверхности, не переводящее ни одной точки в диаметрально противоположную (например, всякая малая деформация), непременно имеет неподвижные точки.
Теоремы о неподвижных точках вроде перечисленных выше доставляют могущественный метод для доказательства многих «теорем существования» в разных областях математики, причем геометрический характер этих теорем часто далеко не очевиден. Замечательным примером может служить теорема Пуанкаре, высказанная им незадолго до смерти, в 1912 г., без доказательства. Из этой теоремы непосредственно вытекает существование бесчисленного множества периодических орбит в ограниченной проблеме трех тел. Пуанкаре не сумел обосновать своей догадки, доказательство этого замечательного факта получил через год американский математик Г. Д. Биркгофф. С тех пор топологические методы неоднократно и с большим успехом применялись к изучению качественного поведения динамических систем.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму русскому изданию
- Как пользоваться книгой
- Что такое математика?
- Глава I. Натуральные числа
- § 1. Операции над целыми числами
- 2. Представление целых чисел с помощью письменных знаков (нумерация).
- 3. Арифметические действия в недесятичных системах счисления.
- § 2. Бесконечность системы натуральных чисел. Математическая индукция
- 2. Арифметическая прогрессия.
- 3. Геометрическая прогрессия.
- 4. Сумма n первых квадратов.
- 5. Одно важное неравенство.
- 6. Биномиальная теорема.
- 7. Дальнейшие замечания по поводу метода математической индукции.
- Дополнение к главе I
- Теория чисел
- 2. Распределение простых чисел.
- § 2. Сравнения
- 2. Теорема Ферма.
- 3. Квадратические вычеты.
- § 3. Пифагоровы числа и большая теорема Ферма
- § 4. Алгоритм Евклида
- 2. Применение к основной теореме арифметики
- 3. Функция Эйлера. Еще раз о теореме Ферма.
- 4. Непрерывные дроби. Диофантовы уравнения
- Глава II. Математическая числовая система
- § 1. Рациональные числа
- 2. Возникновение надобности в рациональных числах внутри самой математики. Принцип обобщения.
- 3. Геометрическое представление рациональных чисел.
- § 2. Несоизмеримые отрезки. Иррациональные числа, пределы
- 2. Десятичные дроби: конечные и бесконечные.
- 3. Пределы. Бесконечные геометрические прогрессии.
- 4. Рациональные числа и периодические десятичные дроби.
- 5. Общее определение иррациональных чисел посредством стягивающихся отрезков.
- 6. Иные методы определения иррациональных чисел.Декиндовы сечения.
- § 3. Замечания из области аналитической геометрии
- 2. Уравнения прямых и кривых линий.
- § 4. Математический анализ бесконечного
- 2. Счетность множества рациональных чисел и несчетность континуума.
- 3. «Кардинальные числа» Кантора.
- 4. Косвенный метод доказательства.
- 5. Парадоксы бесконечного.
- 6. Основания математики.
- § 5. Комплексные числа
- 2. Геометрическое представление комплексных чисел.
- 3. Формула Муавра и корни из единицы.
- 4. Основная теорема алгебры.
- § 6. Алгебраические и трансцендентные числа
- 2. Теорема Лиувилля и конструирование трансцендентных чисел.
- Дополнение к главе II. Алгебра множеств
- 2. Применение к математической логике.
- 3. Одно из применений к теории вероятностей.
- Глава III. Геометрические построения. Алгебра числовых полей
- Часть 1. Доказательства невозможности и алгебра
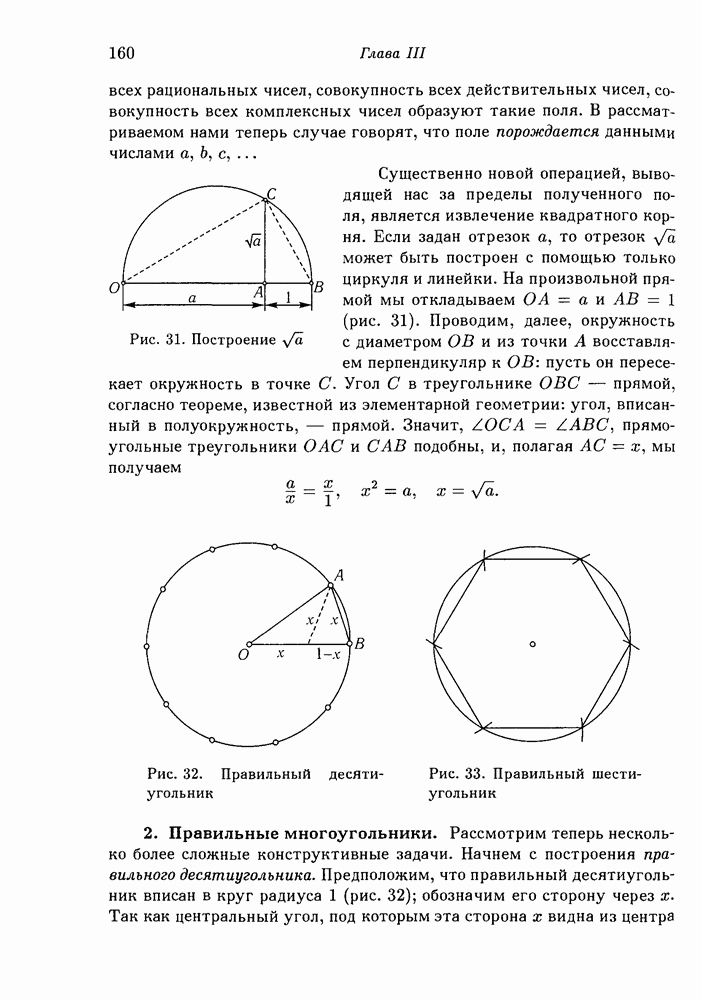
- 1. Построение полей и извлечение квадратных корней.
- 2. Правильные многоугольники.
- 3. Проблема Аполлония.
- § 2. Числа, допускающие построение, и числовые поля
- 2. Все числа, допускающие построение, — алгебраические.
- § 3. Неразрешимость трех классических проблем
- 2. Одна теорема о кубических уравнениях.
- 3. Трисекция угла.
- 4. Правильный семиугольник.
- 5. Замечания по поводу квадратуры круга.
- Часть 2. Различные методы выполнения построений
- § 4. Геометрические преобразования. Инверсия
- 2. Свойства инверсии.
- 3. Геометрическое построение обратных точек.
- 4. Как разделить отрезок пополам и как найти центр данного круга с помощью одного циркуля.
- § 5. Построения с помощью иных инструментов. Построения Маскерони с помощью одного циркуля
- 1. Классическая конструкция, служащая для удвоения куба.
- 2. Построения с помощью одного циркуля.
- 3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды.
- 4. Шарнирные механизмы. Инверсоры Поселье и Гарта.
- § 6. Еще об одной инверсии и ее применениях
- 1. Инвариантность углов. Семейства окружностей.
- 2. Применение к проблеме Аполлония.
- 3. Повторные отражения.
- Глава IV. Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- 1. Классификация геометрических свойств. Инвариантность при преобразованиях.
- 2. Проективные преобразования.
- § 2. Основные понятия
- 1. Группа проективных преобразований.
- 2. Теорема Дезарга.
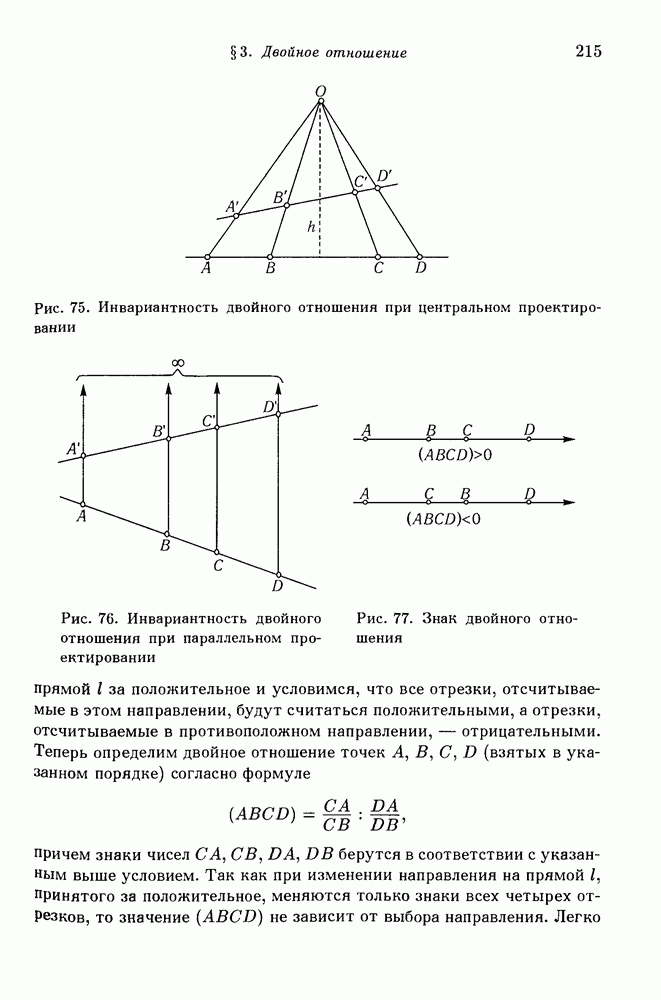
- § 3. Двойное отношение
- § 4. Параллельность и бесконечность
- 2. Идеальные элементы и проектирование.
- 3. Двойное отношение с бесконечно удаленными элементами.
- § 5. Применения
- 2. Двумерное доказательство теоремы Дезарга.
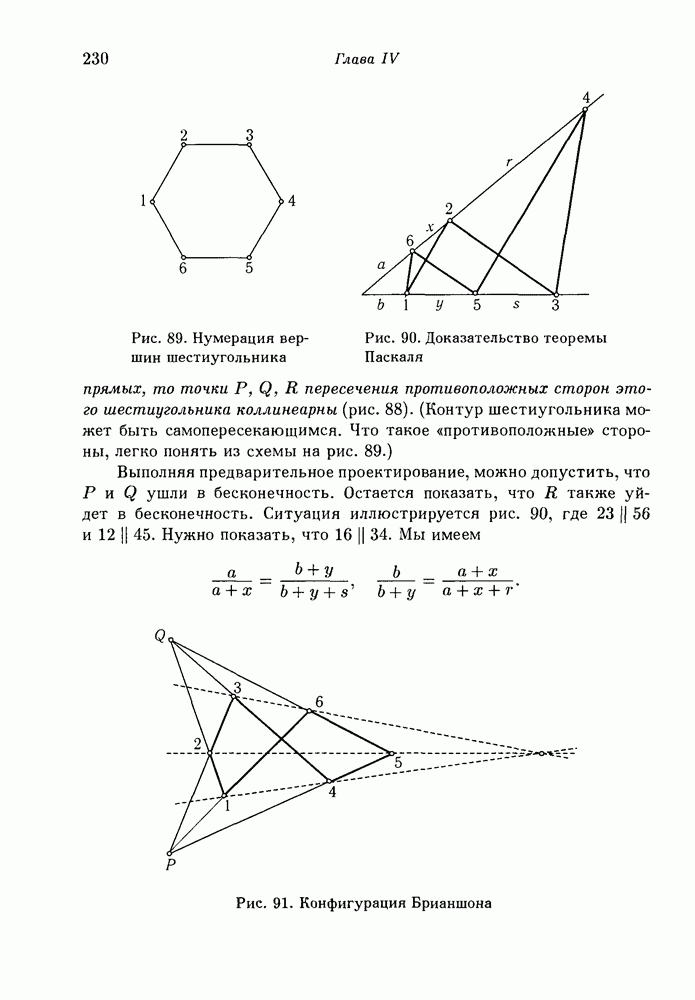
- 3. Теорема Паскаля.
- 4. Теорема Брианшона.
- 5. Замечание по поводу двойственности.
- § 6. Аналитическое представление
- 2. Однородные координаты. Алгебраические основы двойственности.
- § 7. Задачи на построения с помощью одной линейки
- § 8. Конические сечения и квадрики
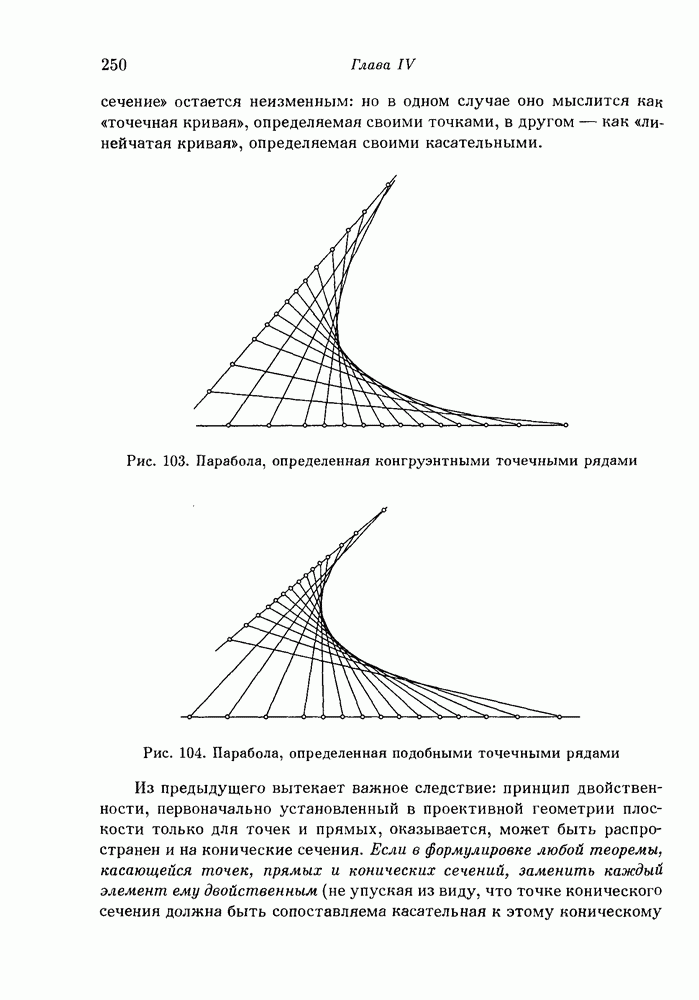
- 2. Проективные свойства конических сечений.
- 3. Конические сечения как «линейчатые кривые».
- 4. Теоремы Паскаля и Брианшона для общего случая произвольных конических сечений.
- 5. Гиперболоид.
- § 9. Аксиоматика и неевклидова геометрия
- 2. Гиперболическая неевклидова геометрия.
- 3. Геометрия и реальность.
- 4. Модель Пуанкаре.
- 5. Эллиптическая, или риманова, геометрия.
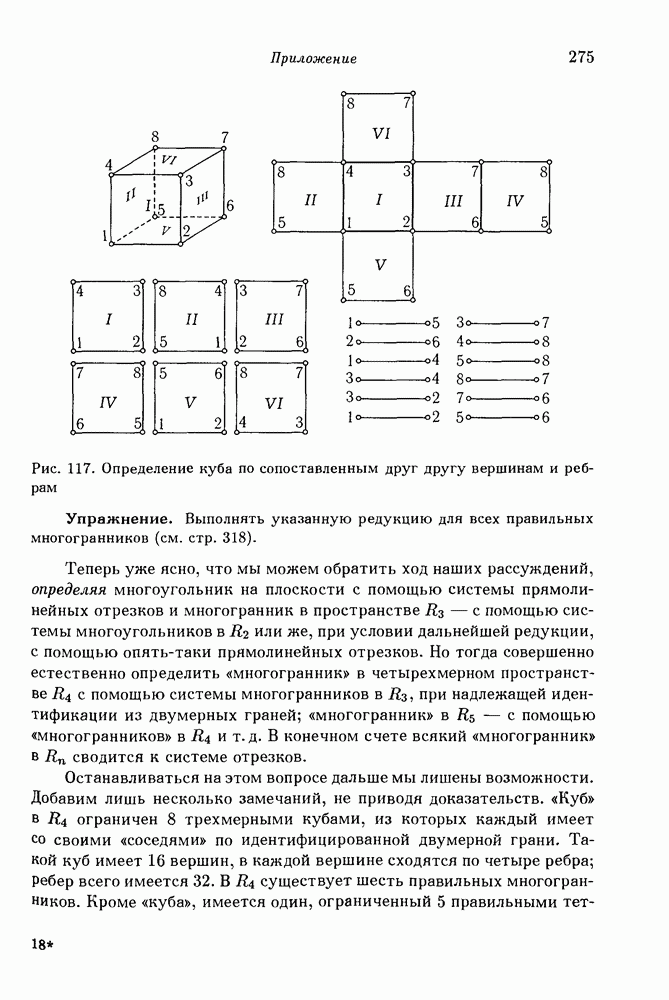
- Приложение. Геометрия в пространствах более чем трех измерений
- Глава V. Топология
- § 1. Формула Эйлера для многогранников
- § 2. Топологические свойства фигур
- 2. Свойства связности.
- § 3. Другие примеры топологических теорем
- 2. Проблема четырех красок.
- 3. Понятие размерности.
- 4. Теорема о неподвижной точке.
- 5. Узлы.
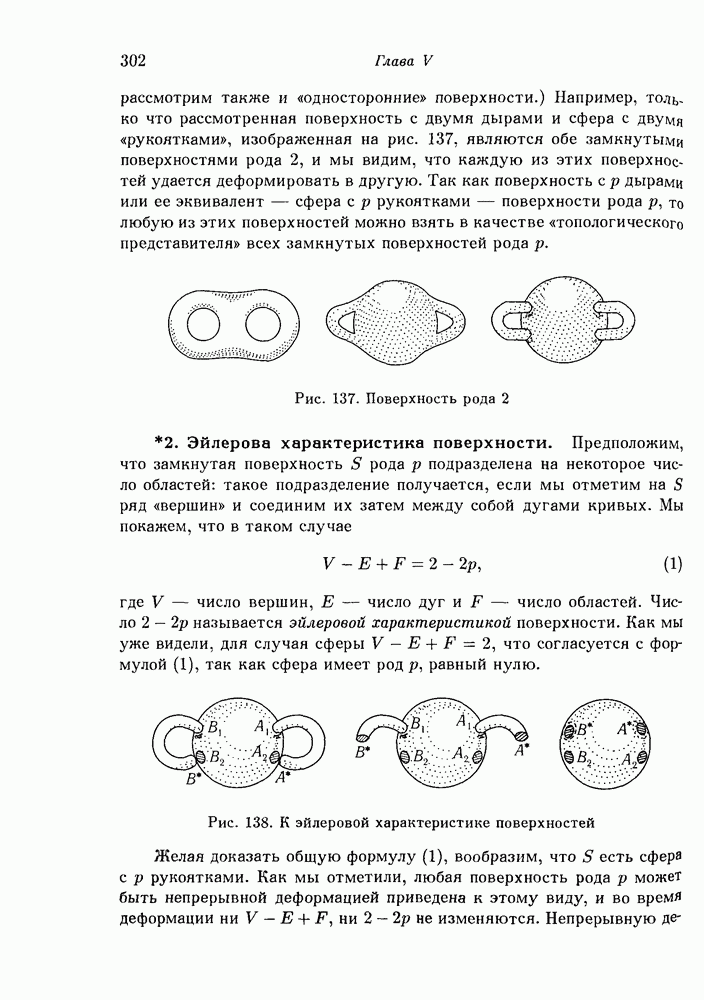
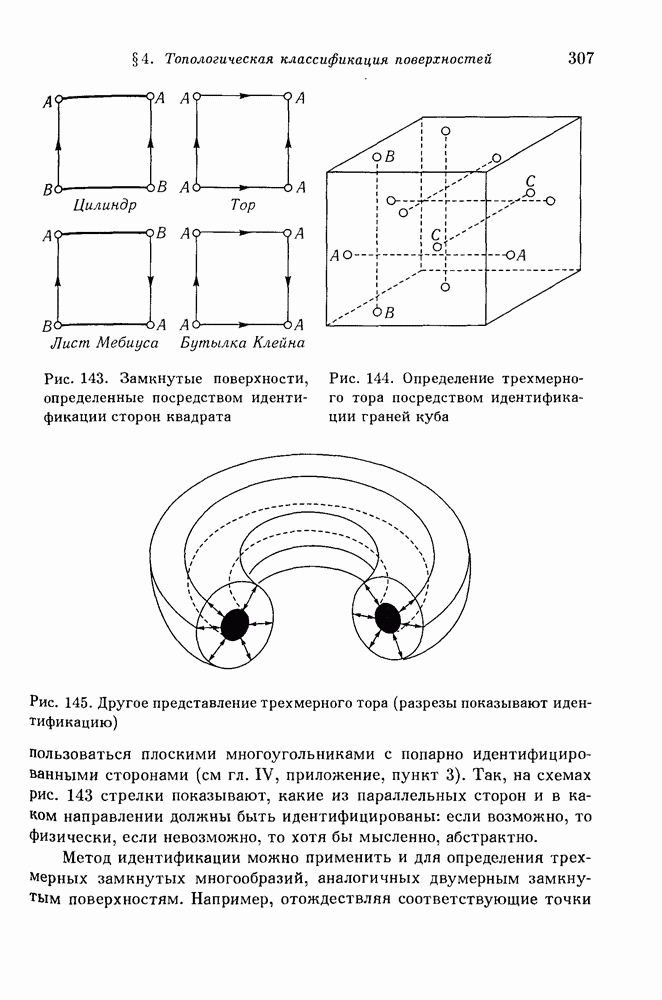
- § 4. Топологическая классификация поверхностей
- 2. Эйлерова характеристика поверхности.
- 3. Односторонние поверхности.
- Приложение
- 2. Теорема Жордана для случая многоугольников.
- 3. Основная теорема алгебры.
- Глава VI. Функции и пределы
- § 1. Независимое переменное и функция
- 2. Радианная мера углов.
- 3. График функции. Обратные функции.
- 4. Сложные функции.
- 5. Непрерывность.
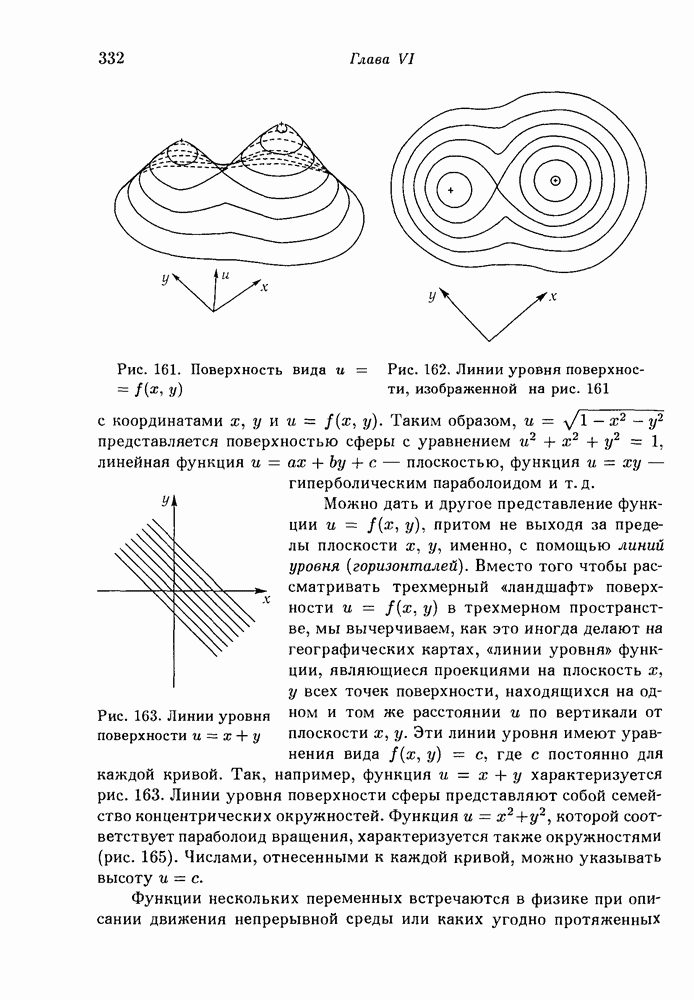
- 6. Функции нескольких переменных.
- 7. Функции и преобразования.
- § 2. Пределы
- 2. Монотонные последовательности.
- 3. Число Эйлера e.
- 4. Число «пи»
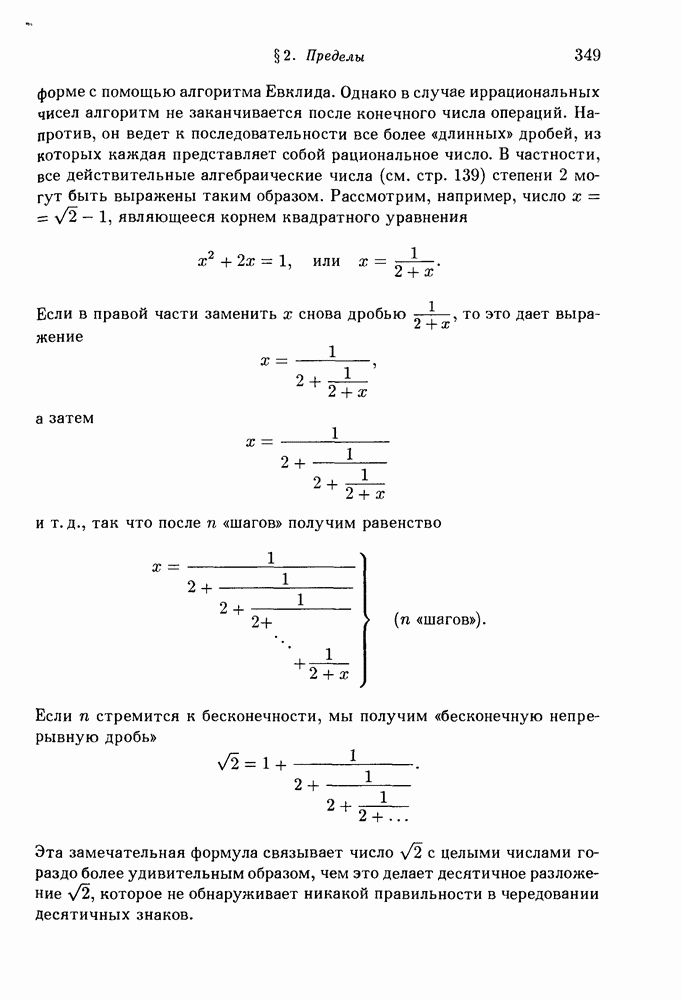
- 5. Непрерывные дроби.
- § 3. Пределы при непрерывном приближении
- 2. Замечания по поводу понятия предела
- 3. Предел sin x/x
- 4. Пределы при х -> оо.
- § 4. Точное определение непрерывности
- § 5. Две основные теоремы о непрерывных функциях
- 2. Доказательство теоремы Больцано.
- 3. Теорема Вейерштрасса об экстремальных значениях.
- 4. Теорема о последовательностях. Компактные множества.
- § 6. Некоторые применения теоремы Больцано
- 2. Применение к одной механической проблеме.
- Дополнение к главе VI. Дальнейшие примеры на пределы и непрерывность
- 4. Разрывные функции как предел непрерывных.
- 5. Пределы при итерации.
- § 2. Пример, относящийся к непрерывности
- Глава VII. Максимумы и минимумы
- § 1. Задачи из области элементарной геометрии
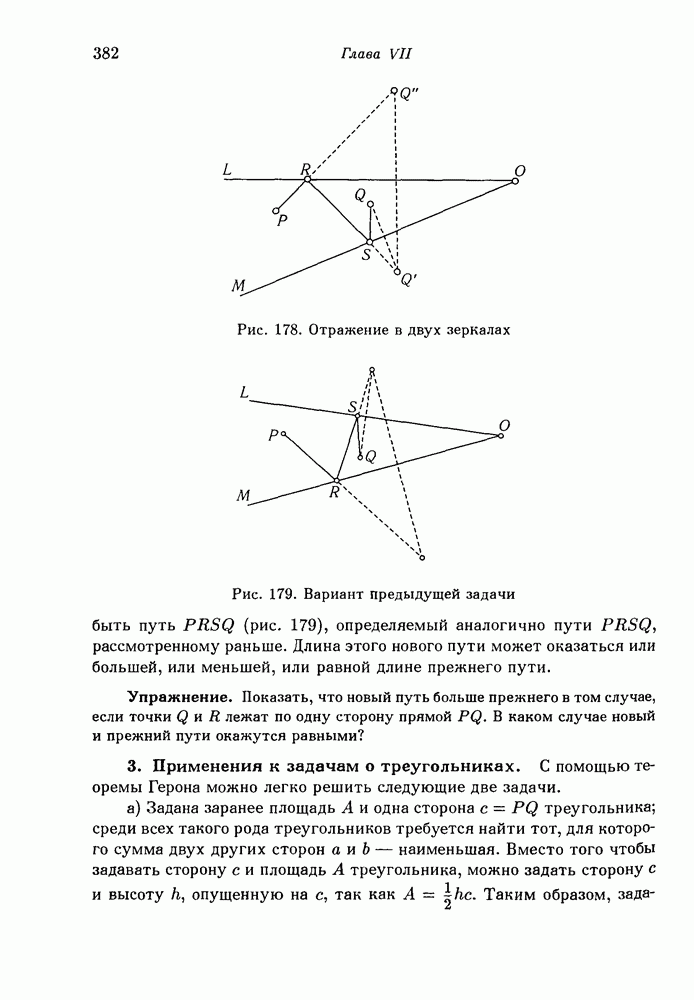
- 2. Теорема Герона. Экстремальное свойство световых лучей.
- 3. Применения к задачам о треугольниках.
- 4. Свойства касательных к эллипсу и гиперболе. Соответствующие экстремальные свойства.
- 5. Экстремальные расстояния точки от данной кривой.
- § 2. Общий принцип, которому подчинены экстремальные задачи
- § 3. Стационарные точки и дифференциальное исчисление
- 2. Максимумы и минимумы функций нескольких переменных. Седловые точки.
- 3. Точки минимакса и топология.
- 4. Расстояние точки от поверхности.
- § 4. Треугольник Шварца
- 4. Треугольники, образованные световыми лучами.
- 5. Замечания, касающиеся задач на отражение и эргодическое движение.
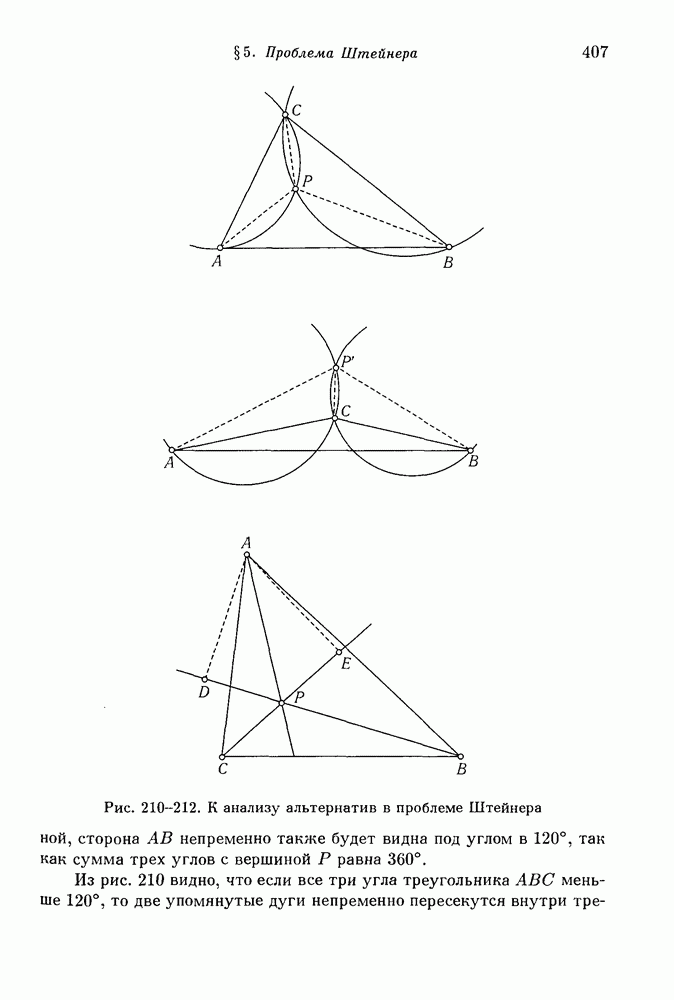
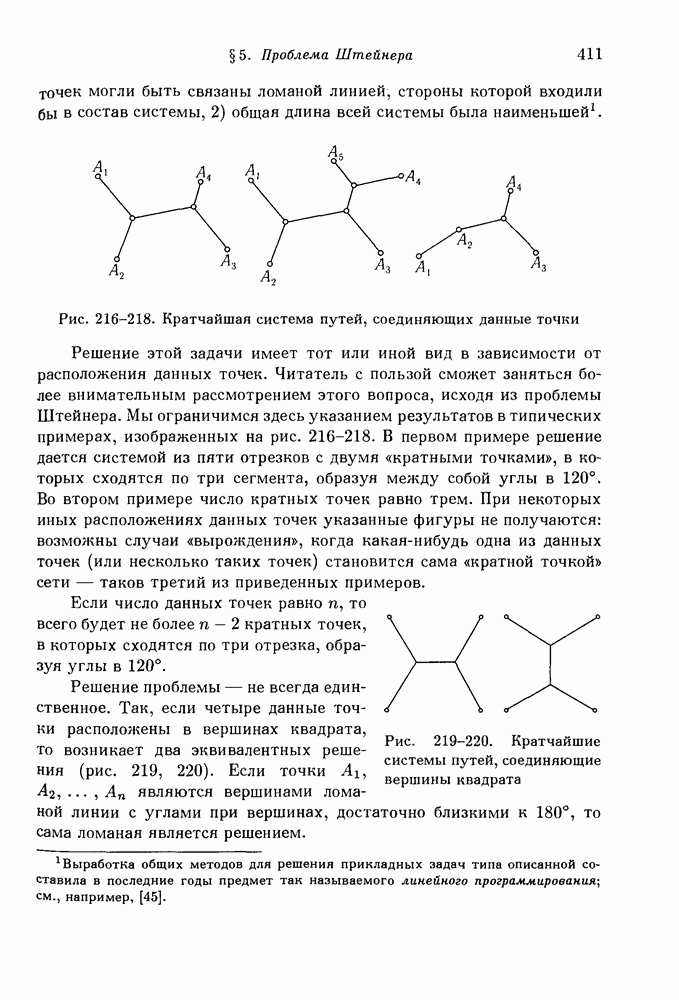
- § 5. Проблема Штейнера
- 2. Анализ возникающих альтернатив.
- 3. Дополнительная проблема.
- 4. Замечания и упражнения.
- 5. Обобщение: проблема уличной сети.
- § 6. Экстремумы и неравенства
- 1. Средние арифметическое и геометрическое двух положительных величин.
- 2. Обобщение на случай n переменных.
- 3. Метод наименьших квадратов.
- § 7. Существование экстремума. Принцип Дирихле
- 3. Экстремальные проблемы элементарного содержания.
- 4. Трудности, возникающие в более сложных случаях.
- § 8. Изопериметрическая проблема
- § 9. Экстремальные проблемы с граничными условиями. Связь между проблемой Штейнера и изопериметрической проблемой
- § 10. Вариационное исчисление
- 2. Вариационное исчисление. Принцип Ферма в оптике.
- 3. Решение задачи о брахистохроне, принадлежащее Якобу Бернулли.
- 4. Геодезические линии на сфере. Минимаксы.
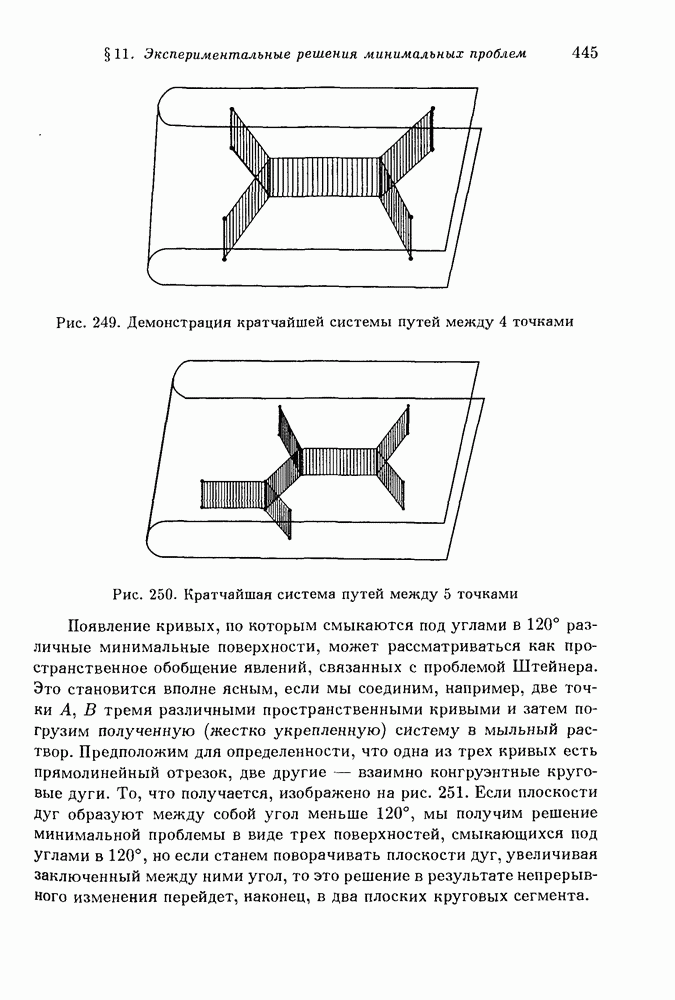
- § 11. Экспериментальные решения минимальных проблем. Опыты с мыльными пленками
- 2. Опыты с мыльными пленками.
- 3. Новые опыты, относящиеся к проблеме Плато.
- 4. Экспериментальные решения других математических проблем.
- Глава VIII. Математический анализ
- § 1. Интеграл
- 2. Интеграл.
- 3. Общие замечания о понятии интеграла. Общее определение.
- 4. Примеры интегрирования. Интегрирование x^r.
- 5. Правила «интегрального исчисления».
- § 2. Производная
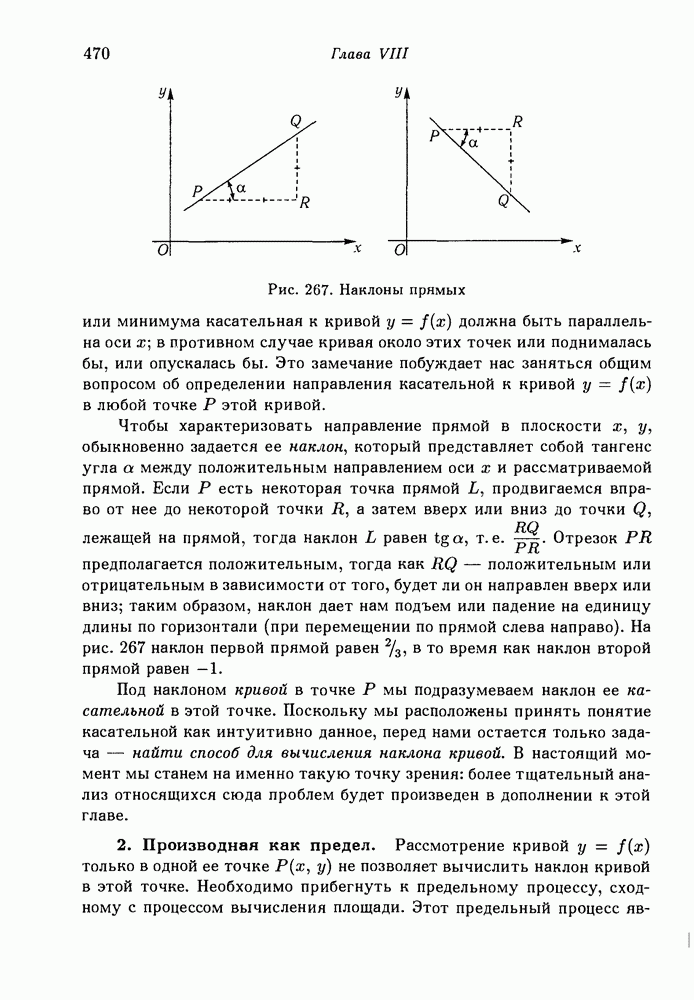
- 2. Производная как предел.
- 3. Примеры.
- 4. Производные от тригонометрических функций.
- 5. Дифференцируемость и непрерывность.
- 6. Производная и скорость. Вторая производная и ускорение.
- 7. Геометрический смысл второй производной.
- 8. Максимумы и минимумы.
- § 3. Техника дифференцирования
- § 4. Обозначения Лейбница и «бесконечно малые»
- § 5. Основная теорема анализа
- 2. Первые применения. Интегрирование функций x^r, cosx, sinx. Функция arctgx
- 3. Формула Лейбница для «пи»
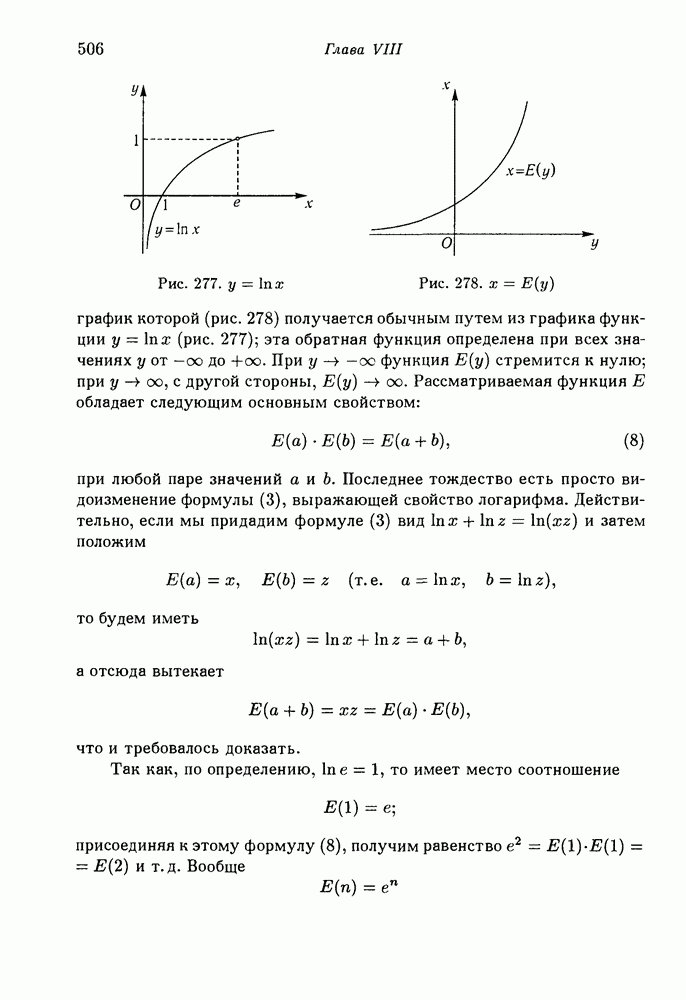
- § 6. Показательная (экспоненциальная) функция и логарифм
- 2. Показательная (экспоненциальная) функция.
- 3. Формулы дифференцирования функций е^х, а^х, x^s.
- 4. Явные выражения числа е^x и функций lnx в виде пределов.
- 5. Бесконечный ряд для логарифма. Вычисление логарифмов.
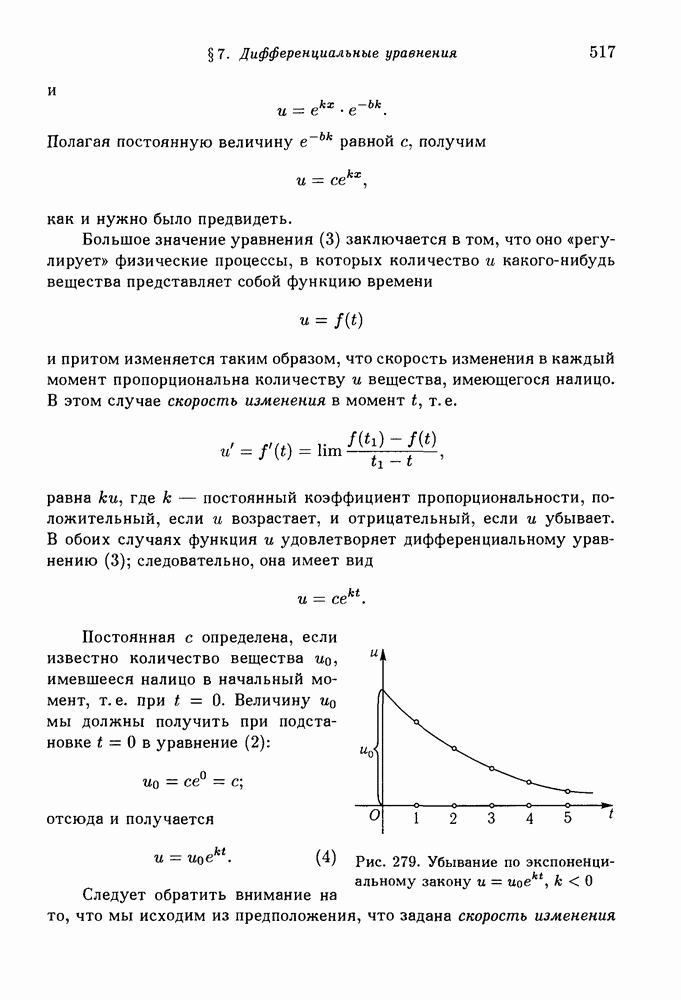
- § 7. Дифференциальные уравнения
- 2. Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- 3. Другие примеры. Простейшие колебания.
- 4. Закон движения Ньютона.
- Дополнение к главе VIII
- § 1. Вопросы принципиального порядка
- 3. Другие приложения понятия интеграла. Работа. Длина кривой.
- § 2. Порядки возрастания
- 2. Порядок возрастания ln(n!)
- § 3. Бесконечные ряды и бесконечные произведения
- 2. Формула Эйлера cos x + i sin x = exp(ix).
- 3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin x в виде бесконечного произведения.
- § 4. Доказательство теоремы о простых числах на основе статистического метода
- Приложение. Дополнительные замечания, задачи и упражнения
- Аналитическая геометрия
- Геометрические построения
- Проективная и неевклидова геометрия
- Топология
- Функции, пределы, непрерывность
- Максимумы и минимумы
- Дифференциальное и интегральное исчисления
- Техника интегрирования
- Рекомендуемая литература