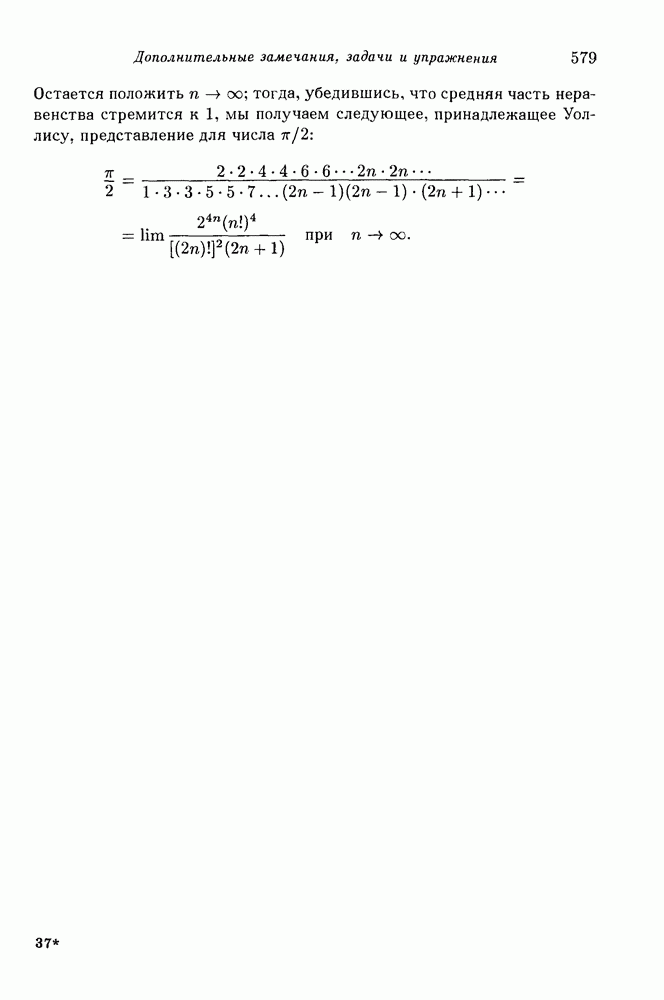| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 3. Бесконечные ряды и бесконечные произведения
1. Бесконечные ряды функций.
Мы не раз уже имели случай указать, что, выражая величину  в виде «суммы бесконечного ряда»
в виде «суммы бесконечного ряда»

мы не утверждаем ничего иного, кроме того, что  есть предел при возрастающем
есть предел при возрастающем  последовательности конечных «частных сумм»
последовательности конечных «частных сумм»

где

Таким образом, равенство (1) равносильно предельному соотношению

где  определено с помощью (2). Если предел (3) существует, то мы говорим, что ряд (1) сходится к значению
определено с помощью (2). Если предел (3) существует, то мы говорим, что ряд (1) сходится к значению  напротив, если предел (3) не существует, то мы говорим, что этот ряд расходится.
напротив, если предел (3) не существует, то мы говорим, что этот ряд расходится.
Например, ряд

сходится к значению  а ряд
а ряд

сходится к значению  но, напротив, ряд
но, напротив, ряд

расходится, так как частные суммы здесь равны поочередно то 1, то 0; а ряд

расходится по той причине, что частные суммы стремятся к бесконечности.
Нам приходилось уже встречаться с рядами, у которых общий член есть функция переменной х, имеющая вид

причем  не зависит от х. Такие ряды называются степенными, для них частными суммами являются многочлены
не зависит от х. Такие ряды называются степенными, для них частными суммами являются многочлены

прибавление постоянного члена со потребует лишь несущественного изменения обозначений в формуле (2).
Разложение функции  в степенной ряд
в степенной ряд

есть, таким образом, один из способов представить функцию  приближенно с помощью простейших функций — полиномов. Подводя итоги предыдущим результатам и несколько дополняя их, составим следующий список уже известных нам разложений в степенные ряды:
приближенно с помощью простейших функций — полиномов. Подводя итоги предыдущим результатам и несколько дополняя их, составим следующий список уже известных нам разложений в степенные ряды:

Сюда же мы присоединим еще два важных разложения

Доказательство этих разложений может быть построено как простое следствие из соотношений (см. стр. 499)

Мы отправляемся от следующего очевидного неравенства:

Интегрируя от 0 до  где
где  есть некоторое фиксированное положительное число, мы находим по формуле (13), стр. 468:
есть некоторое фиксированное положительное число, мы находим по формуле (13), стр. 468:

интегрируя это еще раз, получим

что равносильно

Проинтегрировав последнее неравенство, найдем

Продолжая таким же способом до бесконечности, мы получаем две серии неравенств:

Установим теперь, что при неограниченном возрастании и имеет место соотношение 
Для того чтобы это доказать, выберем некоторое фиксированное число  такое, что и введем обозначение
такое, что и введем обозначение  Любое целое
Любое целое  представим в виде суммы
представим в виде суммы  тогда
тогда

так как из того, что  следует, что
следует, что  то с
то с  Отсюда и вытекает, что справедливы тождества
Отсюда и вытекает, что справедливы тождества

Поскольку члены этих рядов, меняя поочередно знаки, убывают по величине (по крайней мере, при  , то ошибки, совершаемые при обрывании каждого из рядов на некотором члене, не превышают по абсолютной величине первого из отброшенных членов.
, то ошибки, совершаемые при обрывании каждого из рядов на некотором члене, не превышают по абсолютной величине первого из отброшенных членов.
Эти ряды можно использовать при составлении таблиц.
Пример. Чему равен  равен в радианном измерении числу
равен в радианном измерении числу  следовательно,
следовательно,

Если ограничиться выписанными двумя членами, то совершаемая при этом ошибка не будет превышать числа  которое меньше, чем
которое меньше, чем  Итак,
Итак,  и 0,017 452 4064, с 10 десятичными знаками. Наконец, упомянем без доказательства о «биномиальном ряде»
и 0,017 452 4064, с 10 десятичными знаками. Наконец, упомянем без доказательства о «биномиальном ряде»

где  «биномиальный коэффициент»
«биномиальный коэффициент»

Если  есть целое положительное число, то
есть целое положительное число, то  и в формуле (11) все коэффициенты
и в формуле (11) все коэффициенты  при
при  обращаются в нуль, так что мы просто получаем конечную формулу обыкновенной биномиальной теоремы. Одно из крупных открытий Ньютона, сделанных им в начале его деятельности, заключалось в том, что он обобщил биномиальную теорему на случай всех возможных значений показателя а как положительных, так и отрицательных, как рациональных, так и иррациональных. Если а не есть целое положительное число, то правая часть формулы (11) дает бесконечный ряд, сходящийся к значению, равному левой части,
обращаются в нуль, так что мы просто получаем конечную формулу обыкновенной биномиальной теоремы. Одно из крупных открытий Ньютона, сделанных им в начале его деятельности, заключалось в том, что он обобщил биномиальную теорему на случай всех возможных значений показателя а как положительных, так и отрицательных, как рациональных, так и иррациональных. Если а не есть целое положительное число, то правая часть формулы (11) дает бесконечный ряд, сходящийся к значению, равному левой части,
при  Если же
Если же  то ряд (11) расходится, и знак равенства теряет всякий смысл.
то ряд (11) расходится, и знак равенства теряет всякий смысл.
В частности, подставляя в формулу (11) значение  мы найдем разложение
мы найдем разложение

Подобно другим математикам XVIII в., Ньютон не дал настоящего доказательства своей формулы. Удовлетворительный анализ сходимости и пределы, в которых разложение оказывается справедливым, не были установлены для подобных рядов вплоть до XIX в.
Упражнение. Написать степенные ряды, в которые разлагаются функции 
Разложения (4)-(11) являются частными случаями общей формулы Брука Тейлора (1685-1731), дающей разложение функции  в степенной ряд вида
в степенной ряд вида

Подмечая закон, выражающий коэффициенты этого ряда  с помощью функции
с помощью функции  и ее производных, можно утверждать справедливость этого разложения для очень обширного класса функций.
и ее производных, можно утверждать справедливость этого разложения для очень обширного класса функций.
Здесь невозможно привести строгое доказательство формулы Тейлора; невозможно также точно сформулировать условия, при которых она справедлива. Но следующие общедоступные соображения прольют некоторый свет на относящиеся сюда взаимоотношения и существенные факты.
Допустим предварительно, что разложение (13) возможно. Далее предположим, что функция  дифференцируема, что ее производная
дифференцируема, что ее производная  дифференцируема, и так далее, так что существует бесконечная последовательность производных
дифференцируема, и так далее, так что существует бесконечная последовательность производных

Наконец будем дифференцировать бесконечный степенной ряд почленно точно так, как если бы это был конечный многочлен, не озабочиваясь вопросом о законности такой процедуры. После всех этих допущений можно определить коэффициенты  зная поведение функции
зная поведение функции 
в окрестности точки  Прежде всего, подставляя в формулу
Прежде всего, подставляя в формулу  мы находим
мы находим

так как все члены ряда, содержащие переменное х, исчезают. Дифференцируя тождество (13), мы получаем

снова подставляя значение  но на этот раз в формулу (13), мы находим
но на этот раз в формулу (13), мы находим

Дифференцируя (13), мы получаем

подставляя затем в полученную формулу  мы видим, что
мы видим, что

Аналогично, продифференцировав  и затем подставив
и затем подставив  получаем
получаем

и, продолжая дальше таким же образом, мы найдем общую формулу для коэффициента 

где  представляет собой значение
представляет собой значение  производной от функции
производной от функции  при
при  В результате получим ряд Тейлора
В результате получим ряд Тейлора

Пусть читатель в качестве упражнения проверит, что в примерах (4)-(11) коэффициенты степенных рядов составлены как раз по этому закону.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие ко второму русскому изданию
- Как пользоваться книгой
- Что такое математика?
- Глава I. Натуральные числа
- § 1. Операции над целыми числами
- 2. Представление целых чисел с помощью письменных знаков (нумерация).
- 3. Арифметические действия в недесятичных системах счисления.
- § 2. Бесконечность системы натуральных чисел. Математическая индукция
- 2. Арифметическая прогрессия.
- 3. Геометрическая прогрессия.
- 4. Сумма n первых квадратов.
- 5. Одно важное неравенство.
- 6. Биномиальная теорема.
- 7. Дальнейшие замечания по поводу метода математической индукции.
- Дополнение к главе I
- Теория чисел
- 2. Распределение простых чисел.
- § 2. Сравнения
- 2. Теорема Ферма.
- 3. Квадратические вычеты.
- § 3. Пифагоровы числа и большая теорема Ферма
- § 4. Алгоритм Евклида
- 2. Применение к основной теореме арифметики
- 3. Функция Эйлера. Еще раз о теореме Ферма.
- 4. Непрерывные дроби. Диофантовы уравнения
- Глава II. Математическая числовая система
- § 1. Рациональные числа
- 2. Возникновение надобности в рациональных числах внутри самой математики. Принцип обобщения.
- 3. Геометрическое представление рациональных чисел.
- § 2. Несоизмеримые отрезки. Иррациональные числа, пределы
- 2. Десятичные дроби: конечные и бесконечные.
- 3. Пределы. Бесконечные геометрические прогрессии.
- 4. Рациональные числа и периодические десятичные дроби.
- 5. Общее определение иррациональных чисел посредством стягивающихся отрезков.
- 6. Иные методы определения иррациональных чисел.Декиндовы сечения.
- § 3. Замечания из области аналитической геометрии
- 2. Уравнения прямых и кривых линий.
- § 4. Математический анализ бесконечного
- 2. Счетность множества рациональных чисел и несчетность континуума.
- 3. «Кардинальные числа» Кантора.
- 4. Косвенный метод доказательства.
- 5. Парадоксы бесконечного.
- 6. Основания математики.
- § 5. Комплексные числа
- 2. Геометрическое представление комплексных чисел.
- 3. Формула Муавра и корни из единицы.
- 4. Основная теорема алгебры.
- § 6. Алгебраические и трансцендентные числа
- 2. Теорема Лиувилля и конструирование трансцендентных чисел.
- Дополнение к главе II. Алгебра множеств
- 2. Применение к математической логике.
- 3. Одно из применений к теории вероятностей.
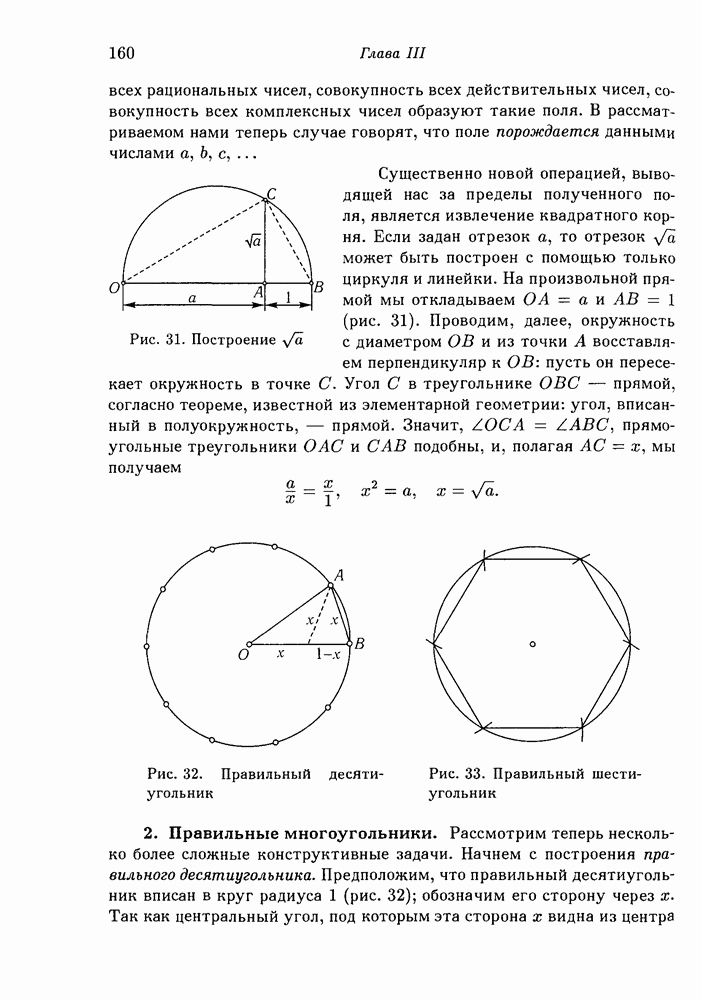
- Глава III. Геометрические построения. Алгебра числовых полей
- Часть 1. Доказательства невозможности и алгебра
- 1. Построение полей и извлечение квадратных корней.
- 2. Правильные многоугольники.
- 3. Проблема Аполлония.
- § 2. Числа, допускающие построение, и числовые поля
- 2. Все числа, допускающие построение, — алгебраические.
- § 3. Неразрешимость трех классических проблем
- 2. Одна теорема о кубических уравнениях.
- 3. Трисекция угла.
- 4. Правильный семиугольник.
- 5. Замечания по поводу квадратуры круга.
- Часть 2. Различные методы выполнения построений
- § 4. Геометрические преобразования. Инверсия
- 2. Свойства инверсии.
- 3. Геометрическое построение обратных точек.
- 4. Как разделить отрезок пополам и как найти центр данного круга с помощью одного циркуля.
- § 5. Построения с помощью иных инструментов. Построения Маскерони с помощью одного циркуля
- 1. Классическая конструкция, служащая для удвоения куба.
- 2. Построения с помощью одного циркуля.
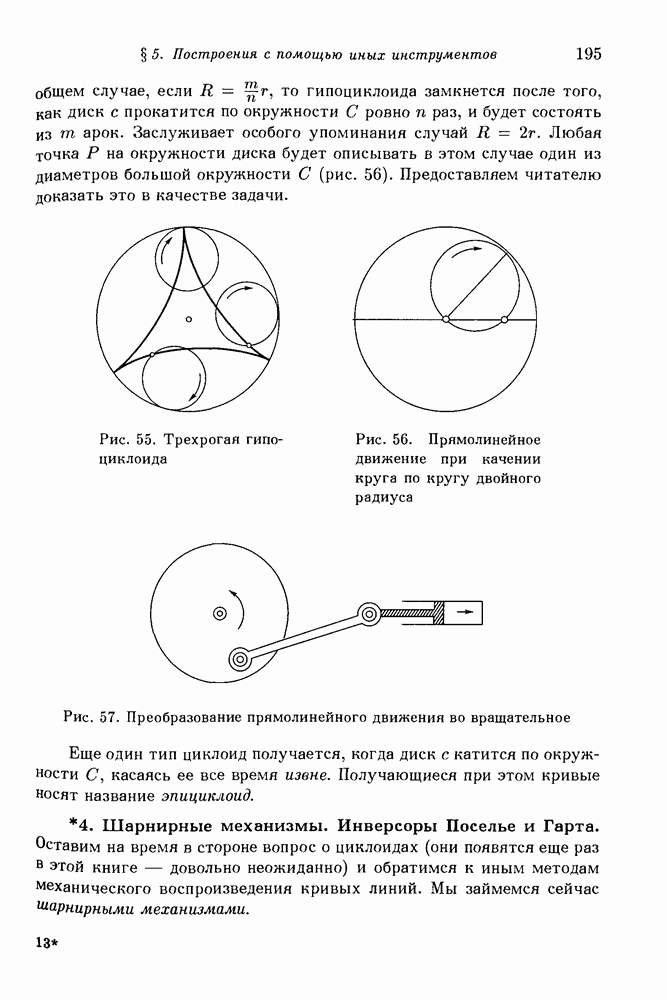
- 3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды.
- 4. Шарнирные механизмы. Инверсоры Поселье и Гарта.
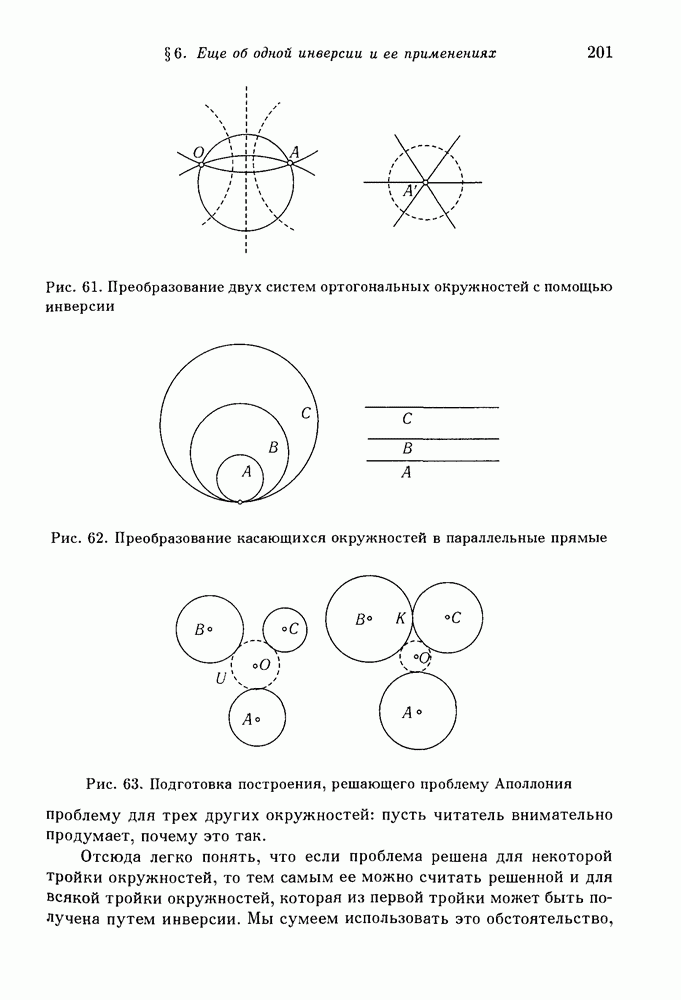
- § 6. Еще об одной инверсии и ее применениях
- 1. Инвариантность углов. Семейства окружностей.
- 2. Применение к проблеме Аполлония.
- 3. Повторные отражения.
- Глава IV. Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- 1. Классификация геометрических свойств. Инвариантность при преобразованиях.
- 2. Проективные преобразования.
- § 2. Основные понятия
- 1. Группа проективных преобразований.
- 2. Теорема Дезарга.
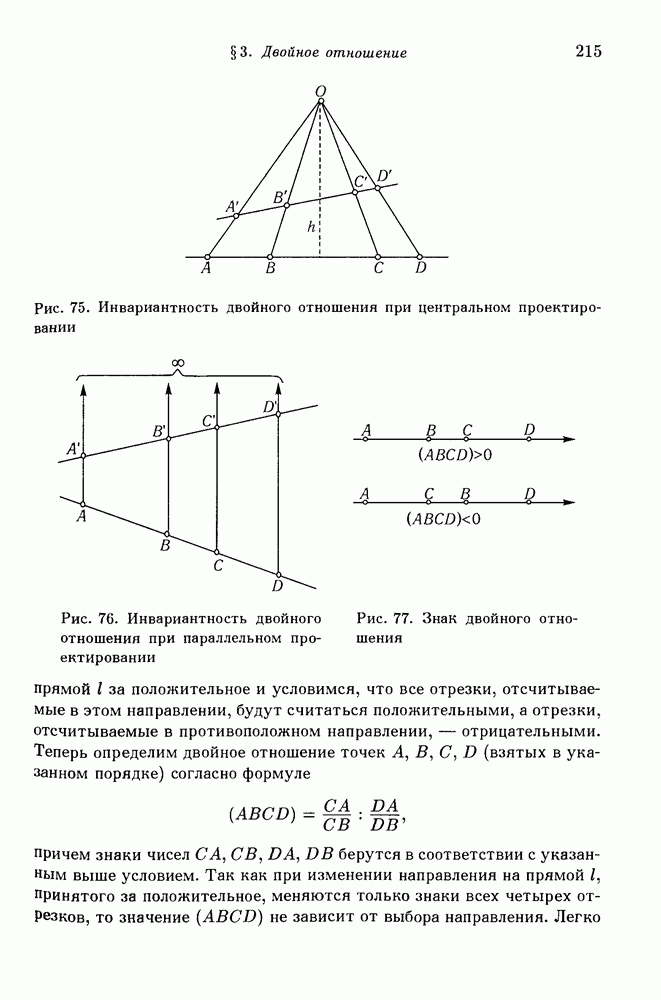
- § 3. Двойное отношение
- § 4. Параллельность и бесконечность
- 2. Идеальные элементы и проектирование.
- 3. Двойное отношение с бесконечно удаленными элементами.
- § 5. Применения
- 2. Двумерное доказательство теоремы Дезарга.
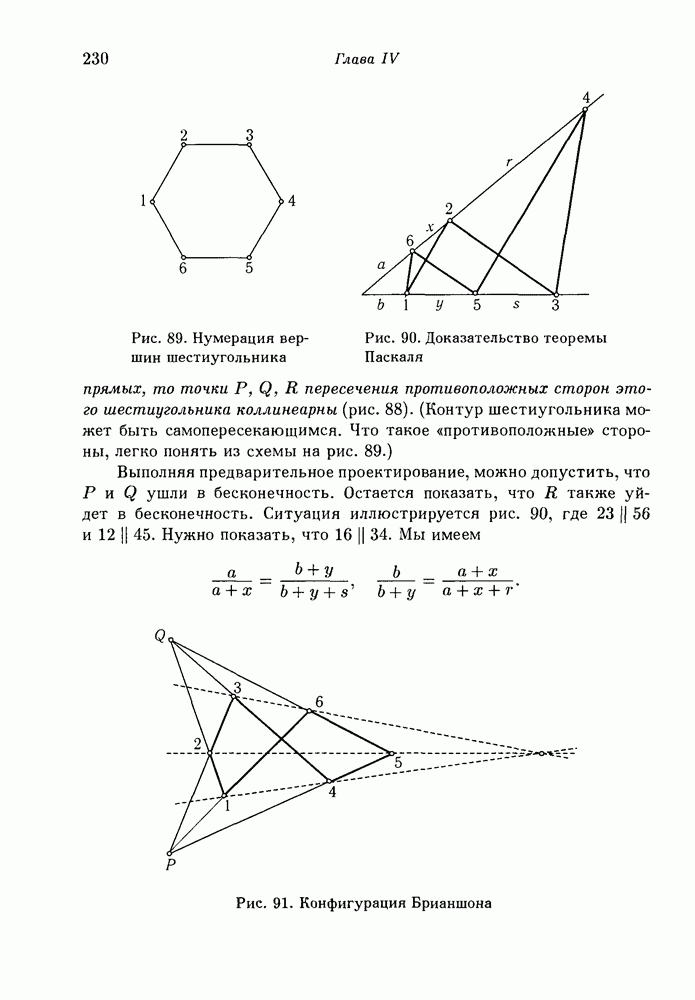
- 3. Теорема Паскаля.
- 4. Теорема Брианшона.
- 5. Замечание по поводу двойственности.
- § 6. Аналитическое представление
- 2. Однородные координаты. Алгебраические основы двойственности.
- § 7. Задачи на построения с помощью одной линейки
- § 8. Конические сечения и квадрики
- 2. Проективные свойства конических сечений.
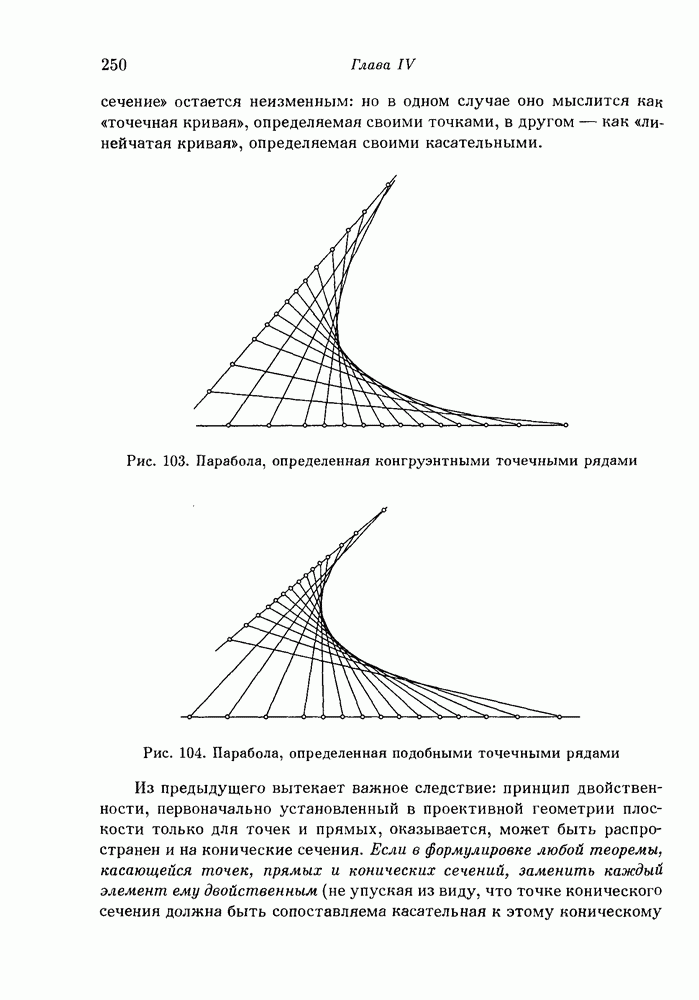
- 3. Конические сечения как «линейчатые кривые».
- 4. Теоремы Паскаля и Брианшона для общего случая произвольных конических сечений.
- 5. Гиперболоид.
- § 9. Аксиоматика и неевклидова геометрия
- 2. Гиперболическая неевклидова геометрия.
- 3. Геометрия и реальность.
- 4. Модель Пуанкаре.
- 5. Эллиптическая, или риманова, геометрия.
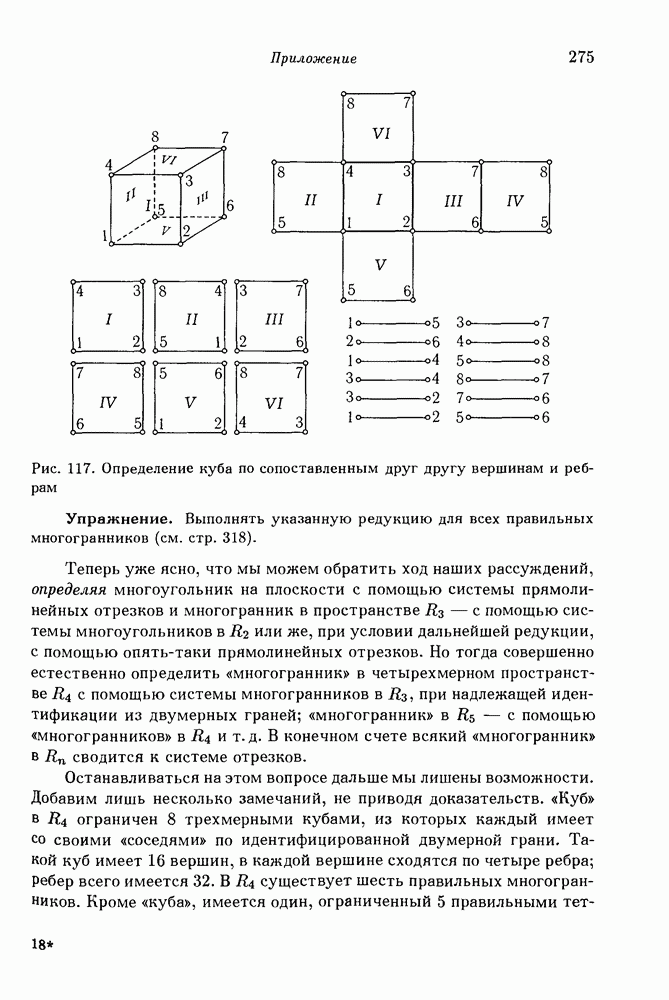
- Приложение. Геометрия в пространствах более чем трех измерений
- Глава V. Топология
- § 1. Формула Эйлера для многогранников
- § 2. Топологические свойства фигур
- 2. Свойства связности.
- § 3. Другие примеры топологических теорем
- 2. Проблема четырех красок.
- 3. Понятие размерности.
- 4. Теорема о неподвижной точке.
- 5. Узлы.
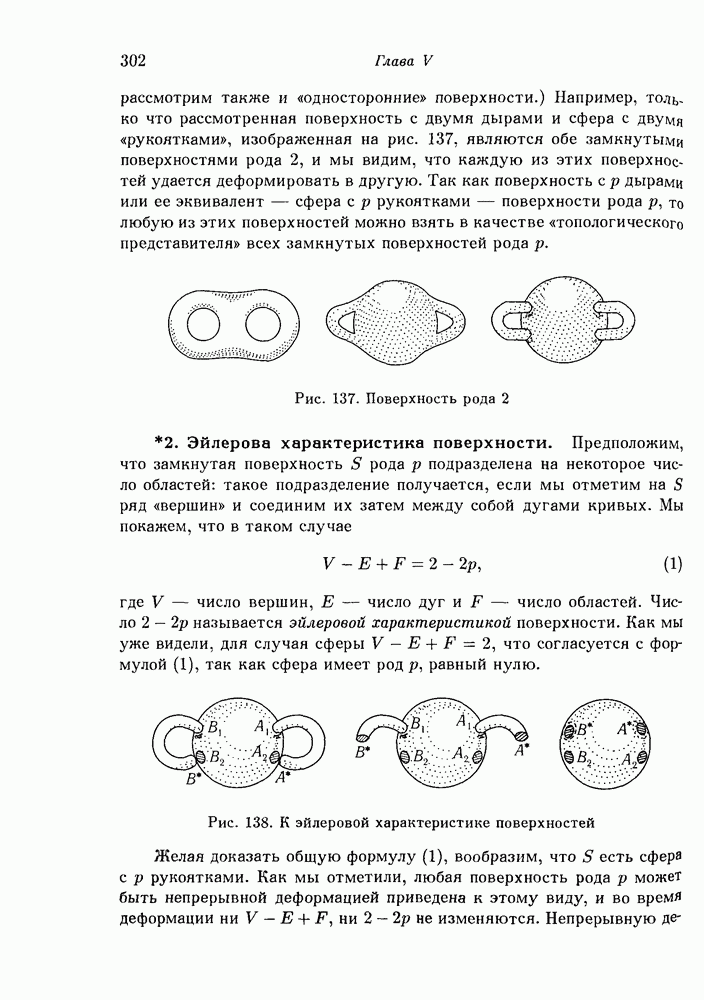
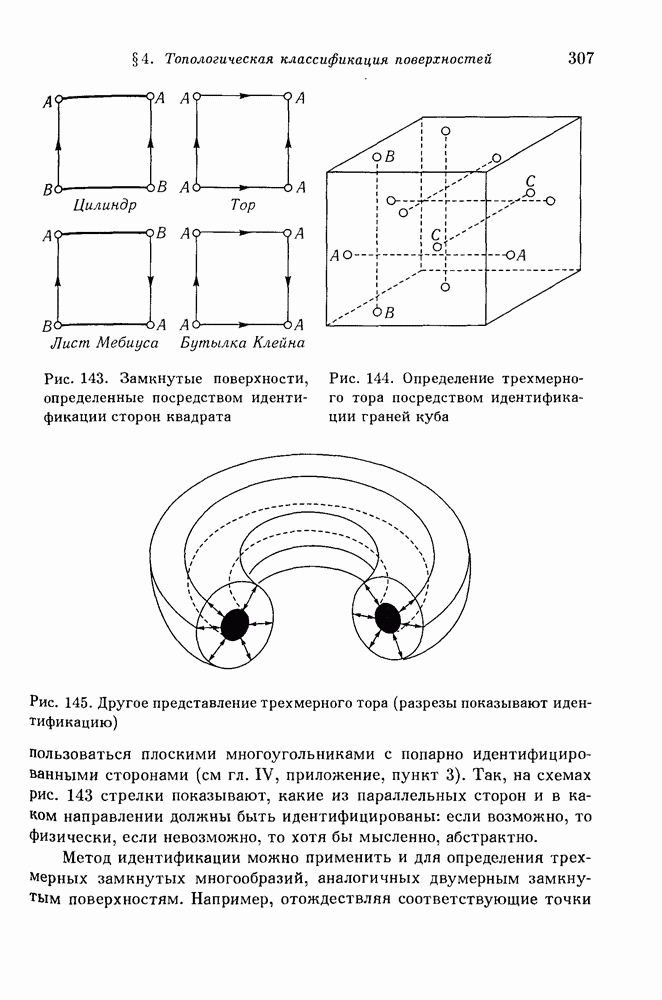
- § 4. Топологическая классификация поверхностей
- 2. Эйлерова характеристика поверхности.
- 3. Односторонние поверхности.
- Приложение
- 2. Теорема Жордана для случая многоугольников.
- 3. Основная теорема алгебры.
- Глава VI. Функции и пределы
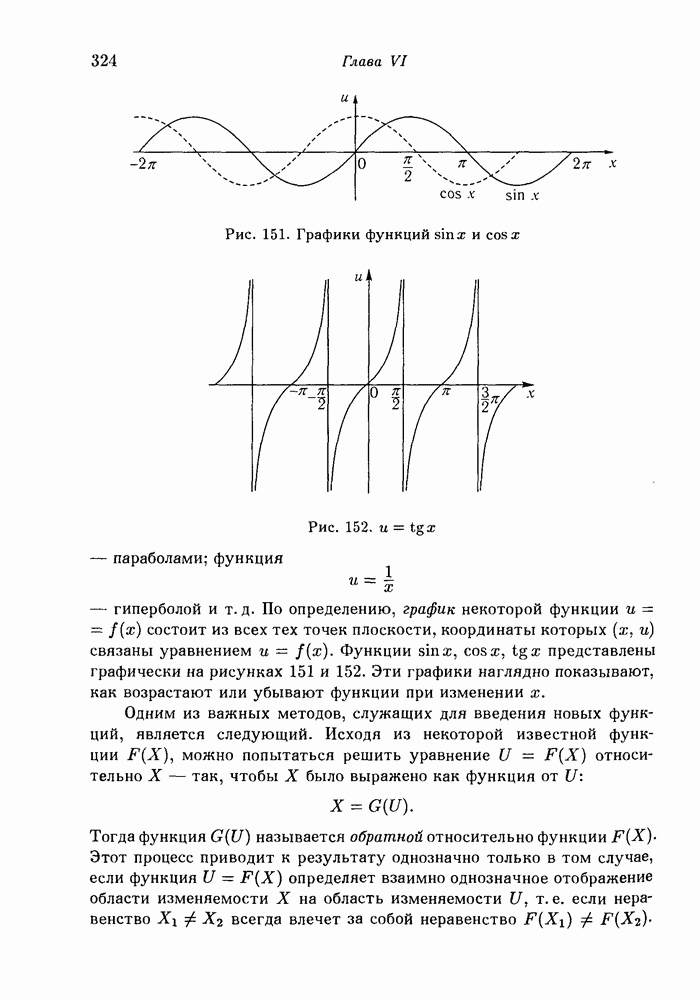
- § 1. Независимое переменное и функция
- 2. Радианная мера углов.
- 3. График функции. Обратные функции.
- 4. Сложные функции.
- 5. Непрерывность.
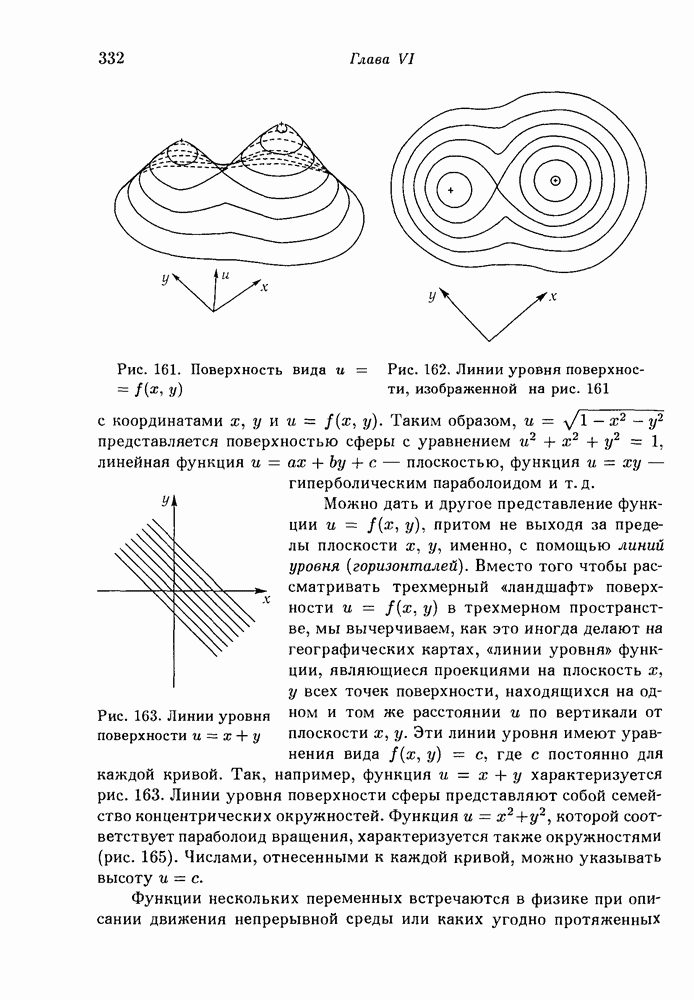
- 6. Функции нескольких переменных.
- 7. Функции и преобразования.
- § 2. Пределы
- 2. Монотонные последовательности.
- 3. Число Эйлера e.
- 4. Число «пи»
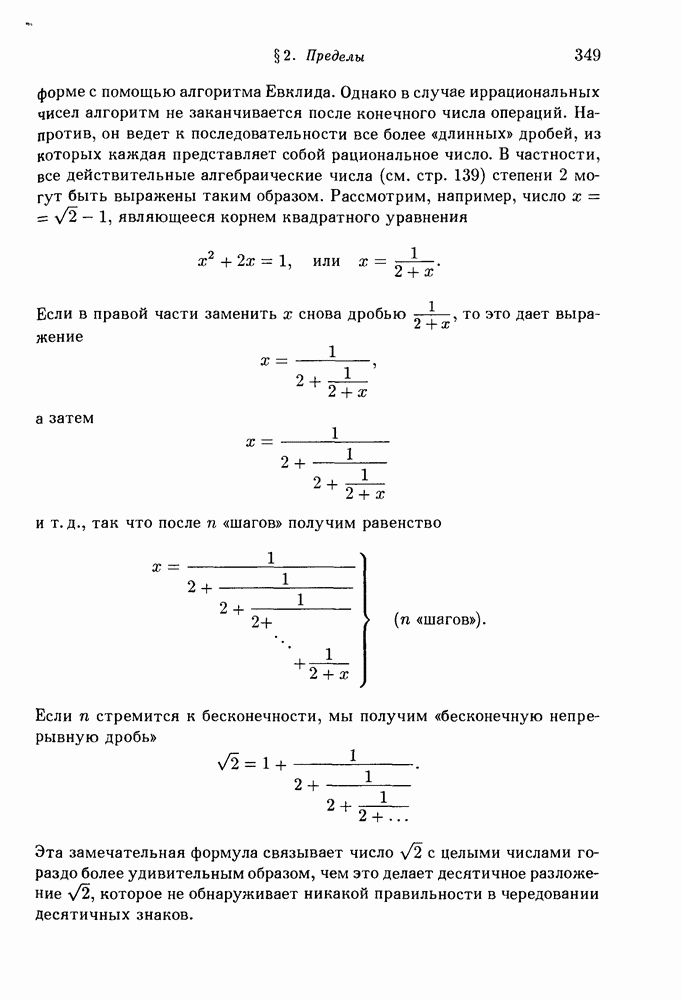
- 5. Непрерывные дроби.
- § 3. Пределы при непрерывном приближении
- 2. Замечания по поводу понятия предела
- 3. Предел sin x/x
- 4. Пределы при х -> оо.
- § 4. Точное определение непрерывности
- § 5. Две основные теоремы о непрерывных функциях
- 2. Доказательство теоремы Больцано.
- 3. Теорема Вейерштрасса об экстремальных значениях.
- 4. Теорема о последовательностях. Компактные множества.
- § 6. Некоторые применения теоремы Больцано
- 2. Применение к одной механической проблеме.
- Дополнение к главе VI. Дальнейшие примеры на пределы и непрерывность
- 4. Разрывные функции как предел непрерывных.
- 5. Пределы при итерации.
- § 2. Пример, относящийся к непрерывности
- Глава VII. Максимумы и минимумы
- § 1. Задачи из области элементарной геометрии
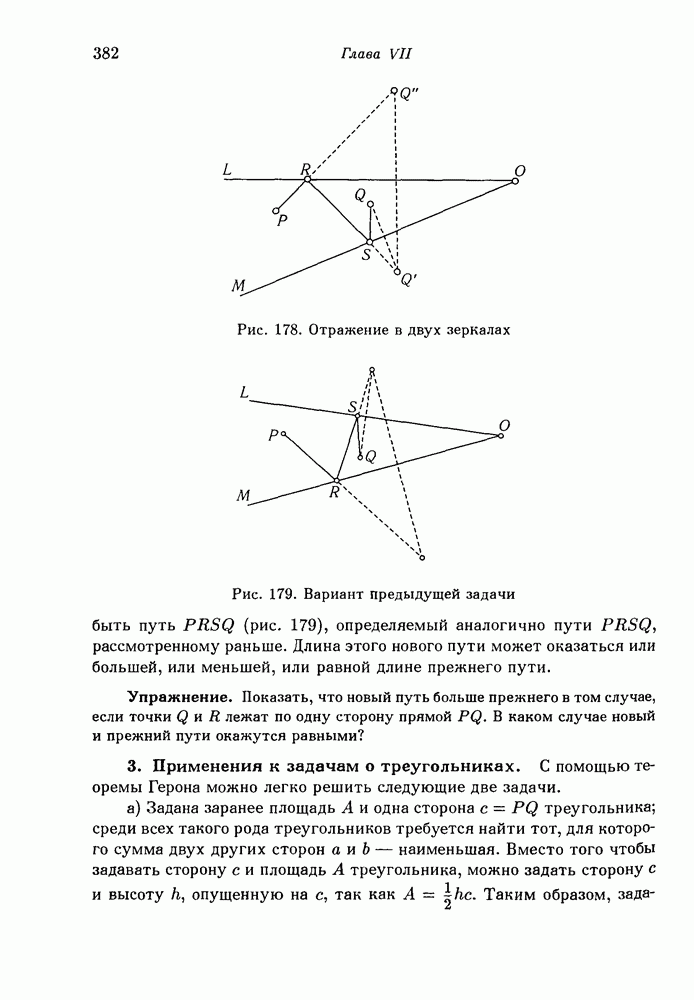
- 2. Теорема Герона. Экстремальное свойство световых лучей.
- 3. Применения к задачам о треугольниках.
- 4. Свойства касательных к эллипсу и гиперболе. Соответствующие экстремальные свойства.
- 5. Экстремальные расстояния точки от данной кривой.
- § 2. Общий принцип, которому подчинены экстремальные задачи
- § 3. Стационарные точки и дифференциальное исчисление
- 2. Максимумы и минимумы функций нескольких переменных. Седловые точки.
- 3. Точки минимакса и топология.
- 4. Расстояние точки от поверхности.
- § 4. Треугольник Шварца
- 4. Треугольники, образованные световыми лучами.
- 5. Замечания, касающиеся задач на отражение и эргодическое движение.
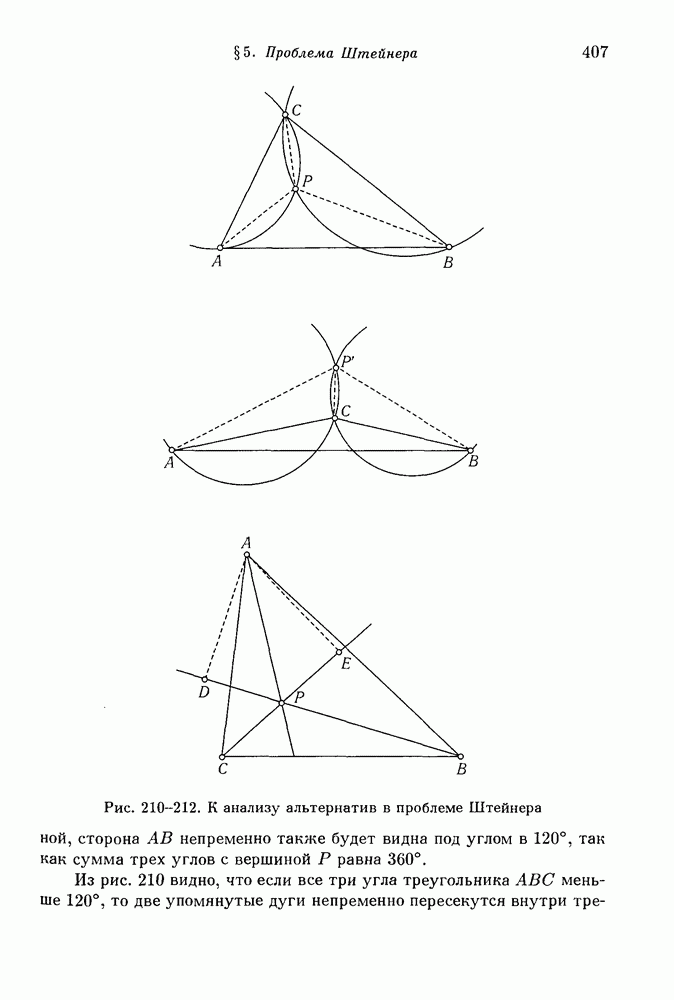
- § 5. Проблема Штейнера
- 2. Анализ возникающих альтернатив.
- 3. Дополнительная проблема.
- 4. Замечания и упражнения.
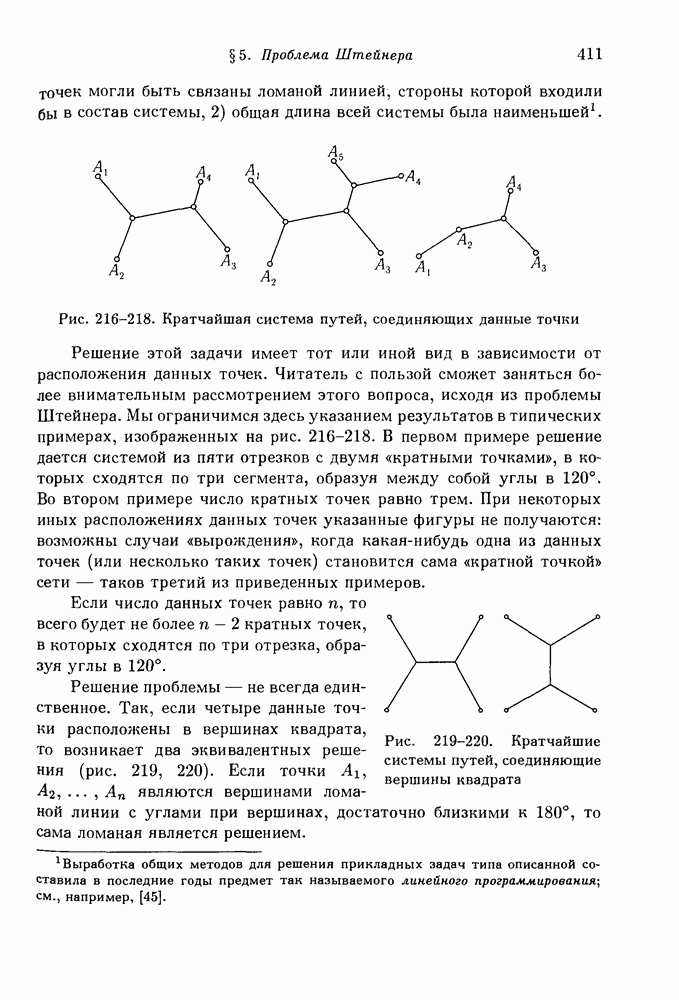
- 5. Обобщение: проблема уличной сети.
- § 6. Экстремумы и неравенства
- 1. Средние арифметическое и геометрическое двух положительных величин.
- 2. Обобщение на случай n переменных.
- 3. Метод наименьших квадратов.
- § 7. Существование экстремума. Принцип Дирихле
- 3. Экстремальные проблемы элементарного содержания.
- 4. Трудности, возникающие в более сложных случаях.
- § 8. Изопериметрическая проблема
- § 9. Экстремальные проблемы с граничными условиями. Связь между проблемой Штейнера и изопериметрической проблемой
- § 10. Вариационное исчисление
- 2. Вариационное исчисление. Принцип Ферма в оптике.
- 3. Решение задачи о брахистохроне, принадлежащее Якобу Бернулли.
- 4. Геодезические линии на сфере. Минимаксы.
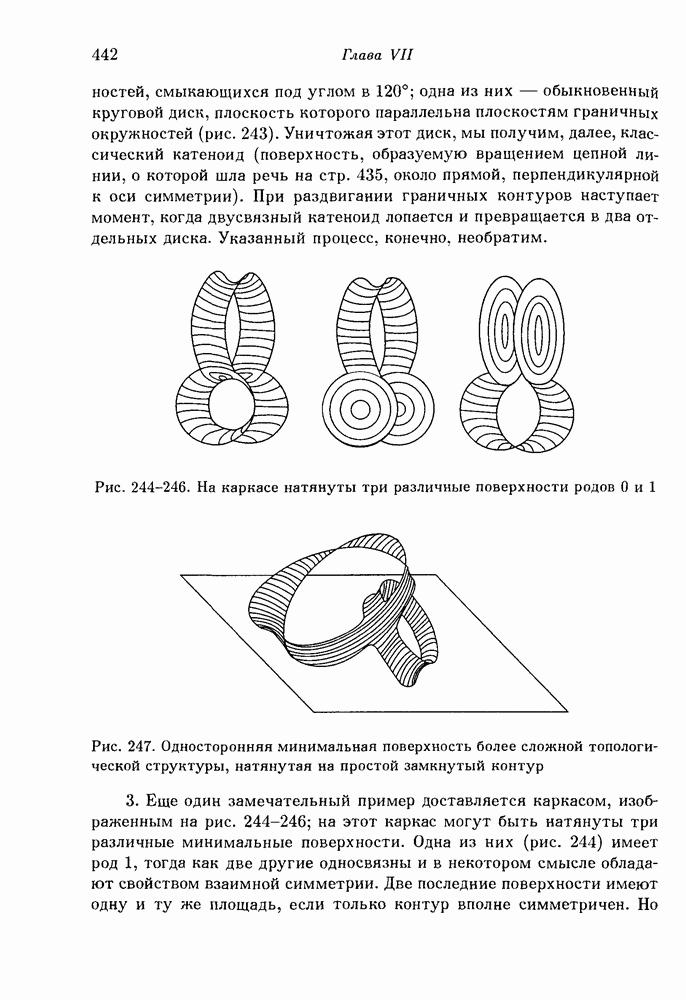
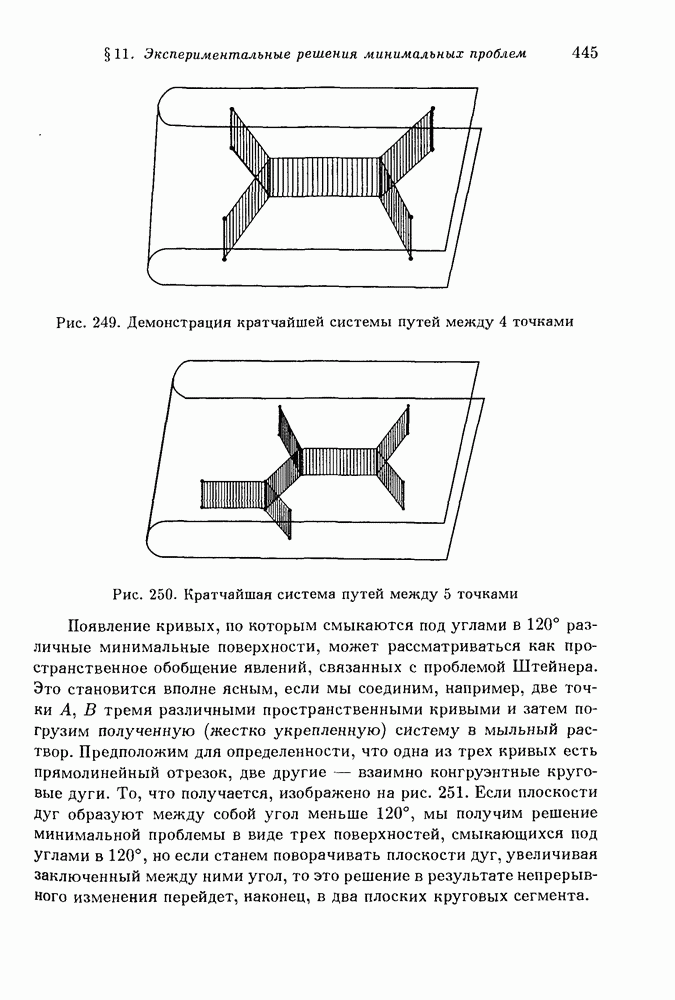
- § 11. Экспериментальные решения минимальных проблем. Опыты с мыльными пленками
- 2. Опыты с мыльными пленками.
- 3. Новые опыты, относящиеся к проблеме Плато.
- 4. Экспериментальные решения других математических проблем.
- Глава VIII. Математический анализ
- § 1. Интеграл
- 2. Интеграл.
- 3. Общие замечания о понятии интеграла. Общее определение.
- 4. Примеры интегрирования. Интегрирование x^r.
- 5. Правила «интегрального исчисления».
- § 2. Производная
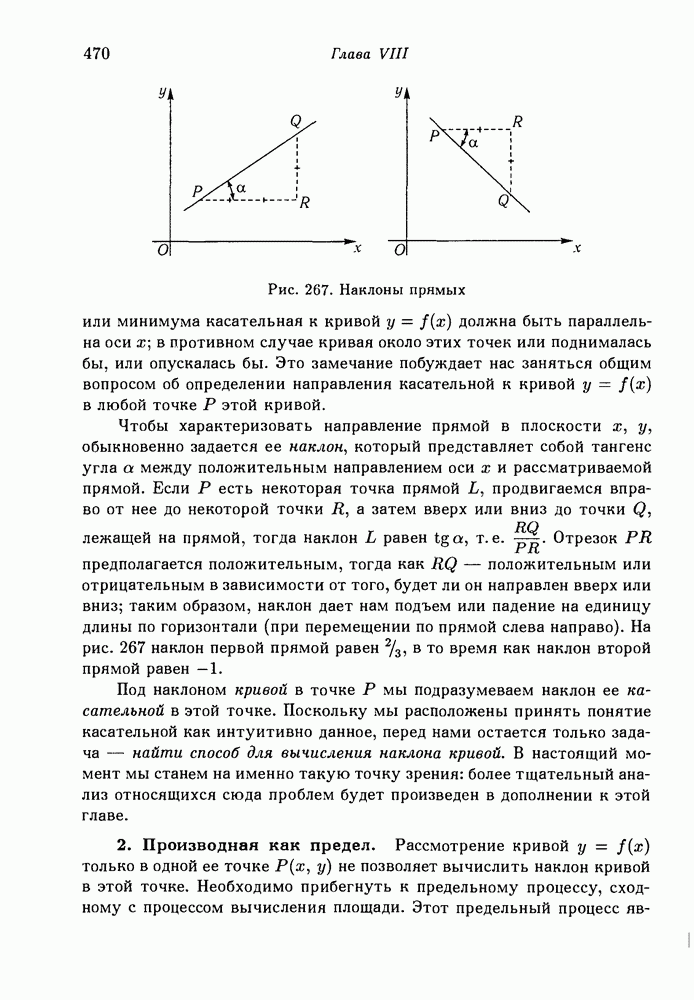
- 2. Производная как предел.
- 3. Примеры.
- 4. Производные от тригонометрических функций.
- 5. Дифференцируемость и непрерывность.
- 6. Производная и скорость. Вторая производная и ускорение.
- 7. Геометрический смысл второй производной.
- 8. Максимумы и минимумы.
- § 3. Техника дифференцирования
- § 4. Обозначения Лейбница и «бесконечно малые»
- § 5. Основная теорема анализа
- 2. Первые применения. Интегрирование функций x^r, cosx, sinx. Функция arctgx
- 3. Формула Лейбница для «пи»
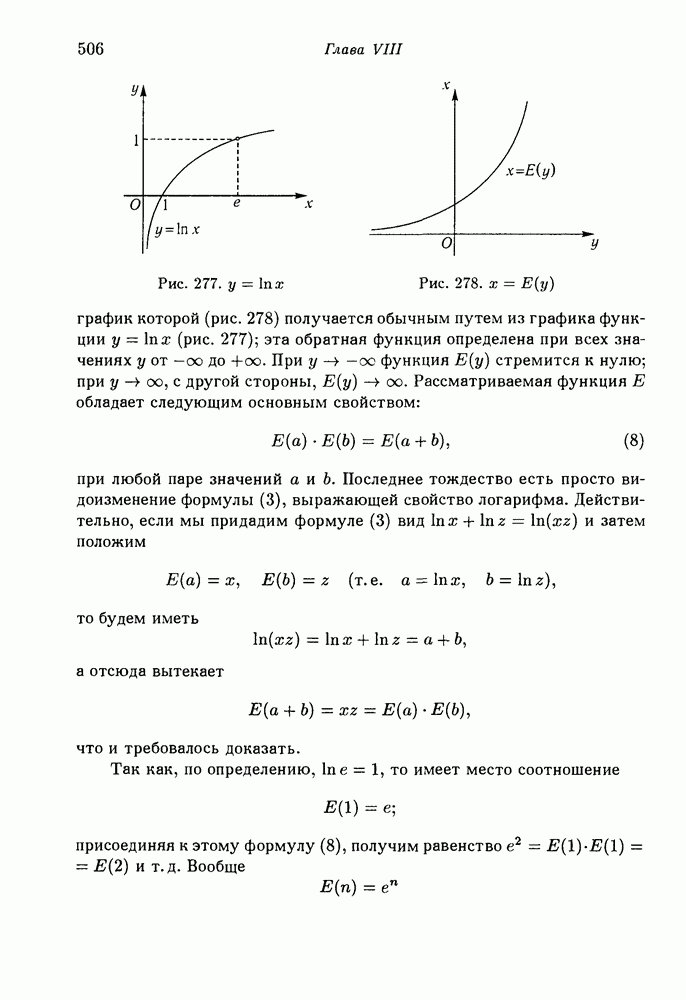
- § 6. Показательная (экспоненциальная) функция и логарифм
- 2. Показательная (экспоненциальная) функция.
- 3. Формулы дифференцирования функций е^х, а^х, x^s.
- 4. Явные выражения числа е^x и функций lnx в виде пределов.
- 5. Бесконечный ряд для логарифма. Вычисление логарифмов.
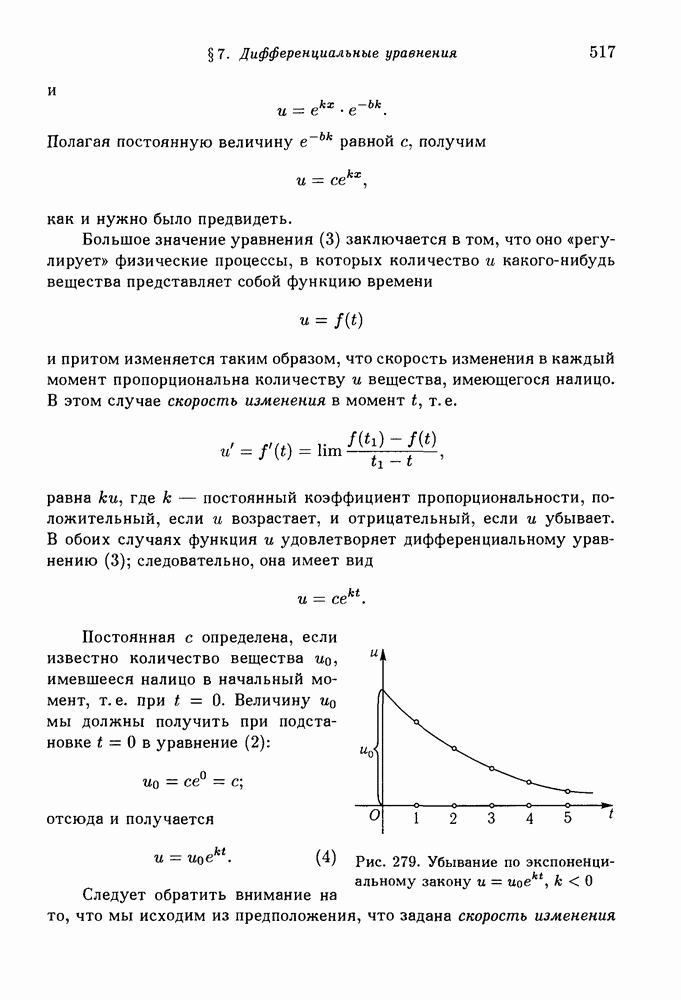
- § 7. Дифференциальные уравнения
- 2. Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- 3. Другие примеры. Простейшие колебания.
- 4. Закон движения Ньютона.
- Дополнение к главе VIII
- § 1. Вопросы принципиального порядка
- 3. Другие приложения понятия интеграла. Работа. Длина кривой.
- § 2. Порядки возрастания
- 2. Порядок возрастания ln(n!)
- § 3. Бесконечные ряды и бесконечные произведения
- 2. Формула Эйлера cos x + i sin x = exp(ix).
- 3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin x в виде бесконечного произведения.
- § 4. Доказательство теоремы о простых числах на основе статистического метода
- Приложение. Дополнительные замечания, задачи и упражнения
- Аналитическая геометрия
- Геометрические построения
- Проективная и неевклидова геометрия
- Топология
- Функции, пределы, непрерывность
- Максимумы и минимумы
- Дифференциальное и интегральное исчисления
- Техника интегрирования
- Рекомендуемая литература