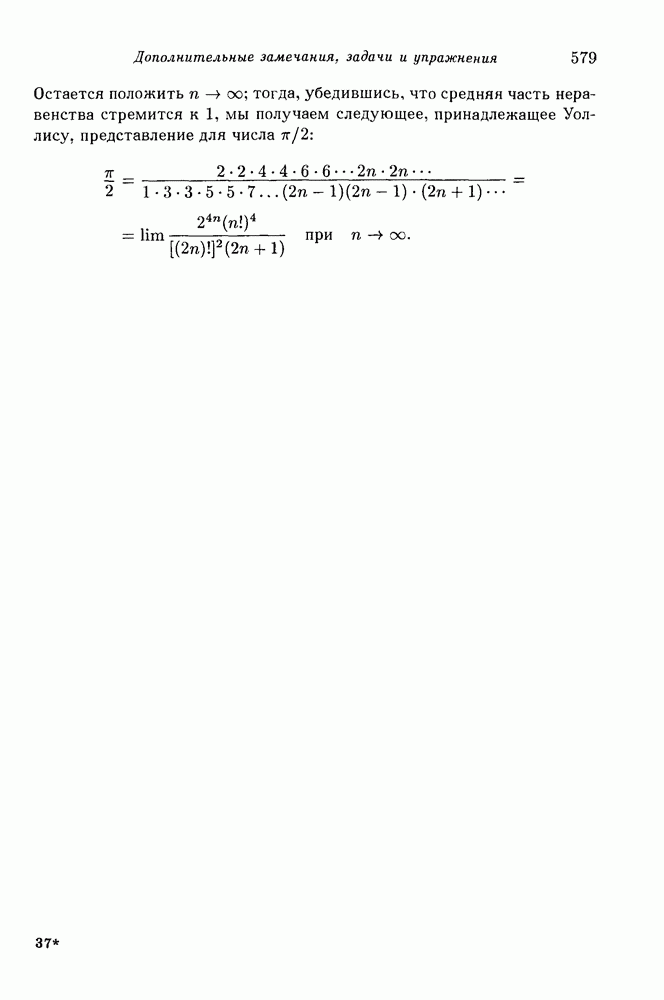| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 8. Изопериметрическая проблема
Что среди всех замкнутых кривых данной длины именно окружность охватывает наибольшую площадь — это один из «очевидных» фактов математики, строгое доказательство которых возможно только на основе новейших методов. Несколько остроумных способов доказательства этой теоремы предложил Штейнер; мы рассмотрим одно из его доказательств.

Рис. 226. К доказательству решения изопериметрической проблемы
Начнем с допущения, что решение проблемы существует. Приняв это, предположим, что это решение осуществляется некоторой кривой С, имеющей длину  и охватывающей максимальную площадь. Легко доказать, что кривая С выпуклая: это значит, что прямолинейный отрезок, соединяющий любые две точки С, лежит целиком внутри или на С. Если бы кривая С не была выпуклой, то, как показано на рис. 226, можно было бы указать отрезок
и охватывающей максимальную площадь. Легко доказать, что кривая С выпуклая: это значит, что прямолинейный отрезок, соединяющий любые две точки С, лежит целиком внутри или на С. Если бы кривая С не была выпуклой, то, как показано на рис. 226, можно было бы указать отрезок  конечные точки которого находились бы на С, а сам он был бы вне С. Дуга
конечные точки которого находились бы на С, а сам он был бы вне С. Дуга  отражение дуги
отражение дуги  относительно
относительно  образовывала бы вместе с дугой
образовывала бы вместе с дугой  кривую длины
кривую длины  охватывающую площадь, большую, чем охватывает данная кривая С, так как включала бы дополнительно площади I и II. Это противоречило бы допущению, что при данной длине
охватывающую площадь, большую, чем охватывает данная кривая С, так как включала бы дополнительно площади I и II. Это противоречило бы допущению, что при данной длине  кривая С охватывает наибольшую площадь. Итак, кривая С должна быть выпуклой. Возьмем теперь какие-нибудь две точки
кривая С охватывает наибольшую площадь. Итак, кривая С должна быть выпуклой. Возьмем теперь какие-нибудь две точки  которые делят кривую С (являющуюся решением проблемы) на две дуги равной длины. Тогда отрезок
которые делят кривую С (являющуюся решением проблемы) на две дуги равной длины. Тогда отрезок  разделит область, ограниченную кривой С, на две равновеликие области.
разделит область, ограниченную кривой С, на две равновеликие области.
В самом деле, если бы площади двух областей не были равны, то область большей площади можно было бы отразить относительно  (рис. 227), и тогда получилась бы замкнутая кривая длины
(рис. 227), и тогда получилась бы замкнутая кривая длины  охватывающая площадь, большую чем та, которую охватывает кривая С.
охватывающая площадь, большую чем та, которую охватывает кривая С.

Рис. 227. К доказательству решения изопериметрической проблемы
Отсюда следует, что любая незамкнутая кривая, представляющая собой половину (по длине) кривой С, является решением следующей проблемы: найти дугу длины  с конечными точками
с конечными точками  охватывающую вместе с отрезком
охватывающую вместе с отрезком  максимальную площадь. Мы покажем теперь, что решением этой новой проблемы является полуокружность, и тогда будет ясно, что решением основной проблемы является окружность. Итак, пусть дуга
максимальную площадь. Мы покажем теперь, что решением этой новой проблемы является полуокружность, и тогда будет ясно, что решением основной проблемы является окружность. Итак, пусть дуга  решает новую проблему. Достаточно убедиться в том, что всякий вписанный угол, например,
решает новую проблему. Достаточно убедиться в том, что всякий вписанный угол, например,  (рис. 228), будет прямым: отсюда будет вытекать, что дуга
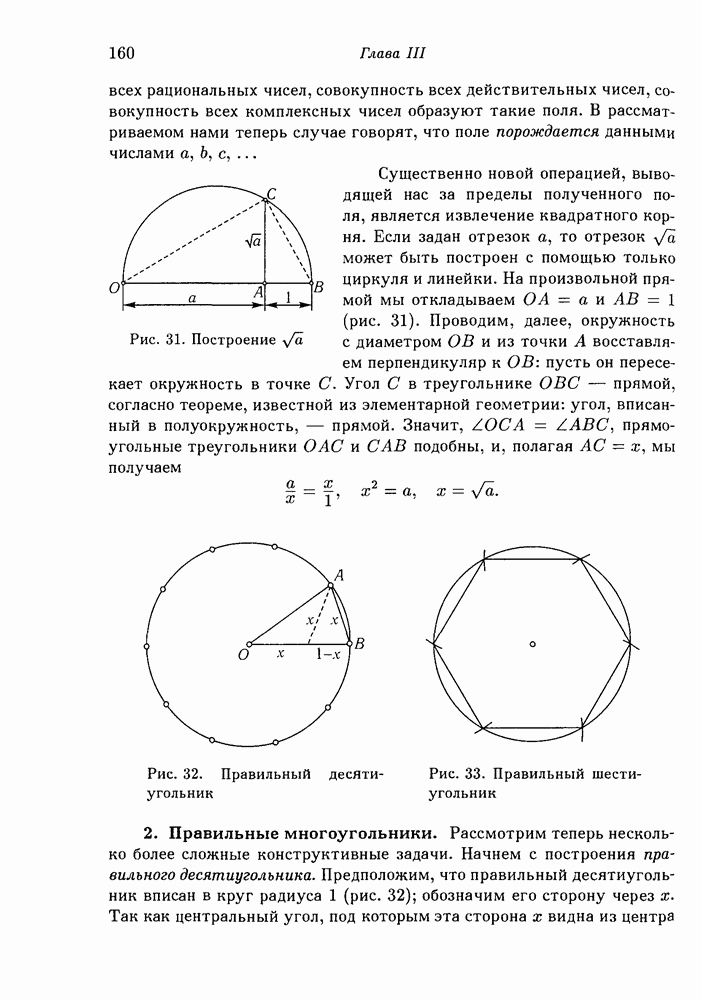
(рис. 228), будет прямым: отсюда будет вытекать, что дуга  полуокружность. Допустим, напротив, что угол
полуокружность. Допустим, напротив, что угол  не прямой. Заменим тогда треугольник
не прямой. Заменим тогда треугольник  другим треугольником с теми же сторонами
другим треугольником с теми же сторонами  и
и  но с заключенным между ними углом в
но с заключенным между ними углом в  тогда длина дуги
тогда длина дуги  останется та же
останется та же  и притом заштрихованные фигуры не изменятся. Но площадь треугольника
и притом заштрихованные фигуры не изменятся. Но площадь треугольника  при этом увеличится, так как треугольник с двумя данными сторонами имеет максимальную площадь при условии, что заключенный между ними угол — прямой (см. стр. 380). Итак, новая дуга
при этом увеличится, так как треугольник с двумя данными сторонами имеет максимальную площадь при условии, что заключенный между ними угол — прямой (см. стр. 380). Итак, новая дуга  (рис. 229) вместе с отрезком
(рис. 229) вместе с отрезком  охватит большую площадь, чем первоначальная. Полученное противоречие приводит к заключению, что, какова бы ни была точка О на рассматриваемой дуге
охватит большую площадь, чем первоначальная. Полученное противоречие приводит к заключению, что, какова бы ни была точка О на рассматриваемой дуге  угол
угол  должен быть прямым. В таком случае доказательство можно считать законченным: кривая, решающая изопериметрическую проблему, есть окружность.
должен быть прямым. В таком случае доказательство можно считать законченным: кривая, решающая изопериметрическую проблему, есть окружность.

Рис. 228. К доказательству решения изопериметрической проблемы

Рис. 229. К доказательству решения изопериметрической проблемы
Изопериметрическое свойство окружности может быть выражено в форме неравенства. Если  есть длина окружности, то охватываемая ею площадь равна
есть длина окружности, то охватываемая ею площадь равна  и потому, какова бы ни была замкнутая кривая, непременно оправдывается следующее изопериметрическое неравенство, связывающее длину кривой С и охватываемую ею площадь А:
и потому, какова бы ни была замкнутая кривая, непременно оправдывается следующее изопериметрическое неравенство, связывающее длину кривой С и охватываемую ею площадь А:

Равенство здесь имеет место только в случае окружности.
Как ясно из соображений, приведенных в § 7, доказательство Штейнера имеет лишь условное значение: «Если существует кривая С длины  охватывающая максимальную площадь, то эта кривая — окружность». Чтобы установить справедливость указанной предпосылки, нужна существенно иная аргументация. Прежде всего установим теорему элементарного содержания: среди всевозможных замкнутых многоугольников
охватывающая максимальную площадь, то эта кривая — окружность». Чтобы установить справедливость указанной предпосылки, нужна существенно иная аргументация. Прежде всего установим теорему элементарного содержания: среди всевозможных замкнутых многоугольников  с четным числом сторон
с четным числом сторон  и обладающих периметром заданной длины наибольшую площадь имеет правильный
и обладающих периметром заданной длины наибольшую площадь имеет правильный  -угольник. Доказательство строится по тому же образцу, что и приведенное выше доказательство Штейнера, со следующими изменениями. С вопросом о существовании решения здесь трудностей не возникает:
-угольник. Доказательство строится по тому же образцу, что и приведенное выше доказательство Штейнера, со следующими изменениями. С вопросом о существовании решения здесь трудностей не возникает:  -угольник, а также его периметр и площадь, зависит непрерывно от
-угольник, а также его периметр и площадь, зависит непрерывно от  координат его вершин, и, не ограничивая общности, область изменения этих координат
координат его вершин, и, не ограничивая общности, область изменения этих координат  -мерном пространстве) можно сделать компактной. Таким образом, мы можем смело начинать с утверждения, что некоторый
-мерном пространстве) можно сделать компактной. Таким образом, мы можем смело начинать с утверждения, что некоторый  -угольник Р есть решение рассматриваемой теперь проблемы, и затем переходить к анализу его свойств. Как и в штейнеровском доказательстве, доказывается, что многоугольник Р выпуклый. Затем убедимся, что все
-угольник Р есть решение рассматриваемой теперь проблемы, и затем переходить к анализу его свойств. Как и в штейнеровском доказательстве, доказывается, что многоугольник Р выпуклый. Затем убедимся, что все  сторон Р равны между собой. Допустим, напротив, что две смежные стороны
сторон Р равны между собой. Допустим, напротив, что две смежные стороны  и
и  имеют различные длины; тогда можно от многоугольника Р отрезать треугольник
имеют различные длины; тогда можно от многоугольника Р отрезать треугольник  и заменить его равнобедренным треугольником
и заменить его равнобедренным треугольником  в котором
в котором  и площадь которого больше (см. § 1). Тогда мы получим многоугольник Р с тем же периметром, но с большей площадью, вопреки сделанному допущению. Итак, все стороны Р должны быть равны между собой. Остается показать, что многоугольник Р правильный: для этого достаточно убедиться, что около Р можно описать окружность. Доказательство строится дальше, как у Штейнера. Устанавливаем прежде всего, что всякая диагональ, соединяющая противоположные вершины, делит площадь на две равные части. Затем Доказываем, что все вершины одного из многоугольников,
и площадь которого больше (см. § 1). Тогда мы получим многоугольник Р с тем же периметром, но с большей площадью, вопреки сделанному допущению. Итак, все стороны Р должны быть равны между собой. Остается показать, что многоугольник Р правильный: для этого достаточно убедиться, что около Р можно описать окружность. Доказательство строится дальше, как у Штейнера. Устанавливаем прежде всего, что всякая диагональ, соединяющая противоположные вершины, делит площадь на две равные части. Затем Доказываем, что все вершины одного из многоугольников,
возникающего при разрезании по диагонали, лежат на одной и той же окружности. Восстановить подробности намеченных доказательств (следующих образцу Штейнера) предоставляем читателю в качестве упражнения.

Рис. 230. К доказательству решения изопериметрической проблемы
Существование решения изопериметрической проблемы доказывается с помощью предельного перехода: когда мы увеличиваем неограниченно число сторон  многоугольника Р, он в пределе переходит в окружность. Этот же предельный переход дает, очевидно, и само решение.
многоугольника Р, он в пределе переходит в окружность. Этот же предельный переход дает, очевидно, и само решение.
Рассуждение Штейнера непригодно для доказательства изопериметрического свойства сферы в трехмерном пространстве. Сам Штейнер дал несколько иную, более сложную трактовку этой проблемы, пригодную для пространственного случая, но мы не приводим ее, так как на ее основе трудно получить доказательство существования решения. Вообще доказательство изопериметрического свойства сферы гораздо труднее, чем доказательство соответствующего свойства окружности; в достаточно полном и строгом изложении оно было дано позднее Г. А. Шварцем в работе, чтение которой довольно затруднительно. Свойство, о котором мы говорим, выражается в виде неравенства

где А — площадь замкнутой поверхости, V — охватываемый ею объем; равенство осуществляется лишь для сферы.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие ко второму русскому изданию
- Как пользоваться книгой
- Что такое математика?
- Глава I. Натуральные числа
- § 1. Операции над целыми числами
- 2. Представление целых чисел с помощью письменных знаков (нумерация).
- 3. Арифметические действия в недесятичных системах счисления.
- § 2. Бесконечность системы натуральных чисел. Математическая индукция
- 2. Арифметическая прогрессия.
- 3. Геометрическая прогрессия.
- 4. Сумма n первых квадратов.
- 5. Одно важное неравенство.
- 6. Биномиальная теорема.
- 7. Дальнейшие замечания по поводу метода математической индукции.
- Дополнение к главе I
- Теория чисел
- 2. Распределение простых чисел.
- § 2. Сравнения
- 2. Теорема Ферма.
- 3. Квадратические вычеты.
- § 3. Пифагоровы числа и большая теорема Ферма
- § 4. Алгоритм Евклида
- 2. Применение к основной теореме арифметики
- 3. Функция Эйлера. Еще раз о теореме Ферма.
- 4. Непрерывные дроби. Диофантовы уравнения
- Глава II. Математическая числовая система
- § 1. Рациональные числа
- 2. Возникновение надобности в рациональных числах внутри самой математики. Принцип обобщения.
- 3. Геометрическое представление рациональных чисел.
- § 2. Несоизмеримые отрезки. Иррациональные числа, пределы
- 2. Десятичные дроби: конечные и бесконечные.
- 3. Пределы. Бесконечные геометрические прогрессии.
- 4. Рациональные числа и периодические десятичные дроби.
- 5. Общее определение иррациональных чисел посредством стягивающихся отрезков.
- 6. Иные методы определения иррациональных чисел.Декиндовы сечения.
- § 3. Замечания из области аналитической геометрии
- 2. Уравнения прямых и кривых линий.
- § 4. Математический анализ бесконечного
- 2. Счетность множества рациональных чисел и несчетность континуума.
- 3. «Кардинальные числа» Кантора.
- 4. Косвенный метод доказательства.
- 5. Парадоксы бесконечного.
- 6. Основания математики.
- § 5. Комплексные числа
- 2. Геометрическое представление комплексных чисел.
- 3. Формула Муавра и корни из единицы.
- 4. Основная теорема алгебры.
- § 6. Алгебраические и трансцендентные числа
- 2. Теорема Лиувилля и конструирование трансцендентных чисел.
- Дополнение к главе II. Алгебра множеств
- 2. Применение к математической логике.
- 3. Одно из применений к теории вероятностей.
- Глава III. Геометрические построения. Алгебра числовых полей
- Часть 1. Доказательства невозможности и алгебра
- 1. Построение полей и извлечение квадратных корней.
- 2. Правильные многоугольники.
- 3. Проблема Аполлония.
- § 2. Числа, допускающие построение, и числовые поля
- 2. Все числа, допускающие построение, — алгебраические.
- § 3. Неразрешимость трех классических проблем
- 2. Одна теорема о кубических уравнениях.
- 3. Трисекция угла.
- 4. Правильный семиугольник.
- 5. Замечания по поводу квадратуры круга.
- Часть 2. Различные методы выполнения построений
- § 4. Геометрические преобразования. Инверсия
- 2. Свойства инверсии.
- 3. Геометрическое построение обратных точек.
- 4. Как разделить отрезок пополам и как найти центр данного круга с помощью одного циркуля.
- § 5. Построения с помощью иных инструментов. Построения Маскерони с помощью одного циркуля
- 1. Классическая конструкция, служащая для удвоения куба.
- 2. Построения с помощью одного циркуля.
- 3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды.
- 4. Шарнирные механизмы. Инверсоры Поселье и Гарта.
- § 6. Еще об одной инверсии и ее применениях
- 1. Инвариантность углов. Семейства окружностей.
- 2. Применение к проблеме Аполлония.
- 3. Повторные отражения.
- Глава IV. Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- 1. Классификация геометрических свойств. Инвариантность при преобразованиях.
- 2. Проективные преобразования.
- § 2. Основные понятия
- 1. Группа проективных преобразований.
- 2. Теорема Дезарга.
- § 3. Двойное отношение
- § 4. Параллельность и бесконечность
- 2. Идеальные элементы и проектирование.
- 3. Двойное отношение с бесконечно удаленными элементами.
- § 5. Применения
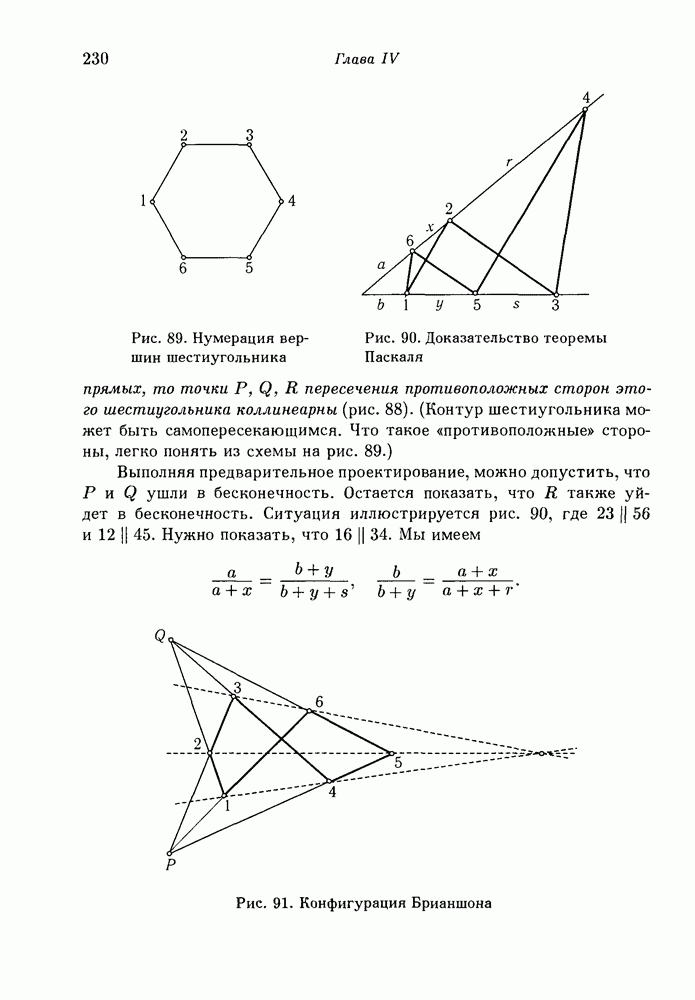
- 2. Двумерное доказательство теоремы Дезарга.
- 3. Теорема Паскаля.
- 4. Теорема Брианшона.
- 5. Замечание по поводу двойственности.
- § 6. Аналитическое представление
- 2. Однородные координаты. Алгебраические основы двойственности.
- § 7. Задачи на построения с помощью одной линейки
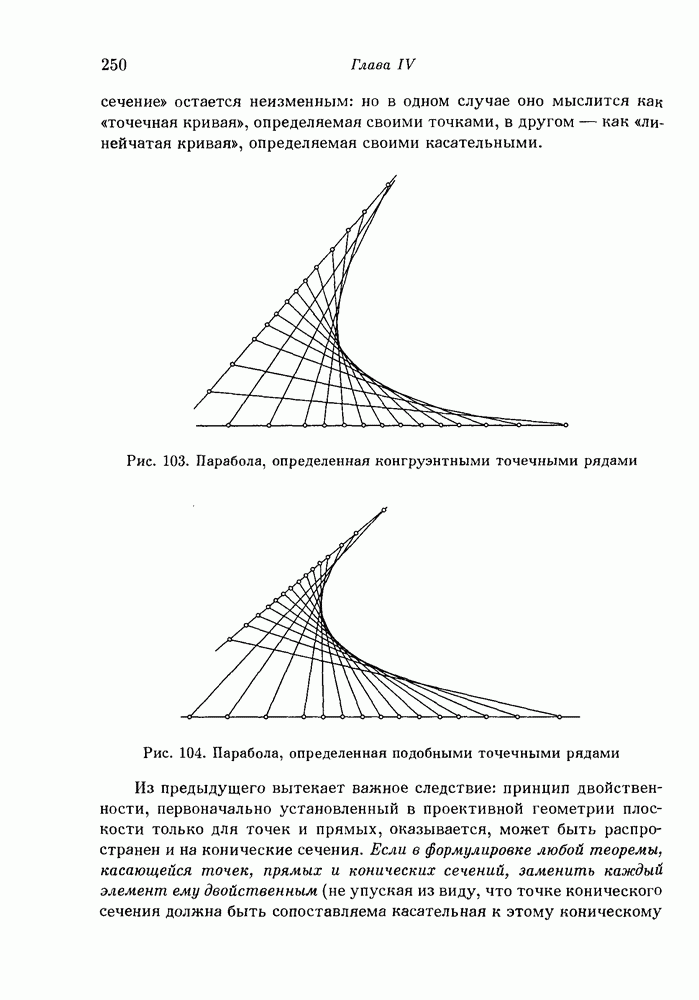
- § 8. Конические сечения и квадрики
- 2. Проективные свойства конических сечений.
- 3. Конические сечения как «линейчатые кривые».
- 4. Теоремы Паскаля и Брианшона для общего случая произвольных конических сечений.
- 5. Гиперболоид.
- § 9. Аксиоматика и неевклидова геометрия
- 2. Гиперболическая неевклидова геометрия.
- 3. Геометрия и реальность.
- 4. Модель Пуанкаре.
- 5. Эллиптическая, или риманова, геометрия.
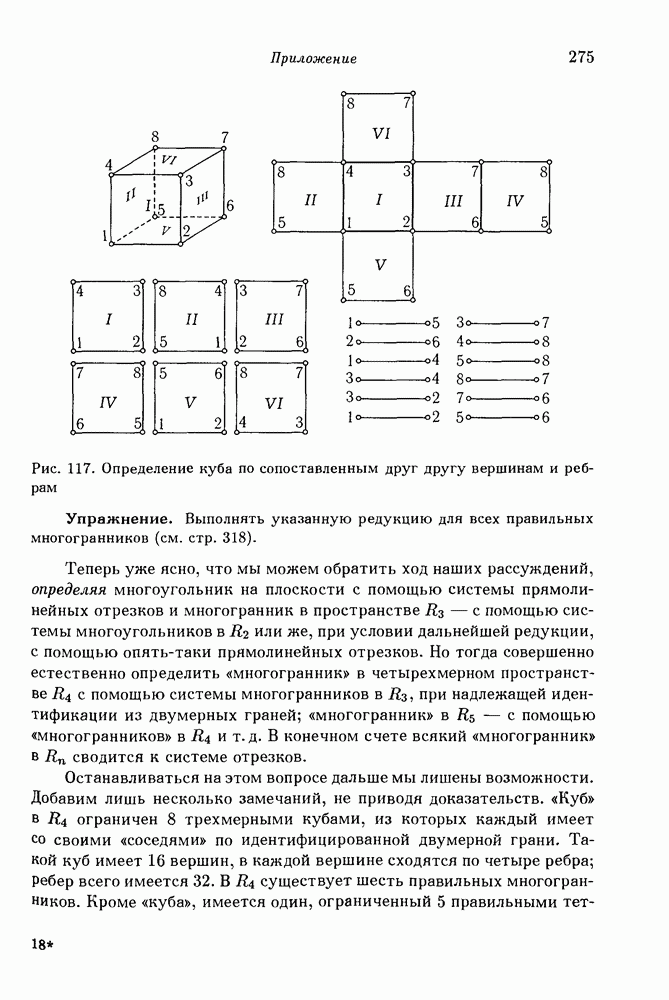
- Приложение. Геометрия в пространствах более чем трех измерений
- Глава V. Топология
- § 1. Формула Эйлера для многогранников
- § 2. Топологические свойства фигур
- 2. Свойства связности.
- § 3. Другие примеры топологических теорем
- 2. Проблема четырех красок.
- 3. Понятие размерности.
- 4. Теорема о неподвижной точке.
- 5. Узлы.
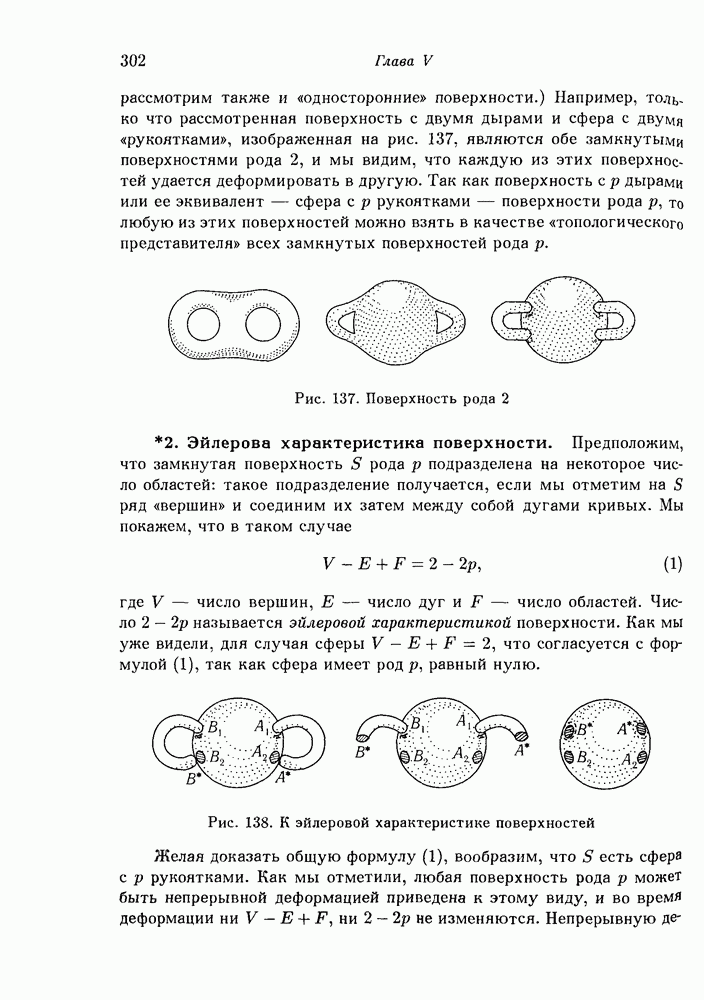
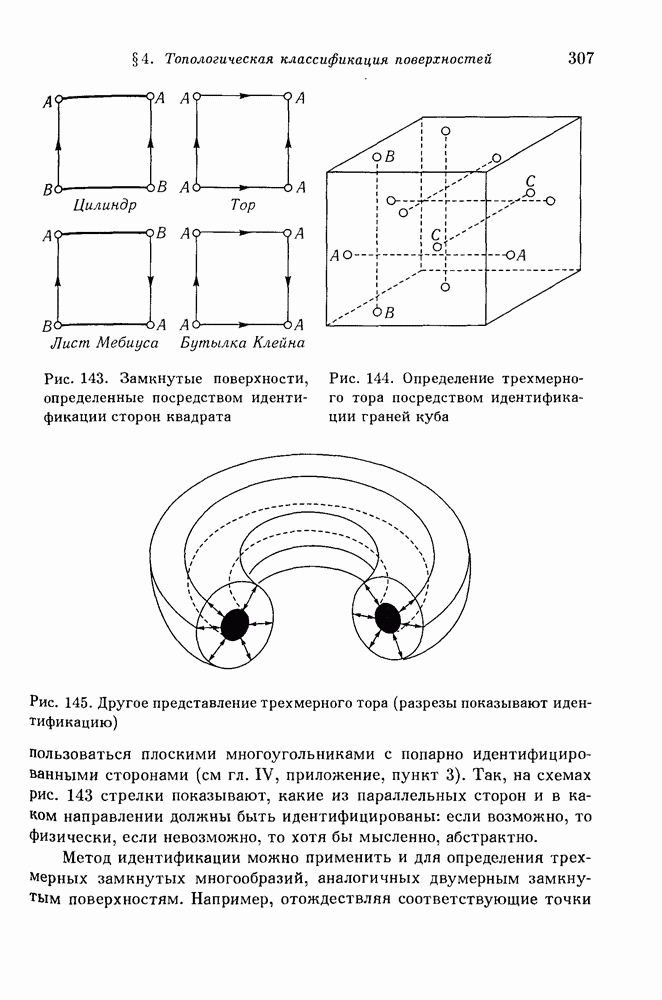
- § 4. Топологическая классификация поверхностей
- 2. Эйлерова характеристика поверхности.
- 3. Односторонние поверхности.
- Приложение
- 2. Теорема Жордана для случая многоугольников.
- 3. Основная теорема алгебры.
- Глава VI. Функции и пределы
- § 1. Независимое переменное и функция
- 2. Радианная мера углов.
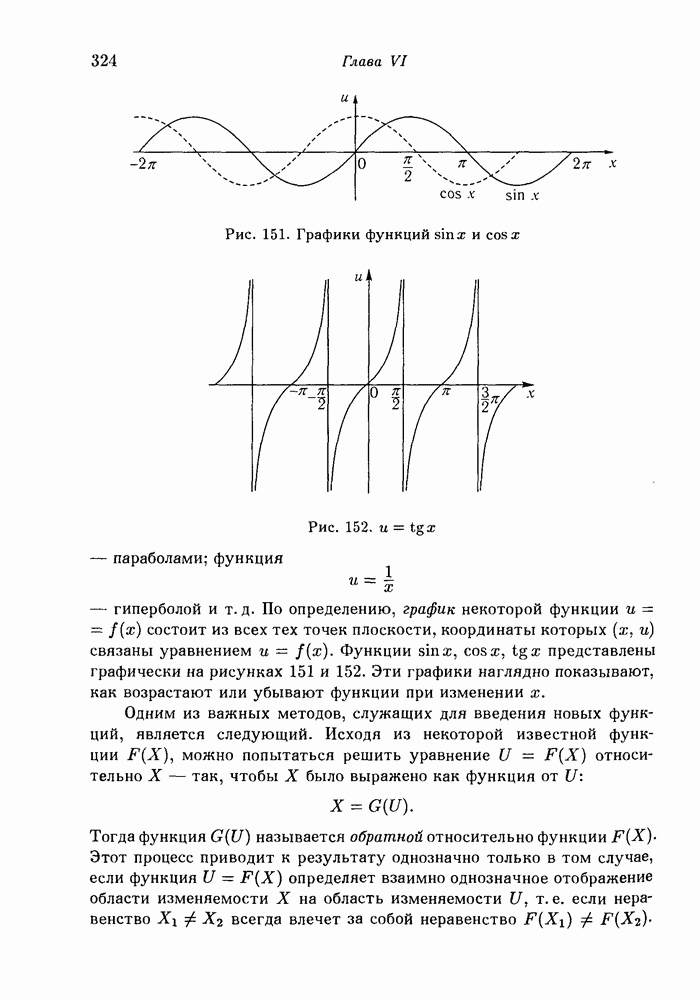
- 3. График функции. Обратные функции.
- 4. Сложные функции.
- 5. Непрерывность.
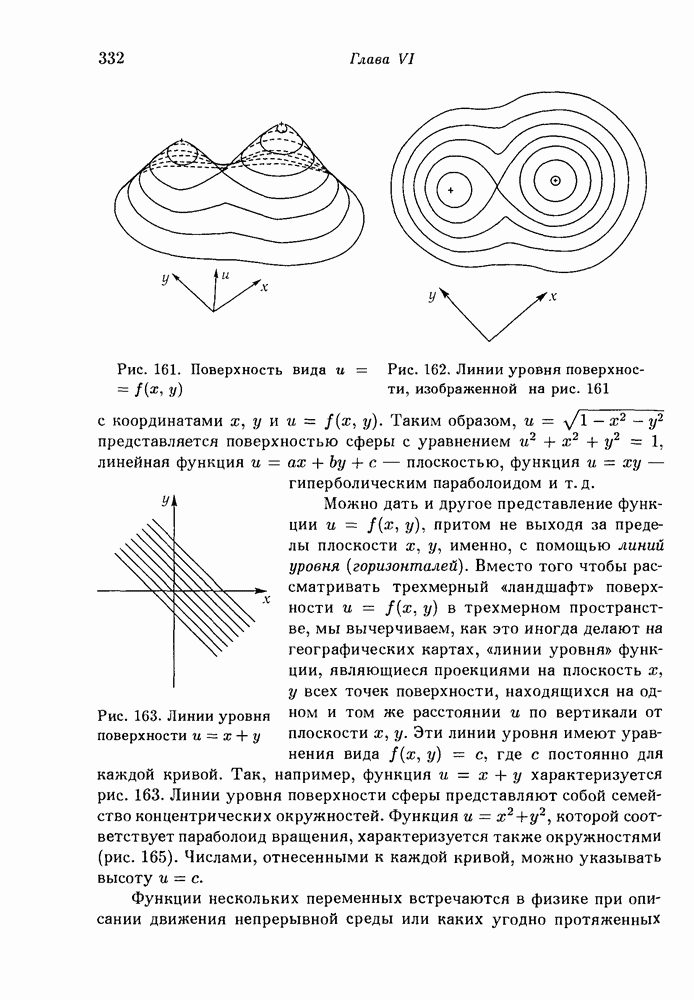
- 6. Функции нескольких переменных.
- 7. Функции и преобразования.
- § 2. Пределы
- 2. Монотонные последовательности.
- 3. Число Эйлера e.
- 4. Число «пи»
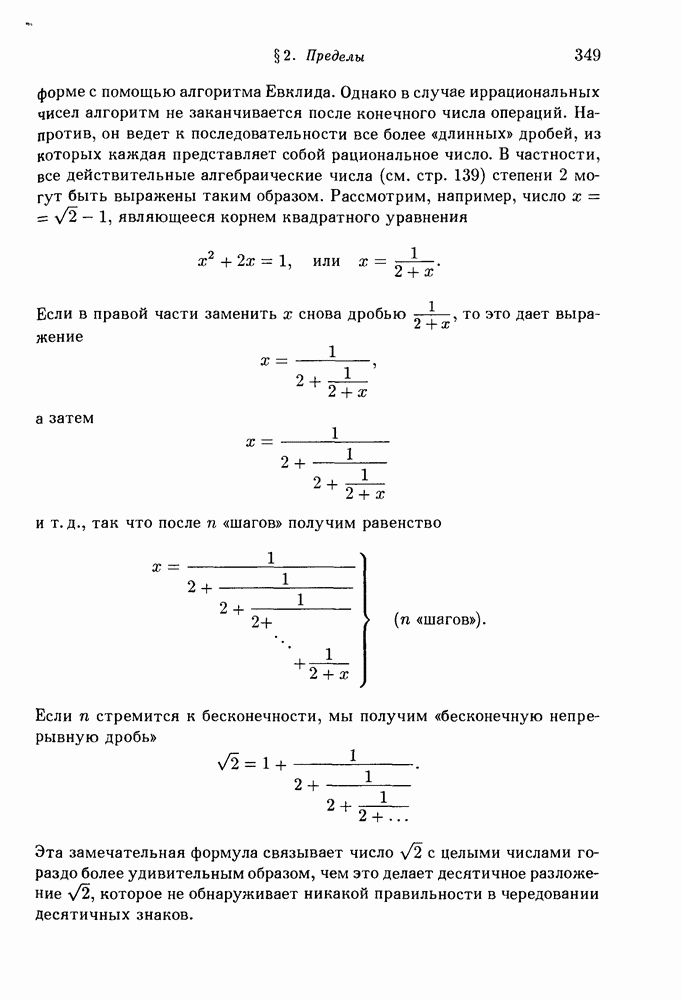
- 5. Непрерывные дроби.
- § 3. Пределы при непрерывном приближении
- 2. Замечания по поводу понятия предела
- 3. Предел sin x/x
- 4. Пределы при х -> оо.
- § 4. Точное определение непрерывности
- § 5. Две основные теоремы о непрерывных функциях
- 2. Доказательство теоремы Больцано.
- 3. Теорема Вейерштрасса об экстремальных значениях.
- 4. Теорема о последовательностях. Компактные множества.
- § 6. Некоторые применения теоремы Больцано
- 2. Применение к одной механической проблеме.
- Дополнение к главе VI. Дальнейшие примеры на пределы и непрерывность
- 4. Разрывные функции как предел непрерывных.
- 5. Пределы при итерации.
- § 2. Пример, относящийся к непрерывности
- Глава VII. Максимумы и минимумы
- § 1. Задачи из области элементарной геометрии
- 2. Теорема Герона. Экстремальное свойство световых лучей.
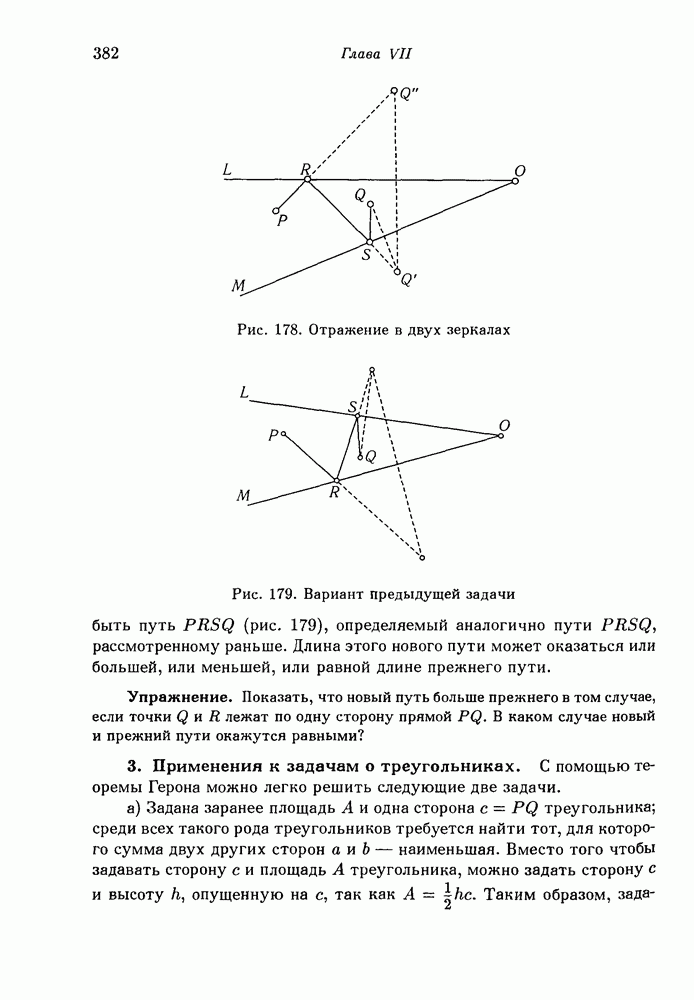
- 3. Применения к задачам о треугольниках.
- 4. Свойства касательных к эллипсу и гиперболе. Соответствующие экстремальные свойства.
- 5. Экстремальные расстояния точки от данной кривой.
- § 2. Общий принцип, которому подчинены экстремальные задачи
- § 3. Стационарные точки и дифференциальное исчисление
- 2. Максимумы и минимумы функций нескольких переменных. Седловые точки.
- 3. Точки минимакса и топология.
- 4. Расстояние точки от поверхности.
- § 4. Треугольник Шварца
- 4. Треугольники, образованные световыми лучами.
- 5. Замечания, касающиеся задач на отражение и эргодическое движение.
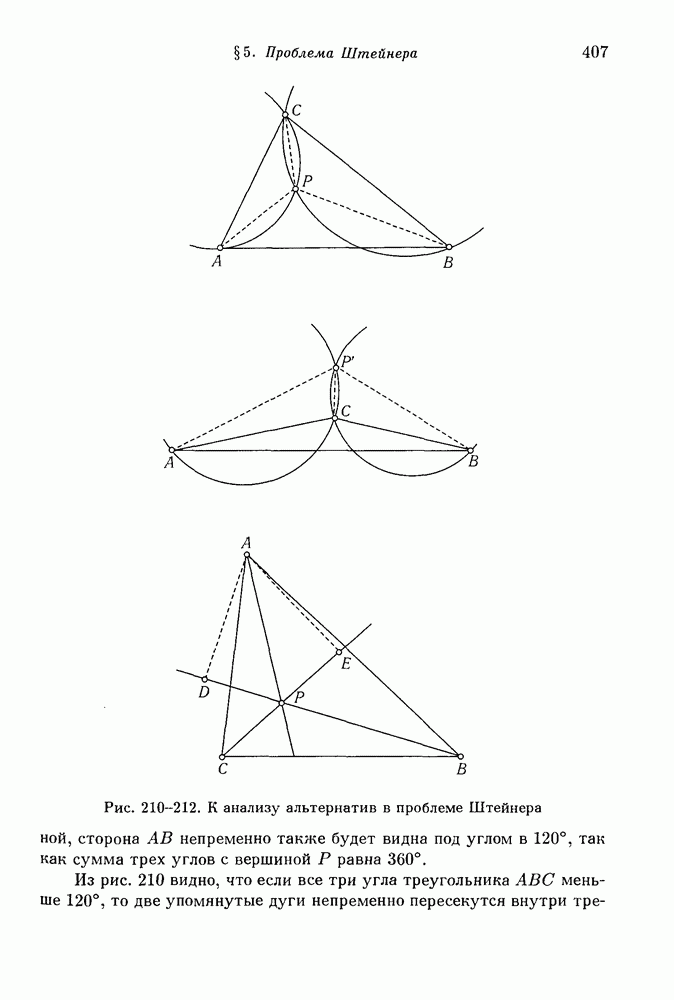
- § 5. Проблема Штейнера
- 2. Анализ возникающих альтернатив.
- 3. Дополнительная проблема.
- 4. Замечания и упражнения.
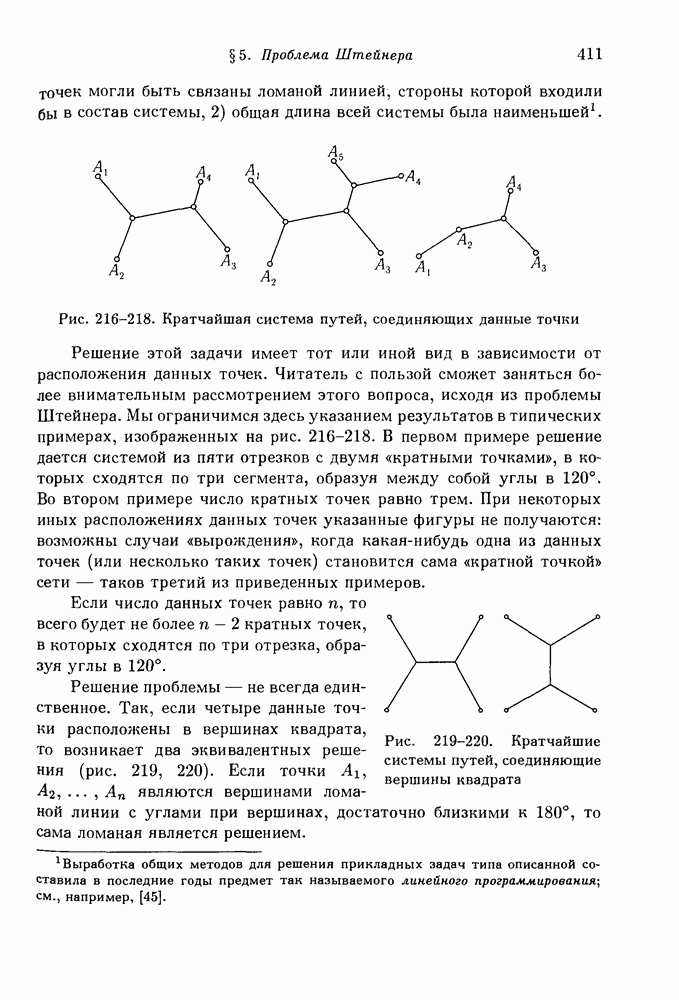
- 5. Обобщение: проблема уличной сети.
- § 6. Экстремумы и неравенства
- 1. Средние арифметическое и геометрическое двух положительных величин.
- 2. Обобщение на случай n переменных.
- 3. Метод наименьших квадратов.
- § 7. Существование экстремума. Принцип Дирихле
- 3. Экстремальные проблемы элементарного содержания.
- 4. Трудности, возникающие в более сложных случаях.
- § 8. Изопериметрическая проблема
- § 9. Экстремальные проблемы с граничными условиями. Связь между проблемой Штейнера и изопериметрической проблемой
- § 10. Вариационное исчисление
- 2. Вариационное исчисление. Принцип Ферма в оптике.
- 3. Решение задачи о брахистохроне, принадлежащее Якобу Бернулли.
- 4. Геодезические линии на сфере. Минимаксы.
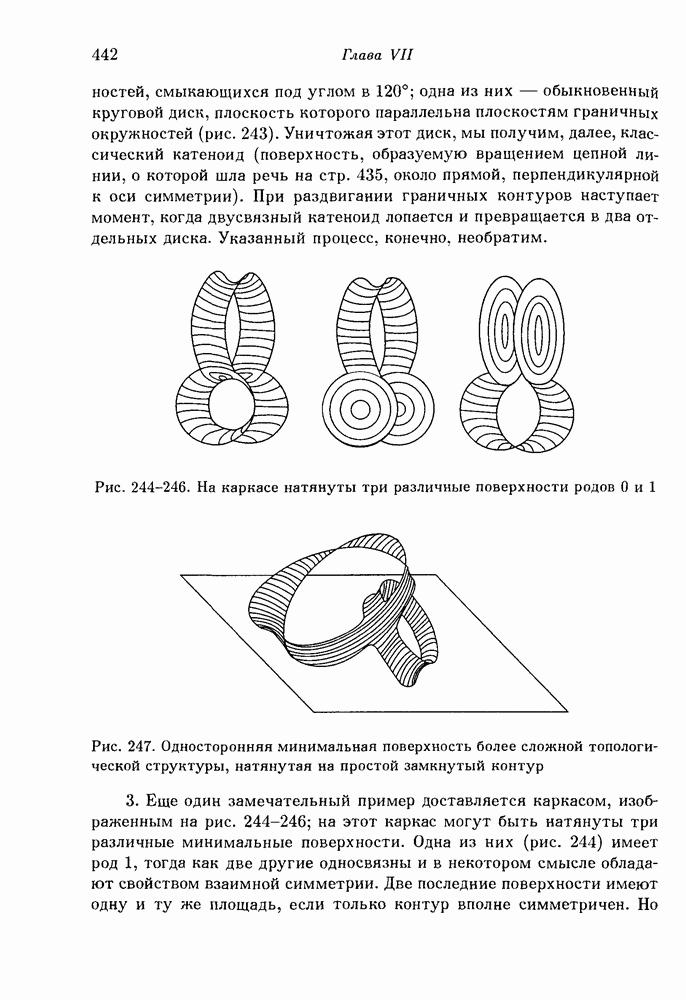
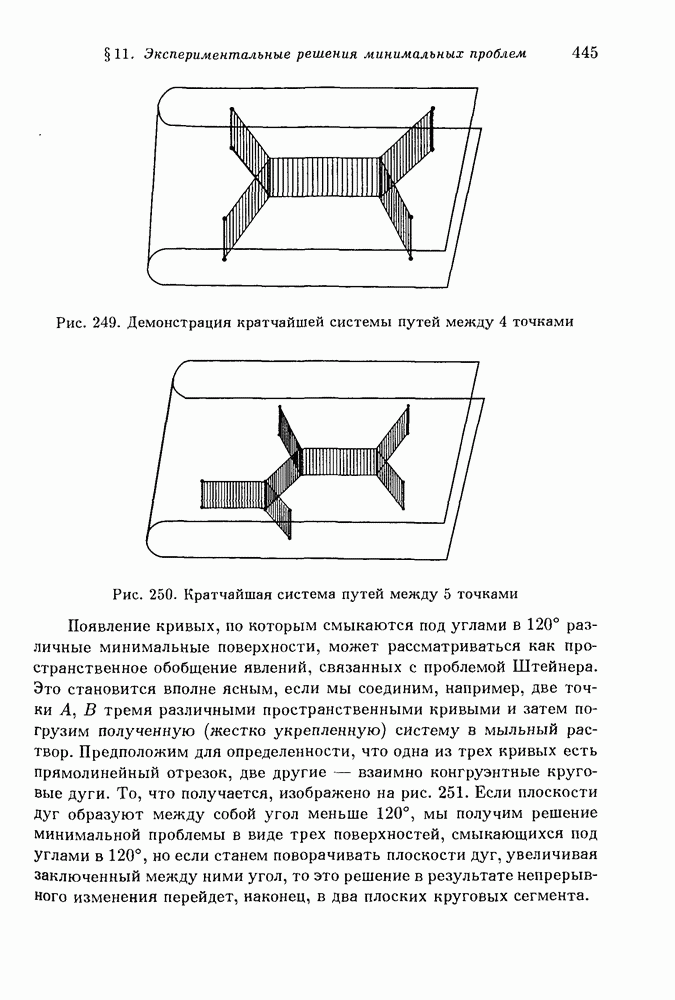
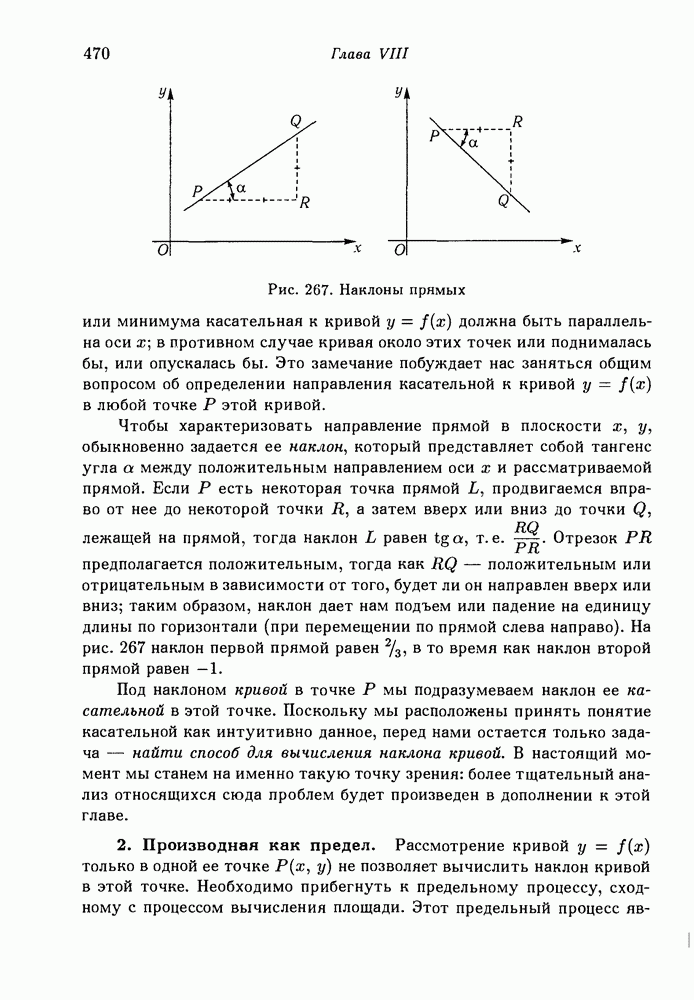
- § 11. Экспериментальные решения минимальных проблем. Опыты с мыльными пленками
- 2. Опыты с мыльными пленками.
- 3. Новые опыты, относящиеся к проблеме Плато.
- 4. Экспериментальные решения других математических проблем.
- Глава VIII. Математический анализ
- § 1. Интеграл
- 2. Интеграл.
- 3. Общие замечания о понятии интеграла. Общее определение.
- 4. Примеры интегрирования. Интегрирование x^r.
- 5. Правила «интегрального исчисления».
- § 2. Производная
- 2. Производная как предел.
- 3. Примеры.
- 4. Производные от тригонометрических функций.
- 5. Дифференцируемость и непрерывность.
- 6. Производная и скорость. Вторая производная и ускорение.
- 7. Геометрический смысл второй производной.
- 8. Максимумы и минимумы.
- § 3. Техника дифференцирования
- § 4. Обозначения Лейбница и «бесконечно малые»
- § 5. Основная теорема анализа
- 2. Первые применения. Интегрирование функций x^r, cosx, sinx. Функция arctgx
- 3. Формула Лейбница для «пи»
- § 6. Показательная (экспоненциальная) функция и логарифм
- 2. Показательная (экспоненциальная) функция.
- 3. Формулы дифференцирования функций е^х, а^х, x^s.
- 4. Явные выражения числа е^x и функций lnx в виде пределов.
- 5. Бесконечный ряд для логарифма. Вычисление логарифмов.
- § 7. Дифференциальные уравнения
- 2. Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- 3. Другие примеры. Простейшие колебания.
- 4. Закон движения Ньютона.
- Дополнение к главе VIII
- § 1. Вопросы принципиального порядка
- 3. Другие приложения понятия интеграла. Работа. Длина кривой.
- § 2. Порядки возрастания
- 2. Порядок возрастания ln(n!)
- § 3. Бесконечные ряды и бесконечные произведения
- 2. Формула Эйлера cos x + i sin x = exp(ix).
- 3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin x в виде бесконечного произведения.
- § 4. Доказательство теоремы о простых числах на основе статистического метода
- Приложение. Дополнительные замечания, задачи и упражнения
- Аналитическая геометрия
- Геометрические построения
- Проективная и неевклидова геометрия
- Топология
- Функции, пределы, непрерывность
- Максимумы и минимумы
- Дифференциальное и интегральное исчисления
- Техника интегрирования
- Рекомендуемая литература