| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Приложение. Геометрия в пространствах более чем трех измерений
1. Введение.
То «реальное» пространство, которое служит средой нашего физического опыта, имеет три измерения, плоскость имеет два измерения, прямая — одно. Наша, в обычном смысле понимаемая, пространственная интуиция решительно ограничена тремя измерениями — и дальше не простирается. Тем не менее во многих случаях вполне уместно говорить о «пространствах», имеющих четыре или более измерений. В каком же смысле допустимо говорить об  -мерном пространстве, где
-мерном пространстве, где  и для чего могут быть полезны такие пространства? Ответ можно дать, став или на аналитическую, или на геометрическую точку зрения. Терминологию
и для чего могут быть полезны такие пространства? Ответ можно дать, став или на аналитическую, или на геометрическую точку зрения. Терминологию  -мерного пространства дозволительно рассматривать только как образный язык, служащий для выражения математических идей, находящихся вне пределов обыкновенной геометрической интуиции.
-мерного пространства дозволительно рассматривать только как образный язык, служащий для выражения математических идей, находящихся вне пределов обыкновенной геометрической интуиции.
2. Аналитический подход.
Мы уже имели случай обратить внимание читателя на изменение роли аналитической геометрии, происшедшее на протяжении ее развития. Точки, прямые, кривые линии и т.д. первоначально рассматривались как чисто геометрические
объекты, и задачей аналитической геометрии было всего-навсего, сопоставляя им координаты или уравнения, интерпретировать и развивать дальше геометрическую теорию алгебраическими или аналитическими методами. Но с течением времени постепенно начала утверждаться противоположная точка зрения. Число х, или пара чисел х, у, или тройка чисел х, у, z стали рассматриваться как исходные, основные объекты и эти аналитические объекты, далее, конкретизировались, или, еще лучше сказать, «визуализировались» в виде точек на прямой, на плоскости, в пространстве. И тогда геометрический язык стал служить для того, чтобы констатировать наличие тех или иных соотношений между числами. При этом мы лишаем геометрические объекты их самостоятельного и независимого значения и говорим, что пара чисел х, у есть точка на плоскости, совокупность всех пар х, у, удовлетворяющих линейному уравнению  с — данные постоянные числа), есть прямая линия и т. д. Такие же определения устанавливаются и для трехмерного пространства.
с — данные постоянные числа), есть прямая линия и т. д. Такие же определения устанавливаются и для трехмерного пространства.
Даже в том случае, когда мы занимаемся собственно алгебраической проблемой, язык геометрии нередко представляется вполне удобным для краткого и совершенно точного описания фактов, и геометрическая интуиция начинает работать, подсказывая правильные алгебраические процедуры. Например, решая систему трех линейных уравнений с тремя неизвестными х, у, z

мы истолковываем стоящую перед нами задачу геометрически и говорим, что в трехмерном пространстве  требуется найти точку пересечения трех плоскостей, заданных уравнениями
требуется найти точку пересечения трех плоскостей, заданных уравнениями  Другой пример: рассматривая все такие числовые пары х, у, что
Другой пример: рассматривая все такие числовые пары х, у, что  мы скажем, что имеем дело с полуплоскостью, расположенной вправо от оси у. В более общем случае совокупность числовых пар х, у, для которых выполняется неравенство
мы скажем, что имеем дело с полуплоскостью, расположенной вправо от оси у. В более общем случае совокупность числовых пар х, у, для которых выполняется неравенство

интерпретируется как полуплоскость, лежащая по одну сторону прямой  а совокупность таких числовых троек х, у, z, что
а совокупность таких числовых троек х, у, z, что

 Как «полупространство», определяемое плоскостью
Как «полупространство», определяемое плоскостью 
После этих разъяснений нам совсем легко перейти к «четырехмерному» или даже к « -мерному» пространству. Рассмотрим четверку чисел
-мерному» пространству. Рассмотрим четверку чисел  Скажем, что такая четверка представляет собой точку, или, еще проще, есть точка в четырехмерном пространстве
Скажем, что такая четверка представляет собой точку, или, еще проще, есть точка в четырехмерном пространстве  Вообще, по определению, точка
Вообще, по определению, точка  -мерного пространства
-мерного пространства  есть не что иное, как система из
есть не что иное, как система из  действительных чисел
действительных чисел  записанных в определенном порядке. Не так важно, что мы не «видим» этой точки. Геометрический язык не перестает быть вполне понятным в случае, если идет речь об алгебраических свойствах
записанных в определенном порядке. Не так важно, что мы не «видим» этой точки. Геометрический язык не перестает быть вполне понятным в случае, если идет речь об алгебраических свойствах  переменных. Дело в том, что многие алгебраические свойства линейных уравнений и т.п. совершенно не зависят от числа входящих переменных, или, как принято говорить, от размерности пространства этих переменных. Мы назовем, таким образом, «гиперплоскостью» совокупность всех таких точек
переменных. Дело в том, что многие алгебраические свойства линейных уравнений и т.п. совершенно не зависят от числа входящих переменных, или, как принято говорить, от размерности пространства этих переменных. Мы назовем, таким образом, «гиперплоскостью» совокупность всех таких точек  в
в  -мерном пространстве
-мерном пространстве  которые удовлетворяют линейному уравнению
которые удовлетворяют линейному уравнению

Точно так же основная алгебраическая задача решения системы  линейных уравнений с
линейных уравнений с  неизвестными
неизвестными

истолковывается на геометрическом языке как нахождение точки пересечения  гиперплоскостей
гиперплоскостей 
Преимущество такого геометрического способа описывать математические факты заключаются в том, что он подчеркивает некоторые обстоятельства алгебраического порядка, которые не зависят от числа измерений  и вместе с тем в случае
и вместе с тем в случае  могут быть наглядно интерпретированы. Во многих приложениях употребление геометрической терминологии имеет также преимущество краткости, а вместе с тем облегчает аналитические рассуждения, а иногда руководит ими и направляет их в должную сторону. Теория относительности снова может быть приведена здесь в качестве примера области, в которой существенный успех был достигнут по той причине, что три пространственные координаты х, у, z и временная координата
могут быть наглядно интерпретированы. Во многих приложениях употребление геометрической терминологии имеет также преимущество краткости, а вместе с тем облегчает аналитические рассуждения, а иногда руководит ими и направляет их в должную сторону. Теория относительности снова может быть приведена здесь в качестве примера области, в которой существенный успех был достигнут по той причине, что три пространственные координаты х, у, z и временная координата  «события» были объединены в одно «пространственно-временное» четырехмерное многообразие
«события» были объединены в одно «пространственно-временное» четырехмерное многообразие  Подчиняя, таким образом, «пространство-время»
Подчиняя, таким образом, «пространство-время»
этой аналитической схеме и наделяя его, кроме того, свойствами неевклидовой геометрии, удалось описать многие весьма сложные ситуации с замечательной простотой. Столь же полезными оказались  -мерные пространства в механике, в статистической физике, не говоря уже о самой математике.
-мерные пространства в механике, в статистической физике, не говоря уже о самой математике.
Приведем еще кое-какие чисто математические примеры. Совокупность всех кругов на плоскости образует трехмерное многообразие, так как круг с центром  у и радиусом
у и радиусом  может быть изображен точкой с координатами
может быть изображен точкой с координатами  Так как радиус круга есть положительное число, то совокупность рассматриваемых точек заполняет полупространство. Таким же образом совокупность всех сфер в обыкновенном трехмерном пространстве образует четырехмерное многообразие, так как каждая сфера с центром
Так как радиус круга есть положительное число, то совокупность рассматриваемых точек заполняет полупространство. Таким же образом совокупность всех сфер в обыкновенном трехмерном пространстве образует четырехмерное многообразие, так как каждая сфера с центром  и радиусом
и радиусом  может быть представлена точкой с координатами
может быть представлена точкой с координатами  Куб в трехмерном пространстве с центром в начале координат, ребрами длины 2 и гранями, параллельными координатным плоскостям, состоит из совокупности всех точек
Куб в трехмерном пространстве с центром в начале координат, ребрами длины 2 и гранями, параллельными координатным плоскостям, состоит из совокупности всех точек  для которых
для которых  Так же точно «куб» в
Так же точно «куб» в  -мерном пространстве
-мерном пространстве  с центром в начале координат, «ребрами» длины 2 и «гранями», параллельными координатным плоскостям, определяется как совокупность точек
с центром в начале координат, «ребрами» длины 2 и «гранями», параллельными координатным плоскостям, определяется как совокупность точек  для которых одновременно справедливы неравенства
для которых одновременно справедливы неравенства  «Поверхность» такого куба состоит из всех точек, для которых хотя бы в одном из этих соотношений имеет место знак равенства. Поверхностные элементы размерности
«Поверхность» такого куба состоит из всех точек, для которых хотя бы в одном из этих соотношений имеет место знак равенства. Поверхностные элементы размерности  состоят из точек, для которых знак равенства стоит по меньшей мере два раза; и т.д.
состоят из точек, для которых знак равенства стоит по меньшей мере два раза; и т.д.
Упражнение. Дайте описание поверхности такого куба в трехмерном, четырехмерном,  -мерном пространствах.
-мерном пространствах.
3. Геометрический, или комбинаторный, подход.
Хотя аналитический подход к  -мерной геометрии чрезвычайно прост и удобен для многих приложений, все же следует упомянуть и о другом методе, носящем чисто геометрический смысл. Он основан на редукции от
-мерной геометрии чрезвычайно прост и удобен для многих приложений, все же следует упомянуть и о другом методе, носящем чисто геометрический смысл. Он основан на редукции от  -мерных к
-мерных к  -мерным данным и тем открывает возможность определять многомерные геометрии с помощью процесса математической индукции.
-мерным данным и тем открывает возможность определять многомерные геометрии с помощью процесса математической индукции.
Начнем с того, что рассмотрим контур треугольника  в двух Измерениях. Разрезая его в точке С и затем поворачивая стороны
в двух Измерениях. Разрезая его в точке С и затем поворачивая стороны  и
и  соответственно около
соответственно около  мы выпрямим контур в прямолинейный отрезок (рис. 116), на котором точка С будет фигурировать
мы выпрямим контур в прямолинейный отрезок (рис. 116), на котором точка С будет фигурировать  Полученная одномерная фигура дает исчерпывающее представление контура двумерного треугольника. Сгибая фигуру в точках А и В
Полученная одномерная фигура дает исчерпывающее представление контура двумерного треугольника. Сгибая фигуру в точках А и В

Рис. 116. Определение треугольника по сторонам с сопоставленными друг другу концами
и добившись совпадения двух точек С, мы имеем возможность восстановить треугольник. Но важно то, что сгибать вовсе и не нужно. Достаточно условиться, что мы «идентифицируем» (т. е. не будем различать) обе точки С, несмотря на то, что эти две точки и не совпадают в обычном смысле. Можно сделать еще следующий шаг: разрезая фигуру также и в точках  мы получим три отрезка
мы получим три отрезка  которые при желании можно опять сложить таким образом, чтобы был восстановлен «настоящий» треугольник
которые при желании можно опять сложить таким образом, чтобы был восстановлен «настоящий» треугольник  причем пары идентифицируемых точек совпадут между собой. Идея идентифицировать различные точки в данной совокупности отрезков, чтобы из них построить многоугольный контур (в нашем случае — треугольник), практически иногда оказывается очень полезной. Если нужно отправить в дальнее путешествие какое-нибудь соединение из металлических балок, например, мостовую ферму, то удобнее всего упаковать сложенные вместе, предварительно разъединенные балки, обозначив одними и теми же знаками те концы различных балок, которые должны быть соединены вместе. Такое собрание балок с мечеными концами совершенно эквивалентно пространственной конструкции. Предыдущее замечание приводит к мысли о том, как можно «разнять» двумерный многогранник в трехмерном пространстве, заменяя его фигурами низших измерений. Возьмем, например, поверхность куба (рис. 117). Ее сейчас же можно свести к системе из шести квадратов, стороны которых надлежащим образом идентифицированы; следующий шаг будет состоять в том, чтобы, заменить эту систему квадратов системой из 12 прямолинейных отрезков с надлежащим образом идентифицированными концами.
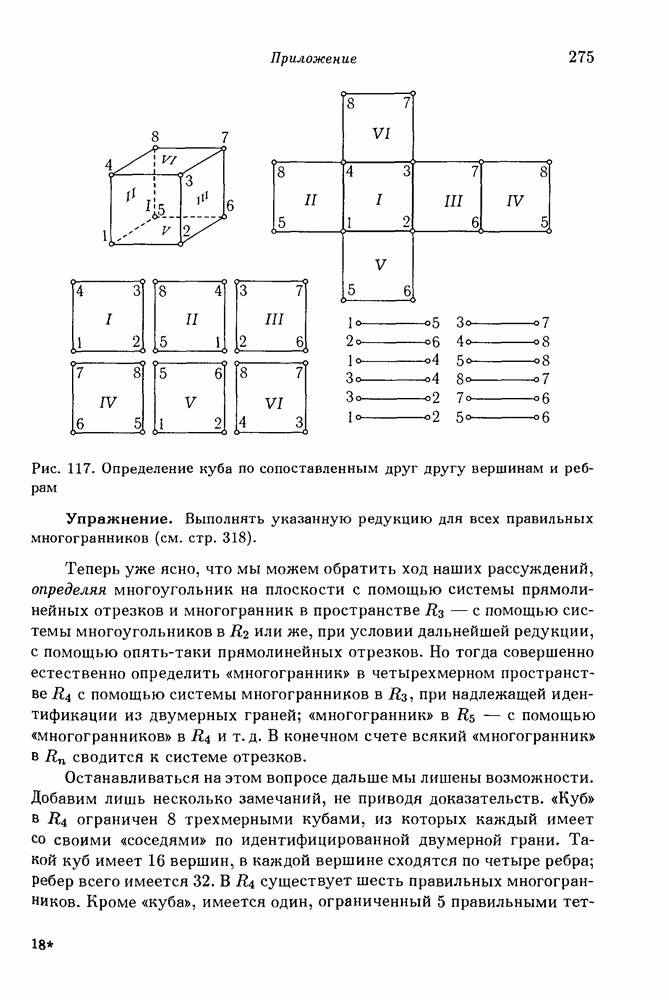
причем пары идентифицируемых точек совпадут между собой. Идея идентифицировать различные точки в данной совокупности отрезков, чтобы из них построить многоугольный контур (в нашем случае — треугольник), практически иногда оказывается очень полезной. Если нужно отправить в дальнее путешествие какое-нибудь соединение из металлических балок, например, мостовую ферму, то удобнее всего упаковать сложенные вместе, предварительно разъединенные балки, обозначив одними и теми же знаками те концы различных балок, которые должны быть соединены вместе. Такое собрание балок с мечеными концами совершенно эквивалентно пространственной конструкции. Предыдущее замечание приводит к мысли о том, как можно «разнять» двумерный многогранник в трехмерном пространстве, заменяя его фигурами низших измерений. Возьмем, например, поверхность куба (рис. 117). Ее сейчас же можно свести к системе из шести квадратов, стороны которых надлежащим образом идентифицированы; следующий шаг будет состоять в том, чтобы, заменить эту систему квадратов системой из 12 прямолинейных отрезков с надлежащим образом идентифицированными концами.
Вообще какой угодно многогранник в трехмерном пространстве  приводится таким образом или к системе плоских многоугольников, или к системе прямолинейных отрезков.
приводится таким образом или к системе плоских многоугольников, или к системе прямолинейных отрезков.

Рис. 117. Определение куба по сопоставленным друг другу вершинам и ребрам
Упражнение. Выполнять указанную редукцию для всех правильных многогранников (см. стр. 318).
Теперь уже ясно, что мы можем обратить ход наших рассуждений, определяя многоугольник на плоскости с помощью системы прямолинейных отрезков и многогранник в пространстве  с помощью системы многоугольников в
с помощью системы многоугольников в  или же, при условии дальнейшей редукции, с помощью опять-таки прямолинейных отрезков. Но тогда совершенно естественно определить «многогранник» в четырехмерном пространстве
или же, при условии дальнейшей редукции, с помощью опять-таки прямолинейных отрезков. Но тогда совершенно естественно определить «многогранник» в четырехмерном пространстве  с помощью системы многогранников в
с помощью системы многогранников в  при надлежащей идентификации из двумерных граней; «многогранник» в
при надлежащей идентификации из двумерных граней; «многогранник» в  с помощью «многогранников» в
с помощью «многогранников» в  и т. д. В конечном счете всякий «многогранник» в
и т. д. В конечном счете всякий «многогранник» в  сводится к системе отрезков.
сводится к системе отрезков.
Останавливаться на этом вопросе дальше мы лишены возможности. Добавим лишь несколько замечаний, не приводя доказательств. «Куб» в  ограничен 8 трехмерными кубами, из которых каждый имеет со своими «соседями» по идентифицированной двумерной грани. Такой куб имеет 16 вершин, в каждой вершине сходятся по четыре ребра; ребер всего имеется 32. В
ограничен 8 трехмерными кубами, из которых каждый имеет со своими «соседями» по идентифицированной двумерной грани. Такой куб имеет 16 вершин, в каждой вершине сходятся по четыре ребра; ребер всего имеется 32. В  существует шесть правильных многогранников. Кроме «куба», имеется один, ограниченный 5 правильными
существует шесть правильных многогранников. Кроме «куба», имеется один, ограниченный 5 правильными

Рис. 118. Простейшие элементы в 1, 2, 3, 4 измерениях
тетраэдрами, один, ограниченный 16 тетраэдрами, один, ограниченный 24 октаэдрами, один, ограниченный 120 додекаэдрами, и еще один, ограниченный 600 тетраэдрами. Доказано, что в  при
при  существует только 3 правильных многогранника: один с
существует только 3 правильных многогранника: один с  вершинами, ограниченный
вершинами, ограниченный  многогранниками из
многогранниками из  имеющими по
имеющими по  -мер-ных граней; один с
-мер-ных граней; один с  вершинами, ограниченный
вершинами, ограниченный  многогранниками из
многогранниками из  имеющими по
имеющими по  -мерных граней; и еще один с
-мерных граней; и еще один с  вершинами, ограниченный
вершинами, ограниченный  многогранниками из
многогранниками из  имеющими по
имеющими по  -мерных граней.
-мерных граней.
Упражнение. Сравнить определение «куба» из  данное в пункте 2, с определением, данным в настоящем пункте, и установить, что прежнее «аналитическое» определение куба равносильно настоящему «комбинаторному».
данное в пункте 2, с определением, данным в настоящем пункте, и установить, что прежнее «аналитическое» определение куба равносильно настоящему «комбинаторному».
Со структурной, или «комбинаторной», точки зрения простейшими геометрическими фигурами размерности 0, 1, 2, 3 являются соответственно точка, отрезок, треугольник, тетраэдр. Ради единообразия символики обозначим фигуры этого типа соответственно То,  (Значки указывают на размерность.) Структура каждой из этих фигур характеризуется тем, что каждая фигура типа
(Значки указывают на размерность.) Структура каждой из этих фигур характеризуется тем, что каждая фигура типа  имеет
имеет  вершин и каждое подмножество из
вершин и каждое подмножество из  вершин фигуры типа
вершин фигуры типа  определяет некоторую фигуру типа
определяет некоторую фигуру типа  Например, трехмерный тетраэдр
Например, трехмерный тетраэдр  имеет 4 вершины, 6 ребер и 4 грани.
имеет 4 вершины, 6 ребер и 4 грани.
Ясно, как будет дальше. Мы определим четырехмерный «тетраэдр»  как множество, состоящее из 5 вершин, причем каждое подмножество из 4 вершин порождает фигуру типа
как множество, состоящее из 5 вершин, причем каждое подмножество из 4 вершин порождает фигуру типа  каждое подмножество из 3 вершин — фигуру типа
каждое подмножество из 3 вершин — фигуру типа  и т.д. Фигура типа
и т.д. Фигура типа  схематически показана на рис. 118: мы видим, что у нее 5 вершин, 10 ребер, 10 треугольных граней и 5 тетраэдров.
схематически показана на рис. 118: мы видим, что у нее 5 вершин, 10 ребер, 10 треугольных граней и 5 тетраэдров.
Обобщение на  измерений не представляет труда. Из теории соединений известно, что существует ровно
измерений не представляет труда. Из теории соединений известно, что существует ровно  таких
таких
различных подмножеств по  объектов, которые могут быть составлены из множества
объектов, которые могут быть составлены из множества  объектов. Поэтому
объектов. Поэтому  -мерный «тетраэдр» содержит
-мерный «тетраэдр» содержит  вершин (фигур типа
вершин (фигур типа 

Упражнение. Нарисовать схематически фигуру типа  и определить число фигур типа
и определить число фигур типа  в ней содержащихся
в ней содержащихся  .
.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму русскому изданию
- Как пользоваться книгой
- Что такое математика?
- Глава I. Натуральные числа
- § 1. Операции над целыми числами
- 2. Представление целых чисел с помощью письменных знаков (нумерация).
- 3. Арифметические действия в недесятичных системах счисления.
- § 2. Бесконечность системы натуральных чисел. Математическая индукция
- 2. Арифметическая прогрессия.
- 3. Геометрическая прогрессия.
- 4. Сумма n первых квадратов.
- 5. Одно важное неравенство.
- 6. Биномиальная теорема.
- 7. Дальнейшие замечания по поводу метода математической индукции.
- Дополнение к главе I
- Теория чисел
- 2. Распределение простых чисел.
- § 2. Сравнения
- 2. Теорема Ферма.
- 3. Квадратические вычеты.
- § 3. Пифагоровы числа и большая теорема Ферма
- § 4. Алгоритм Евклида
- 2. Применение к основной теореме арифметики
- 3. Функция Эйлера. Еще раз о теореме Ферма.
- 4. Непрерывные дроби. Диофантовы уравнения
- Глава II. Математическая числовая система
- § 1. Рациональные числа
- 2. Возникновение надобности в рациональных числах внутри самой математики. Принцип обобщения.
- 3. Геометрическое представление рациональных чисел.
- § 2. Несоизмеримые отрезки. Иррациональные числа, пределы
- 2. Десятичные дроби: конечные и бесконечные.
- 3. Пределы. Бесконечные геометрические прогрессии.
- 4. Рациональные числа и периодические десятичные дроби.
- 5. Общее определение иррациональных чисел посредством стягивающихся отрезков.
- 6. Иные методы определения иррациональных чисел.Декиндовы сечения.
- § 3. Замечания из области аналитической геометрии
- 2. Уравнения прямых и кривых линий.
- § 4. Математический анализ бесконечного
- 2. Счетность множества рациональных чисел и несчетность континуума.
- 3. «Кардинальные числа» Кантора.
- 4. Косвенный метод доказательства.
- 5. Парадоксы бесконечного.
- 6. Основания математики.
- § 5. Комплексные числа
- 2. Геометрическое представление комплексных чисел.
- 3. Формула Муавра и корни из единицы.
- 4. Основная теорема алгебры.
- § 6. Алгебраические и трансцендентные числа
- 2. Теорема Лиувилля и конструирование трансцендентных чисел.
- Дополнение к главе II. Алгебра множеств
- 2. Применение к математической логике.
- 3. Одно из применений к теории вероятностей.
- Глава III. Геометрические построения. Алгебра числовых полей
- Часть 1. Доказательства невозможности и алгебра
- 1. Построение полей и извлечение квадратных корней.
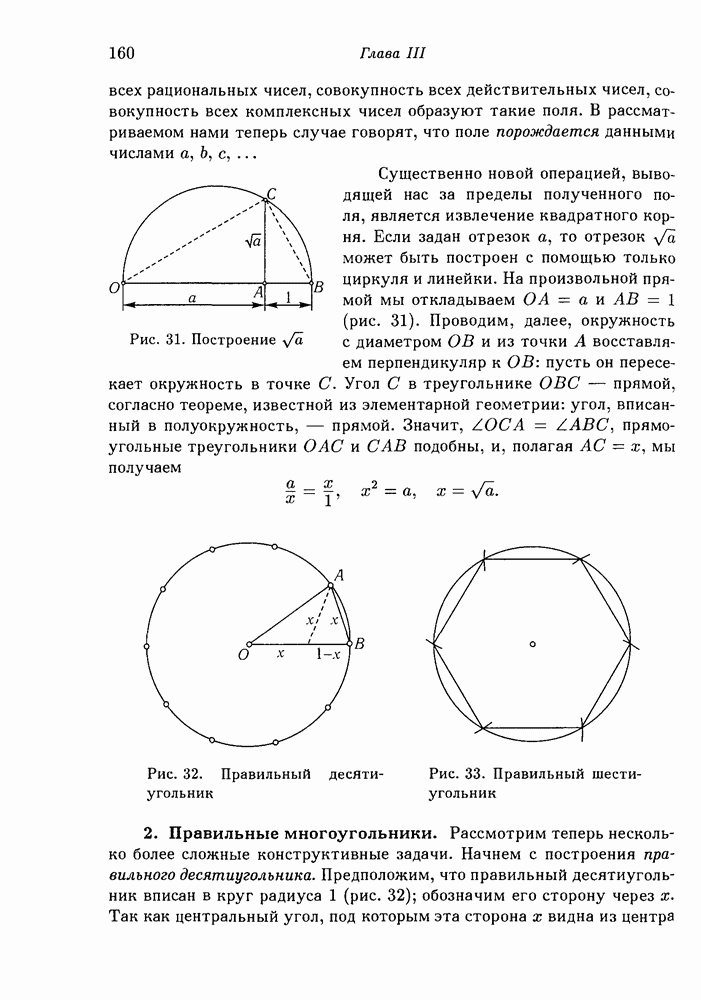
- 2. Правильные многоугольники.
- 3. Проблема Аполлония.
- § 2. Числа, допускающие построение, и числовые поля
- 2. Все числа, допускающие построение, — алгебраические.
- § 3. Неразрешимость трех классических проблем
- 2. Одна теорема о кубических уравнениях.
- 3. Трисекция угла.
- 4. Правильный семиугольник.
- 5. Замечания по поводу квадратуры круга.
- Часть 2. Различные методы выполнения построений
- § 4. Геометрические преобразования. Инверсия
- 2. Свойства инверсии.
- 3. Геометрическое построение обратных точек.
- 4. Как разделить отрезок пополам и как найти центр данного круга с помощью одного циркуля.
- § 5. Построения с помощью иных инструментов. Построения Маскерони с помощью одного циркуля
- 1. Классическая конструкция, служащая для удвоения куба.
- 2. Построения с помощью одного циркуля.
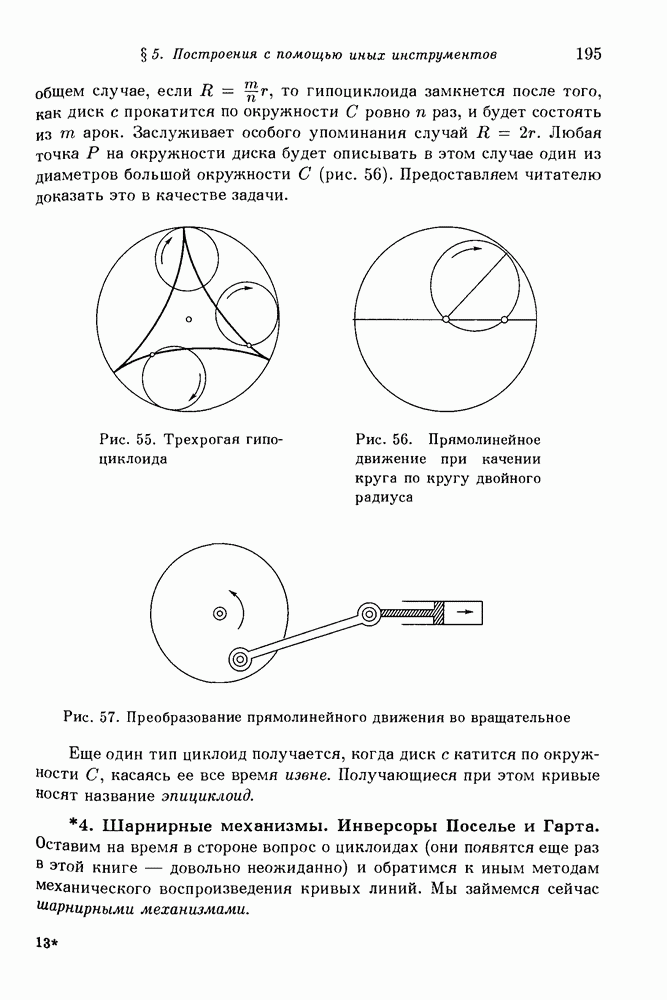
- 3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды.
- 4. Шарнирные механизмы. Инверсоры Поселье и Гарта.
- § 6. Еще об одной инверсии и ее применениях
- 1. Инвариантность углов. Семейства окружностей.
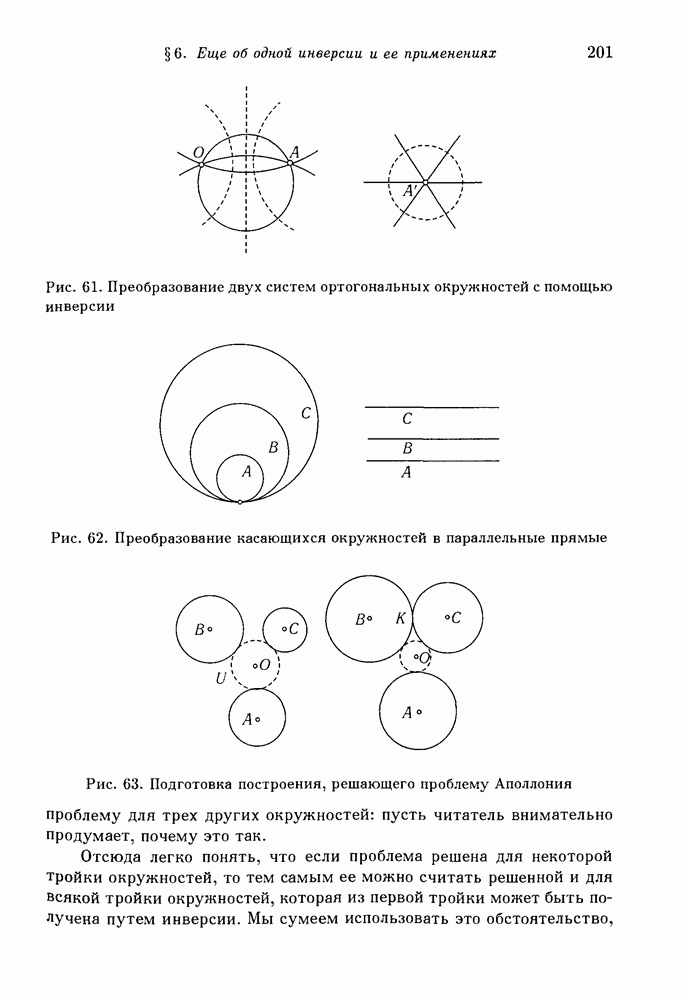
- 2. Применение к проблеме Аполлония.
- 3. Повторные отражения.
- Глава IV. Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- 1. Классификация геометрических свойств. Инвариантность при преобразованиях.
- 2. Проективные преобразования.
- § 2. Основные понятия
- 1. Группа проективных преобразований.
- 2. Теорема Дезарга.
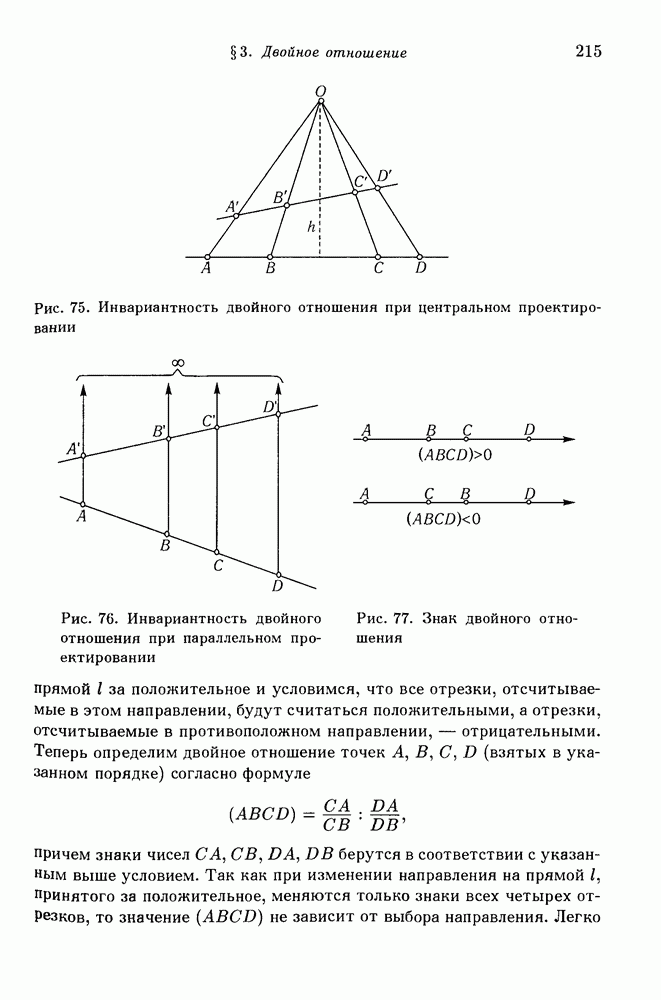
- § 3. Двойное отношение
- § 4. Параллельность и бесконечность
- 2. Идеальные элементы и проектирование.
- 3. Двойное отношение с бесконечно удаленными элементами.
- § 5. Применения
- 2. Двумерное доказательство теоремы Дезарга.
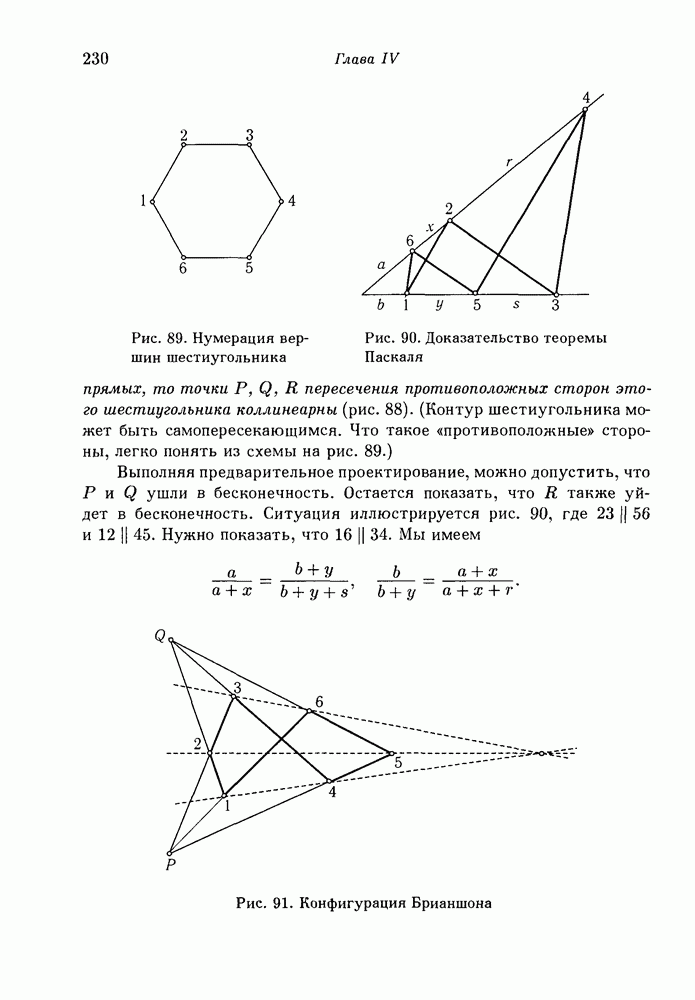
- 3. Теорема Паскаля.
- 4. Теорема Брианшона.
- 5. Замечание по поводу двойственности.
- § 6. Аналитическое представление
- 2. Однородные координаты. Алгебраические основы двойственности.
- § 7. Задачи на построения с помощью одной линейки
- § 8. Конические сечения и квадрики
- 2. Проективные свойства конических сечений.
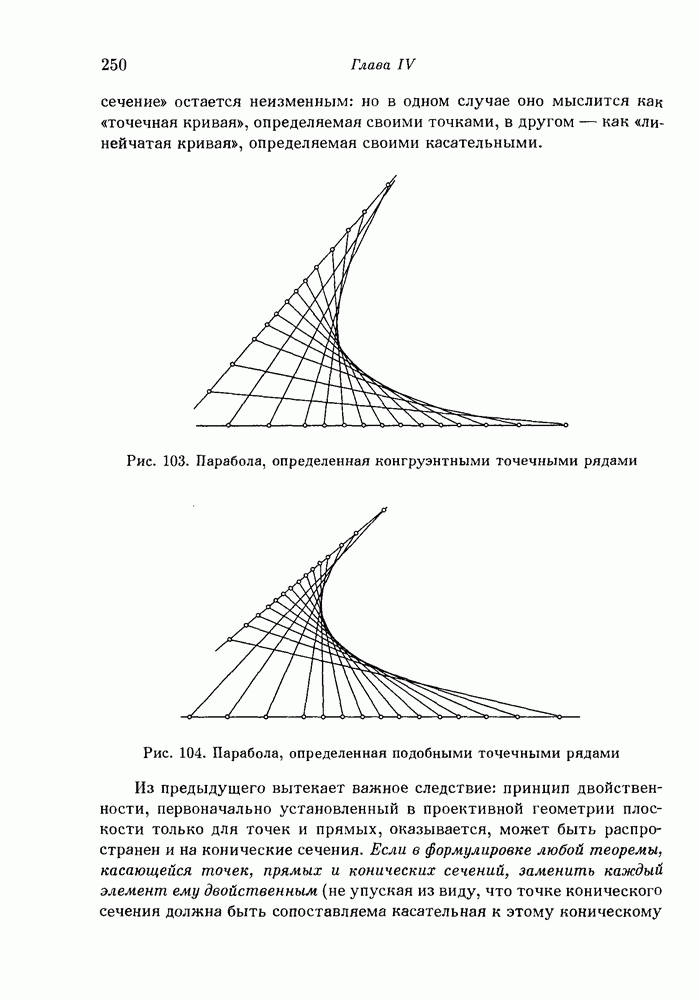
- 3. Конические сечения как «линейчатые кривые».
- 4. Теоремы Паскаля и Брианшона для общего случая произвольных конических сечений.
- 5. Гиперболоид.
- § 9. Аксиоматика и неевклидова геометрия
- 2. Гиперболическая неевклидова геометрия.
- 3. Геометрия и реальность.
- 4. Модель Пуанкаре.
- 5. Эллиптическая, или риманова, геометрия.
- Приложение. Геометрия в пространствах более чем трех измерений
- Глава V. Топология
- § 1. Формула Эйлера для многогранников
- § 2. Топологические свойства фигур
- 2. Свойства связности.
- § 3. Другие примеры топологических теорем
- 2. Проблема четырех красок.
- 3. Понятие размерности.
- 4. Теорема о неподвижной точке.
- 5. Узлы.
- § 4. Топологическая классификация поверхностей
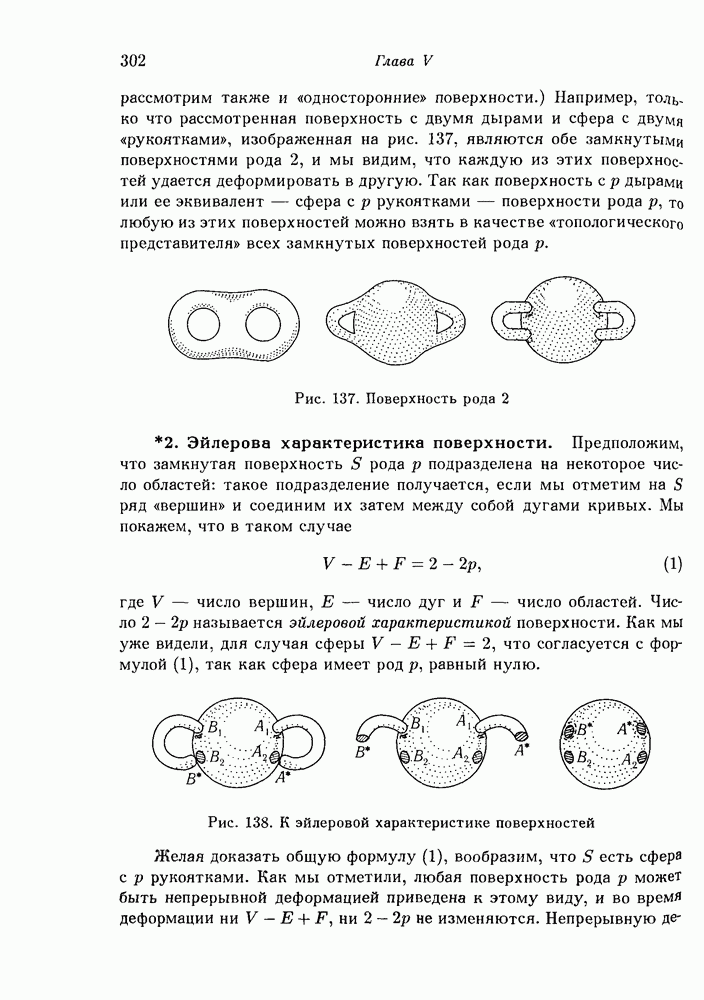
- 2. Эйлерова характеристика поверхности.
- 3. Односторонние поверхности.
- Приложение
- 2. Теорема Жордана для случая многоугольников.
- 3. Основная теорема алгебры.
- Глава VI. Функции и пределы
- § 1. Независимое переменное и функция
- 2. Радианная мера углов.
- 3. График функции. Обратные функции.
- 4. Сложные функции.
- 5. Непрерывность.
- 6. Функции нескольких переменных.
- 7. Функции и преобразования.
- § 2. Пределы
- 2. Монотонные последовательности.
- 3. Число Эйлера e.
- 4. Число «пи»
- 5. Непрерывные дроби.
- § 3. Пределы при непрерывном приближении
- 2. Замечания по поводу понятия предела
- 3. Предел sin x/x
- 4. Пределы при х -> оо.
- § 4. Точное определение непрерывности
- § 5. Две основные теоремы о непрерывных функциях
- 2. Доказательство теоремы Больцано.
- 3. Теорема Вейерштрасса об экстремальных значениях.
- 4. Теорема о последовательностях. Компактные множества.
- § 6. Некоторые применения теоремы Больцано
- 2. Применение к одной механической проблеме.
- Дополнение к главе VI. Дальнейшие примеры на пределы и непрерывность
- 4. Разрывные функции как предел непрерывных.
- 5. Пределы при итерации.
- § 2. Пример, относящийся к непрерывности
- Глава VII. Максимумы и минимумы
- § 1. Задачи из области элементарной геометрии
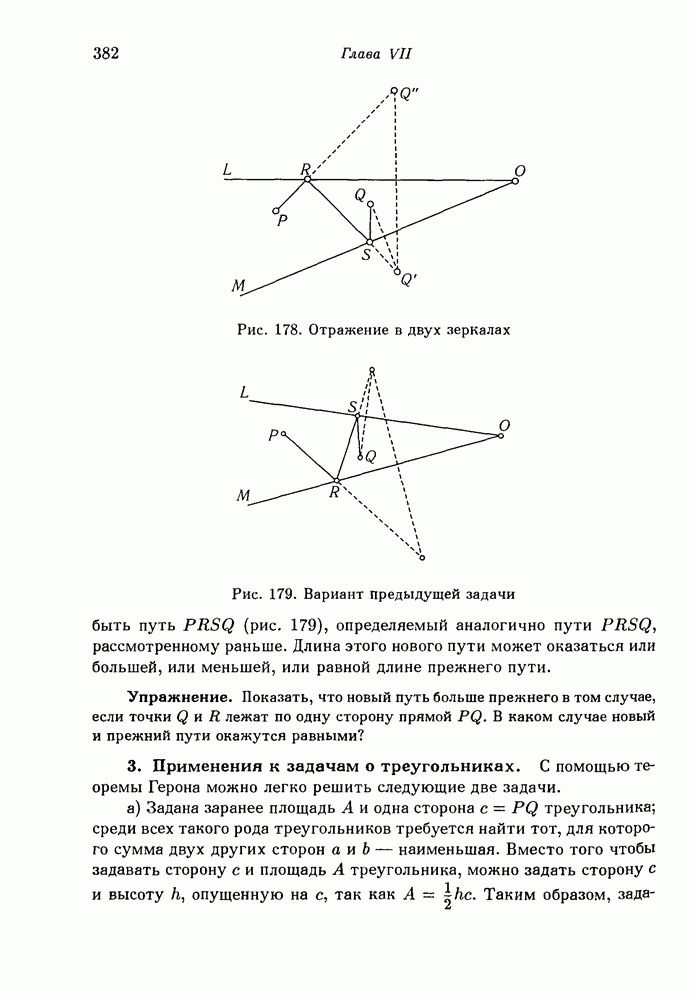
- 2. Теорема Герона. Экстремальное свойство световых лучей.
- 3. Применения к задачам о треугольниках.
- 4. Свойства касательных к эллипсу и гиперболе. Соответствующие экстремальные свойства.
- 5. Экстремальные расстояния точки от данной кривой.
- § 2. Общий принцип, которому подчинены экстремальные задачи
- § 3. Стационарные точки и дифференциальное исчисление
- 2. Максимумы и минимумы функций нескольких переменных. Седловые точки.
- 3. Точки минимакса и топология.
- 4. Расстояние точки от поверхности.
- § 4. Треугольник Шварца
- 4. Треугольники, образованные световыми лучами.
- 5. Замечания, касающиеся задач на отражение и эргодическое движение.
- § 5. Проблема Штейнера
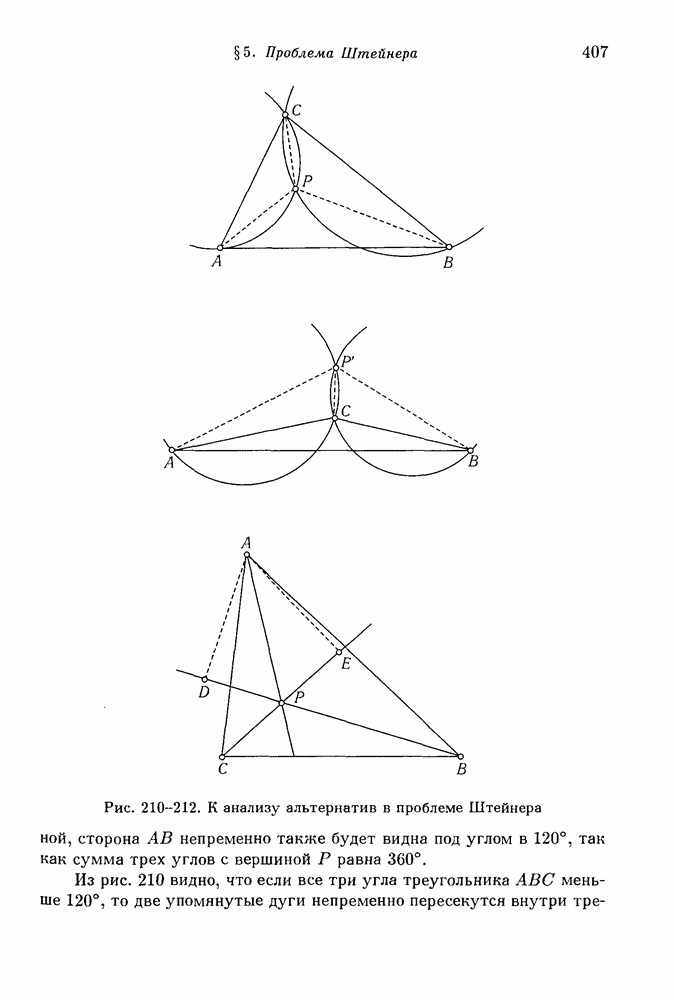
- 2. Анализ возникающих альтернатив.
- 3. Дополнительная проблема.
- 4. Замечания и упражнения.
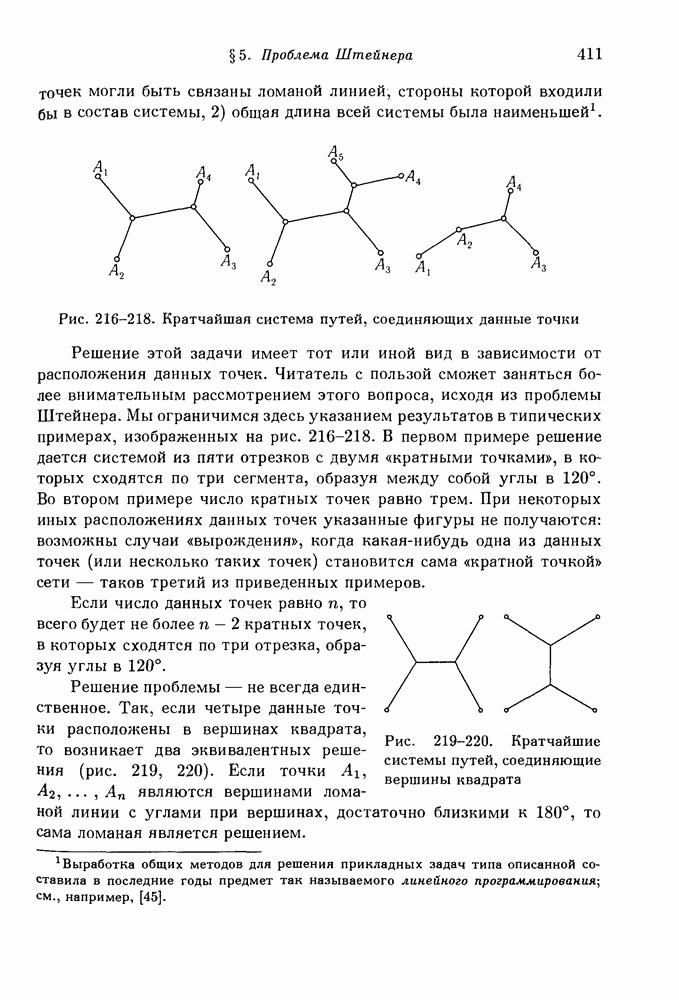
- 5. Обобщение: проблема уличной сети.
- § 6. Экстремумы и неравенства
- 1. Средние арифметическое и геометрическое двух положительных величин.
- 2. Обобщение на случай n переменных.
- 3. Метод наименьших квадратов.
- § 7. Существование экстремума. Принцип Дирихле
- 3. Экстремальные проблемы элементарного содержания.
- 4. Трудности, возникающие в более сложных случаях.
- § 8. Изопериметрическая проблема
- § 9. Экстремальные проблемы с граничными условиями. Связь между проблемой Штейнера и изопериметрической проблемой
- § 10. Вариационное исчисление
- 2. Вариационное исчисление. Принцип Ферма в оптике.
- 3. Решение задачи о брахистохроне, принадлежащее Якобу Бернулли.
- 4. Геодезические линии на сфере. Минимаксы.
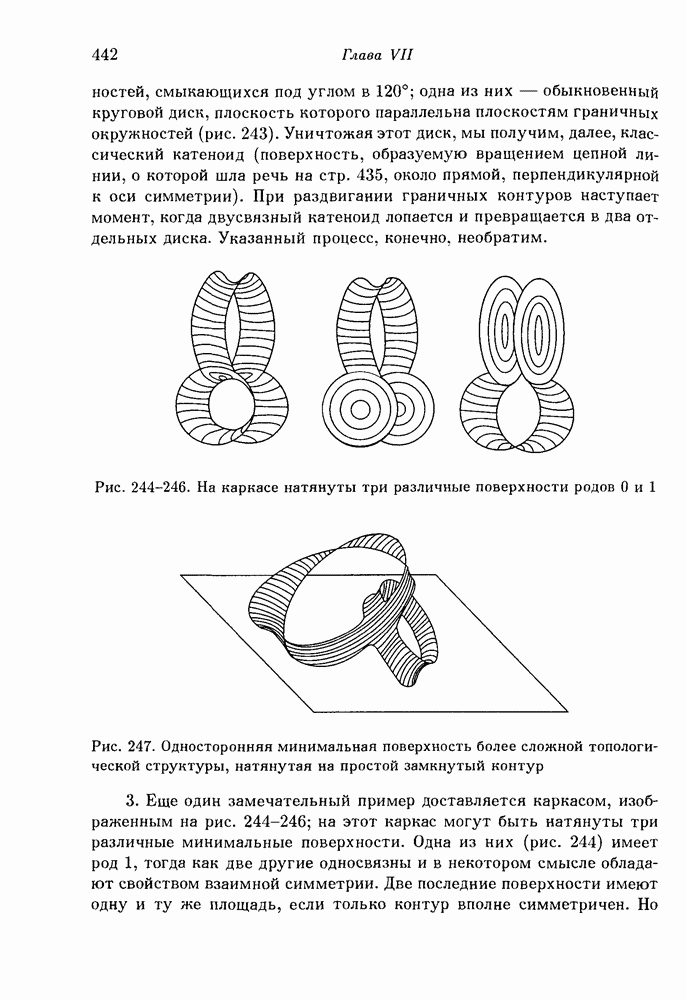
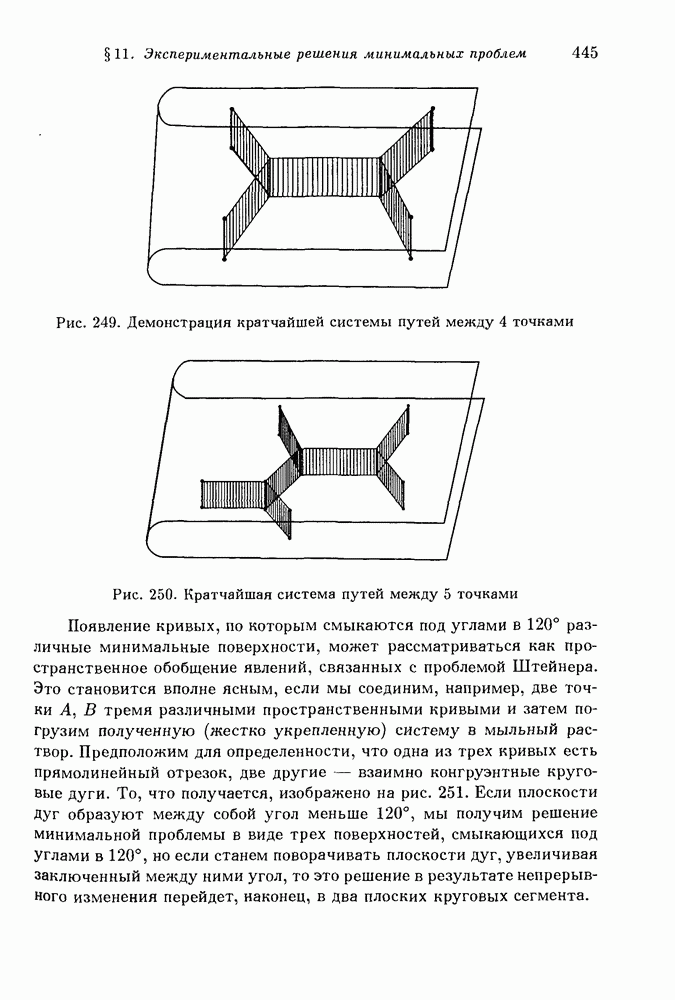
- § 11. Экспериментальные решения минимальных проблем. Опыты с мыльными пленками
- 2. Опыты с мыльными пленками.
- 3. Новые опыты, относящиеся к проблеме Плато.
- 4. Экспериментальные решения других математических проблем.
- Глава VIII. Математический анализ
- § 1. Интеграл
- 2. Интеграл.
- 3. Общие замечания о понятии интеграла. Общее определение.
- 4. Примеры интегрирования. Интегрирование x^r.
- 5. Правила «интегрального исчисления».
- § 2. Производная
- 2. Производная как предел.
- 3. Примеры.
- 4. Производные от тригонометрических функций.
- 5. Дифференцируемость и непрерывность.
- 6. Производная и скорость. Вторая производная и ускорение.
- 7. Геометрический смысл второй производной.
- 8. Максимумы и минимумы.
- § 3. Техника дифференцирования
- § 4. Обозначения Лейбница и «бесконечно малые»
- § 5. Основная теорема анализа
- 2. Первые применения. Интегрирование функций x^r, cosx, sinx. Функция arctgx
- 3. Формула Лейбница для «пи»
- § 6. Показательная (экспоненциальная) функция и логарифм
- 2. Показательная (экспоненциальная) функция.
- 3. Формулы дифференцирования функций е^х, а^х, x^s.
- 4. Явные выражения числа е^x и функций lnx в виде пределов.
- 5. Бесконечный ряд для логарифма. Вычисление логарифмов.
- § 7. Дифференциальные уравнения
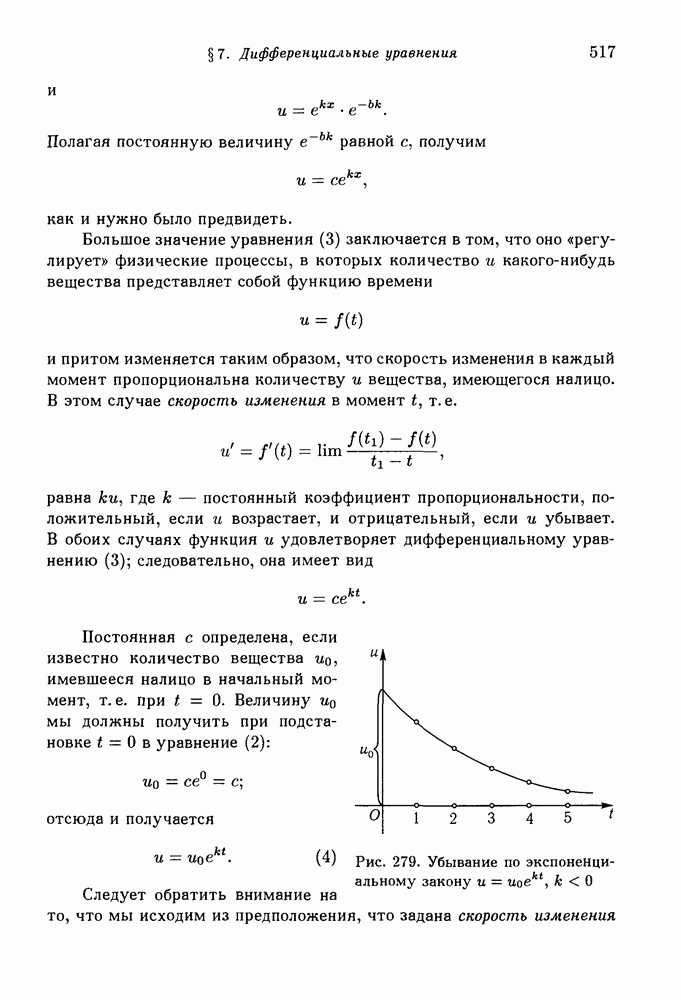
- 2. Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- 3. Другие примеры. Простейшие колебания.
- 4. Закон движения Ньютона.
- Дополнение к главе VIII
- § 1. Вопросы принципиального порядка
- 3. Другие приложения понятия интеграла. Работа. Длина кривой.
- § 2. Порядки возрастания
- 2. Порядок возрастания ln(n!)
- § 3. Бесконечные ряды и бесконечные произведения
- 2. Формула Эйлера cos x + i sin x = exp(ix).
- 3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin x в виде бесконечного произведения.
- § 4. Доказательство теоремы о простых числах на основе статистического метода
- Приложение. Дополнительные замечания, задачи и упражнения
- Аналитическая геометрия
- Геометрические построения
- Проективная и неевклидова геометрия
- Топология
- Функции, пределы, непрерывность
- Максимумы и минимумы
- Дифференциальное и интегральное исчисления
- Техника интегрирования
- Рекомендуемая литература