| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 5. Применения
1. Предварительные замечания.
После введения бесконечно удаленных элементов уже нет необходимости явно оговаривать все исключительные случаи параллельности, возникающие при построениях и доказательствах теорем. Достаточно помнить, что если точка является бесконечно удаленной, то все проходящие через нее прямые параллельны. Отпадает и необходимость делать различие между центральной и параллельной проекциями, так как параллельная проекция есть не что иное, как проекция из бесконечно удаленной точки. На рис. 72 точка О или прямая  могут оказаться бесконечно удаленными (рис. 85
могут оказаться бесконечно удаленными (рис. 85

Рис. 85. Дезаргова конфигурация с центром в бесконечности
изображает первый из упомянутых случаев); мы предоставляем читателю в качестве упражнения сформулировать в «финитных» (т. е. не содержащих упоминания о бесконечности) терминах соответствующие утверждения дезарговой теоремы.
Не только формулировка, но и доказательство теоремы, принадлежащей проективной геометрии, нередко упрощаются в результате введения бесконечно удаленных элементов. Общий принцип заключается в следующем. Условимся под «проективным классом» некоторой геометрической фигуры  понимать класс всех фигур, в которые
понимать класс всех фигур, в которые  может быть переведена проективными преобразованиями. Проективные свойства
может быть переведена проективными преобразованиями. Проективные свойства  ничем не отличаются от проективных свойств любой фигуры ее проективного класса, так как — по самому определению — проективные свойства сохраняются при проектировании. Таким образом, любая проективная теорема (т. е. теорема, говорящая только о проективных свойствах), которая верна для фигуры
ничем не отличаются от проективных свойств любой фигуры ее проективного класса, так как — по самому определению — проективные свойства сохраняются при проектировании. Таким образом, любая проективная теорема (т. е. теорема, говорящая только о проективных свойствах), которая верна для фигуры  будет также верна для любого «представителя» проективного класса этой фигуры, и обратно. Поэтому, чтобы доказать такую теорему для
будет также верна для любого «представителя» проективного класса этой фигуры, и обратно. Поэтому, чтобы доказать такую теорему для  достаточно доказать ее для некоторого «представителя» проективного класса
достаточно доказать ее для некоторого «представителя» проективного класса  Мы можем воспользоваться указанным обстоятельством и выбрать такого «представителя», для которого доказательство проще, чем для самой фигуры
Мы можем воспользоваться указанным обстоятельством и выбрать такого «представителя», для которого доказательство проще, чем для самой фигуры  Например, произвольные две точки
Например, произвольные две точки  плоскости
плоскости  могут быть спроектированы в бесконечность из данного центра О, если проектировать на плоскость, параллельную плоскости, проходящей через точки
могут быть спроектированы в бесконечность из данного центра О, если проектировать на плоскость, параллельную плоскости, проходящей через точки  прямые, проходящие через А или через В, при этом превратятся в семейства параллельных прямых. Именно такое предварительное преобразование мы выполним при доказательстве проективных теорем, которыми займемся в этом параграфе.
прямые, проходящие через А или через В, при этом превратятся в семейства параллельных прямых. Именно такое предварительное преобразование мы выполним при доказательстве проективных теорем, которыми займемся в этом параграфе.

Рис. 86. Подобие треугольников, образованных параллельными прямыми
В дальнейшем нам придется воспользоваться следующим обстоятельством, относящимся к параллельным прямым. Пусть две прямые, проходящие через точку О, пересекаются прямыми  и 12, в точках А, В, С, D, как показано на рис. 86. Если прямые
и 12, в точках А, В, С, D, как показано на рис. 86. Если прямые  и 12 параллельны, то
и 12 параллельны, то  обратно, если выполнено последнее соотношение, то прямые
обратно, если выполнено последнее соотношение, то прямые  и
и  параллельны. Доказательство, вытекающее из элементарных свойств подобных треугольников, предоставляется читателю.
параллельны. Доказательство, вытекающее из элементарных свойств подобных треугольников, предоставляется читателю.

Рис. 87. Доказательство теоремы Дезарга
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие ко второму русскому изданию
- Как пользоваться книгой
- Что такое математика?
- Глава I. Натуральные числа
- § 1. Операции над целыми числами
- 2. Представление целых чисел с помощью письменных знаков (нумерация).
- 3. Арифметические действия в недесятичных системах счисления.
- § 2. Бесконечность системы натуральных чисел. Математическая индукция
- 2. Арифметическая прогрессия.
- 3. Геометрическая прогрессия.
- 4. Сумма n первых квадратов.
- 5. Одно важное неравенство.
- 6. Биномиальная теорема.
- 7. Дальнейшие замечания по поводу метода математической индукции.
- Дополнение к главе I
- Теория чисел
- 2. Распределение простых чисел.
- § 2. Сравнения
- 2. Теорема Ферма.
- 3. Квадратические вычеты.
- § 3. Пифагоровы числа и большая теорема Ферма
- § 4. Алгоритм Евклида
- 2. Применение к основной теореме арифметики
- 3. Функция Эйлера. Еще раз о теореме Ферма.
- 4. Непрерывные дроби. Диофантовы уравнения
- Глава II. Математическая числовая система
- § 1. Рациональные числа
- 2. Возникновение надобности в рациональных числах внутри самой математики. Принцип обобщения.
- 3. Геометрическое представление рациональных чисел.
- § 2. Несоизмеримые отрезки. Иррациональные числа, пределы
- 2. Десятичные дроби: конечные и бесконечные.
- 3. Пределы. Бесконечные геометрические прогрессии.
- 4. Рациональные числа и периодические десятичные дроби.
- 5. Общее определение иррациональных чисел посредством стягивающихся отрезков.
- 6. Иные методы определения иррациональных чисел.Декиндовы сечения.
- § 3. Замечания из области аналитической геометрии
- 2. Уравнения прямых и кривых линий.
- § 4. Математический анализ бесконечного
- 2. Счетность множества рациональных чисел и несчетность континуума.
- 3. «Кардинальные числа» Кантора.
- 4. Косвенный метод доказательства.
- 5. Парадоксы бесконечного.
- 6. Основания математики.
- § 5. Комплексные числа
- 2. Геометрическое представление комплексных чисел.
- 3. Формула Муавра и корни из единицы.
- 4. Основная теорема алгебры.
- § 6. Алгебраические и трансцендентные числа
- 2. Теорема Лиувилля и конструирование трансцендентных чисел.
- Дополнение к главе II. Алгебра множеств
- 2. Применение к математической логике.
- 3. Одно из применений к теории вероятностей.
- Глава III. Геометрические построения. Алгебра числовых полей
- Часть 1. Доказательства невозможности и алгебра
- 1. Построение полей и извлечение квадратных корней.
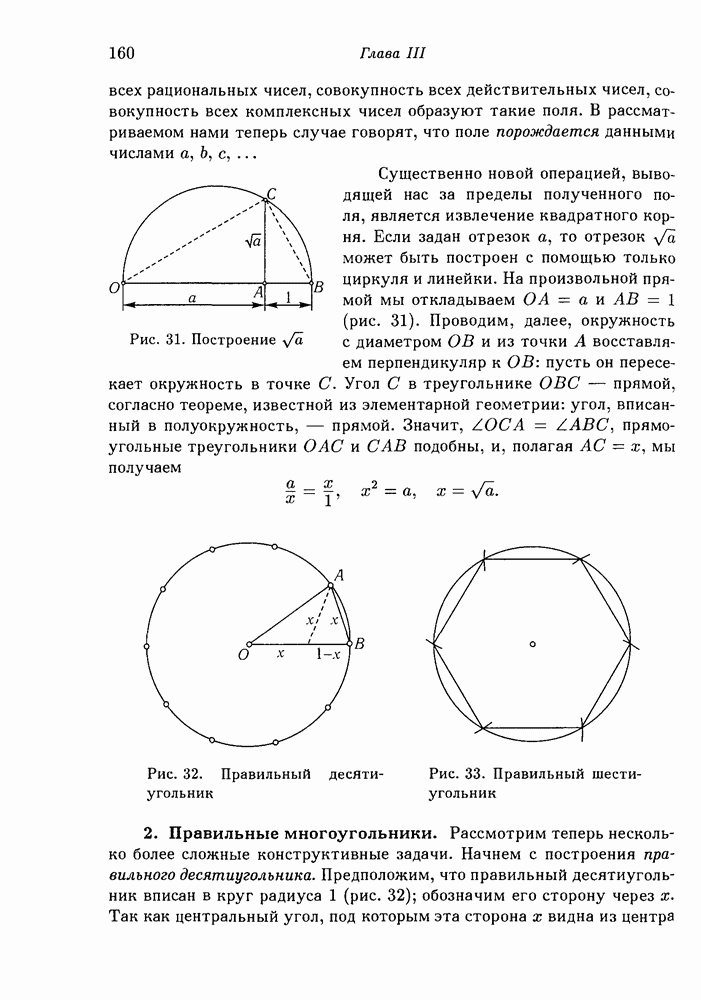
- 2. Правильные многоугольники.
- 3. Проблема Аполлония.
- § 2. Числа, допускающие построение, и числовые поля
- 2. Все числа, допускающие построение, — алгебраические.
- § 3. Неразрешимость трех классических проблем
- 2. Одна теорема о кубических уравнениях.
- 3. Трисекция угла.
- 4. Правильный семиугольник.
- 5. Замечания по поводу квадратуры круга.
- Часть 2. Различные методы выполнения построений
- § 4. Геометрические преобразования. Инверсия
- 2. Свойства инверсии.
- 3. Геометрическое построение обратных точек.
- 4. Как разделить отрезок пополам и как найти центр данного круга с помощью одного циркуля.
- § 5. Построения с помощью иных инструментов. Построения Маскерони с помощью одного циркуля
- 1. Классическая конструкция, служащая для удвоения куба.
- 2. Построения с помощью одного циркуля.
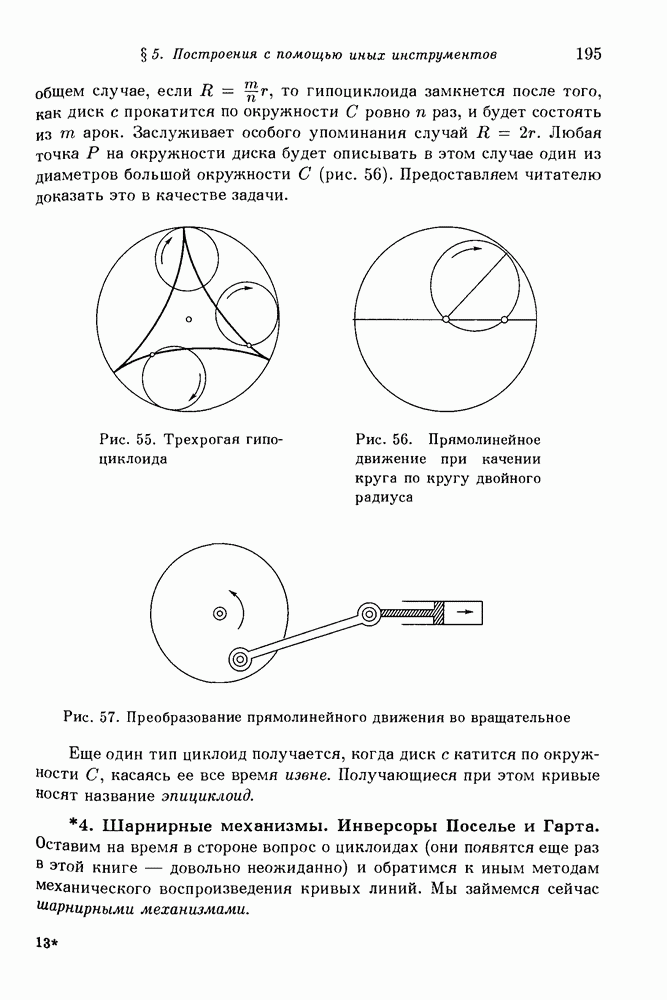
- 3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды.
- 4. Шарнирные механизмы. Инверсоры Поселье и Гарта.
- § 6. Еще об одной инверсии и ее применениях
- 1. Инвариантность углов. Семейства окружностей.
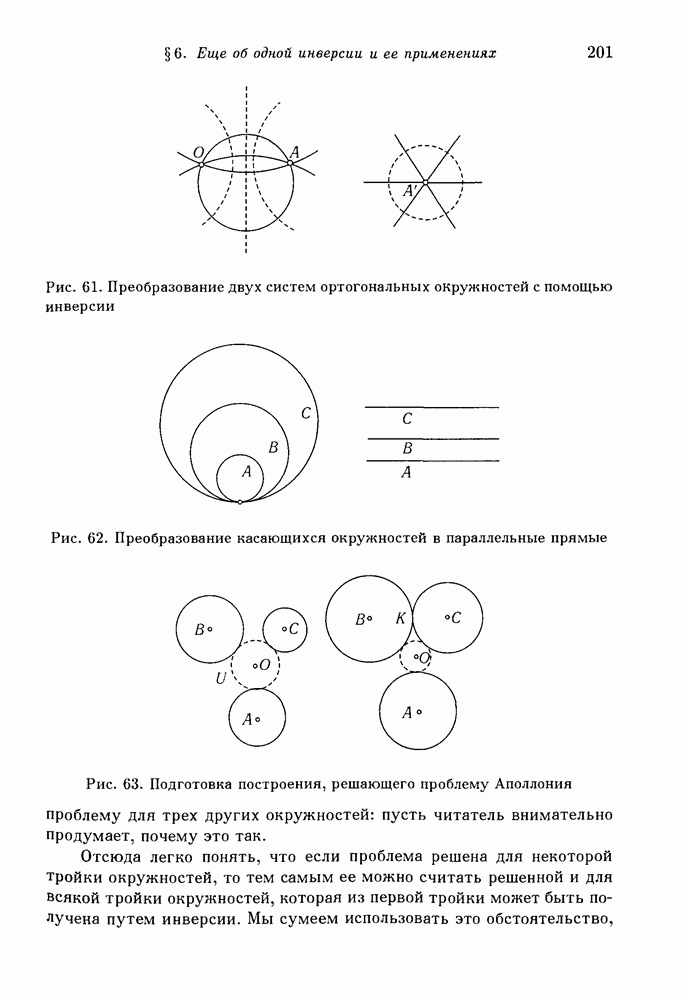
- 2. Применение к проблеме Аполлония.
- 3. Повторные отражения.
- Глава IV. Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- 1. Классификация геометрических свойств. Инвариантность при преобразованиях.
- 2. Проективные преобразования.
- § 2. Основные понятия
- 1. Группа проективных преобразований.
- 2. Теорема Дезарга.
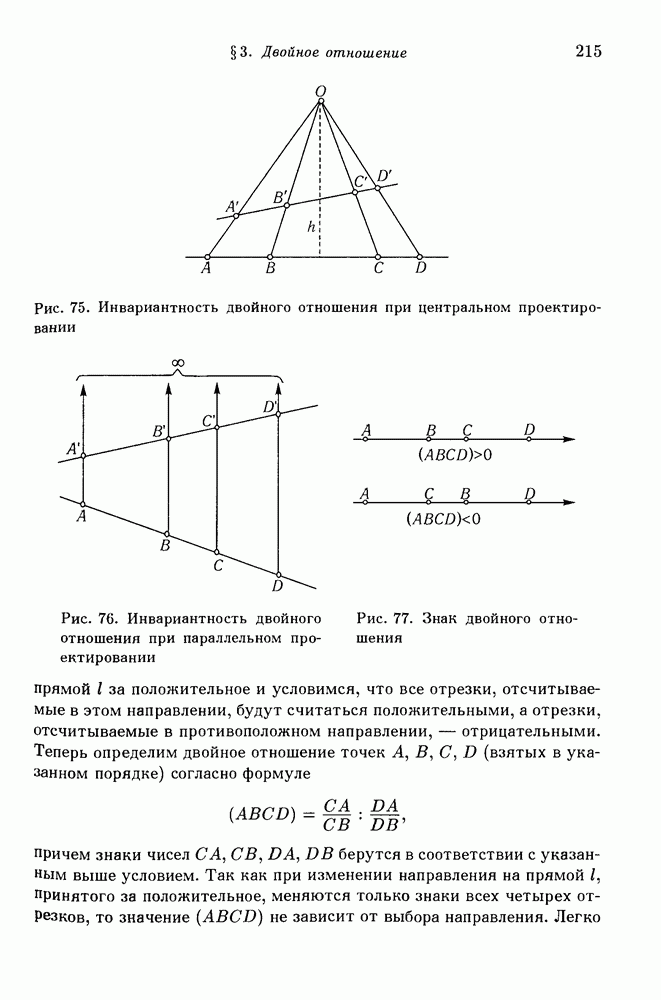
- § 3. Двойное отношение
- § 4. Параллельность и бесконечность
- 2. Идеальные элементы и проектирование.
- 3. Двойное отношение с бесконечно удаленными элементами.
- § 5. Применения
- 2. Двумерное доказательство теоремы Дезарга.
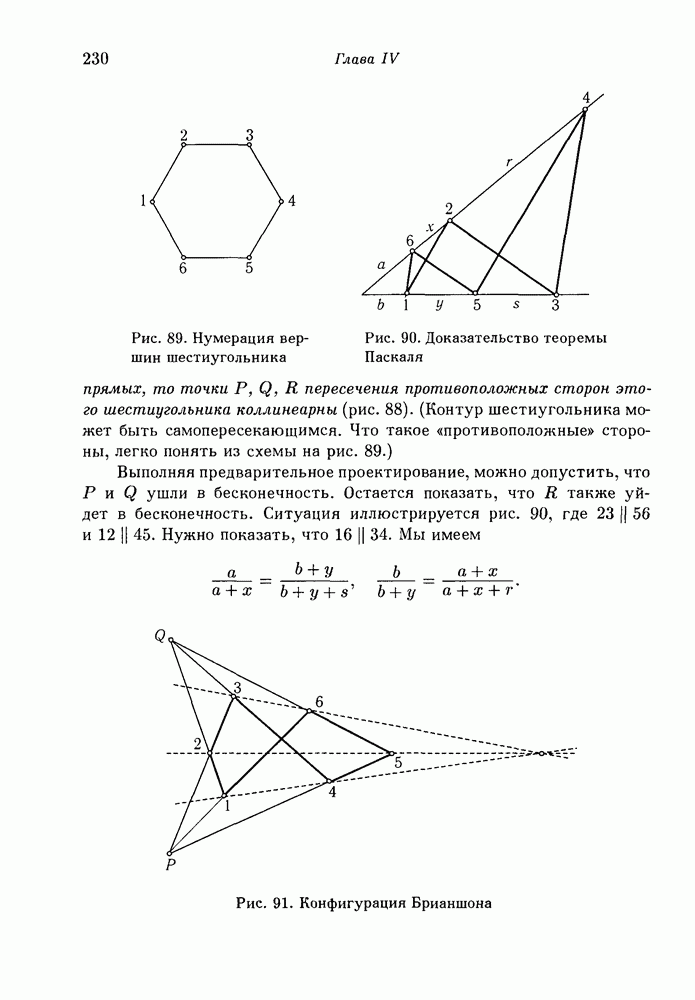
- 3. Теорема Паскаля.
- 4. Теорема Брианшона.
- 5. Замечание по поводу двойственности.
- § 6. Аналитическое представление
- 2. Однородные координаты. Алгебраические основы двойственности.
- § 7. Задачи на построения с помощью одной линейки
- § 8. Конические сечения и квадрики
- 2. Проективные свойства конических сечений.
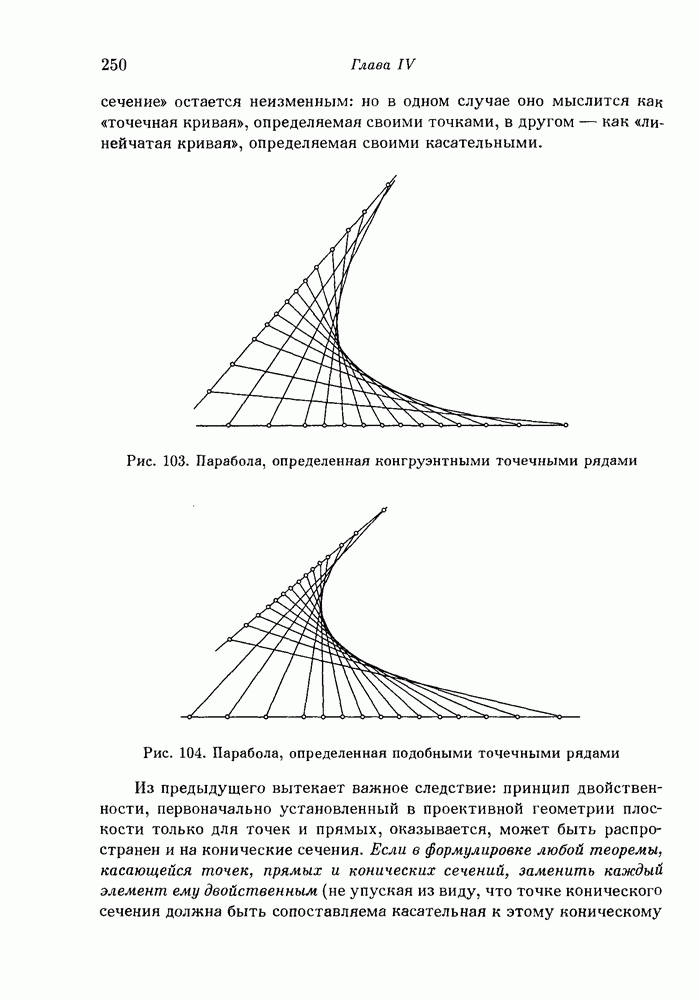
- 3. Конические сечения как «линейчатые кривые».
- 4. Теоремы Паскаля и Брианшона для общего случая произвольных конических сечений.
- 5. Гиперболоид.
- § 9. Аксиоматика и неевклидова геометрия
- 2. Гиперболическая неевклидова геометрия.
- 3. Геометрия и реальность.
- 4. Модель Пуанкаре.
- 5. Эллиптическая, или риманова, геометрия.
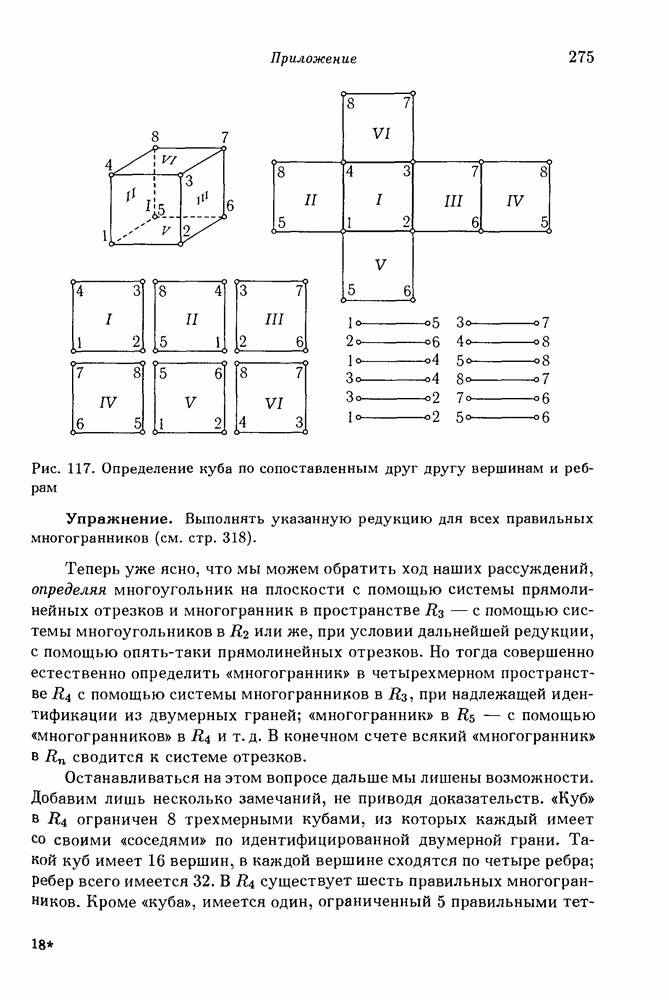
- Приложение. Геометрия в пространствах более чем трех измерений
- Глава V. Топология
- § 1. Формула Эйлера для многогранников
- § 2. Топологические свойства фигур
- 2. Свойства связности.
- § 3. Другие примеры топологических теорем
- 2. Проблема четырех красок.
- 3. Понятие размерности.
- 4. Теорема о неподвижной точке.
- 5. Узлы.
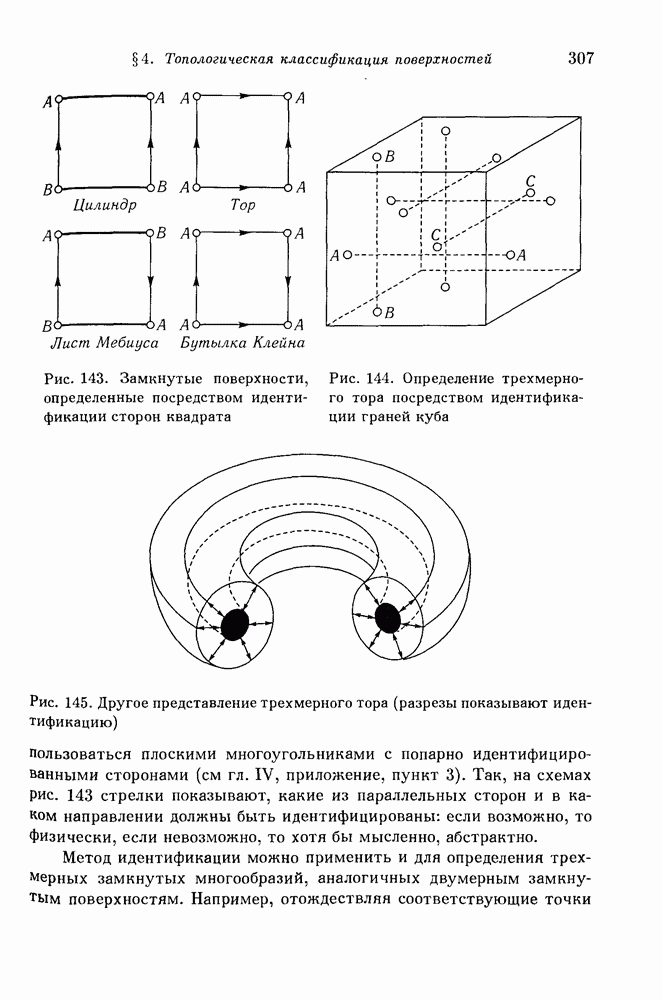
- § 4. Топологическая классификация поверхностей
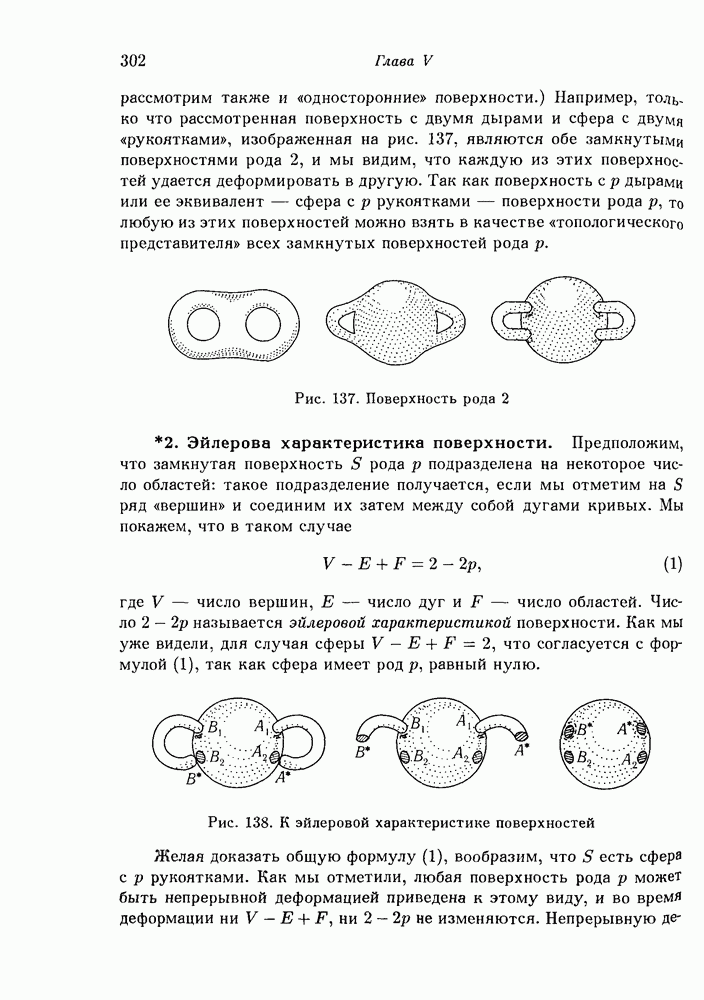
- 2. Эйлерова характеристика поверхности.
- 3. Односторонние поверхности.
- Приложение
- 2. Теорема Жордана для случая многоугольников.
- 3. Основная теорема алгебры.
- Глава VI. Функции и пределы
- § 1. Независимое переменное и функция
- 2. Радианная мера углов.
- 3. График функции. Обратные функции.
- 4. Сложные функции.
- 5. Непрерывность.
- 6. Функции нескольких переменных.
- 7. Функции и преобразования.
- § 2. Пределы
- 2. Монотонные последовательности.
- 3. Число Эйлера e.
- 4. Число «пи»
- 5. Непрерывные дроби.
- § 3. Пределы при непрерывном приближении
- 2. Замечания по поводу понятия предела
- 3. Предел sin x/x
- 4. Пределы при х -> оо.
- § 4. Точное определение непрерывности
- § 5. Две основные теоремы о непрерывных функциях
- 2. Доказательство теоремы Больцано.
- 3. Теорема Вейерштрасса об экстремальных значениях.
- 4. Теорема о последовательностях. Компактные множества.
- § 6. Некоторые применения теоремы Больцано
- 2. Применение к одной механической проблеме.
- Дополнение к главе VI. Дальнейшие примеры на пределы и непрерывность
- 4. Разрывные функции как предел непрерывных.
- 5. Пределы при итерации.
- § 2. Пример, относящийся к непрерывности
- Глава VII. Максимумы и минимумы
- § 1. Задачи из области элементарной геометрии
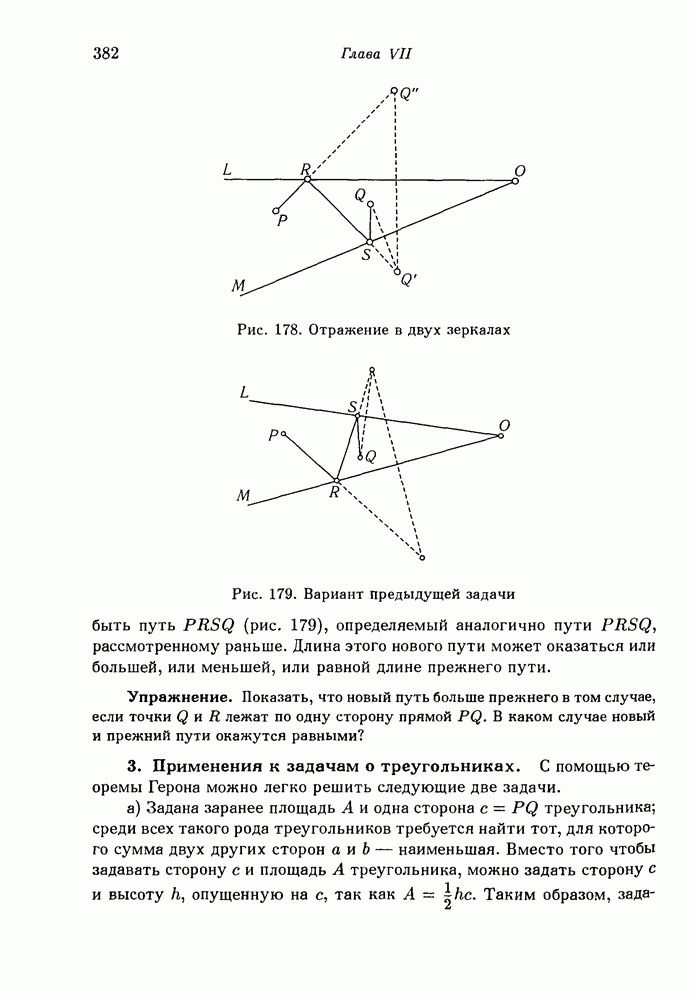
- 2. Теорема Герона. Экстремальное свойство световых лучей.
- 3. Применения к задачам о треугольниках.
- 4. Свойства касательных к эллипсу и гиперболе. Соответствующие экстремальные свойства.
- 5. Экстремальные расстояния точки от данной кривой.
- § 2. Общий принцип, которому подчинены экстремальные задачи
- § 3. Стационарные точки и дифференциальное исчисление
- 2. Максимумы и минимумы функций нескольких переменных. Седловые точки.
- 3. Точки минимакса и топология.
- 4. Расстояние точки от поверхности.
- § 4. Треугольник Шварца
- 4. Треугольники, образованные световыми лучами.
- 5. Замечания, касающиеся задач на отражение и эргодическое движение.
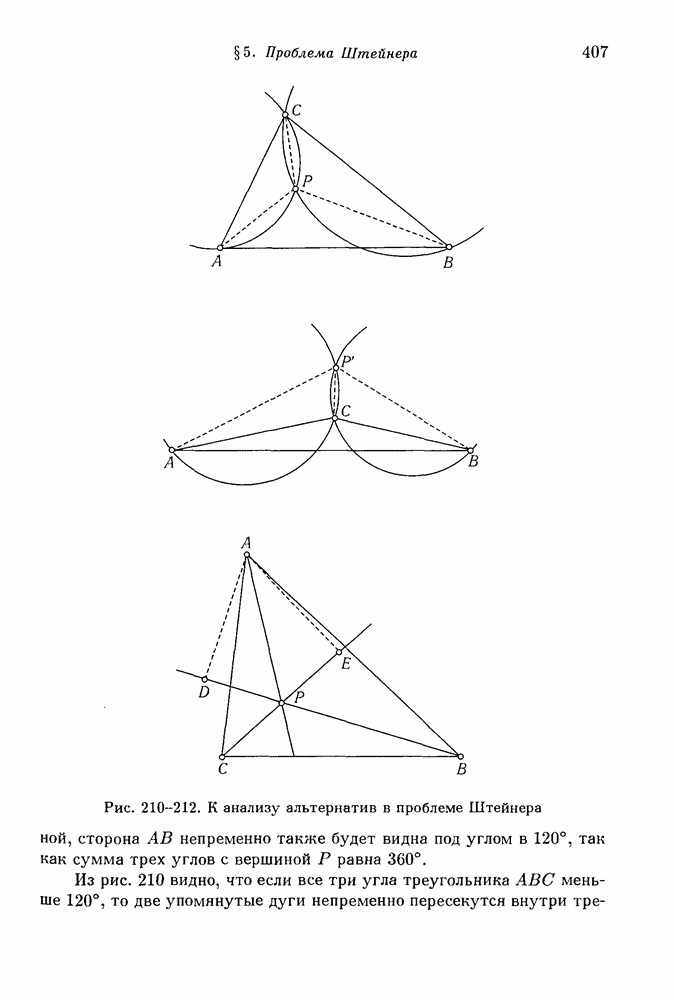
- § 5. Проблема Штейнера
- 2. Анализ возникающих альтернатив.
- 3. Дополнительная проблема.
- 4. Замечания и упражнения.
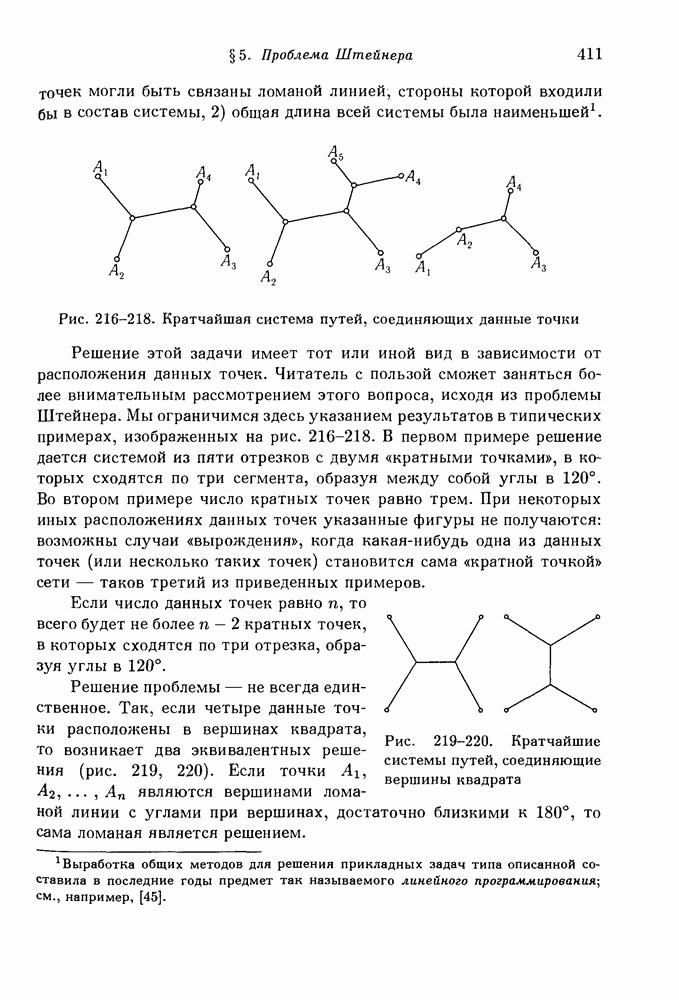
- 5. Обобщение: проблема уличной сети.
- § 6. Экстремумы и неравенства
- 1. Средние арифметическое и геометрическое двух положительных величин.
- 2. Обобщение на случай n переменных.
- 3. Метод наименьших квадратов.
- § 7. Существование экстремума. Принцип Дирихле
- 3. Экстремальные проблемы элементарного содержания.
- 4. Трудности, возникающие в более сложных случаях.
- § 8. Изопериметрическая проблема
- § 9. Экстремальные проблемы с граничными условиями. Связь между проблемой Штейнера и изопериметрической проблемой
- § 10. Вариационное исчисление
- 2. Вариационное исчисление. Принцип Ферма в оптике.
- 3. Решение задачи о брахистохроне, принадлежащее Якобу Бернулли.
- 4. Геодезические линии на сфере. Минимаксы.
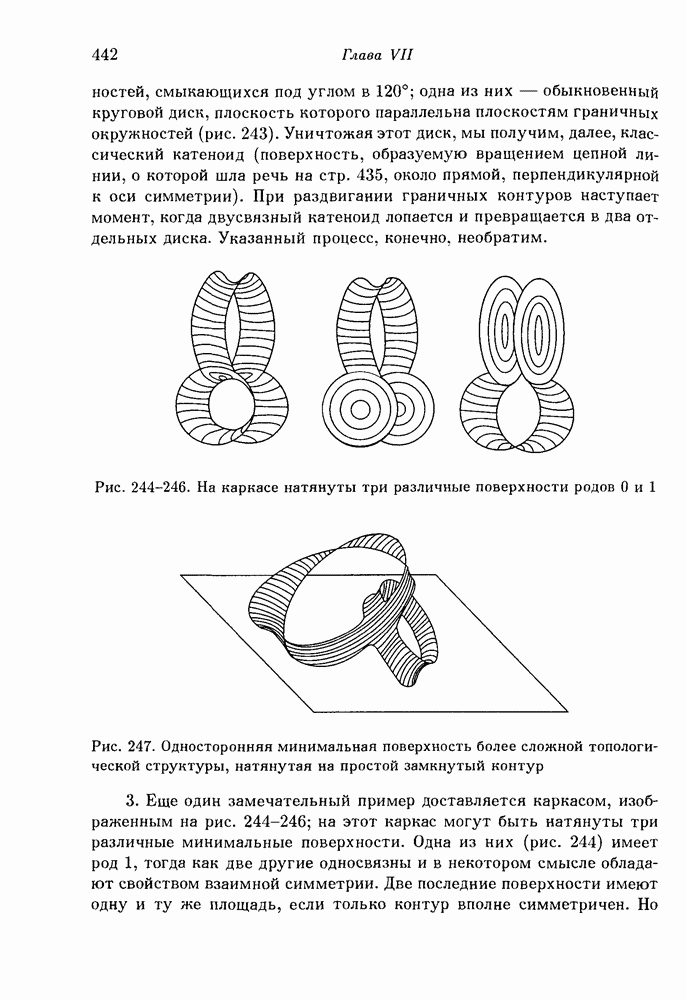
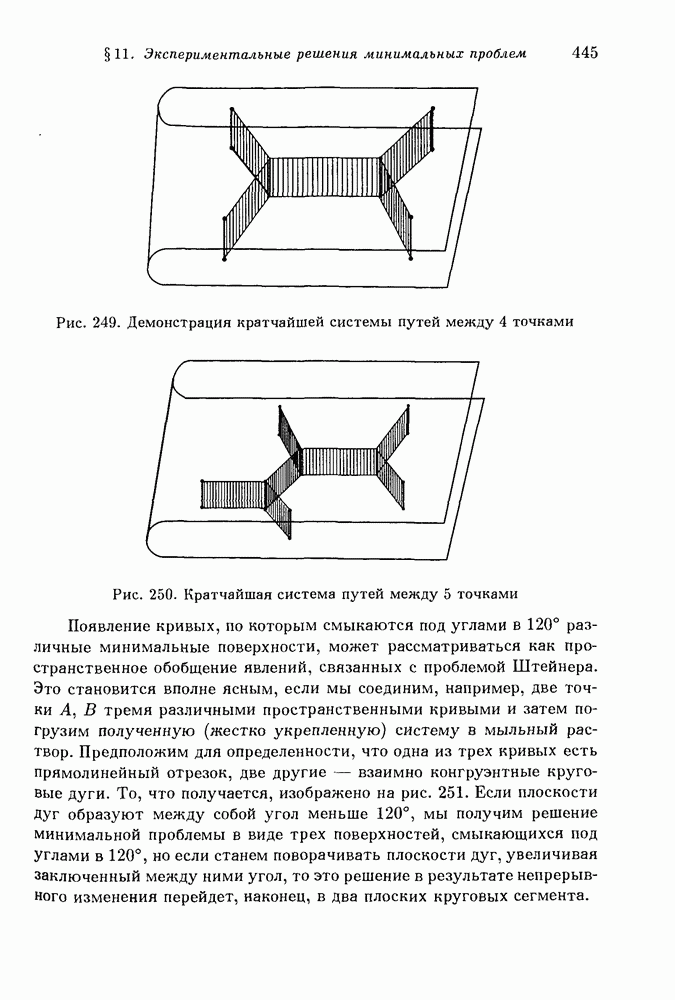
- § 11. Экспериментальные решения минимальных проблем. Опыты с мыльными пленками
- 2. Опыты с мыльными пленками.
- 3. Новые опыты, относящиеся к проблеме Плато.
- 4. Экспериментальные решения других математических проблем.
- Глава VIII. Математический анализ
- § 1. Интеграл
- 2. Интеграл.
- 3. Общие замечания о понятии интеграла. Общее определение.
- 4. Примеры интегрирования. Интегрирование x^r.
- 5. Правила «интегрального исчисления».
- § 2. Производная
- 2. Производная как предел.
- 3. Примеры.
- 4. Производные от тригонометрических функций.
- 5. Дифференцируемость и непрерывность.
- 6. Производная и скорость. Вторая производная и ускорение.
- 7. Геометрический смысл второй производной.
- 8. Максимумы и минимумы.
- § 3. Техника дифференцирования
- § 4. Обозначения Лейбница и «бесконечно малые»
- § 5. Основная теорема анализа
- 2. Первые применения. Интегрирование функций x^r, cosx, sinx. Функция arctgx
- 3. Формула Лейбница для «пи»
- § 6. Показательная (экспоненциальная) функция и логарифм
- 2. Показательная (экспоненциальная) функция.
- 3. Формулы дифференцирования функций е^х, а^х, x^s.
- 4. Явные выражения числа е^x и функций lnx в виде пределов.
- 5. Бесконечный ряд для логарифма. Вычисление логарифмов.
- § 7. Дифференциальные уравнения
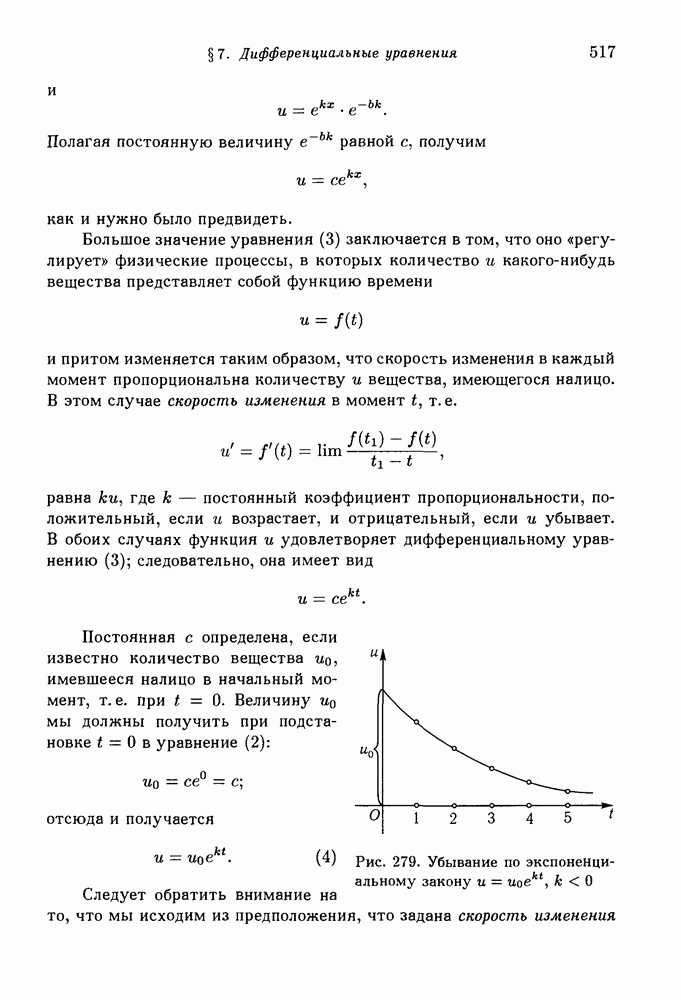
- 2. Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- 3. Другие примеры. Простейшие колебания.
- 4. Закон движения Ньютона.
- Дополнение к главе VIII
- § 1. Вопросы принципиального порядка
- 3. Другие приложения понятия интеграла. Работа. Длина кривой.
- § 2. Порядки возрастания
- 2. Порядок возрастания ln(n!)
- § 3. Бесконечные ряды и бесконечные произведения
- 2. Формула Эйлера cos x + i sin x = exp(ix).
- 3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin x в виде бесконечного произведения.
- § 4. Доказательство теоремы о простых числах на основе статистического метода
- Приложение. Дополнительные замечания, задачи и упражнения
- Аналитическая геометрия
- Геометрические построения
- Проективная и неевклидова геометрия
- Топология
- Функции, пределы, непрерывность
- Максимумы и минимумы
- Дифференциальное и интегральное исчисления
- Техника интегрирования
- Рекомендуемая литература