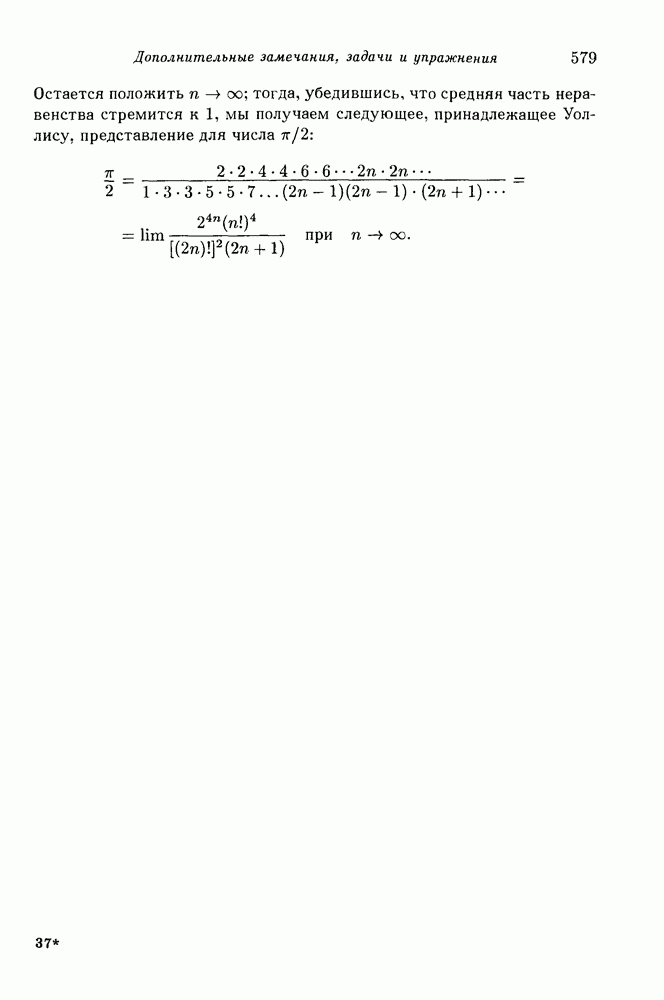| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. Понятие размерности.
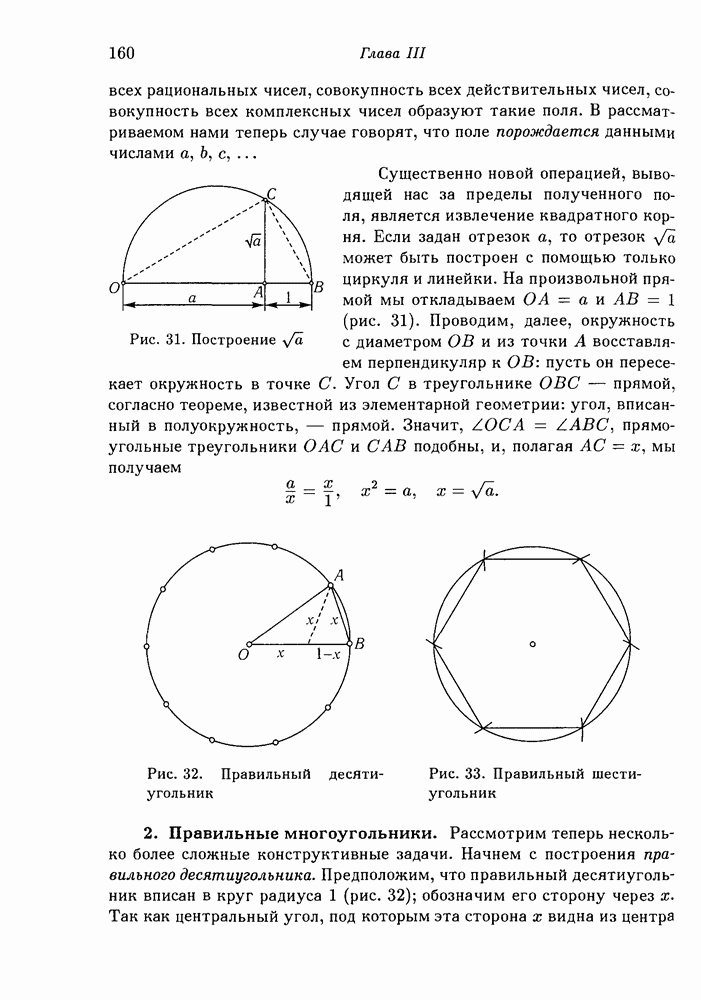
Понятие о «числе измерений», или о «размерности», не представляет особых затруднений, поскольку речь идет о простых геометрических образах, каковы точки, линии, треугольники или многогранники. Отдельная точка или любое конечное множество точек имеет размерность нуль, отрезок — размерность 1, поверхность треугольника или сферы — размерность 2. Множество всех точек куба имеет размерность 3. Однако при желании обобщить понятие размерности на точечные множества более общих типов возникает необходимость в точном определении. Какую размерность следует, например, приписать множеству  состоящему из всех точек
состоящему из всех точек  -оси, у которых координаты
-оси, у которых координаты  рациональные числа? Множество рациональных точек на
рациональные числа? Множество рациональных точек на  -оси везде плотно и потому, казалось бы, ему, как и самому отрезку прямой, надлежало бы приписать размерность 1. С другой стороны, между всякими двумя рациональными точками существуют иррациональные «дыры», как между всякими двумя точками конечного множества, и это говорит в пользу размерности 0.
-оси везде плотно и потому, казалось бы, ему, как и самому отрезку прямой, надлежало бы приписать размерность 1. С другой стороны, между всякими двумя рациональными точками существуют иррациональные «дыры», как между всякими двумя точками конечного множества, и это говорит в пользу размерности 0.
Еще запутаннее обстоит дело с размерностью любопытного множества, впервые рассмотренного Кантором, построенного следующим образом. Из единичного отрезка  удалим среднюю треть (интервал), т. е. все точки х, удовлетворяющие неравенству
удалим среднюю треть (интервал), т. е. все точки х, удовлетворяющие неравенству  Оставшееся точечное Множество обозначим через
Оставшееся точечное Множество обозначим через  Множество
Множество  состоит из двух отрезков; Удалим теперь из каждого отрезка его среднюю треть и то множество, которое останется, обозначим через С. Повторим опять эту процедуру, удаляя среднюю треть у всех четырех отрезков; получим
состоит из двух отрезков; Удалим теперь из каждого отрезка его среднюю треть и то множество, которое останется, обозначим через С. Повторим опять эту процедуру, удаляя среднюю треть у всех четырех отрезков; получим  Дальше таким же образом получим
Дальше таким же образом получим  Обозначим через С множество точек, которое останется, когда все средние трети будут удалены; т. е. С есть, другими словами, множество точек, принадлежащих одновременно всем множествам
Обозначим через С множество точек, которое останется, когда все средние трети будут удалены; т. е. С есть, другими словами, множество точек, принадлежащих одновременно всем множествам  В первой операции был удален интервал длины
В первой операции был удален интервал длины  во второй операции — два интервала, каждый длины
во второй операции — два интервала, каждый длины  сумма длин всех удаленных
сумма длин всех удаленных

Рис. 130. Канторово множество
интервалов равна

Бесконечный ряд в больших скобках есть геометрическая прогрессия, сумма которой равна  итак, сумма длин удаленных промежутков составляет 1. И все-таки далеко не все точки отрезка удалены: множество С не пустое. Например, все точки, являющиеся концами удаленных отрезков
итак, сумма длин удаленных промежутков составляет 1. И все-таки далеко не все точки отрезка удалены: множество С не пустое. Например, все точки, являющиеся концами удаленных отрезков

ему принадлежат. Можно легко убедиться, что множество С состоит из всех тех чисел х, разложения которых в бесконечную дробь по основанию 3 могут быть написаны в форме

где всякое  есть 0 или 2, тогда как в аналогичном разложении для всякой удаленной точки среди чисел а" хоть раз встретится 1.
есть 0 или 2, тогда как в аналогичном разложении для всякой удаленной точки среди чисел а" хоть раз встретится 1.
Какова же размерность множества С? Диагональный процесс, с помощью которого была доказана несчетность множества всех действительных чисел, может быть видоизменен таким образом, чтобы тот же результат получился и для множества С. Отсюда было бы естественно заключить, что множеству С надлежит приписать размерность 1. С другой стороны, С не содержит никакого, даже самого малого, промежутка, как и любое конечное множество; это сближает С с множествами размерности 0. Таким же образом, восставив в плоскости х, у из каждой рациональной точки или из каждой точки канторова множества перпендикуляр длины 1 к оси х (направляя его в сторону положительных значений  мы получим множества, относительно которых может возникнуть сомнение — приписать ли ему размерность 2 или 1.
мы получим множества, относительно которых может возникнуть сомнение — приписать ли ему размерность 2 или 1.
Впервые Пуанкаре (в 1912 г.) обратил внимание на необходимость более глубокого анализа и более точного определения размерности. Пуанкаре заметил, что прямая или кривая имеет размерность 1, так как любые две точки на ней можно разделить, удаляя одну единственную точку (множество размерности 0); плоскость же имеет размерность 2 по той причине, что для разделения двух точек на плоскости нужно удалить целую замкнутую кривую (множество размерности 1). Это приводит к мысли о том, что понятие размерности имеет «индуктивную» природу: некоторому «пространству» следует приписать размерность  если две точки в нем разделяются при удалении подмножества точек размерности
если две точки в нем разделяются при удалении подмножества точек размерности  удаления подмножества меньшей размерности уже не было бы достаточно). В сущности такого рода индуктивное определение неявно содержится уже в евклидовых «Началах», где одномерный образ толкуется как нечто, граница чего состоит из точек; двумерный образ — как нечто, граница чего состоит из линий; наконец, трехмерный образ — как нечто, граница чего состоит из поверхностей.
удаления подмножества меньшей размерности уже не было бы достаточно). В сущности такого рода индуктивное определение неявно содержится уже в евклидовых «Началах», где одномерный образ толкуется как нечто, граница чего состоит из точек; двумерный образ — как нечто, граница чего состоит из линий; наконец, трехмерный образ — как нечто, граница чего состоит из поверхностей.
За последние годы была развита обширная теория — теория размерности. Определение размерности начинается с того, что разъясняется смысл термина «точечное множество размерности 0». Любое конечное точечное множество обладает тем свойством, что каждая его точка может быть заключена в сколь угодно малую область пространства, причем на границе области нет точек множества. Это свойство принимается теперь за определение размерности 0. Условимся ради удобства говорить, что пустое множество имеет размерность —1. В таком случае множество S имеет размерность 0, если оно не имеет размерности —1 (т. е. если S содержит хоть одну точку) и если каждая точка S может быть заключена в произвольно малую область, граница которой пересекает S по множеству размерности —1 (т. е. совсем не содержит ни одной точки  Так, например, множество рациональных точек на прямой имеет размерность 0, так как каждая рациональная точка может быть рассматриваема как центр произвольно малого промежутка с иррациональными концами. Канторово множество
Так, например, множество рациональных точек на прямой имеет размерность 0, так как каждая рациональная точка может быть рассматриваема как центр произвольно малого промежутка с иррациональными концами. Канторово множество  также размерности 0, так как, подобно множеству рациональных точек, оно получается посредством удаления везде плотного множества точек прямой.
также размерности 0, так как, подобно множеству рациональных точек, оно получается посредством удаления везде плотного множества точек прямой.
Итак, мы уже определили понятия «размерность —1» и «размерность 0». Теперь легко понять, что такое «размерность 1»: говорят, что множество S имеет «размерность 1», если оно не есть ни размерности —1, ни размерности 0 и если каждая точка S может быть заключена в произвольно малую область, граница которой пересекается с 5 по множеству размерности 0. Отрезок прямой обладает этим свойством, так как границей каждого промежутка является пара точек, т. е. множество размерности 0 по предыдущему определению. Дальше, продолжая таким же образом, мы можем последовательно определить, что такое размерность 2, размерность 3 и т.д., причем каждое следующее определение основывается на предыдущем.
Таким образом, говорят, что множество S имеет размерность  если оно не имеет меньшей размерности и если каждая точка S может быть
если оно не имеет меньшей размерности и если каждая точка S может быть
заключена в произвольно малую область, граница которой пересекается с 5 по множеству размерности  Например, плоскость имеет размерность 2, так как любая точка плоскости может быть заключена в кружок произвольно малого радиуса, граница которой имеет размерность
Например, плоскость имеет размерность 2, так как любая точка плоскости может быть заключена в кружок произвольно малого радиуса, граница которой имеет размерность  В обыкновенном пространстве никакое множество точек не может иметь размерность, большую чем 3, так как любая точка пространства есть центр произвольно малой сферы, граница которой имеет размерность 2. Но в современной математике термин «пространство» употребляется в более общем смысле; он обозначает любую систему объектов, для которой введено понятие «расстояния» или «окрестности», и такого рода абстрактные «пространства» могут иметь размерность, большую чем 3. Простым примером является декартово
В обыкновенном пространстве никакое множество точек не может иметь размерность, большую чем 3, так как любая точка пространства есть центр произвольно малой сферы, граница которой имеет размерность 2. Но в современной математике термин «пространство» употребляется в более общем смысле; он обозначает любую систему объектов, для которой введено понятие «расстояния» или «окрестности», и такого рода абстрактные «пространства» могут иметь размерность, большую чем 3. Простым примером является декартово  -пространство, «точки» которого суть системы из
-пространство, «точки» которого суть системы из  действительных чисел, взятых в определенном порядке:
действительных чисел, взятых в определенном порядке:

а «расстояние» между  определяется по формуле
определяется по формуле

Можно показать, что это пространство имеет размерность  Пространство, которое не имеет размерности
Пространство, которое не имеет размерности  как бы велико ни было
как бы велико ни было  называется пространством бесконечной размерности. Известно много примеров таких пространств.
называется пространством бесконечной размерности. Известно много примеров таких пространств.
В теории размерности устанавливается одно чрезвычайно интересное свойство двумерных, трехмерных и вообще  -мерных фигур. Начнем с двумерного случая. Если какая-то простая двумерная фигура подразделена на достаточно маленькие «ячейки» (причем предполагается, что каждая ячейка содержит свою границу), то непременно найдутся такие точки, которые принадлежат сразу по меньшей мере трем ячейкам, какова бы ни была форма выбранных ячеек. Вместе с тем существуют такие подразделения фигуры на ячейки, что никакая точка фигуры не принадлежит сразу больше чем трем ячейкам. Так, если рассматриваемая двумерная фигура есть квадрат (рис. 131), то непременно имеются точки вроде той, которая сразу принадлежит трем ячейкам 1, 2 и 3, но для указанного на рисунке подразделения не существует точки, которая сразу принадлежала бы большему числу ячеек. Точно так же в трехмерном случае можно доказать, что если некоторая
-мерных фигур. Начнем с двумерного случая. Если какая-то простая двумерная фигура подразделена на достаточно маленькие «ячейки» (причем предполагается, что каждая ячейка содержит свою границу), то непременно найдутся такие точки, которые принадлежат сразу по меньшей мере трем ячейкам, какова бы ни была форма выбранных ячеек. Вместе с тем существуют такие подразделения фигуры на ячейки, что никакая точка фигуры не принадлежит сразу больше чем трем ячейкам. Так, если рассматриваемая двумерная фигура есть квадрат (рис. 131), то непременно имеются точки вроде той, которая сразу принадлежит трем ячейкам 1, 2 и 3, но для указанного на рисунке подразделения не существует точки, которая сразу принадлежала бы большему числу ячеек. Точно так же в трехмерном случае можно доказать, что если некоторая
объемная фигура (тело) разбита на достаточно маленькие ячейки, то наверное существуют точки, принадлежащие по меньшей мере четырем ячейкам, и вместе с тем можно выбрать такие подразделения, что никакая точка не будет принадлежать сразу больше чем четырем ячейкам.

Рис. 131. Теорема о покрытии
Все эти соображения приводят нас к следующей теореме, высказанной Лебегом и Брауэром: если  -мерная фигура подразделена на достаточно маленькие ячейки, то непременно существуют точки этой фигуры, принадлежащие сразу по меньшей мере
-мерная фигура подразделена на достаточно маленькие ячейки, то непременно существуют точки этой фигуры, принадлежащие сразу по меньшей мере  ячейкам; вместе с тем возможно указать и такие подразделения, что ни одна точка фигуры не будет принадлежать сразу более чем
ячейкам; вместе с тем возможно указать и такие подразделения, что ни одна точка фигуры не будет принадлежать сразу более чем  ячейкам. Эта теорема характеризует размерность рассматриваемой фигуры: все фигуры, для которых теорема верна, являются
ячейкам. Эта теорема характеризует размерность рассматриваемой фигуры: все фигуры, для которых теорема верна, являются  -мерными, все прочие имеют иную размерность. По этой причине указанная теорема может быть взята за определение размерности (так и делают некоторые авторы).
-мерными, все прочие имеют иную размерность. По этой причине указанная теорема может быть взята за определение размерности (так и делают некоторые авторы).
Размерность фигуры относится к числу топологических ее свойств: никакие две фигуры различных размерностей не могут быть топологически эквивалентными. В этом заключается замечательная теорема об «инвариантности размерности»: чтобы оценить ее должным образом, стоит напомнить другую теорему (доказанную на стр. 120), согласно которой множество точек квадрата имеет ту же мощность, что и множество точек отрезка. Соответствие между точками, установленное при доказательстве этой теоремы, не топологическое, так как требование непрерывности нарушается.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму русскому изданию
- Как пользоваться книгой
- Что такое математика?
- Глава I. Натуральные числа
- § 1. Операции над целыми числами
- 2. Представление целых чисел с помощью письменных знаков (нумерация).
- 3. Арифметические действия в недесятичных системах счисления.
- § 2. Бесконечность системы натуральных чисел. Математическая индукция
- 2. Арифметическая прогрессия.
- 3. Геометрическая прогрессия.
- 4. Сумма n первых квадратов.
- 5. Одно важное неравенство.
- 6. Биномиальная теорема.
- 7. Дальнейшие замечания по поводу метода математической индукции.
- Дополнение к главе I
- Теория чисел
- 2. Распределение простых чисел.
- § 2. Сравнения
- 2. Теорема Ферма.
- 3. Квадратические вычеты.
- § 3. Пифагоровы числа и большая теорема Ферма
- § 4. Алгоритм Евклида
- 2. Применение к основной теореме арифметики
- 3. Функция Эйлера. Еще раз о теореме Ферма.
- 4. Непрерывные дроби. Диофантовы уравнения
- Глава II. Математическая числовая система
- § 1. Рациональные числа
- 2. Возникновение надобности в рациональных числах внутри самой математики. Принцип обобщения.
- 3. Геометрическое представление рациональных чисел.
- § 2. Несоизмеримые отрезки. Иррациональные числа, пределы
- 2. Десятичные дроби: конечные и бесконечные.
- 3. Пределы. Бесконечные геометрические прогрессии.
- 4. Рациональные числа и периодические десятичные дроби.
- 5. Общее определение иррациональных чисел посредством стягивающихся отрезков.
- 6. Иные методы определения иррациональных чисел.Декиндовы сечения.
- § 3. Замечания из области аналитической геометрии
- 2. Уравнения прямых и кривых линий.
- § 4. Математический анализ бесконечного
- 2. Счетность множества рациональных чисел и несчетность континуума.
- 3. «Кардинальные числа» Кантора.
- 4. Косвенный метод доказательства.
- 5. Парадоксы бесконечного.
- 6. Основания математики.
- § 5. Комплексные числа
- 2. Геометрическое представление комплексных чисел.
- 3. Формула Муавра и корни из единицы.
- 4. Основная теорема алгебры.
- § 6. Алгебраические и трансцендентные числа
- 2. Теорема Лиувилля и конструирование трансцендентных чисел.
- Дополнение к главе II. Алгебра множеств
- 2. Применение к математической логике.
- 3. Одно из применений к теории вероятностей.
- Глава III. Геометрические построения. Алгебра числовых полей
- Часть 1. Доказательства невозможности и алгебра
- 1. Построение полей и извлечение квадратных корней.
- 2. Правильные многоугольники.
- 3. Проблема Аполлония.
- § 2. Числа, допускающие построение, и числовые поля
- 2. Все числа, допускающие построение, — алгебраические.
- § 3. Неразрешимость трех классических проблем
- 2. Одна теорема о кубических уравнениях.
- 3. Трисекция угла.
- 4. Правильный семиугольник.
- 5. Замечания по поводу квадратуры круга.
- Часть 2. Различные методы выполнения построений
- § 4. Геометрические преобразования. Инверсия
- 2. Свойства инверсии.
- 3. Геометрическое построение обратных точек.
- 4. Как разделить отрезок пополам и как найти центр данного круга с помощью одного циркуля.
- § 5. Построения с помощью иных инструментов. Построения Маскерони с помощью одного циркуля
- 1. Классическая конструкция, служащая для удвоения куба.
- 2. Построения с помощью одного циркуля.
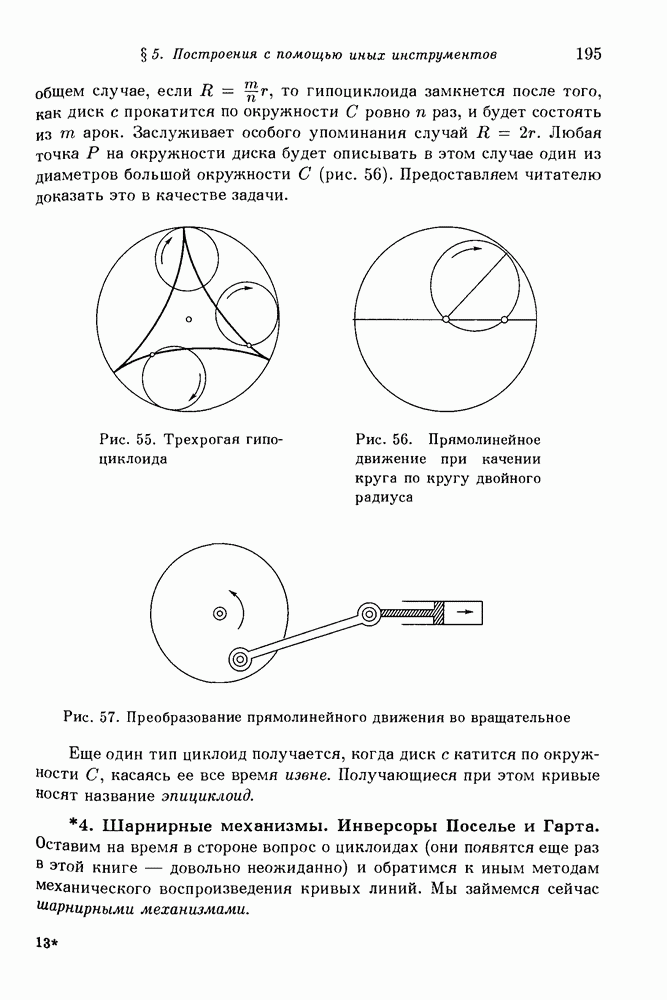
- 3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды.
- 4. Шарнирные механизмы. Инверсоры Поселье и Гарта.
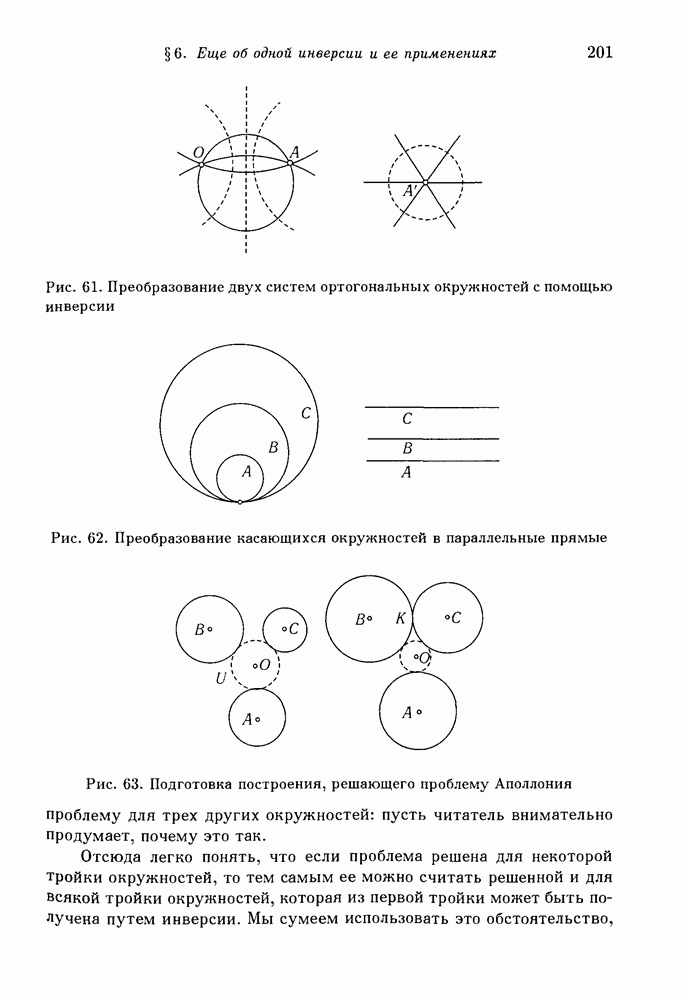
- § 6. Еще об одной инверсии и ее применениях
- 1. Инвариантность углов. Семейства окружностей.
- 2. Применение к проблеме Аполлония.
- 3. Повторные отражения.
- Глава IV. Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- 1. Классификация геометрических свойств. Инвариантность при преобразованиях.
- 2. Проективные преобразования.
- § 2. Основные понятия
- 1. Группа проективных преобразований.
- 2. Теорема Дезарга.
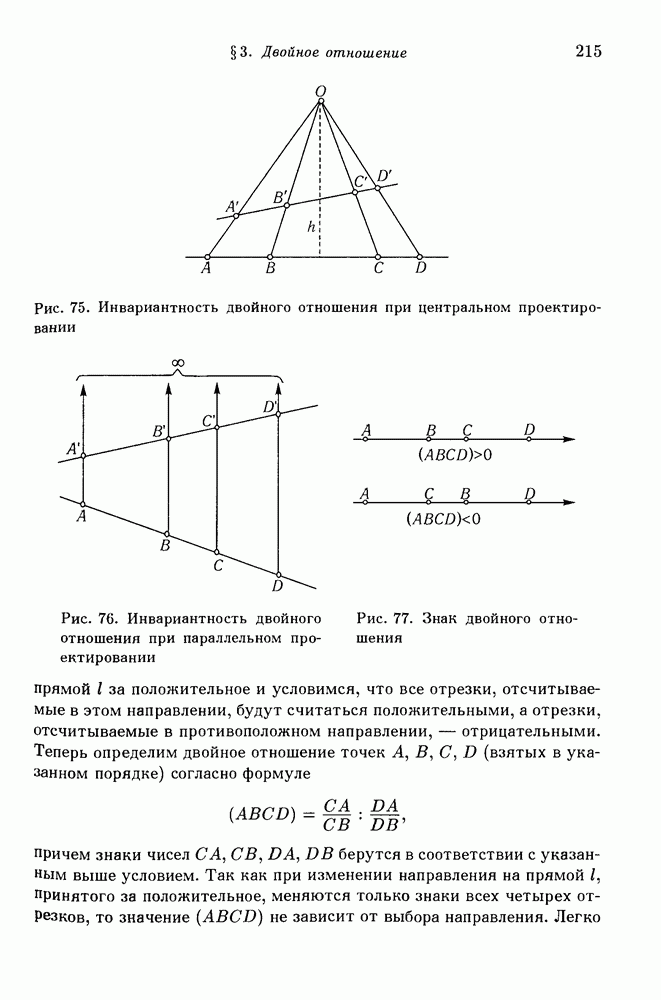
- § 3. Двойное отношение
- § 4. Параллельность и бесконечность
- 2. Идеальные элементы и проектирование.
- 3. Двойное отношение с бесконечно удаленными элементами.
- § 5. Применения
- 2. Двумерное доказательство теоремы Дезарга.
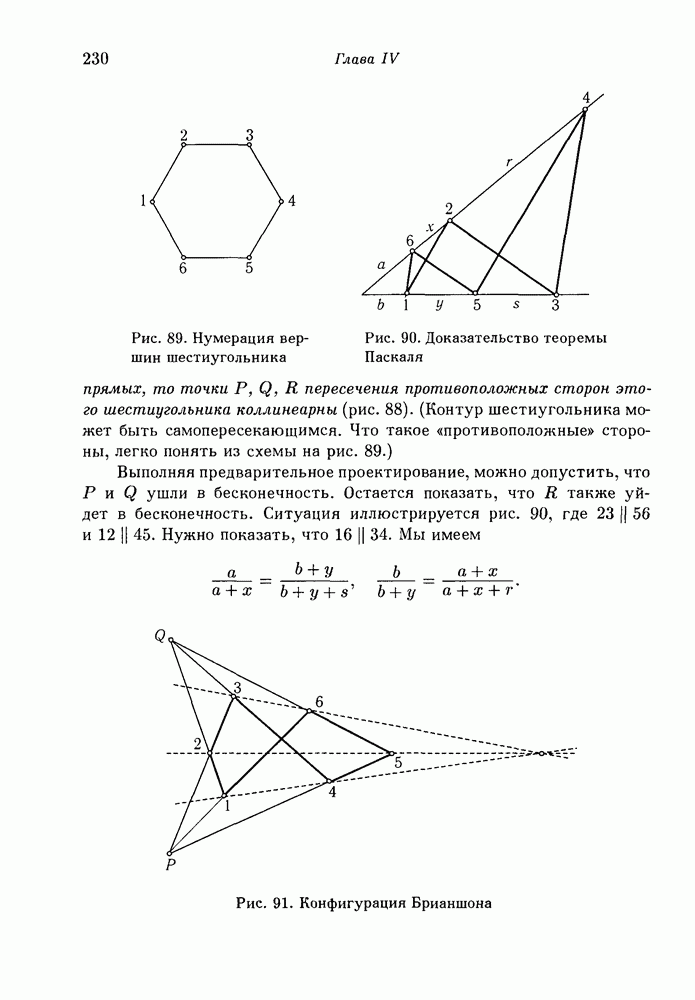
- 3. Теорема Паскаля.
- 4. Теорема Брианшона.
- 5. Замечание по поводу двойственности.
- § 6. Аналитическое представление
- 2. Однородные координаты. Алгебраические основы двойственности.
- § 7. Задачи на построения с помощью одной линейки
- § 8. Конические сечения и квадрики
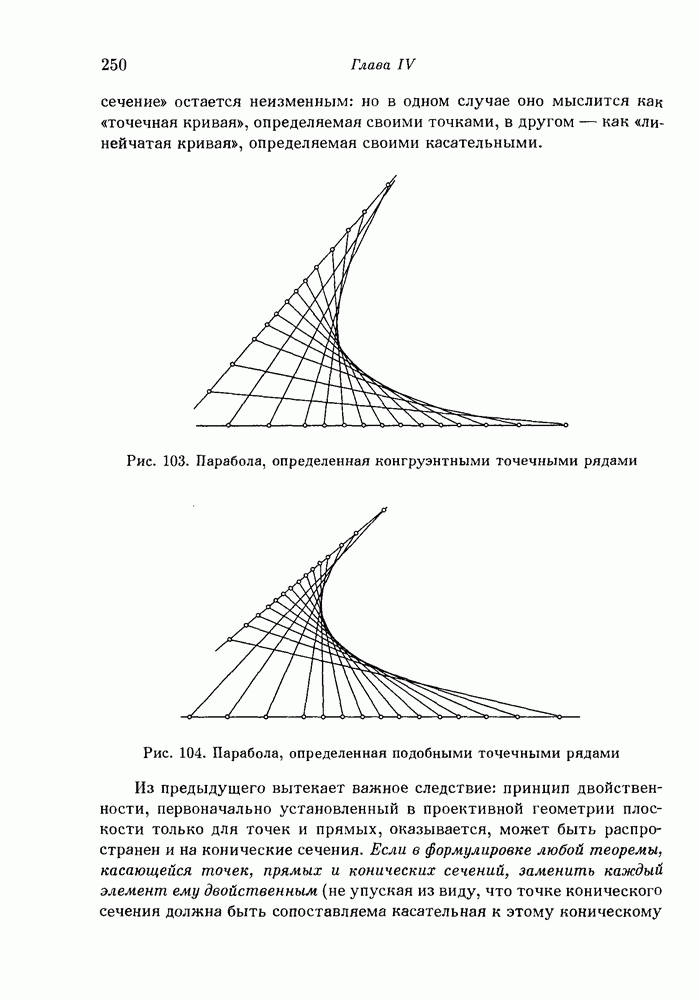
- 2. Проективные свойства конических сечений.
- 3. Конические сечения как «линейчатые кривые».
- 4. Теоремы Паскаля и Брианшона для общего случая произвольных конических сечений.
- 5. Гиперболоид.
- § 9. Аксиоматика и неевклидова геометрия
- 2. Гиперболическая неевклидова геометрия.
- 3. Геометрия и реальность.
- 4. Модель Пуанкаре.
- 5. Эллиптическая, или риманова, геометрия.
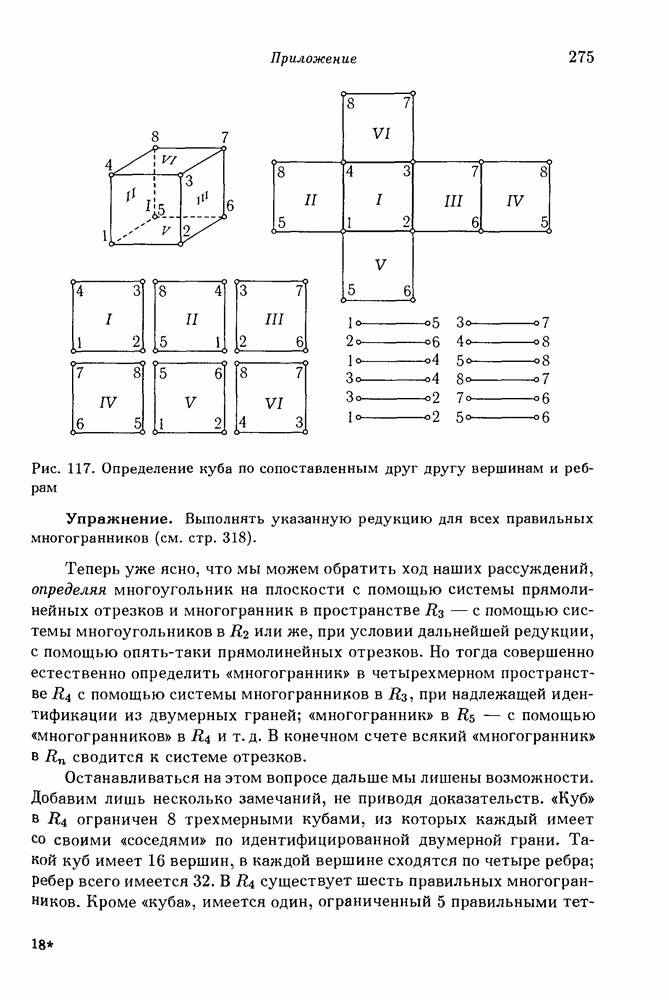
- Приложение. Геометрия в пространствах более чем трех измерений
- Глава V. Топология
- § 1. Формула Эйлера для многогранников
- § 2. Топологические свойства фигур
- 2. Свойства связности.
- § 3. Другие примеры топологических теорем
- 2. Проблема четырех красок.
- 3. Понятие размерности.
- 4. Теорема о неподвижной точке.
- 5. Узлы.
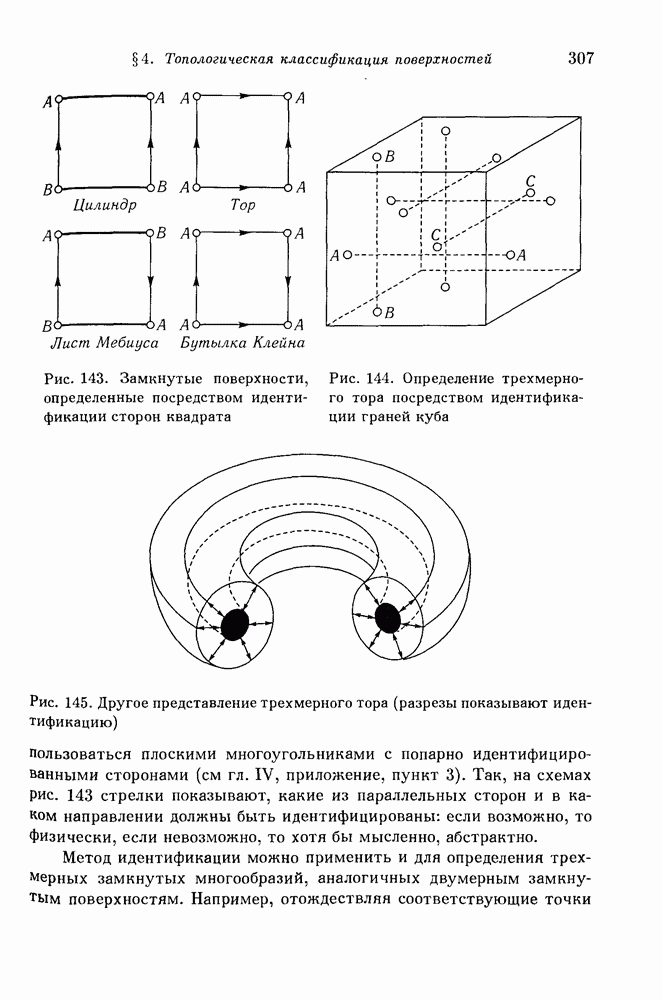
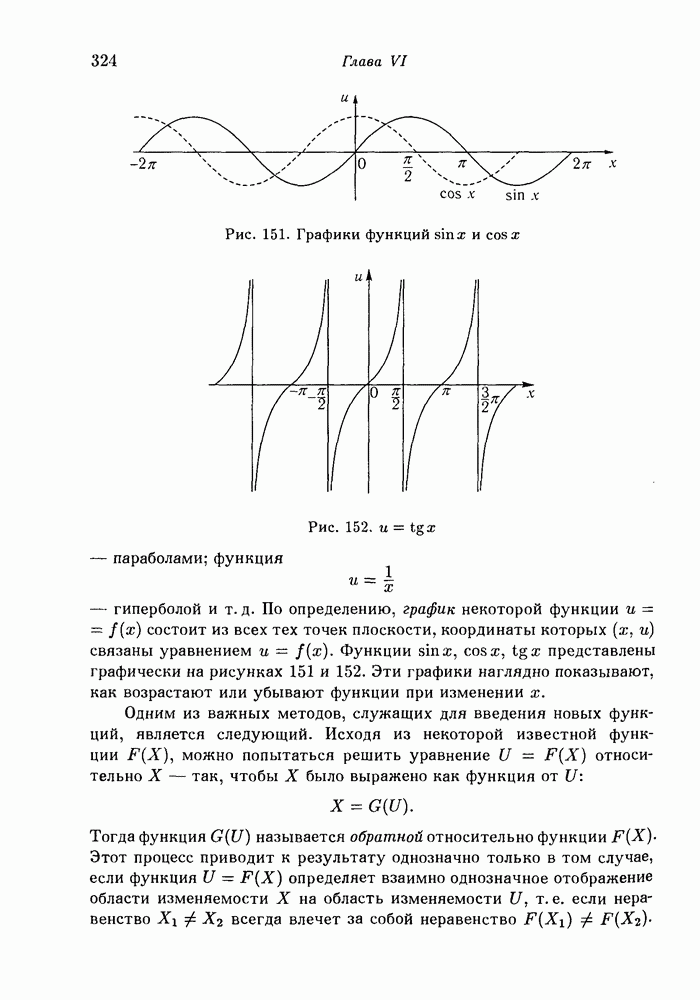
- § 4. Топологическая классификация поверхностей
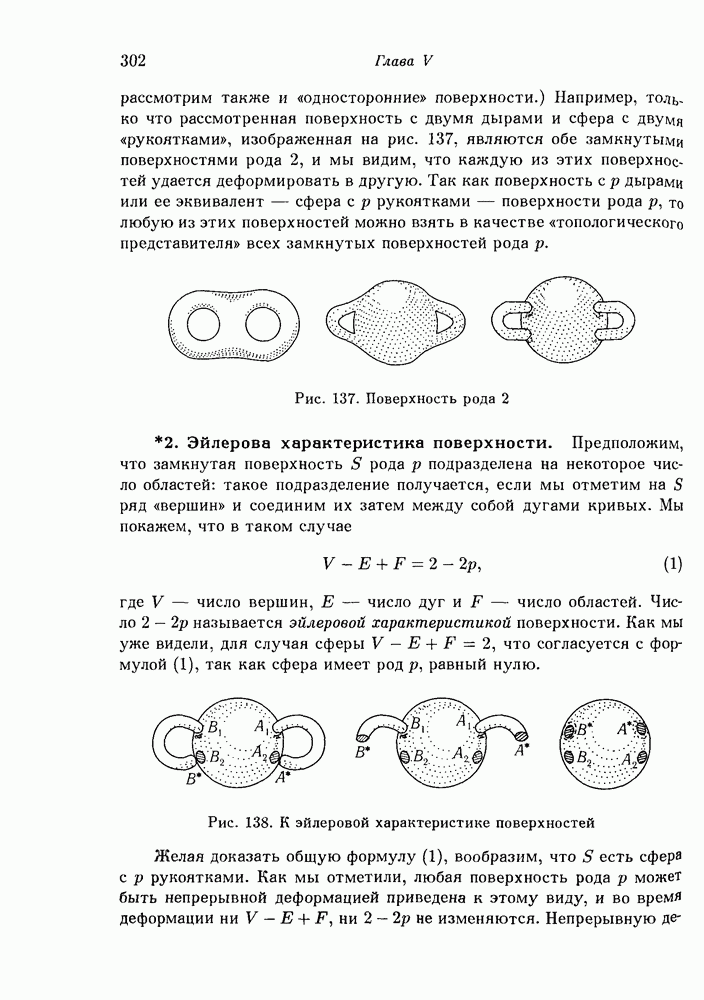
- 2. Эйлерова характеристика поверхности.
- 3. Односторонние поверхности.
- Приложение
- 2. Теорема Жордана для случая многоугольников.
- 3. Основная теорема алгебры.
- Глава VI. Функции и пределы
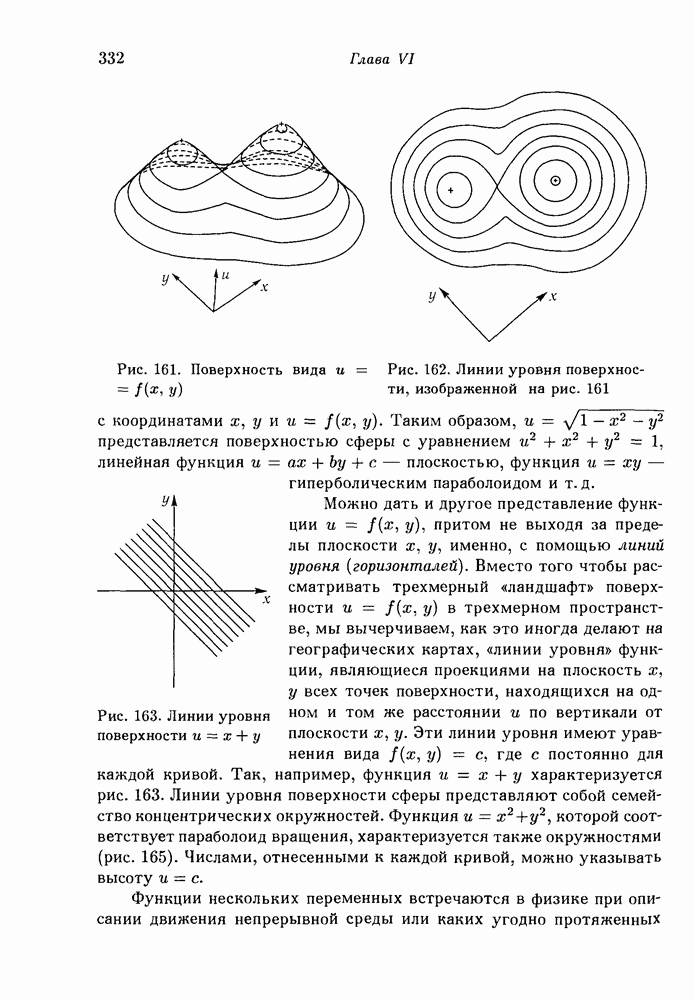
- § 1. Независимое переменное и функция
- 2. Радианная мера углов.
- 3. График функции. Обратные функции.
- 4. Сложные функции.
- 5. Непрерывность.
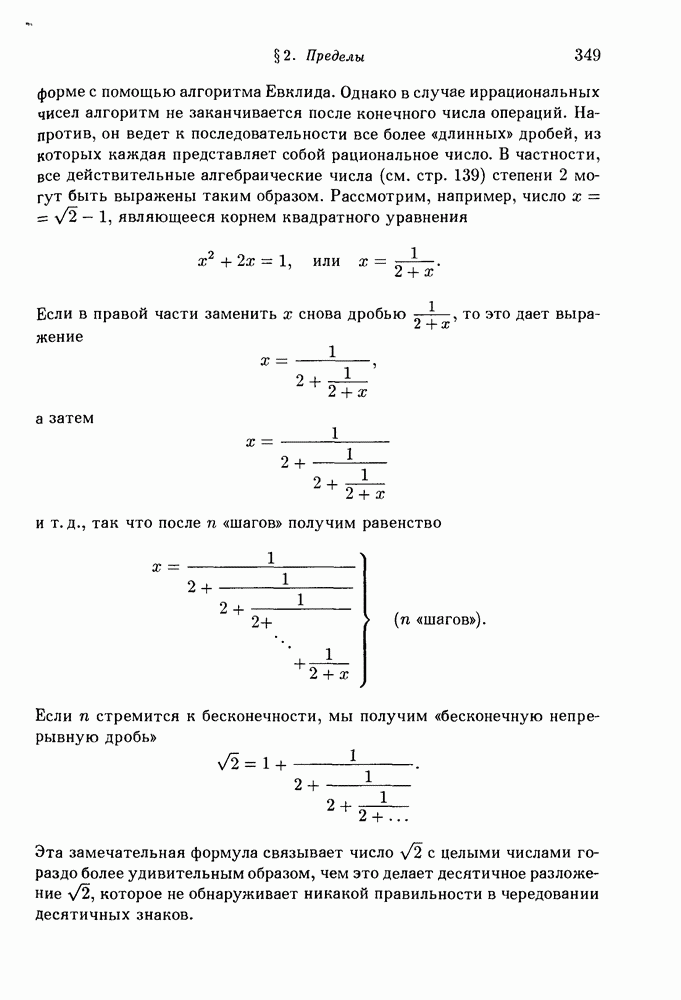
- 6. Функции нескольких переменных.
- 7. Функции и преобразования.
- § 2. Пределы
- 2. Монотонные последовательности.
- 3. Число Эйлера e.
- 4. Число «пи»
- 5. Непрерывные дроби.
- § 3. Пределы при непрерывном приближении
- 2. Замечания по поводу понятия предела
- 3. Предел sin x/x
- 4. Пределы при х -> оо.
- § 4. Точное определение непрерывности
- § 5. Две основные теоремы о непрерывных функциях
- 2. Доказательство теоремы Больцано.
- 3. Теорема Вейерштрасса об экстремальных значениях.
- 4. Теорема о последовательностях. Компактные множества.
- § 6. Некоторые применения теоремы Больцано
- 2. Применение к одной механической проблеме.
- Дополнение к главе VI. Дальнейшие примеры на пределы и непрерывность
- 4. Разрывные функции как предел непрерывных.
- 5. Пределы при итерации.
- § 2. Пример, относящийся к непрерывности
- Глава VII. Максимумы и минимумы
- § 1. Задачи из области элементарной геометрии
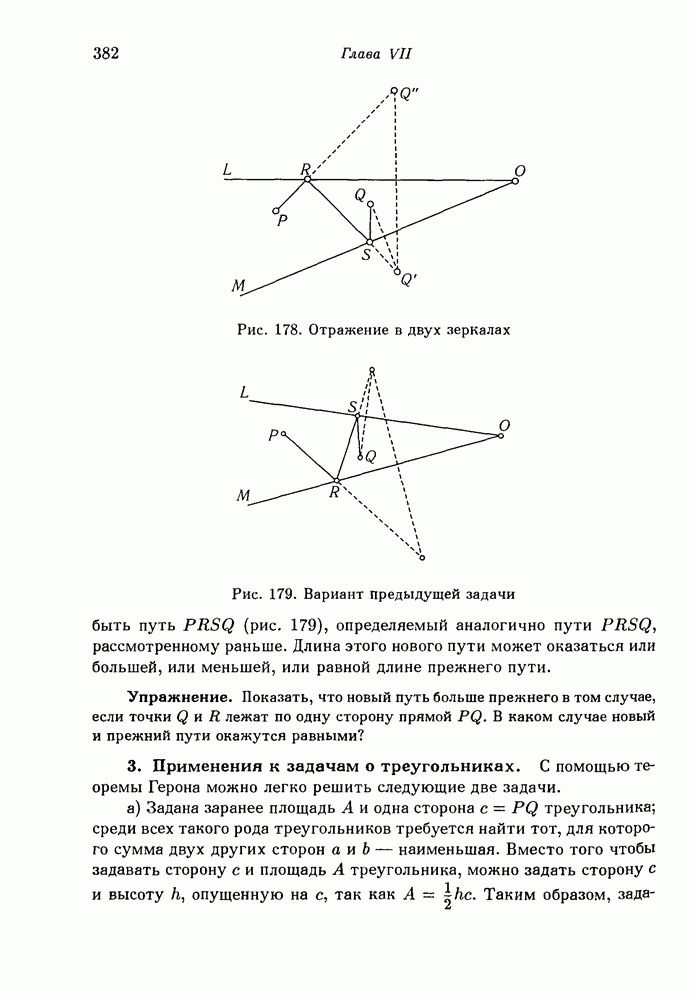
- 2. Теорема Герона. Экстремальное свойство световых лучей.
- 3. Применения к задачам о треугольниках.
- 4. Свойства касательных к эллипсу и гиперболе. Соответствующие экстремальные свойства.
- 5. Экстремальные расстояния точки от данной кривой.
- § 2. Общий принцип, которому подчинены экстремальные задачи
- § 3. Стационарные точки и дифференциальное исчисление
- 2. Максимумы и минимумы функций нескольких переменных. Седловые точки.
- 3. Точки минимакса и топология.
- 4. Расстояние точки от поверхности.
- § 4. Треугольник Шварца
- 4. Треугольники, образованные световыми лучами.
- 5. Замечания, касающиеся задач на отражение и эргодическое движение.
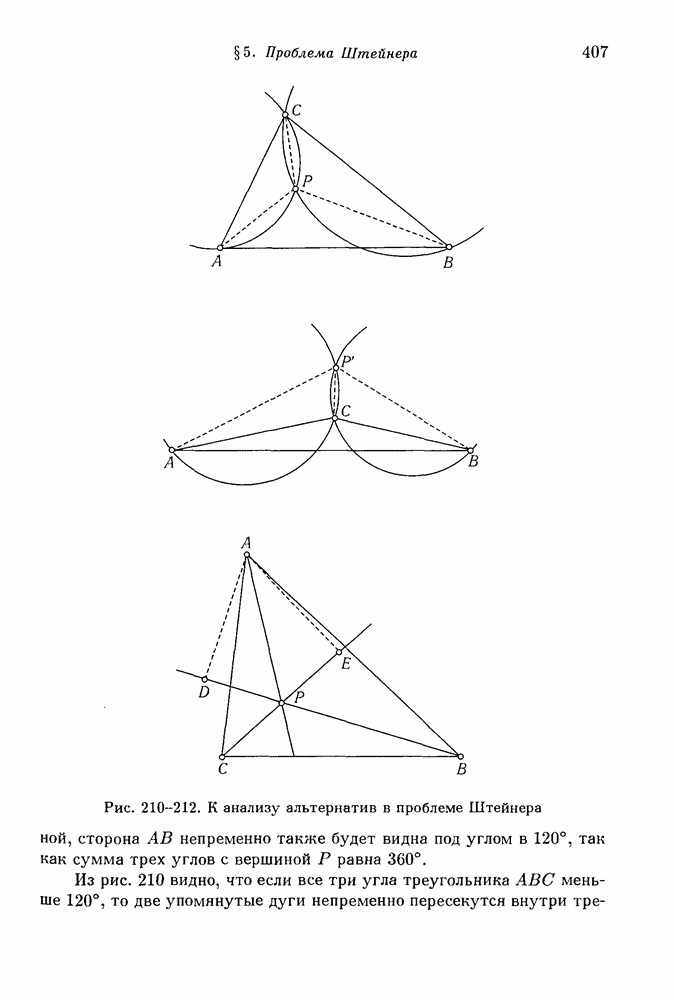
- § 5. Проблема Штейнера
- 2. Анализ возникающих альтернатив.
- 3. Дополнительная проблема.
- 4. Замечания и упражнения.
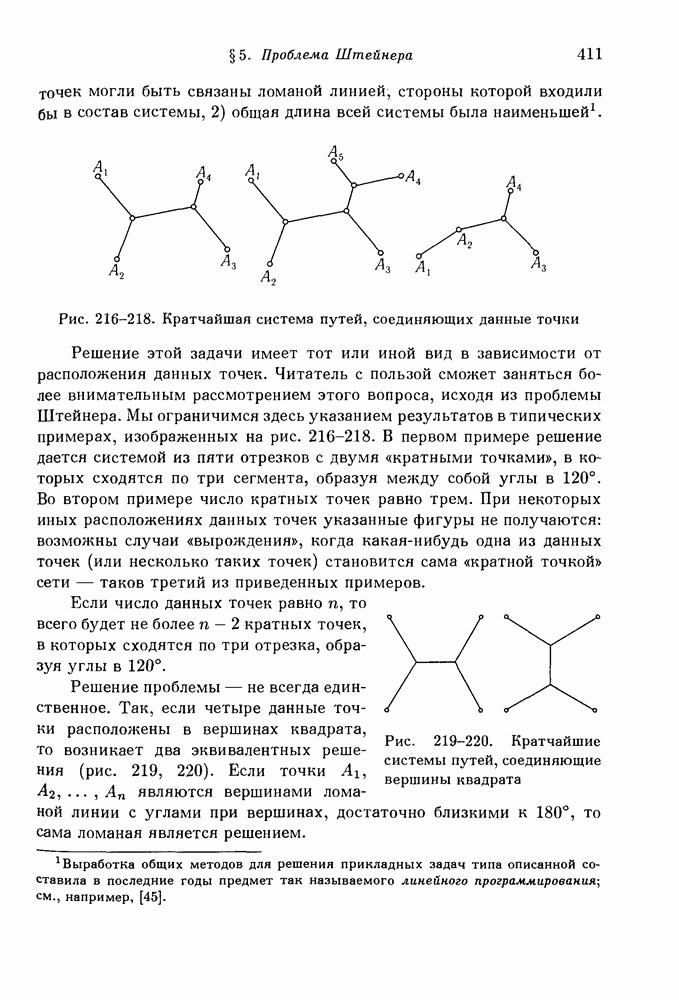
- 5. Обобщение: проблема уличной сети.
- § 6. Экстремумы и неравенства
- 1. Средние арифметическое и геометрическое двух положительных величин.
- 2. Обобщение на случай n переменных.
- 3. Метод наименьших квадратов.
- § 7. Существование экстремума. Принцип Дирихле
- 3. Экстремальные проблемы элементарного содержания.
- 4. Трудности, возникающие в более сложных случаях.
- § 8. Изопериметрическая проблема
- § 9. Экстремальные проблемы с граничными условиями. Связь между проблемой Штейнера и изопериметрической проблемой
- § 10. Вариационное исчисление
- 2. Вариационное исчисление. Принцип Ферма в оптике.
- 3. Решение задачи о брахистохроне, принадлежащее Якобу Бернулли.
- 4. Геодезические линии на сфере. Минимаксы.
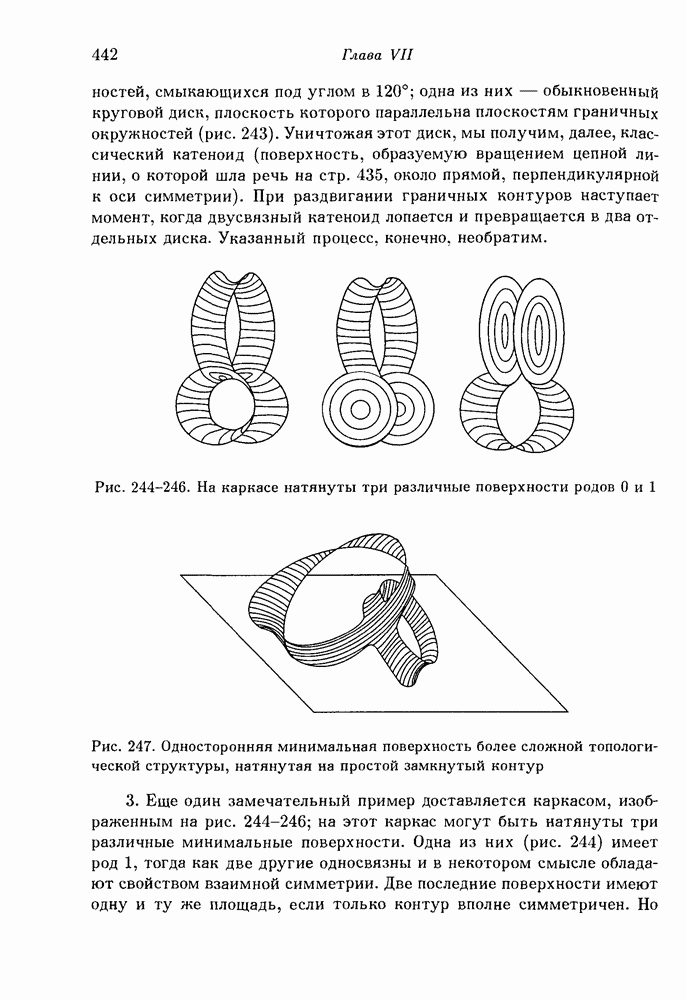
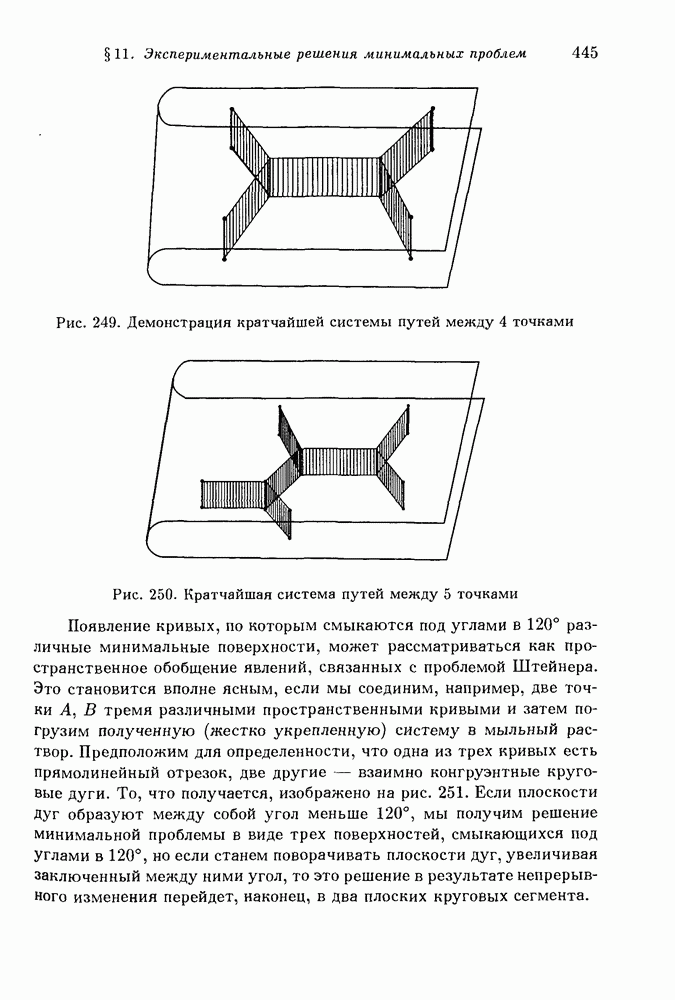
- § 11. Экспериментальные решения минимальных проблем. Опыты с мыльными пленками
- 2. Опыты с мыльными пленками.
- 3. Новые опыты, относящиеся к проблеме Плато.
- 4. Экспериментальные решения других математических проблем.
- Глава VIII. Математический анализ
- § 1. Интеграл
- 2. Интеграл.
- 3. Общие замечания о понятии интеграла. Общее определение.
- 4. Примеры интегрирования. Интегрирование x^r.
- 5. Правила «интегрального исчисления».
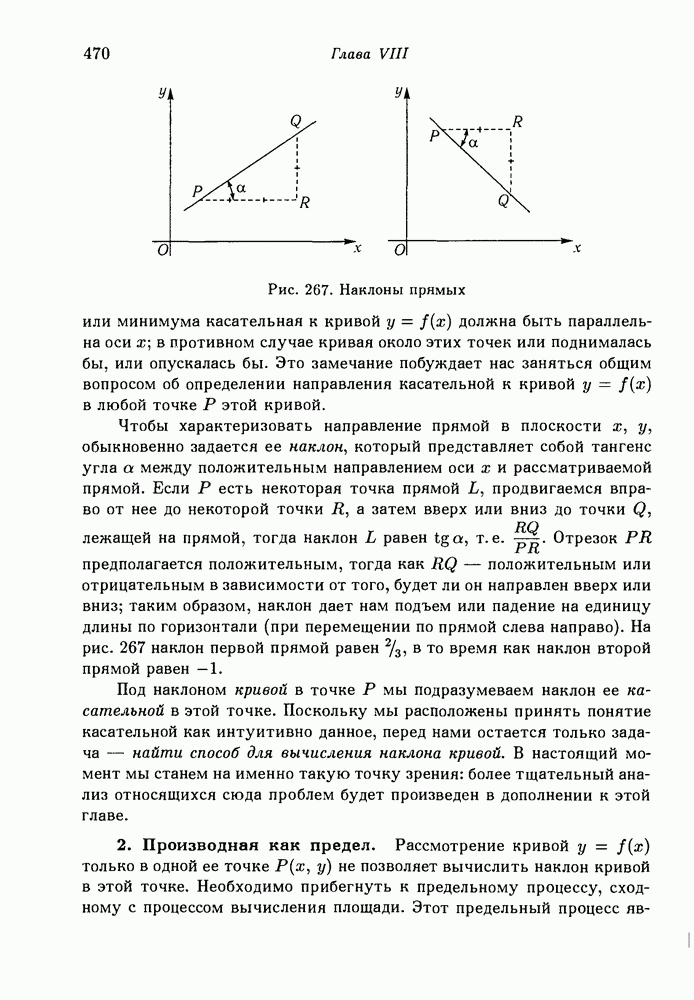
- § 2. Производная
- 2. Производная как предел.
- 3. Примеры.
- 4. Производные от тригонометрических функций.
- 5. Дифференцируемость и непрерывность.
- 6. Производная и скорость. Вторая производная и ускорение.
- 7. Геометрический смысл второй производной.
- 8. Максимумы и минимумы.
- § 3. Техника дифференцирования
- § 4. Обозначения Лейбница и «бесконечно малые»
- § 5. Основная теорема анализа
- 2. Первые применения. Интегрирование функций x^r, cosx, sinx. Функция arctgx
- 3. Формула Лейбница для «пи»
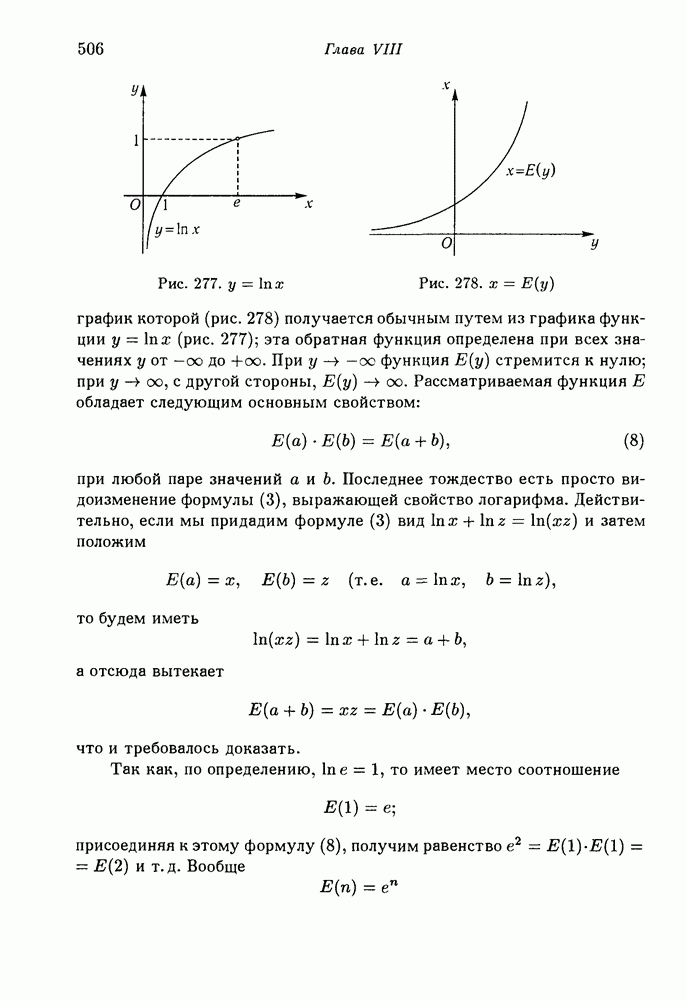
- § 6. Показательная (экспоненциальная) функция и логарифм
- 2. Показательная (экспоненциальная) функция.
- 3. Формулы дифференцирования функций е^х, а^х, x^s.
- 4. Явные выражения числа е^x и функций lnx в виде пределов.
- 5. Бесконечный ряд для логарифма. Вычисление логарифмов.
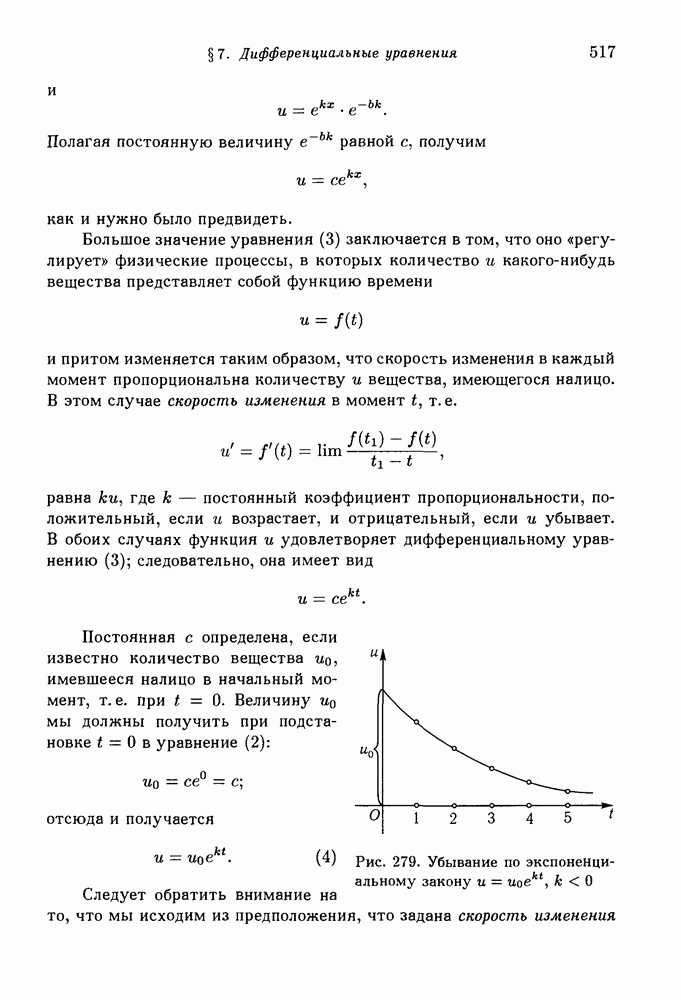
- § 7. Дифференциальные уравнения
- 2. Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- 3. Другие примеры. Простейшие колебания.
- 4. Закон движения Ньютона.
- Дополнение к главе VIII
- § 1. Вопросы принципиального порядка
- 3. Другие приложения понятия интеграла. Работа. Длина кривой.
- § 2. Порядки возрастания
- 2. Порядок возрастания ln(n!)
- § 3. Бесконечные ряды и бесконечные произведения
- 2. Формула Эйлера cos x + i sin x = exp(ix).
- 3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin x в виде бесконечного произведения.
- § 4. Доказательство теоремы о простых числах на основе статистического метода
- Приложение. Дополнительные замечания, задачи и упражнения
- Аналитическая геометрия
- Геометрические построения
- Проективная и неевклидова геометрия
- Топология
- Функции, пределы, непрерывность
- Максимумы и минимумы
- Дифференциальное и интегральное исчисления
- Техника интегрирования
- Рекомендуемая литература