| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Распределение простых чисел.
Можно составить список всех простых чисел, не превышающих какого-то данного числа  следующим образом. Напишем подряд все натуральные числа от 2 до
следующим образом. Напишем подряд все натуральные числа от 2 до  затем вычеркнем все числа, являющиеся кратными 2 (не считая самого числа 2), все числа, являющиеся кратными 3 (не считая 3), и т.д. — пока не будут вычеркнуты все составные числа. Эта процедура, известная под названием «решета Эратосфена», позволит выловить все простые числа в пределах от 2 до
затем вычеркнем все числа, являющиеся кратными 2 (не считая самого числа 2), все числа, являющиеся кратными 3 (не считая 3), и т.д. — пока не будут вычеркнуты все составные числа. Эта процедура, известная под названием «решета Эратосфена», позволит выловить все простые числа в пределах от 2 до  Усовершенствования этого метода мало-помалу привели к тому, что в настоящее время составлены вполне надежные таблицы простых чисел примерно до 10 000 000. Они предоставляют в наше распоряжение обширнейший эмпирический материал,
Усовершенствования этого метода мало-помалу привели к тому, что в настоящее время составлены вполне надежные таблицы простых чисел примерно до 10 000 000. Они предоставляют в наше распоряжение обширнейший эмпирический материал,
позволяющий судить о распределении и свойствах простых чисел. Основываясь на этих таблицах, мы можем высказать ряд в высшей степени правдоподобных гипотез — совершенно так, как будто бы теория чисел была экспериментальной наукой. Часто доказательство этих гипотез оказывается необычайно затруднительным.
а) Формулы, дающие простые числа
Были сделаны попытки найти элементарные арифметические формулы, которые давали бы только простые числа, хотя бы и не требуя того, чтобы они давали все простые числа. Ферма высказал предположение (не выставляя его в качестве положительного утверждения), что все числа вида

являются простыми. В самом деле при  мы получаем
мы получаем

— только простые числа. Но в 1732 г. Эйлер разложил на множители число  ; таким образом, число
; таким образом, число  уже не простое. Позднее среди этих «чисел Ферма» удалось обнаружить другие составные числа, причем ввиду непреодолимых трудностей, с которыми были связаны непосредственные пробы, в каждом случае были выработаны более глубокие теоретико-числовые методы. В настоящее время остается неизвестным даже то, дает ли формула Ферма бесконечное множество простых чисел.
уже не простое. Позднее среди этих «чисел Ферма» удалось обнаружить другие составные числа, причем ввиду непреодолимых трудностей, с которыми были связаны непосредственные пробы, в каждом случае были выработаны более глубокие теоретико-числовые методы. В настоящее время остается неизвестным даже то, дает ли формула Ферма бесконечное множество простых чисел.
Вот другое простое и замечательное выражение, дающее много простых чисел:

При  есть простое число; но уже при
есть простое число; но уже при  простого числа не получается:
простого числа не получается:

Выражение

дает простые числа до  включительно; при
включительно; при  получается составное число.
получается составное число.
В итоге можно сказать, что поиски элементарных формул, дающих только простые числа, оказались тщетными. Еще менее обнадеживающей следует считать задачу нахождения такой формулы, которая давала бы только простые числа и притом все простые числа.
b) Простые числа в арифметических прогрессиях
Если доказательство того, что в последовательности всех натуральных чисел  содержится бесконечное множество простых чисел, носит вполне элементарный характер, то следующий шаг в сторону таких последовательностей, как, например,
содержится бесконечное множество простых чисел, носит вполне элементарный характер, то следующий шаг в сторону таких последовательностей, как, например,  или
или  или, вообще говоря, в сторону произвольной арифметической прогрессии а, а
или, вообще говоря, в сторону произвольной арифметической прогрессии а, а  (где а и
(где а и  не имеют общих множителей) оказался связанным с гораздо большими трудностями. Все наблюдения только подтверждали тот факт, что в каждой такой прогрессии содержится бесконечное число простых чисел, как и в простейшей из них
не имеют общих множителей) оказался связанным с гораздо большими трудностями. Все наблюдения только подтверждали тот факт, что в каждой такой прогрессии содержится бесконечное число простых чисел, как и в простейшей из них  Но понадобились величайшие усилия для того, чтобы доказать эту общую теорему. Успех был достигнут Леженом Дирихле (1805-1859), одним из ведущих математиков прошлого столетия, который применил при доказательстве самые усовершенствованные средства математического анализа из известных в то время. Его замечательные работы в этой области даже для настоящего времени остаются непревзойденными; прошло около ста лет, но доказательства Дирихле все еще не упрощены настолько, чтобы они могли быть поняты теми, кто не овладел полностью техникой математического анализа и теорией функций.
Но понадобились величайшие усилия для того, чтобы доказать эту общую теорему. Успех был достигнут Леженом Дирихле (1805-1859), одним из ведущих математиков прошлого столетия, который применил при доказательстве самые усовершенствованные средства математического анализа из известных в то время. Его замечательные работы в этой области даже для настоящего времени остаются непревзойденными; прошло около ста лет, но доказательства Дирихле все еще не упрощены настолько, чтобы они могли быть поняты теми, кто не овладел полностью техникой математического анализа и теорией функций.
Мы не будем здесь пытаться привести доказательство общей теоремы Дирихле и ограничимся рассмотрением более легкой задачи: обобщим Евклидово доказательство о существовании бесконечного множества простых чисел таким образом, чтобы оно охватило некоторые специальные прогрессии, например,  или
или  Рассмотрим первую из этих прогрессий. Заметим прежде всего, что всякое простое число, большее чем 2, — непременно нечетное (иначе оно делилось бы на 2) и, следовательно, имеет вид
Рассмотрим первую из этих прогрессий. Заметим прежде всего, что всякое простое число, большее чем 2, — непременно нечетное (иначе оно делилось бы на 2) и, следовательно, имеет вид  или
или  (при целом
(при целом  Далее, произведение двух чисел вида
Далее, произведение двух чисел вида  также есть число того же вида, так как
также есть число того же вида, так как

Допустим теперь, что существует лишь конечное число простых чисел вида  обозначим их
обозначим их  и рассмотрим число
и рассмотрим число

Одно из двух: или число  простое, или оно разлагается на произведение простых чисел, среди которых, однако, не может быть ни одного из чисел
простое, или оно разлагается на произведение простых чисел, среди которых, однако, не может быть ни одного из чисел  так как эти числа делят N с остатком —1.
так как эти числа делят N с остатком —1.
Заметим дальше, что все множители, входящие в  не могут быть вида
не могут быть вида  так как само
так как само  не этого вида, тогда как мы видели, что произведение чисел вида
не этого вида, тогда как мы видели, что произведение чисел вида  является числом того же вида. Итак, хоть один из множителей, входящих в
является числом того же вида. Итак, хоть один из множителей, входящих в  должен быть вида
должен быть вида  а это невозможно, так как ни одно из чисел
а это невозможно, так как ни одно из чисел  не входит множителем в
не входит множителем в  а числами
а числами  все простые числа вида
все простые числа вида  по предположению, исчерпываются. Таким образом, допуская, что существует лишь конечное число простых чисел вида
по предположению, исчерпываются. Таким образом, допуская, что существует лишь конечное число простых чисел вида  мы приходим к противоречию, и значит, число таких чисел бесконечно.
мы приходим к противоречию, и значит, число таких чисел бесконечно.
Упражнение. Докажите соответствующую теорему для прогрессии 
с) Теорема о распределении простых чисел
В исследованиях, связанных с законом распределения простых чисел, решительный шаг был сделан тогда, когда математики отказались от тщетных попыток найти элементарную математическую формулу, которая давала бы все простые числа или же точное число простых чисел, содержащихся среди  первых натуральных чисел, и сосредоточили вместо того внимание на распределении в среднем простых чисел среди всех натуральных.
первых натуральных чисел, и сосредоточили вместо того внимание на распределении в среднем простых чисел среди всех натуральных.
При всяком целом  обозначим через
обозначим через  число простых чисел среди чисел
число простых чисел среди чисел  Если мы выделим среди первых чисел натурального ряда
Если мы выделим среди первых чисел натурального ряда

те, которые являются простыми, то не представит труда подсчитать ряд значений 

Возьмем теперь какую-нибудь неограниченно возрастающую последовательность значений  например,
например,

тогда соответствующие значения 

также будут возрастать безгранично (хотя и более медленно). Действительно, множество простых чисел, как мы уже знаем, бесконечно, и потому значения  рано или поздно станут больше любого назначенного числа. «Плотность» распределения простых чисел среди
рано или поздно станут больше любого назначенного числа. «Плотность» распределения простых чисел среди  первых чисел натурального ряда дается отношением не представляет особого труда с помощью таблиц простых чисел подсчитать значения при достаточно больших значениях
первых чисел натурального ряда дается отношением не представляет особого труда с помощью таблиц простых чисел подсчитать значения при достаточно больших значениях 

Последняя, скажем, из выписанных строчек в приведенной табличке дает вероятность того, что число, случайно выхваченное из  первых чисел натурального ряда, окажется простым: всего имеется
первых чисел натурального ряда, окажется простым: всего имеется  возможных выборов, из них
возможных выборов, из них  соответствуют простым числам.
соответствуют простым числам.

Рис. 5. Площадь заштрихованной области под гиперболой определяет 
Распределение отдельных простых чисел отличается чрезвычайно неправильным характером. Но эта неправильность «в малом» исчезает, если мы направим внимание к распределению «в среднем», находящему свое выражение в изменениях отношения при неограниченно растущем  Простой закон, которому подчиняется поведение этого отношения, следует отнести к числу самых замечательных открытий, сделанных во всей математике. Для того чтобы сформулировать теорему о распределении простых чисел, к которой мы теперь подходим, необходимо предварительно разъяснить, что такое «натуральный логарифм» числа
Простой закон, которому подчиняется поведение этого отношения, следует отнести к числу самых замечательных открытий, сделанных во всей математике. Для того чтобы сформулировать теорему о распределении простых чисел, к которой мы теперь подходим, необходимо предварительно разъяснить, что такое «натуральный логарифм» числа  Для этой цели возьмем в плоскости две взаимно перпендикулярные оси и рассмотрим геометрическое место таких точек на плоскости, для которых произведение расстояний х и у от двух осей равно единице. В терминах координат х
Для этой цели возьмем в плоскости две взаимно перпендикулярные оси и рассмотрим геометрическое место таких точек на плоскости, для которых произведение расстояний х и у от двух осей равно единице. В терминах координат х
и у это геометрическое место есть равносторонняя гипербола, уравнение которой имеет вид  Мы определим
Мы определим  как площадь (рис. 5) фигуры, ограниченной гиперболой и двумя вертикальными прямыми
как площадь (рис. 5) фигуры, ограниченной гиперболой и двумя вертикальными прямыми  . (Более детально логарифм и его свойства будут рассмотрены в главе VIII.) Чисто случайно, в связи с изучением таблицы простых чисел, Гаусс заметил, что отношение приблизительно равно и что точность этого приближения, по-видимому, улучшается при возрастании
. (Более детально логарифм и его свойства будут рассмотрены в главе VIII.) Чисто случайно, в связи с изучением таблицы простых чисел, Гаусс заметил, что отношение приблизительно равно и что точность этого приближения, по-видимому, улучшается при возрастании  Насколько удовлетворительно приближение, можно судить по отношению
Насколько удовлетворительно приближение, можно судить по отношению  значения которого при
значения которого при  показаны в следующей табличке:
показаны в следующей табличке:

Основываясь на такого рода эмпирической очевидности, Гаусс высказал в качестве предположения, что отношение «асимптотически равно»  Смысл этого утверждения заключается в следующем: если возьмем последовательность значений
Смысл этого утверждения заключается в следующем: если возьмем последовательность значений  становящихся все больше и больше, например,
становящихся все больше и больше, например,

(как мы делали и раньше), то отношение

вычисляемое для этих последовательно рассматриваемых значений  будет становиться все более и более близким к числу 1, а именно, разность между указанным отношением и единицей будет делаться столь малой, сколь будет назначено, лишь бы только мы рассматривали достаточно большие значения
будет становиться все более и более близким к числу 1, а именно, разность между указанным отношением и единицей будет делаться столь малой, сколь будет назначено, лишь бы только мы рассматривали достаточно большие значения  Такого рода соотношение символически выражается знаком
Такого рода соотношение символически выражается знаком  означает, что
означает, что  при возрастении
при возрастении  стремится к 1. Что знак
стремится к 1. Что знак  не может быть заменен знаком обыкновенного равенства
не может быть заменен знаком обыкновенного равенства  ясно хотя бы из того факта, что
ясно хотя бы из того факта, что  непременно целое число, тогда как не является таковым.
непременно целое число, тогда как не является таковым.
То обстоятельство, что распределение простых чисел хорошо описывается с помощью логарифмической функции, нельзя не признать поистине поразительным, так как здесь вступают в тесное соприкосновение два математических понятия, казалось бы, не имеющие друг к другу никакого отношения.
Хотя схватить содержание высказанного Гауссом предположения не представляет особой трудности, однако его строгое математическое доказательство во времена Гаусса было за пределами возможностей математической науки. Для того чтобы доказать теорему о распределении простых чисел, говорящую лишь о самых элементарных математических понятиях, неизбежно нужно прибегнуть к самым мощным методам современной математики. Пришлось ждать почти сто лет, пока анализ получил достаточное развитие для того, чтобы Адамар (1896) в Париже и Валле-Пуссен (1896) в Лувэне смогли дать исчерпывающее доказательство теоремы о распределении простых чисел. Упрощения и важные дополнения были затем внесены Мангольдтом и Э. Ландау. Задолго до Адамара значительное продвижение в этой области было сделано Риманом (1826-1866) в его знаменитой работе, намечающей основные стратегические линии предстоящей атаки. Совсем недавно американский математик Норберт Винер сумел видоизменить доказательство таким образом, чтобы избежать применения комплексных чисел в узловых моментах проводимых рассуждений. Но все же доказательство теоремы о распределении простых чисел остается слишком сложным для того, чтобы его можно было предложить начинающему. Мы вернемся к этому вопросу на стр. 548 и следующих.
d) Две еще не решенные задачи о простых числах
Если проблема распределения простых чисел («в среднем») была разрешена удовлетворительно, то справедливость ряда других гипотез, эмпирически совершенно несомненная, все еще не доказана.
Сюда относится прежде всего знаменитая гипотеза Гольдбаха. Гольдбах (1690-1764) сам по себе не оставил никакого следа в истории математики: он прославился только проблемой, которую предложил Эйлеру в письме, относящемся к 1742 г. Он обратил внимание на тот факт, что ему всегда удавалось представить любое четное число (кроме 2, которое само есть простое число) в виде суммы двух простых. Например, 
Гольдбах спрашивал у Эйлера, может ли он доказать, что такого рода представление возможно для всякого четного числа, или же, напротив, сможет указать пример, опровергающий такое предположение. Эйлер так и не дал ответа; не дал его никто и в дальнейшем. Эмпирическая очевидность гипотезы Гольдбаха, как легко проверить, вполне убедительна. Источник же возникающих затруднений — в том, что понятие простого числа определяется в терминах умножения, тогда как сама проблема касается сложения. Вообще, находить связи между мультипликативными и аддитивными свойствами чисел очень трудно.
До недавнего времени доказательство гипотезы Гольдбаха казалось задачей совершенно неприступной. Сегодня дело обстоит уже не так. Очень значительный успех, оказавшийся неожиданным и поразительным для всех специалистов по данному вопросу, был достигнут в 1931 г. тогда неизвестным молодым русским математиком Шнирельманом (1905-1938), который доказал, что всякое целое положительное число может быть представлено в виде суммы не более чем 800 000 простых. Хотя этот результат и производит несколько комическое впечатление (по сравнению с первоначально поставленной целью доказать гипотезу Гольдбаха), тем не менее он представлял первый шаг в должном направлении. Доказательство Шнирельмана — прямое и носит конструктивный характер, хотя и не обеспечивает практического метода для представления произвольного целого числа в виде суммы простых. Еще позднее русский же математик Виноградов, пользуясь методами Гарди, Литтлвуда и их поистине великого сотрудника по работе индуса Рамануджана, сумел понизить число слагаемых в формулировке Шнирельмана с 800 000 до 4. Это уже гораздо ближе к решению проблемы Гольдбаха. Но существует очень резкое различие между результатами Шнирельмана и Виноградова: более резкое, чем различие между числами 800 000 и 4. Теорема Виноградова была им доказана лишь для всех «достаточно больших» чисел; точнее говоря, Виноградов установил существование такого числа  что всякое целое число
что всякое целое число  может быть представлено в виде суммы четырех простых чисел. Метод Виноградова не позволяет никак судить о величине
может быть представлено в виде суммы четырех простых чисел. Метод Виноградова не позволяет никак судить о величине  в противоположность методу Шнирельмана он — существенно «косвенный» и неконструктивный. По существу Виноградов доказал следующее: допуская, что существует бесконечное множество чисел, не представимых в виде суммы четырех (или менее того) простых чисел, можно получить противоречие. Здесь перед нами прекрасный пример, показывающий глубокое различие между двумя типами
в противоположность методу Шнирельмана он — существенно «косвенный» и неконструктивный. По существу Виноградов доказал следующее: допуская, что существует бесконечное множество чисел, не представимых в виде суммы четырех (или менее того) простых чисел, можно получить противоречие. Здесь перед нами прекрасный пример, показывающий глубокое различие между двумя типами
доказательств — прямым и косвенным (см. общее обсуждение этого вопроса на стр. 49).
Следующая проблема, еще более любопытная, чем проблема Гольдбаха, нисколько не приблизилась к своему разрешению. Было подмечено, что простые числа нередко встречаются парами в виде  Таковы 3 и 5,11 и 13, 29 и 31 и т. д. Предположение о существовании бесконечного множества таких «близнецов» кажется весьма правдоподобно, но до сих пор не удалось даже приблизиться к его доказательству.
Таковы 3 и 5,11 и 13, 29 и 31 и т. д. Предположение о существовании бесконечного множества таких «близнецов» кажется весьма правдоподобно, но до сих пор не удалось даже приблизиться к его доказательству.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму русскому изданию
- Как пользоваться книгой
- Что такое математика?
- Глава I. Натуральные числа
- § 1. Операции над целыми числами
- 2. Представление целых чисел с помощью письменных знаков (нумерация).
- 3. Арифметические действия в недесятичных системах счисления.
- § 2. Бесконечность системы натуральных чисел. Математическая индукция
- 2. Арифметическая прогрессия.
- 3. Геометрическая прогрессия.
- 4. Сумма n первых квадратов.
- 5. Одно важное неравенство.
- 6. Биномиальная теорема.
- 7. Дальнейшие замечания по поводу метода математической индукции.
- Дополнение к главе I
- Теория чисел
- 2. Распределение простых чисел.
- § 2. Сравнения
- 2. Теорема Ферма.
- 3. Квадратические вычеты.
- § 3. Пифагоровы числа и большая теорема Ферма
- § 4. Алгоритм Евклида
- 2. Применение к основной теореме арифметики
- 3. Функция Эйлера. Еще раз о теореме Ферма.
- 4. Непрерывные дроби. Диофантовы уравнения
- Глава II. Математическая числовая система
- § 1. Рациональные числа
- 2. Возникновение надобности в рациональных числах внутри самой математики. Принцип обобщения.
- 3. Геометрическое представление рациональных чисел.
- § 2. Несоизмеримые отрезки. Иррациональные числа, пределы
- 2. Десятичные дроби: конечные и бесконечные.
- 3. Пределы. Бесконечные геометрические прогрессии.
- 4. Рациональные числа и периодические десятичные дроби.
- 5. Общее определение иррациональных чисел посредством стягивающихся отрезков.
- 6. Иные методы определения иррациональных чисел.Декиндовы сечения.
- § 3. Замечания из области аналитической геометрии
- 2. Уравнения прямых и кривых линий.
- § 4. Математический анализ бесконечного
- 2. Счетность множества рациональных чисел и несчетность континуума.
- 3. «Кардинальные числа» Кантора.
- 4. Косвенный метод доказательства.
- 5. Парадоксы бесконечного.
- 6. Основания математики.
- § 5. Комплексные числа
- 2. Геометрическое представление комплексных чисел.
- 3. Формула Муавра и корни из единицы.
- 4. Основная теорема алгебры.
- § 6. Алгебраические и трансцендентные числа
- 2. Теорема Лиувилля и конструирование трансцендентных чисел.
- Дополнение к главе II. Алгебра множеств
- 2. Применение к математической логике.
- 3. Одно из применений к теории вероятностей.
- Глава III. Геометрические построения. Алгебра числовых полей
- Часть 1. Доказательства невозможности и алгебра
- 1. Построение полей и извлечение квадратных корней.
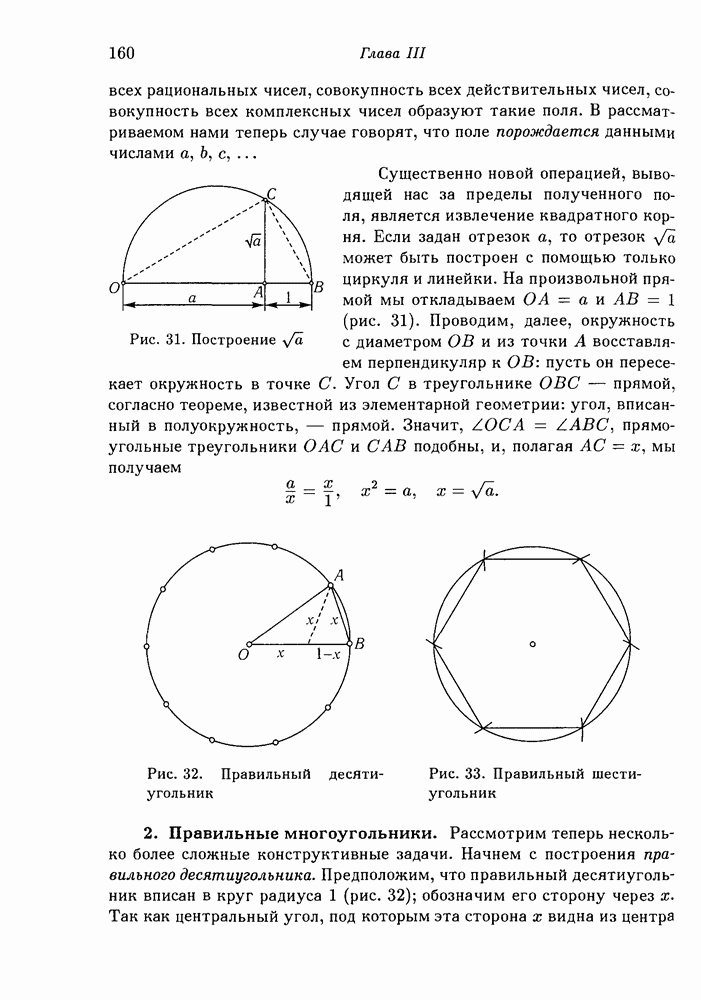
- 2. Правильные многоугольники.
- 3. Проблема Аполлония.
- § 2. Числа, допускающие построение, и числовые поля
- 2. Все числа, допускающие построение, — алгебраические.
- § 3. Неразрешимость трех классических проблем
- 2. Одна теорема о кубических уравнениях.
- 3. Трисекция угла.
- 4. Правильный семиугольник.
- 5. Замечания по поводу квадратуры круга.
- Часть 2. Различные методы выполнения построений
- § 4. Геометрические преобразования. Инверсия
- 2. Свойства инверсии.
- 3. Геометрическое построение обратных точек.
- 4. Как разделить отрезок пополам и как найти центр данного круга с помощью одного циркуля.
- § 5. Построения с помощью иных инструментов. Построения Маскерони с помощью одного циркуля
- 1. Классическая конструкция, служащая для удвоения куба.
- 2. Построения с помощью одного циркуля.
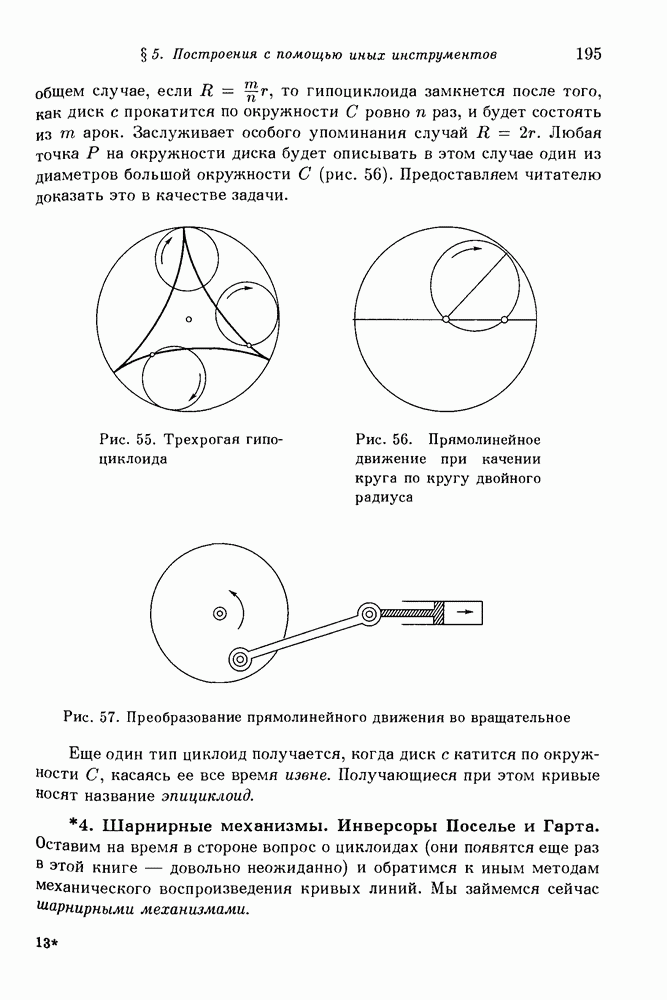
- 3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды.
- 4. Шарнирные механизмы. Инверсоры Поселье и Гарта.
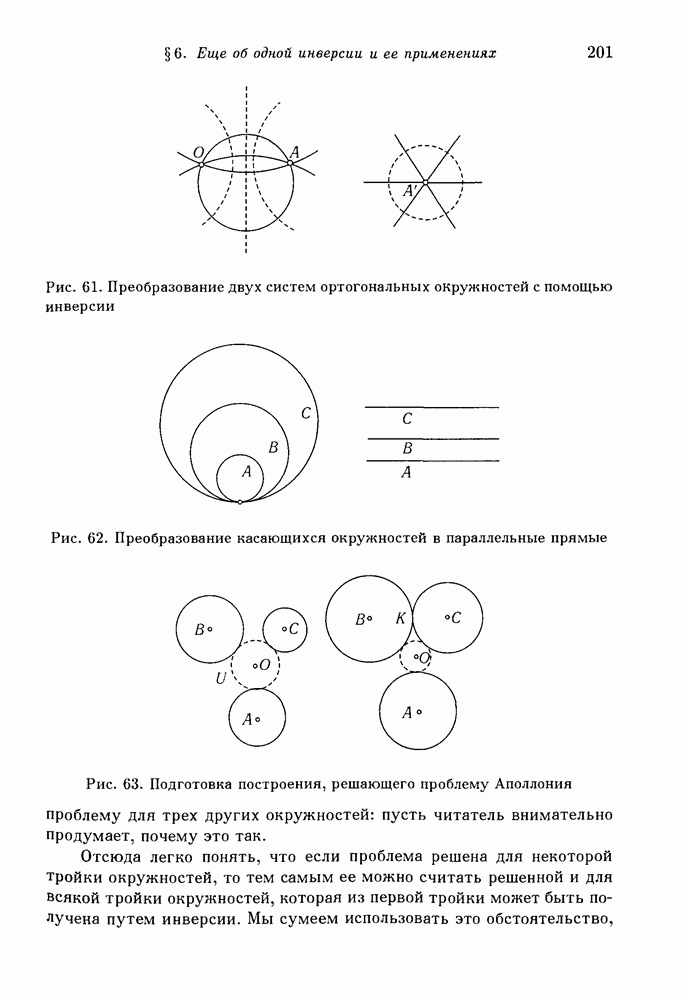
- § 6. Еще об одной инверсии и ее применениях
- 1. Инвариантность углов. Семейства окружностей.
- 2. Применение к проблеме Аполлония.
- 3. Повторные отражения.
- Глава IV. Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- 1. Классификация геометрических свойств. Инвариантность при преобразованиях.
- 2. Проективные преобразования.
- § 2. Основные понятия
- 1. Группа проективных преобразований.
- 2. Теорема Дезарга.
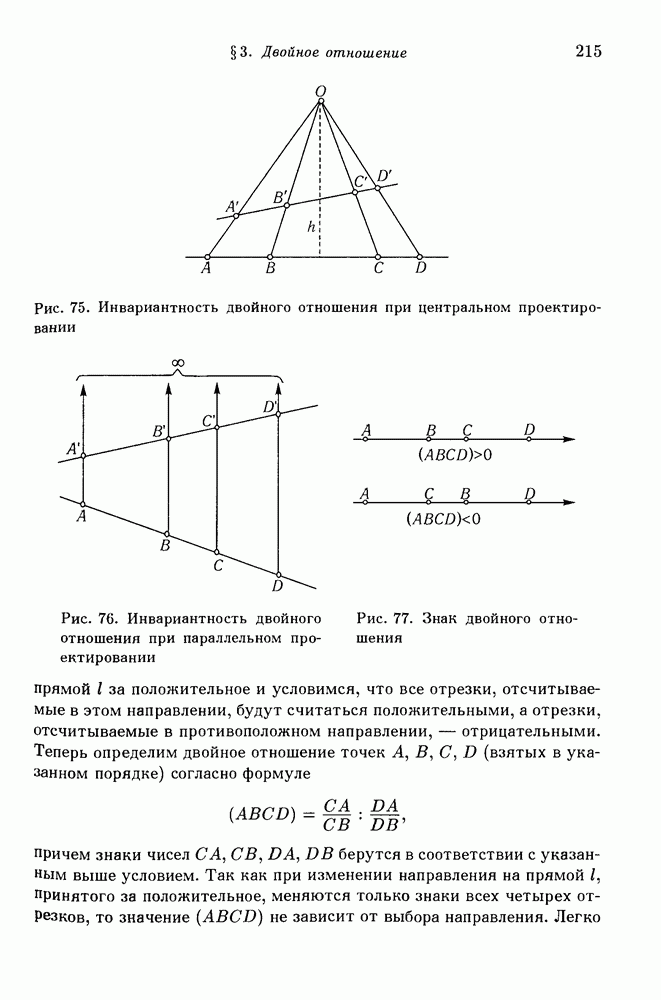
- § 3. Двойное отношение
- § 4. Параллельность и бесконечность
- 2. Идеальные элементы и проектирование.
- 3. Двойное отношение с бесконечно удаленными элементами.
- § 5. Применения
- 2. Двумерное доказательство теоремы Дезарга.
- 3. Теорема Паскаля.
- 4. Теорема Брианшона.
- 5. Замечание по поводу двойственности.
- § 6. Аналитическое представление
- 2. Однородные координаты. Алгебраические основы двойственности.
- § 7. Задачи на построения с помощью одной линейки
- § 8. Конические сечения и квадрики
- 2. Проективные свойства конических сечений.
- 3. Конические сечения как «линейчатые кривые».
- 4. Теоремы Паскаля и Брианшона для общего случая произвольных конических сечений.
- 5. Гиперболоид.
- § 9. Аксиоматика и неевклидова геометрия
- 2. Гиперболическая неевклидова геометрия.
- 3. Геометрия и реальность.
- 4. Модель Пуанкаре.
- 5. Эллиптическая, или риманова, геометрия.
- Приложение. Геометрия в пространствах более чем трех измерений
- Глава V. Топология
- § 1. Формула Эйлера для многогранников
- § 2. Топологические свойства фигур
- 2. Свойства связности.
- § 3. Другие примеры топологических теорем
- 2. Проблема четырех красок.
- 3. Понятие размерности.
- 4. Теорема о неподвижной точке.
- 5. Узлы.
- § 4. Топологическая классификация поверхностей
- 2. Эйлерова характеристика поверхности.
- 3. Односторонние поверхности.
- Приложение
- 2. Теорема Жордана для случая многоугольников.
- 3. Основная теорема алгебры.
- Глава VI. Функции и пределы
- § 1. Независимое переменное и функция
- 2. Радианная мера углов.
- 3. График функции. Обратные функции.
- 4. Сложные функции.
- 5. Непрерывность.
- 6. Функции нескольких переменных.
- 7. Функции и преобразования.
- § 2. Пределы
- 2. Монотонные последовательности.
- 3. Число Эйлера e.
- 4. Число «пи»
- 5. Непрерывные дроби.
- § 3. Пределы при непрерывном приближении
- 2. Замечания по поводу понятия предела
- 3. Предел sin x/x
- 4. Пределы при х -> оо.
- § 4. Точное определение непрерывности
- § 5. Две основные теоремы о непрерывных функциях
- 2. Доказательство теоремы Больцано.
- 3. Теорема Вейерштрасса об экстремальных значениях.
- 4. Теорема о последовательностях. Компактные множества.
- § 6. Некоторые применения теоремы Больцано
- 2. Применение к одной механической проблеме.
- Дополнение к главе VI. Дальнейшие примеры на пределы и непрерывность
- 4. Разрывные функции как предел непрерывных.
- 5. Пределы при итерации.
- § 2. Пример, относящийся к непрерывности
- Глава VII. Максимумы и минимумы
- § 1. Задачи из области элементарной геометрии
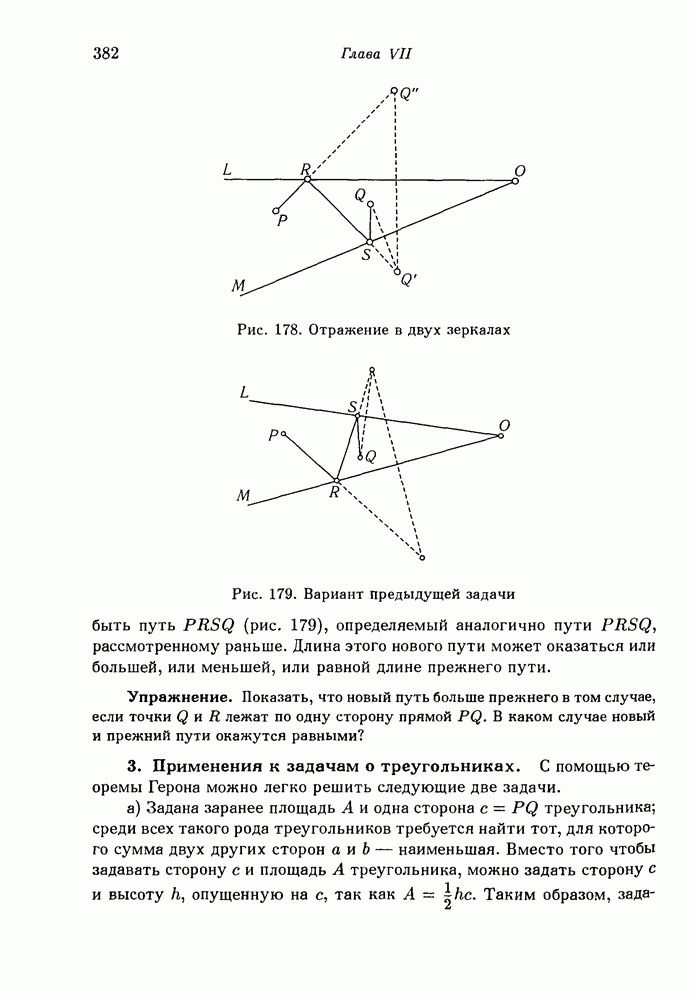
- 2. Теорема Герона. Экстремальное свойство световых лучей.
- 3. Применения к задачам о треугольниках.
- 4. Свойства касательных к эллипсу и гиперболе. Соответствующие экстремальные свойства.
- 5. Экстремальные расстояния точки от данной кривой.
- § 2. Общий принцип, которому подчинены экстремальные задачи
- § 3. Стационарные точки и дифференциальное исчисление
- 2. Максимумы и минимумы функций нескольких переменных. Седловые точки.
- 3. Точки минимакса и топология.
- 4. Расстояние точки от поверхности.
- § 4. Треугольник Шварца
- 4. Треугольники, образованные световыми лучами.
- 5. Замечания, касающиеся задач на отражение и эргодическое движение.
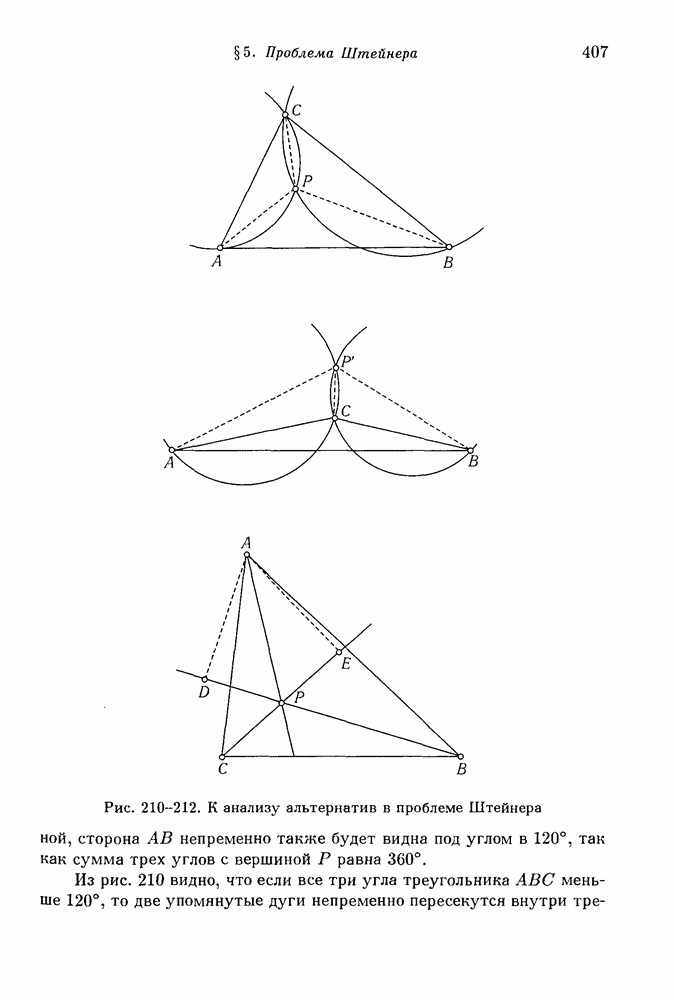
- § 5. Проблема Штейнера
- 2. Анализ возникающих альтернатив.
- 3. Дополнительная проблема.
- 4. Замечания и упражнения.
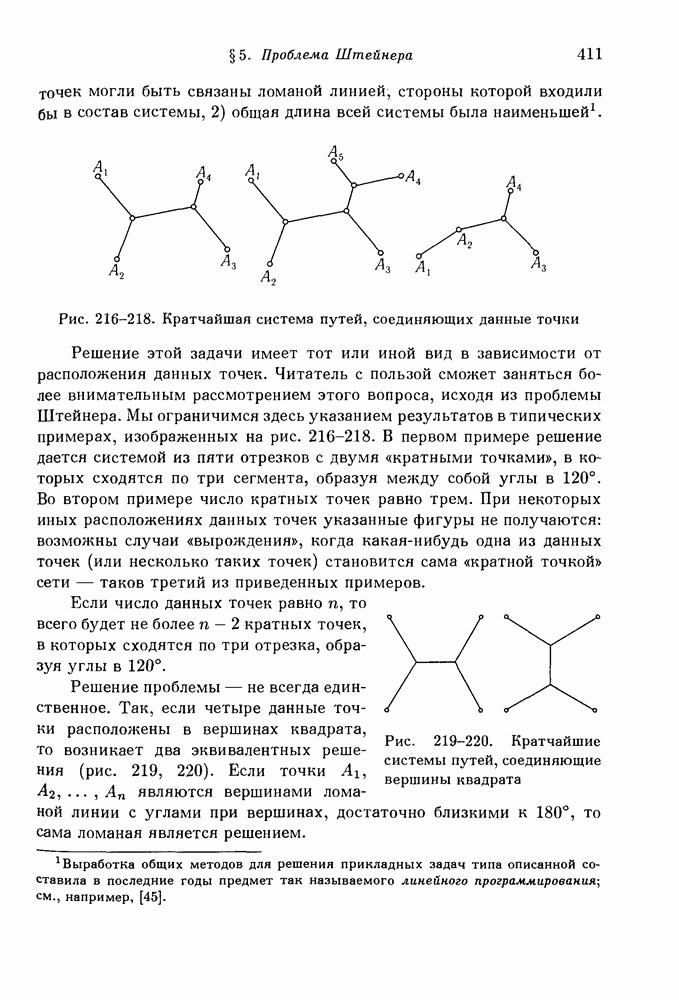
- 5. Обобщение: проблема уличной сети.
- § 6. Экстремумы и неравенства
- 1. Средние арифметическое и геометрическое двух положительных величин.
- 2. Обобщение на случай n переменных.
- 3. Метод наименьших квадратов.
- § 7. Существование экстремума. Принцип Дирихле
- 3. Экстремальные проблемы элементарного содержания.
- 4. Трудности, возникающие в более сложных случаях.
- § 8. Изопериметрическая проблема
- § 9. Экстремальные проблемы с граничными условиями. Связь между проблемой Штейнера и изопериметрической проблемой
- § 10. Вариационное исчисление
- 2. Вариационное исчисление. Принцип Ферма в оптике.
- 3. Решение задачи о брахистохроне, принадлежащее Якобу Бернулли.
- 4. Геодезические линии на сфере. Минимаксы.
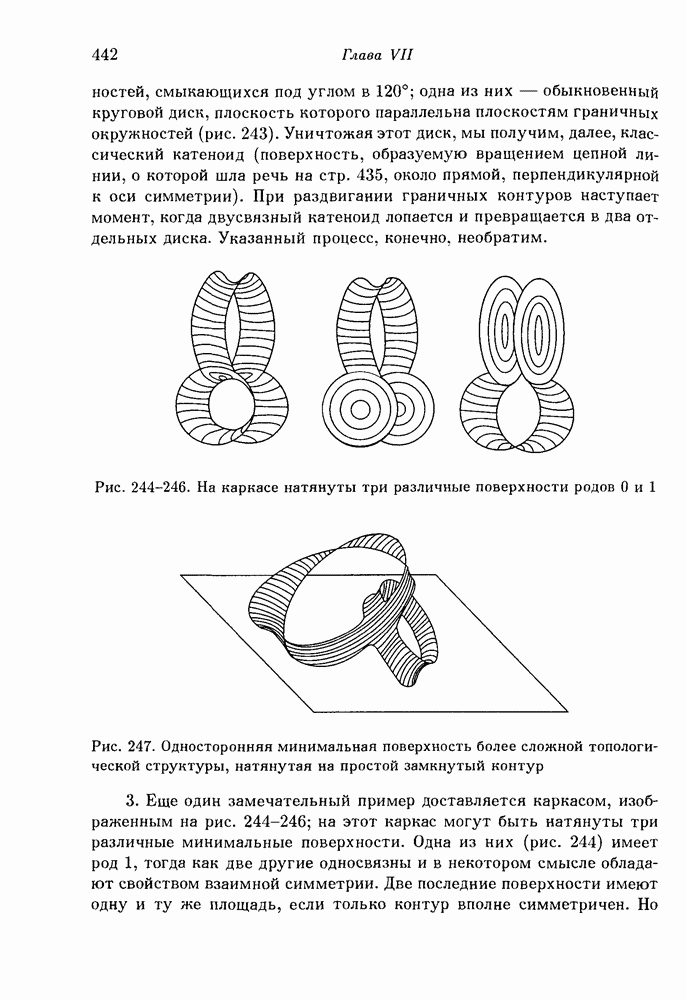
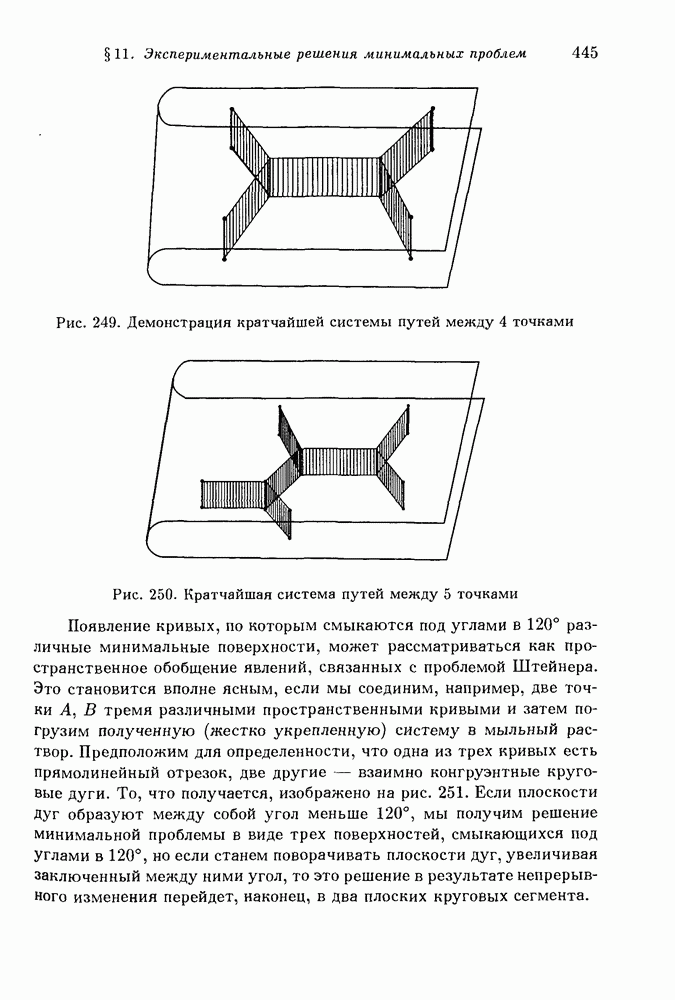
- § 11. Экспериментальные решения минимальных проблем. Опыты с мыльными пленками
- 2. Опыты с мыльными пленками.
- 3. Новые опыты, относящиеся к проблеме Плато.
- 4. Экспериментальные решения других математических проблем.
- Глава VIII. Математический анализ
- § 1. Интеграл
- 2. Интеграл.
- 3. Общие замечания о понятии интеграла. Общее определение.
- 4. Примеры интегрирования. Интегрирование x^r.
- 5. Правила «интегрального исчисления».
- § 2. Производная
- 2. Производная как предел.
- 3. Примеры.
- 4. Производные от тригонометрических функций.
- 5. Дифференцируемость и непрерывность.
- 6. Производная и скорость. Вторая производная и ускорение.
- 7. Геометрический смысл второй производной.
- 8. Максимумы и минимумы.
- § 3. Техника дифференцирования
- § 4. Обозначения Лейбница и «бесконечно малые»
- § 5. Основная теорема анализа
- 2. Первые применения. Интегрирование функций x^r, cosx, sinx. Функция arctgx
- 3. Формула Лейбница для «пи»
- § 6. Показательная (экспоненциальная) функция и логарифм
- 2. Показательная (экспоненциальная) функция.
- 3. Формулы дифференцирования функций е^х, а^х, x^s.
- 4. Явные выражения числа е^x и функций lnx в виде пределов.
- 5. Бесконечный ряд для логарифма. Вычисление логарифмов.
- § 7. Дифференциальные уравнения
- 2. Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- 3. Другие примеры. Простейшие колебания.
- 4. Закон движения Ньютона.
- Дополнение к главе VIII
- § 1. Вопросы принципиального порядка
- 3. Другие приложения понятия интеграла. Работа. Длина кривой.
- § 2. Порядки возрастания
- 2. Порядок возрастания ln(n!)
- § 3. Бесконечные ряды и бесконечные произведения
- 2. Формула Эйлера cos x + i sin x = exp(ix).
- 3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin x в виде бесконечного произведения.
- § 4. Доказательство теоремы о простых числах на основе статистического метода
- Приложение. Дополнительные замечания, задачи и упражнения
- Аналитическая геометрия
- Геометрические построения
- Проективная и неевклидова геометрия
- Топология
- Функции, пределы, непрерывность
- Максимумы и минимумы
- Дифференциальное и интегральное исчисления
- Техника интегрирования
- Рекомендуемая литература