| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 7. Существование экстремума. Принцип Дирихле
1. Общие замечания.
В некоторых из рассмотренных нами экстремальных проблем прямо доказывалось, что решение дает наилучший результат из числа прочих возможных. Ярким примером является принадлежащее Шварцу решение задачи о треугольнике: здесь сразу видно, что никакой вписанный треугольник не может иметь меньший периметр, чем высотный треугольник. Некоторые примеры такого же типа связаны с явно написанными неравенствами, каково, например, неравенство между средними арифметическим и геометрическим. Но при решении других проблем мы шли по иному пути. Мы допускали
прежде всего, что решение уже найдено, и затем, анализируя это допущение, получали заключения, иногда позволяющие дать полную характеристику решения и выполнить соответствующее его построение. Так именно обстояло дело с проблемой Штейнера и таков же был план второго решения проблемы Шварца. Названные два метода логически различны. Первый метод, пожалуй, можно считать более совершенным, так как он дает конструктивное доказательство правильности результата. Второй метод, если судить по примеру проблемы Шварца (второе решение), кажется более простым. Но он является не прямым, а косвенным и, самое главное, он условен по самой своей структуре, так как предполагает существование решения. Он приводит к окончательному результату лишь постольку, поскольку существование решения или постулировано, или доказано. Без этой предпосылки он показывает всего-навсего, что если решение существует, то оно обладает такими-то свойствами.
Вследствие кажущейся очевидности предпосылки о существовании решения математики вплоть до конца прошлого столетия не обращали особенного внимания на указанное логическое обстоятельство и допускали существование решения экстремальных проблем как нечто само собой разумеющееся. Некоторые из величайших ученых XIX в. — Гаусс, Дирихле, Риман — основывали некритически на такого рода допущении глубокие и иначе трудно доказуемые предложения в области математической физики и теории функций. Кризис наступил вскоре после того, как Риман в 1849 г. опубликовал свою докторскую диссертацию, посвященную основаниям теории функций комплексного переменного. Эта сжато написанная работа, представляющая собой один из величайших подвигов математической мысли в новейшую эпоху, была до такой степени неортодоксальной в трактовке вопроса, что многие предпочли попросту ее игнорировать. Вейерштрасс в то время был уже знаменитым профессором Берлинского университета и пользовался репутацией основателя строго построенной теории функций. Вначале пораженный, но все же исполненный сомнений, он вскоре обнаружил в работе Римана логическую брешь, о восполнении которой сам автор не позаботился. Уничтожающая критика Вейерштрасса не поколебала уверенности Римана в справедливости полученных им результатов, но долгое время его теория не пользовалась признанием. Головокружительная научная
карьера Римана вскоре внезапно оборвалась: он умер от туберкулеза. Все же его идеи поддерживались и дальше несколькими убежденными и преданными учениками. Только через пятьдесят лет после появления диссертации Римана Гильберту удалось, наконец, открыть пути, приводящие к исчерпывающему ответу на все вопросы, оставленные в стороне и неразрешенные Риманом. Начатое Риманом и развернувшееся во второй половине столетия развитие математических теорий, глубоко проникающих в область физики, представляет одну из самых блестящих страниц в истории современной науки.
Уязвимое место в работе Римана — как раз вопрос о существовании минимума. Свою теорию Риман основывает на принципе Дирихле (так он сам его назвал по имени своего учителя: Дирихле, читая лекции в Гёттингене, пользовался этим принципом, но ни в одной из своих работ о нем не писал). Предположим, для большей определенности, что некоторая часть плоскости или какой-нибудь поверхности покрыта слоем станиоля и что стационарный электрический ток проходит по слою, соединенному в двух точках с полюсами батареи. Нет сомнений, что такой эксперимент приведет к некоторому однозначно определенному распределению токов. Но как обстоит дело с соответствующей математической проблемой — проблемой, имеющей первостепенное значение в теории функций и в других областях? В теории электричества рассматриваемое нами физическое явление описывается как «дифференциальное уравнение в частных производных с граничными условиями». Именно эта математическая проблема нас и интересует; возможность ее решения кажется правдоподобной именно по той причине, что мы допустили ее эквивалентность физическому явлению; но математическое доказательство этой возможности никоим образом не может базироваться на сделанном допущении. В подходе Римана к решению рассматриваемого им математического вопроса можно различить два этапа. Во-первых, он показывает, что проблема эквивалентна некоторой минимальной проблеме: некоторая величина, выражающая энергию потока электричества, минимизируется некоторыми реально осуществляющимся потоком (по сравнению с иными потоками, совместными с предписанными граничными условиями). Во-вторых, в качестве «принципа Дирихле» он вводит постулат о том, что такого рода минимальная проблема допускает решение. Риман решительно ничего не предпринял для того, чтобы найти хоть какое-нибудь математическое оправдание для этого постулата, и именно в этом пункте его настигли атаки со стороны Вейерштрасса. Не только существование минимума само по себе не было очевидным, но, как выяснилось впоследствии,
вопрос оказался чрезвычайно тонким: математика того времени еще не была подготовлена к его решению, и только через несколько десятилетий напряженные усилия исследовательской мысли привели к законченным результатам.
2. Примеры.
Мы проиллюстрируем возникающую трудность двумя примерами.
1) Отметим на прямой  две точки
две точки  находящиеся на расстоянии
находящиеся на расстоянии  и поставим задачу — отыскать ломаную линию кратчайшей длины, которая, выходя из точки А по направлению, перпендикулярному к
и поставим задачу — отыскать ломаную линию кратчайшей длины, которая, выходя из точки А по направлению, перпендикулярному к  заканчивалась бы в точке В. Так как прямолинейный отрезок
заканчивалась бы в точке В. Так как прямолинейный отрезок  безусловно короче всех других путей, связывающих точки
безусловно короче всех других путей, связывающих точки  то можно быть уверенным, что любой допустимый (удовлетворяющий требованиям задачи) путь имеет длину, большую, чем
то можно быть уверенным, что любой допустимый (удовлетворяющий требованиям задачи) путь имеет длину, большую, чем  в самом деле, единственный путь, длина которого равна
в самом деле, единственный путь, длина которого равна  есть прямолинейный отрезок
есть прямолинейный отрезок  а он не удовлетворяет требованию относительно направления в точке А, т. е. не является допустимым. Рассмотрим, с другой стороны, допустимый путь
а он не удовлетворяет требованию относительно направления в точке А, т. е. не является допустимым. Рассмотрим, с другой стороны, допустимый путь  на рис. 222. Заменяя точку О точкой О, расположенной ближе к А, мы можем получить новый допустимый путь, длина которого как угодно мало отличается от
на рис. 222. Заменяя точку О точкой О, расположенной ближе к А, мы можем получить новый допустимый путь, длина которого как угодно мало отличается от  значит, если существует кратчайший допустимый путь, то длина его не может быть больше, чем
значит, если существует кратчайший допустимый путь, то длина его не может быть больше, чем  и, следовательно, должна быть в точности равна
и, следовательно, должна быть в точности равна  Но мы видели, что единственный путь, имеющий такую длину, не является допустимым. Итак, кратчайшего допустимого пути не существует, и задача наша не имеет решения.
Но мы видели, что единственный путь, имеющий такую длину, не является допустимым. Итак, кратчайшего допустимого пути не существует, и задача наша не имеет решения.

Рис. 222-223. К вопросу о существовании минимума
2) Пусть С — некоторый круг,  точка, лежащая выше его центра на расстоянии 1 (рис. 223). Рассмотрим множество поверхностей, ограниченных окружностью С и проходящих через точку
точка, лежащая выше его центра на расстоянии 1 (рис. 223). Рассмотрим множество поверхностей, ограниченных окружностью С и проходящих через точку 
при том лежащих «над» кругом С (в том смысле, что никакие две различные точки этой поверхности не могут вертикально проектироваться в одну и ту же точку круга С). Какая поверхность из рассматриваемого множества обладает наименьшей площадью? Каким бы естественным ни казался этот вопрос, положительного ответа на него дать нельзя: допустимой поверхности с наименьшей площадью не существует. Если бы поверхность не была подчинена условию проходить через точку  тогда решением задачи был бы, очевидно, плоский диск, ограниченный окружностью С. Обозначим площадь этого диска через А. Всякая другая поверхность, ограниченная окружностью С, непременно имеет площадь большую, чем А. Но можно указать допустимую поверхность, площадь которой будет отличаться от А как угодно мало. В самом деле, возьмем коническую поверхность высоты, равной 1 — такую «тоненькую», чтобы ее площадь была меньше заранее назначенного маленького числа. Поместим эту поверхность посреди диска так, чтобы ее вершина попала в точку
тогда решением задачи был бы, очевидно, плоский диск, ограниченный окружностью С. Обозначим площадь этого диска через А. Всякая другая поверхность, ограниченная окружностью С, непременно имеет площадь большую, чем А. Но можно указать допустимую поверхность, площадь которой будет отличаться от А как угодно мало. В самом деле, возьмем коническую поверхность высоты, равной 1 — такую «тоненькую», чтобы ее площадь была меньше заранее назначенного маленького числа. Поместим эту поверхность посреди диска так, чтобы ее вершина попала в точку  и затем рассмотрим поверхность, образованную из нашей конической поверхности и той части диска, которая окажется вне основания конуса. Совершенно ясно, что построенная таким образом поверхность, только вблизи центра диска отличающаяся от самого диска, обладает площадью, превосходящей А меньше, чем на заранее назначенное число. Так как это последнее число может быть выбрано сколь угодно малым, то отсюда следует, что минимум площади (если он существует) не может отличаться от площади диска А. Но среди поверхностей, ограниченных контуром С, только сам диск обладает площадью
и затем рассмотрим поверхность, образованную из нашей конической поверхности и той части диска, которая окажется вне основания конуса. Совершенно ясно, что построенная таким образом поверхность, только вблизи центра диска отличающаяся от самого диска, обладает площадью, превосходящей А меньше, чем на заранее назначенное число. Так как это последнее число может быть выбрано сколь угодно малым, то отсюда следует, что минимум площади (если он существует) не может отличаться от площади диска А. Но среди поверхностей, ограниченных контуром С, только сам диск обладает площадью  однако диск не проходит через точку S и, значит, не является допустимой поверхностью; следовательно, решения задачи не существует.
однако диск не проходит через точку S и, значит, не является допустимой поверхностью; следовательно, решения задачи не существует.
Мы можем избавить себя от труда приводить дальнейшие относящиеся сюда софистически утонченные примеры, указанные Вейерштрассом. Уже приведенные примеры достаточно убедительно показывают, что существование минимума не является тривиальным моментом в математическом доказательстве. Попробуем взглянуть на рассматриваемый вопрос с более отвлеченной точки зрения. Представим себе некоторый определенный класс объектов, например, кривых или поверхностей; пусть каждому объекту этого класса поставлено в соответствие — как функция этого объекта — некоторое число, например, Длина или площадь. Если в классе содержится лишь конечное число объектов, то среди соответствующих чисел неизбежно имеется наибольшее и наименьшее. Но если в классе содержится бесконечное множество объектов, то даже в том случае, если все соответствующие
числа заключены между двумя конечными границами, среди них вовсе не обязательно найдется наибольшее и наименьшее. На числовой оси множество чисел изображается в виде множества точек. Предположим, ограничившись простейшим случаем, что все числа множества положительные. Такое множество непременно имеет «нижнюю границу» — такое число а, меньше которого в нашем множестве нет ни одного числа и которое или само есть элемент множества, или как угодно мало отличается от некоторого элемента множества. Если а само принадлежит множеству, то оно является его наименьшим элементом; в противном случае множество не содержит вовсе наименьшего элемента. Например, множество чисел  не содержит наименьшего элемента, так как нижняя граница 0 не принадлежит множеству. Такого рода отвлеченные примеры иллюстрируют логические трудности, связанные с проблемой существования. Математическое решение минимальной проблемы нельзя назвать исчерпывающим, если в явной или в неявной форме не устанавливается, что среди элементов числового множества, рассматриваемого в связи с проблемой, существует наименьший.
не содержит наименьшего элемента, так как нижняя граница 0 не принадлежит множеству. Такого рода отвлеченные примеры иллюстрируют логические трудности, связанные с проблемой существования. Математическое решение минимальной проблемы нельзя назвать исчерпывающим, если в явной или в неявной форме не устанавливается, что среди элементов числового множества, рассматриваемого в связи с проблемой, существует наименьший.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие ко второму русскому изданию
- Как пользоваться книгой
- Что такое математика?
- Глава I. Натуральные числа
- § 1. Операции над целыми числами
- 2. Представление целых чисел с помощью письменных знаков (нумерация).
- 3. Арифметические действия в недесятичных системах счисления.
- § 2. Бесконечность системы натуральных чисел. Математическая индукция
- 2. Арифметическая прогрессия.
- 3. Геометрическая прогрессия.
- 4. Сумма n первых квадратов.
- 5. Одно важное неравенство.
- 6. Биномиальная теорема.
- 7. Дальнейшие замечания по поводу метода математической индукции.
- Дополнение к главе I
- Теория чисел
- 2. Распределение простых чисел.
- § 2. Сравнения
- 2. Теорема Ферма.
- 3. Квадратические вычеты.
- § 3. Пифагоровы числа и большая теорема Ферма
- § 4. Алгоритм Евклида
- 2. Применение к основной теореме арифметики
- 3. Функция Эйлера. Еще раз о теореме Ферма.
- 4. Непрерывные дроби. Диофантовы уравнения
- Глава II. Математическая числовая система
- § 1. Рациональные числа
- 2. Возникновение надобности в рациональных числах внутри самой математики. Принцип обобщения.
- 3. Геометрическое представление рациональных чисел.
- § 2. Несоизмеримые отрезки. Иррациональные числа, пределы
- 2. Десятичные дроби: конечные и бесконечные.
- 3. Пределы. Бесконечные геометрические прогрессии.
- 4. Рациональные числа и периодические десятичные дроби.
- 5. Общее определение иррациональных чисел посредством стягивающихся отрезков.
- 6. Иные методы определения иррациональных чисел.Декиндовы сечения.
- § 3. Замечания из области аналитической геометрии
- 2. Уравнения прямых и кривых линий.
- § 4. Математический анализ бесконечного
- 2. Счетность множества рациональных чисел и несчетность континуума.
- 3. «Кардинальные числа» Кантора.
- 4. Косвенный метод доказательства.
- 5. Парадоксы бесконечного.
- 6. Основания математики.
- § 5. Комплексные числа
- 2. Геометрическое представление комплексных чисел.
- 3. Формула Муавра и корни из единицы.
- 4. Основная теорема алгебры.
- § 6. Алгебраические и трансцендентные числа
- 2. Теорема Лиувилля и конструирование трансцендентных чисел.
- Дополнение к главе II. Алгебра множеств
- 2. Применение к математической логике.
- 3. Одно из применений к теории вероятностей.
- Глава III. Геометрические построения. Алгебра числовых полей
- Часть 1. Доказательства невозможности и алгебра
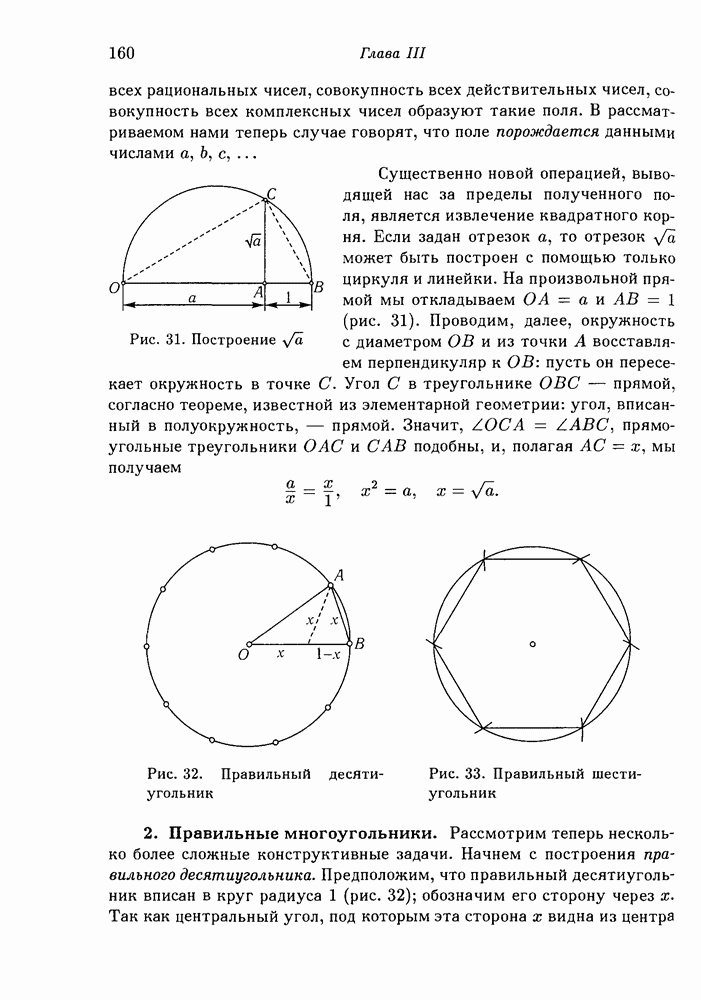
- 1. Построение полей и извлечение квадратных корней.
- 2. Правильные многоугольники.
- 3. Проблема Аполлония.
- § 2. Числа, допускающие построение, и числовые поля
- 2. Все числа, допускающие построение, — алгебраические.
- § 3. Неразрешимость трех классических проблем
- 2. Одна теорема о кубических уравнениях.
- 3. Трисекция угла.
- 4. Правильный семиугольник.
- 5. Замечания по поводу квадратуры круга.
- Часть 2. Различные методы выполнения построений
- § 4. Геометрические преобразования. Инверсия
- 2. Свойства инверсии.
- 3. Геометрическое построение обратных точек.
- 4. Как разделить отрезок пополам и как найти центр данного круга с помощью одного циркуля.
- § 5. Построения с помощью иных инструментов. Построения Маскерони с помощью одного циркуля
- 1. Классическая конструкция, служащая для удвоения куба.
- 2. Построения с помощью одного циркуля.
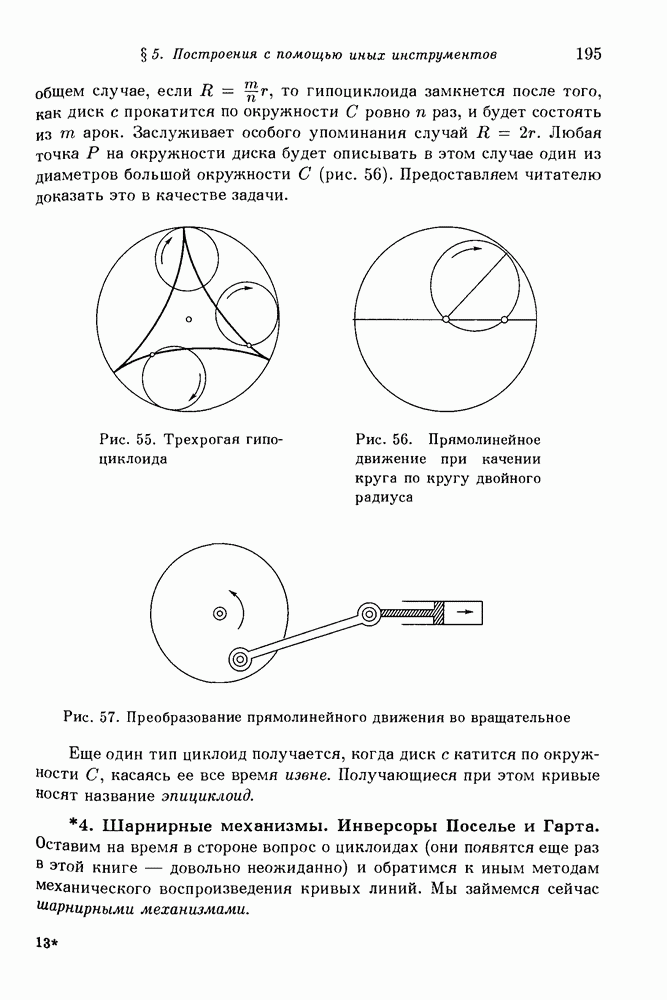
- 3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды.
- 4. Шарнирные механизмы. Инверсоры Поселье и Гарта.
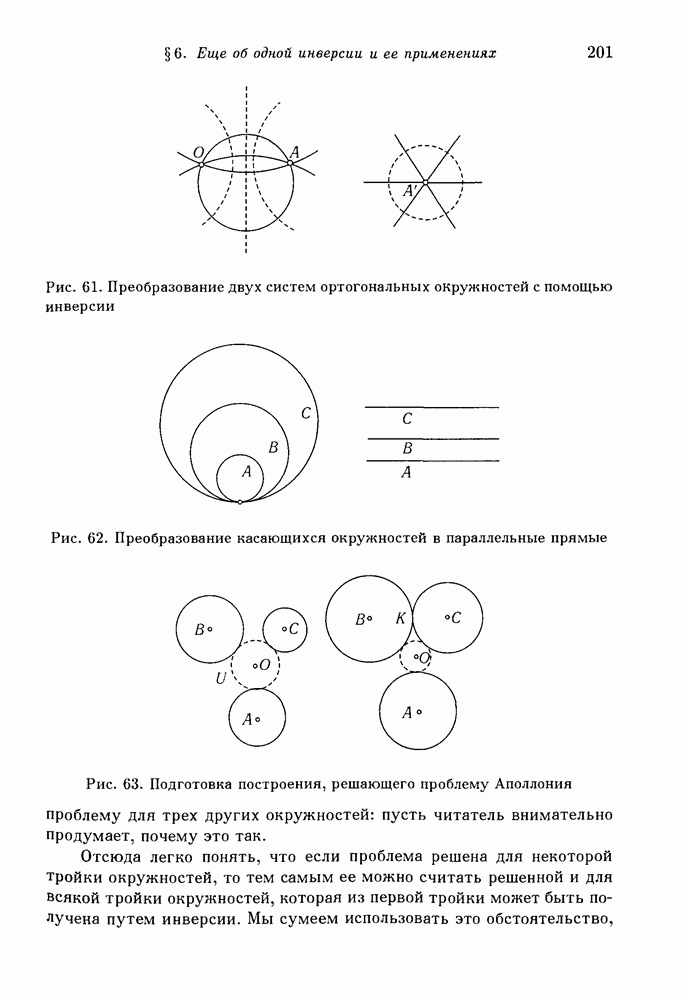
- § 6. Еще об одной инверсии и ее применениях
- 1. Инвариантность углов. Семейства окружностей.
- 2. Применение к проблеме Аполлония.
- 3. Повторные отражения.
- Глава IV. Проективная геометрия. Аксиоматика. Неевклидовы геометрии
- 1. Классификация геометрических свойств. Инвариантность при преобразованиях.
- 2. Проективные преобразования.
- § 2. Основные понятия
- 1. Группа проективных преобразований.
- 2. Теорема Дезарга.
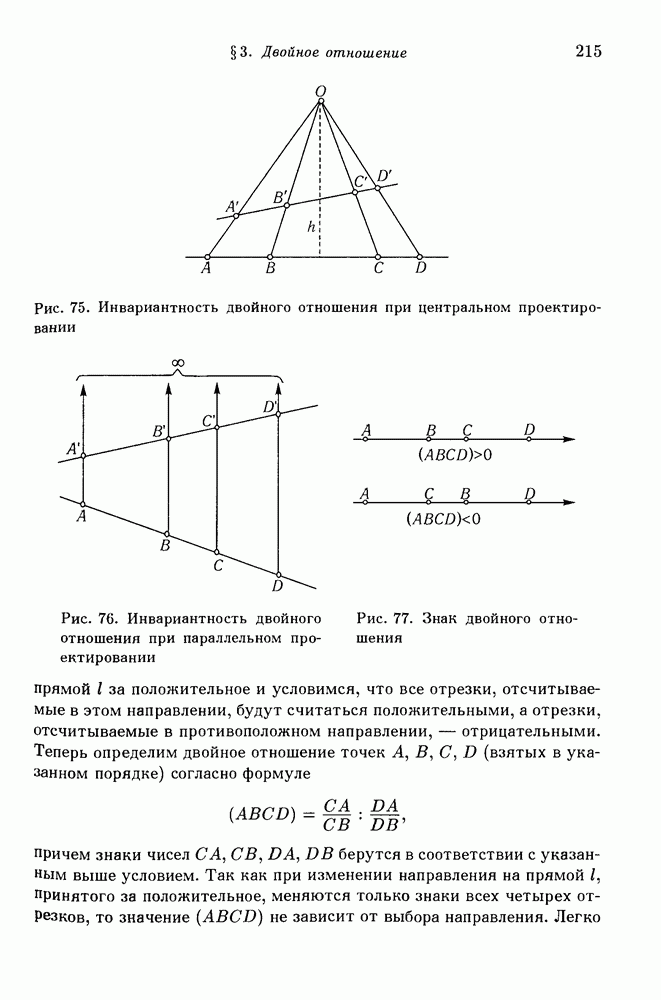
- § 3. Двойное отношение
- § 4. Параллельность и бесконечность
- 2. Идеальные элементы и проектирование.
- 3. Двойное отношение с бесконечно удаленными элементами.
- § 5. Применения
- 2. Двумерное доказательство теоремы Дезарга.
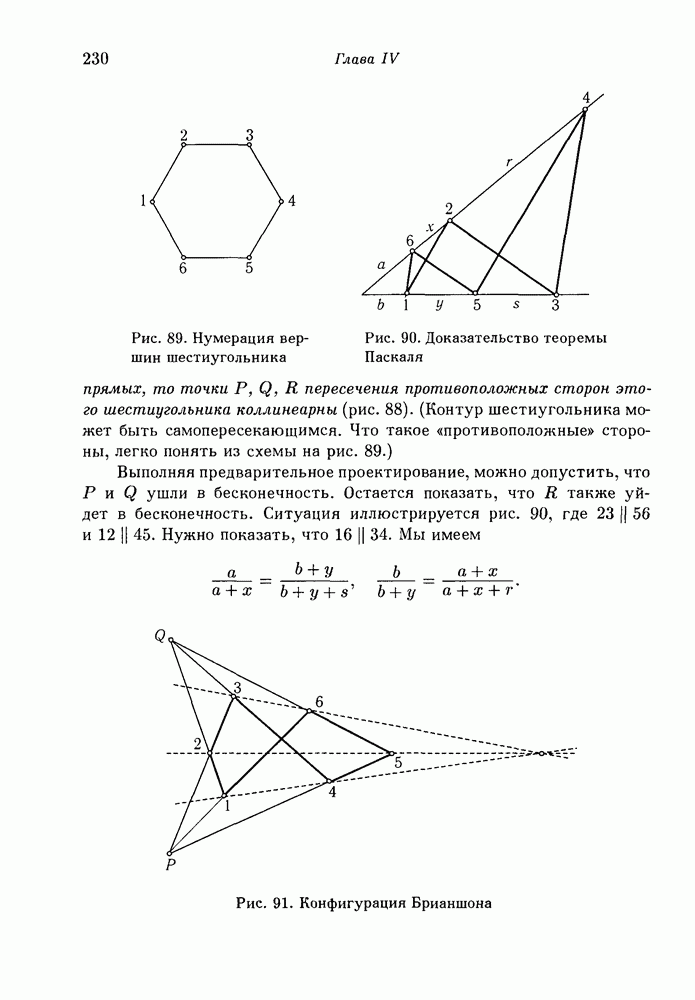
- 3. Теорема Паскаля.
- 4. Теорема Брианшона.
- 5. Замечание по поводу двойственности.
- § 6. Аналитическое представление
- 2. Однородные координаты. Алгебраические основы двойственности.
- § 7. Задачи на построения с помощью одной линейки
- § 8. Конические сечения и квадрики
- 2. Проективные свойства конических сечений.
- 3. Конические сечения как «линейчатые кривые».
- 4. Теоремы Паскаля и Брианшона для общего случая произвольных конических сечений.
- 5. Гиперболоид.
- § 9. Аксиоматика и неевклидова геометрия
- 2. Гиперболическая неевклидова геометрия.
- 3. Геометрия и реальность.
- 4. Модель Пуанкаре.
- 5. Эллиптическая, или риманова, геометрия.
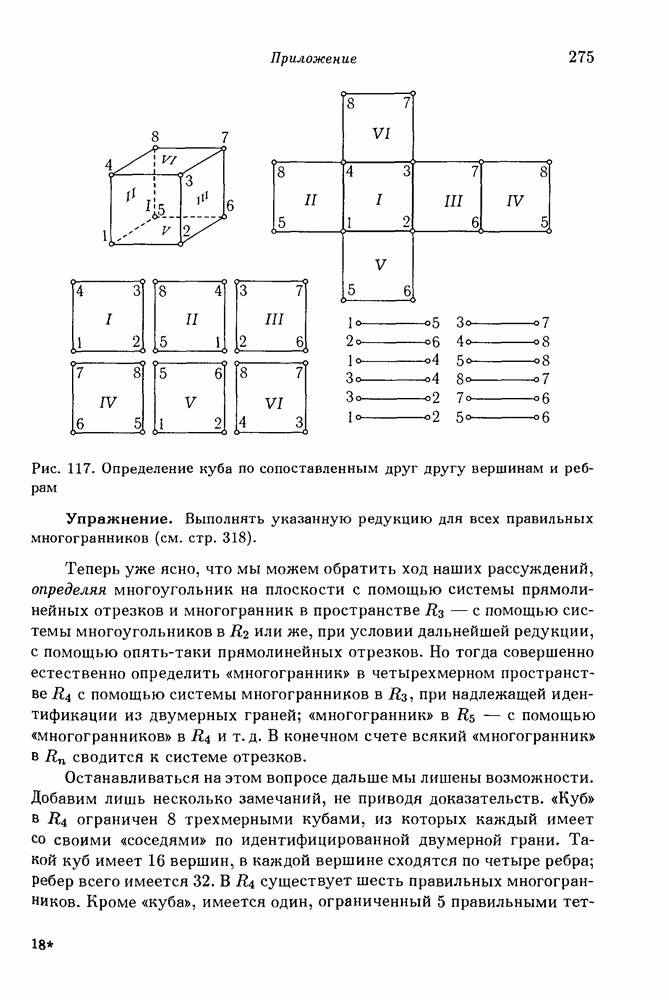
- Приложение. Геометрия в пространствах более чем трех измерений
- Глава V. Топология
- § 1. Формула Эйлера для многогранников
- § 2. Топологические свойства фигур
- 2. Свойства связности.
- § 3. Другие примеры топологических теорем
- 2. Проблема четырех красок.
- 3. Понятие размерности.
- 4. Теорема о неподвижной точке.
- 5. Узлы.
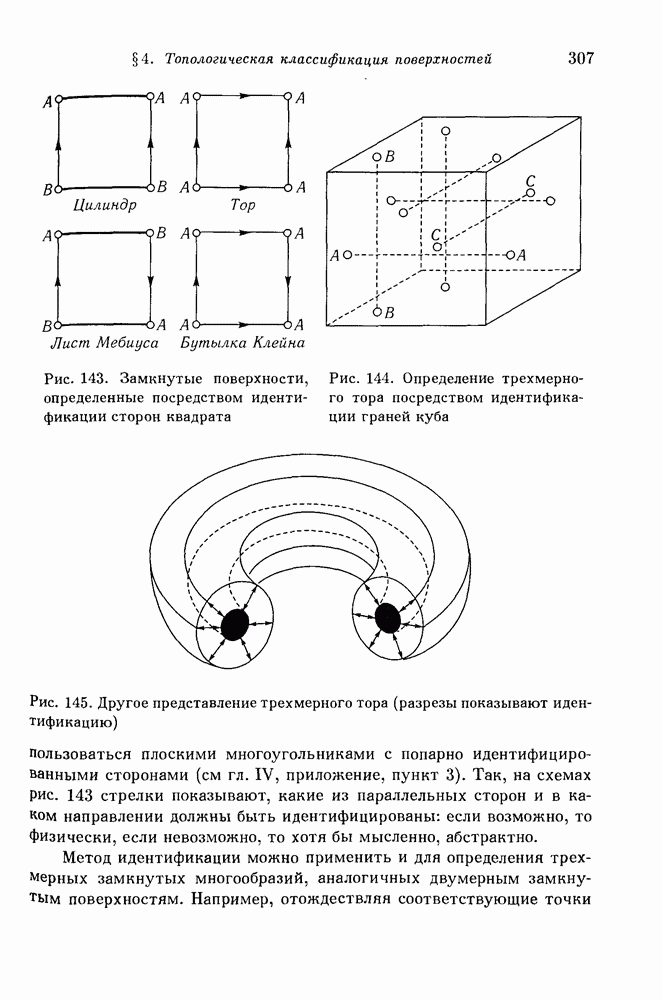
- § 4. Топологическая классификация поверхностей
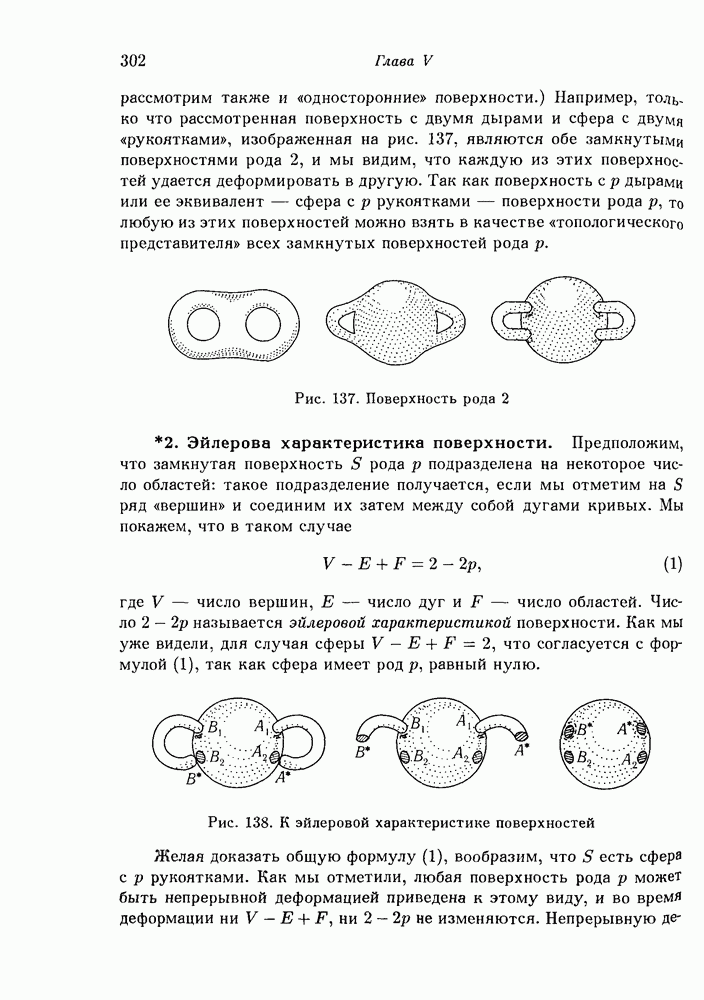
- 2. Эйлерова характеристика поверхности.
- 3. Односторонние поверхности.
- Приложение
- 2. Теорема Жордана для случая многоугольников.
- 3. Основная теорема алгебры.
- Глава VI. Функции и пределы
- § 1. Независимое переменное и функция
- 2. Радианная мера углов.
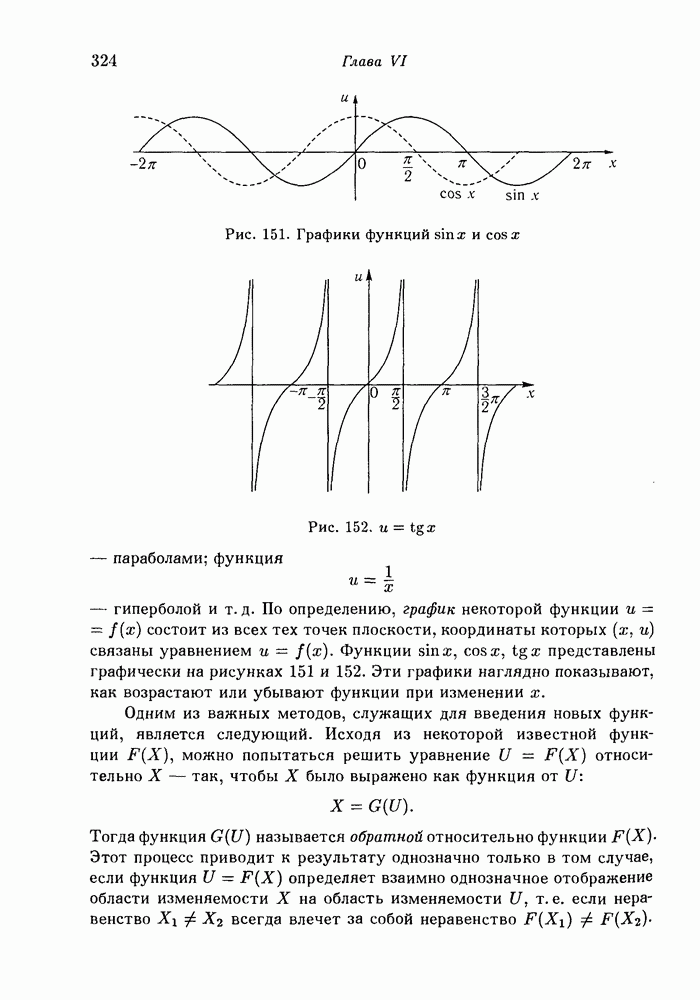
- 3. График функции. Обратные функции.
- 4. Сложные функции.
- 5. Непрерывность.
- 6. Функции нескольких переменных.
- 7. Функции и преобразования.
- § 2. Пределы
- 2. Монотонные последовательности.
- 3. Число Эйлера e.
- 4. Число «пи»
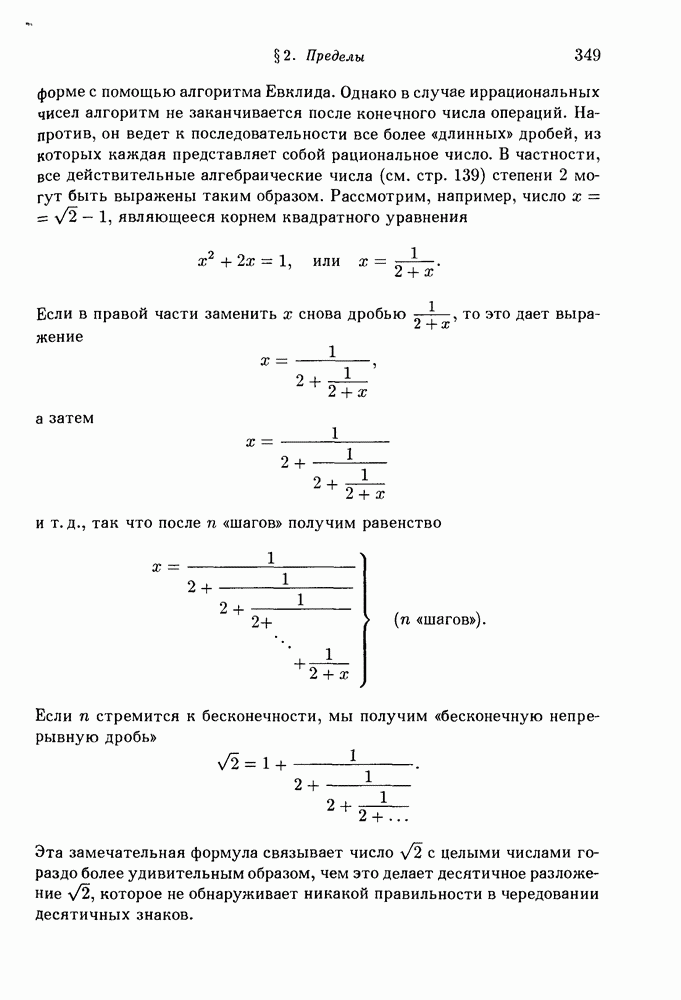
- 5. Непрерывные дроби.
- § 3. Пределы при непрерывном приближении
- 2. Замечания по поводу понятия предела
- 3. Предел sin x/x
- 4. Пределы при х -> оо.
- § 4. Точное определение непрерывности
- § 5. Две основные теоремы о непрерывных функциях
- 2. Доказательство теоремы Больцано.
- 3. Теорема Вейерштрасса об экстремальных значениях.
- 4. Теорема о последовательностях. Компактные множества.
- § 6. Некоторые применения теоремы Больцано
- 2. Применение к одной механической проблеме.
- Дополнение к главе VI. Дальнейшие примеры на пределы и непрерывность
- 4. Разрывные функции как предел непрерывных.
- 5. Пределы при итерации.
- § 2. Пример, относящийся к непрерывности
- Глава VII. Максимумы и минимумы
- § 1. Задачи из области элементарной геометрии
- 2. Теорема Герона. Экстремальное свойство световых лучей.
- 3. Применения к задачам о треугольниках.
- 4. Свойства касательных к эллипсу и гиперболе. Соответствующие экстремальные свойства.
- 5. Экстремальные расстояния точки от данной кривой.
- § 2. Общий принцип, которому подчинены экстремальные задачи
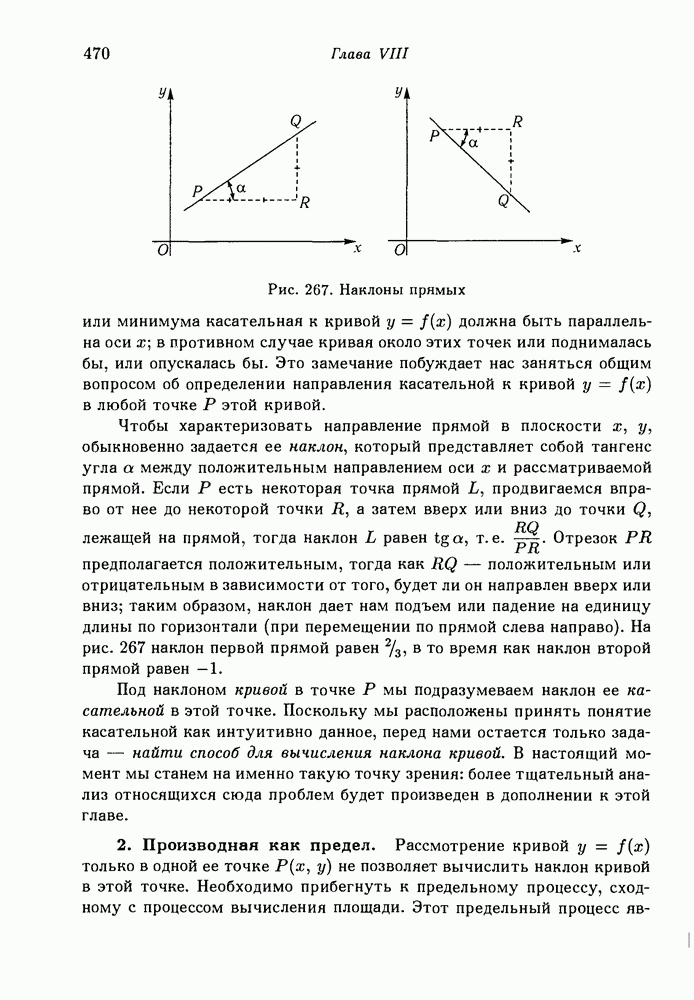
- § 3. Стационарные точки и дифференциальное исчисление
- 2. Максимумы и минимумы функций нескольких переменных. Седловые точки.
- 3. Точки минимакса и топология.
- 4. Расстояние точки от поверхности.
- § 4. Треугольник Шварца
- 4. Треугольники, образованные световыми лучами.
- 5. Замечания, касающиеся задач на отражение и эргодическое движение.
- § 5. Проблема Штейнера
- 2. Анализ возникающих альтернатив.
- 3. Дополнительная проблема.
- 4. Замечания и упражнения.
- 5. Обобщение: проблема уличной сети.
- § 6. Экстремумы и неравенства
- 1. Средние арифметическое и геометрическое двух положительных величин.
- 2. Обобщение на случай n переменных.
- 3. Метод наименьших квадратов.
- § 7. Существование экстремума. Принцип Дирихле
- 3. Экстремальные проблемы элементарного содержания.
- 4. Трудности, возникающие в более сложных случаях.
- § 8. Изопериметрическая проблема
- § 9. Экстремальные проблемы с граничными условиями. Связь между проблемой Штейнера и изопериметрической проблемой
- § 10. Вариационное исчисление
- 2. Вариационное исчисление. Принцип Ферма в оптике.
- 3. Решение задачи о брахистохроне, принадлежащее Якобу Бернулли.
- 4. Геодезические линии на сфере. Минимаксы.
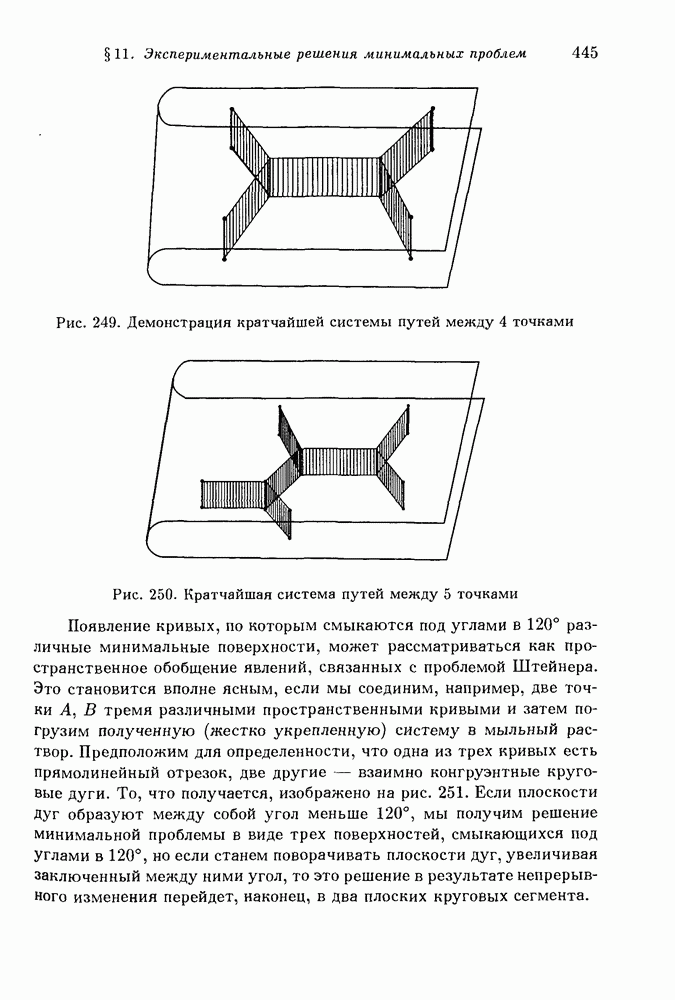
- § 11. Экспериментальные решения минимальных проблем. Опыты с мыльными пленками
- 2. Опыты с мыльными пленками.
- 3. Новые опыты, относящиеся к проблеме Плато.
- 4. Экспериментальные решения других математических проблем.
- Глава VIII. Математический анализ
- § 1. Интеграл
- 2. Интеграл.
- 3. Общие замечания о понятии интеграла. Общее определение.
- 4. Примеры интегрирования. Интегрирование x^r.
- 5. Правила «интегрального исчисления».
- § 2. Производная
- 2. Производная как предел.
- 3. Примеры.
- 4. Производные от тригонометрических функций.
- 5. Дифференцируемость и непрерывность.
- 6. Производная и скорость. Вторая производная и ускорение.
- 7. Геометрический смысл второй производной.
- 8. Максимумы и минимумы.
- § 3. Техника дифференцирования
- § 4. Обозначения Лейбница и «бесконечно малые»
- § 5. Основная теорема анализа
- 2. Первые применения. Интегрирование функций x^r, cosx, sinx. Функция arctgx
- 3. Формула Лейбница для «пи»
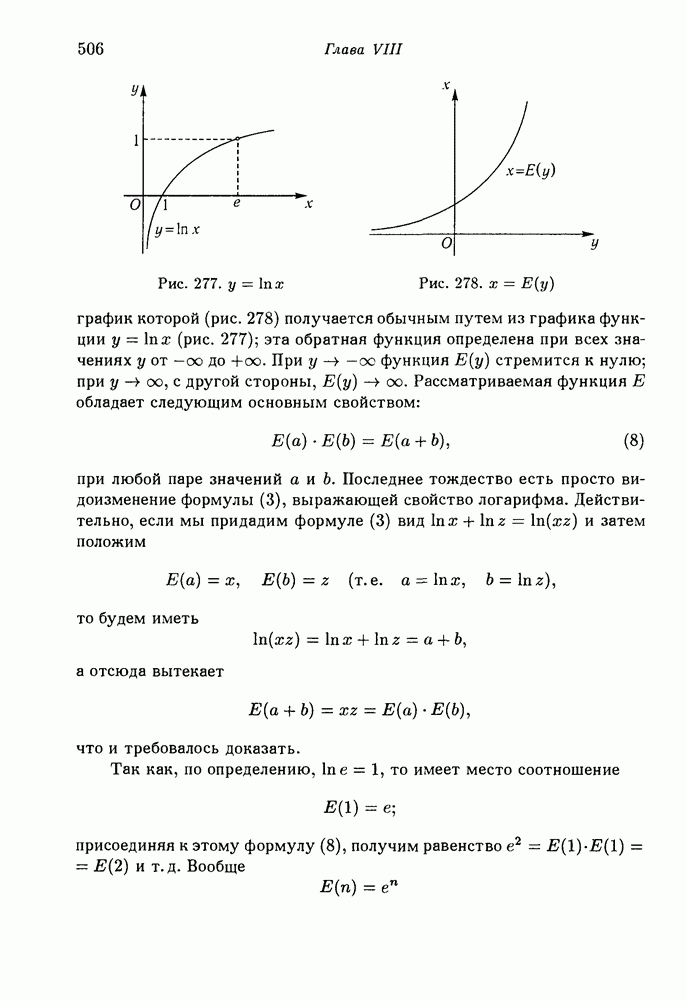
- § 6. Показательная (экспоненциальная) функция и логарифм
- 2. Показательная (экспоненциальная) функция.
- 3. Формулы дифференцирования функций е^х, а^х, x^s.
- 4. Явные выражения числа е^x и функций lnx в виде пределов.
- 5. Бесконечный ряд для логарифма. Вычисление логарифмов.
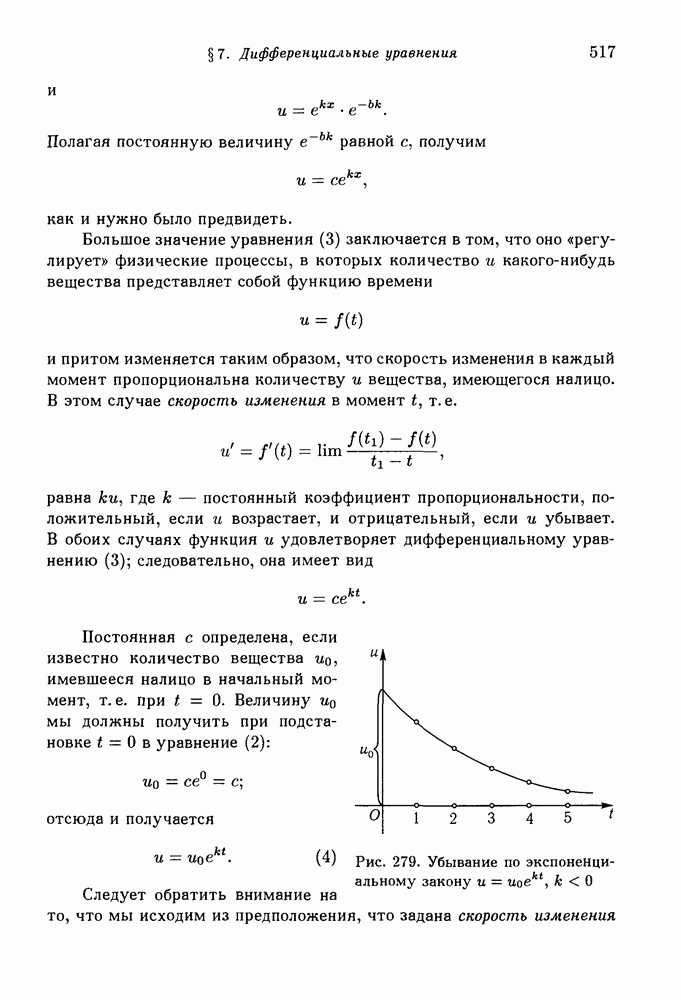
- § 7. Дифференциальные уравнения
- 2. Дифференциальное уравнение экспоненциальной функции. Радиоактивный распад. Закон роста. Сложные проценты.
- 3. Другие примеры. Простейшие колебания.
- 4. Закон движения Ньютона.
- Дополнение к главе VIII
- § 1. Вопросы принципиального порядка
- 3. Другие приложения понятия интеграла. Работа. Длина кривой.
- § 2. Порядки возрастания
- 2. Порядок возрастания ln(n!)
- § 3. Бесконечные ряды и бесконечные произведения
- 2. Формула Эйлера cos x + i sin x = exp(ix).
- 3. Гармонический ряд и дзета-функция. Формула Эйлера, выражающая sin x в виде бесконечного произведения.
- § 4. Доказательство теоремы о простых числах на основе статистического метода
- Приложение. Дополнительные замечания, задачи и упражнения
- Аналитическая геометрия
- Геометрические построения
- Проективная и неевклидова геометрия
- Топология
- Функции, пределы, непрерывность
- Максимумы и минимумы
- Дифференциальное и интегральное исчисления
- Техника интегрирования
- Рекомендуемая литература