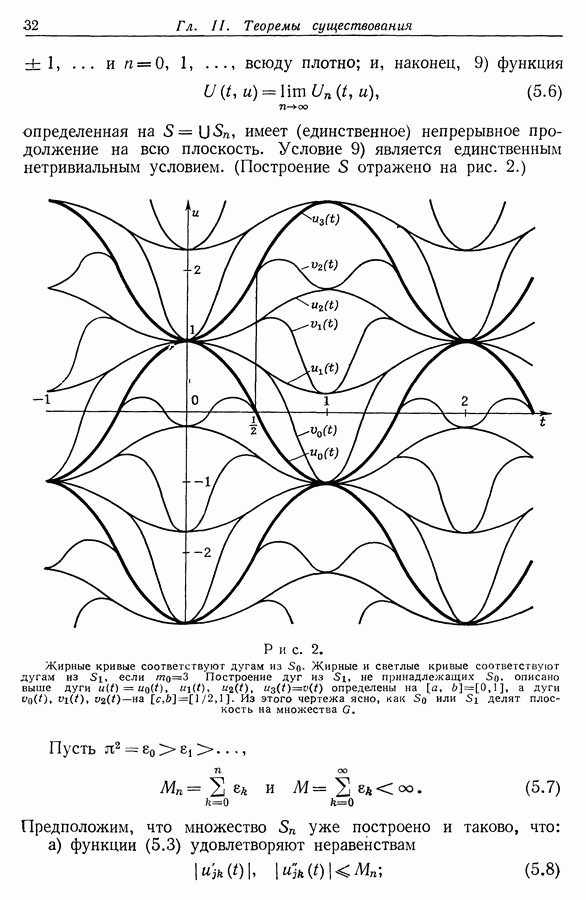
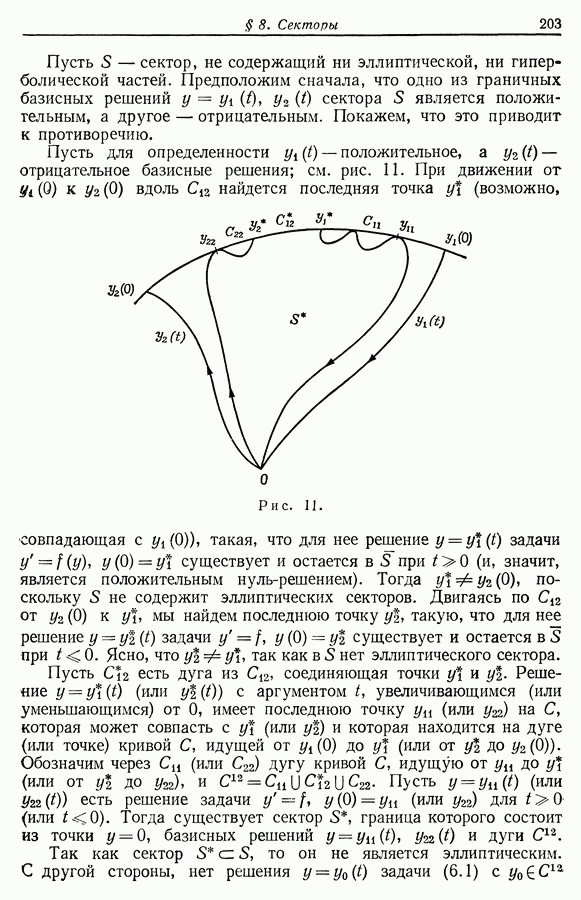
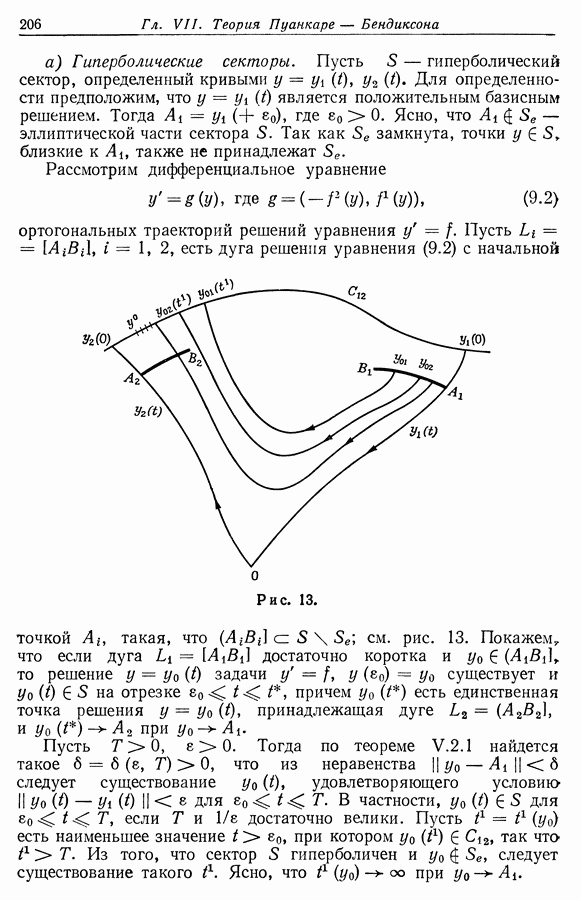
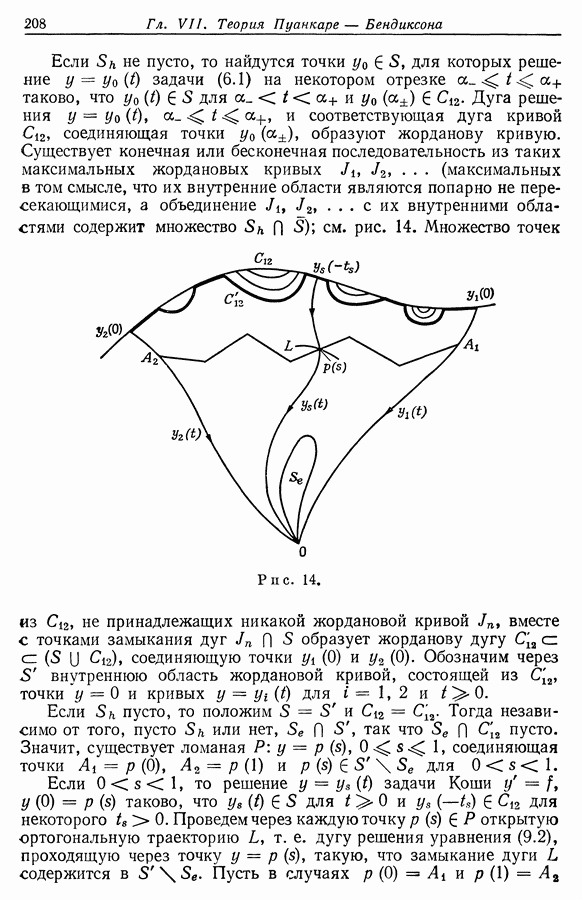
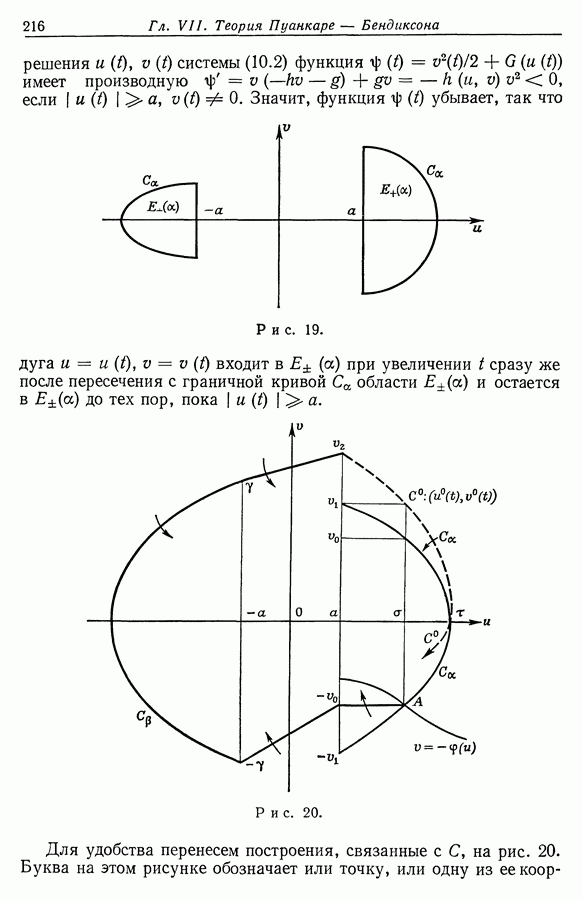
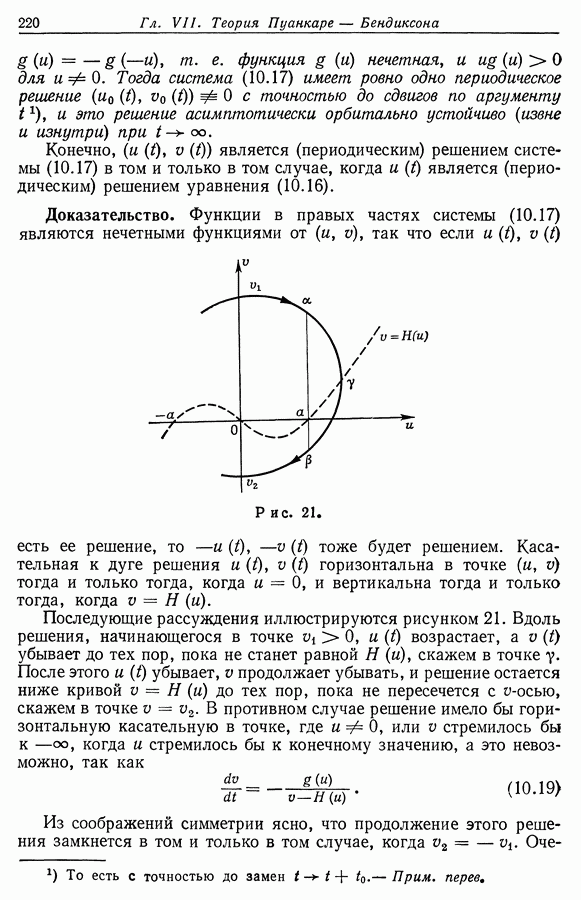
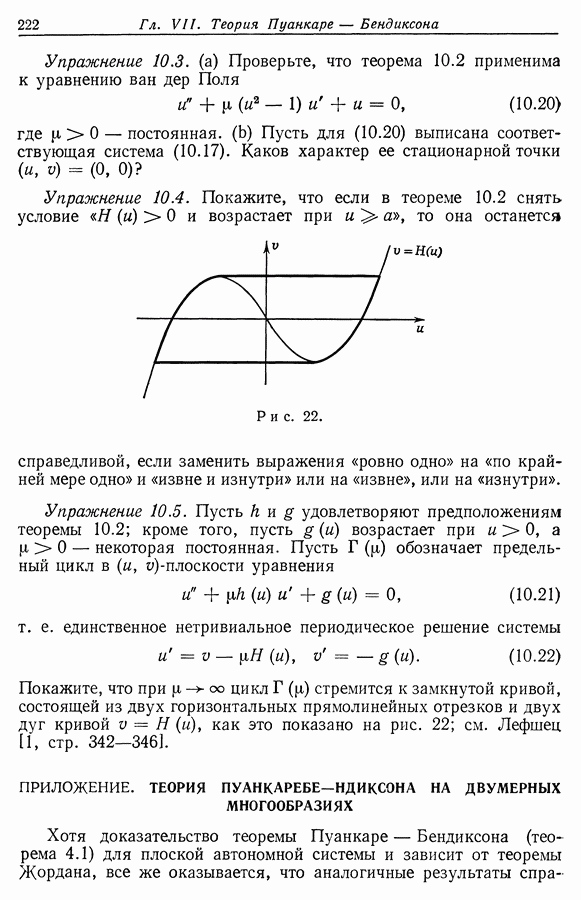
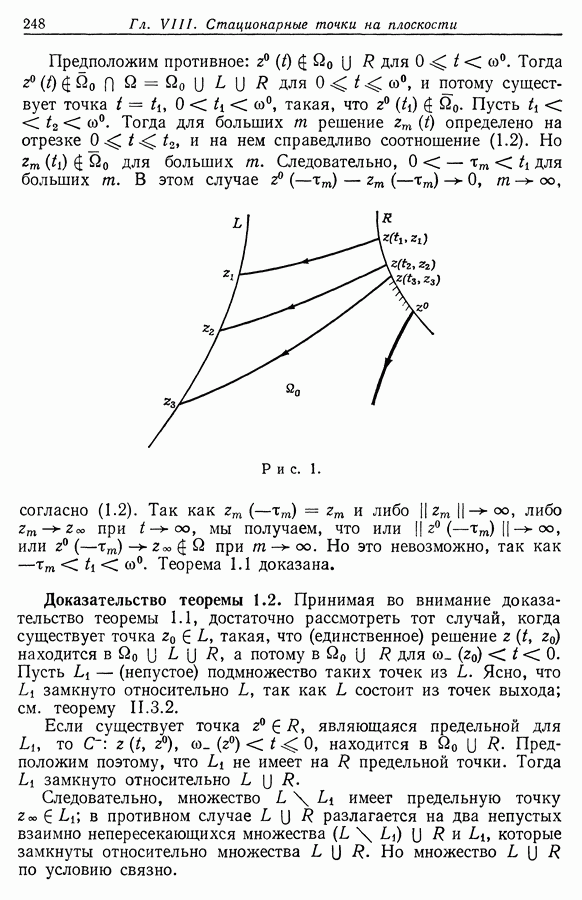
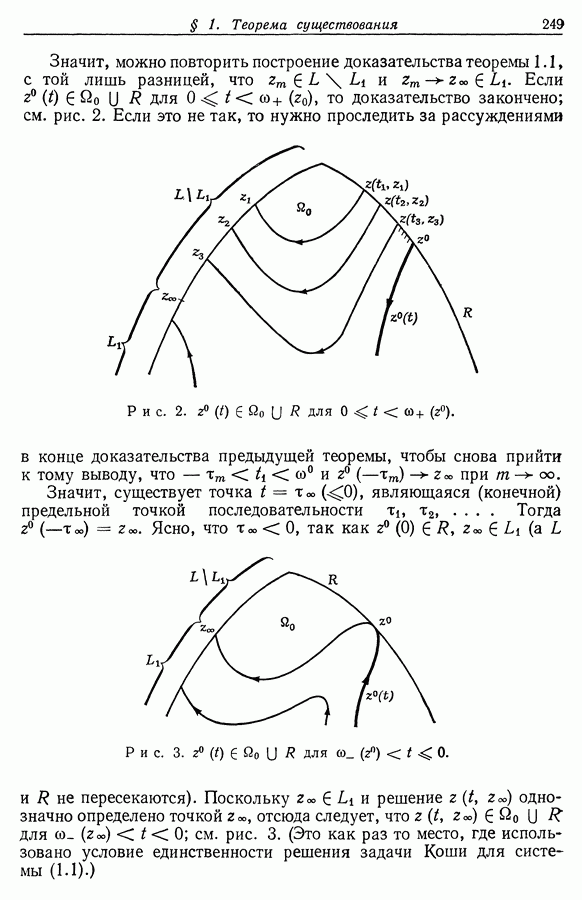
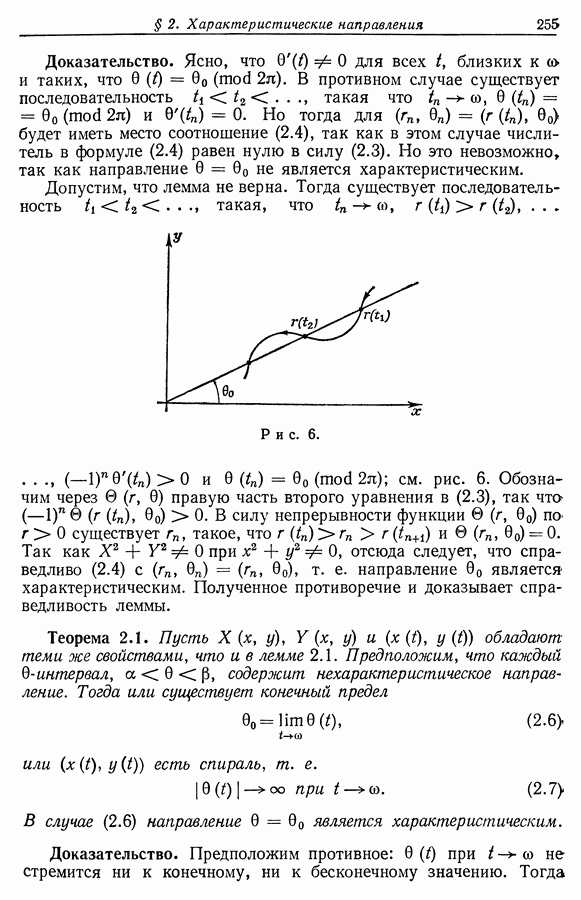
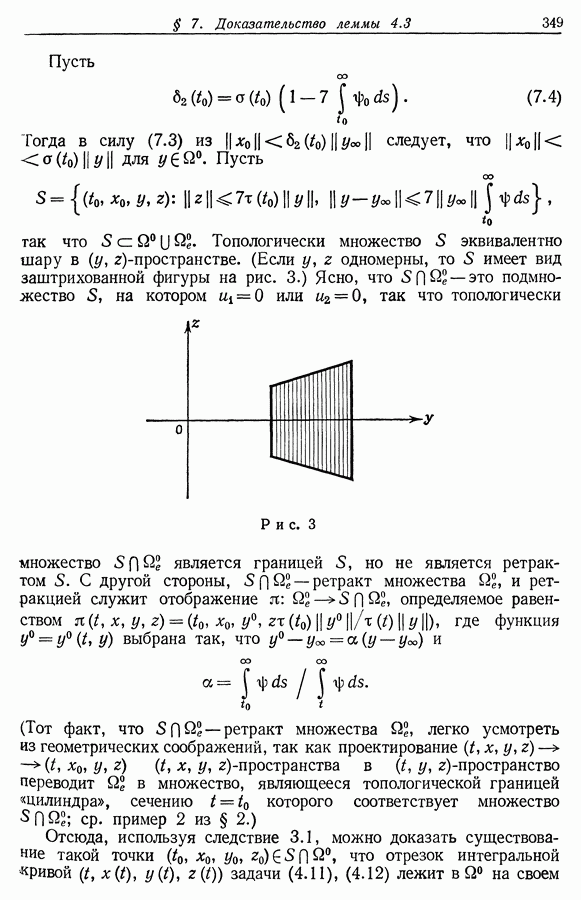
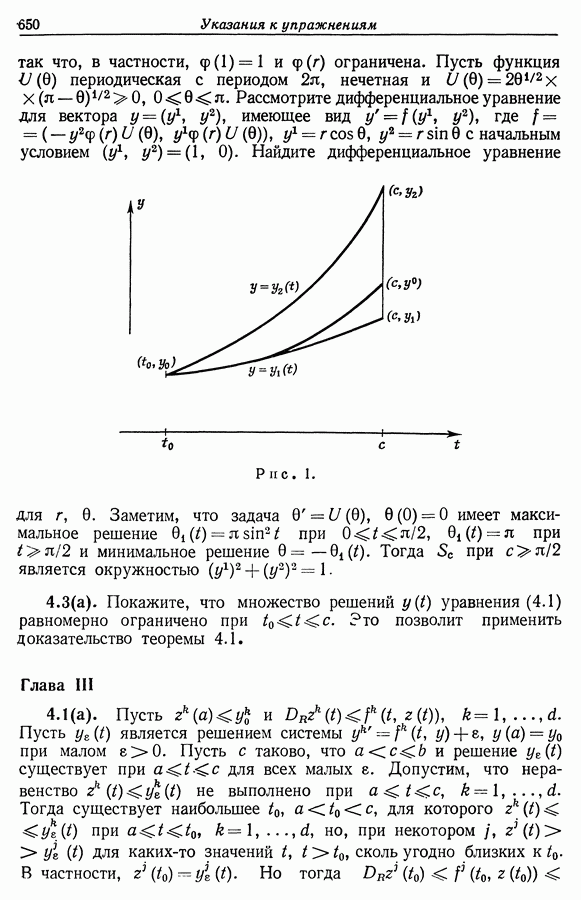
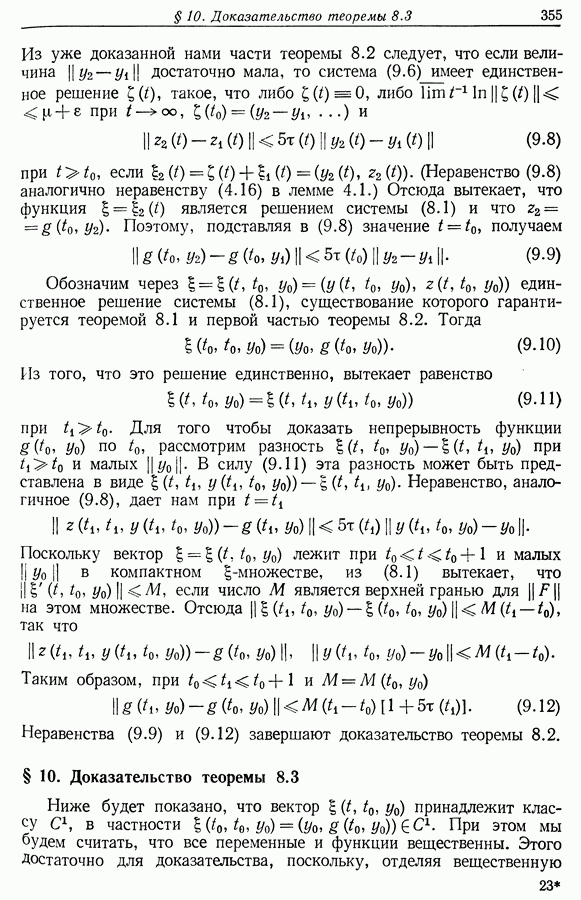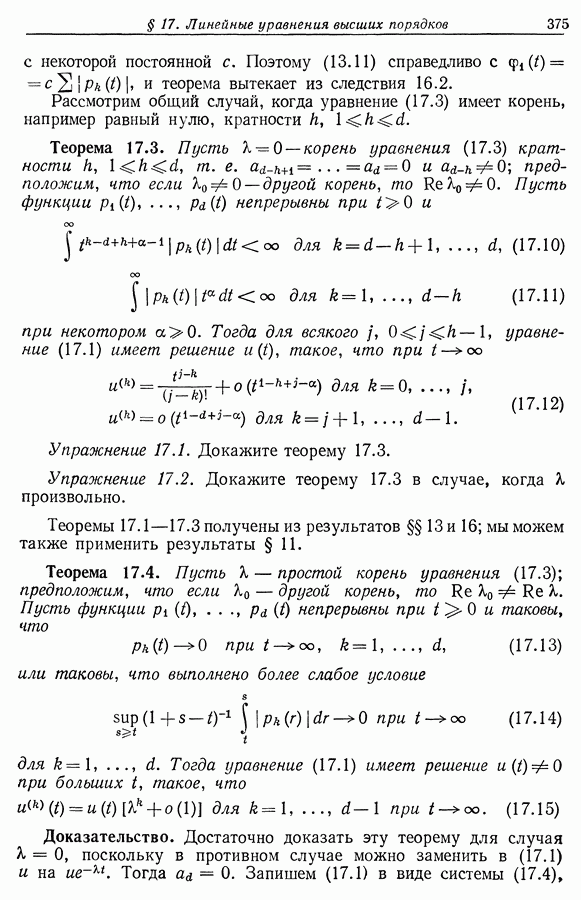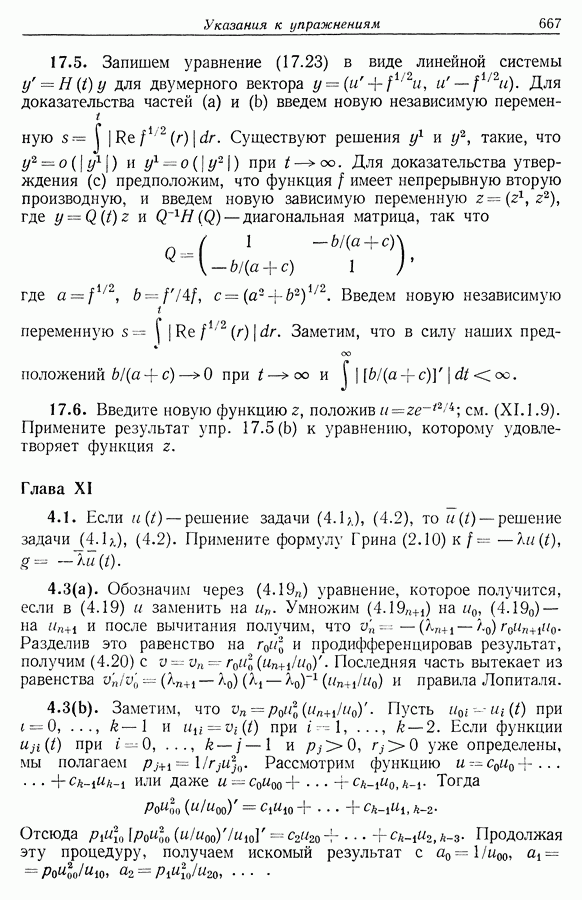| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Априорные оценки
Доказательства теорем существования решений граничных задач в последнем параграфе зависели от нахождения верхних границ решения и его производных. В этом параграфе мы рассмотрим более подробно вопрос об априорных оценках и их применениях. Основная задача, которую мы будем рассматривать, такова: заданы  -мерная вектор-функция
-мерная вектор-функция  принадлежащая на некотором отрезке
принадлежащая на некотором отрезке  классу
классу  граница для
граница для  и некоторая мажоранта для
и некоторая мажоранта для  требуется оценить
требуется оценить  Для случая вещественных
Для случая вещественных  верен следующий результат.
верен следующий результат.
Лемма 5.1. Пусть  где
где  есть положительная непрерывная функция, удовлетворяющая условию
есть положительная непрерывная функция, удовлетворяющая условию

Пусть  Тогда существует число
Тогда существует число  (зависящее только от
(зависящее только от  и
и  такое, что если
такое, что если  -вещественная функция класса
-вещественная функция класса  на
на  где
где  удовлетворяющая условиям
удовлетворяющая условиям

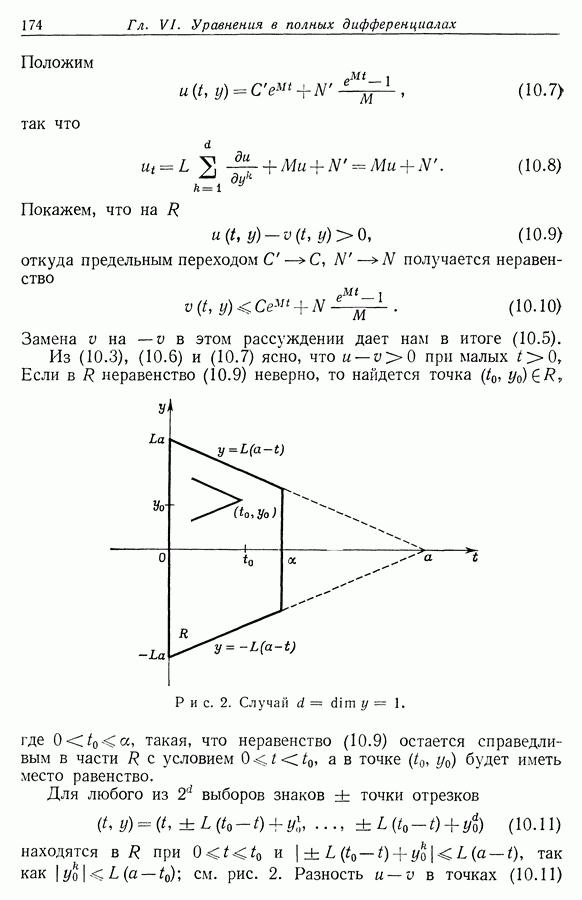
Доказательство. В силу (5.1) существует такое число  что
что

Покажем, что это число  и обладает требуемым свойством. (Поэтому вместо (5.1) достаточно было бы предположить, что существует
и обладает требуемым свойством. (Поэтому вместо (5.1) достаточно было бы предположить, что существует  удовлетворяющее
удовлетворяющее 
Пусть  достигает своего максимума в точке
достигает своего максимума в точке  Мы можем считать, что
Мы можем считать, что  в противном случае
в противном случае  можно заменить на
можно заменить на  Если
Если  то существует некоторая точка
то существует некоторая точка  где
где  В противном случае мы имели бы
В противном случае мы имели бы  что противоречит неравенству
что противоречит неравенству  Предположим, что
Предположим, что  и пусть
и пусть  есть ближайшая к
есть ближайшая к  точка, где
точка, где  Пусть для определенности
Пусть для определенности  Тогда
Тогда  для
для 
Если второе неравенство в (5.2) умножить на  то интегрирование по
то интегрирование по  дает
дает

Даже если не предполагать, что  то в левой части этого неравенства все же возможна формальная замена переменной
то в левой части этого неравенства все же возможна формальная замена переменной  после которой мы получаем, что
после которой мы получаем, что

см. лемму 1.4.1. Из (5.3) видно, что  Значит, или
Значит, или  или
или  В любом случае
В любом случае  Так как
Так как  для
для  то лемма тем самым доказана.
то лемма тем самым доказана.
Лемма 5.1 неверна, если  есть
есть  -мерный вектор,
-мерный вектор,  а абсолютные величины в (5.2) заменены нормами. Чтобы в этом убедиться, заметим, что функция
а абсолютные величины в (5.2) заменены нормами. Чтобы в этом убедиться, заметим, что функция  где
где  — постоянные, удовлетворяет условиям леммы 5.1. Пусть
— постоянные, удовлетворяет условиям леммы 5.1. Пусть  обозначает двумерный вектор
обозначает двумерный вектор  Тогда
Тогда  Значит, при
Значит, при  выполнены неравенства, аналогичные (5.2):
выполнены неравенства, аналогичные (5.2):

но такого числа  что
что  при любом
при любом  не существует.
не существует.
Основной результат, относящийся к вектор-функциям, содержится в следующей лемме:
Лемма 5.2. Пусть  где
где  есть положительная непрерывная функция, удовлетворяющая (5.1). Пусть
есть положительная непрерывная функция, удовлетворяющая (5.1). Пусть  неотрицательные постоянные. Тогда существует постоянная
неотрицательные постоянные. Тогда существует постоянная  (зависящая только от
(зависящая только от  и К), обладающая следующим свойством: если
и К), обладающая следующим свойством: если  есть вектор-функция класса
есть вектор-функция класса  на
на  где
где  удовлетворяющая (5.4), и
удовлетворяющая (5.4), и

то 
Доказательство. Покажем сначала, что из одних только неравенств (5.5) можно вывести существование оценки для  на любом отрезке
на любом отрезке  Пусть
Пусть  ; тогда
; тогда

 согласно (5.5), имеем
согласно (5.5), имеем

Это неравенство и аналог равенства (5.6), в котором  заменено на
заменено на  дают
дают

отсюда

Аналогично для  соотношение
соотношение

приводит к неравенству

Функция  определенная соотношениями
определенная соотношениями

является непрерывной и невозрастающей функцией от  (это можно проверить вычислением производной
(это можно проверить вычислением производной  Если
Если  то, полагая
то, полагая  в (5.7), находим, что
в (5.7), находим, что

Если  то мы получаем (5.10) при
то мы получаем (5.10) при  Аналогично из (5.8) следует, что
Аналогично из (5.8) следует, что

Складывая (5.10) и (5.11) при  получаем
получаем

Из предположений (5.4) и (5.10), (5.11) вытекает, что

где знак  берется в соответствии с тем, будет ли
берется в соответствии с тем, будет ли  или 2. Пусть функция
или 2. Пусть функция  определена равенством
определена равенством

Тогда по лемме 1.4.1

где интеграл берется по  -интервалу с концевыми точками
-интервалу с концевыми точками  В силу (5.13) подинтегральное выражение мажорируется функцией
В силу (5.13) подинтегральное выражение мажорируется функцией

Отсюда

Поскольку функция  возрастает, из (5.12) получаем оценку
возрастает, из (5.12) получаем оценку  где
где

а  - функция, обратная к
- функция, обратная к  Если
Если  то точка
то точка  содержится в интервале длины
содержится в интервале длины  из
из  Только что проведенные рассуждения показывают, что
Только что проведенные рассуждения показывают, что  может быть заменено на
может быть заменено на  и лемма доказана с
и лемма доказана с  в качестве допустимого выбора
в качестве допустимого выбора 
Упражнение 5.1. Покажите, что справедлив аналог леммы 5.2, в котором условие (5.5) заменено неравенствами

где  вещественная функция класса
вещественная функция класса  на
на  такая, что
такая, что  В этом случае
В этом случае  зависит только от
зависит только от 
Если в лемме 5.1 положить  то мы получим такое
то мы получим такое
Следствие 5.1. Пусть  неотрицательные постоянные. Тогда существует такая постоянная
неотрицательные постоянные. Тогда существует такая постоянная  (зависящая только от
(зависящая только от  что если функция
что если функция  принадлежит классу
принадлежит классу  на
на  удовлетворяет
удовлетворяет 

Замечание 1. Если  в (5.16) удовлетворяет условию
в (5.16) удовлетворяет условию  то выполнено неравенство (5.5) с
то выполнено неравенство (5.5) с

Значит, в следствии. 1 предположение (5.5) при  излишне (но пример, предшествующий лемме 5.2, показывает, что при
излишне (но пример, предшествующий лемме 5.2, показывает, что при  условие (5.5) отбросить нельзя). Далее, если для а в (5.5) имеет место неравенство
условие (5.5) отбросить нельзя). Далее, если для а в (5.5) имеет место неравенство  то выполняется (5.16) с
то выполняется (5.16) с

так что в этом случае условие (5.16) излишне. Но даже если  (так что
(так что  вещественная функция), то условие (5.16) при
вещественная функция), то условие (5.16) при  не может быть отброшено.
не может быть отброшено.
Для проверки первой части замечания 1 отметим, что

Отсюда и из (5.16) видно, что  Повторное применение неравенства (5.16) дает соотношение
Повторное применение неравенства (5.16) дает соотношение

а это есть не что иное, как (5.5) при  и К из (5.17). Доказательство той части замечания, которая относится к (5.18), проводится аналогично.
и К из (5.17). Доказательство той части замечания, которая относится к (5.18), проводится аналогично.
Упражнение 5.2. Покажите, что если  то условие (5.5) из следствия 5.1 не может быть отброшено.
то условие (5.5) из следствия 5.1 не может быть отброшено.
В последующем нам пригодится следующий простой факт:
Лемма 5.3. Пусть  функция, непрерывная на множестве
функция, непрерывная на множестве

и пусть  обладает одним (или несколькими) из следующих свойств:
обладает одним (или несколькими) из следующих свойств:

Пусть  Тогда существует непрерывная ограниченная функция
Тогда существует непрерывная ограниченная функция  определенная при
определенная при  и произвольных
и произвольных  удовлетворяющая условию
удовлетворяющая условию

и обладающая соответствующими свойствами из следующей их совокупности:

Доказательство. Искомую функцию  мы можем получить следующим образом. Пусть
мы можем получить следующим образом. Пусть  где
где  есть вещественная непрерывная функция, определенная следующим образом:
есть вещественная непрерывная функция, определенная следующим образом:  когда
когда 
соответственно. Положим

На  имеем тождество
имеем тождество

из которого ясно, что  обладает там требуемыми свойствами. Далее, из справедливости любого из соотношений (5.21) — (5.24) для
обладает там требуемыми свойствами. Далее, из справедливости любого из соотношений (5.21) — (5.24) для  вытекает его справедливость и для
вытекает его справедливость и для  Лемма доказана.
Лемма доказана.
Заметим, что из неравенств типа (5.23), (5.24) следует, что решения уравнения

удовлетворяют соответственно условиям (5.4), (5.5); см. (5.19).
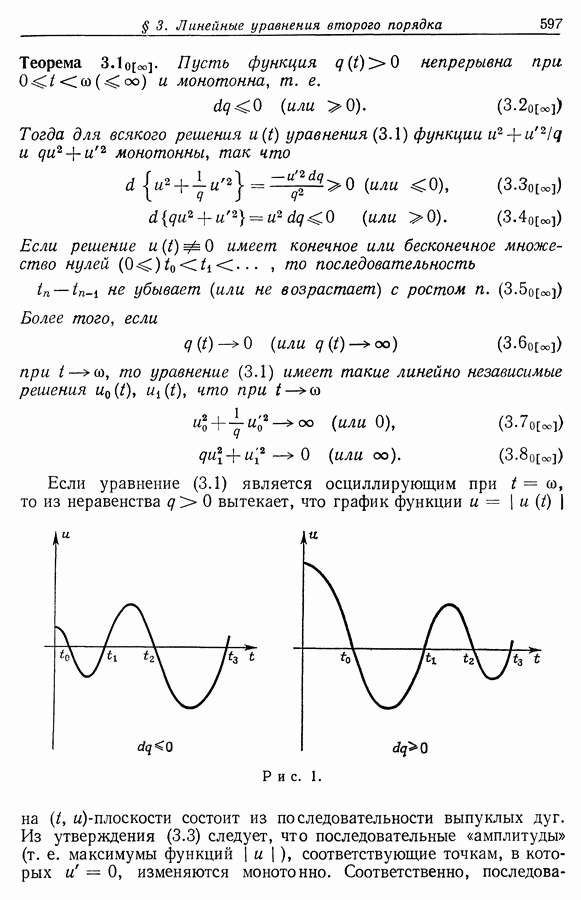
Теорема 5.1. Пусть функция  непрерывна на множестве
непрерывна на множестве  определенном в (5.20), и удовлетворяет неравенствам
определенном в (5.20), и удовлетворяет неравенствам

(5.24) и (5.23), где  положительная непрерывная функция, удовлетворяющая (5.1). Пусть
положительная непрерывная функция, удовлетворяющая (5.1). Пусть  Тогда уравнение (5.26) имеет по крайней мере одно решение, удовлетворяющее условиям
Тогда уравнение (5.26) имеет по крайней мере одно решение, удовлетворяющее условиям 
Из доказательства будет ясно, что условие (5.23) при  может быть отброшено. Далее, если
может быть отброшено. Далее, если

где  — неотрицательные постоянные и
— неотрицательные постоянные и  то могут быть отброшены оба условия (5.23) и (5.24).
то могут быть отброшены оба условия (5.23) и (5.24).
Если  числовая функция
числовая функция  -мерный вектор), то вместо леммы 5.2 в доказательстве можно использовать лемму 5.1. Это приводит к такому результату:
-мерный вектор), то вместо леммы 5.2 в доказательстве можно использовать лемму 5.1. Это приводит к такому результату:
Следствие 5.2. Пусть  вещественная переменная и
вещественная переменная и  вещественная функция из теоремы 5.1. Тогда утверждение теоремы 5.1 будет справедливым, если условие (5.24) отсутствует.
вещественная функция из теоремы 5.1. Тогда утверждение теоремы 5.1 будет справедливым, если условие (5.24) отсутствует.
Заметим, что в этом случае условие (5.27) принимает простой вид:  для
для 
Доказательство теоремы 5.1. Доказательство сначала будет проводиться для случая, когда  удовлетворяет не (5.27), а неравенству (5.22). Пусть
удовлетворяет не (5.27), а неравенству (5.22). Пусть  есть постоянная, существование которой гарантируется леммой 5.2 (при
есть постоянная, существование которой гарантируется леммой 5.2 (при  Пусть
Пусть  непрерывная ограниченная функция для
непрерывная ограниченная функция для  и
и
произвольных  удовлетворяющая неравенствам (5.25), (5.22), (5.23) и (5.24). По теореме 4.2 граничная задача
удовлетворяющая неравенствам (5.25), (5.22), (5.23) и (5.24). По теореме 4.2 граничная задача

имеет решение  Условие (5.22) означает, что
Условие (5.22) означает, что  удовлетворяет неравенству
удовлетворяет неравенству  при
при  см. (5.19). Значит,
см. (5.19). Значит,  ни в одной точке
ни в одной точке  где
где  не достигает максимума. Так как
не достигает максимума. Так как  то
то  удовлетворяют условиям
удовлетворяют условиям  и потому
и потому  для
для  Используя неравенства (5.23) и (5.24) и равенство
Используя неравенства (5.23) и (5.24) и равенство  получаем, что к
получаем, что к  применима лемма 5.2 и потому
применима лемма 5.2 и потому  для
для 
Соответственно из (5.25) видно, что  есть решение уравнения
есть решение уравнения  Тем самым теорема 5.1 доказана для того случая, когда условие (5.27) усилено до (5.22). Чтобы устранить это ограничение, заметим, что при
Тем самым теорема 5.1 доказана для того случая, когда условие (5.27) усилено до (5.22). Чтобы устранить это ограничение, заметим, что при  функция
функция  удовлетворяет условиям теоремы 5.1 так же, как и условию (5.22), если
удовлетворяет условиям теоремы 5.1 так же, как и условию (5.22), если  в (5.23) и (5.24) заменены соответственно на
в (5.23) и (5.24) заменены соответственно на  . Значит, уравнение
. Значит, уравнение

имеет решение  удовлетворяющее заданным выше граничным условиям. Ясно, что
удовлетворяющее заданным выше граничным условиям. Ясно, что  и существует постоянная
и существует постоянная  зависящая от
зависящая от  такая, что
такая, что  Следовательно, если
Следовательно, если  для
для  то
то  II Значит, семейство функций
II Значит, семейство функций  на
на  равномерно ограничено и равностепенно непрерывно. Тогда по теореме Арцела существует последовательность
равномерно ограничено и равностепенно непрерывно. Тогда по теореме Арцела существует последовательность  такая, что
такая, что  при
при  существует и является решением уравнения (5.26), удовлетворяющим условиям
существует и является решением уравнения (5.26), удовлетворяющим условиям  Теорема 5.1 доказана.
Теорема 5.1 доказана.
Упражнение 5.3. Покажите, что если в теореме 5.1 условие (5.27) усилено следующим образом:

то уравнение (5.26) имеет решение  удовлетворяющее граничным условиям
удовлетворяющее граничным условиям  и
и

Упражнение 5.4. Пусть и — вещественная переменная. Пусть  — вещественная функция, непрерывная для
— вещественная функция, непрерывная для  и всех
и всех  и удовлетворяющая следующим условиям: i) при фиксированных
и удовлетворяющая следующим условиям: i) при фиксированных  функция
функция  не убывает по
не убывает по  где
где  положительная непрерывная неубывающая для
положительная непрерывная неубывающая для  функция, удовлетворяющая (5.1); iii) уравнение
функция, удовлетворяющая (5.1); iii) уравнение 
 имеет по крайней мере одно решение
имеет по крайней мере одно решение  которое существует на
которое существует на  (например, выполнены условия
(например, выполнены условия  если
если  с постоянными
с постоянными  Пусть
Пусть  произвольные числа. Тогда уравнение
произвольные числа. Тогда уравнение  имеет по крайней мере одно решение, удовлетворяющее условиям и
имеет по крайней мере одно решение, удовлетворяющее условиям и  относящейся сюда теореме единственности см. упр. 4.5(c)).
относящейся сюда теореме единственности см. упр. 4.5(c)).
Теорема 5.2. Пусть функция  непрерывна в
непрерывна в

Пусть  для каждого
для каждого  удовлетворяет на
удовлетворяет на  условиям теоремы 5.1, где
условиям теоремы 5.1, где  постоянные а, К в (5.23), (5.24) могут зависеть от
постоянные а, К в (5.23), (5.24) могут зависеть от  Пусть Тогда уравнение (5.26) имеет решение
Пусть Тогда уравнение (5.26) имеет решение  которое существует при
которое существует при  и удовлетворяет условию
и удовлетворяет условию 
Упражнение  Докажите теорему
Докажите теорему  Покажите, что если в теореме 5.2 условие (5.27) усилено до (5.29), то решение
Покажите, что если в теореме 5.2 условие (5.27) усилено до (5.29), то решение  может быть выбрано так, что будет иметь место (5.30). (с) Далее, если (5.29) усилено до
может быть выбрано так, что будет иметь место (5.30). (с) Далее, если (5.29) усилено до  то
то  для
для  Покажите, что в случае, когда
Покажите, что в случае, когда  есть
есть  -мерный вектор (т. е. числовая функция), условие (5.29) в теореме 5.2 и частях
-мерный вектор (т. е. числовая функция), условие (5.29) в теореме 5.2 и частях  настоящего упражнения может быть отброшено.
настоящего упражнения может быть отброшено.
Упражнение 5.6. Пусть  непрерывна на множестве
непрерывна на множестве  из (5.31). Пусть для каждого
из (5.31). Пусть для каждого  и больших
и больших  существует непрерывная функция
существует непрерывная функция  такая, что
такая, что  для больших
для больших  произвольно. Пусть
произвольно. Пусть  решение уравнения (5.26) при больших
решение уравнения (5.26) при больших  Тогда
Тогда  при
при 
Упражнение 5.7. Пусть  непрерывна на множестве
непрерывна на множестве  (см. (5.31)) и имеет непрерывные частные производные по компонентам векторов
(см. (5.31)) и имеет непрерывные частные производные по компонентам векторов  пусть матрицы Якоби (4.23) удовлетворяют условию
пусть матрицы Якоби (4.23) удовлетворяют условию  см. (3.17). Пусть
см. (3.17). Пусть  Тогда уравнение (5.26) имеет самое большее одно решение, удовлетворяющее условиям
Тогда уравнение (5.26) имеет самое большее одно решение, удовлетворяющее условиям 
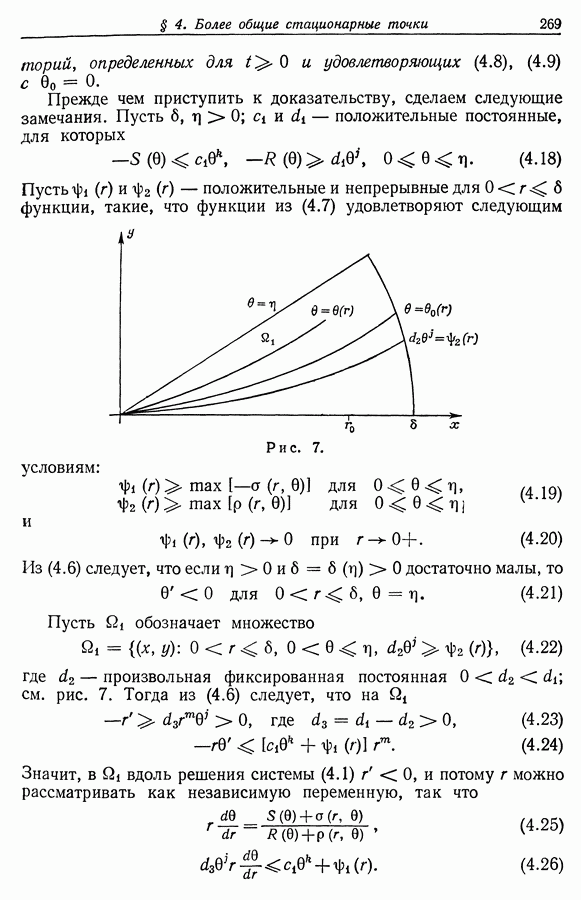
Замечание 2. Основное назначение предположений, связанных в теоремах 5.1, 5.2 с (5.23) и/или (5.24), состоит в том, чтобы выполнялось следующее условие:
Условие  Существует постоянная
Существует постоянная  обладающая тем свойством, что если
обладающая тем свойством, что если  есть решение уравнения
есть решение уравнения  для
для  удовлетворяющее условию
удовлетворяющее условию 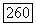
Упражнение 5.8. Покажите, что если (5.27) заменено на (5.22) и условия, включающие (5.23) и/или (5.24), заменены условием 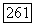 то теорема 5.1, следствие 5.2 и теорема 5.2 остаются справедливыми. (В случае теоремы 5.2, конечно, предполагается, что условие
то теорема 5.1, следствие 5.2 и теорема 5.2 остаются справедливыми. (В случае теоремы 5.2, конечно, предполагается, что условие 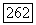 имеет место для всех больших
имеет место для всех больших 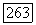
Упражнение 5.9. Пусть 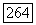 непрерывна на множестве
непрерывна на множестве 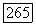 из (5.31) и удовлетворяет условию
из (5.31) и удовлетворяет условию 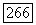 для всех
для всех 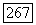 Предположим, что для каждого
Предположим, что для каждого 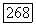 из
из 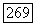 уравнение (5.26) имеет ровно одно решение
уравнение (5.26) имеет ровно одно решение 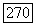 существующее при и удовлетворяющее условию
существующее при и удовлетворяющее условию 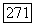 (см., например, теорему 5.2 и упр. 5.7). (а) Покажите, что
(см., например, теорему 5.2 и упр. 5.7). (а) Покажите, что 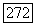 непрерывно зависит от
непрерывно зависит от 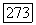 для
для 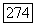 Предположим, кроме того, что
Предположим, кроме того, что 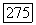 при фиксированных
при фиксированных 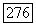 периодична по
периодична по 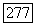 с периодом
с периодом 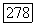 Тогда (5.26) имеет по крайней мере одно решение
Тогда (5.26) имеет по крайней мере одно решение 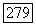 с периодом
с периодом 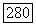
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- Глава I. Предварительные сведения
- § 2. Основные теоремы
- § 3. Гладкие аппроксимации
- § 4. Замена переменных в интегралах
- Глава II. Теоремы существования
- § 1. Теорема Пикара — Линделёфа
- § 2. Теорема Пеано
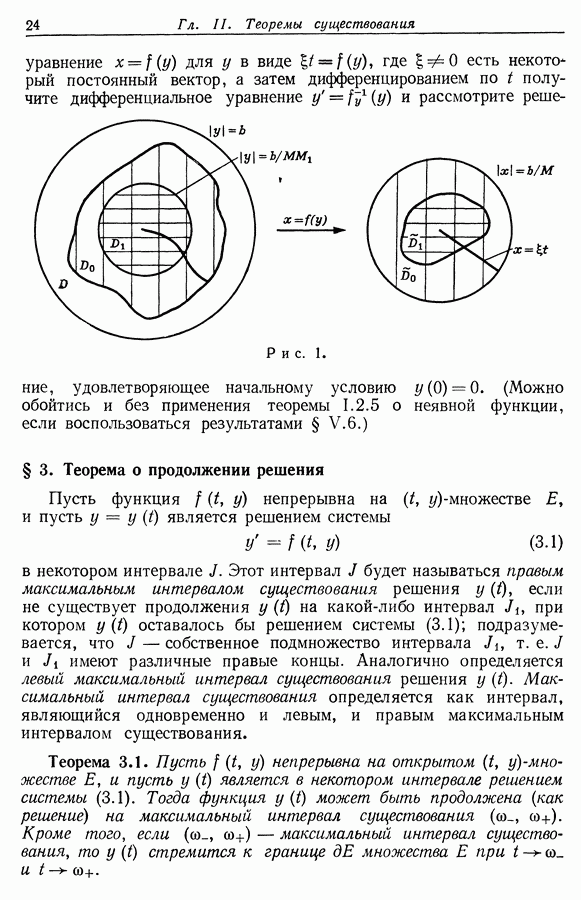
- § 3. Теорема о продолжении решения
- § 4. Теорема Кнезера
- § 5. Пример неединственности
- Глава III. Дифференциальные неравенства и единственность
- § 1. Неравенство Гронуолла
- § 2. Максимальные и минимальные решения
- § 3. Правые производные
- § 4. Дифференциальные неравенства
- § 5. Теорема Уинтнера
- § 6. Теоремы единственности
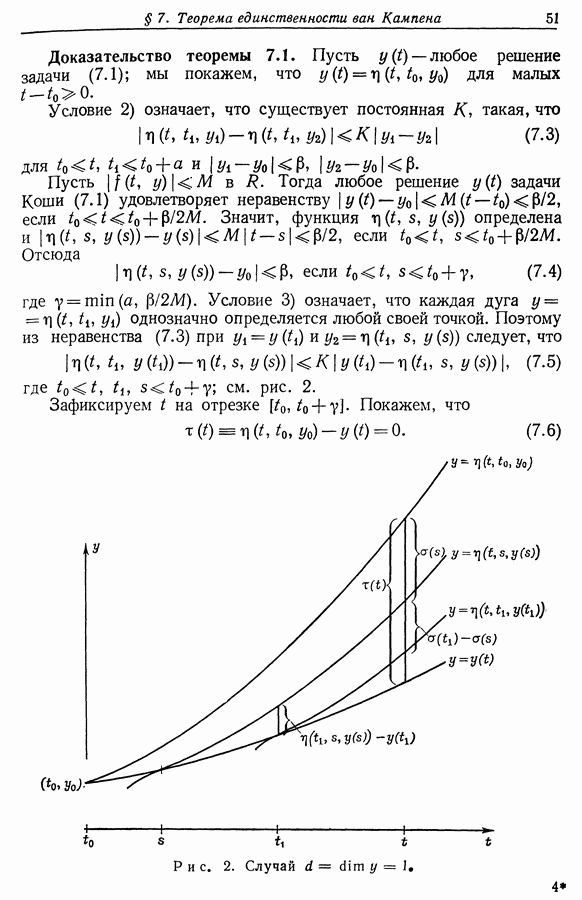
- § 7. Теорема единственности ван Кампена
- § 8. Точки выхода и функции Ляпунова
- § 9. Последовательные приближения
- Глава IV. Линейные дифференциальные уравнения
- § 2. Вариация постоянных
- § 3. Редукция к системам меньшего, порядка
- § 4. Основные неравенства
- § 5. Системы с постоянными коэффициентами
- § 6. Теория Флоке
- § 7. Сопряженные системы
- § 8. Линейные уравнения высших порядков
- § 9. Замечания о замене переменных
- ДОБАВЛЕНИЕ. ЛИНЕЙНЫЕ АНАЛИТИЧЕСКИЕ УРАВНЕНИЯ
- § 10. Фундаментальные матрицы
- § 11. Простые особенности
- § 12. Уравнения высших порядков
- § 13. Кратные особенности
- Глава V. Зависимость от начальных условий и параметров
- § 2. Непрерывность
- § 3. Дифференцируемость
- § 4. Существование производных высших порядков
- § 5. Внешние производные
- § 6. Дальнейшие теоремы о дифференцируемости
- § 7. S- и L-липшицевы формы
- § 8. Теорема единственности
- § 9. Лемма
- § 10. Доказательство теоремы 8.1
- § 11. Доказательство теоремы 6.1
- § 12. Первые интегралы
- Глава VI. Уравнения в полных дифференциалах Уравнения с частными производными
- § 1. Уравнения в полных дифференциалах
- § 2. Алгебра внешних форм
- § 3. Теорема Фробениуса
- § 4. Доказательство теоремы 3.1
- § 5. Доказательство леммы 3.1
- § 6. Система (1.1)
- ЧАСТЬ II. МЕТОД ХАРАКТЕРИСТИК (МЕТОД КОШИ)
- § 7. Нелинейные уравнения в частных производных
- § 8. Характеристики
- § 9. Теорема существования и единственности
- § 10. Лемма Хаара и единственность
- Глава VII. Теория Пуанкаре — Бендиксона
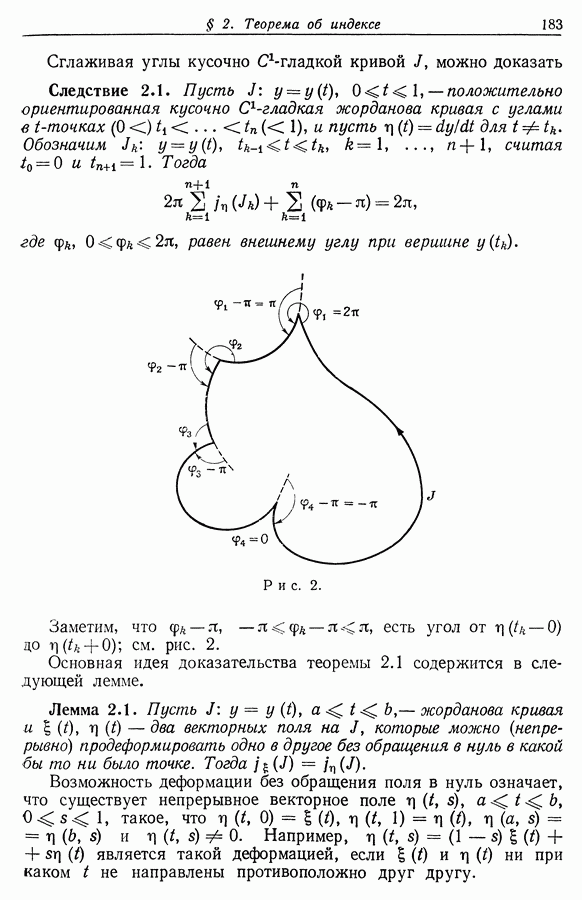
- § 2. Теорема об индексе
- § 3. Индекс стационарной точки
- § 4. Теорема Пуанкаре — Бендиксона
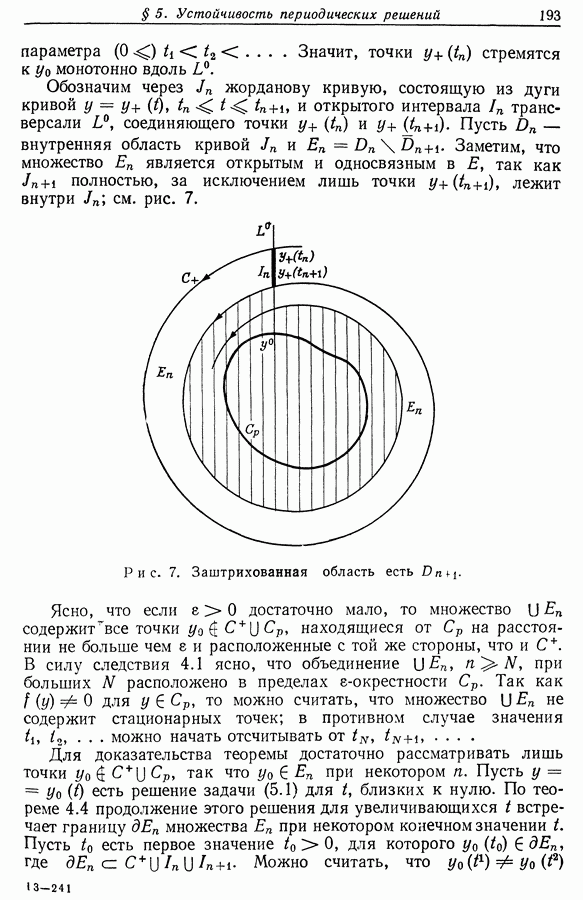
- § 5. Устойчивость периодических решений
- § 6. Точки вращения
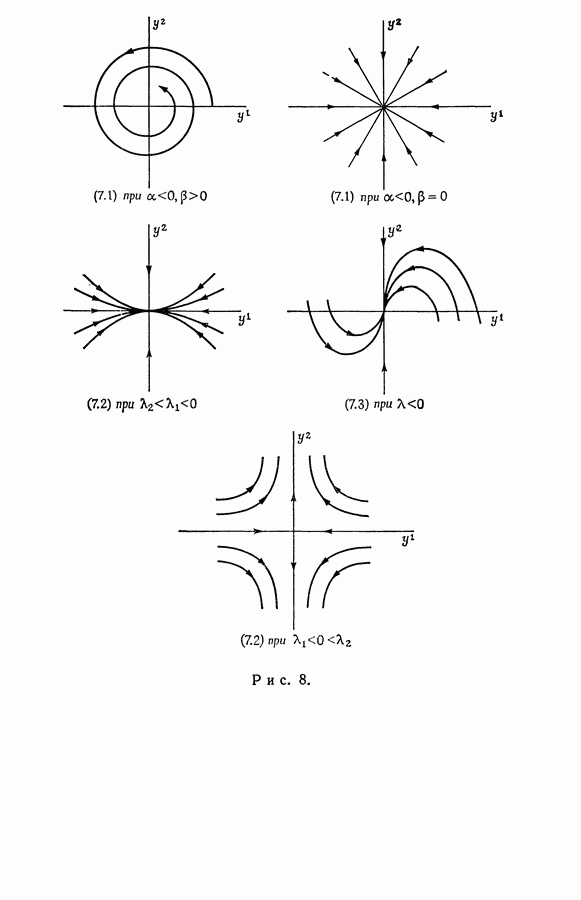
- § 7. Фокусы, узлы и седловые точки
- § 8. Секторы
- § 9. Стационарная точка общего вида
- § 10. Уравнения второго порядка
- ПРИЛОЖЕНИЕ. ТЕОРИЯ ПУАНКАРЕБЕ—НДИКСОНА НА ДВУМЕРНЫХ МНОГООБРАЗИЯХ
- § 12. Аналог теоремы Пуанкаре-Бендиксона
- § 13. Каскады на замкнутой кривой
- § 14. Потоки на торе
- Глава VIII. Стационарные точки на плоскости
- § 2. Характеристические направления
- § 3. Системы, близкие к линейным
- § 4. Более общие стационарные точки
- Глава IX. Инвариантные многообразия и линеаризация
- § 2. Отображения Т
- § 3. Модификация функции F(s)
- § 4. Приведение системы к нормальному виду
- § 5. Инвариантные многообразия отображения
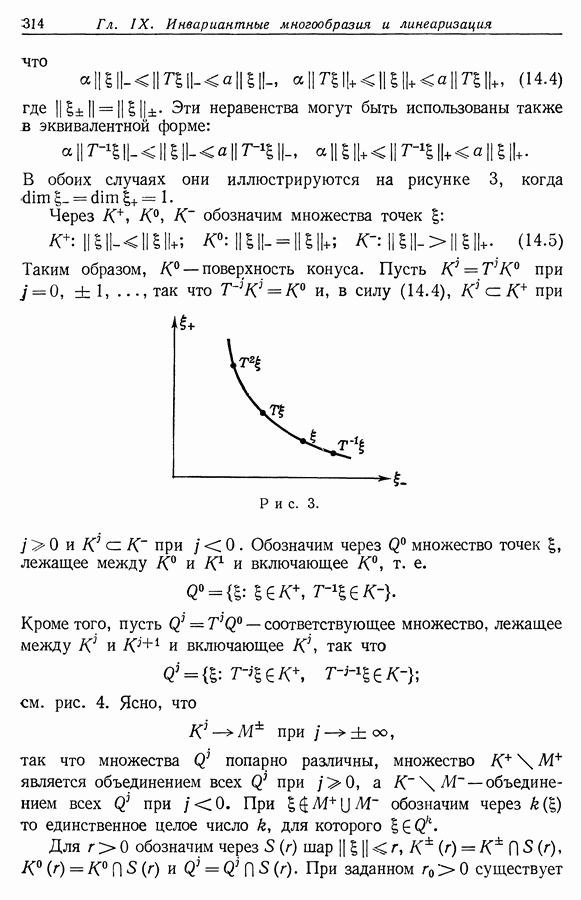
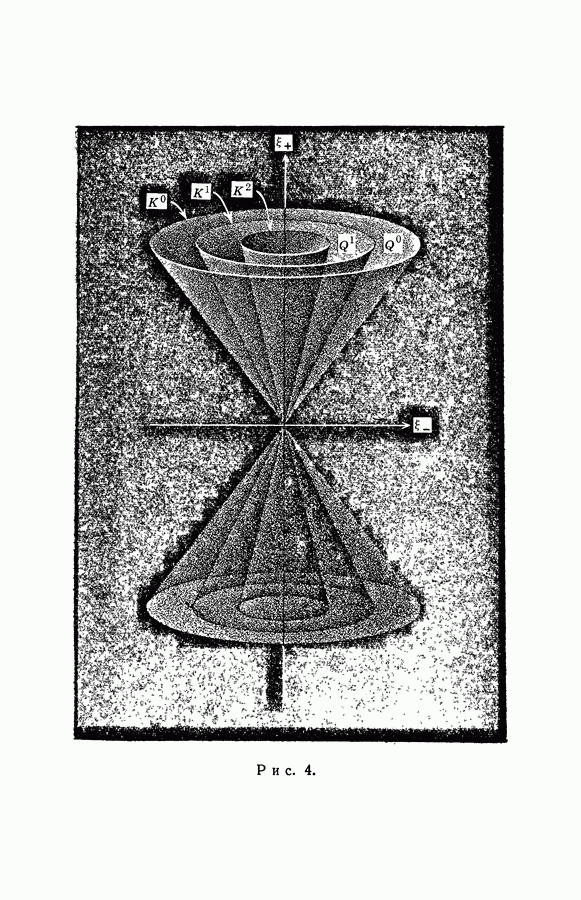
- § 6. Существование инвариантных многообразий
- § 7. Линеаризации
- § 8. Линеаризация отображения
- § 9. Доказательство теоремы 7.1
- § 10. Периодические решения
- § 11. Предельные циклы
- ПРИЛОЖЕНИЕ. ГЛАДКО ЭКВИВАЛЕНТНЫЕ ОТОБРАЖЕНИЯ
- § 12. Гладкие линеаризации
- § 9. Доказательство теоремы 7.12
- § 14. Доказательство теоремы 12.2
- Глава X. Возмущенные линейные системы
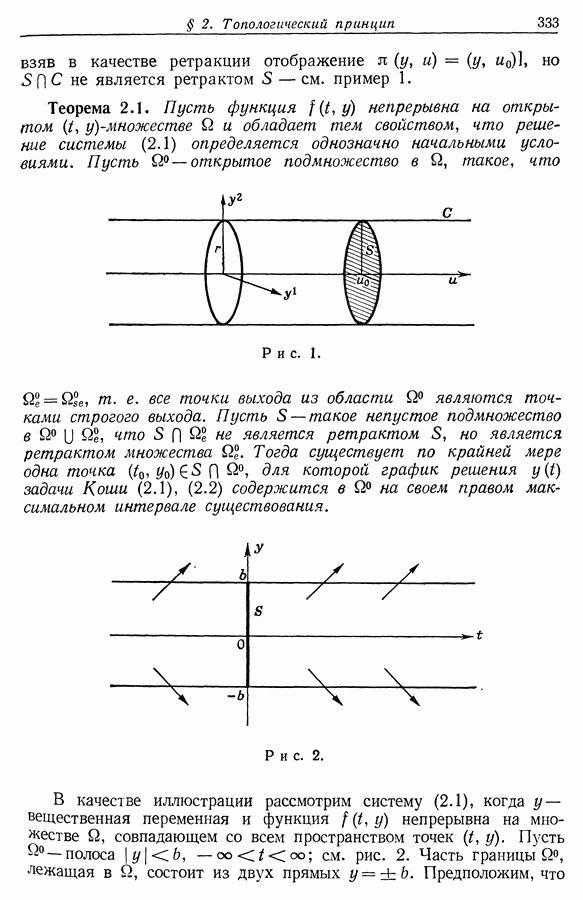
- § 2. Топологический принцип
- § 3. Теорема Важевского
- § 4. Подготовительные леммы
- § 5. Доказательство леммы 4.1
- § 6. Доказательство леммы 4.2
- § 7. Доказательство леммы 4.3
- § 8. Асимптотическое интегрирование. Логарифмическая шкала
- § 9. Доказательство теоремы 8.2
- § 10. Доказательство теоремы 8.3
- § 11. Логарифмическая шкала (продолжение)
- § 12. Доказательство теоремы 11.2
- § 13. Асимптотическое интегрирование
- § 14. Доказательство теоремы 13.1
- § 15. Доказательство теоремы 13.2
- § 16. Следствия и уточнения
- § 17. Линейные уравнения высших порядков
- Глава XI. Линейные уравнения второго порядка
- § 2. Основные факты
- § 3. Теоремы Штурма
- § 4. Краевые задачи Штурма — Лиувилля
- § 5. Число нулей
- § 6. Неосциллирующие уравнения и главные решения
- § 7. Теоремы о неосциллирующих уравнениях
- § 8. Асимптотическое интегрирование. Эллиптические случаи
- § 9. Асимптотическое интегрирование. Неэллиптические случаи
- ПРИЛОЖЕНИЕ. СИСТЕМЫ БЕЗ СОПРЯЖЕННЫХ ТОЧЕК
- § 11. Обобщения
- Глава XII. Некоторые применения теорем о неявных функциях и неподвижных точках
- ЧАСТЬ I. ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ
- § 2. Нелинейные задачи
- ЧАСТЬ II. ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
- § 4. Нелинейные задачи
- § 5. Априорные оценки
- ЧАСТЬ III. ОБЩАЯ ТЕОРИЯ
- § 7. Функции Грина
- § 8. Нелинейные уравнения
- § 9. Асимптотическое интегрирование
- Глава XIII. Дихотомии для решений линейных уравнений
- § 2. Предварительные леммы
- § 3. Оператор T
- § 4. Оценки для ||Py(t)||
- § 5. Оценки для ||y(t)||
- § 6. Приложения к системам первого порядка
- § 7. Приложения к системам высшего порядка
- § 8. P(B,D)-многообразия
- ЧАСТЬ II. СОПРЯЖЕННЫЕ УРАВНЕНИЯ
- § 10. Оператор T’
- § 11. Индивидуальные дихотомии
- § 12. Р-допустимые пространства для T’
- § 13. Приложения к дифференциальным уравнениям
- § 14. Существование PD решений
- Глава XIV. Монотонность
- ЧАСТЬ I. МОНОТОННЫЕ РЕШЕНИЯ
- § 2. Монотонные решения
- § 3. Линейные уравнения второго порядка
- § 4. Линейные уравнения второго порядка (продолжение)
- ЧАСТЬ II. ОДНА ЗАДАЧА ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
- § 6. Случай «лямбда» больше 0
- § 7. Случай «лямбда» меньше 0
- § 8. Случай «лямбда» равна 0
- § 9. Асимптотическое поведение
- ЧАСТЬ III. АСИМПТОТИЧЕСКАЯ УСТОЙЧИВОСТЬ В ЦЕЛОМ
- § 11. Функции Ляпунова
- § 12. Переменная матрица G
- § 13. О следствии 11.2
- § 14. «J(y) x*x меньше либо равно 0, если x*f(y) = 0»
- § 15. Доказательство теоремы 14.2
- § 16. Доказательство теоремы 14.1