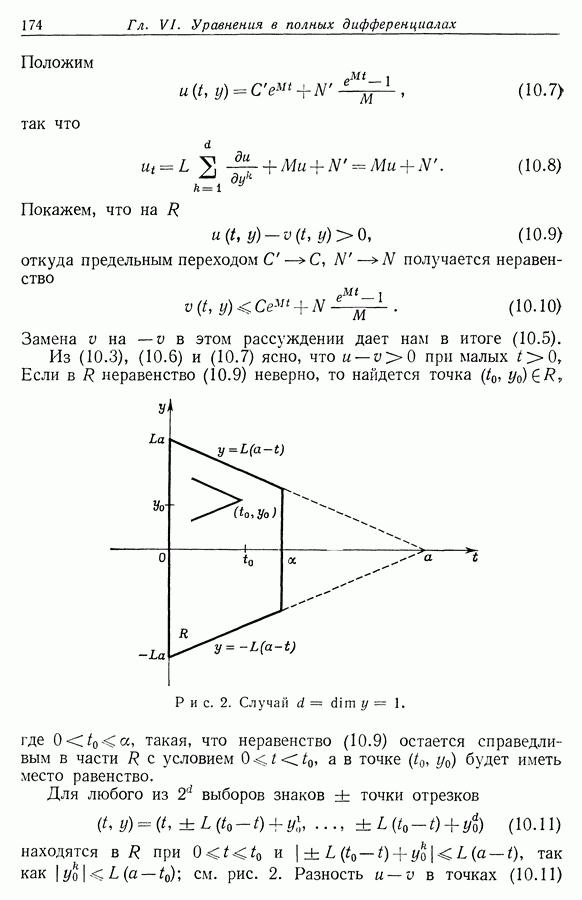
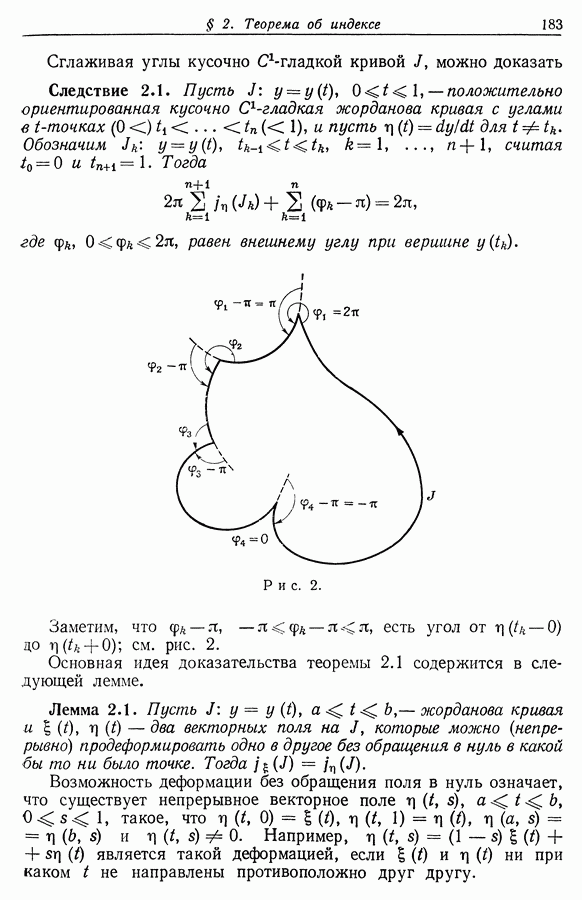
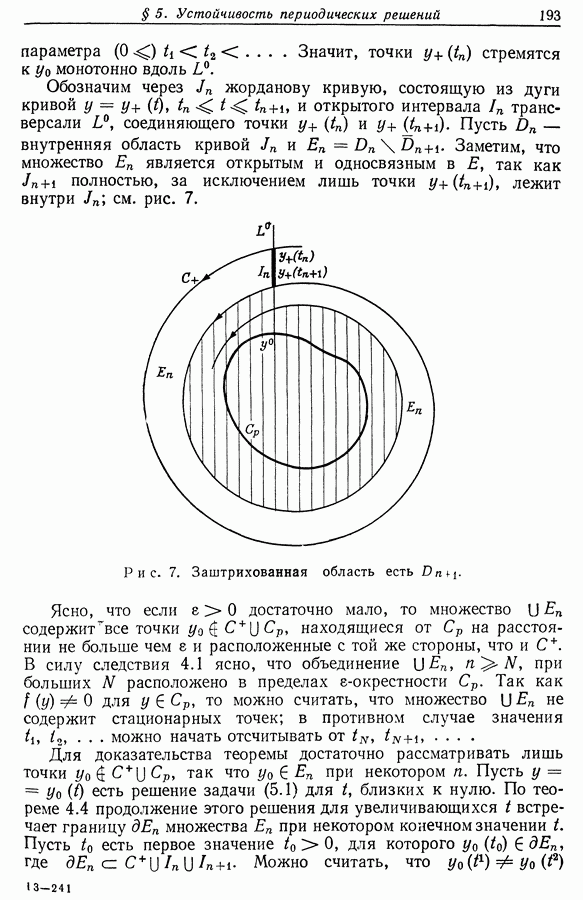
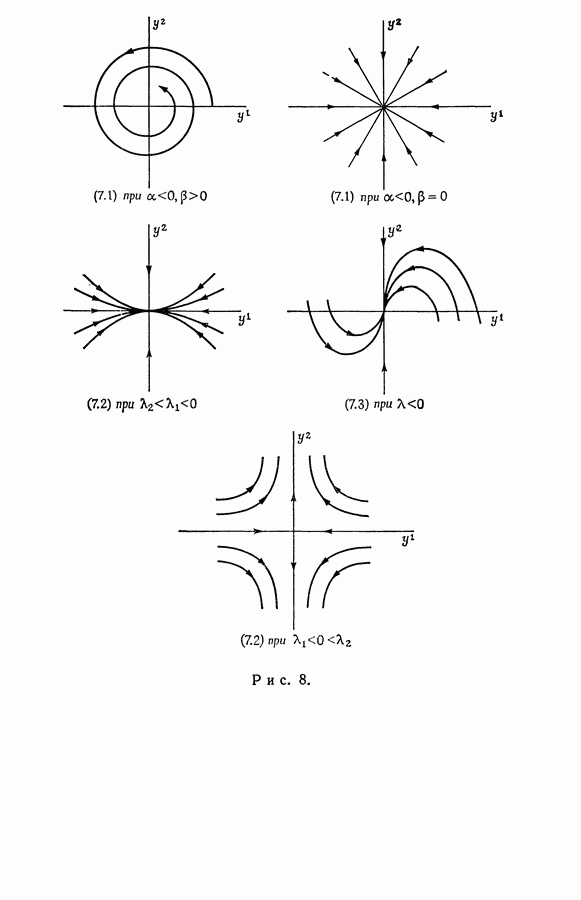
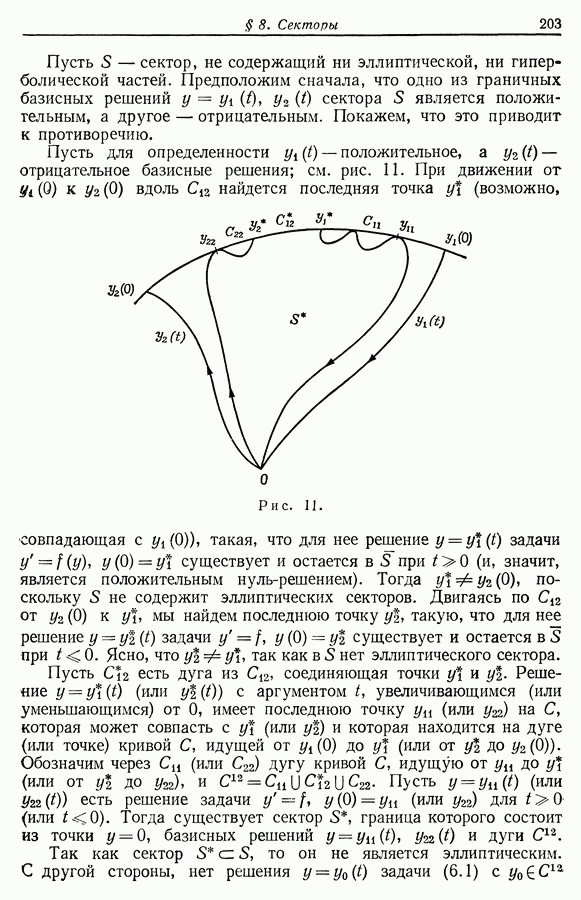
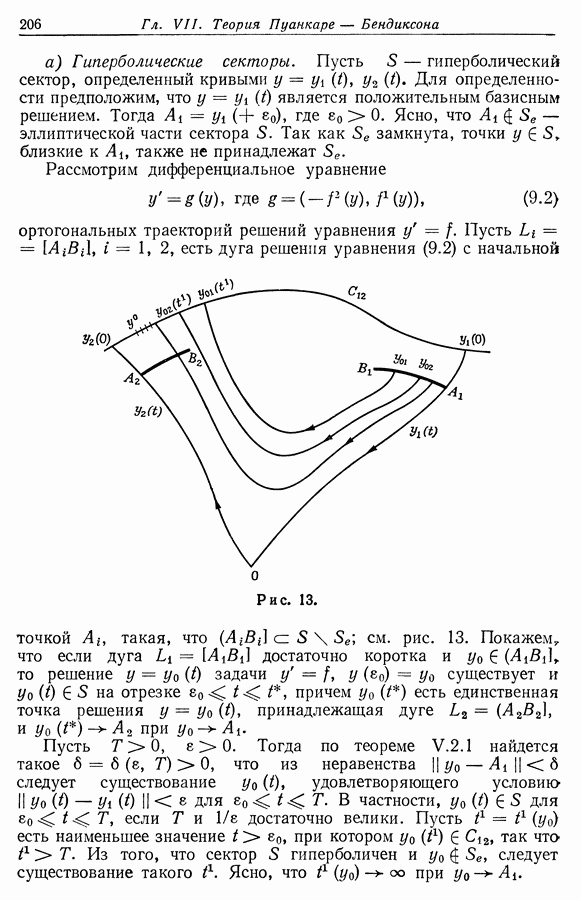
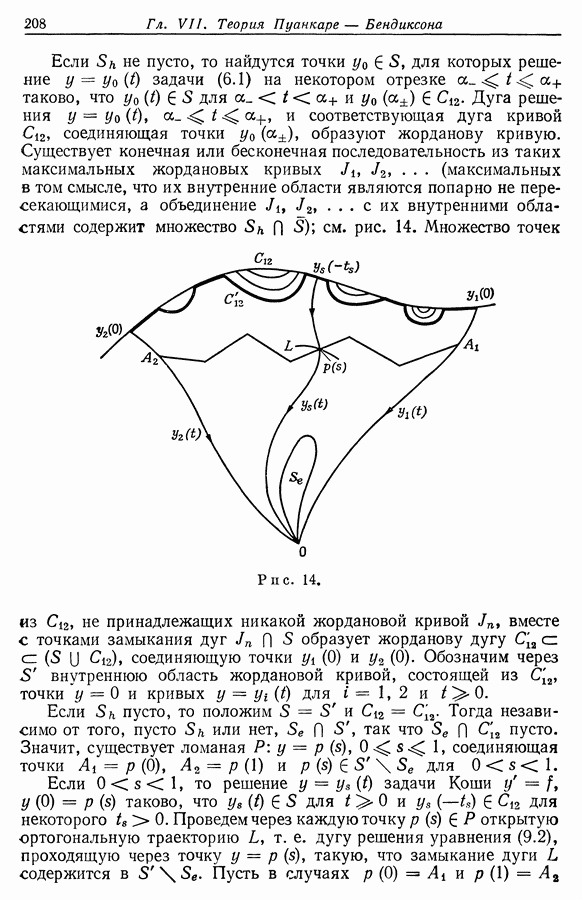
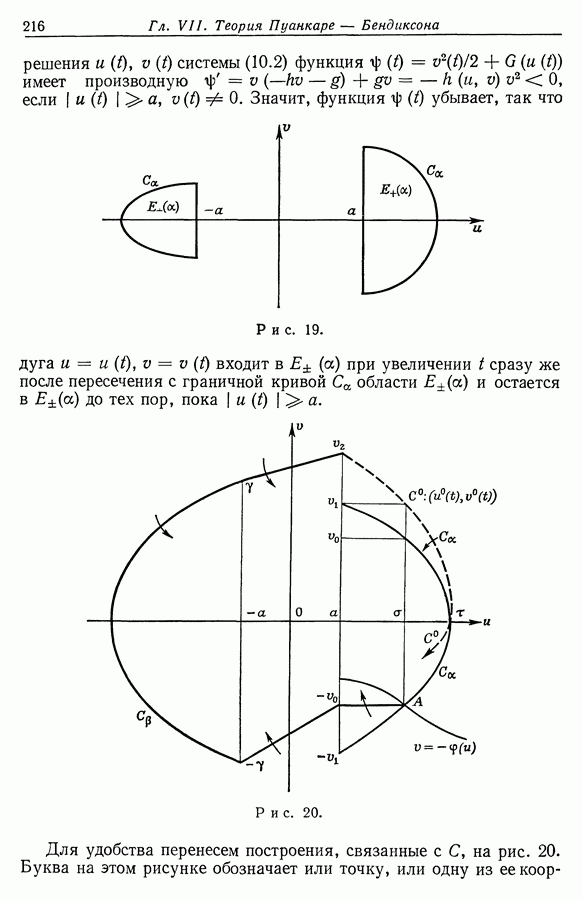
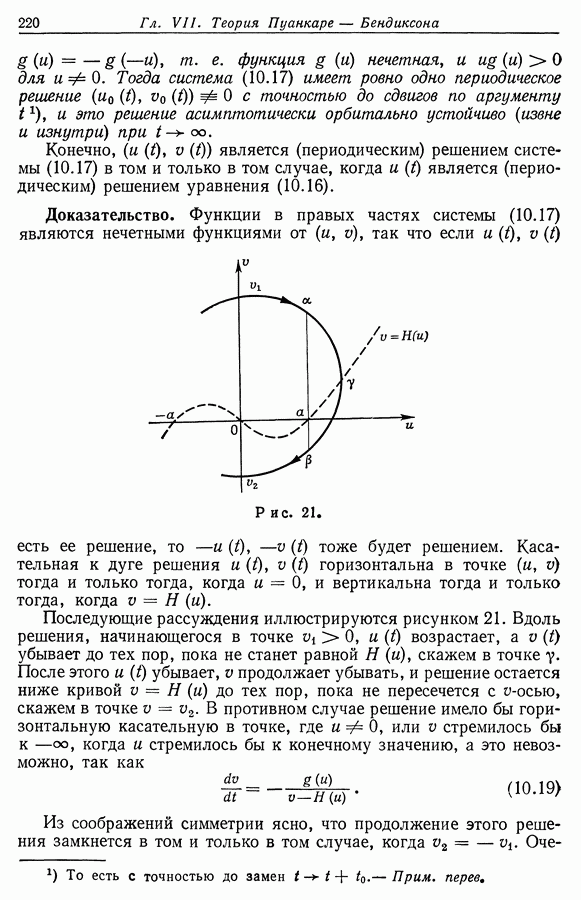
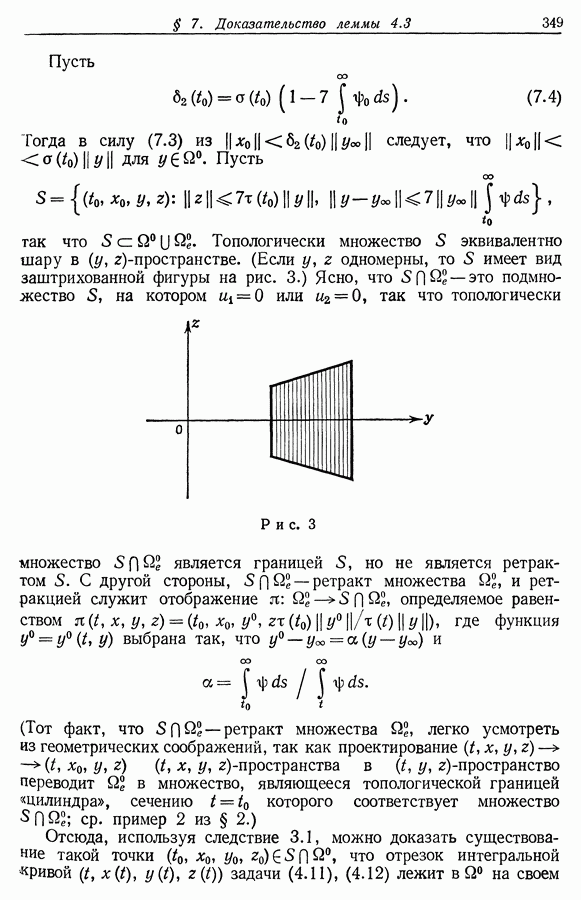
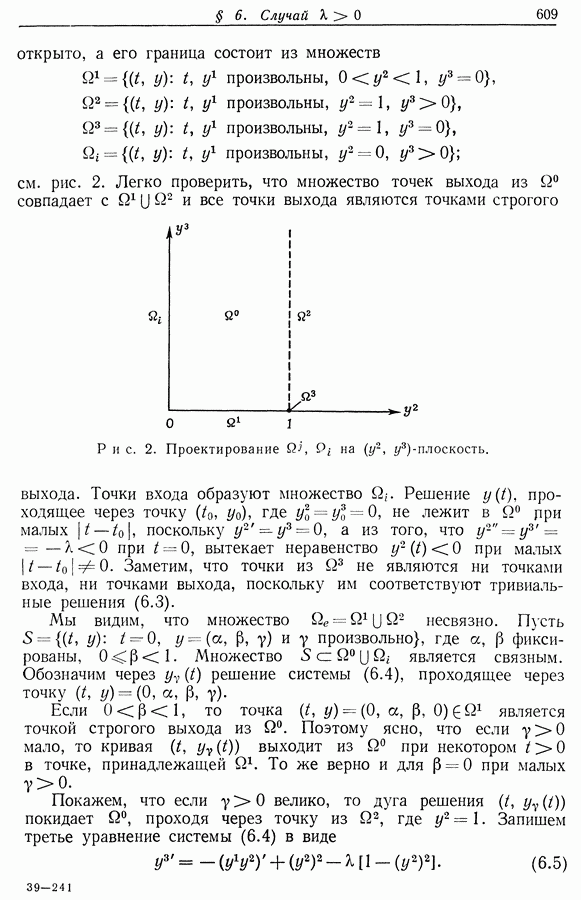
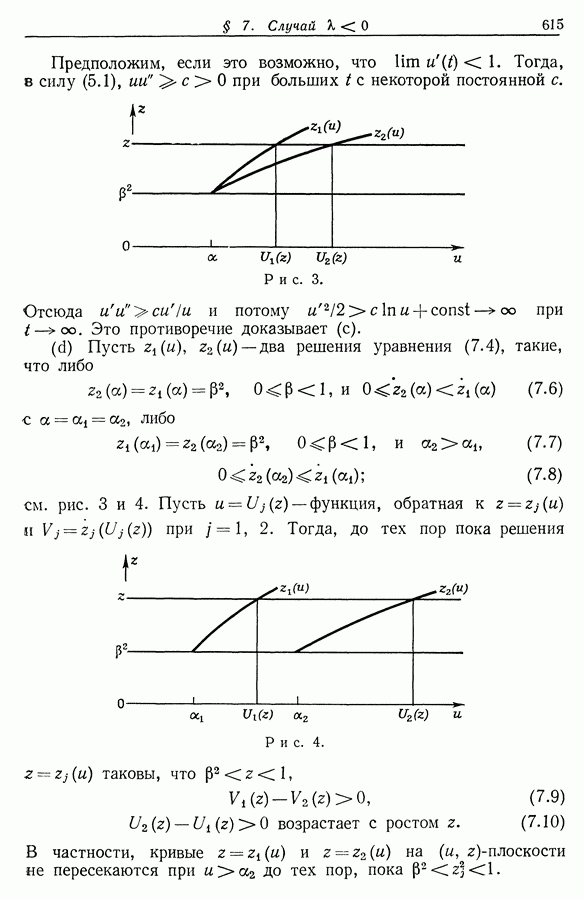
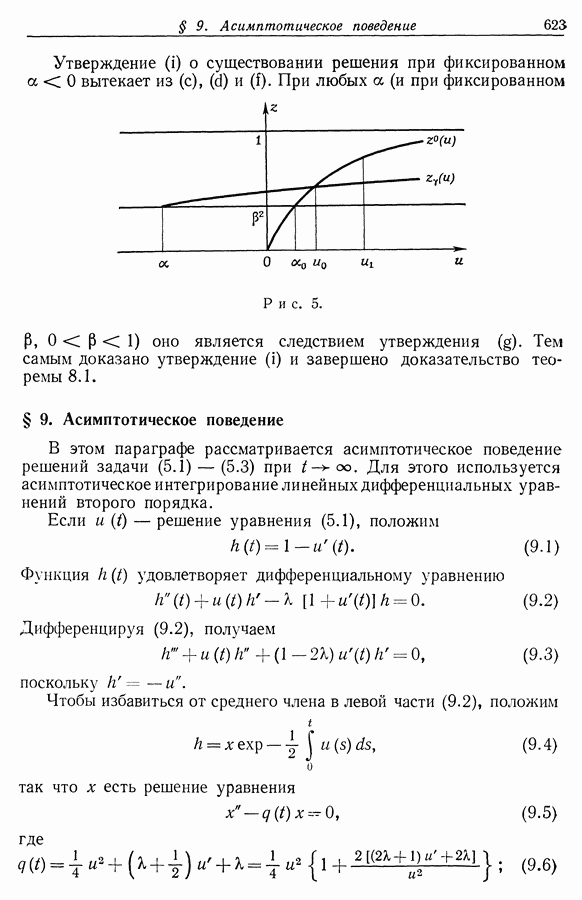
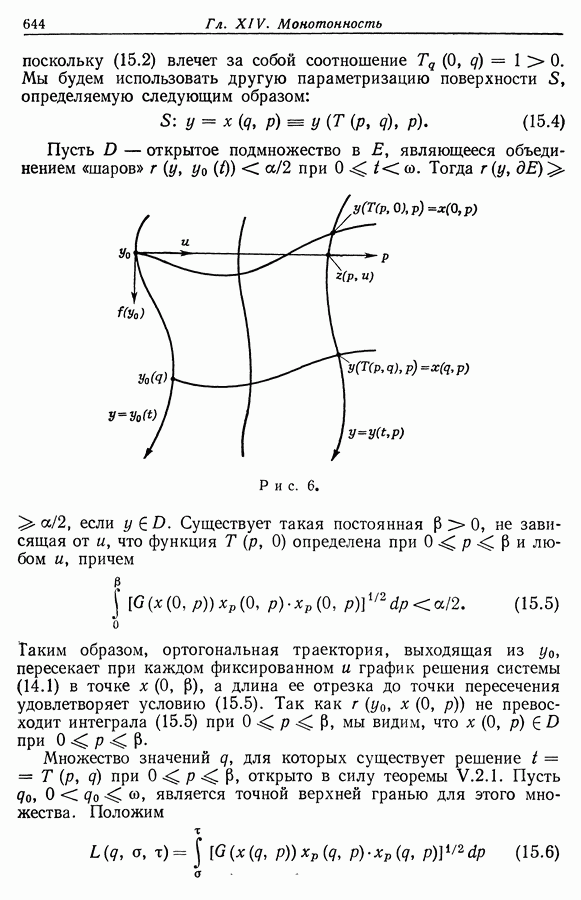
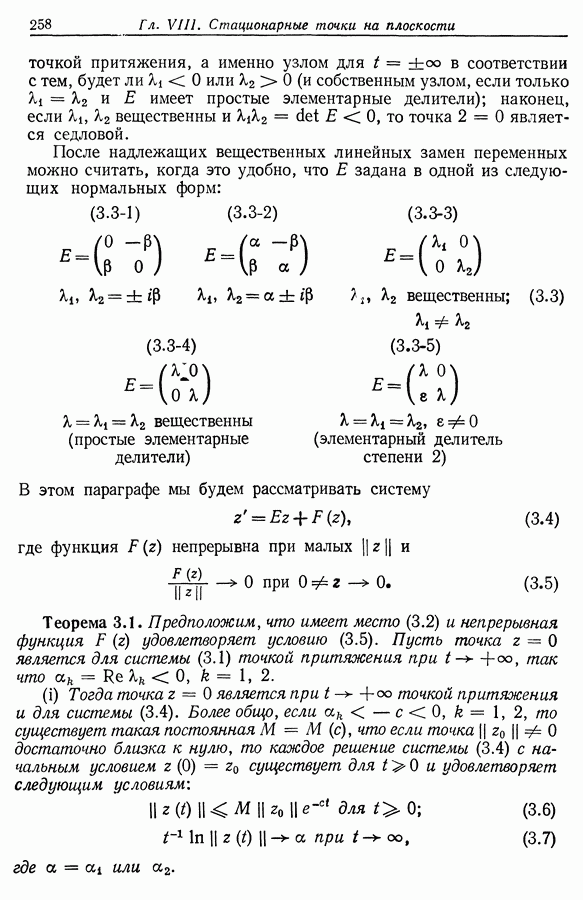| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
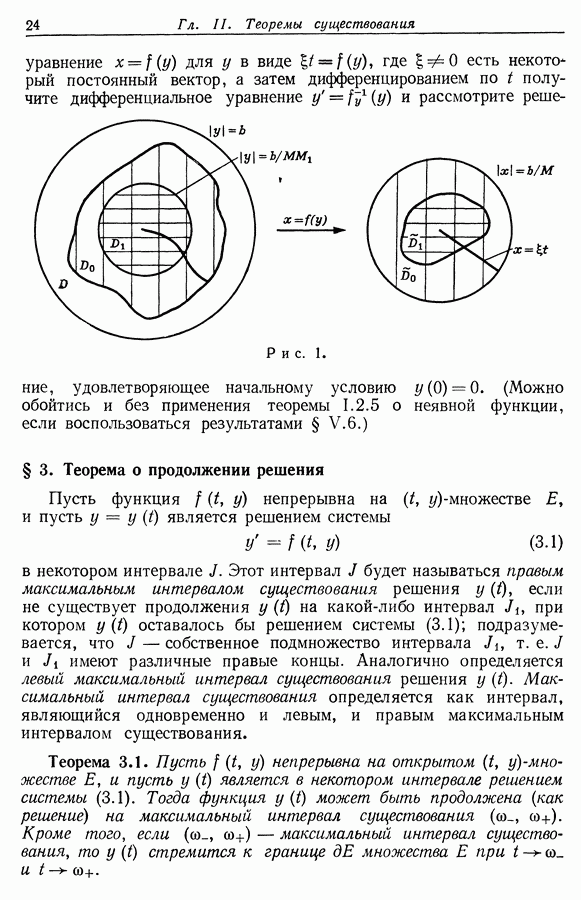
§ 13. О следствии 11.2
Для того чтобы доказать утверждение, аналогичное следствию 11.2, но с заменой  матрицей
матрицей  зависящей от у, нам понадобится некоторое свойство полных элементов длины дуги в римановой метрике.
зависящей от у, нам понадобится некоторое свойство полных элементов длины дуги в римановой метрике.
Множество точек у на  называется ограниченным относительно метрики
называется ограниченным относительно метрики  если для некоторой (а следовательно, и для каждой) фиксированной точки
если для некоторой (а следовательно, и для каждой) фиксированной точки  существует такая постоянная с, что
существует такая постоянная с, что  с для всех точек у из этого множества.
с для всех точек у из этого множества.
Лемма 13.1. Пусть матрица  непрерывна на связном открытом у-множестве
непрерывна на связном открытом у-множестве  и положительно определена при каждом
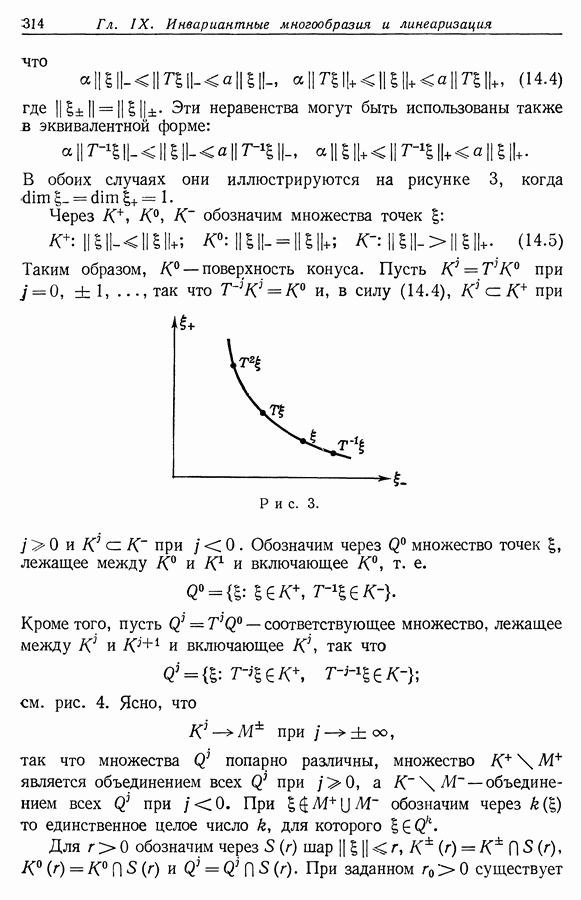
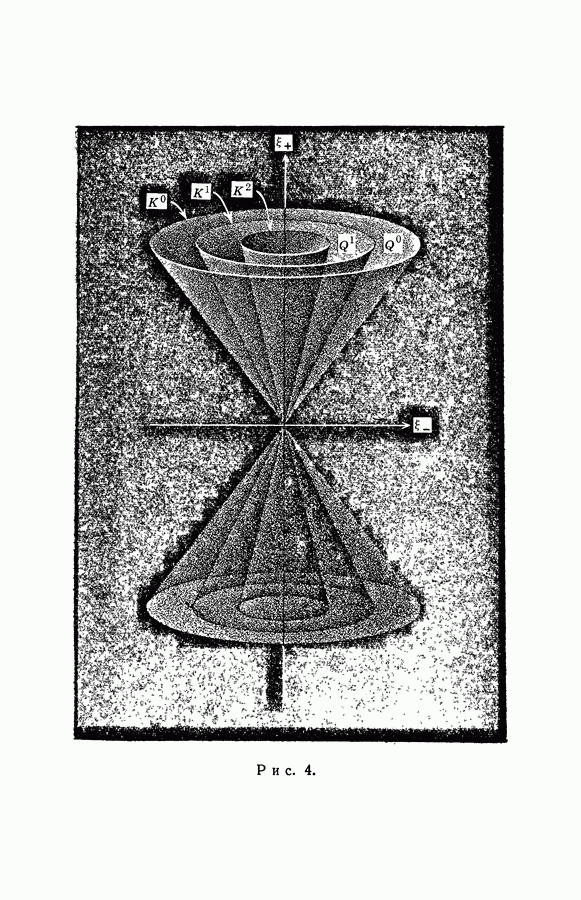
и положительно определена при каждом  Если элемент
Если элемент  в (12.1) является полным на
в (12.1) является полным на  то каждое подмножество из
то каждое подмножество из  ограниченное относительно метрики
ограниченное относительно метрики  имеет по крайней мере одну предельную точку в
имеет по крайней мере одну предельную точку в  а следовательно, и компактное замыкание в
а следовательно, и компактное замыкание в  В частности, каждое такое подмножество в
В частности, каждое такое подмножество в  ограничено (относительно евклидовой метрики в
ограничено (относительно евклидовой метрики в 
Обратное утверждение очевидно. Лемма 13.1 нам понадобится только при доказательстве теоремы 13.1. Можно, конечно, обойтись и без нее, если в теореме 13.1 сделать дополнительное предположение о том, что для  выполнено свойство, которое по лемме 13.1 вытекает из полноты. Доказательство леммы 13.1 имеется в книге Хопфа и Ринова [1]; см. также Милнор [1].
выполнено свойство, которое по лемме 13.1 вытекает из полноты. Доказательство леммы 13.1 имеется в книге Хопфа и Ринова [1]; см. также Милнор [1].
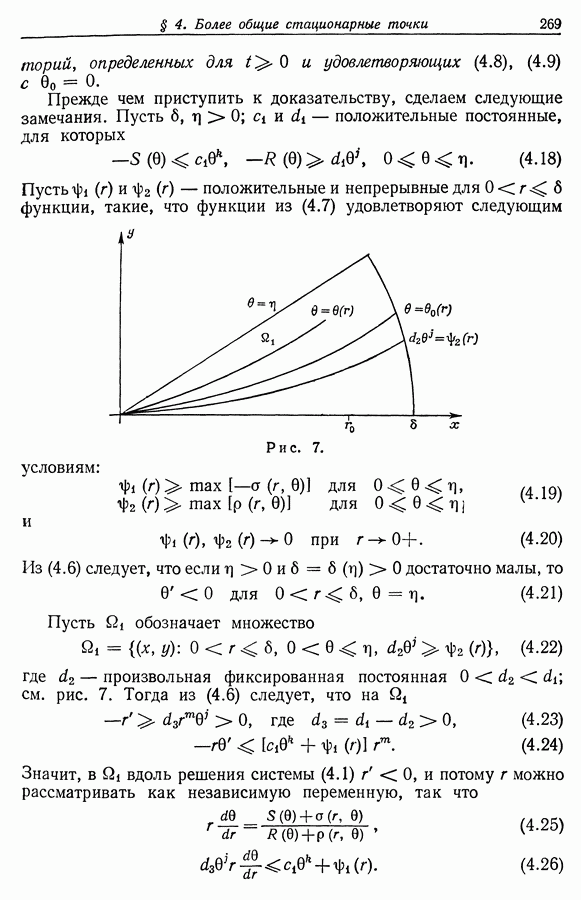
Теорема 13.1. Пусть  на некотором открытом связном у-множестве
на некотором открытом связном у-множестве  Пусть матрица
Пусть матрица  принадлежит классу
принадлежит классу  на положительно определена при фиксированном у и такова, что элемент
на положительно определена при фиксированном у и такова, что элемент  в (12.1) является полным на
в (12.1) является полным на  Пусть матрица
Пусть матрица  определенная формулой (12.10), такова, что
определенная формулой (12.10), такова, что

Тогда каждое решение  системы
системы  начинающееся при
начинающееся при  существует при всех
существует при всех  кроме того, если
кроме того, если  два различных решения при то функция
два различных решения при то функция

В частности, если существует стационарная точка  так что
так что  то для каждого решения
то для каждого решения  функция
функция

Следующее доказательство можно упростить, используя  известный факт, что если
известный факт, что если  две точки в
две точки в  то существует отрезок геодезической кривой С из класса
то существует отрезок геодезической кривой С из класса  соединяющий их. и такой, что величина
соединяющий их. и такой, что величина  равна римановой длине
равна римановой длине  дуги С.
дуги С.
Доказательство. Пусть  решение системы
решение системы  при
при  Пусть
Пусть  Множество точек
Множество точек

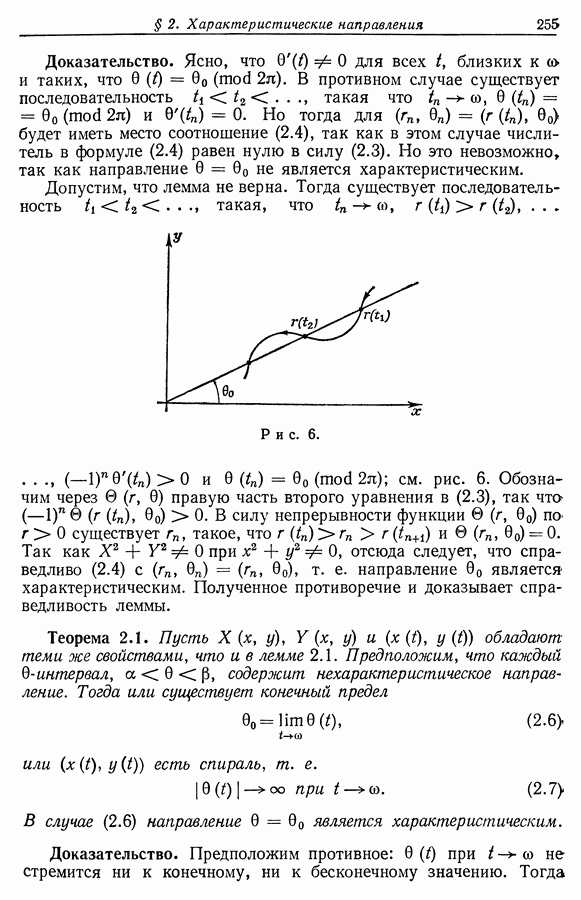
имеет компактное замыкание в  в силу леммы 13.1. Поэтому в силу замечания, сделанного после формулы (12.4), и аналогичного замечания для формы
в силу леммы 13.1. Поэтому в силу замечания, сделанного после формулы (12.4), и аналогичного замечания для формы  в (13.1) отсюда следует,
в (13.1) отсюда следует,  найдется такая постоянная
найдется такая постоянная  что
что

Пусть  кривая класса
кривая класса  удовлетворяющая условиям
удовлетворяющая условиям  и величина
и величина  настолько близка к
настолько близка к  что
что

Отсюда следует, что 
Пусть  решение системы
решение системы  удовлетворяющее условию
удовлетворяющее условию  так что
так что  решение, начинающееся в точке
решение, начинающееся в точке  при
при  Тогда
Тогда  на ее области определения; см. теорему V.3.I.
на ее области определения; см. теорему V.3.I.
По теореме существования Пеано найдется такое  не зависящее от и, что решение
не зависящее от и, что решение  существует при
существует при  для каждого фиксированного и, и
для каждого фиксированного и, и  Покажем, что
Покажем, что  существует при
существует при  Это очевидно для малых
Это очевидно для малых  в силу теоремы V.2.I. Предположим, что найдется наименьшее значение
в силу теоремы V.2.I. Предположим, что найдется наименьшее значение  , такое, что если правый максимальный интервал для
, такое, что если правый максимальный интервал для  равен
равен  то
то 
При фиксированном  обозначим через
обозначим через  длину
длину  дуги
дуги  т. е.
т. е.

где  Заметим, что
Заметим, что  решение системы уравнений в вариациях (12.7) с
решение системы уравнений в вариациях (12.7) с  Поэтому подинтегральное выражение в (13.6) равно где
Поэтому подинтегральное выражение в (13.6) равно где  функция, определенная в (12.8) при фиксированном и с
функция, определенная в (12.8) при фиксированном и с 

Для малого фиксированного  дуга
дуга  лежит в
лежит в  поскольку
поскольку  В этом случае из (13.4) вытекает неравенство
В этом случае из (13.4) вытекает неравенство

Следовательно, в силу (13.5)

до тех пор, пока  Неравенство (13.7) показывает, что при возрастании
Неравенство (13.7) показывает, что при возрастании  от
от  до
до  точка
точка  не может выйти из
не может выйти из  Следовательно, это неравенство выполнено при
Следовательно, это неравенство выполнено при 
Отсюда вытекает, что интеграл (13.6) с  сходится. Поэтому из полноты
сходится. Поэтому из полноты  в (12.1) следует существование предела
в (12.1) следует существование предела  при и
при и  который принадлежит
который принадлежит  при
при  (так же, как и при
(так же, как и при  Этот предел равен
Этот предел равен  так что решение определено при
так что решение определено при  Это противоречит тому факту, что
Это противоречит тому факту, что  правый максимальный интервал существования решения
правый максимальный интервал существования решения  Следовательно, решение
Следовательно, решение  существует при для каждого
существует при для каждого  и 1.
и 1.
В частности, решение  существует при
существует при  Следовательно, если
Следовательно, если  в (13.6) и (13.7), то, в силу (12.3),
в (13.6) и (13.7), то, в силу (12.3),  Поэтому
Поэтому  в силу (13.5). Так как
в силу (13.5). Так как  можно заменить в этом рассуждении любым значением
можно заменить в этом рассуждении любым значением  из полуинтервала
из полуинтервала  отсюда вытекает, что (13.2) выполняется на каждом интервале, на котором существует
отсюда вытекает, что (13.2) выполняется на каждом интервале, на котором существует 
Покажем теперь, что  существует при 0. Если
существует при 0. Если  то решение
то решение  является периодическим и существует при всех
является периодическим и существует при всех  Если
Если  то мы можем использовать то же рассуждение с
то мы можем использовать то же рассуждение с  Тогда решение
Тогда решение  существует при
существует при  т.е.
т.е.  существует при
существует при  Повторяя это рассуждение, можно доказать, что
Повторяя это рассуждение, можно доказать, что  существует при
существует при 
Если  стационарная точка и
стационарная точка и  решение системы
решение системы  то функция
то функция  убывает. В частности,
убывает. В частности,  при
при  и функция
и функция  ограничена при 0. Поэтому кривая
ограничена при 0. Поэтому кривая  имеет компактное замыкание в
имеет компактное замыкание в  в силу леммы 13.1.
в силу леммы 13.1.
Заметим, что функция  удовлетворяет, в силу (12.11) и (13.1), соотношению
удовлетворяет, в силу (12.11) и (13.1), соотношению 
0. Следовательно, по лемме 11.1,  -предельные точки кривой С
-предельные точки кривой С 
-являются нулями функции  Но из (13.1) видно, что
Но из (13.1) видно, что  тогда и только тогда, когда
тогда и только тогда, когда  Поэтому
Поэтому  о при
о при  Тем самым теорема 13.1 доказана.
Тем самым теорема 13.1 доказана.
Упражнение 13.1. Замените в теореме 13.1 условие (13.1) более слабым:  для
для  и всех
и всех  Покажите, что справедливо следующее утверждение, аналогичное первой части теоремы 13.1: (а) функция
Покажите, что справедливо следующее утверждение, аналогичное первой части теоремы 13.1: (а) функция  не возрастает и (b) если
не возрастает и (b) если  решение системы
решение системы  начинающееся при
начинающееся при  то
то  существует при
существует при 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- Глава I. Предварительные сведения
- § 2. Основные теоремы
- § 3. Гладкие аппроксимации
- § 4. Замена переменных в интегралах
- Глава II. Теоремы существования
- § 1. Теорема Пикара — Линделёфа
- § 2. Теорема Пеано
- § 3. Теорема о продолжении решения
- § 4. Теорема Кнезера
- § 5. Пример неединственности
- Глава III. Дифференциальные неравенства и единственность
- § 1. Неравенство Гронуолла
- § 2. Максимальные и минимальные решения
- § 3. Правые производные
- § 4. Дифференциальные неравенства
- § 5. Теорема Уинтнера
- § 6. Теоремы единственности
- § 7. Теорема единственности ван Кампена
- § 8. Точки выхода и функции Ляпунова
- § 9. Последовательные приближения
- Глава IV. Линейные дифференциальные уравнения
- § 2. Вариация постоянных
- § 3. Редукция к системам меньшего, порядка
- § 4. Основные неравенства
- § 5. Системы с постоянными коэффициентами
- § 6. Теория Флоке
- § 7. Сопряженные системы
- § 8. Линейные уравнения высших порядков
- § 9. Замечания о замене переменных
- ДОБАВЛЕНИЕ. ЛИНЕЙНЫЕ АНАЛИТИЧЕСКИЕ УРАВНЕНИЯ
- § 10. Фундаментальные матрицы
- § 11. Простые особенности
- § 12. Уравнения высших порядков
- § 13. Кратные особенности
- Глава V. Зависимость от начальных условий и параметров
- § 2. Непрерывность
- § 3. Дифференцируемость
- § 4. Существование производных высших порядков
- § 5. Внешние производные
- § 6. Дальнейшие теоремы о дифференцируемости
- § 7. S- и L-липшицевы формы
- § 8. Теорема единственности
- § 9. Лемма
- § 10. Доказательство теоремы 8.1
- § 11. Доказательство теоремы 6.1
- § 12. Первые интегралы
- Глава VI. Уравнения в полных дифференциалах Уравнения с частными производными
- § 1. Уравнения в полных дифференциалах
- § 2. Алгебра внешних форм
- § 3. Теорема Фробениуса
- § 4. Доказательство теоремы 3.1
- § 5. Доказательство леммы 3.1
- § 6. Система (1.1)
- ЧАСТЬ II. МЕТОД ХАРАКТЕРИСТИК (МЕТОД КОШИ)
- § 7. Нелинейные уравнения в частных производных
- § 8. Характеристики
- § 9. Теорема существования и единственности
- § 10. Лемма Хаара и единственность
- Глава VII. Теория Пуанкаре — Бендиксона
- § 2. Теорема об индексе
- § 3. Индекс стационарной точки
- § 4. Теорема Пуанкаре — Бендиксона
- § 5. Устойчивость периодических решений
- § 6. Точки вращения
- § 7. Фокусы, узлы и седловые точки
- § 8. Секторы
- § 9. Стационарная точка общего вида
- § 10. Уравнения второго порядка
- ПРИЛОЖЕНИЕ. ТЕОРИЯ ПУАНКАРЕБЕ—НДИКСОНА НА ДВУМЕРНЫХ МНОГООБРАЗИЯХ
- § 12. Аналог теоремы Пуанкаре-Бендиксона
- § 13. Каскады на замкнутой кривой
- § 14. Потоки на торе
- Глава VIII. Стационарные точки на плоскости
- § 2. Характеристические направления
- § 3. Системы, близкие к линейным
- § 4. Более общие стационарные точки
- Глава IX. Инвариантные многообразия и линеаризация
- § 2. Отображения Т
- § 3. Модификация функции F(s)
- § 4. Приведение системы к нормальному виду
- § 5. Инвариантные многообразия отображения
- § 6. Существование инвариантных многообразий
- § 7. Линеаризации
- § 8. Линеаризация отображения
- § 9. Доказательство теоремы 7.1
- § 10. Периодические решения
- § 11. Предельные циклы
- ПРИЛОЖЕНИЕ. ГЛАДКО ЭКВИВАЛЕНТНЫЕ ОТОБРАЖЕНИЯ
- § 12. Гладкие линеаризации
- § 9. Доказательство теоремы 7.12
- § 14. Доказательство теоремы 12.2
- Глава X. Возмущенные линейные системы
- § 2. Топологический принцип
- § 3. Теорема Важевского
- § 4. Подготовительные леммы
- § 5. Доказательство леммы 4.1
- § 6. Доказательство леммы 4.2
- § 7. Доказательство леммы 4.3
- § 8. Асимптотическое интегрирование. Логарифмическая шкала
- § 9. Доказательство теоремы 8.2
- § 10. Доказательство теоремы 8.3
- § 11. Логарифмическая шкала (продолжение)
- § 12. Доказательство теоремы 11.2
- § 13. Асимптотическое интегрирование
- § 14. Доказательство теоремы 13.1
- § 15. Доказательство теоремы 13.2
- § 16. Следствия и уточнения
- § 17. Линейные уравнения высших порядков
- Глава XI. Линейные уравнения второго порядка
- § 2. Основные факты
- § 3. Теоремы Штурма
- § 4. Краевые задачи Штурма — Лиувилля
- § 5. Число нулей
- § 6. Неосциллирующие уравнения и главные решения
- § 7. Теоремы о неосциллирующих уравнениях
- § 8. Асимптотическое интегрирование. Эллиптические случаи
- § 9. Асимптотическое интегрирование. Неэллиптические случаи
- ПРИЛОЖЕНИЕ. СИСТЕМЫ БЕЗ СОПРЯЖЕННЫХ ТОЧЕК
- § 11. Обобщения
- Глава XII. Некоторые применения теорем о неявных функциях и неподвижных точках
- ЧАСТЬ I. ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ
- § 2. Нелинейные задачи
- ЧАСТЬ II. ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
- § 4. Нелинейные задачи
- § 5. Априорные оценки
- ЧАСТЬ III. ОБЩАЯ ТЕОРИЯ
- § 7. Функции Грина
- § 8. Нелинейные уравнения
- § 9. Асимптотическое интегрирование
- Глава XIII. Дихотомии для решений линейных уравнений
- § 2. Предварительные леммы
- § 3. Оператор T
- § 4. Оценки для ||Py(t)||
- § 5. Оценки для ||y(t)||
- § 6. Приложения к системам первого порядка
- § 7. Приложения к системам высшего порядка
- § 8. P(B,D)-многообразия
- ЧАСТЬ II. СОПРЯЖЕННЫЕ УРАВНЕНИЯ
- § 10. Оператор T’
- § 11. Индивидуальные дихотомии
- § 12. Р-допустимые пространства для T’
- § 13. Приложения к дифференциальным уравнениям
- § 14. Существование PD решений
- Глава XIV. Монотонность
- ЧАСТЬ I. МОНОТОННЫЕ РЕШЕНИЯ
- § 2. Монотонные решения
- § 3. Линейные уравнения второго порядка
- § 4. Линейные уравнения второго порядка (продолжение)
- ЧАСТЬ II. ОДНА ЗАДАЧА ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
- § 6. Случай «лямбда» больше 0
- § 7. Случай «лямбда» меньше 0
- § 8. Случай «лямбда» равна 0
- § 9. Асимптотическое поведение
- ЧАСТЬ III. АСИМПТОТИЧЕСКАЯ УСТОЙЧИВОСТЬ В ЦЕЛОМ
- § 11. Функции Ляпунова
- § 12. Переменная матрица G
- § 13. О следствии 11.2
- § 14. «J(y) x*x меньше либо равно 0, если x*f(y) = 0»
- § 15. Доказательство теоремы 14.2
- § 16. Доказательство теоремы 14.1