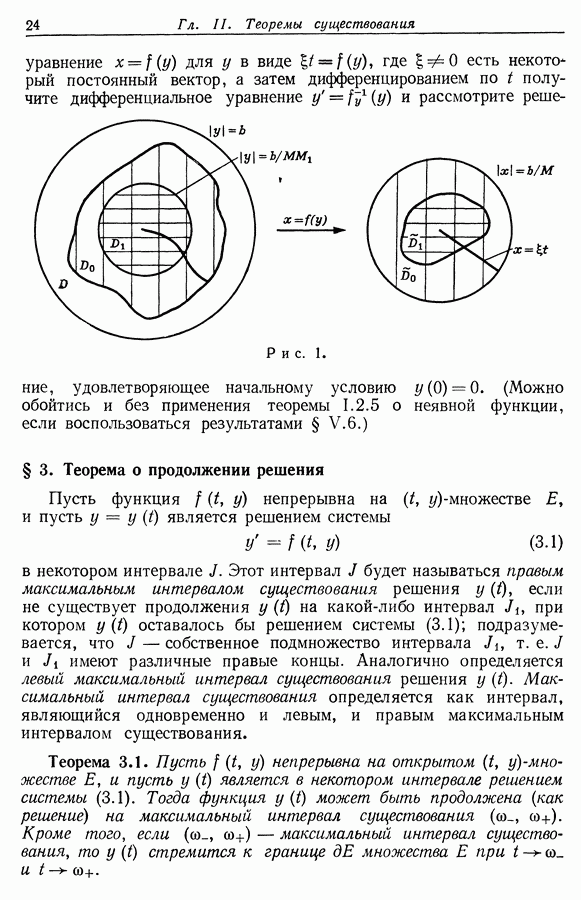
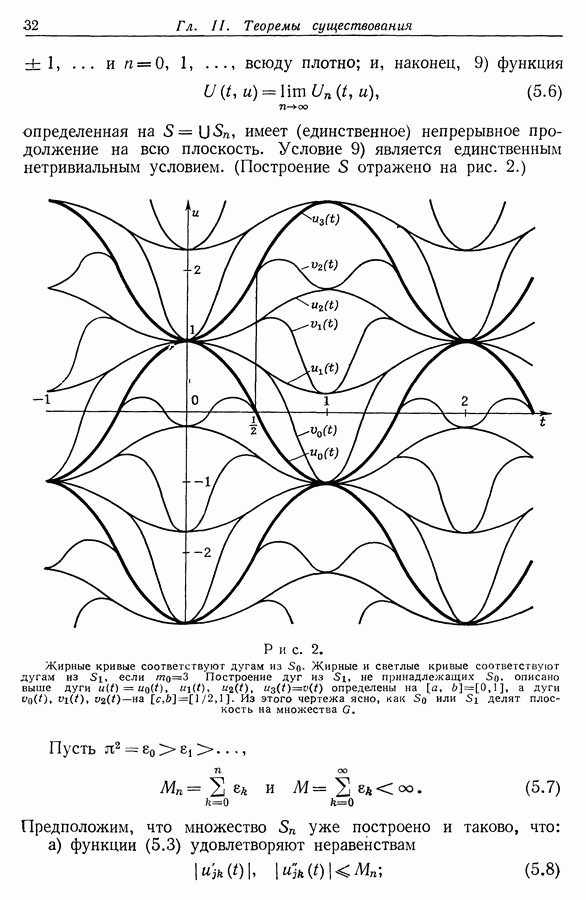
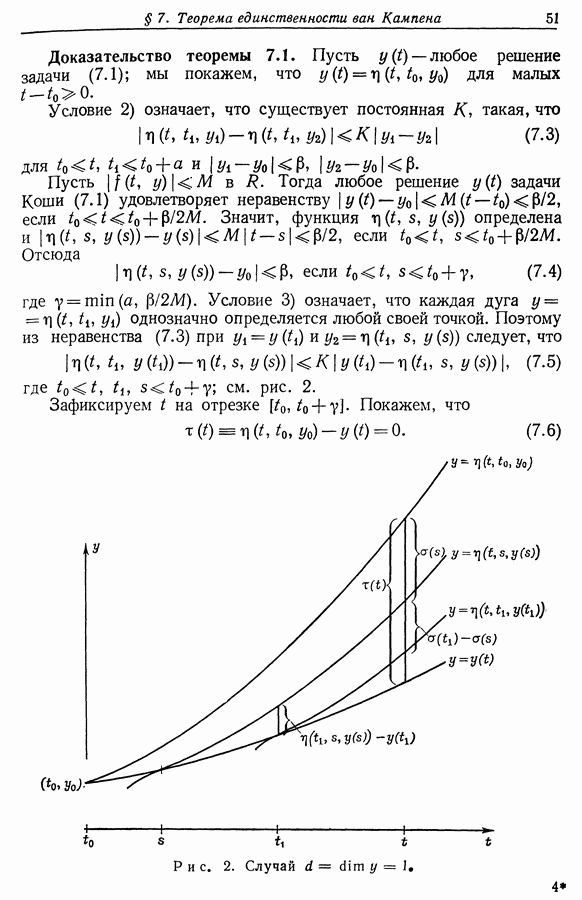
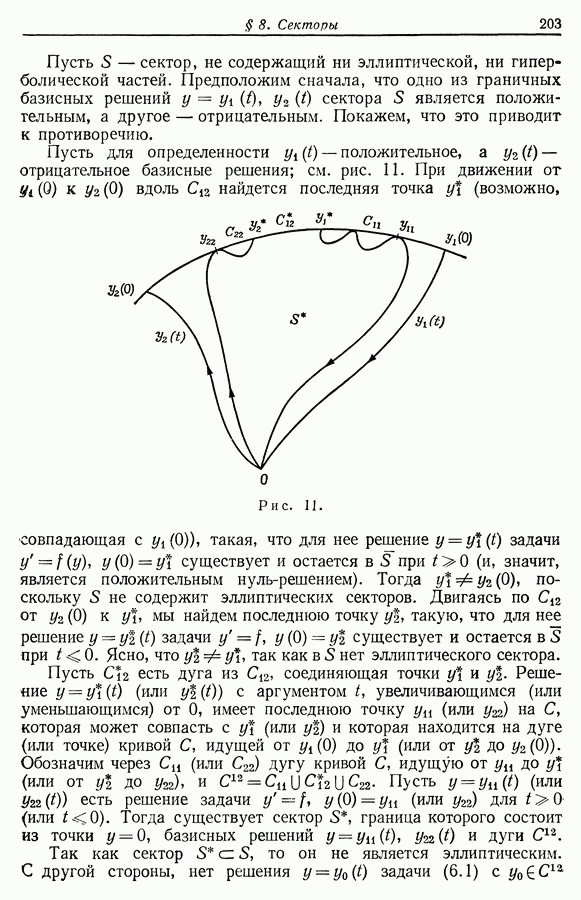
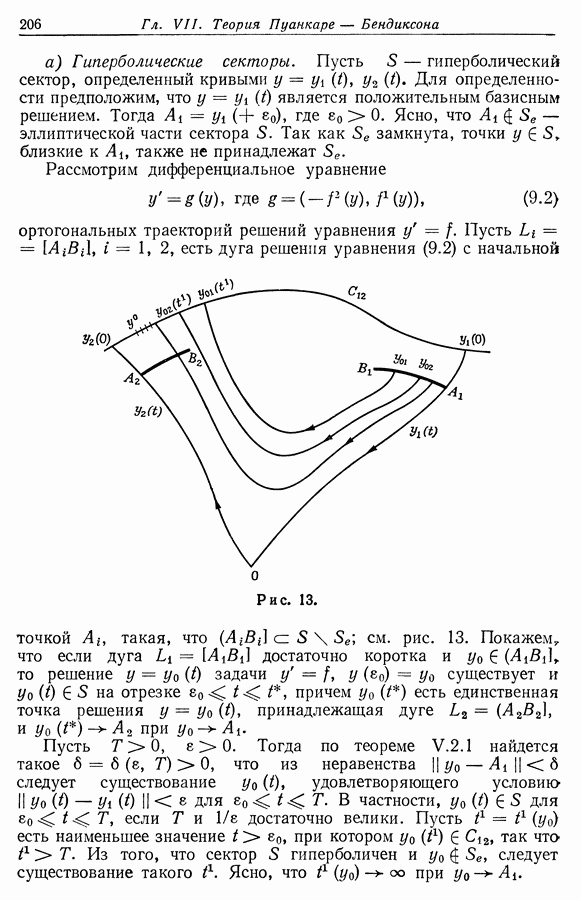
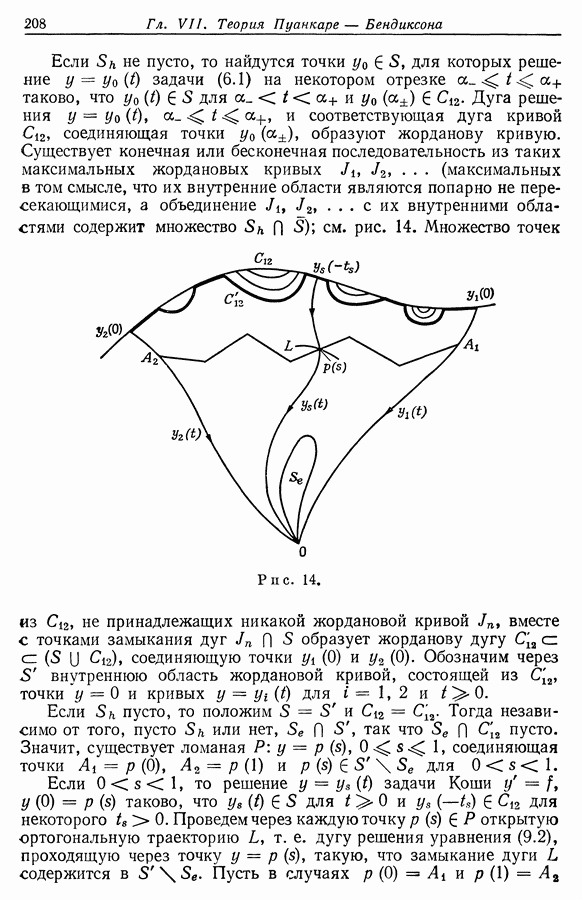
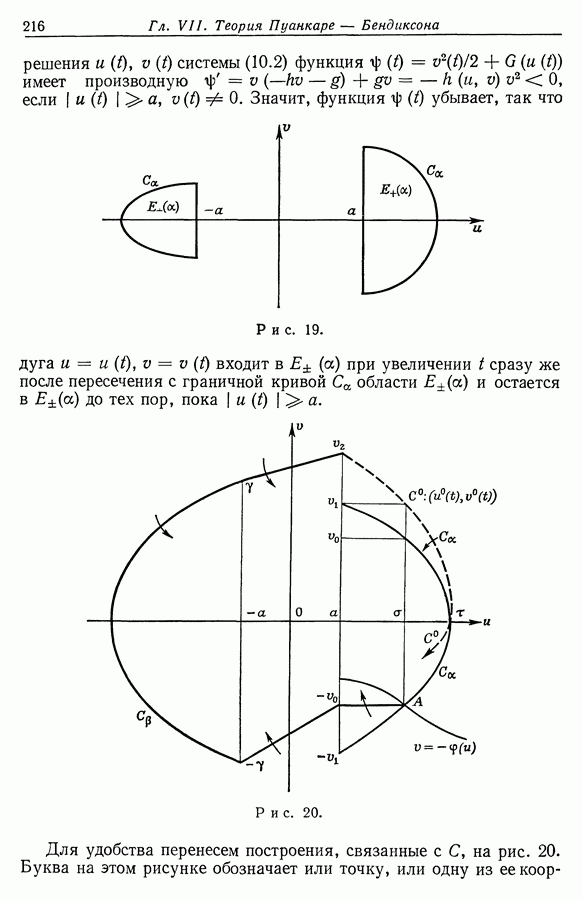
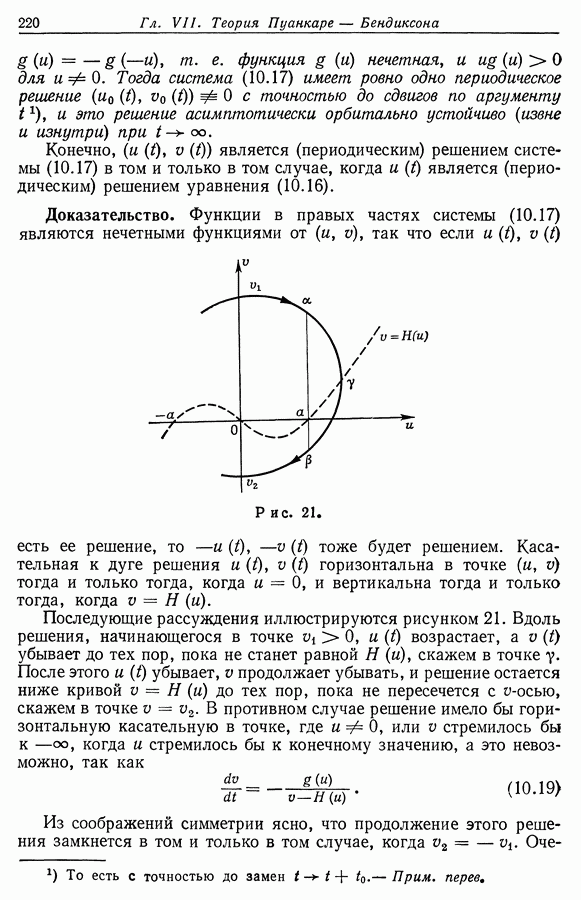
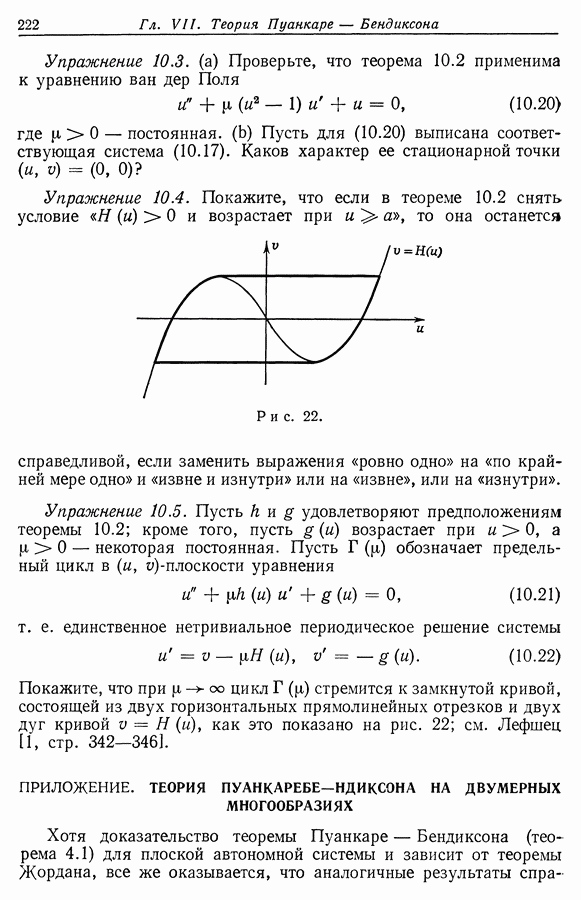
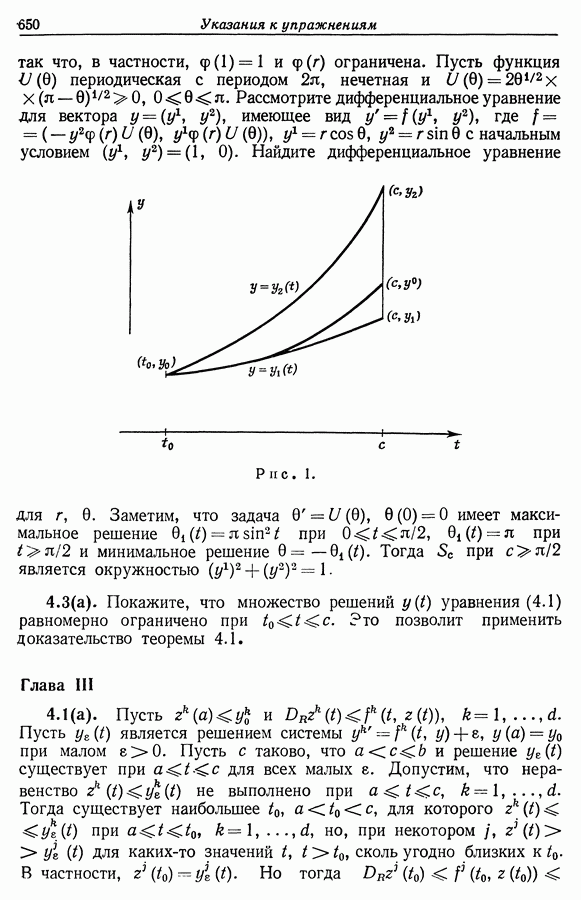
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
Глава X. Возмущенные линейные системы
В этой главе излагаются методы асимптотического интегрирования системы дифференциальных уравнений  которую можно рассматривать как возмущенную линейную систему уравнений с постоянными коэффициентами
которую можно рассматривать как возмущенную линейную систему уравнений с постоянными коэффициентами 
В § 1 этой главы исследуется простой, но важный случай  Поскольку результат достигается в этом случае с помощью очень простых соображений, имеющих, однако, широкое применение, мы сочли нужным выделить его.
Поскольку результат достигается в этом случае с помощью очень простых соображений, имеющих, однако, широкое применение, мы сочли нужным выделить его.
Один из самых важных методов, используемых в общем случае произвольного основан на простом топологическом принципе, излагаемом в §§ 2 и 3. Он широко применяется и в других главах. Совсем другой подход, приводящий к результатам, аналогичным тем, которые получены в §§ 13 и 16, обсуждается в части III гл. XII.
Для удобства изложения и большей общности мы рассматриваем в этой главе векторы  с комплексными компонентами, что позволяет привести
с комплексными компонентами, что позволяет привести  к подходящей нормальной форме с помощью линейной замены переменных; ср. § IV.9. Соответственно, если
к подходящей нормальной форме с помощью линейной замены переменных; ср. § IV.9. Соответственно, если  — два вектора, то через
— два вектора, то через  обозначается их скалярное произведение 2
обозначается их скалярное произведение 2
§ 1. Случай Е = 0
В этом параграфе рассматривается уравнение

где вектор  «мал» в некотором смысле. Основной результат содержится в следующей теореме.
«мал» в некотором смысле. Основной результат содержится в следующей теореме.
Теорема 1.1. Пусть вектор-функция  непрерывна при
непрерывна при  и удовлетворяет неравенству
и удовлетворяет неравенству

где функция непрерывна при  и такова, что
и такова, что

Если норма  достаточно мала, например
достаточно мала, например

то решение  уравнения (1.1), удовлетворяющее условию
уравнения (1.1), удовлетворяющее условию  существует при
существует при  Кроме того, если функция
Кроме того, если функция  удовлетворяет уравнению (1.1) при больших
удовлетворяет уравнению (1.1) при больших  например при
например при  то
то

существует и  если
если 
Иными словами, решения системы (1.1) при больших  ведут себя так же, как решения системы
ведут себя так же, как решения системы  а именно как постоянные. Теорема 1.1 допускает следующее обобщение.
а именно как постоянные. Теорема 1.1 допускает следующее обобщение.
Теорема 1.2. Пусть вектор  удовлетворяет предположениям теоремы 1.1, и пусть
удовлетворяет предположениям теоремы 1.1, и пусть  произвольный вектор, для которого
произвольный вектор, для которого

Тогда система (1.1) имеет по крайней мере одно решение  удовлетворяющее условию (1.5) при 0. Если, кроме того,
удовлетворяющее условию (1.5) при 0. Если, кроме того,  удовлетворяет условию Липшица следующего вида:
удовлетворяет условию Липшица следующего вида:

то для данного  существует в точности одно решение системы (1.1), определенное для больших
существует в точности одно решение системы (1.1), определенное для больших  и удовлетворяющее (1.5).
и удовлетворяющее (1.5).
В последней части теоремы 1.2 утверждается, что условие (1.7) позволяет установить взаимно однозначное соответствие между решениями  системы
системы  и решениями системы (1.1), если предполагается, что
и решениями системы (1.1), если предполагается, что  достаточно мала и
достаточно мала и 
Доказательство теоремы 1.1. Если умножить (1.1) скалярно на  то из (1.1), (1.2) вытекает, что
то из (1.1), (1.2) вытекает, что

Поскольку  интегрирование неравенства (1.8) дает
интегрирование неравенства (1.8) дает

если  существует на
существует на  -интервале, содержащем точки
-интервале, содержащем точки  где
где  В частности, если
В частности, если  и вектор
и вектор  удовлетворяет условию (1.4), то
удовлетворяет условию (1.4), то  существует при всех
существует при всех 
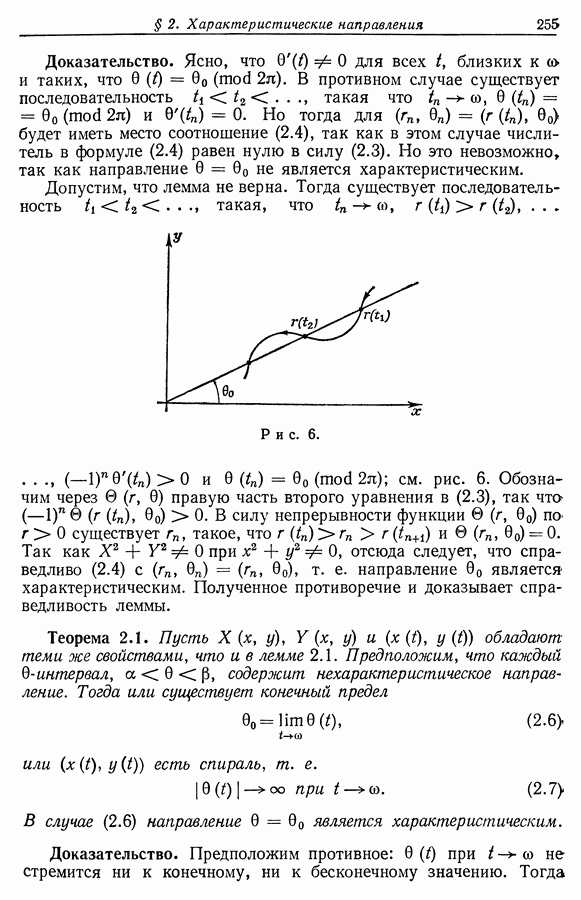
В общем случае, если решение  существует при
существует при  то оно ограничено:
то оно ограничено:

Отсюда получаем, что  (используя для этого (1.1) и (1.2)). Следовательно, интеграл
(используя для этого (1.1) и (1.2)). Следовательно, интеграл  абсолютно сходится и предел (1.5) существует. В самом деле,
абсолютно сходится и предел (1.5) существует. В самом деле,

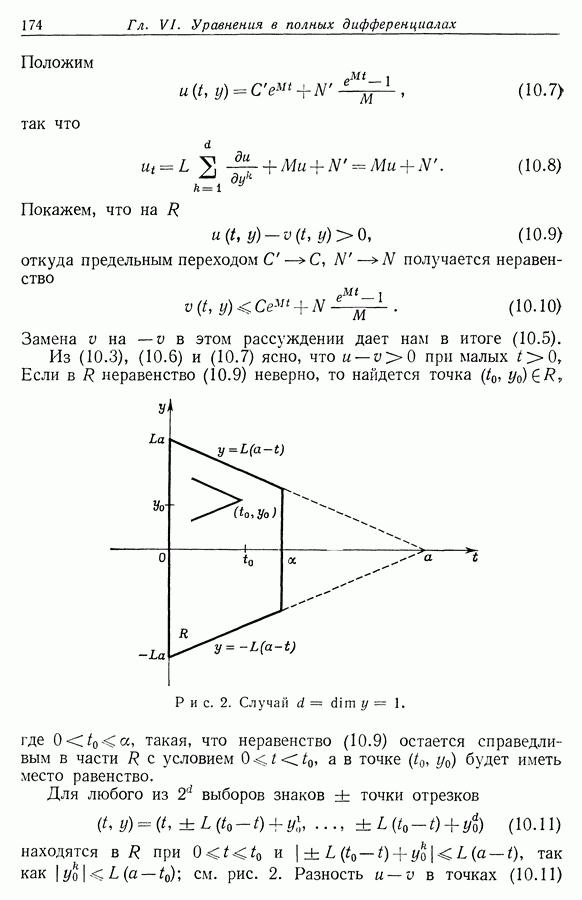
Заметим, что из неравенства (1.9) следует, что  тогда и только тогда, когда
тогда и только тогда, когда  обращается в нуль в некоторой точке
обращается в нуль в некоторой точке  Если
Если  то из первого неравенства в (1.9) следует, что
то из первого неравенства в (1.9) следует, что  Тем самым теорема 1.1 доказана.
Тем самым теорема 1.1 доказана.
Доказательство теоремы 1.2. Докажем вначале утверждение о существовании. Для данного  обозначим через
обозначим через  фиксированное решение (оно не обязательно единственно) следующей задачи Коши:
фиксированное решение (оно не обязательно единственно) следующей задачи Коши:

Поскольку неравенство (1.9) имеет место для любого для которого определено решение  из (1.6) и
из (1.6) и  следует, что
следует, что  существует при всех
существует при всех  Следовательно,
Следовательно,  где
где  определено в (1.10). Поэтому из (1.2) следует, что
определено в (1.10). Поэтому из (1.2) следует, что  при всех
при всех  следовательно, при
следовательно, при  имеем
имеем

В частности, семейство функций  равномерно ограничено и равностепенно непрерывно на каждом ограниченном
равномерно ограничено и равностепенно непрерывно на каждом ограниченном  -интервале. Следовательно, существует последовательность
-интервале. Следовательно, существует последовательность  значений
значений  такая, что
такая, что  при
при  и предел
и предел

существует равномерно на каждом ограниченном  -интервале. Далее,
-интервале. Далее,  есть решение уравнения (1.1). Полагая
есть решение уравнения (1.1). Полагая  в (1.13) и устремляя
в (1.13) и устремляя  при фиксированном получаем
при фиксированном получаем

Отсюда вытекает (1.5), и теорема существования доказана.
Докажем теперь единственность при условии (1.7). Пусть  решения системы (1.1) при больших например при
решения системы (1.1) при больших например при  удовлетворяющих условию (1.5). Пусть
удовлетворяющих условию (1.5). Пусть  Тогда из (1.1) и (1.7) следует (1.8), а потому и (1.9) при
Тогда из (1.1) и (1.7) следует (1.8), а потому и (1.9) при  Если
Если  фиксировано, а в
фиксировано, а в  то отсюда вытекает, что
то отсюда вытекает, что  поскольку
поскольку  при
при 
Этим завершается доказательство теоремы 1.2.
Мажоранта  в (1.2), содержащая множитель
в (1.2), содержащая множитель  удобна тем, что она позволяет доказать в теоремах 1.1 и 1.2 существование некоторых решений при всех
удобна тем, что она позволяет доказать в теоремах 1.1 и 1.2 существование некоторых решений при всех  Более простой результат о существовании решения при «больших
Более простой результат о существовании решения при «больших  содержится в следующем упражнении.
содержится в следующем упражнении.
Упражнение 1.1. Пусть функция  непрерывна на произведении
непрерывна на произведении  где
где  ограниченное открытое
ограниченное открытое  -множество. Пусть
-множество. Пусть  при
при  где
где  непрерывная функция, удовлетворяющая (1.3). (а) Пусть
непрерывная функция, удовлетворяющая (1.3). (а) Пусть  Тогда существует число
Тогда существует число  зависящее только от
зависящее только от  и функции
и функции  такое, что если
такое, что если  то решение
то решение  уравнения (1.1), удовлетворяющее условию
уравнения (1.1), удовлетворяющее условию  существует при всех
существует при всех  Кроме того, всякое решение системы (1.1) при больших
Кроме того, всякое решение системы (1.1) при больших  имеет предел
имеет предел  при
при  Пусть
Пусть  Тогда существует число
Тогда существует число  зависящее только от
зависящее только от  и функции
и функции  такое, что система (1.1) имеет при
такое, что система (1.1) имеет при  решение
решение  удовлетворяющее (1.5).
удовлетворяющее (1.5).
Упражнение 1.2. Покажите, что теорема 1.1 и первая часть теоремы 1.2 остаются справедливыми, если вектор  непрерывен при
непрерывен при  и всех
и всех  если
если  произвольны, а условие (1.2) заменено условием
произвольны, а условие (1.2) заменено условием

где  удовлетворяет условиям теоремы 1.1, а
удовлетворяет условиям теоремы 1.1, а  непрерывная при
непрерывная при  функция, такая, что
функция, такая, что

Из теорем 1.1 и 1.2 можно вывести некоторые следствия, если заменить (1.1) системой

где  непрерывная матрица порядка
непрерывная матрица порядка  Решения системы (1.15) следует сравнивать с решениями системы
Решения системы (1.15) следует сравнивать с решениями системы

Пусть  фундаментальная матрица системы (1.16), так что замена переменных
фундаментальная матрица системы (1.16), так что замена переменных

приводит систему (1.15) к виду

Применяя к (1.18) теоремы 1.1 и 1.2, получаем
Следствие 1.1. Пусть матрица  непрерывна при
непрерывна при  фундаментальная матрица системы (1.16). Предположим, что функция
фундаментальная матрица системы (1.16). Предположим, что функция  непрерывна при
непрерывна при  и всех
и всех  причем
причем

где функция  удовлетворяет предположениям теоремы 1.1. Обозначим через
удовлетворяет предположениям теоремы 1.1. Обозначим через  решение системы (1.15), определенное на некотором
решение системы (1.15), определенное на некотором  -интервале. Тогда
-интервале. Тогда  существует при всех
существует при всех  , предел
, предел

существует и  если
если  обратно, для заданного
обратно, для заданного  существует решение
существует решение  системы (1.15), удовлетворяющее (1.20).
системы (1.15), удовлетворяющее (1.20).
Если матрица  ограничена при
ограничена при  то мы можем сформулировать соответствующий результат, если
то мы можем сформулировать соответствующий результат, если  определена лишь при
определена лишь при  Кроме того, мы можем получить аналог утверждения о единственности в теореме 1.2. Если
Кроме того, мы можем получить аналог утверждения о единственности в теореме 1.2. Если  — постоянная матрица, то следствие 1.1 принимает следующий вид:
— постоянная матрица, то следствие 1.1 принимает следующий вид:
Следствие 1.2. Пусть функция  непрерывна при
непрерывна при  и всех
и всех  и удовлетворяет неравенству
и удовлетворяет неравенству

где  — такая же функция, как и в теореме 1.1. Пусть
— такая же функция, как и в теореме 1.1. Пусть  решение уравнения
решение уравнения

определенное на некотором  -интервале. Тогда
-интервале. Тогда  определено при всех 0, существует
определено при всех 0, существует

 если
если  кроме того, если задано
кроме того, если задано  то существует решение системы (1.22), определенное при всех
то существует решение системы (1.22), определенное при всех  и удовлетворяющее (1.20).
и удовлетворяющее (1.20).
Упражнение 1.3. Сформулируйте теоремы, соответствующие следствиям 1.1 и 1.2 так же, как упражнения 1.1 и 1.2 соответствуют теоремам 1.1 и 1.2.
В общем случае результат такого  который сформулирован в следствии 1.2, удобен только тогда, когда матрицы
который сформулирован в следствии 1.2, удобен только тогда, когда матрицы 
ограничены при  Например, предположим, что
Например, предположим, что  так что
так что  Тогда, если выполнены условия следствия 1.2, система (1.22) имеет решение вида
Тогда, если выполнены условия следствия 1.2, система (1.22) имеет решение вида  при
при  но не обязательно имеет решение вида
но не обязательно имеет решение вида  при
при  Кроме того, условие (1.21) может оказаться слишком жестким для того, чтобы иметь возможность делать такие же выводы, как в следствии 1.2. Результаты, полученные в оставшейся части этой главы, гораздо сильнее; они получены при менее ограничительных условиях, чем те, которые рассматривались выше.
Кроме того, условие (1.21) может оказаться слишком жестким для того, чтобы иметь возможность делать такие же выводы, как в следствии 1.2. Результаты, полученные в оставшейся части этой главы, гораздо сильнее; они получены при менее ограничительных условиях, чем те, которые рассматривались выше.
Упражнение 1.4. Предположим, что (1.1) является линейной однородной системой вида

и матрица  непрерывна при
непрерывна при  Будем говорить, что система (1.23) принадлежит классу
Будем говорить, что система (1.23) принадлежит классу  если (i) каждое решение
если (i) каждое решение  системы (1.23) имеет предел
системы (1.23) имеет предел  при
при  для каждого постоянного вектора
для каждого постоянного вектора  существует решение
существует решение  системы (1.23), такое, что
системы (1.23), такое, что  при
при  Покажите, что (1.23) принадлежит классу
Покажите, что (1.23) принадлежит классу  тогда и только тогда, когда для каждой (или для какой-нибудь одной) фундаментальной матрицы
тогда и только тогда, когда для каждой (или для какой-нибудь одной) фундаментальной матрицы  системы (1.23) существует предел
системы (1.23) существует предел  при
при  который является невырожденной матрицей (и что это верно тогда и только тогда, когда существует
который является невырожденной матрицей (и что это верно тогда и только тогда, когда существует  при
при  сходится хотя бы условно), (b) Система (1.23) принадлежит классу
сходится хотя бы условно), (b) Система (1.23) принадлежит классу  в том и только в том случае, если сопряженная система
в том и только в том случае, если сопряженная система  принадлежит классу
принадлежит классу  Система (1.23) принадлежит классу
Система (1.23) принадлежит классу  если
если  (или, что эквивалентно, если
(или, что эквивалентно, если  при
при 
Это сразу же следует из теорем 1.1, 1.2. (d) Покажите, что (с) имеет следующее следствие (являющееся уточнением  система (1.23) принадлежит классу
система (1.23) принадлежит классу  если
если  сходится (возможно, только условно) и либо
сходится (возможно, только условно) и либо  либо
либо 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- Глава I. Предварительные сведения
- § 2. Основные теоремы
- § 3. Гладкие аппроксимации
- § 4. Замена переменных в интегралах
- Глава II. Теоремы существования
- § 1. Теорема Пикара — Линделёфа
- § 2. Теорема Пеано
- § 3. Теорема о продолжении решения
- § 4. Теорема Кнезера
- § 5. Пример неединственности
- Глава III. Дифференциальные неравенства и единственность
- § 1. Неравенство Гронуолла
- § 2. Максимальные и минимальные решения
- § 3. Правые производные
- § 4. Дифференциальные неравенства
- § 5. Теорема Уинтнера
- § 6. Теоремы единственности
- § 7. Теорема единственности ван Кампена
- § 8. Точки выхода и функции Ляпунова
- § 9. Последовательные приближения
- Глава IV. Линейные дифференциальные уравнения
- § 2. Вариация постоянных
- § 3. Редукция к системам меньшего, порядка
- § 4. Основные неравенства
- § 5. Системы с постоянными коэффициентами
- § 6. Теория Флоке
- § 7. Сопряженные системы
- § 8. Линейные уравнения высших порядков
- § 9. Замечания о замене переменных
- ДОБАВЛЕНИЕ. ЛИНЕЙНЫЕ АНАЛИТИЧЕСКИЕ УРАВНЕНИЯ
- § 10. Фундаментальные матрицы
- § 11. Простые особенности
- § 12. Уравнения высших порядков
- § 13. Кратные особенности
- Глава V. Зависимость от начальных условий и параметров
- § 2. Непрерывность
- § 3. Дифференцируемость
- § 4. Существование производных высших порядков
- § 5. Внешние производные
- § 6. Дальнейшие теоремы о дифференцируемости
- § 7. S- и L-липшицевы формы
- § 8. Теорема единственности
- § 9. Лемма
- § 10. Доказательство теоремы 8.1
- § 11. Доказательство теоремы 6.1
- § 12. Первые интегралы
- Глава VI. Уравнения в полных дифференциалах Уравнения с частными производными
- § 1. Уравнения в полных дифференциалах
- § 2. Алгебра внешних форм
- § 3. Теорема Фробениуса
- § 4. Доказательство теоремы 3.1
- § 5. Доказательство леммы 3.1
- § 6. Система (1.1)
- ЧАСТЬ II. МЕТОД ХАРАКТЕРИСТИК (МЕТОД КОШИ)
- § 7. Нелинейные уравнения в частных производных
- § 8. Характеристики
- § 9. Теорема существования и единственности
- § 10. Лемма Хаара и единственность
- Глава VII. Теория Пуанкаре — Бендиксона
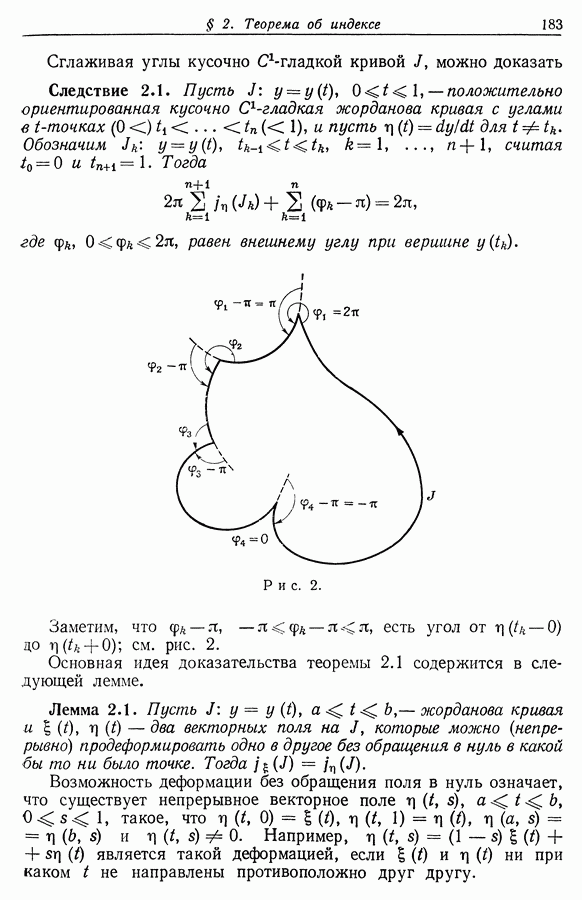
- § 2. Теорема об индексе
- § 3. Индекс стационарной точки
- § 4. Теорема Пуанкаре — Бендиксона
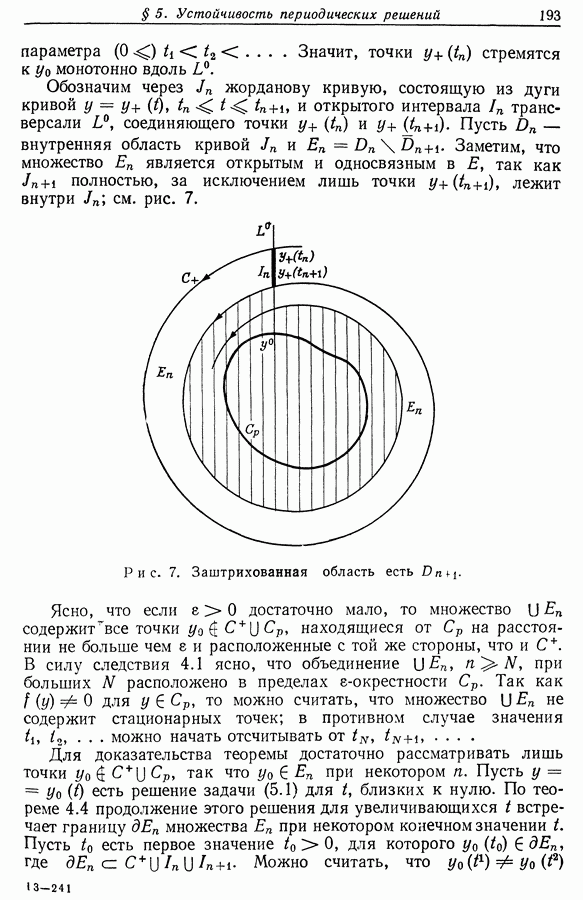
- § 5. Устойчивость периодических решений
- § 6. Точки вращения
- § 7. Фокусы, узлы и седловые точки
- § 8. Секторы
- § 9. Стационарная точка общего вида
- § 10. Уравнения второго порядка
- ПРИЛОЖЕНИЕ. ТЕОРИЯ ПУАНКАРЕБЕ—НДИКСОНА НА ДВУМЕРНЫХ МНОГООБРАЗИЯХ
- § 12. Аналог теоремы Пуанкаре-Бендиксона
- § 13. Каскады на замкнутой кривой
- § 14. Потоки на торе
- Глава VIII. Стационарные точки на плоскости
- § 2. Характеристические направления
- § 3. Системы, близкие к линейным
- § 4. Более общие стационарные точки
- Глава IX. Инвариантные многообразия и линеаризация
- § 2. Отображения Т
- § 3. Модификация функции F(s)
- § 4. Приведение системы к нормальному виду
- § 5. Инвариантные многообразия отображения
- § 6. Существование инвариантных многообразий
- § 7. Линеаризации
- § 8. Линеаризация отображения
- § 9. Доказательство теоремы 7.1
- § 10. Периодические решения
- § 11. Предельные циклы
- ПРИЛОЖЕНИЕ. ГЛАДКО ЭКВИВАЛЕНТНЫЕ ОТОБРАЖЕНИЯ
- § 12. Гладкие линеаризации
- § 9. Доказательство теоремы 7.12
- § 14. Доказательство теоремы 12.2
- Глава X. Возмущенные линейные системы
- § 2. Топологический принцип
- § 3. Теорема Важевского
- § 4. Подготовительные леммы
- § 5. Доказательство леммы 4.1
- § 6. Доказательство леммы 4.2
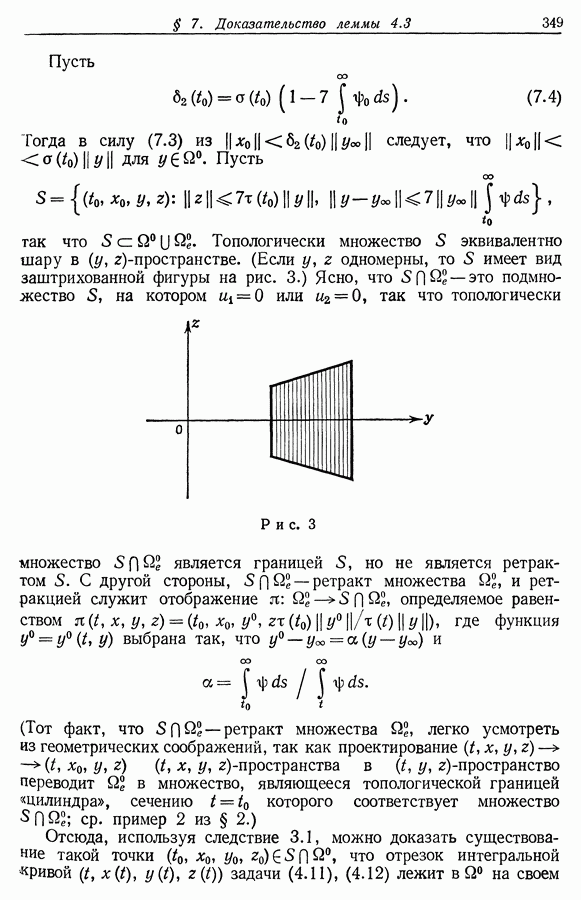
- § 7. Доказательство леммы 4.3
- § 8. Асимптотическое интегрирование. Логарифмическая шкала
- § 9. Доказательство теоремы 8.2
- § 10. Доказательство теоремы 8.3
- § 11. Логарифмическая шкала (продолжение)
- § 12. Доказательство теоремы 11.2
- § 13. Асимптотическое интегрирование
- § 14. Доказательство теоремы 13.1
- § 15. Доказательство теоремы 13.2
- § 16. Следствия и уточнения
- § 17. Линейные уравнения высших порядков
- Глава XI. Линейные уравнения второго порядка
- § 2. Основные факты
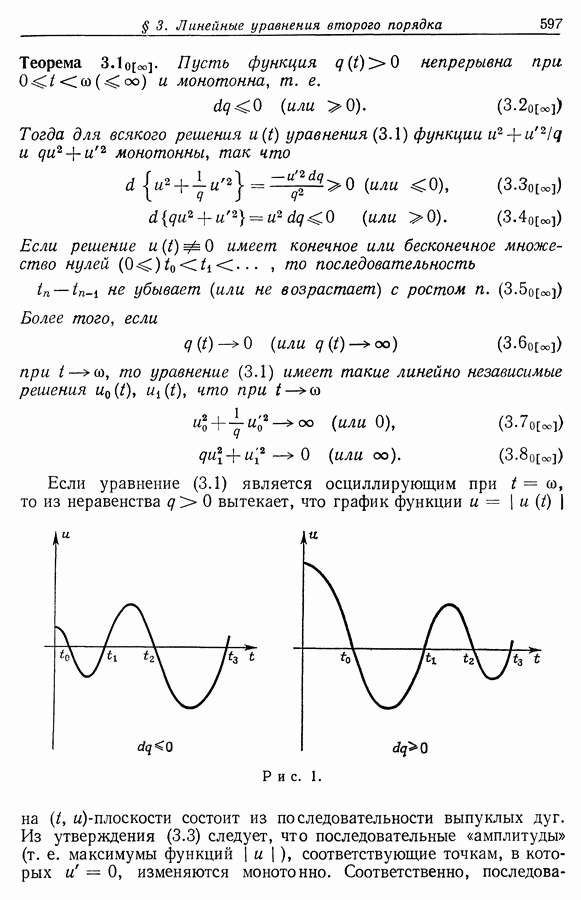
- § 3. Теоремы Штурма
- § 4. Краевые задачи Штурма — Лиувилля
- § 5. Число нулей
- § 6. Неосциллирующие уравнения и главные решения
- § 7. Теоремы о неосциллирующих уравнениях
- § 8. Асимптотическое интегрирование. Эллиптические случаи
- § 9. Асимптотическое интегрирование. Неэллиптические случаи
- ПРИЛОЖЕНИЕ. СИСТЕМЫ БЕЗ СОПРЯЖЕННЫХ ТОЧЕК
- § 11. Обобщения
- Глава XII. Некоторые применения теорем о неявных функциях и неподвижных точках
- ЧАСТЬ I. ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ
- § 2. Нелинейные задачи
- ЧАСТЬ II. ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
- § 4. Нелинейные задачи
- § 5. Априорные оценки
- ЧАСТЬ III. ОБЩАЯ ТЕОРИЯ
- § 7. Функции Грина
- § 8. Нелинейные уравнения
- § 9. Асимптотическое интегрирование
- Глава XIII. Дихотомии для решений линейных уравнений
- § 2. Предварительные леммы
- § 3. Оператор T
- § 4. Оценки для ||Py(t)||
- § 5. Оценки для ||y(t)||
- § 6. Приложения к системам первого порядка
- § 7. Приложения к системам высшего порядка
- § 8. P(B,D)-многообразия
- ЧАСТЬ II. СОПРЯЖЕННЫЕ УРАВНЕНИЯ
- § 10. Оператор T’
- § 11. Индивидуальные дихотомии
- § 12. Р-допустимые пространства для T’
- § 13. Приложения к дифференциальным уравнениям
- § 14. Существование PD решений
- Глава XIV. Монотонность
- ЧАСТЬ I. МОНОТОННЫЕ РЕШЕНИЯ
- § 2. Монотонные решения
- § 3. Линейные уравнения второго порядка
- § 4. Линейные уравнения второго порядка (продолжение)
- ЧАСТЬ II. ОДНА ЗАДАЧА ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
- § 6. Случай «лямбда» больше 0
- § 7. Случай «лямбда» меньше 0
- § 8. Случай «лямбда» равна 0
- § 9. Асимптотическое поведение
- ЧАСТЬ III. АСИМПТОТИЧЕСКАЯ УСТОЙЧИВОСТЬ В ЦЕЛОМ
- § 11. Функции Ляпунова
- § 12. Переменная матрица G
- § 13. О следствии 11.2
- § 14. «J(y) x*x меньше либо равно 0, если x*f(y) = 0»
- § 15. Доказательство теоремы 14.2
- § 16. Доказательство теоремы 14.1