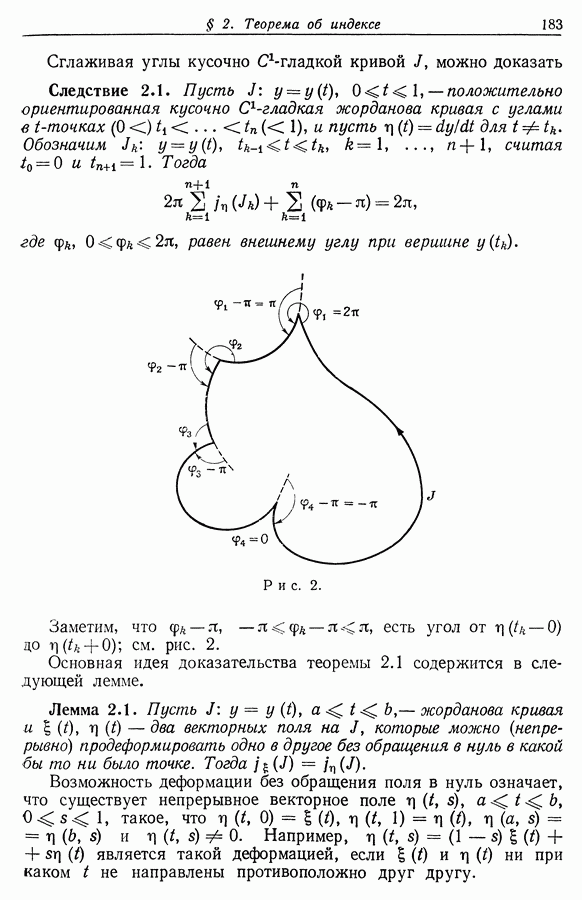
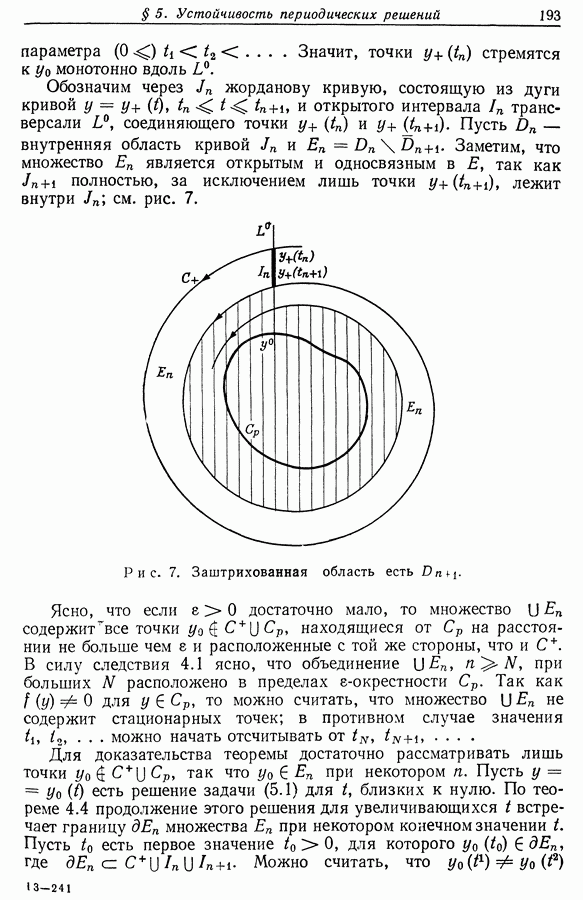
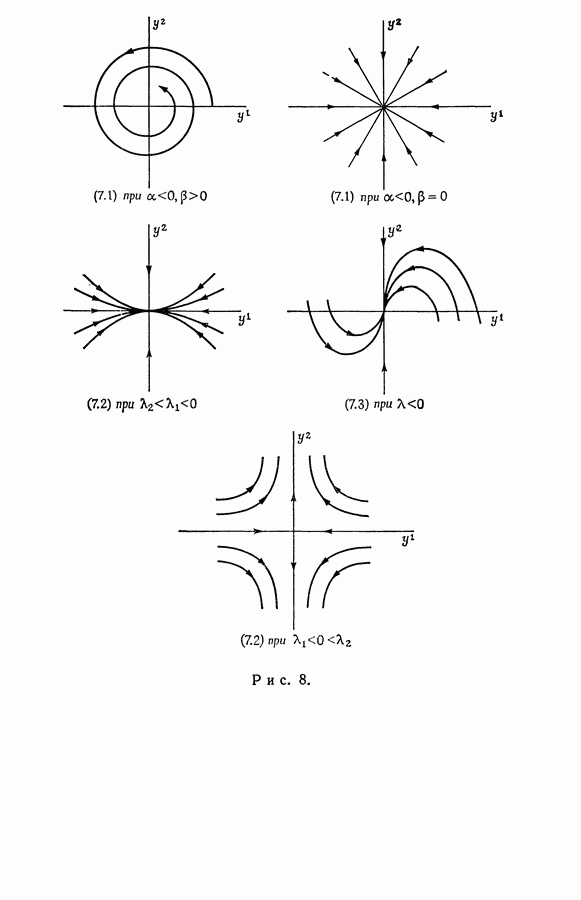
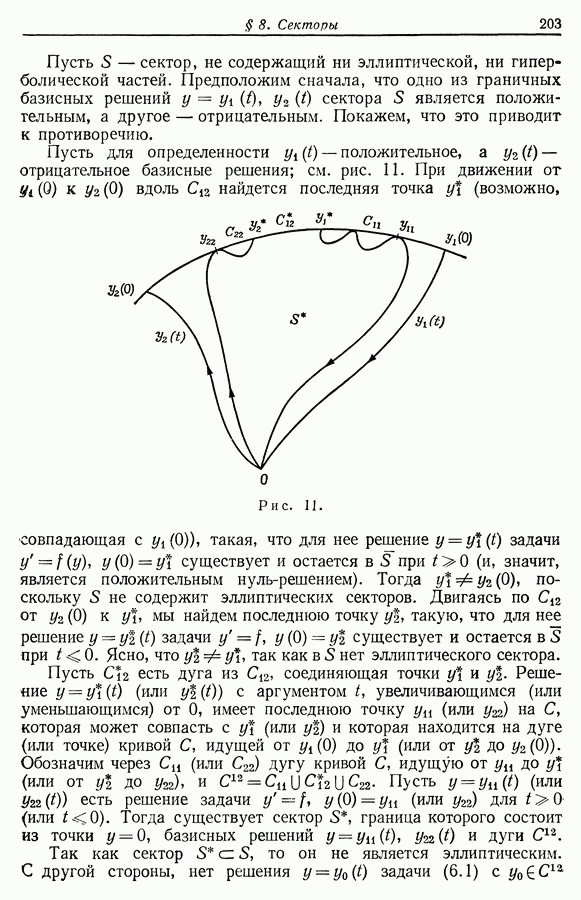
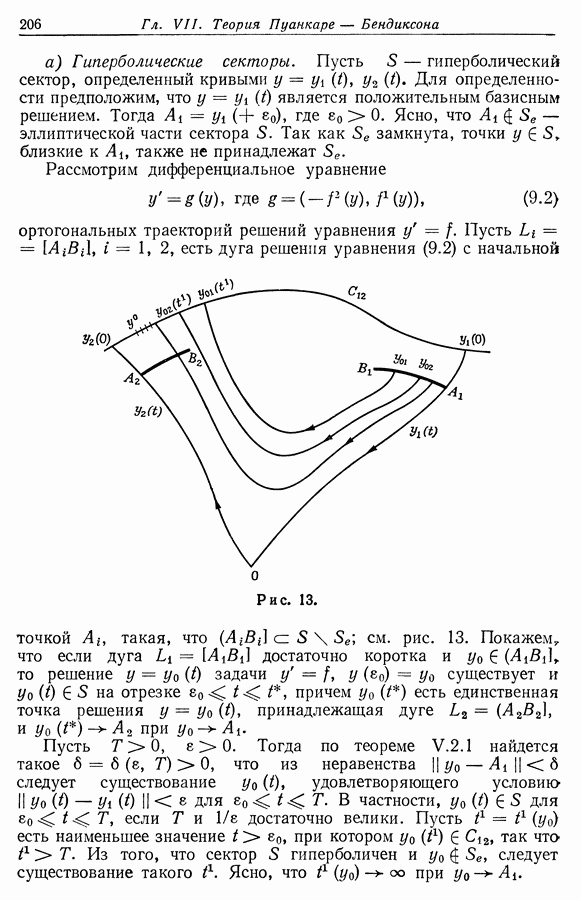
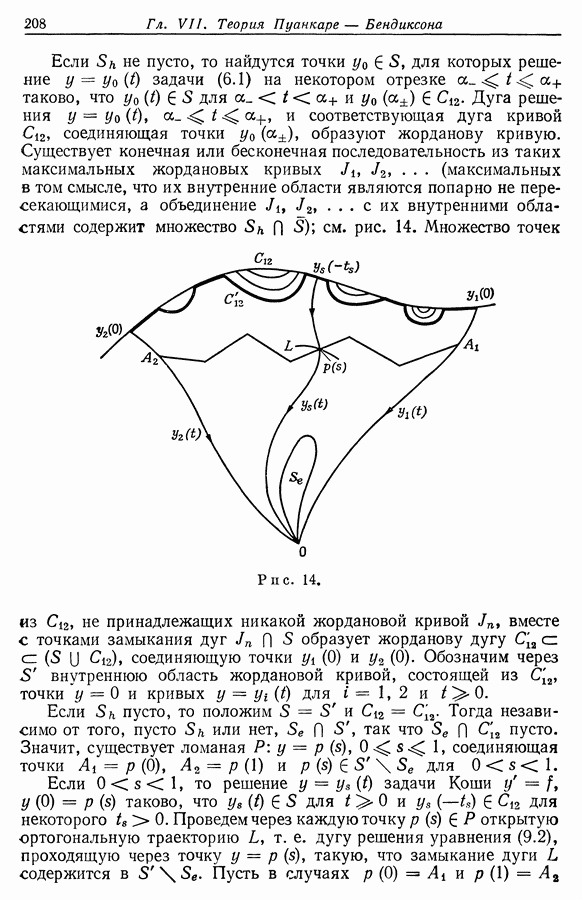
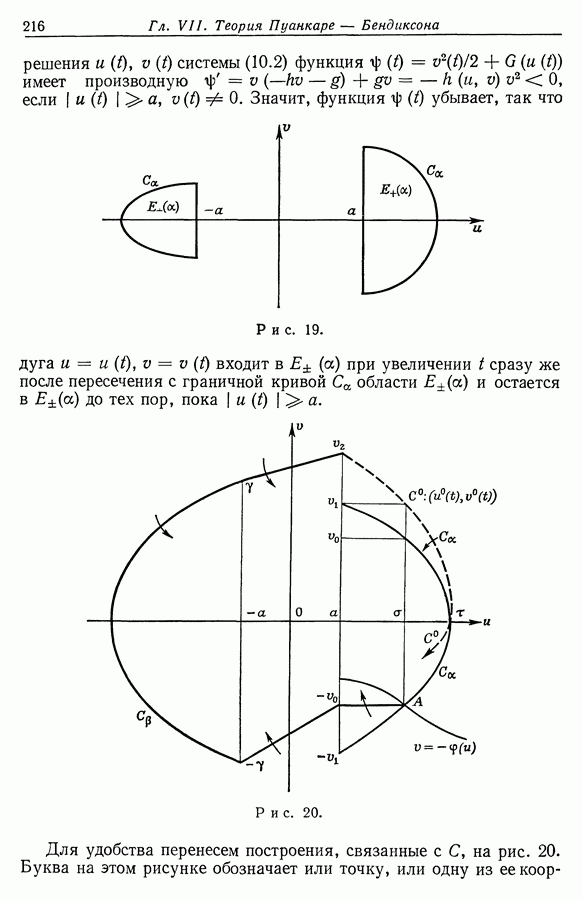
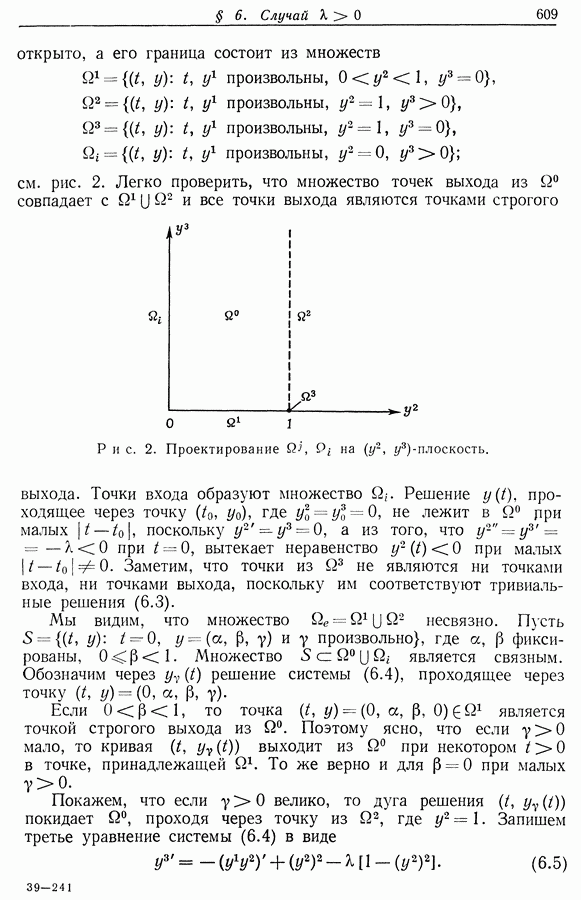
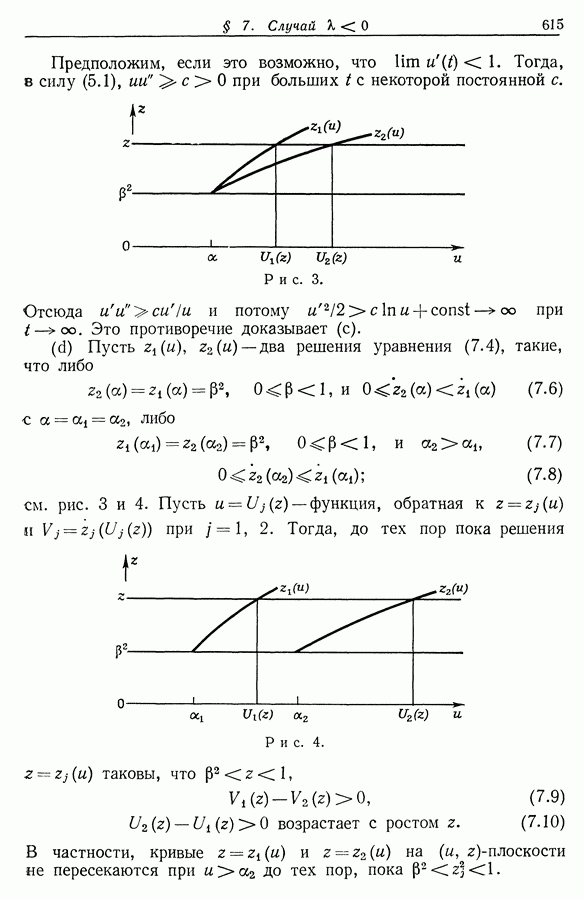
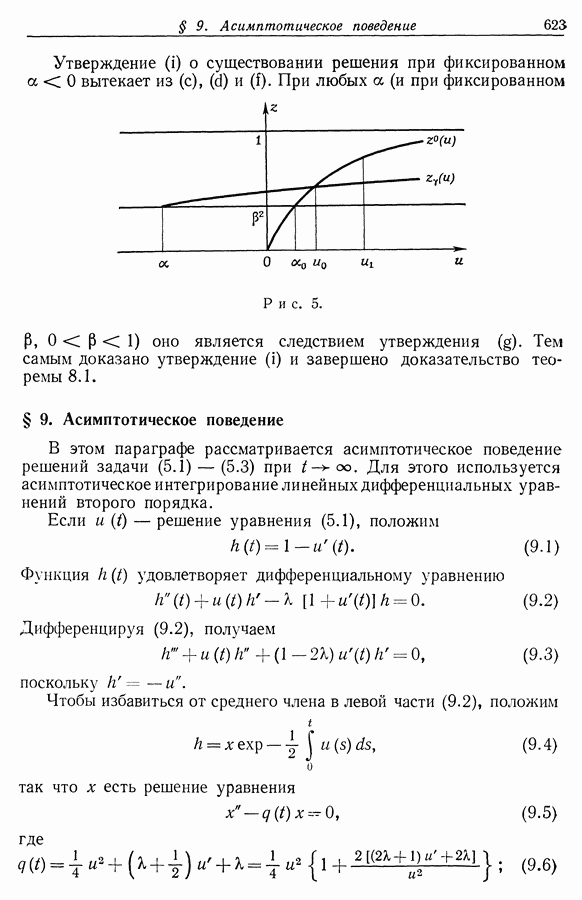
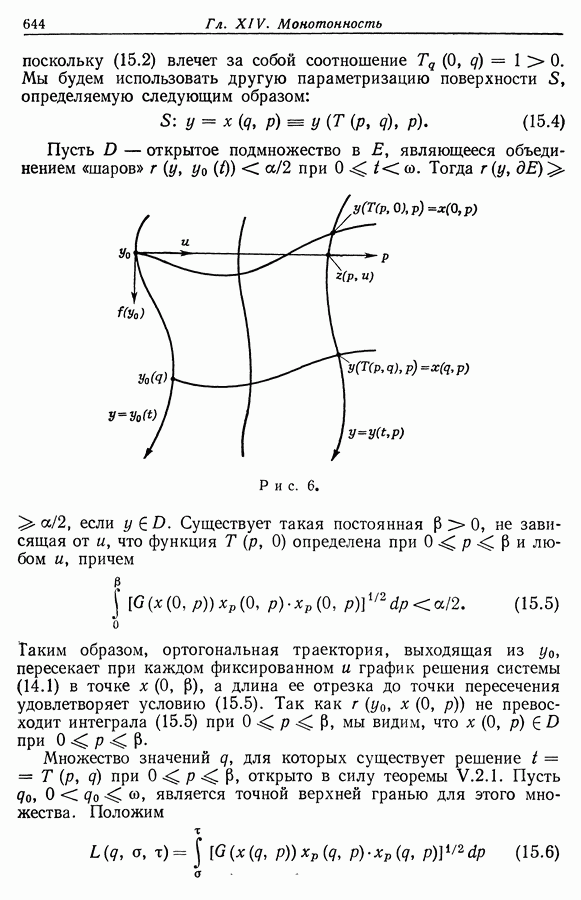
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 4. Теорема Пуанкаре — Бендиксона
Рассмотрение дифференциального уравнения  начатое в § 1, теперь будет продолжено для плоского случая
начатое в § 1, теперь будет продолжено для плоского случая  с применением теоремы Жордана. Основным результатом здесь является следующая теорема Пуанкаре — Бендиксона:
с применением теоремы Жордана. Основным результатом здесь является следующая теорема Пуанкаре — Бендиксона:
Теорема 4.1. Пусть поле  непрерывно в открытом плоском множестве
непрерывно в открытом плоском множестве  и пусть
и пусть  есть решение уравнения
есть решение уравнения

 имеющее компактное замыкание в
имеющее компактное замыкание в  Предположим, кроме того,
Предположим, кроме того,  для
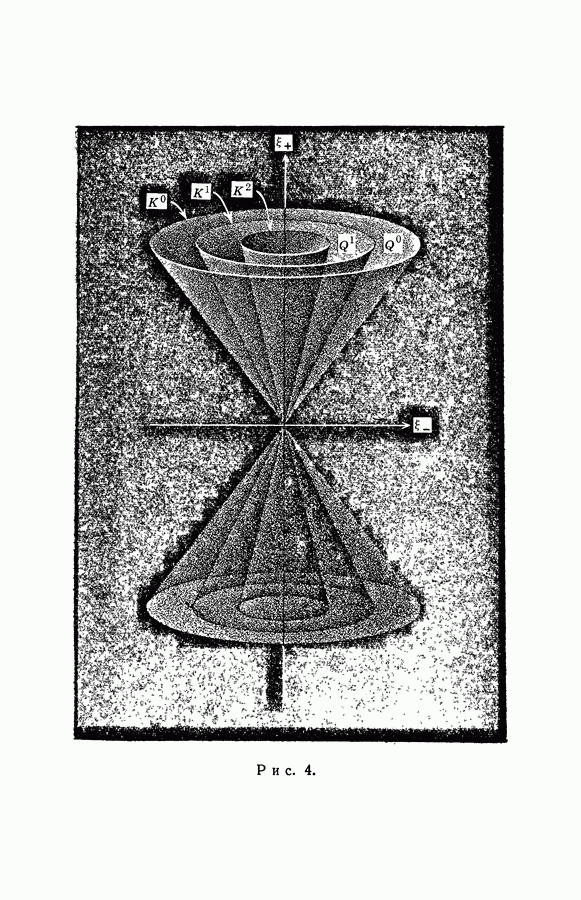
для  что
что  не содержит стационарных точек. Тогда
не содержит стационарных точек. Тогда  состоит из точек у периодического решения
состоит из точек у периодического решения  уравнения (4.1). Далее, если
уравнения (4.1). Далее, если  наименьший период решения
наименьший период решения  то
то  для
для  т. е. кривая
т. е. кривая  является жордановой.
является жордановой.
Если задачи Коши для уравнения (4.1) имеют единственные решения, то либо  для
для  либо решение
либо решение  является периодическим (т. е.
является периодическим (т. е.  при всех
при всех  для некоторого фиксированного положительного числа
для некоторого фиксированного положительного числа  В последнем случае (исключенном в теореме 4.1) множество
В последнем случае (исключенном в теореме 4.1) множество  совпадает с множеством
совпадает с множеством 
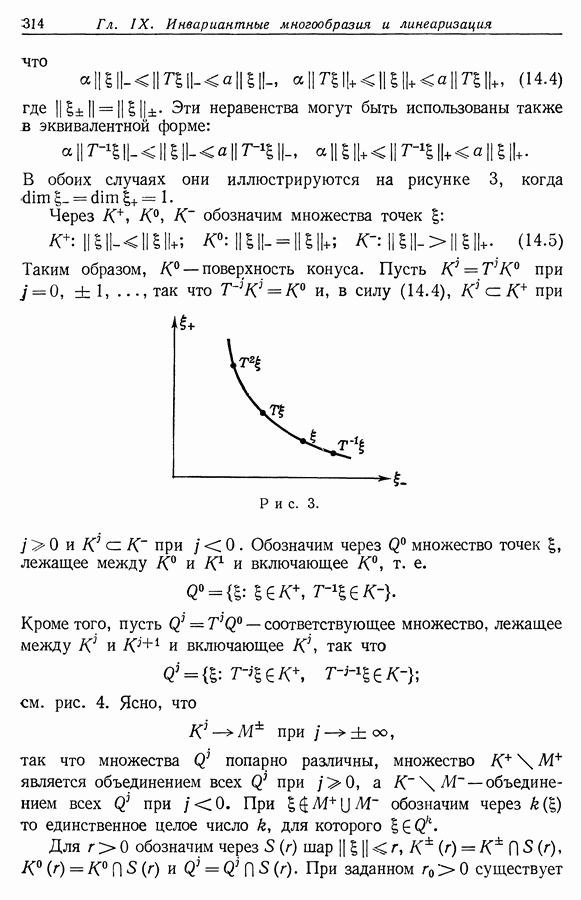
Из доказательства теоремы 4.1 будет видно, что  является спиралью, наворачивающейся на замкнутую кривую
является спиралью, наворачивающейся на замкнутую кривую  или извне, или изнутри; см. рис. 4. Будет установлено также такое
или извне, или изнутри; см. рис. 4. Будет установлено также такое
Следствие 4.1. Пусть выполнены предположения теоремы 4.1, и пусть  период решения
период решения  Тогда существует последовательность
Тогда существует последовательность  такая, что
такая, что

равномерно относительно  и
и

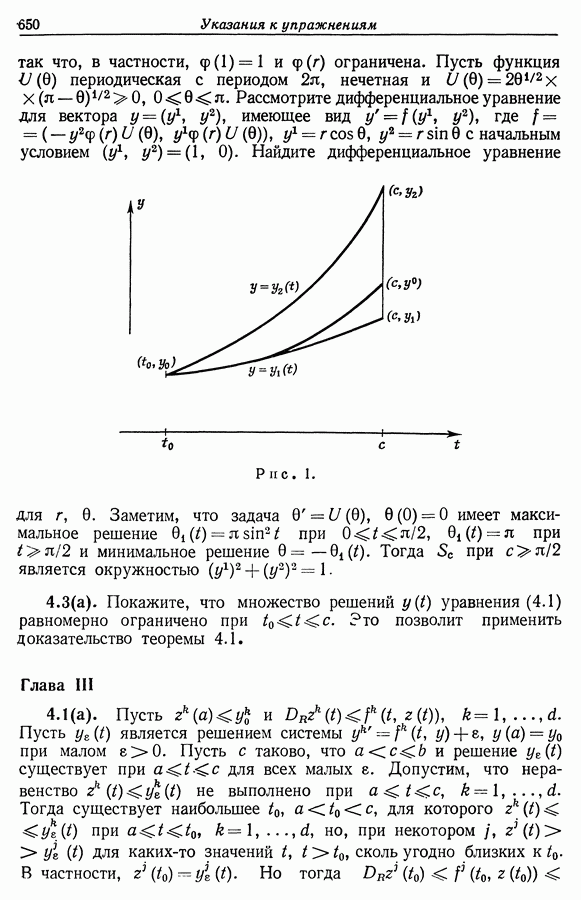
Доказательство теоремы 4.1. Прямолинейный отрезок  называется трансверсалью для уравнения (4.1), если ни в одной точке
называется трансверсалью для уравнения (4.1), если ни в одной точке  вектор
вектор  и не параллелен отрезку
и не параллелен отрезку 

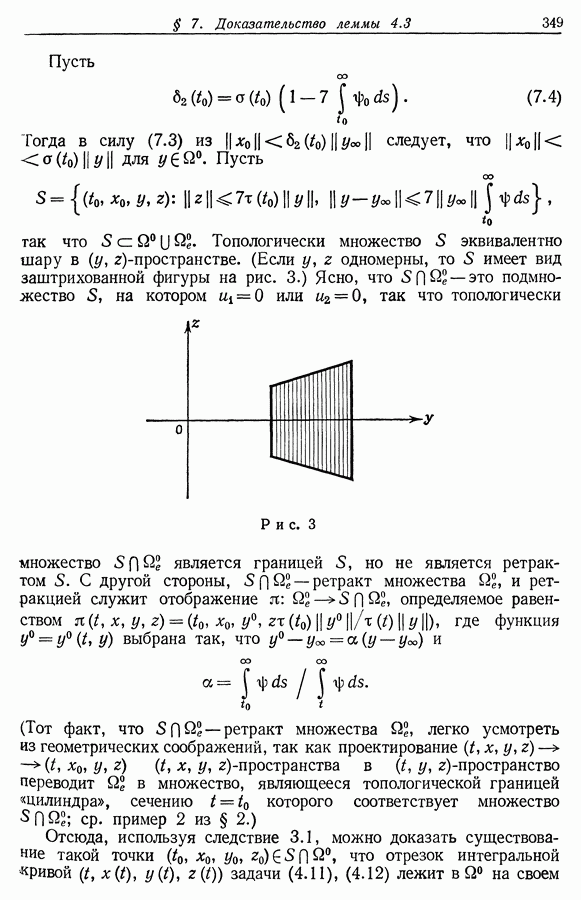
Рис. 4.
Все пересечения  с решением
с решением  уравнения
уравнения  происходят в одном и том же направлении при увеличивающемся
происходят в одном и том же направлении при увеличивающемся 
Доказательство разобьем на пять этапов.
(a) Пусть  трансверсаль, проходящая через
трансверсаль, проходящая через  Тогда из теоремы Пеано следует, что найдутся малая окрестность
Тогда из теоремы Пеано следует, что найдутся малая окрестность  точки
точки  и число
и число  такие, что каждое решение
такие, что каждое решение  задачи Коши
задачи Коши  для
для  существует в отрезке
существует в отрезке  и пересекает
и пересекает  при этих значениях
при этих значениях  точно один раз. В самом деле, если взять произвольное
точно один раз. В самом деле, если взять произвольное  то
то  могут быть выбраны так, что
могут быть выбраны так, что  существует и отличается от
существует и отличается от  при
при  не больше чем на
не больше чем на  Значит, если окрестность
Значит, если окрестность  достаточно мала, то решение
достаточно мала, то решение  пересекает
пересекает  по крайней мере один раз, но в то же время оно при
по крайней мере один раз, но в то же время оно при  может пересечься с
может пересечься с  не больше одного раза, так как пересечения его с
не больше одного раза, так как пересечения его с  должны иметь одинаковые направления.
должны иметь одинаковые направления.
В частности, отсюда следует, что если  решение уравнения
решение уравнения  в некотором конечном отрезке, то
в некотором конечном отрезке, то  пересекается с
пересекается с  самое большее конечное число раз.
самое большее конечное число раз.
(b) Пусть  трансверсаль, которую без потери общности можно считать отрезком
трансверсаль, которую без потери общности можно считать отрезком  -оси, где
-оси, где  Предположим,
Предположим,
что  пересекается с
пересекается с  в точках, отвечающих значениям
в точках, отвечающих значениям  тогда (4) будет строго монотонной функцией от
тогда (4) будет строго монотонной функцией от 
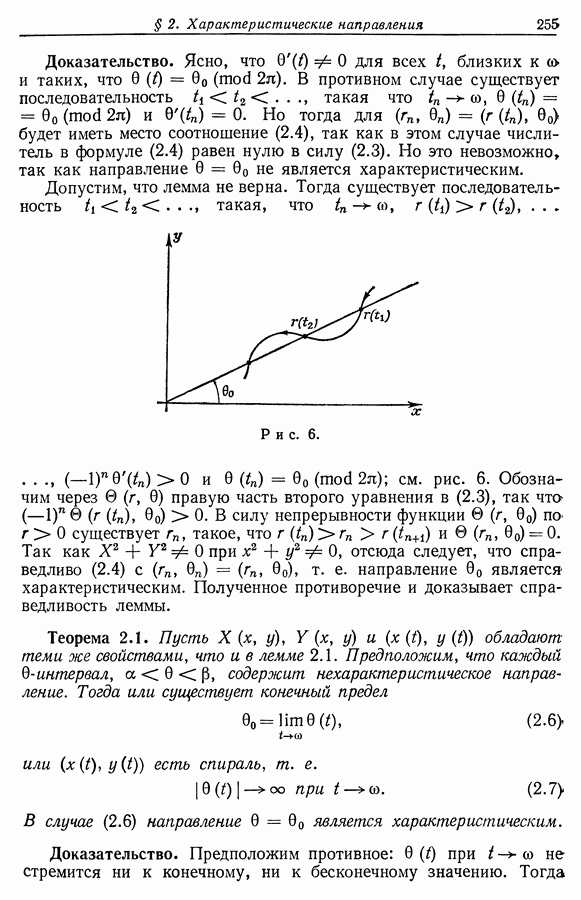
Чтобы убедиться в этом, предположим без потери общности, что при пересечениях с  значение
значение  возрастает (т. е.
возрастает (т. е.  при пересечении меняет знак с минуса на плюс). Рассмотрим случай
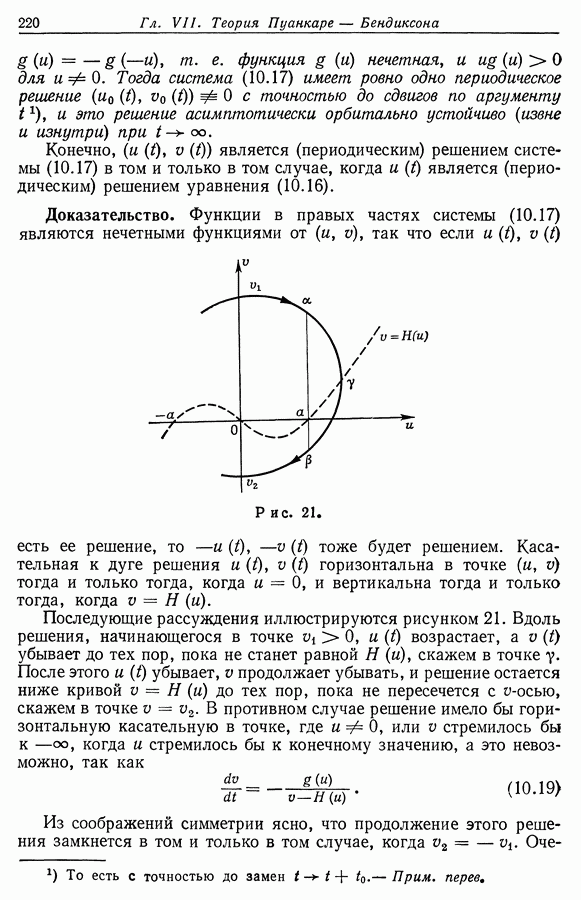
при пересечении меняет знак с минуса на плюс). Рассмотрим случай  см. рис. 5. Множество, состоящее из дуги
см. рис. 5. Множество, состоящее из дуги  и прямолинейного отрезка
и прямолинейного отрезка  на
на  -оси, образует жорданову кривую Для всех
-оси, образует жорданову кривую Для всех  точки
точки  лежат или во внешней, или во внутренней областях кривой
лежат или во внешней, или во внутренней областях кривой  в силу предположений относительно
в силу предположений относительно  и того факта, что пересечения
и того факта, что пересечения  происходят только в одном направлении. Отсюда ясно, что
происходят только в одном направлении. Отсюда ясно, что  и это рассуждение можно продолжить далее для остальных точек.
и это рассуждение можно продолжить далее для остальных точек.

Рис. 5.
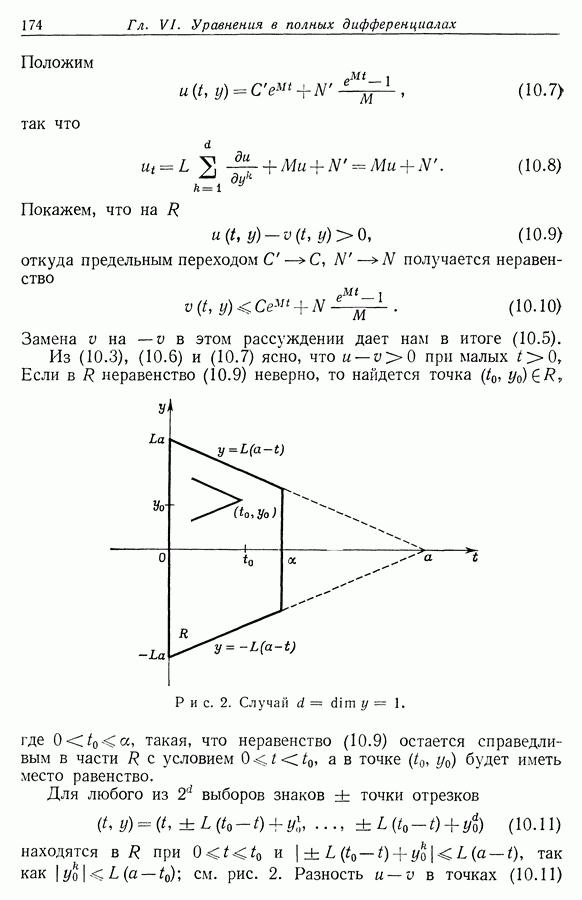
(c) Проверим теперь, что если  трансверсаль, то
трансверсаль, то  содержит самое большее одну точку из
содержит самое большее одну точку из  Действительно, если
Действительно, если  то из (а) следует, что
то из (а) следует, что  пересекает
пересекает  бесконечное число раз (а именно всякий раз, когда она проходит достаточно близко от точки
бесконечное число раз (а именно всякий раз, когда она проходит достаточно близко от точки  С увеличением
С увеличением  точки пересечения
точки пересечения  монотонно стремятся к
монотонно стремятся к  вдоль
вдоль  согласно
согласно  Значит, множество
Значит, множество  не может содержать точки, отличной от
не может содержать точки, отличной от 
Так как  ограничено, то
ограничено, то  не пусто. Пусть
не пусто. Пусть  По теореме 1.2 задача Коши
По теореме 1.2 задача Коши  имеет решение
имеет решение  содержащееся в
содержащееся в  значит,
значит, 
Множество  не пусто. Пусть
не пусто. Пусть  так что точка
так что точка  регулярная, поскольку
регулярная, поскольку  не содержит стационарных точек. Поэтому через точку
не содержит стационарных точек. Поэтому через точку  проходит трансверсаль
проходит трансверсаль  имеет вблизи
имеет вблизи  бесконечное число пересечений с
бесконечное число пересечений с  но
но  и каждое пересечение
и каждое пересечение  принадлежит
принадлежит  Согласно (с), все эти точки должны совпадать. В частности, существуют
Согласно (с), все эти точки должны совпадать. В частности, существуют  такие,
такие,
что  Значит, уравнение (4.1) имеет периодическое решение
Значит, уравнение (4.1) имеет периодическое решение  периода
периода  такое, что
такое, что  о (0 для
о (0 для  Поскольку
Поскольку  ни на одном
ни на одном  -интервале не обращается в постоянную, можно считать, что
-интервале не обращается в постоянную, можно считать, что  для
для 
Покажем, что  совпадает со своим подмножеством
совпадает со своим подмножеством  Если это не так, то множество
Если это не так, то множество  не пусто. Тогда
не пусто. Тогда  содержит точку
содержит точку  являющуюся предельной точкой для
являющуюся предельной точкой для  так как
так как  связно по теореме 1.1.
связно по теореме 1.1.

Рис. 6.
Пусть  трансверсаль, проходящая через
трансверсаль, проходящая через  Любой малый шар с центром в
Любой малый шар с центром в  содержит точки
содержит точки  Для любой такой точки
Для любой такой точки  уравнение
уравнение  имеет решение
имеет решение  такое, что
такое, что  в силу теоремы 1.2. Если точка
в силу теоремы 1.2. Если точка  достаточно близка к
достаточно близка к  то
то  пересекает трансверсаль
пересекает трансверсаль  Согласно (с), это пересечение должно быть обязательно в точке
Согласно (с), это пересечение должно быть обязательно в точке 
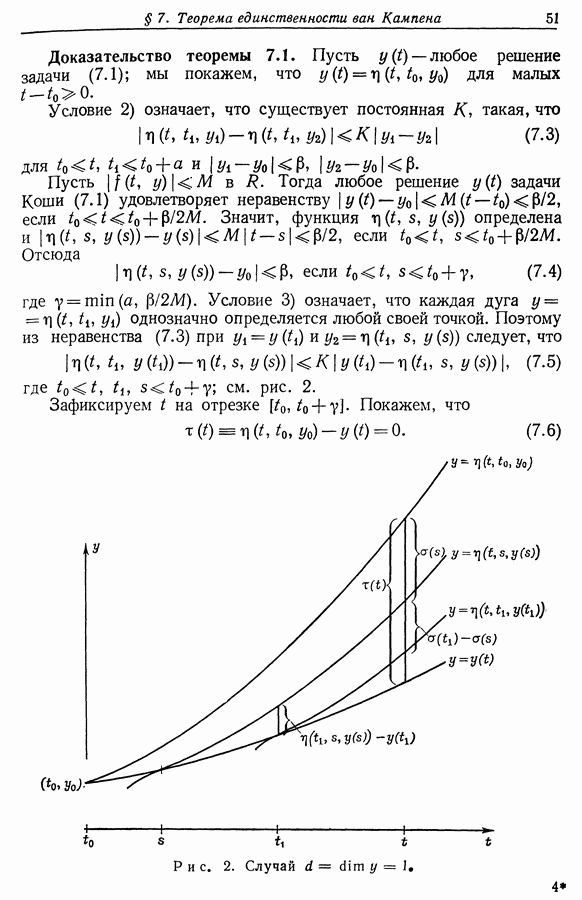
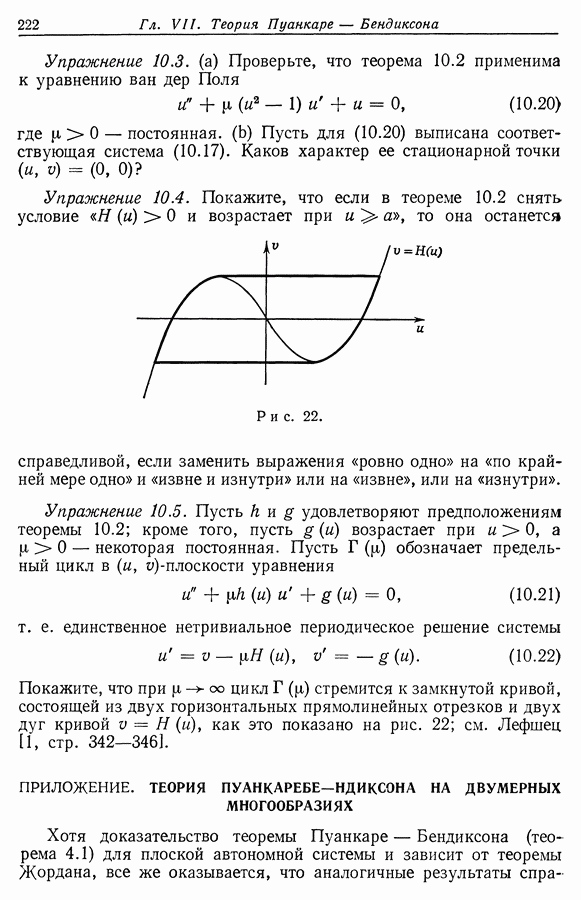
Так как  то такое пересечение невозможно, если задачи Коши для (4.1) имеют единственные решения. В общем случае этот факт можно доказать следующим образом. Пусть
то такое пересечение невозможно, если задачи Коши для (4.1) имеют единственные решения. В общем случае этот факт можно доказать следующим образом. Пусть  в то время как
в то время как  для
для  Так как точка
Так как точка  регулярная, найдется трансверсаль
регулярная, найдется трансверсаль  проходящая через
проходящая через  Тогда малое смещение трансверсали
Тогда малое смещение трансверсали  в подходящем направлении дает трансверсаль
в подходящем направлении дает трансверсаль  которая пересекает
которая пересекает  в двух различных точках; см. рис. 6. Это противоречит части (с). Теорема доказана.
в двух различных точках; см. рис. 6. Это противоречит части (с). Теорема доказана.
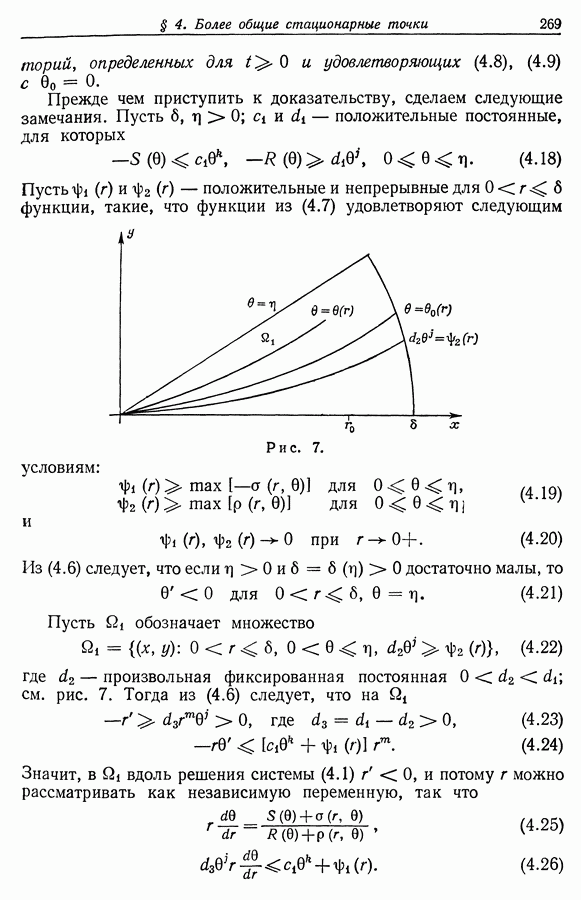
Замечание. В последующем нам потребуется такой факт: рассуждения пункта  показывают, что если
показывают, что если  обладает свойством
обладает свойством  и если точка
и если точка  регулярная, то у точки
регулярная, то у точки  найдется такая окрестность
найдется такая окрестность  что решение задачи
что решение задачи  единственно. Если, кроме того,
единственно. Если, кроме того,  связно и в
связно и в  существует периодическая орбита
существует периодическая орбита  состоящая только из регулярных точек, то
состоящая только из регулярных точек, то 
Доказательство следствия 4.1. Пусть  и пусть
и пусть  трансверсаль, проходящая через
трансверсаль, проходящая через  Пусть последовательные пересечения
Пусть последовательные пересечения  происходят в точках
происходят в точках  Тогда
Тогда  стремится к
стремится к  монотонно вдоль
монотонно вдоль  Поскольку
Поскольку  единственное решение задачи
единственное решение задачи  то из аналога замечания 2 к теореме 1.2 видно, что в (4.2) сходимость равномерна на каждом отрезке, в частности на
то из аналога замечания 2 к теореме 1.2 видно, что в (4.2) сходимость равномерна на каждом отрезке, в частности на 
Заметим, что  при
при  Следовательно, если
Следовательно, если  велико, то
велико, то  пересекает
пересекает  в отрезке
в отрезке  Отсюда
Отсюда  Кроме
Кроме  величина
величина  мала при больших
мала при больших  откуда следует, что существует
откуда следует, что существует  такое, что
такое, что  для
для  В частности, для значений
В частности, для значений  не существует пересечений с
не существует пересечений с  Следовательно,
Следовательно,  при больших
при больших  Тем самым следствие 4.1 доказано.
Тем самым следствие 4.1 доказано.
Теорема 4.2. Пусть  определены так же, как в теореме 4.1 с той лишь разницей, что
определены так же, как в теореме 4.1 с той лишь разницей, что  содержит конечное число
содержит конечное число  стационарных точек уравнения (4.1). Если
стационарных точек уравнения (4.1). Если  то применима теорема 4.1. Если
то применима теорема 4.1. Если  состоит из одной точки, то применимо следствие 1.1. Если
состоит из одной точки, то применимо следствие 1.1. Если  не вырождается в точку, то
не вырождается в точку, то  состоит из стационарных точек
состоит из стационарных точек  и конечной или бесконечной совокупности орбит
и конечной или бесконечной совокупности орбит  проходящих через стационарные точки и таких, что пределы
проходящих через стационарные точки и таких, что пределы  при
при  существуют и совпадают с одной из точек
существуют и совпадают с одной из точек 
Может оказаться, что  Не утверждается, что
Не утверждается, что  есть максимальный интервал существования решения
есть максимальный интервал существования решения  Но если начальные условия определяют решение уравнения (4.1) единственным образом, так что единственное решение уравнения (4.1), проходящее через стационарную точку
Но если начальные условия определяют решение уравнения (4.1) единственным образом, так что единственное решение уравнения (4.1), проходящее через стационарную точку  есть
есть  то тогда
то тогда  см. лемму II.3.1.
см. лемму II.3.1.
Доказательство. Рассмотрим случай, когда  не вырождается в точку. Так как множество
не вырождается в точку. Так как множество  по теореме 1.1 связно, оно содержит регулярные точки
по теореме 1.1 связно, оно содержит регулярные точки  Для любой такой точки у о у задачи
Для любой такой точки у о у задачи  существуют решения
существуют решения  остающиеся при всех
остающиеся при всех  Пусть С обозначает любое такое решение.
Пусть С обозначает любое такое решение.
Рассмотрим только  Случай
Случай  разбирается аналогично. Могут быть две возможности: (i) существует первое положительное значение
разбирается аналогично. Могут быть две возможности: (i) существует первое положительное значение  для которого
для которого  является стационарной точкой (т. е. одной из точек
является стационарной точкой (т. е. одной из точек  или
или  не является стационарной точкой ни при каком конечном
не является стационарной точкой ни при каком конечном 
Рассмотрим случай  Если
Если  содержит регулярную точку
содержит регулярную точку  согласно части (d) доказательства теоремы 4.1, содержит траекторию периодического решения
согласно части (d) доказательства теоремы 4.1, содержит траекторию периодического решения  Но тогда
Но тогда  содержит стационарную точку
содержит стационарную точку  в противном случае, согласно части
в противном случае, согласно части  и замечанию к доказательству теоремы 4.1,
и замечанию к доказательству теоремы 4.1,  . Но это невозможно, так как
. Но это невозможно, так как  при Значит, в случае (ii) множество
при Значит, в случае (ii) множество  может содержать только стационарные точки, и так как оно связно, то состоит лишь из одной стационарной точки у.
может содержать только стационарные точки, и так как оно связно, то состоит лишь из одной стационарной точки у.
Итак, в случае  есть стационарная точка и
есть стационарная точка и  при
при  согласно следствию 1.1. Значит, любая регулярная точка
согласно следствию 1.1. Значит, любая регулярная точка  принадлежащая множеству
принадлежащая множеству  указанного типа, находится на дуге
указанного типа, находится на дуге 
Остается показать, что множество таких дуг  не более чем счетно. Заметим, что если точка
не более чем счетно. Заметим, что если точка  регулярная, то указанное выше решение
регулярная, то указанное выше решение  является единственным в достаточно малом интервале
является единственным в достаточно малом интервале  с частью
с частью  и замечанием после доказательства теоремы 4.1. Следовательно, никакие две дуги решения
и замечанием после доказательства теоремы 4.1. Следовательно, никакие две дуги решения  друг с другом встретиться не могут.
друг с другом встретиться не могут.
Так как  то можно считать, что
то можно считать, что  при
при  не совпадает ни с одной из стационарных точек
не совпадает ни с одной из стационарных точек  В противном случае
В противном случае  можно заменить на
можно заменить на  при подходящем
при подходящем  Кроме того, если точка
Кроме того, если точка  регулярная, то
регулярная, то  для
для 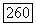 так как последовательность пересечений
так как последовательность пересечений 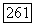 с трансверсалью, проходящей через
с трансверсалью, проходящей через 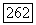 стремится к
стремится к 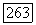 строго монотонно; см. часть (b) доказательства теоремы 4.1. Значит,
строго монотонно; см. часть (b) доказательства теоремы 4.1. Значит, 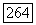 не могут иметь общей точки.
не могут иметь общей точки.
Допустим, что существует несчетное множество дуг Со, относительно которых тогда можно предположить, что они соединяют одну и ту же пару стационарных (не обязательно различных) точек. Любая пара этих соединяющих дуг (или одна дуга) образует жорданову кривую 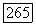 Так как жордановых кривых с попарно непересекающимися внутренними областями существует не более чем счетное множество, то найдутся три различные кривые скажем
Так как жордановых кривых с попарно непересекающимися внутренними областями существует не более чем счетное множество, то найдутся три различные кривые скажем 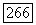 такие, что
такие, что 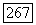 будет содержаться в замыкании внутренних областей
будет содержаться в замыкании внутренних областей 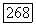 кривых
кривых 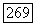 Но это невозможно, так как
Но это невозможно, так как 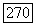 не пересекается с
не пересекается с 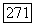 и находится или между
и находится или между 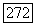 и или между
и или между 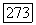
В следующей теореме мы снимаем предположение о том, что 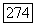
Теорема 4.3. Пусть 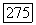 непрерывна в открытом плоском множестве
непрерывна в открытом плоском множестве 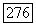 и пусть
и пусть 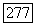 есть решение уравнения (4.1) для
есть решение уравнения (4.1) для 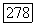 с компактным замыканием в
с компактным замыканием в 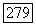 Тогда
Тогда 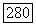 содержит замкнутую (периодическую) орбиту
содержит замкнутую (периодическую) орбиту 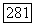 уравнения (4.1), которая может свестись к одной стационарной точке
уравнения (4.1), которая может свестись к одной стационарной точке 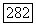
Доказательство. Предположим, что 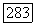 не содержит стационарных точек. Пусть
не содержит стационарных точек. Пусть  и пусть
и пусть 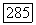 есть решение, существование которого гарантируется теоремой 1.2, так что
есть решение, существование которого гарантируется теоремой 1.2, так что 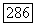 Так как
Так как 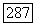 замкнуто,
замкнуто,  Если
Если 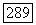 Для
Для 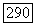 то
то  является по теореме 4.1 замкнутой орбитой
является по теореме 4.1 замкнутой орбитой 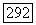 Если же
Если же 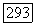 для некоторых
для некоторых 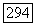 с условием
с условием 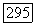 то
то 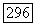 содержит периодическую траекторию
содержит периодическую траекторию 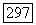 с периодом
с периодом 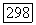 совпадающую с
совпадающую с 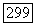 при
при 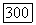 Значит, в любом случае
Значит, в любом случае  содержит замкнутую орбиту
содержит замкнутую орбиту 
Теорема 4.4. Пусть функция  непрерывна в открытой односвязной плоской области
непрерывна в открытой односвязной плоской области  где
где  и пусть
и пусть  есть решение уравнения (4.1) на его максимальном интервале существования
есть решение уравнения (4.1) на его максимальном интервале существования  Тогда
Тогда  выходит из любого компактного подмножества
выходит из любого компактного подмножества  когда
когда 
Доказательство. Если, например,  содержится в некотором компактном подмножестве
содержится в некотором компактном подмножестве  для некоторого то
для некоторого то  по теореме II.3.1 и
по теореме II.3.1 и  содержит периодическое решение
содержит периодическое решение  в силу теоремы 4.3. Так как
в силу теоремы 4.3. Так как  в
в  то функция
то функция  ни на каком
ни на каком  -интервале не может быть постоянной. Пусть
-интервале не может быть постоянной. Пусть  будет первым значением
будет первым значением  для которого
для которого  Тогда кривая
Тогда кривая  является жордановой. Значит, уравнение (4.1) имеет периодическое решение
является жордановой. Значит, уравнение (4.1) имеет периодическое решение  о (0 периода
о (0 периода  такое, что
такое, что  для
для  Так как область
Так как область  односвязна, то внутренняя область кривой
односвязна, то внутренняя область кривой  содержится в
содержится в  По теореме 3.1 во внутренней области кривой
По теореме 3.1 во внутренней области кривой  тогда должна содержаться стационарная точка, что противоречит условию
тогда должна содержаться стационарная точка, что противоречит условию  Теорема доказана.
Теорема доказана.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
- ИЗ ПРЕДИСЛОВИЯ АВТОРА
- Глава I. Предварительные сведения
- § 2. Основные теоремы
- § 3. Гладкие аппроксимации
- § 4. Замена переменных в интегралах
- Глава II. Теоремы существования
- § 1. Теорема Пикара — Линделёфа
- § 2. Теорема Пеано
- § 3. Теорема о продолжении решения
- § 4. Теорема Кнезера
- § 5. Пример неединственности
- Глава III. Дифференциальные неравенства и единственность
- § 1. Неравенство Гронуолла
- § 2. Максимальные и минимальные решения
- § 3. Правые производные
- § 4. Дифференциальные неравенства
- § 5. Теорема Уинтнера
- § 6. Теоремы единственности
- § 7. Теорема единственности ван Кампена
- § 8. Точки выхода и функции Ляпунова
- § 9. Последовательные приближения
- Глава IV. Линейные дифференциальные уравнения
- § 2. Вариация постоянных
- § 3. Редукция к системам меньшего, порядка
- § 4. Основные неравенства
- § 5. Системы с постоянными коэффициентами
- § 6. Теория Флоке
- § 7. Сопряженные системы
- § 8. Линейные уравнения высших порядков
- § 9. Замечания о замене переменных
- ДОБАВЛЕНИЕ. ЛИНЕЙНЫЕ АНАЛИТИЧЕСКИЕ УРАВНЕНИЯ
- § 10. Фундаментальные матрицы
- § 11. Простые особенности
- § 12. Уравнения высших порядков
- § 13. Кратные особенности
- Глава V. Зависимость от начальных условий и параметров
- § 2. Непрерывность
- § 3. Дифференцируемость
- § 4. Существование производных высших порядков
- § 5. Внешние производные
- § 6. Дальнейшие теоремы о дифференцируемости
- § 7. S- и L-липшицевы формы
- § 8. Теорема единственности
- § 9. Лемма
- § 10. Доказательство теоремы 8.1
- § 11. Доказательство теоремы 6.1
- § 12. Первые интегралы
- Глава VI. Уравнения в полных дифференциалах Уравнения с частными производными
- § 1. Уравнения в полных дифференциалах
- § 2. Алгебра внешних форм
- § 3. Теорема Фробениуса
- § 4. Доказательство теоремы 3.1
- § 5. Доказательство леммы 3.1
- § 6. Система (1.1)
- ЧАСТЬ II. МЕТОД ХАРАКТЕРИСТИК (МЕТОД КОШИ)
- § 7. Нелинейные уравнения в частных производных
- § 8. Характеристики
- § 9. Теорема существования и единственности
- § 10. Лемма Хаара и единственность
- Глава VII. Теория Пуанкаре — Бендиксона
- § 2. Теорема об индексе
- § 3. Индекс стационарной точки
- § 4. Теорема Пуанкаре — Бендиксона
- § 5. Устойчивость периодических решений
- § 6. Точки вращения
- § 7. Фокусы, узлы и седловые точки
- § 8. Секторы
- § 9. Стационарная точка общего вида
- § 10. Уравнения второго порядка
- ПРИЛОЖЕНИЕ. ТЕОРИЯ ПУАНКАРЕБЕ—НДИКСОНА НА ДВУМЕРНЫХ МНОГООБРАЗИЯХ
- § 12. Аналог теоремы Пуанкаре-Бендиксона
- § 13. Каскады на замкнутой кривой
- § 14. Потоки на торе
- Глава VIII. Стационарные точки на плоскости
- § 2. Характеристические направления
- § 3. Системы, близкие к линейным
- § 4. Более общие стационарные точки
- Глава IX. Инвариантные многообразия и линеаризация
- § 2. Отображения Т
- § 3. Модификация функции F(s)
- § 4. Приведение системы к нормальному виду
- § 5. Инвариантные многообразия отображения
- § 6. Существование инвариантных многообразий
- § 7. Линеаризации
- § 8. Линеаризация отображения
- § 9. Доказательство теоремы 7.1
- § 10. Периодические решения
- § 11. Предельные циклы
- ПРИЛОЖЕНИЕ. ГЛАДКО ЭКВИВАЛЕНТНЫЕ ОТОБРАЖЕНИЯ
- § 12. Гладкие линеаризации
- § 9. Доказательство теоремы 7.12
- § 14. Доказательство теоремы 12.2
- Глава X. Возмущенные линейные системы
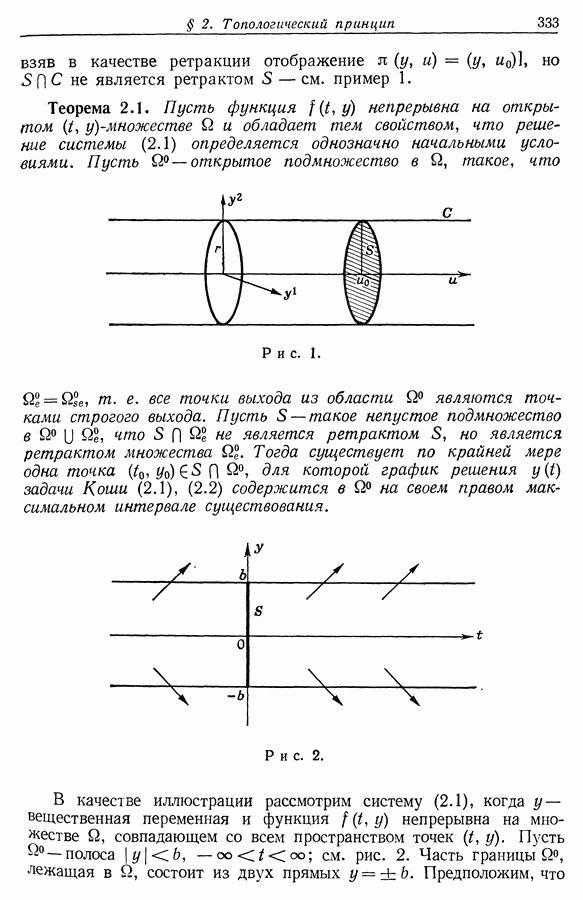
- § 2. Топологический принцип
- § 3. Теорема Важевского
- § 4. Подготовительные леммы
- § 5. Доказательство леммы 4.1
- § 6. Доказательство леммы 4.2
- § 7. Доказательство леммы 4.3
- § 8. Асимптотическое интегрирование. Логарифмическая шкала
- § 9. Доказательство теоремы 8.2
- § 10. Доказательство теоремы 8.3
- § 11. Логарифмическая шкала (продолжение)
- § 12. Доказательство теоремы 11.2
- § 13. Асимптотическое интегрирование
- § 14. Доказательство теоремы 13.1
- § 15. Доказательство теоремы 13.2
- § 16. Следствия и уточнения
- § 17. Линейные уравнения высших порядков
- Глава XI. Линейные уравнения второго порядка
- § 2. Основные факты
- § 3. Теоремы Штурма
- § 4. Краевые задачи Штурма — Лиувилля
- § 5. Число нулей
- § 6. Неосциллирующие уравнения и главные решения
- § 7. Теоремы о неосциллирующих уравнениях
- § 8. Асимптотическое интегрирование. Эллиптические случаи
- § 9. Асимптотическое интегрирование. Неэллиптические случаи
- ПРИЛОЖЕНИЕ. СИСТЕМЫ БЕЗ СОПРЯЖЕННЫХ ТОЧЕК
- § 11. Обобщения
- Глава XII. Некоторые применения теорем о неявных функциях и неподвижных точках
- ЧАСТЬ I. ПЕРИОДИЧЕСКИЕ РЕШЕНИЯ
- § 2. Нелинейные задачи
- ЧАСТЬ II. ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ УРАВНЕНИЙ ВТОРОГО ПОРЯДКА
- § 4. Нелинейные задачи
- § 5. Априорные оценки
- ЧАСТЬ III. ОБЩАЯ ТЕОРИЯ
- § 7. Функции Грина
- § 8. Нелинейные уравнения
- § 9. Асимптотическое интегрирование
- Глава XIII. Дихотомии для решений линейных уравнений
- § 2. Предварительные леммы
- § 3. Оператор T
- § 4. Оценки для ||Py(t)||
- § 5. Оценки для ||y(t)||
- § 6. Приложения к системам первого порядка
- § 7. Приложения к системам высшего порядка
- § 8. P(B,D)-многообразия
- ЧАСТЬ II. СОПРЯЖЕННЫЕ УРАВНЕНИЯ
- § 10. Оператор T’
- § 11. Индивидуальные дихотомии
- § 12. Р-допустимые пространства для T’
- § 13. Приложения к дифференциальным уравнениям
- § 14. Существование PD решений
- Глава XIV. Монотонность
- ЧАСТЬ I. МОНОТОННЫЕ РЕШЕНИЯ
- § 2. Монотонные решения
- § 3. Линейные уравнения второго порядка
- § 4. Линейные уравнения второго порядка (продолжение)
- ЧАСТЬ II. ОДНА ЗАДАЧА ТЕОРИИ ПОГРАНИЧНОГО СЛОЯ
- § 6. Случай «лямбда» больше 0
- § 7. Случай «лямбда» меньше 0
- § 8. Случай «лямбда» равна 0
- § 9. Асимптотическое поведение
- ЧАСТЬ III. АСИМПТОТИЧЕСКАЯ УСТОЙЧИВОСТЬ В ЦЕЛОМ
- § 11. Функции Ляпунова
- § 12. Переменная матрица G
- § 13. О следствии 11.2
- § 14. «J(y) x*x меньше либо равно 0, если x*f(y) = 0»
- § 15. Доказательство теоремы 14.2
- § 16. Доказательство теоремы 14.1