| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
6.4.г. Распределение расстояний между уровнями
Берри  отметил, что для более полного выявления различий между регулярными и нерегулярными спектрами важно изучить энергетические спектры в различных масштабах
отметил, что для более полного выявления различий между регулярными и нерегулярными спектрами важно изучить энергетические спектры в различных масштабах  При наибольших разрешениях идентифицируются отдельные собственные значения. Для регулярных состояний это может быть сделано с помощью правил ЭБК, но для нерегулярных состояний такой возможности, как говорилось выше, не существует. На больших масштабах, напротив, спектр может быть охарактеризован лишь в терминах средней плотности состояний
При наибольших разрешениях идентифицируются отдельные собственные значения. Для регулярных состояний это может быть сделано с помощью правил ЭБК, но для нерегулярных состояний такой возможности, как говорилось выше, не существует. На больших масштабах, напротив, спектр может быть охарактеризован лишь в терминах средней плотности состояний  задаваемой формулой Томаса-Ферми
задаваемой формулой Томаса-Ферми

которое представляет собой меру Лиувилля классического фазового пространства при значении энергии  отнесенному к статистическому объему
отнесенному к статистическому объему  «занимаемому» квантовым состоянием. Понятно, что в этом самом грубом масштабе не существует способов различать проявления регулярного и нерегулярного классического движений. При промежуточных степенях разрешения различные группы и распределения уровней энергии дают больше информации об описываемом движении.
«занимаемому» квантовым состоянием. Понятно, что в этом самом грубом масштабе не существует способов различать проявления регулярного и нерегулярного классического движений. При промежуточных степенях разрешения различные группы и распределения уровней энергии дают больше информации об описываемом движении.
Одной из характеристик спектров мощности, наиболее активно изучаемой на этих промежуточных масштабах, является статистика распределений расстояний между уровнями. Эти распределения представляют собой свойства спектра в масштабах порядка среднего расстояния между уровнями, т. е., как видно из (6.4.5), порядка  или
или  Обзор этих вопросов был дан в 1987 году Бэрри в [13]. Наиболее важной величиной является распределение расстояний между близко расположенными соседними уровнями, характеризуемое функцией вероятности
Обзор этих вопросов был дан в 1987 году Бэрри в [13]. Наиболее важной величиной является распределение расстояний между близко расположенными соседними уровнями, характеризуемое функцией вероятности  которая задает вероятность того, что расстояние между двумя соседними (по энергии) уровнями заключено в интервале между
которая задает вероятность того, что расстояние между двумя соседними (по энергии) уровнями заключено в интервале между  Эта величина широко использовалась при изучении статистических свойств энергетических уровней ядра, характеризуемых очень высокой плотностью состояний. Полагая, что моделью энергетических уровней ядра могут служить собственные значения случайных матриц, элементы которых определяются из гауссова ансамбля, Вигнер [23] высказал замечательное предположение, что
Эта величина широко использовалась при изучении статистических свойств энергетических уровней ядра, характеризуемых очень высокой плотностью состояний. Полагая, что моделью энергетических уровней ядра могут служить собственные значения случайных матриц, элементы которых определяются из гауссова ансамбля, Вигнер [23] высказал замечательное предположение, что

В дальнейшем было показано, что этот результат почти идеально согласуется с точным решением модели (вывод которого — сложнейшая задача математической физики; см. [19]). Экспериментальные данные по энергетическим уровням ядра вполне подтвердили предположение Вигнера. Важно отметить, что  при
при 
что подразумевает некоторое «отталкивание» или «избегание пересечения» уровней. Кроме того (ядерные) энергетические уровни могут принадлежать различным классам симметрии, тогда как с помощью распределения Вигнера (6.4.6) каждый такой класс можно описать только в отдельности. Поэтому при смешении распределений, принадлежащих различным классам, возникает распределение Пуассона

которое соответствует совершенно случайной, несогласованной организации уровней.
Для того, чтобы изучать связанные с расстоянием между уровнями статистические свойства собственных значений единственного гамильтониана, можно создать «ансамбль», перейдя к пределу  таким образом, что плотность состояний при данном значении энергии
таким образом, что плотность состояний при данном значении энергии  стремится к бесконечности. Таким образом, в малой энергетической зоне можно получить значимые статистические выборки расстояний между уровнями.
стремится к бесконечности. Таким образом, в малой энергетической зоне можно получить значимые статистические выборки расстояний между уровнями.
Для полностью интегрируемых систем (т. е. таких систем, все состояния которых могут быть проквантованы по правилам ЭБК) было доказано [14], что  является распределением Пуассона (6.4.7) при условии невырожденности гамильтониана
является распределением Пуассона (6.4.7) при условии невырожденности гамильтониана

Поэтому наиболее вероятное расстояние между уровнями равно нулю, что подразумевает сильное группирование уровней. Это не должно удивлять. Регулярные состояния имеют полный набор «хороших» квантовых чисел и могут, следовательно, образовывать сильно коррелированные последовательности по квантовому числу:  Именно такие последовательности могут приводить к строгим правилам отбора Персиваля. Вместе с тем, с точки зрения расстояний по энергии все эти последовательности должны перемешиваться, и следует ожидать, что корреляция будет невелика. В случаях вырожденных гамильтонианов, таких, как системы гармонических осцилляторов, получены различные распределения, которые зависят от тонких теоретико-числовых свойств фундаментальных частот.
Именно такие последовательности могут приводить к строгим правилам отбора Персиваля. Вместе с тем, с точки зрения расстояний по энергии все эти последовательности должны перемешиваться, и следует ожидать, что корреляция будет невелика. В случаях вырожденных гамильтонианов, таких, как системы гармонических осцилляторов, получены различные распределения, которые зависят от тонких теоретико-числовых свойств фундаментальных частот.
Для неинтегрируемых систем высказывалось множество предположений относительно вида  основанных на том, что «неупорядоченность» нерегулярного спектра скорее всего может, в определенном смысле, найти свое выражение в распределении, близком к вигнеровскому. Было проведено множество численных исследований, и все они указывали на переход от распределения Пуассона в интегрируемых режимах к некоторому распределению вигнеровского типа, стремящемуся к нулю при
основанных на том, что «неупорядоченность» нерегулярного спектра скорее всего может, в определенном смысле, найти свое выражение в распределении, близком к вигнеровскому. Было проведено множество численных исследований, и все они указывали на переход от распределения Пуассона в интегрируемых режимах к некоторому распределению вигнеровского типа, стремящемуся к нулю при  в хаотических режимах. Многие исследователи приводили аргументы в пользу утверждения, что
в хаотических режимах. Многие исследователи приводили аргументы в пользу утверждения, что

где  — некоторый показатель степени. Бэрри [11] привел доводы в пользу того, что
— некоторый показатель степени. Бэрри [11] привел доводы в пользу того, что  где
где  число параметров системы, которые надо варьировать, чтобы достичь вырождения энергетических уровней. Идея о взаимосвязи между квазиклассическим нерегулярным спектром и спектром собственных значений, определяемых различными ансамблями матриц, весьма привлекательна, но требуется дать строгое ее обоснование. Не ясно также, возможно ли экспериментально определять распределения расстояний между уровнями с точностью, достаточной для однозначного решения вопроса о регулярности или нерегулярности спектра.
число параметров системы, которые надо варьировать, чтобы достичь вырождения энергетических уровней. Идея о взаимосвязи между квазиклассическим нерегулярным спектром и спектром собственных значений, определяемых различными ансамблями матриц, весьма привлекательна, но требуется дать строгое ее обоснование. Не ясно также, возможно ли экспериментально определять распределения расстояний между уровнями с точностью, достаточной для однозначного решения вопроса о регулярности или нерегулярности спектра.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
- 1.3.б. фазовые портреты консервативных систем
- 1.4. Линейный анализ устойчивости
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
- 4.7.б. Перемешивание
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
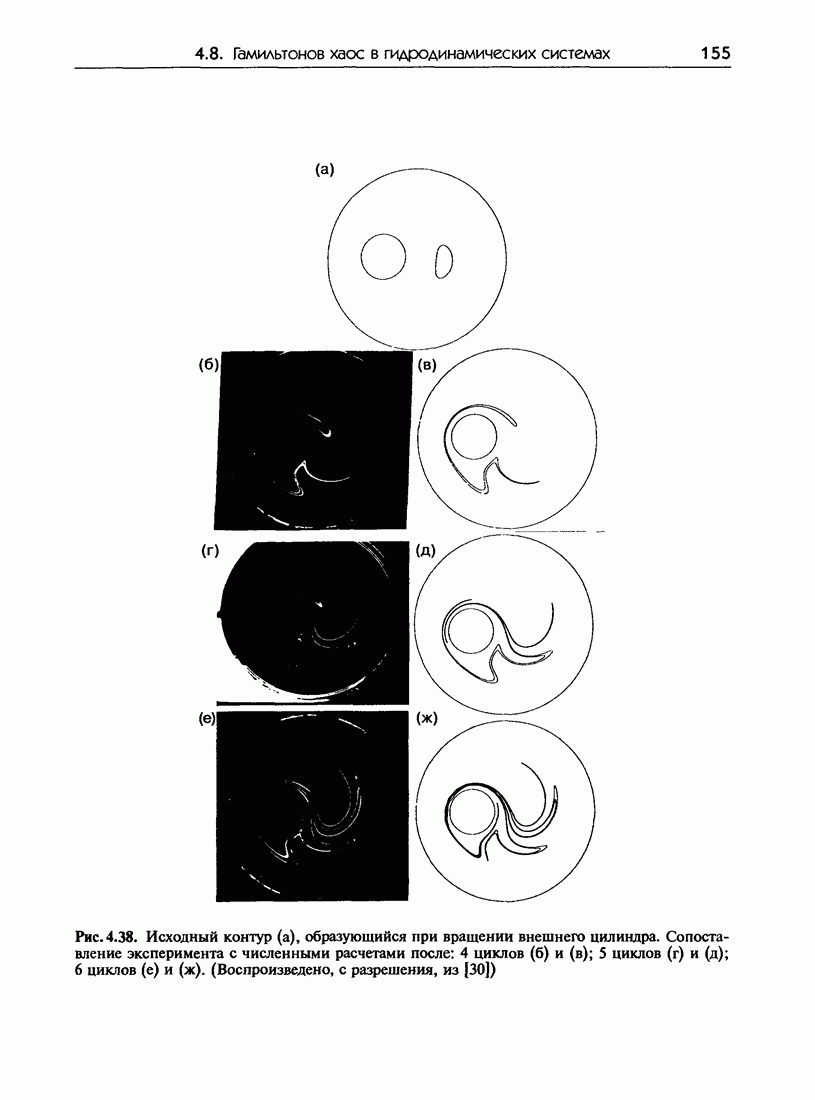
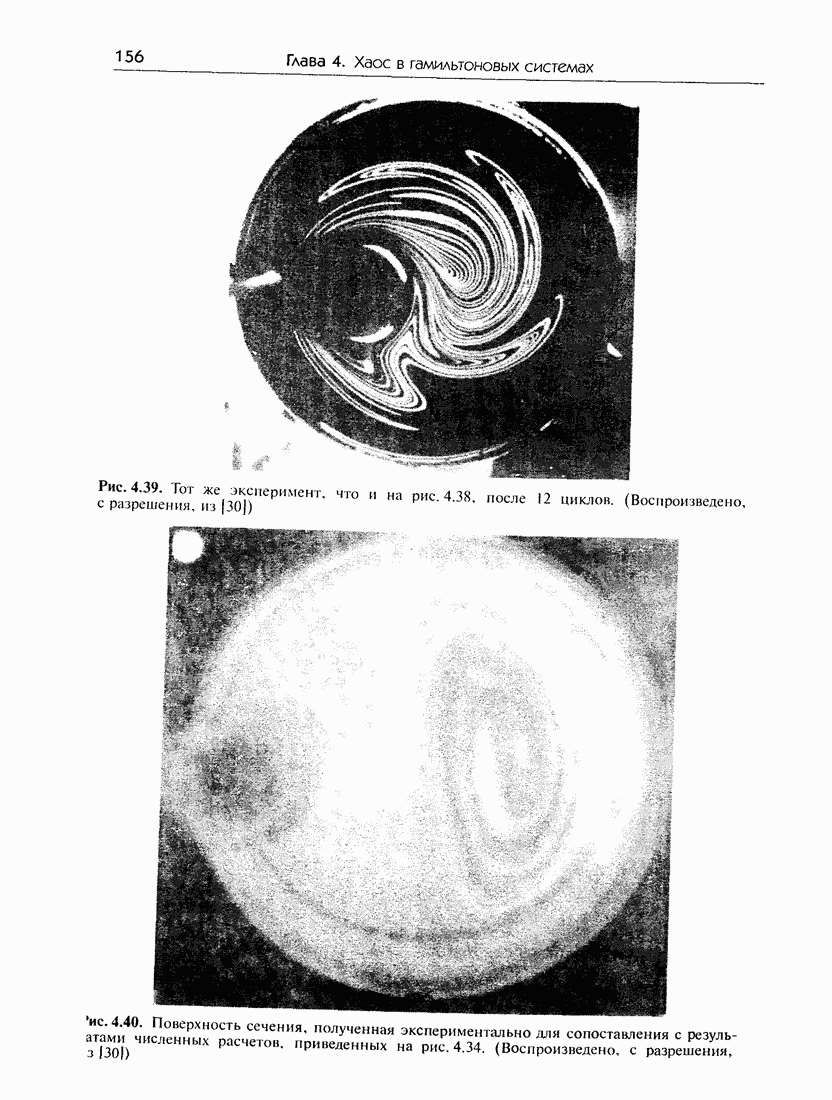
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
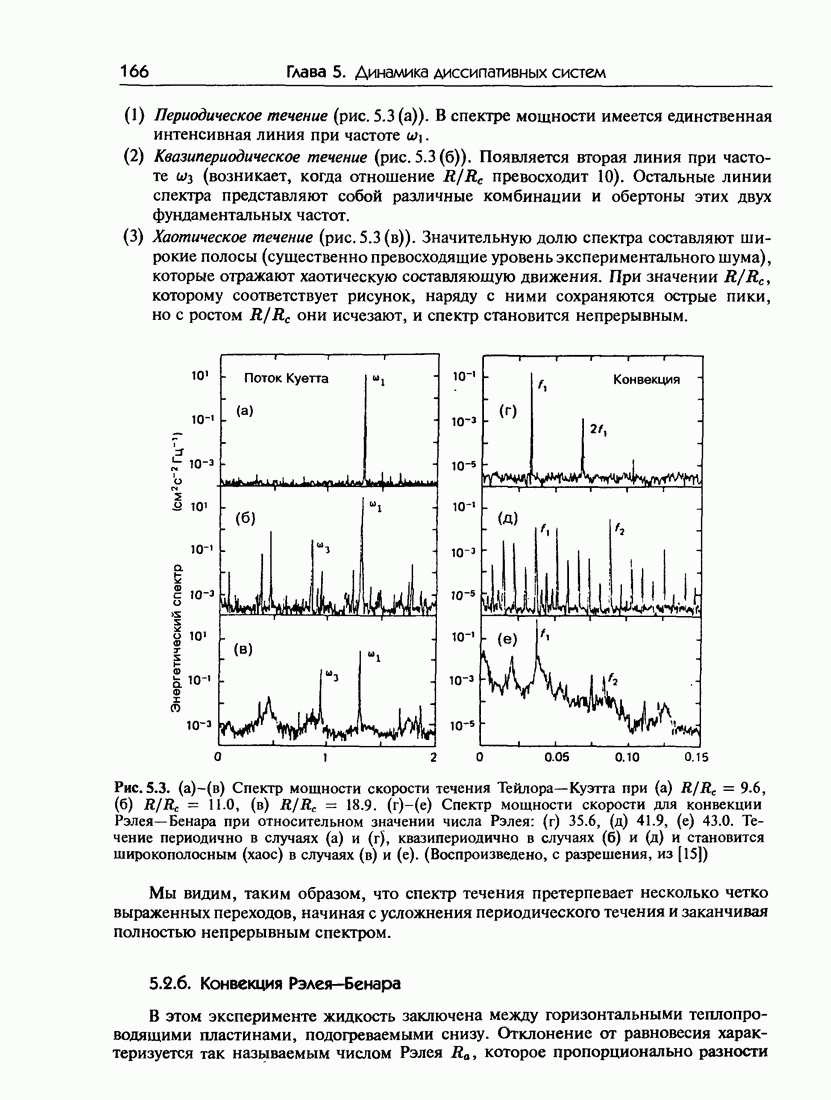
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
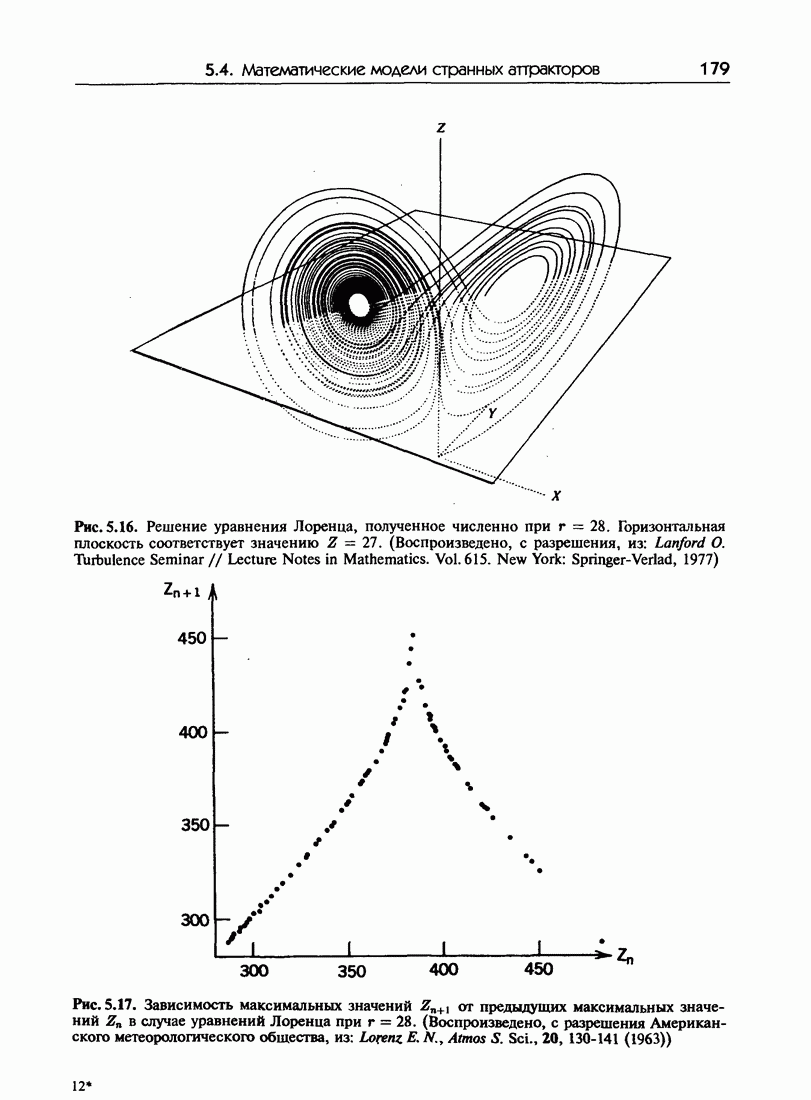
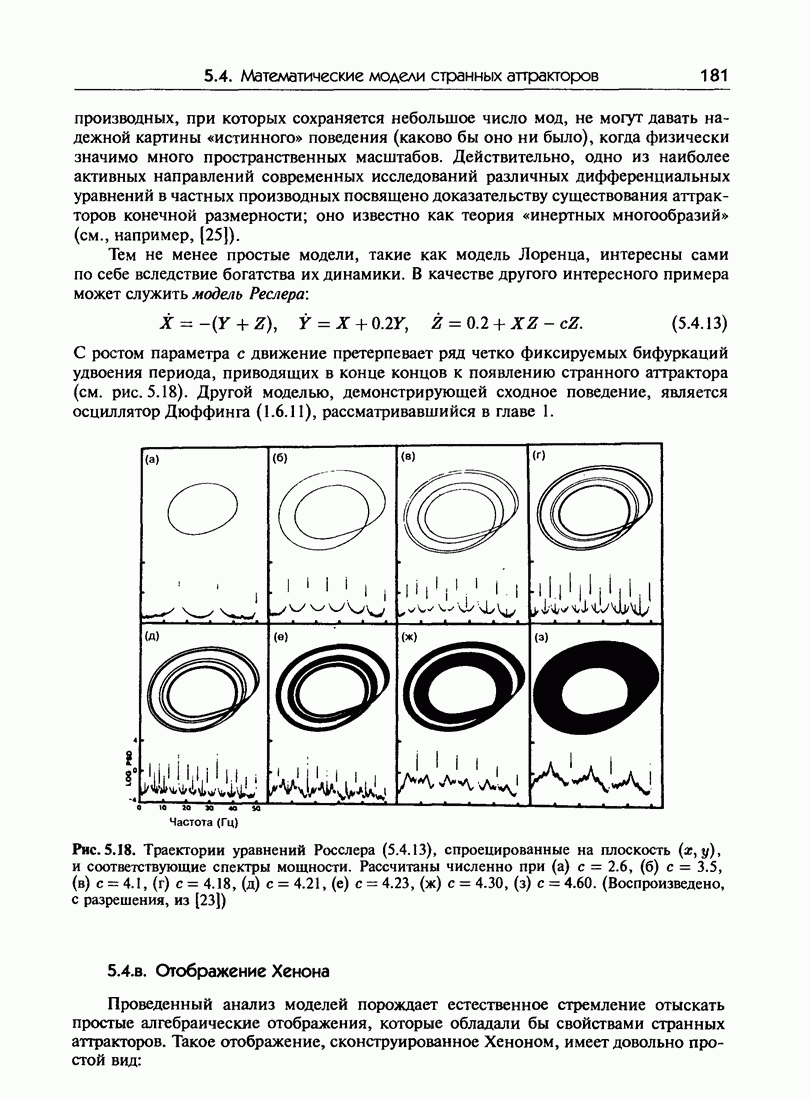
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
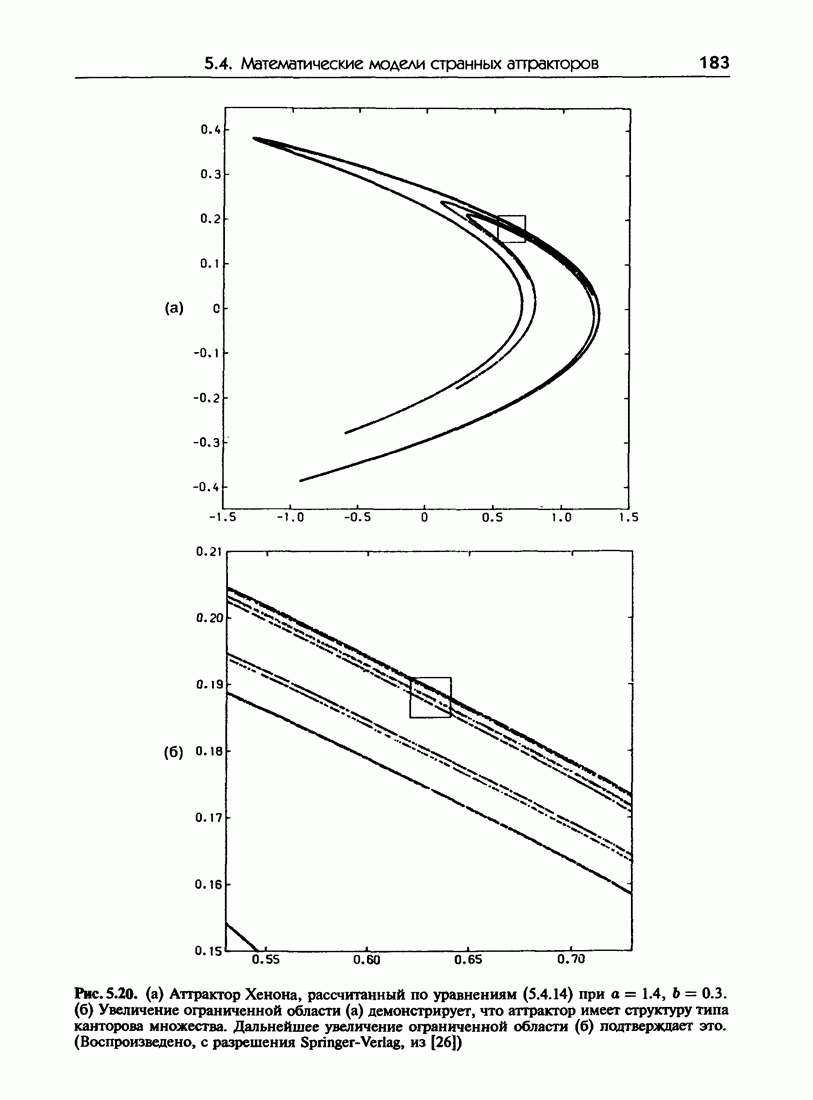
- 5.4.в. Отображение Хенона
- 5.5. Бифуркации удвоения периода
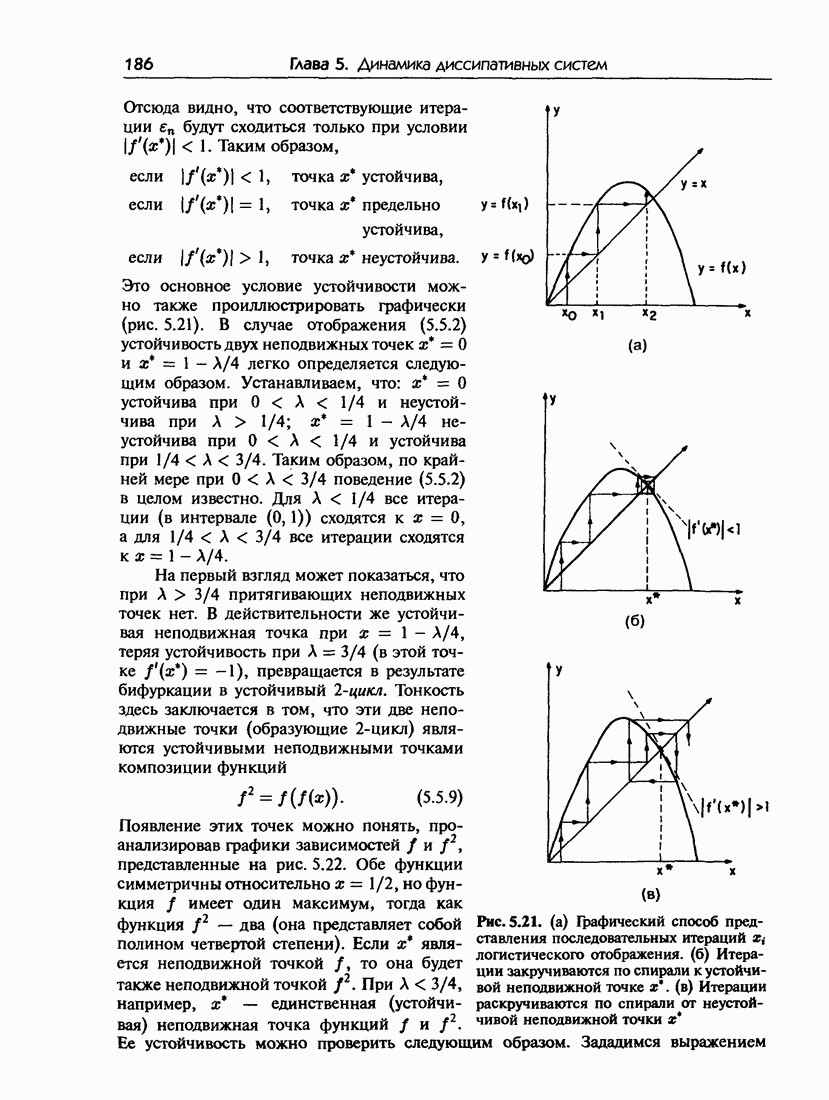
- 5.5.а. Механизм удвоения периода
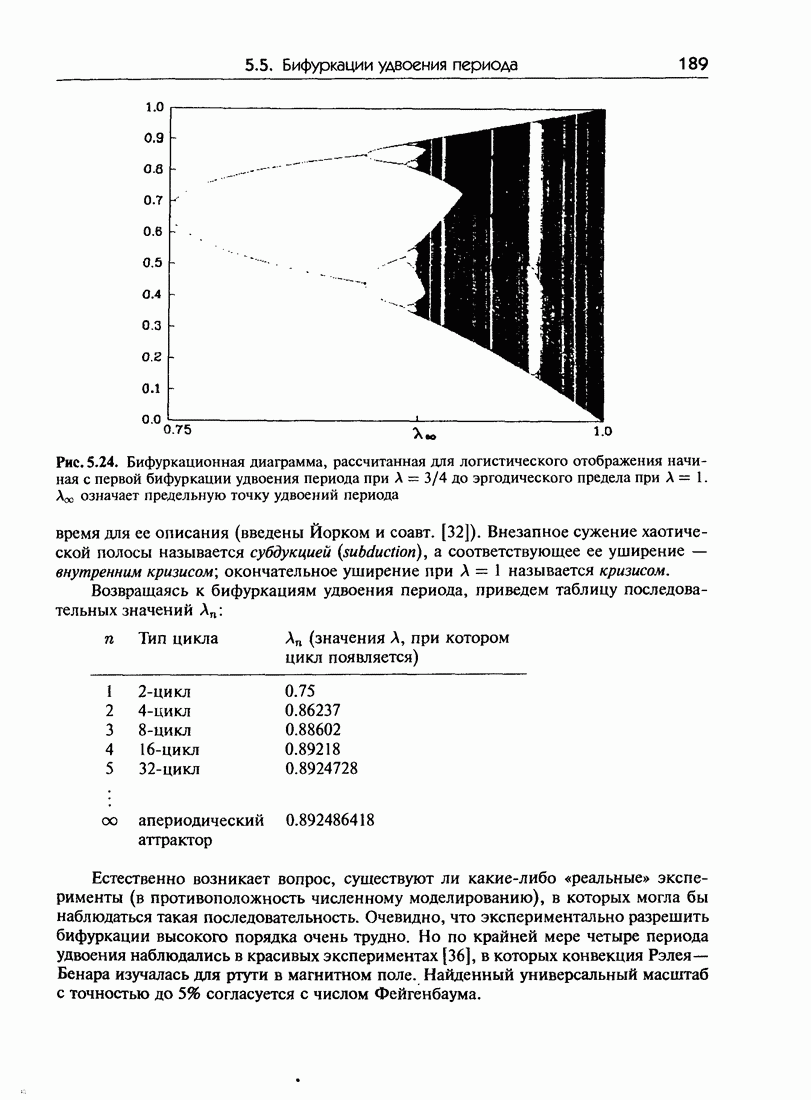
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
- 5.5.г. Другие классы универсальности
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
- 7.5. Другие солитонные системы
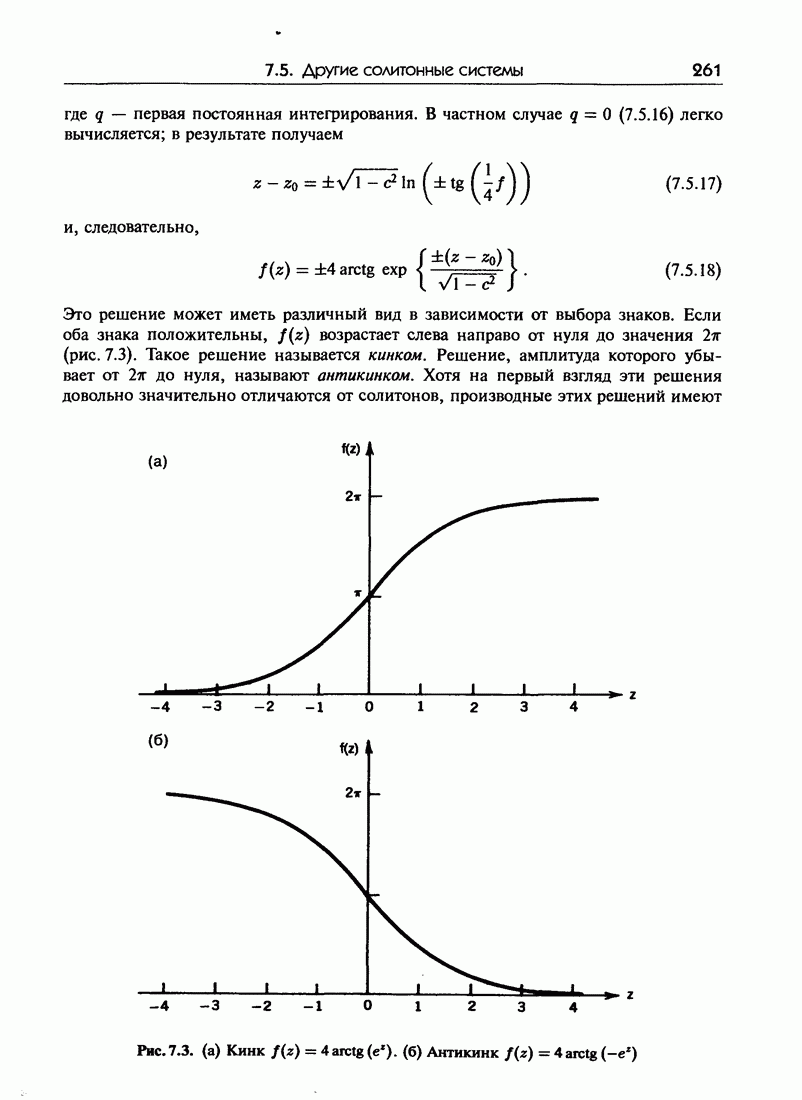
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
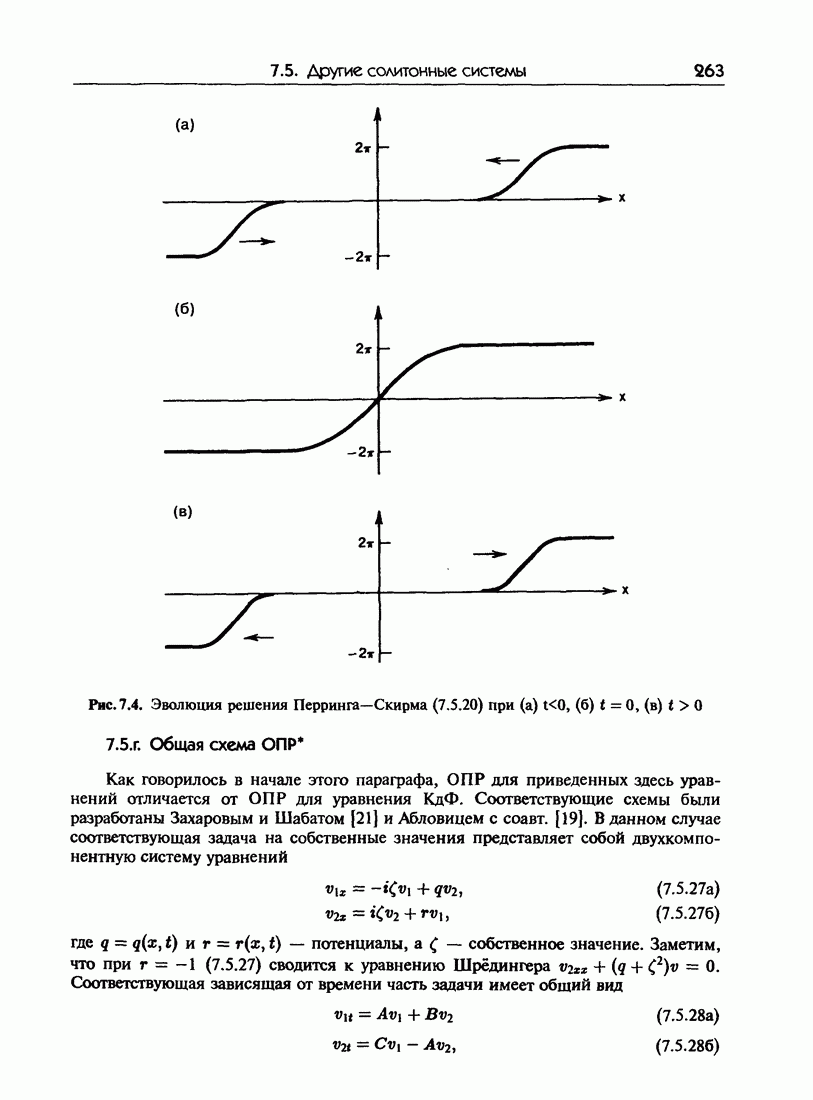
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
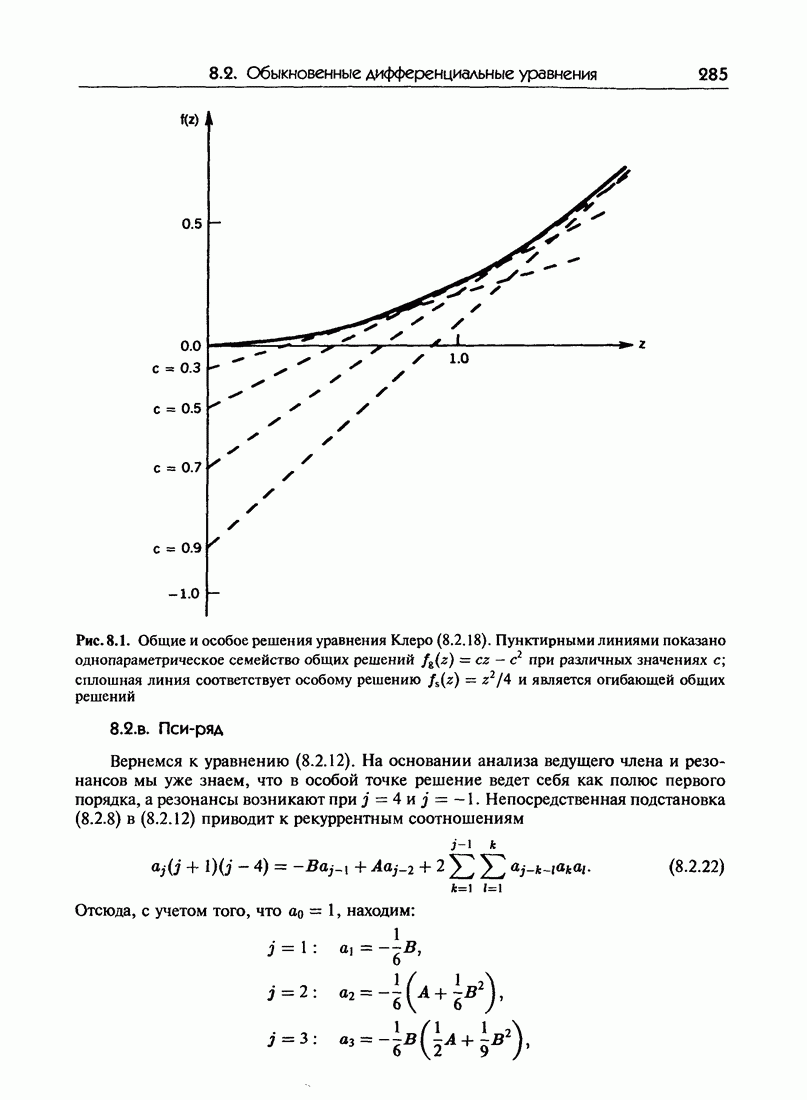
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда