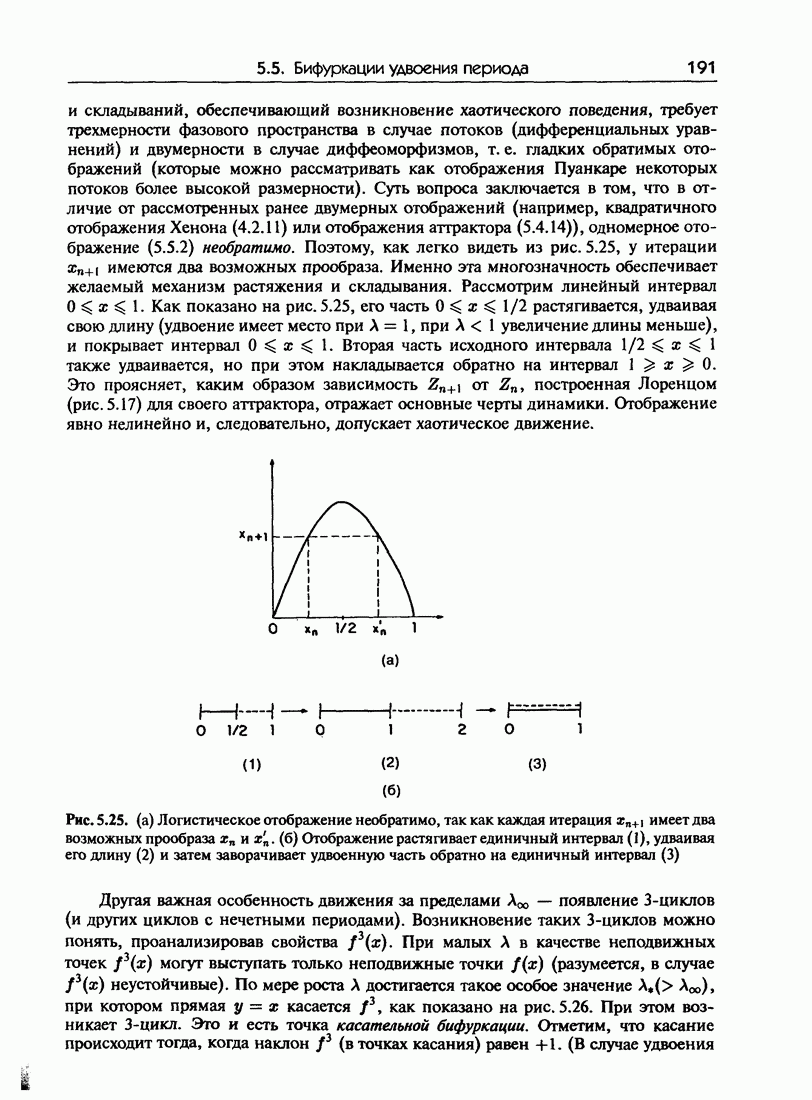
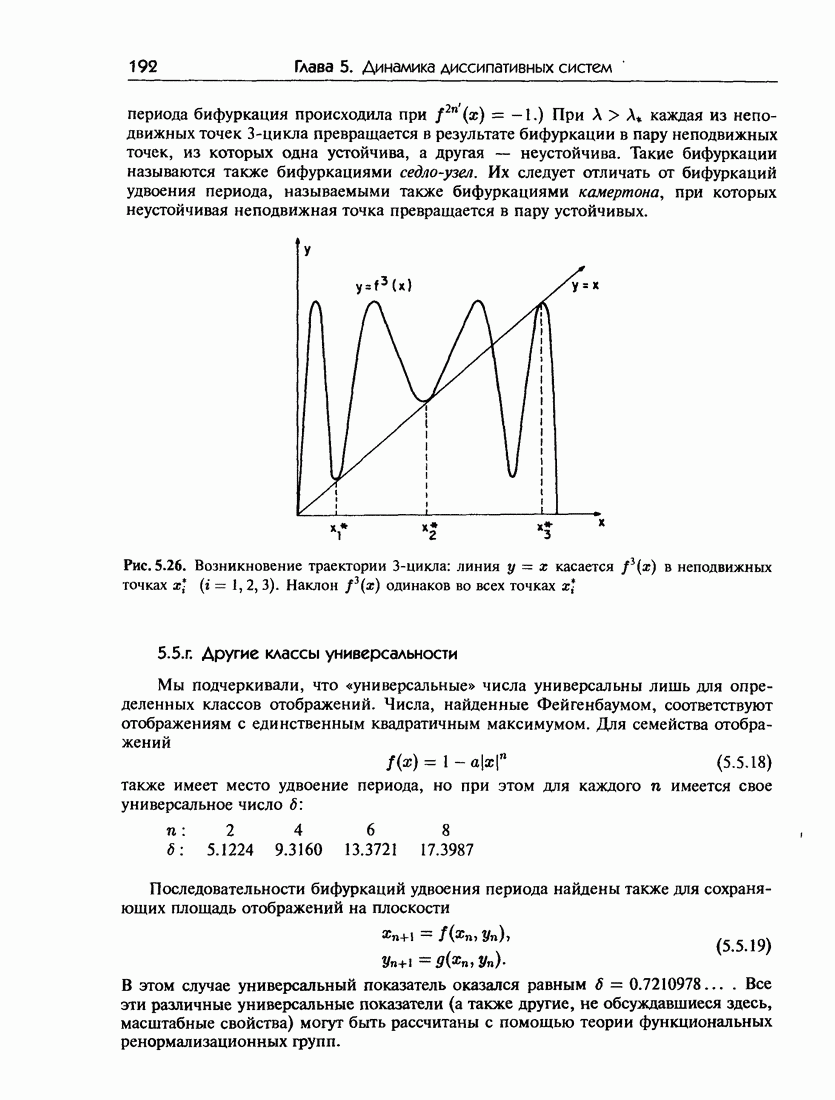
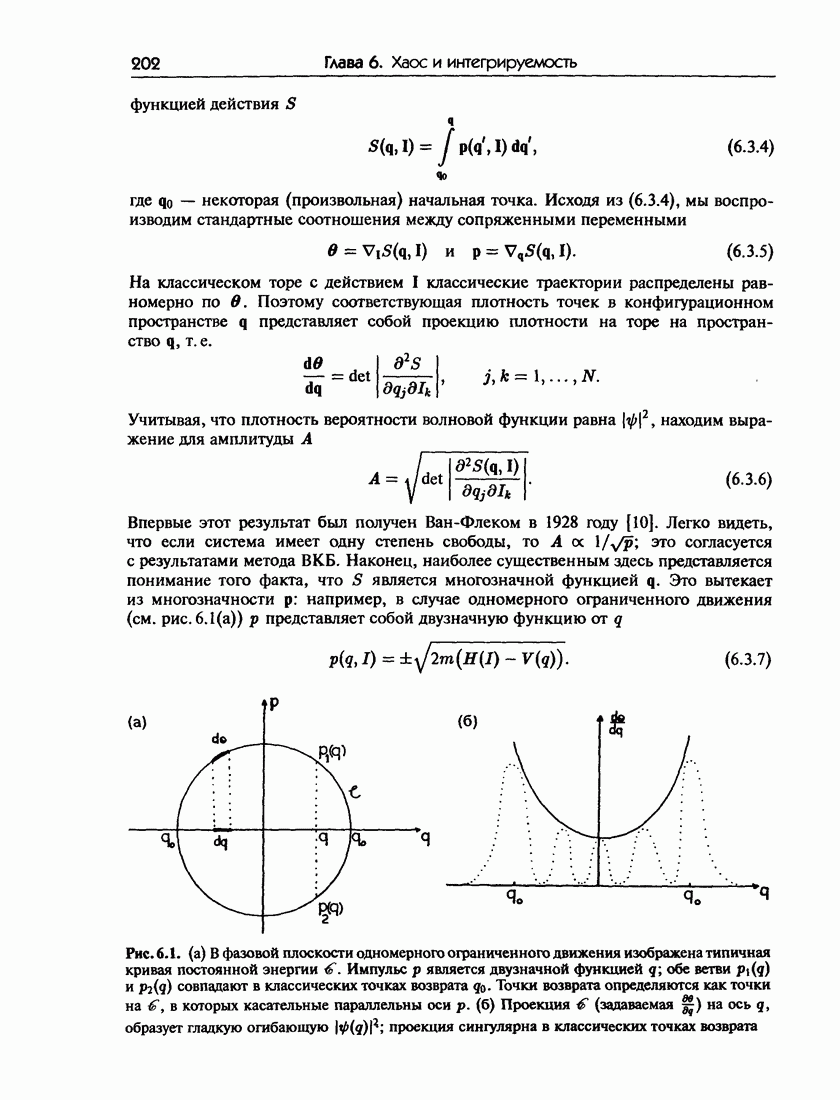
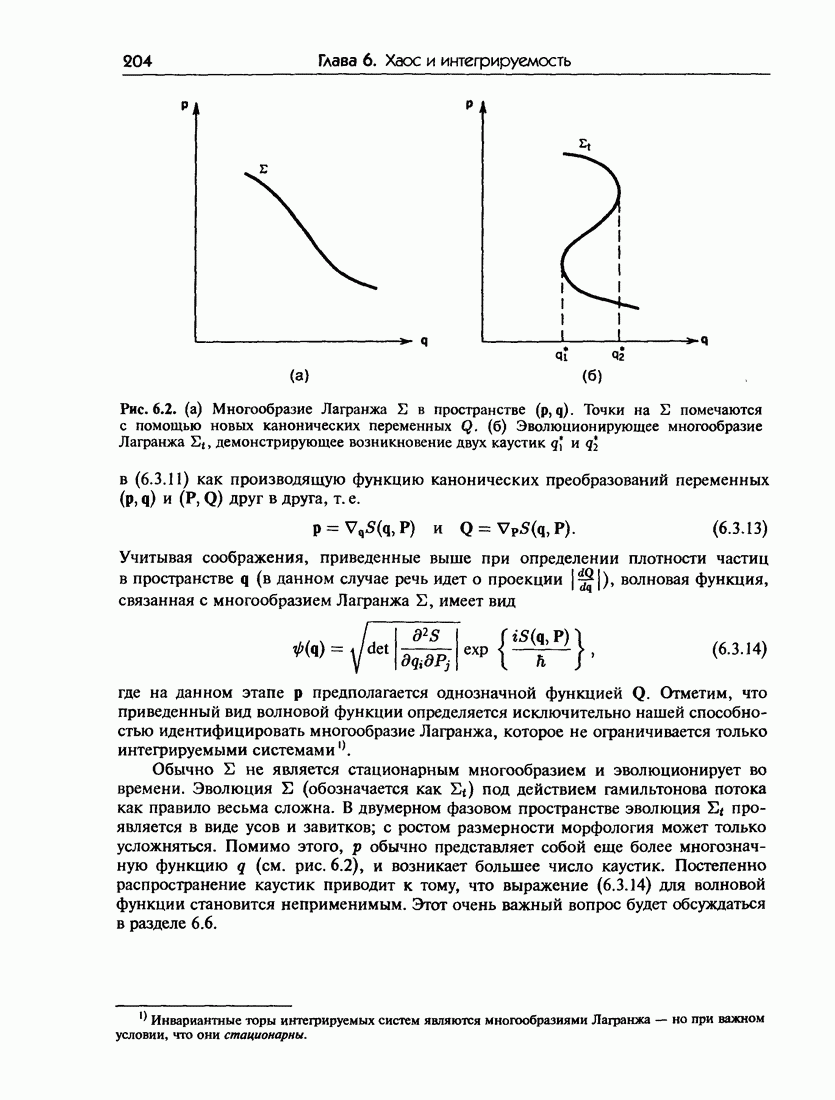
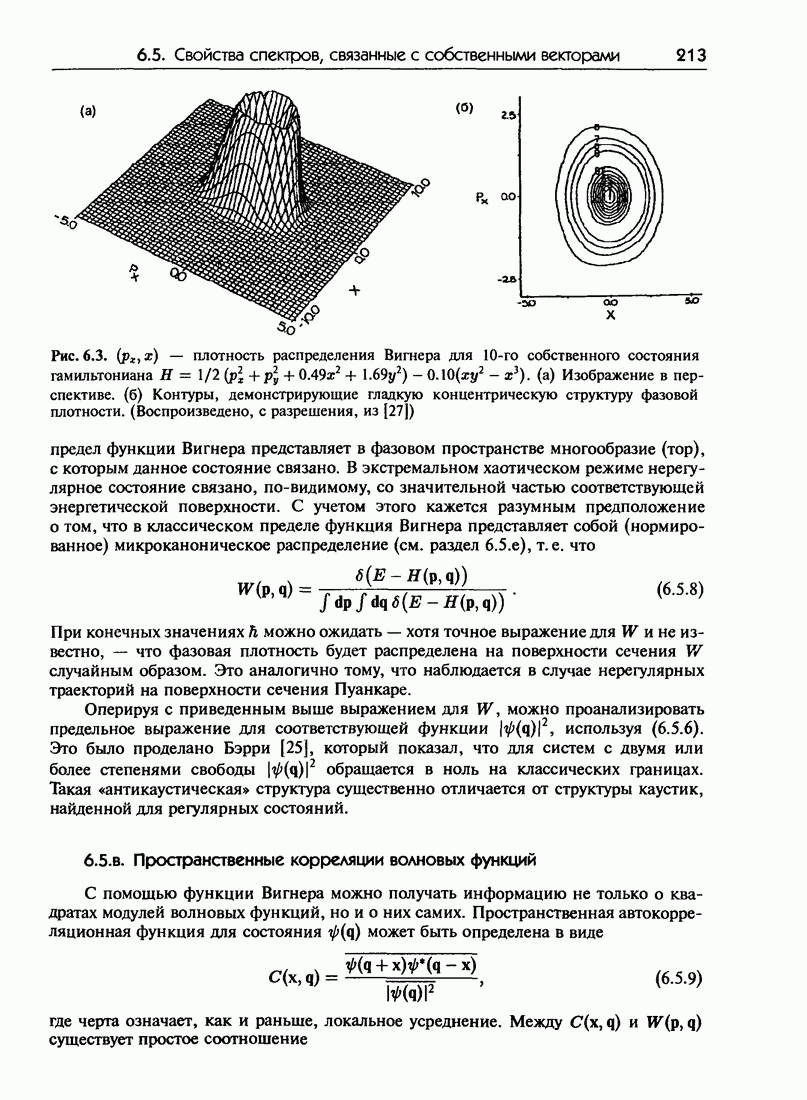
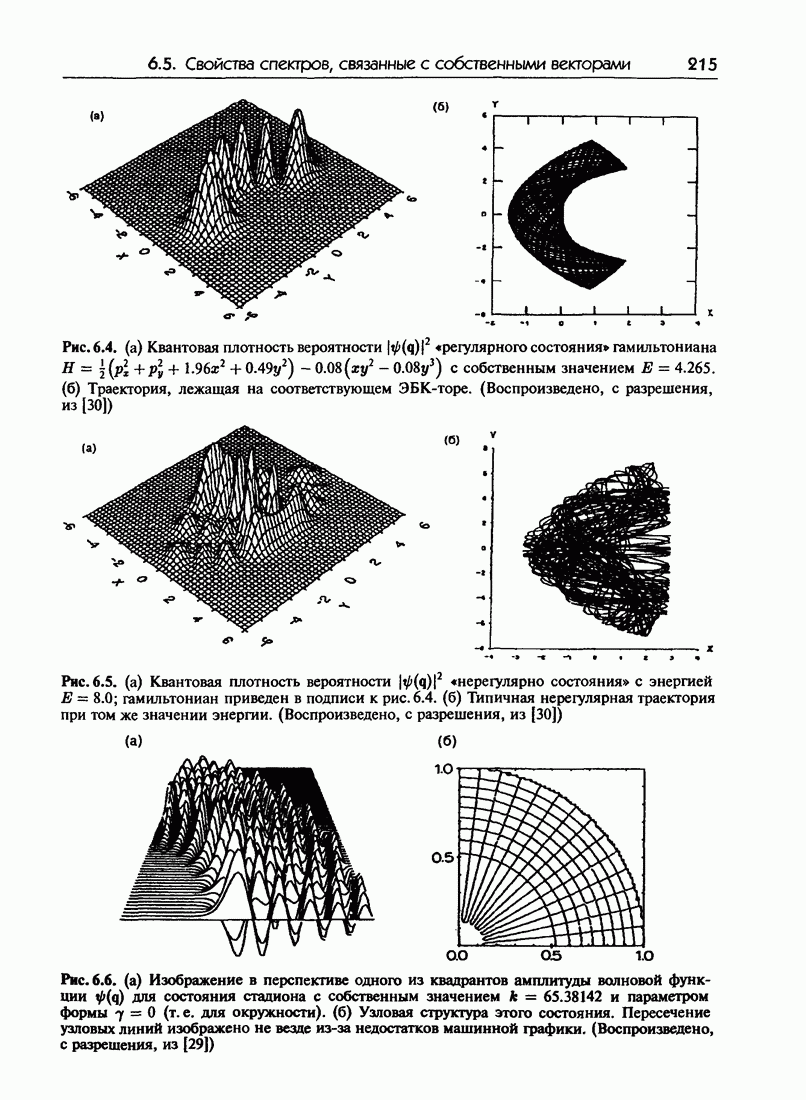
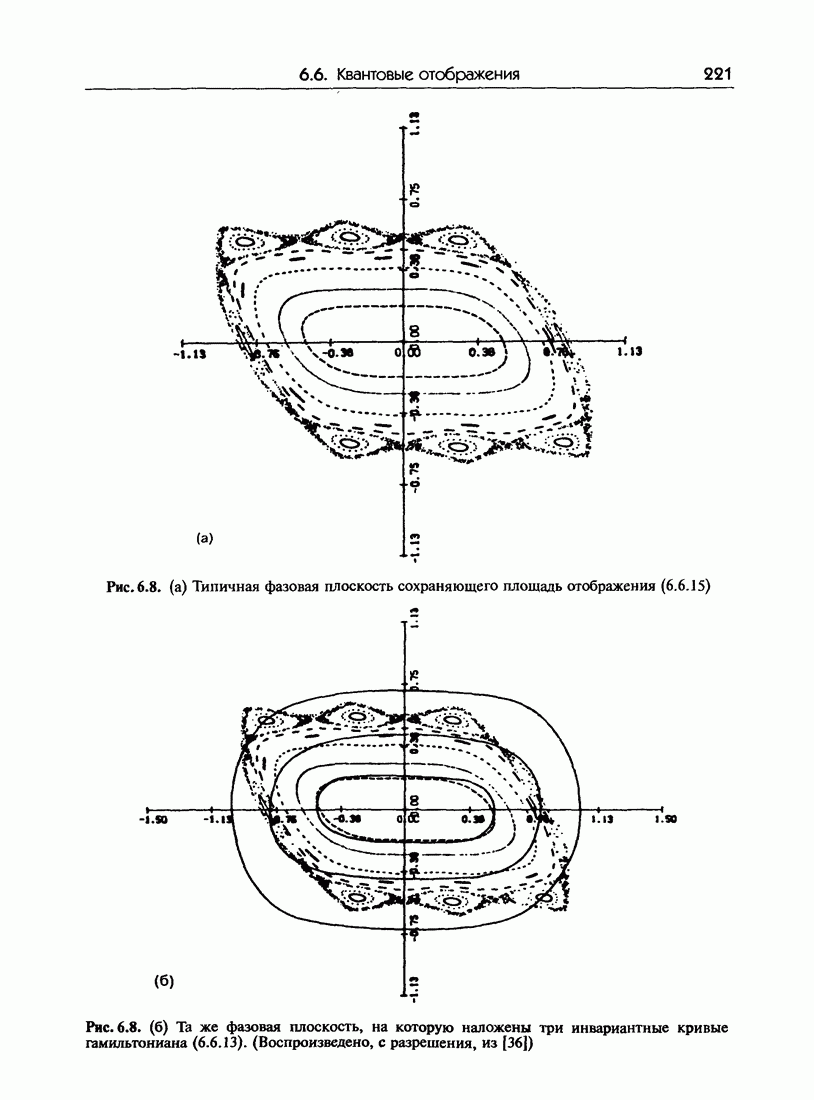
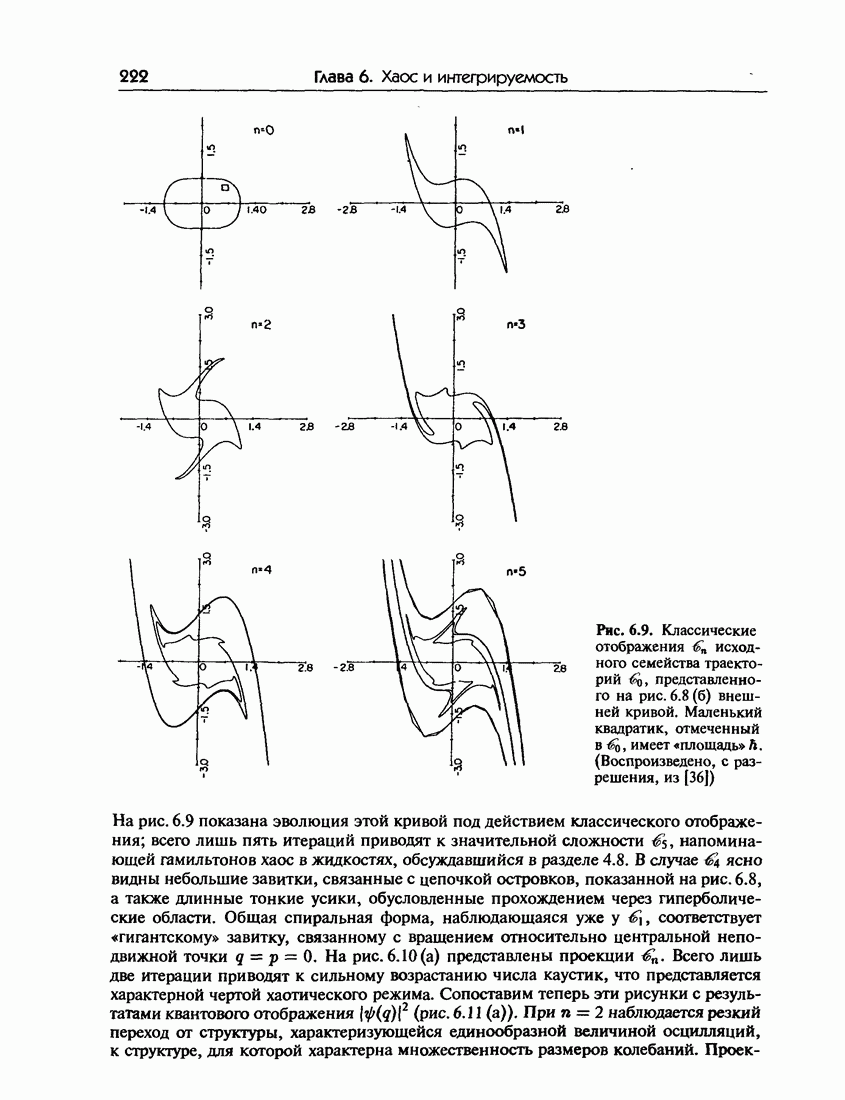
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7.7. Динамика неинтегрируемых эволюционных уравнений
Интегрируемые уравнения в частных производных, допускающие солитонные решения, удивительно часто возникают при выводе реалистических физических моделей для различных одномерных волновых процессов. (В качестве вводного обзора читателю рекомендуется работа Гиббона [27]). Не менее важны тесно связанные с ними нелинейные эволюционные уравнения, которые не являются интегрируемыми и не допускают решений методом ОПР. Поведение таких уравнений варьируется от ограниченных во времени сингулярностей («вспышек») до пространственного хаоса. В этой связи кажется очень вероятным, что проникновение в понимание пространственно-временного хаоса (и, возможно, даже динамической турбулентности в жидкости) может быть достигнуто путем изучения некоторых таких модельных
уравнений. Это необъятное поле для деятельности, однако, чтобы довершить картину исследования хаоса и интегрируемости в динамических системах (в нашем изложении эти два понятия оказались в определенном смысле связанными), мы кратко упомянем некоторые «канонические» модели и их поведение.
7.7.а. Самофокусирующиеся сингулярности
Двумерное нелинейное уравнение Шрёдингера

где  обозначает двумерный лапласиан, не может быть решено с помощью метода ОПР. Кроме того, оно допускает решения в виде ограниченных во времени «вспышек» или «самофокусирующихся» сингулярностей. Обычно изучение подобных особенностей решений уравнения (7.7.1) проводят в полярных координатах, в которых уравнение принимает вид
обозначает двумерный лапласиан, не может быть решено с помощью метода ОПР. Кроме того, оно допускает решения в виде ограниченных во времени «вспышек» или «самофокусирующихся» сингулярностей. Обычно изучение подобных особенностей решений уравнения (7.7.1) проводят в полярных координатах, в которых уравнение принимает вид

где  Выявить наличие особенности можно при помощи довольно простых динамических принципов (см., например, работу Беркшайра и Гиббона [24]). Запишем интегралы движения для уравнения (7.7.2), соответствующие сохранению массы и энергии:
Выявить наличие особенности можно при помощи довольно простых динамических принципов (см., например, работу Беркшайра и Гиббона [24]). Запишем интегралы движения для уравнения (7.7.2), соответствующие сохранению массы и энергии:

и

Кроме этого, можно определить также момент инерции

который, как можно показать, связан с интегралом энергии соотношением

При подходящем выборе начальных условий и  можно добиться, чтобы
можно добиться, чтобы  что, в свою очередь, влечет
что, в свою очередь, влечет  Таким образом, за ограниченный промежуток времени момент инерции сколлапсирует, т.е. обратится в нуль.
Таким образом, за ограниченный промежуток времени момент инерции сколлапсирует, т.е. обратится в нуль.
Очень сложно определить истинную природу сингулярности. Этой тематике посвящены многочисленные теоретические исследования (многие из которых восходят к Захарову и его соавторам; см., например, статью Захарова и Сынах [32]). В этой работе было высказано предположение, что сингулярность (во времени) является
алгебраической; другими словами, решение ведет себя как  по мере того как время приближается к критическому значению
по мере того как время приближается к критическому значению  («момент вспышки»), В последующих работах предлагалось рассматривать особенности гораздо более сложной логарифмической структуры (см., например, статью Мак-Лафлина и др. [29]). Присутствие особенностей в решениях нелинейного уравнении Шрёдингера не ограничивается двумерным случаем. Они могут присутствовать и в общем уравнении
(«момент вспышки»), В последующих работах предлагалось рассматривать особенности гораздо более сложной логарифмической структуры (см., например, статью Мак-Лафлина и др. [29]). Присутствие особенностей в решениях нелинейного уравнении Шрёдингера не ограничивается двумерным случаем. Они могут присутствовать и в общем уравнении

где  -мерный лапласиан, а а указывает на порядок нелинейности. Для каждого
-мерный лапласиан, а а указывает на порядок нелинейности. Для каждого  найдется такое значение
найдется такое значение  для которого будет наблюдаться самофокусирующаяся сингулярность в решении. Например, одномерное нелинейное уравнение Шрёдингера четвертого порядка
для которого будет наблюдаться самофокусирующаяся сингулярность в решении. Например, одномерное нелинейное уравнение Шрёдингера четвертого порядка

допускает сингулярные решения. В цитированной выше работе Захарова и Сынах предполагалось алгебраическое поведение этой сингулярности:  однако опять-таки кажется, что реальная ситуация гораздо сложнее.
однако опять-таки кажется, что реальная ситуация гораздо сложнее.
7.7.б. Уравнения Захарова
Во многих физических областях возникает интерес смоделировать взаимодействие длинных волн с короткими. Так, например, в теории ленгмюровских волн в физике плазмы взаимодействие между быстро осциллирующим электрическим полем и и медленно меняющейся плотностью ионов  имеет вид
имеет вид

Эта система известна как одномерные уравнения Захарова. Уравнения подобного типа возникают также в моделях возбуждений в идеализированных цепочках  предложенных Давыдовым [26]. Важная черта уравнений (7.7.9) проявляется в пределе больших С. В этом случае уравнение (7.7.96) принимает вид
предложенных Давыдовым [26]. Важная черта уравнений (7.7.9) проявляется в пределе больших С. В этом случае уравнение (7.7.96) принимает вид  другими словами,
другими словами,  оказывается прямо пропорциональным и и (7.7.9а) сводится к интегрируемому нелинейному уравнению Шрёдингера, обладающему солитонными решениями. Однако общая система (7.7.9) не является интегрируемой и не может быть решена методом ОПР. Численные расчеты показывают, что система способна на очень сложное поведение. Напротив, если уравнения (7.7.9) сводятся к «одноволновой» форме путем факторизации оператора
оказывается прямо пропорциональным и и (7.7.9а) сводится к интегрируемому нелинейному уравнению Шрёдингера, обладающему солитонными решениями. Однако общая система (7.7.9) не является интегрируемой и не может быть решена методом ОПР. Численные расчеты показывают, что система способна на очень сложное поведение. Напротив, если уравнения (7.7.9) сводятся к «одноволновой» форме путем факторизации оператора  к виду
к виду  получаем систему
получаем систему

которая является интегрируемой и допускает применение метода ОПР.
Для физически более реалистичных приложений особенно важным оказывается двумерный вариант (7.7.9), а именно

В этом случае в пределе больших С (7.7.11а) сводится к двумерному нелинейному уравнению Шрёдингера, в котором возможно появление самофокусирующейся сингулярности. Путем численного моделирования системы (7.7.11) обнаружена богатая структура ее решений, включающая «вспышку», сопровождающуюся «затуханием». (Неплохой обзор этих явлений в контексте физики плазмы был дан Голдманом [28].)
7.7.в. Когерентность и хаос
Хорошей моделью для изучения пространственно-временного хаоса является одномерное уравнение  -Гордона в поле внешней силы (с затуханием):
-Гордона в поле внешней силы (с затуханием):

Обычно рассматривают решения этого уравнения с периодическими граничными условиями, когда  Детальный численный анализ уравнения (7.7.12), проведенный Бишопом и др. [25], показал, что данная система обладает богатым поведением по мере варьирования параметров внешней силы
Детальный численный анализ уравнения (7.7.12), проведенный Бишопом и др. [25], показал, что данная система обладает богатым поведением по мере варьирования параметров внешней силы  и затухания а. Однако структура пространственной части решений оказывается обычно когерентной, т. е. проявляются черты лишь небольшого числа хорошо выраженных пространственных мод. Особенно впечатляет тот факт, что эта пространственная когерентность сохраняется даже тогда, когда временная эволюция становится хаотичной. Становится ясным, что солитонная структура невозмущенной системы
и затухания а. Однако структура пространственной части решений оказывается обычно когерентной, т. е. проявляются черты лишь небольшого числа хорошо выраженных пространственных мод. Особенно впечатляет тот факт, что эта пространственная когерентность сохраняется даже тогда, когда временная эволюция становится хаотичной. Становится ясным, что солитонная структура невозмущенной системы  может быть довольно стабильной.
может быть довольно стабильной.
Во многих задачах статистической механики и динамики жидкости часто фигурируют два уравнения: уравнение Гинзбурга-Ландау и тесно связанное с ним уравнение Ньюеля-Уайтхеда. Типичный вид этих уравнений в случае одного пространственного измерения следующий:

где  (комплексная) амплитуда некоторой нестабильной моды,
(комплексная) амплитуда некоторой нестабильной моды,  являются подгоночными параметрами, которые могут быть комплексными. Это уравнение может быть обобщено на высшие размерности; оно характеризуется огромным разнообразием в поведении — от когерентности до хаоса — в зависимости от выбранных значений параметров. Выяснение свойств этих уравнений является бурно развивающейся областью исследований.
являются подгоночными параметрами, которые могут быть комплексными. Это уравнение может быть обобщено на высшие размерности; оно характеризуется огромным разнообразием в поведении — от когерентности до хаоса — в зависимости от выбранных значений параметров. Выяснение свойств этих уравнений является бурно развивающейся областью исследований.
Список литературы
(см. скан)
(см. скан)
(см. скан)
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
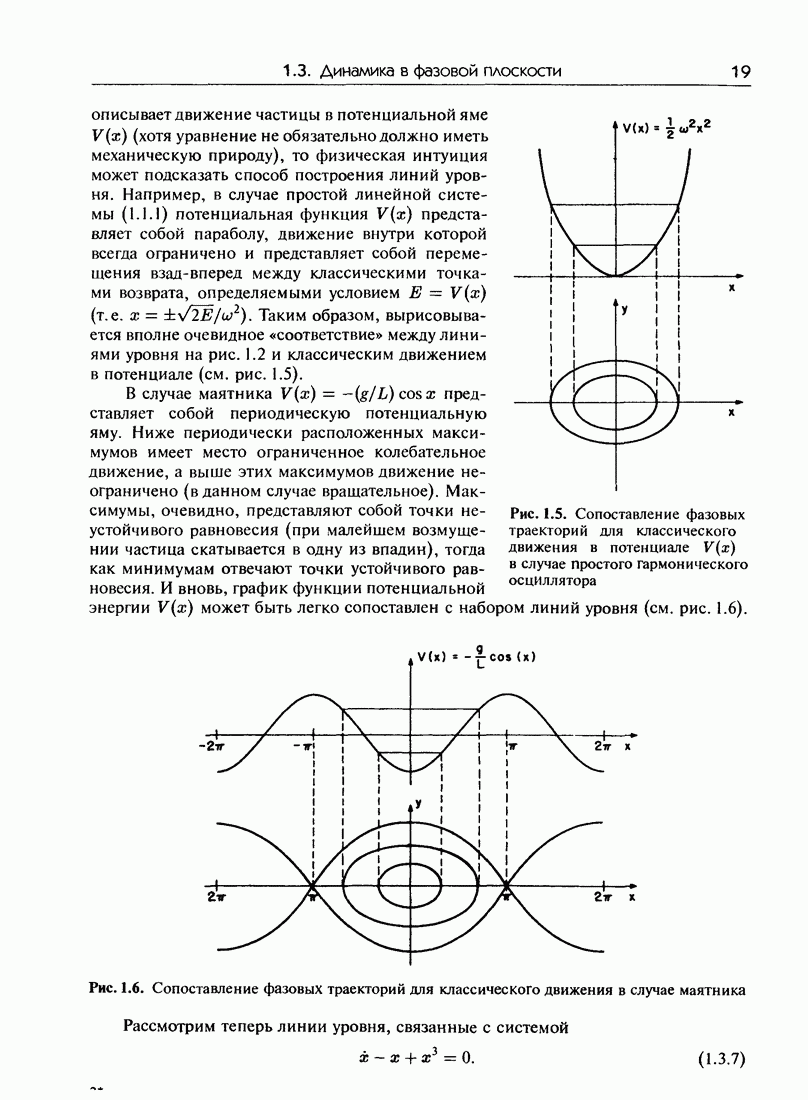
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
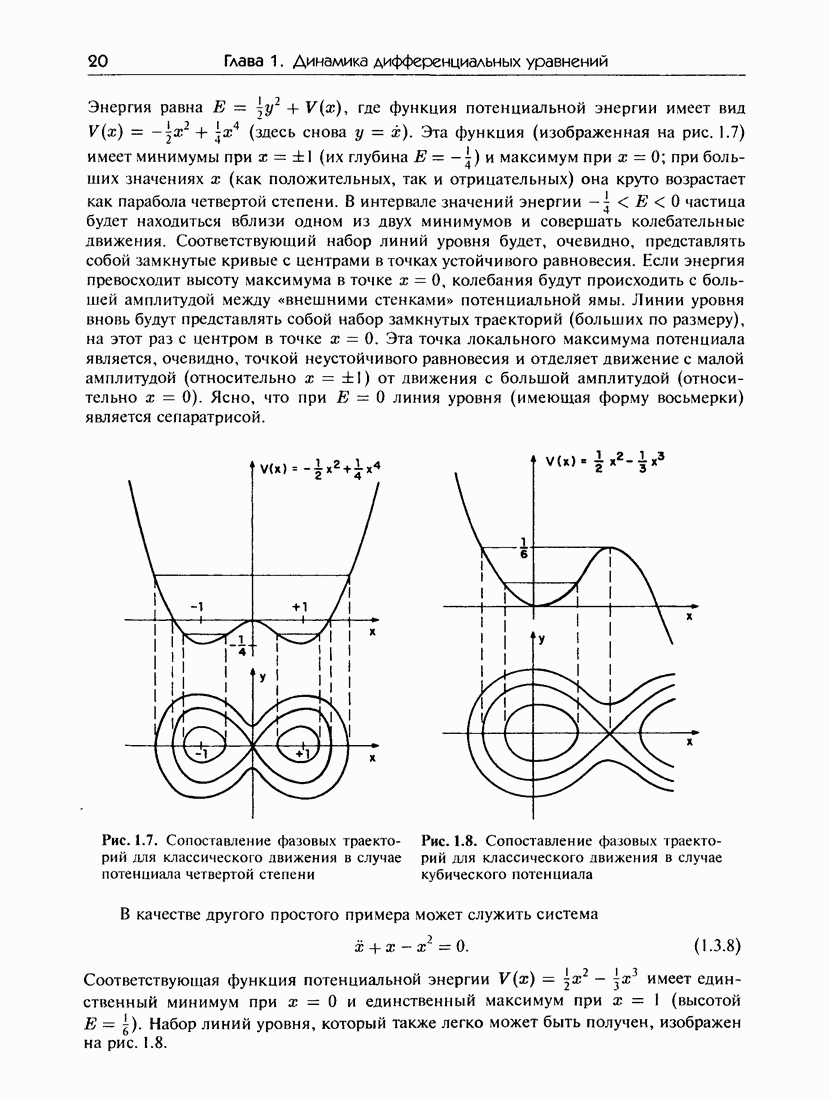
- 1.3.б. фазовые портреты консервативных систем
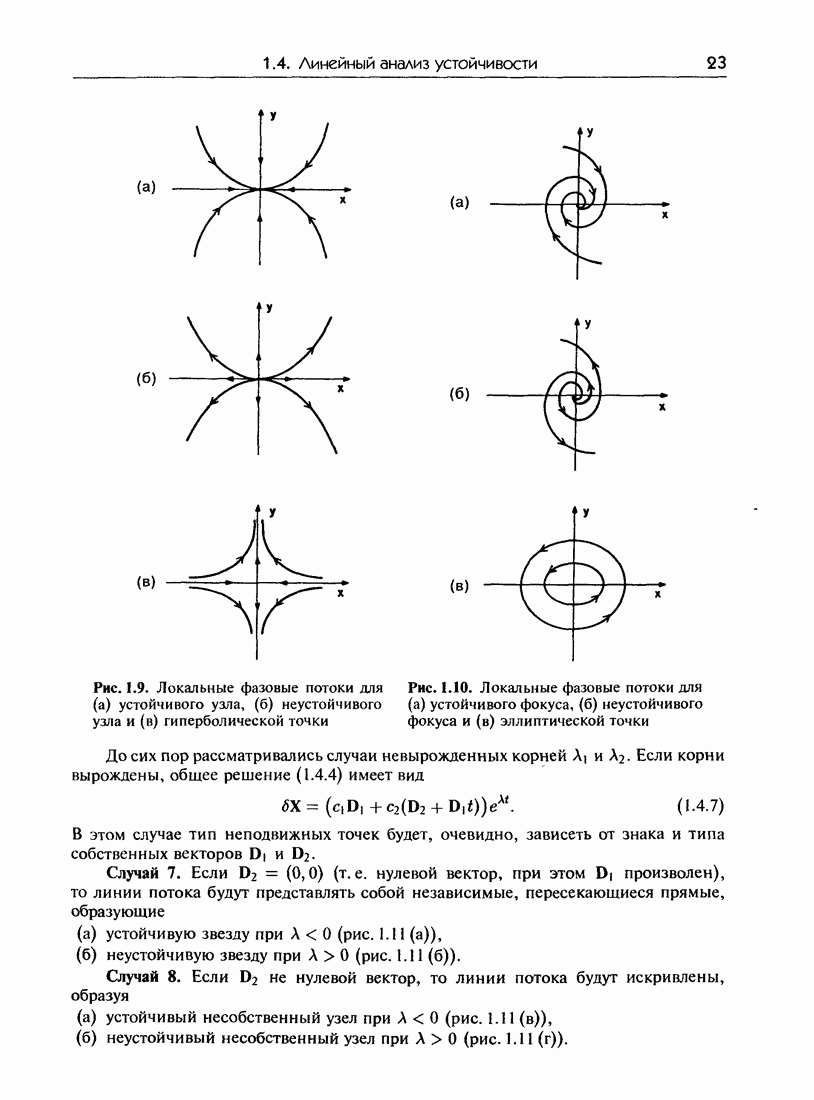
- 1.4. Линейный анализ устойчивости
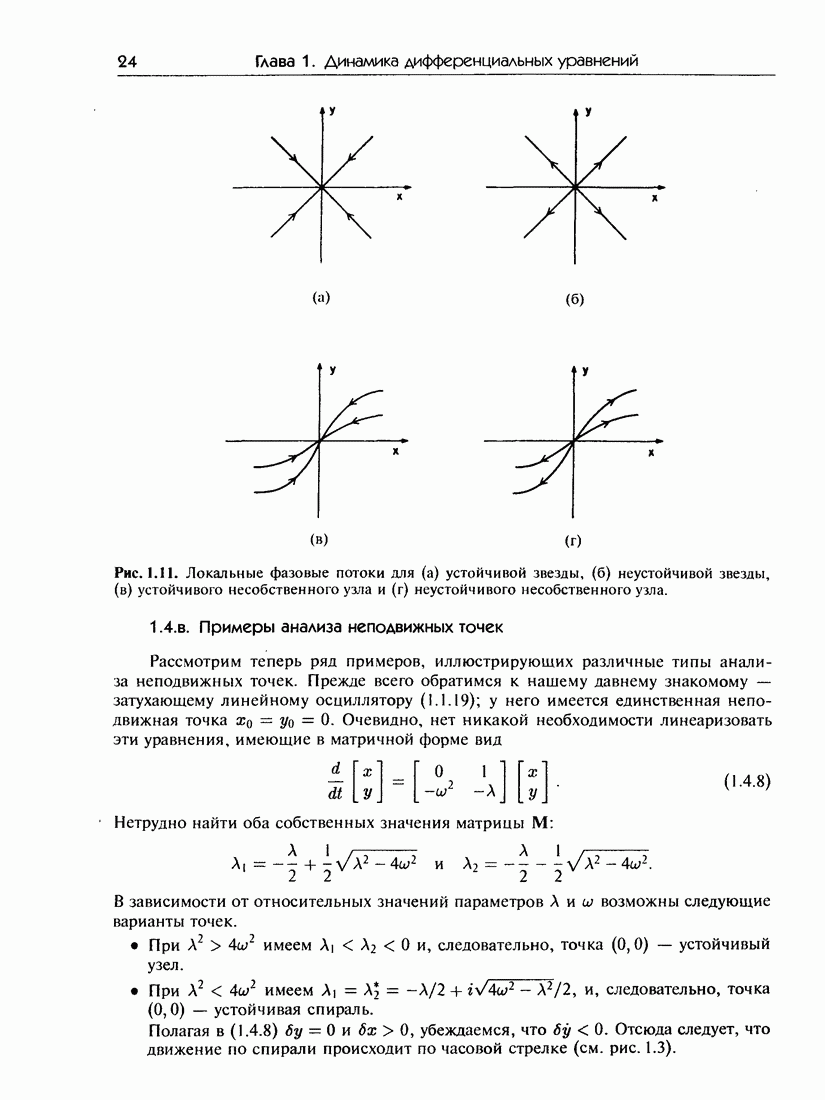
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
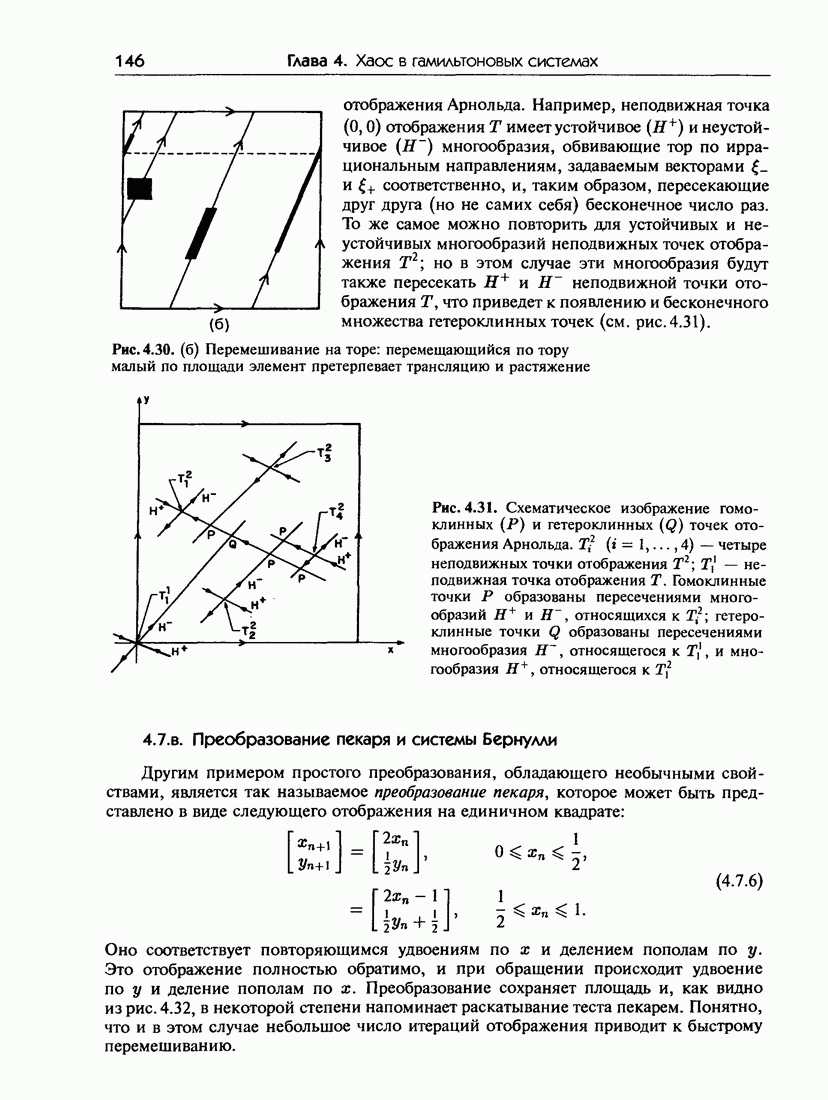
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
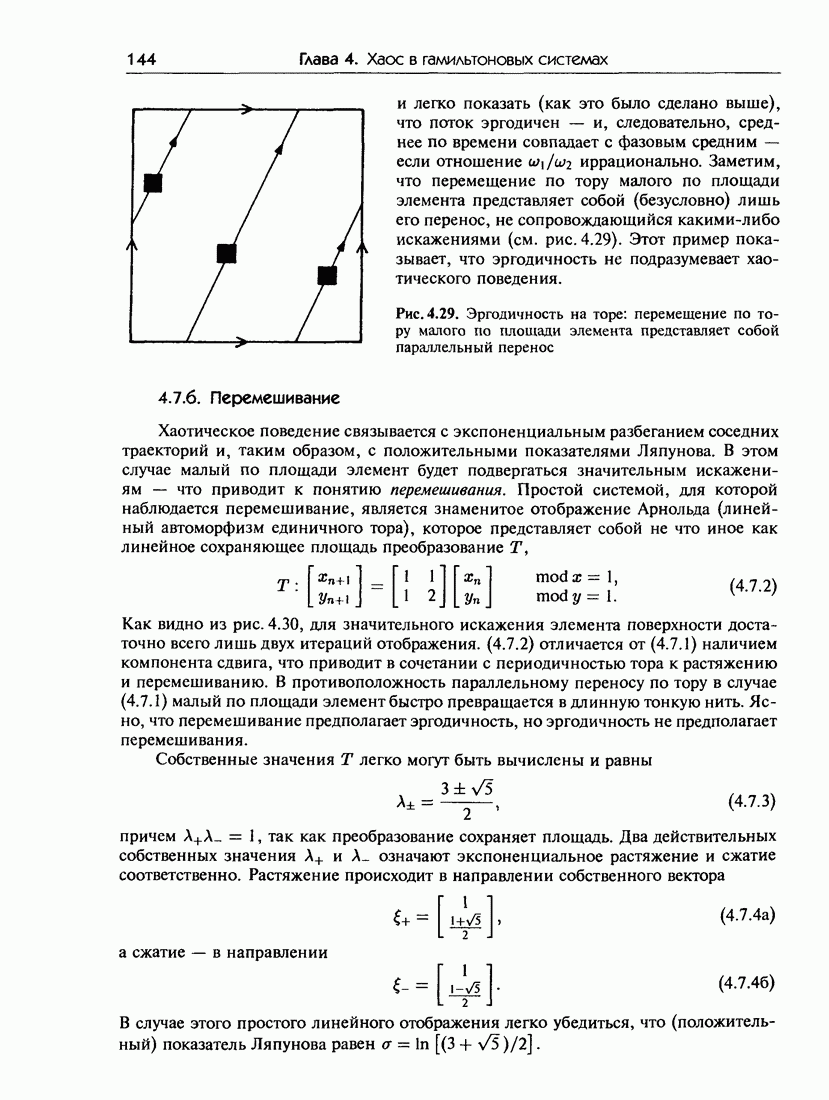
- 4.7. Статистические понятия сильно хаотических систем
- 4.7.б. Перемешивание
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
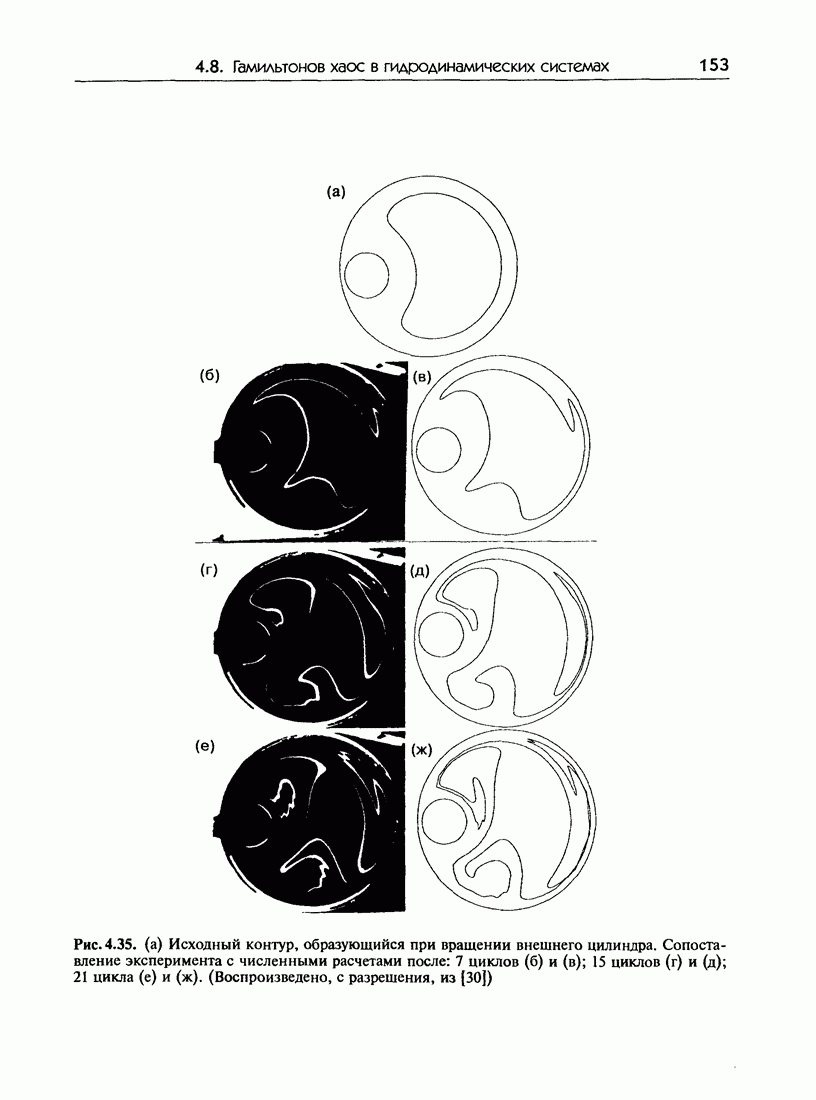
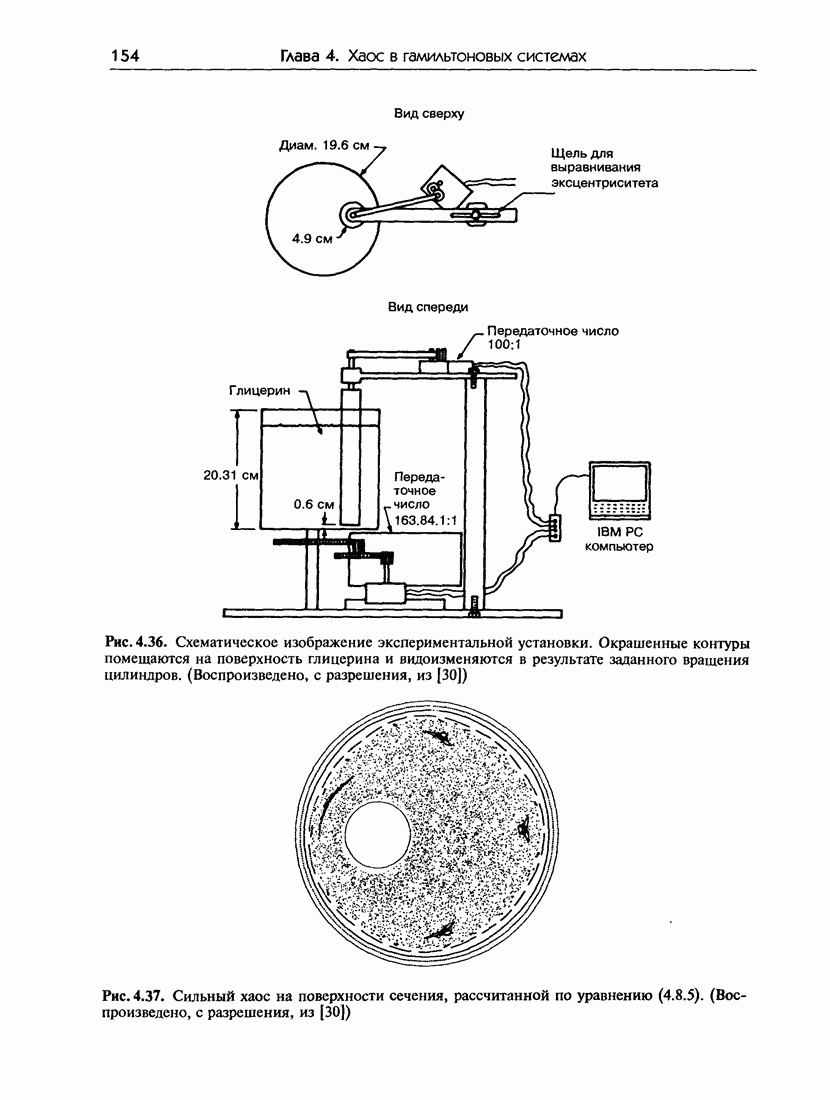
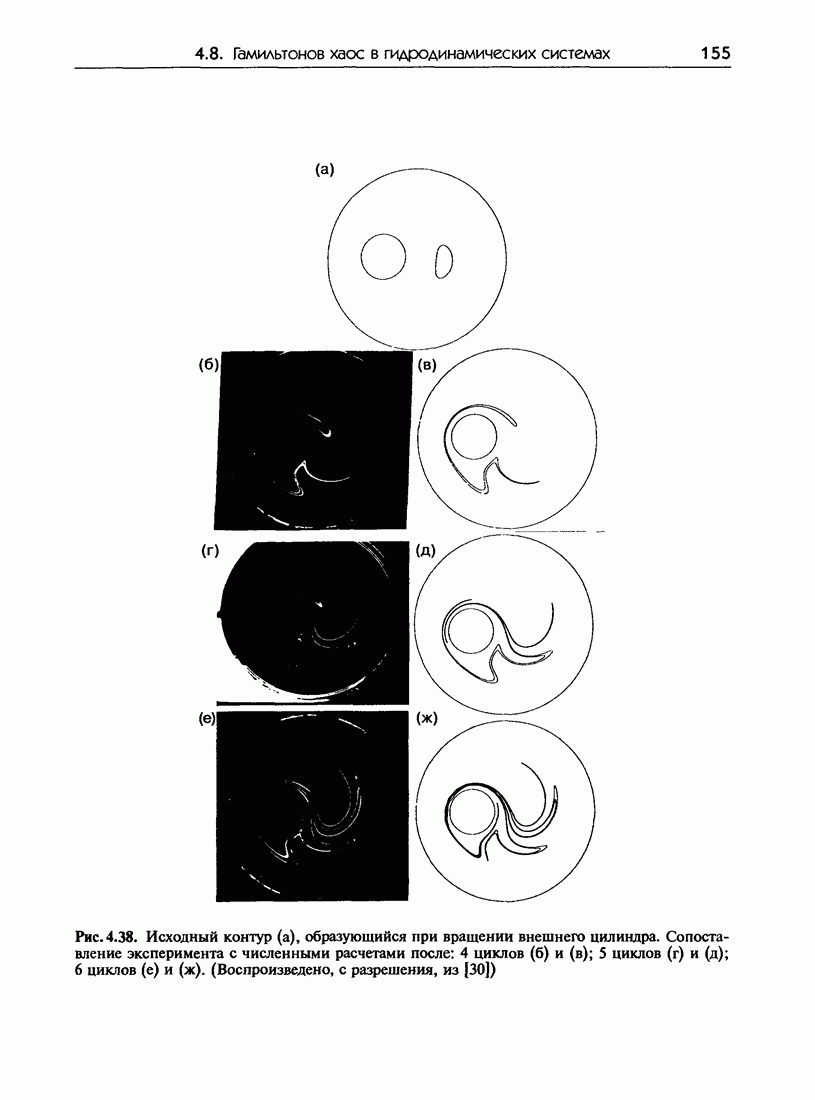
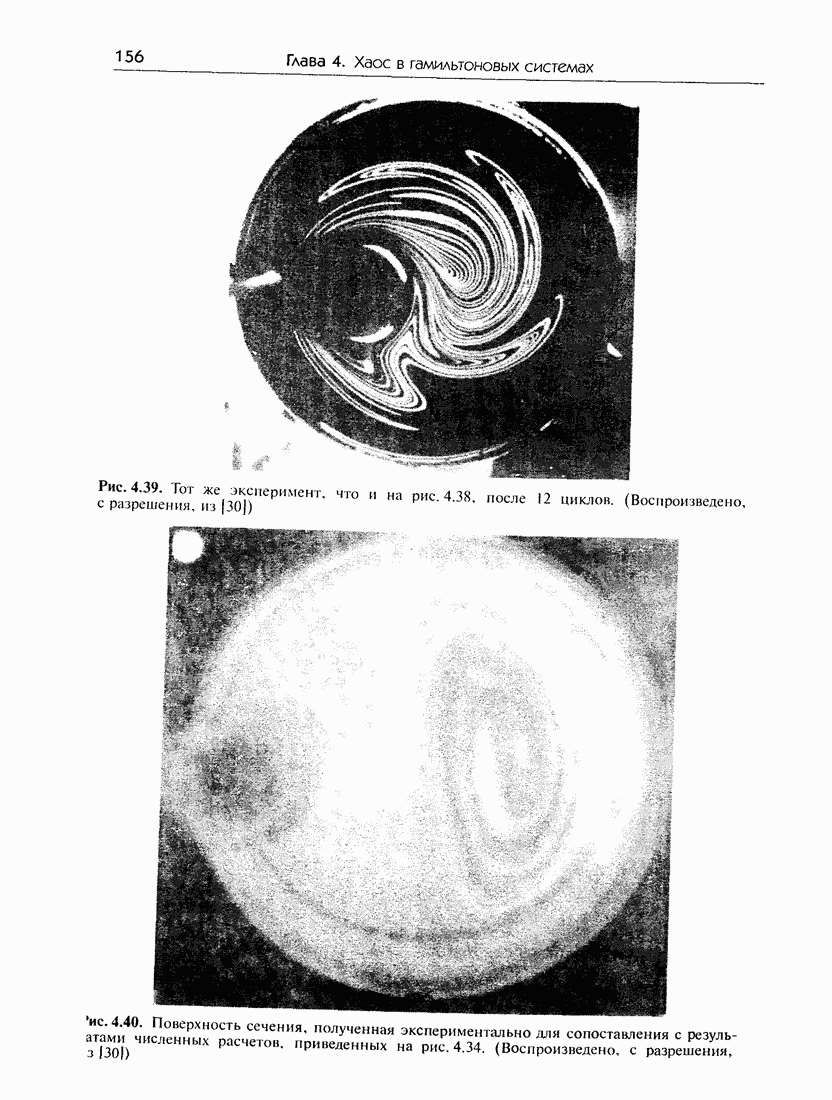
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
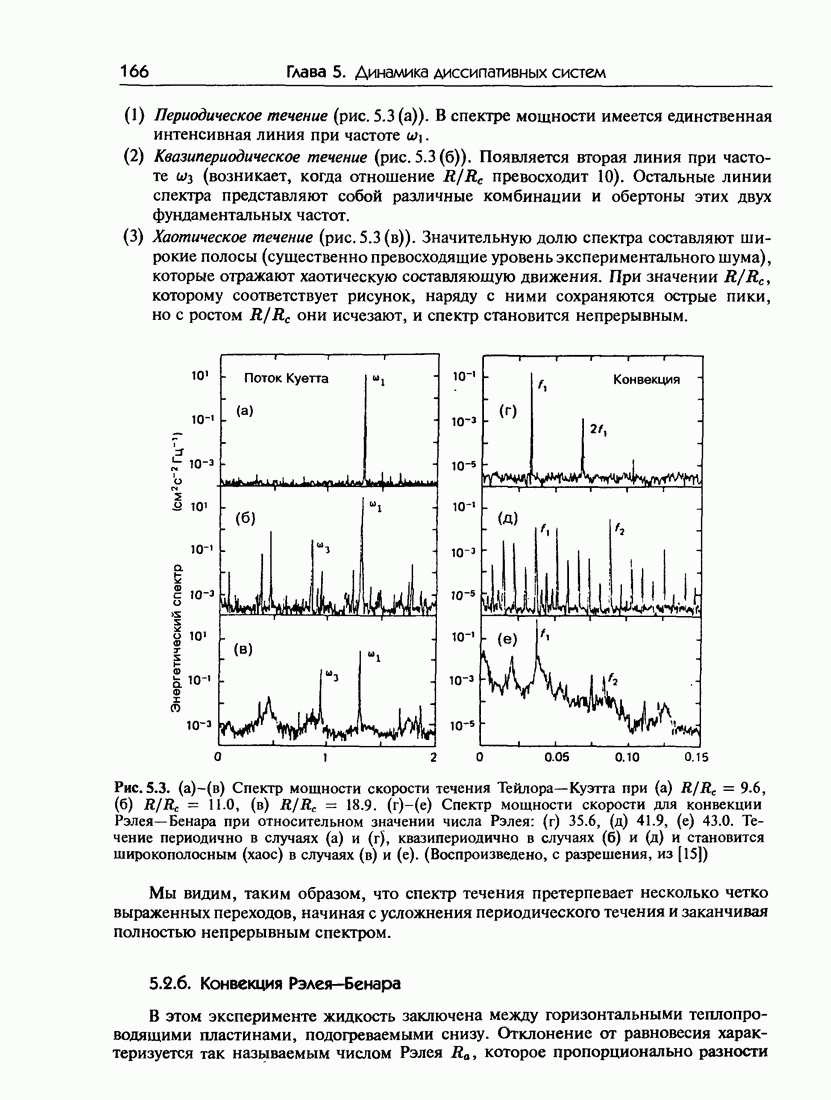
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
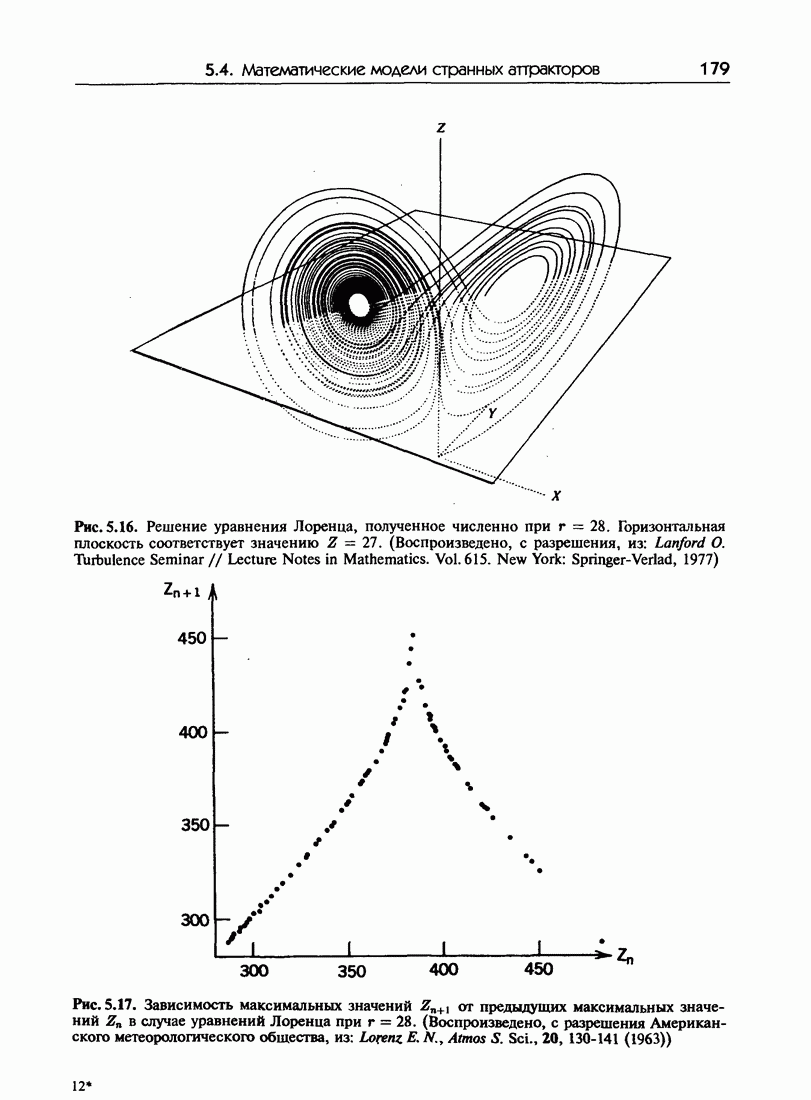
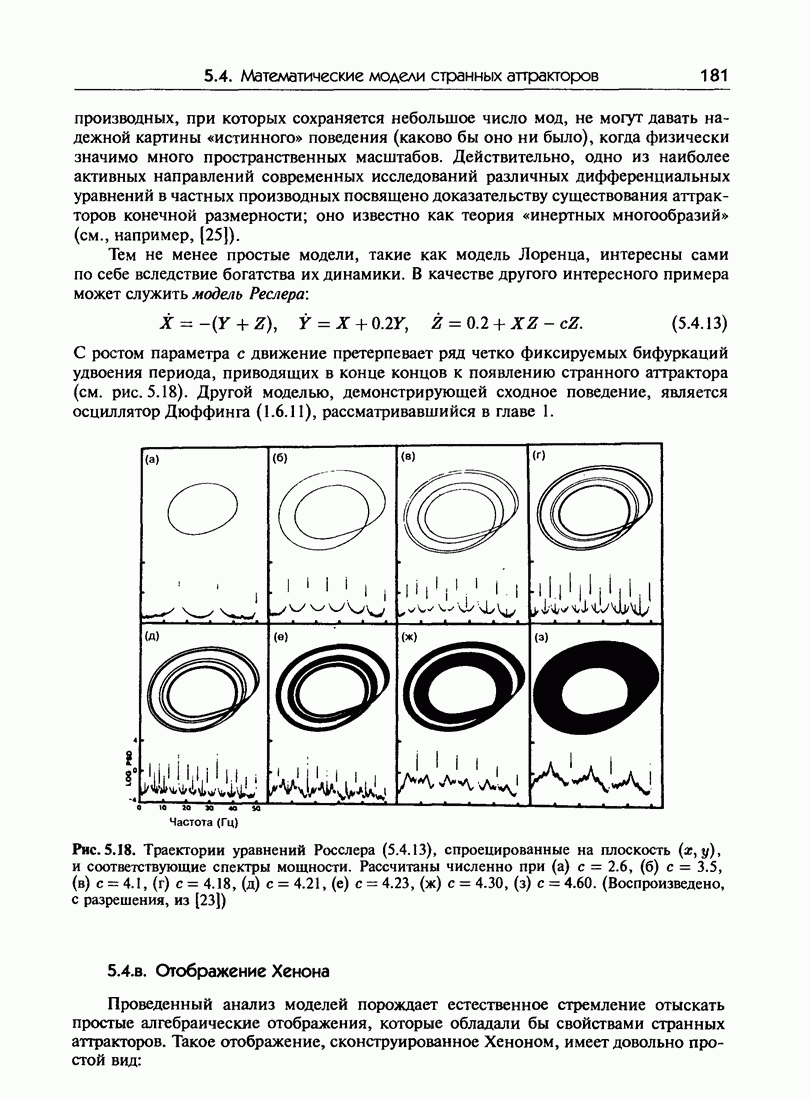
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
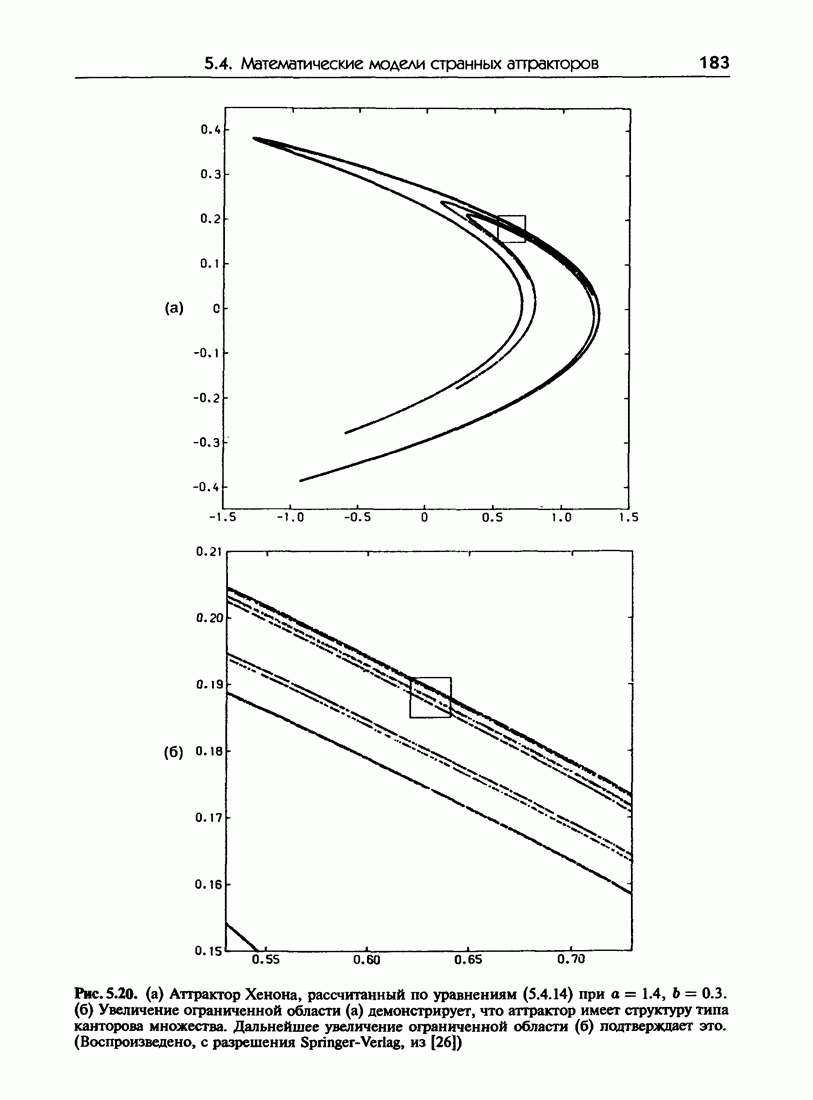
- 5.4.в. Отображение Хенона
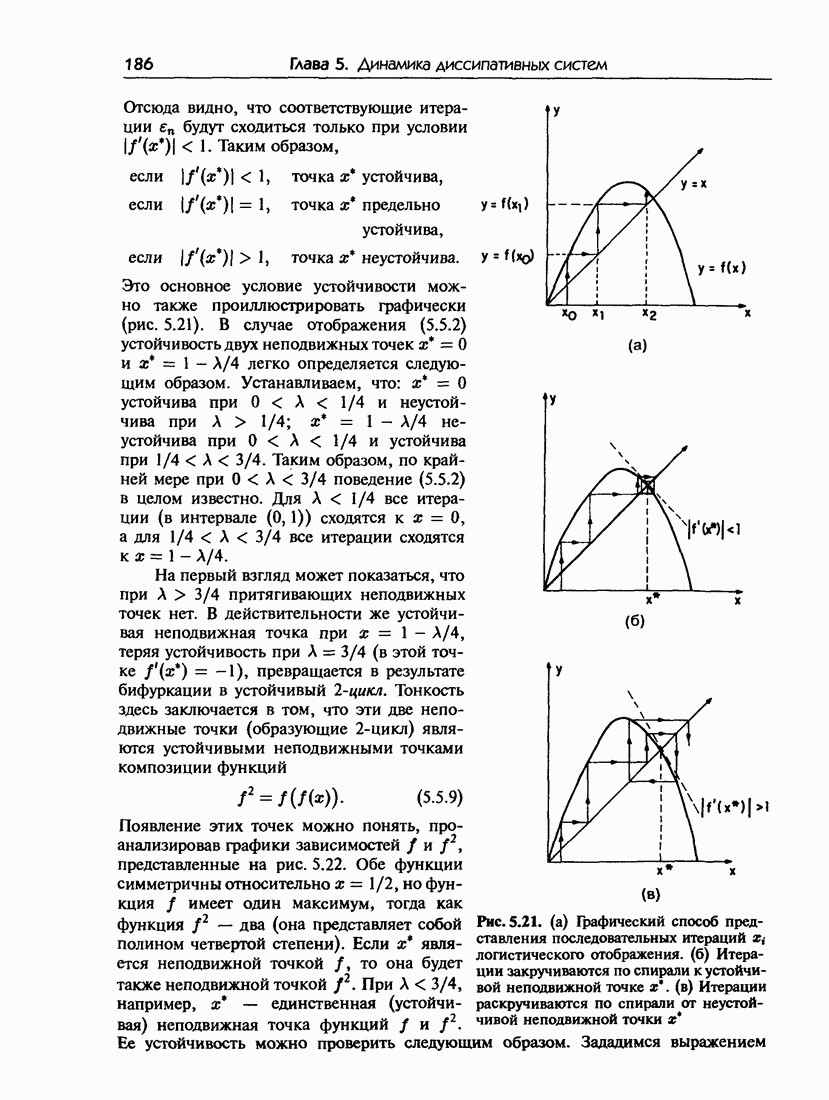
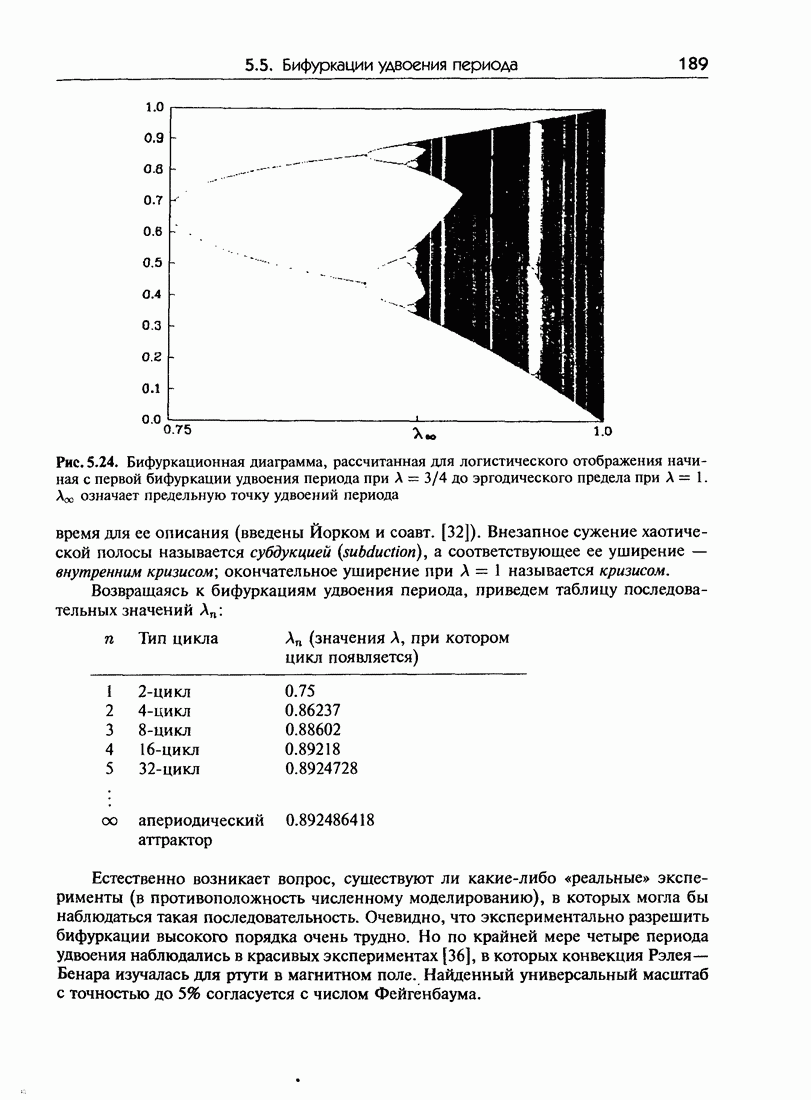
- 5.5. Бифуркации удвоения периода
- 5.5.а. Механизм удвоения периода
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
- 5.5.г. Другие классы универсальности
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
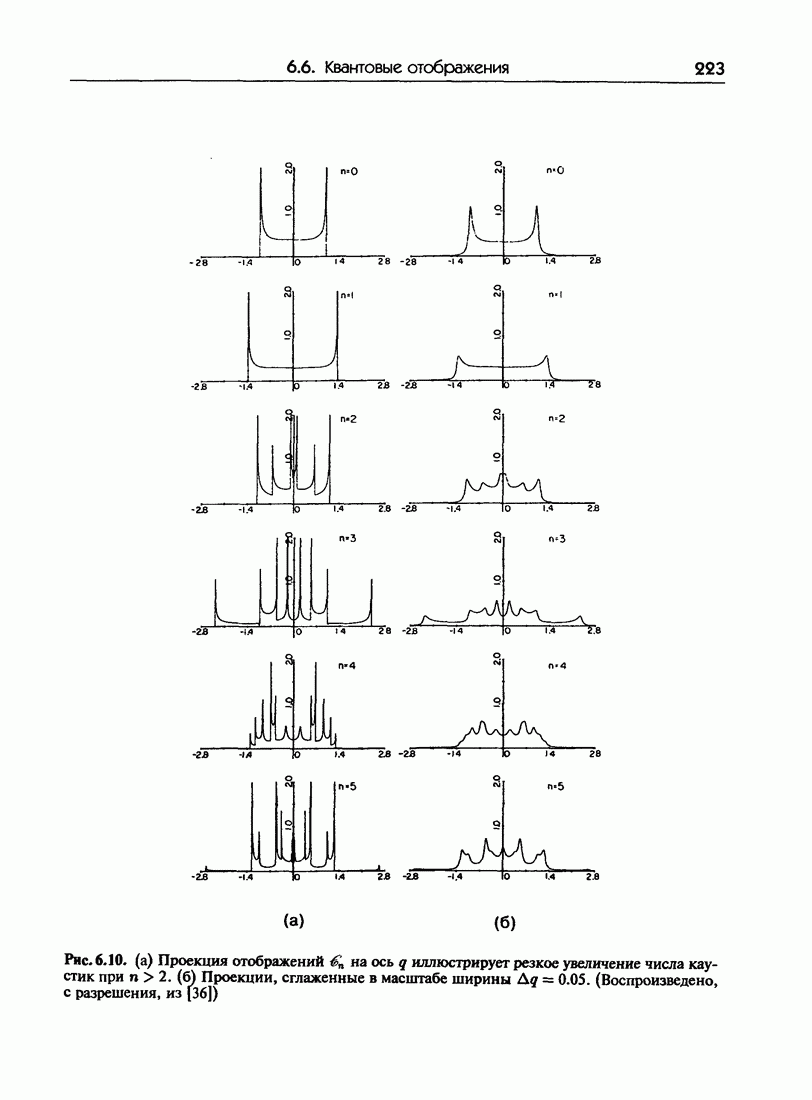
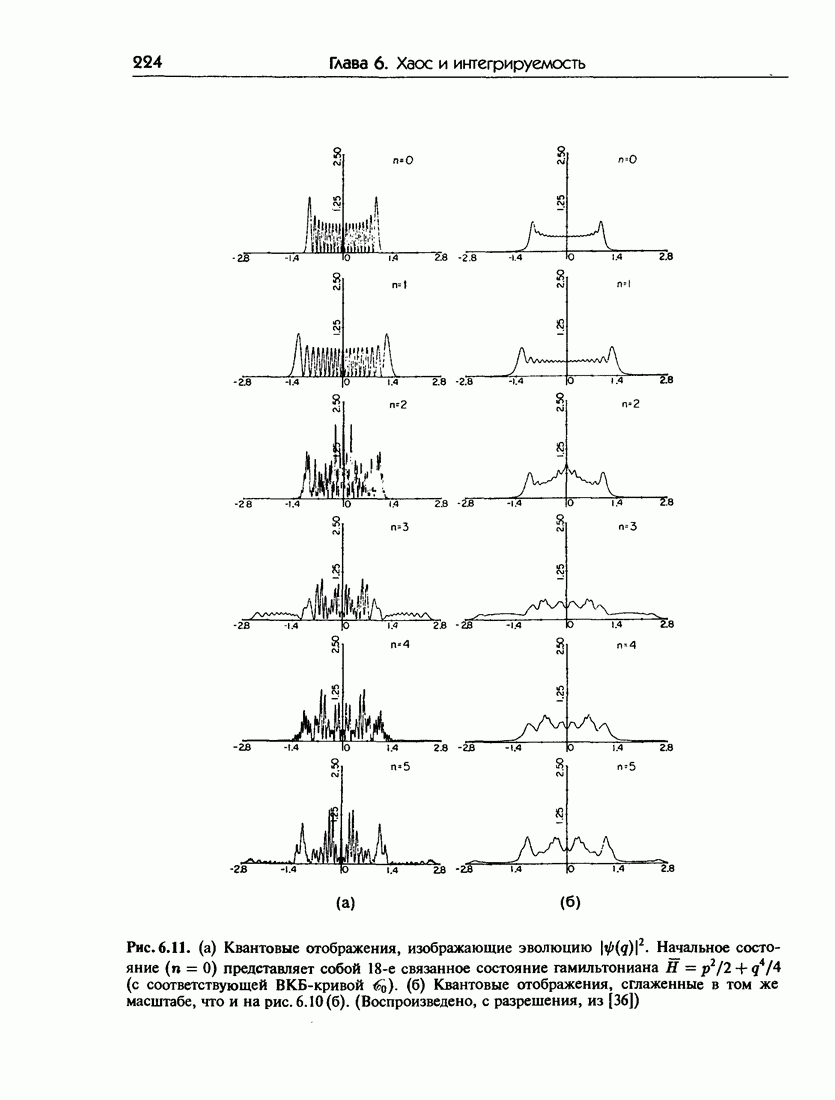
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
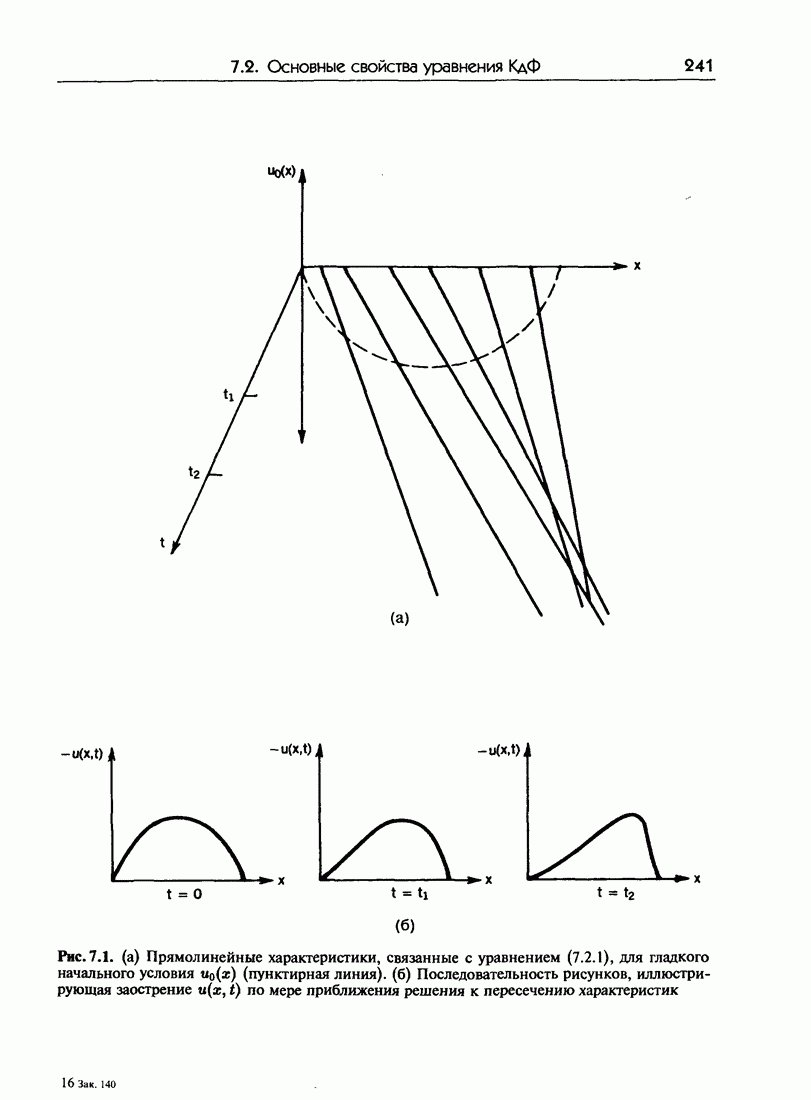
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
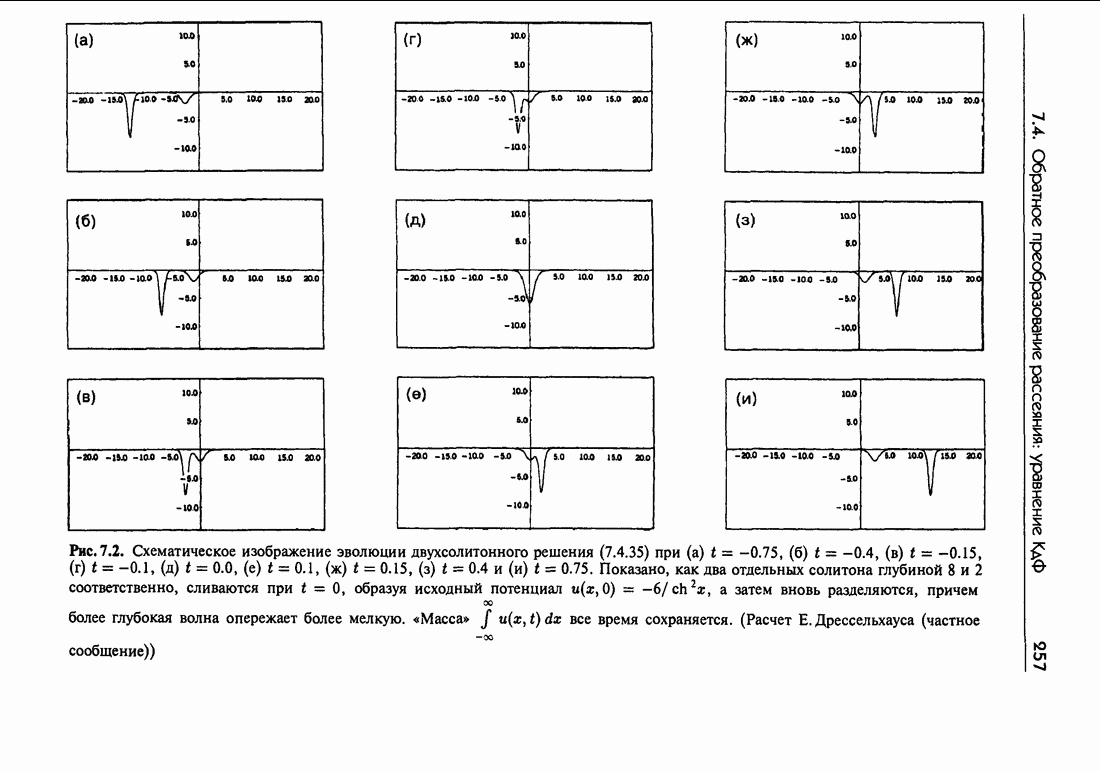
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
- 7.5. Другие солитонные системы
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда