| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
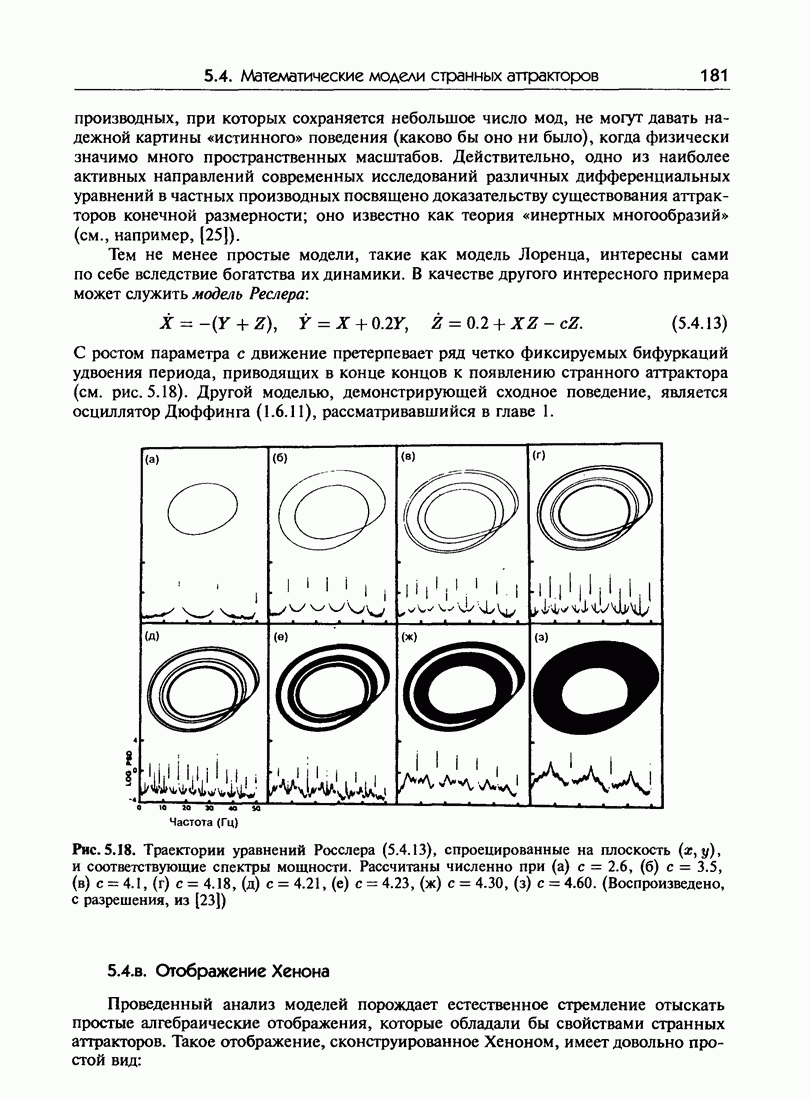
181
182
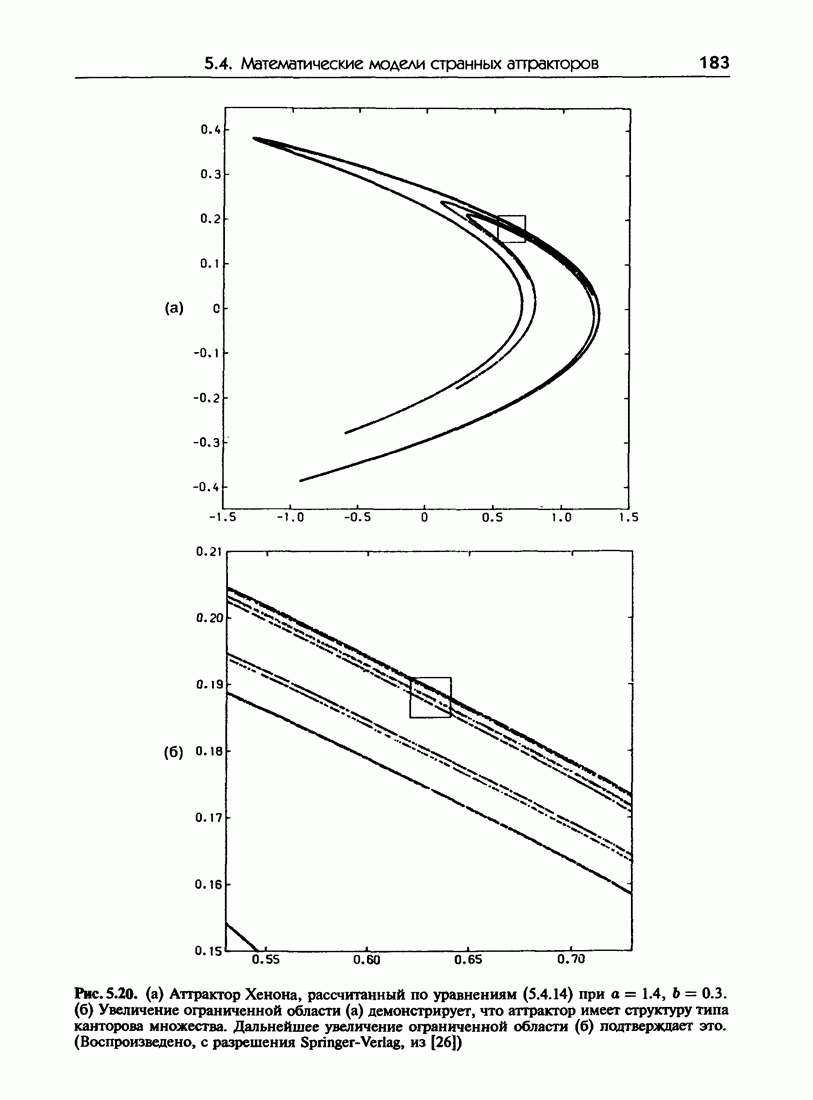
183
184
185
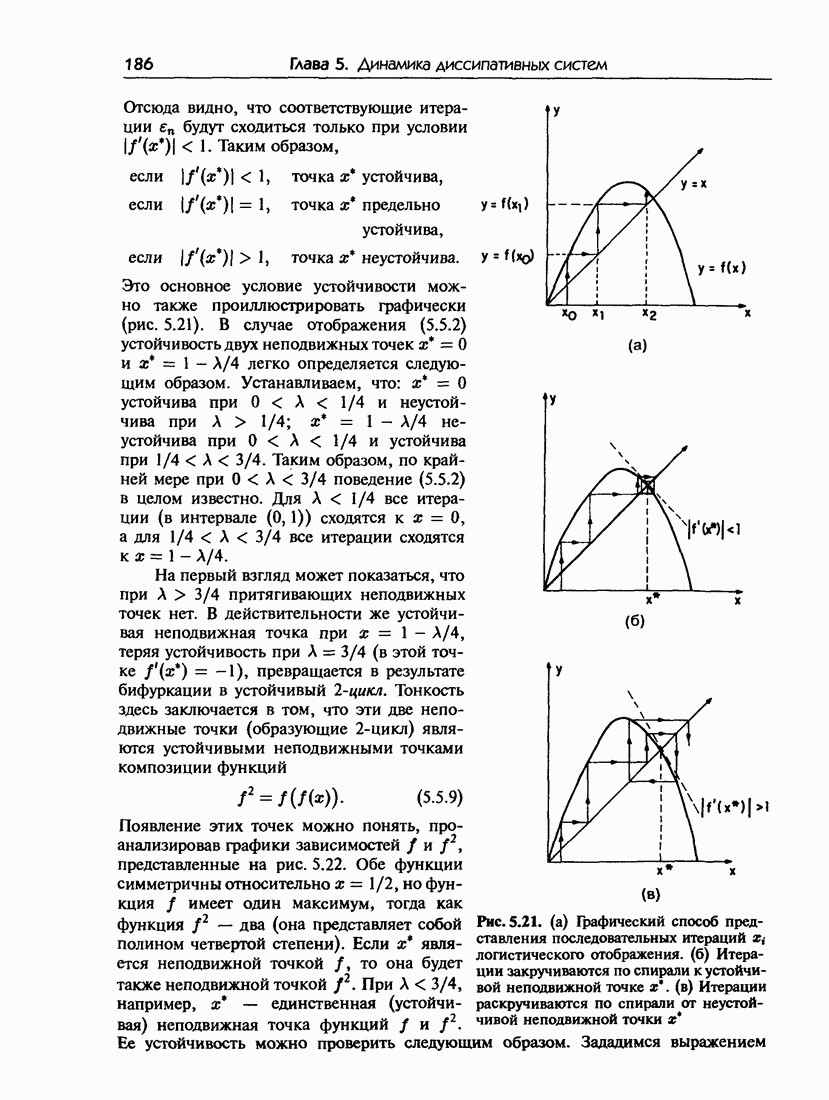
186
187
188
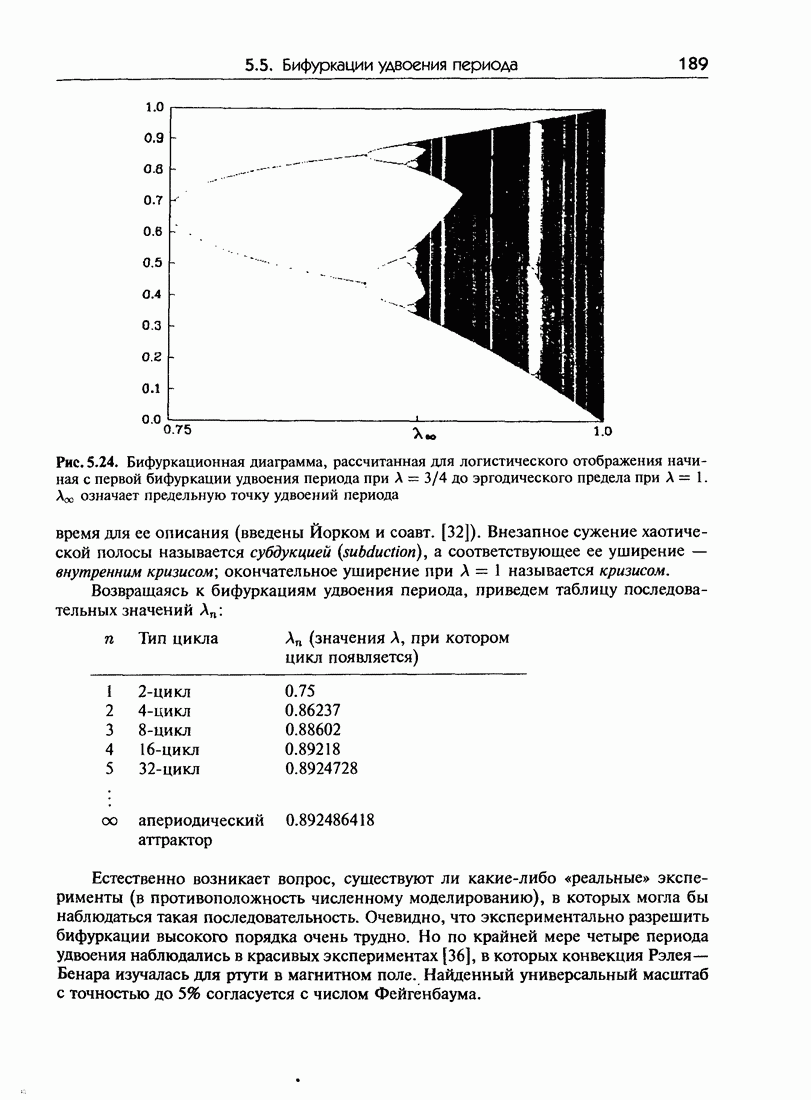
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
КАМ-теорема утверждает, что в случае неинтегрируемых гамильтоновых систем с ростом (неинтегрируемого) возмущения все большее и большее число торов разрушается. Движение в сильно неинтегрируемых системах преимущественно хаотическое, и сохраняется лишь небольшое число торов. Для большинства связанных состояний правила ЭБК при таких значениях энергии больше неприменимы; мы уже говорили, что это отмечалось довольно давно Эйнштейном. Однако в полной мере значение обсуждаемых трудностей оценил значительно позже Персиваль [4], который предложил подразделять энергетический спектр связанного состояния в квазиклассическом пределе  на две части.
на две части.
1. Регулярный спектр, соответствующий режиму интегрируемого (регулярного) движения, при котором все состояния могут быть проквантованы в соответствии с правилами ЭБК.
2. Нерегулярный спектр, соответствующий режиму преимущественно хаотического (нерегулярного) движения, при котором правила ЭБК уже неприменимы.
Эти два различных класса спектров могут обладать совершенно разными свойствами, отражая различия классического движения, «лежащего в их основе». Понятие нерегулярного спектра представляет особый интерес, поскольку оно в некотором смысле подразумевает, что в пределе  «лежащий в основе» классический хаос будет проявляться в квантовомеханических свойствах системы. Такая возможность даже послужила для некоторых исследователей основанием ввести понятие «квантовый хаос», которое не всегда ассоциируется с пределом
«лежащий в основе» классический хаос будет проявляться в квантовомеханических свойствах системы. Такая возможность даже послужила для некоторых исследователей основанием ввести понятие «квантовый хаос», которое не всегда ассоциируется с пределом  Вместе с тем, все обсуждаемое здесь неразрывно связано с квазиклассическим пределом, и любое представление о «квантовом хаосе» предполагает взаимосвязь с классическим хаосом.
Вместе с тем, все обсуждаемое здесь неразрывно связано с квазиклассическим пределом, и любое представление о «квантовом хаосе» предполагает взаимосвязь с классическим хаосом.
Наше обсуждение существенных различий в свойствах регулярных и нерегулярных спектров условно распадается на две части. Первая часть, составляющая содержание настоящего раздела, посвящена в основном свойствам, связанным с собственными значениями; содержание второй части, излагаемой в следующем разделе, составляют главным образом свойства, связанные с собственными векторами (волновыми функциями).
6.4.а. Регулярные и нерегулярные связанные состояния
Принципиальное отличие регулярных и нерегулярных (квазиклассических) состояний заключается в том, что регулярное состояние может быть описано с помощью полного набора «хороших» квантовых чисел  где
где  число степеней свободы. Состоянию с квантовыми числами
число степеней свободы. Состоянию с квантовыми числами  можно, таким образом, поставить в соответствие семейство траекторий на
можно, таким образом, поставить в соответствие семейство траекторий на  -мерном торе с постоянным действием, задаваемым правилами ЭБК (6.3.10). Следовательно, существует взаимно-однозначное соответствие между регулярным состоянием и классическим тором. В случае состояния с нерегулярным спектром, напротив, не только не существует способа разумно задать «хорошие» квантовые числа, но и представления о взаимном соответствии такого состояния и данной области фазового пространства
-мерном торе с постоянным действием, задаваемым правилами ЭБК (6.3.10). Следовательно, существует взаимно-однозначное соответствие между регулярным состоянием и классическим тором. В случае состояния с нерегулярным спектром, напротив, не только не существует способа разумно задать «хорошие» квантовые числа, но и представления о взаимном соответствии такого состояния и данной области фазового пространства
ограничиваются лишь тем, что состояние должно «занимать» объем порядка  Некоторые авторы тем не менее считают, что в хаотических режимах все же можно, используя определенные методы классической теории возмущений, построить «приближенные торы (в конце концов, разумеется, соответствующие ряды должны в этих режимах расходиться) и использовать для квантования правила ЭБК (см. [16]). В подвергнутых анализу модельных системах полученные таким образом уровни энергии достаточно хорошо согласовывались с точными квантовомеханическими расчетами. Обсуждаемые результаты затрагивают очень важный вопрос, связанный с тем, что рассмотренные системы не содержали достаточно большого числа связанных состояний — ситуация, когда
Некоторые авторы тем не менее считают, что в хаотических режимах все же можно, используя определенные методы классической теории возмущений, построить «приближенные торы (в конце концов, разумеется, соответствующие ряды должны в этих режимах расходиться) и использовать для квантования правила ЭБК (см. [16]). В подвергнутых анализу модельных системах полученные таким образом уровни энергии достаточно хорошо согласовывались с точными квантовомеханическими расчетами. Обсуждаемые результаты затрагивают очень важный вопрос, связанный с тем, что рассмотренные системы не содержали достаточно большого числа связанных состояний — ситуация, когда  относительно «велико». Понятно, что случай, когда области фазового пространства, занятые хаотическим движением, существенно меньше, чем
относительно «велико». Понятно, что случай, когда области фазового пространства, занятые хаотическим движением, существенно меньше, чем  , т.е. «размера» квантового состояния, не представляет сколь-нибудь существенного интереса с точки зрения квантовой механики. Из сказанного следует, что
, т.е. «размера» квантового состояния, не представляет сколь-нибудь существенного интереса с точки зрения квантовой механики. Из сказанного следует, что  играет в некотором смысле «сглаживающую» роль, способствуя сохранению торов, которые, вообще говоря, должны разрушаться. Вместе с тем очевидно, что как только
играет в некотором смысле «сглаживающую» роль, способствуя сохранению торов, которые, вообще говоря, должны разрушаться. Вместе с тем очевидно, что как только  становится достаточно мало, такой подход более не применим, и возникает фундаментальная проблема поиска квазиклассических условий квантования для хаотических систем. До настоящего времени не было предложено ни одного «прямого» подхода, но существует «косвенный» метод, основанный на использовании классических периодических траекторий. Этот важный метод будет изложен в контексте «квантовых отображений» в разделе 6.7.
становится достаточно мало, такой подход более не применим, и возникает фундаментальная проблема поиска квазиклассических условий квантования для хаотических систем. До настоящего времени не было предложено ни одного «прямого» подхода, но существует «косвенный» метод, основанный на использовании классических периодических траекторий. Этот важный метод будет изложен в контексте «квантовых отображений» в разделе 6.7.
Основываясь на отсутствии «хороших» квантовых чисел в случае нерегулярных состояний, Персиваль [4] пришел к выводу, что регулярные и нерегулярные спектры должны различаться по их вероятностям переходов. Переходы между состояниями регулярного спектра должны характеризоваться строгими правилами отбора; это предполагает, что спектр (в смысле спектроскопически наблюдаемых величин) состоит из небольшого числа интенсивных линий, соответствующих сильно связанным состояниям. С другой стороны предполагается, что состояния нерегулярного (энергетического) спектра будут в одинаковой мере связаны со всеми теми состояниями с близкой энергией, которые соответствуют одним и тем же «хаотическим» областям фазового пространства; таким образом ожидается, что спектр будет состоять из большого числа слабых линий. Пока не известны экспериментальные данные, однозначно подтверждающие существование нерегулярных спектров.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
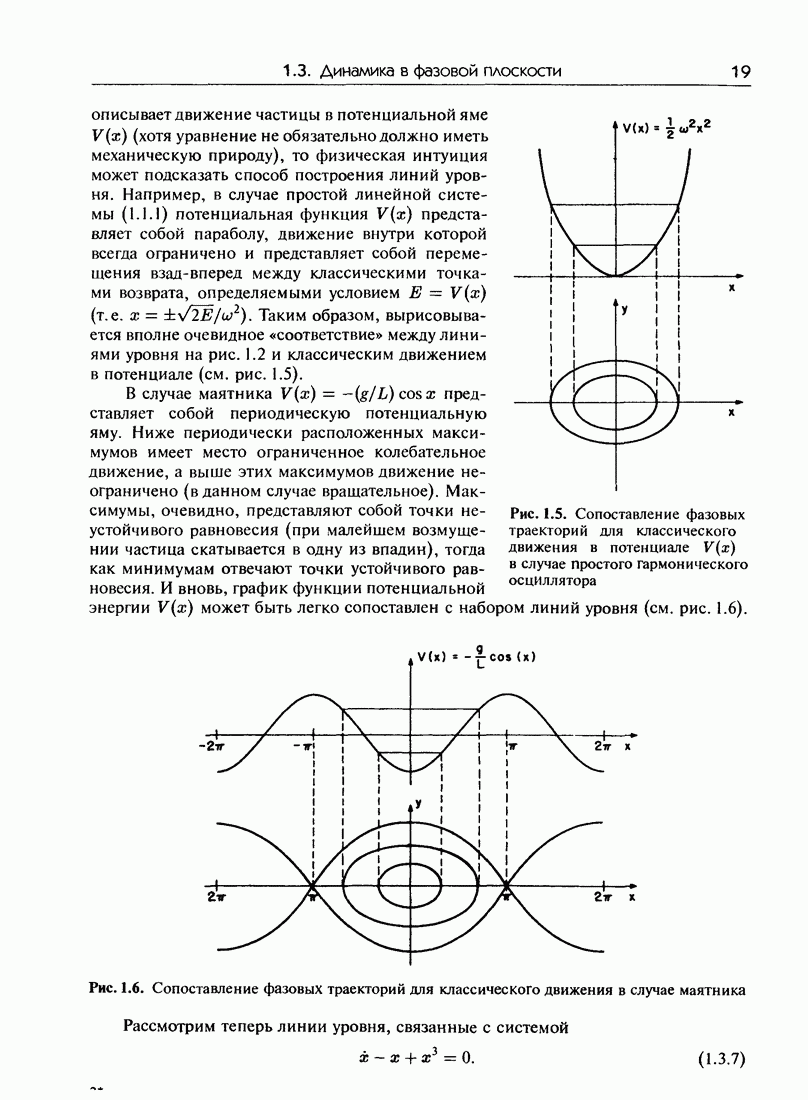
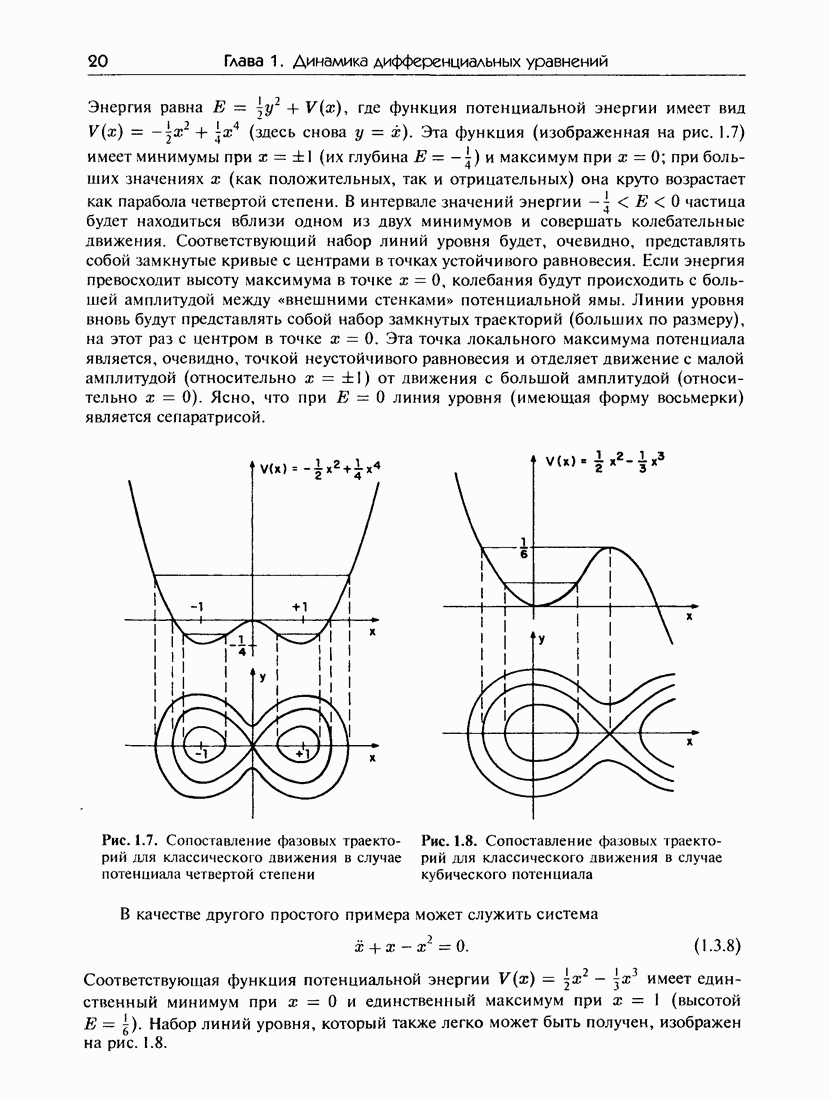
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
- 1.3.б. фазовые портреты консервативных систем
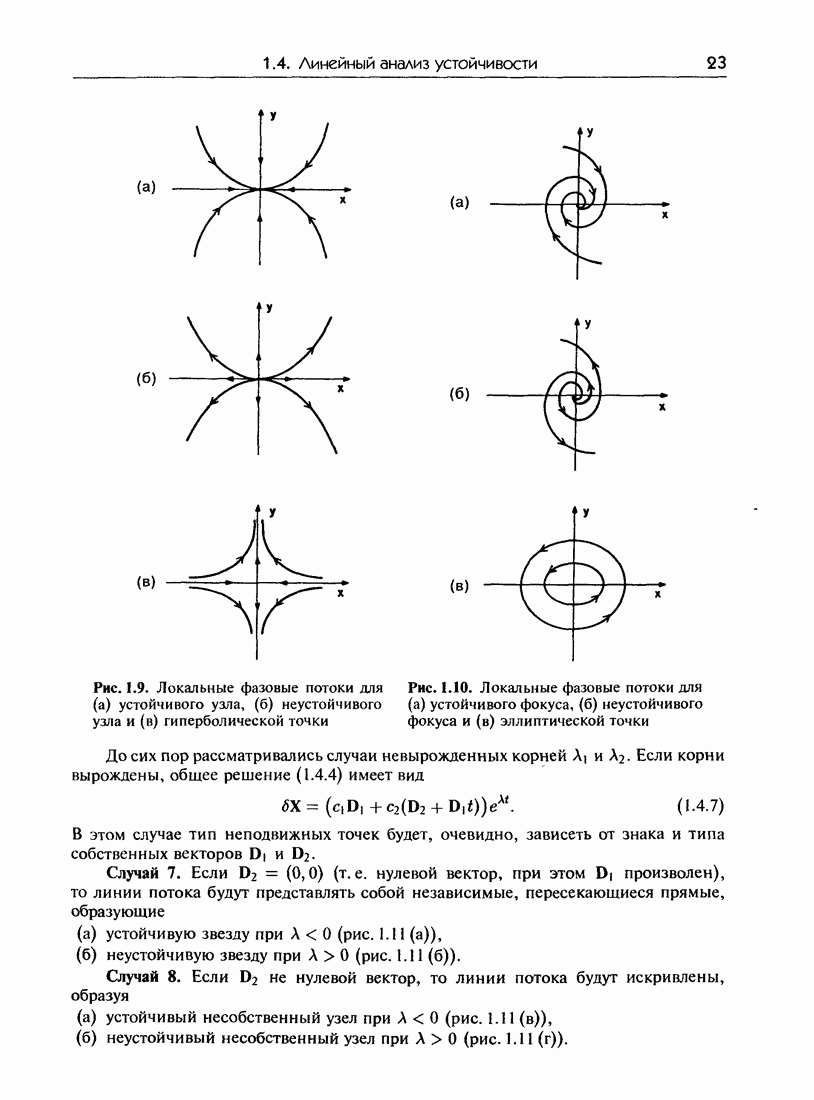
- 1.4. Линейный анализ устойчивости
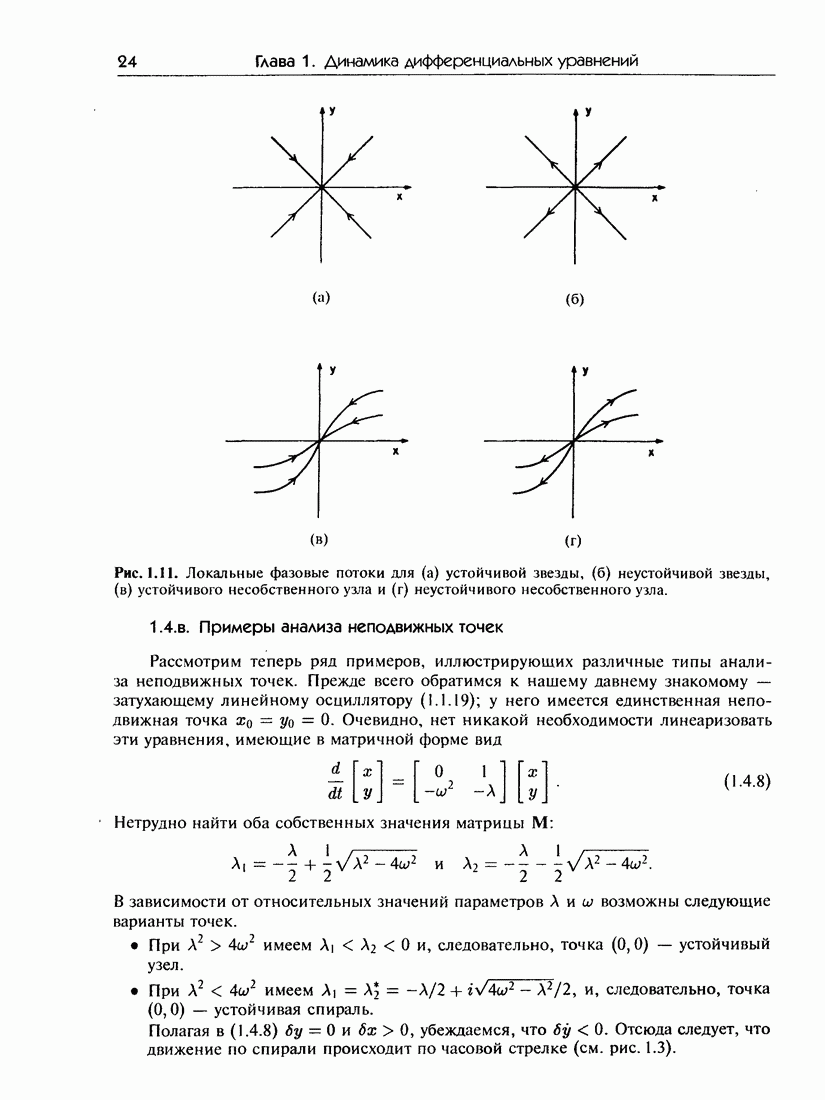
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
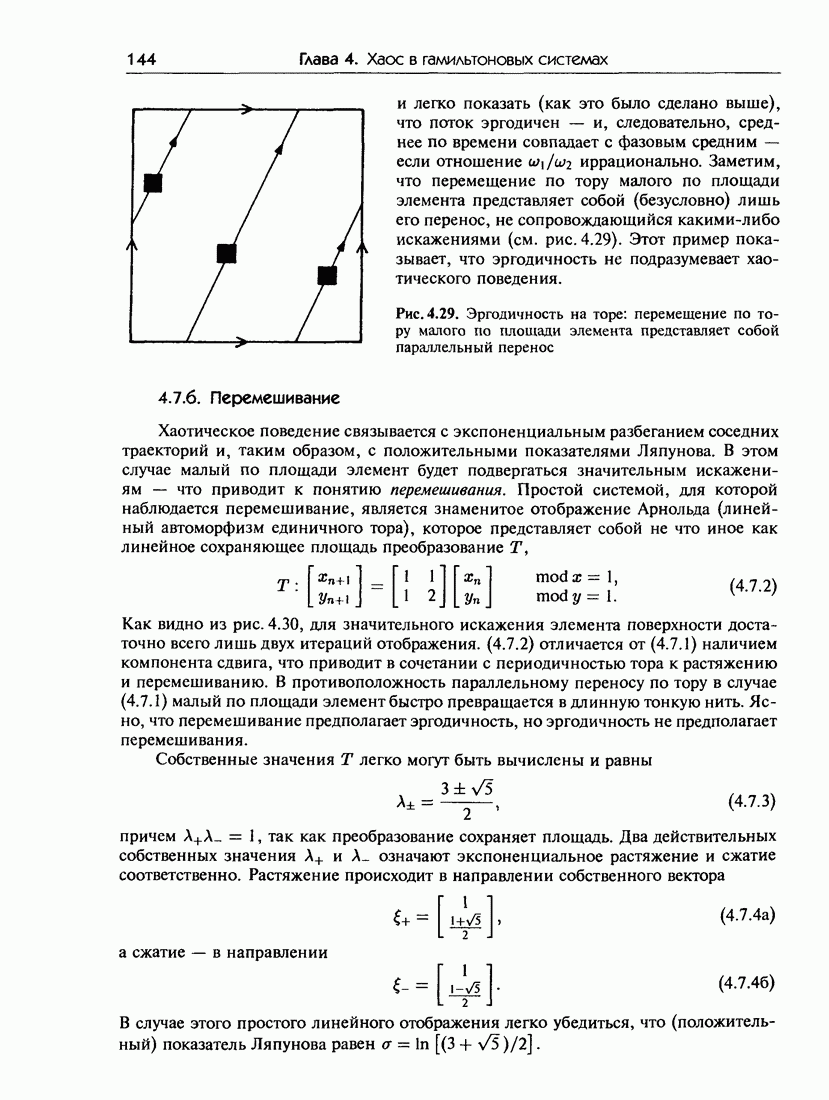
- 4.7.б. Перемешивание
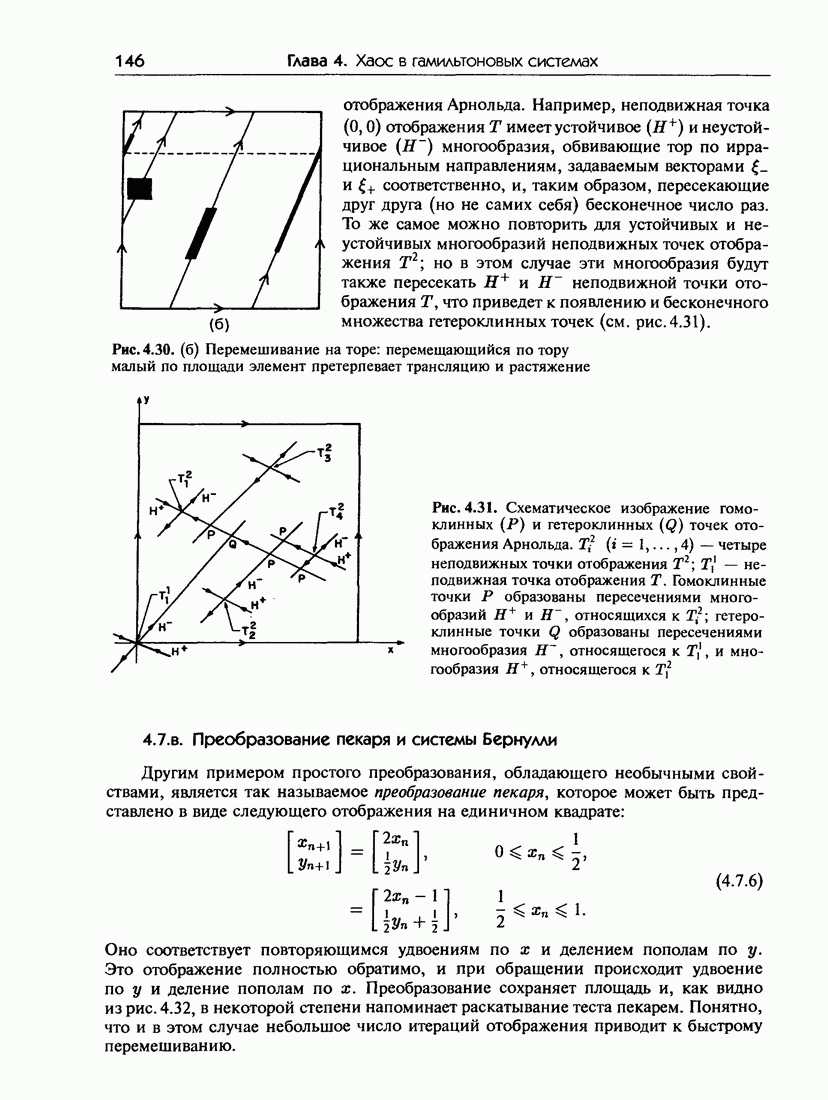
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
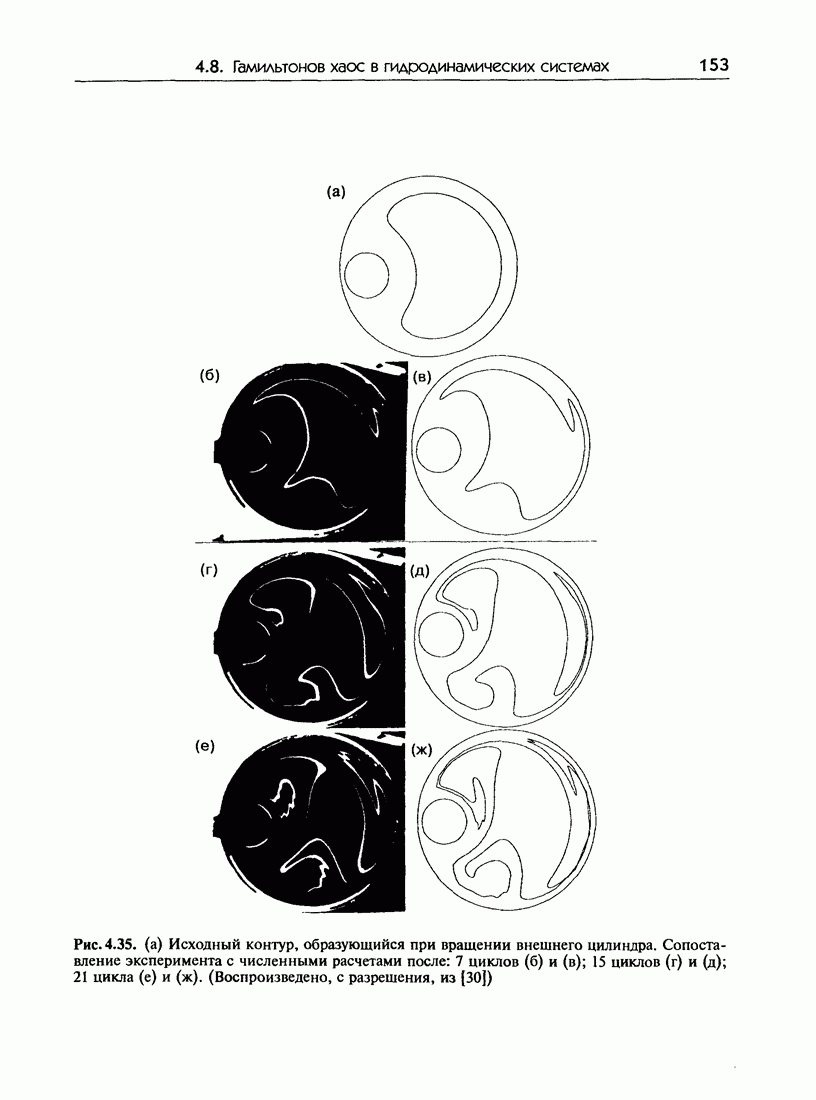
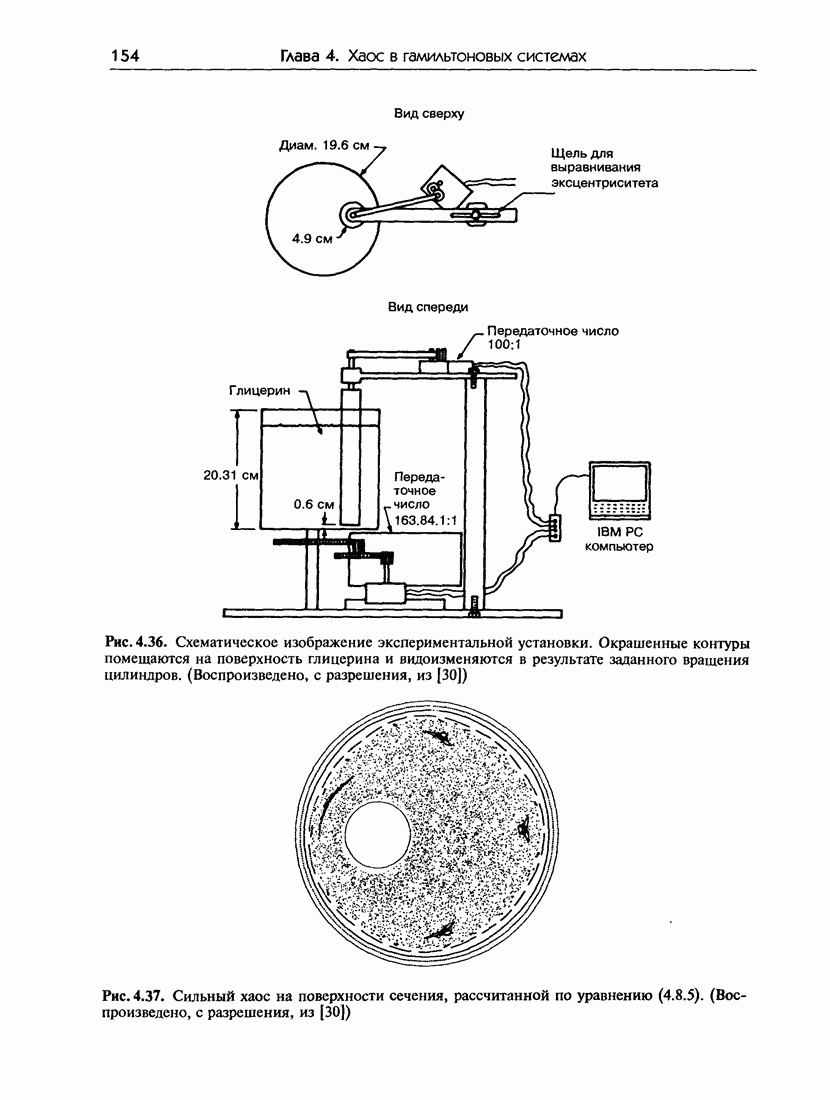
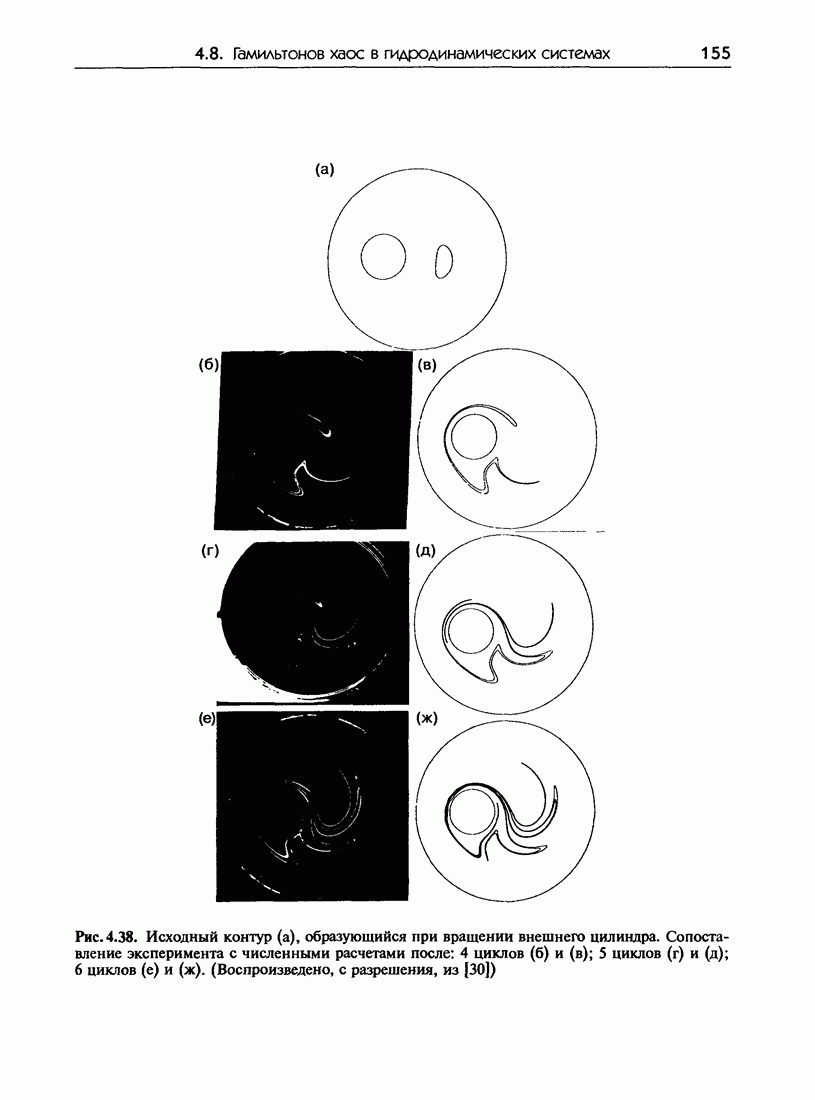
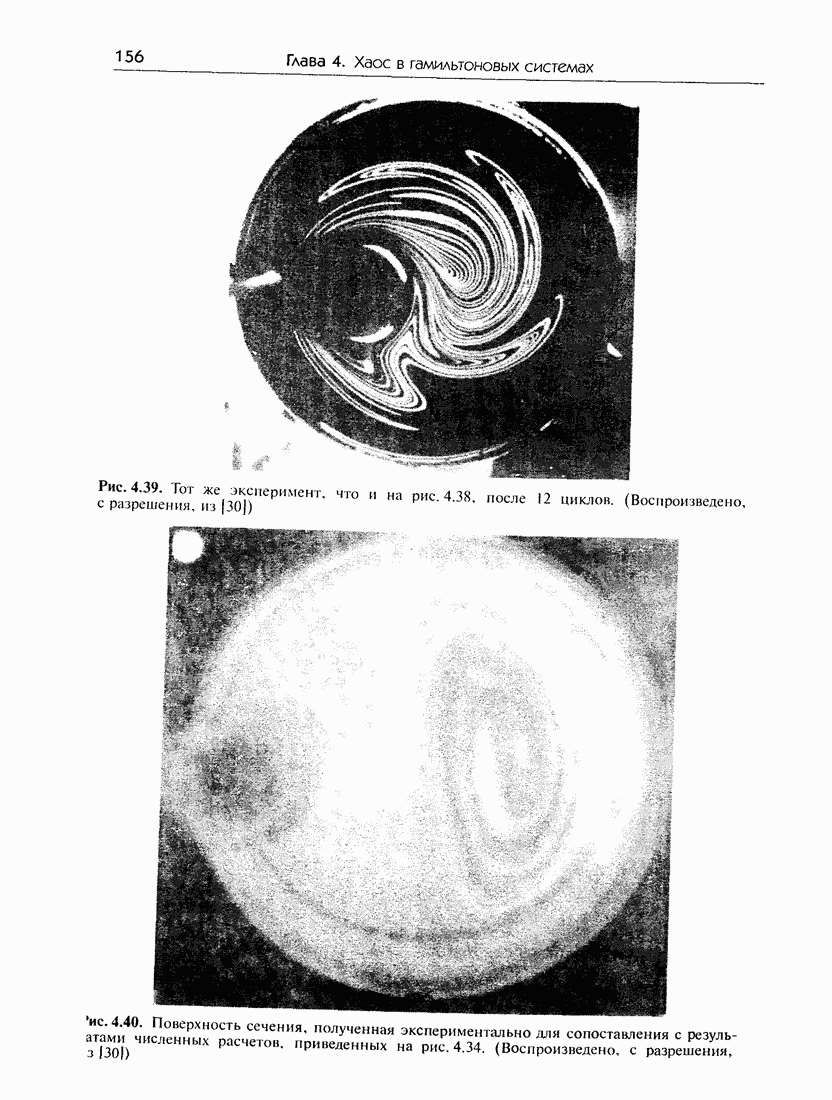
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
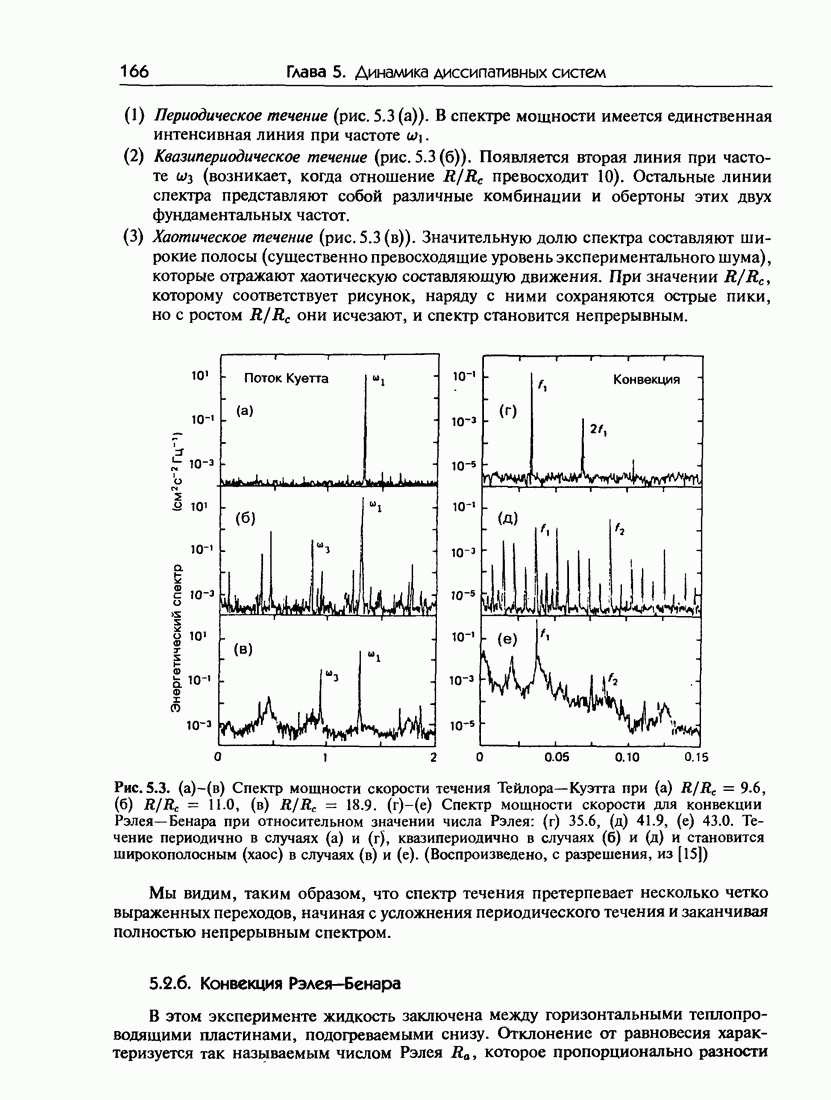
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
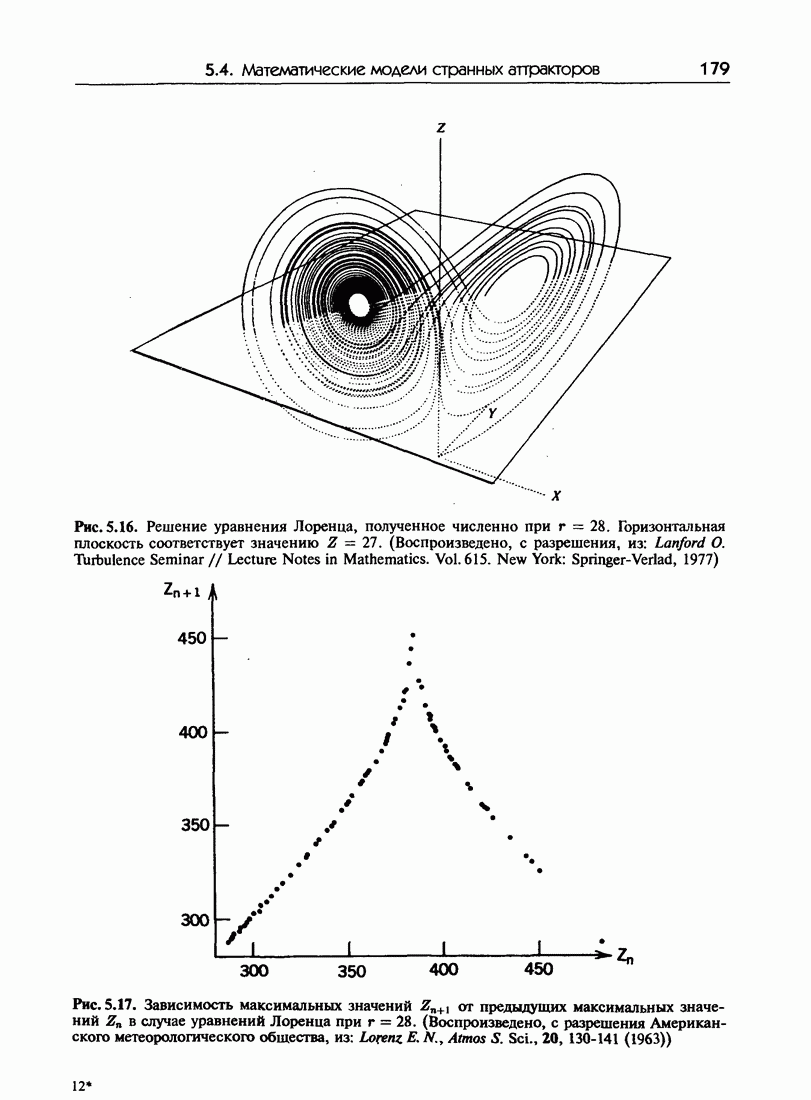
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
- 5.4.в. Отображение Хенона
- 5.5. Бифуркации удвоения периода
- 5.5.а. Механизм удвоения периода
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
- 5.5.г. Другие классы универсальности
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
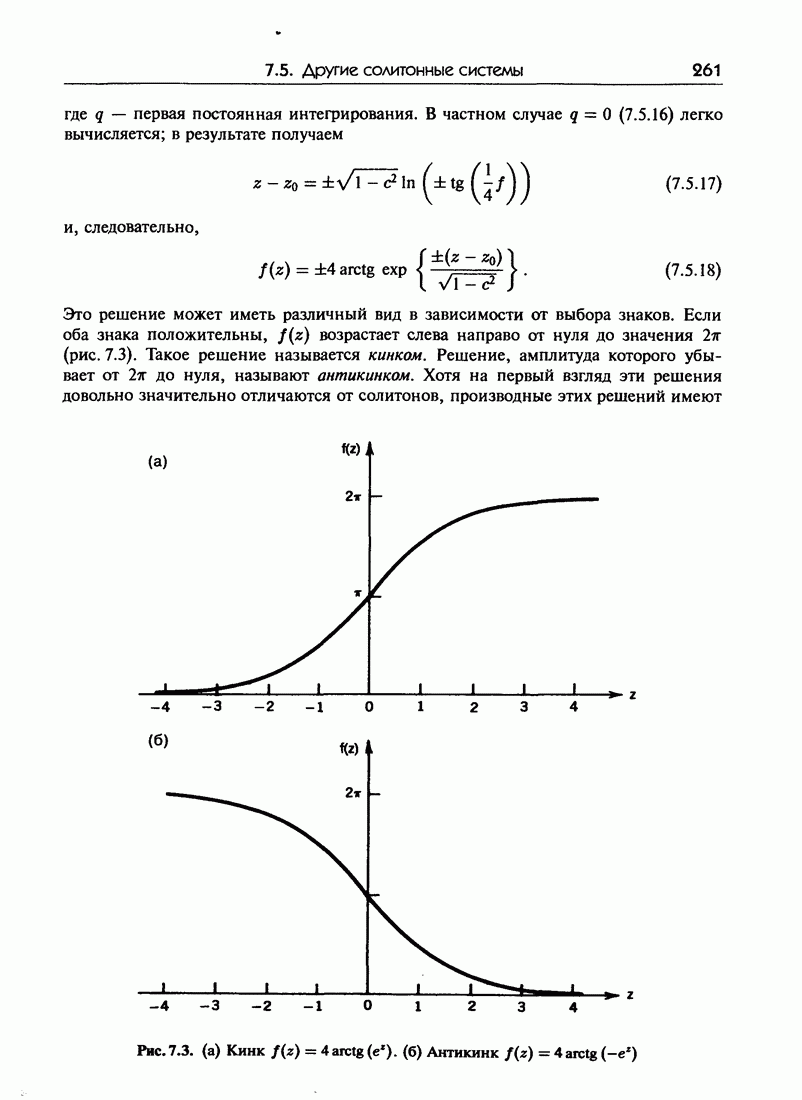
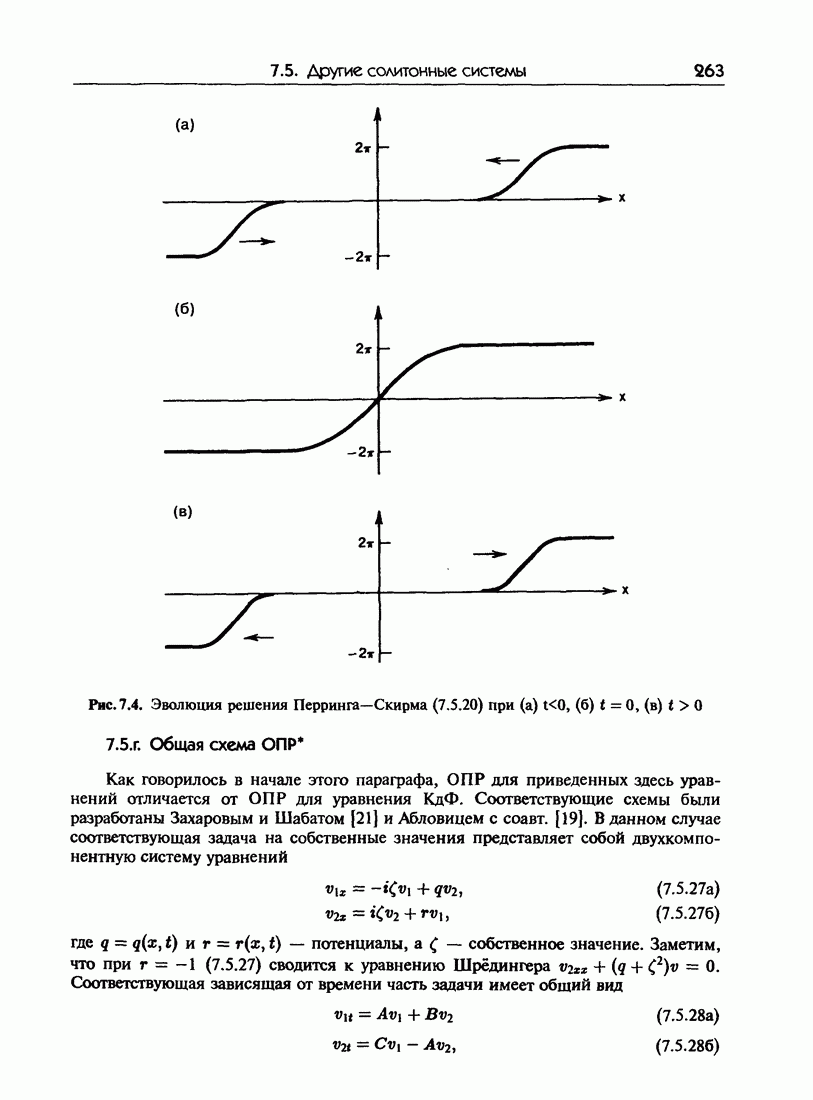
- 7.5. Другие солитонные системы
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
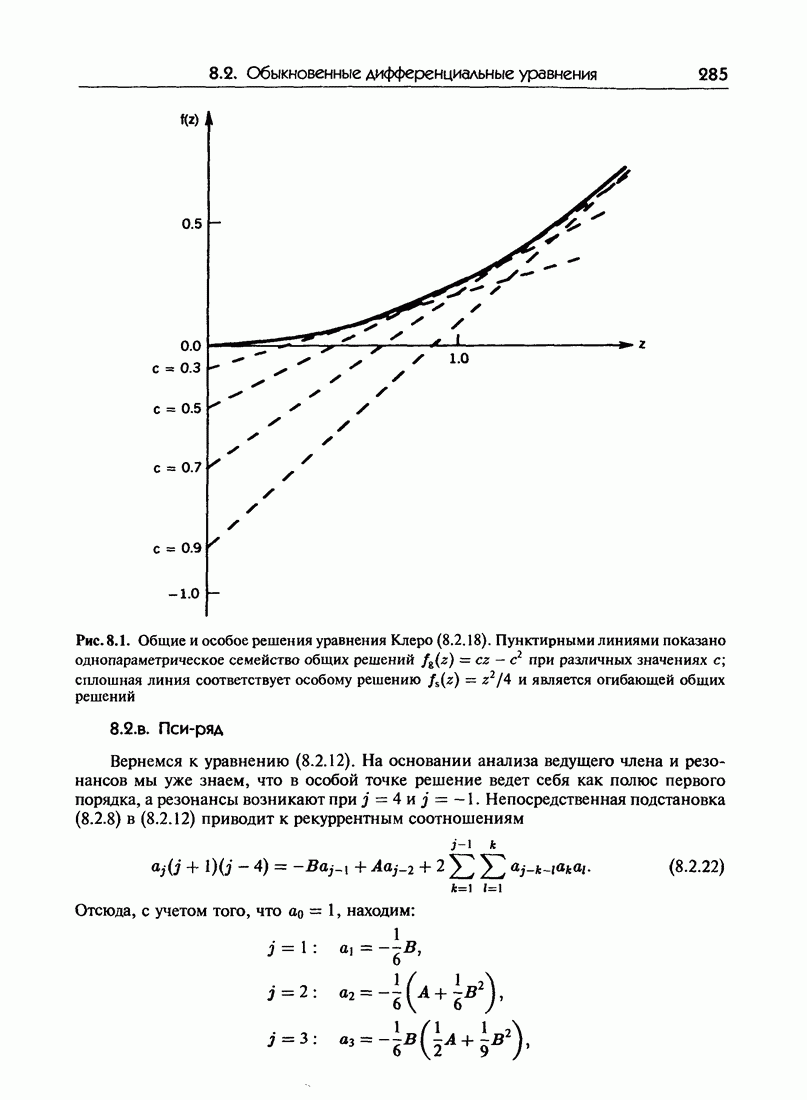
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
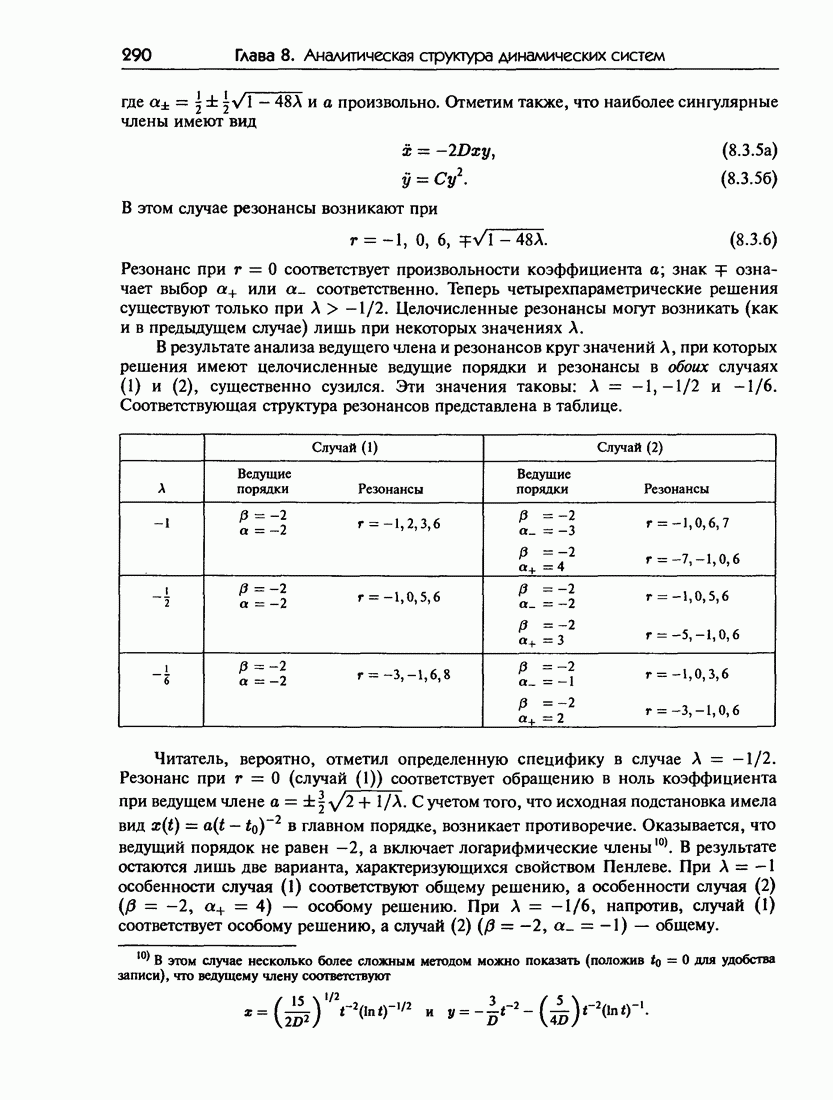
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда