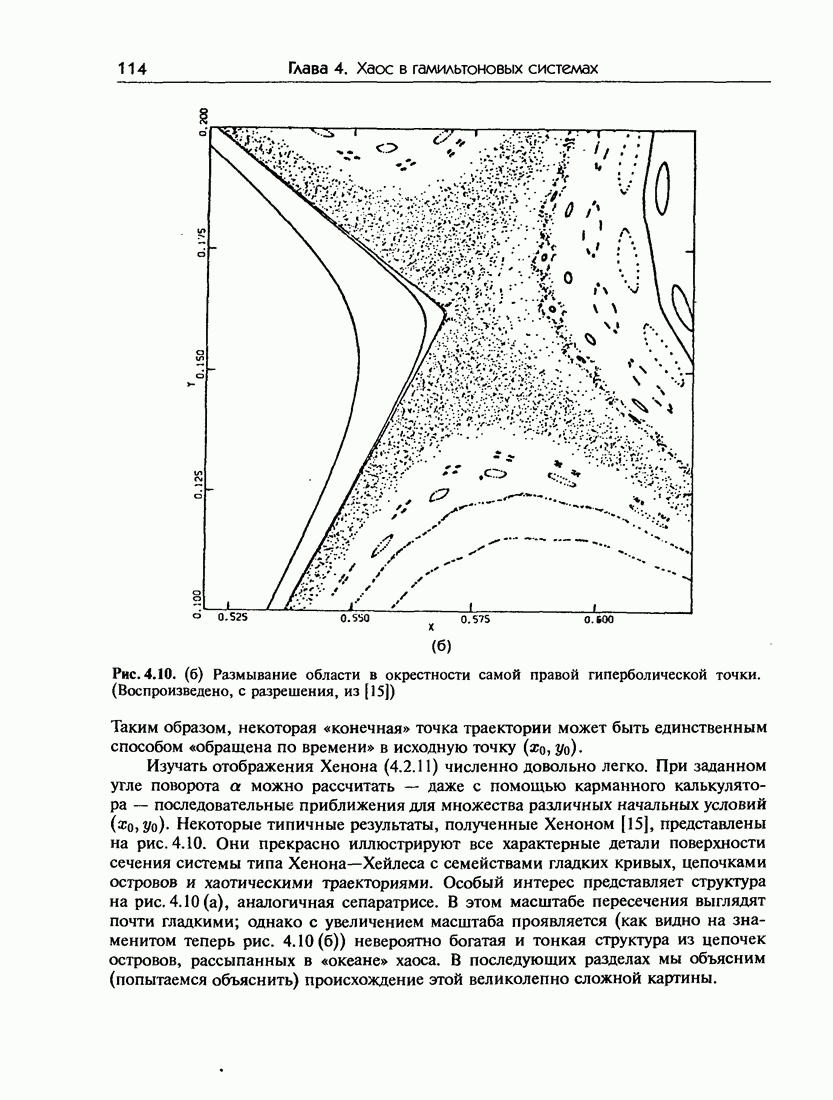
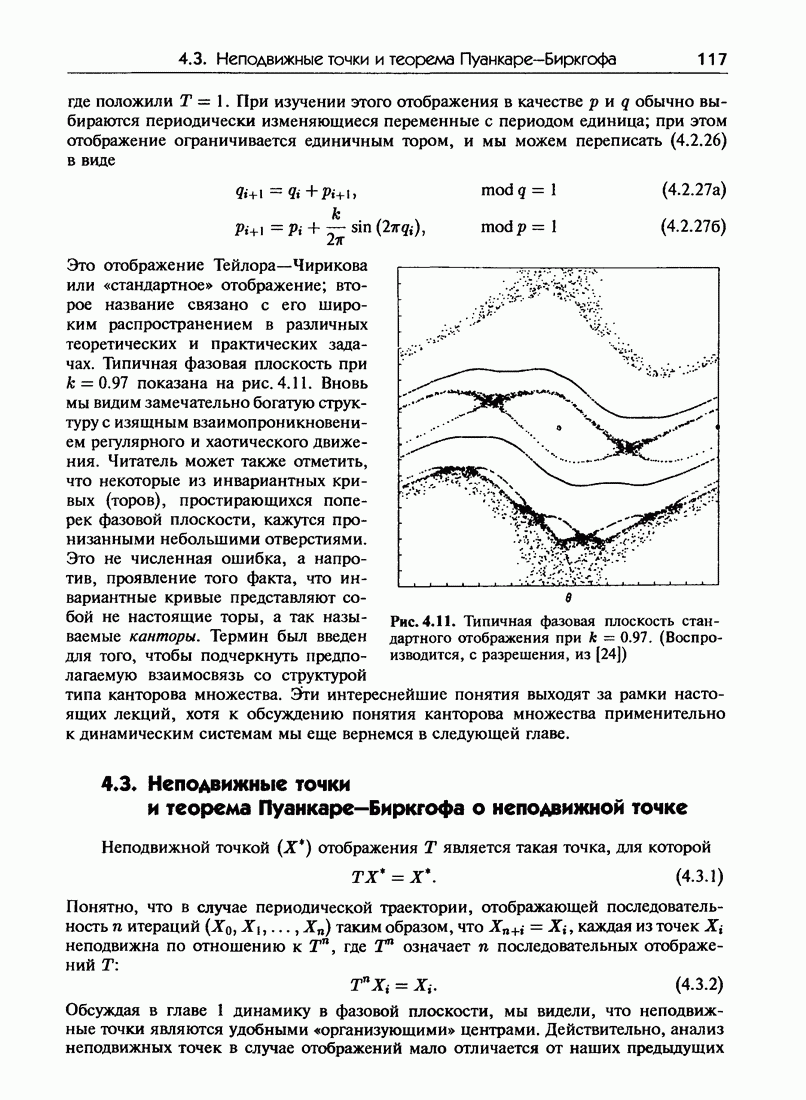
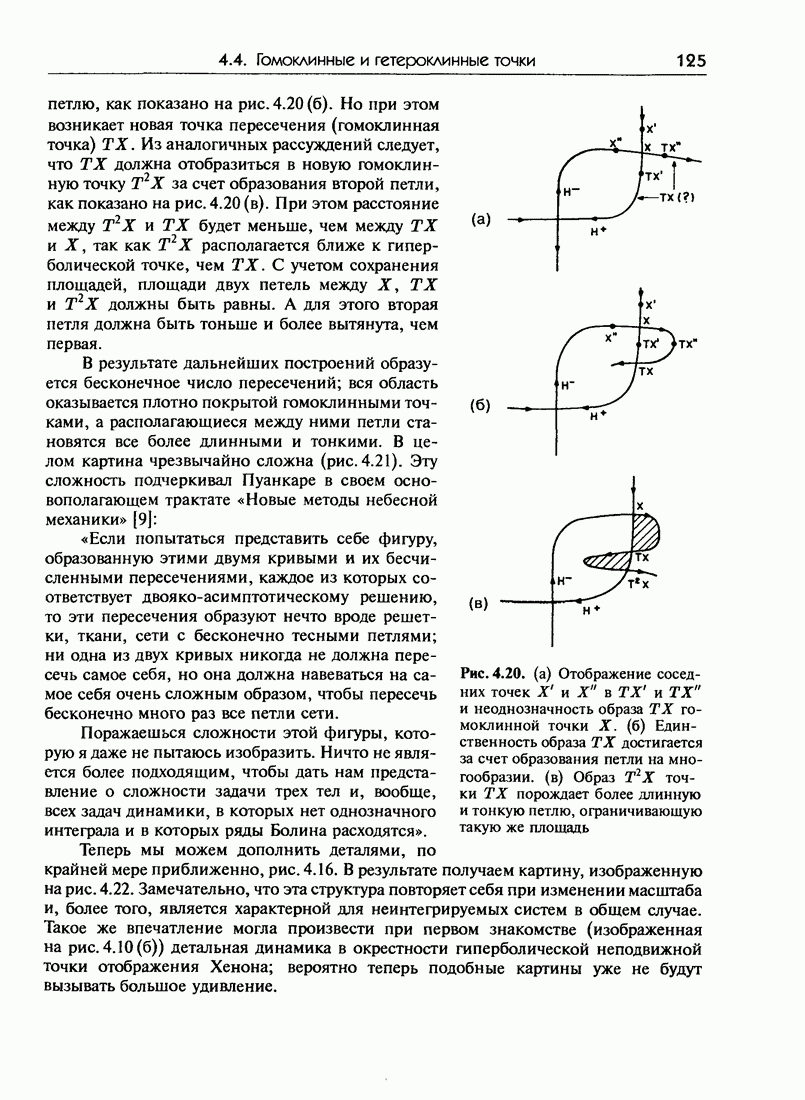
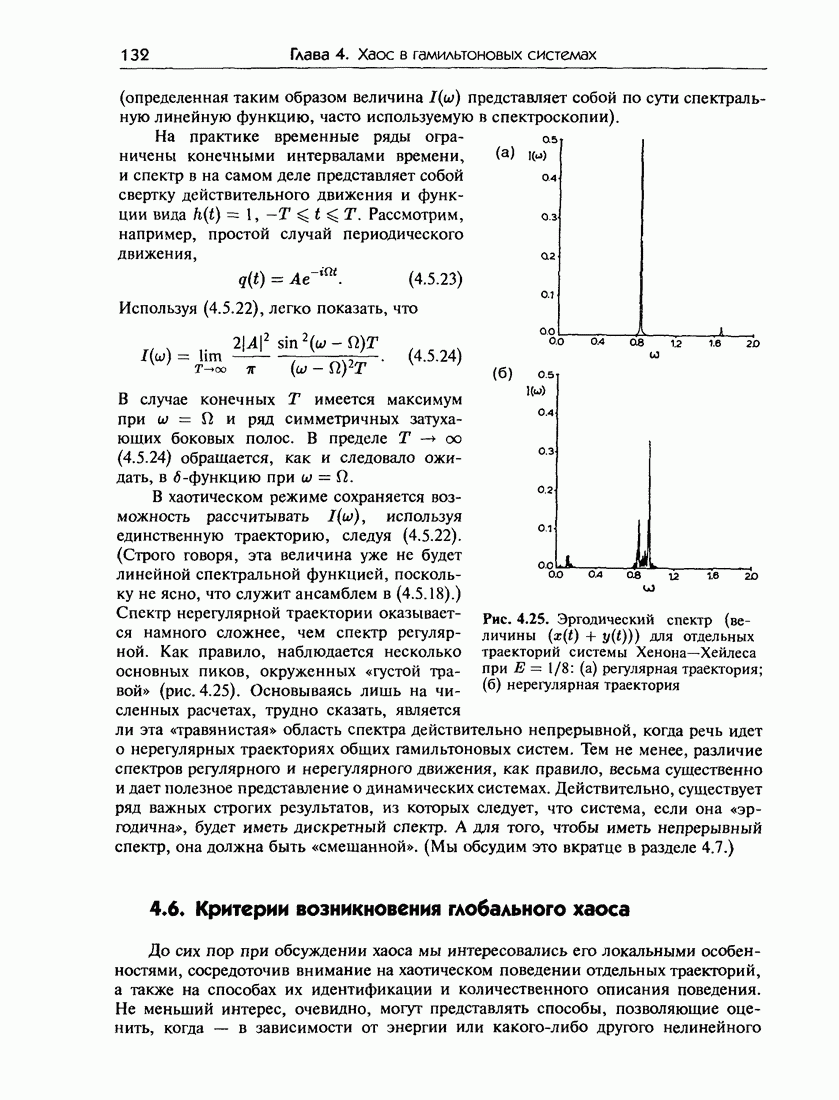
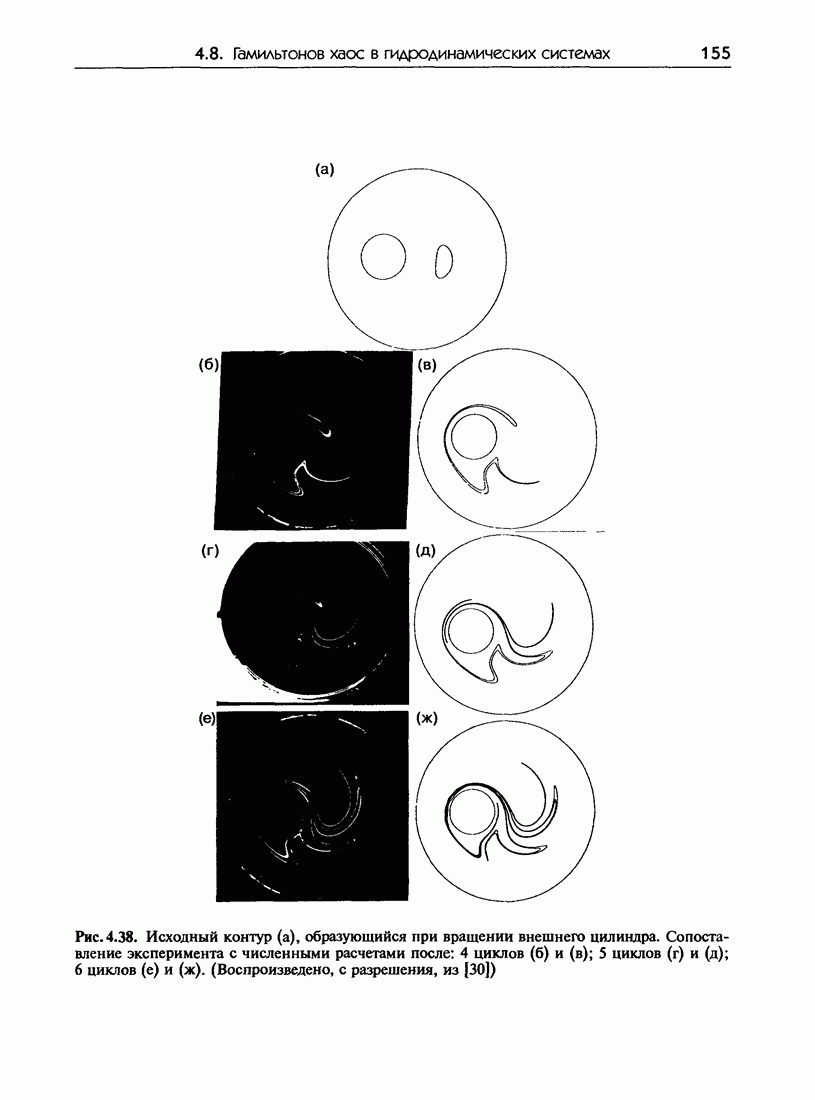
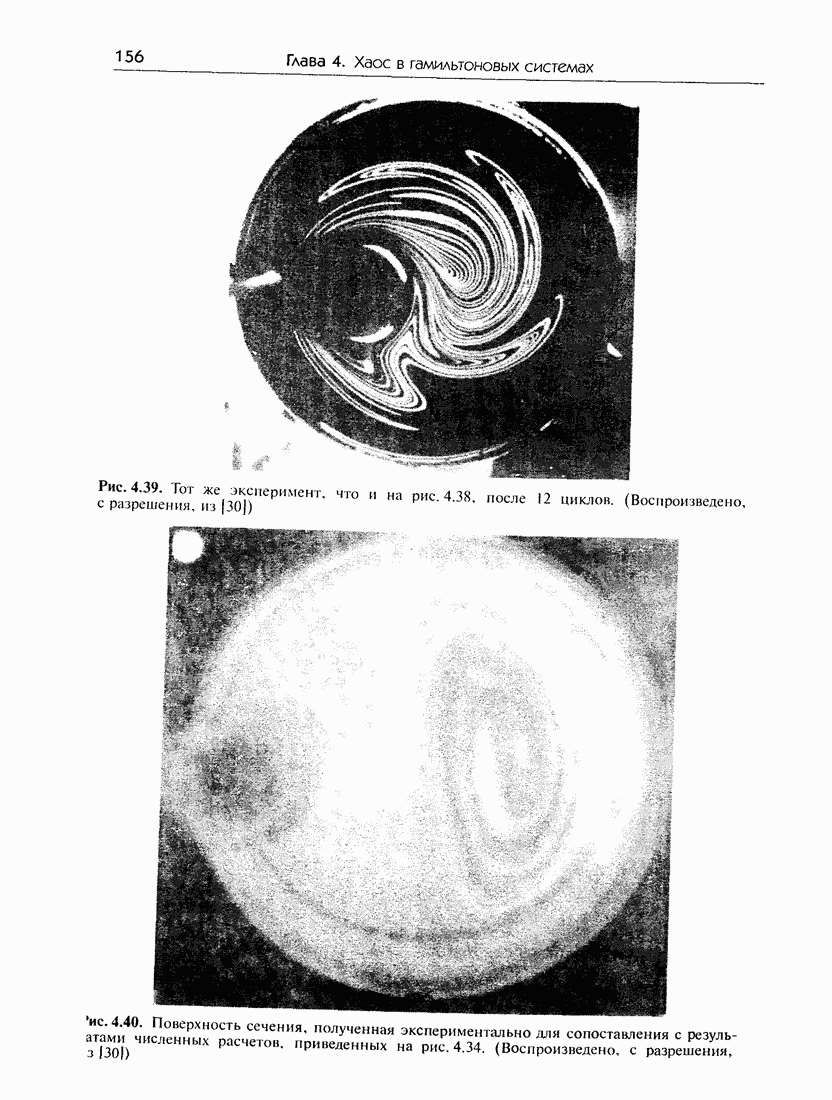
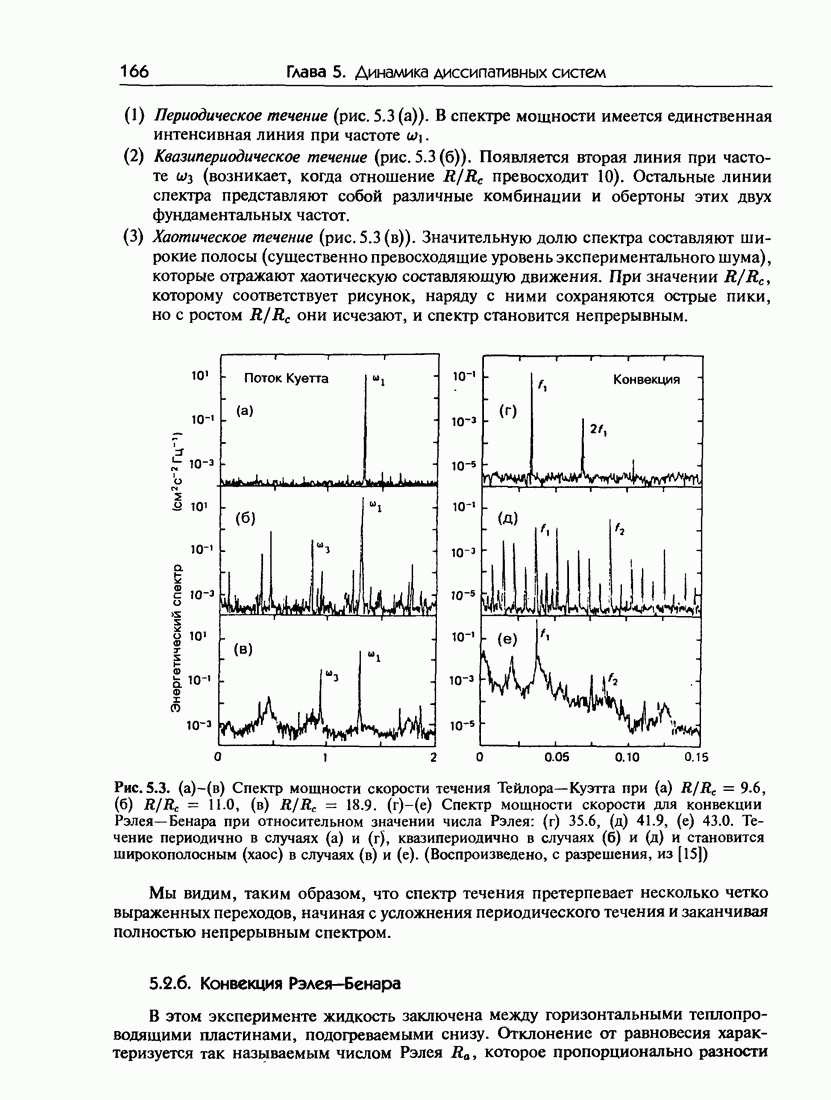
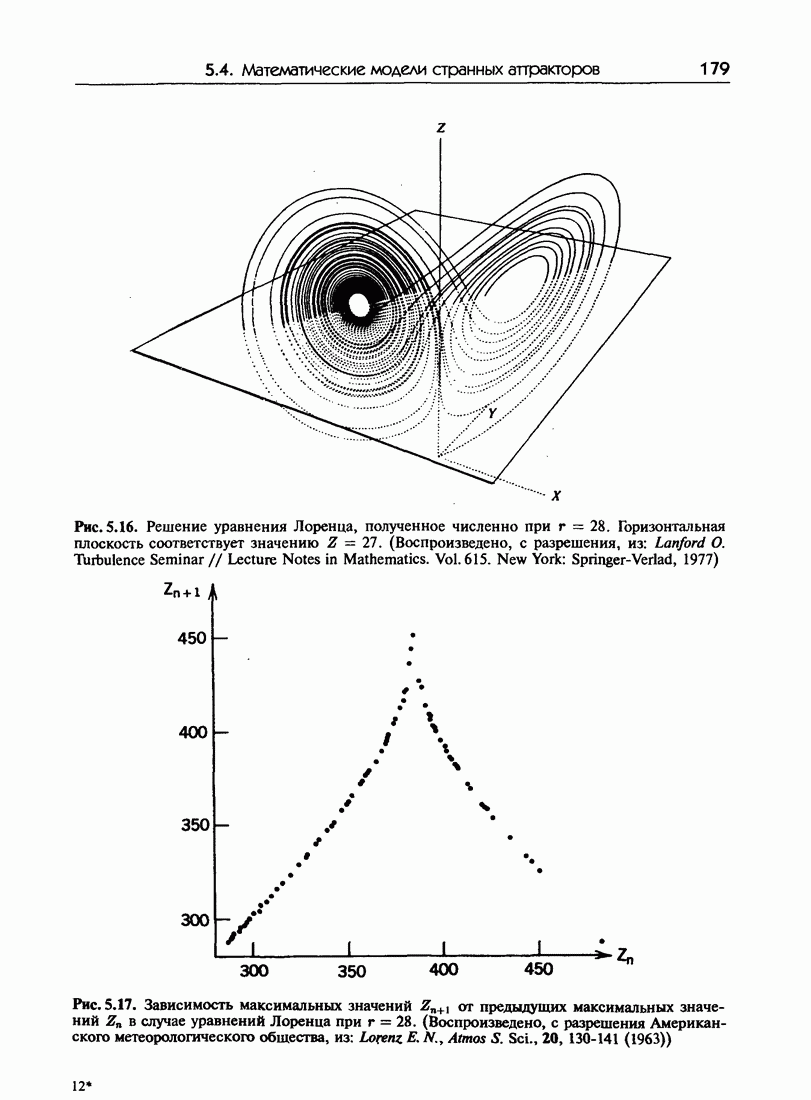
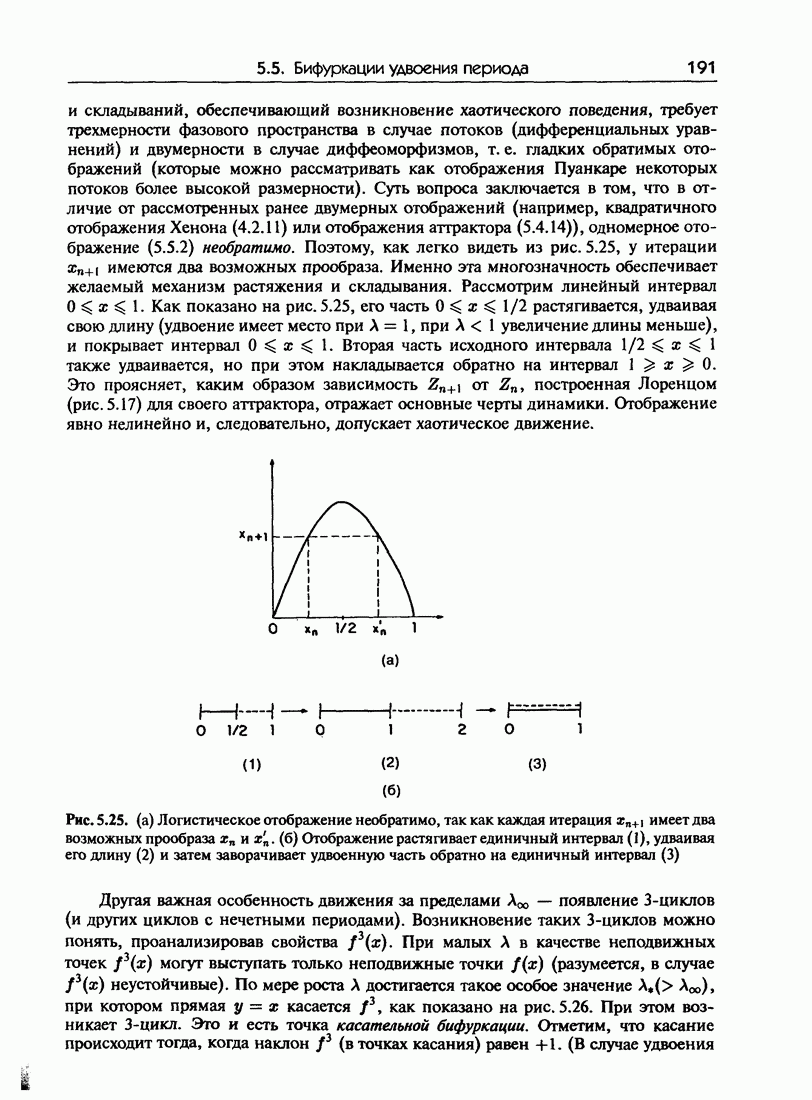
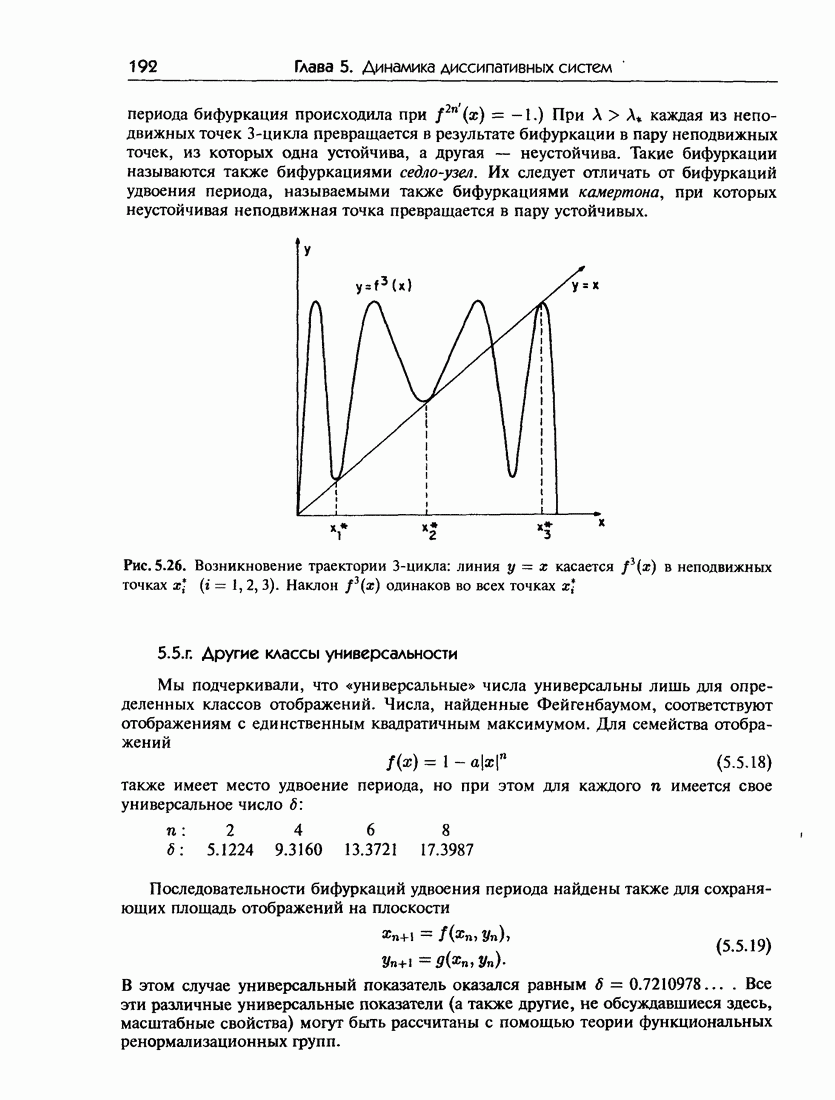
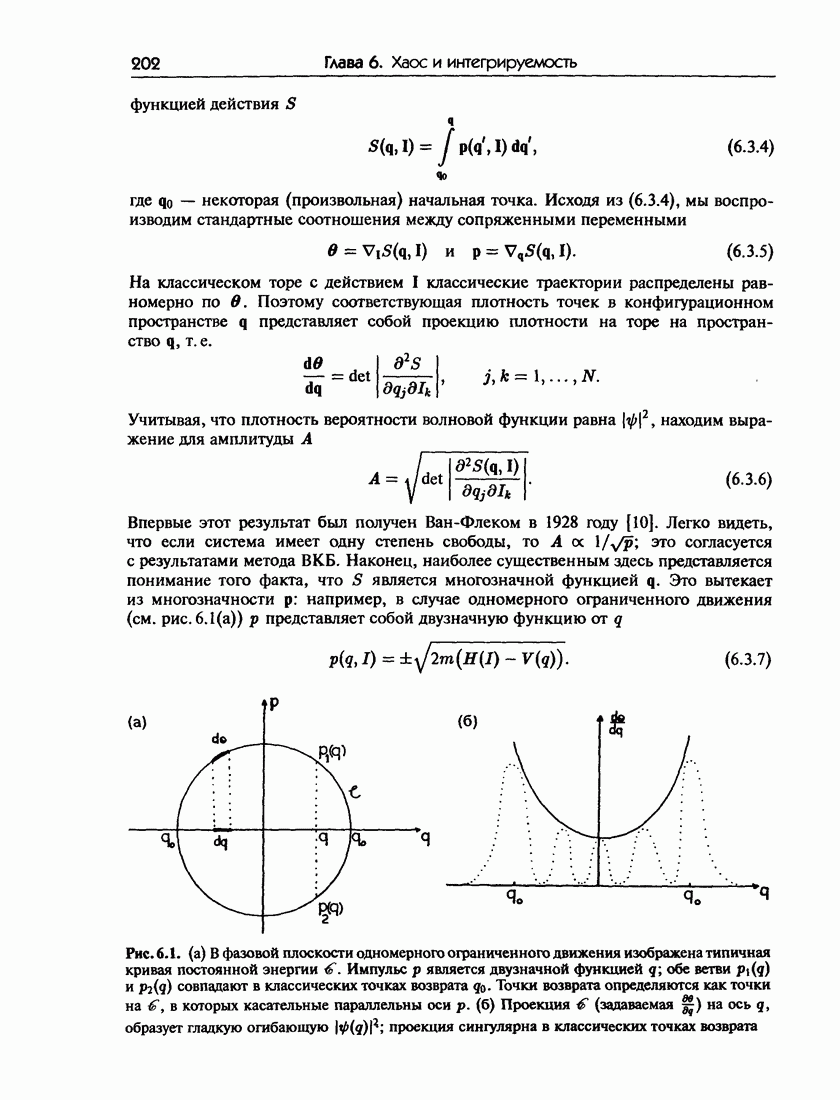
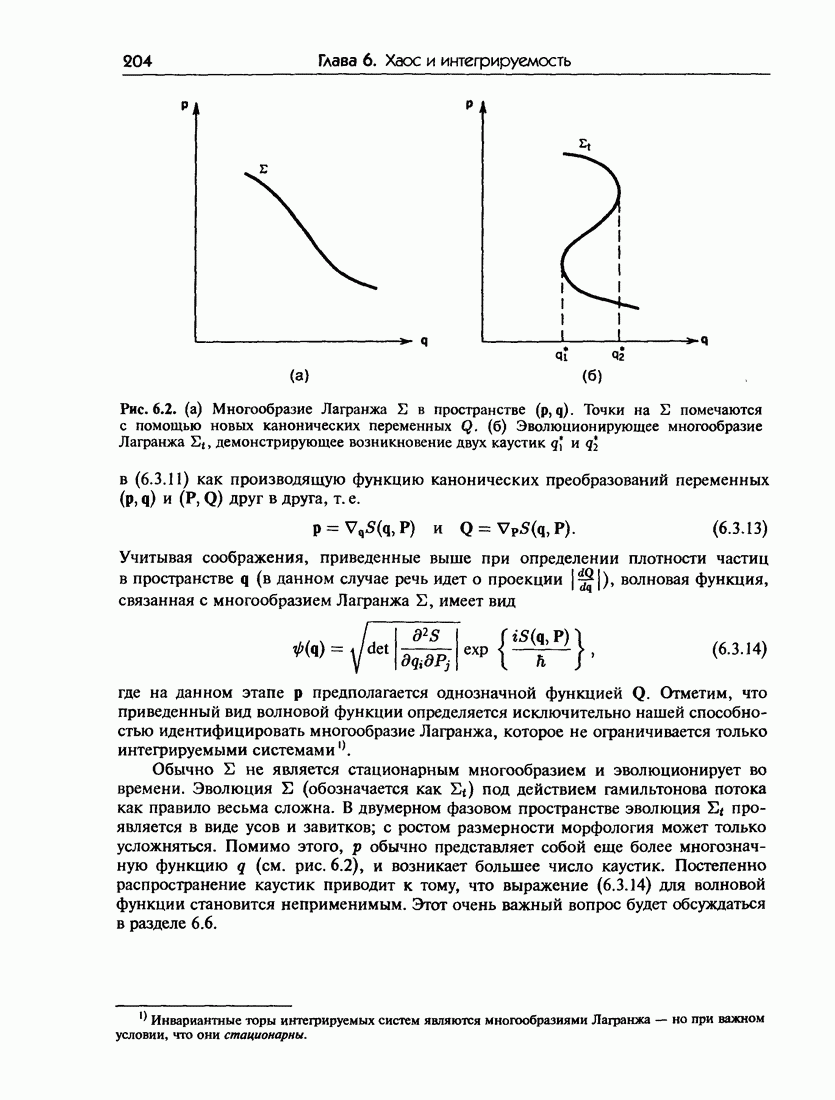
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
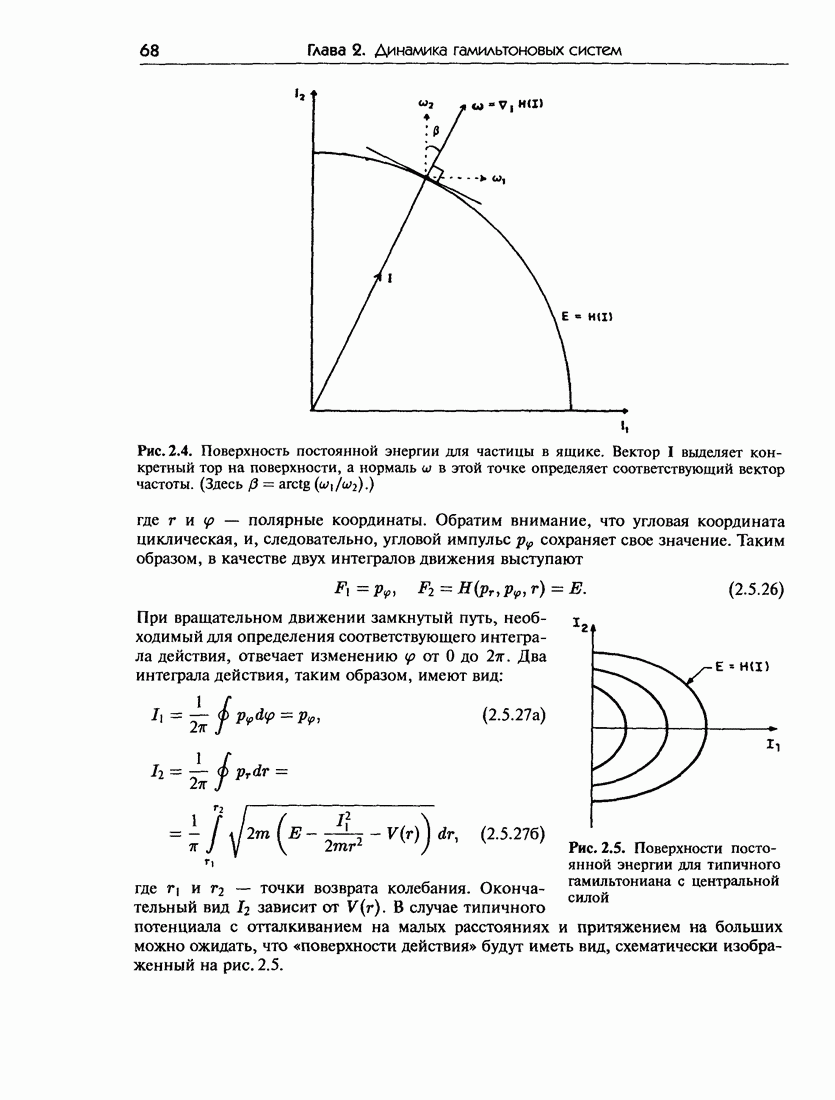
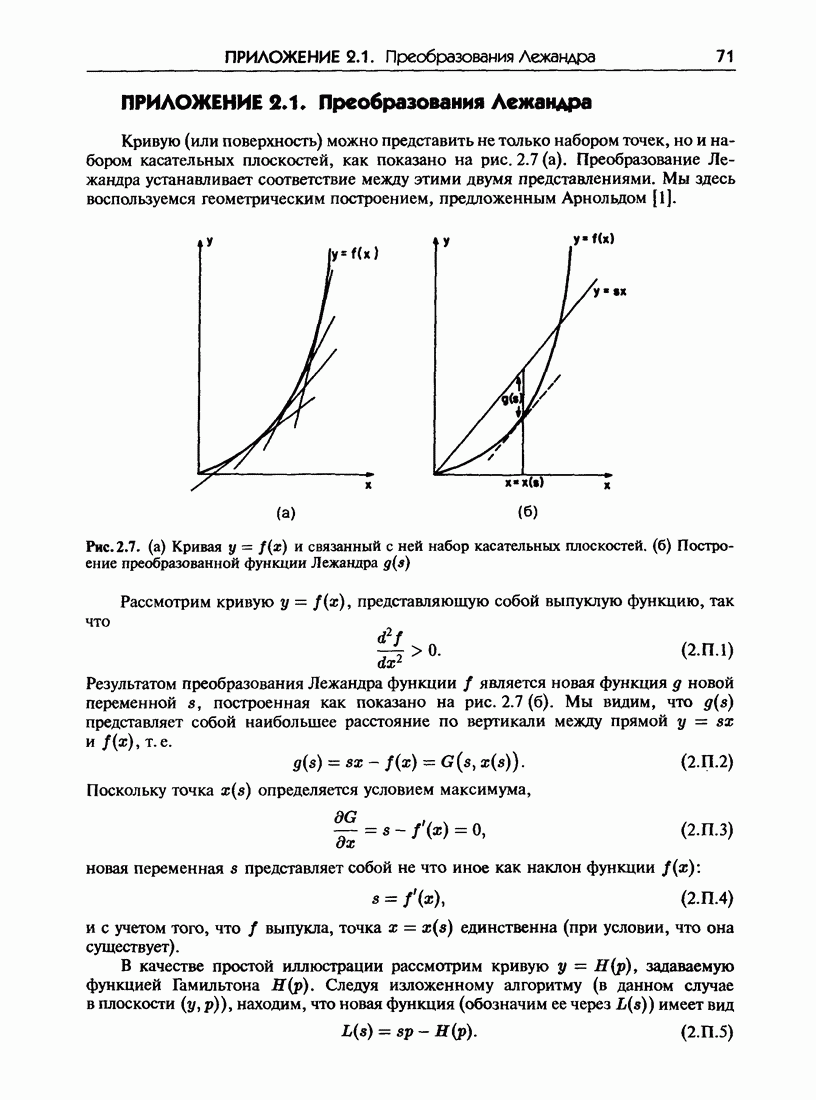
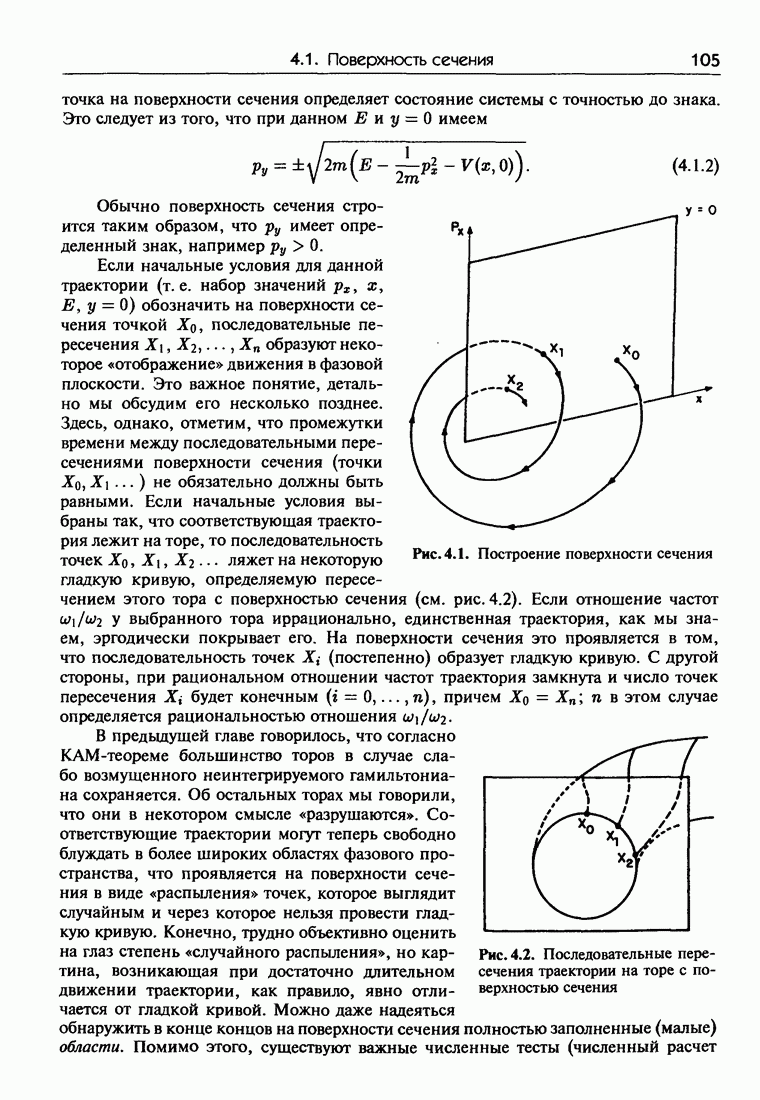
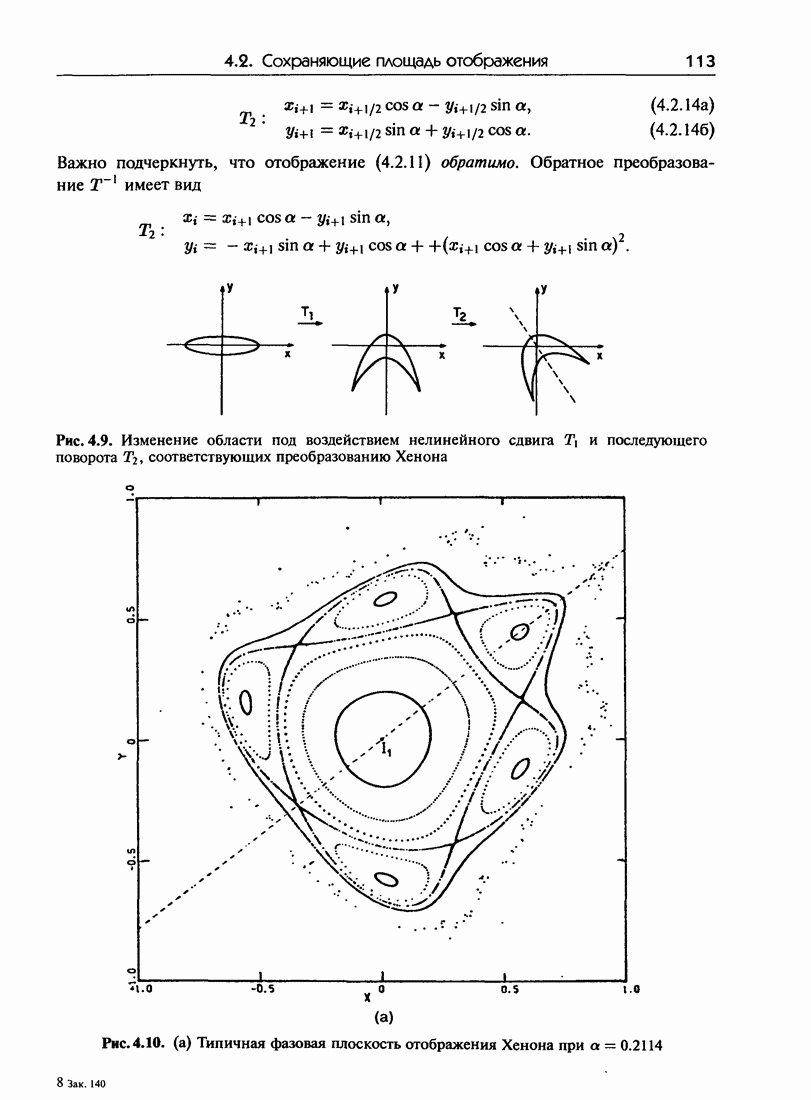
3.3. Большое число степеней свободы и проблема малых знаменателей
Каноническая теория возмущений для систем с двумя и более степенями свободы формулируется точно так же, как и для систем с одной степенью свободы — но при этом возникают значительные трудности, проявляющиеся уже в первом порядке по  Рассмотрим систему
Рассмотрим систему

где  -мерные векторы действий и углов соответственно. Уравнения Гамильтона имеют вид
-мерные векторы действий и углов соответственно. Уравнения Гамильтона имеют вид

и

где  представляет собой
представляет собой  -мерный вектор частот. Нашей целью вновь является отыскание в рамках теории возмущений нового набора канонических переменных
-мерный вектор частот. Нашей целью вновь является отыскание в рамках теории возмущений нового набора канонических переменных  который допускает преобразование возмущенной системы к интегрируемому виду (т.е.
который допускает преобразование возмущенной системы к интегрируемому виду (т.е.  с помощью производящей функции
с помощью производящей функции  удовлетворяющей соотношениям
удовлетворяющей соотношениям

5 разлагается по степеням  в ряд вида
в ряд вида

где основной член соответствует обычному тождественному преобразованию. Уравнение Гамильтона-Якоби

преобразуется точно таким же образом, как и ранее, что дает

и т.д., где мы снова заменяем I на  в левой части (3.3.66). Из (3.3.66) с учетом (3.3.26) получаем
в левой части (3.3.66). Из (3.3.66) с учетом (3.3.26) получаем

Поправку первого порядка для энергии снова находим, полагая периодичность  по в и проводя усреднение по всем угловым переменным:
по в и проводя усреднение по всем угловым переменным:

где

Существенные трудности возникают при попытке разрешить (3.3.7) относительно  Разлагая 51 и «периодическую» часть
Разлагая 51 и «периодическую» часть  в
в  -мерные ряды Фурье,
-мерные ряды Фурье,

где  и штрих означает отсутствие в сумме члена
и штрих означает отсутствие в сумме члена  , легко находим, что
, легко находим, что

3.3.а. Малые знаменатели
На основании результатов, полученных для систем с одной степенью свободы, может показаться, что таким же образом можно продолжать действовать и в случае более высоких порядков по  Однако понятно, что если фундаментальные частоты
Однако понятно, что если фундаментальные частоты  соизмеримы (т. е.
соизмеримы (т. е.  то сумма в (3.3.12) будет расходиться. При этом, даже если
то сумма в (3.3.12) будет расходиться. При этом, даже если  несоизмерима, всегда можно отыскать такое (большое)
несоизмерима, всегда можно отыскать такое (большое)  что произведение
что произведение  окажется сколь угодно мало. Это известная в классической механике проблема малых знаменателей, претерпевшая за последние сто лет столь незначительное развитие.
окажется сколь угодно мало. Это известная в классической механике проблема малых знаменателей, претерпевшая за последние сто лет столь незначительное развитие.
В некоторых случаях сходимость ряда может быть достигнута за счет соответствующего уменьшения числителя. Однако Брунс уже довольно давно показал, что (грубо говоря) значения  для которых ряд (абсолютно) сходится, и значения, для которых он не сходится, лежат сколь угодно близко друг к другу. Отсюда вытекает, вследствие зависимости
для которых ряд (абсолютно) сходится, и значения, для которых он не сходится, лежат сколь угодно близко друг к другу. Отсюда вытекает, вследствие зависимости  от
от  что получаемая описанным выше способом
что получаемая описанным выше способом  не является непрерывной функцией
не является непрерывной функцией  А поскольку предположение непрерывности лежит в основе всей процедуры теории возмущений (см. уравнения (3.3.2) и (3.3.3)), то соответствующий ряд — даже если окажется, что он сходится при некотором значении
А поскольку предположение непрерывности лежит в основе всей процедуры теории возмущений (см. уравнения (3.3.2) и (3.3.3)), то соответствующий ряд — даже если окажется, что он сходится при некотором значении  не обязательно представляет действительное движение. Дальнейшие исследования Пуанкаре убедительно показали, что ряд Фурье (такой как (3.3.10) и
не обязательно представляет действительное движение. Дальнейшие исследования Пуанкаре убедительно показали, что ряд Фурье (такой как (3.3.10) и  не может служить сходящимся представлением для возмущенной системы. Поэтому такие важные задачи, как устойчивость орбит планет солнечной системы на протяжении длительного промежутка времени, удовлетворительно решены быть не могут. Оценка устойчивости на протяжении ограниченного промежутка времени, основанная на некоторых усечениях ряда — максимум того, что может быть здесь достигнуто.
не может служить сходящимся представлением для возмущенной системы. Поэтому такие важные задачи, как устойчивость орбит планет солнечной системы на протяжении длительного промежутка времени, удовлетворительно решены быть не могут. Оценка устойчивости на протяжении ограниченного промежутка времени, основанная на некоторых усечениях ряда — максимум того, что может быть здесь достигнуто.
3.3.б. Фундаментальная проблема
Для решения проблемы малых знаменателей некоторые из наиболее выдающихся математиков своего времени приложили немалые усилия, но успехом они не увенчались. Пуанкаре назвал эту проблему «фундаментальной проблемой» классической механики; представлялось, что на пути дальнейшего прогресса имеются непреодолимые препятствия. Состояние вопроса удачно подытожил Макс Борн, интересовавшийся классической теорией возмущений в связи с решением задач «старой квантовой теории» [5]: «Было бы поистине замечательно, если бы Природа оградила себя от дальнейшего развития знаний посредством аналитических трудностей в задачах многих тел».
Одна из точек зрения состояла в том, что добавка даже малейшего неинтегрируемого возмущения сделает систему эргодической; т. е. система будет полностью заполнять энергетическую поверхность так, что среднее по времени будет равно среднему по фазовому пространству. Таковы были взгляды накануне знаменитого расчета Ферми-Улама-Паста - одного из первых динамических расчетов, проведенных с использованием компьютера в начале 1950-х годов. Эти авторы рассмотрели цепочку гармонических осцилляторов, связанных кубической нелинейностью, и проанализировали, каким образом энергия одной из мод будет распределяться между остальными. Они предполагали обнаружить статистическое распределение по энергии. К своему большому удивлению они обнаружили периодическую циркуляцию энергии, откуда следовало, что система интегрируема в «значительно большей степени», чем предполагалось. (В действительности интегрируемость этой системы оказалась за пределами самых необузданных фантазий — в непрерывном пределе рассматриваемая модель сводится к известному нелинейному дифференциальному уравнению в частных производных, называемому уравнением Кортевегаде Фриза)
«Фундаментальная проблема» была решена в самом начале 1960-х годов с появлением знаменитой теперь теоремы Колмогорова-Арнольда-Мозера (КАМ-теоремы). Эта теорема излагается в следующем разделе. А в заключение этого раздела отметим, что теория возмущений и ее различные варианты, включая, например, разработанные недавно методы преобразований Ли, остаются до сих пор весьма ценным средством. Хороший обзор и иллюстрация многих из этих методов даны в книге [7].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
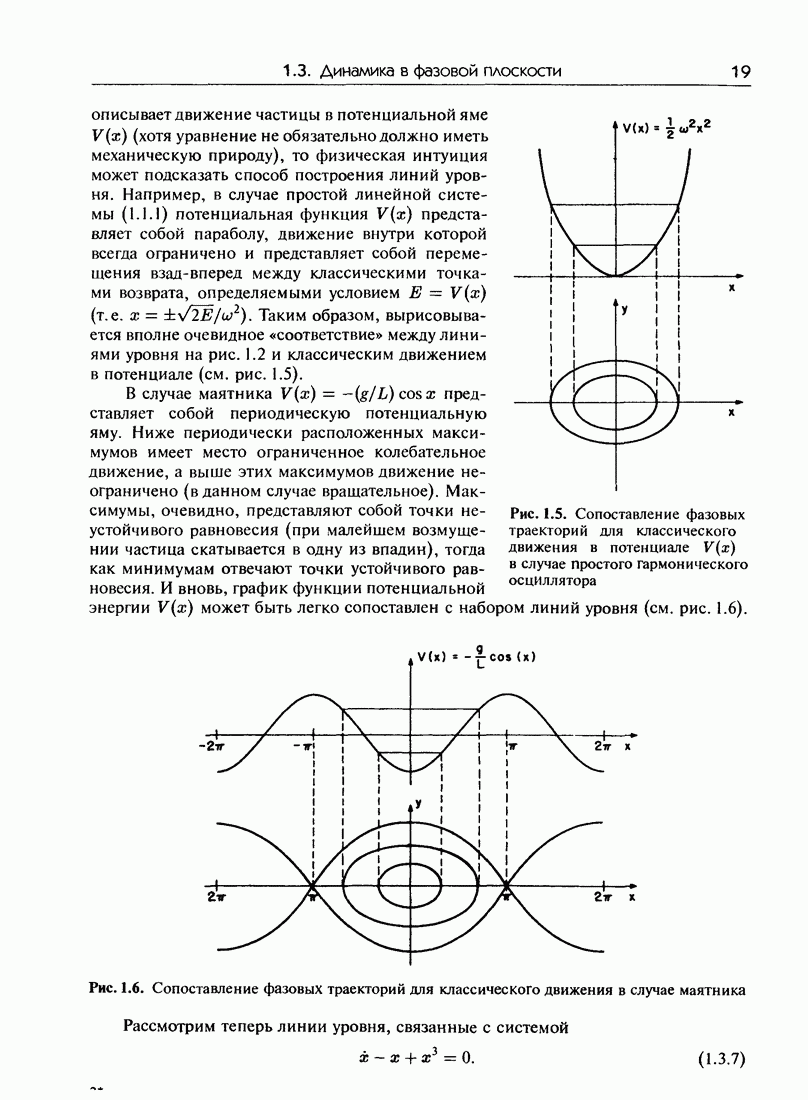
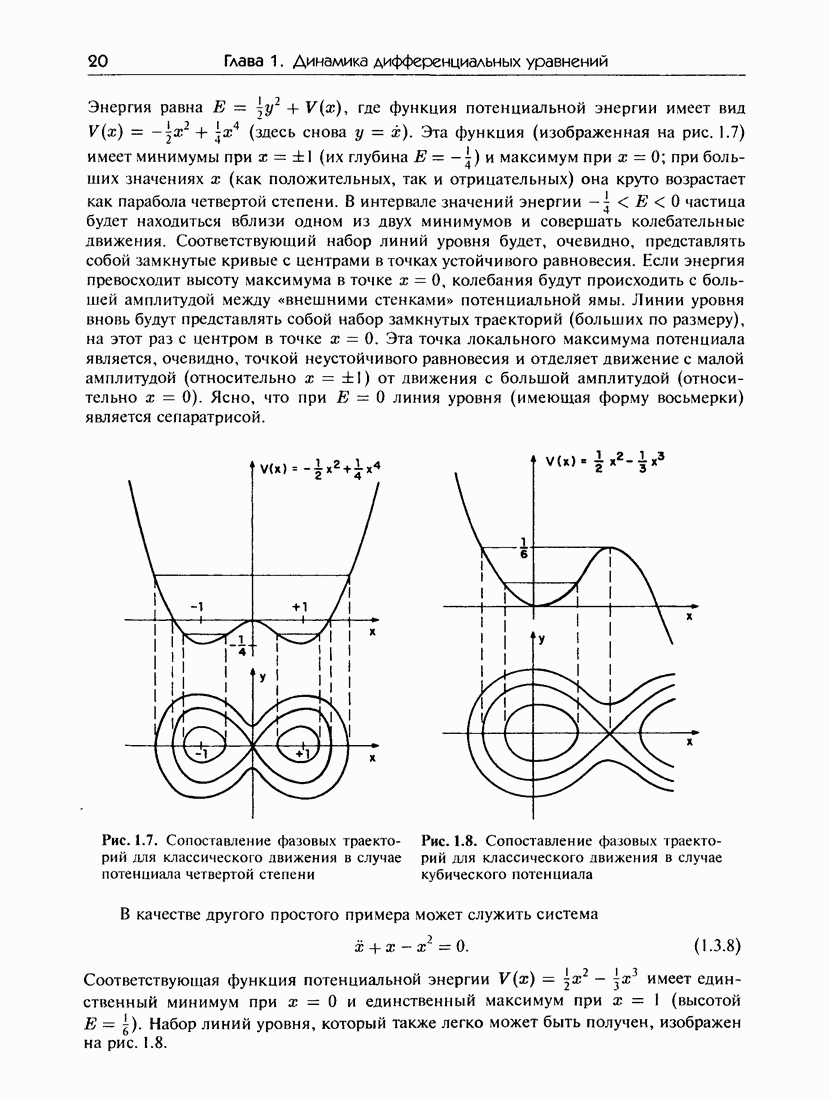
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
- 1.3.б. фазовые портреты консервативных систем
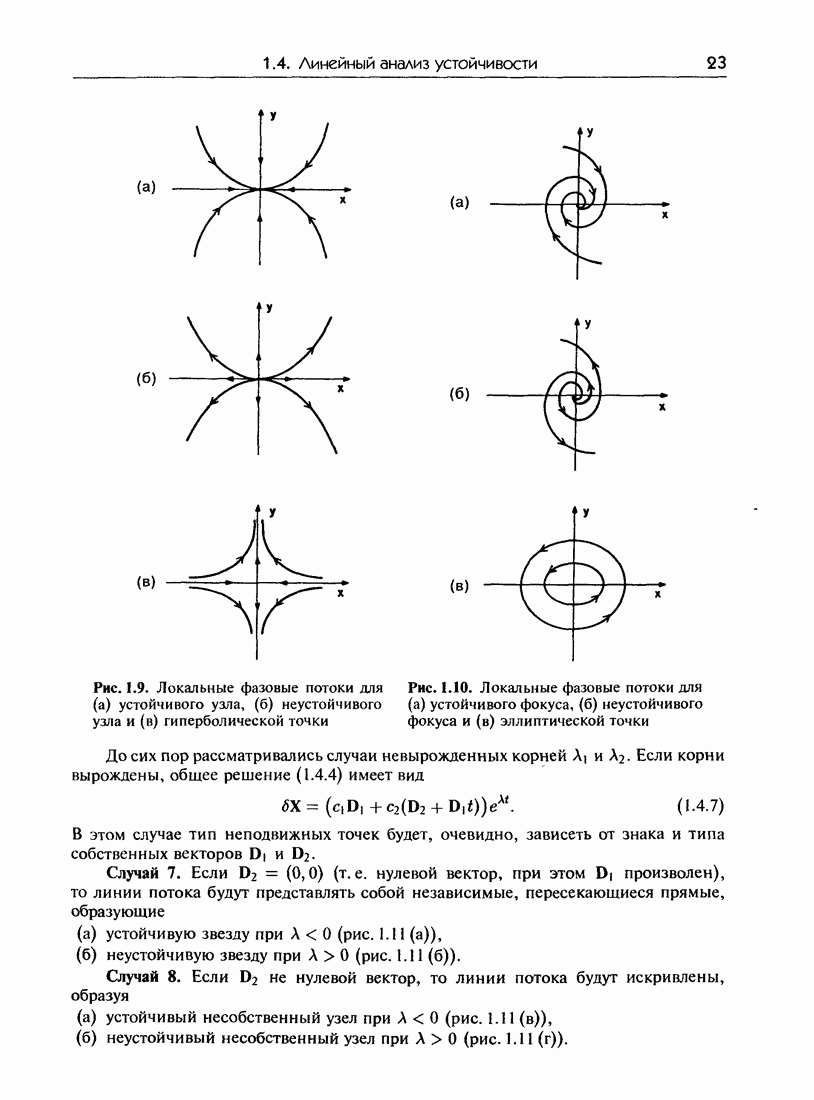
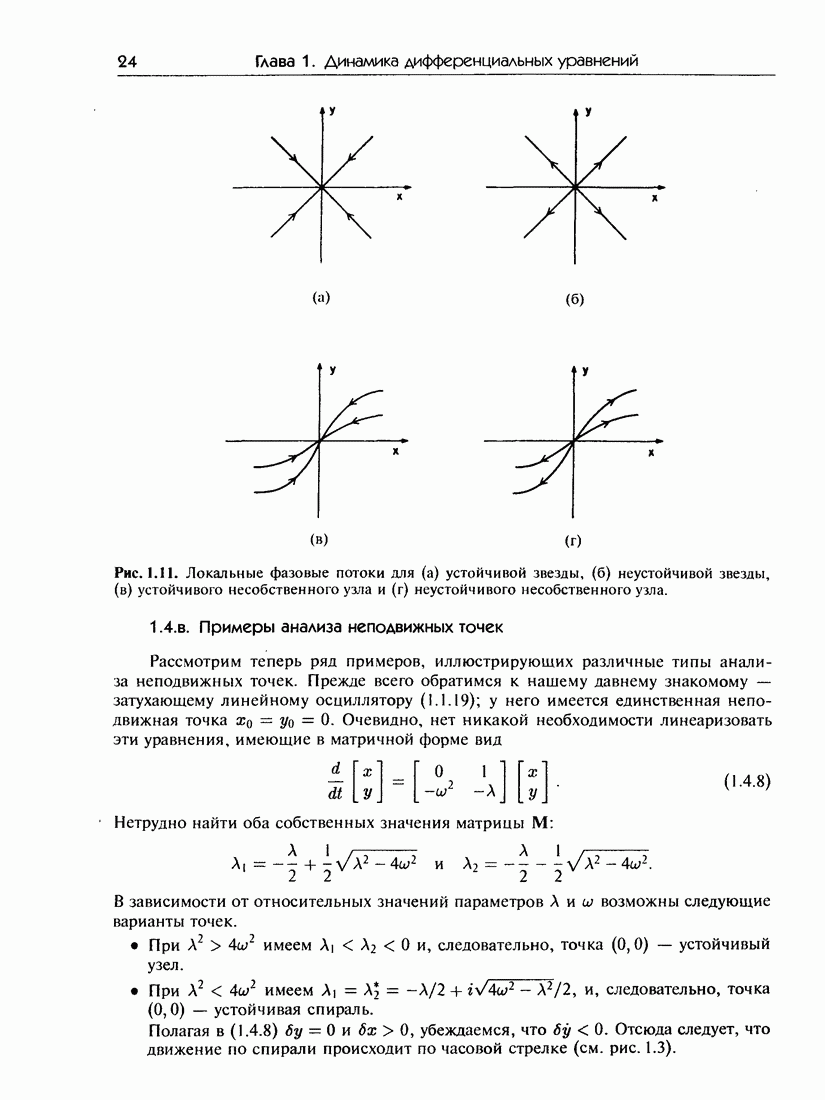
- 1.4. Линейный анализ устойчивости
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
- 4.7.б. Перемешивание
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
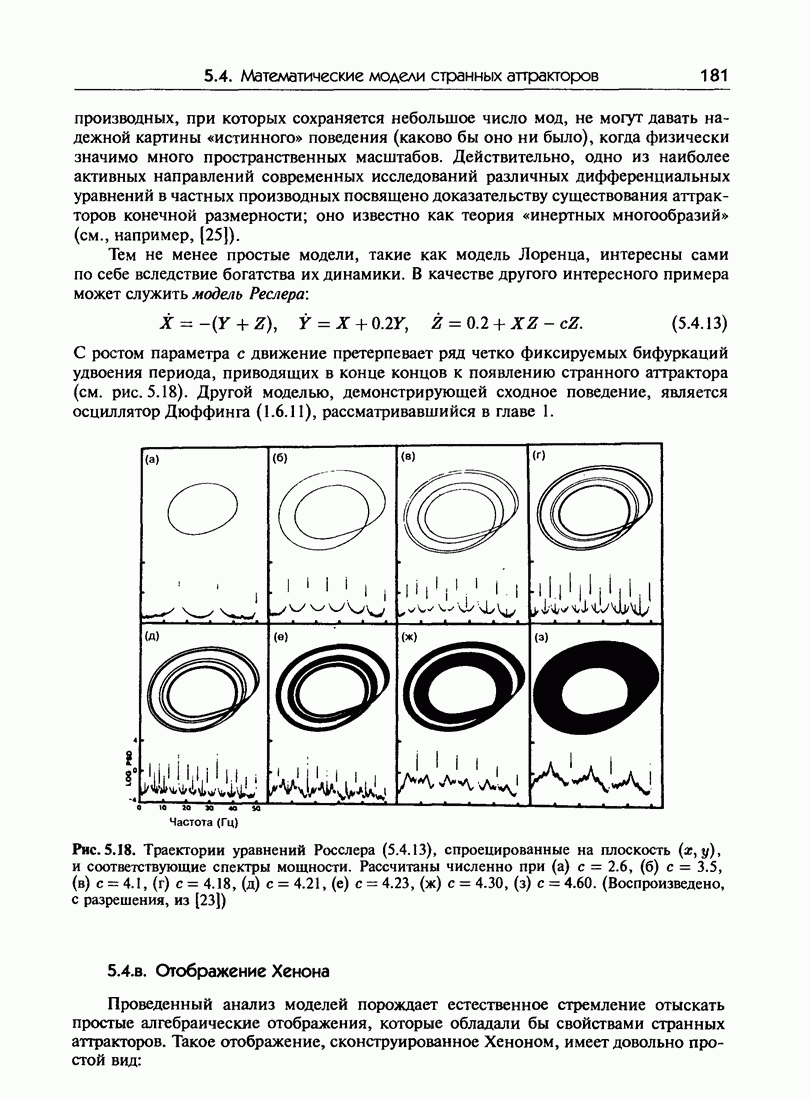
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
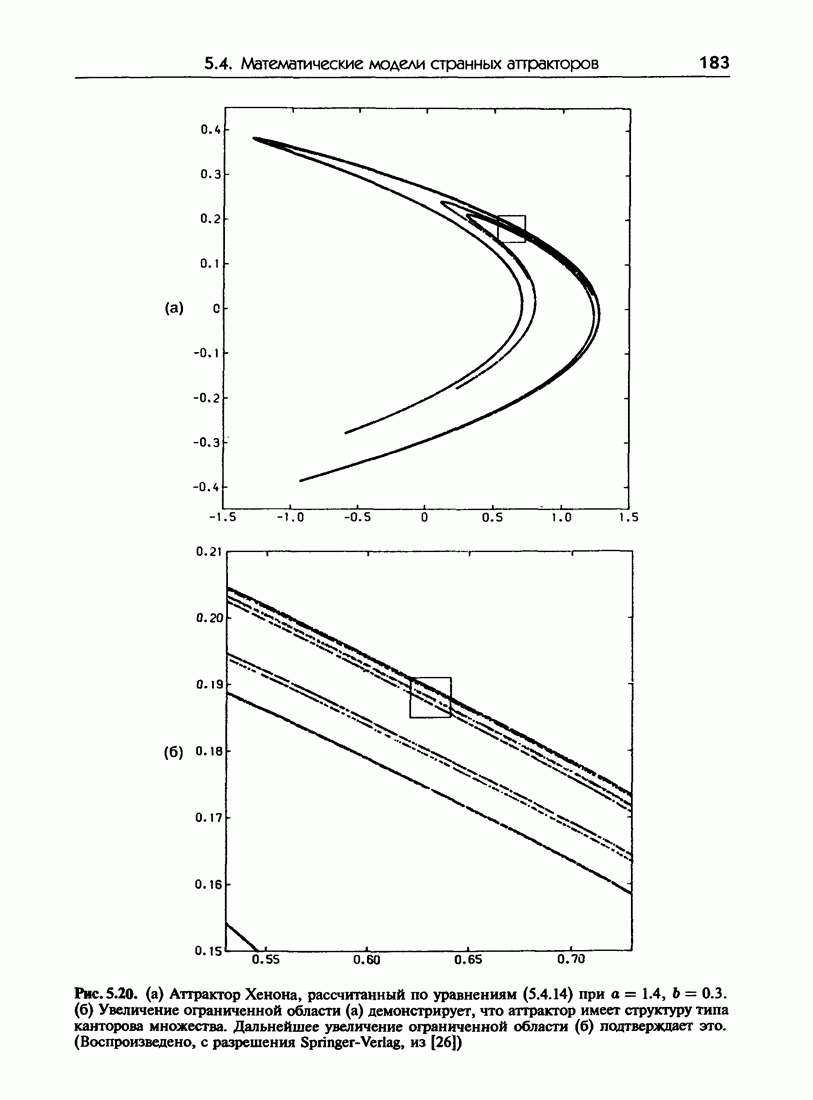
- 5.4.в. Отображение Хенона
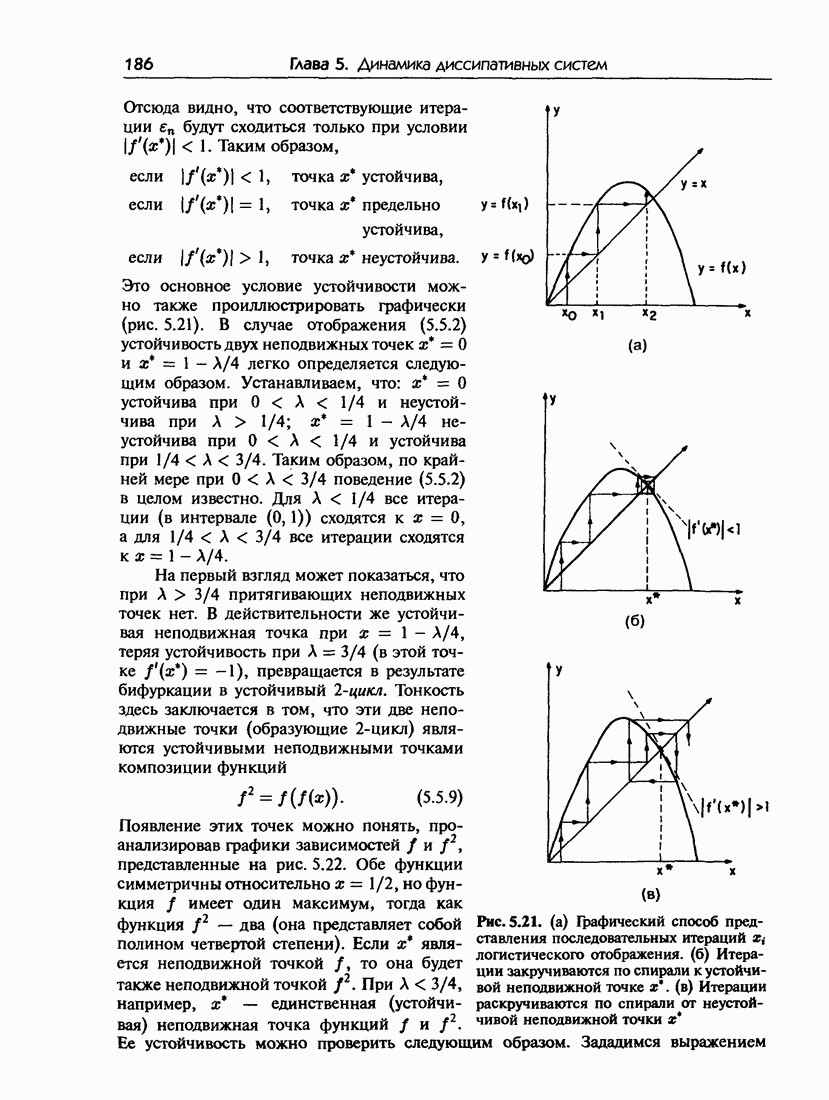
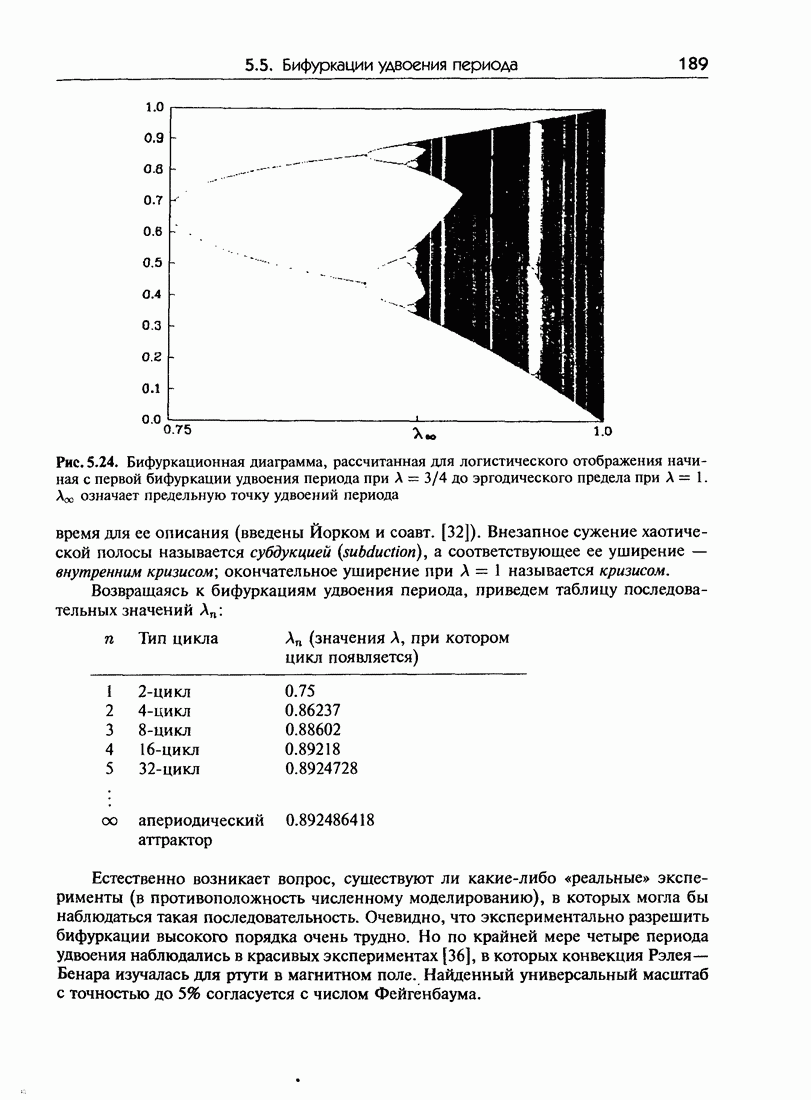
- 5.5. Бифуркации удвоения периода
- 5.5.а. Механизм удвоения периода
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
- 5.5.г. Другие классы универсальности
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
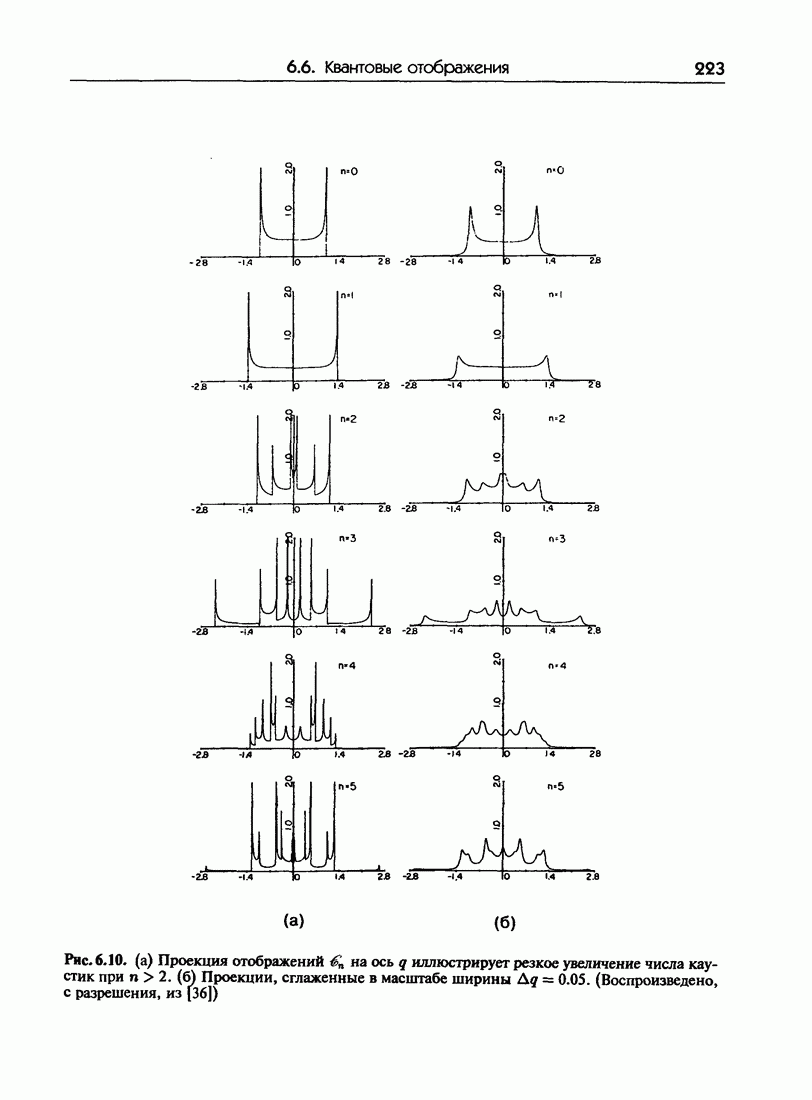
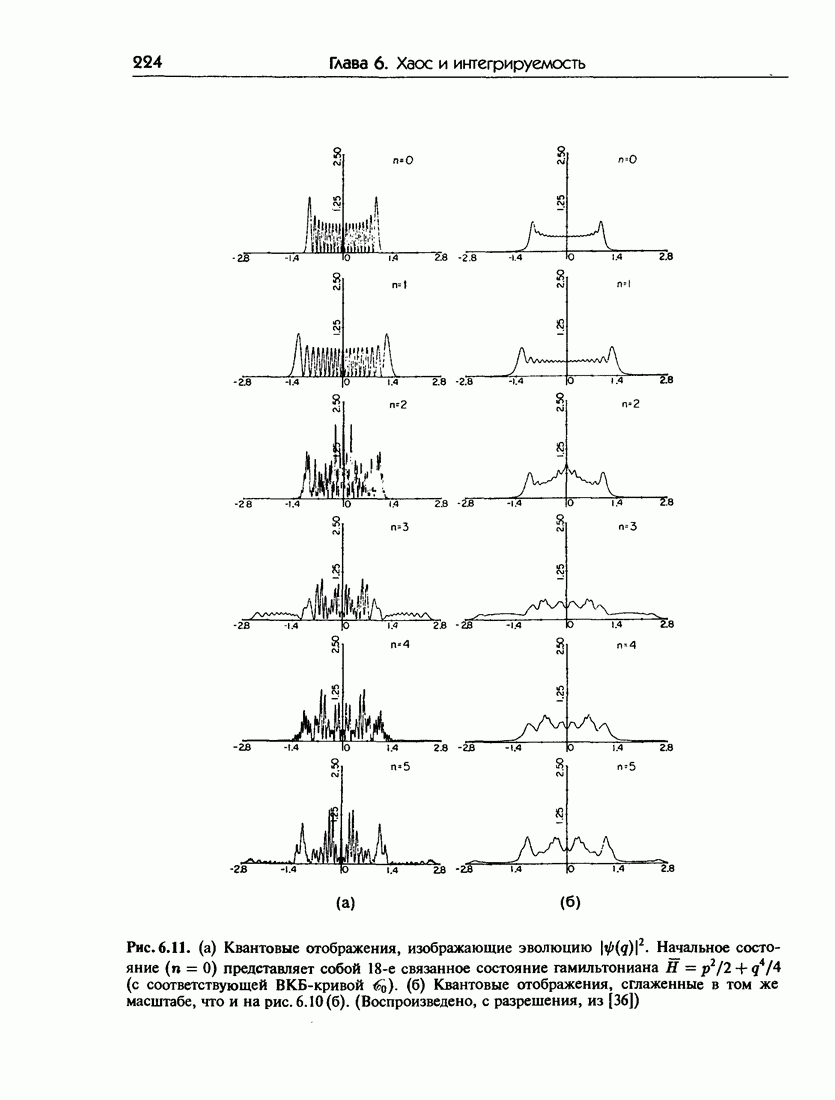
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
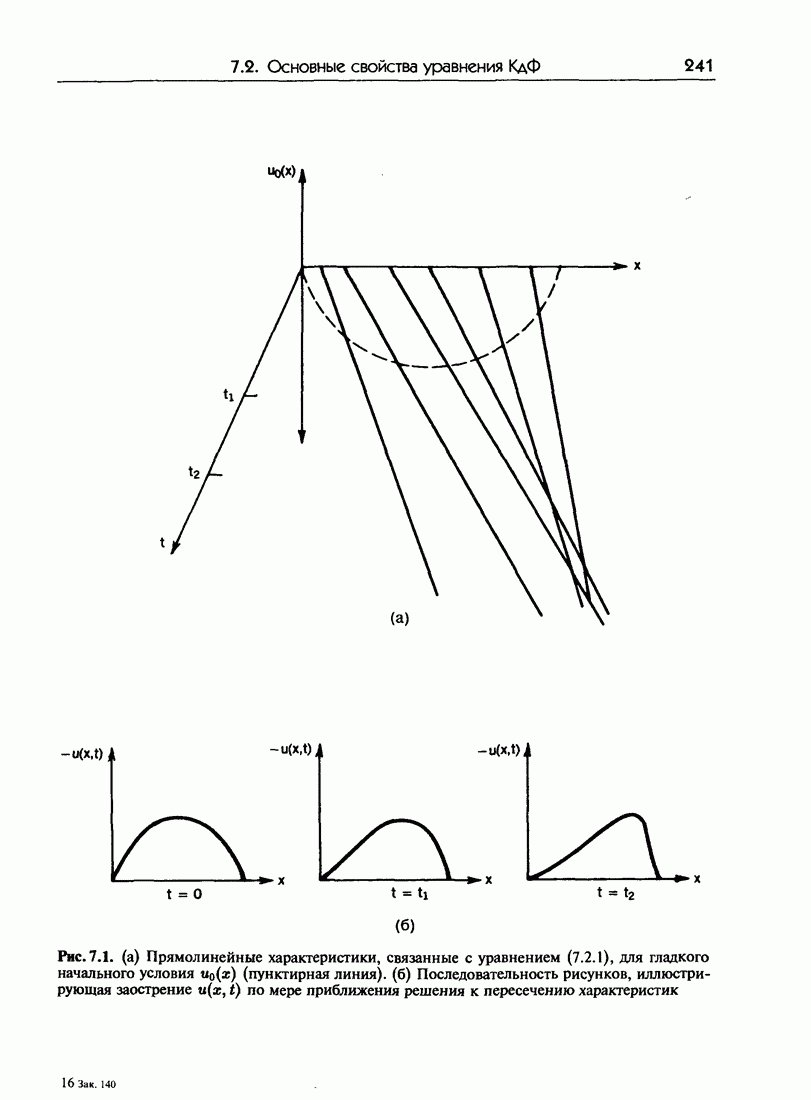
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
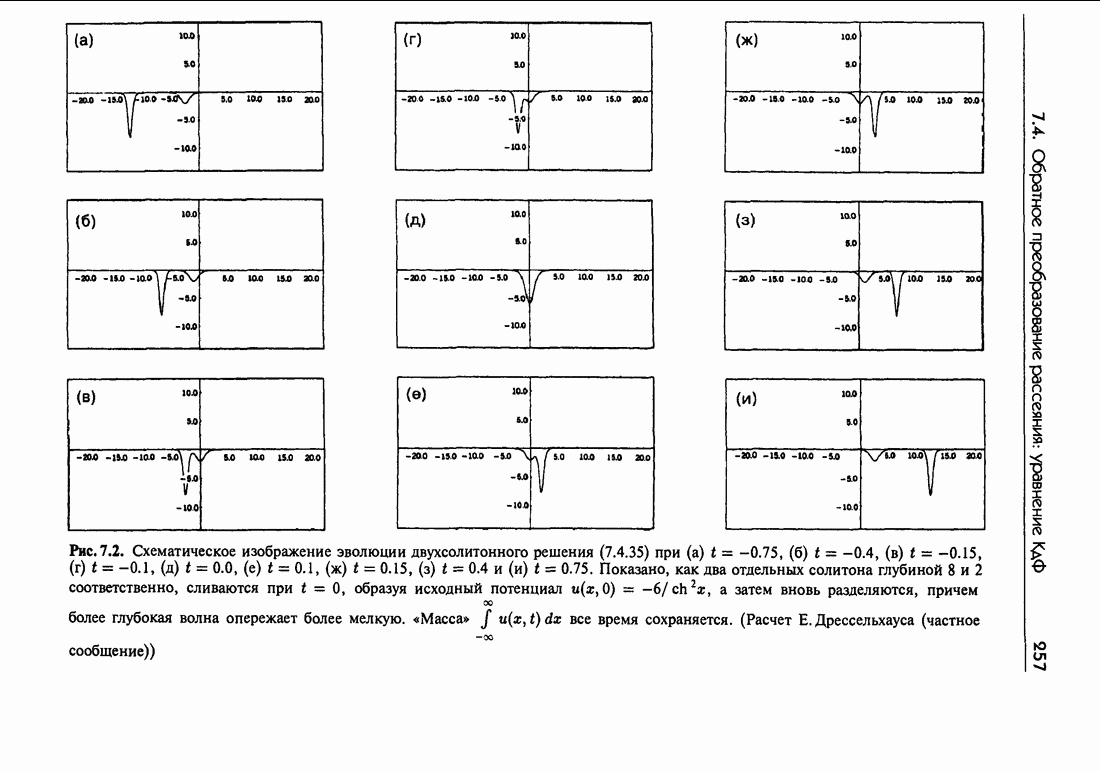
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
- 7.5. Другие солитонные системы
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда