| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.6.б. Метод Грина
Перейдем к обсуждению (хотя и очень краткому) важного метода, развитого Грином [24], который позволяет предсказывать возникновение хаотического движения, основываясь на анализе устойчивости замкнутых траекторий. В основе метода лежит гипотеза о том, что «размывание» инвариантной кривой (тора) может быть связано с внезапной потерей устойчивости соседними замкнутыми траекториями. Чтобы представить себе это более подробно, рассмотрим слабо возмущенную интегрируемую систему. В соответствии с КАМ-теоремой сохраняются инвариантные кривые с «достаточно» иррациональным числом вращения. Соседние рациональные (и близкие к рациональным) кривые разрушаются таким образом, как мы ранее описывали (теорема Пуанкаре-Биркгофа о неподвижной точке): в одинаковом числе эллиптических (устойчивых) и гиперболических (неустойчивых) неподвижных точек. Метод Грина основан на наблюдении, что, когда возмущение становится достаточно сильным (или энергия достаточно велика), устойчивые неподвижные точки также превращаются в неустойчивые («гиперболические с отражением») неподвижные точки. Такой переход и сигнализирует о «размывании» инвариантной кривой, расположенной «близко» к множеству неподвижных точек, потерявших устойчивость. Вернемся к обсуждению КАМ-теоремы в главе 3; вполне удовлетворительный способ оценить близость замкнутой траектории к данной инвариантной кривой состоит в том, чтобы выразить число вращения этой кривой в виде цепной дроби

где  положительные целые числа. При этом последовательные усечения такой дроби, представляющей иррациональное число вращения, дают числа вращения замкнутых траекторий, все более «близких» к выбранной инвариантной кривой. Анализируя устойчивость такой последовательности замкнутых траекторий по мере их «приближения» к инвариантной кривой, Грин [24] сумел предсказать разрушение этой кривой.
положительные целые числа. При этом последовательные усечения такой дроби, представляющей иррациональное число вращения, дают числа вращения замкнутых траекторий, все более «близких» к выбранной инвариантной кривой. Анализируя устойчивость такой последовательности замкнутых траекторий по мере их «приближения» к инвариантной кривой, Грин [24] сумел предсказать разрушение этой кривой.
Обсуждаемый метод включает два существенных этапа: (1) отыскание замкнутых траекторий и (2) определение их устойчивости. Подробное обсуждение первого вопроса выходит за рамки этой главы. Достаточно сказать, что имеется целый ряд хорошо разработанных и эффективных методов отыскания замкнутых траекторий с любой требуемой топологией (числами вращения). Упомянем, в частности, подход, описанный Грином [24], и метод, разработанный Хеллеманом и Бунтисом [25]. Анализ устойчивости мы рассмотрим на примере, подробно изученном Грином, а именно, на примере «стандартного отображения» (на единичном торе):

Параметр к можно рассматривать как параметр возмущения; при  отображение становится тривиальным:
отображение становится тривиальным:

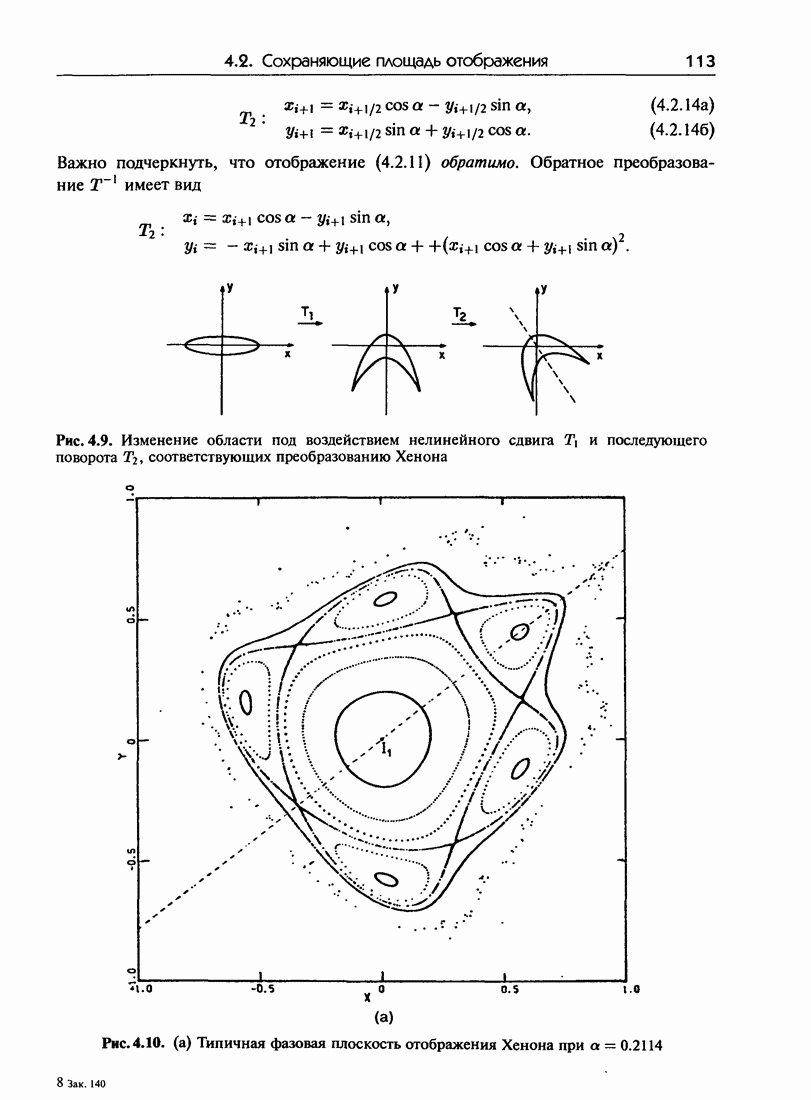
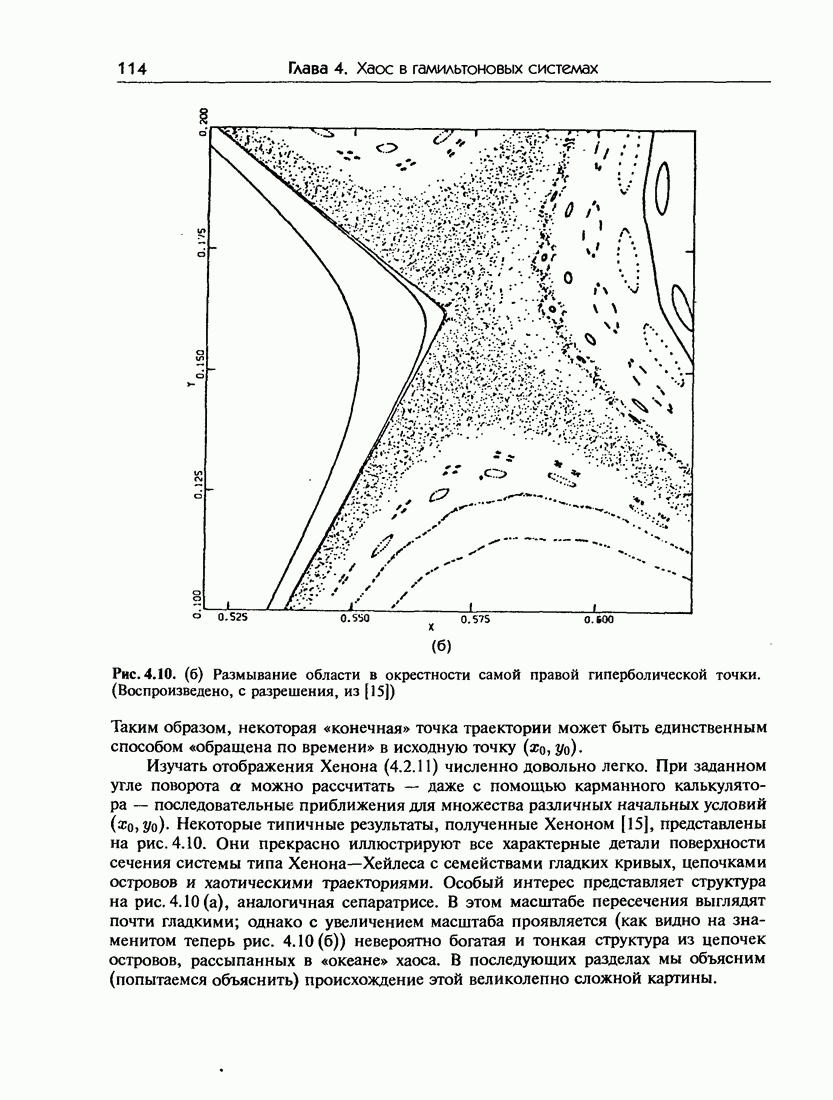
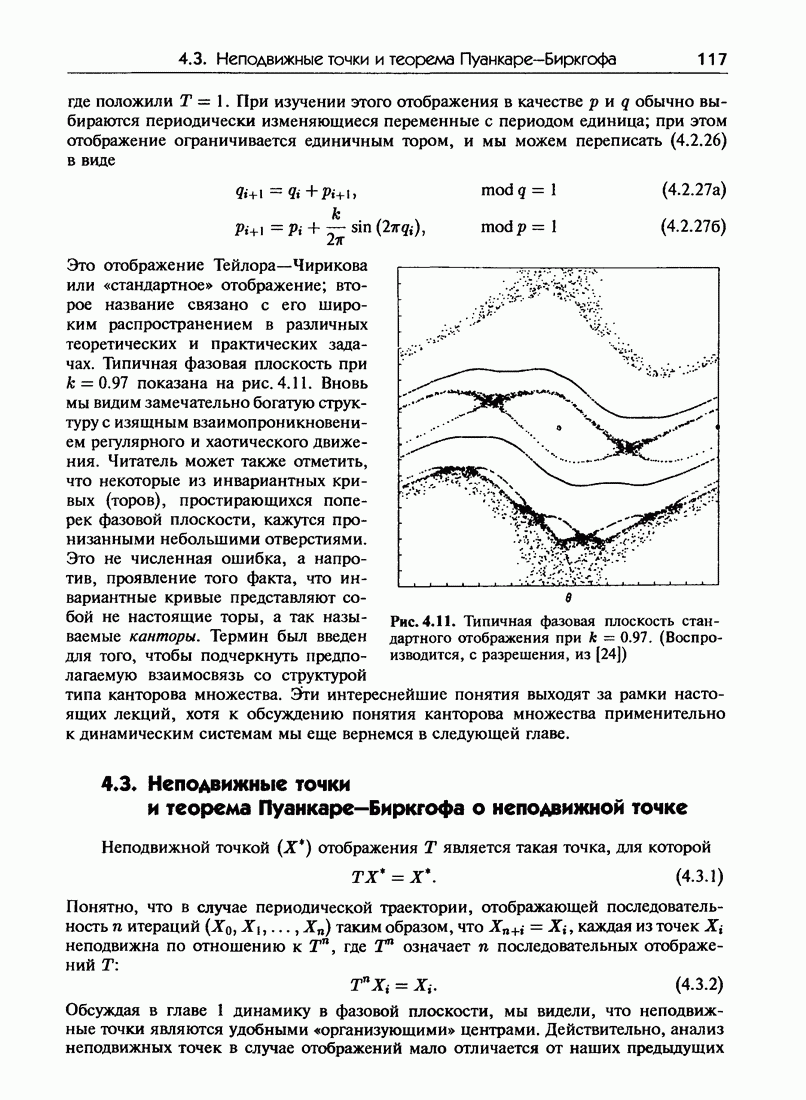
При этом оно, очевидно, «интегрируемо», поскольку все траектории лежат на прямой. Они же являются инвариантными кривыми невозмущенного отображения. Возвращаясь к рис. 4.11, на котором представлено стандартное отображение, рассчитанное при  мы видим несколько сильно нерегулярных траекторий, заполняющих значительные области фазовой плоскости, а также типичную структуру из чередующихся гиперболических и эллиптических неподвижных точек. Заметим, что существуют также инвариантные кривые, разделяющие фазовое пространство и тем самым не позволяющие траектории блуждать по всему фазовому пространству. До тех пор, пока эти кривые не разрушатся, «хаос», очевидно, не будет действительно глобальным.
мы видим несколько сильно нерегулярных траекторий, заполняющих значительные области фазовой плоскости, а также типичную структуру из чередующихся гиперболических и эллиптических неподвижных точек. Заметим, что существуют также инвариантные кривые, разделяющие фазовое пространство и тем самым не позволяющие траектории блуждать по всему фазовому пространству. До тех пор, пока эти кривые не разрушатся, «хаос», очевидно, не будет действительно глобальным.
Для определения устойчивости данной замкнутой траектории необходимо построить касательное отображение. Это соответствует линеаризации отображения каждой итерации. Определив переменные «касательного пространства» (61,60), получаем касательное отображение

где

Касательное отображение относится к сохраняющим площадь, так как

Для траектории, замыкающейся после  итераций этого отображения, собственные значения
итераций этого отображения, собственные значения  матрицы
матрицы 

задают индексы устойчивости, или множители Флоке. Обозначая элементы матрицы  через
через  получаем в явном виде
получаем в явном виде

где мы использовали условие (4.6.42):

Ранее было показано, что в случае комплексных собственных значений траектории устойчивы, тогда как в случае действительных — неустойчивы. Грин [24] ввел величину, называемую вычетом, которая определяется следующим образом:

где  обозначает след матрицы.
обозначает след матрицы.
Из (4.6.44) следует, что при  собственные значения мнимые и, следовательно, траектория устойчива, т. е. неподвижные точки являются эллиптическими. При
собственные значения мнимые и, следовательно, траектория устойчива, т. е. неподвижные точки являются эллиптическими. При  или
или  собственные значения действительны, и, следовательно, траектория неустойчива. При этом случаю
собственные значения действительны, и, следовательно, траектория неустойчива. При этом случаю  соответствуют гиперболические неподвижные точки, а случаю
соответствуют гиперболические неподвижные точки, а случаю  «гиперболические-с-отражением». (Для параболических неподвижных точек
«гиперболические-с-отражением». (Для параболических неподвижных точек  Можно показать, что для траектории «длины»
Можно показать, что для траектории «длины»  вычет пропорционален
вычет пропорционален  как для больших, так и для малых
как для больших, так и для малых  . (Напомним, что для рассматриваемой системы
. (Напомним, что для рассматриваемой системы  — это параметр возмущения.) Такая экспоненциальная зависимость от
— это параметр возмущения.) Такая экспоненциальная зависимость от  устраняется путем введения величины, называемой средним вычетом,
устраняется путем введения величины, называемой средним вычетом,

где  некоторая произвольная постоянная, задаваемая из соображений практического удобства. Теперь мы можем охарактеризовать устойчивость последовательности замкнутых траекторий, сходящихся к выбранной инвариантной кривой. Каждая последующая замкнутая траектория (определяемая последующим усечением цепной дроби, которая служит представлением числа вращений выбранной кривой) характеризуется большим значением
некоторая произвольная постоянная, задаваемая из соображений практического удобства. Теперь мы можем охарактеризовать устойчивость последовательности замкнутых траекторий, сходящихся к выбранной инвариантной кривой. Каждая последующая замкнутая траектория (определяемая последующим усечением цепной дроби, которая служит представлением числа вращений выбранной кривой) характеризуется большим значением  что соответствует возрастанию топологической сложности этой траектории. Замечательно, что при этом последовательность средних вычетов сходится, как оказалось, к некоторой конечной величине. Скорость сходимости определяется
что соответствует возрастанию топологической сложности этой траектории. Замечательно, что при этом последовательность средних вычетов сходится, как оказалось, к некоторой конечной величине. Скорость сходимости определяется  по-видимому, значением
по-видимому, значением  ; для рассматриваемой задачи было найдено оптимальное значение
; для рассматриваемой задачи было найдено оптимальное значение  Более подробное обсуждение этого вопроса читатель может найти в оригинальной работе Грина [24]. Показано (эмпирически), что, если последовательность средних вычетов сходится к величине, превосходящей
Более подробное обсуждение этого вопроса читатель может найти в оригинальной работе Грина [24]. Показано (эмпирически), что, если последовательность средних вычетов сходится к величине, превосходящей
единицу (в предположении  то инвариантная кривая, связанная с данной последовательностью замкнутых траекторий, разрушается.
то инвариантная кривая, связанная с данной последовательностью замкнутых траекторий, разрушается.
Этот критерий позволяет найти для любой инвариантной кривой значение параметра возмущения к, при котором она разрушается. В случае рассматриваемой системы метод дал очень точные результаты. В дополнение к этому Грин [24] предложил нестандартное обобщение своего метода для предсказания возникновения глобального хаоса. Оно основывается на предположении, что чем лучше иррациональная кривая может быть приближена последовательностью рациональных, тем меньшее возмущение  требуется для ее разрушения. Естественно предположить, что в последнюю очередь будет разрушена кривая, число вращения которой хуже всего приближается посредством последовательности рациональных чисел. Представление в виде цепной дроби для числа вращения такой инвариантной кривой имеет вид
требуется для ее разрушения. Естественно предположить, что в последнюю очередь будет разрушена кривая, число вращения которой хуже всего приближается посредством последовательности рациональных чисел. Представление в виде цепной дроби для числа вращения такой инвариантной кривой имеет вид

и представляет собой знаменитое «золотое сечение». Таким образом, когда к становится достаточно большим для того, чтобы разрушить эту инвариантную кривую, можно с достаточной уверенностью считать, что все остальные кривые за это время также разрушились. После этого ничто не препятствует нерегулярной траектории блуждать по всей фазовой плоскости — возникает глобальный хаос. Было найдено, что критическое значение к, при котором разрушается кривая, соответствующая золотому сечению, близко к единице. Это хорошо согласуется с наблюдаемым возникновением глобального хаоса.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
- 1.3.б. фазовые портреты консервативных систем
- 1.4. Линейный анализ устойчивости
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
- 4.7.б. Перемешивание
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
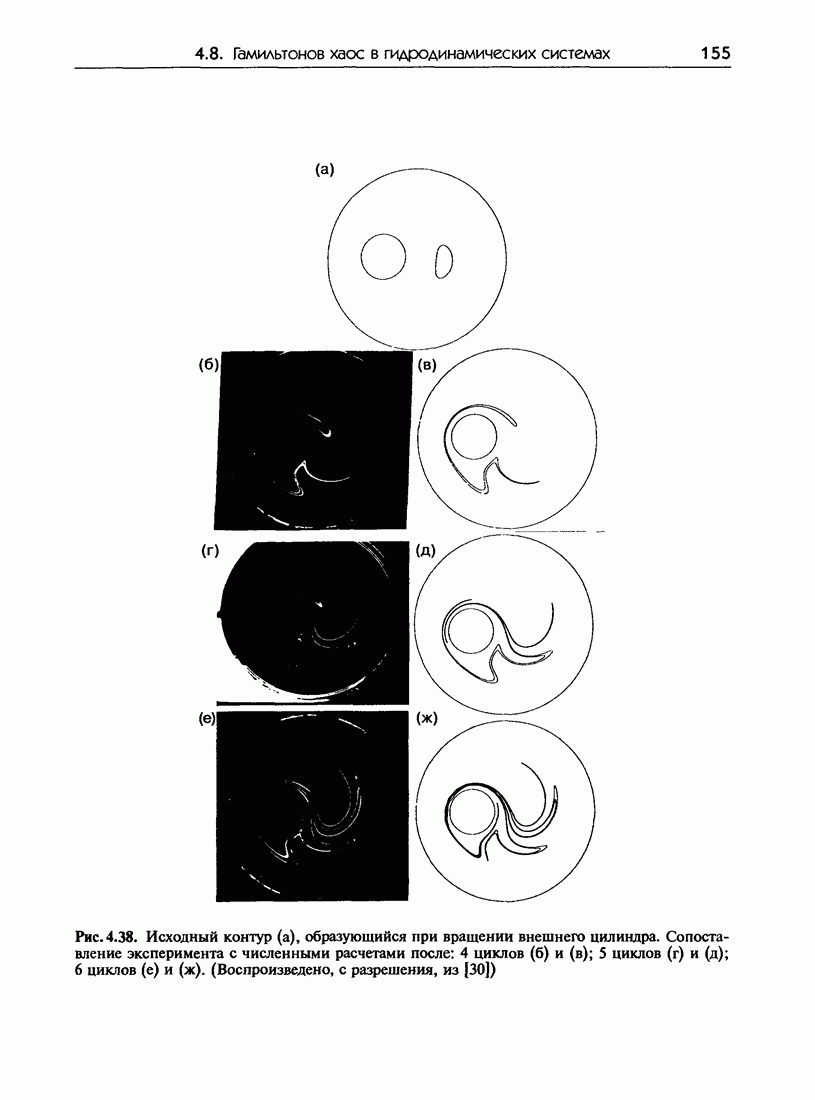
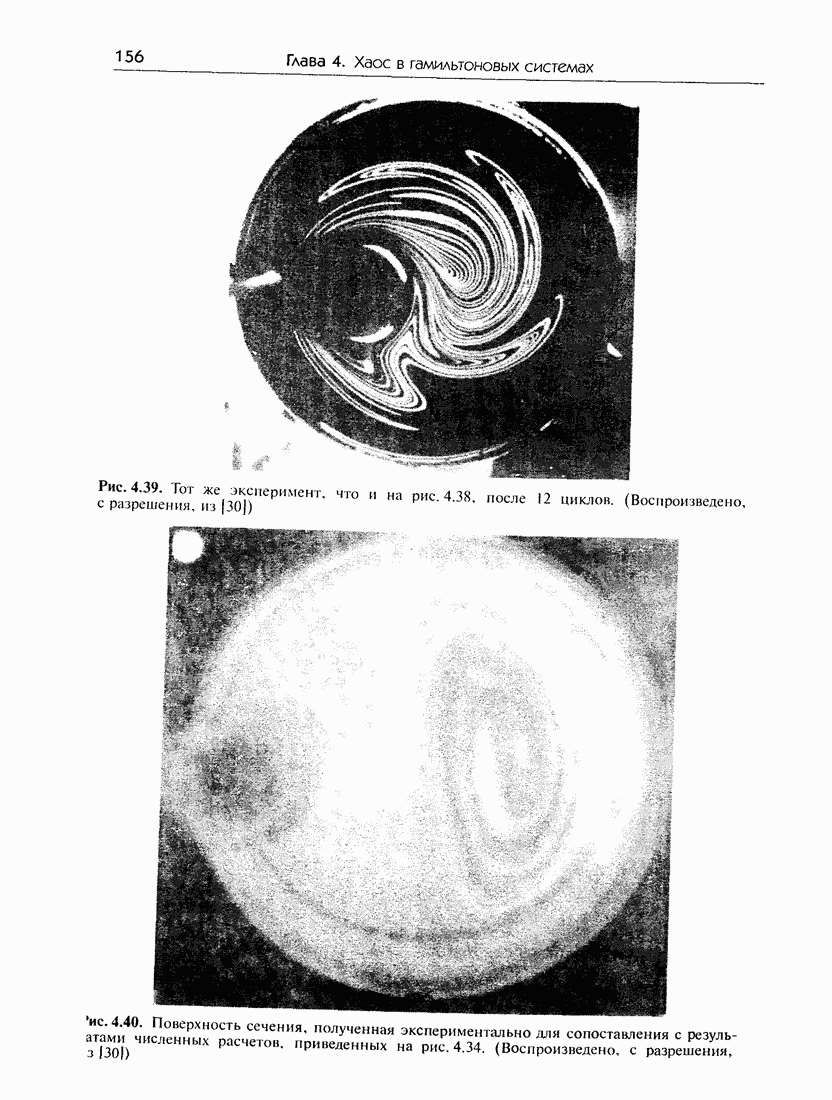
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
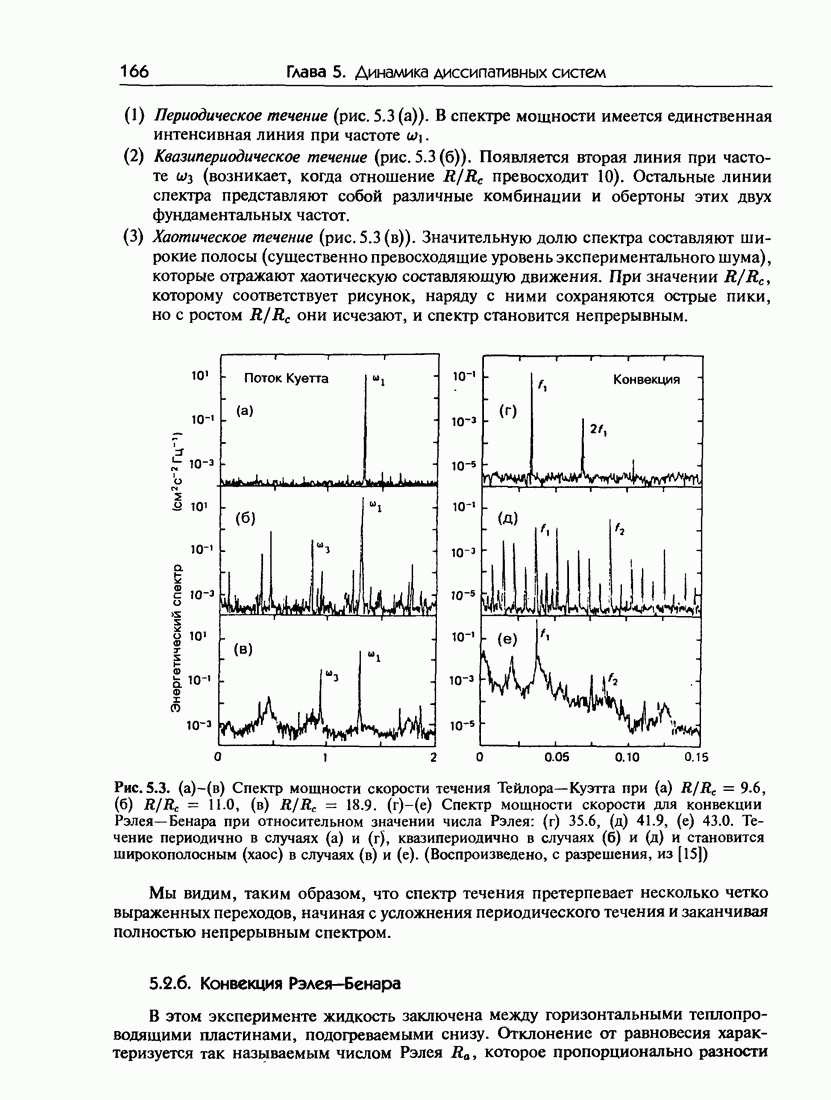
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
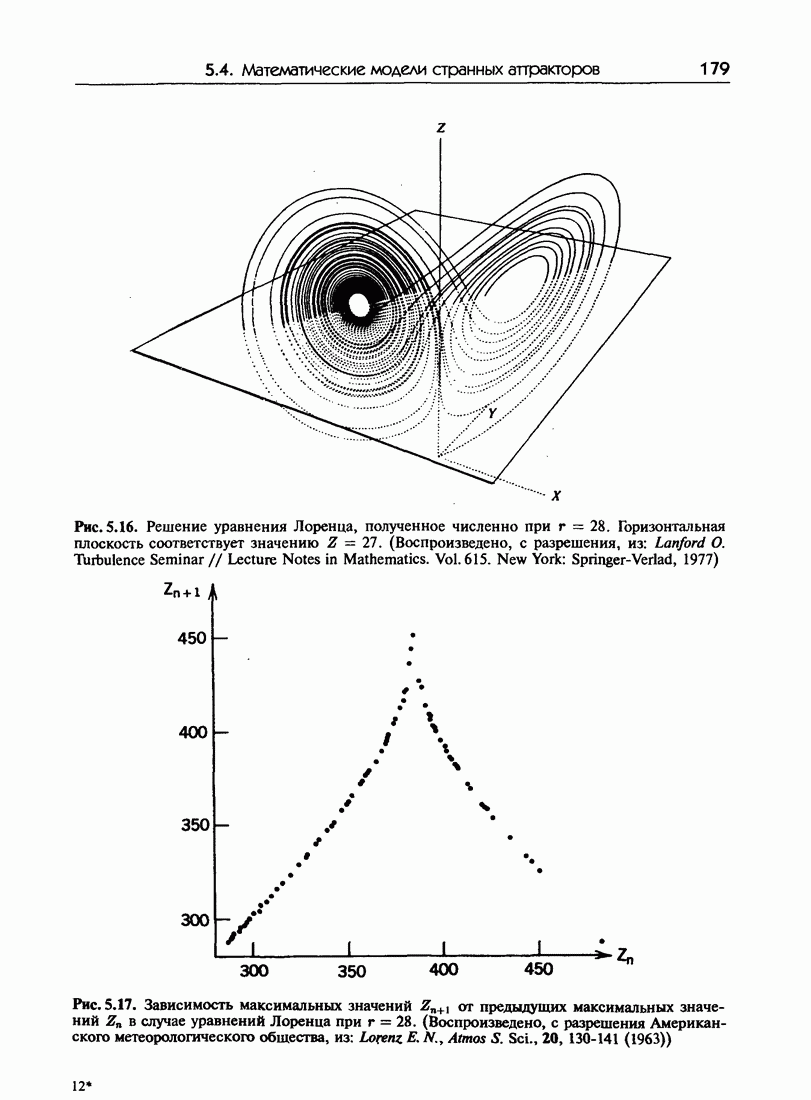
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
- 5.4.в. Отображение Хенона
- 5.5. Бифуркации удвоения периода
- 5.5.а. Механизм удвоения периода
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
- 5.5.г. Другие классы универсальности
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
- 7.5. Другие солитонные системы
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда