| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
8.2. Обыкновенные дифференциальные уравнения в комплексной области
8.2.а. Локальные представления
В случае самых простых нелинейных дифференциальных уравнений, таких как (8.1.9) и (8.1.11), характер подвижных особенностей можно определить исходя из вида точного решения. В большинстве случаев точные решения получить не удается, и характер подвижных особенностей устанавливают исходя из «локальных» свойств решений.
Пусть дано обыкновенное дифференциальное уравнение  порядка вида
порядка вида

где  функция аналитическая по независимой переменной z и рациональная по всем остальным аргументам. Поведение решения (решений) такого уравнения в подвижной особой точке определяется посредством анализа ведущего члена разложения. Записываем подстановку
функция аналитическая по независимой переменной z и рациональная по всем остальным аргументам. Поведение решения (решений) такого уравнения в подвижной особой точке определяется посредством анализа ведущего члена разложения. Записываем подстановку

где а и а необходимо определить,  произвольная точка в комплексной z-плоскости (т.е. положение подвижной особенности). Подставляя (8.2.2) в (8.2.1) и приравнивая наиболее сингулярные члены, определяем а и а. Рассмотрим, например, уравнение второго порядка
произвольная точка в комплексной z-плоскости (т.е. положение подвижной особенности). Подставляя (8.2.2) в (8.2.1) и приравнивая наиболее сингулярные члены, определяем а и а. Рассмотрим, например, уравнение второго порядка

В главе 1 было показано, что оно имеет точное решение в терминах эллиптических функций Вейерштрасса. Подстановка (8.2.2) дает

Наиболее сингулярные члены (т. е. вторая производная и  должны совпадать в особой точке
должны совпадать в особой точке  Приравнивание показателей степени
Приравнивание показателей степени  дает значение
дает значение  Аналогично, должны быть равны и коэффициенты при этих сингулярных членах
Аналогично, должны быть равны и коэффициенты при этих сингулярных членах  откуда находим
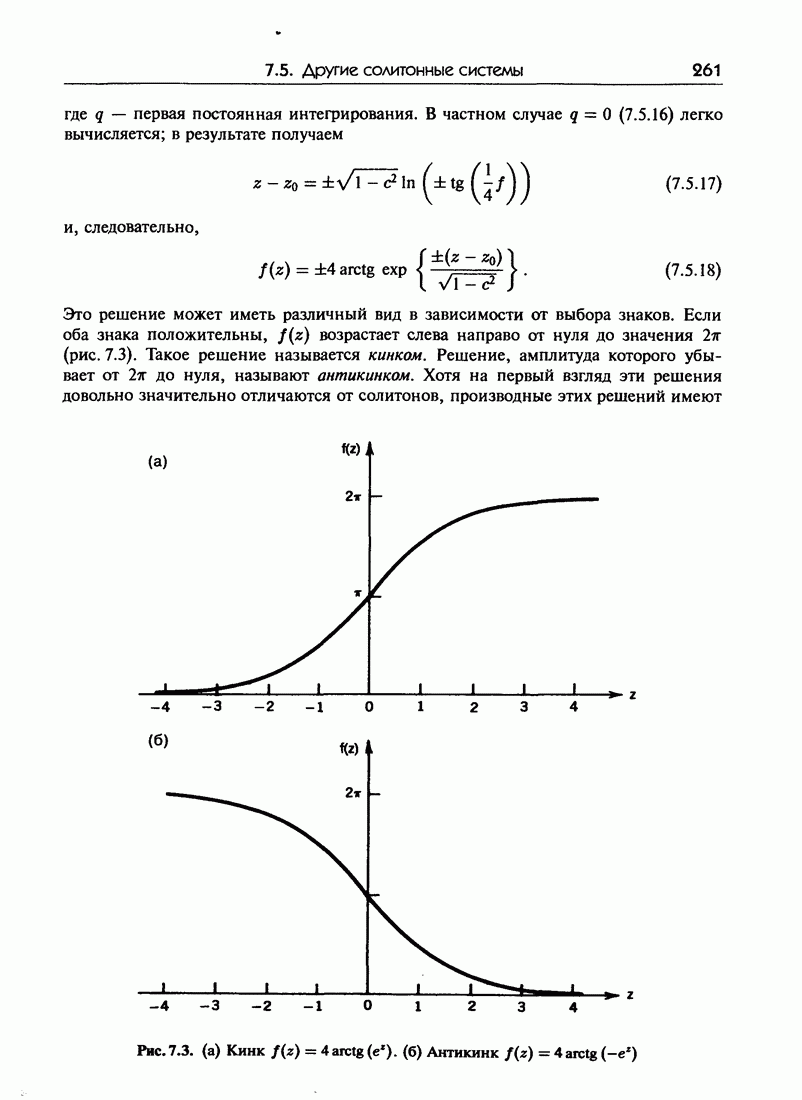
откуда находим  Таким образом, в точке
Таким образом, в точке  решение уравнения (8.2.3) ведет себя как
решение уравнения (8.2.3) ведет себя как  (полюс второго порядка).
(полюс второго порядка).
Отметим, что член более низкого порядка в этом уравнении  не влияет на поведение в точке
не влияет на поведение в точке  Усиление нелинейности в (8.2.3) приводит к изменению порядка сингулярности. Нетрудно показать, что уравнение
Усиление нелинейности в (8.2.3) приводит к изменению порядка сингулярности. Нетрудно показать, что уравнение

допускающее, как мы знаем, решение в терминах эллиптических функций Якоби, ведет себя в подвижной особой точке как  (полюс первого порядка). Легко видеть, что дальнейшее усиление нелинейности приведет к подвижной точке ветвления.
(полюс первого порядка). Легко видеть, что дальнейшее усиление нелинейности приведет к подвижной точке ветвления.
Анализ ведущего члена позволяет охарактеризовать поведение решения только в особой точке. Для того, чтобы установить поведение в окрестности сингулярности, необходимо прибегнуть к локальному разложению в ряд. Если особенность действительно является неподвижным полюсом, такое разложение будет представлять собой простой ряд Лорана. Рассмотрим, например, уравнение (8.2.3). Мы уже установили, что в особой точке оно ведет себя как полюс второго порядка. Исходя из этого, ряд Лорана должен иметь вид

Самосогласованность этого разложения может быть проверена непосредственной подстановкой в уравнение. Это приводит к соотношению

которое можно упростить и свести к рекуррентным соотношениям для 

где мы воспользовались тем, что  Вычисления по этим рекуррентным соотношениям дают:
Вычисления по этим рекуррентным соотношениям дают:

При  получаем соотношение
получаем соотношение

правая часть которого обращается с учетом значений  в ноль. Это означает произвольность а. Мы видим, таким образом, что ряд Лорана (8.2.5) имеет два произвольных параметра,
в ноль. Это означает произвольность а. Мы видим, таким образом, что ряд Лорана (8.2.5) имеет два произвольных параметра,  последний характеризует произвольность положения полюса. Поскольку уравнение (8.2.3) представляет собой о. д. у. второго
последний характеризует произвольность положения полюса. Поскольку уравнение (8.2.3) представляет собой о. д. у. второго
порядка, его общее решение включает два произвольных параметра. Проведенный анализ показывает, что в (локальном) разложении Лорана это проявляется в виде произвольности  Мы можем, таким образом, заключить, что в окрестности подвижной особой точки
Мы можем, таким образом, заключить, что в окрестности подвижной особой точки  общее решение уравнения (8.2.3) действительно ведет себя как полюс второго порядка. Мы будем часто обращаться к этому результату, говоря, что уравнение (8.2.3) обладает свойством Пенлеве. В качестве упражнения можно показать, что уравнение (8.2.4) также обладает свойством Пенлеве; произвольными параметрами локального разложения
общее решение уравнения (8.2.3) действительно ведет себя как полюс второго порядка. Мы будем часто обращаться к этому результату, говоря, что уравнение (8.2.3) обладает свойством Пенлеве. В качестве упражнения можно показать, что уравнение (8.2.4) также обладает свойством Пенлеве; произвольными параметрами локального разложения

являются 
Степени  при которых появляются произвольные коэффициенты, часто называют резонансами. Резонансы можно находить с помощью простого метода без полных расчетов по рекуррентным соотношениям. Он основывается на подстановке
при которых появляются произвольные коэффициенты, часто называют резонансами. Резонансы можно находить с помощью простого метода без полных расчетов по рекуррентным соотношениям. Он основывается на подстановке

где  должны быть определены посредством анализа ведущего члена. Исходя из (8.2.9), можно записать линейное относительно
должны быть определены посредством анализа ведущего члена. Исходя из (8.2.9), можно записать линейное относительно  уравнение и определить значения
уравнение и определить значения  при которых
при которых  произвольно. Так, например, в случае уравнения (8.2.3) подстановка имеет вид
произвольно. Так, например, в случае уравнения (8.2.3) подстановка имеет вид

Оперируя наиболее сингулярными членами, получаем

Приравнивая линейные по  члены, приходим к
члены, приходим к

Таким образом, для того, чтобы  было произвольным, необходимо, чтобы либо
было произвольным, необходимо, чтобы либо  либо
либо  Корень
Корень  отвечает произвольности коэффициента
отвечает произвольности коэффициента  соответствующего степеням
соответствующего степеням  в (8.2.5). Второй корень
в (8.2.5). Второй корень  соответствует не степени
соответствует не степени  (что не согласуется с уравнением), а определяет произвольность
(что не согласуется с уравнением), а определяет произвольность 
Такой анализ позволяет определить лишь, какие коэффициенты должны быть произвольными. Так это или нет, необходимо затем проверить с помощью полного набора рекуррентных соотношений. Резонансам соответствуют как правило некоторые соотношения, называемые условиями совместности, которые должны быть выполнены для того, чтобы обеспечить произвольность коэффициента. Для уравнения (8.2.3), например, соответствующее условие совместности имеет вид  В данном случае оно удовлетворяется при любом значении А. Для более сложных
В данном случае оно удовлетворяется при любом значении А. Для более сложных
задач часто оказывается, что произвольность может быть получена лишь при некоторых определенных значениях параметров системы. Если, например, уравнение (8.2.4) модифицировать, включив в него член, содержащий первую производную:

то коэффициент  ряда (8.2.8) будет произвольным лишь при условии, что
ряда (8.2.8) будет произвольным лишь при условии, что  Если это условие не выполняется, простой ряд Лорана не может служить локальным представлением общего решения. В этом случае ряд необходимо обобщить таким образом, чтобы коэффициент при
Если это условие не выполняется, простой ряд Лорана не может служить локальным представлением общего решения. В этом случае ряд необходимо обобщить таким образом, чтобы коэффициент при  вновь стал произвольным. Новый ряд, называемый пси-рядом, указывает на то, что особенность уже не является простым полюсом и характеризуется сложной логарифмической многозначностью. Этот метод будет изложен в разделе 8.2.в.
вновь стал произвольным. Новый ряд, называемый пси-рядом, указывает на то, что особенность уже не является простым полюсом и характеризуется сложной логарифмической многозначностью. Этот метод будет изложен в разделе 8.2.в.
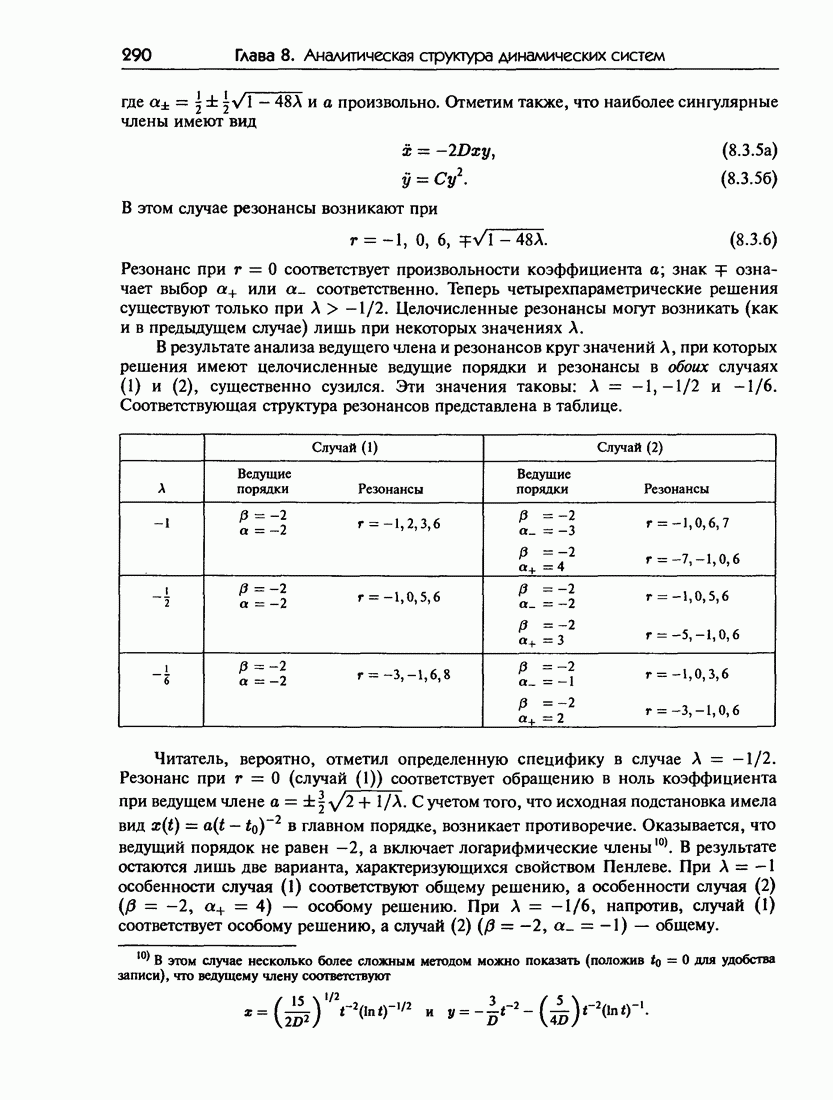
До сих пор мы все время подразумевали целочисленность ведущих порядков и резонансов. Одна из этих величин или обе — в зависимости от порядка и характера нелинейности уравнения — вполне могут оказаться не целыми (например, иррациональными или комплексными). Понятно, что в этом случае особенности не являются простыми полюсами и рассматриваемая система не обладает свойством Пенлеве. А поскольку, как следует из работы Ковалевской, свойство Пенлеве является критерием интегрируемости, мы видим, что уже на уровне анализа ведущих членов и резонансов это дает простой аналитический «намек» на неинтегрируемость системы.
В заключение этого подраздела сделаем несколько замечаний относительно существенных особенностей. Это такие особенности, локальные разложения которых имеют бесконечное число отрицательных степеней. В качестве простого примера может служить неподвижная существенная особенность решения  линейного уравнения первого порядка (8.1.8). В этом случае локальное разложение записывается следующим образом:
линейного уравнения первого порядка (8.1.8). В этом случае локальное разложение записывается следующим образом:

В случае нелинейных уравнений первого порядка вида

оказывается, что для широкого класса  такие уравнения могут иметь только подвижные полюсы и алгебраические точки ветвления и при этом только неподвижные существенные особенности. Однако в случае нелинейных о. д. у. второго порядка существенная особенность может стать подвижной. Простым примером является о. д. у.
такие уравнения могут иметь только подвижные полюсы и алгебраические точки ветвления и при этом только неподвижные существенные особенности. Однако в случае нелинейных о. д. у. второго порядка существенная особенность может стать подвижной. Простым примером является о. д. у.

где у означает общее решение имеет вид

и обладает подвижной существенной особенностью при  Наряду с подвижными существенными особенностями нелинейные о. д. у. второго порядка могут также
Наряду с подвижными существенными особенностями нелинейные о. д. у. второго порядка могут также
обладать подвижными логарифмическими и трансцендентными точками ветвления. Эти два типа особенностей могут быть определены в рамках локального анализа, тогда как нахождение существенных особенностей затруднительно, если решение не известно в явном виде. В настоящее время роль подвижных существенных особенностей в установлении интегрируемости конкретной системы понята недостаточно. Отметим также, что с повышением порядка дифференциальных уравнений могут возникать подвижные особенности еще более сложных типов.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
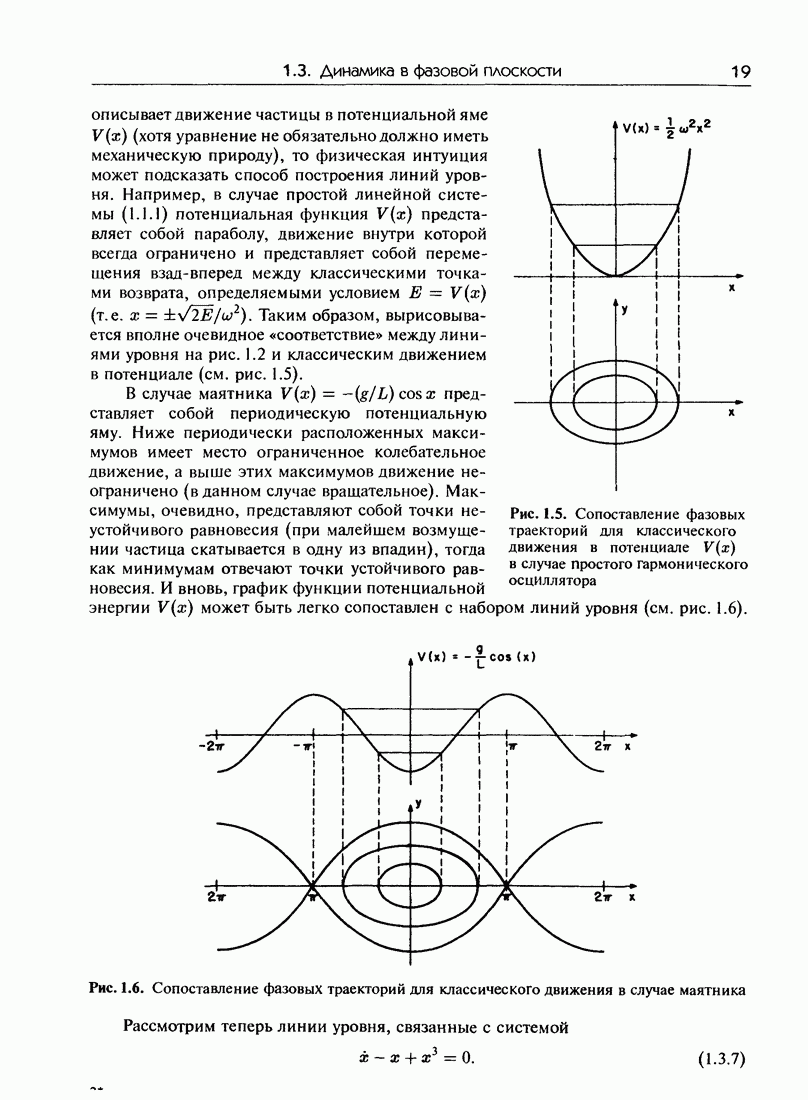
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
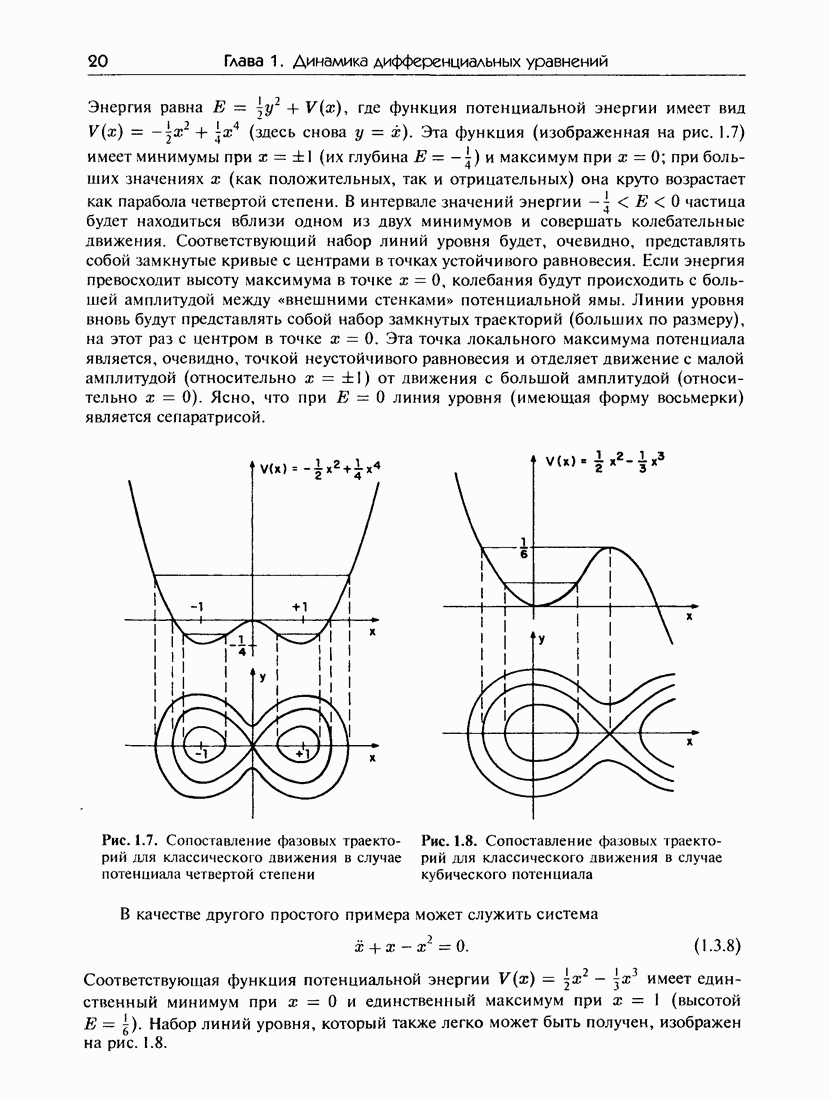
- 1.3.б. фазовые портреты консервативных систем
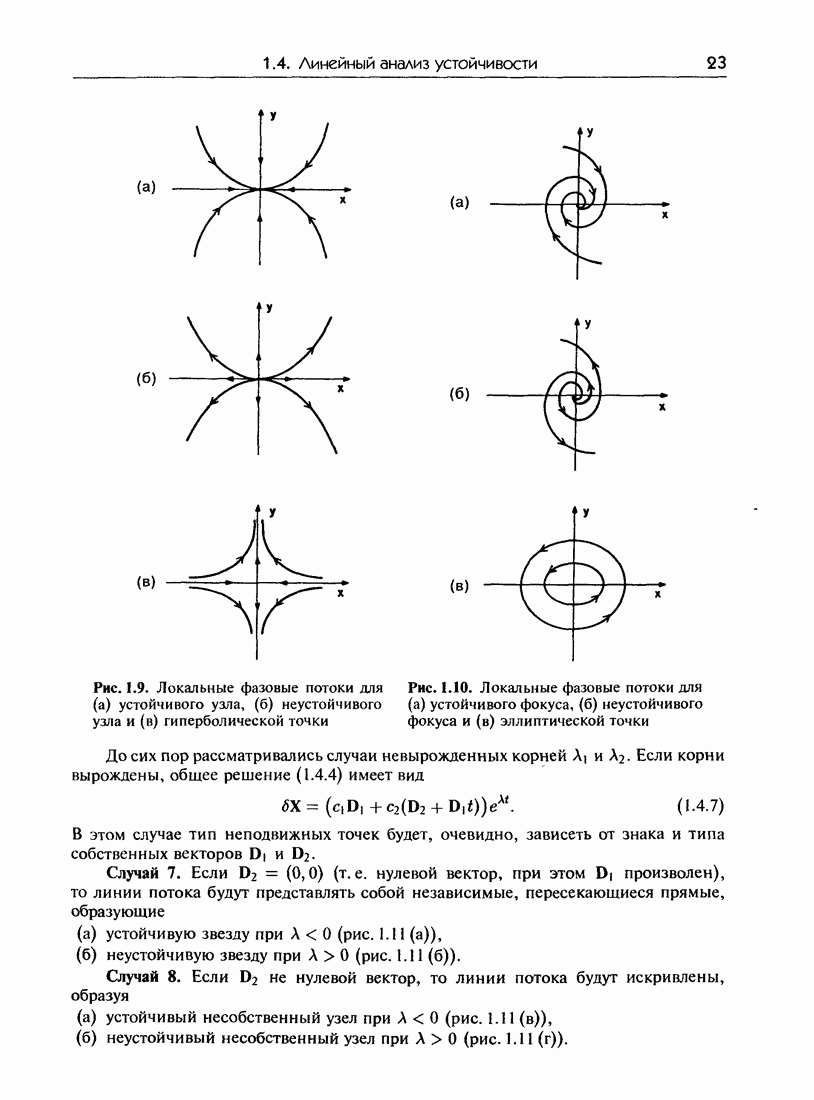
- 1.4. Линейный анализ устойчивости
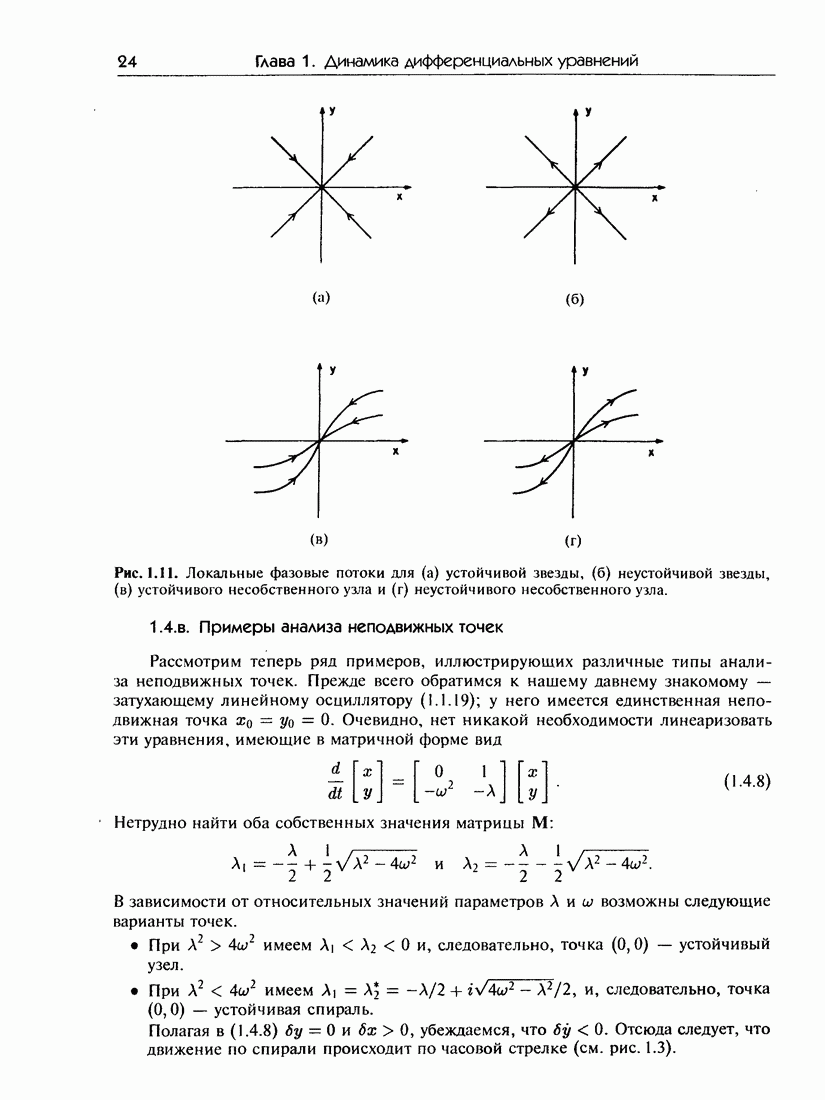
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
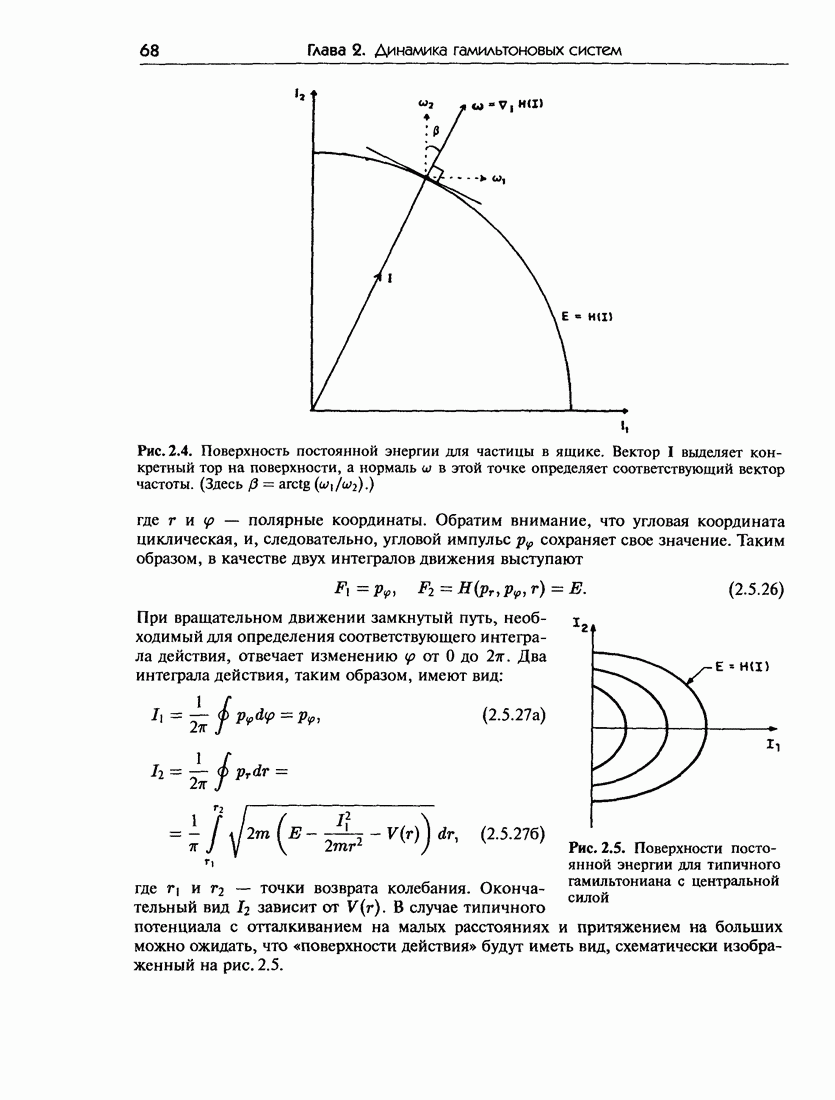
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
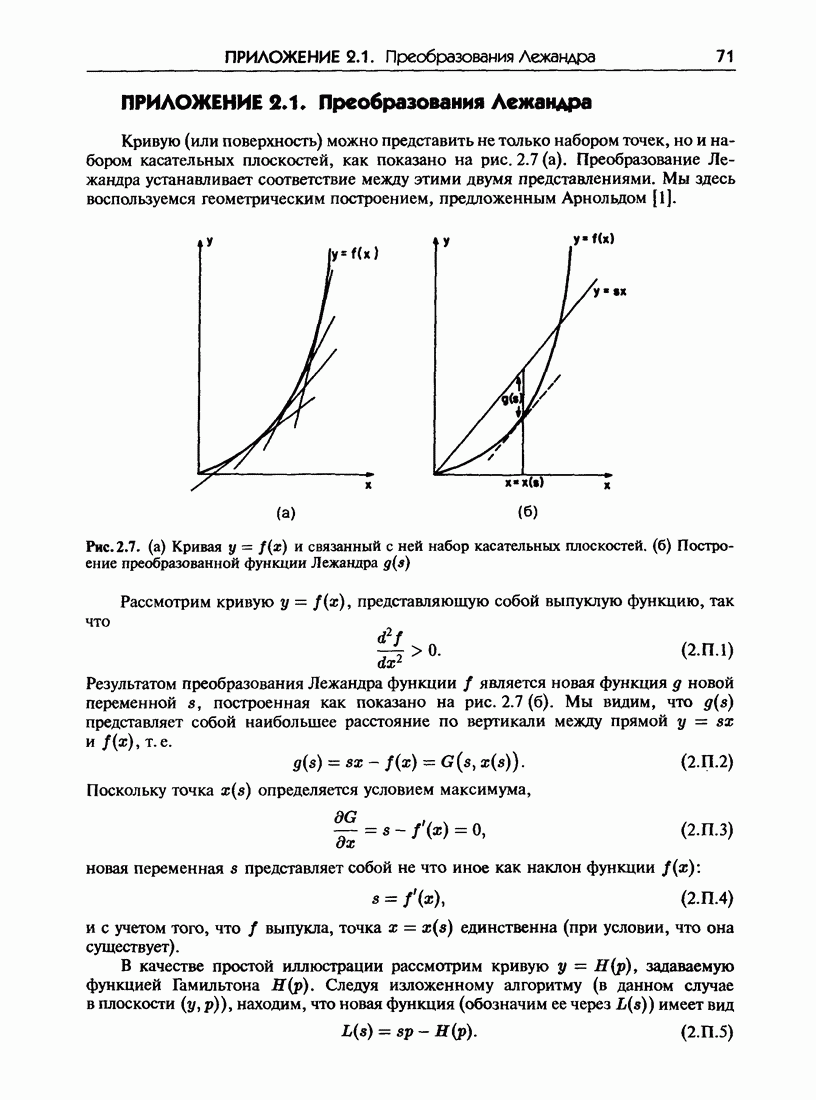
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
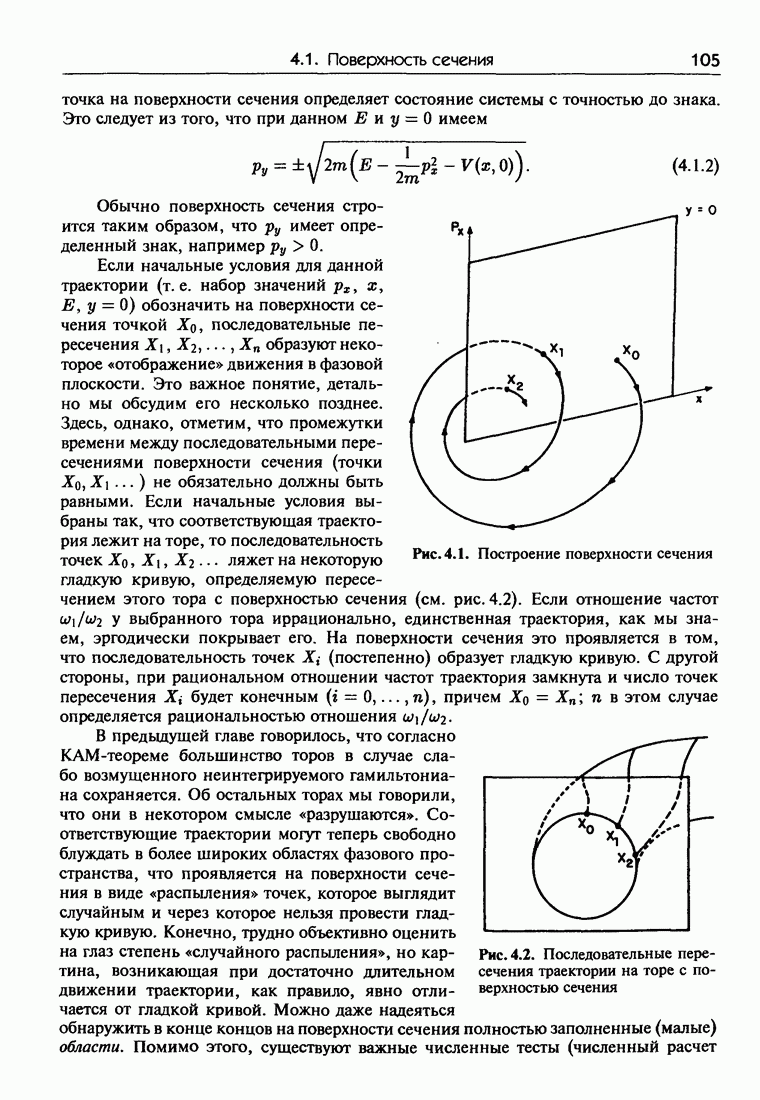
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
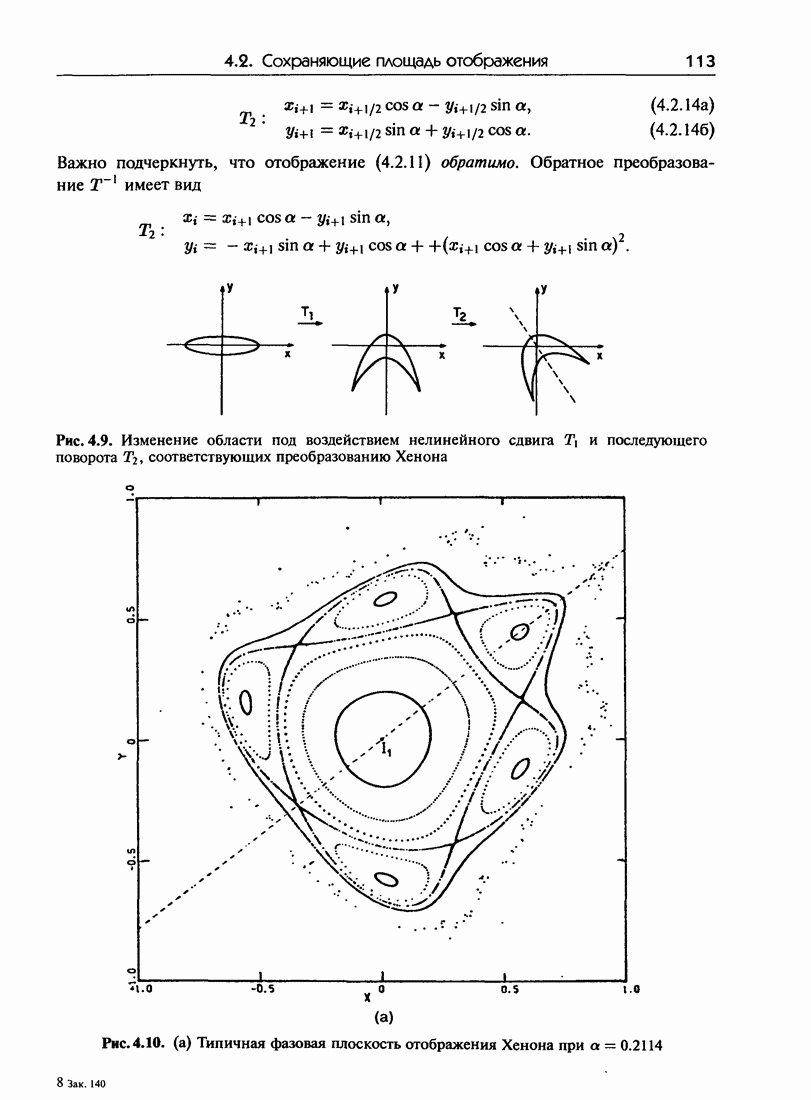
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
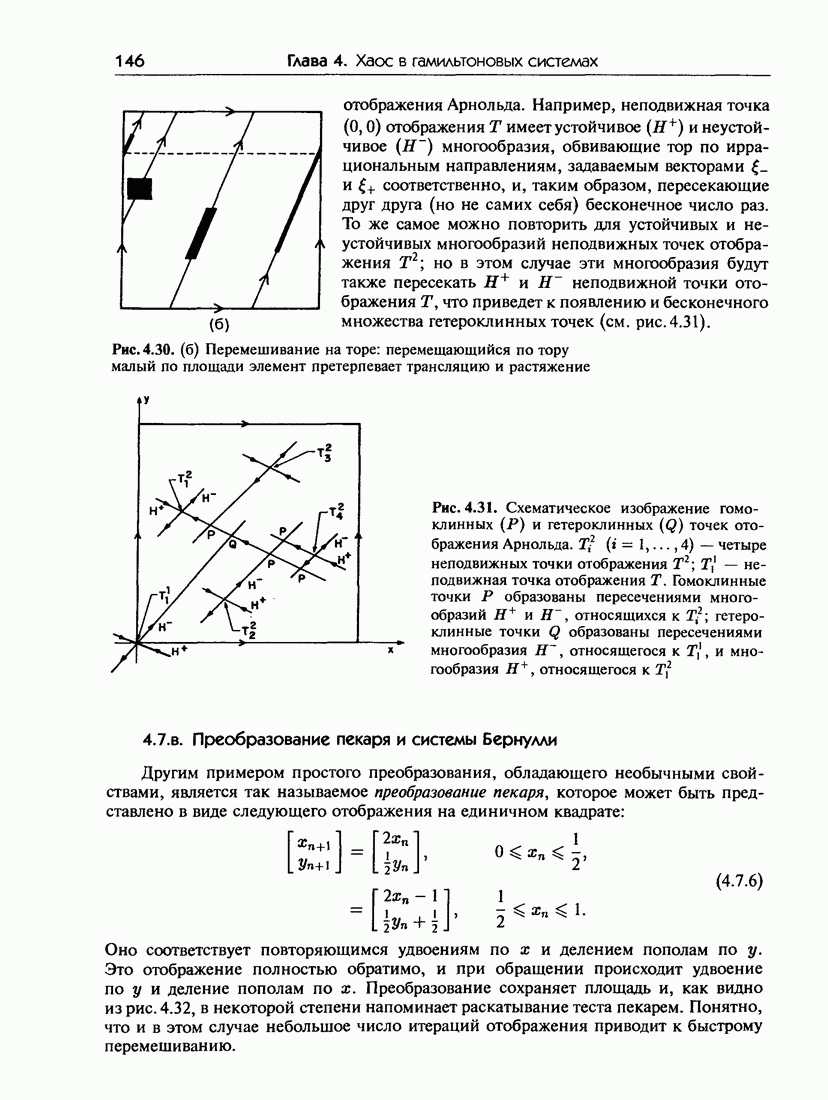
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
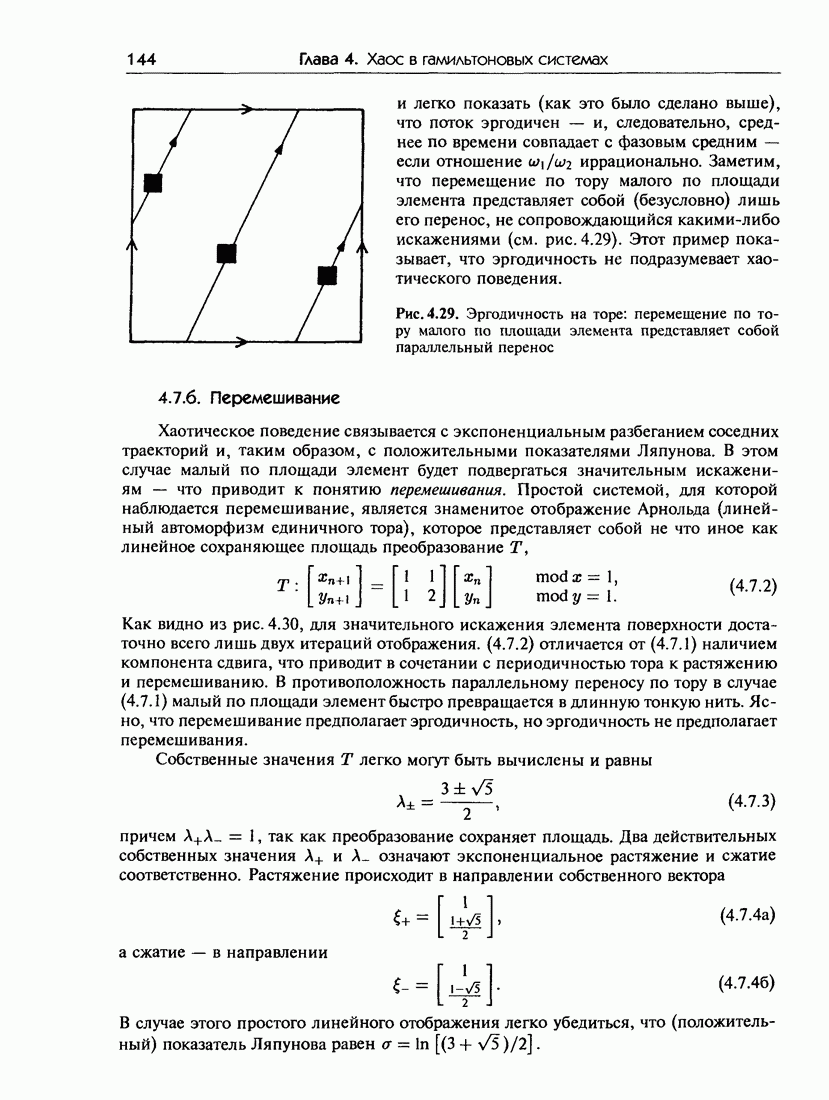
- 4.7.б. Перемешивание
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
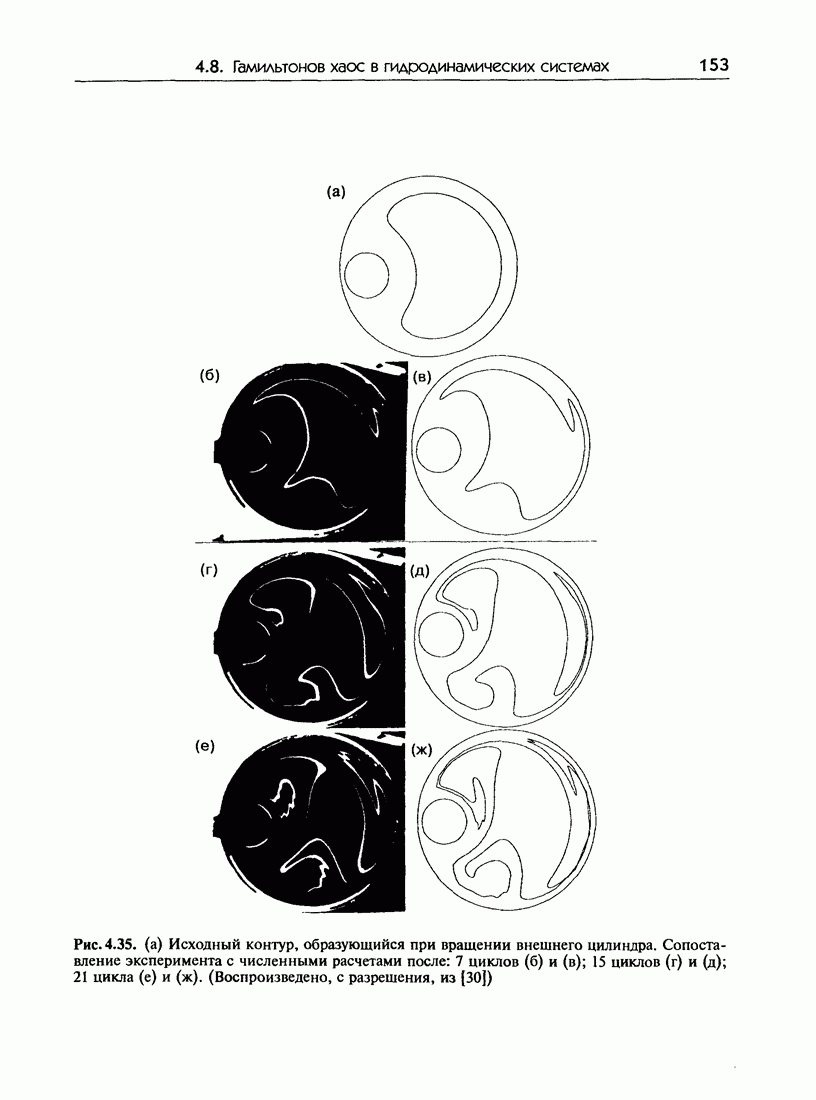
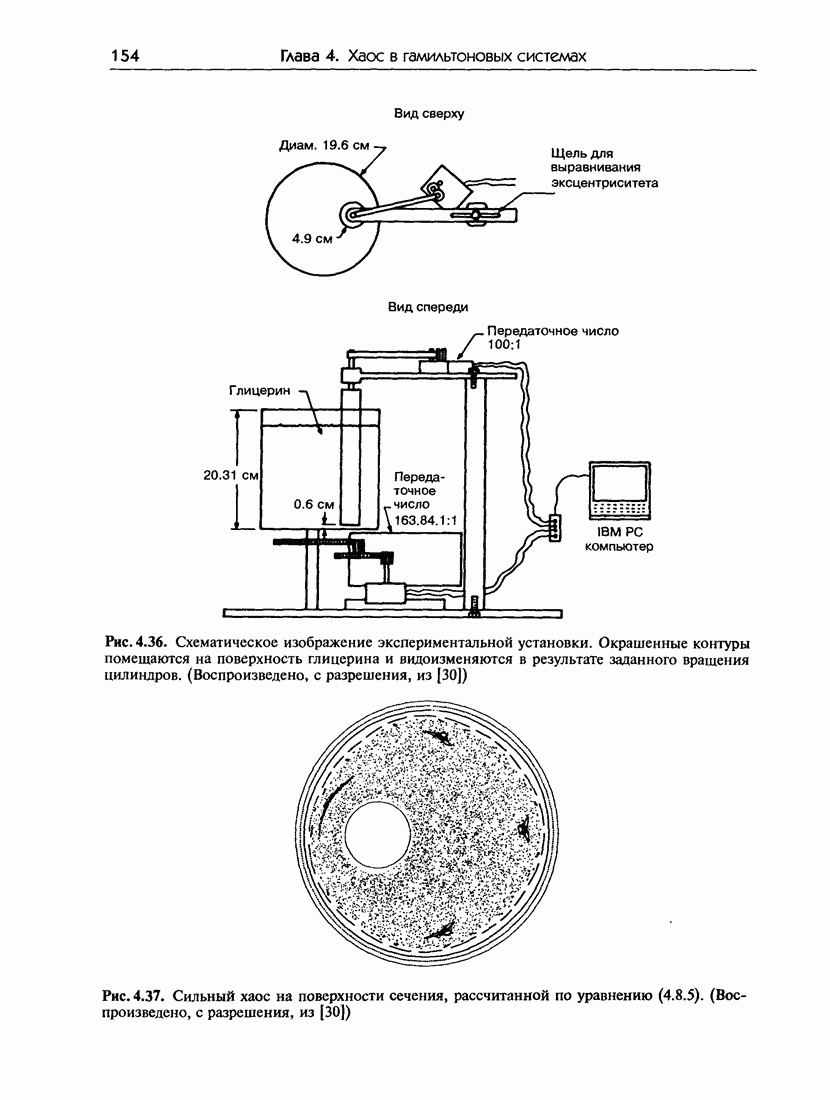
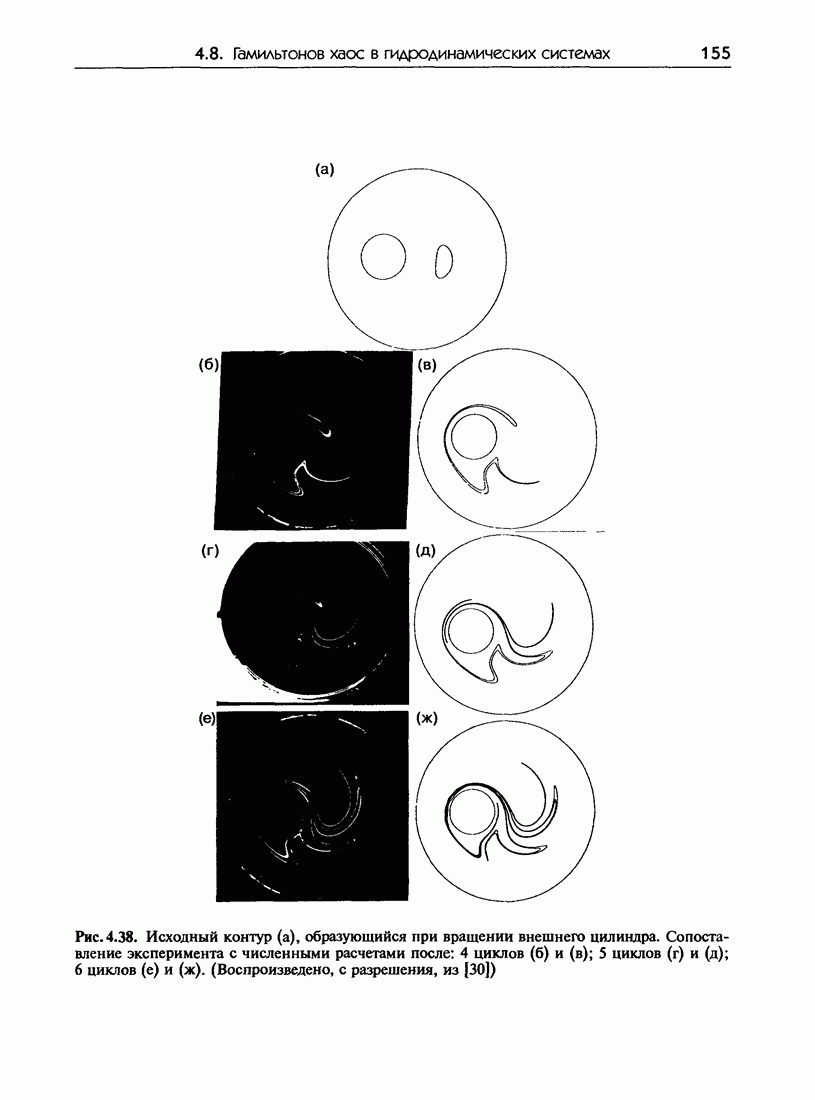
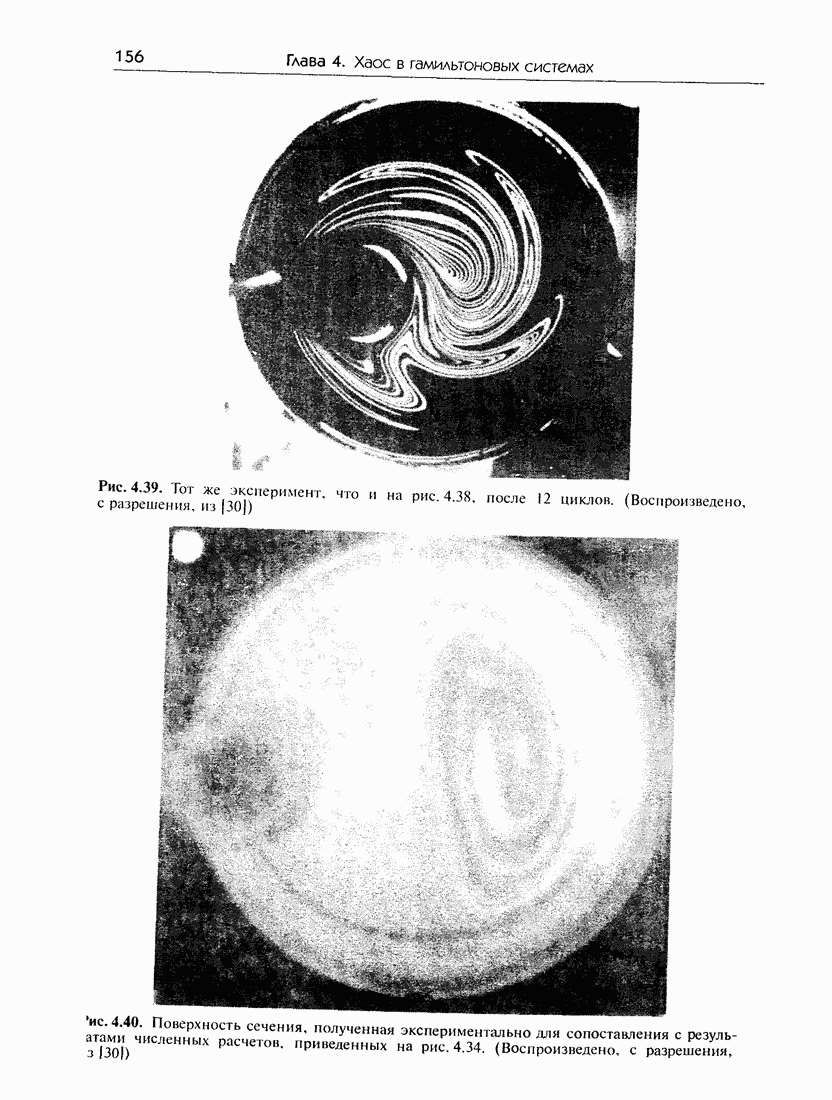
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
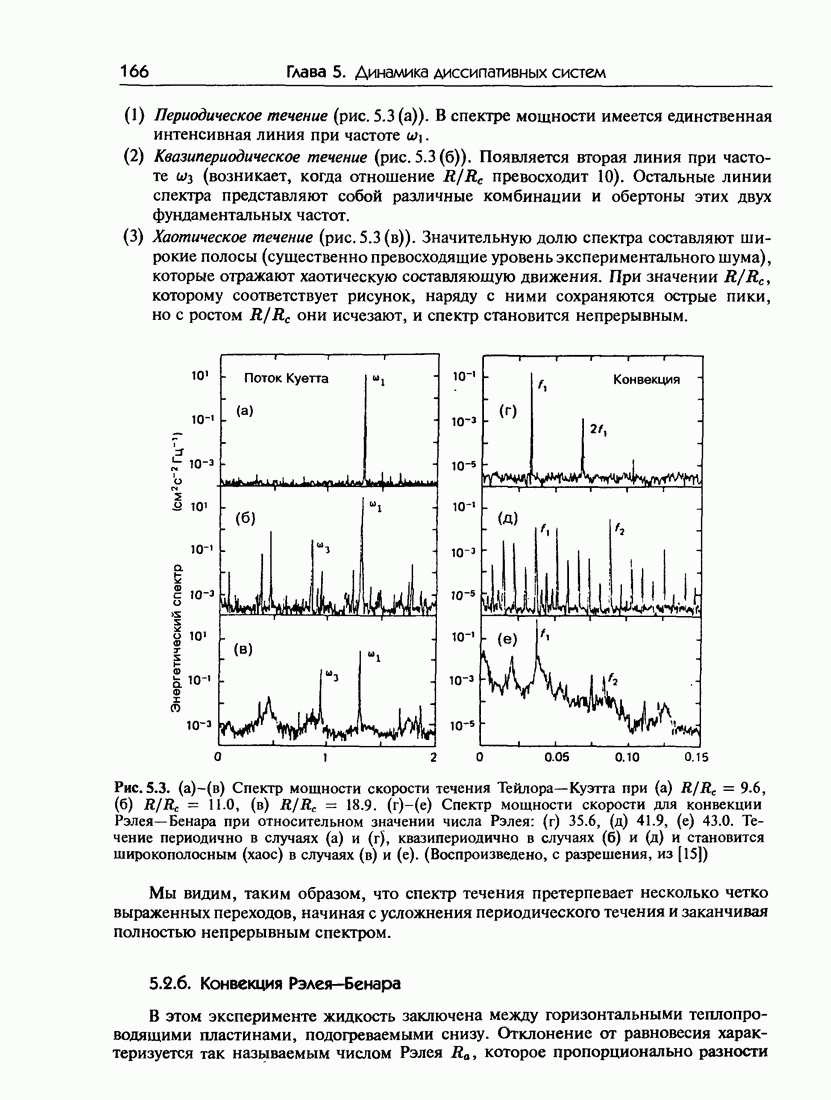
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
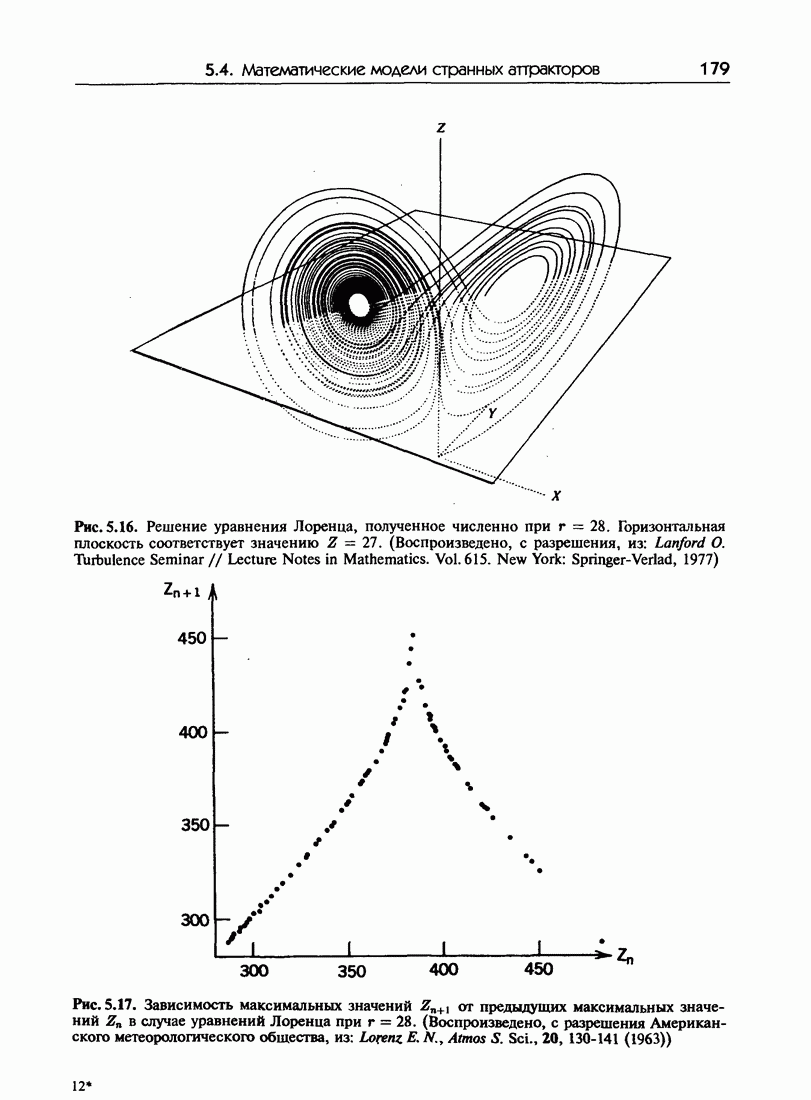
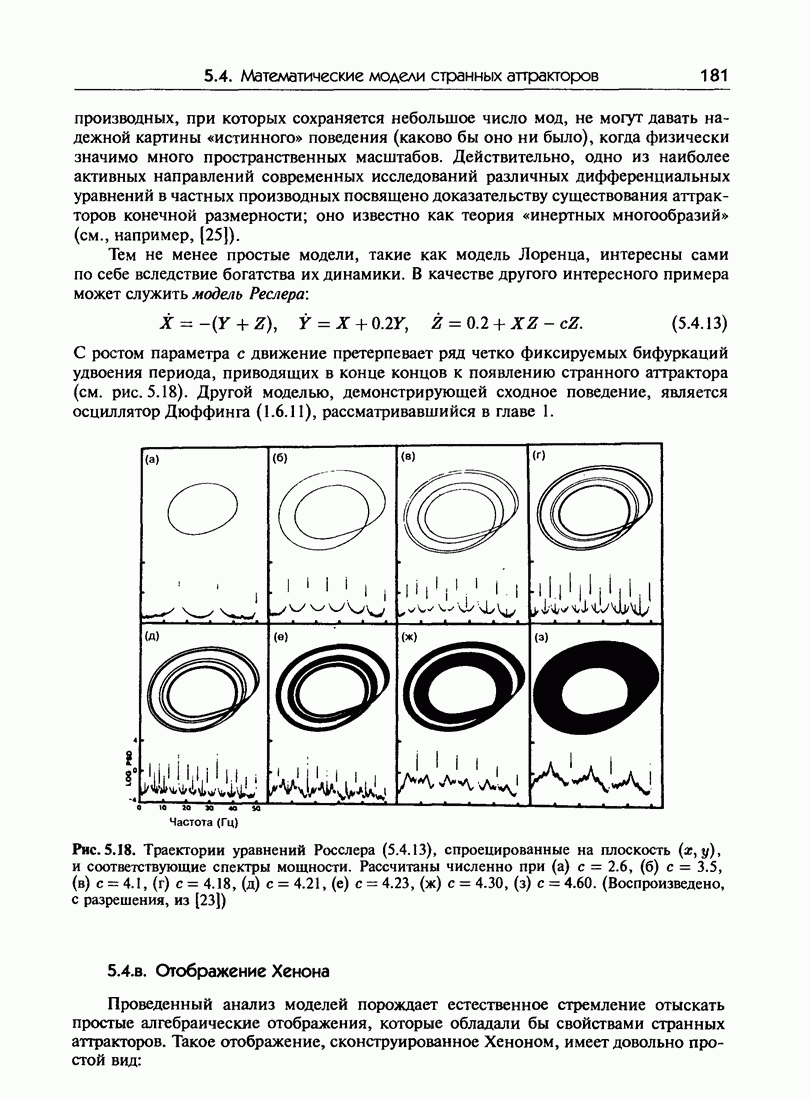
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
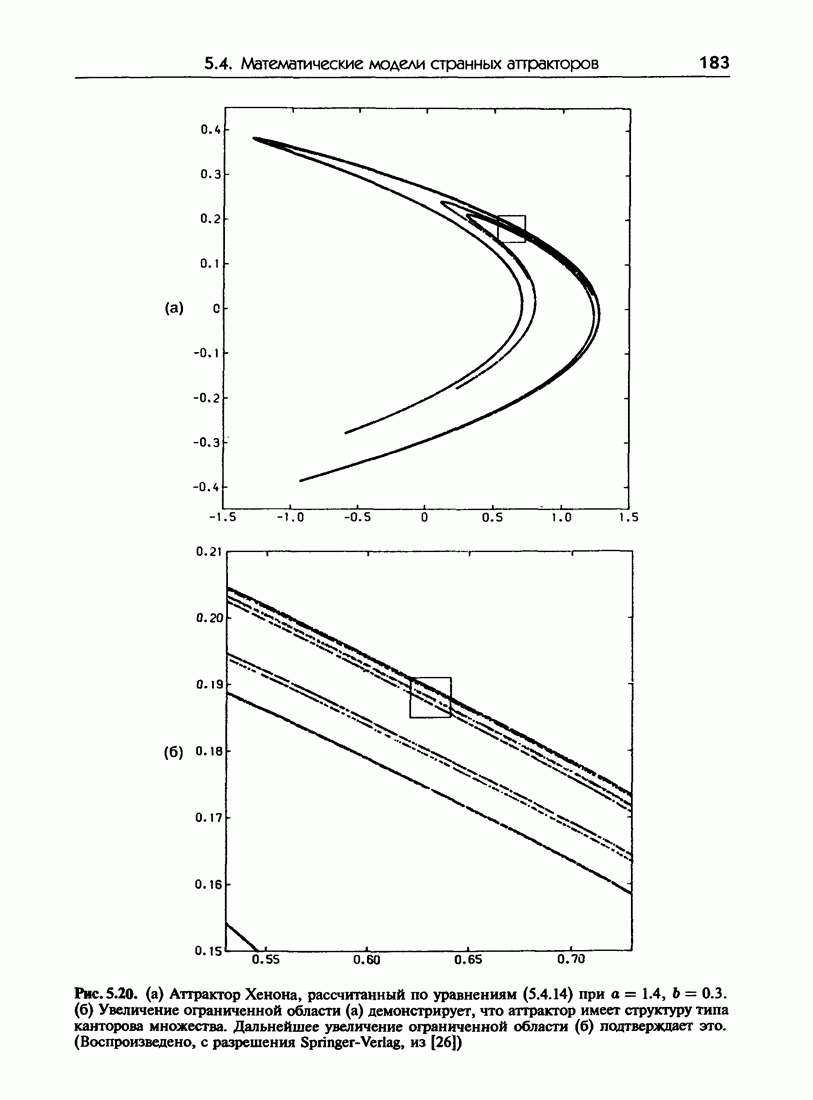
- 5.4.в. Отображение Хенона
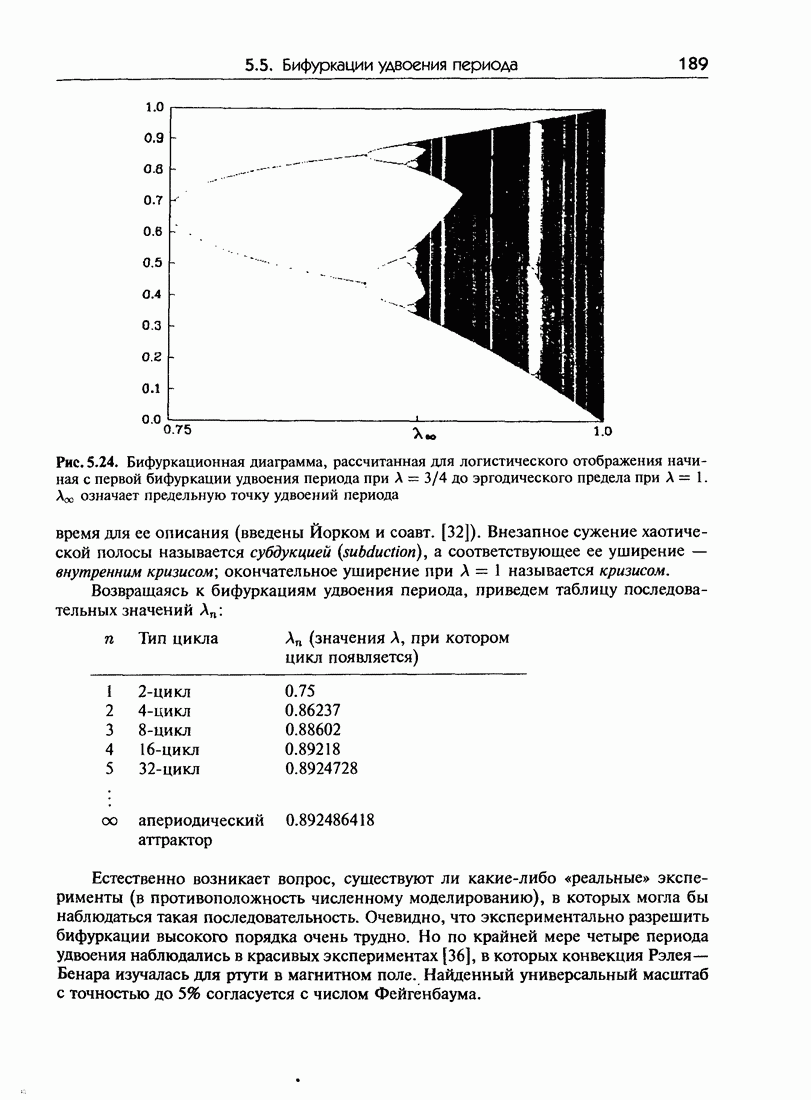
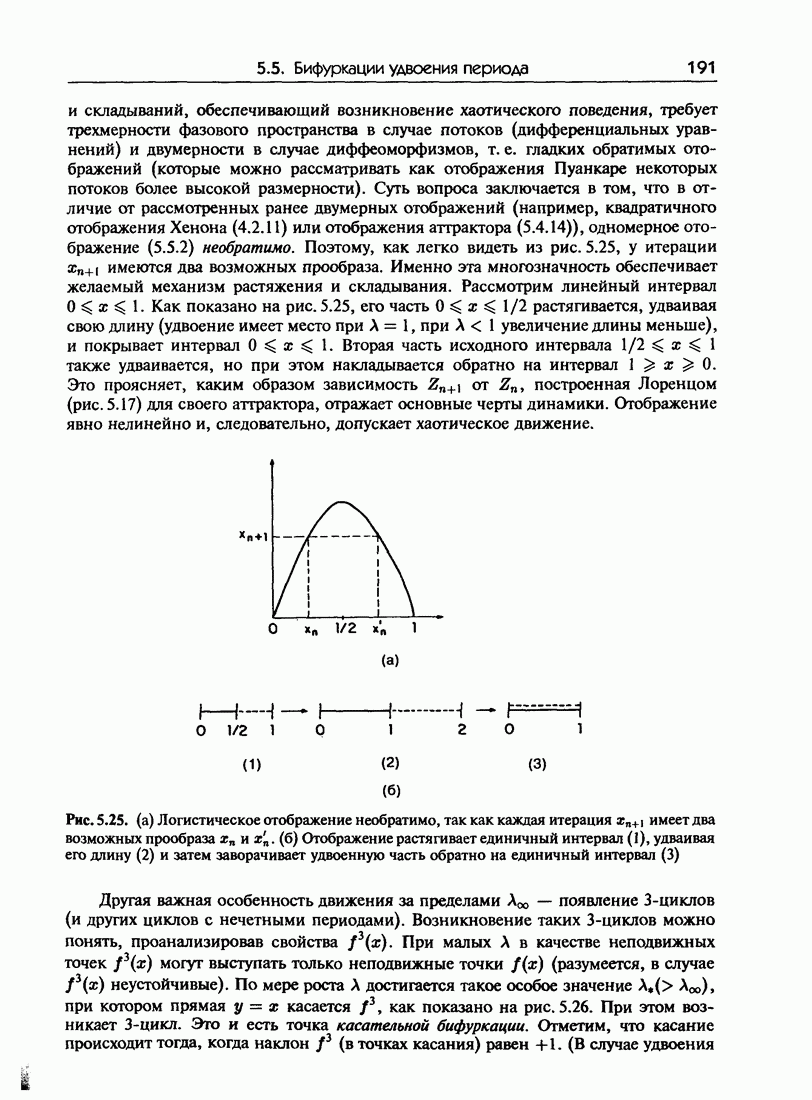
- 5.5. Бифуркации удвоения периода
- 5.5.а. Механизм удвоения периода
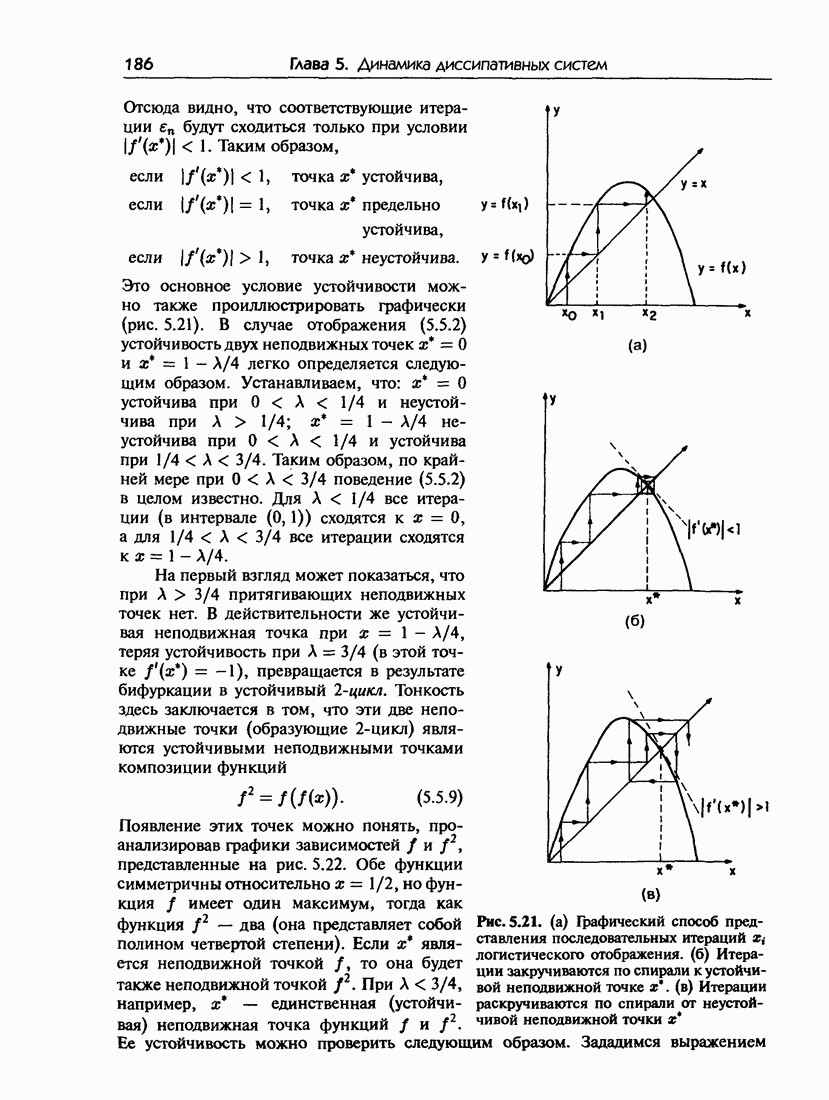
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
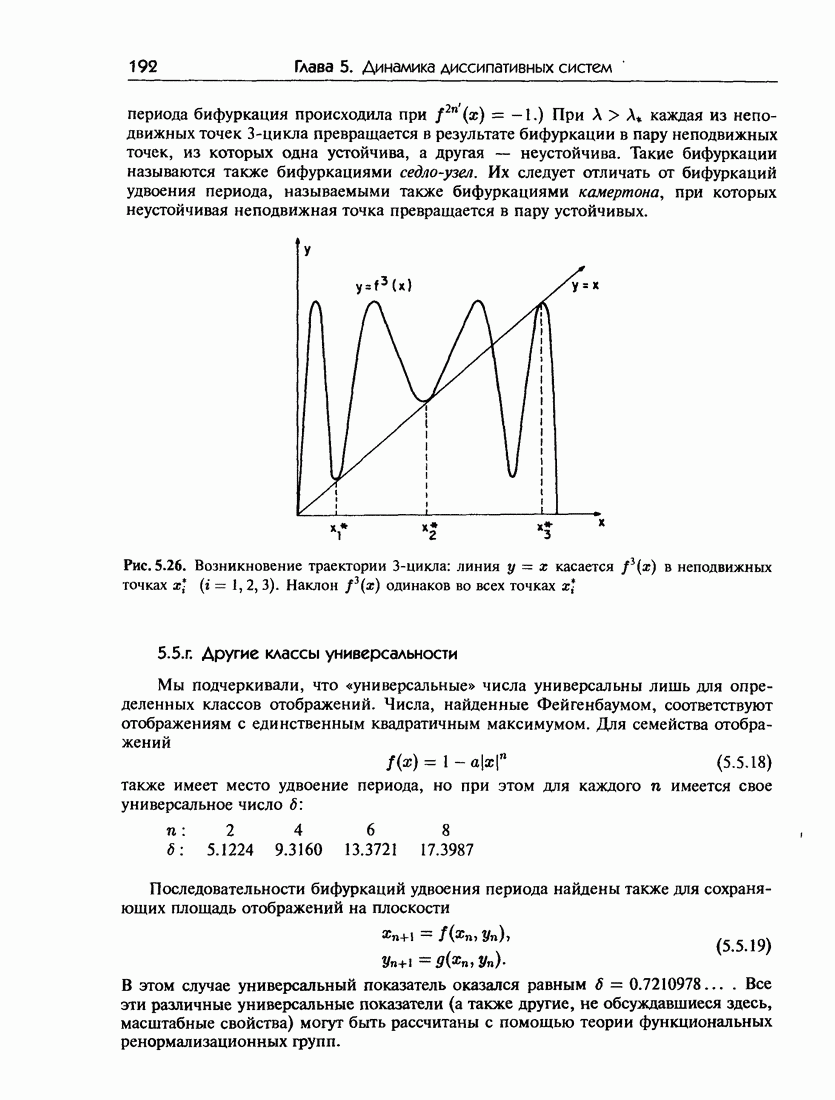
- 5.5.г. Другие классы универсальности
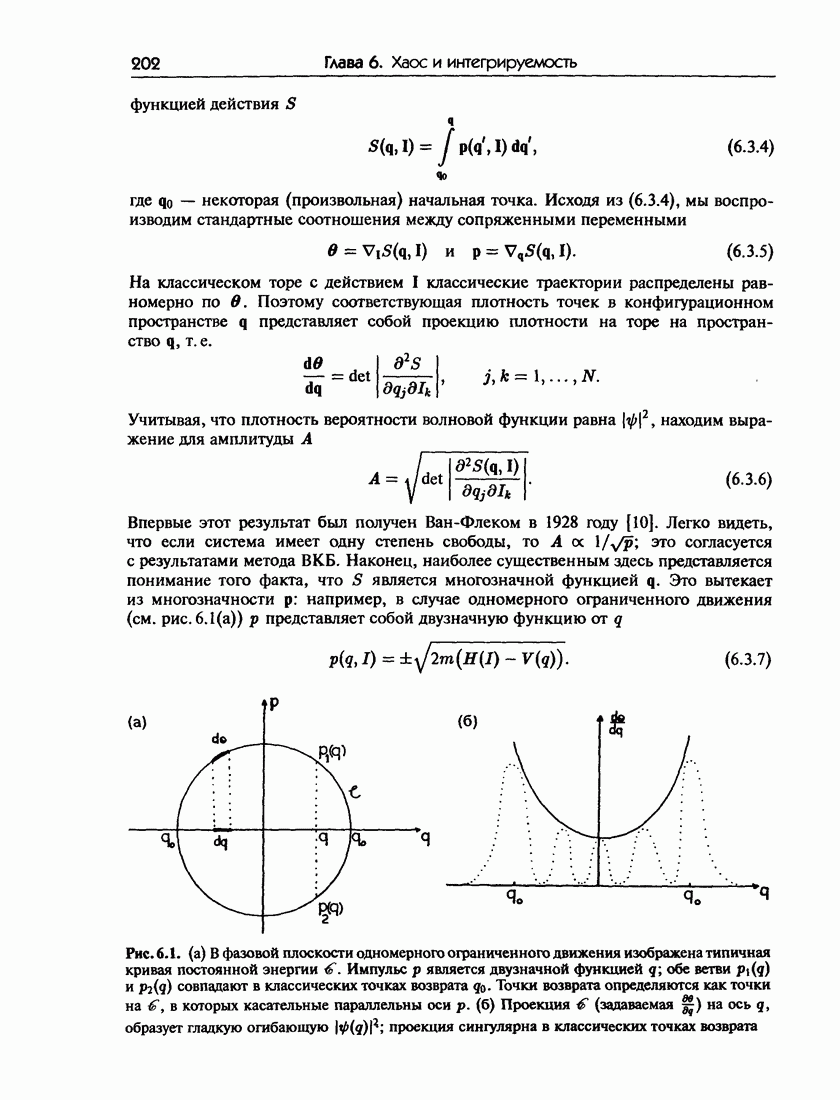
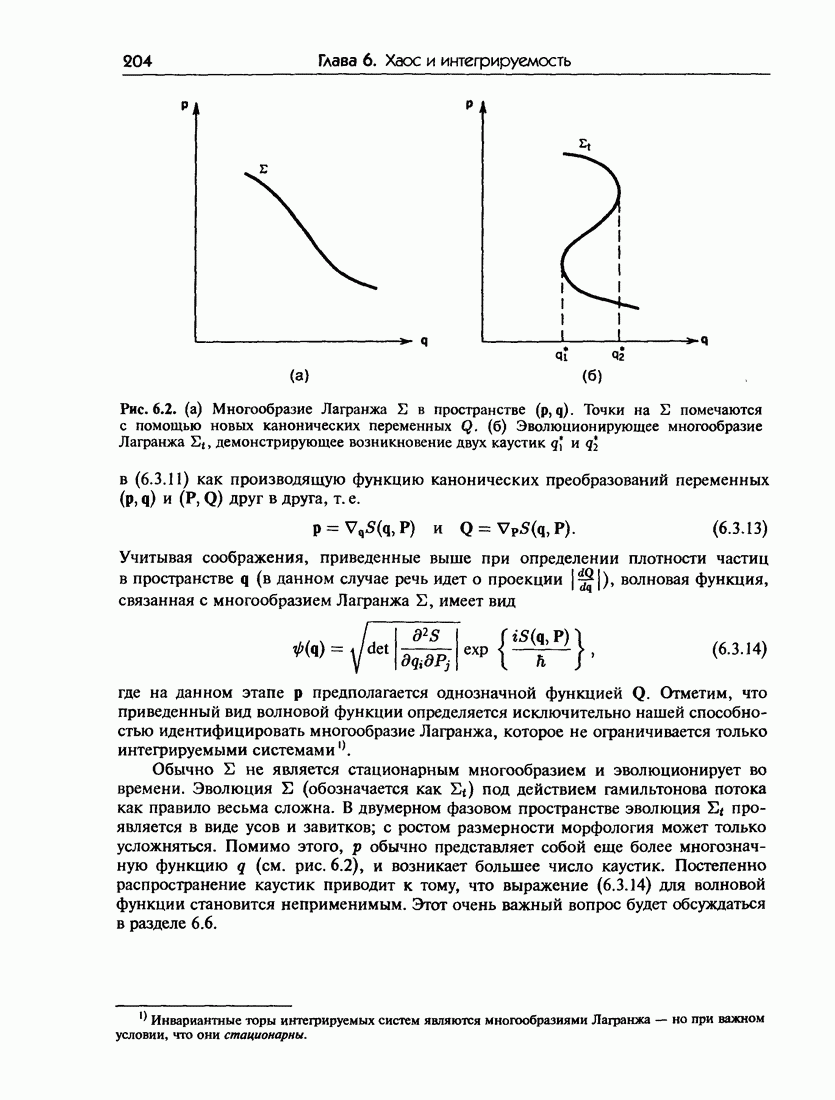
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
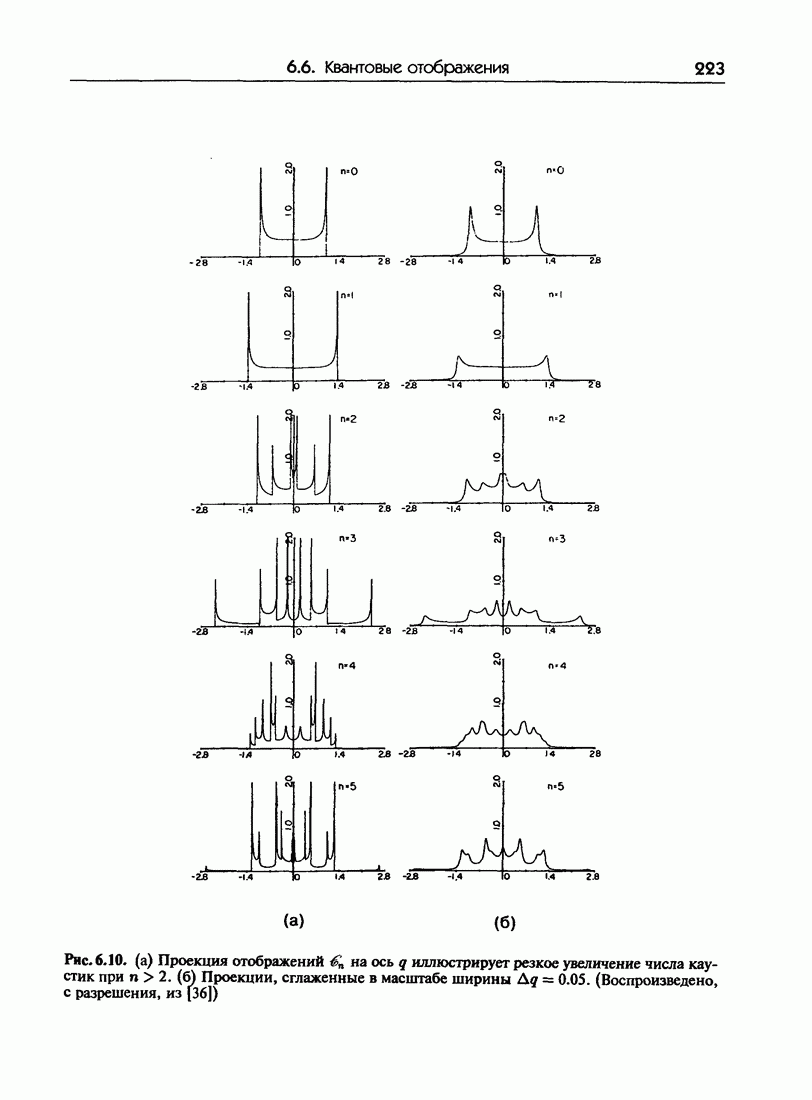
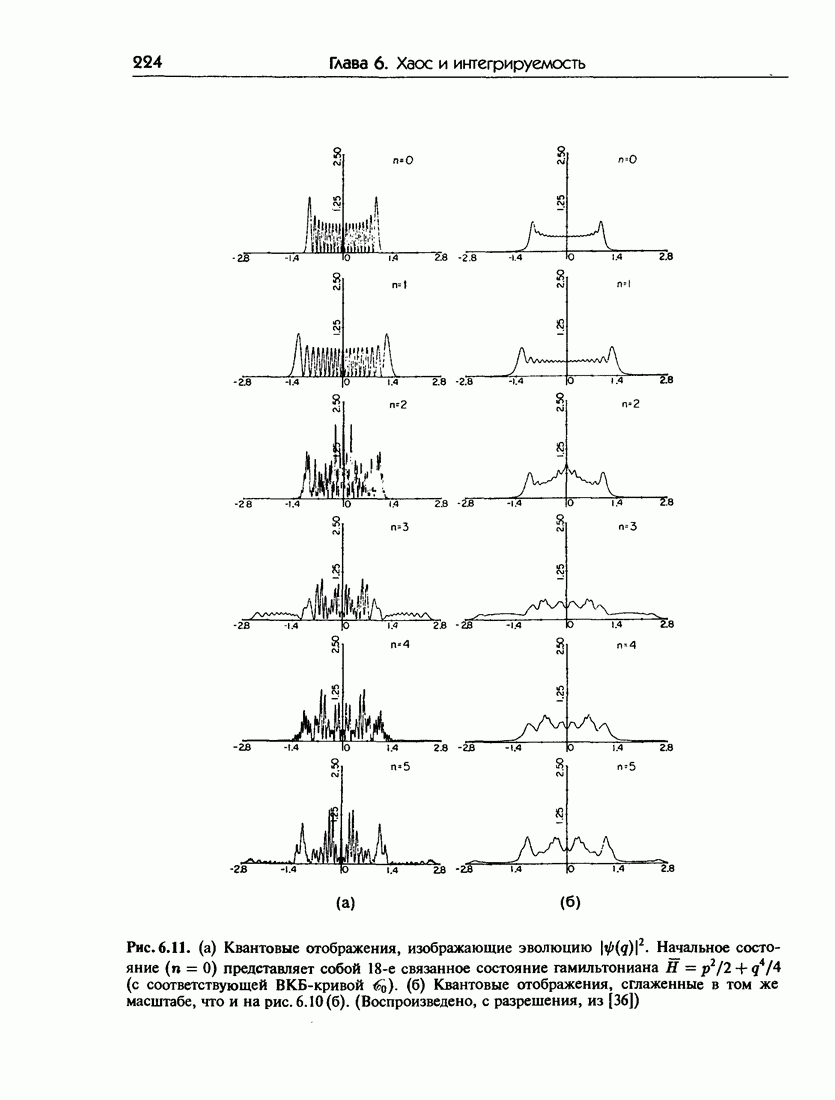
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
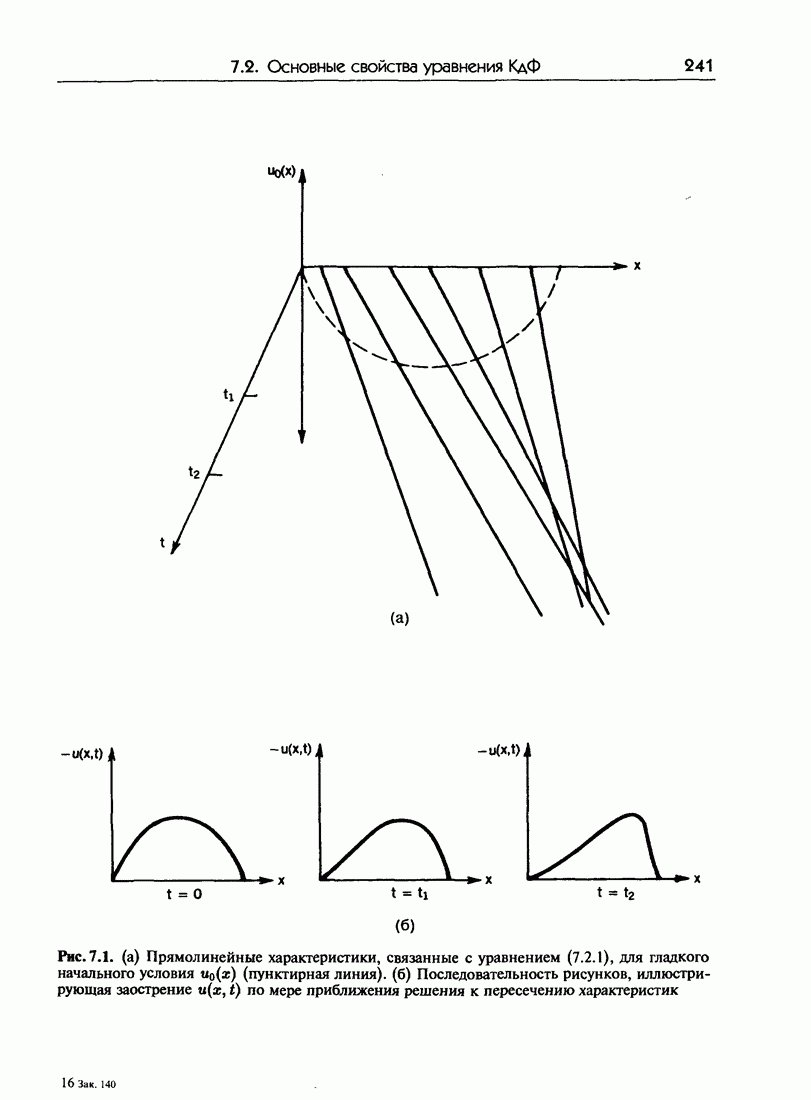
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
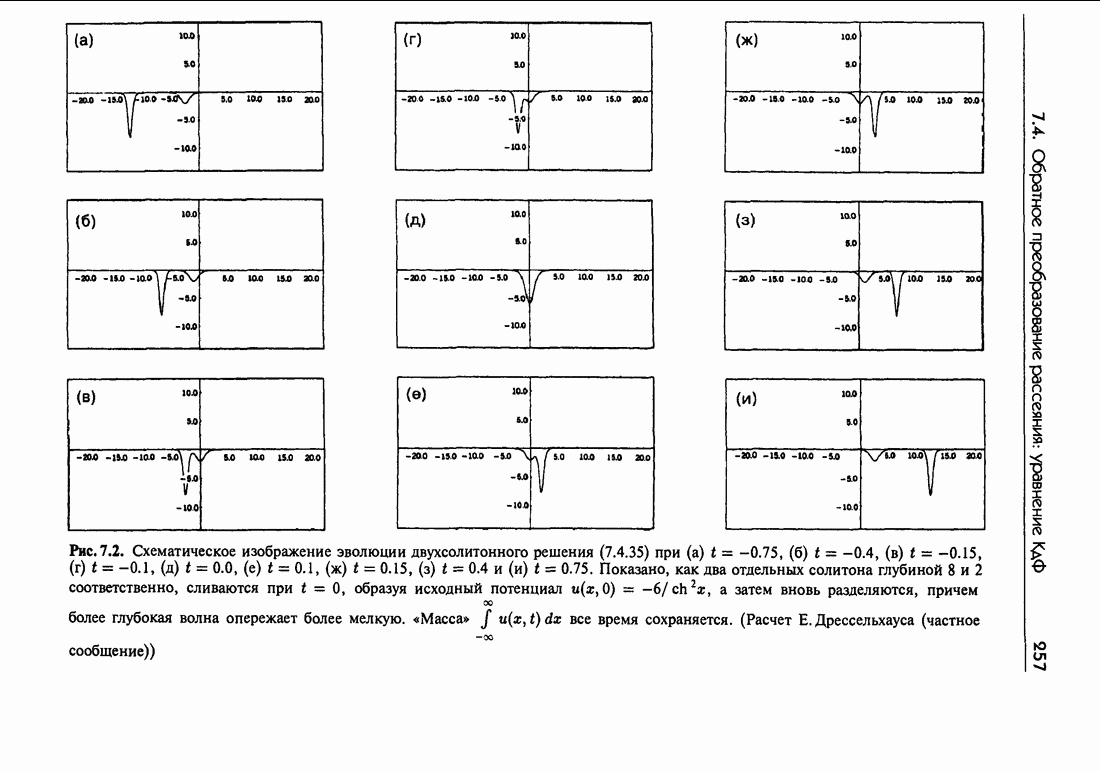
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
- 7.5. Другие солитонные системы
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
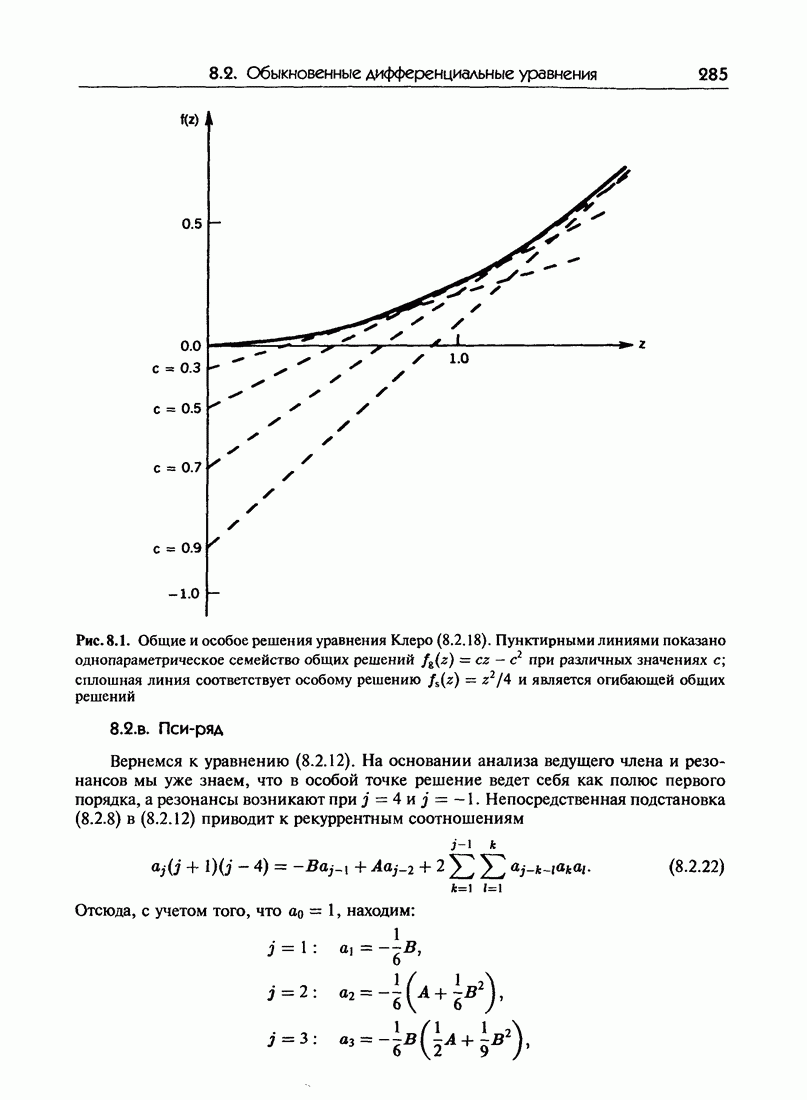
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда