| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
4.5. Критерии локального хаоса
4.5.а. Показатели Ляпунова
Важная особенность хаотического движения — чрезвычайная чувствительность к малым изменениям в начальных условиях. Близко расположенные траектории экспоненциально разбегаются во времени в отличие от регулярных траекторий, которые разбегаются лишь линейно. (Отметим, что такое разбегание не может, безусловно, продолжаться бесконечно в ограниченном фазовом пространстве.) Точная количественная оценка скорости разбегания может быть дана в терминах показателей Ляпунова, которые служат мерой средней скорости экспоненциального разбегания соседних траекторий. Показатели Ляпунова чрезвычайно полезны при описании
динамических систем, и возможность их использования ни коим образом не ограничивается гамильтоновыми системами, рассматриваемыми в этой главе. Поэтому, чтобы не утрачивать общность рассуждений, мы будем рассматривать некоторую (автономную) систему, описываемую дифференциальными уравнениями 

При изучении устойчивости данной неподвижной точки мы подвергали линеаризации уравнения движения в окрестности этой точки. Теперь мы будем линеаризовать уравнения движения в окрестности произвольной базовой траектории  с целью получить касательное отображение:
с целью получить касательное отображение:

Норма

задает меру разбегания двух соседних траекторий, т. е. базовой траектории х и соседней с ней траектории, имеющей начальные условия  Средняя скорость экспоненциального разбегания определяется следующим образом:
Средняя скорость экспоненциального разбегания определяется следующим образом:

где  Помимо этого, можно показать (пояснения будут даны ниже), что существует набор из
Помимо этого, можно показать (пояснения будут даны ниже), что существует набор из  таких величин
таких величин  Эти величины называются характеристическими показателями Ляпунова и могут быть упорядочены:
Эти величины называются характеристическими показателями Ляпунова и могут быть упорядочены:

В случае регулярного движения показатели равны нулю, поскольку  возрастает со временем лишь линейно (либо алгебраически).
возрастает со временем лишь линейно (либо алгебраически).
Чтобы лучше понять обсуждаемые идеи, целесообразно прежде всего рассмотреть показатели Ляпунова для отображений. Простейший возможный случай — одномерное отображение вида

где  некоторая простая нелинейная функция х, например,
некоторая простая нелинейная функция х, например,  Замечательные динамические свойства такого отображения будут более подробно описаны в главе 5. Касательное отображение имеет простой вид
Замечательные динамические свойства такого отображения будут более подробно описаны в главе 5. Касательное отображение имеет простой вид

где  производная от
производная от  вычисляемая в каждой точке
вычисляемая в каждой точке  вдоль данной траектории. Соответствующий показатель Ляпунова легко находится по аналогии с (4.5.3):
вдоль данной траектории. Соответствующий показатель Ляпунова легко находится по аналогии с (4.5.3):

Показатель а не зависит от начальной точки  (кроме множества меры ноль начальных условий). Читателю, вероятно, не составит труда проверить для случая
(кроме множества меры ноль начальных условий). Читателю, вероятно, не составит труда проверить для случая  что
что 
В случае многомерных отображений

где  -мерные векторы, имеется набор из
-мерные векторы, имеется набор из  характеристических показателей, соответствующих
характеристических показателей, соответствующих  собственным значениям соответствующего касательного отображения. Вводя в рассмотрение собственные значения
собственным значениям соответствующего касательного отображения. Вводя в рассмотрение собственные значения  матрицы
матрицы

где  линеаризация
линеаризация  в точке
в точке  показатели можно определить в виде
показатели можно определить в виде

Должно быть понятно, что в случае сохраняющих площадь отображений и гамильтоновых потоков сумма показателей должна равняться нулю, что гарантирует сохранение фазового объема.
Теперь вернемся к случаю потоков, описываемых уравнениями (4.5.1), и запишем (4.5.2) в векторном виде:

где  и
и  линеаризованная матрица с элементами
линеаризованная матрица с элементами  Должен существовать такой набор базисных векторов
Должен существовать такой набор базисных векторов  что
что  Скорости растяжения (или сжатия) в каждом из направлений
Скорости растяжения (или сжатия) в каждом из направлений  задают набор показателей
задают набор показателей  которые могут быть упорядочены так же, как в (4.5.5). Понятно, что с течением времени малый элемент объема будет в наибольшей степени растянут в том направлении
которые могут быть упорядочены так же, как в (4.5.5). Понятно, что с течением времени малый элемент объема будет в наибольшей степени растянут в том направлении  которому соответствует наибольший показатель. В конкретном случае (4.5.4) будет давать именно это значение показателя
которому соответствует наибольший показатель. В конкретном случае (4.5.4) будет давать именно это значение показателя  согласно
согласно  В случае гамильтоновых систем с
В случае гамильтоновых систем с  степенями свободы вектор
степенями свободы вектор  становится
становится  -мерным
-мерным  соответственно, показателей будет
соответственно, показателей будет  штук. Но при этом они обладают определенной симметрией, а именно
штук. Но при этом они обладают определенной симметрией, а именно

То есть любое растяжение в одном «направлении» компенсируется сжатием в другом, что и обеспечивает выполнение теоремы Лиувилля. Если же показатели вычисляются на заданной энергетической поверхности, то пространство имеет размерность  . При этом из (4.5.12) следует, что два (или более, в зависимости от динамики) показателя
. При этом из (4.5.12) следует, что два (или более, в зависимости от динамики) показателя  должны равняться нулю.
должны равняться нулю.
Расчет показателей в случае  -мерных потоков (в отличие от отображений) нетривиален. Рассмотрим, например, вычисления в соответствии с определением (4.5.4). Если норма
-мерных потоков (в отличие от отображений) нетривиален. Рассмотрим, например, вычисления в соответствии с определением (4.5.4). Если норма  возрастает экспоненциально, возникает опасность переполнения компьютера и связанных с этим ошибок. Чтобы избежать этого, можно использовать схему, предложенную Бенеттин с соавт. [19]. Исходная норма
возрастает экспоненциально, возникает опасность переполнения компьютера и связанных с этим ошибок. Чтобы избежать этого, можно использовать схему, предложенную Бенеттин с соавт. [19]. Исходная норма  в этом методе нормируется на единицу, и производится расчет разбегания за некоторый период времени
в этом методе нормируется на единицу, и производится расчет разбегания за некоторый период времени  после чего норма вновь перенормируется на единицу.
после чего норма вновь перенормируется на единицу.
Таким образом (см. рис. 4.24) вычисляется последовательность величин

Здесь  означает евклидову норму и
означает евклидову норму и

где  рассчитывается из (4.5.2) с начальными значениями
рассчитывается из (4.5.2) с начальными значениями  вдоль базовой траектории х от
вдоль базовой траектории х от  до
до  По аналогии с (4.5.4) можно определить
По аналогии с (4.5.4) можно определить

Более того, для не слишком больших  можно показать, что предел
можно показать, что предел  существует и не зависит от
существует и не зависит от  Действительно, может быть показано, что
Действительно, может быть показано, что

где  наибольший показатель из набора (4.5.5). Расчет полного спектра показателей Ляпунова а...
наибольший показатель из набора (4.5.5). Расчет полного спектра показателей Ляпунова а...  требует более изощренных методов; обсуждение этого важного вопроса лучше оставить специалистам (см. [20]).
требует более изощренных методов; обсуждение этого важного вопроса лучше оставить специалистам (см. [20]).

Рис. 4.24. Расчет наибольшего показателя Ляпунова. В конце каждого периода расстояние от базовой траектории вновь приводится к 
Существует величина, так называемая энтропия Колмогорова (КС-энтропия), которая связана с показателями Ляпунова, но гораздо труднее вычисляется на практике. Формально она определяется по аналогии с энтропией в статистической механике (т. е. учитывает разбиения фазового пространства и т. д.) и служит мерой количества информации, потерянной или приобретенной системой в ходе эволюции. Замечательный результат Песина [21] дает возможность рассчитывать энтропию Колмогорова, исходя из показателей Ляпунова посредством соотношения

которое представляет собой сумму всех положительных показателей Ляпунова, усредненную по некоторой (связной) области фазового пространства  с мерой
с мерой  Очень ясное введение в круг этих идей, включающее расчет
Очень ясное введение в круг этих идей, включающее расчет  для системы Хенона—Хейлеса, было дано Бенеттин с соавторами [19].
для системы Хенона—Хейлеса, было дано Бенеттин с соавторами [19].
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
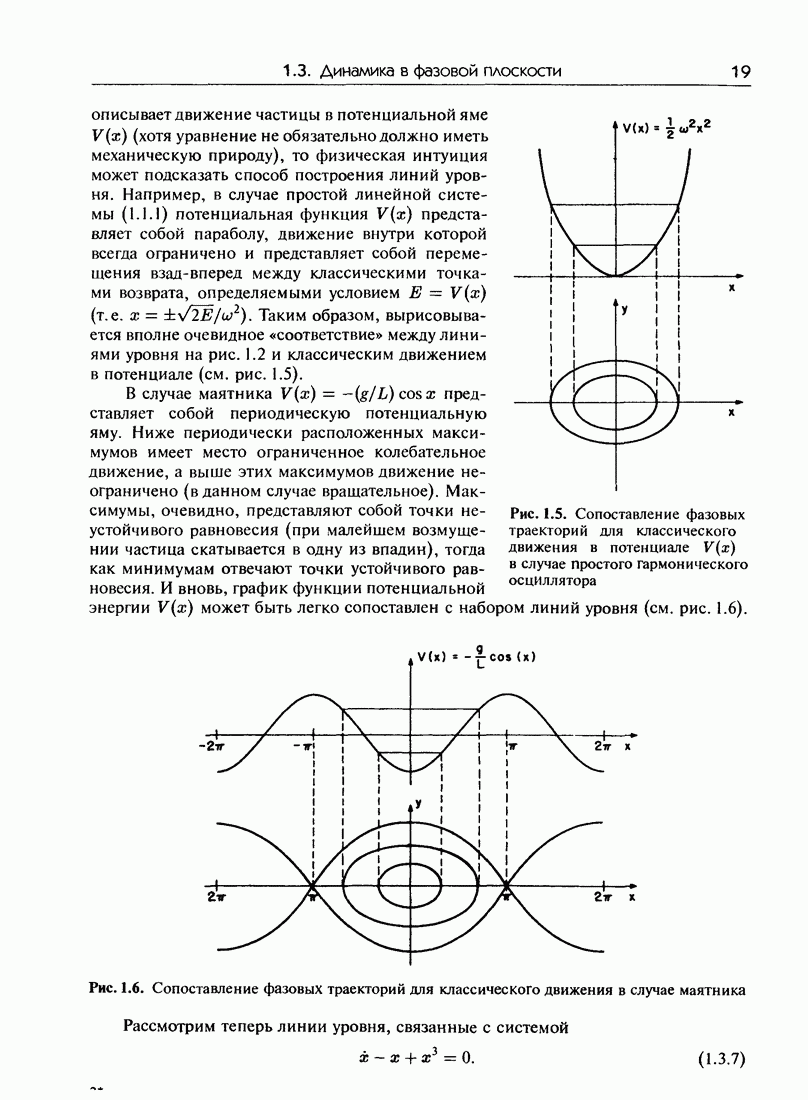
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
- 1.3.б. фазовые портреты консервативных систем
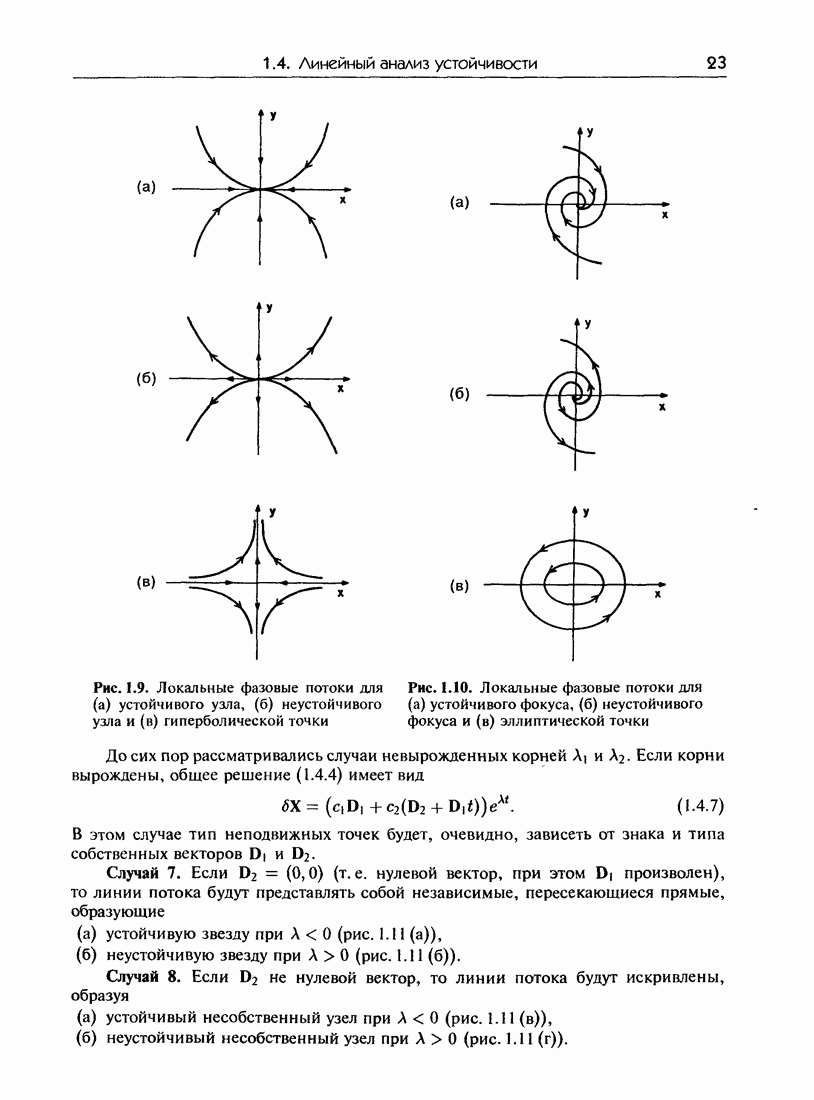
- 1.4. Линейный анализ устойчивости
- 1.4.б. Классификация неподвижных точек
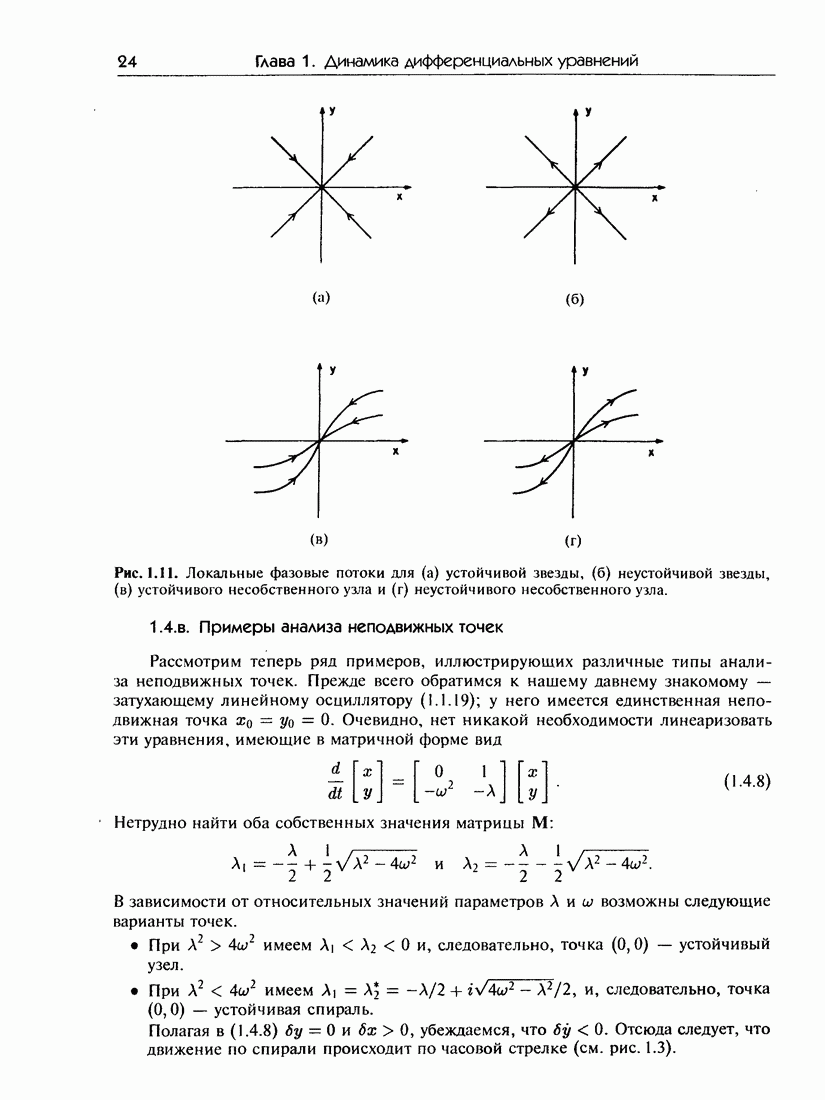
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
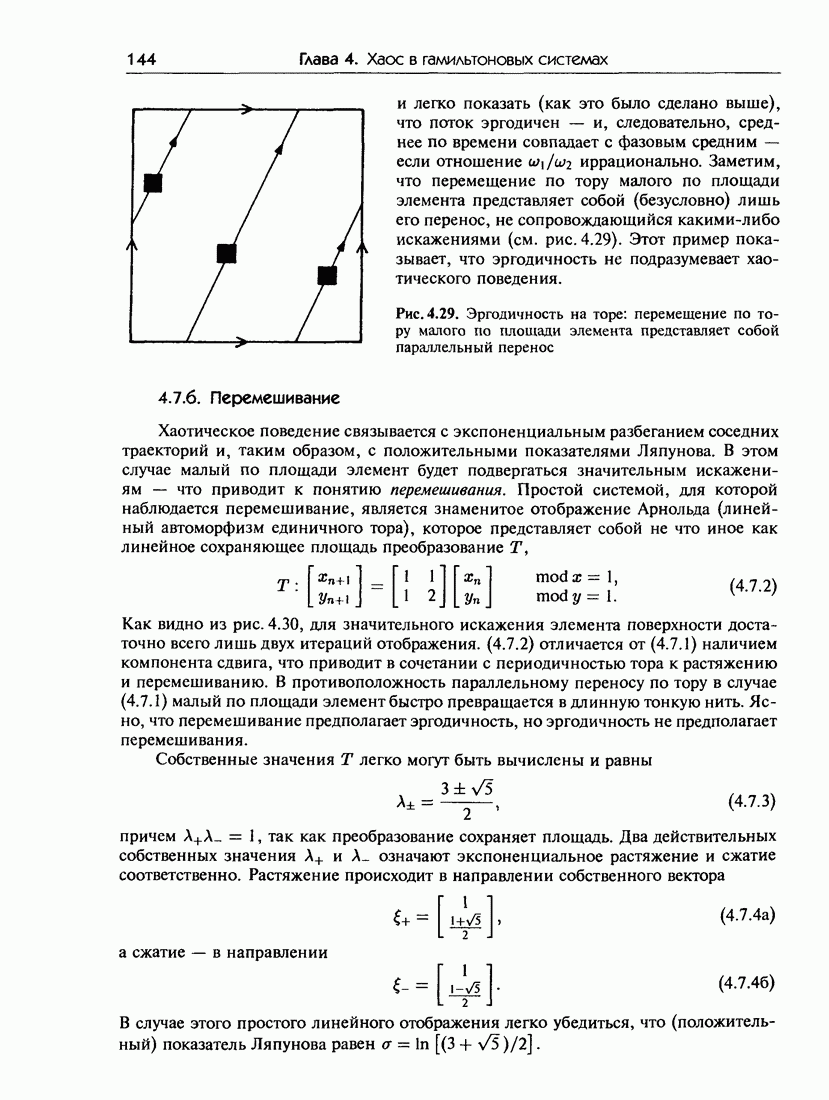
- 4.7.б. Перемешивание
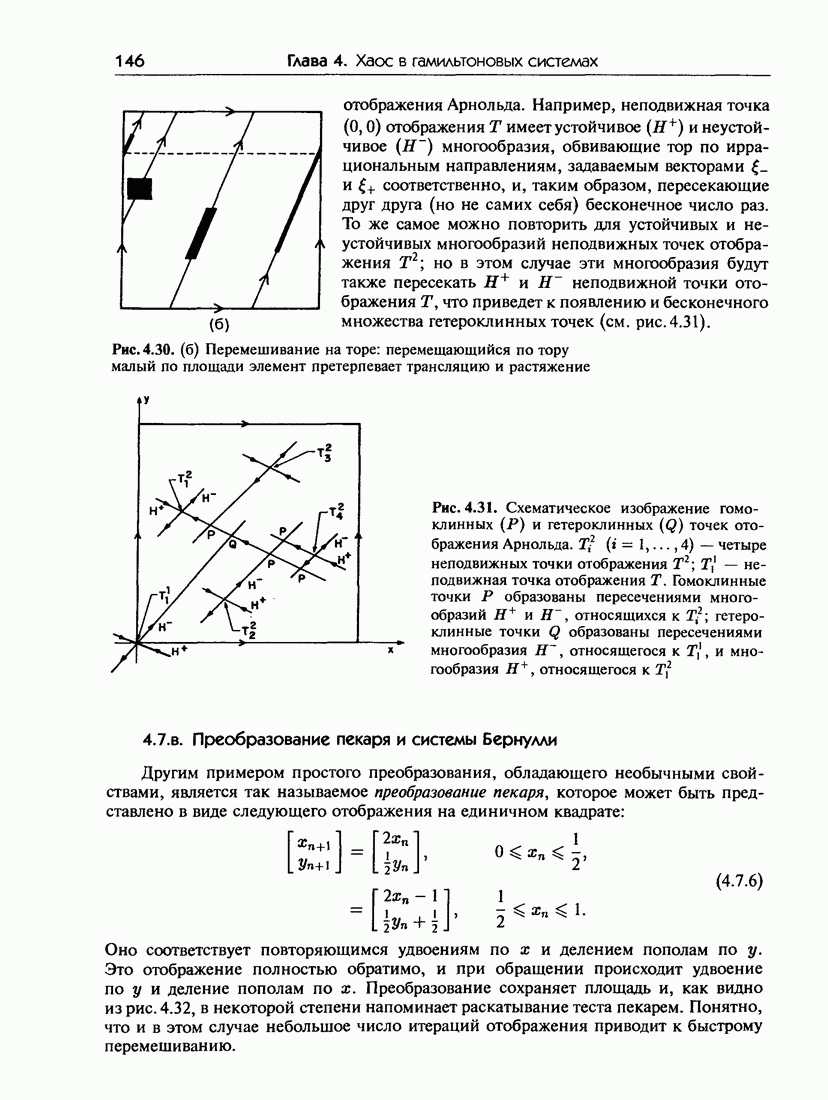
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
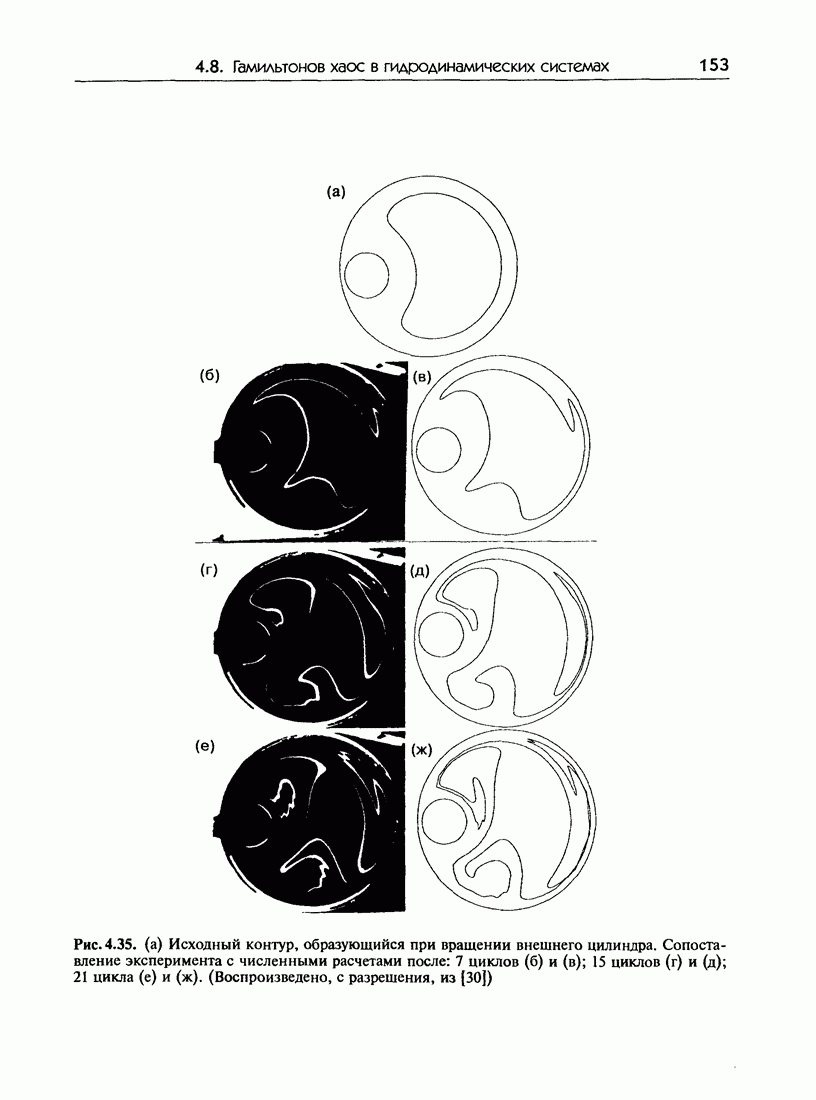
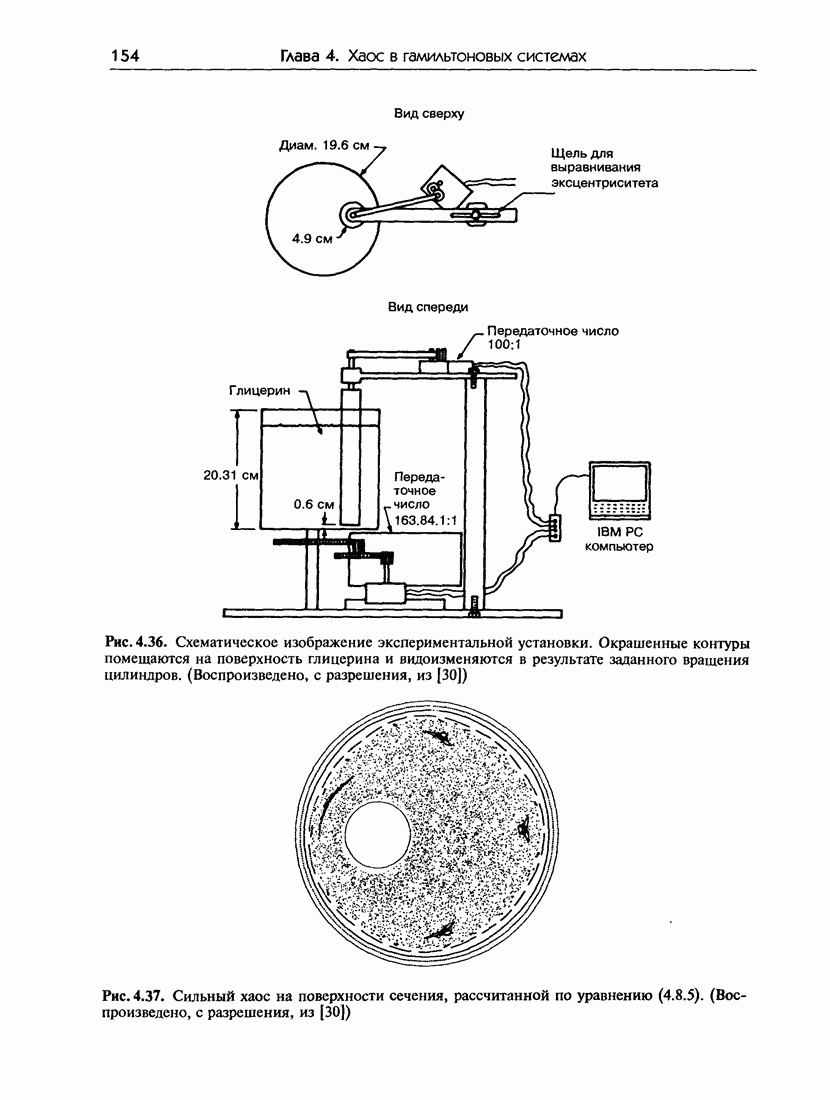
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
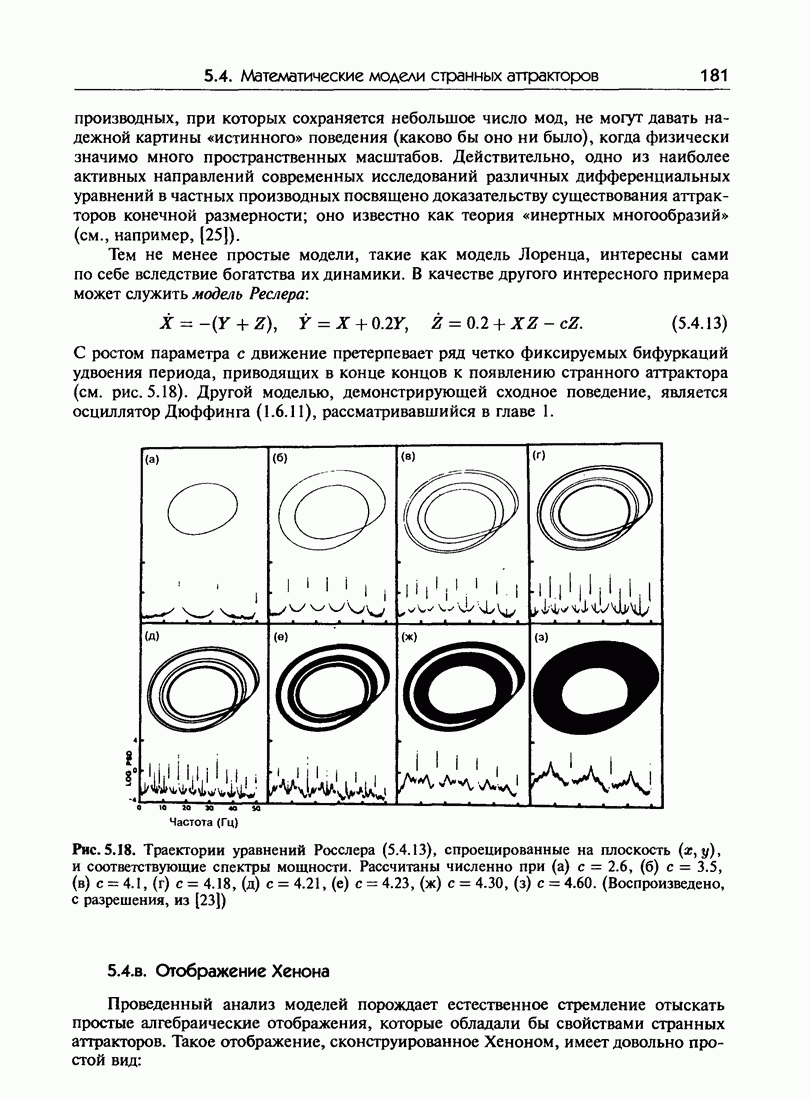
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
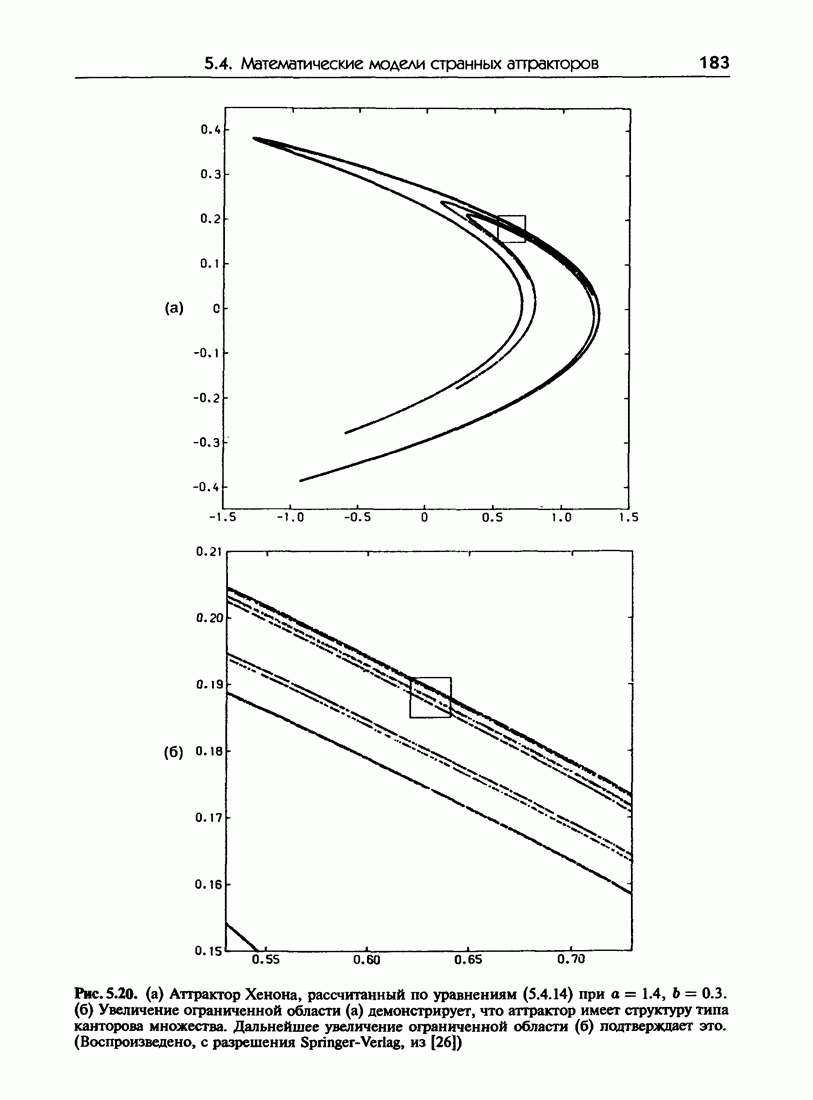
- 5.4.в. Отображение Хенона
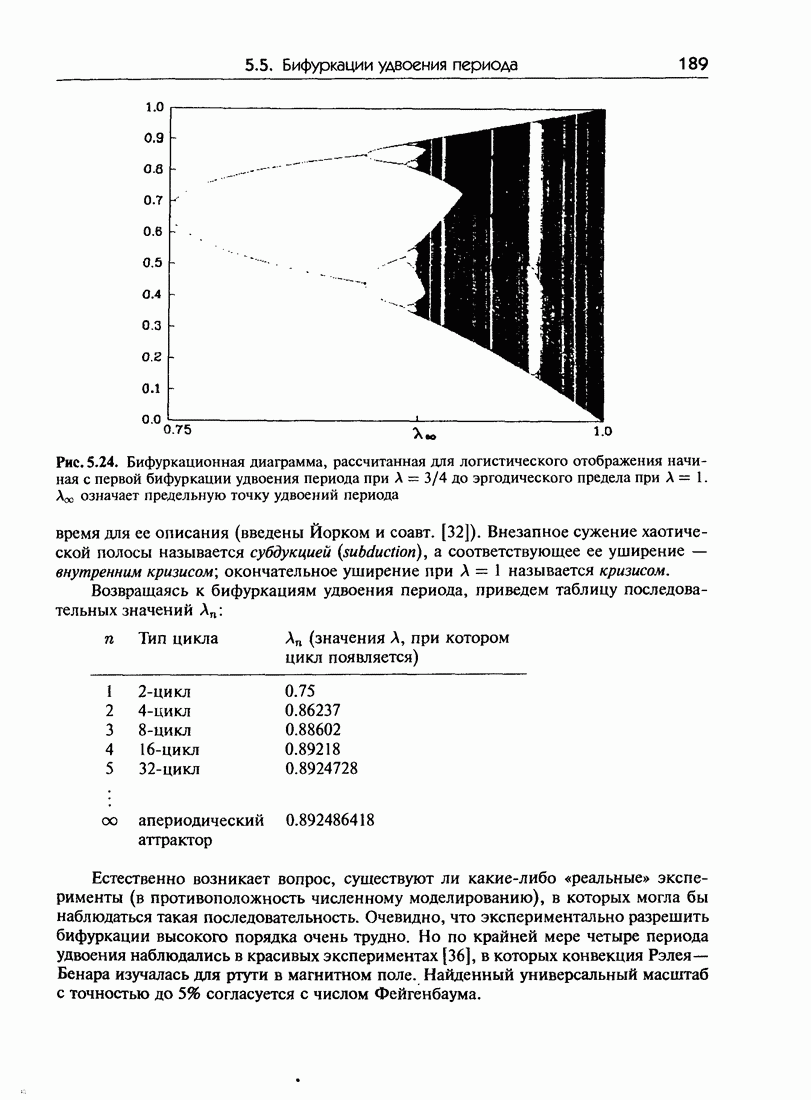
- 5.5. Бифуркации удвоения периода
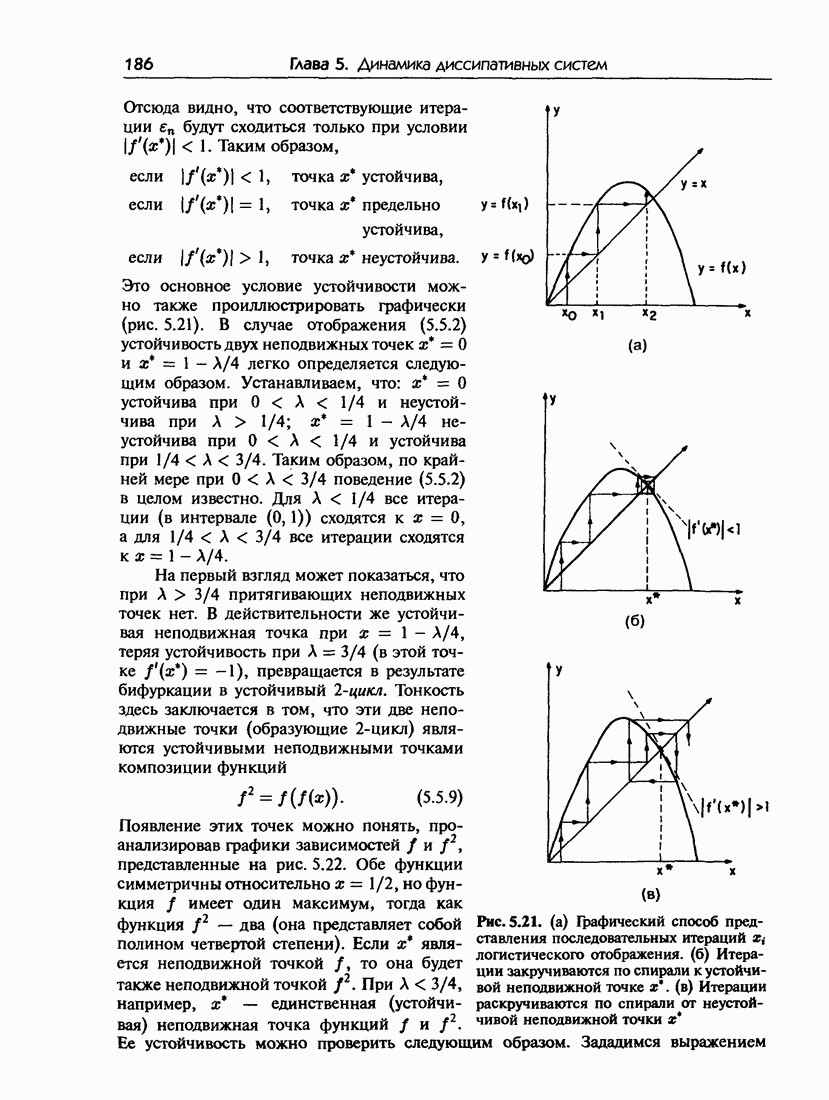
- 5.5.а. Механизм удвоения периода
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
- 5.5.г. Другие классы универсальности
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
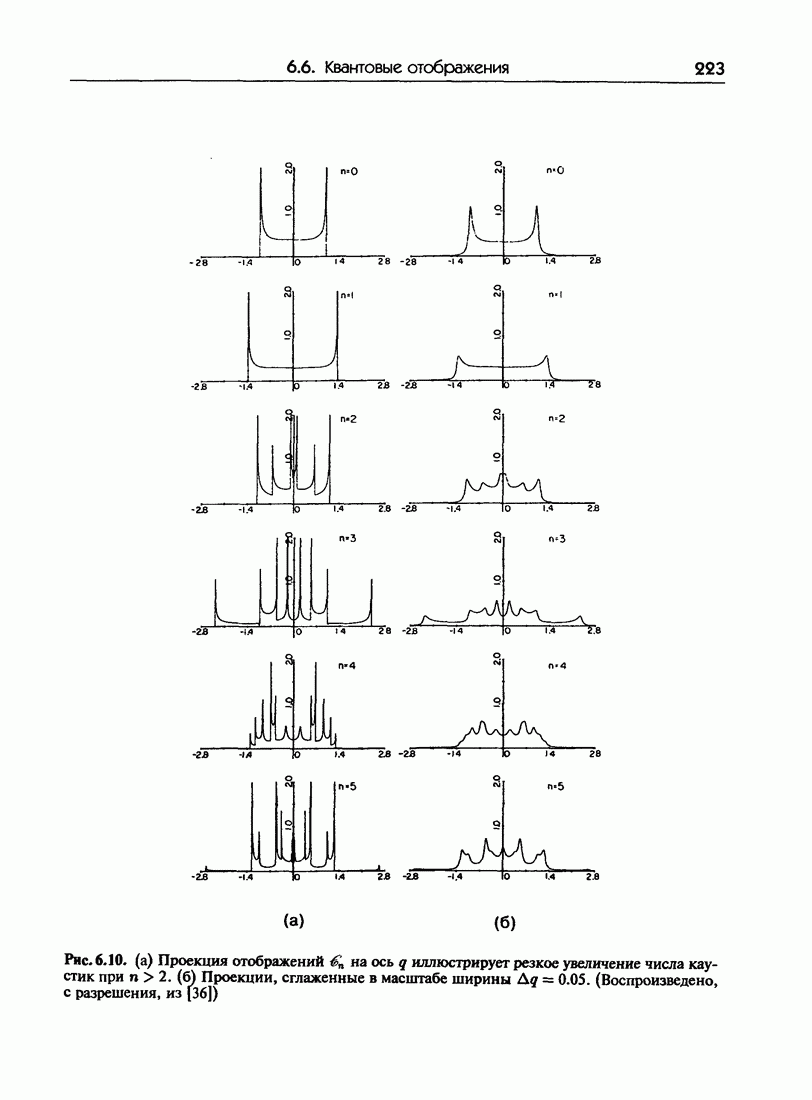
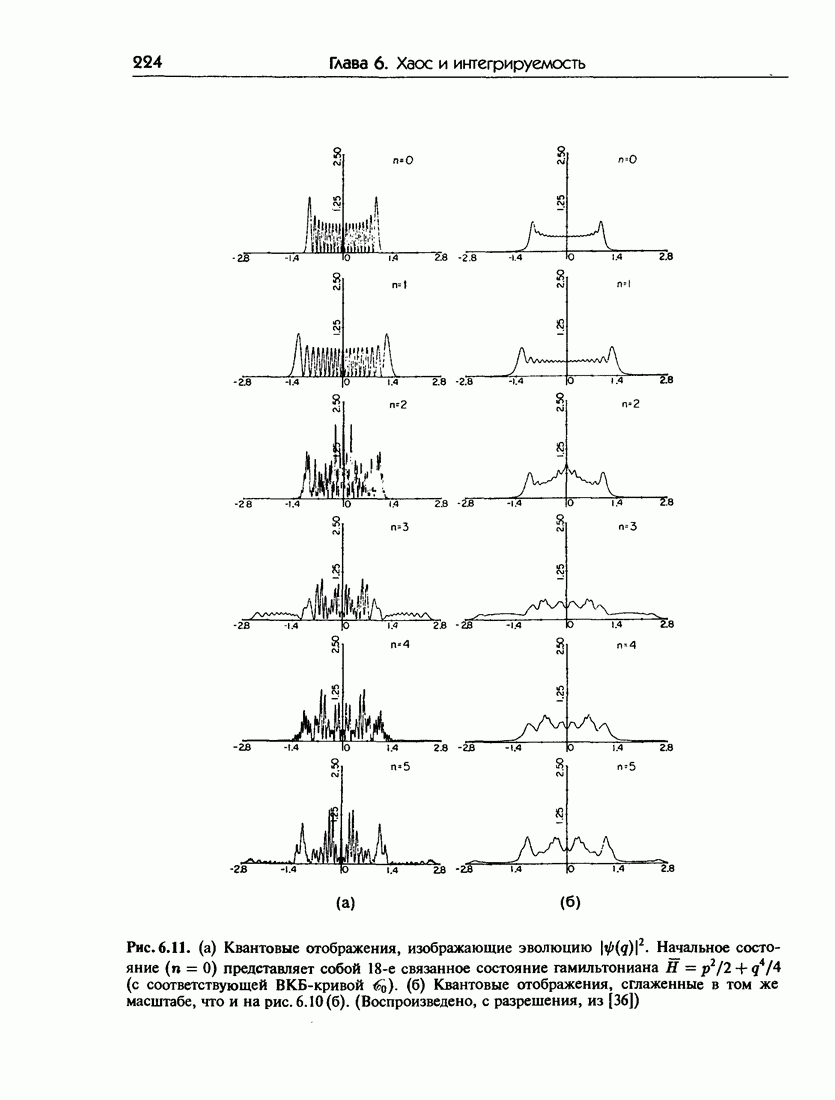
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
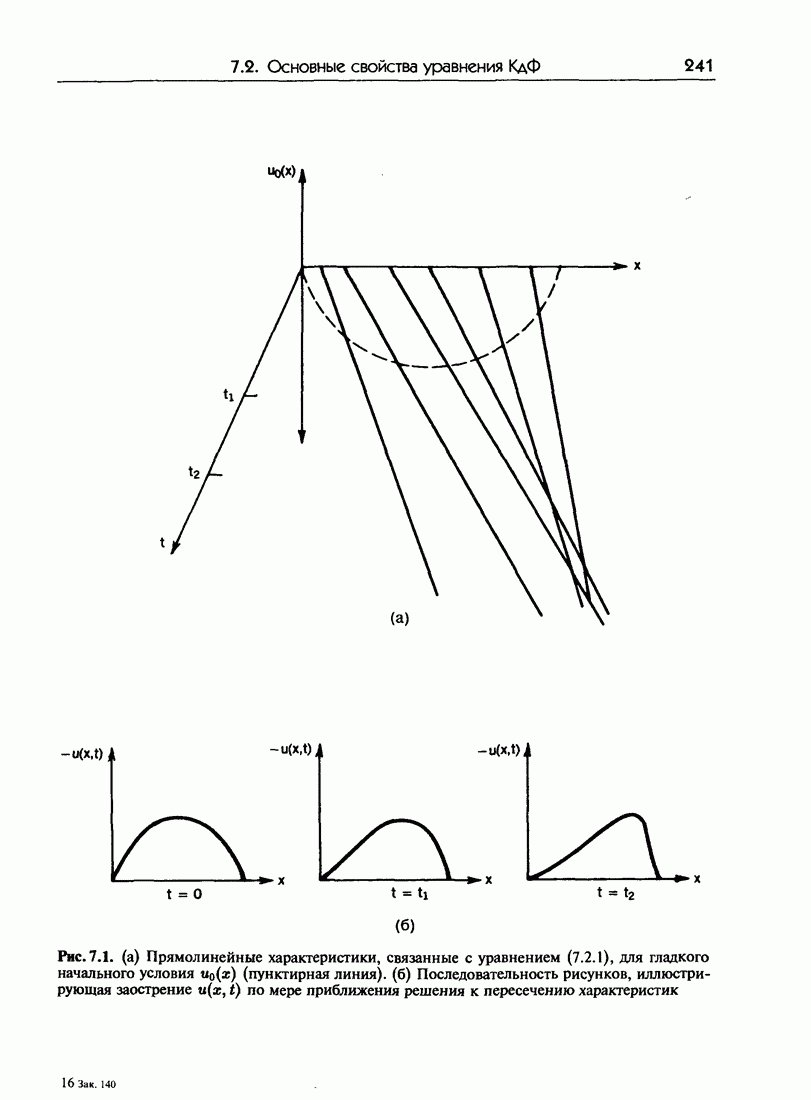
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
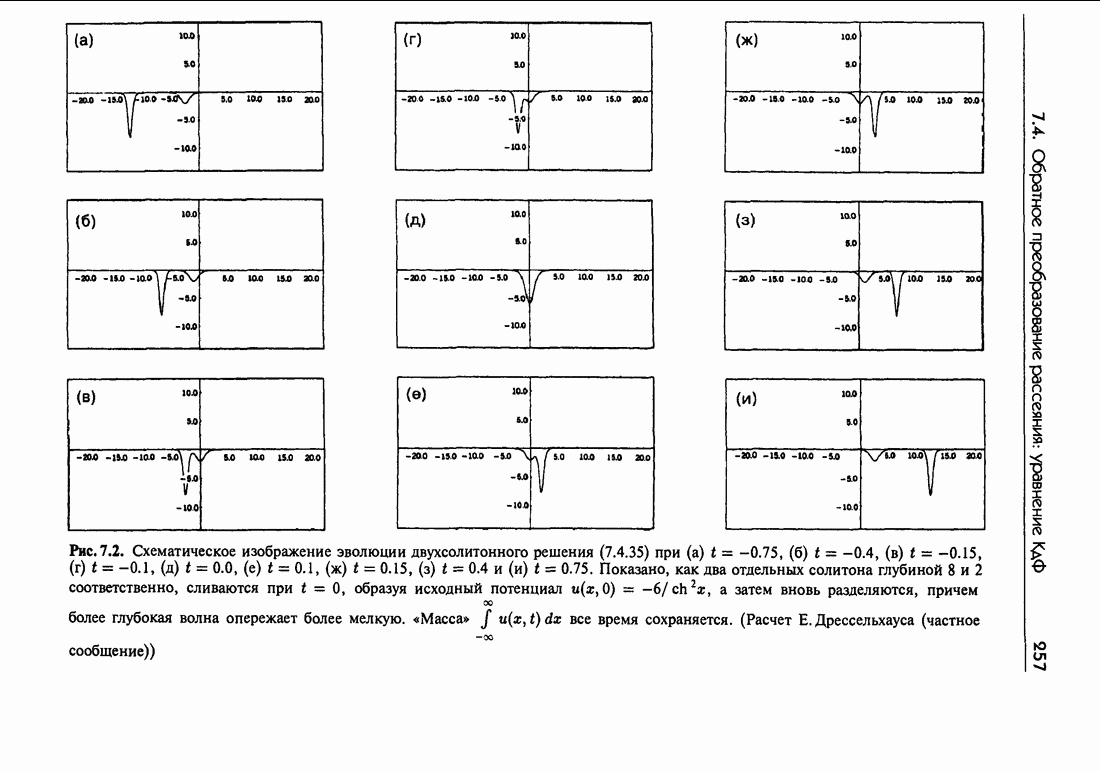
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
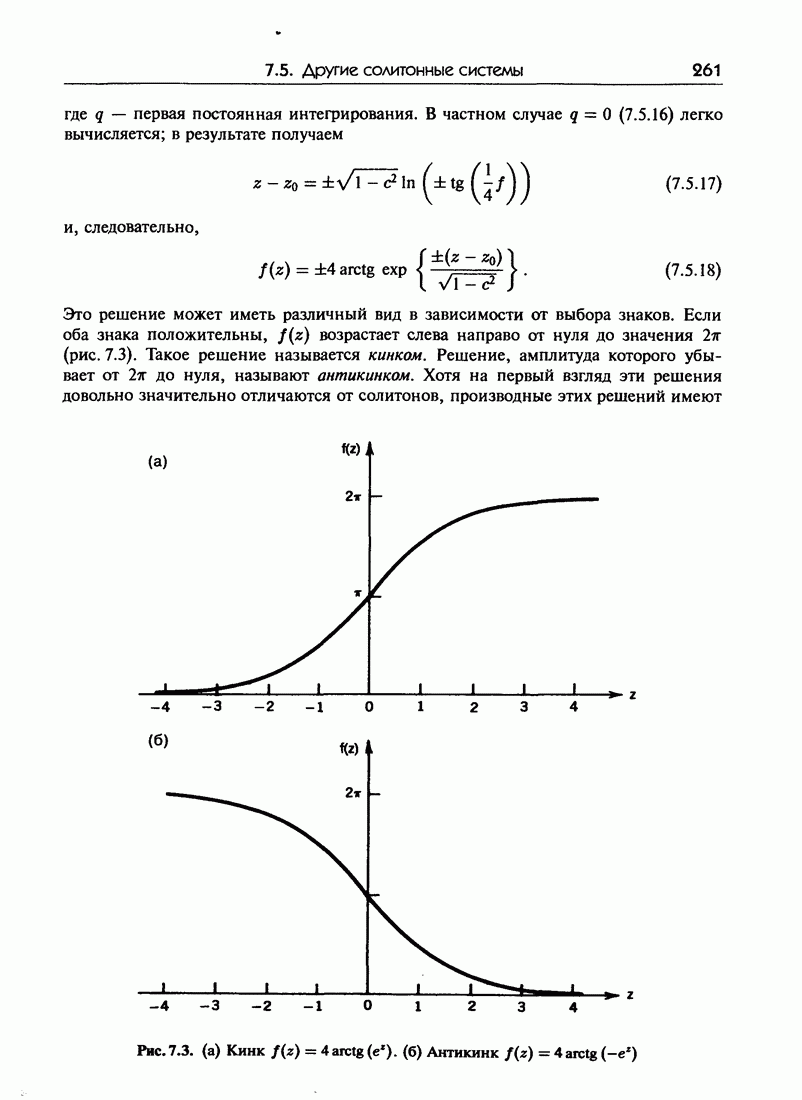
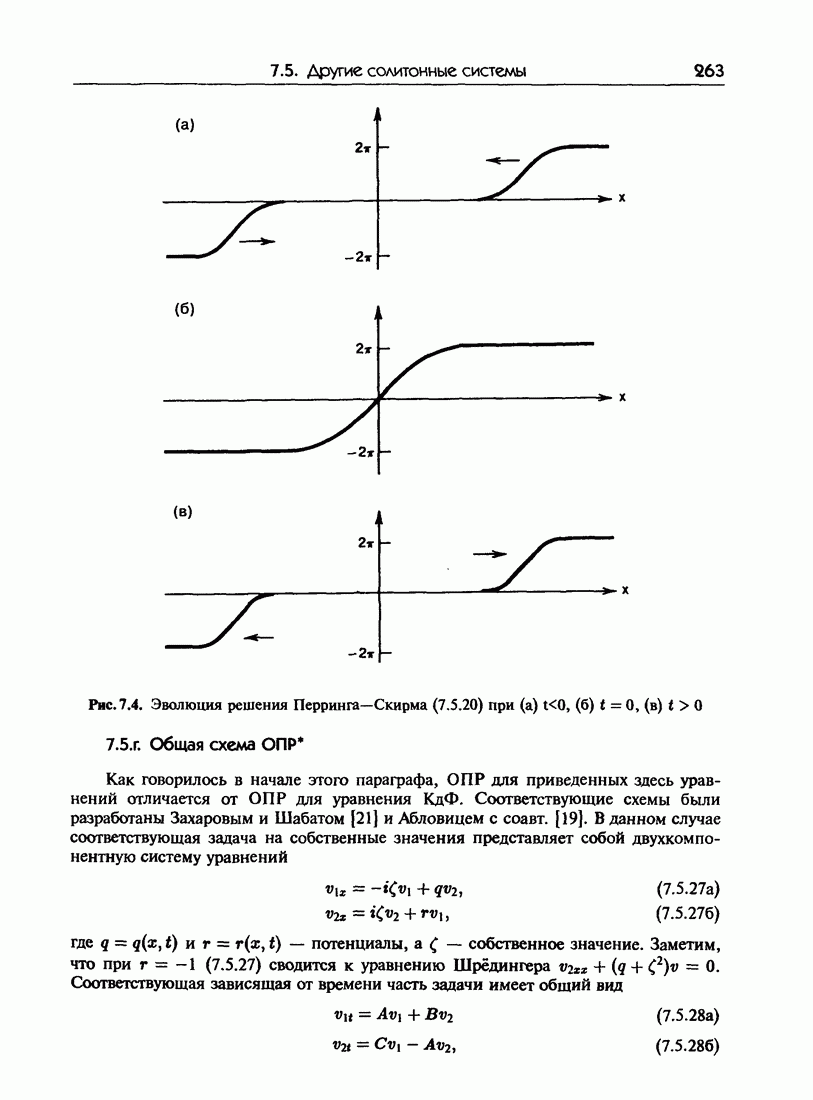
- 7.5. Другие солитонные системы
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
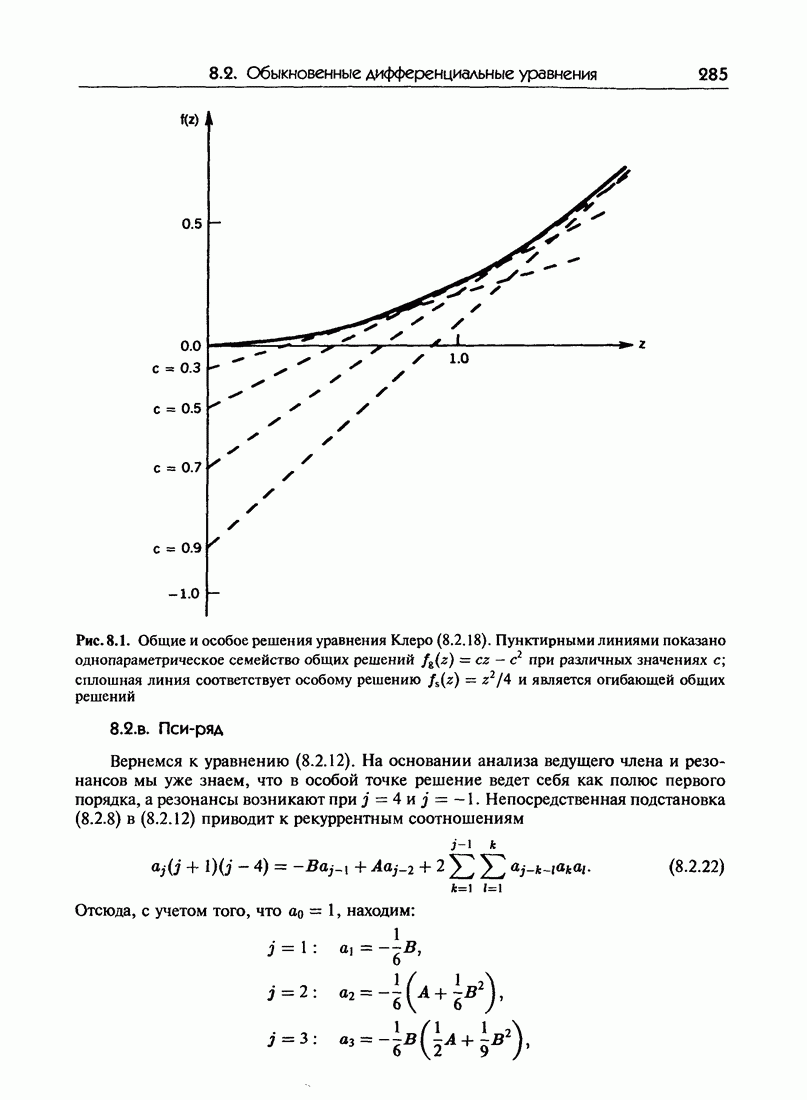
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда