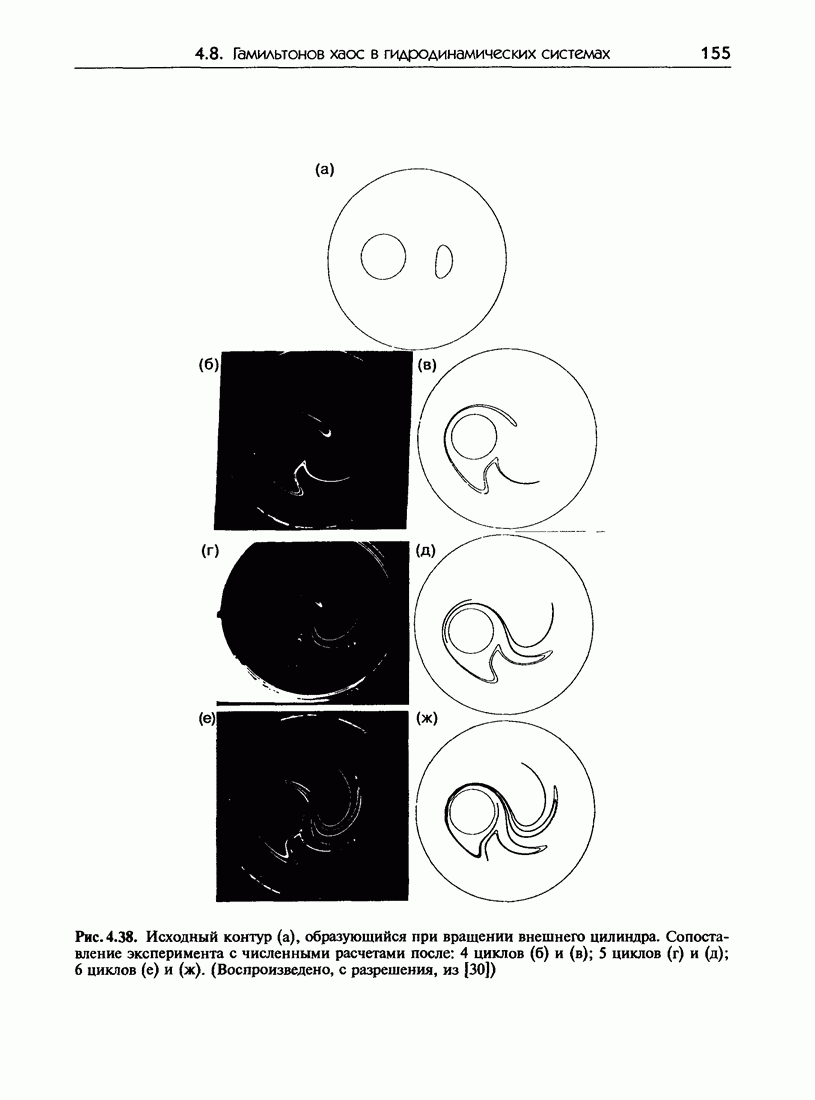
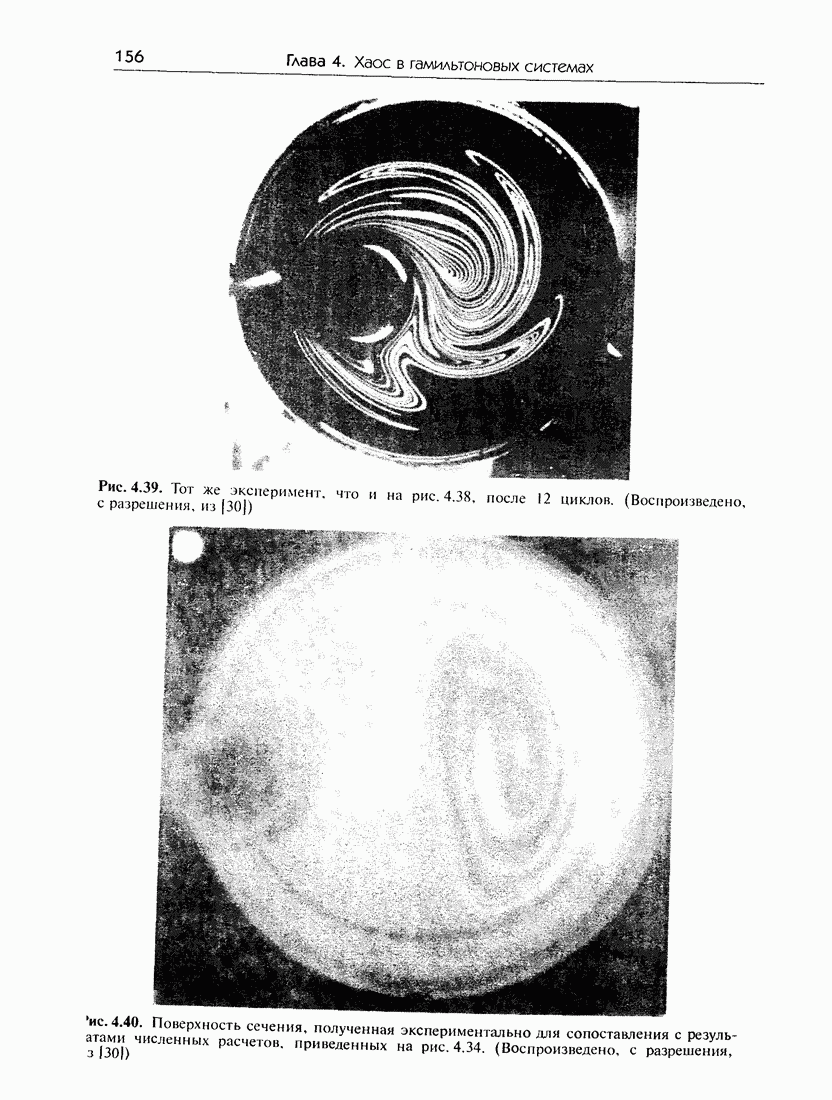
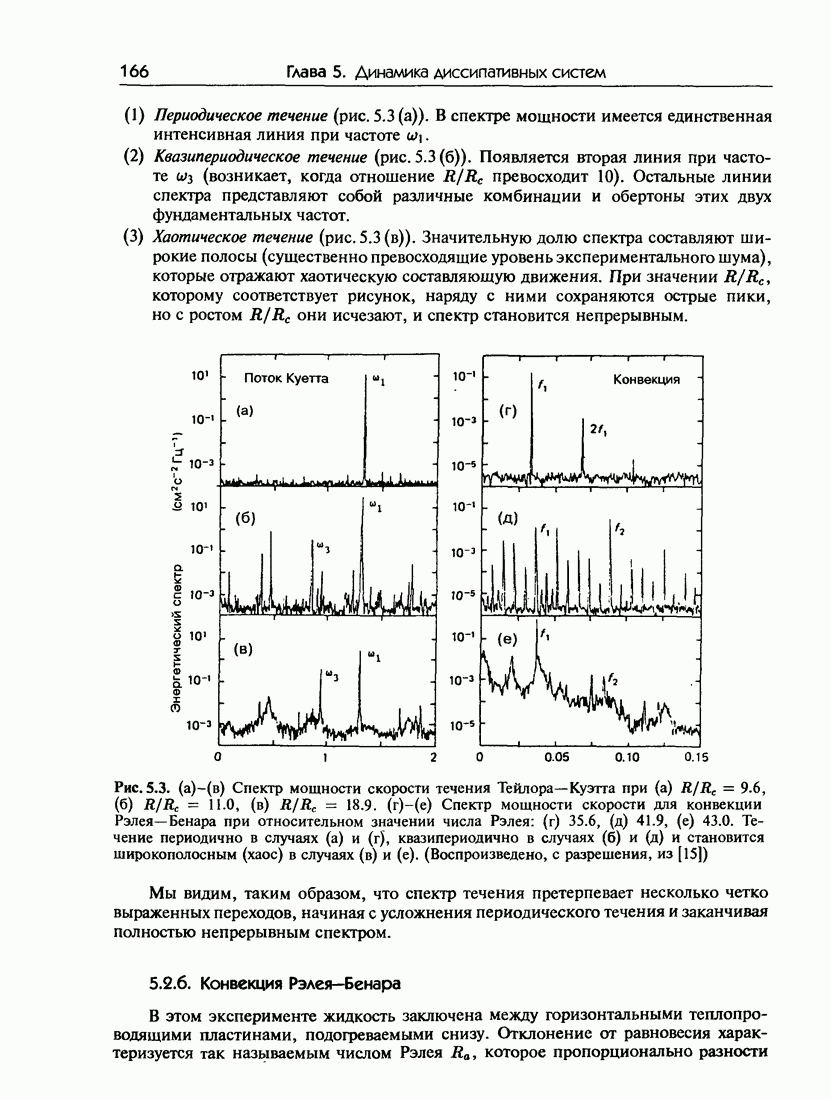
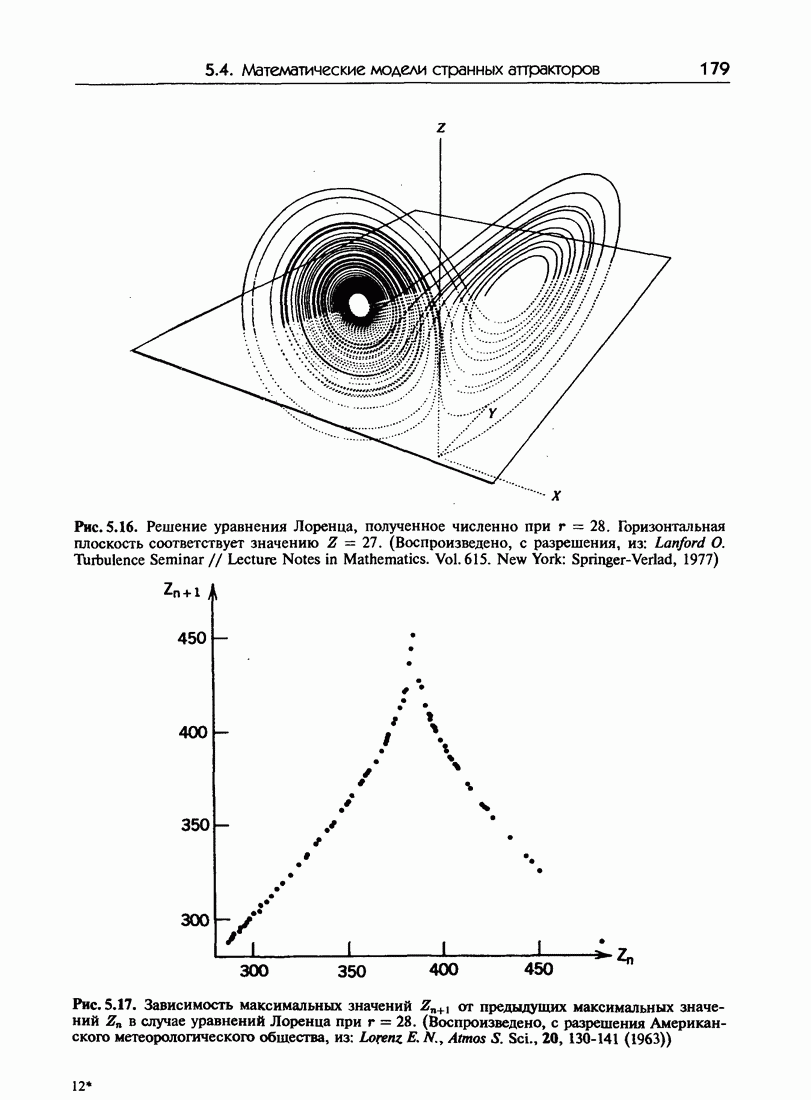
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
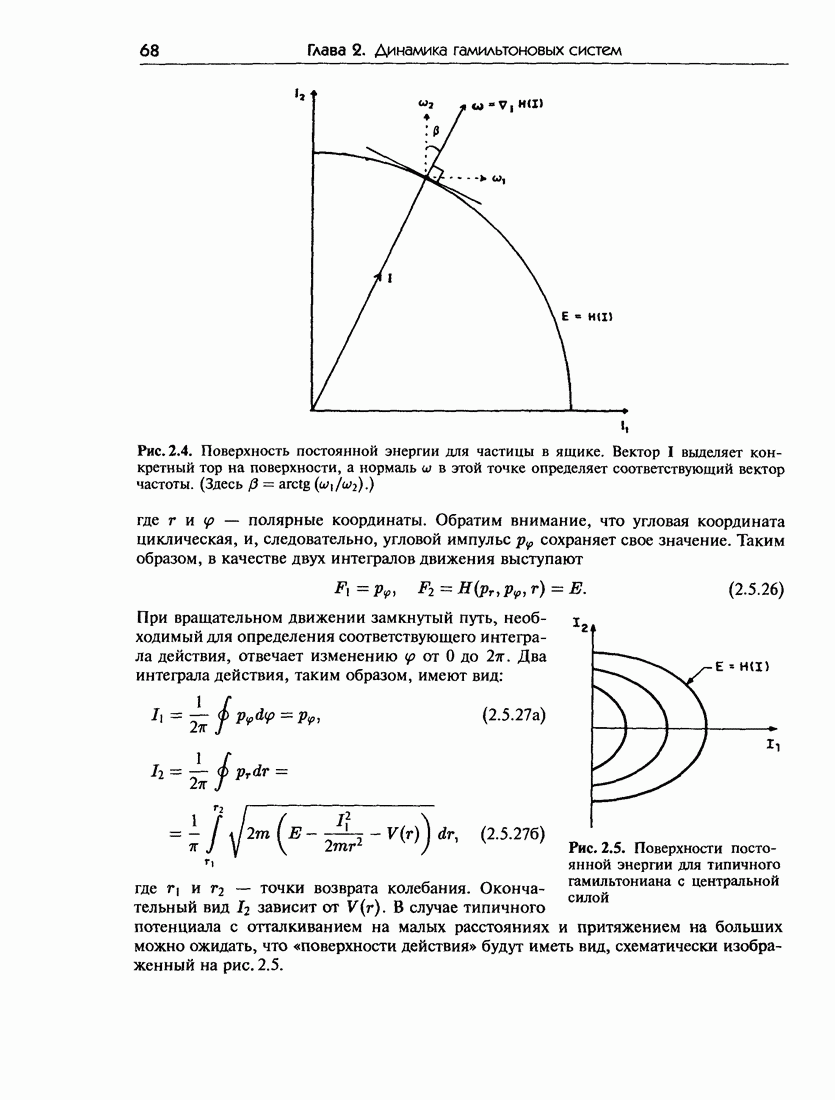
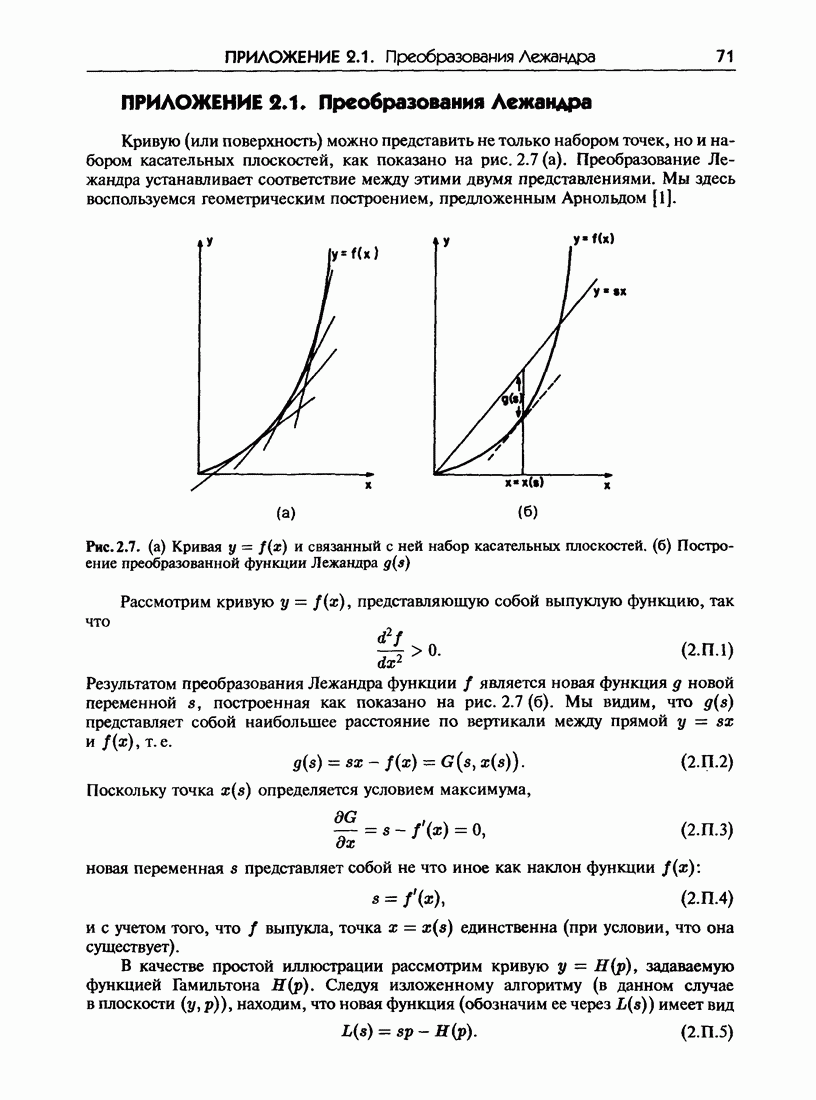
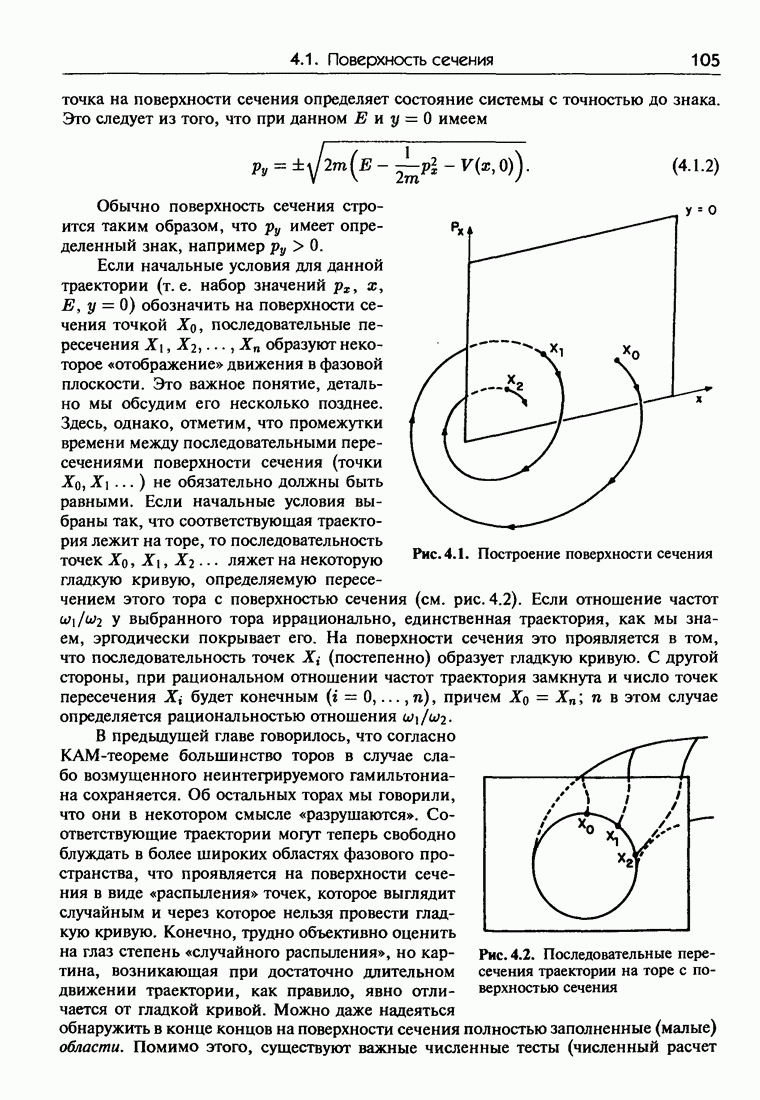
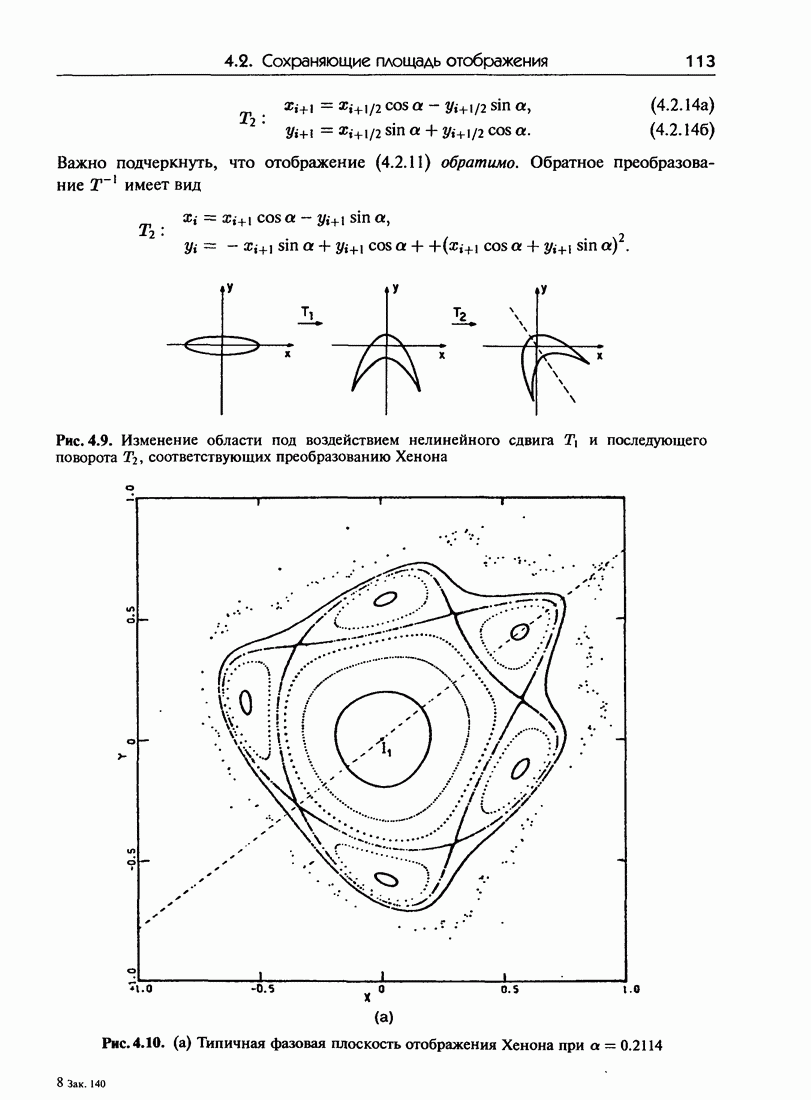
7.6. Гамильтонова структура интегрируемых систем
Одним из важнейших свойств солитонных уравнений является то, что они представляют собой интегрируемые гамильтоновы системы. Здесь мы дадим лишь беглый обзор этого факта, который, в свою очередь, поможет установить связь между свойствами систем с конечными степенями свободы, описанными в главах 2 и 3, и их непрерывными аналогами, которые будут обсуждаться в настоящей главе.
7.6.а. Функциональная производная
Для дальнейшего анализа нам понадобится такое важное математическое понятие как вариация или вариационная производная, получить представление о котором совсем нетрудно, если вспомнить вариационный принцип, описанный в главе 2. Рассмотрим некоторый функционал  вида
вида

где  является некоторой функцией от
является некоторой функцией от  и (здесь
и (здесь  Очевидным примером функционала (7.6.1) является функционал действия, в котором роль
Очевидным примером функционала (7.6.1) является функционал действия, в котором роль  играет лагранжиан, а роль
играет лагранжиан, а роль  координата
координата  Обычная производная (скажем, некоторой функции
Обычная производная (скажем, некоторой функции  определятся как результат придания аргументу функции малого приращения, т.е.
определятся как результат придания аргументу функции малого приращения, т.е.  Вариационная производная отражает эффект малой вариации функции
Вариационная производная отражает эффект малой вариации функции  т.е.
т.е.  входящей в
входящей в  . Соответственно, мы можем вычислить первую вариацию функционала
. Соответственно, мы можем вычислить первую вариацию функционала  обычным способом, полагая
обычным способом, полагая

где подразумевается, что вариация  обращается в нуль в конечных точках
обращается в нуль в конечных точках  Разлагая подынтегральное выражение в первом слагаемом с точностью до первого порядка по
Разлагая подынтегральное выражение в первом слагаемом с точностью до первого порядка по  получаем
получаем

где  Интегрируя второе слагаемое по частям (и предполагая, что
Интегрируя второе слагаемое по частям (и предполагая, что  приходим к стандартному результату
приходим к стандартному результату

Выражение, стоящее под знаком интеграла, называется вариационной производной и обозначается  Таким образом,
Таким образом,

Рассмотрим теперь более общий случай, когда  является функцией произвольного числа производных от и,
является функцией произвольного числа производных от и,

где введено обозначение  Нетрудно показать, что в данном случае вариационная производная вычисляется по формуле
Нетрудно показать, что в данном случае вариационная производная вычисляется по формуле

где чередование знаков объясняется многократным интегрированием по частям, необходимым для того, чтобы привести  к виду
к виду 
Приведем несколько простых примеров. Для функционала

получаем

а для функционала

имеем

В качестве менее тривиального примера функционала рассмотрим сохраняющуюся плотность в уравнении  т.е.
т.е.

для которой вариационная производная равняется

Таким образом, уравнение КдФ может быть записано в виде

где выражение для функционала  дается формулой (7.6.10).
дается формулой (7.6.10).
Функциональную производную можно определить и следующим образом. Рассмотрим функционал (7.6.1), в котором и является функцией также и некоторого параметра а (т. е.  так что
так что

Производная от  по а легко находится в соответствии с правилом дифференцирования сложных функций:
по а легко находится в соответствии с правилом дифференцирования сложных функций:

здесь  Интегрируя снова по частям (и считая вклад от конечных точек нулевым), приходим к следующему выражению:
Интегрируя снова по частям (и считая вклад от конечных точек нулевым), приходим к следующему выражению:

которая также может быть записана в виде

Последнее выражение, по сути, служит определением (Оно может быть очевидным образом обобщено и для случая (7.6.6).)
7.6.б. Гамильтонова структура уравнения Кортвега—де Фриза
Впервые на гамильтонова природа уравнения (7.6.12) была показана в работе Гарднера [22]. В нашем изложении мы будем следовать его подходу. При выводе решения  уравнения КдФ Гарднер предположил, что это решение является периодичным на интервале
уравнения КдФ Гарднер предположил, что это решение является периодичным на интервале  Следовательно, и может быть разложено в ряд Фурье,
Следовательно, и может быть разложено в ряд Фурье,

где  набор комплексных коэффициентов. Рассматривая заданный в (7.6.10) функционал
набор комплексных коэффициентов. Рассматривая заданный в (7.6.10) функционал  как функцию от множества «параметров» и и используя (7.6.16), получаем выражение
как функцию от множества «параметров» и и используя (7.6.16), получаем выражение

при выводе которого также было использовано разложение (7.6.17). Равенство (7.6.18) позволяет получить разложение в ряд Фурье величины  Имеем
Имеем

С учетом (7.6.12) уравнение движения для отдельной моды и принимает вид

Если при  определить переменные
определить переменные

то (7.6.20) можно представить в явно гамильтоновой форме:

Следовательно, можно определить скобки Пуассона двух функционалов  как
как 

Опираясь на формулу (7.6.19), легко показать, что (7.6.23) может быть представлено в виде

которое можно принять за определение скобок Пуассона  Несложно показать, что так определенные скобки Пуассона удовлетворяют тождеству Якоби.
Несложно показать, что так определенные скобки Пуассона удовлетворяют тождеству Якоби.
Напомним, в разделе 7.2 было показано, что уравнение КдФ обладает бесконечным числом сохраняющихся плотностей вида

где для периодических систем интегрирование ведется в пределах ( а для неограниченных систем — в пределах
а для неограниченных систем — в пределах  Ввиду того, что
Ввиду того, что  являются сохраняющимися величинами (т. е. константами движения), их скобки Пуассона с гамильтонианом
являются сохраняющимися величинами (т. е. константами движения), их скобки Пуассона с гамильтонианом  определенным формулами (7.6.21) и (7.6.10), должны обращаться
определенным формулами (7.6.21) и (7.6.10), должны обращаться
в нуль:

Кроме того, можно показать, что  попарно коммутируют между собой,
попарно коммутируют между собой,

для всех тип. Это свойство является непрерывным аналогом (2.5.11) для интегрируемых гамильтоновых систем с конечным числом степеней свободы. Таким образом, уравнение КдФ может рассматриваться как полностью интегрируемая гамильтонова система с бесконечным числом степеней свободы. Продолжая аналогию с конечномерными системами, можно предположить, что поток системы КдФ должен быть ограничен (в некотором смысле) бесконечномерным тором. Кроме того, в великолепной работе Захарова и Фаддеева [23] было установлено, что каноническое преобразование гамильтониана к переменным действие-угол может быть проведено в терминах ОПР.
7.6.в. Гамильтонова структура нелинейного уравнения Шредингера
Можно показать, что все солитонные уравнения, рассмотренные в этой главе, являются гамильтоновыми системами с соответствующими скобками Пуассона (исходное ограничение на интервал ( на самом деле может быть снято). В завершении нашего обсуждения рассмотрим случай нелинейного уравнения Шрёдингера (7.5.26), которое запишем в виде
на самом деле может быть снято). В завершении нашего обсуждения рассмотрим случай нелинейного уравнения Шрёдингера (7.5.26), которое запишем в виде

где  . В этом случае гамильтониан описывается выражением
. В этом случае гамильтониан описывается выражением

а уравнения (7.6.28) принимают каноническую форму

| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
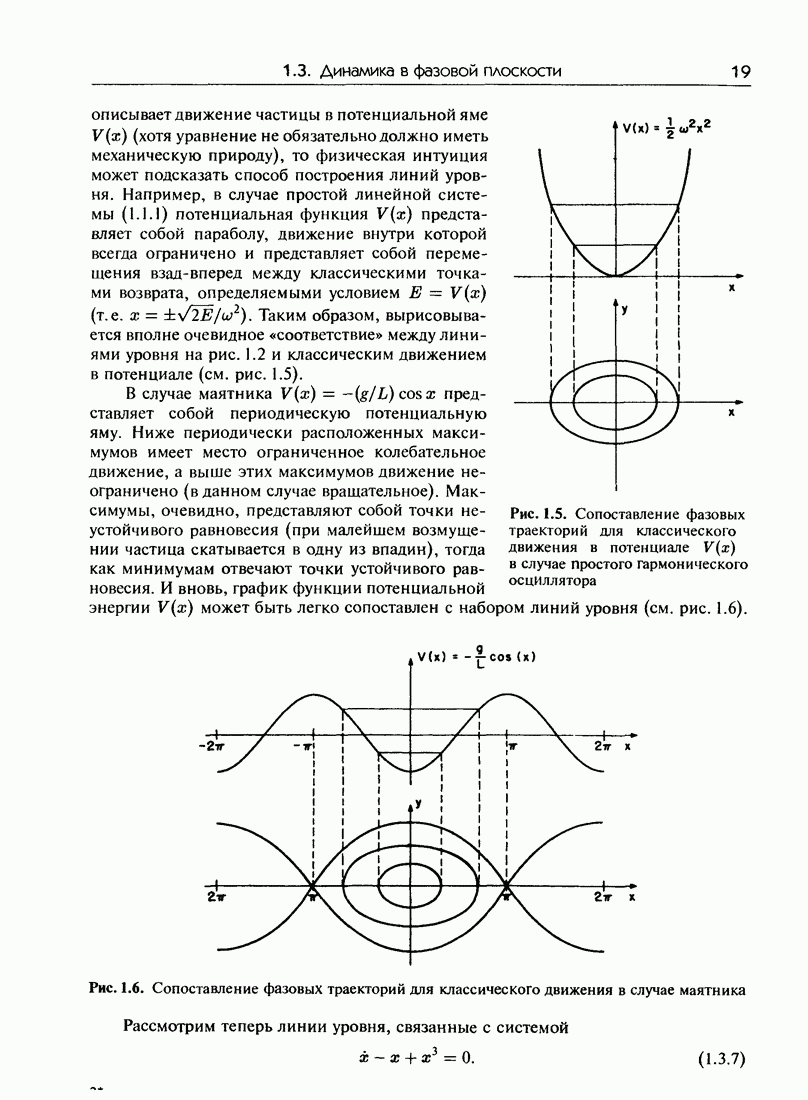
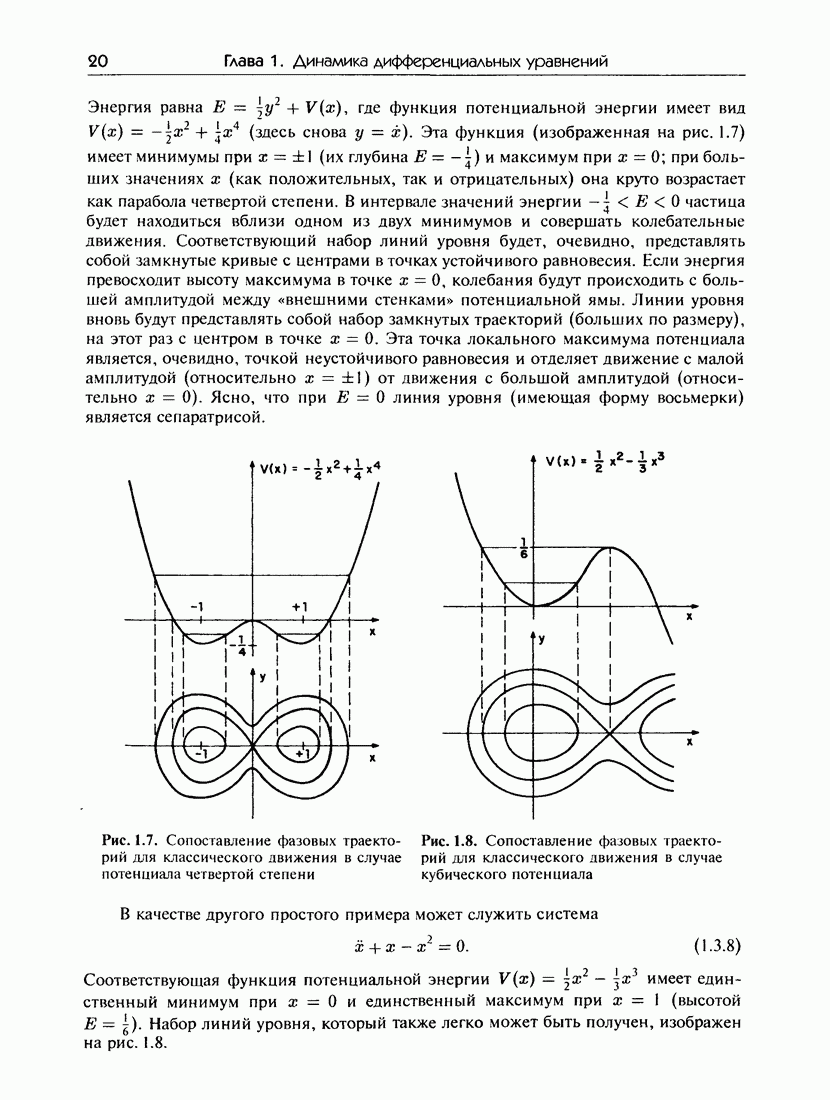
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
- 1.3.б. фазовые портреты консервативных систем
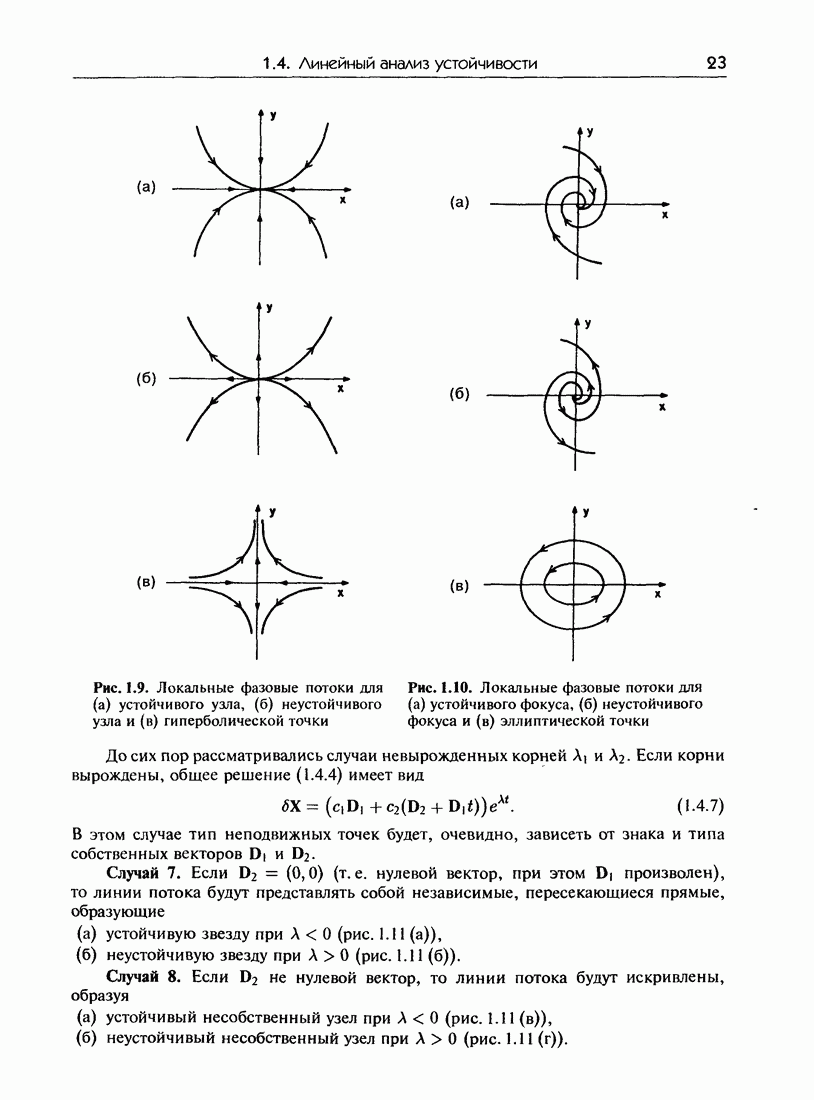
- 1.4. Линейный анализ устойчивости
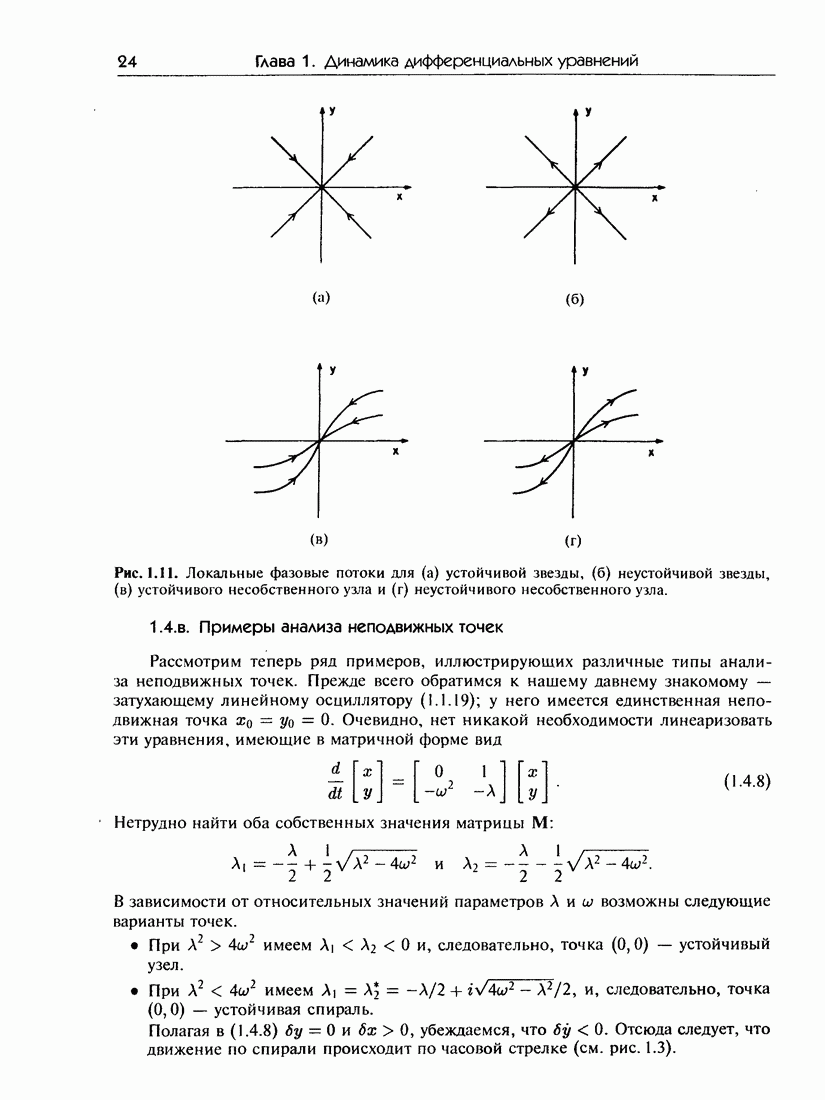
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
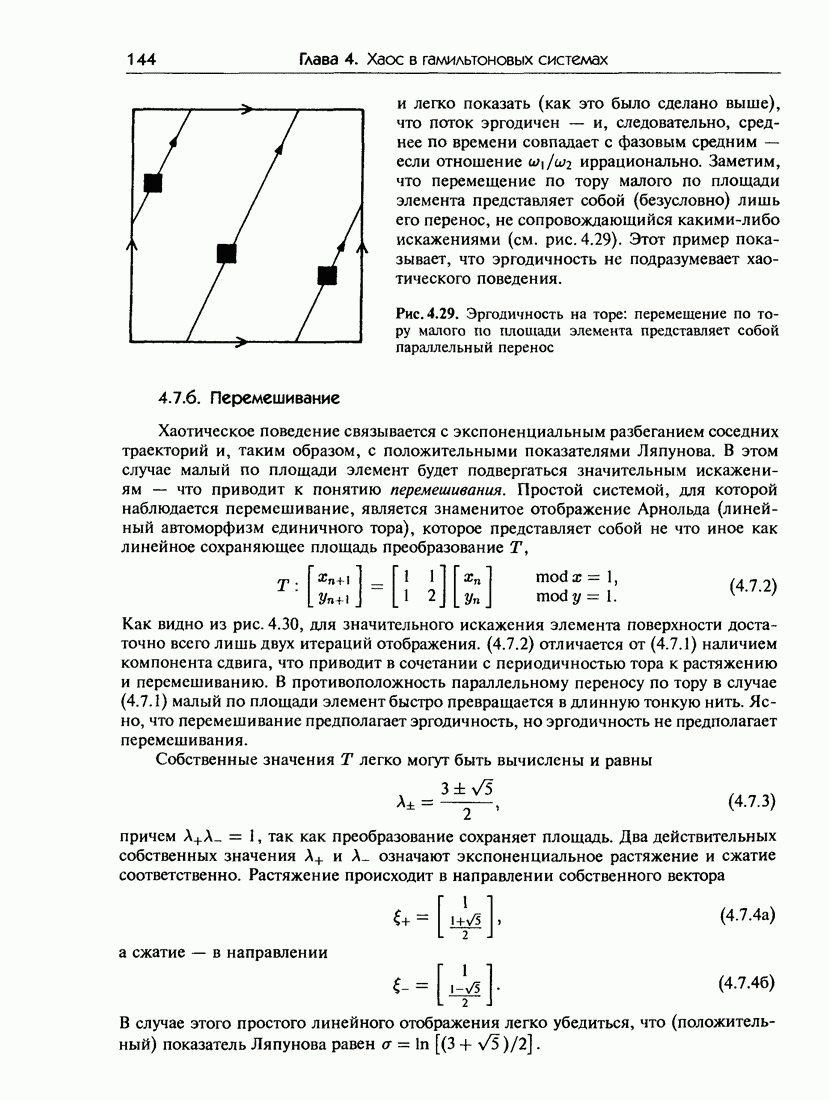
- 4.7.б. Перемешивание
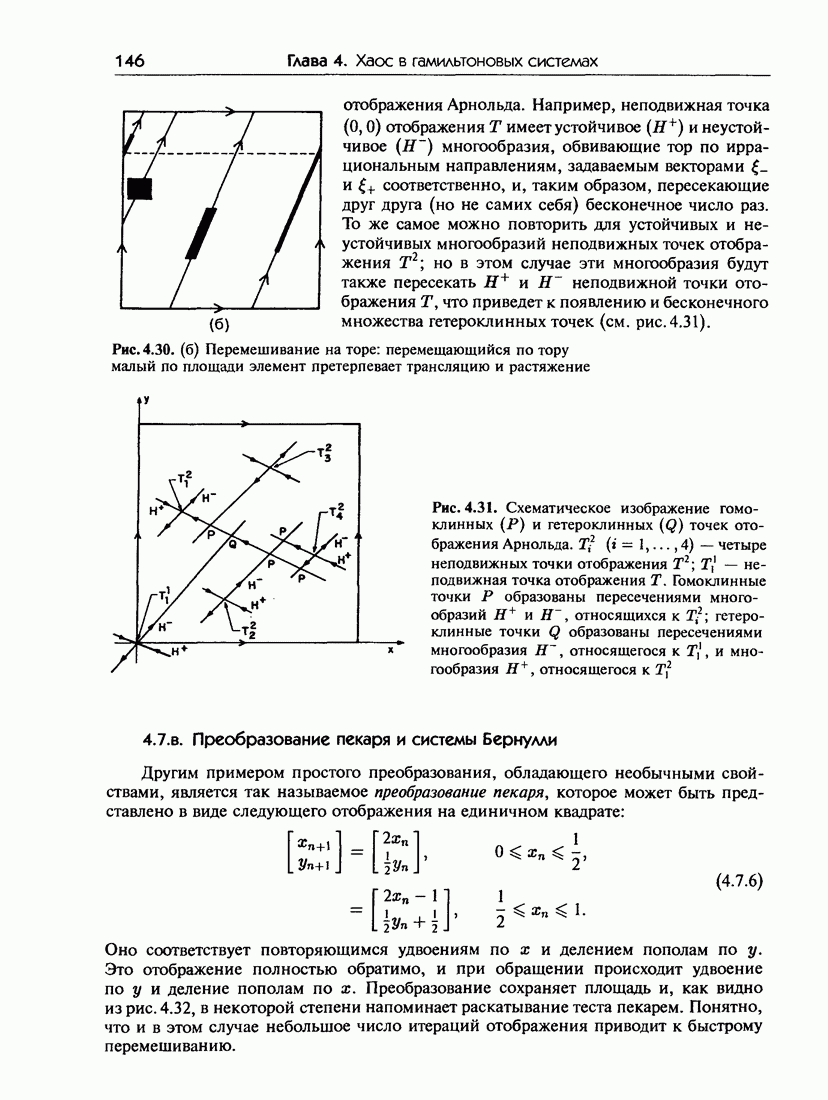
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
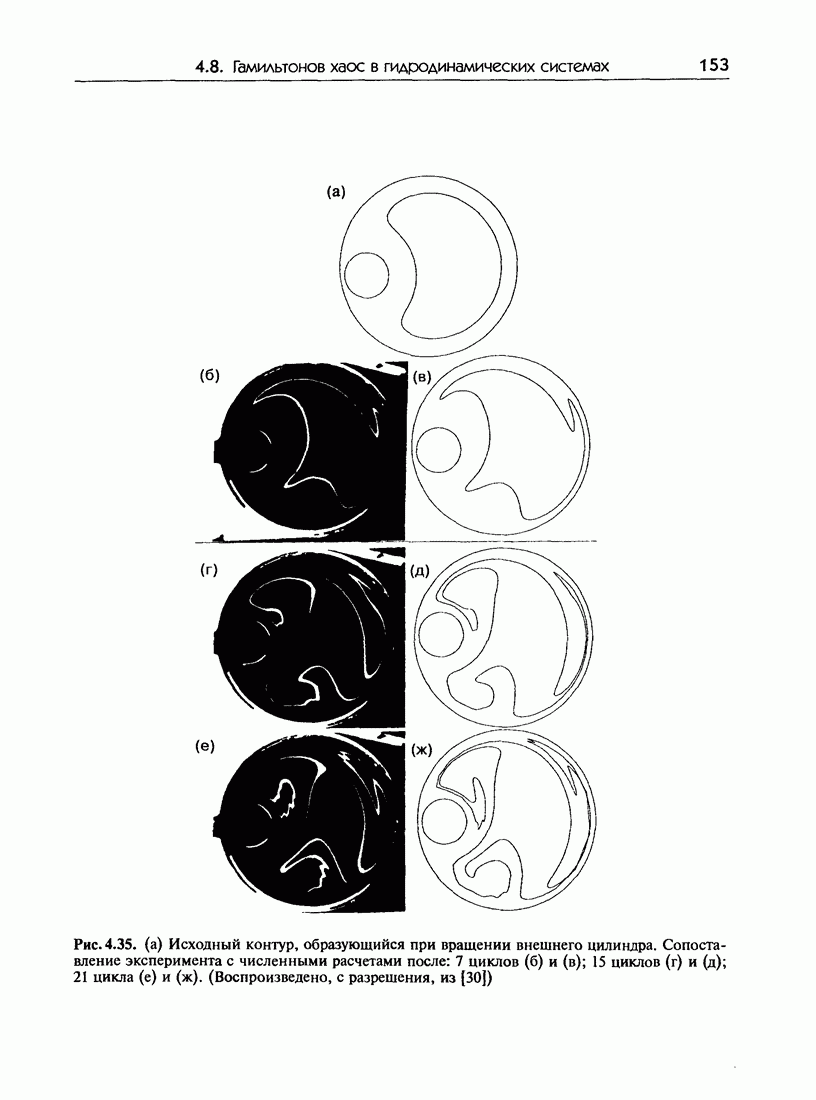
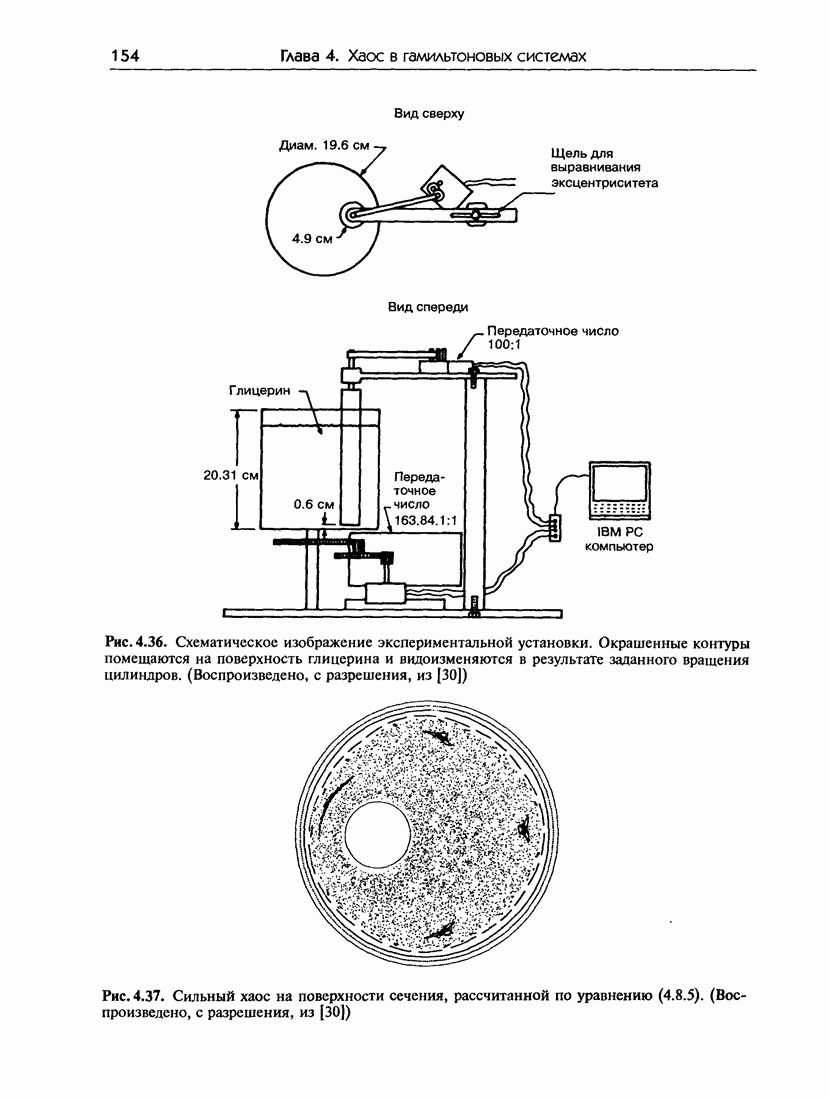
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
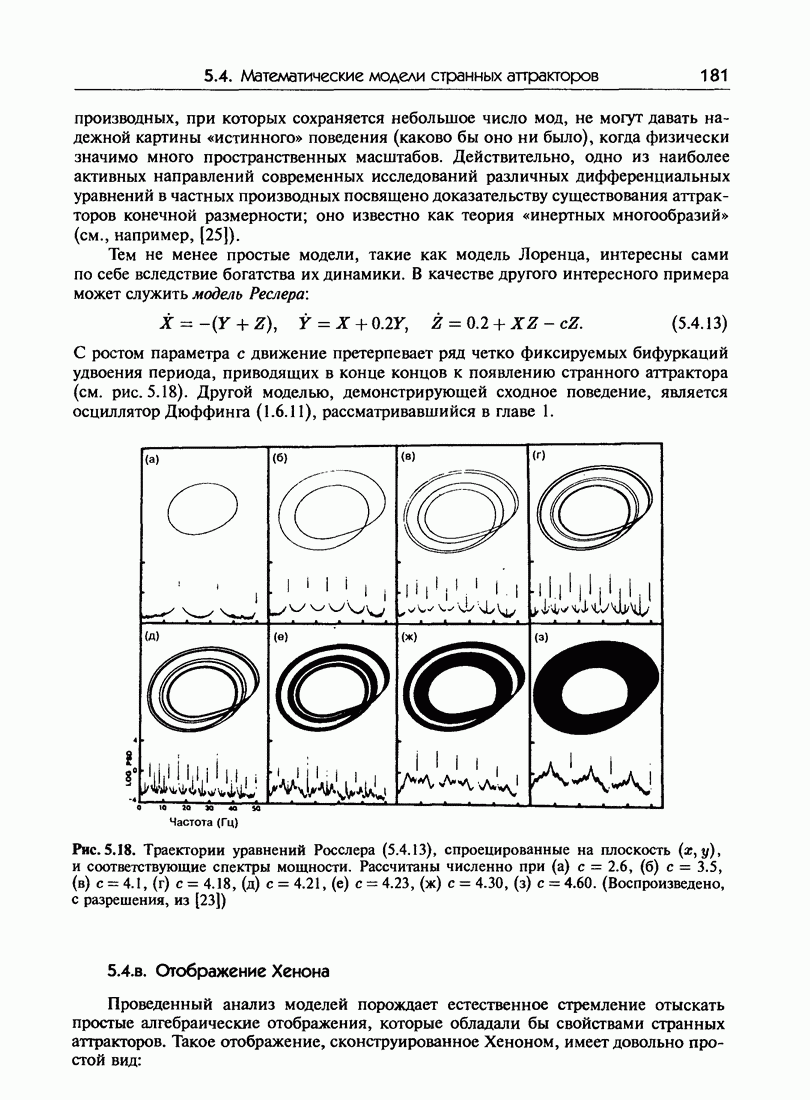
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
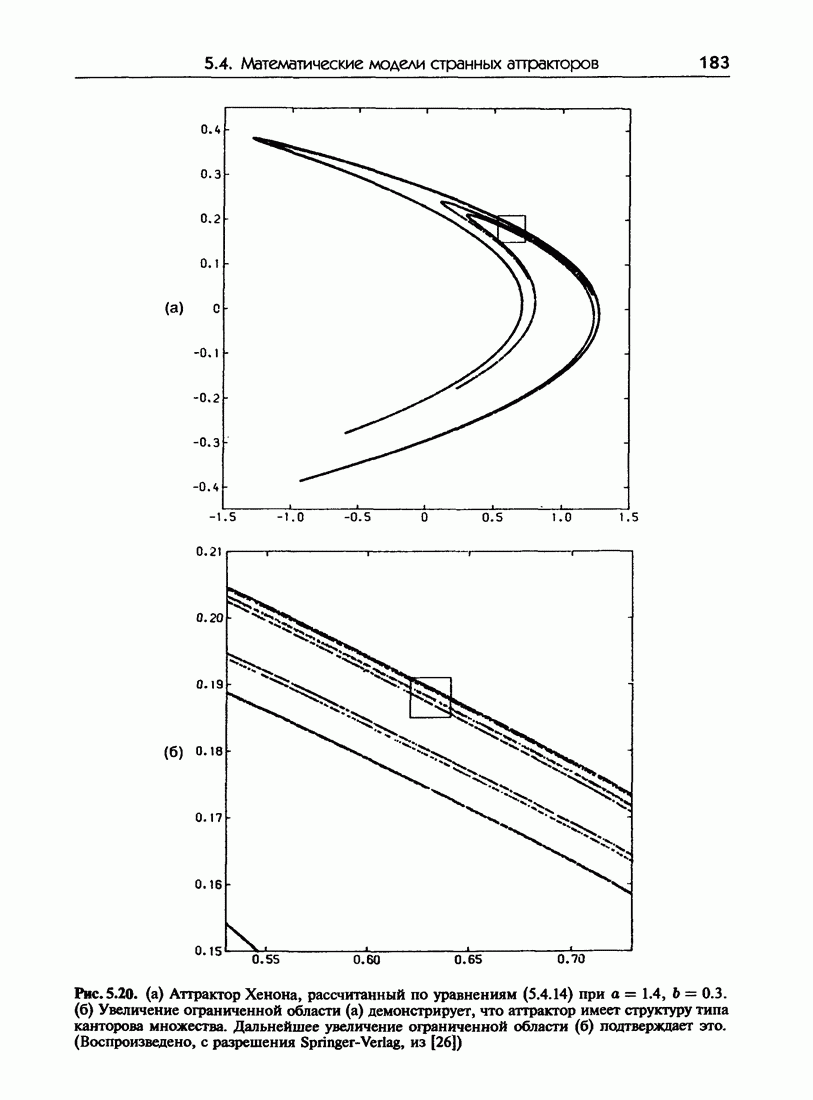
- 5.4.в. Отображение Хенона
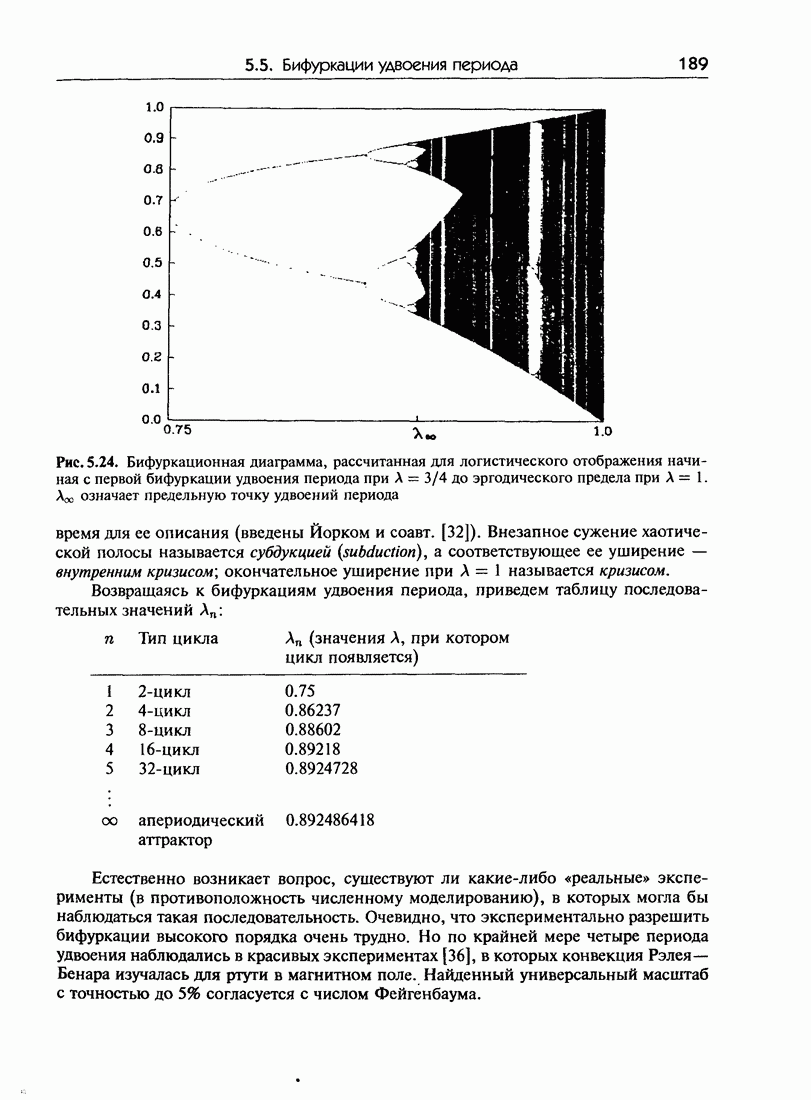
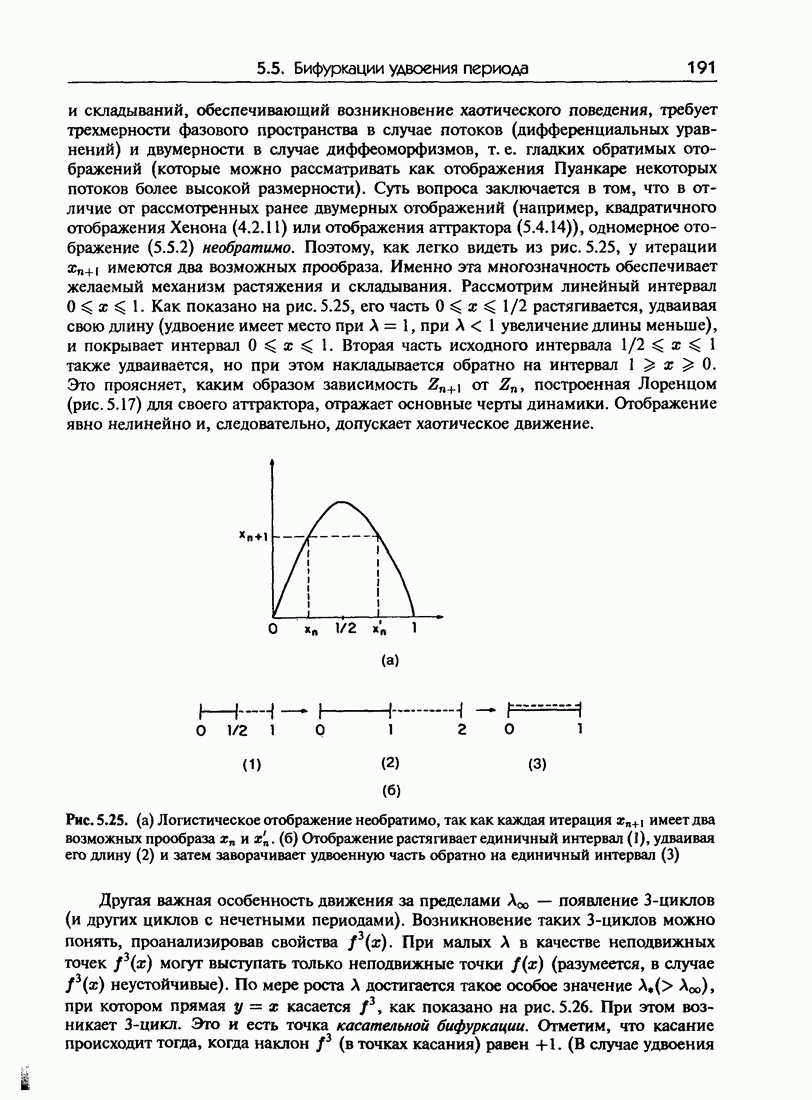
- 5.5. Бифуркации удвоения периода
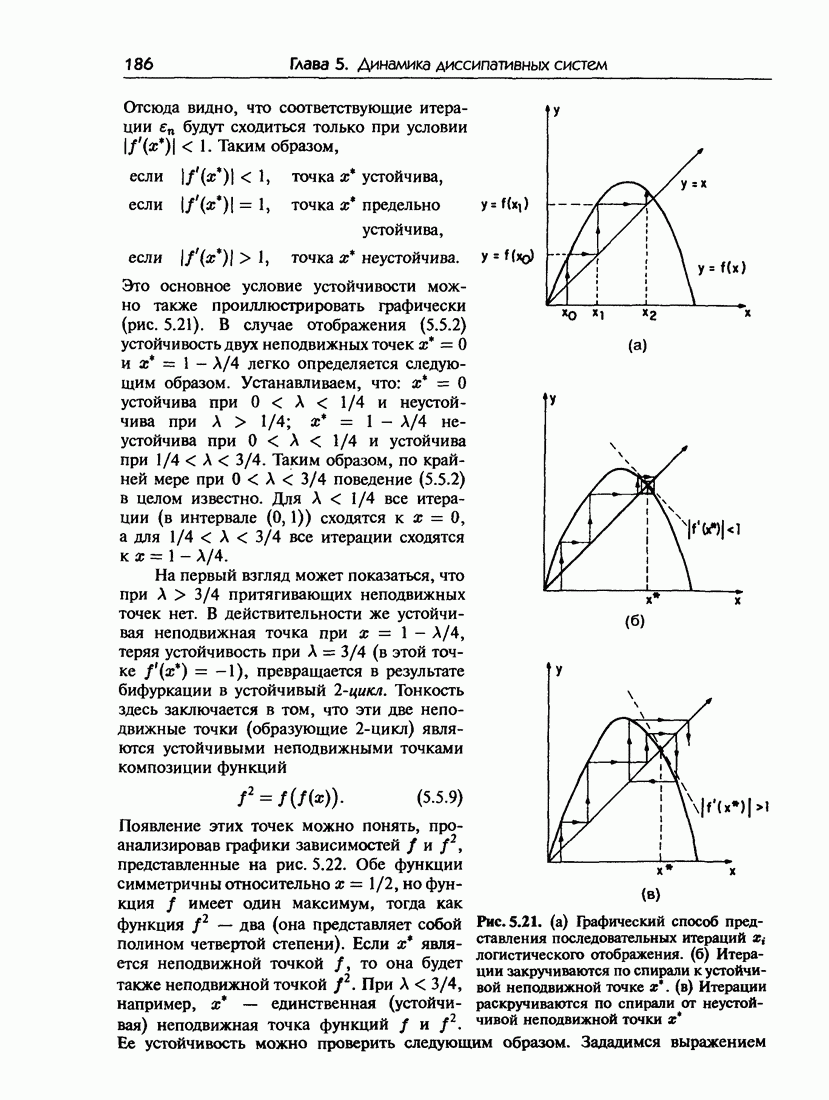
- 5.5.а. Механизм удвоения периода
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
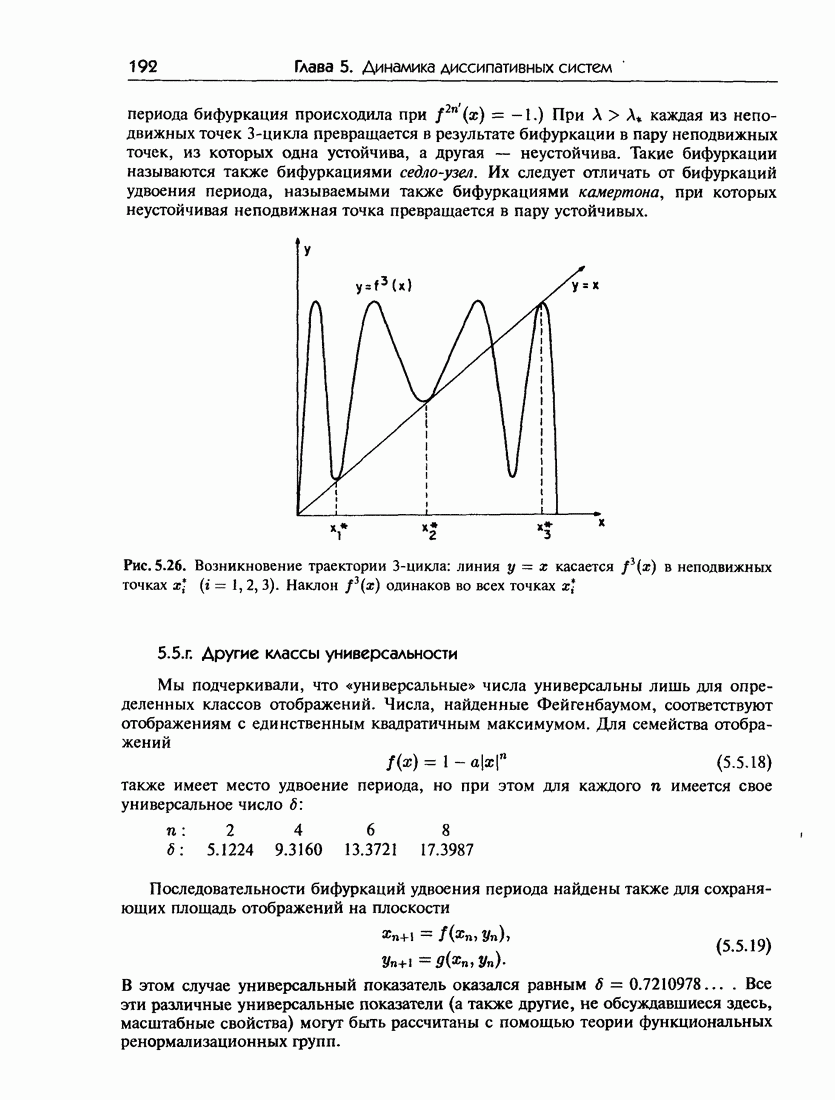
- 5.5.г. Другие классы универсальности
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
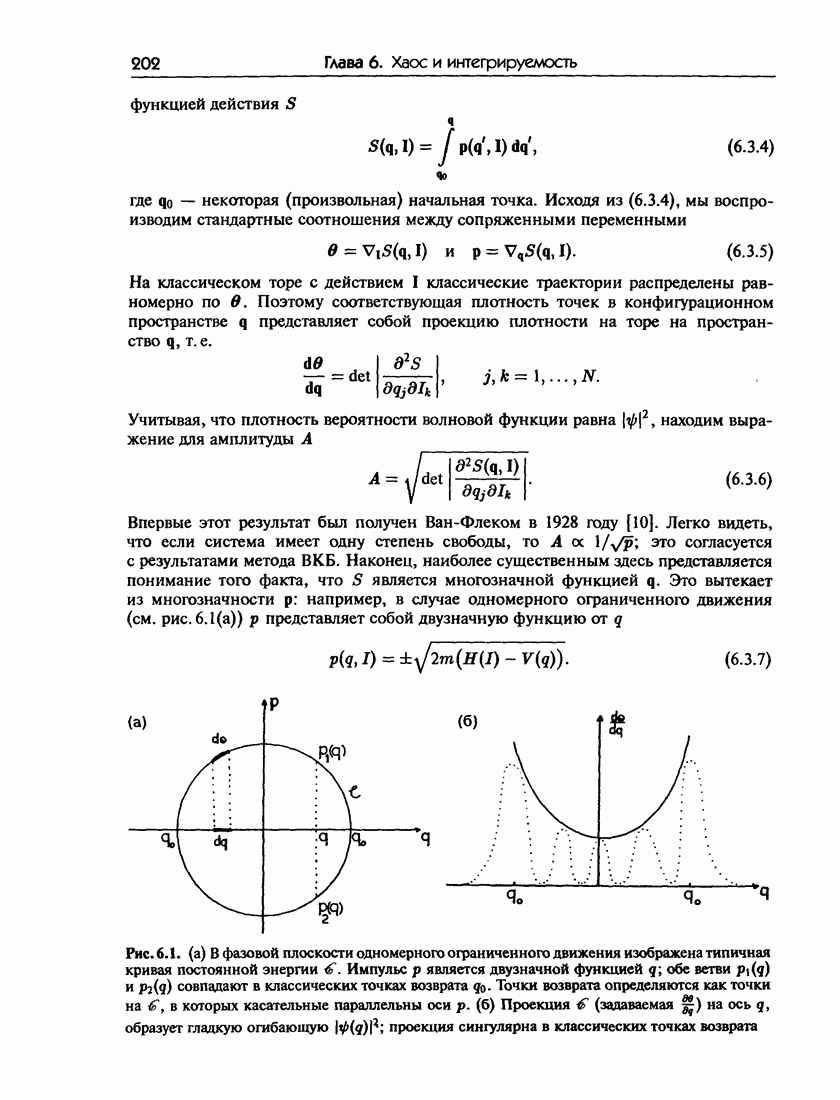
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
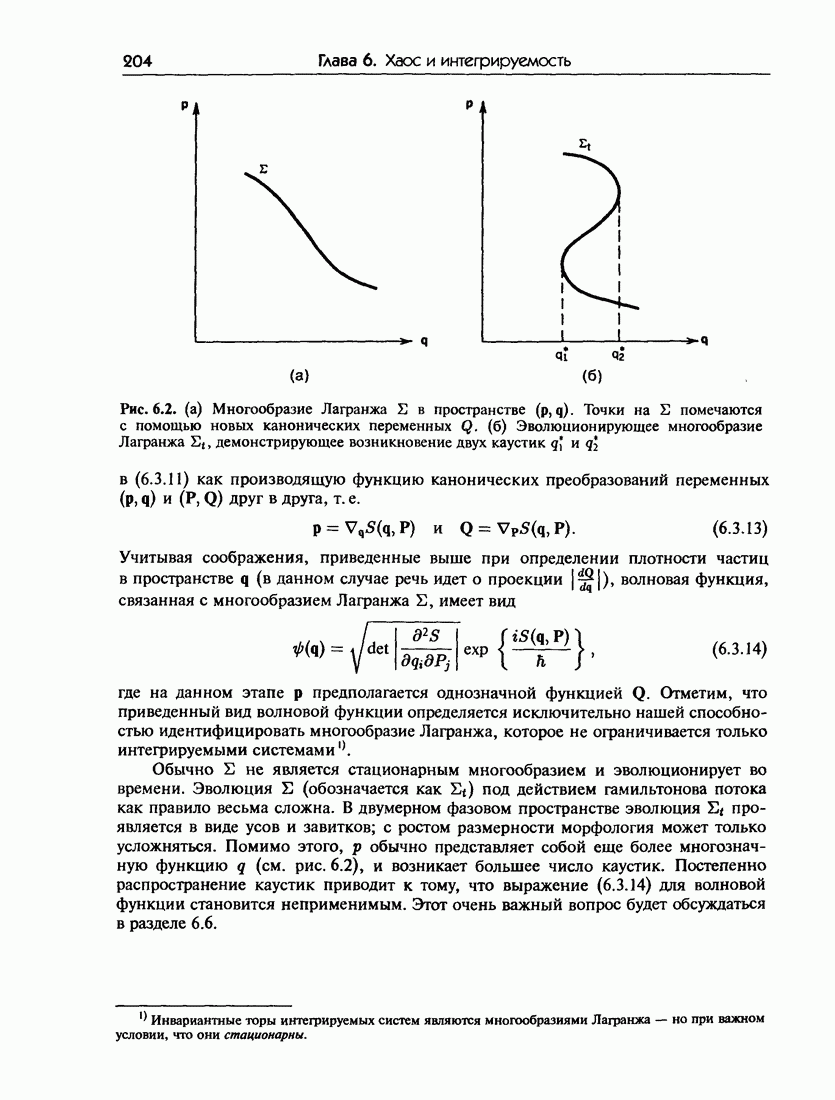
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
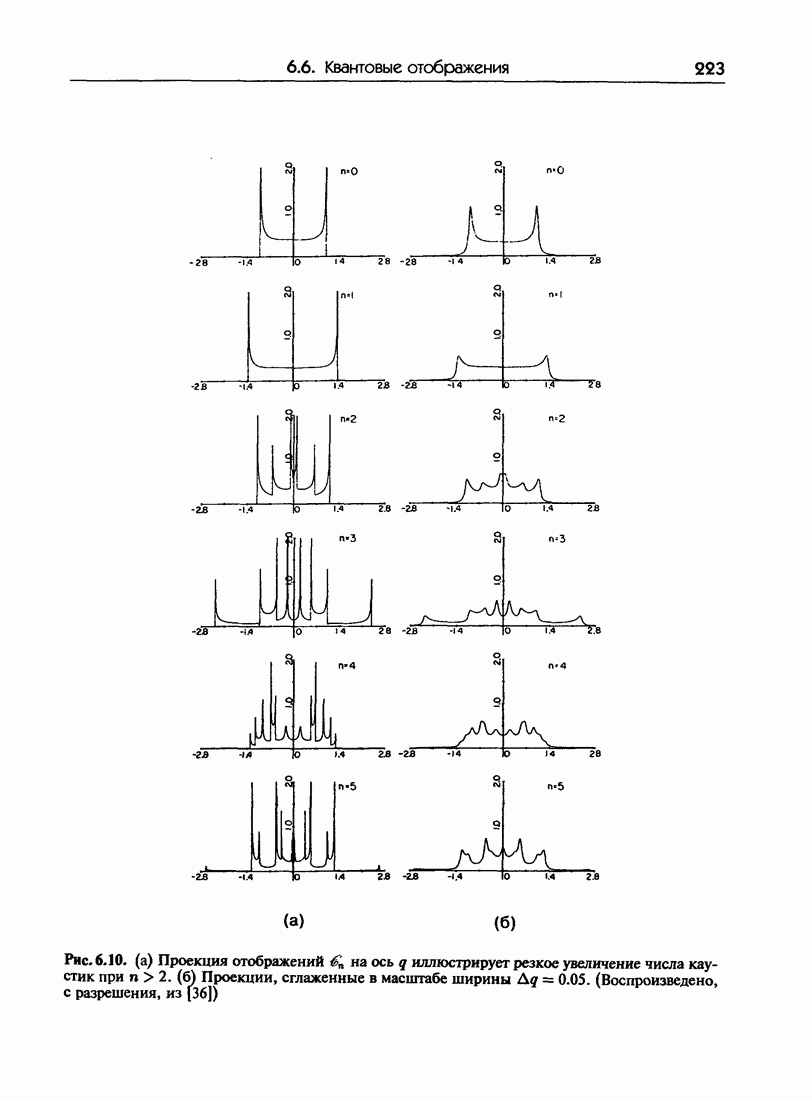
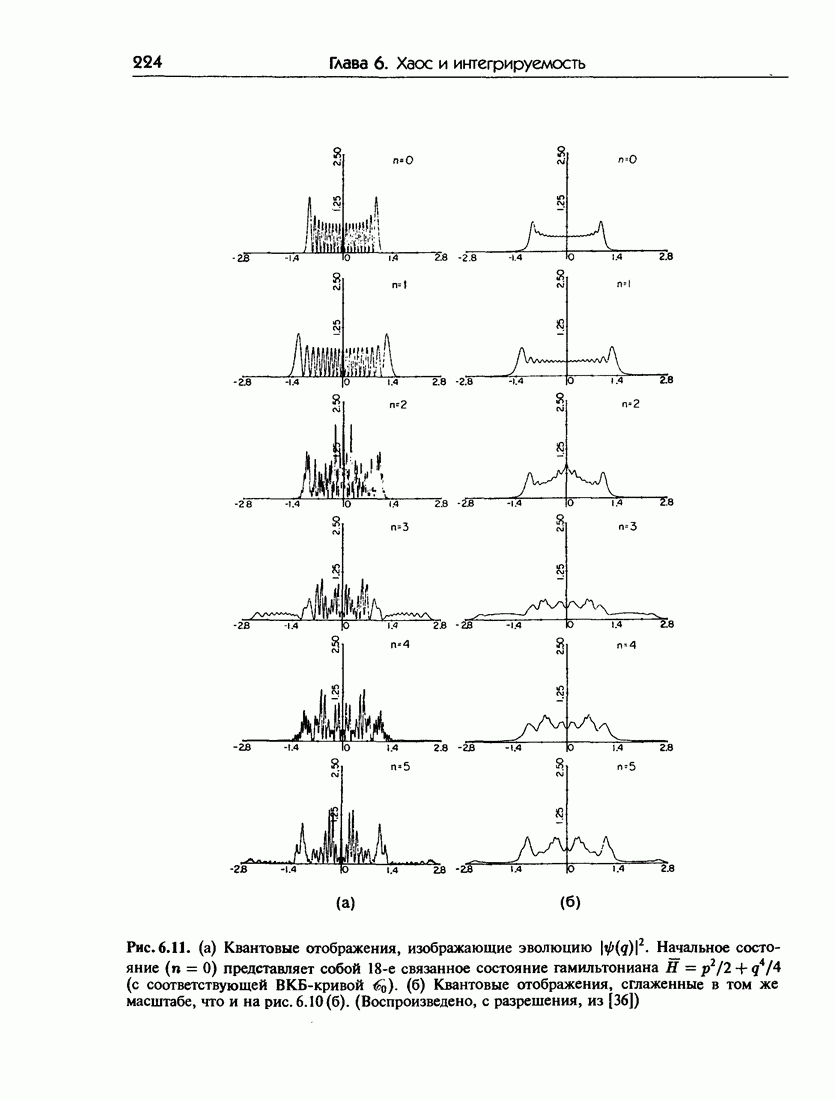
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
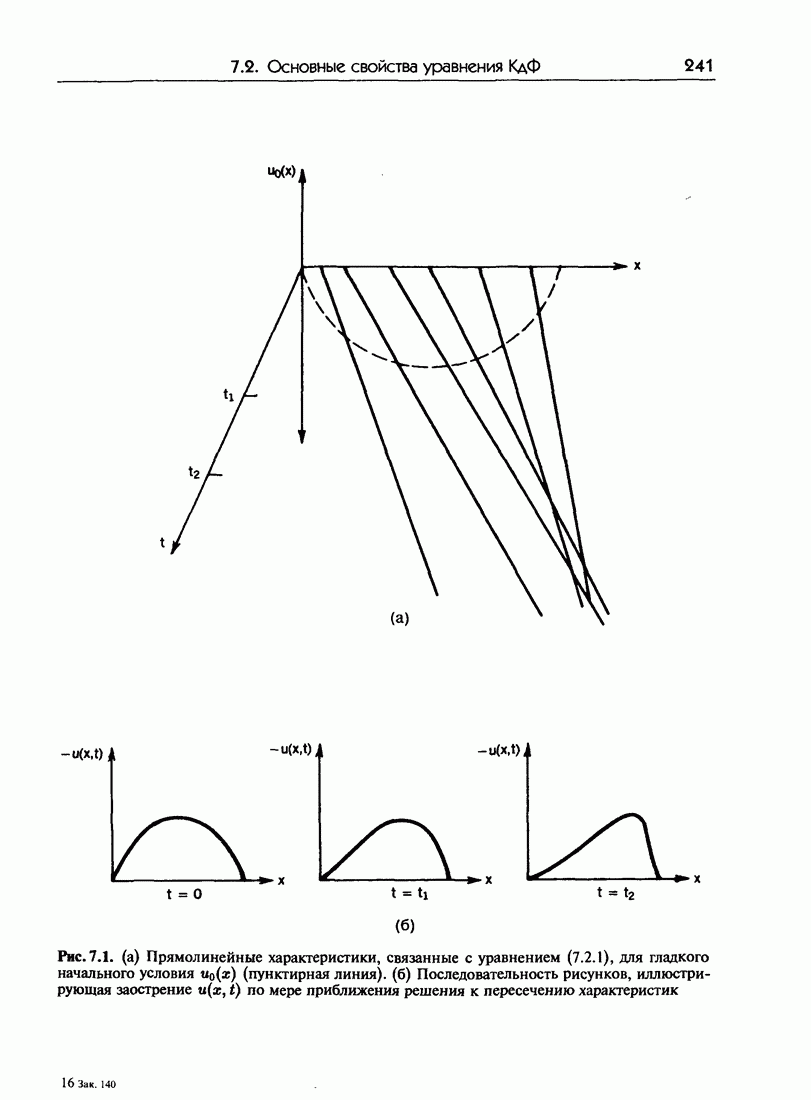
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
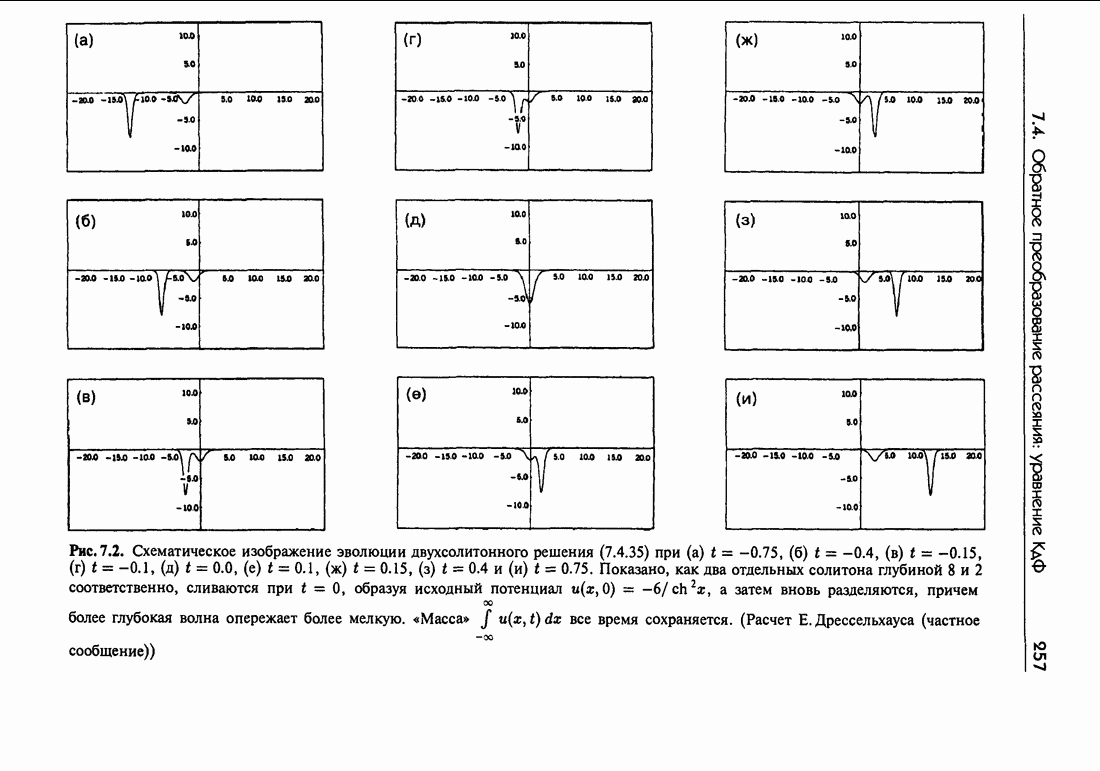
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
- 7.5. Другие солитонные системы
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда