| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
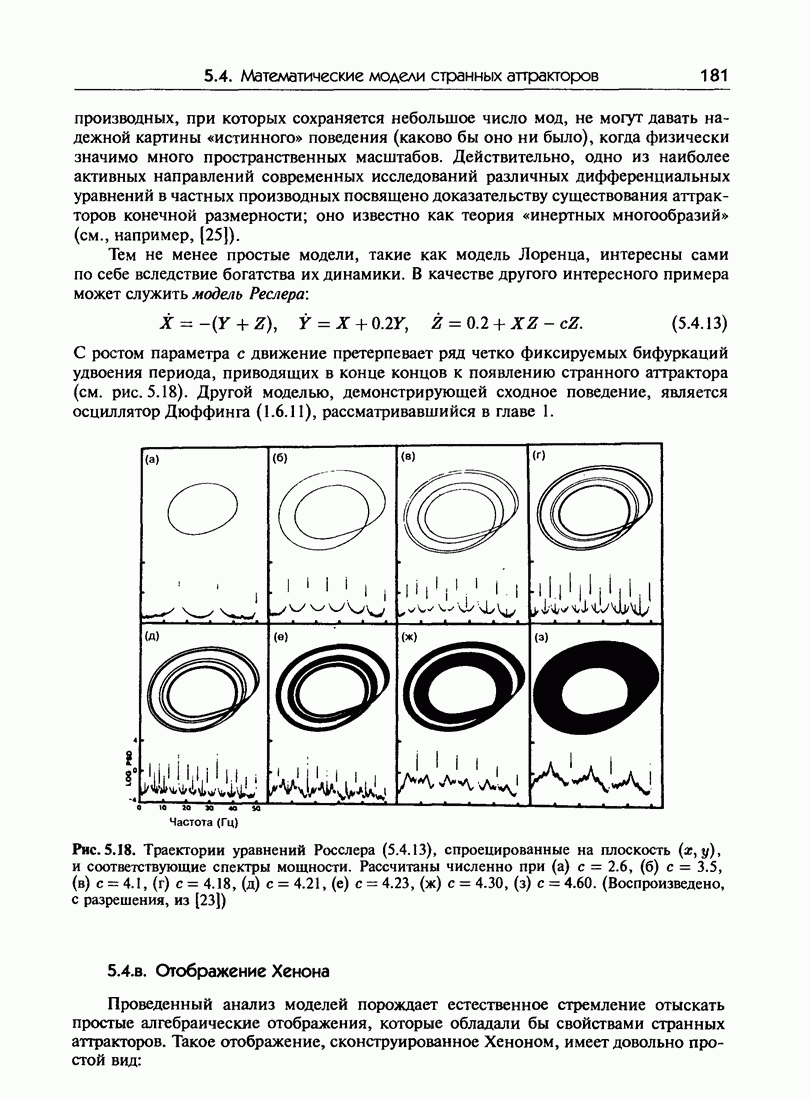
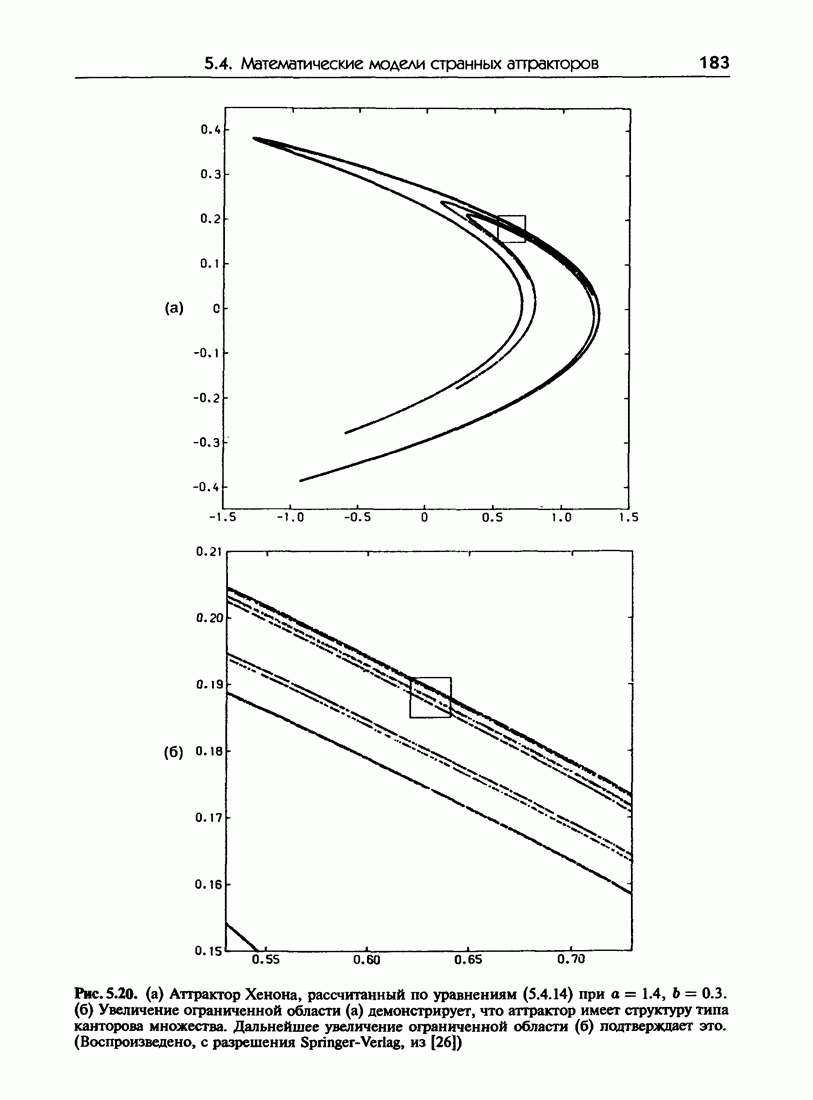
5.4. Математические модели странных аттракторов
Перейдем к рассмотрению некоторых простых математических моделей, позволяющих описывать ряд свойств странного аттрактора.
5.4.а. Модель Лоренца
Эта известная система, исследованная Лоренцем в 1963 году, знаменита в том числе и тем, что была построена задолго до появления понятия странного аттрактора. Она создавалась с целью построить упрощенную модель атмосферной конвекции для решения вопроса о том, возможен ли долгосрочный прогноз погоды. В последующие годы эта система подробно изучалась многими авторами. Большинство полученных результатов собрано в [30].
Рассмотрим слой жидкости постоянной глубины  на которую наложен температурный градиент
на которую наложен температурный градиент  Если все движения параллельны плоскости
Если все движения параллельны плоскости  и однородны в направлении у, то управляющие уравнения движения могут быть представлены в двумерном виде:
и однородны в направлении у, то управляющие уравнения движения могут быть представлены в двумерном виде:

где  функция тока двумерного движения, т. е. компоненты скорости
функция тока двумерного движения, т. е. компоненты скорости  задаются соотношениями
задаются соотношениями

а  — поле температур, характеризующее отклонение от состояния равновесия.
— поле температур, характеризующее отклонение от состояния равновесия.
Коэффициенты:  гравитационная постоянная, а — коэффициент термического расширения,
гравитационная постоянная, а — коэффициент термического расширения,  кинематическая вязкость, k — теплопроводность.
кинематическая вязкость, k — теплопроводность.
Рэлей нашел, что решения вида

должны возрастать в том случае, если число Рэлея, т. е. величина

будет превышать критическую величину

Минимальное значение  достигается при
достигается при  :
:

Для численного решения задачи требуется проинтегрировать пару двумерных дифференциальных уравнений в частных производных (5.4.1). Это всегда неприятная задача. Альтернативой непосредственному численному интегрированию является разложение функций  и в по базисному набору. При этом, задавшись периодическими граничными условиями в обоих направлениях, имеем
и в по базисному набору. При этом, задавшись периодическими граничными условиями в обоих направлениях, имеем

Подстановка этих разложений в дифференциальные уравнения в частных производных дает бесконечное число обыкновенных дифференциальных уравнений. Для осуществления интегрирования требуется конечное усечение этого бесконечного набора.
Лоренц (1963) рассмотрел предельное возможное усечение, включив в рассмотрение лишь коэффициенты три (обозначаемый через X),  В этом случае с помощью масштабных преобразований можно свести систему к следующей системе трех обыкновенных дифференциальных уравнений:
В этом случае с помощью масштабных преобразований можно свести систему к следующей системе трех обыкновенных дифференциальных уравнений:

где  число Прандтля,
число Прандтля,  (нормированное) число Рэлея,
(нормированное) число Рэлея,  геометрический фактор и переменная времени преобразуется как
геометрический фактор и переменная времени преобразуется как  В системе уравнений (5.4.8), обычно называемых уравнениями Лоренца, переменным
В системе уравнений (5.4.8), обычно называемых уравнениями Лоренца, переменным  может быть дана простая физическая интерпретация: X — интенсивность конвекции; У — разность температур между восходящим и нисходящим потоками;
может быть дана простая физическая интерпретация: X — интенсивность конвекции; У — разность температур между восходящим и нисходящим потоками;  отклонение вертикального температурного профиля от линейного.
отклонение вертикального температурного профиля от линейного.
Изучим некоторые свойства уравнений (5.4.8).
(а) Дивергенция

отрицательна, так как  и а положительны. Обозначив элемент объема фазового пространства через
и а положительны. Обозначив элемент объема фазового пространства через  представляем сжатие в виде
представляем сжатие в виде

Таким образом, все траектории ограничиваются в конце концов некоторым предельным многообразием.
(б) Критические точки. Условию

удовлетворяют точки:
(1)  , отвечающая состоянию чистой теплопроводности без конвекции;
, отвечающая состоянию чистой теплопроводности без конвекции;
(2)  , соответствующие состоянию стационарной конвекции. Отметим, что такие состояния существуют только при
, соответствующие состоянию стационарной конвекции. Отметим, что такие состояния существуют только при  Свойства устойчивости. Линеаризованное преобразование имеет вид
Свойства устойчивости. Линеаризованное преобразование имеет вид

и позволяет сделать следующие выводы об устойчивости критических точек.
(1)  : при
: при  точка устойчивости, т.е. все собственные значения имеют отрицательную действительную часть; при
точка устойчивости, т.е. все собственные значения имеют отрицательную действительную часть; при  действительная часть одного из собственных значений становится положительной. Критическая точка неустойчива, и, следовательно, бесконечно малое возмущение может вызвать конвекцию. Отметим, что устойчивость критической точки зависит только от значения числа Рэлея.
действительная часть одного из собственных значений становится положительной. Критическая точка неустойчива, и, следовательно, бесконечно малое возмущение может вызвать конвекцию. Отметим, что устойчивость критической точки зависит только от значения числа Рэлея.
(2)  : при
: при  собственные значения состоят из одного действительного отрицательного корня и пары комплексно сопряженных корней. Можно показать, что эта пара критических точек теряет устойчивость при
собственные значения состоят из одного действительного отрицательного корня и пары комплексно сопряженных корней. Можно показать, что эта пара критических точек теряет устойчивость при

При положительных  это условие выполняется только в том случае, если
это условие выполняется только в том случае, если

Отметим, что устойчивость этих критических точек зависит уже не только от значения числа Рэлея.
В своей работе [27] Лоренц выбрал следующие значения параметров:

При таком выборе стационарное (конвективное) состояние теряет устойчивость при

и скорость сжатия  очень велика.
очень велика.
Сформулируем, что происходит с решениями уравнений Лоренца по мере возрастания 
(1)  . Начало координат является глобальным притягивающим стационарным решением, и все траектории (соответствующие всем различным начальным условиям) постепенно закручиваются по спирали к началу координат.
. Начало координат является глобальным притягивающим стационарным решением, и все траектории (соответствующие всем различным начальным условиям) постепенно закручиваются по спирали к началу координат.
(2)  . Начало координат теряет устойчивость и в результате бифуркации превращается в пару локальных притягивающих стационарных решений
. Начало координат теряет устойчивость и в результате бифуркации превращается в пару локальных притягивающих стационарных решений  . Фактически все траектории стягиваются либо к С, либо к С. Исключение составляет множество траекторий (меры ноль), остающихся в окрестности начала координат. При
. Фактически все траектории стягиваются либо к С, либо к С. Исключение составляет множество траекторий (меры ноль), остающихся в окрестности начала координат. При  начало координат преобразуется в гомоклиническую точку. Дальнейший рост
начало координат преобразуется в гомоклиническую точку. Дальнейший рост  приводит к неразличимости «областей притяжения»
приводит к неразличимости «областей притяжения»  в результате чего траектории могут переходить из одной в другую прежде, чем окончательно зафиксироваться.
в результате чего траектории могут переходить из одной в другую прежде, чем окончательно зафиксироваться.
(3)  . Как уже говорилось, это критическое значение, при котором стационарные состояния
. Как уже говорилось, это критическое значение, при котором стационарные состояния  теряют устойчивость. Однако анализ по Хопфу показал, что при больших значениях
теряют устойчивость. Однако анализ по Хопфу показал, что при больших значениях  существует обратная бифуркация; поэтому предельные точки
существует обратная бифуркация; поэтому предельные точки  не превращаются в предельные циклы.
не превращаются в предельные циклы.
(4)  . Траектории, полученные в этом режиме, ведут себя нетривиально. В оригинальной работе [27] Лоренц рассматривал траекторию с начальными условиями (
. Траектории, полученные в этом режиме, ведут себя нетривиально. В оригинальной работе [27] Лоренц рассматривал траекторию с начальными условиями ( (малое отклонение от равновесия) при значении
(малое отклонение от равновесия) при значении  При этом значении
При этом значении  имеются неустойчивые стационарные состояния
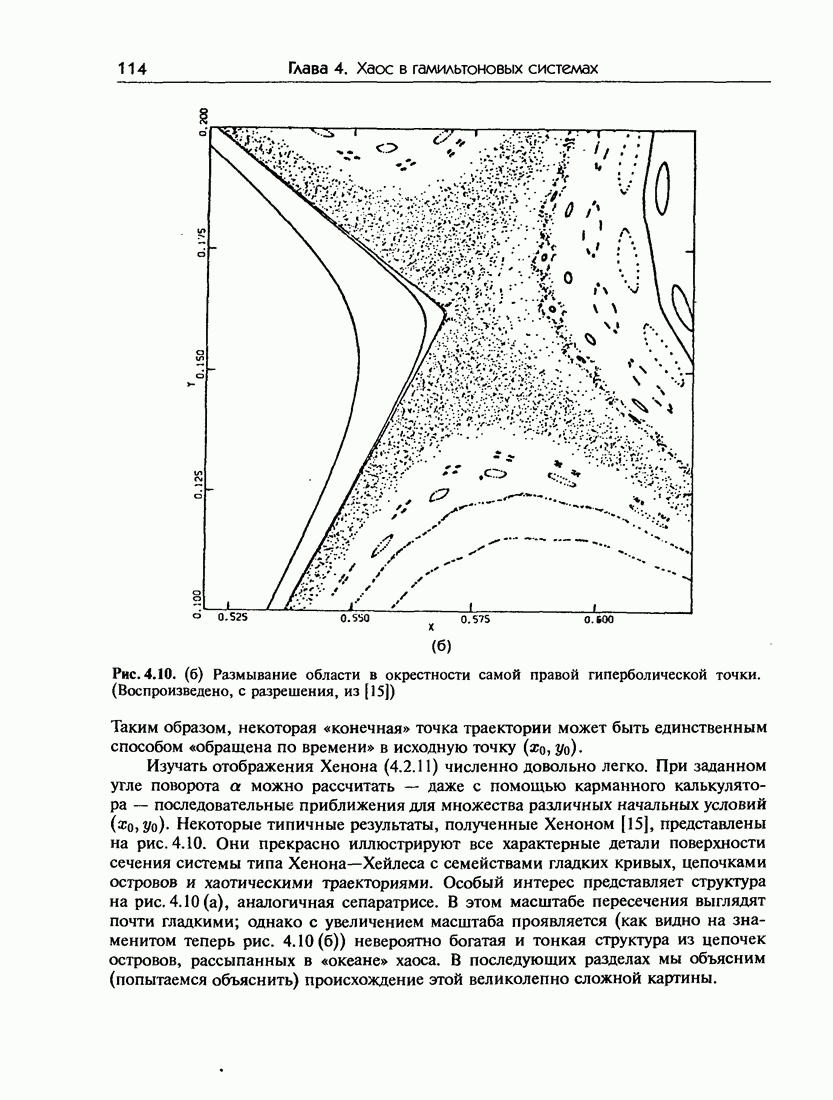
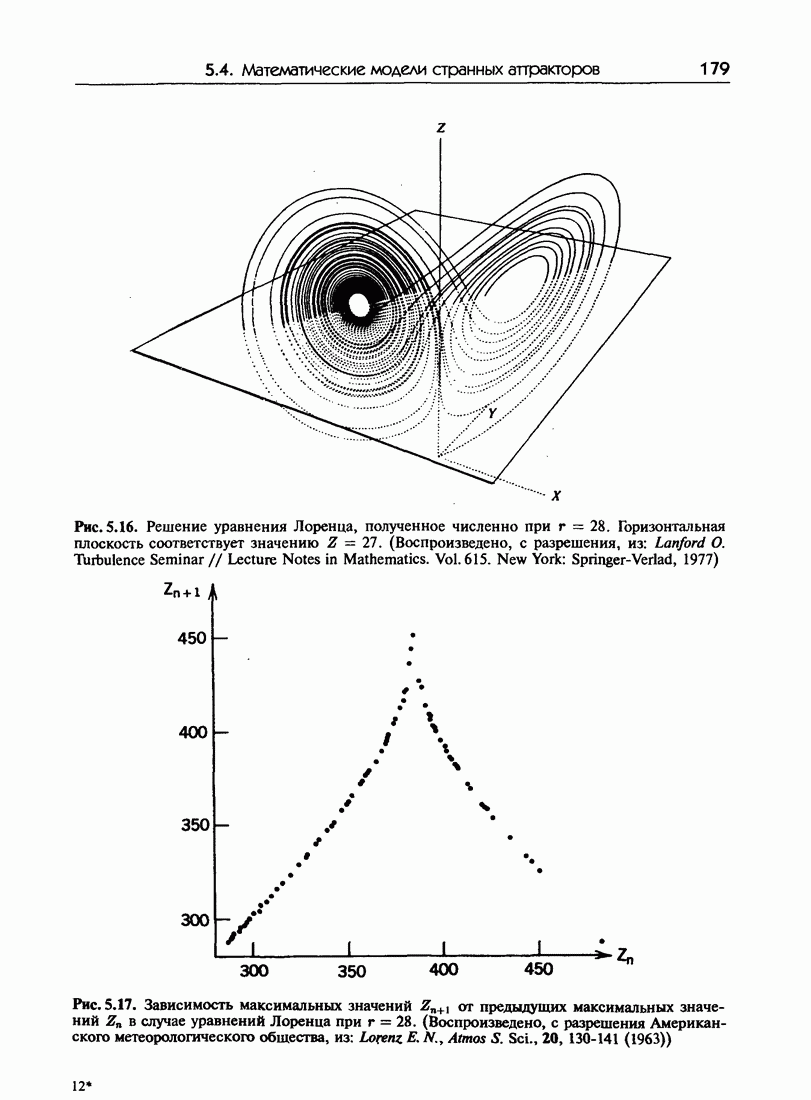
имеются неустойчивые стационарные состояния  . Расчеты Лоренца показали, что после того как некоторые временные колебания затухают, движение становится крайне неупорядоченным. Это является результатом того, что решение, раскручиваясь по спирали в окрестности одной из неподвижных точек (С или С) в течение произвольного периода времени, перепрыгивает затем в окрестность второй неподвижной точки и также некоторое время раскручивается по спирали, а затем перепрыгивает назад и т. д. Такое сочетание движения по спирали (вдоль неустойчивого многообразия) и возврата (вдоль устойчивого многообразия) порождает обсуждавшийся выше механизм растяжений и складываний и приводит к чрезвычайно сложному многообразию, а именно, к странному аттрактору определенного вида. Типичная траектория этого аттрактора показана на рис. 5.16. (Кажущаяся регулярность показанной на рисунке структуры обманчива — аттрактор чрезвычайно сложен.) Спектр мощности траектории существенно непрерывен, что указывает на выраженную хаотичность движения.
. Расчеты Лоренца показали, что после того как некоторые временные колебания затухают, движение становится крайне неупорядоченным. Это является результатом того, что решение, раскручиваясь по спирали в окрестности одной из неподвижных точек (С или С) в течение произвольного периода времени, перепрыгивает затем в окрестность второй неподвижной точки и также некоторое время раскручивается по спирали, а затем перепрыгивает назад и т. д. Такое сочетание движения по спирали (вдоль неустойчивого многообразия) и возврата (вдоль устойчивого многообразия) порождает обсуждавшийся выше механизм растяжений и складываний и приводит к чрезвычайно сложному многообразию, а именно, к странному аттрактору определенного вида. Типичная траектория этого аттрактора показана на рис. 5.16. (Кажущаяся регулярность показанной на рисунке структуры обманчива — аттрактор чрезвычайно сложен.) Спектр мощности траектории существенно непрерывен, что указывает на выраженную хаотичность движения.
Фазовое пространство системы Лоренца трехмерно, и естественно задать вопрос, существует ли способ компактного представления движения аналогичный, возможно, методу поверхности сечения, используемому в случае гамильтоновых систем. После того, как переходные процессы затухают и система «оседает» странный аттрактор, поведение всех индивидуальных переменных  как функций времени становится хаотическим. Нужно отдать должное проницательности Лоренца, который изучил последовательные значения максимумов функции
как функций времени становится хаотическим. Нужно отдать должное проницательности Лоренца, который изучил последовательные значения максимумов функции  достигает максимального значения при движении по спирали в окрестности одной из неподвижных точек С или С (обозначим его через
достигает максимального значения при движении по спирали в окрестности одной из неподвижных точек С или С (обозначим его через  а затем перепрыгивает к другой неподвижной точке и там достигает следующего максимального значения
а затем перепрыгивает к другой неподвижной точке и там достигает следующего максимального значения  и т.д. Зависимость
и т.д. Зависимость  от
от  имеет вид, показанный на
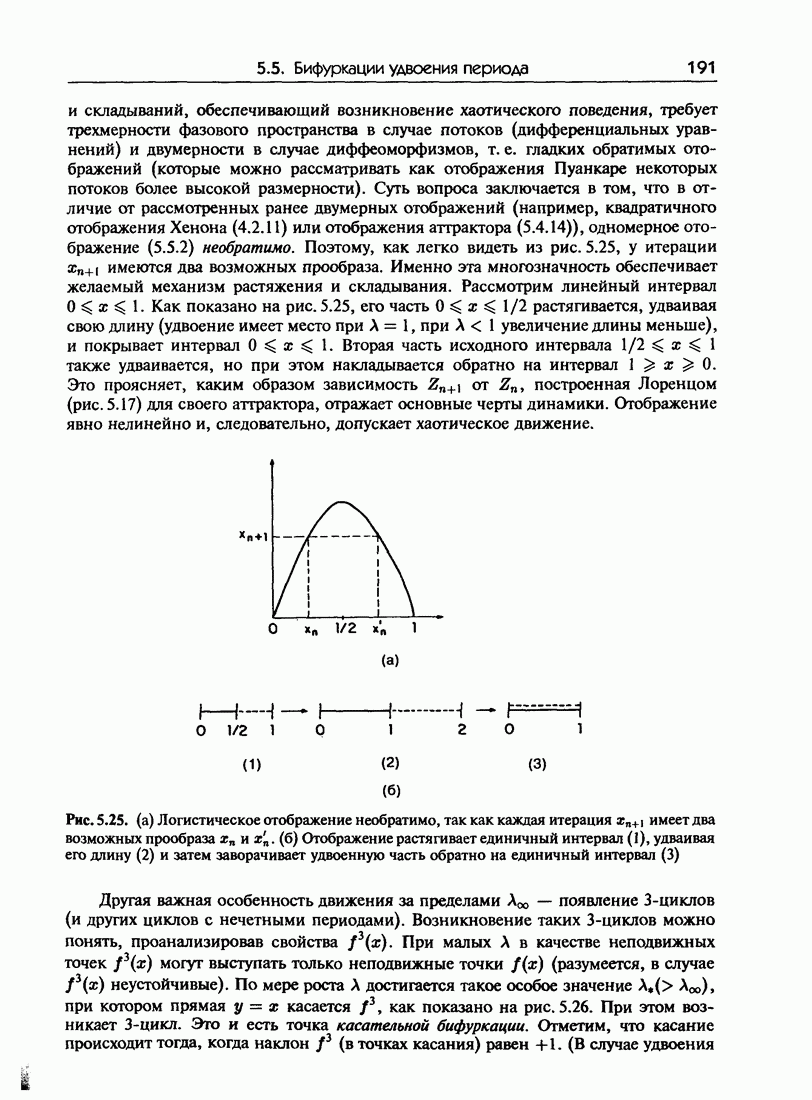
имеет вид, показанный на  Замечательно, что это одномерное «отображение» содержит существенные черты динамики аттрактора Лоренца. Свойства таких одномерных отображений мы будем подробно изучать в разделе 5.5.
Замечательно, что это одномерное «отображение» содержит существенные черты динамики аттрактора Лоренца. Свойства таких одномерных отображений мы будем подробно изучать в разделе 5.5.

(кликните для просмотра скана)
Природа аттрактора Лоренца изучена очень подробно. Это действительно странный аттрактор, хотя он и не относится к аксиоме А. Отметим, что хотя движение явно становится хаотическим по достижении  и 24.74, последовательность событий, приводящих к этому хаосу, не включает в себя никаких периодических режимов, т. е. это не соответствует полному сценарию Рюэля-Тэкенса возникновения турбулентности.
и 24.74, последовательность событий, приводящих к этому хаосу, не включает в себя никаких периодических режимов, т. е. это не соответствует полному сценарию Рюэля-Тэкенса возникновения турбулентности.
Интересно также, что происходит при очень больших значениях  Исследования различных авторов свидетельствуют о существовании чередующихся режимов турбулентности и периодического поведения. При значениях
Исследования различных авторов свидетельствуют о существовании чередующихся режимов турбулентности и периодического поведения. При значениях  превышающих 28, странный аттрактор превращается в периодический предельный цикл (примерно при
превышающих 28, странный аттрактор превращается в периодический предельный цикл (примерно при  . По мере дальнейшего возрастания
. По мере дальнейшего возрастания  этот предельный цикл некоторое время сохраняется, но затем превращается снова в странный аттрактор. При еще больших значениях
этот предельный цикл некоторое время сохраняется, но затем превращается снова в странный аттрактор. При еще больших значениях  вновь происходит превращение в другой предельный цикл (при
вновь происходит превращение в другой предельный цикл (при  . При переходе от предельного цикла к хаотическому режиму наблюдается эффект, называемый перемежаемостью, т. е. «всплески» турбулентности на фоне периодического движения. Эти всплески могут быть различных типов; их подробное обсуждение можно найти в [1]. Заметим в заключение, что насколько такое поведение при больших
. При переходе от предельного цикла к хаотическому режиму наблюдается эффект, называемый перемежаемостью, т. е. «всплески» турбулентности на фоне периодического движения. Эти всплески могут быть различных типов; их подробное обсуждение можно найти в [1]. Заметим в заключение, что насколько такое поведение при больших  (т. е. чередование хаотического и периодического режимов) представляет академический интерес, настолько оно делает модель Лоренца нереалистичной, когда речь идет о «реальной» турбулентности.
(т. е. чередование хаотического и периодического режимов) представляет академический интерес, настолько оно делает модель Лоренца нереалистичной, когда речь идет о «реальной» турбулентности.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
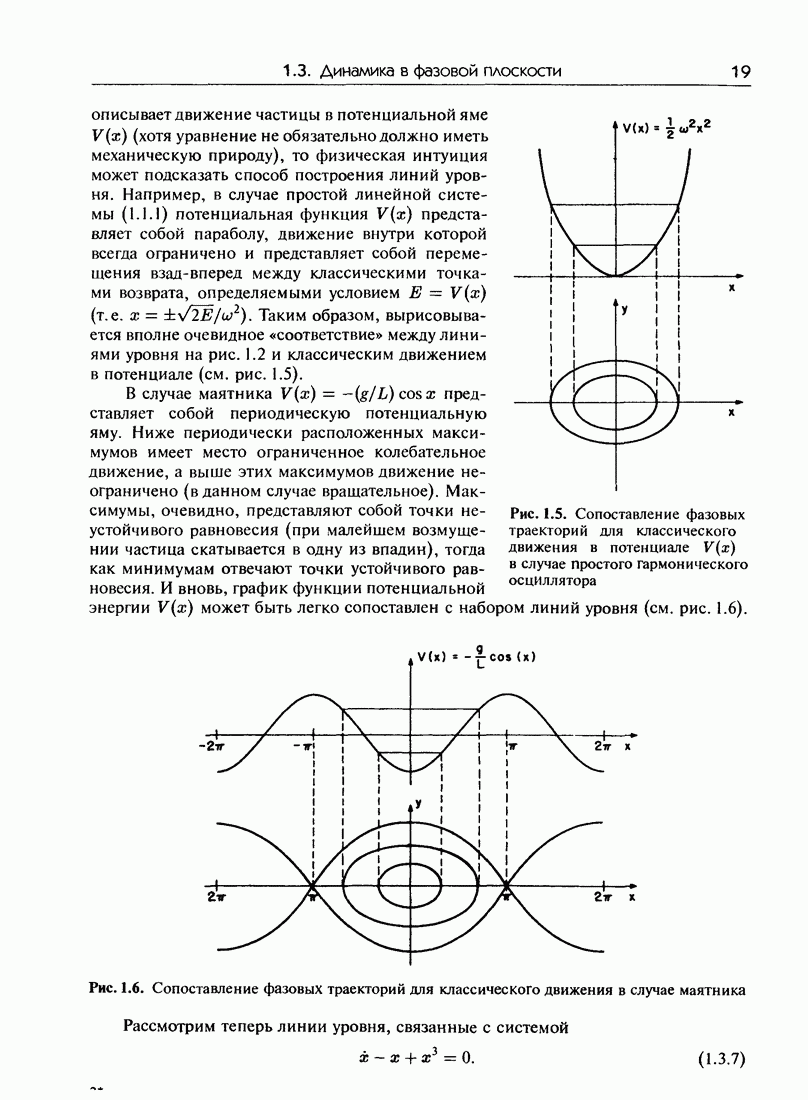
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
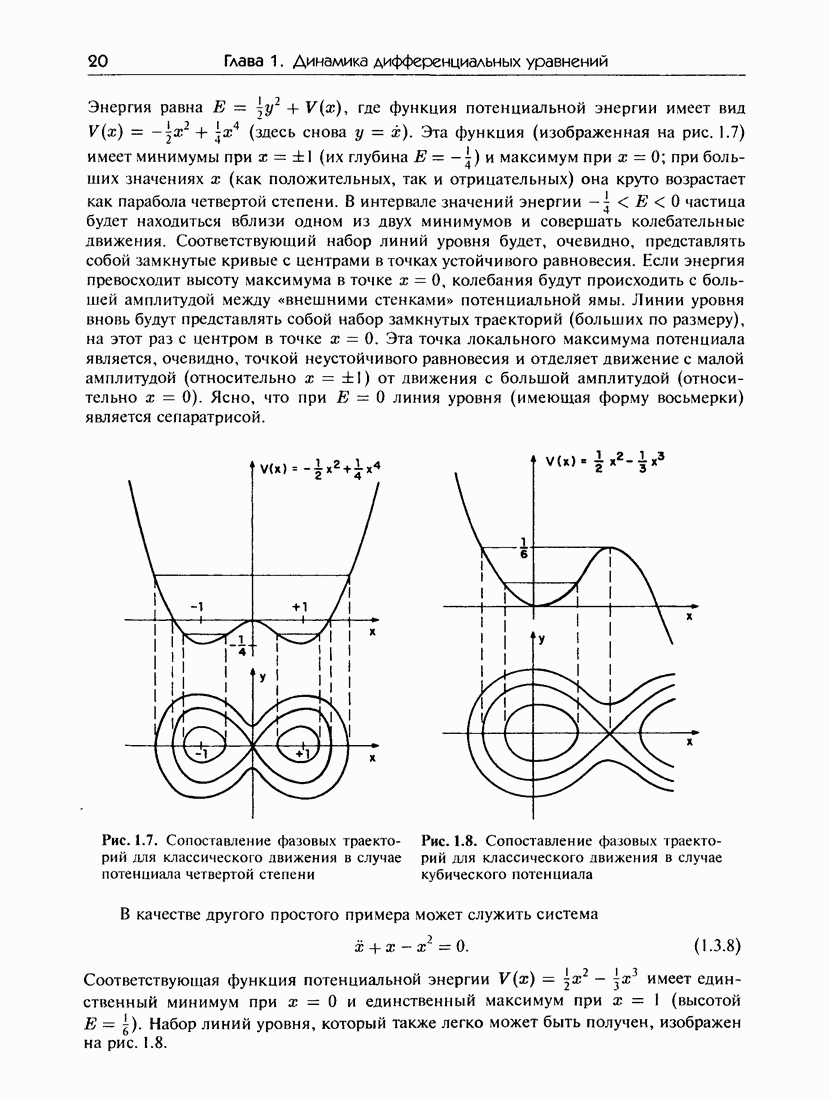
- 1.3.б. фазовые портреты консервативных систем
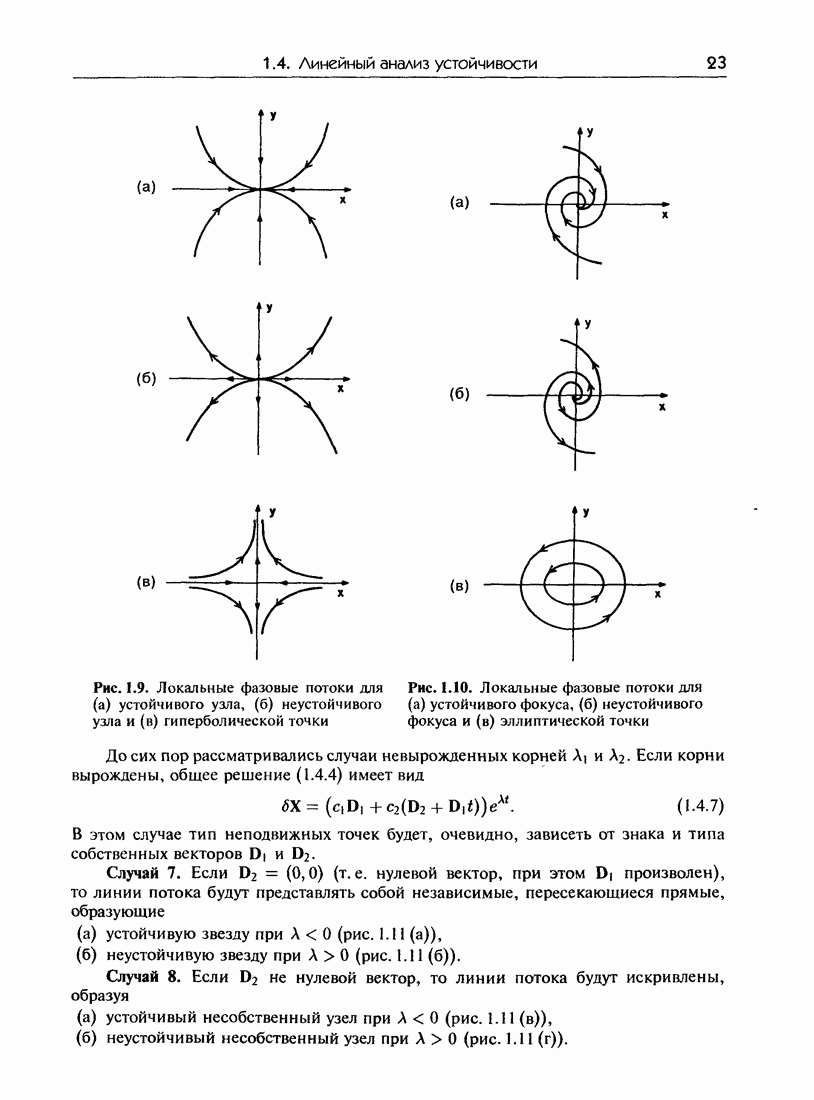
- 1.4. Линейный анализ устойчивости
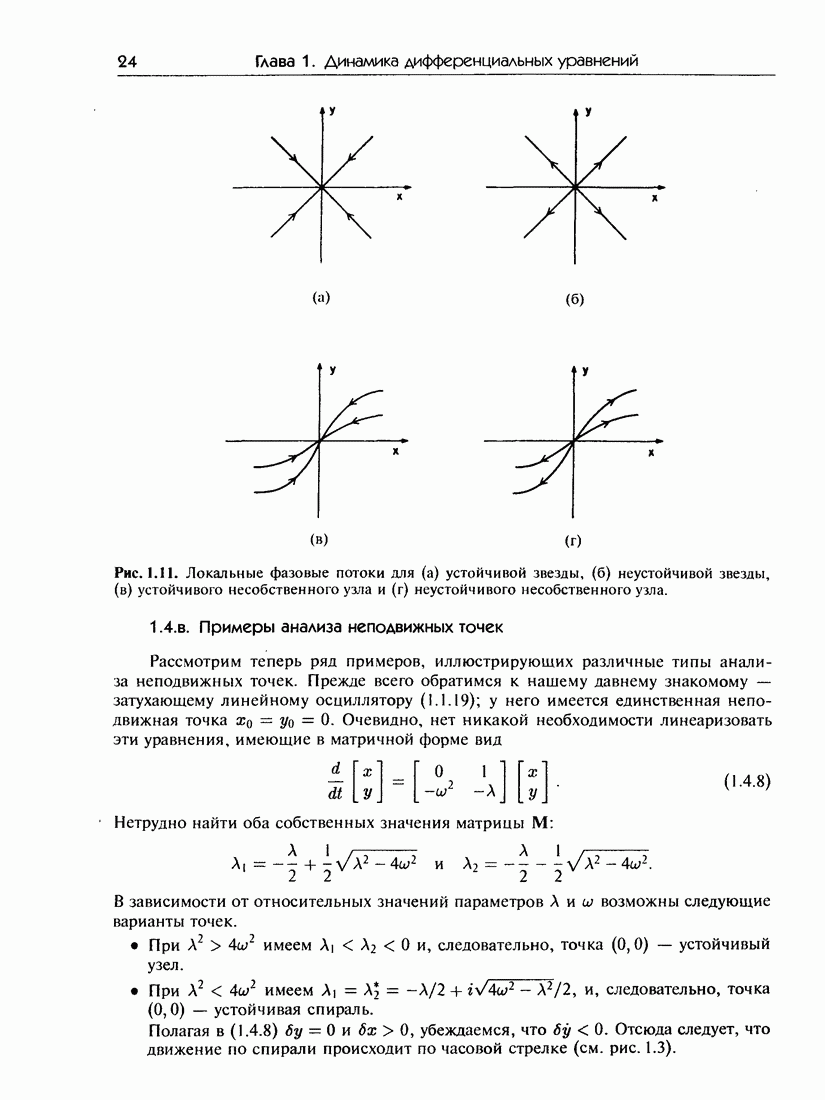
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
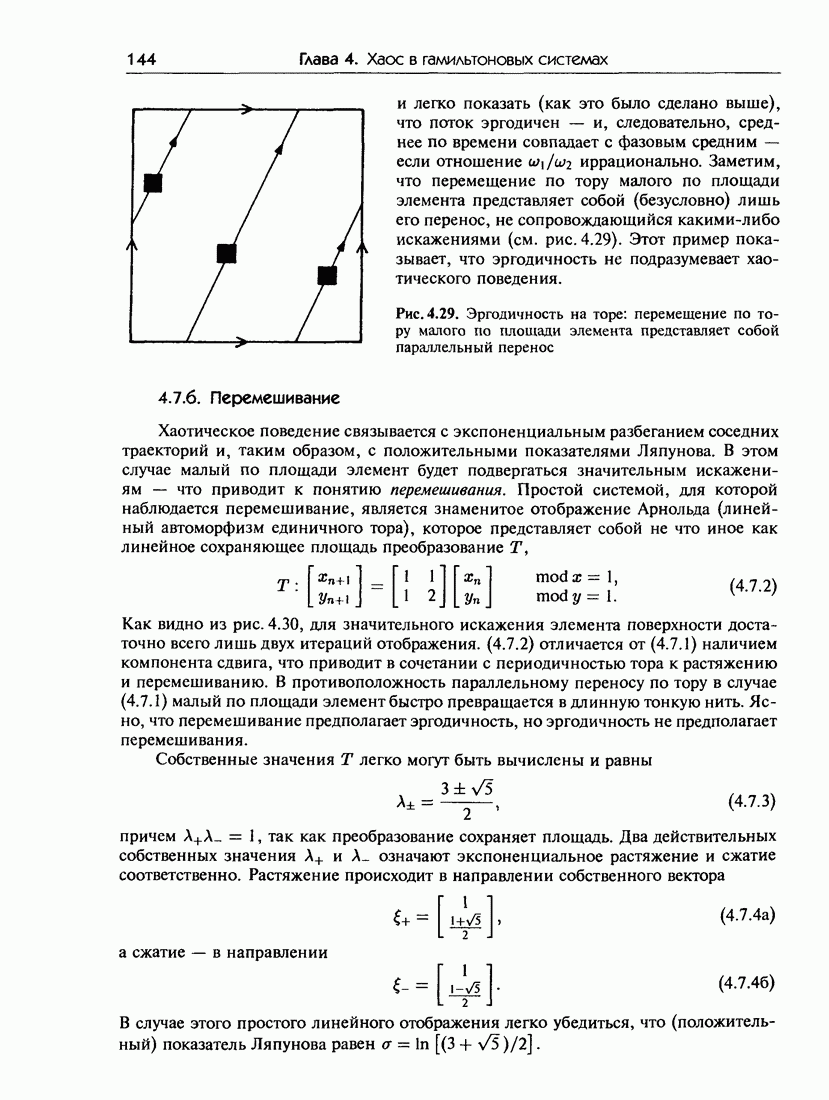
- 4.7.б. Перемешивание
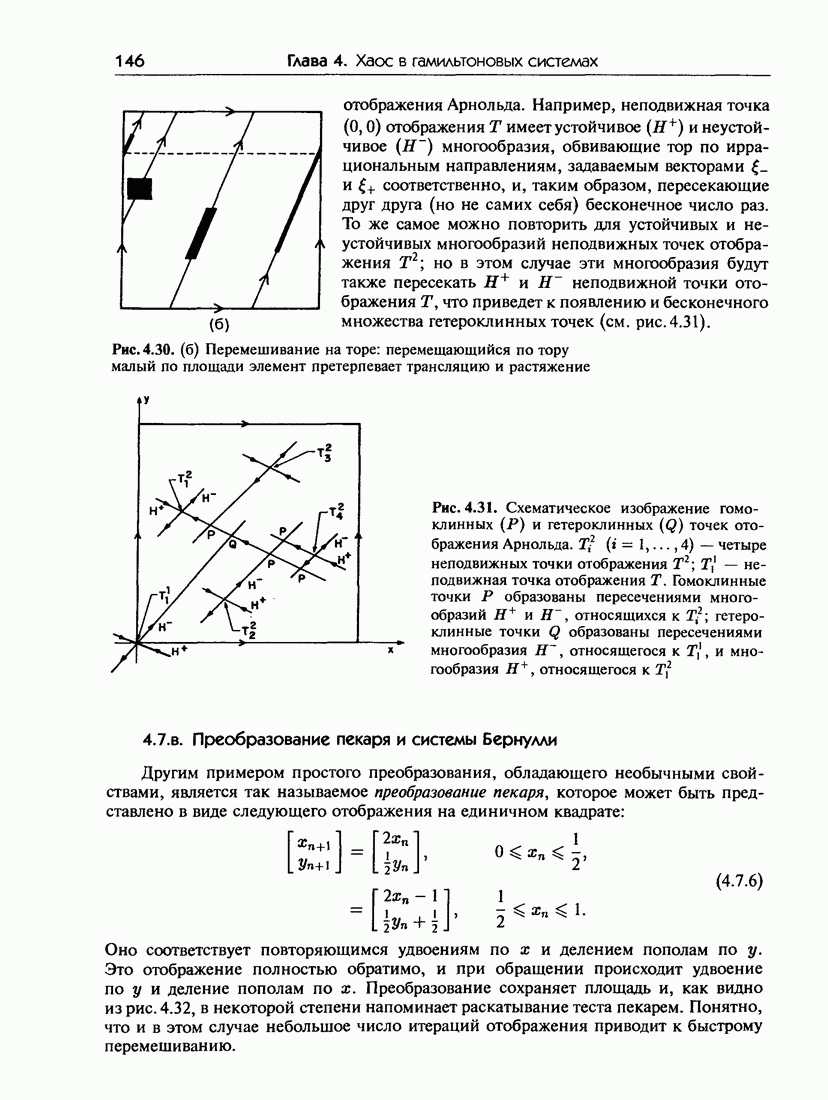
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
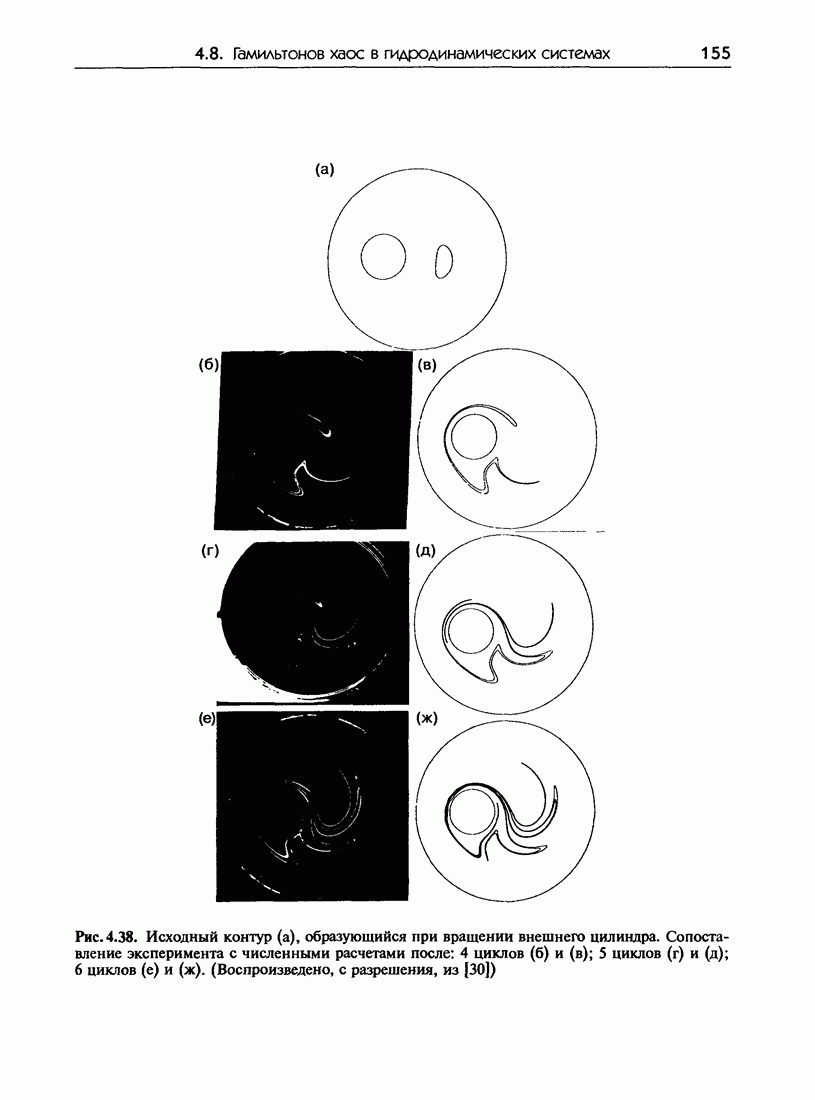
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
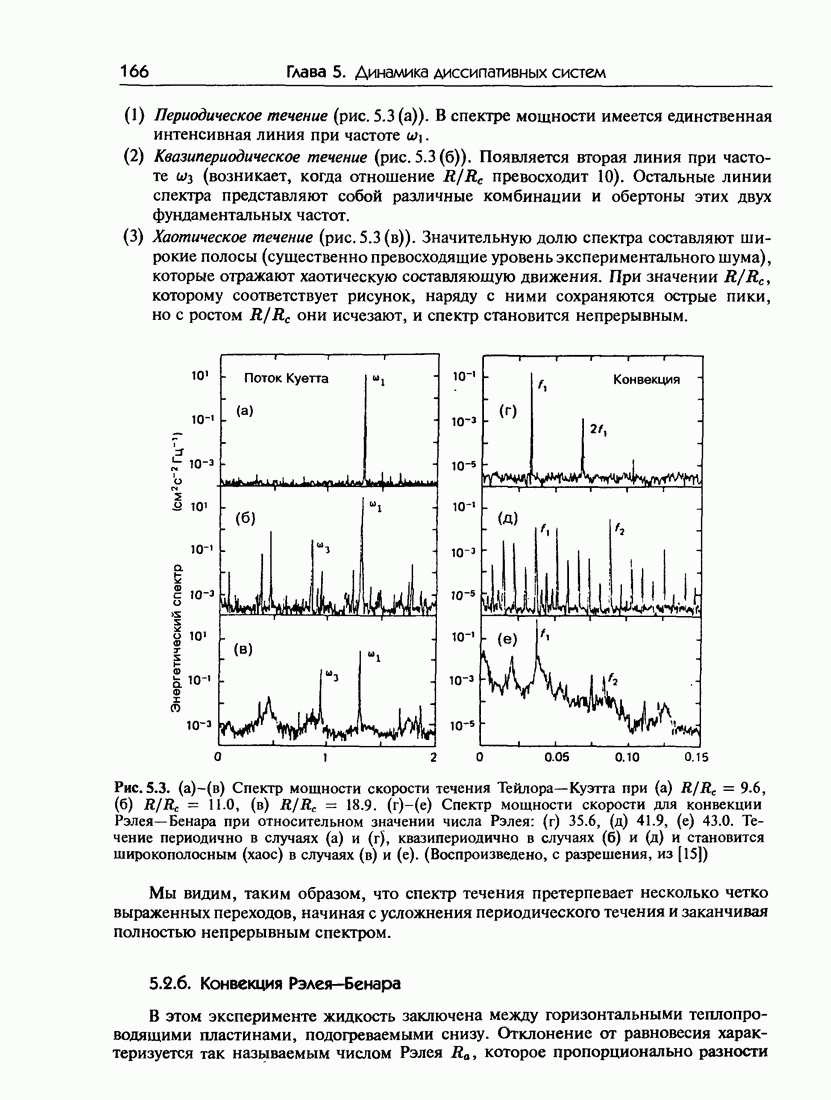
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
- 5.4.в. Отображение Хенона
- 5.5. Бифуркации удвоения периода
- 5.5.а. Механизм удвоения периода
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
- 5.5.г. Другие классы универсальности
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
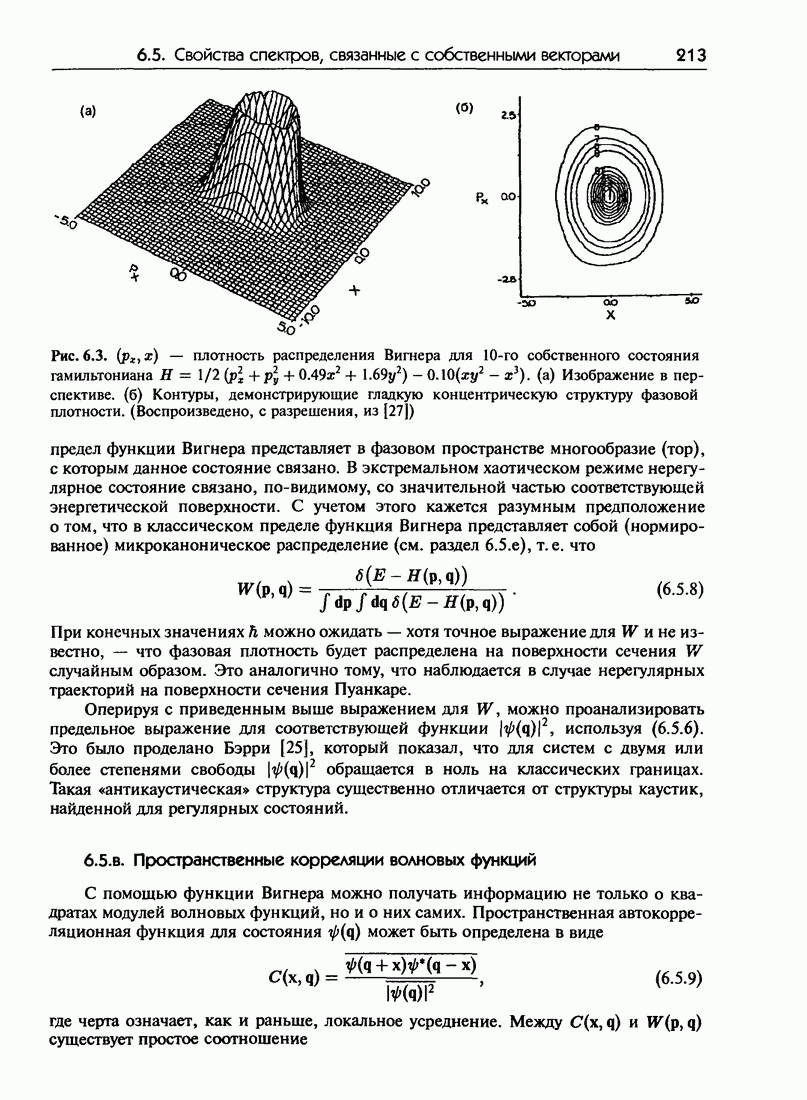
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
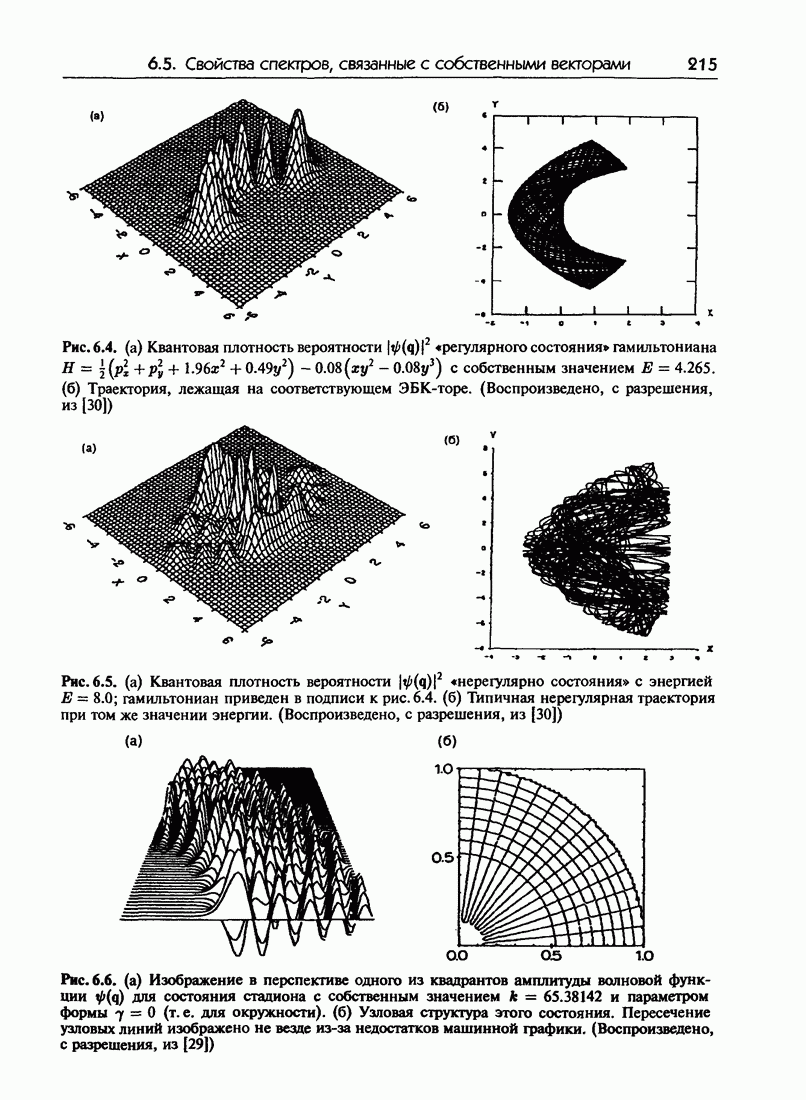
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
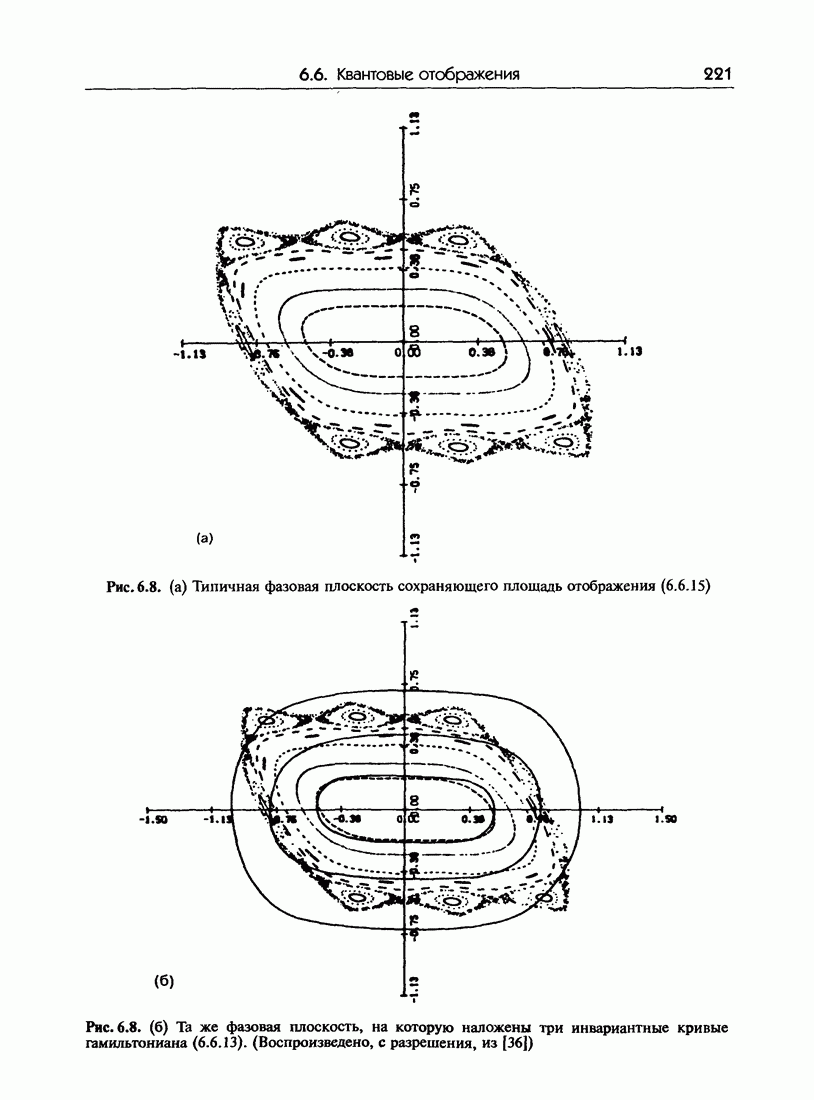
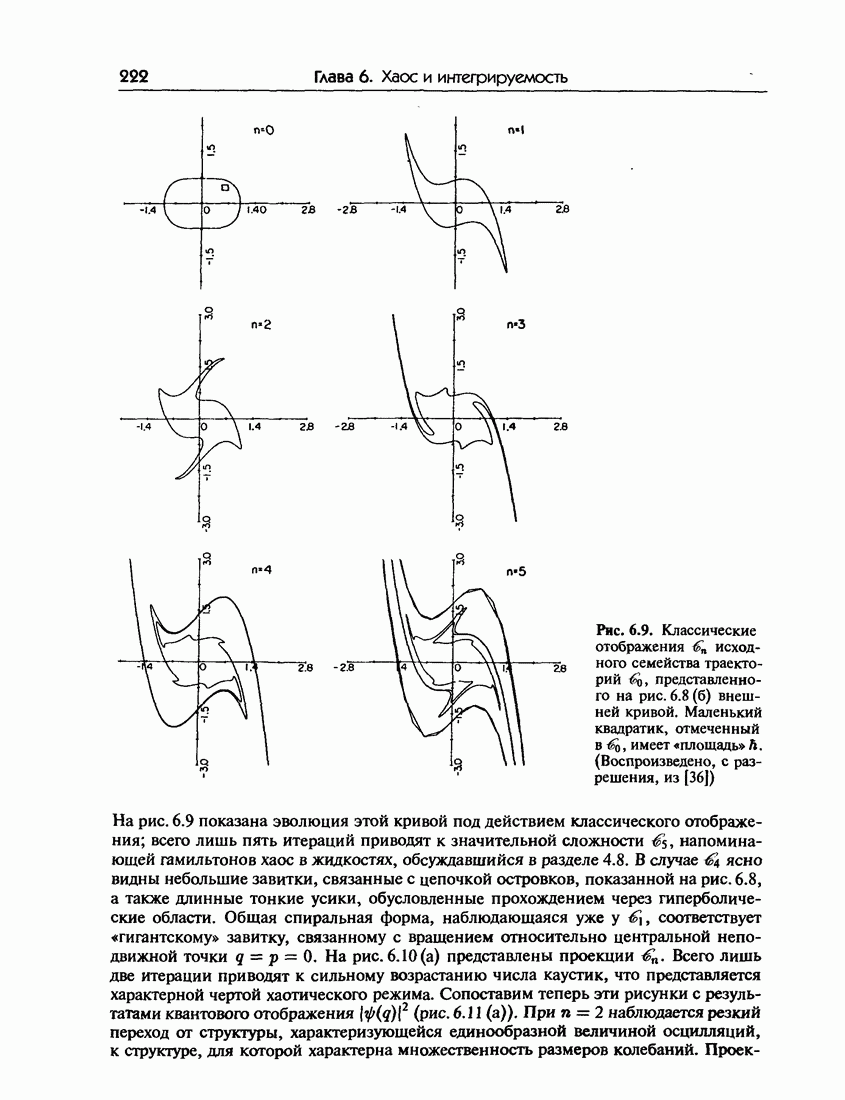
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
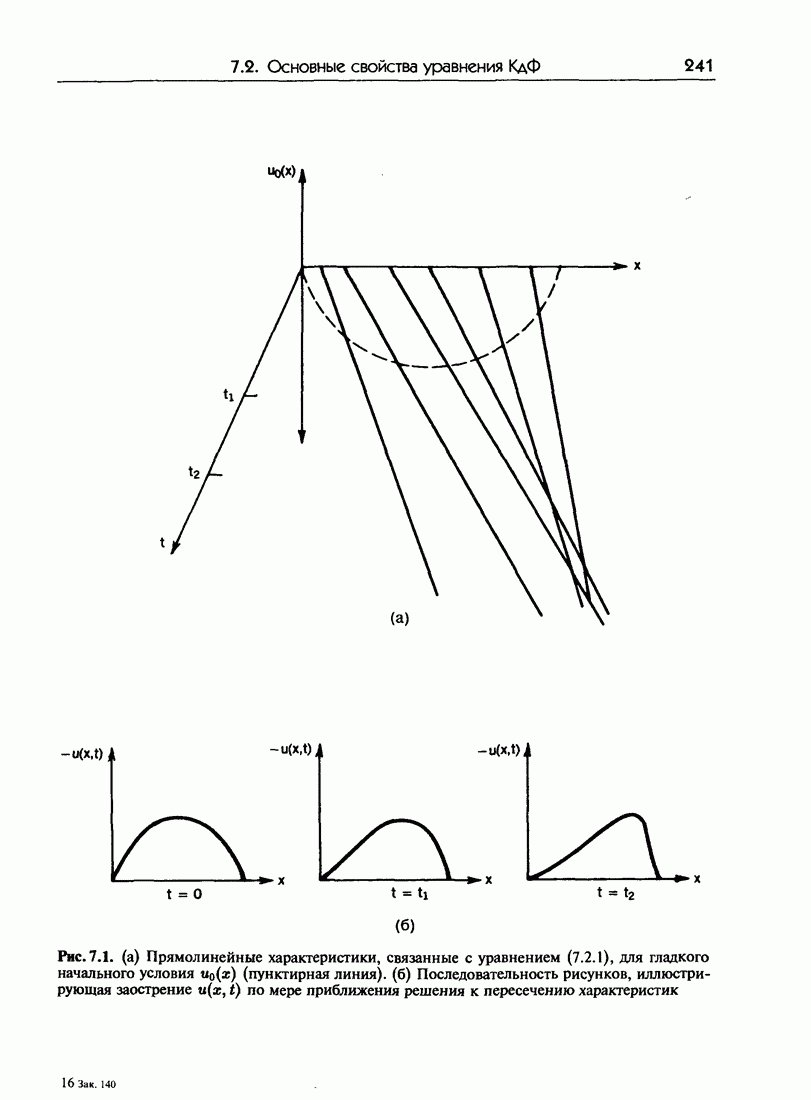
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
- 7.5. Другие солитонные системы
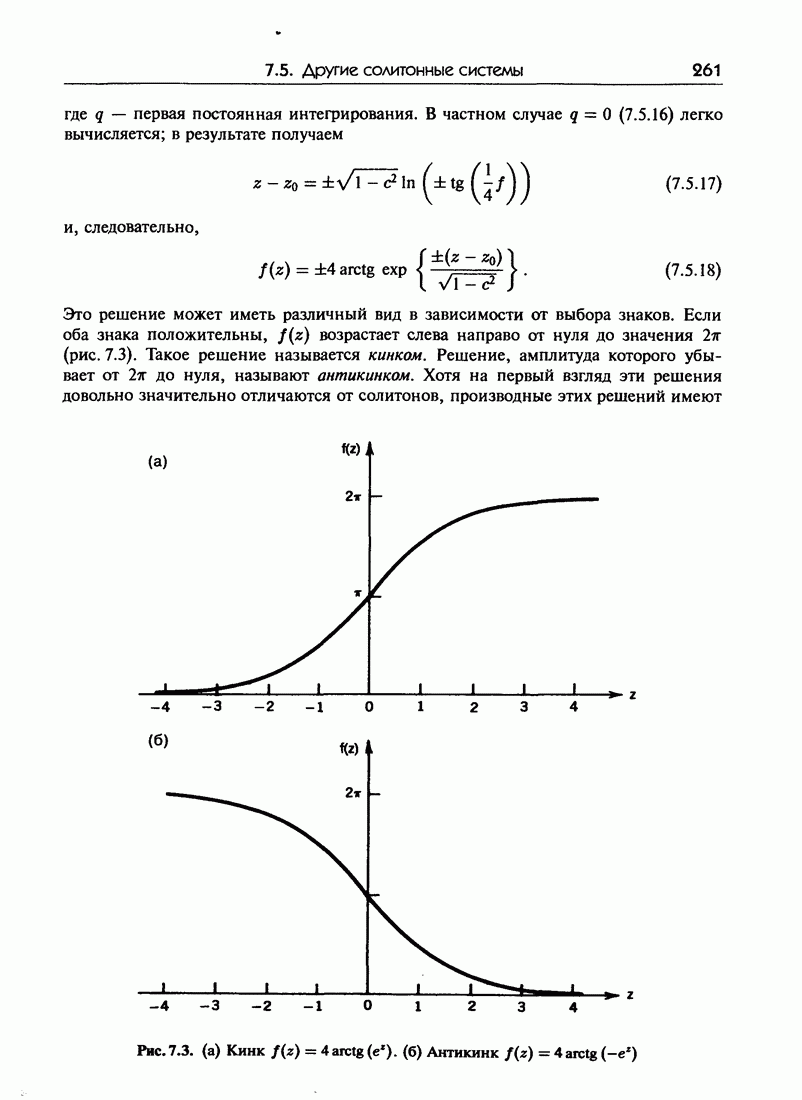
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
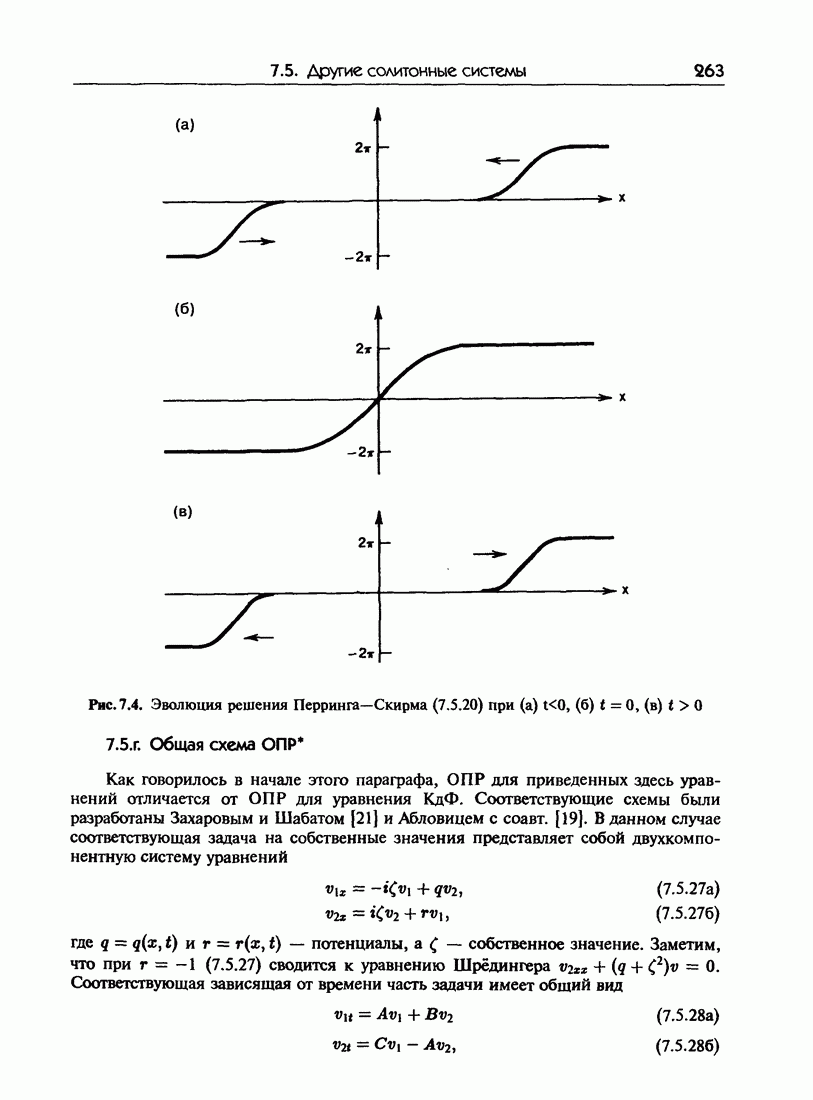
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
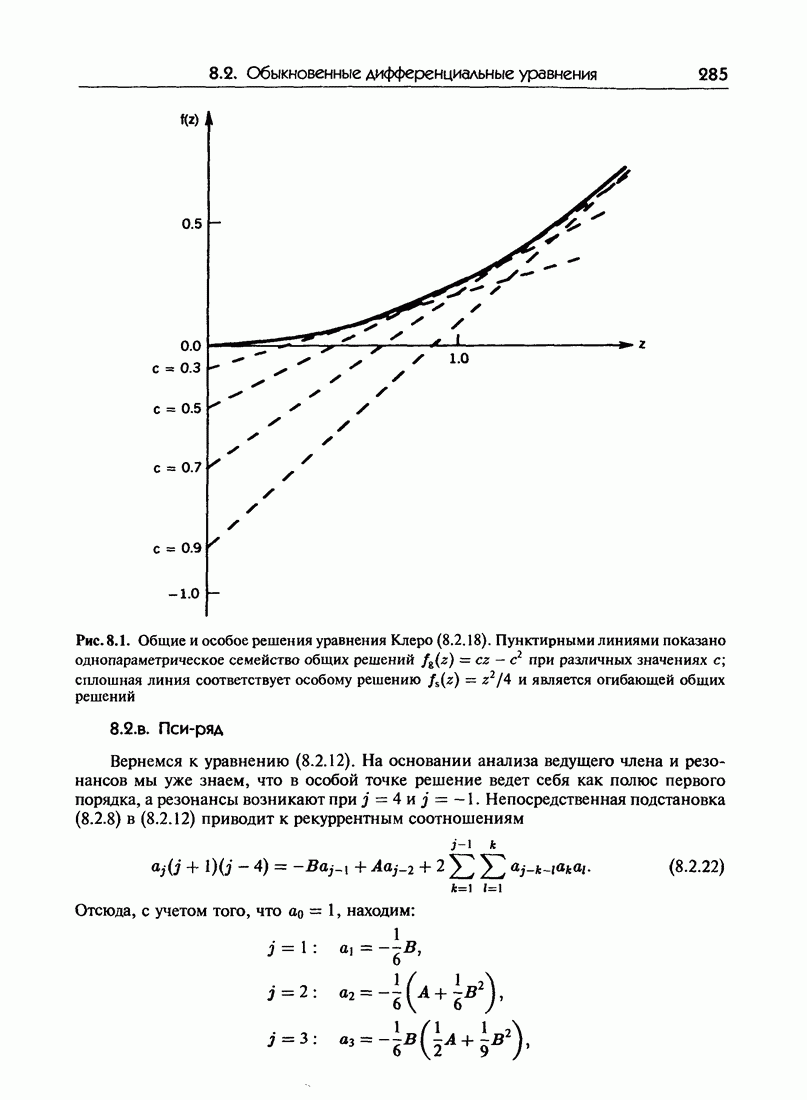
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда