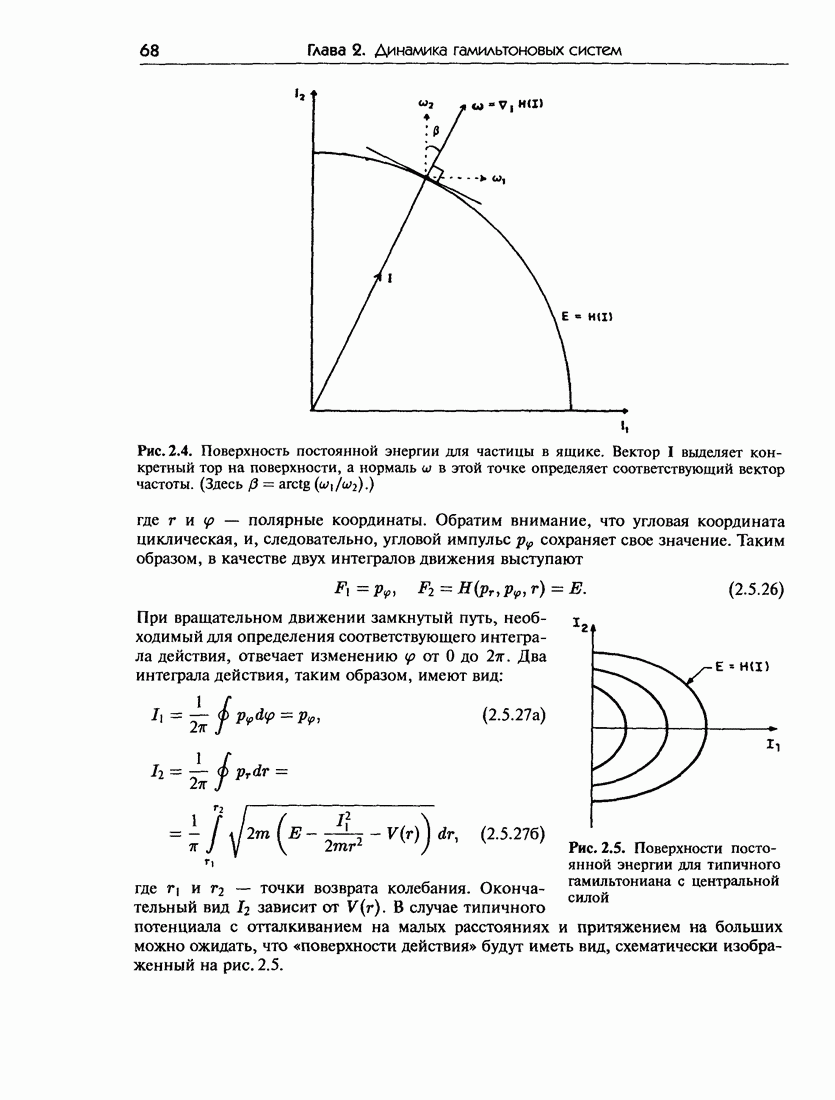
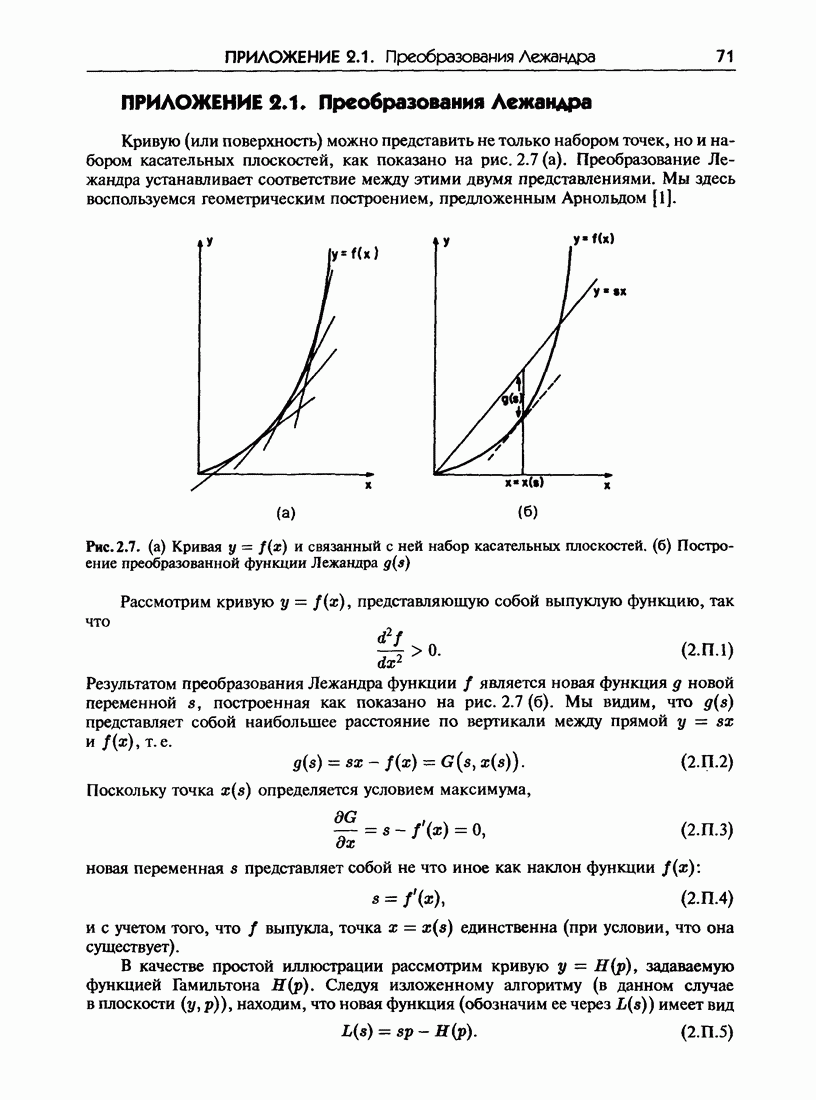
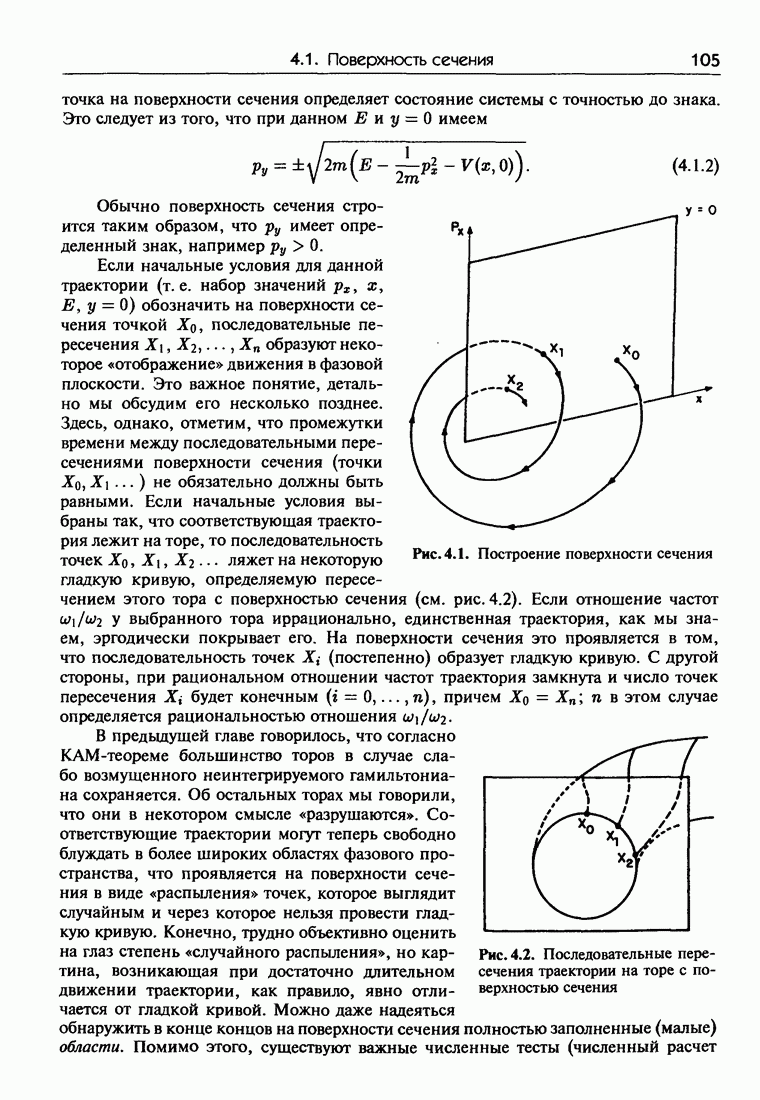
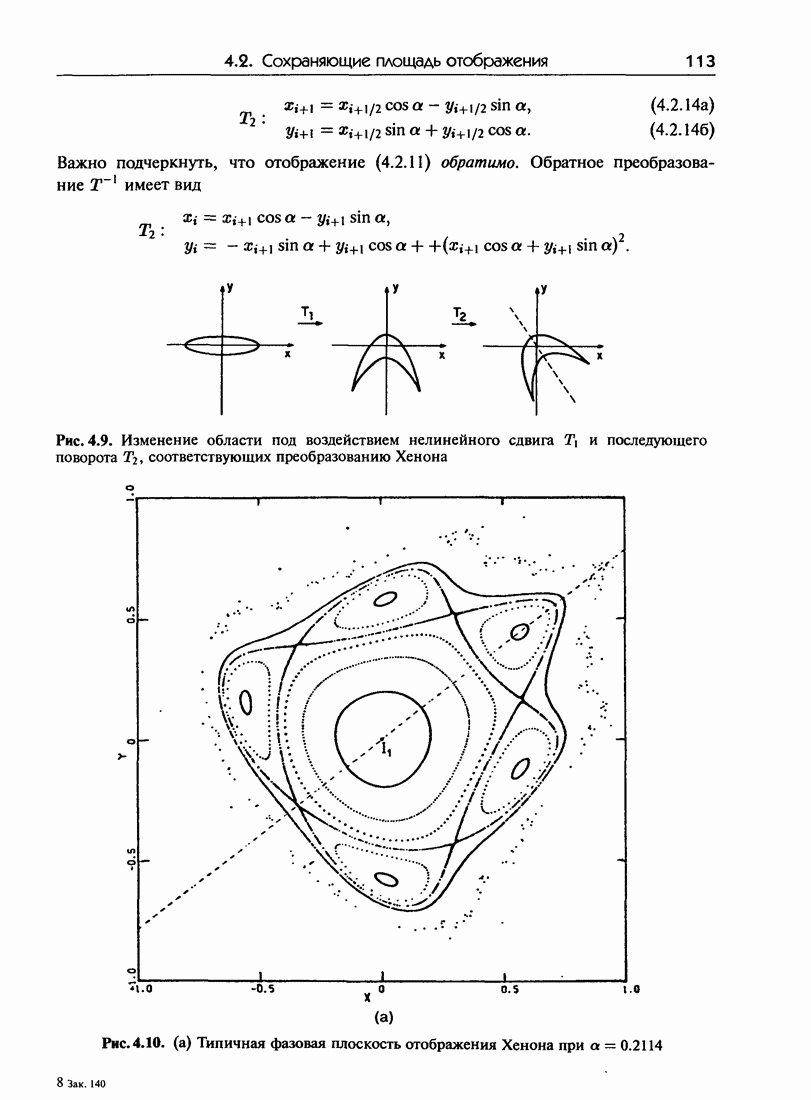
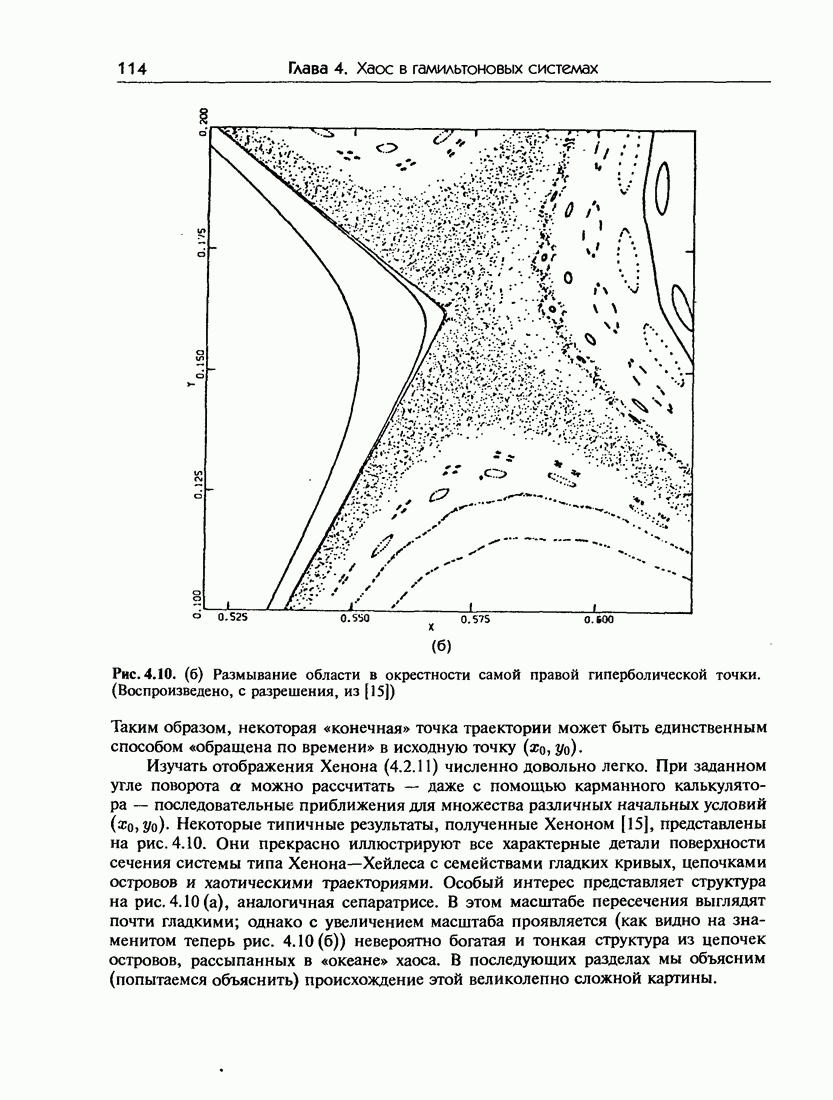
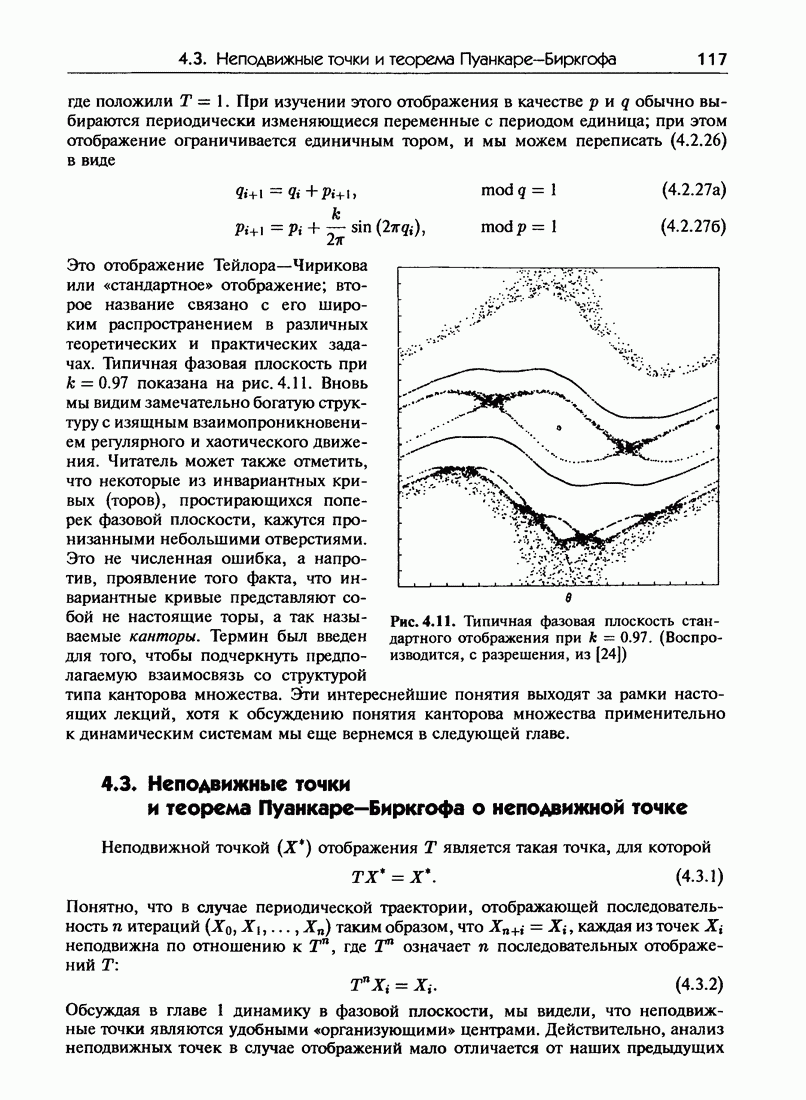
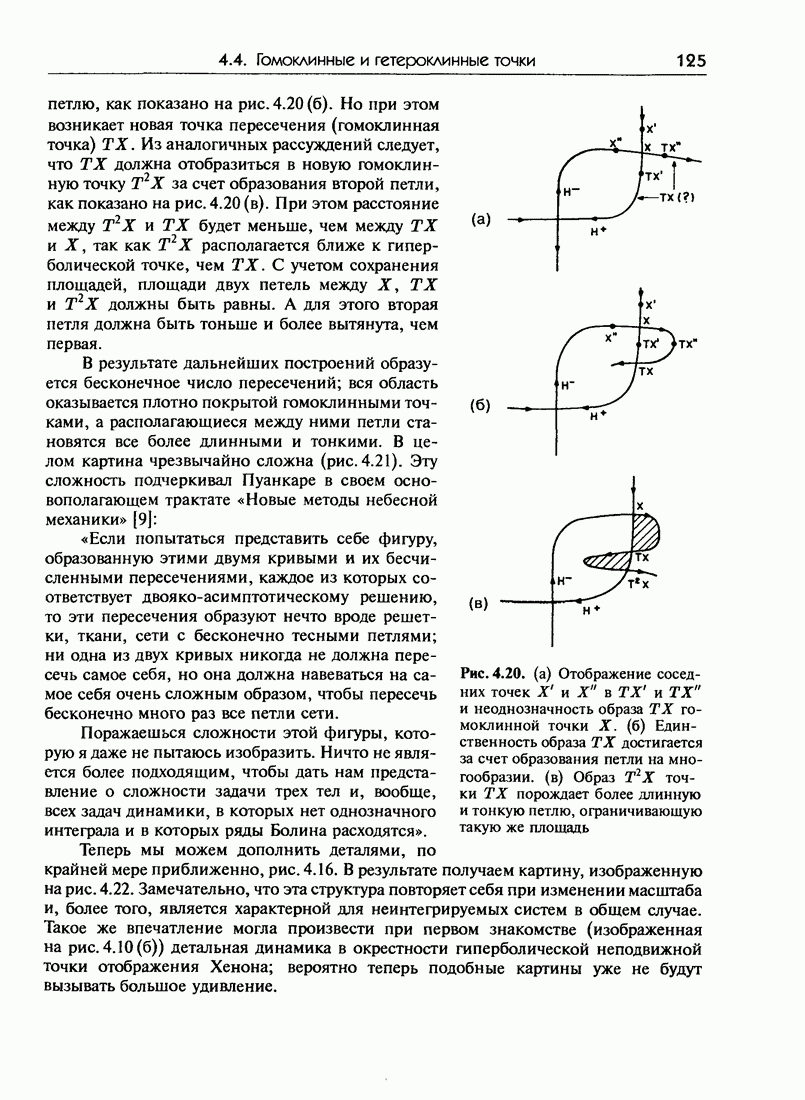
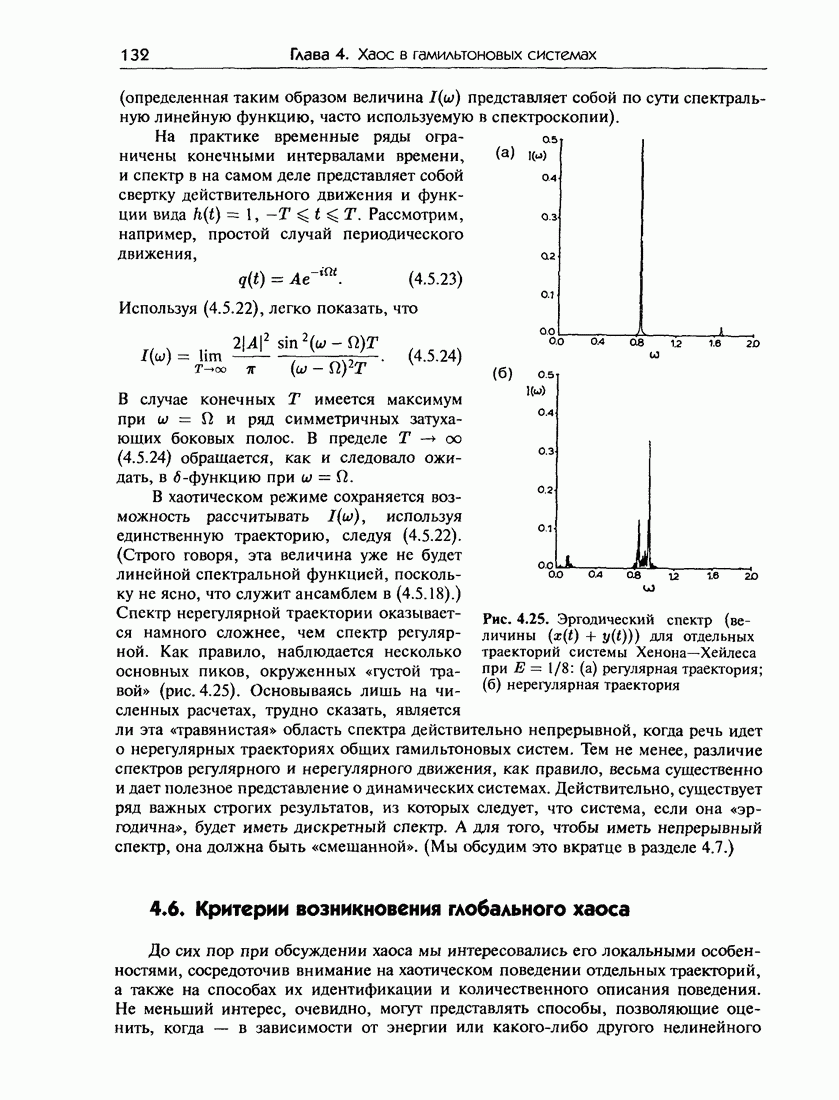
| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
Понятие «интегрирования» дифференциального уравнения является, несомненно, весьма тонким. Для большинства рассмотренных до сих пор систем второго порядка существование постоянного первого интеграла (в консервативных случаях это механическая энергия) позволяло понизить на единицу порядок уравнения, сводя тем самым задачу к отысканию решения в «квадратурах». Выражения типа «точное решение» или «аналитическое решение» дифференциального уравнения использовались здесь (равно как и в других работах) весьма произвольно. Вопрос о том, что подразумевается под этими удобными выражениями, безусловно не является неуместным. В конце концов, можно ли было до появления эллиптических функций не считать неразрешимыми простые нелинейные дифференциальные уравнения кубического осциллятора или маятника? Правомерен вопрос, что происходит «за пределами» эллиптических функций, скажем, с уравнениями типа (1.2.4), когда показатель степени при больше 3. В этом случае, по крайней мере, еще существует интеграл движения (энергия), позволяющий перейти к квадратурам — такие интегралы называются гиперэмипттескими интегралами. Обращение, однако, становится в этом случае гораздо более сложным, и в игру вступают многие результаты из алгебраической геометрии.
В случае неконсервативных систем второго порядка вопрос об «интегрировании» становится более запутанным. В некоторых случаях, обсуждавшихся в разделе 1.5, возможно было отыскать зависящий от времени интеграл, который позволял понизить порядок. Но это, как легко понять, были весьма специальные случаи. Затруднения иного рода связаны с системами уравнений типа


известными как уравнения Пенлеве первого и второго типов соответственно. Для них неизвестны первые интегралы, и они не могут быть «проинтегрированы в квадратурах». И хотя очевидно, что уравнения, подобные этим, имеют «решения», нетривиальным и спорным остается вопрос, в какой степени эти решения могут быть представлены «аналитически» — в противоположность численному результату.
Фактором, существенным при обсуждении этого вопроса, является аналитическая структура решения, т. е. поведение решения в комплексной плоскости. К счастью, целый ряд важных свойств, таких как возможные сингулярности решения, может быть определен непосредственно по виду уравнений движения, без обращения к точному решению (которое мы, естественно, можем и «не знать»). Может быть и так, что аналитическая структура особенно «проста» и соответствующее уравнение оказывается в некотором смысле «интегрируемым». Эта возможность будет обсуждаться в главе 8.
Может быть вопрос интегрируемости автономных систем второго порядка в определенном смысле довольно академичен. В этих случаях движение всегда ограничено двумерной фазовой плоскостью и никогда не проявляет сколь-нибудь сложного или хаотического поведения. Когда фазовое пространство приобретает третье измерение (или более), что может иметь место в случае неавтономных систем второго порядка или в случае автономных систем третьего порядка, вопрос об интегрируемости становится гораздо более содержательным вследствие возможности хаотического поведения. Здесь важную роль приобретает существование «интегралов движения», поскольку они, как мы видели, налагают геометрические ограничения на фазовый поток. Рассмотрим следующую автономную систему третьего порядка:

Прежде всего заметим, из (1.7.3а) и (1.7.3в) следует, что  Это позволяет найти (постоянный) интеграл движения
Это позволяет найти (постоянный) интеграл движения

и мы видим, таким образом, что траектории в трехмерном фазовом пространстве  ограничены поверхностью, определяемой уравнением (1.7.4). С помощью этого интеграла систему третьего порядка (1.7.3) можно свести к системе второго порядка
ограничены поверхностью, определяемой уравнением (1.7.4). С помощью этого интеграла систему третьего порядка (1.7.3) можно свести к системе второго порядка

Эта система второго порядка в свою очередь может быть сведена к системе первого порядка с помощью второго интеграла

который также можно рассматривать как (другое) геометрическое ограничение на фазовый поток. Уравнение (1.7.6) можно проинтегрировать в терминах эллиптических функций Якоби. Таким образом, отыскание двух интегралов  позволило
позволило
свести решение исходной системы третьего порядка к единственной «квадратуре» — в этом смысле можно считать, что система «проинтегрирована полностью».
Теперь рассмотрим систему

где а и  постоянные. В этом случае оказывается, что при
постоянные. В этом случае оказывается, что при  интегралы типа
интегралы типа  следовательно,
следовательно,  не могут быть найдены явным образом — и система, таким образом, не представляется «интегратируемой» (integratable). Таким образом, без численного анализа не ясно, в какой именно области трехмерного фазового пространства может «блуждать» решение.
не могут быть найдены явным образом — и система, таким образом, не представляется «интегратируемой» (integratable). Таким образом, без численного анализа не ясно, в какой именно области трехмерного фазового пространства может «блуждать» решение.
Простые (и тщательно подобранные!) примеры (1.7.3) и (1.7.7) порождают много фундаментальных вопросов. Первый из них — каким образом находить интегралы движения (если они существуют?). По мере того, как порядок уравнений возрастает, а их функциональный вид усложняется, эта задача становится очень сложной. Действительно, не существует сколь-нибудь систематической процедуры для ее решения — приходится полагаться на опыт, на удачу и, в безнадежных ситуациях, на провидение! Может оказаться, как это вытекает из одной блестящей работы русского математика Софьи Ковалевской, написанной сто лет назад, что существование интегралов может быть связано с аналитической структурой дифференциальных уравнений. Другой фундаментальный вопрос состоит в том, какое именно число интегралов необходимо, чтобы поэтапно осуществить полное «интегрирование». Именно здесь важно отличать различные классы динамических систем. Для гамильтоновых систем (к которым (1.7.3) и (1.7.7) не относятся) имеется ряд весьма сильных результатов. Как будет показано в следующей главе, если система имеет столько же интегралов  сколько степеней свободы (что составляет половину размерности фазового пространства), то она может быть «проинтегрирована в квадратурах». Коротко говоря, это является следствием очень специальных геометрических свойств гамильтониана —
сколько степеней свободы (что составляет половину размерности фазового пространства), то она может быть «проинтегрирована в квадратурах». Коротко говоря, это является следствием очень специальных геометрических свойств гамильтониана —  интегралов достаточно для ограничения потока в определенном направлении, допускающем последующую параметризацию в специальной системе координат, что приводит к тривиальному интегрированию. В случае негамильтоновых систем ситуация не столь благоприятна. Для того, чтобы осуществить полное интегрирование системы
интегралов достаточно для ограничения потока в определенном направлении, допускающем последующую параметризацию в специальной системе координат, что приводит к тривиальному интегрированию. В случае негамильтоновых систем ситуация не столь благоприятна. Для того, чтобы осуществить полное интегрирование системы  порядка
порядка  необходимо иметь
необходимо иметь  интеграл.
интеграл.
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
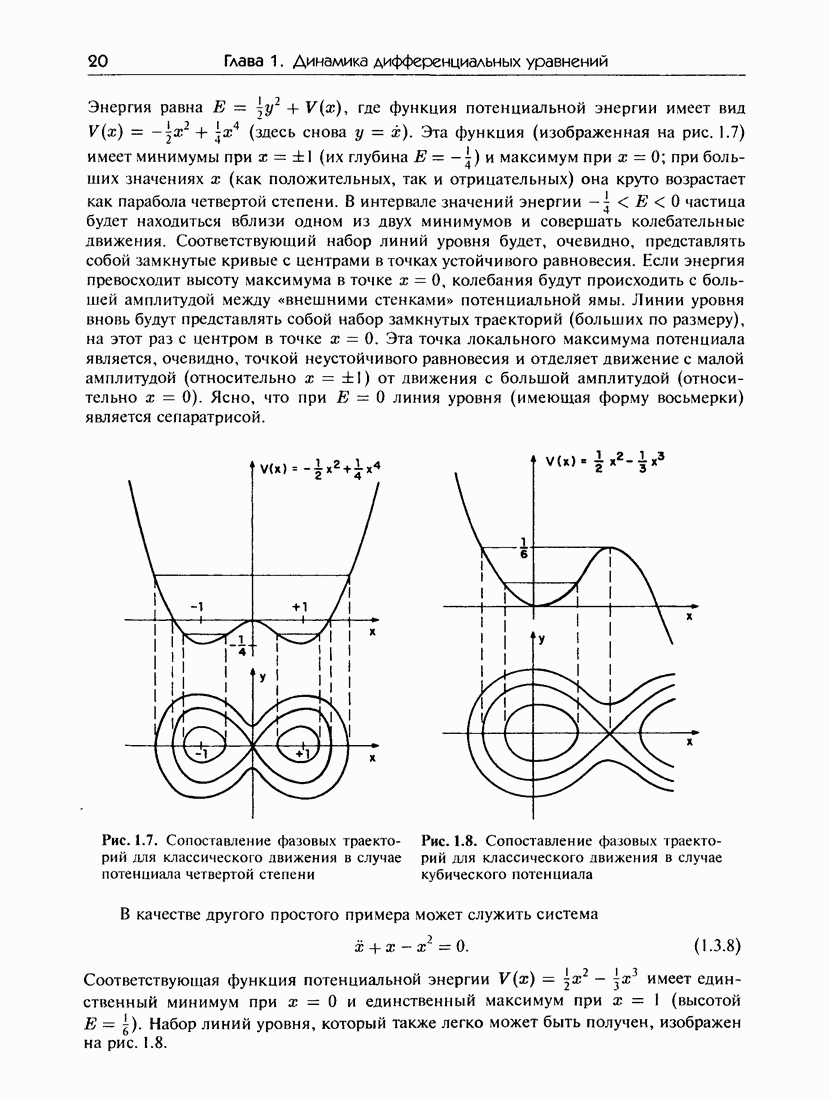
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
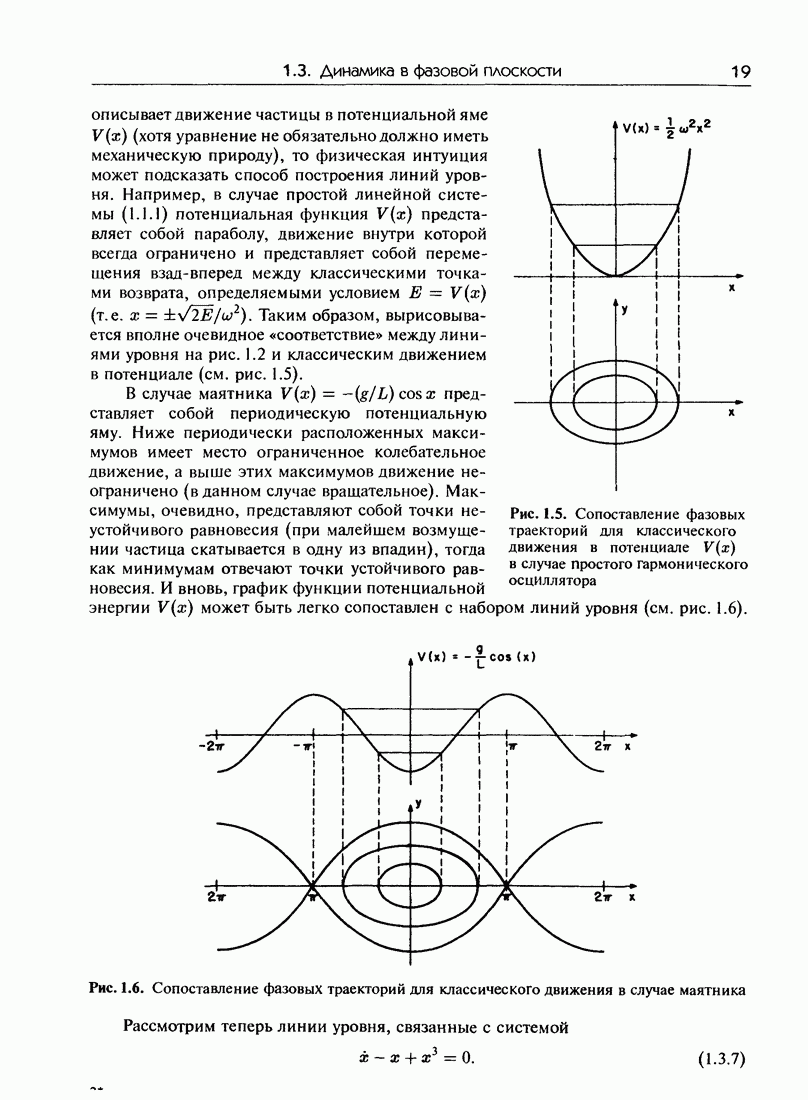
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
- 1.3.б. фазовые портреты консервативных систем
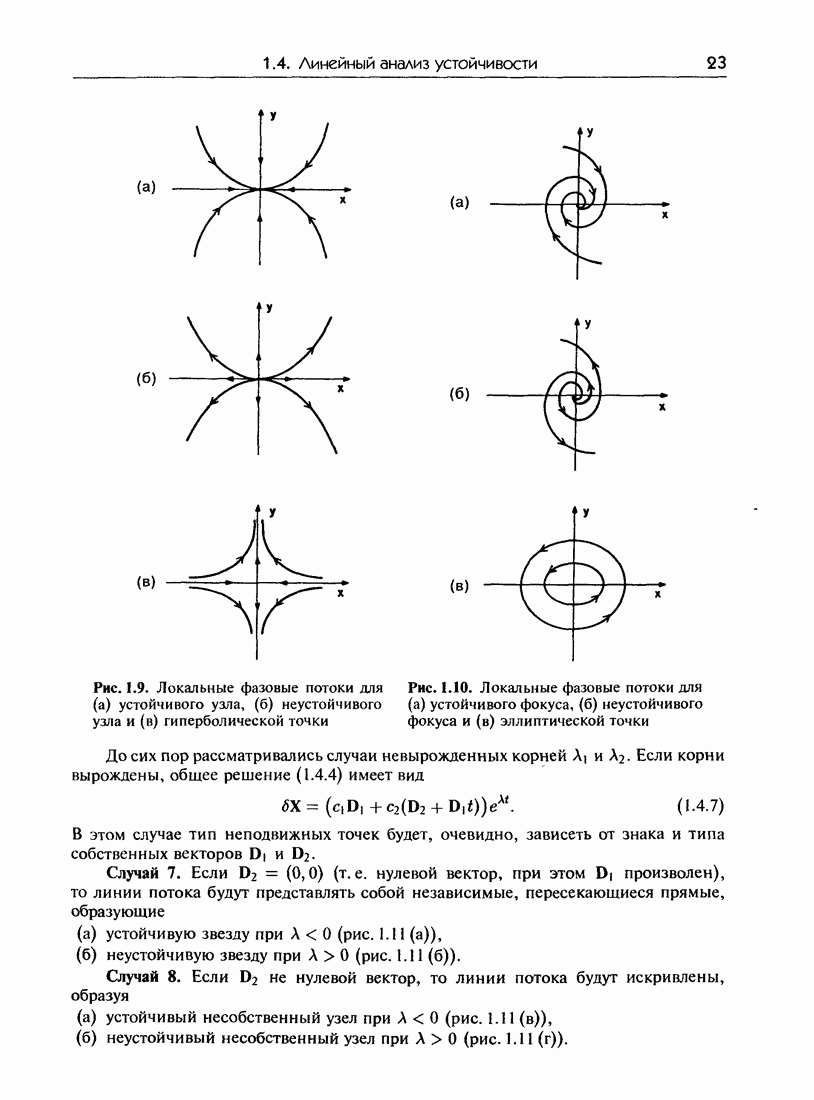
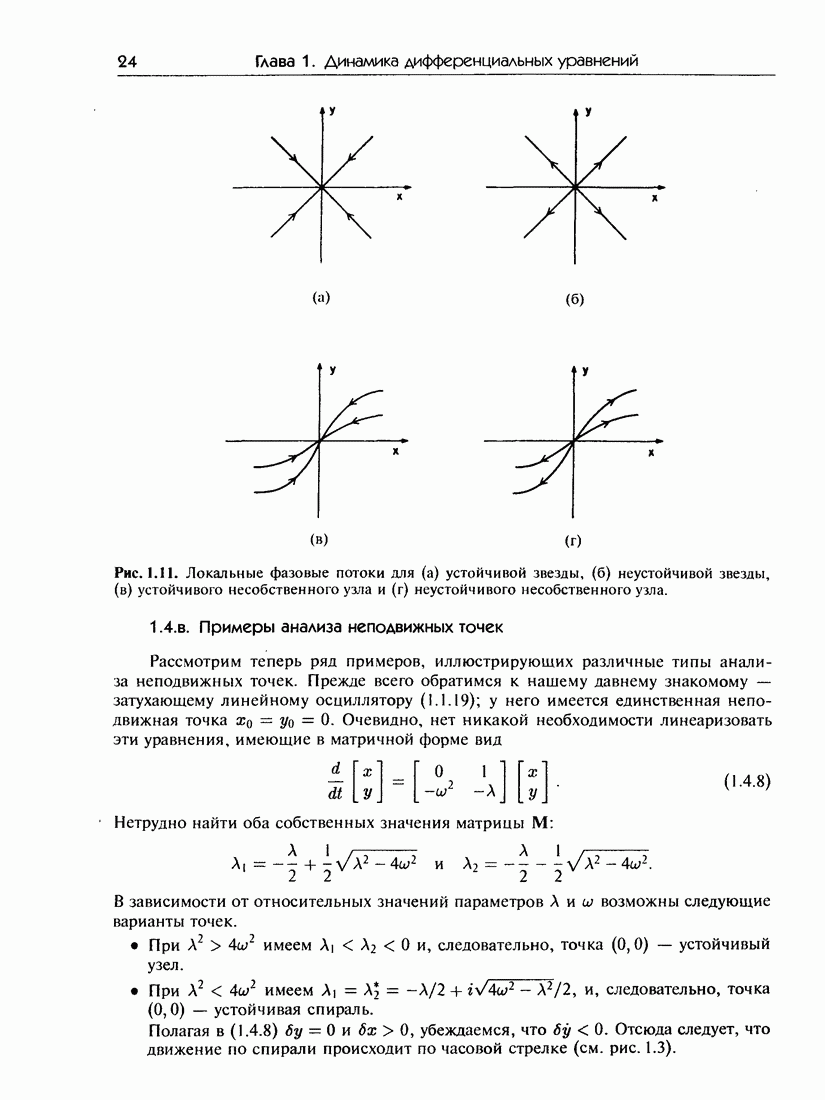
- 1.4. Линейный анализ устойчивости
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
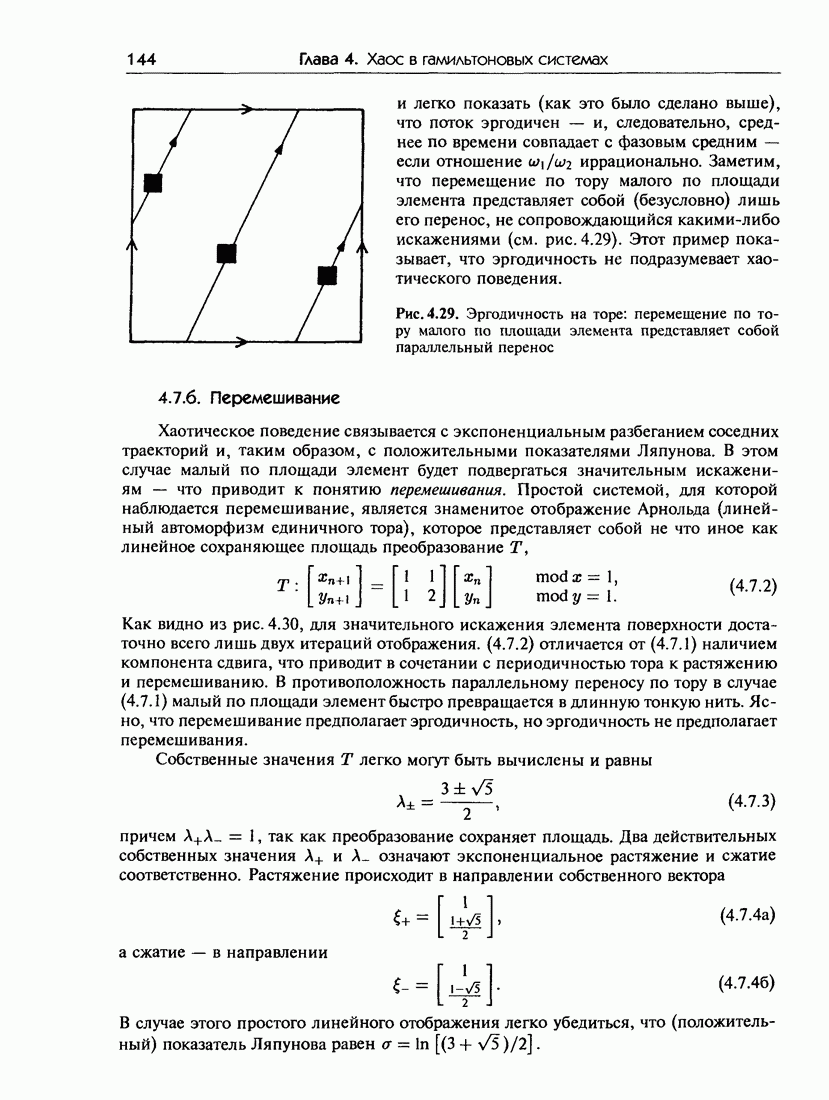
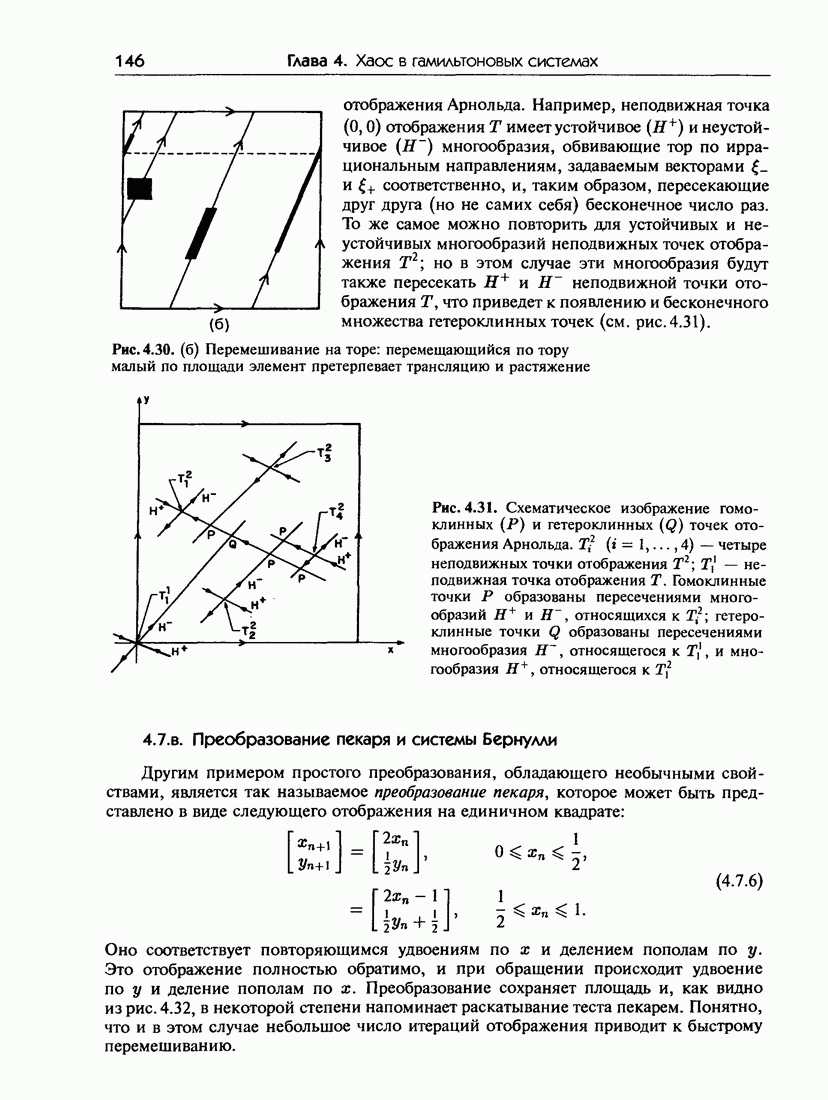
- 4.7.б. Перемешивание
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
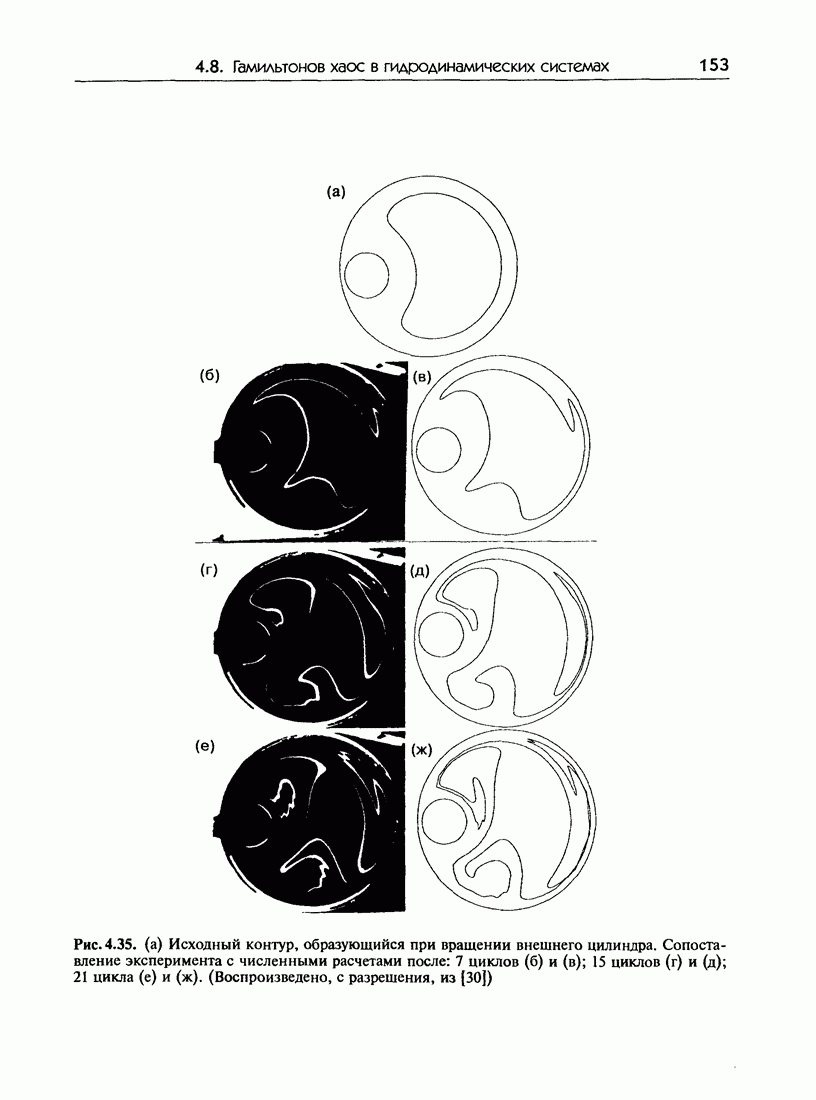
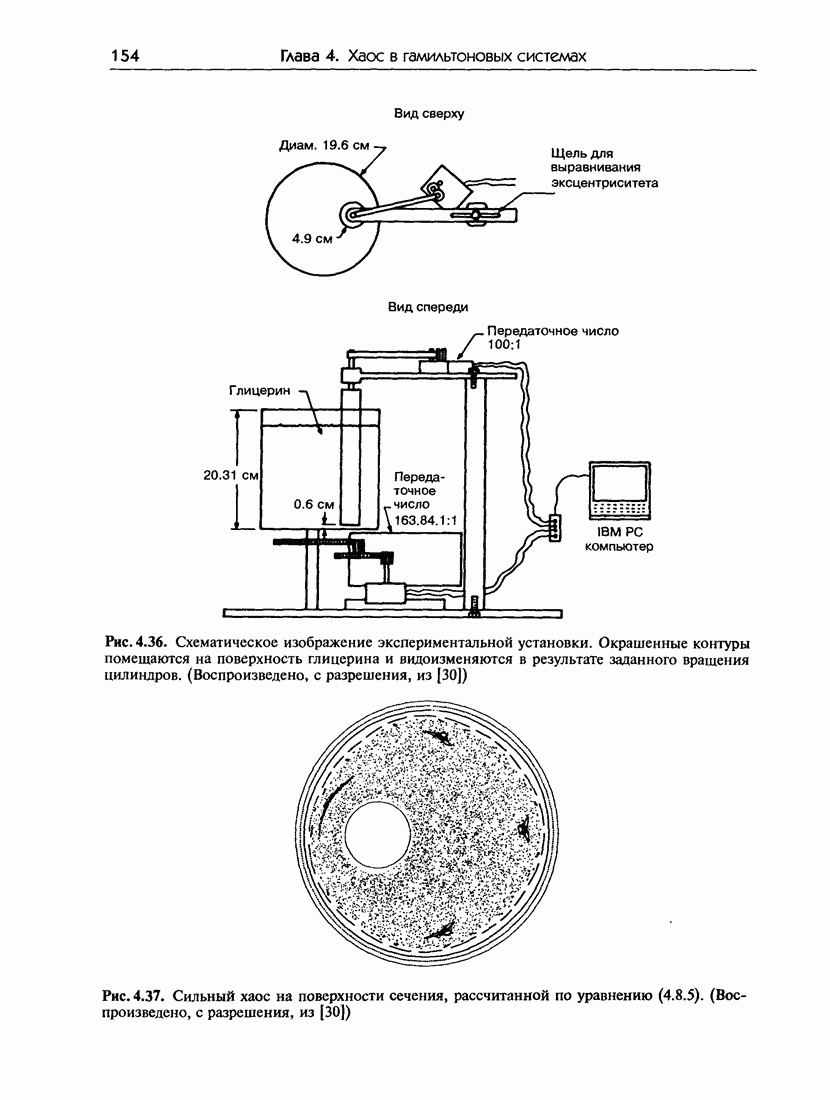
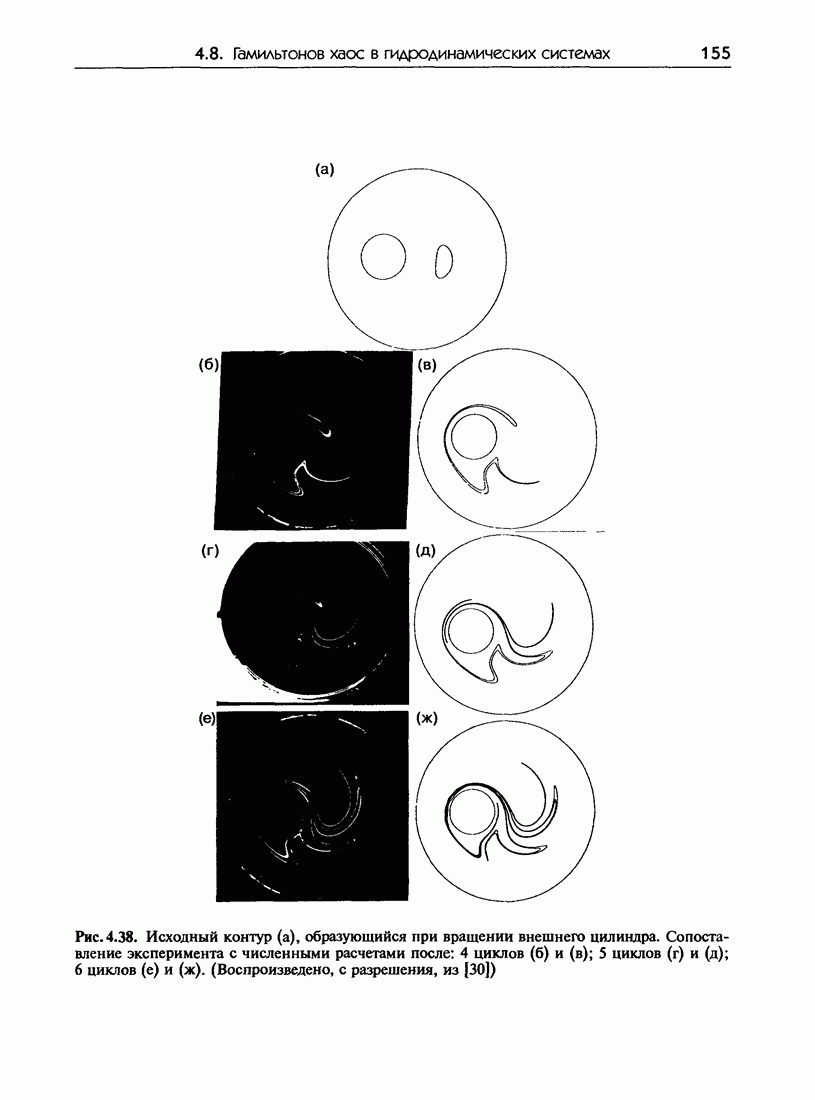
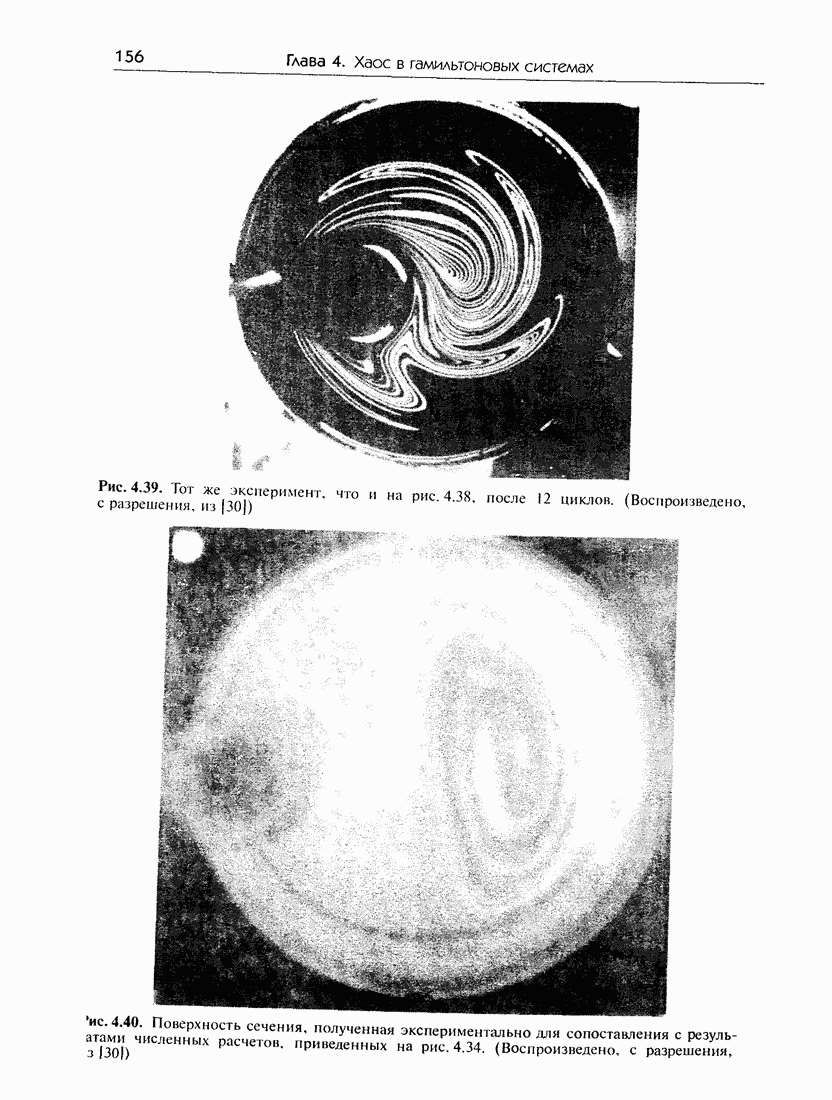
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
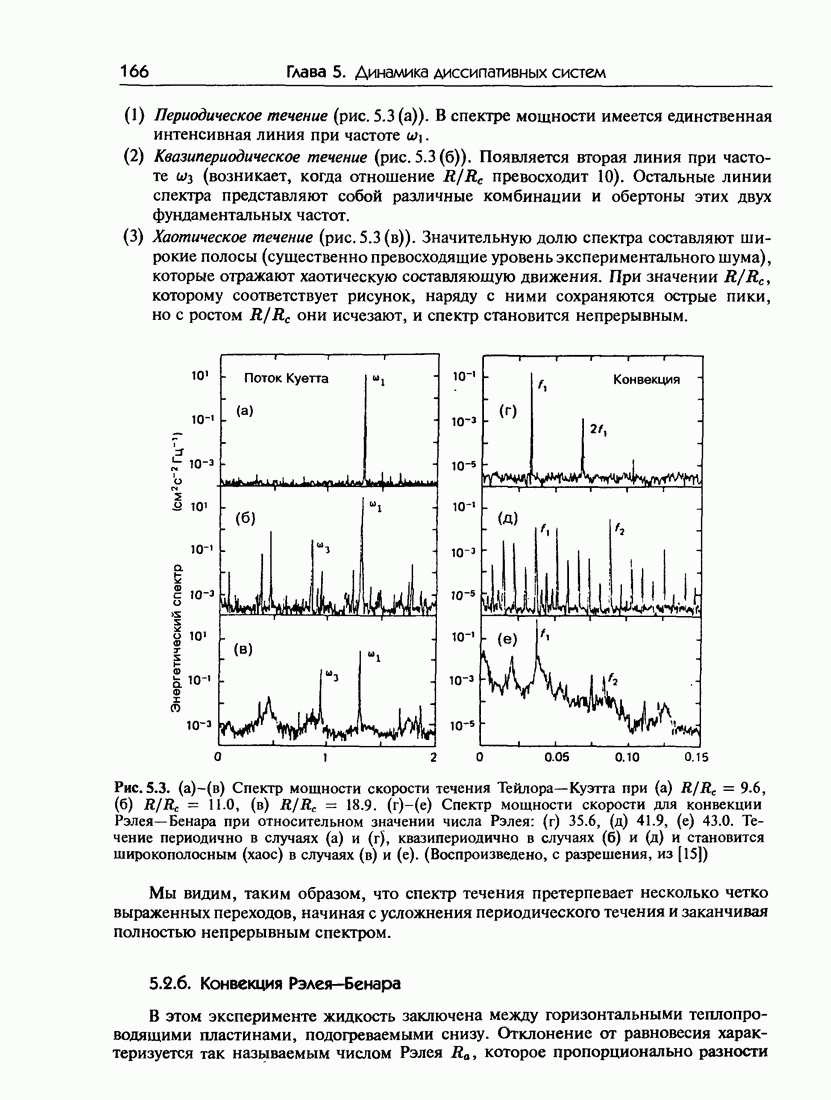
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
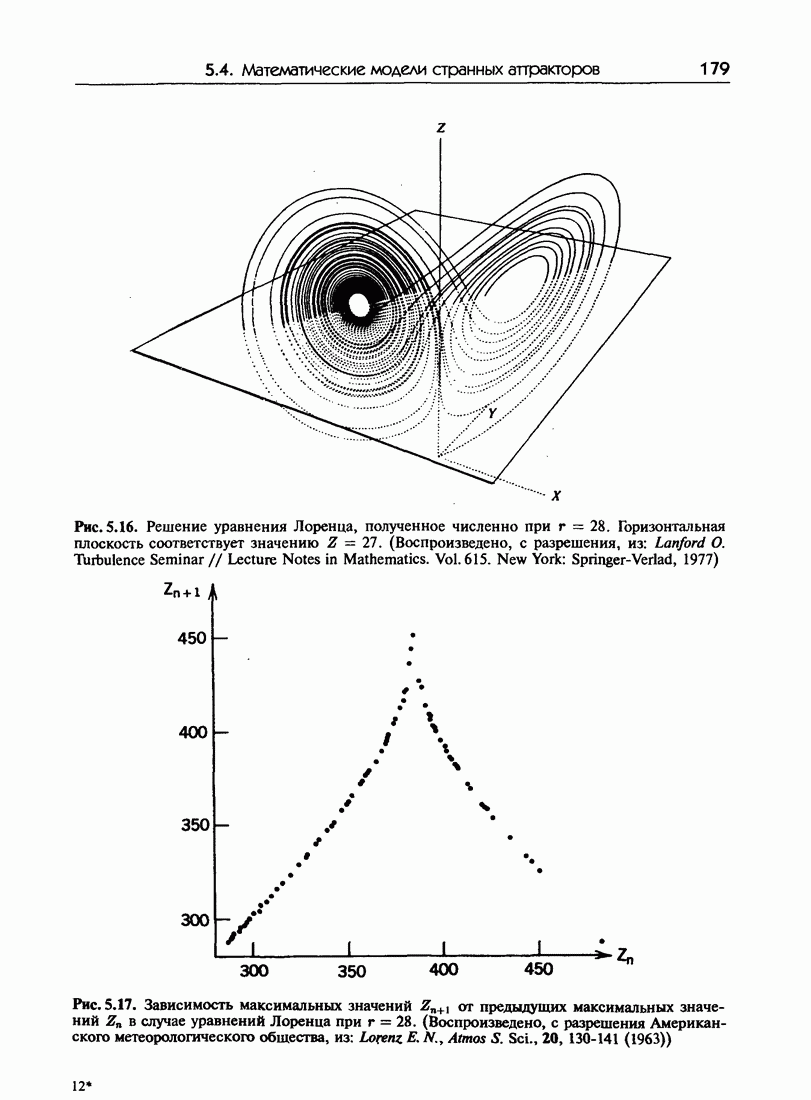
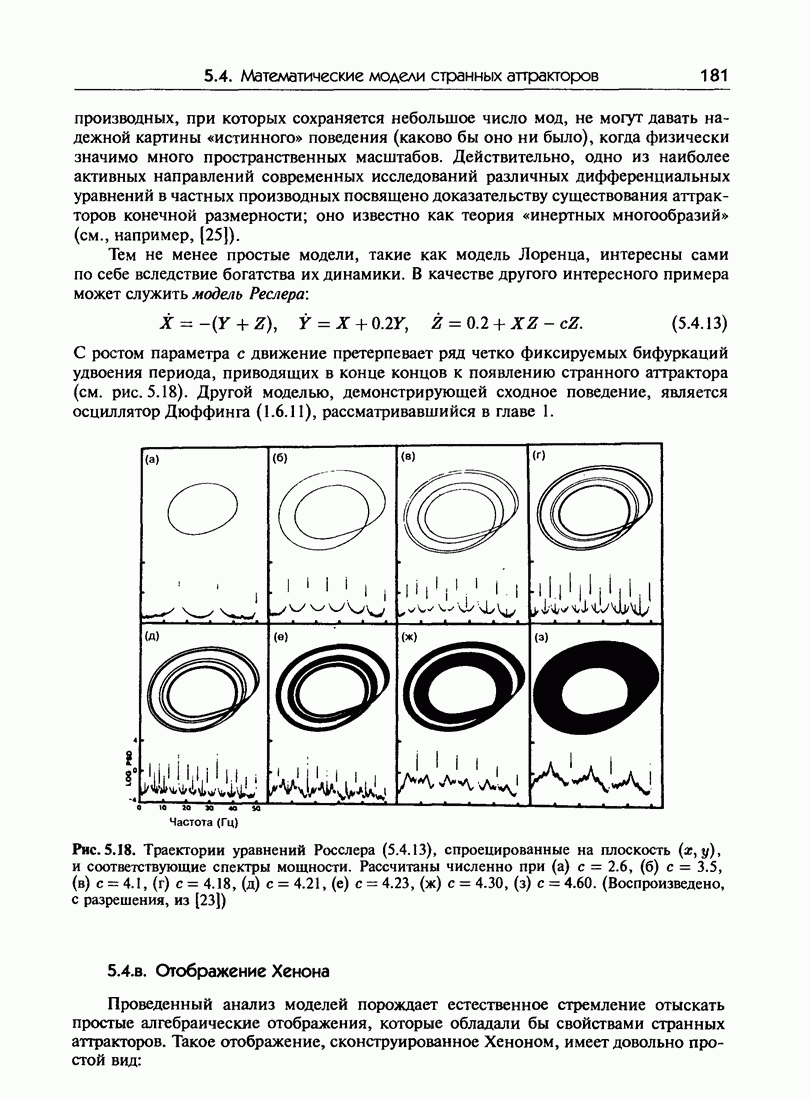
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
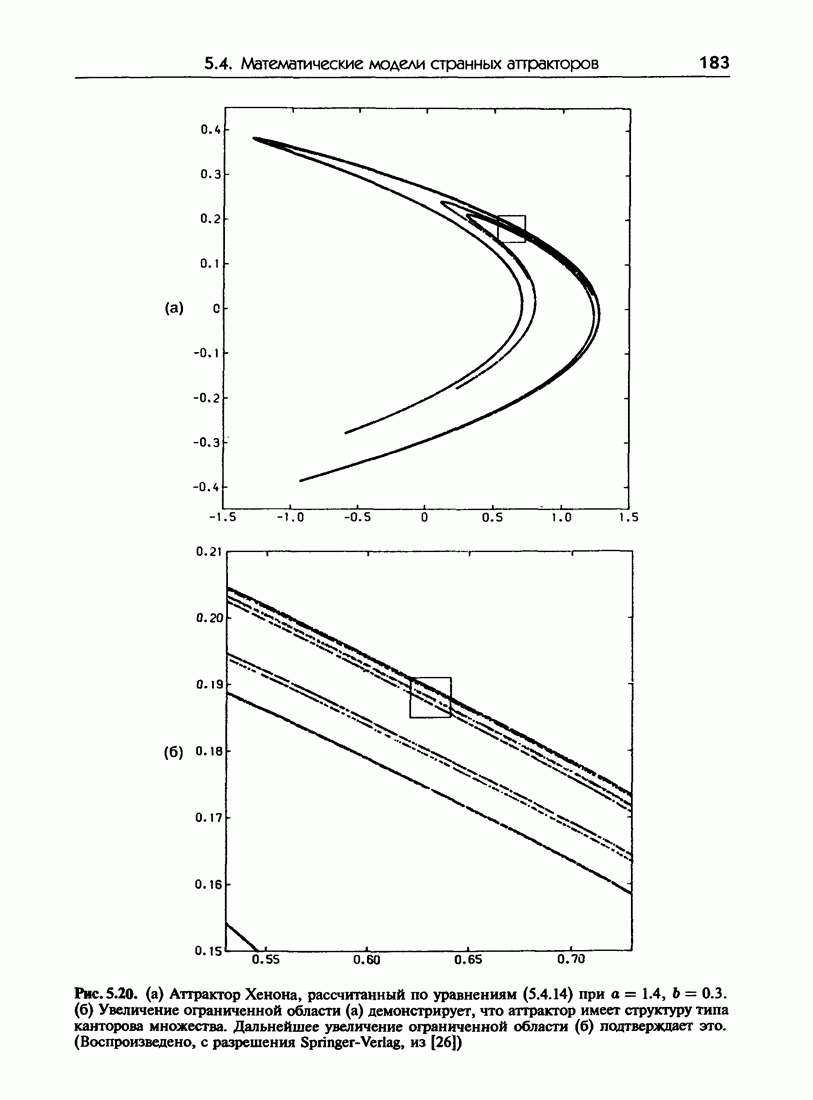
- 5.4.в. Отображение Хенона
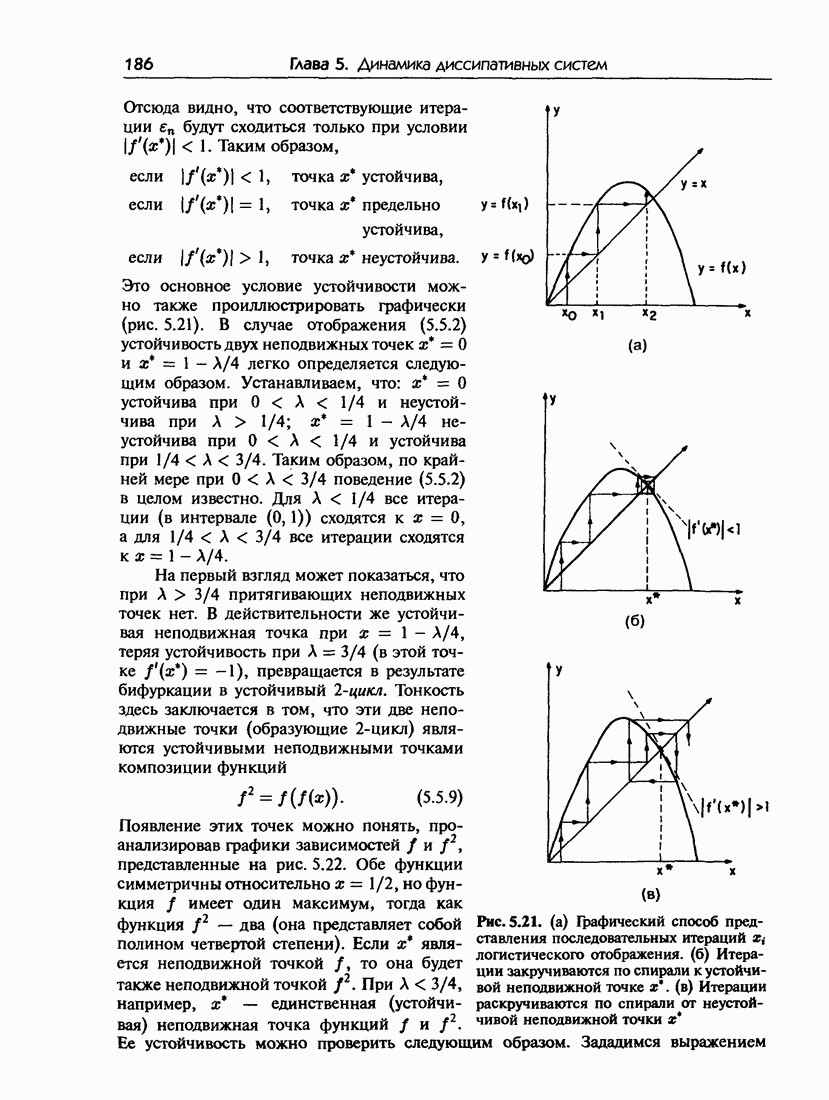
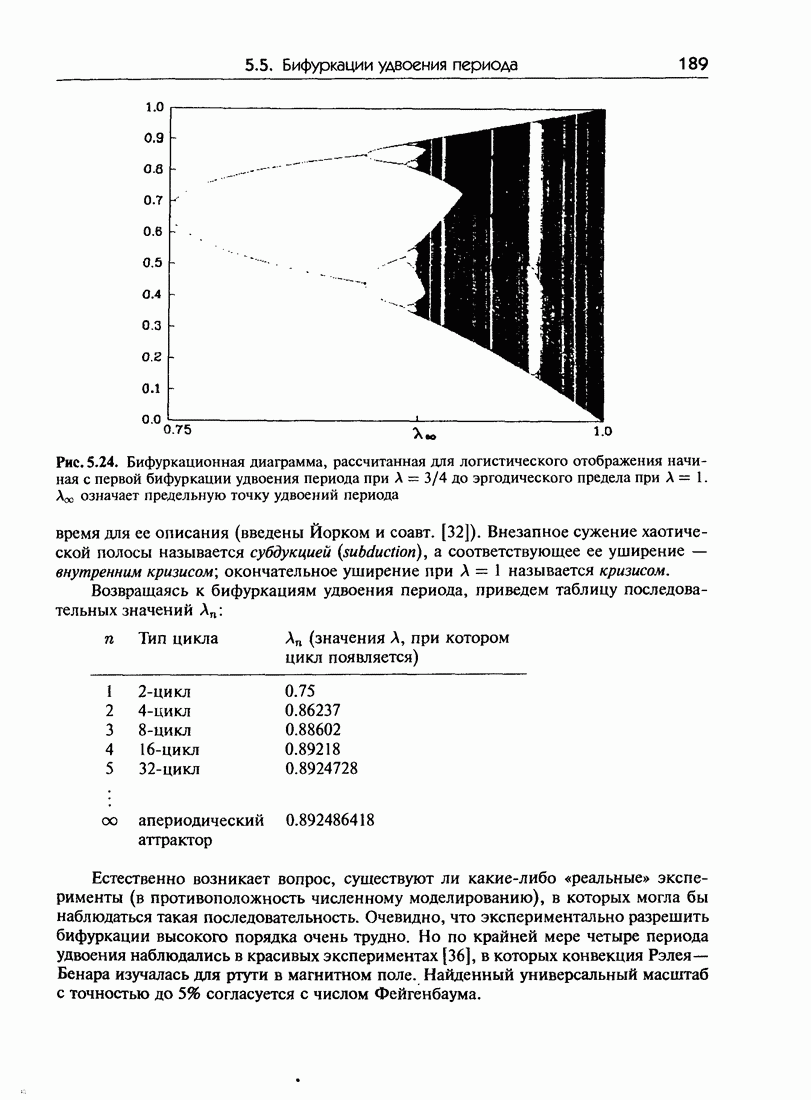
- 5.5. Бифуркации удвоения периода
- 5.5.а. Механизм удвоения периода
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
- 5.5.г. Другие классы универсальности
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
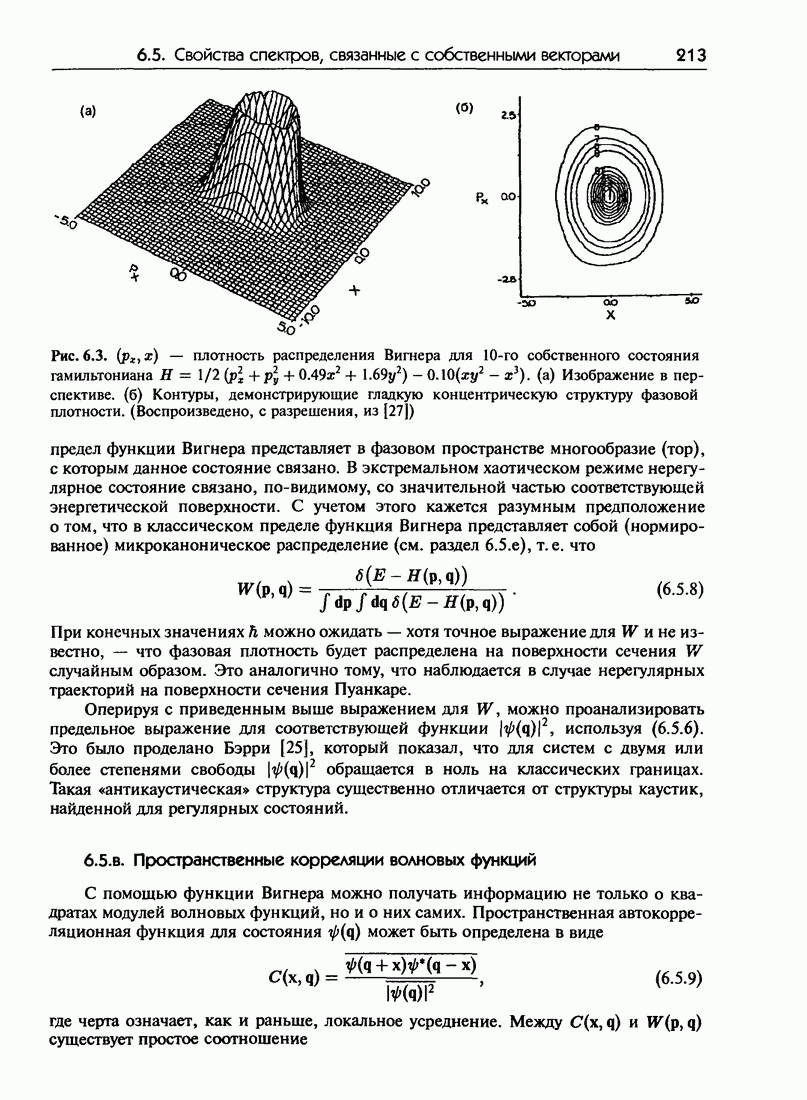
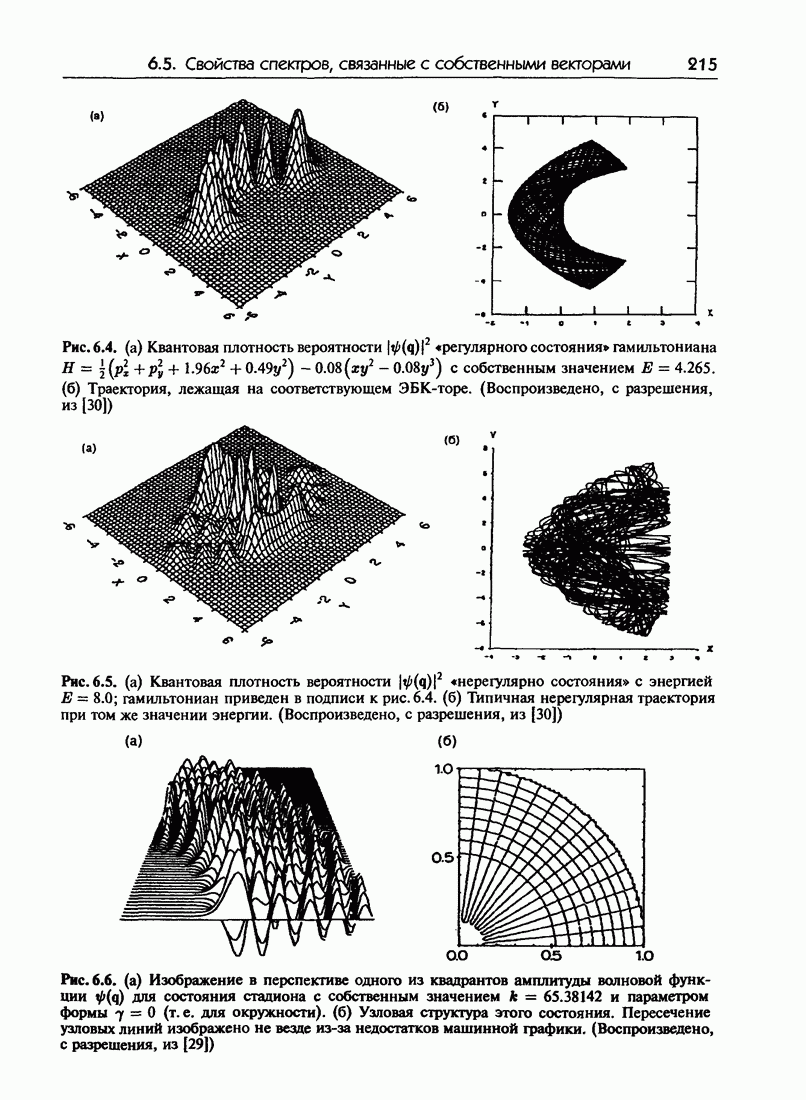
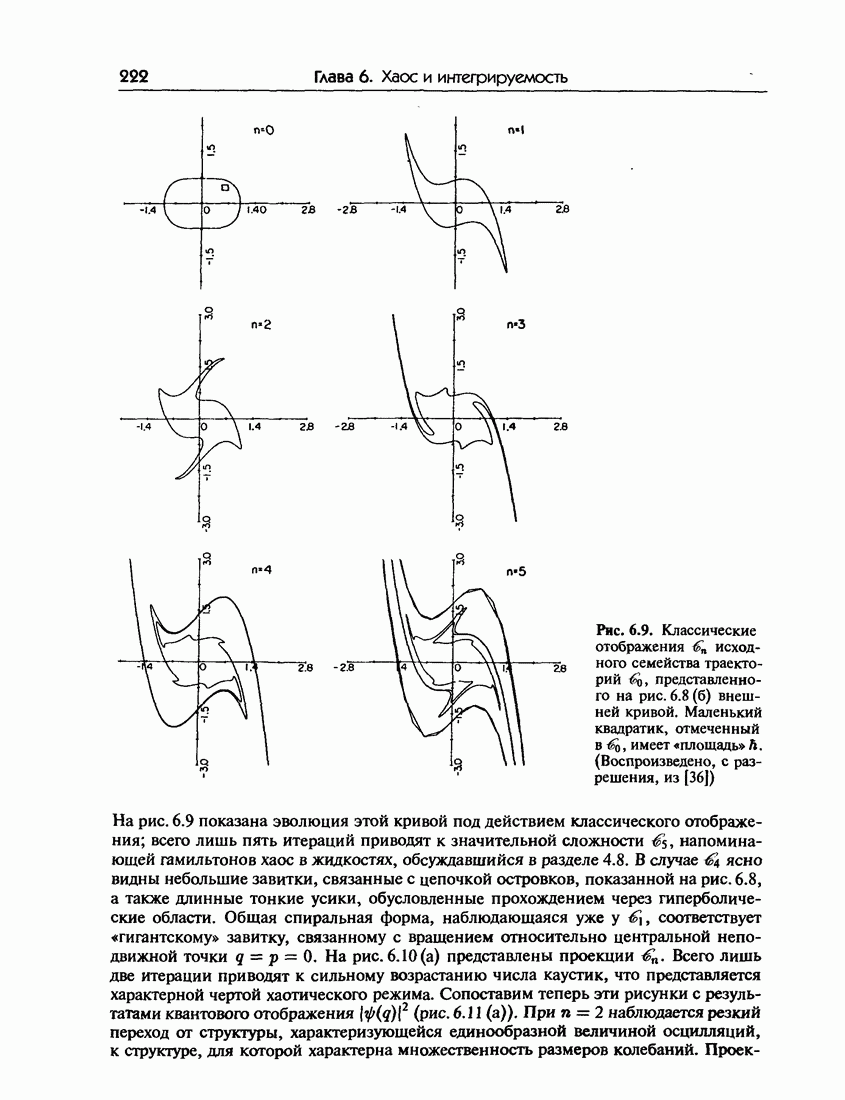
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
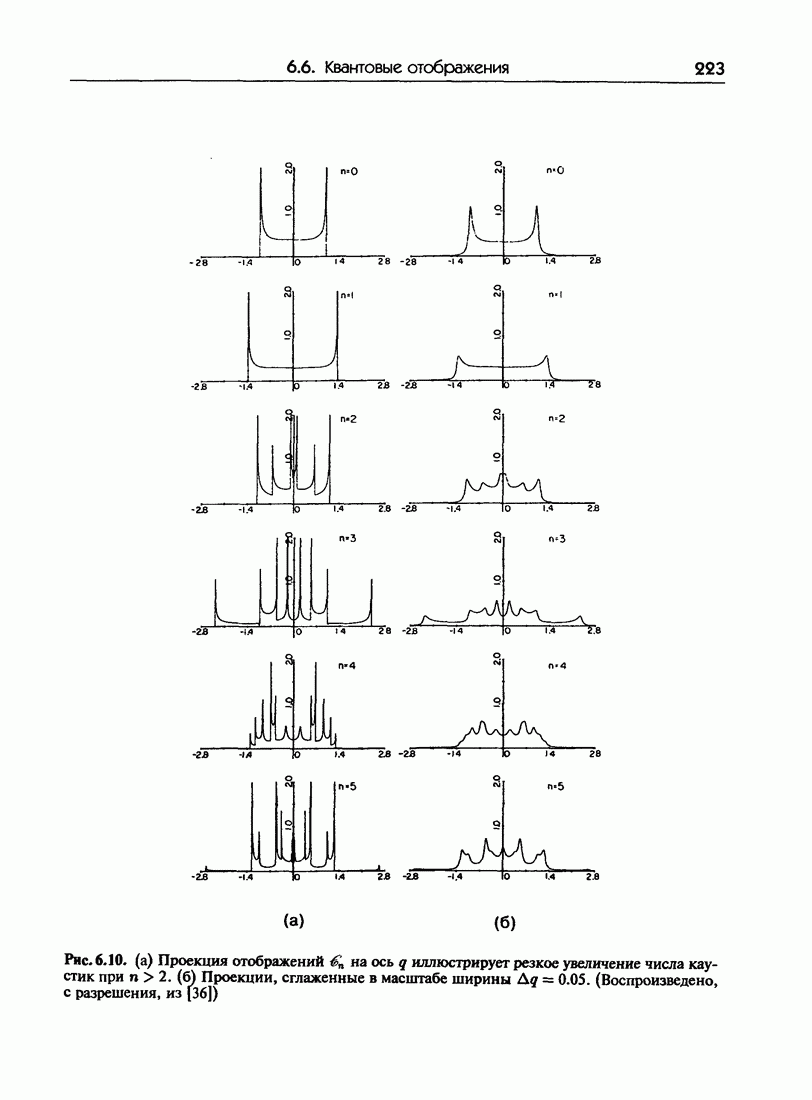
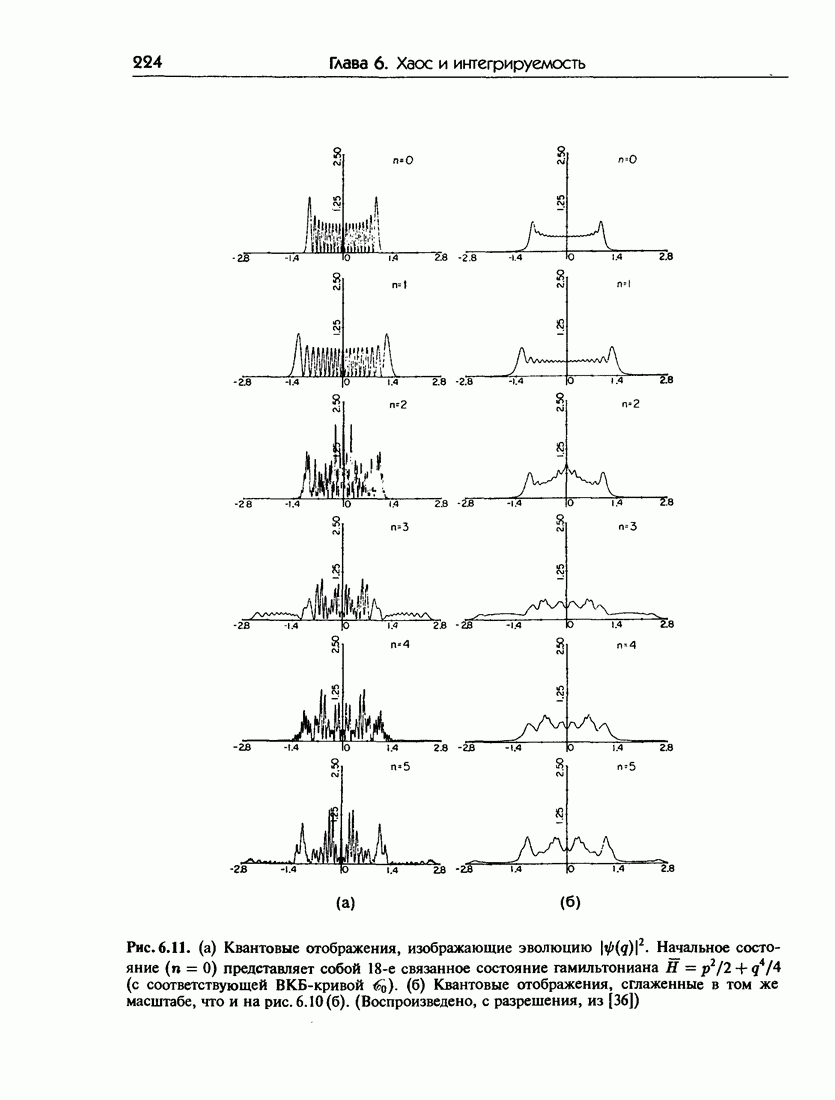
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
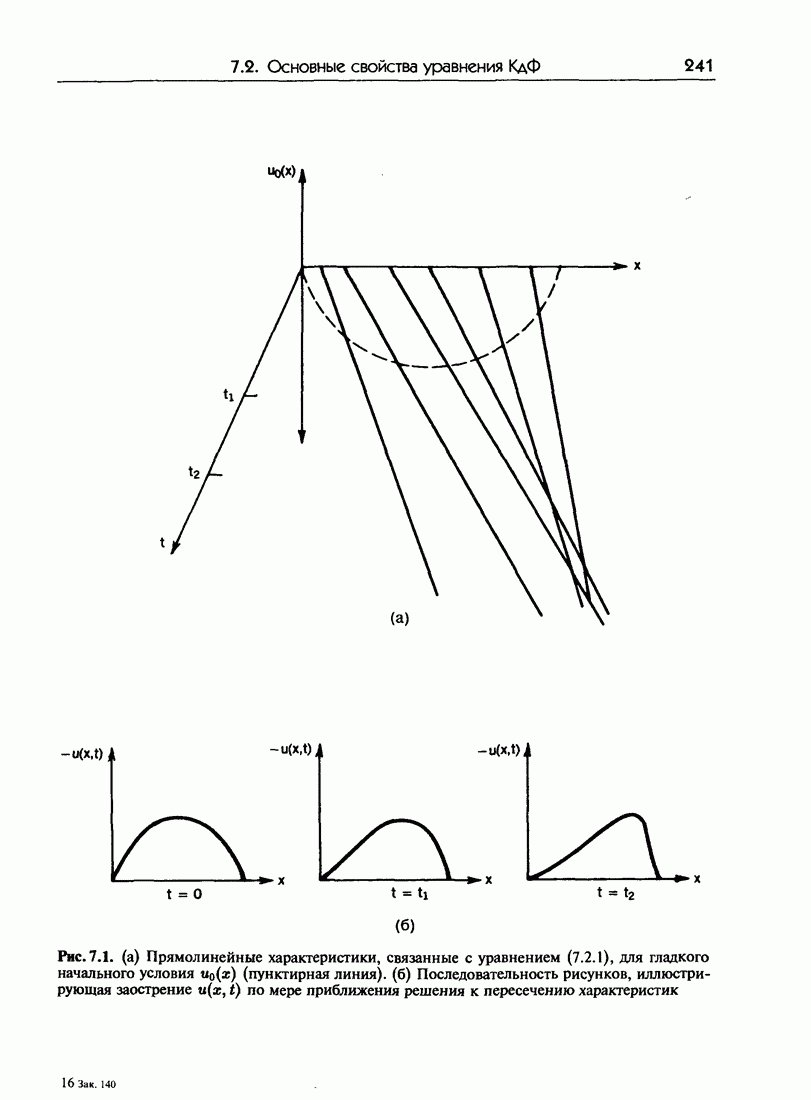
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
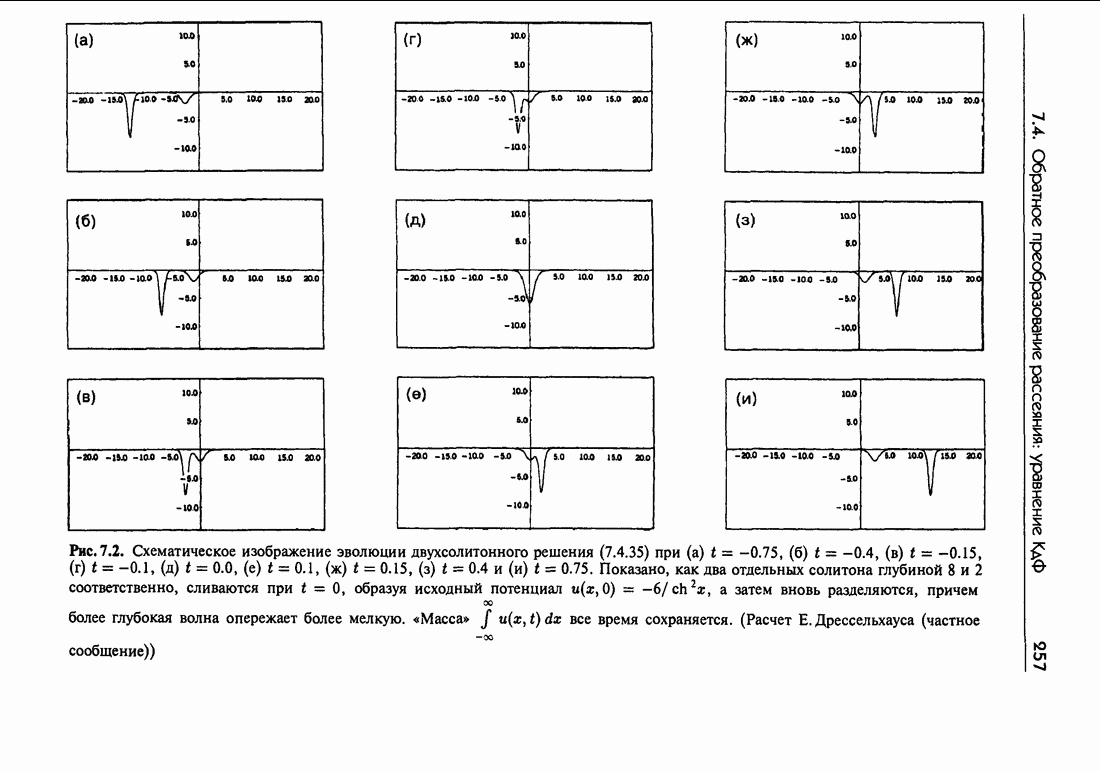
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
- 7.5. Другие солитонные системы
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда