| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4.6.а. Метод перекрытия резонансов
Для того, чтобы понять метод Чирикова, необходимо прежде пояснить, что подразумевается под резонансом. Рассмотрим некоторый интегрируемый гамильтониан Но с  степенями свободы, возмущенный некоторым гамильтонианом
степенями свободы, возмущенный некоторым гамильтонианом 

где  -
-  -компонентные вектора переменных действие—угол. Как обычно, представим
-компонентные вектора переменных действие—угол. Как обычно, представим  в виде ряда Фурье по угловой переменной:
в виде ряда Фурье по угловой переменной:

где  коэффициенты Фурье и
коэффициенты Фурье и  Уравнения для невозмущенных переменных имеют, разумеется, вид
Уравнения для невозмущенных переменных имеют, разумеется, вид

где  начальные значения. Рассмотрим теперь ситуацию, когда
начальные значения. Рассмотрим теперь ситуацию, когда  возмущен только одним членом суммы Фурье:
возмущен только одним членом суммы Фурье:

В этом случае возмущенные переменные удовлетворяют уравнениям движения

где  означает дифференцирование по
означает дифференцирование по  Если ограничиться первым порядком по
Если ограничиться первым порядком по  уравнения (4.6.5) могут быть проинтегрированы просто путем соответствующей подстановки невозмущенного решения (4.6.3); в этом случае (4.6.5а) дает
уравнения (4.6.5) могут быть проинтегрированы просто путем соответствующей подстановки невозмущенного решения (4.6.3); в этом случае (4.6.5а) дает

где  — фазовый фактор. Понятно, что такое приближение нарушается при
— фазовый фактор. Понятно, что такое приближение нарушается при  Это и есть резонанс, и читатель может видеть, что по сути он совпадает с эффектом, порождаемым малыми знаменателями, обсуждавшимися в главе 3. На самом деле мы уже сталкивались с примером резонанса уже в главе 1 в случае вынужденного линейного осциллятора (1.6.4), знаменатель решения которого пропорционален
Это и есть резонанс, и читатель может видеть, что по сути он совпадает с эффектом, порождаемым малыми знаменателями, обсуждавшимися в главе 3. На самом деле мы уже сталкивались с примером резонанса уже в главе 1 в случае вынужденного линейного осциллятора (1.6.4), знаменатель решения которого пропорционален  где
где  собственная частота,
собственная частота,  внешняя вынуждающая частота. В случае единственного возмущающего члена (уравнение (4.6.4)) такой резонанс не вызывает особых затруднений и может быть устранен с помощью подходящего канонического преобразования как описано ниже. Действительно, система (4.6.4) остается полностью интегрируемой, поскольку можно построить новый интеграл движения вида
внешняя вынуждающая частота. В случае единственного возмущающего члена (уравнение (4.6.4)) такой резонанс не вызывает особых затруднений и может быть устранен с помощью подходящего канонического преобразования как описано ниже. Действительно, система (4.6.4) остается полностью интегрируемой, поскольку можно построить новый интеграл движения вида

где  вектор, ортогональный к
вектор, ортогональный к  (т.е.
(т.е.  ). Это легко проверить, вычислив скобки Пуассона для
). Это легко проверить, вычислив скобки Пуассона для  и Н:
и Н:

Таким образом, изолированные резонансы хотя и могут вызывать значительное искажение торов, расположенных в их окрестности, не привносят в систему никакого хаоса. Но одновременное присутствие двух или более резонансов делает систему неинтегрируемой. Более того, если резонансы расположены достаточно близко друг к другу, это приводит, как будет сейчас показано, к возникновению глобального хаоса.
Метод резонансов прекрасно проиллюстрировали Уолкер и Форд [27]. Выбрав интегрируемый гамильтониан

и добавив к нему  резонанс и
резонанс и  резонанс:
резонанс:

они изучили влияние этих резонансов на систему. Влияние каждого из резонансов в отдельности, а также их совместное влияние представлены на рис. 4.26. При низких значениях энергии две резонансные зоны четко разделены. С ростом энергии системы эти две зоны перекрываются и возникают «макроскопические зоны неустойчивости». Под этим термином Уолкер и Форд понимают просто ясно наблюдаемое на поверхности сечения рассеяние точек. Размер такой зоны возрастает с ростом энергии. Структура усложняется еще больше с появлением «вторичных» резонансных зон по мере сближения двух основных зон. Авторы сумели посредством численных расчетов предсказать значение энергии, при котором происходит первое перекрывание резонансов, т. е. (успешно) предсказать возникновение глобального хаотического движения. Это позволяет предположить, что перекрывание резонансов играет ключевую роль в возникновении такого движения. С началом перекрывания основных зон в процесс вовлекается также множество резонансов более высокого порядка, и это в определенной мере дает уверенность в том, что в достаточно больших областях фазового пространства торы (в подавляющем большинстве) разрушаются и что возникающий хаос действительно «глобальный», так как траектории получают возможность блуждать между областями, которые раньше были разделены нерезонансными торами.

Рис. 4.26. Поверхность сечения резонансного гамильтониана (4.6.10): (а) в присутствии только  резонанса
резонанса  в присутствии только
в присутствии только  резонанса
резонанса  оба резонанса присутствуют
оба резонанса присутствуют  , но при
, но при  значительно разделены; (г) две резонансные зоны перекрываются при
значительно разделены; (г) две резонансные зоны перекрываются при  ; случайно разбросанные точки образуются траекторией, начинающейся в области перекрывания резонансов. (Воспроизведено, с разрешения, из [27])
; случайно разбросанные точки образуются траекторией, начинающейся в области перекрывания резонансов. (Воспроизведено, с разрешения, из [27])
Метод, позволяющий приближенно предсказывать начало перекрывания резонансов, был предложен Чириковым [22]. Наилучшие результаты этот метод дает в случае вынужденных одномерных осцилляторов. Модель вынужденного одномерного осциллятора оказывается чрезвычайно полезной при разработке ускорителей, а также при изучении молекулярных связей и атомов в различных полях. Мы рассмотрим одномерный нелинейный осциллятор (например,  возмущенный внешней периодической силой (например,
возмущенный внешней периодической силой (например,  где
где  фаза этой силы. Так как невозмущенная система одномерна, ее всегда можно разрешить в переменных действие — угол
фаза этой силы. Так как невозмущенная система одномерна, ее всегда можно разрешить в переменных действие — угол  ; и мы можем любое (в пределах разумного) внешнее поле представить в виде ряда Фурье по этим переменным:
; и мы можем любое (в пределах разумного) внешнее поле представить в виде ряда Фурье по этим переменным:

Мы знаем, что в случае линейной системы совпадение внешней частоты  с частотой осциллятора
с частотой осциллятора  приводит к тому, что движение носит «взрывной» характер.
приводит к тому, что движение носит «взрывной» характер.
В нелинейном случае в окрестности  также имеется резонанс. Однако, как было показано в главе 1, с ростом амплитуды осциллятора изменяется и зависящая от энергии частота, в результате система выходит из резонанса. В рассматриваемом случае частота осциллятора определяется обычным уравнением
также имеется резонанс. Однако, как было показано в главе 1, с ростом амплитуды осциллятора изменяется и зависящая от энергии частота, в результате система выходит из резонанса. В рассматриваемом случае частота осциллятора определяется обычным уравнением  резонанс существует при таких значениях
резонанс существует при таких значениях  для которых
для которых

В этом случае соответствующая фаза (и ее гармоники)  изменяется медленно по сравнению с другими членами ряда (4.6.11). В силу нелинейности
изменяется медленно по сравнению с другими членами ряда (4.6.11). В силу нелинейности  должны существовать и другие резонансы при других значениях
должны существовать и другие резонансы при других значениях  вообще говоря, множество резонансов всюду плотно. Но для простоты мы начнем с рассмотрения изолированного резонанса (4.6.12) и проанализируем поведение гамильтониана в его окрестности. Попытаемся свести (4.6.11) к более простому виду, из которого можно было бы оценить «ширину резонанса».
вообще говоря, множество резонансов всюду плотно. Но для простоты мы начнем с рассмотрения изолированного резонанса (4.6.12) и проанализируем поведение гамильтониана в его окрестности. Попытаемся свести (4.6.11) к более простому виду, из которого можно было бы оценить «ширину резонанса».
Вспоминая изучение канонических преобразований в главе 2, введем производящую функцию

где  новый импульс, а член
новый импульс, а член  обеспечивает, как мы увидим ниже, подходящий сдвиг начала отсчета новой переменной действия
обеспечивает, как мы увидим ниже, подходящий сдвиг начала отсчета новой переменной действия  Производящая функция приводит к соотношениям
Производящая функция приводит к соотношениям

и

где  новая «резонансная» фаза, сопряженная с новым импульсом 3. Нам понадобится также производная от
новая «резонансная» фаза, сопряженная с новым импульсом 3. Нам понадобится также производная от  по времени,
по времени,

Каноническое преобразование гамильтониана к новым переменным дает

Преобразованный гамильтониан имеет практически такой же вид, как исходный (4.6.11). Но в результате этого преобразования наблюдатель как бы помещается во вращающуюся систему, в которой скорость изменения новой фазы определяет медленное отклонение от резонанса. Хотя неравенство  не обязательно справедливо, мы предположим, что оно выполняется в окрестности резонанса и, следовательно, одному полному циклу по
не обязательно справедливо, мы предположим, что оно выполняется в окрестности резонанса и, следовательно, одному полному циклу по  соответствует много циклов по
соответствует много циклов по  В среднем вклад этих быстро осциллирующих членов равен нулю, и это подводит нас к следующему шагу, состоящему в усреднении гамильтониана по быстрым фазовым переменным:
В среднем вклад этих быстро осциллирующих членов равен нулю, и это подводит нас к следующему шагу, состоящему в усреднении гамильтониана по быстрым фазовым переменным:

В результате «усредненный» гамильтониан  приобретает вид
приобретает вид

где мы перешли к действительным числам (полагая  а также включив множитель 2 в коэффициенты Фурье
а также включив множитель 2 в коэффициенты Фурье  До сих пор мы рассматривали все гармоники, но с этого момента предположим, что
До сих пор мы рассматривали все гармоники, но с этого момента предположим, что

При этом (4.6.19) сводится к

Последний шаг заключается в следующем. Считать, что в области резонанса  разлагаем (4.6.21) в окрестности
разлагаем (4.6.21) в окрестности  в ряд, ограничиваясь членами второго порядка (при этом предполагается, что коэффициент
в ряд, ограничиваясь членами второго порядка (при этом предполагается, что коэффициент  медленно меняющаяся функция I). Таким образом получаем
медленно меняющаяся функция I). Таким образом получаем

Поскольку  условие резонанса (4.6.12) приводит к значительному упрощению за счет уничтожения линейных по
условие резонанса (4.6.12) приводит к значительному упрощению за счет уничтожения линейных по  членов. Опуская постоянный член
членов. Опуская постоянный член  остается «резонансный» гамильтониан
остается «резонансный» гамильтониан

где «масса»  определяется соотношением
определяется соотношением

«Резонансный» гамильтониан (4.6.23) по форме в точности совпадает с гамильтонианом маятника, сепаратриса которого (см. рис. 4.27) определяется уравнением

В старых переменных  оно имеет простой вид
оно имеет простой вид

где

Величина  представляет собой резонансную «полуширину», которая также может быть выражена через частоту:
представляет собой резонансную «полуширину», которая также может быть выражена через частоту:


Рис. 4.27. Фазовая плоскость гамильтониана маятника (4.6.23); показана сепаратриса
Заметим, что поскольку  зависимость резонансной полуширины от величины резонанса содержится лишь в коэффициентах Фурье
зависимость резонансной полуширины от величины резонанса содержится лишь в коэффициентах Фурье  Из (4.6.27) и (4.6.28) видно, что резонансное возмущение имеет порядок
Из (4.6.27) и (4.6.28) видно, что резонансное возмущение имеет порядок 
Важно подчеркнуть, что вывод резонансного гамильтониана (4.6.23) связан с несколькими допущениями. Нерезонансные члены в  опущены на основании того, что они быстро осциллируют, и, следовательно, при усреднении по полному циклу движения дают ноль. Предположение
опущены на основании того, что они быстро осциллируют, и, следовательно, при усреднении по полному циклу движения дают ноль. Предположение  позволило пренебречь резонансными гармониками; кроме того, были опущены члены высших порядков в разложении по
позволило пренебречь резонансными гармониками; кроме того, были опущены члены высших порядков в разложении по  Чириков [22] предложил объединить эти предположения в «условие умеренной нелинейности»,
Чириков [22] предложил объединить эти предположения в «условие умеренной нелинейности»,

где  Дальнейшее обсуждение этого условия можно найти в [22].
Дальнейшее обсуждение этого условия можно найти в [22].
Резонансный гамильтониан (4.6.23) все еще остается интегрируемым, поскольку состоит из единственного изолированного резонанса. «Критерий перекрывания резонансов» Чирикова получается в результате оценивания ширины другого (основного) резонанса и, затем, отыскания такого значения константы связи  при которой оба резонанса соприкоснутся друг с другом; т. е. мы ищем такое
при которой оба резонанса соприкоснутся друг с другом; т. е. мы ищем такое  , что
, что

где  ширины двух резонансов, а
ширины двух резонансов, а  расстояние между ними. Ширина каждой из резонансных зон вычисляется независимо от всех остальных. Понятно, что это является основным приближением, и остается надеяться, что «условие умеренной нелинейности» (4.6.29) обеспечивает приемлемость ошибки.
расстояние между ними. Ширина каждой из резонансных зон вычисляется независимо от всех остальных. Понятно, что это является основным приближением, и остается надеяться, что «условие умеренной нелинейности» (4.6.29) обеспечивает приемлемость ошибки.
Чириков [22] проверил свой метод для ряда простых систем. Особый интерес представляет система с модельным гамильтонианом

С физической точки зрения она представляет собой ротор (единичной массы), на который действует бесконечная последовательность резонансов или, если представить (4.6.31) в эквивалентном виде

маятник, подверженный серии «толчков» в моменты времени  Читатель может убедиться, что интегрирование уравнений Гамильтона дает в случае одного периода в точности «стандартное отображение» (4.2.26), где
Читатель может убедиться, что интегрирование уравнений Гамильтона дает в случае одного периода в точности «стандартное отображение» (4.2.26), где  Каждый член в последовательности резонансов непосредственно дает резонансный гамильтониан (ср.
Каждый член в последовательности резонансов непосредственно дает резонансный гамильтониан (ср. 

где  медленно меняющаяся фаза
медленно меняющаяся фаза  Резонансную полуширину можно получить, исходя непосредственно из (4.6.28):
Резонансную полуширину можно получить, исходя непосредственно из (4.6.28):

Резонансы возникают при каждом целочисленном значении  (схематически это показано на рис. 4.28). Расстояние между резонансами равно единице
(схематически это показано на рис. 4.28). Расстояние между резонансами равно единице  они начинают соприкасаться при
они начинают соприкасаться при

Это позволяет предсказать критическое значение параметра возмущения К, при котором происходит перекрывание резонансов; с учетом

получаем

Численный анализ этой системы показывает, что глобальный хаос возникает при  критерий перекрывания, таким образом, дает ошибку примерно в 2,5 раза. Дальнейшее уточнение, как, например, учет высших гармоник резонансных фаз, позволяет улучшить оценку:
критерий перекрывания, таким образом, дает ошибку примерно в 2,5 раза. Дальнейшее уточнение, как, например, учет высших гармоник резонансных фаз, позволяет улучшить оценку: 
Метод Чирикова стимулировал значительную активность исследователей, в результате чего появились его уточненные версии (учитывающие, например, влияние «вторичных» резонансов), которые позволили гораздо точнее предсказывать возникновение глобального хаоса. Метод также применим к автономным системам с большим числом степеней свободы («наибольшую строгость» теория имеет в случае систем с одной степенью свободы в поле внешней силы). Основные идеи при этом сохраняются, но анализ становится более сложным. Дальнейшую информацию по этому вопросу заинтересованный читатель может найти в других источниках.

Рис. 4.28. Резонансы в фазовой плоскости гамильтониана (4.6.32) маятника, подверженного толчкам
| << Предыдущий параграф | Следующий параграф >> |
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
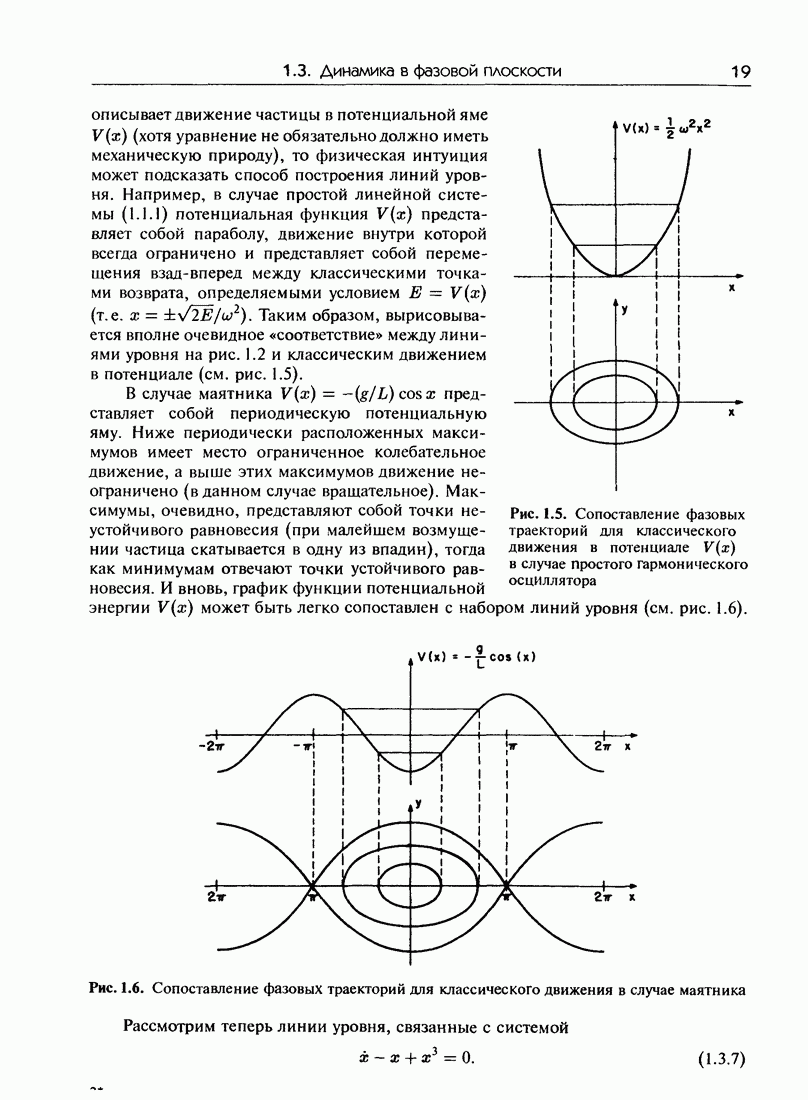
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
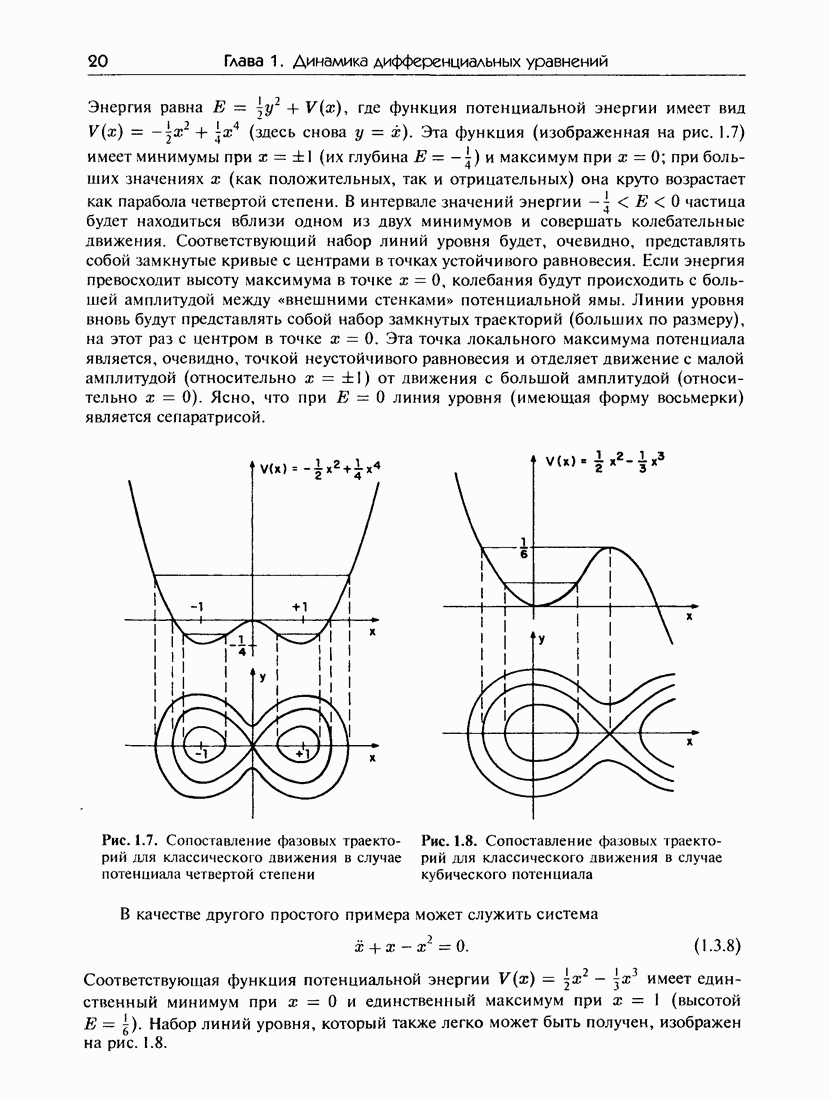
- 1.3.б. фазовые портреты консервативных систем
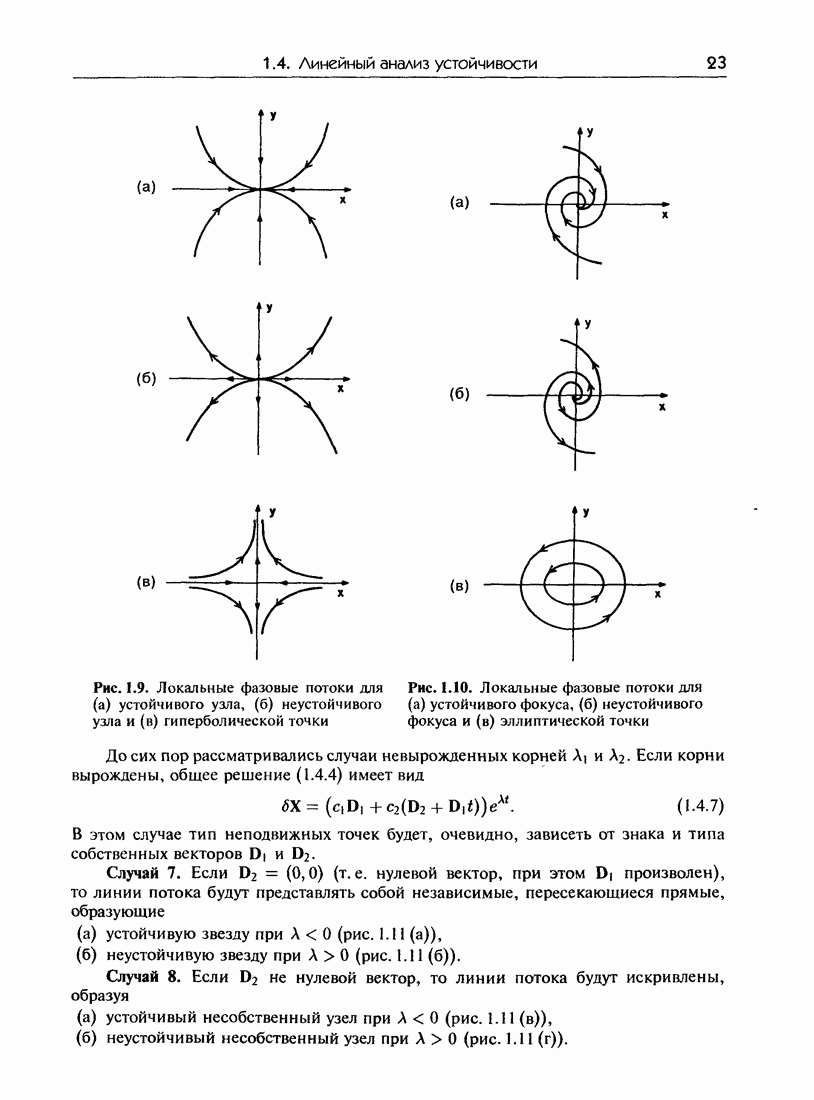
- 1.4. Линейный анализ устойчивости
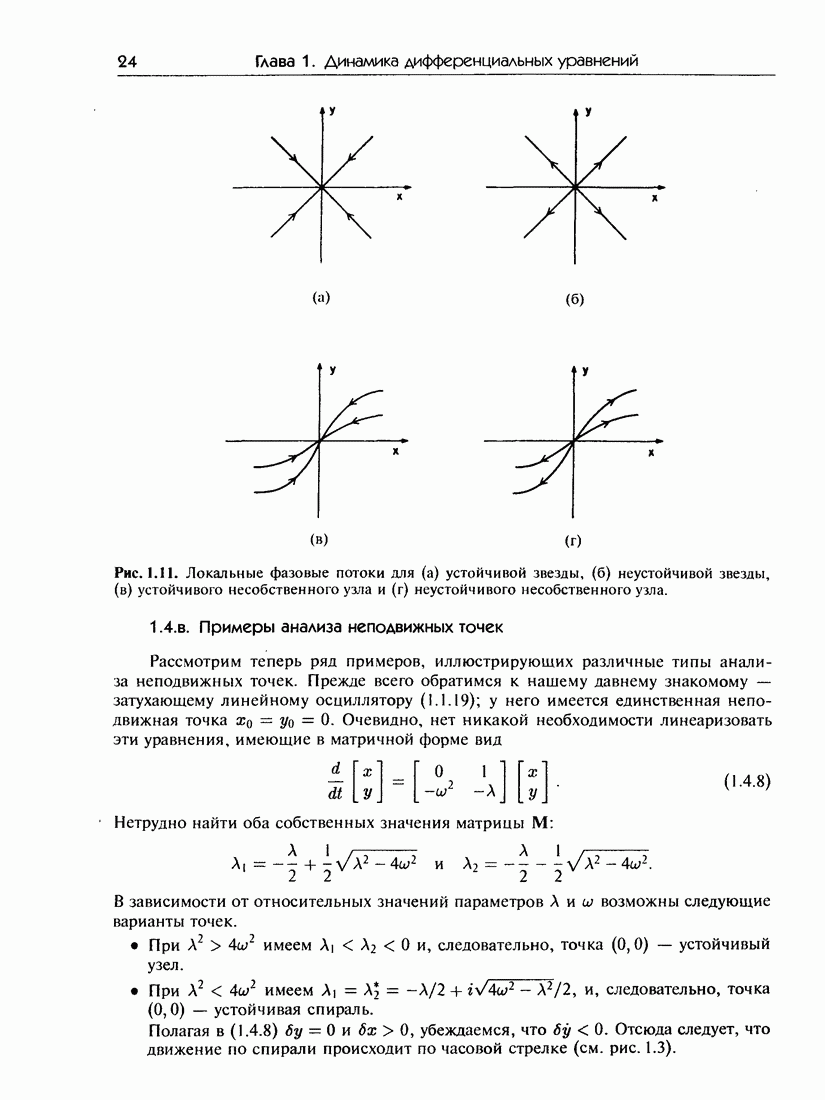
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
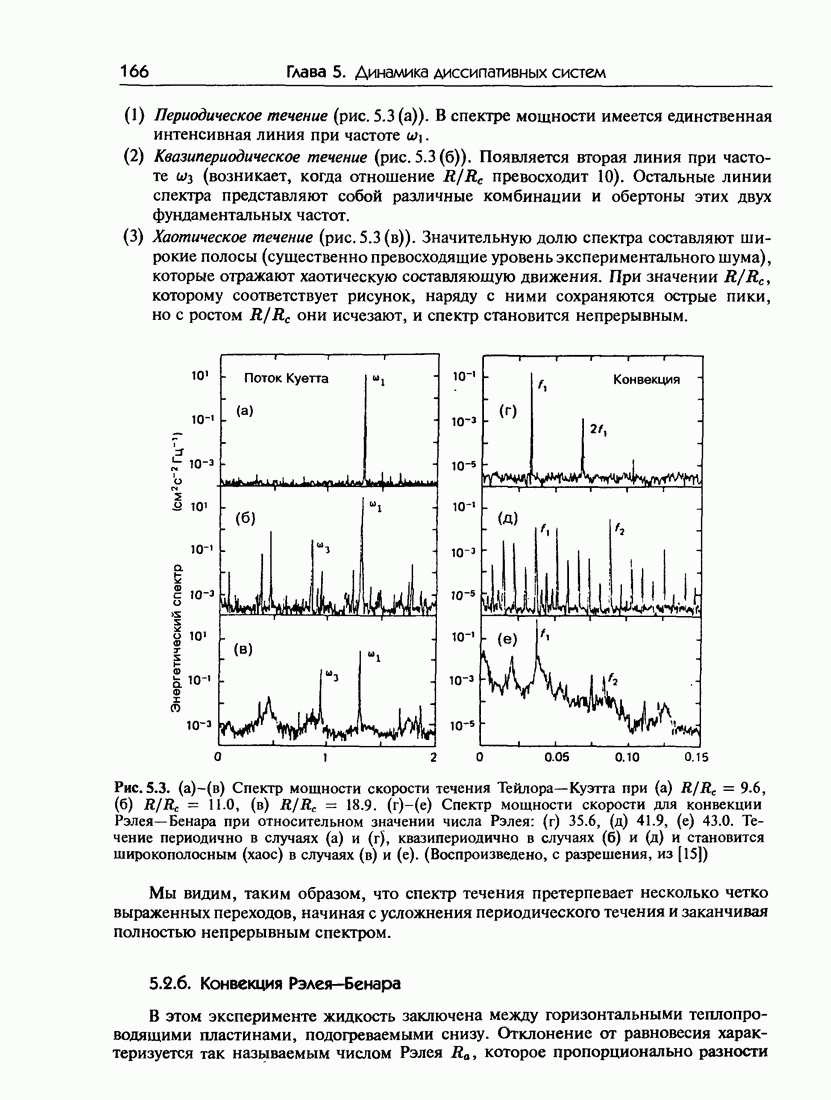
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
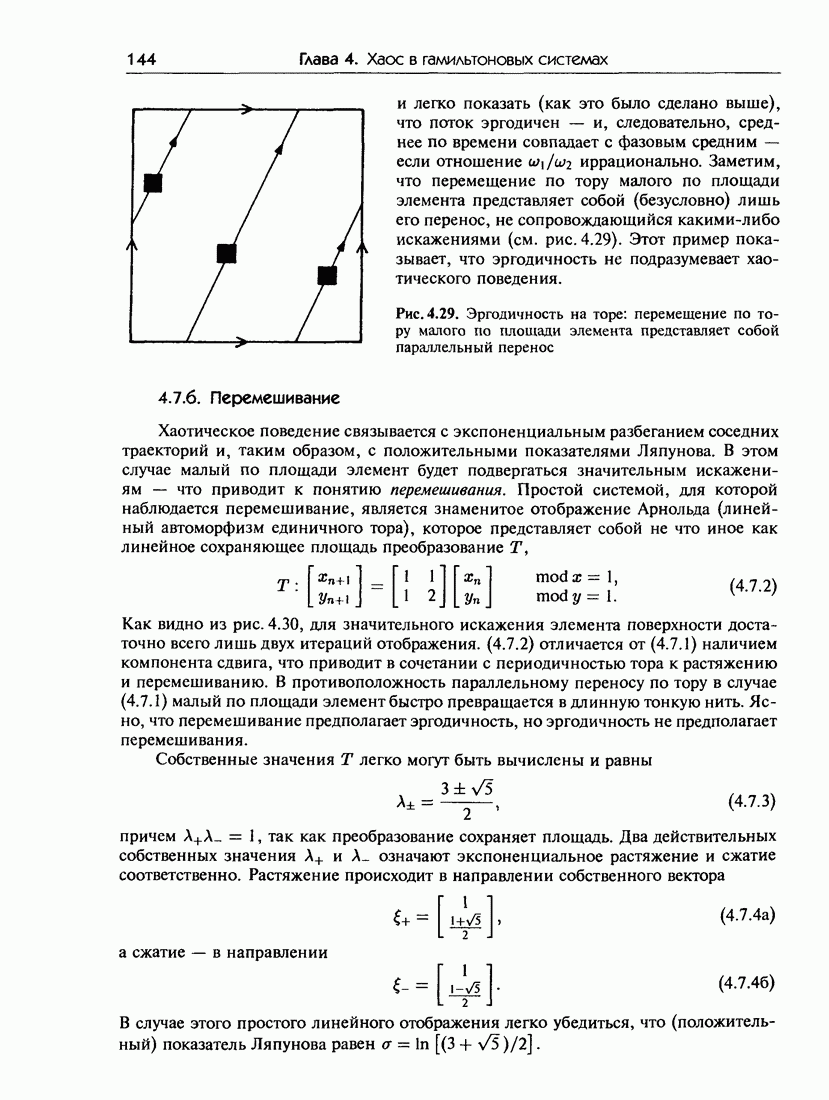
- 4.7.б. Перемешивание
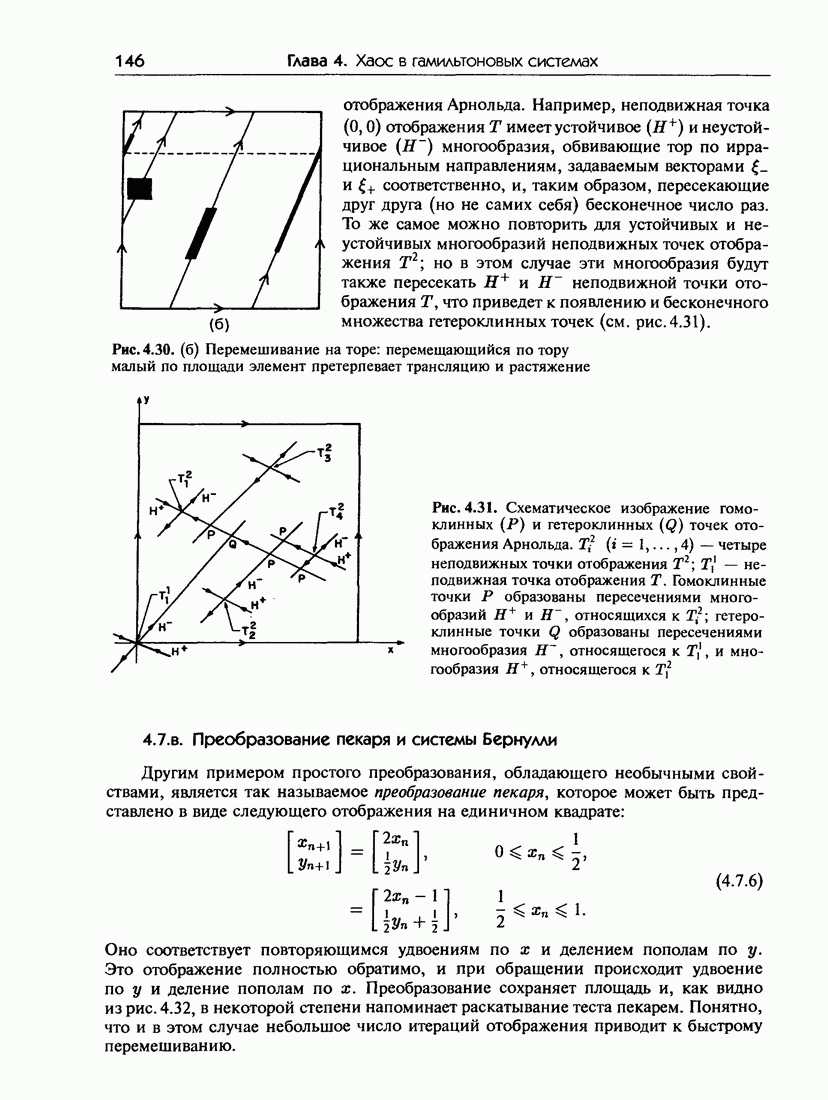
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
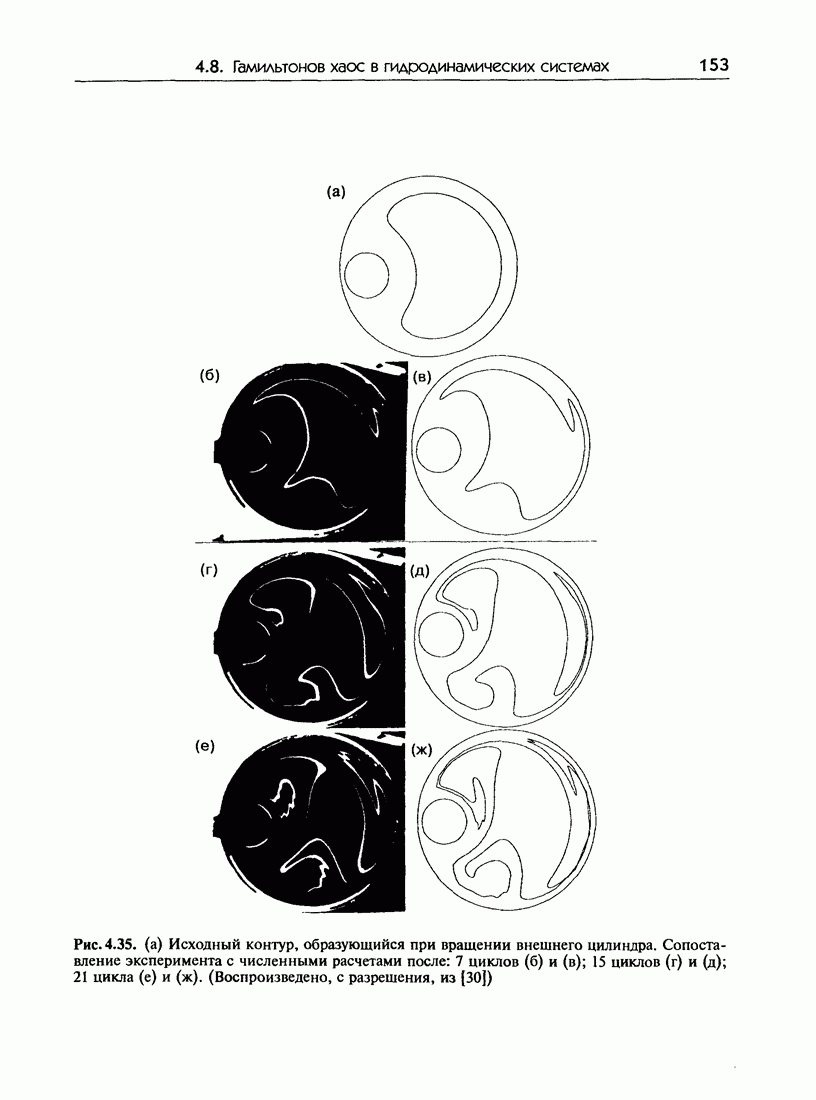
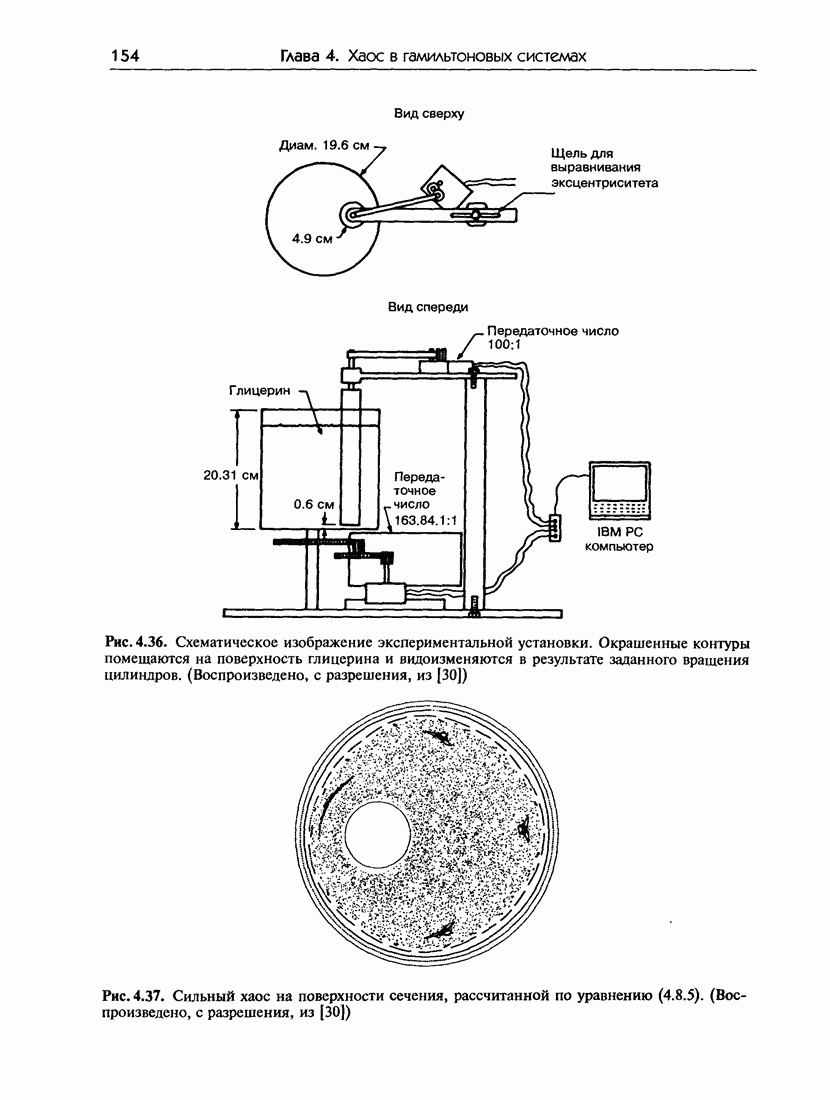
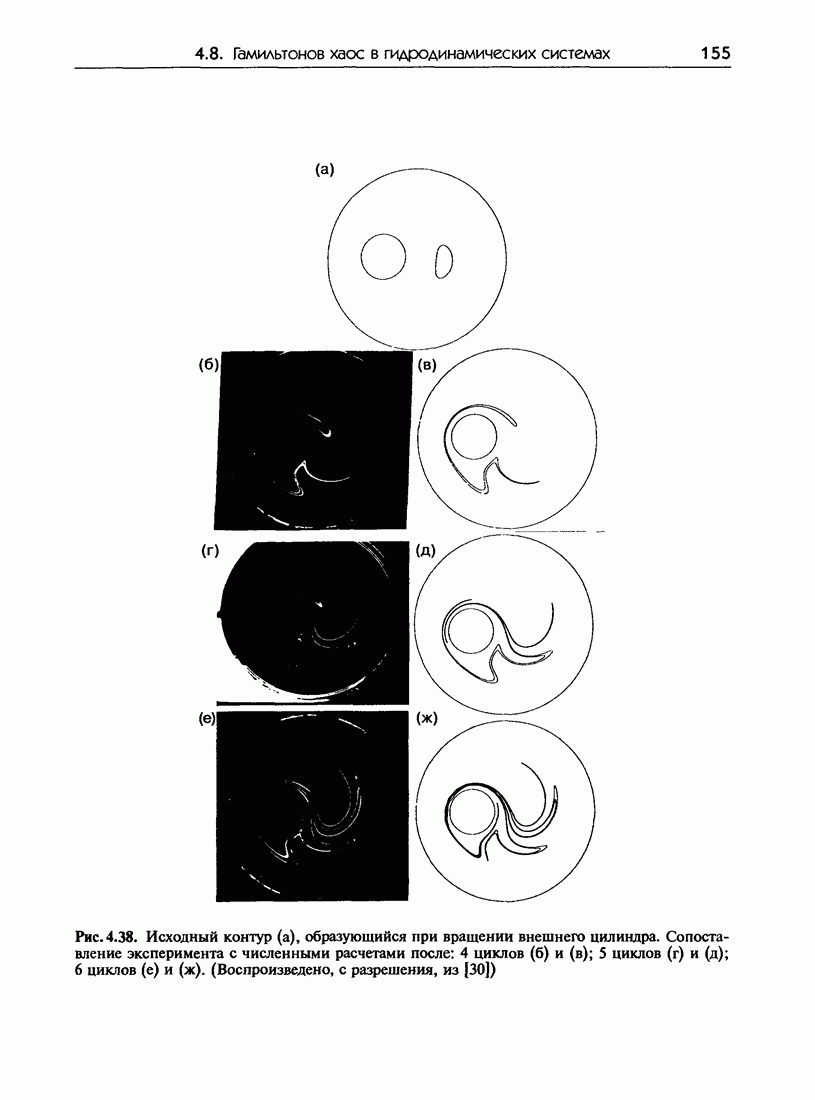
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
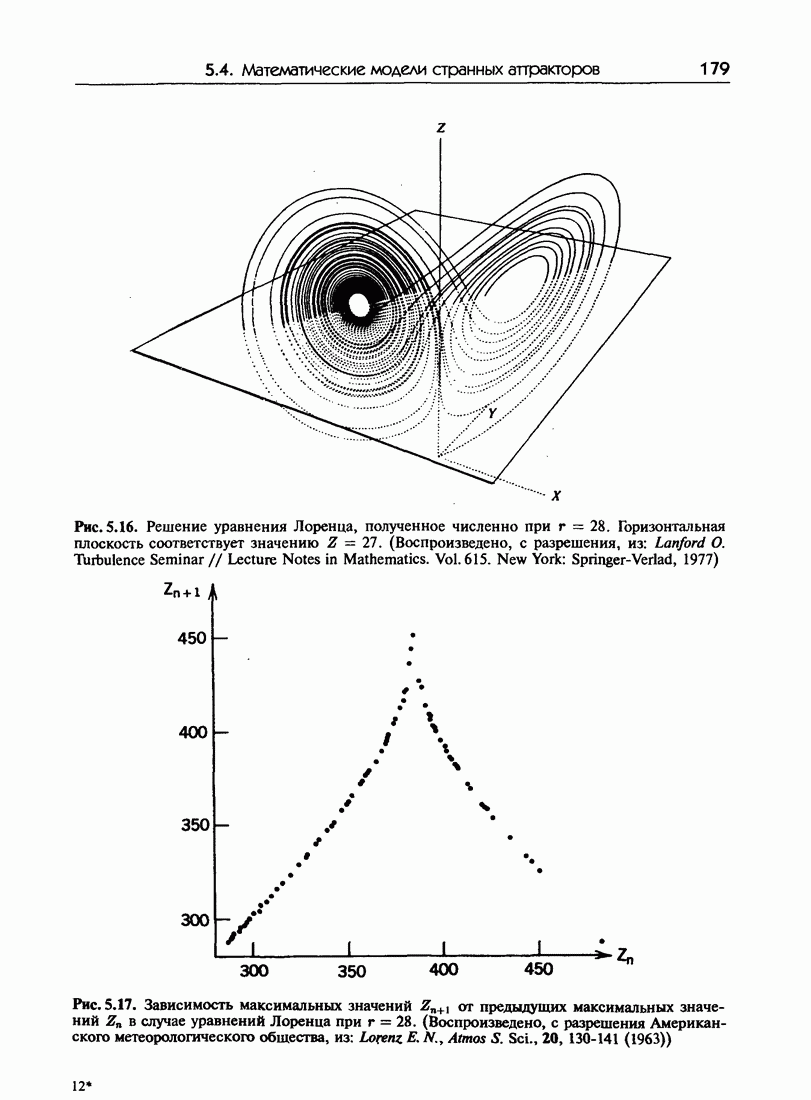
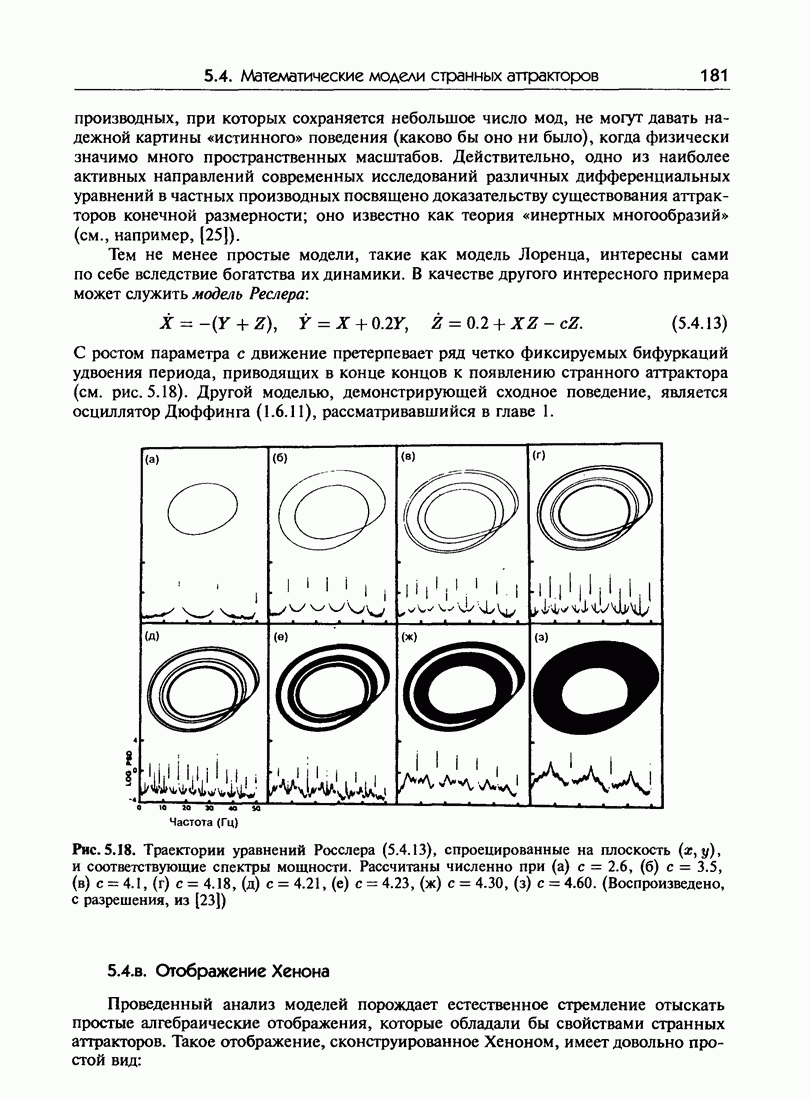
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
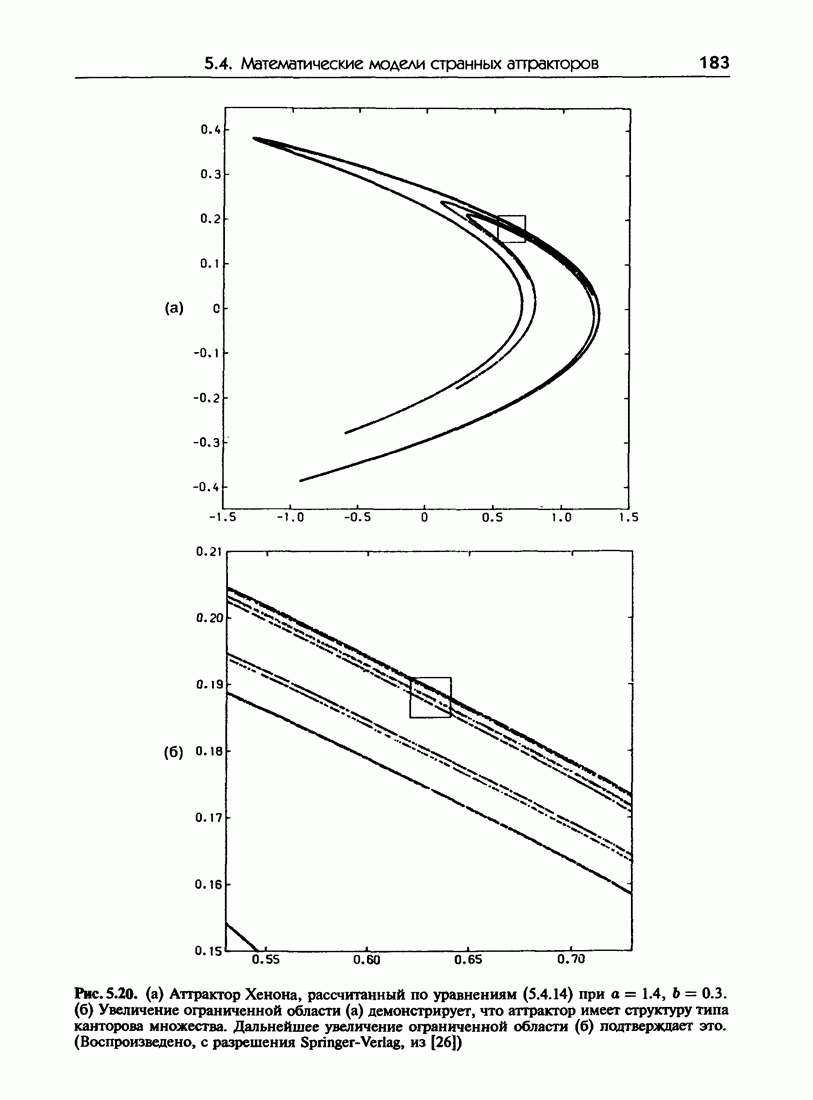
- 5.4.в. Отображение Хенона
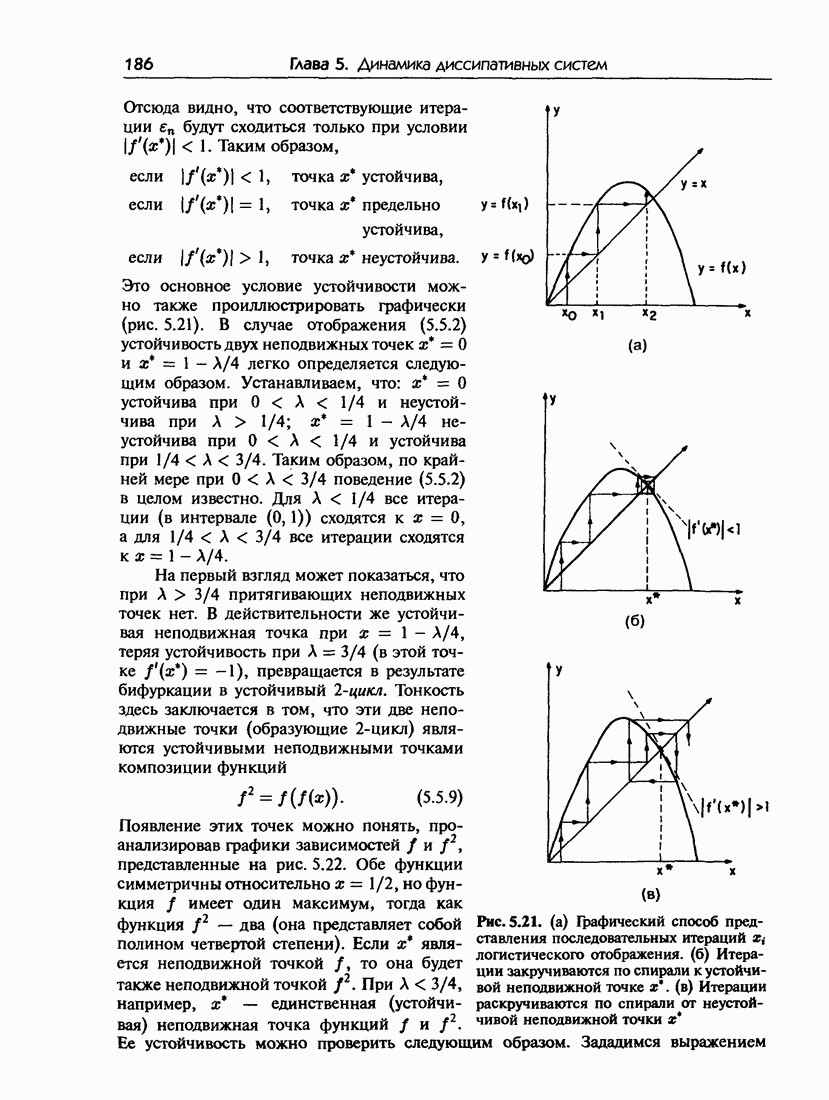
- 5.5. Бифуркации удвоения периода
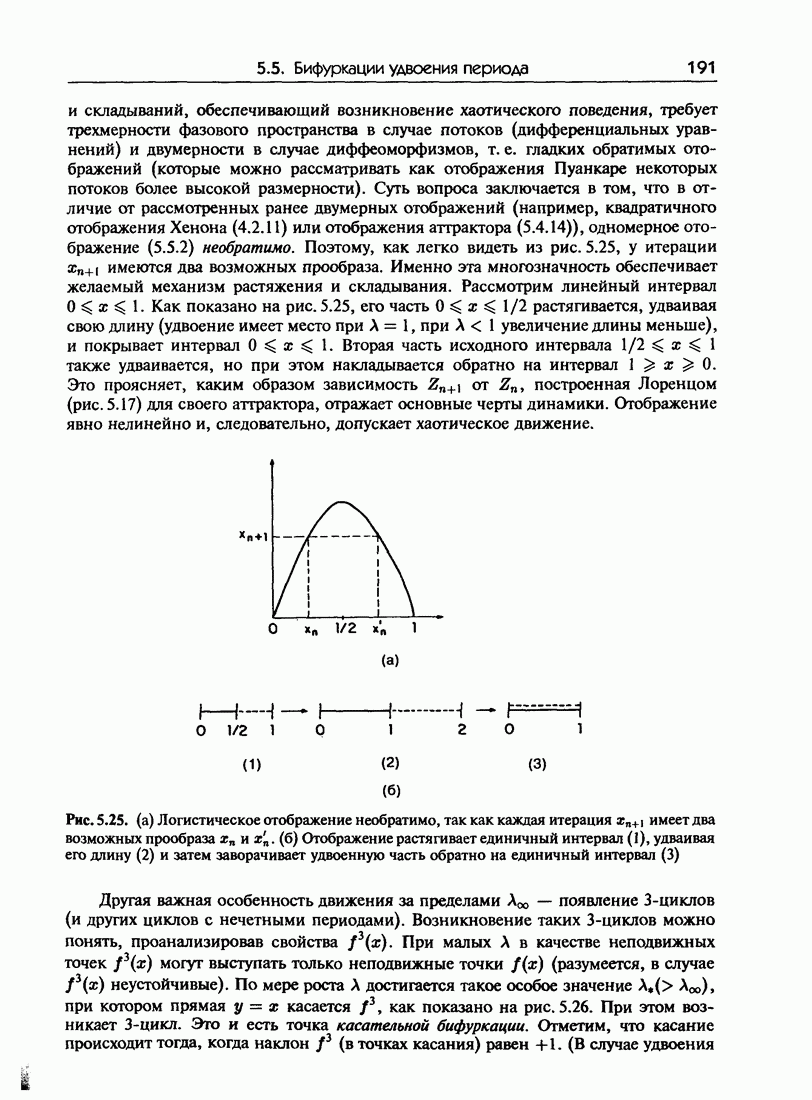
- 5.5.а. Механизм удвоения периода
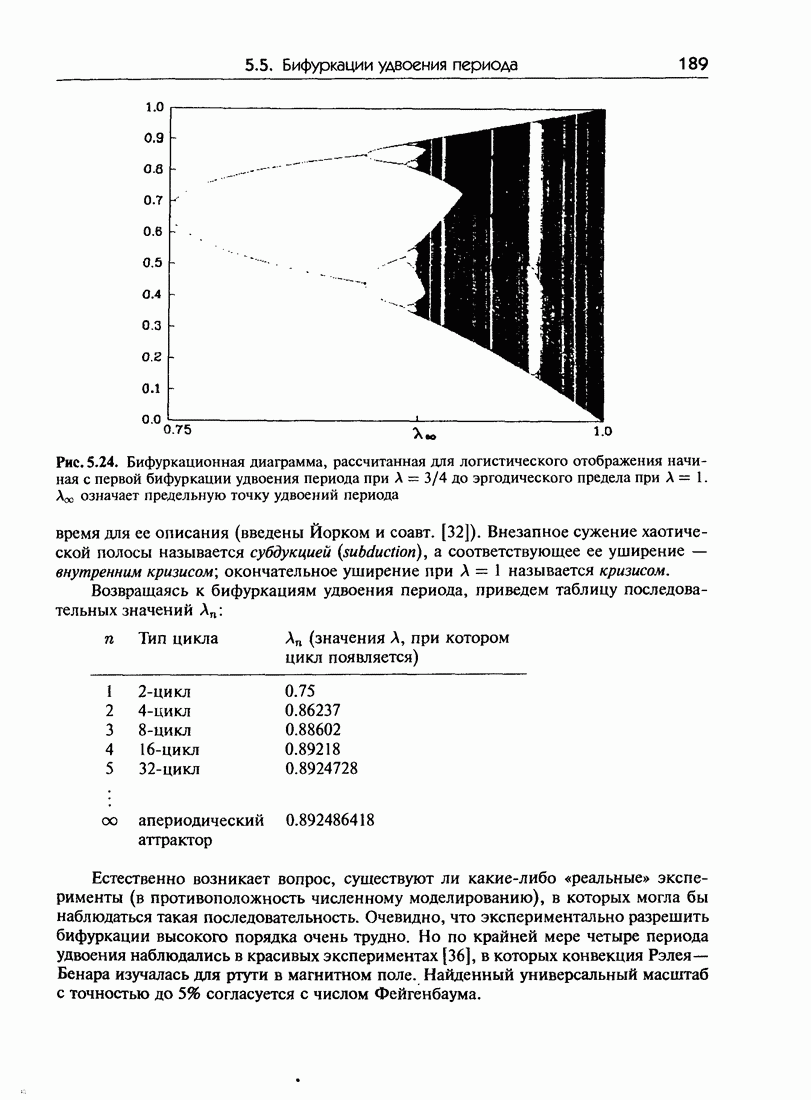
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
- 5.5.г. Другие классы универсальности
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
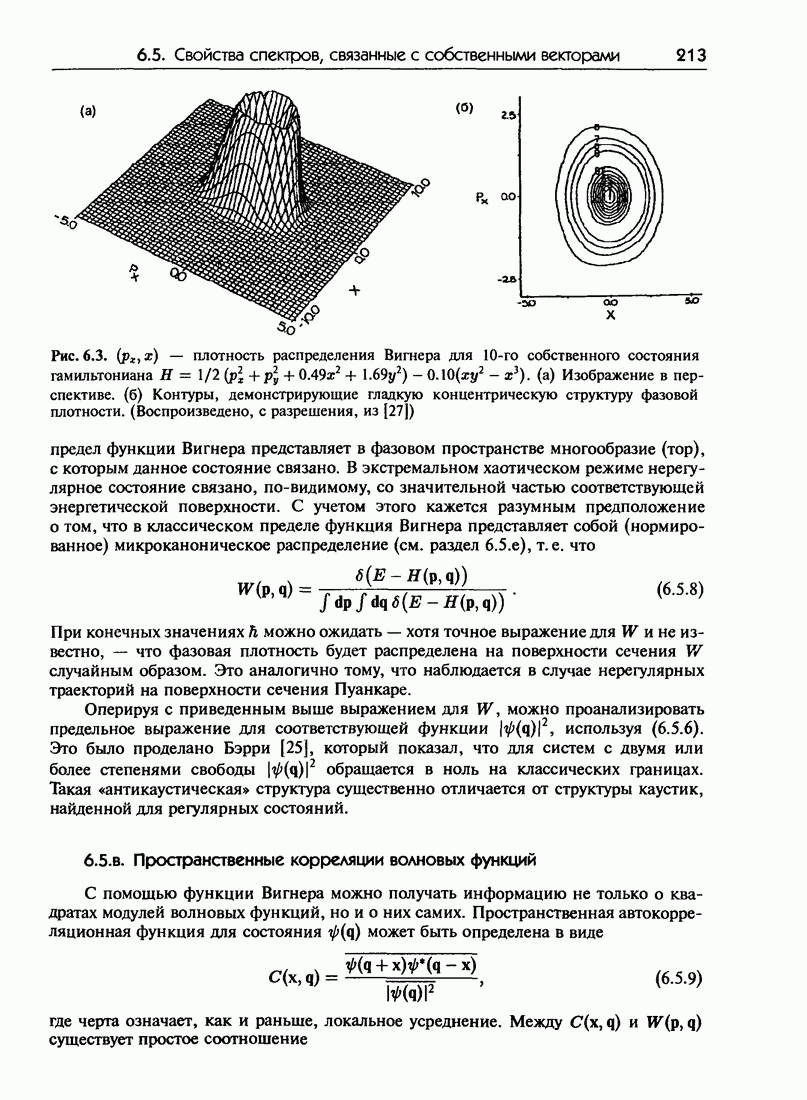
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
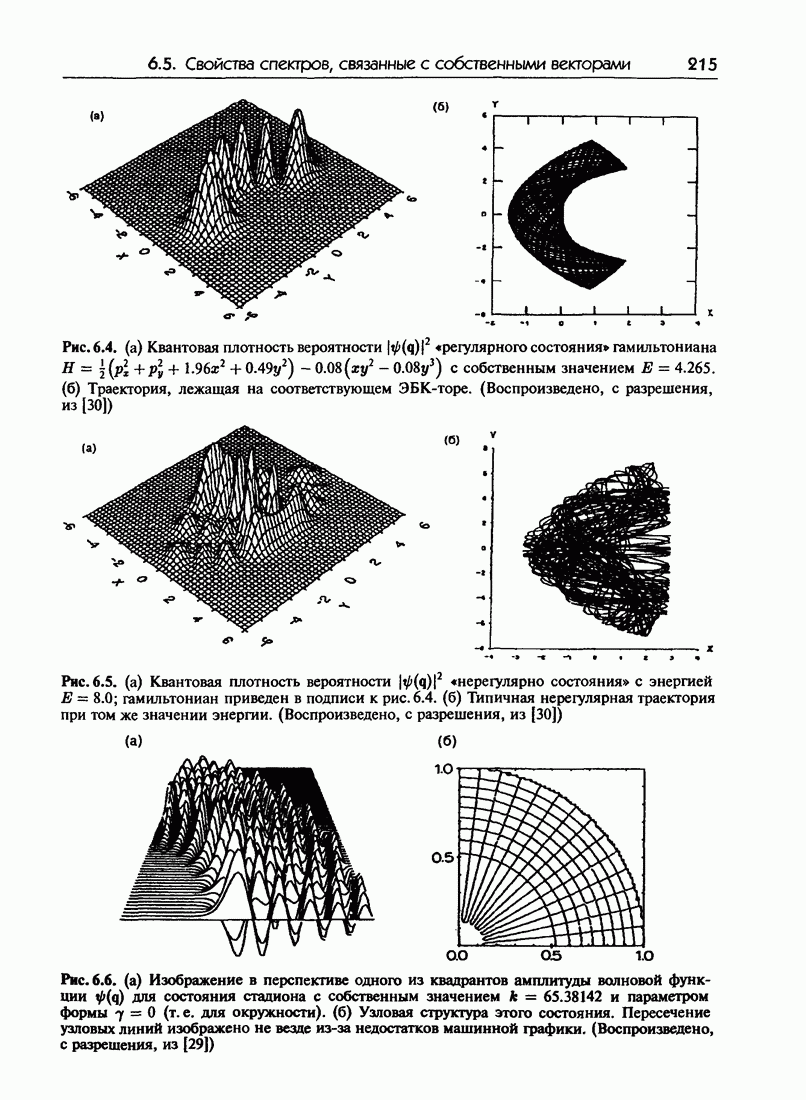
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
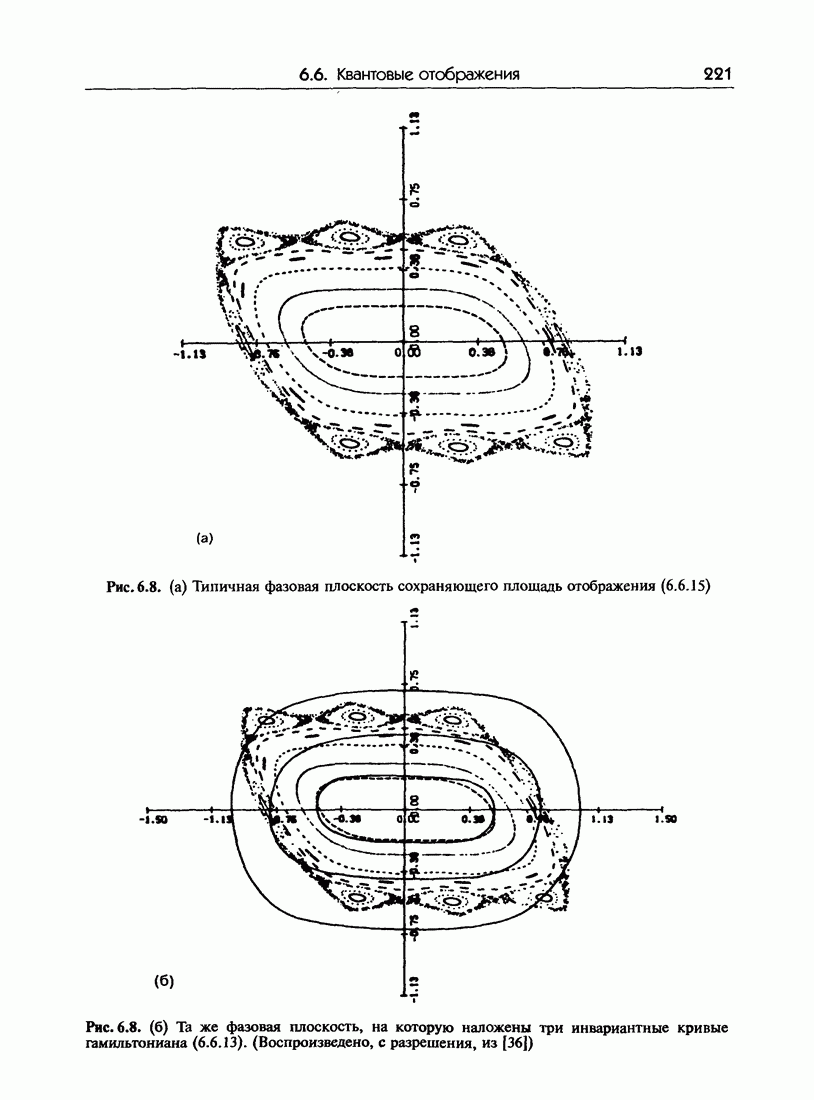
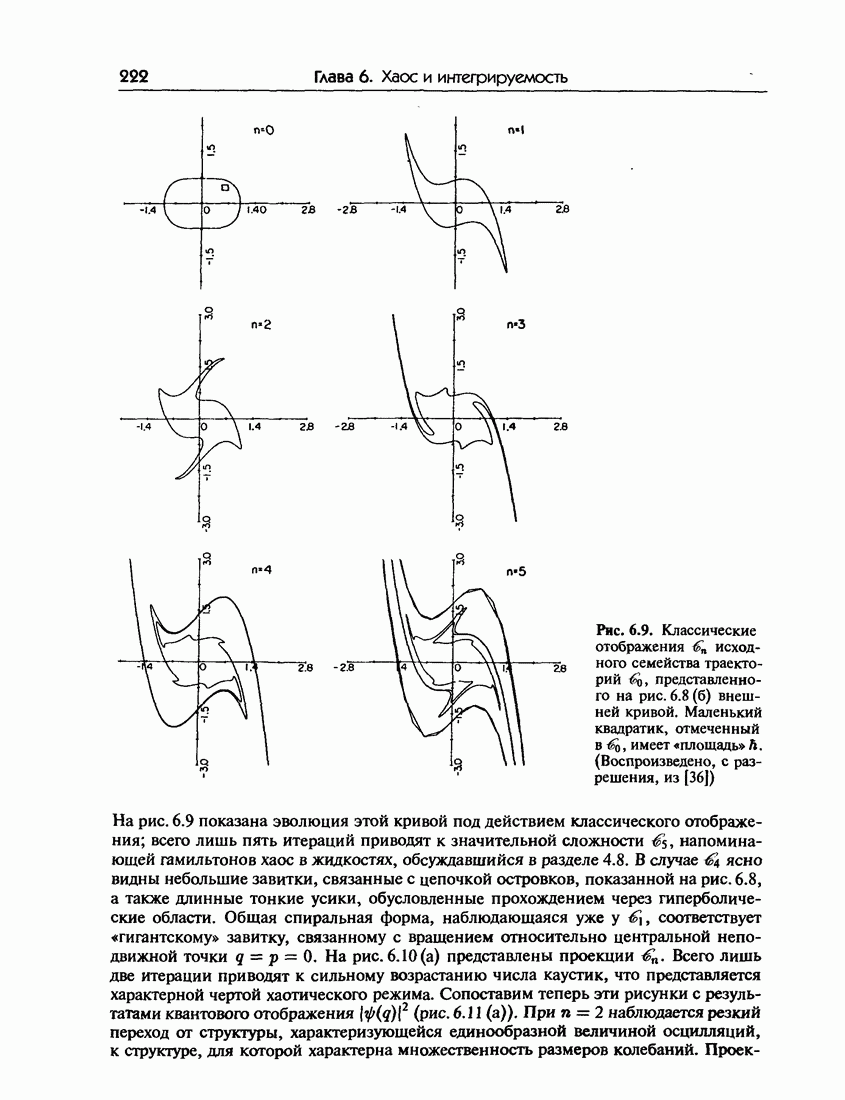
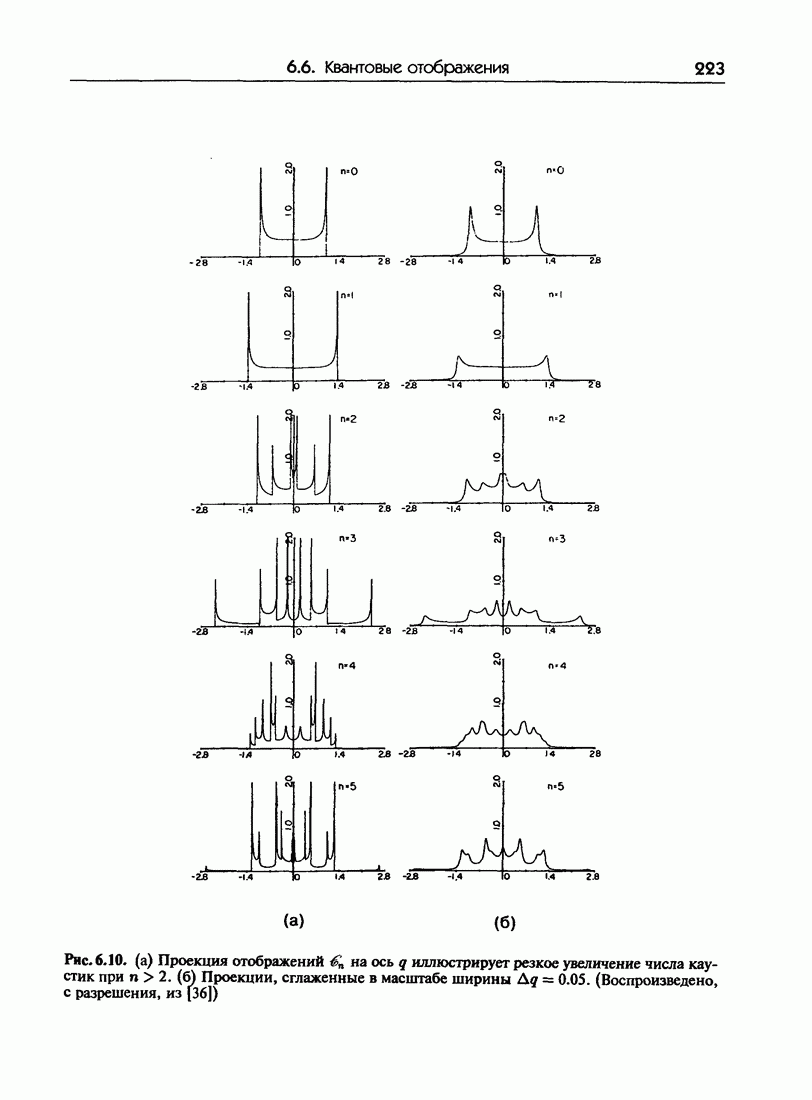
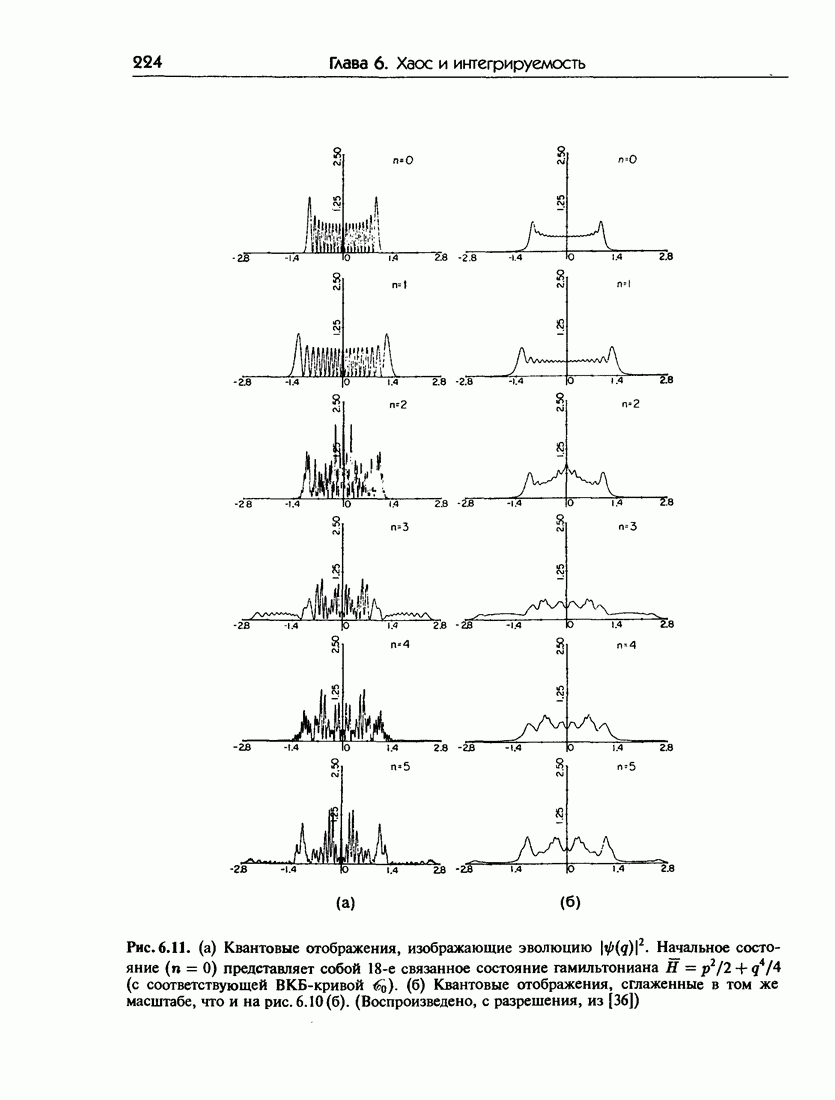
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
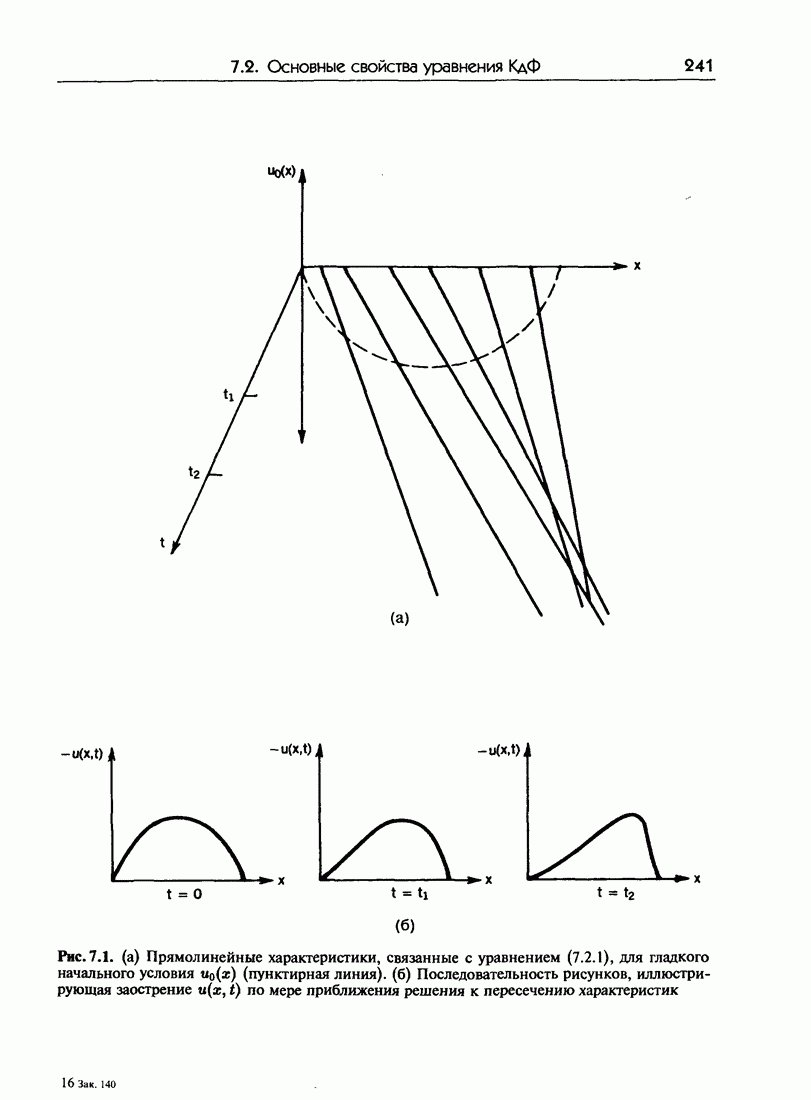
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
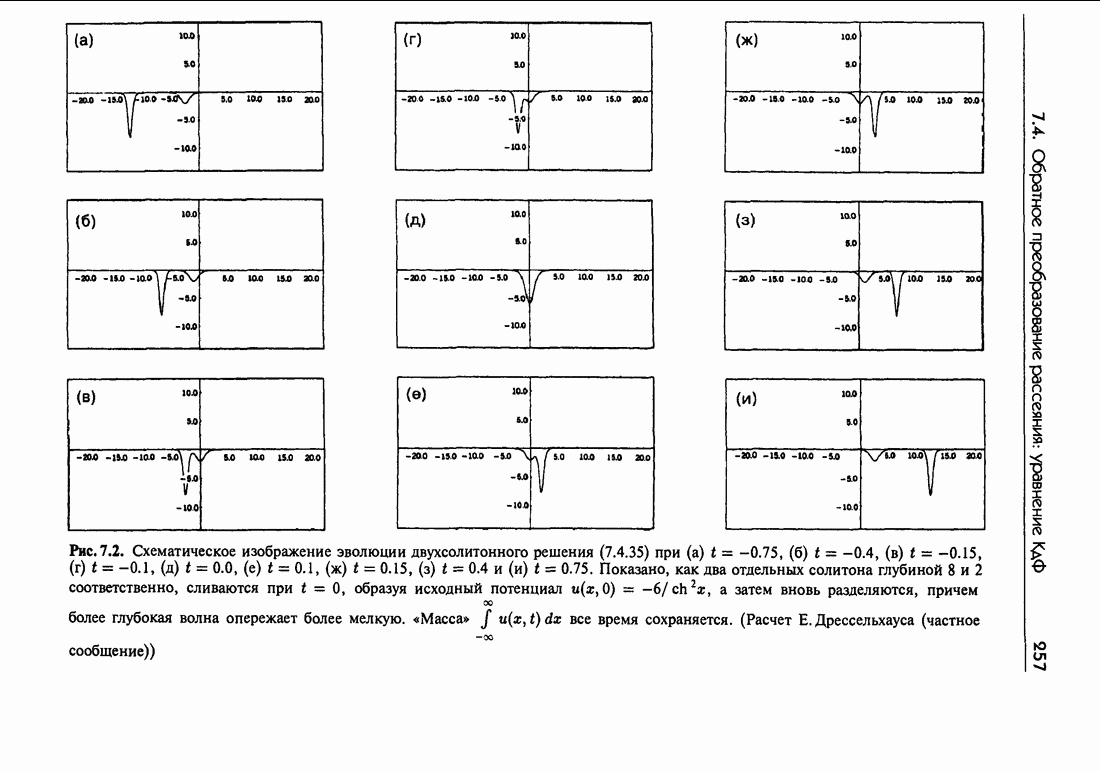
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
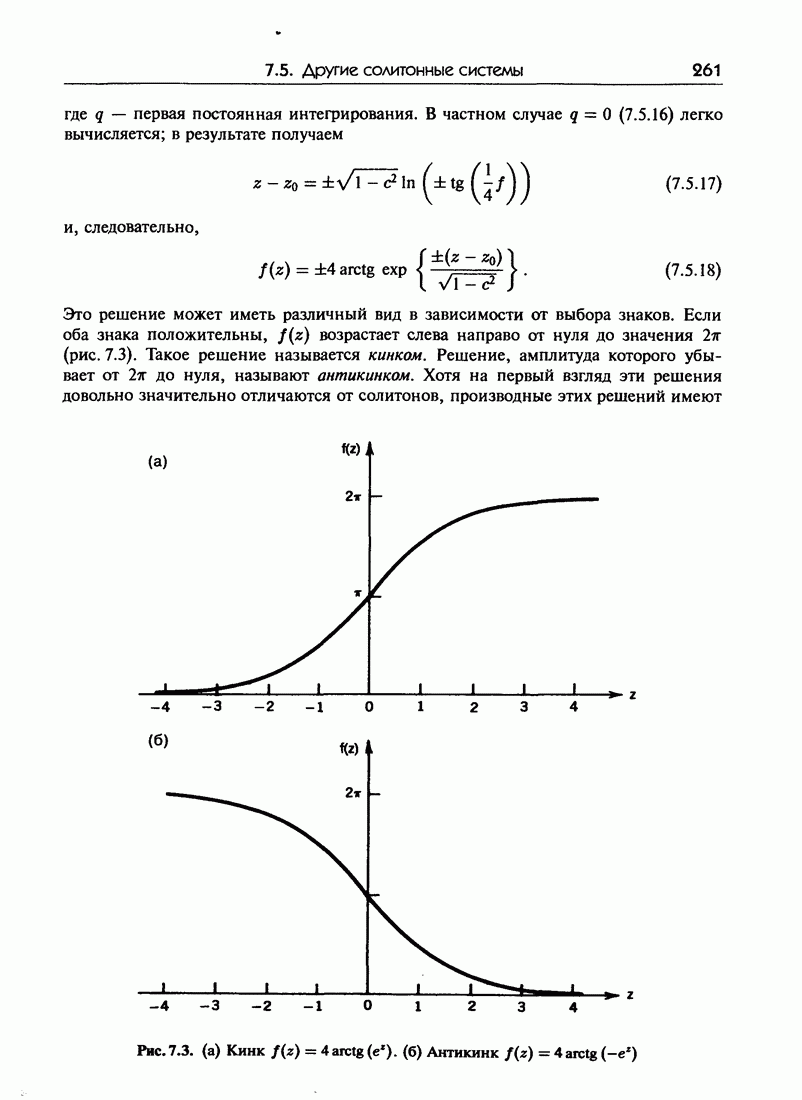
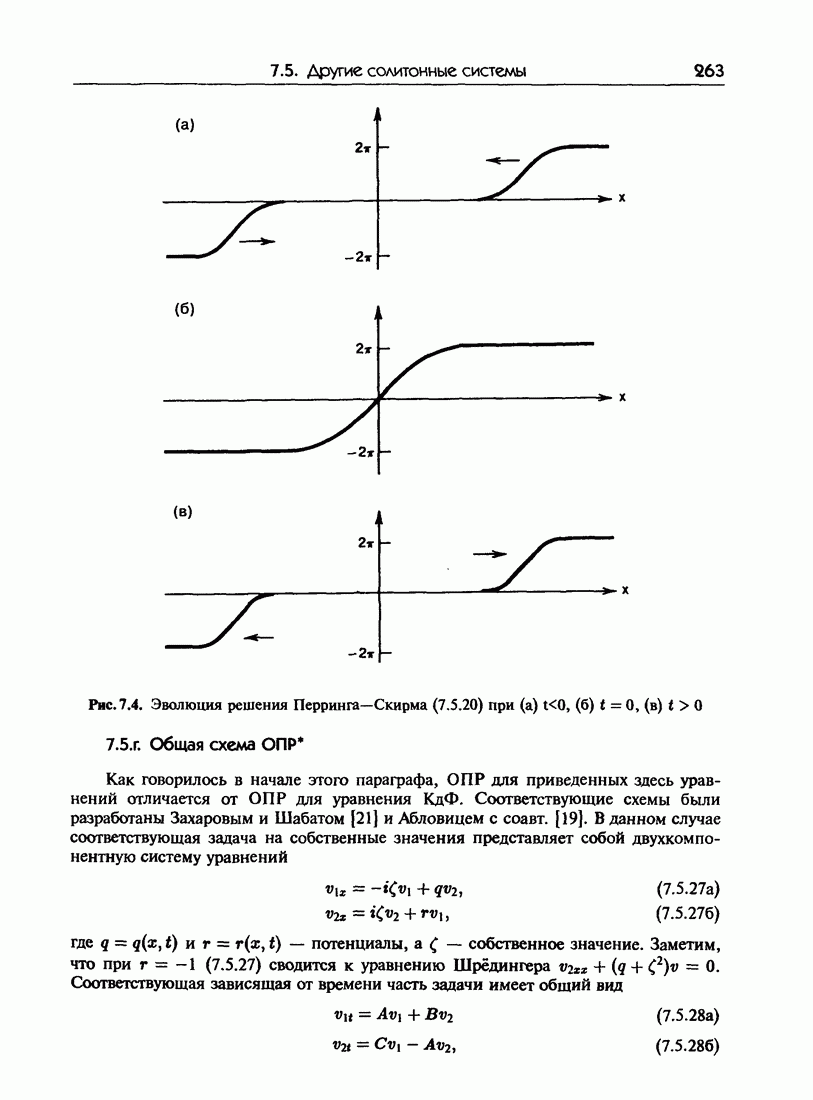
- 7.5. Другие солитонные системы
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
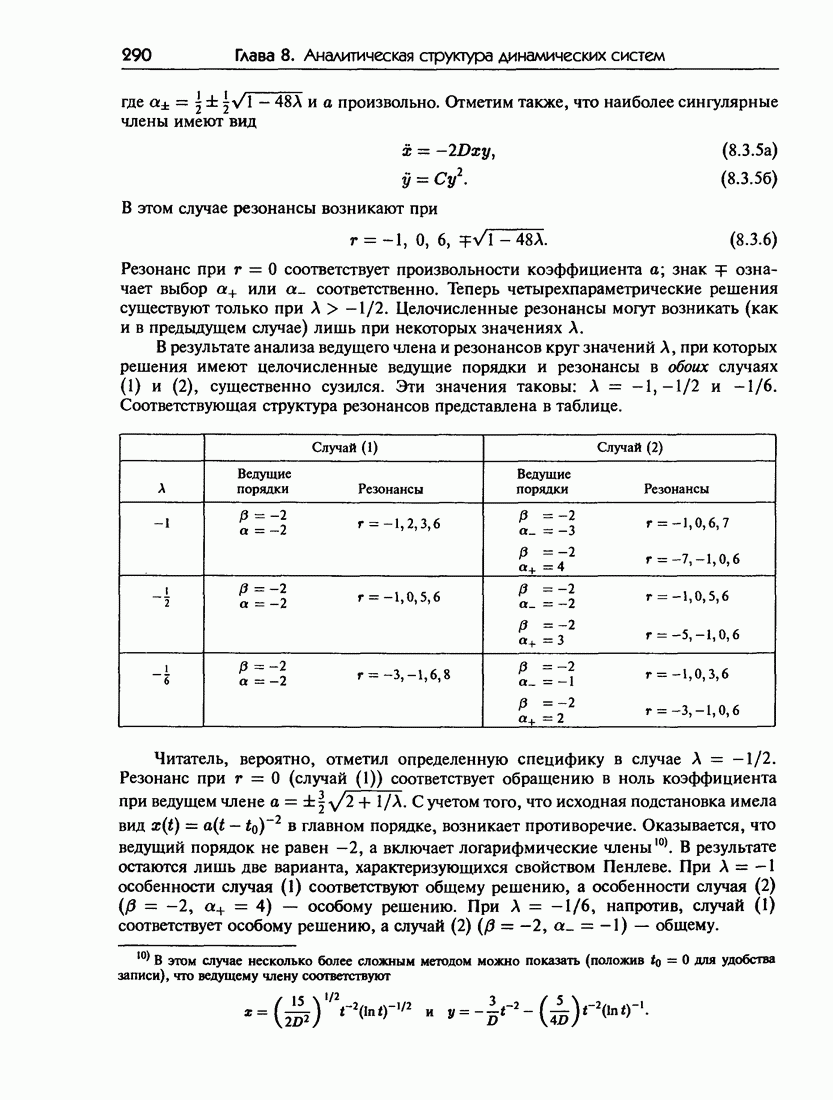
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
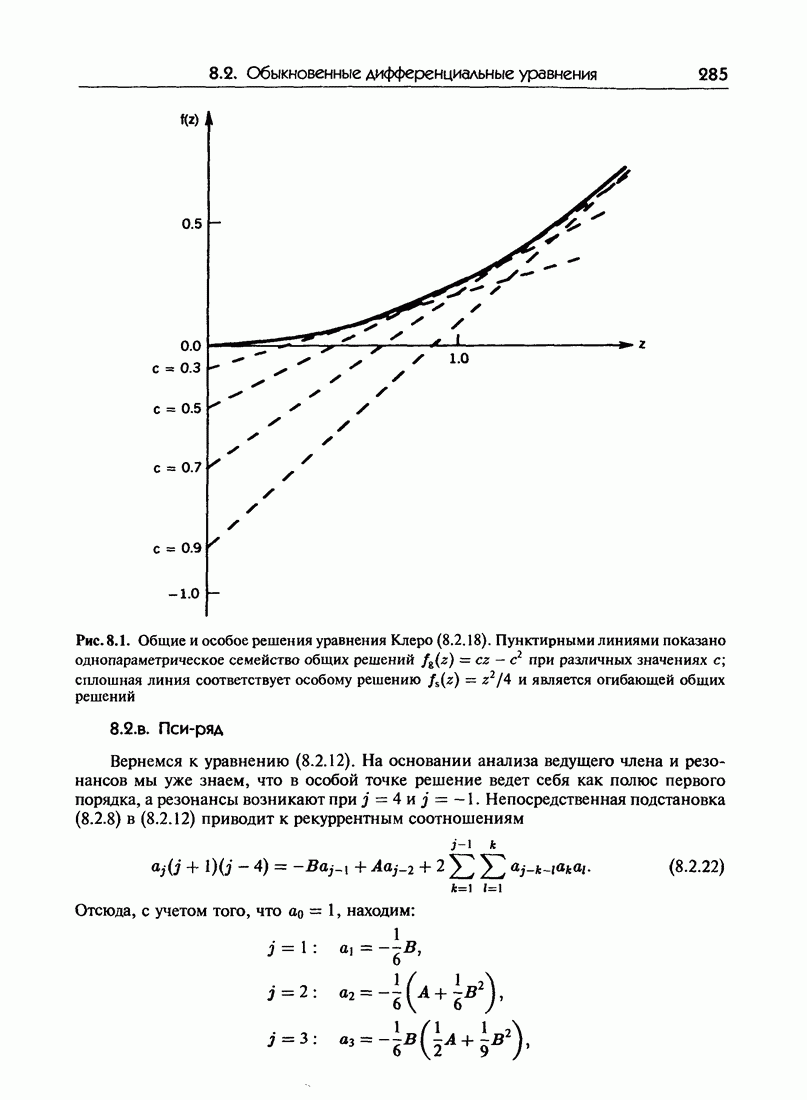
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда