| << Предыдущий параграф | Следующий параграф >> |
Пред.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
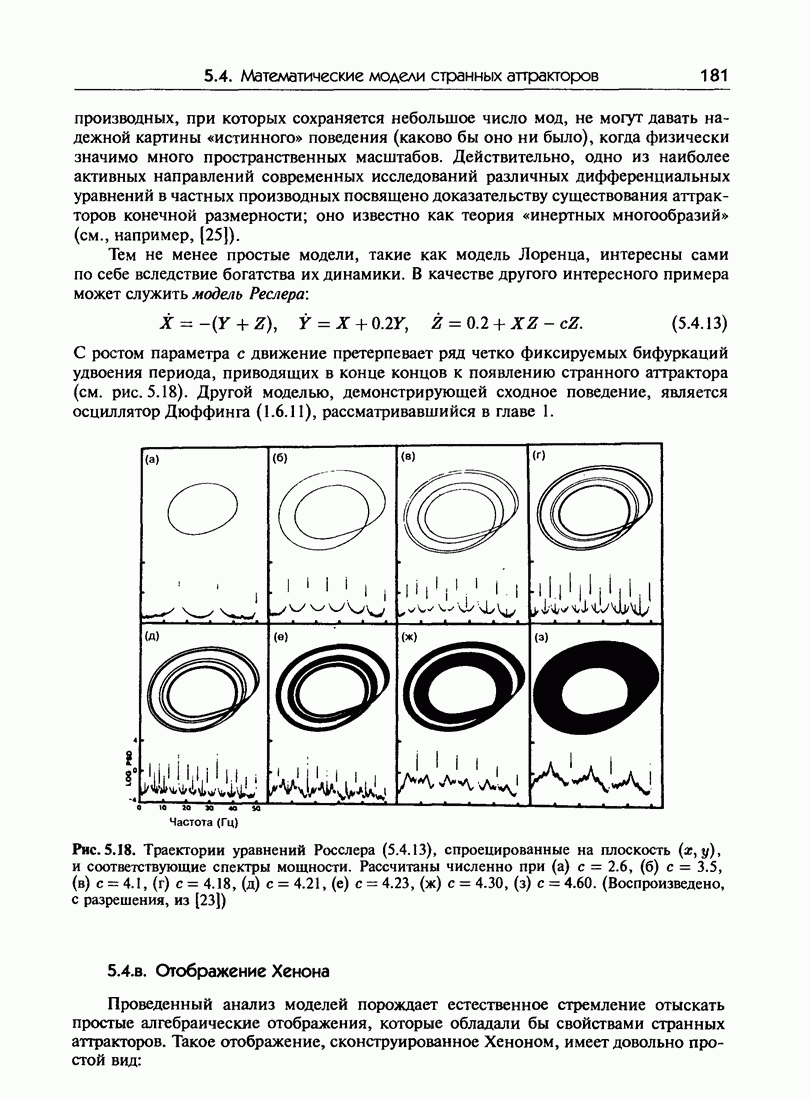
181
182
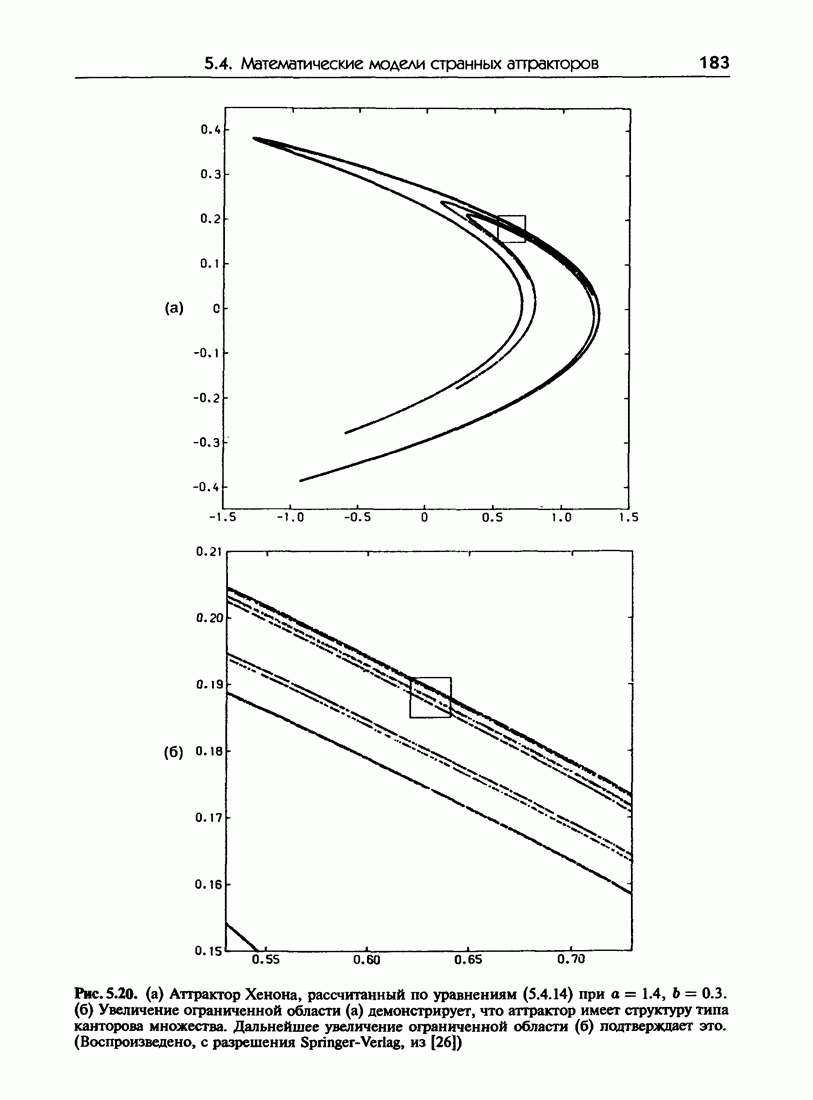
183
184
185
186
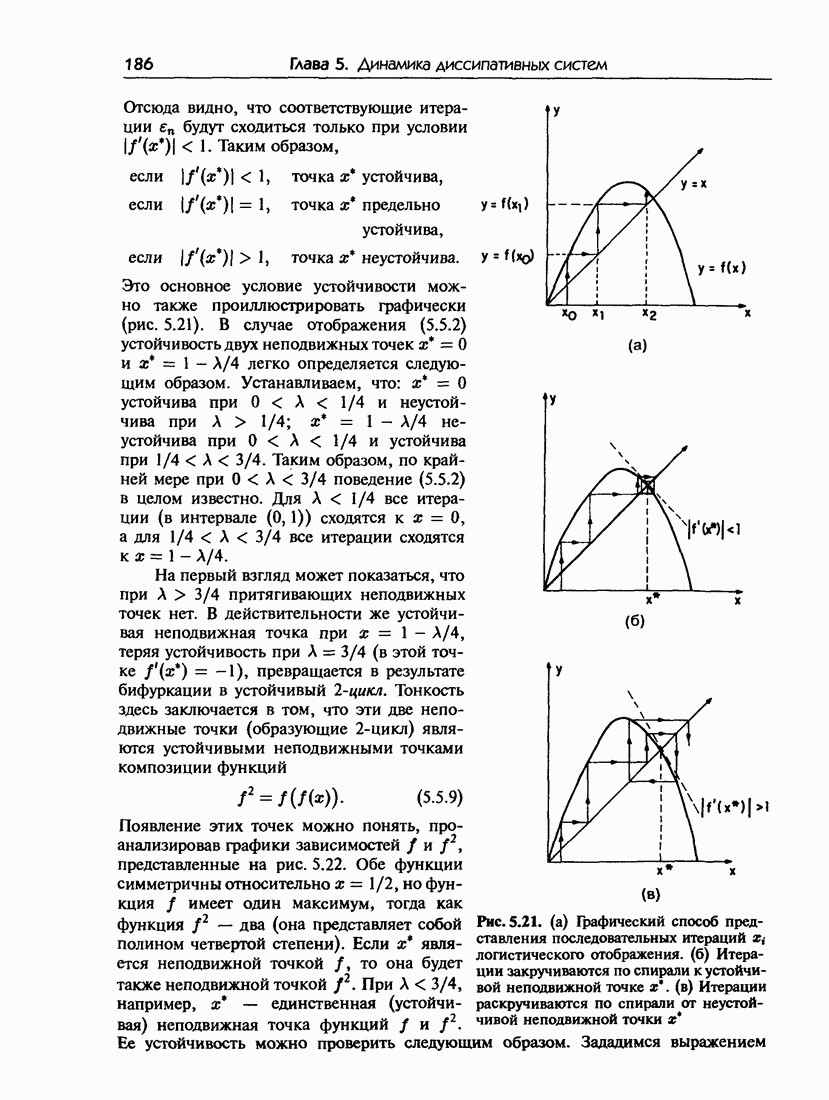
187
188
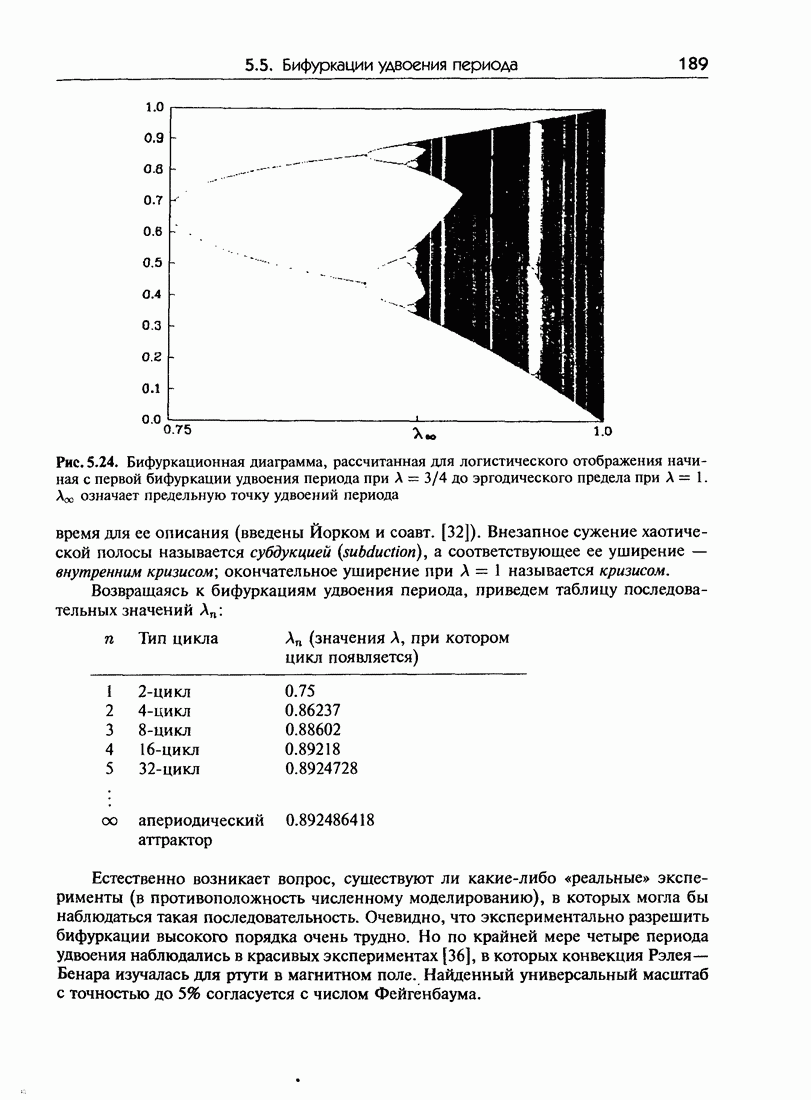
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
303
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
Применение формализма, к рассмотрению которого мы приступаем, не ограничивается рамками квантовомеханических задач; он также широко используется при решении (линейных) дифференциальных уравнений, сингулярно зависящих от малого параметра. Рассмотрим, например, простую краевую задачу

с граничными условиями  Нетрудно показать, что точное решение имеет вид
Нетрудно показать, что точное решение имеет вид

(при условии  в пределе
в пределе  это решение теряет смысл. Понятно, что этот сингулярный предел значительно затрудняет решение уравнений и более общего вида
это решение теряет смысл. Понятно, что этот сингулярный предел значительно затрудняет решение уравнений и более общего вида

где  некая нетривиальная функция от
некая нетривиальная функция от  Наиболее конструктивная процедура (предшествовавшая ВКБ) была разработана Рэлеем, Джефри и др., которые показали,
Наиболее конструктивная процедура (предшествовавшая ВКБ) была разработана Рэлеем, Джефри и др., которые показали,
что решение может быть представлено в виде экспоненты от ряда по степеням  а именно
а именно

(Блестящее обсуждение этого метода дано в [5].)
6.2.а. Разложение ВКБ
В настоящем разделе мы сосредоточим внимание на квантовомеханических вопросах, в рамках которых в качестве малого параметра выступает величина  Рассмотрим вначале одномерное не зависящее от времени уравнение Шрёдингера
Рассмотрим вначале одномерное не зависящее от времени уравнение Шрёдингера

и произведем подстановку

где  представляет собой ряд
представляет собой ряд

Подставляя (6.2.5) в (6.2.4) и приравнивая последовательно степени  получаем иерархию уравнений:
получаем иерархию уравнений:

Вспоминая, что  для двух первых уравнений легко находим решения
для двух первых уравнений легко находим решения

и

где с — постоянная интегрирования, а  некоторая начальная точка на траектории. Для
некоторая начальная точка на траектории. Для  также можно легко получить соответствующие выражения, но их громоздкость быстро возрастает. Исходя из (6.2.8) и (6.2.9), находим вид приближенной волновой функции, соответствующей первому порядку по
также можно легко получить соответствующие выражения, но их громоздкость быстро возрастает. Исходя из (6.2.8) и (6.2.9), находим вид приближенной волновой функции, соответствующей первому порядку по 

где два корня (6.2.8) задают два линейно независимых решения уравнения (6.2.4), которые в виде линейной комбинации с произвольными константами  образуют общее решение (6.2.10). В областях, где
образуют общее решение (6.2.10). В областях, где  положительны; такие области известны как классически разрешенные. Области, в которых
положительны; такие области известны как классически разрешенные. Области, в которых  называются классически запрещенными,
называются классически запрещенными,  в них имеют мнимые значения. Такие области в классической механике не имеют смысла, а в квантовой механике соответствуют областям, через которые может осуществляться «туннелирование». Очевидно, что решение (6.2.10) разрушается в окрестности классических точек возврата
в них имеют мнимые значения. Такие области в классической механике не имеют смысла, а в квантовой механике соответствуют областям, через которые может осуществляться «туннелирование». Очевидно, что решение (6.2.10) разрушается в окрестности классических точек возврата  в которых
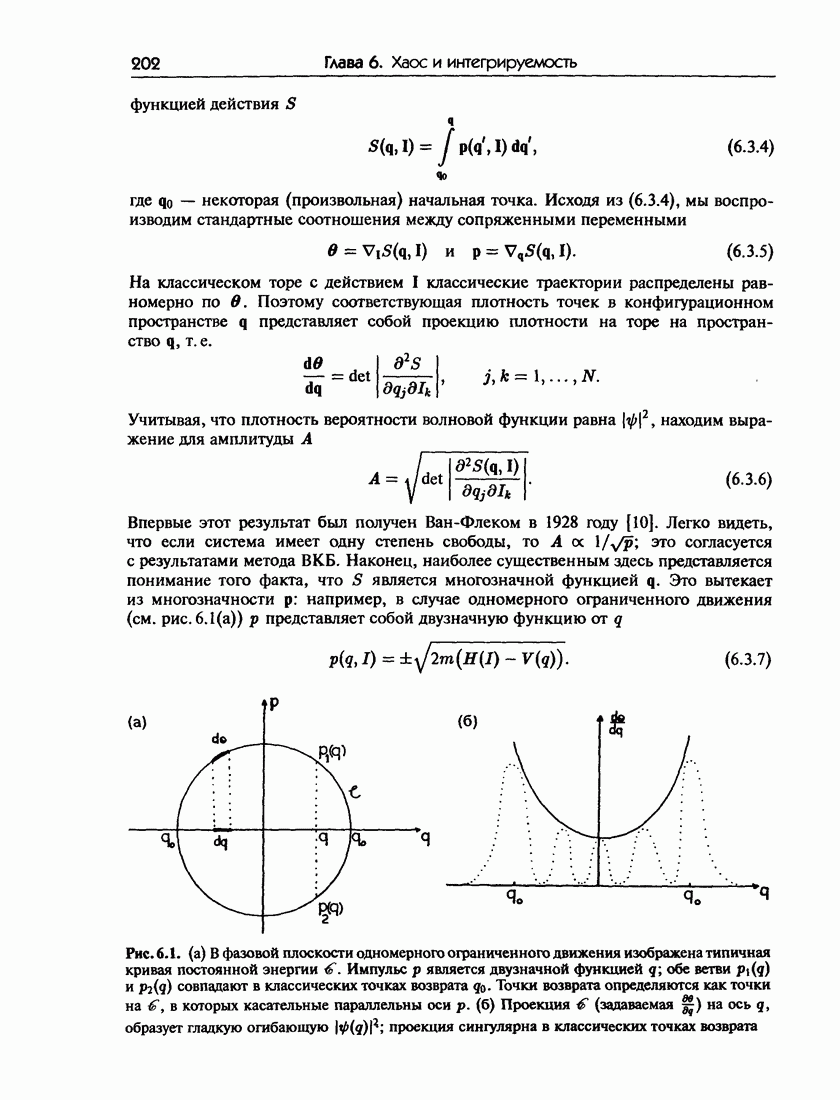
в которых  Плотность вероятности
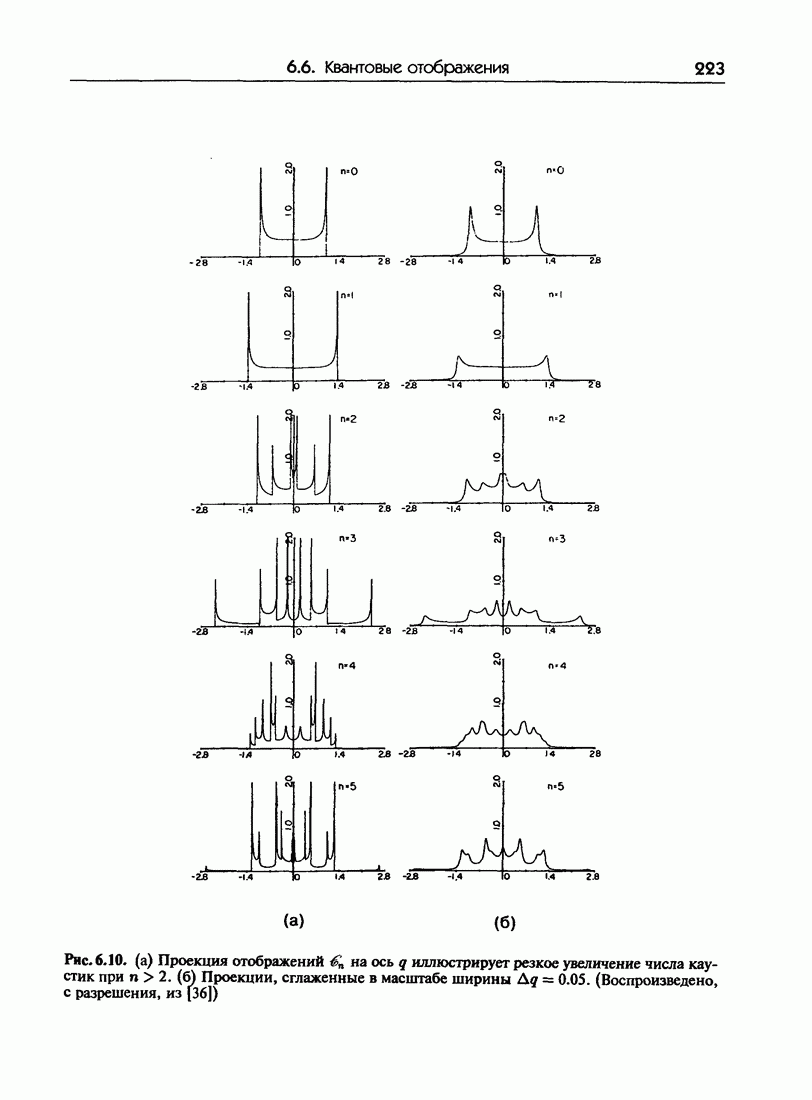
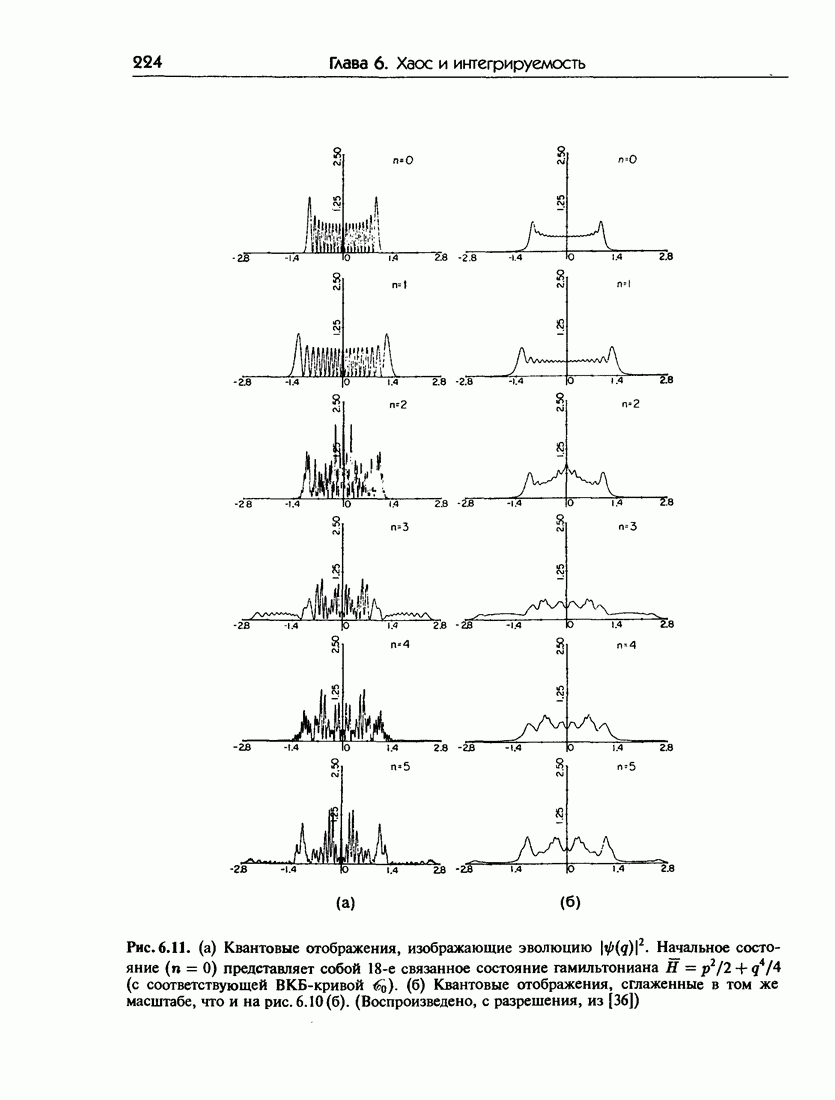
Плотность вероятности  становится здесь очень большой. Это согласуется с классической интуицией, согласно которой частицу вероятнее всего можно обнаружить в тех областях, в которых она проводит больше времени, а именно вблизи точек возврата (где движение наиболее медленное). Расходимость решений (6.2.10) в точках возврата не является непреодолимой проблемой; для отыскания решений, гладко переходящих из разрешенной области в запрещенную без расходимостей была разработана замечательная математическая техника, известная как равномерные приближения. Важный аналог таких классических расходимостей существует в геометрической оптике. Это каустики, которые соответствуют объединению лучей, приводящему к появлению очень интенсивных точек или областей, как это наблюдается, например, при фокусировании (света). Понятие каустик будет играть существенную роль при дальнейшем обсуждении свойств квазиклассических волновых функций.
становится здесь очень большой. Это согласуется с классической интуицией, согласно которой частицу вероятнее всего можно обнаружить в тех областях, в которых она проводит больше времени, а именно вблизи точек возврата (где движение наиболее медленное). Расходимость решений (6.2.10) в точках возврата не является непреодолимой проблемой; для отыскания решений, гладко переходящих из разрешенной области в запрещенную без расходимостей была разработана замечательная математическая техника, известная как равномерные приближения. Важный аналог таких классических расходимостей существует в геометрической оптике. Это каустики, которые соответствуют объединению лучей, приводящему к появлению очень интенсивных точек или областей, как это наблюдается, например, при фокусировании (света). Понятие каустик будет играть существенную роль при дальнейшем обсуждении свойств квазиклассических волновых функций.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- Предисловие
- Глава 1. Динамика дифференциальных уравнений
- 1.1.б. Затухающий осциллятор
- 1.2. Интегрирование нелинейных уравнений второго порядка
- 1.2.а. Эллиптические функции Якоби
- 1.2.б. Эллиптические функции Вейерштрасса
- 1.2.в. Периодическая структура эллиптических функций
- 1.2.г. Уравнение маятника
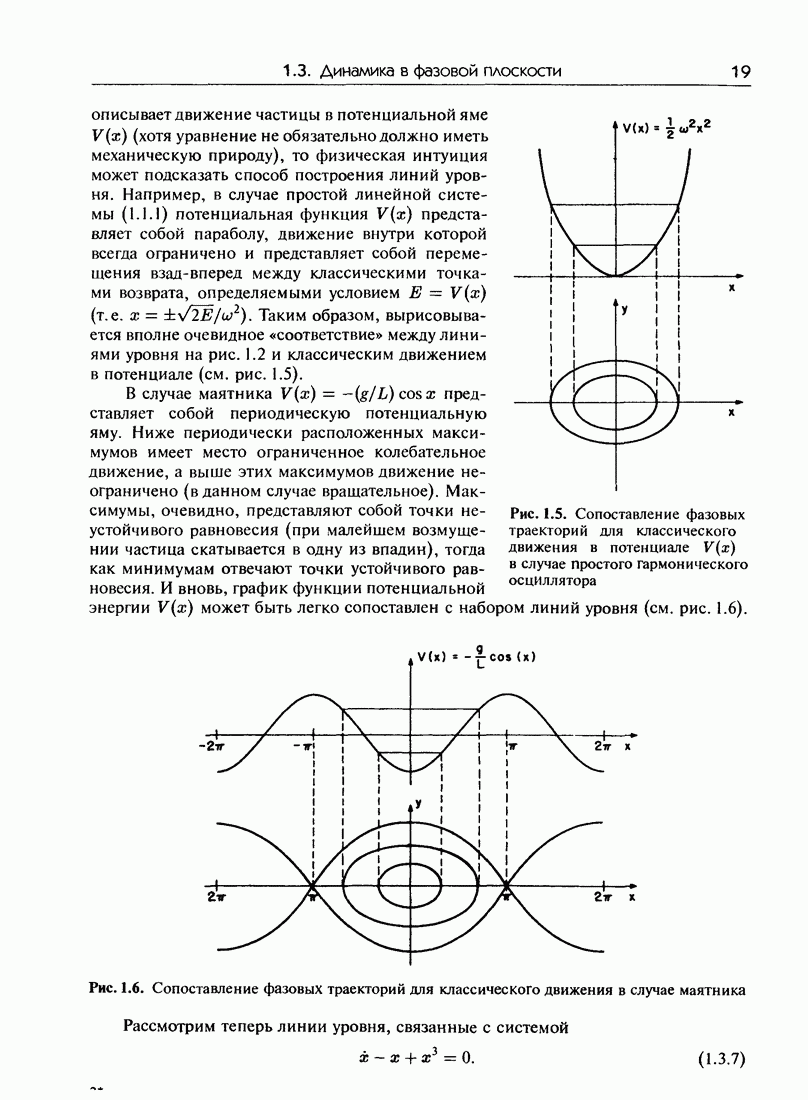
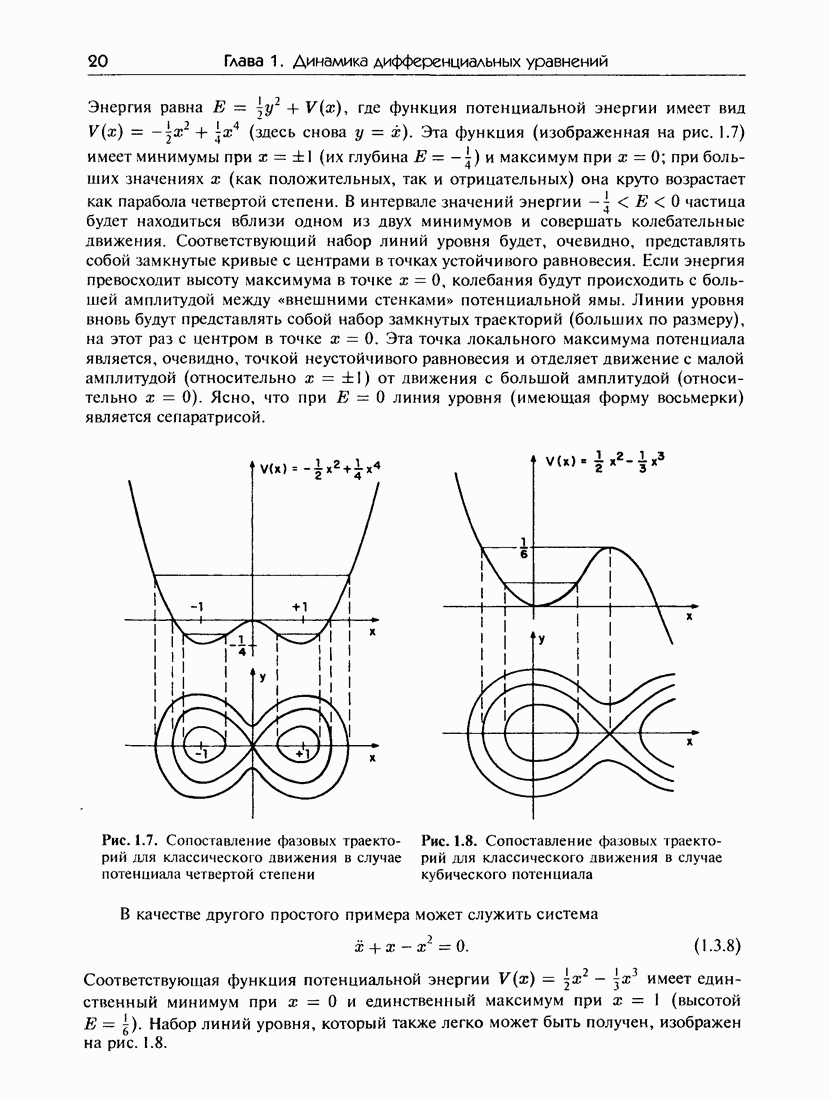
- 1.3. Динамика в фазовой плоскости
- 1.3.а. Фазовый портрет маятника
- 1.3.б. фазовые портреты консервативных систем
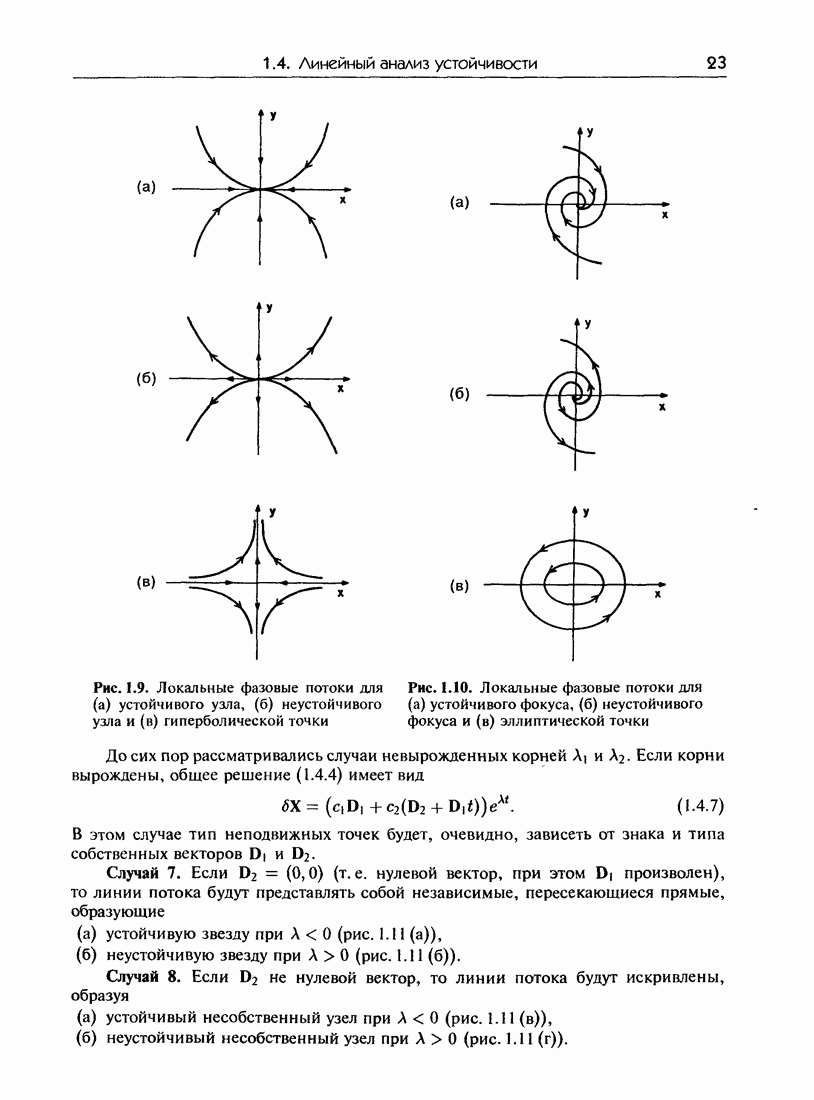
- 1.4. Линейный анализ устойчивости
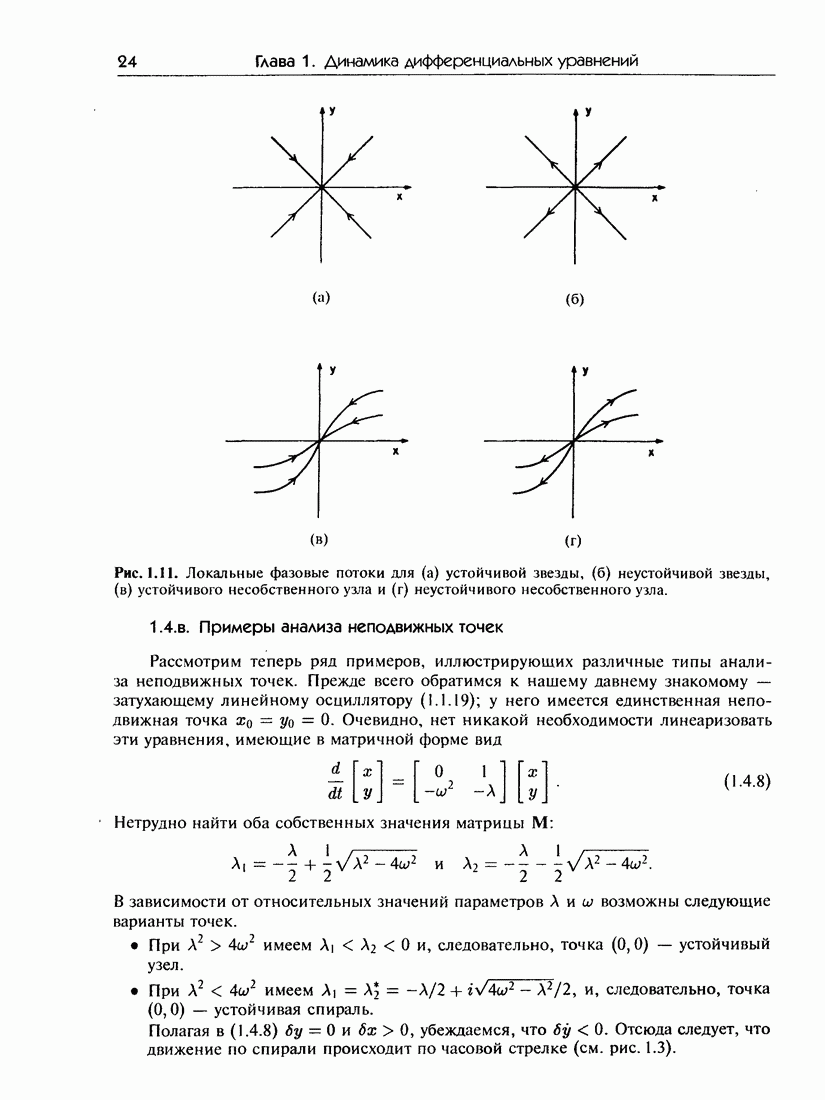
- 1.4.б. Классификация неподвижных точек
- 1.4.в. Примеры анализа неподвижных точек
- 1.4.г. Предельные циклы
- 1.5. Интегралы, зависящие от времени
- 1.6. Неавтономные системы
- 1.6.а. Осциллятор с вынуждающей силой
- 1.6.б. Затухающий осциллятор с вынуждающей внешней силой
- 1.7. Дальнейшие замечания об интегрировании дифференциальных уравнений
- ПРИЛОЖЕНИЕ 1.1. Эллиптические функции
- Глава 2. Динамика гамильтоновых систем
- 2.1.б. Свойства Лагранжиана
- 2.1.в. Свойства обобщенных импульсов
- 2.2. Формализм Гамильтона
- 2.2.б. Уравнения Гамильтона
- 2.2.в. Скобки Пуассона
- 2.3. Канонические преобразования
- 2.3.б. Оптимальное преобразование
- 2.3.в. Производящие функции
- 2.4. Уравнение Гамильтона-Якоби и переменные действие—угол
- 2.4.а. Уравнение Гамильтона-Якоби в случае одной степени свободы
- 2.4.б. Переменные действие—угол в случае одной степени свободы
- 2.5. Интегрируемые гамильтонианы
- 2.5.б. Свойства интегрируемых систем
- 2.5.в. Примеры интегрируемых систем
- 2.5.г. Движение на торах
- 2.5.д. Фундаментальные вопросы
- ПРИЛОЖЕНИЕ 2.1. Преобразования Лежандра
- ПРИЛОЖЕНИЕ 2.2. Геометрические представления в классической механике
- Глава 3. Классическая теория возмущений
- 3.1.б. Сингулярные ряды возмущений
- 3.1.в. Регулярные ряды возмущений для дифференциальных уравнений
- 3.2. Каноническая теория возмущений
- 3.2.б. Решения с точностью до первого порядка по е
- 3.2.в. Решения с точностью до более высоких степеней по е
- 3.2.г. Возмущенный осциллятор
- 3.3. Большое число степеней свободы и проблема малых знаменателей
- 3.4. Теорема Колмогорова-Арнольда-Мозера
- 3.4.а. Суперсходящаяся теория возмущений
- 3.4.б. Теоретико-числовые свойства частот
- 3.4.в. Другие аспекты КАМ-теоремы
- 3.5. Резюме по КАМ-теореме и ее вариантам
- 3.5.б. Отображения
- 3.5.в. Периодические системы
- 3.5.г. Точки устойчивого равновесия
- Глава 4. Хаос в гамильтоновых системах и сохраняющие площадь отображения
- 4.1.б. Гамильтониан Хенона-Хейлеса
- 4.1.в. Цепочка Тода
- 4.1.г. Поверхность сечения как симплекгическое отображение
- 4.2. Сохраняющие площадь отображения
- 4.2.б. Отображения на плоскости
- 4.2.в. Взаимосвязь между сохраняющими площадь отображениями и гамильтонианами
- 4.2.г. Дискретные лагранжианы
- 4.2.д. Стандартное отображение
- 4.3. Неподвижные точки и теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.3.б. Классификация неподвижных точек
- 4.3.в. Теорема Пуанкаре-Биркгофа о неподвижной точке
- 4.4. Гомоклинные и гетероклинные точки
- 4.4.б. Усы и завитки
- 4.5. Критерии локального хаоса
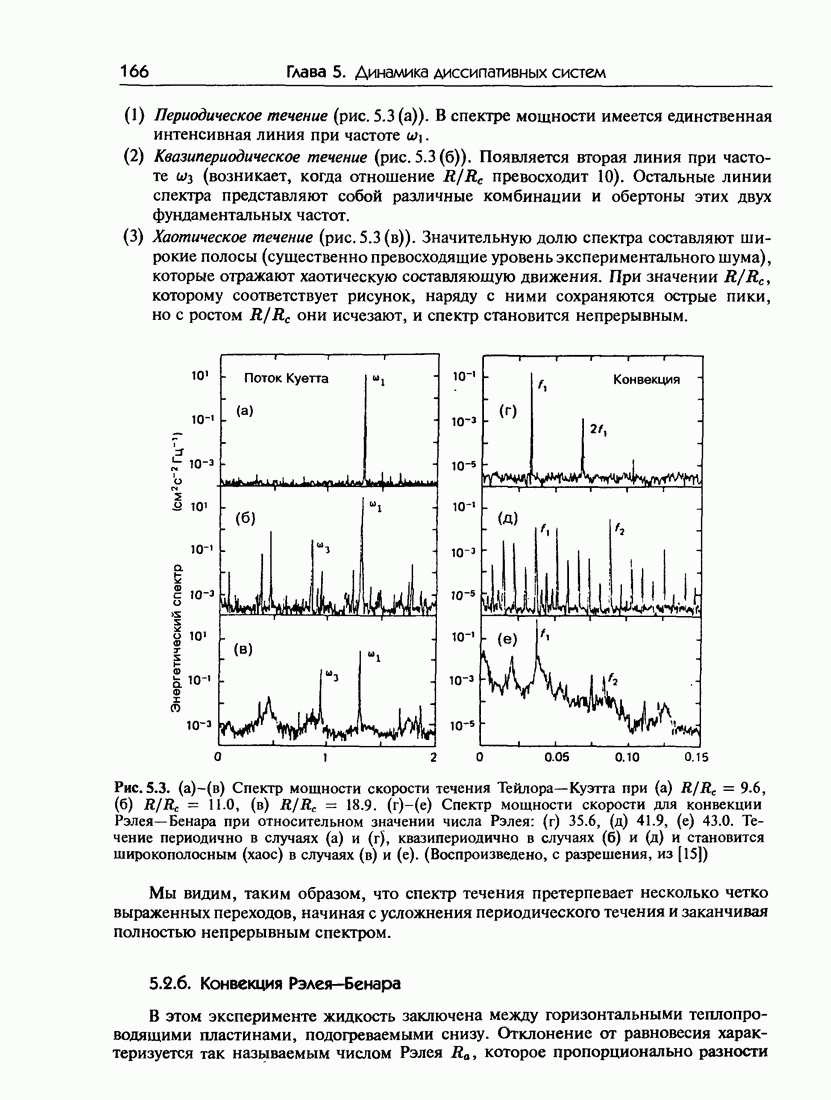
- 4.5.б. Спектры мощности
- 4.6. Критерии возникновения глобального хаоса
- 4.6.а. Метод перекрытия резонансов
- 4.6.б. Метод Грина
- 4.7. Статистические понятия сильно хаотических систем
- 4.7.б. Перемешивание
- 4.7.в. Преобразование пекаря и системы Бернулли
- 4.7.г. Иерархия неупорядоченности
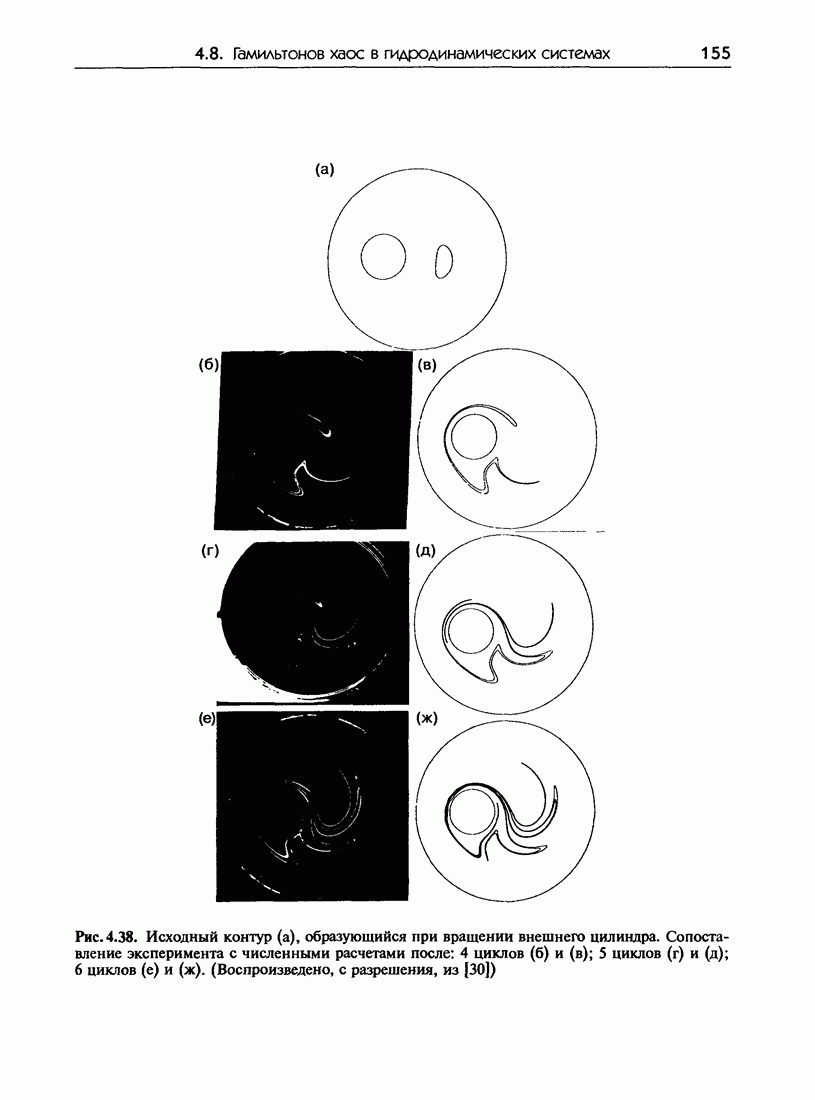
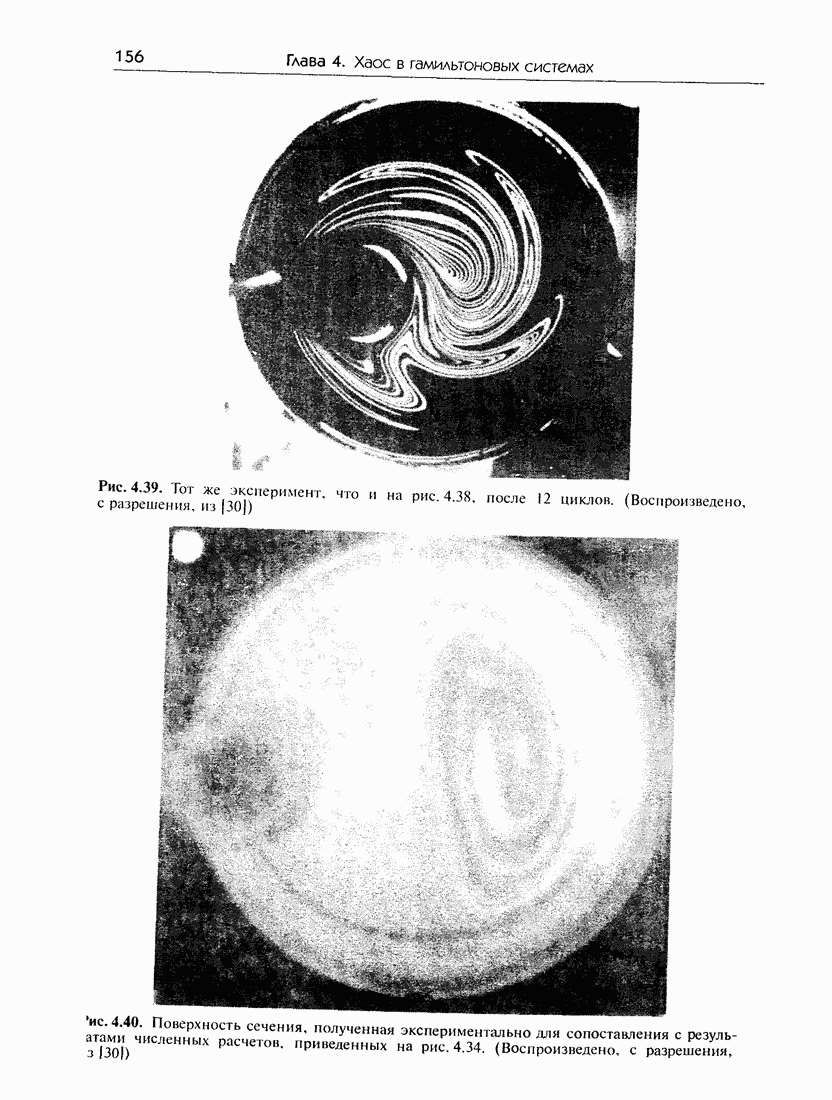
- 4.8. Гамильтонов хаос в гидродинамических системах
- 4.8.б. Модельная система
- 4.8.в. Экспериментальные результаты
- ПРИЛОЖЕНИЕ 4.1. Поверхность сечения как симплектическое отображение
- Глава 5. Динамика диссипативных систем
- 5.1.б. Понятие турбулентности
- 5.1.в. Гамильтонова дигрессия
- 5.2. Экспериментальные наблюдения возникновения турбулентности
- 5.2.б. Конвекция Рэлея-Бенара
- 5.3. Теоретические представления о возникновении турбулентности
- 5.3.б. Теория бифуркации Хопфа
- 5.3.в. Теория Рюэля-Тэкенса
- 5.3.г. Другие сценарии
- 5.3.д. Фракталы
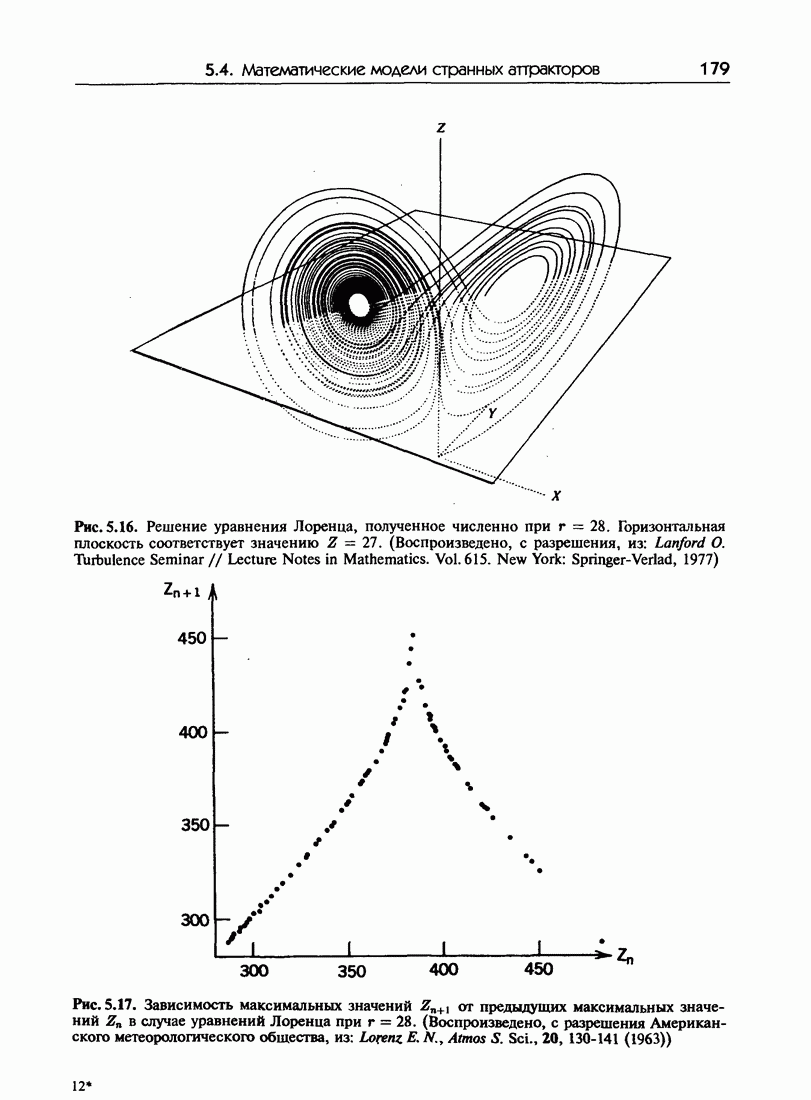
- 5.4. Математические модели странных аттракторов
- 5.4.б. Варианты модели Лоренца
- 5.4.в. Отображение Хенона
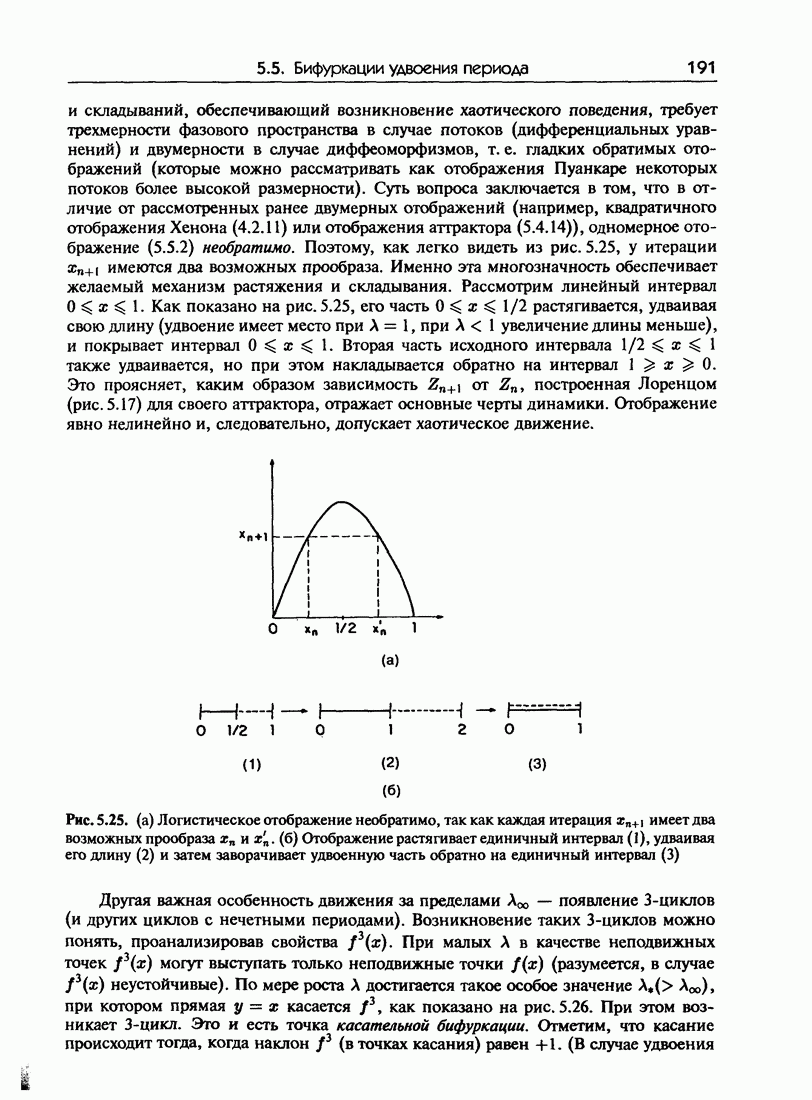
- 5.5. Бифуркации удвоения периода
- 5.5.а. Механизм удвоения периода
- 5.5.б. Бифуркационная диаграмма
- 5.5.в. Поведение за пределами …
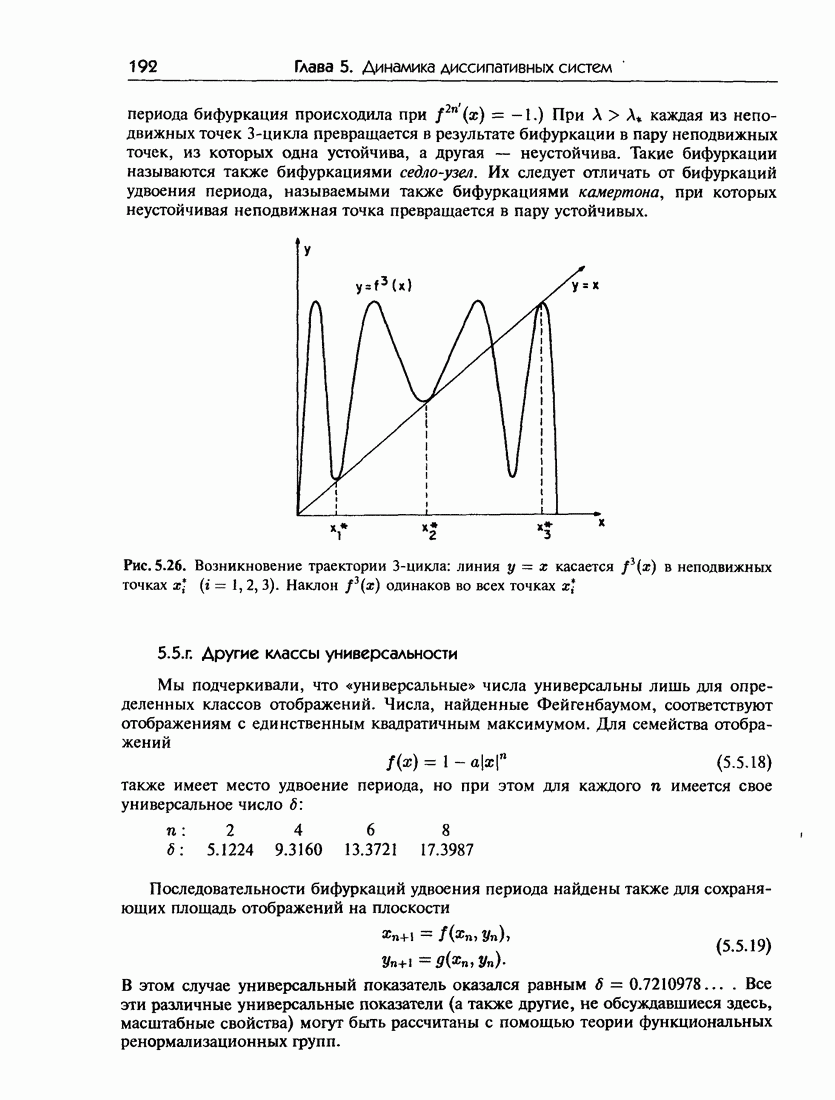
- 5.5.г. Другие классы универсальности
- Глава 6. Хаос и интегрируемость в квазиклассичсской механике
- 6.1.б. Квазиклассический предел для задач, не зависящих от времени
- 6.2. Метод ВКБ и условия квантования Бора-Зоммерфельда
- 6.2.б. Квантование Бора-Зоммерфельда
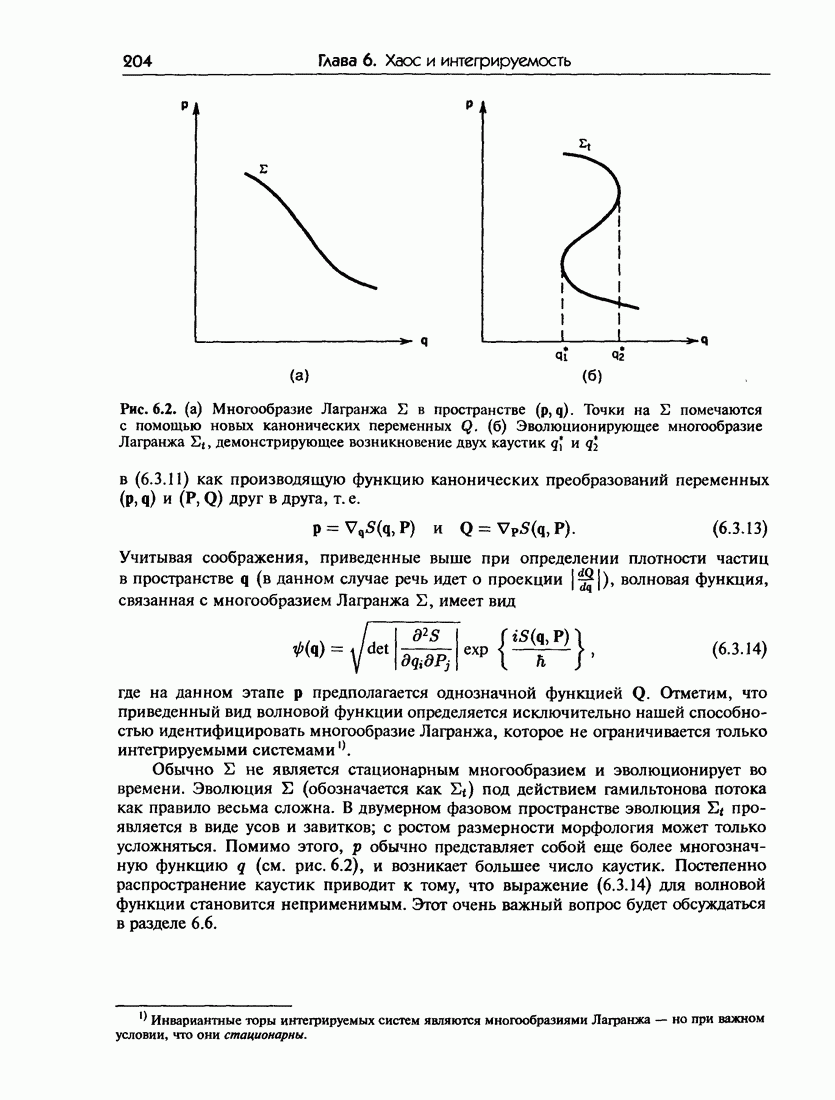
- 6.3. Квазиклассическое квантование в случае большого числа степеней свободы
- 6.3.б. ЭБК-квантование
- 6.3.в. Квазиклассические волновые пакеты
- 6.4. Регулярные и нерегулярные спектры: свойства, связанные с собственными значениями
- 6.4.б. Спектр мощности и принцип соответствия
- 6.4.в. Чувствительность к возмущению
- 6.4.г. Распределение расстояний между уровнями
- 6.4.д. Спектральная жесткость
- 6.5. Регулярные и нерегулярные спектры: свойства, связанные с собственными векторами
- 6.5.б. функция Вигнера
- 6.5.в. Пространственные корреляции волновых функций
- 6.5.г. Некоторые численные результаты
- 6.5.д. Узловые структуры
- 6.5.е. Теоремы локализации
- 6.5.ж. Эксперименты по микроволновой ионизации
- 6.6. Квантовые отображения: эволюция волновых пакетов
- 6.6.б. Квантовое отображение
- 6.6.в. Эволюция классических и квантовых состояний
- 6.7. Квантовые отображения: квантование с использованием замкнутых траекторий
- 6.7.б. Квазиэнергетический спектр
- 6.7.в. Пропагатор квантового отображения
- 6.7.г. Вычисление следа пропагатора
- 6.7.д. Обсуждение метода замкнутых траекторий
- ПРИЛОЖЕНИЕ 6.1. Метод стационарной фазы
- Глава 7. Нелинейные эволюционные уравнения и солитоны
- 7.1.б. Эксперимент ФУП
- 7.1.в. Открытие солитона
- 7.2. Основные свойства уравнения КдФ
- 7.2.б. Решение типа бегущей волны
- 7.2.в. Автомодельные решения
- 7.2.г. Законы сохранения
- 7.2.д. Преобразование Миуры
- 7.2.е. Инвариантность Галилея
- 7.3. Обратное преобразование рассеяния: основные принципы
- 7.3.б. Аналогия с преобразованиями Фурье
- 7.3.в. Прямая задача рассеяния
- 7.3.г. Обратная задача рассеяния
- 7.4. Обратное преобразование рассеяния: уравнение КдФ
- 7.4.б. Эволюция данных рассеяния
- 7.4.в. Двухсолитонное решение
- 7.4.г. Более общие решения
- 7.4.д. Пара Лакса
- 7.5. Другие солитонные системы
- 7.5.б. Уравнение sin-Гордона
- 7.5.в. Нелинейное уравнение Шредингера
- 7.5.г. Общая схема ОПР
- 7.6. Гамильтонова структура интегрируемых систем
- 7.7. Динамика неинтегрируемых эволюционных уравнений
- Глава 8. Аналитическая структура динамических систем
- 8.1.а. Работа Ковалевской
- 8.1.б. Работа Пенлеве
- 8.2. Обыкновенные дифференциальные уравнения в комплексной области
- 8.2.б. Общие и особые решения
- 8.2.в. Пси-ряд
- 8.2.г. Эллиптические функции и алгебраические кривые
- 8.3. Интегрируемые системы обыкновенных дифференциальных уравнений
- 8.3.б. Интегрируемые системы с подвижными точками ветвления
- 8.3.в. Система Лоренца
- 8.3.г. Почему «работает» свойство Пенлеве?
- 8.3.д. Структура сингулярностей неинтегрируемых систем
- 8.4. Свойство Пенлеве дифференциальных уравнений в частных производных
- 8.4.б. Примеры свойства Пенлеве для у. ч. п.
- 8.4.в. Пара Лакса и преобразования Бэклунда