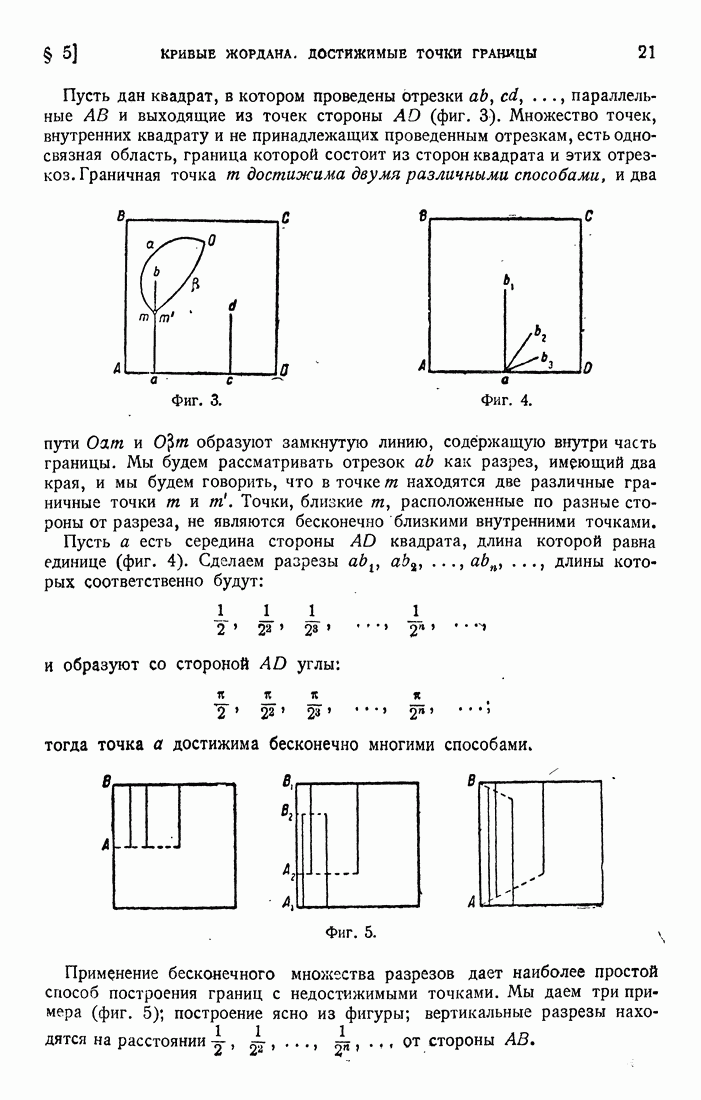
| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
§ 103. Множитель. Область притяжения.
Пусть  есть неподвижная точка преобразования
есть неподвижная точка преобразования  коэфициент
коэфициент  при
при  в разложении функции
в разложении функции  равен
равен 
Мы назовем множителем неподвижной точки  порядка
порядка  число
число  коэфициент в разложении
коэфициент в разложении  (или
(или  , если
, если  есть
есть  конечно удаленная точка).
конечно удаленная точка).
Если  то точка называется неподвижной притягивающей точкой.
то точка называется неподвижной притягивающей точкой.
Если  то она называется неподвижной отталкивающей точкой.
то она называется неподвижной отталкивающей точкой.
Если  то — неподвижной индиферентной точкой
то — неподвижной индиферентной точкой  или
или 
Число  не изменится, если совершить над
не изменится, если совершить над  одно и то же линейное преобразование или вообще преобразование, конформное в соседстве с точкой Следовательно, мы можем всегда предполагать, что
одно и то же линейное преобразование или вообще преобразование, конформное в соседстве с точкой Следовательно, мы можем всегда предполагать, что  находится на конечном расстоянии.
находится на конечном расстоянии.
Пусть  есть иикл» соответствующий точке С порядка
есть иикл» соответствующий точке С порядка  Вычислим множители, соответствующие этим различным неподвижным точкам порядка
Вычислим множители, соответствующие этим различным неподвижным точкам порядка  Имеем:
Имеем:

следовательно,

Итак, все множители равны.
Изучим сначала неподвижную притягивающую точку первого порядка.
Так как  имеет модуль меньше единицы, то можно провести круг
имеет модуль меньше единицы, то можно провести круг  с центром в в котором
с центром в в котором  остается меньше числа а, меньшего единицы. Тогда имеем:
остается меньше числа а, меньшего единицы. Тогда имеем:

откуда

Таким образом последовательность  сходится равномерно к С, когда
сходится равномерно к С, когда  бесконечно растет. Последующие для каждой точки
бесконечно растет. Последующие для каждой точки  круга
круга  сгущаются к точке Множество точек плоскости, для которых
сгущаются к точке Множество точек плоскости, для которых  имеет пределом образуют область притяжения точкой Она вообще состоит из счетного множества открытых областей. Эти области притяжения содержат, конечно, связную область, внутри которой находится
имеет пределом образуют область притяжения точкой Она вообще состоит из счетного множества открытых областей. Эти области притяжения содержат, конечно, связную область, внутри которой находится 
эта последняя область называется областью непосредственного притяжения точкой 
Рассмотрим теперь неподвижную точку  притяжения порядка
притяжения порядка  для
для  это есть точка первого порядка для
это есть точка первого порядка для 
Можно повторить для последовательности  все, что мы только что сказали; функции
все, что мы только что сказали; функции  имеют пределом когда
имеют пределом когда  в (у); последовательность
в (у); последовательность  имеет пределом и т. д. Последовательность
имеет пределом и т. д. Последовательность  имеет пределом
имеет пределом  Мы говорим, что
Мы говорим, что  сходится равномерно к циклу. Пусть
сходится равномерно к циклу. Пусть  есть область непосредственного притяжения точкой области непосредственного притяжения точками
есть область непосредственного притяжения точкой области непосредственного притяжения точками  последующие
последующие  для
для  Множество этих
Множество этих  областей образует область непосредственного притяжения циклом. Так же определяется вся область притяжения.
областей образует область непосредственного притяжения циклом. Так же определяется вся область притяжения.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МНОЖЕСТВА ТОЧЕК. СЕМЕЙСТВА ФУНКЦИЙ. МНОЖЕСТВА ТОЧЕК ОБЛАСТИ
- § 1. Множество. Предельная точка.
- § 2. Производное множество.
- § 3. Внутренние и внешние точки. Границы. Области.
- § 4. Непрерывные множества.
- § 5. Кривые Жордана. Достижимые точки границы.
- § 6. Множества точек в произвольном пространстве.
- § 7. Множества точек в функциональном пространстве.
- СЕМЕЙСТВА ФУНКЦИЙ
- § 8. Теорема Вейерштрасса.
- § 9. Сгущение значений.
- § 10. Функции, ограниченные в своей совокупности
- § 11. Равностепенная непрерывность.
- § 12. Существование предельных функций.
- § 13. Случай открытой области.
- § 14. Случай неаналитических функций.
- § 15. Теорема Стилтьеса.
- § 16. Теорема Витали.
- § 17. Функции, допускающие исключительные области.
- § 18. Определение нормального семейства.
- § 19. Семейство нормальное в точке.
- § 20. Нормальные и ограниченные семейства.
- § 21. Число нулей функций нормального семейства.
- § 22. Иррегулярные точки.
- § 23. Семейство гармонических функций. Теорема Харнака.
- § 24. Частные ограниченных функций.
- § 25. Нормальное семейство функций N.
- ГЛАВА II. ГОЛОМОРФНЫЕ ФУНКЦИИ С ИСКЛЮЧИТЕЛЬНЫМИ ЗНАЧЕНИЯМИ. КВАЗИ-НОРМАЛЬНЫЕ СЕМЕЙСТВА. ФУНКЦИИ ШВАРЦА
- § 26. Теорема Пэнлеве.
- § 27. Метод симметрии.
- § 28. Функции Шварца.
- § 23. Замощение фундаментального круга.
- § 30. Фундаментальные подстановки.
- § 31. Построение функции Шварца.
- СЕМЕЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ С ИСКЛЮЧИТЕЛЬНЫМИ ЗНАЧЕНИЯМИ
- § 32. Основной признак.
- § 33. Обобщение.
- КВАЗИ-НОРМАЛЬНЫЕ СЕМЕЙСТВА
- § 34. Определение квазинормального семейства.
- § 35. Иррегулярные точки.
- § 36. Основной признак.
- § 37. Случай, когда квазинормальное семейство будет нормальным.
- § 38. Расширение признаков нормальности и квазинормальности.
- ГЛАВА III. ИЗУЧЕНИЕ ОДНОЗНАЧНЫХ ФУНКЦИЙ В ОКРЕСТНОСТИ ИЗОЛИРОВАННОЙ СУЩЕСТВЕННО ОСОБОЙ ТОЧКИ
- § 40. Первая теорема Пикара.
- § 41. Обобщения.
- § 42. Вторая теорема Пикара.
- § 43. Обобщения.
- § 44. Теорема Жюлиа.
- § 45. Случай целых функций.
- § 46. Теорема Шоттки (Schottky).
- § 47. Теорема Ландау.
- § 48. Обобщения.
- ГЛАВА IV. КОНФОРМНОЕ ОТОБРАЖЕНИЕ. КОНФОРМНОЕ ОТОБРАЖЕНИЕ ОТКРЫТОЙ ОБЛАСТИ
- § 50. Отображение внутренности области на круг.
- § 51. Теорема Пуанкаре.
- § 52. Теорема Каратеодори.
- СООТВЕТСТВИЕ ГРАНИЦ
- § 53. Достижимые точки границы.
- § 54. Точки, достижимые единственным способом.
- § 55. Множество достижимых точек.
- § 56. Трансверсали области.
- § 57. Прерывное приближение к точкам границы.
- § 58. Простые концы.
- § 59. Области, ограниченные кривой Жордана.
- § 60. Теорема Фейера (Fejer).
- ГЛАВА V. СЕМЕЙСТВО МЕРОМОРФНЫХ ФУНКЦИЙ
- § 62. Нормальное семейство.
- § 63. Иррегулярные точки. Исключительные последовательности.
- § 64. Равностепенная непрерывность на сфере Римана.
- § 65. Число нулей функций нормального семейства.
- § 66. Количественные свойства.
- § 67. Функции с асимптотическими значениями.
- § 68. Тождества Бореля (Borel)
- КВАЗИНОРМАЛЬНЫЕ СЕМЕЙСТВА
- § 69. Определение. Свойства иррегулярных точек.
- § 70. Порядок иррегулярной точки. Полный порядок.
- § 71. Квазинормальные семейства функций, число нулей которых ограничено.
- § 72. Случай, когда предельные функции конечны.
- ГЛАВА VI. ЧАСТНЫЕ КВАЗИ-НОРМАЛЬНЫЕ СЕМЕЙСТВА
- СЕМЕЙСТВА ФУНКЦИЙ С КВАЗИ-ИСКЛЮЧИТЕЛЬНЫМИ ЗНАЧЕНИЯМИ
- § 74. Распространение теоремы Шоттки.
- § 75. Обобщения.
- § 76. Распространение теоремы Ландау.
- § 77. Частные случаи.
- ИСКЛЮЧИТЕЛЬНЫЕ МЕРОМОРФНЫЕ ФУНКЦИИ
- § 82. Условия Островского.
- § 83. Обратное предложение.
- § 84. Общая теорема.
- ГЛАВА VII. ПОСЛЕДОВАТЕЛЬНОСТИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
- ПОСЛЕДОВАТЕЛЬНОСТИ ГОЛОМОРФНЫХ ФУНКЦИЙ
- § 86. Последовательности, сходящиеся на бесконечном множестве внутренних точек.
- § 87. Теорема Бляшке.
- § 88. Распространение на функции N.
- § 89. Распространение на неограниченные функции.
- § 90. Последовательности, сходящиеся на некоторой части границы.
- § 91. Обобщения.
- § 92. Теорема Адамара о трех кругах.
- § 93. Быстрота сходимости. Распространения теоремы Стилтьеса.
- § 94. Сходящиеся ряды голоморфных функций.
- § 95. Теорема Ненча (Jentzsch).
- § 96. Теорема Островского.
- ПОСЛЕДОВАТЕЛЬНОСТИ МЕРОМОРФНЫХ ФУНКЦИЙ
- § 97. Природа сходимости нормально или квази-нормальной последовательности.
- § 98. Последовательности, которые сходятся на бесконечном множестве внутренних точек.
- § 99. Сходящиеся последовательности мероморфных функций.
- § 100. Множество иррегулярных точек.
- ГЛАВА VIII. ИТЕРАЦИЯ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 102. Неподвижные точки. Циклы.
- § 103. Множитель. Область притяжения.
- § 104. Ограниченность числа притягивающих циклов.
- § 105. Связь между итерацией и функциональными уравнениями.
- § 106. Ограниченность числа индиферентных циклов.
- § 107. Неподвижные отталкивающие точки.
- § 108. Примеры итерации.
- § 109. Множество иррегулярных точек
- § 110. Инвариантность множества g.
- § 111. Структура множества g.
- § 112. Однородность множества g.
- § 113. Примеры множества g.
- § 114. Распределение областей притяжения.
- ГЛАВА IX. СЕМЕЙСТВА ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- НОРМАЛЬНЫЕ СЕМЕЙСТВА ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
- § 116. Нормальные семейства голоморфных функций.
- § 117. Функции, ограниченные в своей совокупности.
- § 118. Сгущение значений.
- § 119. Функции, имеющие исключительные области.
- § 120. Функции, имеющие два исключительных значения.
- § 121. Нормальные последовательности, сходящиеся на бесконечном множестве точек.
- § 122. Множество иррегулярных точек.
- § 123. Структура множества (F).
- СЕМЕЙСТВА УНИФОРМИЗИРУЮЩИХ ФУНКЦИЙ
- § 124. Теорема Пикара.
- § 125. Случай алгебраического соотношения жанра единица.
- § 126. Случай алгебраического соотношения жанра нуль.
- ГЛАВА X. СЛОЖНЫЕ СЕМЕЙСТВА И ПРИЛОЖЕНИЯ
- СЛОЖНЫЕ НОРМАЛЬНЫЕ СЕМЕЙСТВА
- § 128. Целые функции. Наибольшее число исключительных комбинаций.
- § 129. Класс системы функций.
- § 130. Треугольные таблицы комбинаций.
- § 131. Определение сложного нормального семейства.
- § 132. Признак нормальности для сложного семейства.
- СПЕЦИАЛЬНЫЕ СЛОЖНЫЕ СЕМЕЙСТВА
- § 133. Система трех голоморфных функций, никогда не равных.
- § 134. Обобщения.
- § 135. Случай, когда функции могут быть равными.
- § 136. О некоторых нормальных семействах.
- § 137. Системы из четырех мероморфных функций, никогда не равных.
- § 138. Обобщения.
- АЛГЕБРОИДНЫЕ ФУНКЦИИ, ДОПУСКАЮЩИЕ ИСКЛЮЧИТЕЛЬНЫЕ ИНВОЛЮЦИИ
- § 140. Алгеброидные функции. Исключительная инволюция.
- § 141. Класс алгеброидных функций.
- § 142. Наибольшее число исключительных инволюций.
- § 143. Порядок исключительного значения.
- § 144. Нормальные семейства алгеброидных функций.
- § 145. Случай неограниченных функций.
- § 146. Признак нормальности семейства.
- § 147. Распространение теоремы Шоттки.
- § 148. Распространение теоремы Ландау.
- § 149. Обобщения.
- § 150. Алгеброидные функции, нецелые.