СООТВЕТСТВИЕ ГРАНИЦ

§ 53. Достижимые точки границы.

Изучим теперь соответствие между точками границ и областей Пусть дана сначала внутри области последовательность точек: имеющих единственную предельную точку на границе (С); пусть соответствующие им точки внутри Всякая точка предельная для находится на потому что если подпоследовательность стремится к внутренней точке которой соответствует внутри то точки должны стремиться к а это противоречит условию. Обратно, если последовательность точек внутренних сходится к некоторой точке границы то соответствующие им точки могут иметь предельной точкой только точку

Фиг. 16.

Пусть теперь даны достижимая точка границы и линия проведенная внутри и оканчивающаяся в Ей соответствует внутри круга линия я утверждаю, что она оканчивается в определенной точке границы т. е. что точки имеют единственную предельную точку на окружности

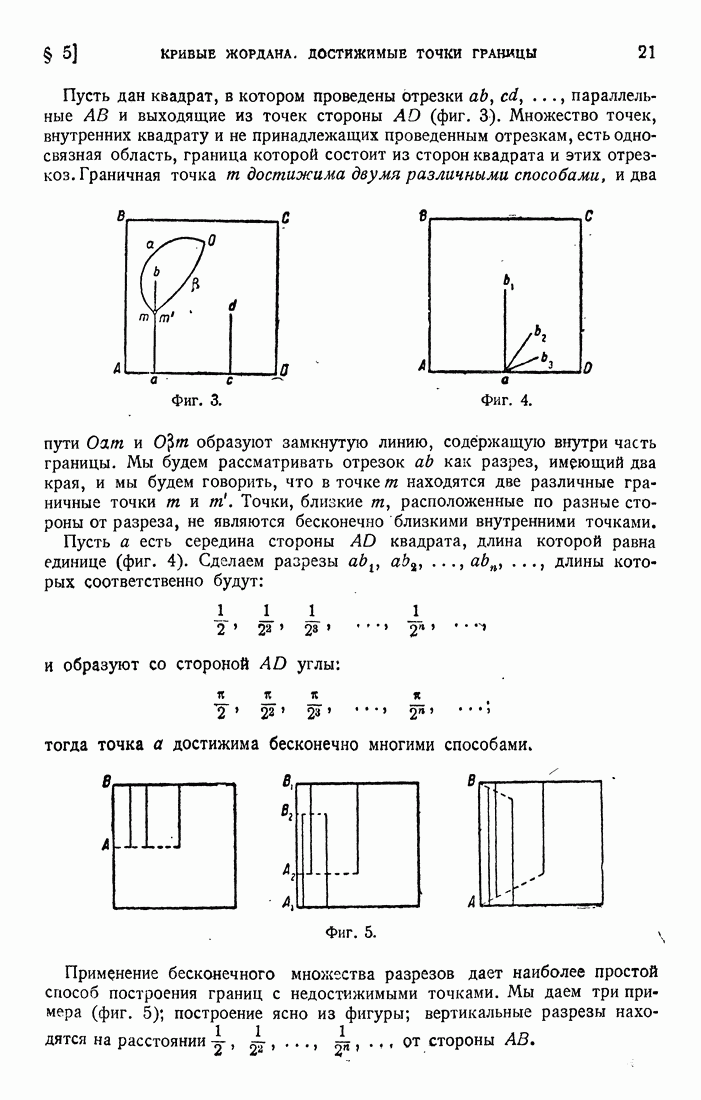
В самом деле, допустим, что существуют две таких точки (фиг. 16): можно найти на линии точки стремящиеся к 20, и точки стремящиеся к Исключая в случае надобности некоторые из этих точек, я могу допустить, что соответствующие им на находятся в следующем порядке: Все точки взяты внутри некоторого круга с центром радиуса пересекающего окружность в двух точках а и также точки взяты внутри круга с центром в радиуса пересекающего окружность в двух точках Точки суть на одной из двух дуг окружности на другой. Наконец, я всегда могу предполагать, что не имеет двойных точек, тогда также не имеет таковых.

Обозначим через последнюю точку встречи дуги линия с малым кругом ; через — первую точку встречи с малым кругом Дуга вся вне кругов Пусть также аналогичные точки встречи Точки которым соответствуют точки стремящиеся к могут иметь предельными точками только а или ; выбрасывая в случае надобности некоторые

дуги, можно предполагать, что сходятся, например к точке а, и более, что находится всегда между Так как дуги не могут пересекаться и не могут переходить через окружности и то точки сходятся к точке а. Всякая бесконечная последовательность точек, выбранных на дугах , имеет предельную точку на дуге Обратно, всякая точка дуги окружности есть предел точек достаточно соединить с центром о кривой, не встречающей кругов и Эта кривая встречает все дуги апап в точках, которые не могут иметь другой предельной точки кроме Дуги стремятся равномерно к это значит, что каждому данному значению соответствует индекс начиная с которого дуга апап всегда заключена между окружностями, имеющими центр в , а радиусы . В противном случае существовало бы число и бесконечное множество точек: расположенных соответственно на дугах того же индекса, для которых расстояние от окружности было бы больше, чем эти точки имели бы предельную точку внутри а это невозможно, потому что соответствующие точки имеют пределом Пусть -данное число; начиная с точки Все точки находятся от точки на расстоянии, меньшем 7); итак, для большего к, на всякой дуге апап имеем:

Допустим, что это неравенство справедливо для всех точек находящихся между дугами, во всем четырехугольнике тогда функция

голоморфна в четырехугольнике и стремится равномерно к нулю вблизи дуги окружности; следовательно, ее можно продолжить методом симметрии: она голоморфна и равна нулю на дуге следовательно, она тождественно равна нулю, что невозможно: итак, не может существовать двух различных предельных точек

Таким образом все сводится к доказательству того, что близка к нулю в четырехугольнике . Проведем два круга с центрами и радиусами меньшими Пусть последняя точка встречи с окружностью - первая точка встречи с окружностью эти точки существуют, если достаточно велико. Можно предполагать, что, начиная с достаточно большого значения на дуге

где произвольно малое число, меньшее единицы.

Изучим функцию в четырехугольнике Гармоническая функция по предположию меньше на сторонах она меньше на дугах окружностей, где диаметр области Мы можем предположить, что

Назовем V гармоническую функцию, равную на окружности на окружности с центром и радиусом большим диаметра увеличенного на

где расстояние между Эта функция больше когда точка лежит в кольце. Пусть V — функция аналогично определенная, отправляясь от точки Гармоническая функция

больше вне кругов и на части, общей кругам и На окружности например, V равно больше следовательно, больше то же самое — на итак меньше на всех четырех сторонах четырехугольника и следовательно, внутри, и это верно, каково бы ни было Но для имеем:

следовательно, вне двух кругов функция удовлетворяет тому же неравенству. Оставляя фиксированными, можно взять настолько малым, чтобы коэфициент при в правой части был, например, больше и чтобы второй член, бесконечно малый вместе с был меньше Тогда будем иметь:

и это неравенство, в котором сколь угодно мало, выполняется в четырехугольнике каково бы ни было т. е. в четырехугольнике

Мы доказали предложение, которое будет использовано в дальнейшем: Для функции, голоморфной внутри круга и не равной постоянному, не может существовать бесконечной последовательности дуг: стремящихся к дуге окружности и таких, чтобы на этих дугах функция равномерно стремилась к одному и тому же пределу.

Из этой теоремы следует, что если есть функция, дающая конформное отображение, и если точки суть точки окружности, то диаметр одной из двух областей, на которые дуга разделяет этот круг, стремится к нулю, когда неограниченно растет и точки дуги имеют пределом В самом деле, точки не могут иметь двух различных предельных точек иначе дуга стремилась

бы к дуге и функция превращалась бы в постоянное. Итак, стремятся к одной и той же точке а окружности и для достаточно большого дуга будет внутри круга с центром а и с произвольно малым радиусом.