| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
§ 5. Кривые Жордана. Достижимые точки границы.
Кривой Жордана называется множество точек, координаты которых выражаются функциями действительного параметра:

определенными и непрерывными в замкнутом интервале, например в интервале 
Кривая Жордана будет без двойных точек, если два различные значения  дают всегда две различные точки кроме, быть может, значений О и 1. Она замкнута или незамкнута в зависимости от того, что значения
дают всегда две различные точки кроме, быть может, значений О и 1. Она замкнута или незамкнута в зависимости от того, что значения  в концах интервала дают одну и ту же точку или различные.
в концах интервала дают одну и ту же точку или различные.
Точки кривой Жордана образуют совершенное множество.
Для незамкнутой кривой Жордана без двойных точек можно найти ломаную без двойных точек, имеющую те же самые концы, все точки которой находятся на сколь угодно малом расстоянии от кривой.
Граничная точка  области
области  достижима изнутри, если можно найти кривую Жордана, выходящую из некоторой внутренней точки О, оканчивающуюся в точке
достижима изнутри, если можно найти кривую Жордана, выходящую из некоторой внутренней точки О, оканчивающуюся в точке  все точки которой кроме А суть внутренние точки области
все точки которой кроме А суть внутренние точки области  точка А есть единственная предельная для них точка, расположенная на границе.
точка А есть единственная предельная для них точка, расположенная на границе.
Множество достижимых точек есть множество, плотное на границе связной области, т. е. всякая неизолированная граничная точка является предельной точкой для множества достижимых точек. Пусть А — неизолированная граничная точка и  — граничные точки, которые стремятся к А. На окружности
— граничные точки, которые стремятся к А. На окружности  , имеющей центр в точке А и проходящей через
, имеющей центр в точке А и проходящей через  найдется внутренняя точка
найдется внутренняя точка  иначе окружность
иначе окружность  разбивает область, которая не будет связной. Следуя по окружности из точки
разбивает область, которая не будет связной. Следуя по окружности из точки  в каком-нибудь направлении, мы встретим первую граничную точку, потому что множество точек, общих окружности
в каком-нибудь направлении, мы встретим первую граничную точку, потому что множество точек, общих окружности  и границе, есть множество замкнутое. Эта точка
и границе, есть множество замкнутое. Эта точка  достижима по дуге
достижима по дуге  окружности, и последовательность точек
окружности, и последовательность точек  стремится к точке А.
стремится к точке А.
Ко  достижимой точке А можно подойти по ломаной линии, расположенной внутри
достижимой точке А можно подойти по ломаной линии, расположенной внутри  и имеющей бесконечное множество звеньев вблизи А. В самом деле, пусть
и имеющей бесконечное множество звеньев вблизи А. В самом деле, пусть  кривая Жордана, расположенная внутри области и оканчивающаяся в точке
кривая Жордана, расположенная внутри области и оканчивающаяся в точке  которая соответствует верхнему пределу единица для параметра.
которая соответствует верхнему пределу единица для параметра.
Возьмем последовательность чисел:  которые, возрастая, стремятся к единице; пусть
которые, возрастая, стремятся к единице; пусть  кратчайшее расстояние между границей и дугой
кратчайшее расстояние между границей и дугой  линии
линии  дугу можно заменить ломаной линией, имеющей те же концы и везде отстоящей от дуги на расстояние, меньшее
дугу можно заменить ломаной линией, имеющей те же концы и везде отстоящей от дуги на расстояние, меньшее  это — линия внутри
это — линия внутри 
Все эти ломаные составляют одну, расположенную внутри  и примыкающую к точке
и примыкающую к точке  Легко видеть, что возможно изменить эту
Легко видеть, что возможно изменить эту
ломаную так, чтобы уничтожить все двойные точки, которые она может содержать.
Вот несколько примеров односвязных областей.
Наиболее простым типом границы после замкнутой кривой, без двойных точек, аналитической или состоящей из аналитических дуг, является замкнутая кривая Жордана без двойных точек.
Жордан доказал, что такая кривая разбивает плоскость на две односвязчые области, а А. Шёнфлис (A. Schoenflies), - что всякая ее точка является достижимой изнутри и извне. Рассмотрим теперь кривую (фиг. 1):

Она содержит бесконечное множество дуг, сжимающихся к отрезку  оси у. Соединим точку А с точкой С линии
оси у. Соединим точку А с точкой С линии  кривой Жордана
кривой Жордана  , расположенной под прямой
, расположенной под прямой  Кривая
Кривая  отрезок
отрезок  и часть линии
и часть линии  точки которой имеют абсциссы, меньшие абсциссы точки С, служат границей односвязной области.
точки которой имеют абсциссы, меньшие абсциссы точки С, служат границей односвязной области.

Фиг. 1.

Фиг. 2.
Кривая  не есть кривая Жордана, потому что, пересекая ее прямой, параллельной оси
не есть кривая Жордана, потому что, пересекая ее прямой, параллельной оси  мы получим точки, имеющие предельной любую точку отрезка
мы получим точки, имеющие предельной любую точку отрезка  Точки отрезка
Точки отрезка  кроме точки А не достижимы изнутри. Если вместо
кроме точки А не достижимы изнутри. Если вместо  взять кривую
взять кривую  примыкающую к точке В, то эти точки будут достижимы изнутри, но не будут достижимыми снаружи.
примыкающую к точке В, то эти точки будут достижимы изнутри, но не будут достижимыми снаружи.
Если граница не является кривой Жордана, то она может разбивать плоскость больше, чем на две части. Например область  заштрихованная на фиг. 2, заключена между двумя спиралями, имеющими одну и ту же асимптотическую окружность
заштрихованная на фиг. 2, заключена между двумя спиралями, имеющими одну и ту же асимптотическую окружность  Граница состоит из этих двух ветвей и из окружности; она разбивает плоскость на три односвязные области: область
Граница состоит из этих двух ветвей и из окружности; она разбивает плоскость на три односвязные области: область  другая область, образованная точками внутренними окружности
другая область, образованная точками внутренними окружности  и внешность окружности
и внешность окружности 
Взяв несколько окружностей, можно получить разбиение плоскости на какое угодно число областей. Существуют даже границы, разбивающие плоскость на счетное множество областей.
Пусть дан квадрат, в котором проведены отрезки  параллельные
параллельные  и выходящие из точек стороны
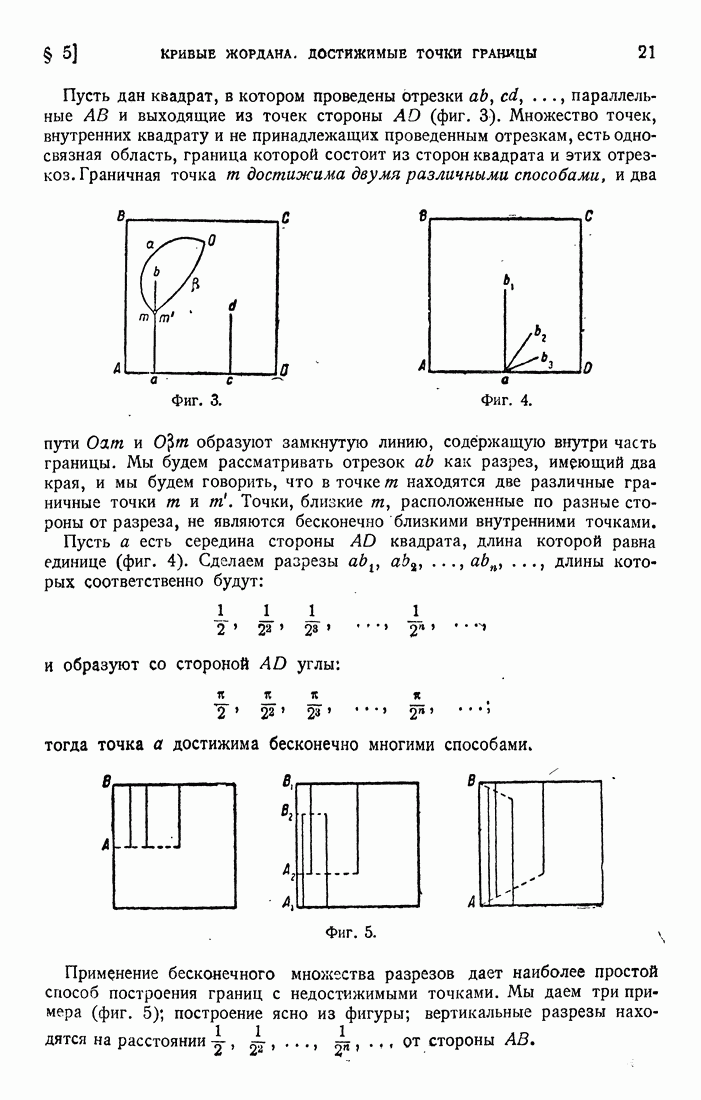
и выходящие из точек стороны  (фиг. 3). Множество точек, внутренних квадрату и не принадлежащих проведенным отрезкам, есть односвязная область, граница которой состоит из сторон квадрата и этих отрезков. Граничная точка
(фиг. 3). Множество точек, внутренних квадрату и не принадлежащих проведенным отрезкам, есть односвязная область, граница которой состоит из сторон квадрата и этих отрезков. Граничная точка  достижима двумя различными способами, и два пути
достижима двумя различными способами, и два пути  образуют замкнутую линию, содержащую внутри часть границы.
образуют замкнутую линию, содержащую внутри часть границы.

Фиг. 3.

Фиг. 4.
Мы будем рассматривать отрезок  как разрез, имеющий два края, и мы будем говорить, что в точке
как разрез, имеющий два края, и мы будем говорить, что в точке  находятся две различные граничные точки
находятся две различные граничные точки  Точки, близкие
Точки, близкие  расположенные по разные стороны от разреза, не являются бесконечно близкими внутренними точками.
расположенные по разные стороны от разреза, не являются бесконечно близкими внутренними точками.
Пусть а есть середина стороны  квадрата, длина которой равна единице (фиг. 4). Сделаем разрезы
квадрата, длина которой равна единице (фиг. 4). Сделаем разрезы  длины которых соответственно будут:
длины которых соответственно будут:

и образуют со стороной  углы:
углы:

тогда точка  достижима бесконечно многими способами.
достижима бесконечно многими способами.

Фиг. 5.
Применение бесконечного множества разрезов дает наиболее простой способ построения границ с недостижимыми точками. Мы даем три примера (фиг. 5); построение ясно из фигуры; вертикальные разрезы находятся на расстоянии  от стороны
от стороны 
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МНОЖЕСТВА ТОЧЕК. СЕМЕЙСТВА ФУНКЦИЙ. МНОЖЕСТВА ТОЧЕК ОБЛАСТИ
- § 1. Множество. Предельная точка.
- § 2. Производное множество.
- § 3. Внутренние и внешние точки. Границы. Области.
- § 4. Непрерывные множества.
- § 5. Кривые Жордана. Достижимые точки границы.
- § 6. Множества точек в произвольном пространстве.
- § 7. Множества точек в функциональном пространстве.
- СЕМЕЙСТВА ФУНКЦИЙ
- § 8. Теорема Вейерштрасса.
- § 9. Сгущение значений.
- § 10. Функции, ограниченные в своей совокупности
- § 11. Равностепенная непрерывность.
- § 12. Существование предельных функций.
- § 13. Случай открытой области.
- § 14. Случай неаналитических функций.
- § 15. Теорема Стилтьеса.
- § 16. Теорема Витали.
- § 17. Функции, допускающие исключительные области.
- § 18. Определение нормального семейства.
- § 19. Семейство нормальное в точке.
- § 20. Нормальные и ограниченные семейства.
- § 21. Число нулей функций нормального семейства.
- § 22. Иррегулярные точки.
- § 23. Семейство гармонических функций. Теорема Харнака.
- § 24. Частные ограниченных функций.
- § 25. Нормальное семейство функций N.
- ГЛАВА II. ГОЛОМОРФНЫЕ ФУНКЦИИ С ИСКЛЮЧИТЕЛЬНЫМИ ЗНАЧЕНИЯМИ. КВАЗИ-НОРМАЛЬНЫЕ СЕМЕЙСТВА. ФУНКЦИИ ШВАРЦА
- § 26. Теорема Пэнлеве.
- § 27. Метод симметрии.
- § 28. Функции Шварца.
- § 23. Замощение фундаментального круга.
- § 30. Фундаментальные подстановки.
- § 31. Построение функции Шварца.
- СЕМЕЙСТВА ГОЛОМОРФНЫХ ФУНКЦИЙ С ИСКЛЮЧИТЕЛЬНЫМИ ЗНАЧЕНИЯМИ
- § 32. Основной признак.
- § 33. Обобщение.
- КВАЗИ-НОРМАЛЬНЫЕ СЕМЕЙСТВА
- § 34. Определение квазинормального семейства.
- § 35. Иррегулярные точки.
- § 36. Основной признак.
- § 37. Случай, когда квазинормальное семейство будет нормальным.
- § 38. Расширение признаков нормальности и квазинормальности.
- ГЛАВА III. ИЗУЧЕНИЕ ОДНОЗНАЧНЫХ ФУНКЦИЙ В ОКРЕСТНОСТИ ИЗОЛИРОВАННОЙ СУЩЕСТВЕННО ОСОБОЙ ТОЧКИ
- § 40. Первая теорема Пикара.
- § 41. Обобщения.
- § 42. Вторая теорема Пикара.
- § 43. Обобщения.
- § 44. Теорема Жюлиа.
- § 45. Случай целых функций.
- § 46. Теорема Шоттки (Schottky).
- § 47. Теорема Ландау.
- § 48. Обобщения.
- ГЛАВА IV. КОНФОРМНОЕ ОТОБРАЖЕНИЕ. КОНФОРМНОЕ ОТОБРАЖЕНИЕ ОТКРЫТОЙ ОБЛАСТИ
- § 50. Отображение внутренности области на круг.
- § 51. Теорема Пуанкаре.
- § 52. Теорема Каратеодори.
- СООТВЕТСТВИЕ ГРАНИЦ
- § 53. Достижимые точки границы.
- § 54. Точки, достижимые единственным способом.
- § 55. Множество достижимых точек.
- § 56. Трансверсали области.
- § 57. Прерывное приближение к точкам границы.
- § 58. Простые концы.
- § 59. Области, ограниченные кривой Жордана.
- § 60. Теорема Фейера (Fejer).
- ГЛАВА V. СЕМЕЙСТВО МЕРОМОРФНЫХ ФУНКЦИЙ
- § 62. Нормальное семейство.
- § 63. Иррегулярные точки. Исключительные последовательности.
- § 64. Равностепенная непрерывность на сфере Римана.
- § 65. Число нулей функций нормального семейства.
- § 66. Количественные свойства.
- § 67. Функции с асимптотическими значениями.
- § 68. Тождества Бореля (Borel)
- КВАЗИНОРМАЛЬНЫЕ СЕМЕЙСТВА
- § 69. Определение. Свойства иррегулярных точек.
- § 70. Порядок иррегулярной точки. Полный порядок.
- § 71. Квазинормальные семейства функций, число нулей которых ограничено.
- § 72. Случай, когда предельные функции конечны.
- ГЛАВА VI. ЧАСТНЫЕ КВАЗИ-НОРМАЛЬНЫЕ СЕМЕЙСТВА
- СЕМЕЙСТВА ФУНКЦИЙ С КВАЗИ-ИСКЛЮЧИТЕЛЬНЫМИ ЗНАЧЕНИЯМИ
- § 74. Распространение теоремы Шоттки.
- § 75. Обобщения.
- § 76. Распространение теоремы Ландау.
- § 77. Частные случаи.
- ИСКЛЮЧИТЕЛЬНЫЕ МЕРОМОРФНЫЕ ФУНКЦИИ
- § 82. Условия Островского.
- § 83. Обратное предложение.
- § 84. Общая теорема.
- ГЛАВА VII. ПОСЛЕДОВАТЕЛЬНОСТИ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
- ПОСЛЕДОВАТЕЛЬНОСТИ ГОЛОМОРФНЫХ ФУНКЦИЙ
- § 86. Последовательности, сходящиеся на бесконечном множестве внутренних точек.
- § 87. Теорема Бляшке.
- § 88. Распространение на функции N.
- § 89. Распространение на неограниченные функции.
- § 90. Последовательности, сходящиеся на некоторой части границы.
- § 91. Обобщения.
- § 92. Теорема Адамара о трех кругах.
- § 93. Быстрота сходимости. Распространения теоремы Стилтьеса.
- § 94. Сходящиеся ряды голоморфных функций.
- § 95. Теорема Ненча (Jentzsch).
- § 96. Теорема Островского.
- ПОСЛЕДОВАТЕЛЬНОСТИ МЕРОМОРФНЫХ ФУНКЦИЙ
- § 97. Природа сходимости нормально или квази-нормальной последовательности.
- § 98. Последовательности, которые сходятся на бесконечном множестве внутренних точек.
- § 99. Сходящиеся последовательности мероморфных функций.
- § 100. Множество иррегулярных точек.
- ГЛАВА VIII. ИТЕРАЦИЯ РАЦИОНАЛЬНЫХ ФУНКЦИЙ
- § 102. Неподвижные точки. Циклы.
- § 103. Множитель. Область притяжения.
- § 104. Ограниченность числа притягивающих циклов.
- § 105. Связь между итерацией и функциональными уравнениями.
- § 106. Ограниченность числа индиферентных циклов.
- § 107. Неподвижные отталкивающие точки.
- § 108. Примеры итерации.
- § 109. Множество иррегулярных точек
- § 110. Инвариантность множества g.
- § 111. Структура множества g.
- § 112. Однородность множества g.
- § 113. Примеры множества g.
- § 114. Распределение областей притяжения.
- ГЛАВА IX. СЕМЕЙСТВА ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- НОРМАЛЬНЫЕ СЕМЕЙСТВА ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ
- § 116. Нормальные семейства голоморфных функций.
- § 117. Функции, ограниченные в своей совокупности.
- § 118. Сгущение значений.
- § 119. Функции, имеющие исключительные области.
- § 120. Функции, имеющие два исключительных значения.
- § 121. Нормальные последовательности, сходящиеся на бесконечном множестве точек.
- § 122. Множество иррегулярных точек.
- § 123. Структура множества (F).
- СЕМЕЙСТВА УНИФОРМИЗИРУЮЩИХ ФУНКЦИЙ
- § 124. Теорема Пикара.
- § 125. Случай алгебраического соотношения жанра единица.
- § 126. Случай алгебраического соотношения жанра нуль.
- ГЛАВА X. СЛОЖНЫЕ СЕМЕЙСТВА И ПРИЛОЖЕНИЯ
- СЛОЖНЫЕ НОРМАЛЬНЫЕ СЕМЕЙСТВА
- § 128. Целые функции. Наибольшее число исключительных комбинаций.
- § 129. Класс системы функций.
- § 130. Треугольные таблицы комбинаций.
- § 131. Определение сложного нормального семейства.
- § 132. Признак нормальности для сложного семейства.
- СПЕЦИАЛЬНЫЕ СЛОЖНЫЕ СЕМЕЙСТВА
- § 133. Система трех голоморфных функций, никогда не равных.
- § 134. Обобщения.
- § 135. Случай, когда функции могут быть равными.
- § 136. О некоторых нормальных семействах.
- § 137. Системы из четырех мероморфных функций, никогда не равных.
- § 138. Обобщения.
- АЛГЕБРОИДНЫЕ ФУНКЦИИ, ДОПУСКАЮЩИЕ ИСКЛЮЧИТЕЛЬНЫЕ ИНВОЛЮЦИИ
- § 140. Алгеброидные функции. Исключительная инволюция.
- § 141. Класс алгеброидных функций.
- § 142. Наибольшее число исключительных инволюций.
- § 143. Порядок исключительного значения.
- § 144. Нормальные семейства алгеброидных функций.
- § 145. Случай неограниченных функций.
- § 146. Признак нормальности семейства.
- § 147. Распространение теоремы Шоттки.
- § 148. Распространение теоремы Ландау.
- § 149. Обобщения.
- § 150. Алгеброидные функции, нецелые.