| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
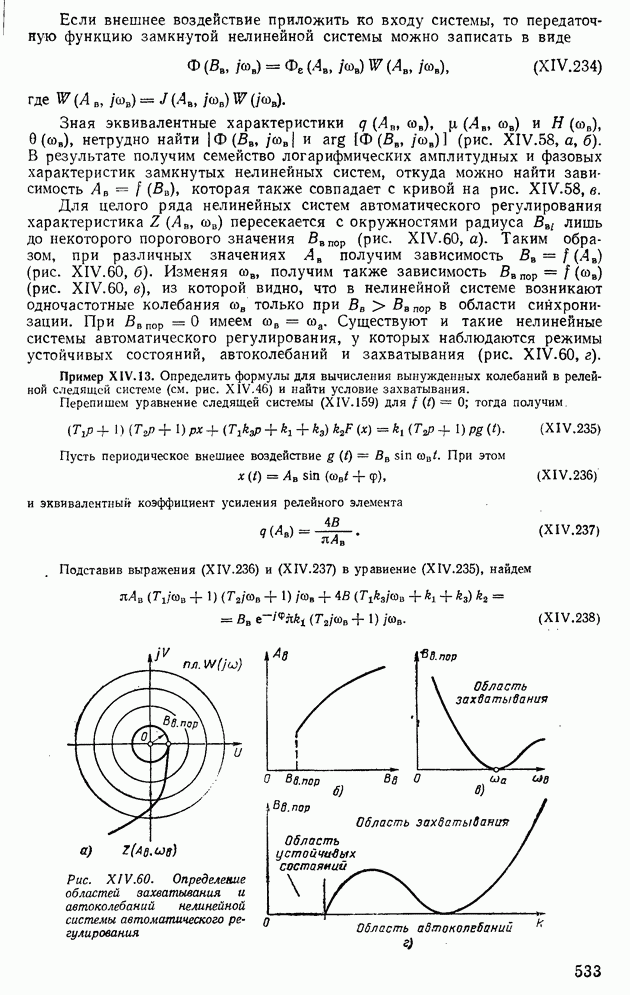
3. АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
Метод фазовой плоскости теории автоматического регулирования был введен А. А. Андроновым [26]. Сущность метода заключается в построении фазовых траекторий по дифференциальным уравнениям в системе координат: отклонение регулируемой величины х и скорость ее изменения 
Процесс изменения траектории представляет собой движение изображающей точки на плоскости. Начальные условия системы определяют первоначальное положение изображающей точки на фазовой плоскости. Совокупность фазовых траекторий в плоскости  представляет собой фазовый портрет.
представляет собой фазовый портрет.
Построим на фазовой плоскости некоторые наиболее характерные фазовые портреты. Для этого воспользуемся дифференциальным уравнением второго порядка:

Рассмотрим следующие случаи.
Случай  т. е.
т. е.

Решение этого уравнения запишем в виде

где
На основании выражений (XIV. 15) нетрудно найти следующее соотношение:

которое представляет собой уравнение эллипса с полуосями А и  При различных начальных значениях А на фазовой плоскости получаемсемейство подобных эллипсов, которые не пересекаются и имеют общий центр (рис. XIV.6, а).
При различных начальных значениях А на фазовой плоскости получаемсемейство подобных эллипсов, которые не пересекаются и имеют общий центр (рис. XIV.6, а).
Уравнение фазовой траектории можно записать и в другом виде. Из уравнения (XIV. 14) имеем

но  откуда
откуда

 Подставив соотношение (XIV. 18) в уравнение (XIV. 17) и сделав ряд преобразований, получим
Подставив соотношение (XIV. 18) в уравнение (XIV. 17) и сделав ряд преобразований, получим

Возьмем на одном из эллипсов (рис. XIV.6, а) точку  с координатами
с координатами  Соответствующее положение этой точки в координатах
Соответствующее положение этой точки в координатах  показано на рис. XIV.6, б. Точка
показано на рис. XIV.6, б. Точка  на рис. XIV.6, а соответствует точке
на рис. XIV.6, а соответствует точке  на рис. XIV.6, б и т. д. Таким образом, движение изображающей точки на фазовой плоскости
на рис. XIV.6, б и т. д. Таким образом, движение изображающей точки на фазовой плоскости  по эллипсу представляет собой периодический процесс с постоянными амплитудой А и частотой
по эллипсу представляет собой периодический процесс с постоянными амплитудой А и частотой  (автоколебания).
(автоколебания).
Случай  . В этом случае уравнение (XIV. 13) имеет комплексно-сопряженные корни
. В этом случае уравнение (XIV. 13) имеет комплексно-сопряженные корни  и его решение имеет вид
и его решение имеет вид

или

При любых начальных условиях имеем действительное решение, т. е. 

где
Отсюда

Пользуясь выражениями (XIV.22) и (XIV.23), нетрудно получить соотношение для радиус-вектора

Данное уравнение соответствует свертывающейся логарифмической спирали, так как при  радиус-вектор
радиус-вектор  стремится к нулю (рис. XIV. 7, а).
стремится к нулю (рис. XIV. 7, а).
Уравнение (XIV. 13) можно переписать в виде


Рис. XIV.6. Фазовый портрет системы второго порядка и перехфдный процесс в ней при 

Рис. XIV.7. Фазовый портрет системы второго порядка и переходный процесс в ней при 
Подставляя соотношение (XIV. 18) в уравнение (XIV.25), получим следующее выражение для фазовых траекторий:

Возьмем на одной из фазовых траекторий (рис. XIV.7, а) точку  . Перенесем эту точку на плоскость
. Перенесем эту точку на плоскость  (рис. XIV.7, б). Двигаясь по фазовой траектории, получим затухающий колебательный процесс (рис. XIV. 7, б).
(рис. XIV.7, б). Двигаясь по фазовой траектории, получим затухающий колебательный процесс (рис. XIV. 7, б).
Точка равновесия является особой точкой фазовой плоскости и называется устойчивым фокусом.
Случай  Корни характеристического уравнения
Корни характеристического уравнения  и решение уравнения (XIV.13) имеет следующий вид:
и решение уравнения (XIV.13) имеет следующий вид:

откуда

Из выражений (XIV.27) и (XIV.28) найдём

Это уравнение соответствует развертывающейся логарифмической спирали, так как при  имеем
имеем  (рис. XIV.8, а).
(рис. XIV.8, а).
Из уравнения (XIV.13) при  получим
получим

т. е. снова имеем уравнение развертывающейся спирали.
На рис. XIV.8, б в плоскости  построен переходный процесс в системе, соответствующий движению Изображающей точки по фазовой траектории из точки
построен переходный процесс в системе, соответствующий движению Изображающей точки по фазовой траектории из точки  .
.
Как видно из рис. XIV.8, б переходный процесс представляет собой незатухающий колебательный процесс

Рис. XIV.8. Фазовый портрет системы второго порядка и переходный процесс в ней при 

Рис. XIV.9. Фазовый портрет системы второго порядка и переходный процесс в ней при 
с неограниченно возрастающей амплитудой. Точка равновесия на фазовой плоскости называется неустойчивым фокусом.
Случай 4:  . В этом случае имеем соотношение для радиус-вектора в виде выражения (XIV.24), а фазовые траектории описываются уравнением. (XIV.26). Фазовые траектории построены на рис. XIV.9, а. Точка равновесия называется устойчивым узлом. Фазовые траектории, имеющие точку равновесия в виде устойчивого узла, соответствуют апериодическому затухающему переходному процессу. Кривые 1—6 на фазовой плоскости соответствуют апериодическим кривым 1—6 на плоскости
. В этом случае имеем соотношение для радиус-вектора в виде выражения (XIV.24), а фазовые траектории описываются уравнением. (XIV.26). Фазовые траектории построены на рис. XIV.9, а. Точка равновесия называется устойчивым узлом. Фазовые траектории, имеющие точку равновесия в виде устойчивого узла, соответствуют апериодическому затухающему переходному процессу. Кривые 1—6 на фазовой плоскости соответствуют апериодическим кривым 1—6 на плоскости  (рис. XIV.9, б).
(рис. XIV.9, б).
Случай  Движение изображающих точек направлено от точки равновесия системы к бесконечно удаленной точке фазовой плоскости (рис. XIV. 10, а). В этом случае положение равновесия системы неустойчивое. Точка равновесия данного типа называется неустойчивым узлом. Переходные процессы построены на рис. XIV. 10, б.
Движение изображающих точек направлено от точки равновесия системы к бесконечно удаленной точке фазовой плоскости (рис. XIV. 10, а). В этом случае положение равновесия системы неустойчивое. Точка равновесия данного типа называется неустойчивым узлом. Переходные процессы построены на рис. XIV. 10, б.
Случай  неустойчивое звено, т. е.
неустойчивое звено, т. е.

Из уравнения (XIV.31) найдем

Интегрируя уравнение (XIV.32), получим

где С — постоянная интегрирования.
Выражение (XIV.33) представляет собой уравнение семейства равносторонних гипербол, симметричных относительно главных осей. На рис. XIV. 11 показан вид семейства фазовых траекторий, построенных по уравнению (XIV.33).
Определим асимптоты семейства гипербол, для чего положим  Уравнения асимптот будут
Уравнения асимптот будут


Рис. XIV.10. Фазовый портрет системы второго порядка и переходный процесс в ней при 

Рис. XIV.11. Фазовый портрет в системе для неустойчивого звена при отсутствии демпфирования 
Направления движения изображающих точек на фазовой плоскости по асимптотам показаны на рис. XIV. 11. Из этого рисунка видно, что движение всех изображающих точек по гиперболам происходит от точки равновесия в бесконечность. Движение точек по асимптотам 1 и 3 также направлено в бесконечность. Изображающие точки по асимптотам 2 и 4 стремятся к положению равновесия. Точка равновесия представляет собой особую точку фазовой плоскости, называемую седлом.
По фазовым траекториям можно судить об устойчивости линейных систем автоматического регулирования, если их поведение описывается дифференциальными уравнениями второго порядка. Рассмотренные выше особые точки фазовой плоскости соответствуют положениям устойчивого или неустойчивого равновесия систем.
Фазовые траектории можно строить и для релейных (нелинейных) систем регулирования второго порядка и с их помощью анализировать устойчивость таких систем. Следует заметить, что для нелинейных систем необходимо знать не только вид особых точек, но и характер особых траекторий. Имея фазовый портрет системы, находят по нему особые точки и траектории и определяют характер устойчивости системы в большом и в малом [21, 63].
Методы построения фазовых портретов. Как было показано раньше, для построения фазового портрета используют различные способы графического интегрирования дифференциальных уравнений. Наибольшее применение получили следующие методы: решения уравнений по участкам, изоклин, Льенара.
Метод решения уравнений по участкам. Зная дифференциальные уравнения систем на отдельных участках, построим их фазовые траектории на плоскости 
Пример XIV.3. Построить фазовые траектории для релейной системы автоматического регулирования температуры печи (см. рис. XIV.1). Уравнение этой системы с идеальным реле с зоной нечувствительности имеет третий порядок. С целью понижения порядка уравнения примем, что  мало, тогда после подстановки выражения (XIV.2) в (XIV.6) получим уравнения для трех участков:
мало, тогда после подстановки выражения (XIV.2) в (XIV.6) получим уравнения для трех участков:


Рис. XIV.12. Построение фазового пдртрета нелинейной системы с идеальным реле с зоной нечувствительности
Уравнение фазовых траекторий по формуле (XIV.35) найдем после подстановки

т. е.

Так как  то последнее уравнение можно переписать в следующем виде:
то последнее уравнение можно переписать в следующем виде:

Решение этого уравнения

где  — произвольная постоянная интегрирования.
— произвольная постоянная интегрирования.
Для построения фазовых траекторий на участке  проведем прямые с наклоном —
проведем прямые с наклоном —  — при различных значениях С. Эти прямые заполняют полосу между линиями переключений реле I—I и II—II (рис. XIV.12). На прямых проставим стрелки В соответствии со следующим правилом: в верхней половине плоскости, где
— при различных значениях С. Эти прямые заполняют полосу между линиями переключений реле I—I и II—II (рис. XIV.12). На прямых проставим стрелки В соответствии со следующим правилом: в верхней половине плоскости, где  изображающая точка всегда движется слева направо, а в ннжней пбловнне плоскости, где
изображающая точка всегда движется слева направо, а в ннжней пбловнне плоскости, где  справа налево, т. е. по часовой стрелке. Правее лннин II—II, где
справа налево, т. е. по часовой стрелке. Правее лннин II—II, где  из уравнения (XIV.36) имеем следующее выражение:
из уравнения (XIV.36) имеем следующее выражение:

или

откуда

Для интегрирования выражение (XIV.40) перепишем в виде

откуда

По уравнений (XIV.41) Правее линии II—II построены фазовый траектории при различных значениях 
Перейдем к решению уравнения (XIV.37) при 

или

откуда

По уравнению (XIV.43) левее линии  на рис. XIV.12 построены фазовые траектории при различных значениях
на рис. XIV.12 построены фазовые траектории при различных значениях  Таким образом был построен фазовый портрет для релейной системы автоматического регулирования температуры печи.
Таким образом был построен фазовый портрет для релейной системы автоматического регулирования температуры печи.
Рассмотрим переходный процесс в этой системе. Для этого на рис.  обозначим характерные точки
обозначим характерные точки  Перенесем эти точки на плоскость
Перенесем эти точки на плоскость  тогда получим переходный процесс в системе (рис. XIV. 13). Как видно из рисунка, переходный Процесс затухает, а остановка процесса регулирования происходит в любой точке зоны нечувствительности реле.
тогда получим переходный процесс в системе (рис. XIV. 13). Как видно из рисунка, переходный Процесс затухает, а остановка процесса регулирования происходит в любой точке зоны нечувствительности реле.
Пример XIV.4. Уравнения системы регулирования температуры печи с двухпозиционным реле с петлей гистерезиса имеют третий порядок. Понизим порядок уравнений до второго, приняв  тогда, подставив
тогда, подставив  в уравнение (XIV.7), получим
в уравнение (XIV.7), получим

Уравнение фазбвых траекторий получим после подстановки в выражения (XIV.44) и (XIV.45)  и исключения времени
и исключения времени  т. е.
т. е.

и

откуда найдем решения в виде уравнений (XIV.41) и (XIV.43).
Для построения фазовых траекторий на рис. XIV. 14 проведем две линии переключений:

при  — вправо от оси ординат на расстоянии — и при
— вправо от оси ординат на расстоянии — и при  влево от оси ординат на расстоянии
влево от оси ординат на расстоянии  Семейство фазовых траекторий построено на фазовой плоскости (рис. XIV. 14).
Семейство фазовых траекторий построено на фазовой плоскости (рис. XIV. 14).
Из рис. XIV. 14 видно, что при больших начальных отклонениях в системе ее фазовые траектории соответствуют затухающему колебательному переходному процессу до установления некоторой амплитуды А и частоты  . При малых начальных отклонениях фазовые траектории соответствуют нарастающему колебательному переходному процессу с установлением тех же значений амплитуды и частоты (рис. XIV.15). Границей между расходящимися и сходящимися фазовыми траекториями служит замкнутая кривая
. При малых начальных отклонениях фазовые траектории соответствуют нарастающему колебательному переходному процессу с установлением тех же значений амплитуды и частоты (рис. XIV.15). Границей между расходящимися и сходящимися фазовыми траекториями служит замкнутая кривая  (см. рис. XIV.14). Эта замкнутая кривая соответствует периодическому колебательному процессу с частотой со и амплитудой А (или автоколебаниям). Амплитуда автоколебаний А определяется длиной отрезка
(см. рис. XIV.14). Эта замкнутая кривая соответствует периодическому колебательному процессу с частотой со и амплитудой А (или автоколебаниям). Амплитуда автоколебаний А определяется длиной отрезка  оси абсцисс, а частоту автоколебаний находят по длине Отрезка
оси абсцисс, а частоту автоколебаний находят по длине Отрезка  оси ординат, равной Лео.
оси ординат, равной Лео.

Рис. XIV.13. Переходный процесс в нёлинейндй системе с идеальным, релейным Элементом

Рис. XIV.14. Построение фазового. портрета нелинейной системы с реальным двухлозициднным релейным элементом

Рис. XIV. 15. Переходные процессы в нелинейной системе с реальным двухпозиционным релейным элементом.

Рис. XIV. 16. К определению амплитуды и частоты автоколебаний в релейной системе
Периодический процесс в данной релейной системе является устойчивым, так как при изменении начальных условий в системе всегда устанавливается процесс с амплитудой А и частотой  Как видно
Как видно  рис. XIV. 14, амплитуда и частота автоколебаний не зависят от начальных условий, а определяются только параметрами системы автоматического регулирования
рис. XIV. 14, амплитуда и частота автоколебаний не зависят от начальных условий, а определяются только параметрами системы автоматического регулирования 
Пример XIV.5. Определить приближенно частоту и амплитуду автоколебаний по фазовому портрету, построенному на рис. XIV.  Для упрощения рассуждений будем считать, что кривая
Для упрощения рассуждений будем считать, что кривая  является эллипсом (рис. XIV. 16); тогда колебания будут синусоидальными, т. е.
является эллипсом (рис. XIV. 16); тогда колебания будут синусоидальными, т. е.

где  — амплитуда автоколебаний;
— амплитуда автоколебаний;  — частота автоколебаний.
— частота автоколебаний.
Отрезок  соответствует амплитуде автоколебаний
соответствует амплитуде автоколебаний  частоту автоколебаний определяют по формуле
частоту автоколебаний определяют по формуле

где  — ось эллипса.
— ось эллипса.
В тех случаях, когда аналитическое решение нелинейного дифференциального уравнения невозможно, применяют приближенные графические способы их интегрирования (методы изоклин и Льенара).
Метод изоклин. Допустим, что нелинейное дифференциальное уравнение второго порядка путем замены у — можно привести к виду

и

откуда

где  — наклон фазовой траектории на плоскости
— наклон фазовой траектории на плоскости 
Итак, в каждой точке фазового пространства можно найти вполне определенное значение наклона фазовой траектории, т. е.

Способ построения заключается в следующем. Из уравнения (XIV.50) находим функцию

представляющую собой уравнение изоклин.
Построим ряд изоклин 1—4 по уравнению (XIV.52) (рис. XIV. 17). В точке  изоклин
изоклин  проведем две прямые
проведем две прямые  с наклонами и
с наклонами и  - соответственно до пересечения с изоклиной 2. Отрезок
- соответственно до пересечения с изоклиной 2. Отрезок  разделим пополам и через точку
разделим пополам и через точку  проведем две прямые
проведем две прямые  и с наклонами
и с наклонами

Рис. XIV. 17. Построение фазовой траектории по изоклинам

Рис. XIV. 18. Фазовый портрет системы, описываемой нелинейным дифференциальным уравнением (XIV.53)
 Затем отрезок
Затем отрезок  на изоклине 3 разделим на две части и найдем точку
на изоклине 3 разделим на две части и найдем точку  через которую проведем две прямые с наклонами
через которую проведем две прямые с наклонами  Через точки
Через точки  проведена фазовая траектория с соответствующими им наклонами. Из данного рассмотрения видно, что точность построения фазовой траектории будет тем больше, чем чаще на графике нанесены изоклины.
проведена фазовая траектория с соответствующими им наклонами. Из данного рассмотрения видно, что точность построения фазовой траектории будет тем больше, чем чаще на графике нанесены изоклины.
Пример XIV.6 [761. Построить фазовый портрет системы, описываемой нелинейным дифференциальным уравнением

пользуясь методом изоклин.
Пусть  тогда уравнение (XIV.53) Примет вид
тогда уравнение (XIV.53) Примет вид

откуда найдем

Из выражения (XIV.55) определим уравнение изоклин в виде

На рис. XIV. 18 построены изоклины и нанесены соответствующие им наклоны  По методике, изложенной выше, на рис. XIV. 18 был построен фазовый портрет системы, описываемой нелинейным дифференциальным уравнением (XIV.53).
По методике, изложенной выше, на рис. XIV. 18 был построен фазовый портрет системы, описываемой нелинейным дифференциальным уравнением (XIV.53).
Метод Льенара [76]. Этот метод позволяет определить наклон фазовой траектории в любой точке фазовой плоскости. Представив нелинейное дифференциальное уравнение в виде

откуда найдем

В выражении (XIV. 58) положим

и построим на фазовой плоскости (рис. XIV.9) по уравнению (XIV.59) кривую 1. Если принять, что начало фазовой траектории находится в точке  то, проведя из нее прямую, параллельную оси абсцисс, до пересечения
то, проведя из нее прямую, параллельную оси абсцисс, до пересечения

Рис. XIV.19. К построению фазового портрета по методу Льенара

Рис. XIV.20. Построение фазового портрета по методу Льенара
с кривой 1, получим точку  Из точки
Из точки  проведем прямую, параллельную оси ординат, до пересечения с осью х (точка
проведем прямую, параллельную оси ординат, до пересечения с осью х (точка  Наклон линии
Наклон линии  к оси абсцисс можно определить по формуле
к оси абсцисс можно определить по формуле

Через точку  проводим прямую
проводим прямую  перпендикулярную к
перпендикулярную к  Направление этой прямой на плоскости определяется
Направление этой прямой на плоскости определяется  с принятым правилом движения изображающей точки по часовой стрелке. Далее на отрезке этого перпендикуляра берут точку
с принятым правилом движения изображающей точки по часовой стрелке. Далее на отрезке этого перпендикуляра берут точку  и находят точки А 2 и
и находят точки А 2 и  Затем строят отрезок, перпендикулярный
Затем строят отрезок, перпендикулярный  на котором находят точку
на котором находят точку  Пользуясь полученными наклонами, можно найти искомую фазовую траекторию. От длины отрезков
Пользуясь полученными наклонами, можно найти искомую фазовую траекторию. От длины отрезков  зависит точность такого построения.
зависит точность такого построения.
Пример XIV.7. Построить фазовый портрет для нелинейного дифференциального уравнения

при следующих начальных условиях:  по методу Льёнара. Соответствующее построение выполнено на рис. XIV.20.
по методу Льёнара. Соответствующее построение выполнено на рис. XIV.20.
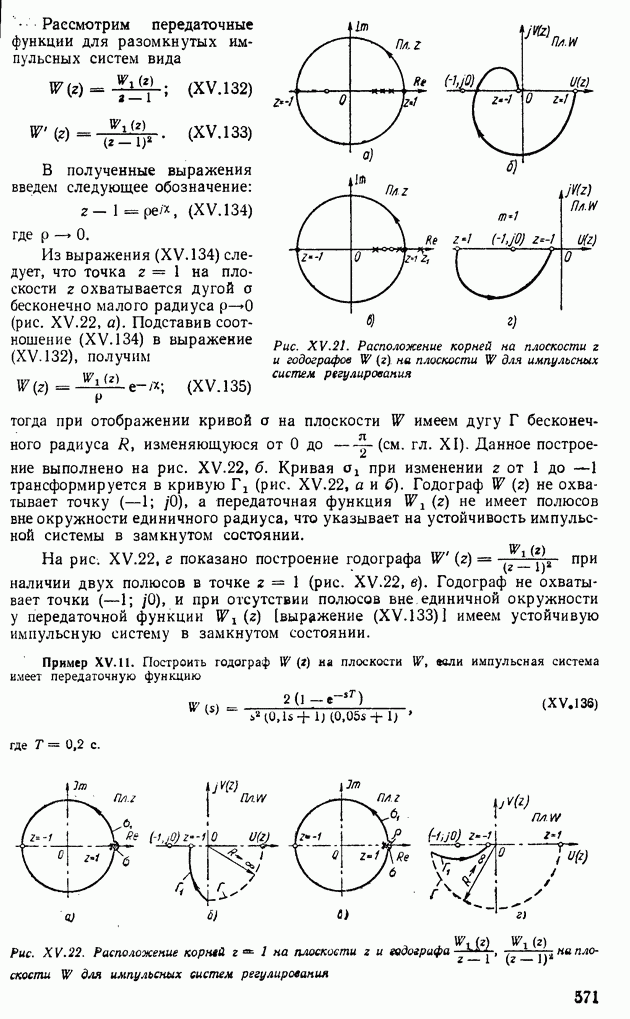
Рассмотрим несколько фазовых портретов, соответствующих нелинейным системам автоматического регулирования. На рис. XIV.21, а показан фазовый портрет для системы с зоной нечувствительности. Установившемуся состоянию равновесия при данной нагрузке соответствует не одна точка на фазовой плоскости, а отрезок с различными возможными состояниями равновесия (жирная линия). Длина этого отрезка зависит от ширины зоны нечувствительности.
На рис. XIV.21, б изображен фазовый портрет для нелинейной системы, неустойчивой в малом, но имеющей устойчивый предельный цикл в большом. На рис. XIV.21, в показан фазовый портрет системы, когда она устойчива в малом, а в большом — неустойчива. В этом случае предельный цикл называется неустойчивым. Неустойчивый предельный цикл характеризуется тем, что изображающая точка практически не может по нему двигаться. При небольшом увеличении отклонения под влиянием воздействий изображающая точка начнет удаляться от предельного цикла в бесконечность.
Возможны случаи, когда нелинейная система имеет несколькб предельных циклов. На рис. XIV.21, г изображен фазовый портрет с двумя

Рис. XIV.21. Особые траектории фазовых портретов нелинейных систем
предельными циклами. Первый из них, расположенный ближе к началу координат, является неустойчивым, а второй, более удаленный — устойчивым [26].
Существуют и такие нелинейные системы, у которых, на фазовом портрете (рис. XIV.21, д), кроме центра, появляются еще две особые точки типа седла, через которые проходят особые траектории, называемые сепаратрисами. Они разделяют всю фазовую плоскость на пять областей, из которых одна, замкнутая сепаратрисами, является областью устойчивого колебательного процесса. Все остальные области являются областями неустойчивых расходящихся процессов [26].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 1. ПРИНЦИПЫ ДЕЙСТВИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
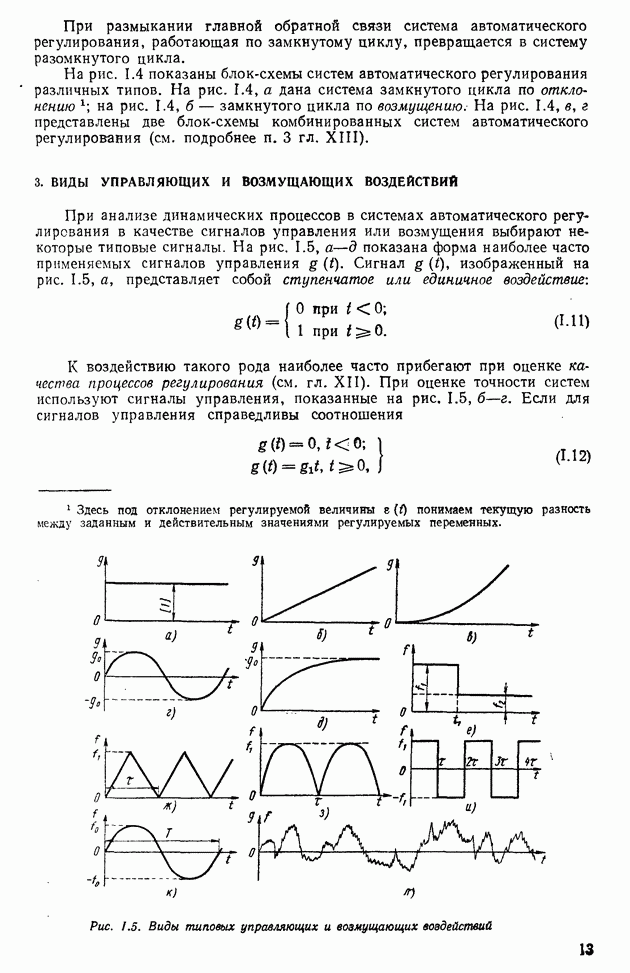
- 3. ВИДЫ УПРАВЛЯЮЩИХ И ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ
- 4. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Глава II. ВИДЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛТРОВАНИЯ
- 1. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
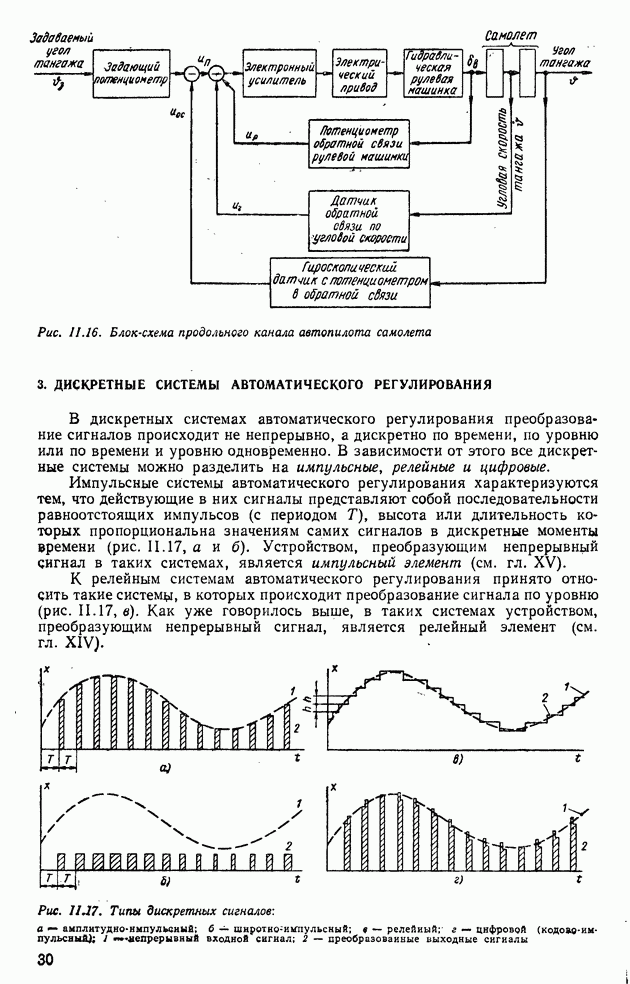
- 3. ДИСКРЕТНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ПРИМЕНЕНИЕ ЦВМ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. ПРИМЕНЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ДЛЯ УПРАВЛЕНИЯ СЛОЖНЫМИ ПРОИЗВОДСТВЕННЫМИ ПРОЦЕССАМИ. СИСТЕМЫ КОМПЛЕКСНОЙ АВТОМАТИЗАЦИИ ПРОИЗВОДСТВА
- Глава III. ОБЪЕКТЫ РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ СВОЙСТВА ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 2. ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 3. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ ДИНАМИКИ
- 4. УСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (ДИЗЕЛЬ, ГИДРОТУРБИНА, САМОЛЕТ)
- 5. НЕУСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (РЕСИВЕР, РАКЕТА-НОСИТЕЛЬ КОСМИЧЕСКИХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ)
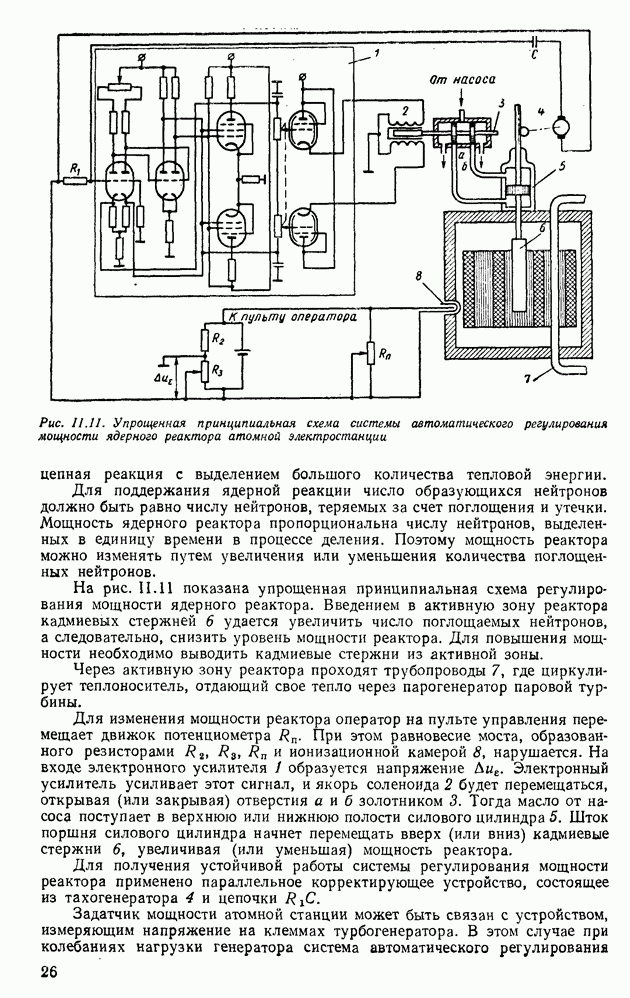
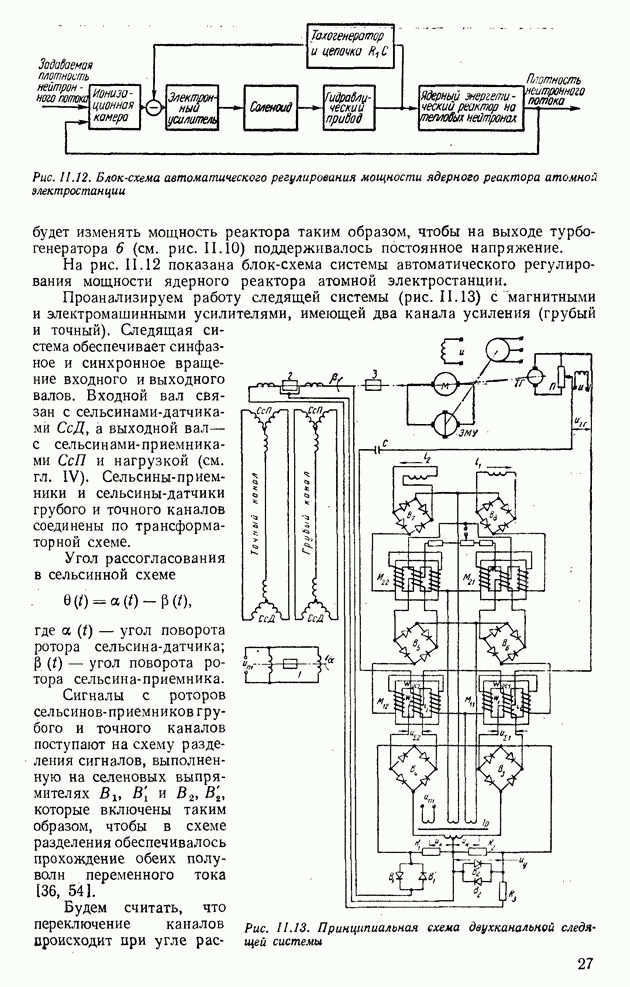
- 6. АСТАТИЧЕСКИЕ ОБЪЕКТЫ (ТРЕХФАЗНЫЙ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ, ЯДЕРНЫЙ ЭНЕРГЕТИЧЕСКИЙ РЕАКТОР НА ТЕПЛОВЫХ НЕЙТРОНАХ, КОСМИЧЕСКИЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ)
- 7. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- Глава IV. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОПРЕДЕЛЕНИЕ ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ИЗМЕРИТЕЛЬНЫХ ПОДСИСТЕМ
- 2. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Индуктивные устройства.
- Емкостные устройства.
- Сельсины.
- Дифференциальный сельсин.
- Погрешность сельсинов.
- Устройства для замера угловых скоростей.
- Устройства замера угловых ускорений.
- 4. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И ТОКА
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕМПЕРАТУР И ИЗЛУЧЕНИЙ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЙ И РАСХОДОВ ЖИДКОСТИ И ГАЗА
- 7. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ ВЕЛИЧИН, УГЛОВЫХ СКОРОСТЕЙ И ЛИНЕЙНЫХ УСКОРЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ
- Устройства для измерения линейных ускорений подвижных объектов (акселерометры).
- 8. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- Глава V. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ
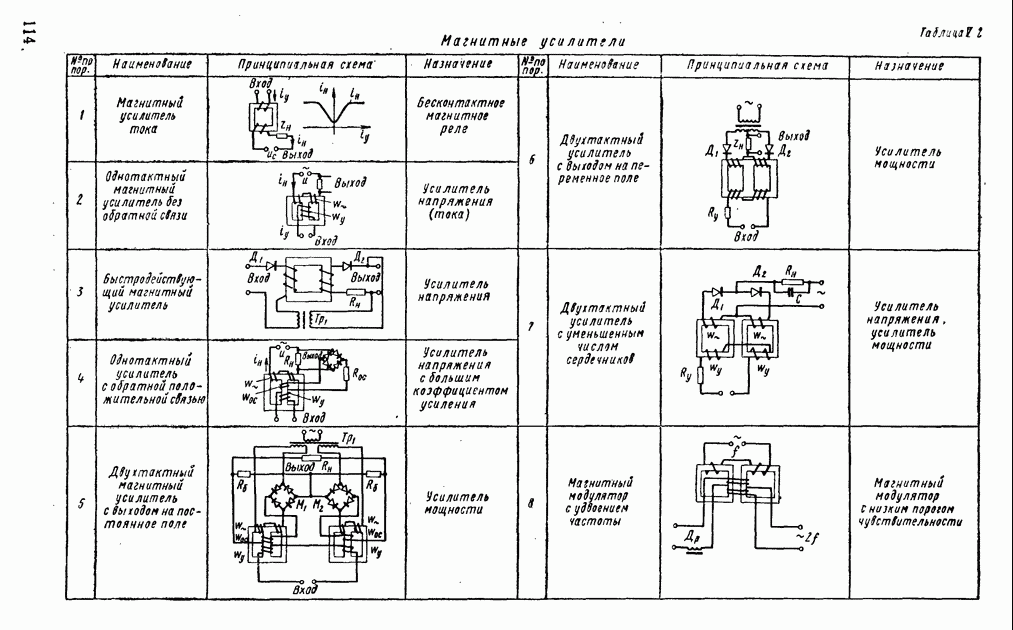
- 2. МАГНИТНЫЕ УСИЛИТЕЛИ
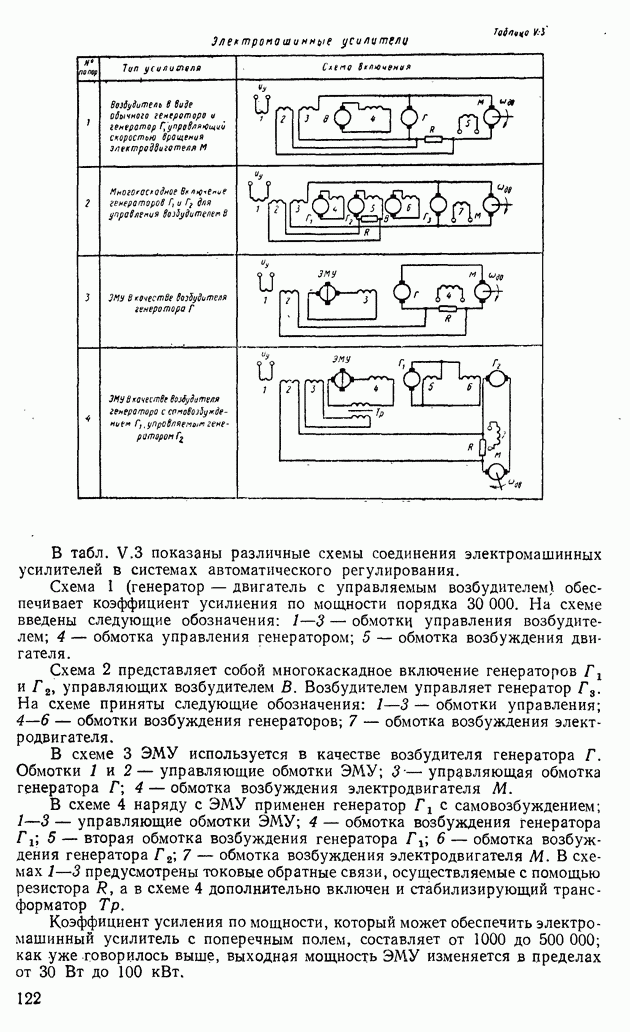
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 4. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 5. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ РАЗЛИЧНЫХ УСИЛИТЕЛЕЙ
- ГЛАВА VI. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА
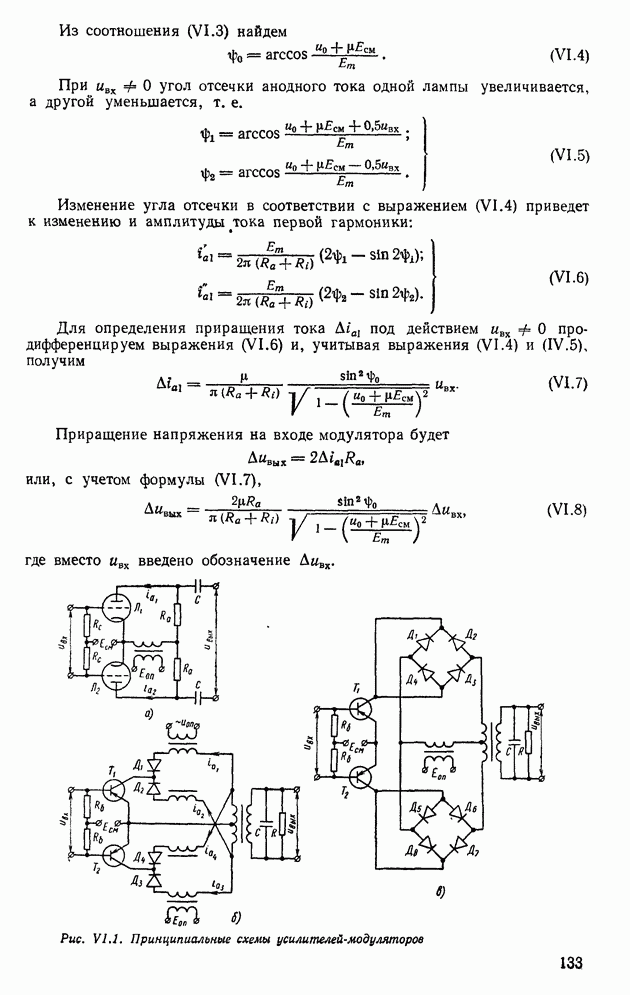
- 1. УСИЛИТЕЛИ-ПРЕОБРАЗОВАТЕЛИ
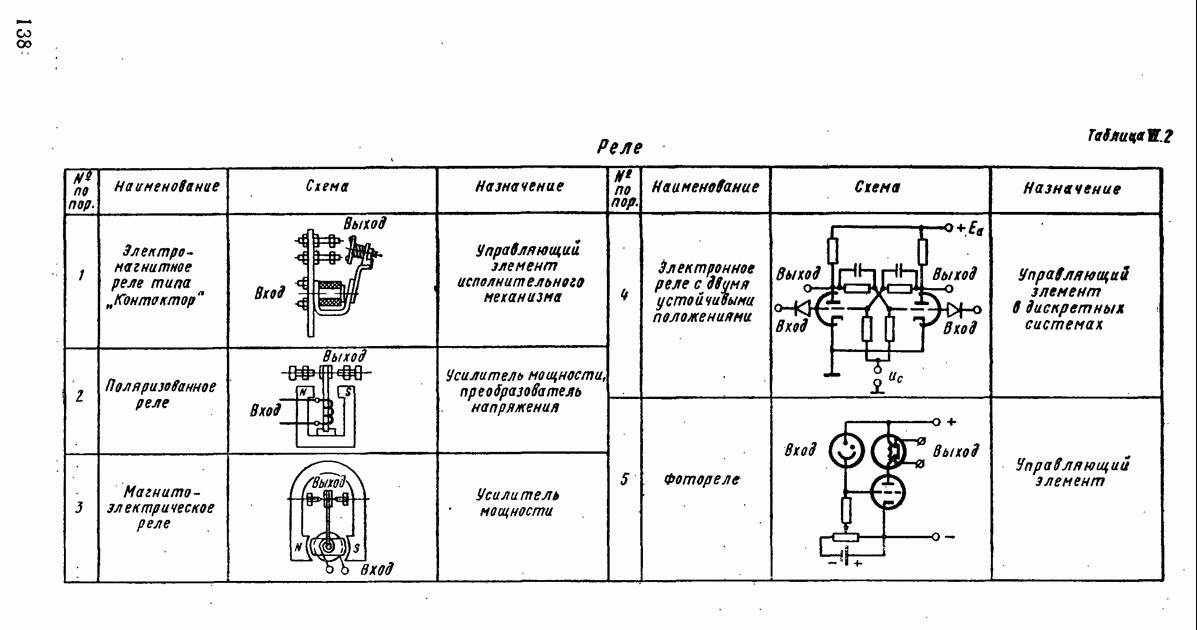
- 2. РЕЛЕ
- 3. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
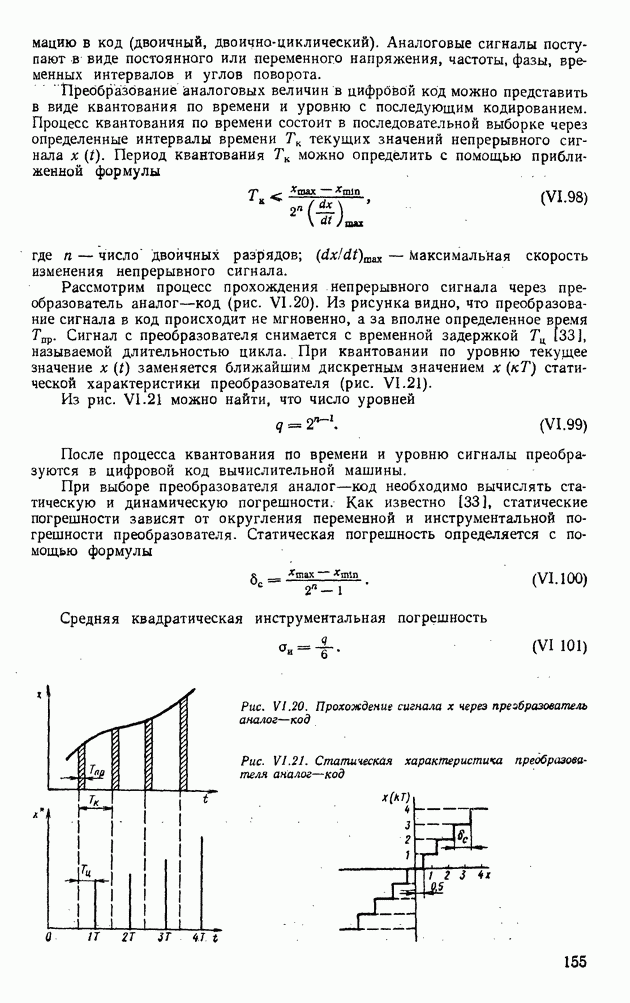
- 4. ПРЕОБРАЗОВАТЕЛИ АНАЛОГ—КОД
- 5. ПРЕОБРАЗОВАТЕЛИ КОД—АНАЛОГ
- 6. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ УПРАВЛЯЮЩИЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
- 8. ПНЕВМАТИЧЕСКИЕ АНАЛОГОВЫЕ И ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 9. ТОЧНОСТЬ РАБОТЫ И БЫСТРОДЕЙСТВИЕ УПРАВЛЯЮЩИХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
- 10. СРАВНИТЕЛЬНАЯ ОЦЕНКА ПРЕОБРАЗУЮЩИХ УСТРОЙСТВ
- Глава VII. ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 1. ЭЛЕКТРИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 2. МЕХАНИЧЕСКИЕ ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. ГИДРАВЛИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 4. ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 5. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- 6. СРАВНИТЕЛЬНАЯ ОЦЕНКА ИСПОЛНИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- Глава VIII. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
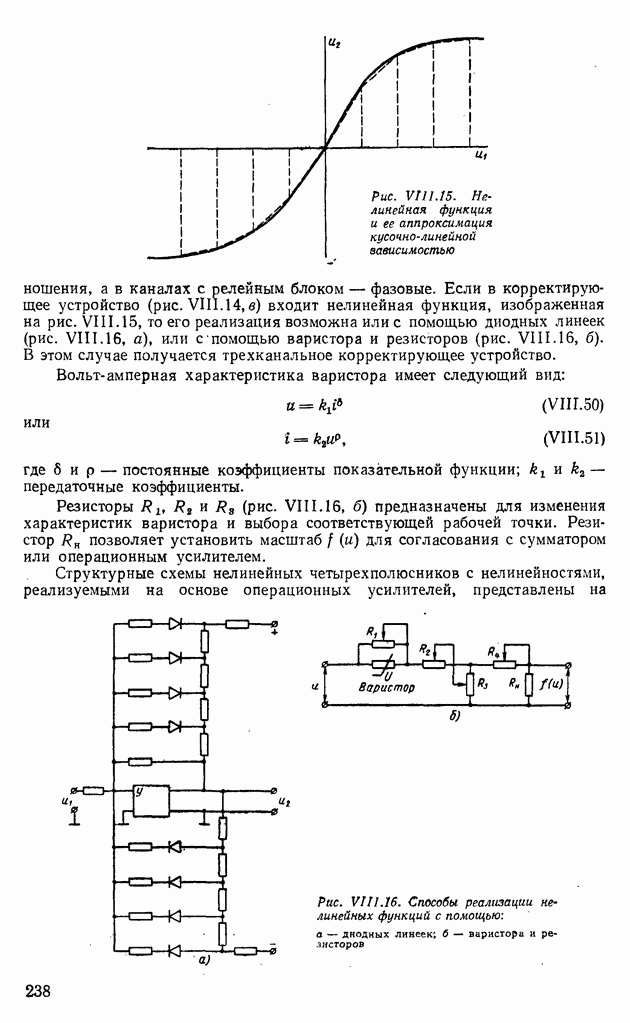
- 2. НЕЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 3. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 4. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ЛИНИЯХ ЗАДЕРЖЕК И ДИСКРЕТНЫХ ЭЛЕМЕНТАХ
- Глава IX. УРАВНЕНИЯ ДИНАМИКИ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
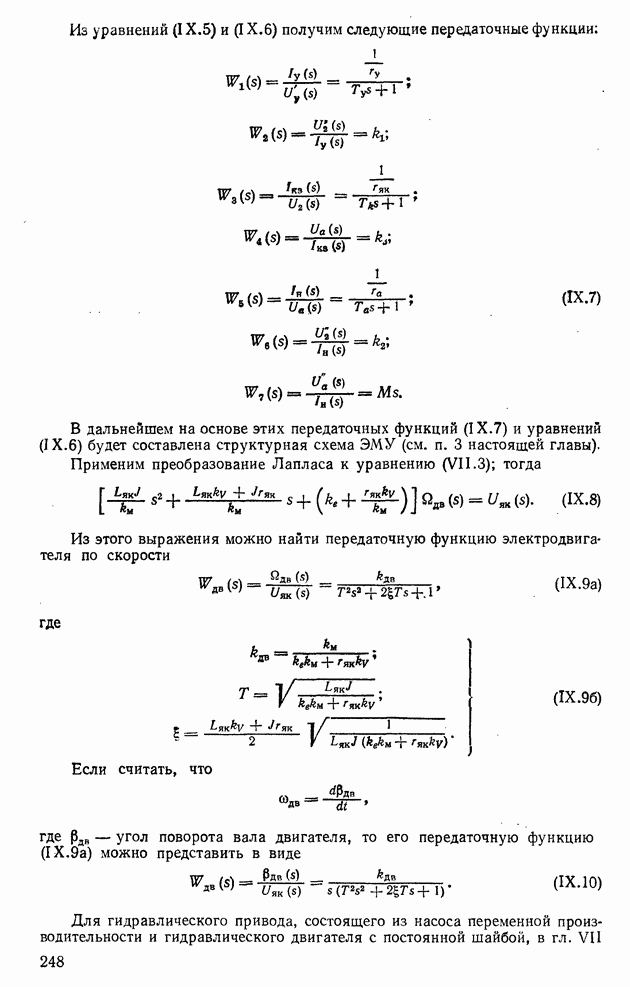
- 1. ПРЕДСТАВЛЕНИЕ ОБЪЕКТОВ И УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С СОСРЕДОТОЧЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
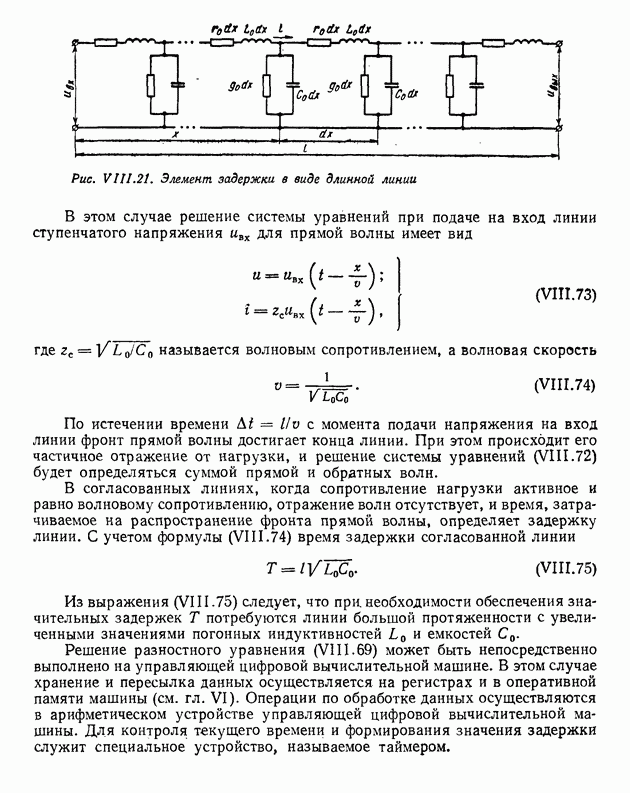
- 2. ПРЕДСТАВЛЕНИЕ УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С РАСПРЕДЕЛЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ТРАНСЦЕДЕНТНЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 3. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
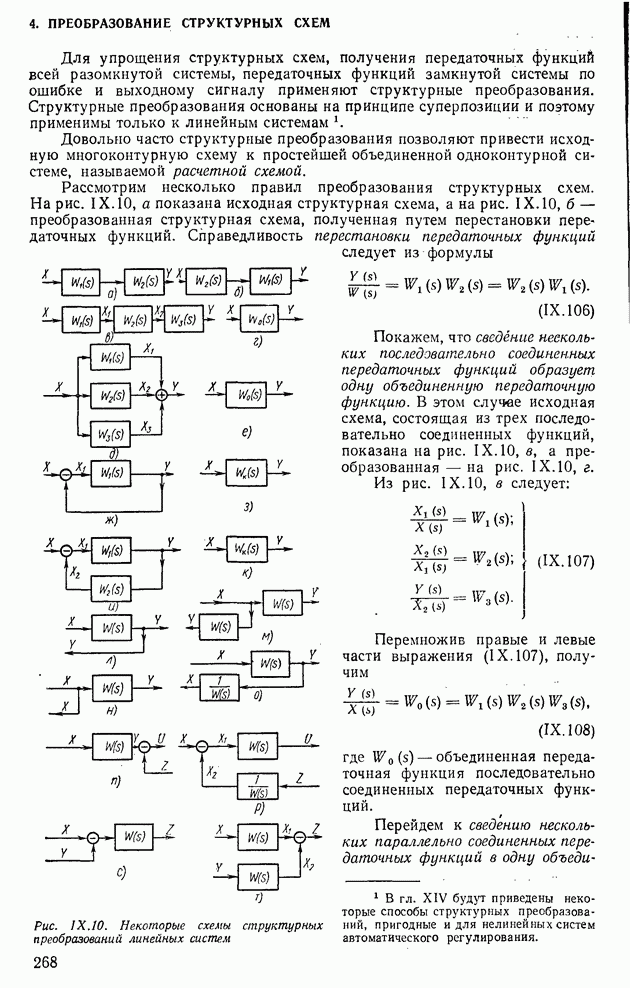
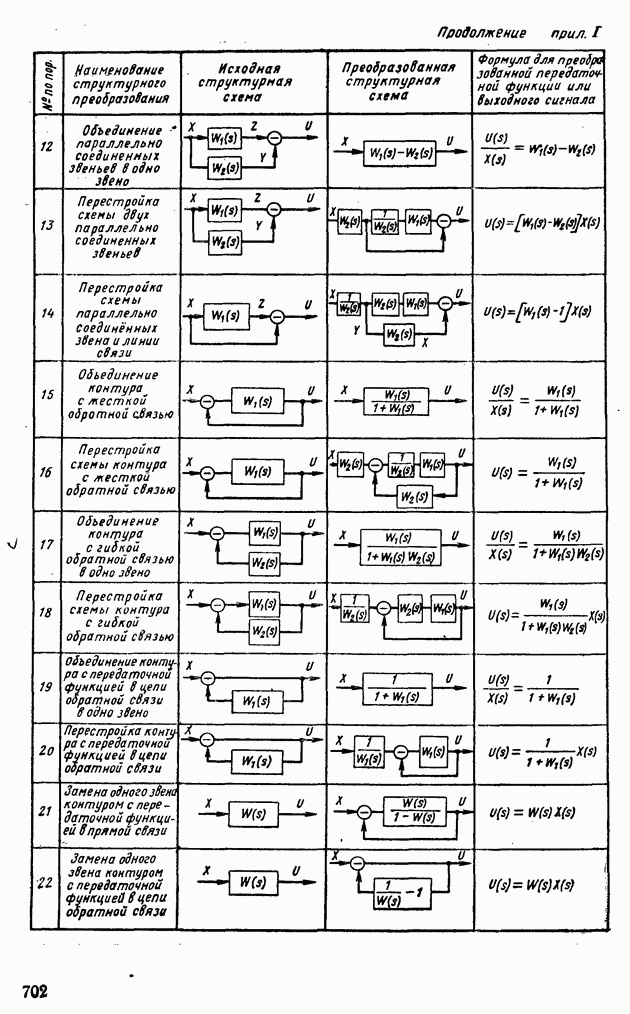
- 4. ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ
- 5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ОПИСАНИЕ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ РЕГУЛИРОВАНИЯ В ВЕКТОРНО-МАТРИЧНОЙ ФОРМЕ
- 7. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 8. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 9. РЕШЕНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ УРАВНЕНИЙ СОСТОЯНИЯ
- 10. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ МАТРИЦ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ ЛИНЕЙНЫХ СИСТЕМ
- 12. ПРЕДСТАВЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ИМПУЛЬСНЫМИ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ
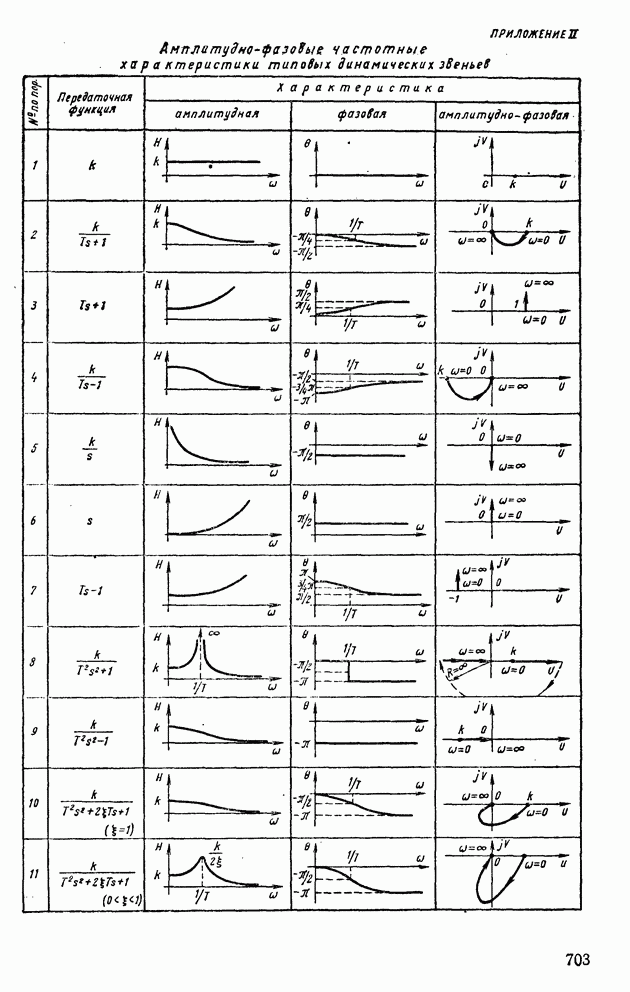
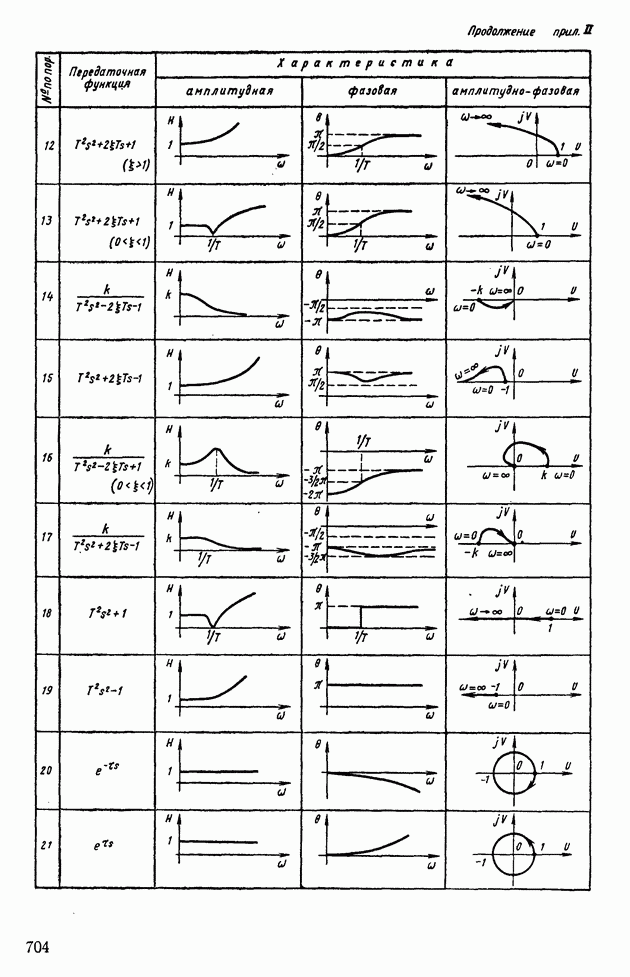
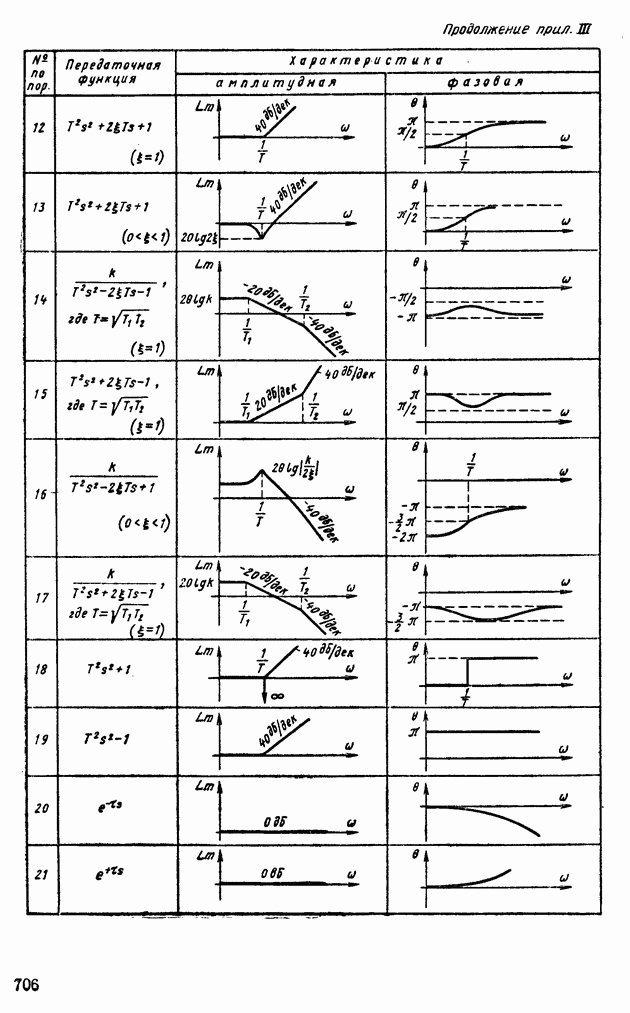
- Глава X. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ АМПЛИТУДНО-ФАЗОВЫЕ И ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 1. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- Логарифмические амплитудная и фазовая частотные характеристики апериодического звена.
- 2. АПЕРИОДИЧЕСКОЕ НЕУСТОЙЧИВОЕ ЗВЕНО
- 4. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 5. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ (УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ)
- 6. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО РОДА
- 7. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО РОДА
- 8. ТРАНСЦЕНДЕНТНЫЕ ЗВЕНЬЯ
- 9. ФАЗОВАЯ ЛИНЕЙКА
- 10. ПОСТРОЕНИЕ АМПЛИТУДНО-ФАЗОВЫХ И ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ ГРУПП ТИПОВЫХ ЗВЕНЬЕВ
- 11. ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ВИДА ПЕРЕДАТОЧНЫХ ФУНКЦИЙ И ПАРАМЕТРОВ ГРУПП ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
- ГЛАВА XI. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ
- 2. ОПРЕДЕЛЕНИЕ ФУНКЦИЙ ЛЯПУНОВА МЕТОДАМИ Г. СЕГЕ И Д. ШУЛЬЦА
- 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 5. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 6. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ТРАНСЦЕНДЕНТНЫМИ ЗВЕНЬЯМИ
- 9. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ С ПОМОЩЬЮ D-РАЗБИЕНИЯ
- Глава XII. ИССЛЕДОВАНИЕ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
- 2. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПО ЗАДАННЫМ ПЕРЕДАТОЧНЫМ ФУНКЦИЯМ ЗАМКНУТЫХ СИСТЕМ
- 3. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПО РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ ЛЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ
- 4. МЕТОД КОРНЕВОГО ГОДОГРАФА
- 5. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА
- 6. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ СИСТЕМ РЕГУЛИРОВАНИЯ И ИХ СВЯЗЬ С ХАРАКТЕРИСТИКАМИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 7. ОПРЕДЕЛЕНИЕ ВЕЩЕСТВЕННЫХ И МНИМЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СИСТЕМ ПО АМПЛИТУДНО-ФАЗОВЫМ И ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ РАЗОМКНУТЫХ СИСТЕМ
- 8. ЧАСТОТНЫЕ ОЦЕНКИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9. ЧАСТОТНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ТРАПЕЦЕИДАЛЬНЫХ ХАРАКТЕРИСТИК
- 10. УСТАНОВЛЕНИЕ НОРМ ЗАПАСОВ УСТОЙЧИВОСТИ ПО ФАЗЕ И МОДУЛЮ, ОБЕСПЕЧИВАЮЩИХ ТРЕБУЕМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМ РЕГУЛИРОВАНИЯ
- ГЛАВА XIII. ДИНАМИЧЕСКАЯ ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ОШИБОК В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ АМПЛИТУДНЫХ ХАРАКТЕРИСТИК
- 3. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПУТЕМ ПРИМЕНЕНИЯ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ
- 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 5. СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ СТАЦИОНАРНЫХ ПРОЦЕССОВ
- 6. СВОЙСТВА СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ
- 7. ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ
- 8. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЛИНЕЙНЫМИ СИСТЕМАМИ
- 9. РАСЧЕТ ОШИБОК В СИСТЕМЕ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ШУМОВ
- 10. ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ВОЗДЕЙСТВИИ СЛУЧАЙНЫХ СИГНАЛОВ И ШУМОВ
- ГЛАВА XIV. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ТИПОВЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ ПО ВТОРОМУ МЕТОДУ ЛЯПУНОВА
- 3. АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
- 4. ПРИМЕНЕНИЕ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. АНАЛИЗ АВТОКОЛЕБАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДВУМЯ НЕЛИНЕЙНОСТЯМИ
- 7. ДВУХКОНТУРНЫЕ НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕДЛЕННО ИЗМЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
- 9. СПОСОБЫ ПОДАВЛЕНИЯ АВТОКОЛЕБАНИЙ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 10. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 11. КРИТЕРИЙ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
- 12. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- Глава XIV. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ИМПУЛЬСНЫХ УСТРОЙСТВ
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. АМПЛИТУДНО-ФАЗОВЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ СИСТЕМ
- 4. ПРИМЕНЕНИЕ ВЕКТОРНО-МАТРИЧНОГО АППАРАТА К ИМПУЛЬСНЫМ СИСТЕМАМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ОСНОВНЫЕ СВОЙСТВА z-ПРЕОБРАЗОВАНИЯ
- 6. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Критерий устойчивости для импульсных систем на плоскостях z и W(z).
- Критерий устойчивости Шур—Кона.
- Критерии устойчивости, основанные на применении билинейного преобразования.
- 7. МЕТОДЫ АНАЛИЗА КАЧЕСТВА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕТОДЫ АНАЛИЗА ТОЧНОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 9. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С УПРАВЛЯЮЩИМИ ЦВМ
- 10. СПОСОБЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ В УПРАВЛЯЮЩИХ ЦВМ И ОПРЕДЕЛЕНИЕ ИХ ОСНОВНЫХ ПАРАМЕТРОВ
- Глава XVI. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МЕТОДЫ ПОИСКА ЭКСТРЕМУМА
- 2. СПОСОБЫ ОРГАНИЗАЦИИ ДВИЖЕНИЯ К ЭКСТРЕМУМУ
- 3. МЕТОДЫ РАСЧЕТА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРОВ
- 4. ВЫБОР КОРРЕКТИРУЮЩИХ УСТРОЙСТВ В ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРАХ
- 5. ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ С ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ
- Глава XVII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ ВОЗДЕЙСТВИЯХ
- 2. ВЫБОР ПАРАМЕТРОВ УСТРОЙСТВ НЕИЗМЕНЯЕМОЙ ЧАСТИ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ПОСТРОЕНИЕ ЖЕЛАЕМОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 4. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. СИНТЕЗ ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 6. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 7. СПОСОБЫ РЕАЛИЗАЦИИ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Глава XVIII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 1. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА НА ОСНОВЕ КРИТЕРИЯ МИНИМУМА ИНТЕГРАЛЬНОЙ ОШИБКИ
- 2. СИНТЕЗ СИСТЕМ РЕГУЛИРОВАНИЯ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЖЕЛАЕМОЙ СИСТЕМЫ
- 4. ПРИМЕР СИНТЕЗА КОРРЕКТИРУЮЩИХ УСТРОЙСТВ СИСТЕМЫ РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- ГЛАВА XIX. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИНТЕЗ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ, ОСНОВАННЫЙ НА ПРИМЕНЕНИИ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- 2. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. РЕАЛИЗАЦИЯ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ ПРИ ПОМОЩИ RC-ЦЕПЕЙ
- 4. РЕАЛИЗАЦИЯ ПРОГРАММ КОРРЕКЦИИ НА УПРАВЛЯЮЩЕЙ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- ГЛАВА XX. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ПРИНЦИП МАКСИМУМА
- 3. ТЕОРЕМА О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
- 4. ПРИМЕРЫ ПРИМЕНЕНИЯ ПРИНЦИПА МАКСИМУМА
- 5. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 6. СИНТЕЗ НЕПРЕРЫВНЫХ ОПТИМАЛЬНЫХ СИСТЕМ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ