| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
3. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
Функциональные преобразователи предназначены для реализации определенной математической зависимости между входными и выходными величинами. Наибольшее распространение эти преобразователи находят в аналоговых вычислителях и счетно-решающих устройствах.
Функциональные зависимости, осуществляемые с помощью вычислительных устройств, могут быть весьма разнообразны. Наряду с устройствами для вычисления алгебраических и трансцендентных функций или для приближенной реализации заданной функции одной или нескольких переменных в системах автоматического регулирования приходится иметь дело с операциями дифференцирования и интегрирования, а также с решением алгебраических и дифференциальных уравнений.
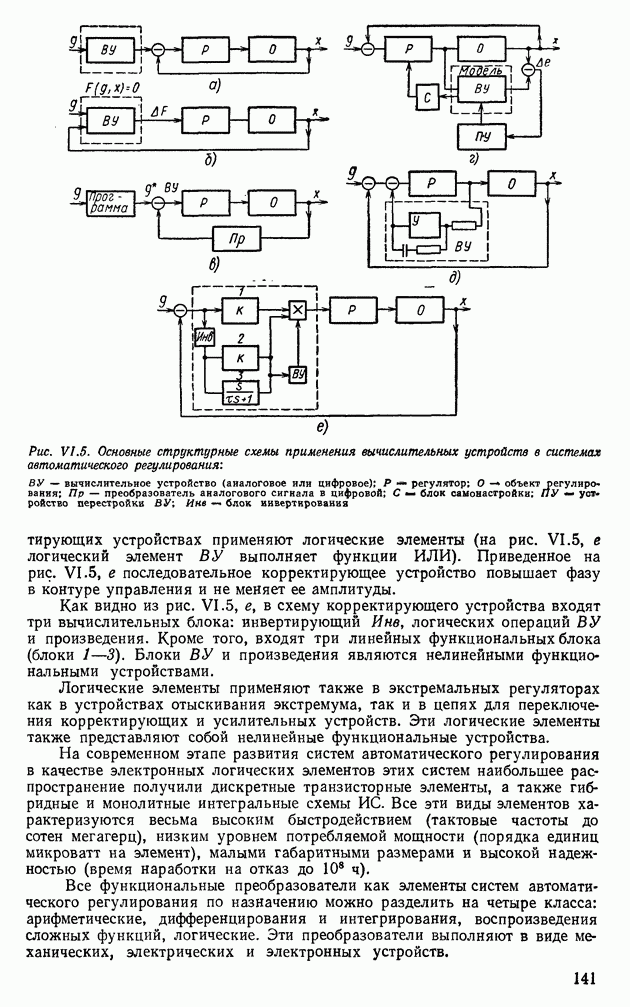
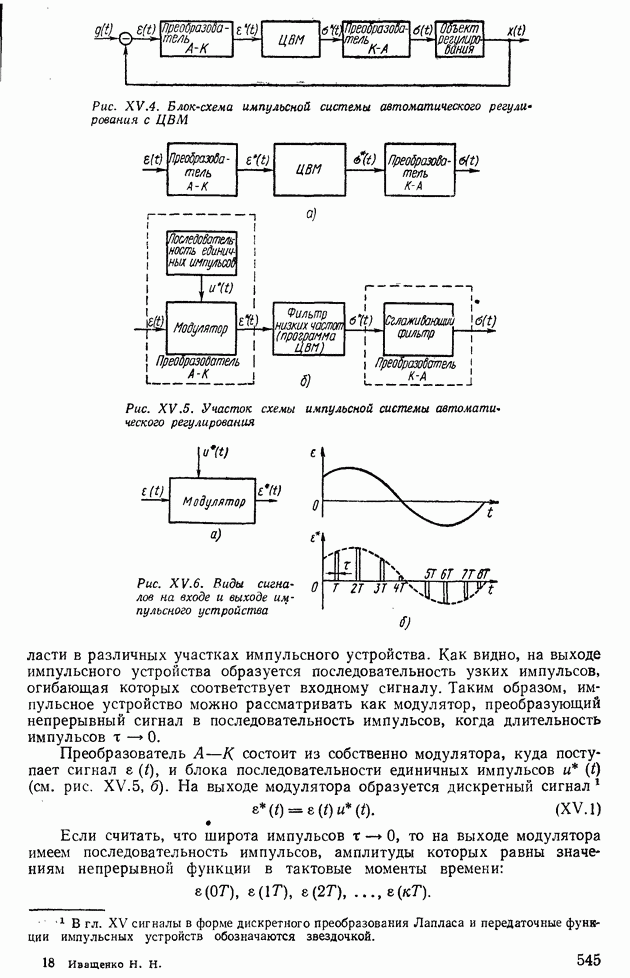
В системах автоматического регулирования вычислительные устройства чаще всего применяют, когда к системе предъявляют требование воспроизведения по заданному закону выходной величины но значениям входной величины. В этом случае вычислительное устройство с В У выполняет функцию задатчика, а схема регулирования имеет вид, изображенный на рис. VI.5, а. В тех случаях, когда закон воспроизведения задан неявной функцией  вычислительное устройство выполняет роль сравнивающего устройства и датчика рассогласования (рис. VI .5, б). Здесь вычислительное устройство или счетно-решающий прибор определяет числовое значение функции
вычислительное устройство выполняет роль сравнивающего устройства и датчика рассогласования (рис. VI .5, б). Здесь вычислительное устройство или счетно-решающий прибор определяет числовое значение функции  в каждый момент времени, и это значение является сигналом рассогласования, на основании которого регулятор вырабатывает регулирующее воздействие.
в каждый момент времени, и это значение является сигналом рассогласования, на основании которого регулятор вырабатывает регулирующее воздействие.
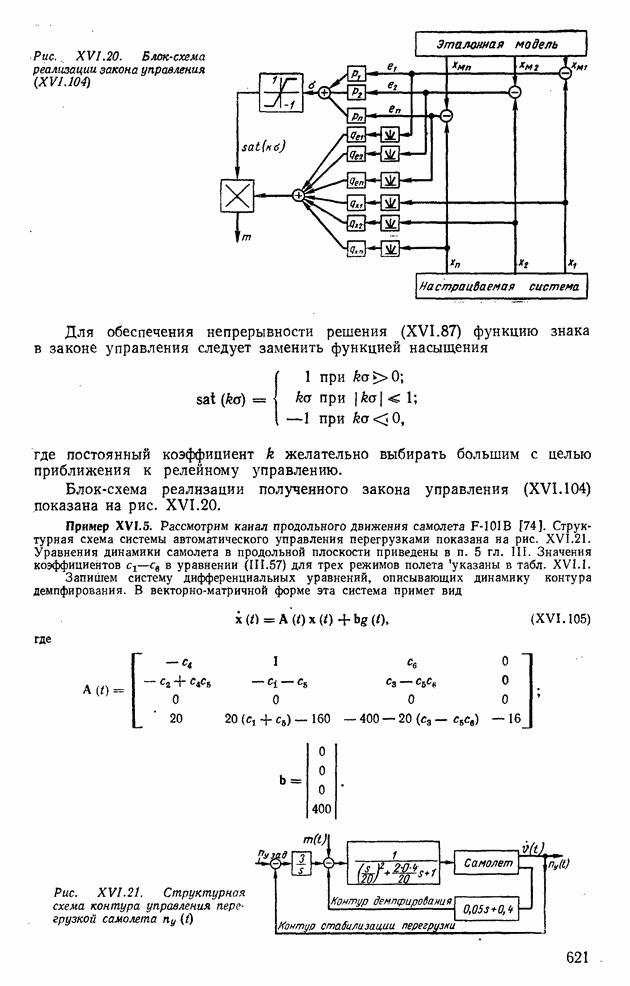
Вычислительные устройства, особенно цифрового действия, применяют в системах программного управления, когда цифровой счетчик (вычислитель) является сравнивающим элементом (рис. VI .5, в). В последнее время вычислительные устройства стали широко применять в самонастраивающихся системах, имеющих модель с перестраиваемыми параметрами (рис. VI.5, г). В зависимости от сигнала ошибки  устройство перестройки
устройство перестройки  изменяет параметры модели до тех пор, пока
изменяет параметры модели до тех пор, пока  не станет равным нулю. По полученным параметрам модели блок самонастройки С перестраивает параметры регулятора Р.
не станет равным нулю. По полученным параметрам модели блок самонастройки С перестраивает параметры регулятора Р.
Вычислительные элементы используют также в цепях обратных связей систем в виде корректирующих устройств (рис. VI.5, д). Иногда в
Рис. VI.5. (см. скан) Основные структурные схемы применения вычислительных устройств в системах автоматического регулирования: ВУ — вычислительное устройство (аналоговое или цифровое); Р регулятор; О — объект регулирования; Пр — преобразователь аналогового сигнала в цифровой; С блок самонастройки; ПУ - устройство перестройки ВУ; Инв - блок инвертирования
корректирующих устройствах применяют логические элементы (на рис. VI.5, е логический элемент ВУ выполняет функции ИЛИ). Приведенное на рис. VI .5, е последовательное корректирующее устройство повышает фазу в контуре управления и не меняет ее амплитуды.
Как видно из рис. VI.5, е, в схему корректирующего устройства входят три вычислительных блока: инвертирующий Инв, логических операций ВУ и произведения. Кроме того, входят три линейных функциональных блока (блоки 1—3). Блоки ВУ и произведения являются нелинейными функциональными устройствами.
Логические элементы применяют также в экстремальных регуляторах как в устройствах отыскивания экстремума, так и в цепях для переключения корректирующих и усилительных устройств. Эти логические элементы также представляют собой нелинейные функциональные устройства.
На современном этапе развития систем автоматического регулирования в качестве электронных логических элементов этих систем наибольшее распространение получили дискретные транзисторные элементы, а также гибридные и монолитные интегральные схемы ИС. Все эти виды элементов характеризуются весьма высоким быстродействием (тактовые частоты до сотен мегагерц), низким уровнем потребляемой мощности (порядка единиц микроватт на элемент), малыми габаритными размерами и высокой надежностью (время наработки на отказ до 
Все функциональные преобразователи как элементы систем автоматического регулирования по назначению можно разделить на четыре класса: арифметические, дифференцирования и интегрирования, воспроизведения сложных функций, логические. Эти преобразователи выполняют в виде механических, электрических и электронных устройств.
Механические устройства характеризуются тем, что их входные и выходные параметры являются механическими величинами (угловое или линейное перемещение, скорость, усилие и т. п.) В электромеханических устройствах выходные параметры чаще всего реализуются в виде электрических величин (тока, напряжения), а входные — как механические. В электронных устройствах как входные, так и выходные сигналы и воздействия реализуются обычно в виде напряжений постоянного или переменного тока.
Как электромеханические, так и электронные устройства могут быть постоянного или переменного тока. При работе на переменном токе обычно применяют модуляцию колебаний входным сигналом, а выходная величина реализуется как мгновенное значение огибающей модулированного выходного напряжения. В устройствах постоянного тока используемые усилители вносят некоторую погрешность, обусловленную нестабильностью характеристики усилителя. Если расчетная характеристика усилителя выражается уравнением  то в действительности выходная величина будет
то в действительности выходная величина будет  , т. е. на выходе появляется дополнительное напряжение, создающее погрешность вычислительного устройства. Эту погрешность называют погрешностью дрейфа усилителя (или погрешностью дрейфа нуля).
, т. е. на выходе появляется дополнительное напряжение, создающее погрешность вычислительного устройства. Эту погрешность называют погрешностью дрейфа усилителя (или погрешностью дрейфа нуля).
В аналоговых вычислителях, чтобы снизить влияние дрейфа нуля до допустимого малого значения, применяют операционные усилители (см. п. 6 данной главы), обеспечивающие требуемую стабилизацию нуля.
В заключение укажем на основные требования, предъявляемые к функциональным преобразователям. Они должны легко включаться в систему, т. е. должны оперировать с величинами той же физической природы, какая принята в системе регулирования. Точность этих устройств в системах регулирования различна. Если вычислительный элемент входит в сравнивающее устройство или в устройство, задающее программу, то его точность должна быть весьма высокой. Если же вычислительный элемент включается после сравнивающего устройства и формирует сигнал ошибки, то требования к его точности значительно снижаются.
Аналоговые электронные функциональные преобразователи. Аналоговые электронные функциональные преобразователи являются в настоящее время  самым распространенным классом устройств. К ним относятся элементы сравнения (компараторы), логарифмические усилители, блоки переключения, дифференцирующие и интегрирующие устройства и т.
самым распространенным классом устройств. К ним относятся элементы сравнения (компараторы), логарифмические усилители, блоки переключения, дифференцирующие и интегрирующие устройства и т. 
Компаратор (рис. VI.6, а). Дифференциальный усилитель ДУ усиливает разность сигналов. При этом  при
при  ияых
ияых  при
при  Если на выходе поставить прибор, регистрирующий полярность выходного сигнала, то он будет показывать, какой из входных сигналов больше, т. е. будет осуществлять сравнение сигналов.
Если на выходе поставить прибор, регистрирующий полярность выходного сигнала, то он будет показывать, какой из входных сигналов больше, т. е. будет осуществлять сравнение сигналов.
Логарифмический усилитель (рис. VI.6, б). Так как входное сопротивление ДУ велико  то
то  Если считать, что ДУ имеет большой коэффициент усиления, то потенциалы обоих входов ДУ весьма близки и равны нулю, так как один из выходов заземлен. Поэтому
Если считать, что ДУ имеет большой коэффициент усиления, то потенциалы обоих входов ДУ весьма близки и равны нулю, так как один из выходов заземлен. Поэтому


Рис. VI.6. Функциональные аналоговые блоки с использованием операционного усилителя: а — компаратор; б — логарифмический усилитель; в - автилогарифматор

Рис. VI.7. Логарифмический умножитель
т. е.

Таким образом, сигнал на выходе пропорционален логарифму входного сигнала. Точность вычисления логарифма зависит от того, насколько характеристика диода близка к логарифмической. При специальном выборе диода и его режима можно получить практически идеальную характеристику на пять-шесть декад изменения тока.
Усилитель, вычисляющий антилогарифмы (рис. VI.6, в). Принцип его действия аналогичен принципу действия логарифмического усилителя. Можно записать

т. е. логарифм выходного сигнала пропорционален величине входного.
Логарифмический умножитель. На рис. VI.7 показана схема логарифмического умножителя. Схема осуществляет логарифмирование входных сигналов, затем сложение логарифмов и получение антилогарифма произведения. Точность такого умножения значительно выше, чем при обычном аналоговом умножении двух величин.
Импульсные умножители. Принцип действия этих устройств состоит в том, что сомножители произведения воспроизводятся различными формами импульсов, причем чаще всего используются импульсы прямоугольной или пилообразной формы. После импульсного умножителя импульсы пропускаются через фильтр, сглаживаются, а затем определяется их среднее значение. Для лучшего уяснения этого обратимся к рис. VI.8.
Генератор импульсов I с модулятором длительности преобразует входной сигнал  в последовательность импульсов с амплитудой
в последовательность импульсов с амплитудой  длительностью
длительностью  и периодом Т, пропорциональным входному сигналу
и периодом Т, пропорциональным входному сигналу  т. е.
т. е.

где  — коэффициент пропорциональности.
— коэффициент пропорциональности.
Импульсная последовательность  поступает в модулятор II, где подвергается модуляции по амплитуде сигналом
поступает в модулятор II, где подвергается модуляции по амплитуде сигналом  . Вследствие этого выходящая последовательность импульсов
. Вследствие этого выходящая последовательность импульсов  имеет амплитуду
имеет амплитуду

и длительность 

Рис. VI.8. Блок-схема пульсного умножителя

Рис. VI.9. Блок-схема множительного импульсного устройства с пилообразными импульсами напряжения

Рис. VI.10. Схема дифференцирующего устройства с транзистором
После прохождения через сглаживающий фильтр III импульсная последовательность с небольшой погрешностью превращается в постоянное напряжение, величина которого

Из полученной формулы следует, что имеется возможность построения импульсных функциональных элементов для умножения переменных величин.
Точность умножения определяется линейностью операций, описываемых выражениями (VI.32) и (VI.33). Это приводит к весьма жестким требованиям по линейности и стабильности блоков I и II, и, несмотря на это, ошибка перемножения составляет ±10%.
Для повышения точности умножения до  и выше применяют множительное импульсное устройство, преобразующее пилообразные импульсы напряжения (рис. VI .9). Генератор задающих импульсов I посылает высокочастотный сигнал на генератор пилообразного напряжения II и модулятор III. Тангенс угла наклона переднего фронта пилообразных импульсов
и выше применяют множительное импульсное устройство, преобразующее пилообразные импульсы напряжения (рис. VI .9). Генератор задающих импульсов I посылает высокочастотный сигнал на генератор пилообразного напряжения II и модулятор III. Тангенс угла наклона переднего фронта пилообразных импульсов  генератора II пропорционален входному напряжению
генератора II пропорционален входному напряжению  Компаратор IV определяет напряжение и пилообразных импульсов в момент времени
Компаратор IV определяет напряжение и пилообразных импульсов в момент времени  . Момент времени
. Момент времени  пропорционален входному напряжению
пропорционален входному напряжению  и зависит от параметров временного модулятора. Напряжение на выходе множительного устройства в этом случае определяется в виде
и зависит от параметров временного модулятора. Напряжение на выходе множительного устройства в этом случае определяется в виде

Точность перемножения в схеме, показанной на рис. VI.9, зависит от линейности пилообразных импульсов; последняя с помощью специальных усилителей может быть получена достаточно высокой.
В заключение рассмотрим одну из схем дифференцирования сигналов, состоящую из  -цепи и транзистора.
-цепи и транзистора.
Схема дифференцирующего устройства на транзисторе (рис. VI. 10). В этой схеме транзистор охвачен параллельной отрицательной обратной связью по напряжению через резистор  Операция дифференцирования осуществляется конденсатором С и резистором
Операция дифференцирования осуществляется конденсатором С и резистором  Резисторы
Резисторы  включены для обеспечения необходимого режима работы транзистора по постоянному току, конденсатор
включены для обеспечения необходимого режима работы транзистора по постоянному току, конденсатор  служит для развязки, а конденсатор
служит для развязки, а конденсатор  выполняет роль разделительного.
выполняет роль разделительного.
При больших значениях коэффициента усиления транзистора по току

имеем

Полученное выражение (VI.36) указывает на то, что схема, показанная на рис. VI. 10, выполняет операцию дифференцирования.
Действительно, не приводя строгих выкладок, можно записать

где  — ток обратной связи через резистор
— ток обратной связи через резистор 
Выражение (VI.37) справедливо, так как токовый сигнал в цепи базы стремится к нулю. Из этого выражения нетрудно получить формулу (VI.36).
Из-за наличия транзистора схема, показанная на рис. VI. 10, имеет более низкое выходное сопротивление и может быть применена совместно с низкоомными усилительными устройствами. Это и является основным преимуществом рассматриваемой схемы.
Схема интегрирующего устройства с транзистором (рис. VI. 11). Транзистор охвачен отрицательной обратной связью через конденсатор  Резистор
Резистор  образует интегрирующую цепочку, а резисторы
образует интегрирующую цепочку, а резисторы  служат для установления необходимого режима питания транзистора. Конденсатор
служат для установления необходимого режима питания транзистора. Конденсатор  предназначен для фильтрации высоких частот, а
предназначен для фильтрации высоких частот, а  являются разделительными.
являются разделительными.
Выходное напряжение можно определить с помощью соотношения:

где  — входное сопротивление транзистора;
— входное сопротивление транзистора;  — коэффициент усиления транзистора по току;
— коэффициент усиления транзистора по току;  — сопротивление транзистора по цепи коллектора.
— сопротивление транзистора по цепи коллектора.
Из анализа выражения (VI.38) видно, что второе слагаемое подынтегрального выражения вносит искажение в интегрирование входного сигнала, но при больших Р его влиянием можно пренебречь. Тогда приведенная схема обеспечивает практически «чистое» интегрирование.
Перейдем теперь к рассмотрению электрических функциональных устройств.
Аналоговые электрические функциональные устройства. Простейшие аналоговые функциональные устройства электрического типа, выполняющие операции суммирования, показаны на рис. VI. 12.
Суммирование при последовательном и параллельном включении напряжений. Схема 

Рис. VI.11. Схема интегрирующего устройства с транзистором

Рис. VI.12. Схема сложения при последовательном и параллельном включении напряжений:  электродвижущие силы источников;
электродвижущие силы источников;  — их внутренние сопротивления;
— их внутренние сопротивления;  — внешние резисторы в цепях источников;
— внешние резисторы в цепях источников;  -выходной резистор;
-выходной резистор;  — выходное напряжение;
— выходное напряжение;  — общий ток;
— общий ток;  -токи в цепях источников;
-токи в цепях источников;  — напряжения на зажимах источников
— напряжения на зажимах источников
мирования, при последовательном включении напряжений изображена на рис. VI. 12, а. В этом случае выходное напряжение можно определить по формуле

где

Отсюда

Обозначив

получим

Пользуясь этой формулой, можно сложить входные величины  и получить на выходе их сумму
и получить на выходе их сумму 
Примем масштабный коэффициент моделирования напряжения входных величин равным  а выходной равным
а выходной равным 
Тогда можно положить

откуда

Если 

Таким образом, схема, приведенная на рис. VI. 12, а, обеспечивает сложение произвольного числа входных величин, если масштабный коэффициент моделирования для выхода  принять равным
принять равным  Если
Если  , то
, то  .
.
Если вместо ЭДС  источников рассматривать напряжения
источников рассматривать напряжения  на их зажимах (рис. VI. 12, б), то всегда нвых
на их зажимах (рис. VI. 12, б), то всегда нвых  Однако для правильной работы схемы как суммирующего устройства необходимо, чтобы выполнилось условие
Однако для правильной работы схемы как суммирующего устройства необходимо, чтобы выполнилось условие 

Рис. VI.13. Алгебраическое суммирование входных величин с помощью усилителя с обратной связью: I, II, III — потенциометры задатчика с нулевой точкой; Е — источник питания;  входные напряжения;
входные напряжения;  выходное напряжение; У — усилитель;
выходное напряжение; У — усилитель;  резисторы входных цепей;
резисторы входных цепей;  резистор обратной связи;
резистор обратной связи;  входное напряжение усилителя:
входное напряжение усилителя:  , — токи входных цепей; С — общий ток;
, — токи входных цепей; С — общий ток;  сеточный ток
сеточный ток
Для случая, изображенного на рис. VI.12, в, имеем следующие соотношения:

Исключая I, придем к формуле для выходного напряжения

Если подобрать сопротивления  так, чтобы соблюдались соотношения
так, чтобы соблюдались соотношения  то
то

где  — число входных величин.
— число входных величин.
С помощью этой формулы также можно реализовать сложение входных величин.
Сохраняя прежние обозначения коэффициентов моделирования, можем написать

при  имеем
имеем 
Операции суммирования могут быть выполнены с помощью сочетания электрических и электронных устройств, например при использовании потенциометров в усилителя с обратной связью.
Суммирование с помощью усилителя с обратной связью. Алгебраическое суммирование входных величин в системах автоматического регулирования может быть реализовано с помощью усилителя с обратной связью. Схема такого устройства представлена на рис. VI.13. Основным требованием к усилителям, применяемым для указанной цели, является обеспечение достаточно высокого коэффициента усиления.
Допустим, что в качестве входных величин на потенциометрах установлены напряжения  тогда сила тока в каждой цепи будет
тогда сила тока в каждой цепи будет

а общий ток

Напряжению  приписывается знак плюс или минус, в зависимости от того, где находится движок потенциометра — выше или ниже нулевой линии. Если обозначить коэффициент усиления усилителя через
приписывается знак плюс или минус, в зависимости от того, где находится движок потенциометра — выше или ниже нулевой линии. Если обозначить коэффициент усиления усилителя через  то
то

С другой стороны,  , где
, где  — входной ток усилителя. Обычно
— входной ток усилителя. Обычно  при больших значениях
при больших значениях  пренебрежимо мал по сравнению с
пренебрежимо мал по сравнению с  поэтому можно принять, что
поэтому можно принять, что

Исключая из уравнений (VI.50), (VI.51)  , придем к зависимости
, придем к зависимости

где

Если  достаточно велико, то
достаточно велико, то  и формула (VI.54) принимает вид
и формула (VI.54) принимает вид

При  получим формулу суммирования
получим формулу суммирования

Можно подобрать значения сопротивлений  так, чтобы отношения
так, чтобы отношения  были равны относительным весам соответствующих входных величин. Тогда устройство, соответствующее схёме рис. VI.13, позволит суммировать входные величины не только с учетом их знаков, но и с учетом их относительных весов
были равны относительным весам соответствующих входных величин. Тогда устройство, соответствующее схёме рис. VI.13, позволит суммировать входные величины не только с учетом их знаков, но и с учетом их относительных весов  и формула примет вид
и формула примет вид

Перейдем к рассмотрению электромеханических устройств.
Электромеханические функциональные устройства. Электромеханические функциональные устройства относятся к наиболее часто встречающимся устройствам в системах автоматического регулирования. Устройства этого типа могут выполнять любые алгебраические операции, дифференцирование и интегрирование функций, а также воспроизводить различные нелинейные зависимости  и т.п.).
и т.п.).
Тахогенератор как дифференцирующий элемент. В системах автоматического регулирования в качестве дифференцирующего элемента наряду с электронными дифференциаторами часто применяют тахогенераторы постоянного тока (рис. VI. 14).
Если использовать прямолинейную часть характеристики холостого хода, магнитопровод тахогенератор а выполнить из ! материала с малыми потерями на гистерезис, а якорь с обмоткой — с пренебрежимо малым

Рис. VI.14. Схема тахогенератора постоянного тока
омическим сопротивлением, то с достаточной для практических целей точностью будет справедливо соотношение

где А — постоянная, зависящая от размеров и конструкции генератора, а также от качества магнитного материала.
Эта формула позволяет использовать тахогенератор как дифференцирующий элемент по времени.
В самом деле, если положить  входную величину представить угловым перемещением а, определяющим коэффициент
входную величину представить угловым перемещением а, определяющим коэффициент  а напряжение а принять за выходную величину у с коэффициентом пропорциональности
а напряжение а принять за выходную величину у с коэффициентом пропорциональности  то получим
то получим

или при 

Если напряжение возбуждения  сделать переменным и использовать его для моделирования второй входной величины и, то получим следующую функцию:
сделать переменным и использовать его для моделирования второй входной величины и, то получим следующую функцию:

или при 

Таким образом, с помощью тахогенератора может быть построен элемент, воспроизводящий функцию

Для уменьшения погрешности тахогенератора, связанной с влиянием сопротивления переходного контакта между коллектором и щетками, применяют коллекторы с большим числом пластинок, а щетки выполняют с малым переходным сопротивлением. Повышая скорость вращения якоря тахогенератора, удается снизить погрешность.
Тахогенератор в качестве интегрирующего элемента. В системах автоматического регулирования применяют схемы интегрирования заданной функции с помощью тахогенератора (рис. VI.15).
Заданная функция  моделируется с помощью каркасного потенциометра 1 в виде напряжения
моделируется с помощью каркасного потенциометра 1 в виде напряжения  при перемещении движка
при перемещении движка 

Рис. VI. 15. Схема интегрирования с помощью тахогенератора: 1 — каркасный потенциометр, моделирующий заданную функцию  — усилитель; 3 — потенциометр тахогенератора для установки коэффициента моделирования; 4 — обмотка возбуждения тахогенератора; 5 — передача от вала тахогенератора к движку
— усилитель; 3 — потенциометр тахогенератора для установки коэффициента моделирования; 4 — обмотка возбуждения тахогенератора; 5 — передача от вала тахогенератора к движку  — потенциометр отсчета выходного напряжения; а, б, в — движки потенциометров. ТГ — тахогенератор; М — электродвигатель механизма автоматической компенсации
— потенциометр отсчета выходного напряжения; а, б, в — движки потенциометров. ТГ — тахогенератор; М — электродвигатель механизма автоматической компенсации

Рис. VI. 16. Моделирование функции с помощью профильного потенциометра
с постоянной скоростью. Напряжение на зажимах тахогенератора, пропорциональное первой производной от углового перемещения  вала, снимается в виде напряжения
вала, снимается в виде напряжения  с потенциометра 3. Коэффициент
с потенциометра 3. Коэффициент  можно, по желанию, изменять путем перемещения движка вручную. В свою очередь, перемещение вала
можно, по желанию, изменять путем перемещения движка вручную. В свою очередь, перемещение вала  тахогенератора снимается в виде выходного напряжения мвых с потенциометра 6, движок которого в связан передачей 5 с валом. Если
тахогенератора снимается в виде выходного напряжения мвых с потенциометра 6, движок которого в связан передачей 5 с валом. Если  — коэффициент моделирования углового перемещения
— коэффициент моделирования углового перемещения  то
то

Тахогенератор  вращается электродвигателем М, получающим питание через усилитель 2. Поскольку электродвигатель М является электродвигателем отработки в схеме автоматической компенсации, то можем написать, что в установившемся состоянии
вращается электродвигателем М, получающим питание через усилитель 2. Поскольку электродвигатель М является электродвигателем отработки в схеме автоматической компенсации, то можем написать, что в установившемся состоянии  и
и

откуда

Таким образом, напряжение ипвт соответствует функции  с коэффициентом
с коэффициентом 
Воспроизведение сложных функций. В счетно-решающих устройствах систем автоматического регулирования для воспроизводства различных сложных функций применяют потенциометры с профилированными каркасами; потенциометры с изогнутыми прямоугольными каркасами; потенциометры со ступенчатыми каркасами; электронно-лучевые трубки; диодные линейки.
Потенциометры с профилированными каркасами. Сечение такого каркаса, на который наматывается провод сопротивления, представляет собой четырехугольник с двумя прямыми углами, переменной высотой  и постоянным основанием
и постоянным основанием  . Длина одного витка, если не учитывать изоляцию, составит
. Длина одного витка, если не учитывать изоляцию, составит  . Допустим, что намотка выполняется равномерно по длине каркаса и на единицу длины укладывается
. Допустим, что намотка выполняется равномерно по длине каркаса и на единицу длины укладывается  витков. Если при этом сопротивление единицы длины наматываемого провода равно
витков. Если при этом сопротивление единицы длины наматываемого провода равно  то на элементарной длине каркаса
то на элементарной длине каркаса  будет уложено
будет уложено  витков с сопротивлением
витков с сопротивлением

Допустим, что требуется напряжением и воспроизвести функцию  на интервале от 0 до
на интервале от 0 до  Рассмотрим случай, когда
Рассмотрим случай, когда  на интервале
на интервале  представляет собой монотонную возрастающую функцию с начальным значением
представляет собой монотонную возрастающую функцию с начальным значением  при
при  График такой функции изображен на рис. VI. 16. Здесь переменная х воспроизводится перемещением движка потенциометра на величину I, отсчитываемую от точки 0.
График такой функции изображен на рис. VI. 16. Здесь переменная х воспроизводится перемещением движка потенциометра на величину I, отсчитываемую от точки 0.
Из. рис. VI. 16 следует, что

Величина потенциала в каждой точке обмотки потенциометра определяется напряжением между. движком и точкой отсчета и соответствует функции  Для обеспечения начального значения функции
Для обеспечения начального значения функции  в цепь потенциометра включается добавочный резистор с сопротивлением
в цепь потенциометра включается добавочный резистор с сопротивлением  За точку отсчета напряжений принят отрицательный полюс источника питания.
За точку отсчета напряжений принят отрицательный полюс источника питания.
Общее сопротивление каркаса на длине  отвечающей заданному интервалу
отвечающей заданному интервалу  будет
будет

Если присоединить потенциометр к источнику питания, как показано на рис. VI. 16, то напряжение на движке в любой точке участка I будет

С другой стороны,

тогда

Если функции  моделируются с коэффициентом
моделируются с коэффициентом  то должны выполняться равенства
то должны выполняться равенства

Дифференцируя по х, найдем

но

тогда

Таким образом,

где

Эта формула позволяет вычислить для любого значения  высоту
высоту  профиля каркаса потенциометра. Значения
профиля каркаса потенциометра. Значения  определяются по краевым значениям функции
определяются по краевым значениям функции  и допускаемой плотности тока в проводе, наматываемом на каркасе, т. е.
и допускаемой плотности тока в проводе, наматываемом на каркасе, т. е.

Если функция  немонотонная и знакопеременная с ненулевыми начальным и конечным значениями на заданном интервале, то интервал разделяют на участки таким образом, чтобы каждый отвечал монотонному отрезку кривой, изображающей функцию. В соответствии с этим каркас потенциометра делят на несколько самостоятельных частей.
немонотонная и знакопеременная с ненулевыми начальным и конечным значениями на заданном интервале, то интервал разделяют на участки таким образом, чтобы каждый отвечал монотонному отрезку кривой, изображающей функцию. В соответствии с этим каркас потенциометра делят на несколько самостоятельных частей.

Рис. VI.17. Потенциометр со ступенчатым каркасом
Потенциометры со ступенчатыми каркасами (рис. VI. 17, а). Если на ступенчатом каркасе намотка равномерная, то сопротивление  участка О А изменяется в зависимости от перемещения ползунка по закону ломаной линии (рис. VI.17, б).
участка О А изменяется в зависимости от перемещения ползунка по закону ломаной линии (рис. VI.17, б).
Определим законы изменения сопротивлений по участкам. На первом участке имеем

на втором участке

на третьем участке

На основании полученных зависимостей (VI.80) — (VI.82) можно найти сопротивления для  участка в виде
участка в виде

Закон изменения выходного напряжения и в пределах  участка будет
участка будет

где Е — напряжение питания потенциометра; R — полное сопротивление потенциометра.
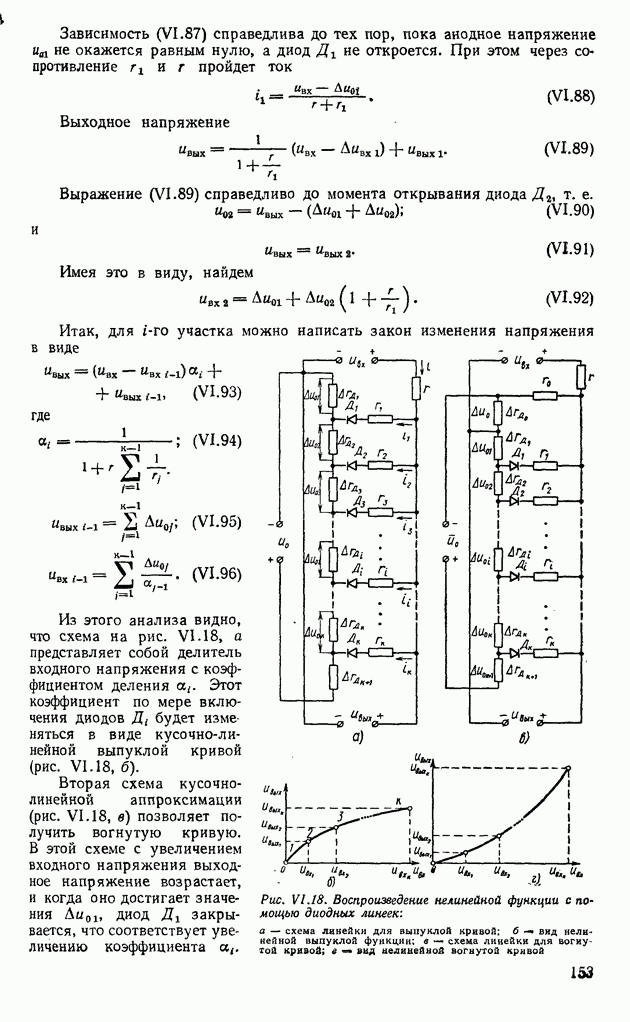
Диодные линейки. В последнее время для воспроизведения сложных нелинейных функций стали применять диодные линейки. На рис. VI. 18, а и в показаны принципиальные схемы таких линеек, обеспечивающих кусочно-линейную аппроксимацию функций (для выпуклой и вогнутой кривых). Как видно из рис. VI. 18, а, анодное напряжение на  диоде
диоде

При малых входных напряжениях цепи всех диодов закрыты и

тогда

Зависимость (VI .87) справедлива до тех пор, пока анодное напряжение ил не окажется равным нулю, а диод не откроется. При этом через сопротивление  пройдет ток
пройдет ток

Выходное напряжение

Выражение (VI.89) справедливо до момента открывания диода  т. е.
т. е.

и

Имея это в виду, найдем

Итак, для  участка можно написать закон изменения напряжения в виде
участка можно написать закон изменения напряжения в виде

где

Из этого анализа видно, что схема на рис. VI. 18, а представляет собой делитель входного напряжения с коэффициентом деления  Этот коэффициент по мере включения диодов
Этот коэффициент по мере включения диодов  будет изменяться в виде кусочно-линейной выпуклой кривой (рис. VI. 18, б).
будет изменяться в виде кусочно-линейной выпуклой кривой (рис. VI. 18, б).
Рис. VI.18. (см. скан) Воспроизведение нелинейной функции с помощью диодных линеек: а — схема линейки для выпуклой кривой; б — вид нелинейной выпуклой функции; в — схема линейки для вогнутой кривой; в - вид нелинейной вогнутой кривой
Вторая схема кусочнолинейной аппроксимации (рис. VI. 18, в) позволяет получить вогнутую кривую.
В этой схеме с увеличением входного напряжения выходное напряжение возрастает, и когда оно достигает значения  диод
диод  закрывается, что соответствует увеличению коэффициента
закрывается, что соответствует увеличению коэффициента 

Рис. VI.19. Воспроизведение нелинейной функции, заданной графически, с помощью следящей системы
При дальнейшем возрастании  последовательно закрываются диоды
последовательно закрываются диоды  т. е.
т. е.

Отсюда видно, что схема, представленная на рис. VI. 18, в, воспроизводит функцию, изображенную на рис. VI. 18, г. Существует еще много других схем воспроизведения нелинейных функций с помощью диодных линеек [73].
Воспроизведение нелинейной функции, заданной графически, с помощью следящей системы. Принцип воспроизведения данным способом может быть уяснен из рис. VI. 19. Здесь функция  задана в виде кривой, нанесенной на бумагу с токопроводящим составом. Бумага с графиком кривой навертывается на барабан 3, вращающийся с постоянной скоростью. Угол поворота барабана воспроизводит в некотором масштабе изменение независимой переменной х. Считывающая головка 2 приводится в движение электродвигателем 5, получающим питание через усилитель 4. Один полюс на входе усилителя связан со средней точкой источника, а другой — со считывающей головкой. Последняя имеет две щетки: щетку-потенциометр а и гладкую щетку б. Гладкая щетка соединена с усилителем, а щетка-потенциометр — с источником напряжения 1. Обе щетки при движении головки имеют контакт с кривой, благодаря чему потенциал гладкой щетки всегда равен потенциалу точки потенциометра, которая находится в соприкосновении с кривой
задана в виде кривой, нанесенной на бумагу с токопроводящим составом. Бумага с графиком кривой навертывается на барабан 3, вращающийся с постоянной скоростью. Угол поворота барабана воспроизводит в некотором масштабе изменение независимой переменной х. Считывающая головка 2 приводится в движение электродвигателем 5, получающим питание через усилитель 4. Один полюс на входе усилителя связан со средней точкой источника, а другой — со считывающей головкой. Последняя имеет две щетки: щетку-потенциометр а и гладкую щетку б. Гладкая щетка соединена с усилителем, а щетка-потенциометр — с источником напряжения 1. Обе щетки при движении головки имеют контакт с кривой, благодаря чему потенциал гладкой щетки всегда равен потенциалу точки потенциометра, которая находится в соприкосновении с кривой  Если точка соприкосновения совпадает с серединой потенциометра, электродвигатель 5 неподвижен. При отклонении ее в ту или другую сторону электродвигатель приходит в движение и перемещает головку. Направление вращения электродвигателя и перемещение считывающей головки связаны таким образом, что отклонение точки кривой от середины потенциометра всегда стремится к нулю. На этом основан процесс считывания заданной кривой.
Если точка соприкосновения совпадает с серединой потенциометра, электродвигатель 5 неподвижен. При отклонении ее в ту или другую сторону электродвигатель приходит в движение и перемещает головку. Направление вращения электродвигателя и перемещение считывающей головки связаны таким образом, что отклонение точки кривой от середины потенциометра всегда стремится к нулю. На этом основан процесс считывания заданной кривой.
Кроме считывающего механизма, устройство имеет потенциометр 7, служащий для моделирования считанного значения функции у. Моделирование осуществляется с помощью привода движка 6 от электродвигателя 5.
Если установить движок 6 в начальное нулевое положение, когда середина потенциометра считывающей головки 2 находится на оси х, то при всяком другом положении головки напряжение и, снятое с потенциометра 7, будет моделировать величину у.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 1. ПРИНЦИПЫ ДЕЙСТВИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ВИДЫ УПРАВЛЯЮЩИХ И ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ
- 4. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Глава II. ВИДЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛТРОВАНИЯ
- 1. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ДИСКРЕТНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ПРИМЕНЕНИЕ ЦВМ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. ПРИМЕНЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ДЛЯ УПРАВЛЕНИЯ СЛОЖНЫМИ ПРОИЗВОДСТВЕННЫМИ ПРОЦЕССАМИ. СИСТЕМЫ КОМПЛЕКСНОЙ АВТОМАТИЗАЦИИ ПРОИЗВОДСТВА
- Глава III. ОБЪЕКТЫ РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ СВОЙСТВА ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 2. ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 3. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ ДИНАМИКИ
- 4. УСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (ДИЗЕЛЬ, ГИДРОТУРБИНА, САМОЛЕТ)
- 5. НЕУСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (РЕСИВЕР, РАКЕТА-НОСИТЕЛЬ КОСМИЧЕСКИХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ)
- 6. АСТАТИЧЕСКИЕ ОБЪЕКТЫ (ТРЕХФАЗНЫЙ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ, ЯДЕРНЫЙ ЭНЕРГЕТИЧЕСКИЙ РЕАКТОР НА ТЕПЛОВЫХ НЕЙТРОНАХ, КОСМИЧЕСКИЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ)
- 7. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- Глава IV. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОПРЕДЕЛЕНИЕ ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ИЗМЕРИТЕЛЬНЫХ ПОДСИСТЕМ
- 2. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Индуктивные устройства.
- Емкостные устройства.
- Сельсины.
- Дифференциальный сельсин.
- Погрешность сельсинов.
- Устройства для замера угловых скоростей.
- Устройства замера угловых ускорений.
- 4. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И ТОКА
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕМПЕРАТУР И ИЗЛУЧЕНИЙ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЙ И РАСХОДОВ ЖИДКОСТИ И ГАЗА
- 7. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ ВЕЛИЧИН, УГЛОВЫХ СКОРОСТЕЙ И ЛИНЕЙНЫХ УСКОРЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ
- Устройства для измерения линейных ускорений подвижных объектов (акселерометры).
- 8. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- Глава V. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ
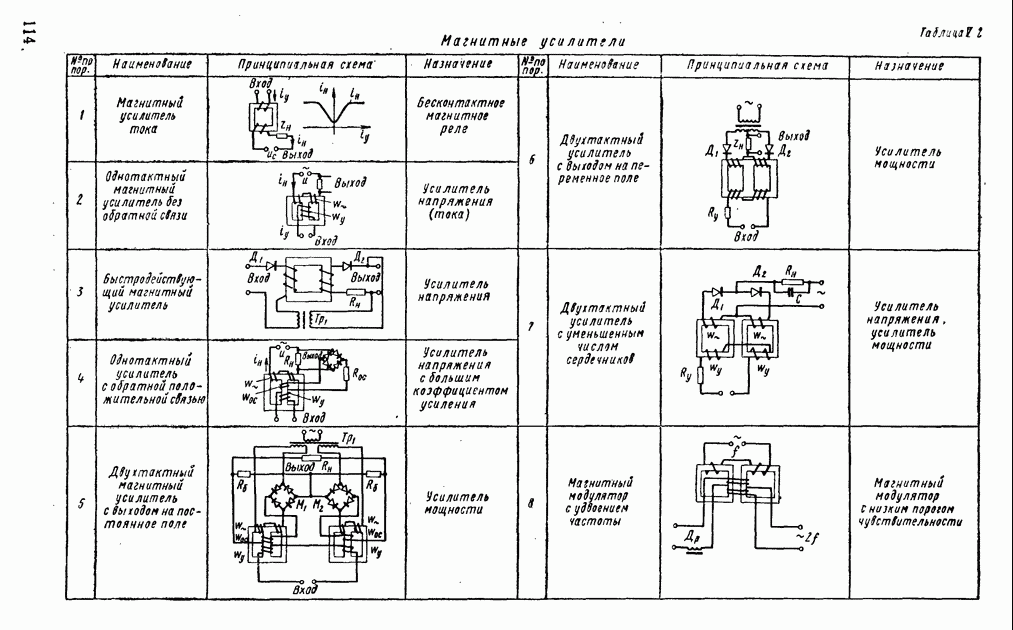
- 2. МАГНИТНЫЕ УСИЛИТЕЛИ
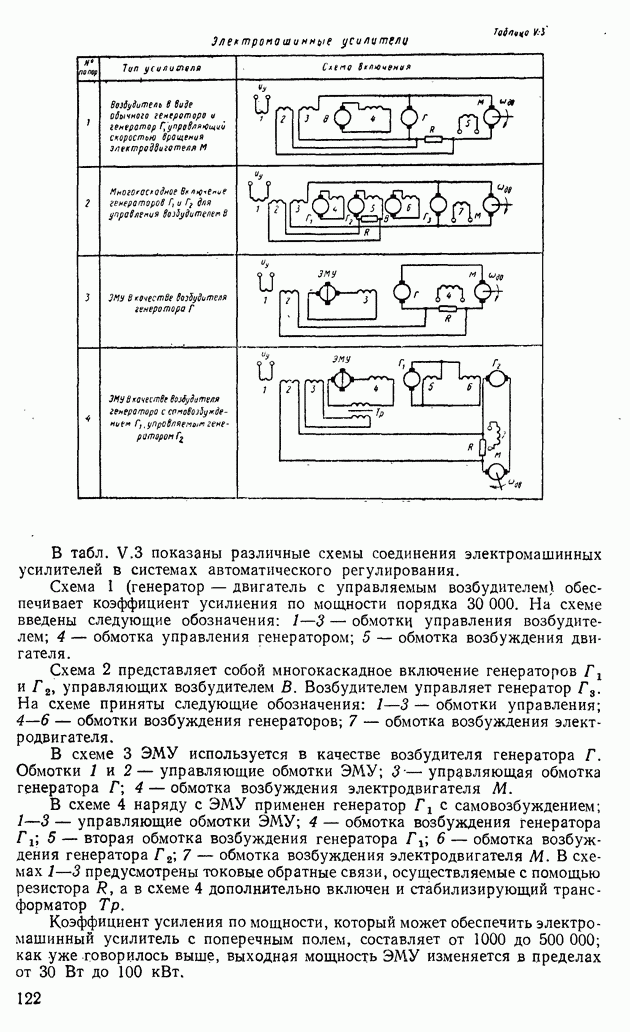
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
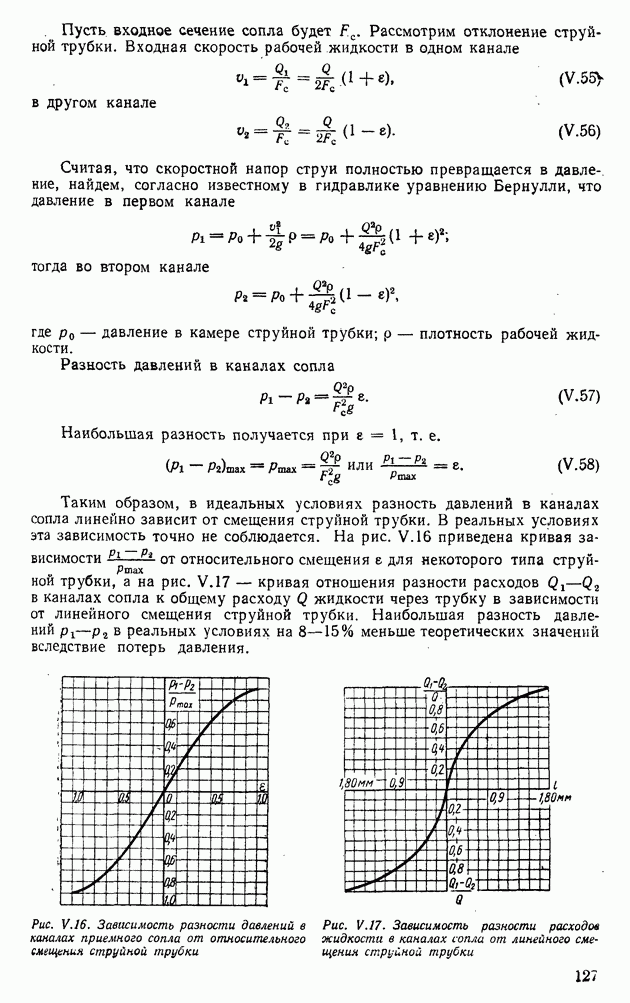
- 4. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 5. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ РАЗЛИЧНЫХ УСИЛИТЕЛЕЙ
- ГЛАВА VI. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА
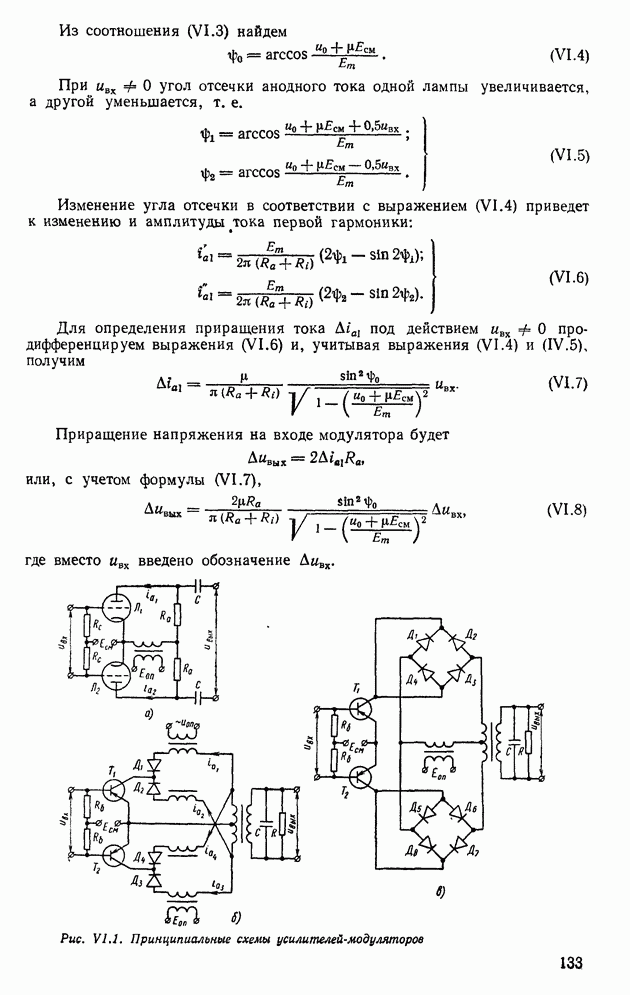
- 1. УСИЛИТЕЛИ-ПРЕОБРАЗОВАТЕЛИ
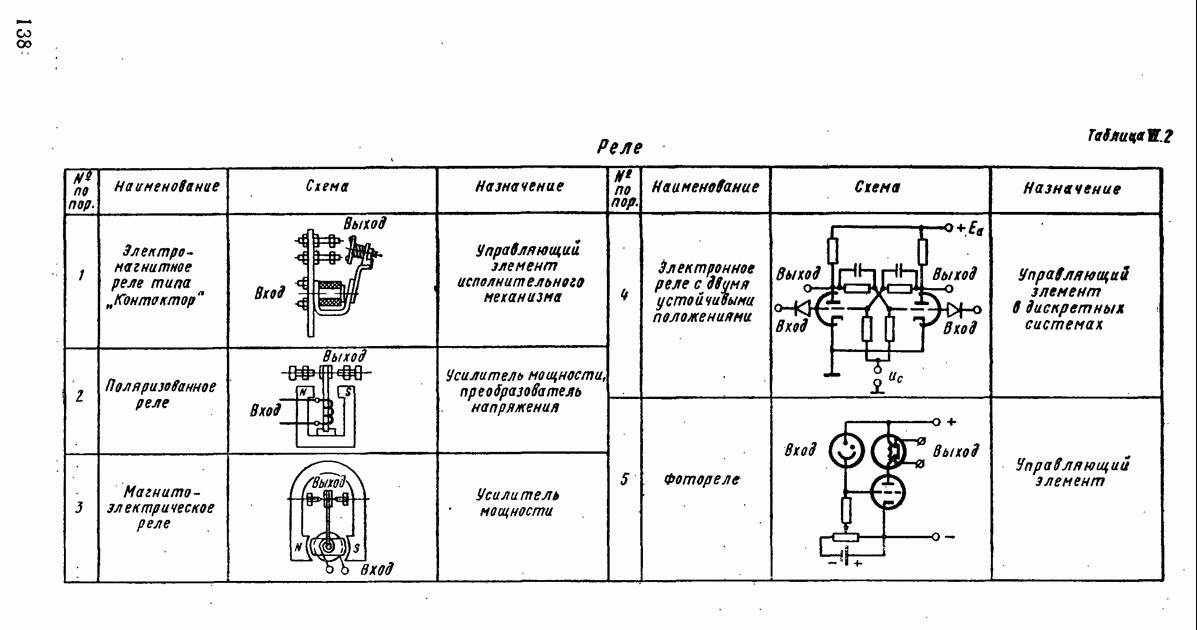
- 2. РЕЛЕ
- 3. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
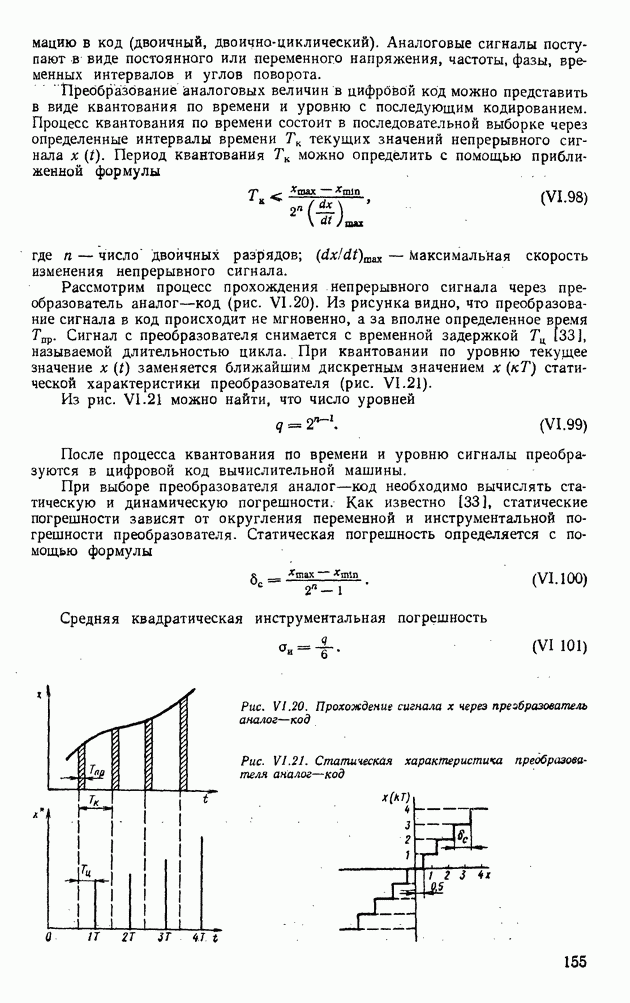
- 4. ПРЕОБРАЗОВАТЕЛИ АНАЛОГ—КОД
- 5. ПРЕОБРАЗОВАТЕЛИ КОД—АНАЛОГ
- 6. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ УПРАВЛЯЮЩИЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
- 8. ПНЕВМАТИЧЕСКИЕ АНАЛОГОВЫЕ И ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 9. ТОЧНОСТЬ РАБОТЫ И БЫСТРОДЕЙСТВИЕ УПРАВЛЯЮЩИХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
- 10. СРАВНИТЕЛЬНАЯ ОЦЕНКА ПРЕОБРАЗУЮЩИХ УСТРОЙСТВ
- Глава VII. ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 1. ЭЛЕКТРИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 2. МЕХАНИЧЕСКИЕ ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. ГИДРАВЛИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 4. ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 5. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- 6. СРАВНИТЕЛЬНАЯ ОЦЕНКА ИСПОЛНИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- Глава VIII. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. НЕЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 3. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 4. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ЛИНИЯХ ЗАДЕРЖЕК И ДИСКРЕТНЫХ ЭЛЕМЕНТАХ
- Глава IX. УРАВНЕНИЯ ДИНАМИКИ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- 1. ПРЕДСТАВЛЕНИЕ ОБЪЕКТОВ И УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С СОСРЕДОТОЧЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 2. ПРЕДСТАВЛЕНИЕ УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С РАСПРЕДЕЛЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ТРАНСЦЕДЕНТНЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 3. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
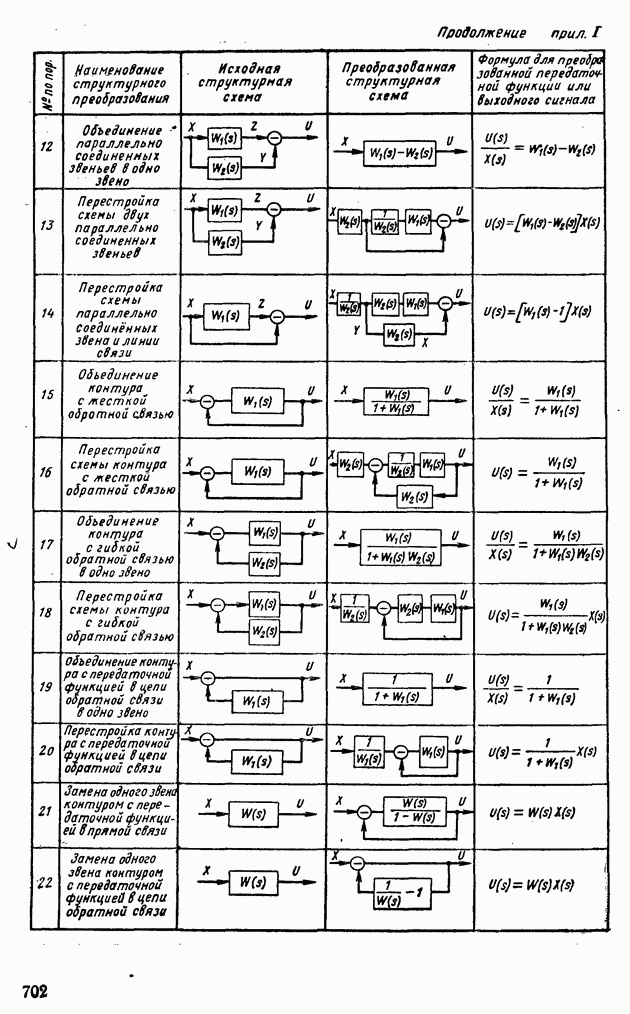
- 4. ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ
- 5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ОПИСАНИЕ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ РЕГУЛИРОВАНИЯ В ВЕКТОРНО-МАТРИЧНОЙ ФОРМЕ
- 7. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 8. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 9. РЕШЕНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ УРАВНЕНИЙ СОСТОЯНИЯ
- 10. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ МАТРИЦ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ ЛИНЕЙНЫХ СИСТЕМ
- 12. ПРЕДСТАВЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ИМПУЛЬСНЫМИ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ
- Глава X. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ АМПЛИТУДНО-ФАЗОВЫЕ И ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 1. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- Логарифмические амплитудная и фазовая частотные характеристики апериодического звена.
- 2. АПЕРИОДИЧЕСКОЕ НЕУСТОЙЧИВОЕ ЗВЕНО
- 4. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 5. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ (УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ)
- 6. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО РОДА
- 7. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО РОДА
- 8. ТРАНСЦЕНДЕНТНЫЕ ЗВЕНЬЯ
- 9. ФАЗОВАЯ ЛИНЕЙКА
- 10. ПОСТРОЕНИЕ АМПЛИТУДНО-ФАЗОВЫХ И ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ ГРУПП ТИПОВЫХ ЗВЕНЬЕВ
- 11. ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ВИДА ПЕРЕДАТОЧНЫХ ФУНКЦИЙ И ПАРАМЕТРОВ ГРУПП ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
- ГЛАВА XI. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ
- 2. ОПРЕДЕЛЕНИЕ ФУНКЦИЙ ЛЯПУНОВА МЕТОДАМИ Г. СЕГЕ И Д. ШУЛЬЦА
- 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 5. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 6. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ТРАНСЦЕНДЕНТНЫМИ ЗВЕНЬЯМИ
- 9. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ С ПОМОЩЬЮ D-РАЗБИЕНИЯ
- Глава XII. ИССЛЕДОВАНИЕ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
- 2. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПО ЗАДАННЫМ ПЕРЕДАТОЧНЫМ ФУНКЦИЯМ ЗАМКНУТЫХ СИСТЕМ
- 3. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПО РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ ЛЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ
- 4. МЕТОД КОРНЕВОГО ГОДОГРАФА
- 5. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА
- 6. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ СИСТЕМ РЕГУЛИРОВАНИЯ И ИХ СВЯЗЬ С ХАРАКТЕРИСТИКАМИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 7. ОПРЕДЕЛЕНИЕ ВЕЩЕСТВЕННЫХ И МНИМЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СИСТЕМ ПО АМПЛИТУДНО-ФАЗОВЫМ И ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ РАЗОМКНУТЫХ СИСТЕМ
- 8. ЧАСТОТНЫЕ ОЦЕНКИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9. ЧАСТОТНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ТРАПЕЦЕИДАЛЬНЫХ ХАРАКТЕРИСТИК
- 10. УСТАНОВЛЕНИЕ НОРМ ЗАПАСОВ УСТОЙЧИВОСТИ ПО ФАЗЕ И МОДУЛЮ, ОБЕСПЕЧИВАЮЩИХ ТРЕБУЕМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМ РЕГУЛИРОВАНИЯ
- ГЛАВА XIII. ДИНАМИЧЕСКАЯ ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ОШИБОК В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ АМПЛИТУДНЫХ ХАРАКТЕРИСТИК
- 3. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПУТЕМ ПРИМЕНЕНИЯ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ
- 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 5. СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ СТАЦИОНАРНЫХ ПРОЦЕССОВ
- 6. СВОЙСТВА СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ
- 7. ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ
- 8. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЛИНЕЙНЫМИ СИСТЕМАМИ
- 9. РАСЧЕТ ОШИБОК В СИСТЕМЕ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ШУМОВ
- 10. ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ВОЗДЕЙСТВИИ СЛУЧАЙНЫХ СИГНАЛОВ И ШУМОВ
- ГЛАВА XIV. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ТИПОВЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ ПО ВТОРОМУ МЕТОДУ ЛЯПУНОВА
- 3. АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
- 4. ПРИМЕНЕНИЕ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. АНАЛИЗ АВТОКОЛЕБАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДВУМЯ НЕЛИНЕЙНОСТЯМИ
- 7. ДВУХКОНТУРНЫЕ НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕДЛЕННО ИЗМЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
- 9. СПОСОБЫ ПОДАВЛЕНИЯ АВТОКОЛЕБАНИЙ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 10. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 11. КРИТЕРИЙ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
- 12. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- Глава XIV. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ИМПУЛЬСНЫХ УСТРОЙСТВ
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. АМПЛИТУДНО-ФАЗОВЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ СИСТЕМ
- 4. ПРИМЕНЕНИЕ ВЕКТОРНО-МАТРИЧНОГО АППАРАТА К ИМПУЛЬСНЫМ СИСТЕМАМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ОСНОВНЫЕ СВОЙСТВА z-ПРЕОБРАЗОВАНИЯ
- 6. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Критерий устойчивости для импульсных систем на плоскостях z и W(z).
- Критерий устойчивости Шур—Кона.
- Критерии устойчивости, основанные на применении билинейного преобразования.
- 7. МЕТОДЫ АНАЛИЗА КАЧЕСТВА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕТОДЫ АНАЛИЗА ТОЧНОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 9. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С УПРАВЛЯЮЩИМИ ЦВМ
- 10. СПОСОБЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ В УПРАВЛЯЮЩИХ ЦВМ И ОПРЕДЕЛЕНИЕ ИХ ОСНОВНЫХ ПАРАМЕТРОВ
- Глава XVI. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МЕТОДЫ ПОИСКА ЭКСТРЕМУМА
- 2. СПОСОБЫ ОРГАНИЗАЦИИ ДВИЖЕНИЯ К ЭКСТРЕМУМУ
- 3. МЕТОДЫ РАСЧЕТА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРОВ
- 4. ВЫБОР КОРРЕКТИРУЮЩИХ УСТРОЙСТВ В ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРАХ
- 5. ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ С ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ
- Глава XVII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ ВОЗДЕЙСТВИЯХ
- 2. ВЫБОР ПАРАМЕТРОВ УСТРОЙСТВ НЕИЗМЕНЯЕМОЙ ЧАСТИ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ПОСТРОЕНИЕ ЖЕЛАЕМОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 4. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. СИНТЕЗ ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 6. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 7. СПОСОБЫ РЕАЛИЗАЦИИ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Глава XVIII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 1. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА НА ОСНОВЕ КРИТЕРИЯ МИНИМУМА ИНТЕГРАЛЬНОЙ ОШИБКИ
- 2. СИНТЕЗ СИСТЕМ РЕГУЛИРОВАНИЯ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЖЕЛАЕМОЙ СИСТЕМЫ
- 4. ПРИМЕР СИНТЕЗА КОРРЕКТИРУЮЩИХ УСТРОЙСТВ СИСТЕМЫ РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- ГЛАВА XIX. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИНТЕЗ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ, ОСНОВАННЫЙ НА ПРИМЕНЕНИИ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- 2. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. РЕАЛИЗАЦИЯ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ ПРИ ПОМОЩИ RC-ЦЕПЕЙ
- 4. РЕАЛИЗАЦИЯ ПРОГРАММ КОРРЕКЦИИ НА УПРАВЛЯЮЩЕЙ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- ГЛАВА XX. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ПРИНЦИП МАКСИМУМА
- 3. ТЕОРЕМА О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
- 4. ПРИМЕРЫ ПРИМЕНЕНИЯ ПРИНЦИПА МАКСИМУМА
- 5. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 6. СИНТЕЗ НЕПРЕРЫВНЫХ ОПТИМАЛЬНЫХ СИСТЕМ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ