| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. СПОСОБЫ ОРГАНИЗАЦИИ ДВИЖЕНИЯ К ЭКСТРЕМУМУ
Организация движения к точке экстремума основана на использовании сигналов, зависящих от градиента функции, или сигналов отклонений от экстремума. Наиболее употребимыми являются методы Гаусса—Зейделя (или поочередного изменения параметров), градиента и наискорейшего спуска.
Метод Гаусса—Зейделя.
Сущность этого метода заключается в поочередном изменении координат  и определении экстремумов вида
и определении экстремумов вида

при  Сперва изменяется координата
Сперва изменяется координата  в направлении уменьшения градиента
в направлении уменьшения градиента  до нулевого значения при постоянных значениях остальных координат. Затем изменяется координата
до нулевого значения при постоянных значениях остальных координат. Затем изменяется координата  в сторону уменьшения
в сторону уменьшения 
После осуществления поиска по всем  координатам (рабочий цикл) снова изменяются координаты
координатам (рабочий цикл) снова изменяются координаты  до обращения в нуль
до обращения в нуль  затем по
затем по  до полного завершения рабочего цикла. Итак, процесс рабочих циклов повторяется до тех пор, пока все
до полного завершения рабочего цикла. Итак, процесс рабочих циклов повторяется до тех пор, пока все  не станут равными нулю. Процесс поиска по этому методу для функции
не станут равными нулю. Процесс поиска по этому методу для функции  от двух переменных
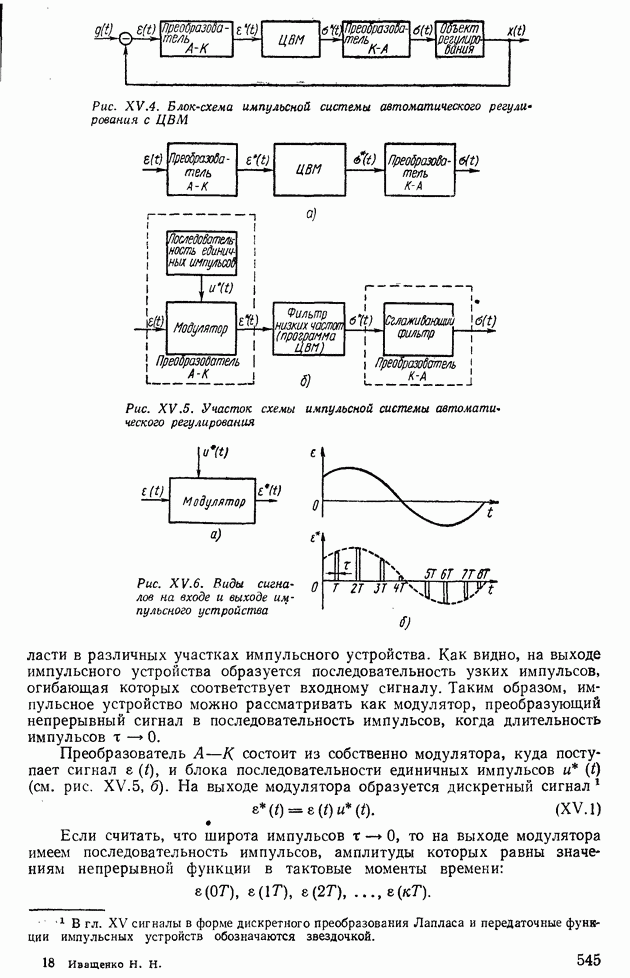
от двух переменных  показан на рис. XVI.7, а. Движение от точки А, параллельное оси
показан на рис. XVI.7, а. Движение от точки А, параллельное оси  происходит прямолинейно, пока
происходит прямолинейно, пока  не обратится в нуль (точка В на рис. XVI.7, а). Затем движение совершается по прямой, параллельной оси
не обратится в нуль (точка В на рис. XVI.7, а). Затем движение совершается по прямой, параллельной оси  до точки С, где
до точки С, где  Далее попадаем в точку
Далее попадаем в точку  где снова
где снова  до точки О, соответствующей экстремальному значению функции
до точки О, соответствующей экстремальному значению функции  На рис. XVI.7, а видно, что при организации движения к экстремуму по методу Гаусса—Зейделя путь не является кратчайшим.
На рис. XVI.7, а видно, что при организации движения к экстремуму по методу Гаусса—Зейделя путь не является кратчайшим.
Метод градиентов (рис. XVI.7, б). Данный метод состоит в том, что движение к минимуму функции  осуществляется в направлении, обратном мгновенному направлению вектора градиента функции
осуществляется в направлении, обратном мгновенному направлению вектора градиента функции
Пусть  — первое приближение
— первое приближение  — значение градиента функции в этой точке. Проведем прямую
— значение градиента функции в этой точке. Проведем прямую


Рис. XV 1.7. Процессы при поиске экстремума тремя методами: а — Гаусса—Зейделя; б — градиента; в — наискорейшего спуска
где  — вещественный параметр. Поскольку вдоль
— вещественный параметр. Поскольку вдоль  функция
функция  в окрестности
в окрестности  возрастает, а в направлении
возрастает, а в направлении  убывает, то для малых
убывает, то для малых  имеем
имеем

Определяем следующий шаг в направлении уменьшения 

для любого шага получим

Каждая координата на  шаге вычисляется по формуле
шаге вычисляется по формуле

Вычисления прекращаются, если для всех  выполняется условие
выполняется условие  где
где  мало.
мало.
В методе градиентов выбор шага  связан условием
связан условием

При этом условии шаг  оказывается обычно очень малым. При большом числе итераций затрачивается много машинного времени, поэтому в таком виде метод градиентного спуска применяется редко. Значительно более экономичным оказывается метод спуска с переменным шагом (или метод наискорейшего спуска).
оказывается обычно очень малым. При большом числе итераций затрачивается много машинного времени, поэтому в таком виде метод градиентного спуска применяется редко. Значительно более экономичным оказывается метод спуска с переменным шагом (или метод наискорейшего спуска).
Метод наискорейшего спуска (рис. XVI.7, в). Этот метод является развитием метода градиентов.
Пусть теперь  — произвольный параметр. Рассмотрим функцию
— произвольный параметр. Рассмотрим функцию 
На каждой итерации величину шага  будем определять из условия
будем определять из условия 
Процесс вычислений, выполняемый по схеме

с шагом  называют методом наискорейшего спуска, где для определения
называют методом наискорейшего спуска, где для определения  на каждой итерации нужно дополнительно решать задачу отыскания минимума функции одной переменной. Эту вспомогательную задачу можно решать по-разному. Обычно поступают следующим образом. Пусть
на каждой итерации нужно дополнительно решать задачу отыскания минимума функции одной переменной. Эту вспомогательную задачу можно решать по-разному. Обычно поступают следующим образом. Пусть  — шаг на
— шаг на  этапе; на
этапе; на  шаге принимаем
шаге принимаем  и проверяем условие (XVI.20). Если оно выполняется, то шаг
и проверяем условие (XVI.20). Если оно выполняется, то шаг  увеличиваем до тех пор, пока при некотором
увеличиваем до тех пор, пока при некотором  не нарушится условие
не нарушится условие

После этого значение  выбираем в качестве начального приближения шага в следующей итерации
выбираем в качестве начального приближения шага в следующей итерации  Если же при
Если же при  выполняется условие (XVI.20), то принимаем
выполняется условие (XVI.20), то принимаем  и снова проверяем условие (XVI.20), и т. д. до тех пор, пока оно не выполнится. Дальнейшее дробление шага выполняется по той же схеме, что и увеличение шага, т. е. с проверкой условия (XVI.21).
и снова проверяем условие (XVI.20), и т. д. до тех пор, пока оно не выполнится. Дальнейшее дробление шага выполняется по той же схеме, что и увеличение шага, т. е. с проверкой условия (XVI.21).
Такая процедура обеспечивает движение с максимально выгодным шагом. Преимуществом этого метода является быстрота прихода в точку экстремума, большие шаги движения на начальном этапе поиска (на отрезке  Возможно сочетание рассмотренных трех методов поиска, например на начальном участке — метод наискорейшего спуска, а на участке подхода к точке экстремума — метод градиента.
Возможно сочетание рассмотренных трех методов поиска, например на начальном участке — метод наискорейшего спуска, а на участке подхода к точке экстремума — метод градиента.
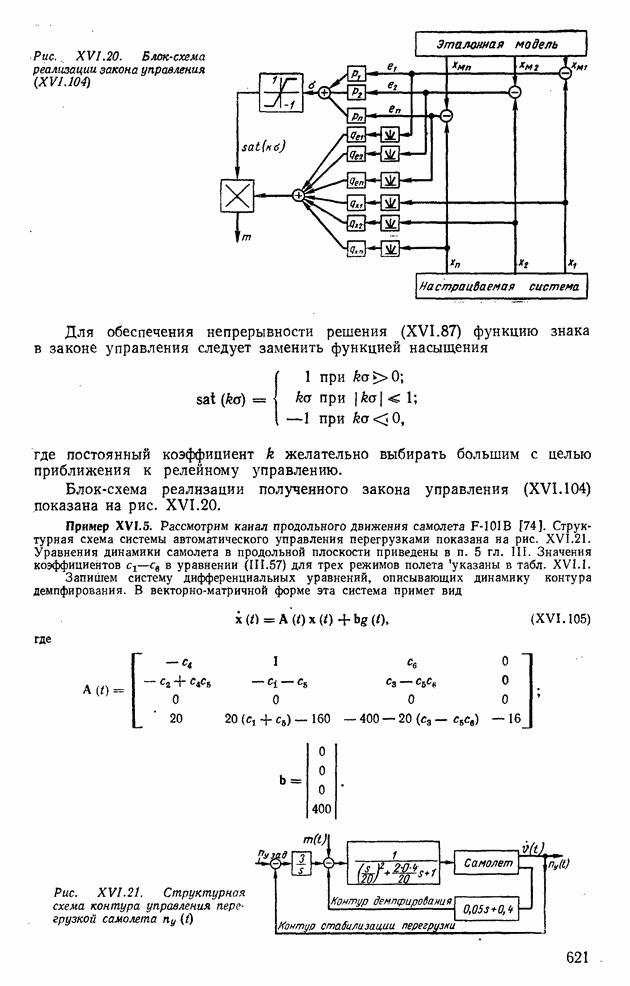
Пример XVI. 1. Определить процесс выхода к экстремуму для экстремального регулятора по методу градиента, если объект регулирования описывается уравнениями вида

а исполнительные устройства уравнениями

Допустим, что параметры системы имеют следующие значения:

Примем, что зона нечувствительности нелинейного элемента  ; начальные условия
; начальные условия  .
.
При поиске по методу градиента сигнал управления пропорционален проекциям градиента

Так как движение совершается в сторону убывания градиента, то, подставив эти значения в дифференциальные уравнения исполнительного устройства с обратным знаком, получим

откуда

Подставим эти соотношения в уравнения (XVI.22), получим

Решая уравнения (XVI.27), найдем

Для определения постоянной с воспользуемся следующими начальными условиями:  . Т. е.
. Т. е.

или

Очевидно, что в выражении (XVI.30)


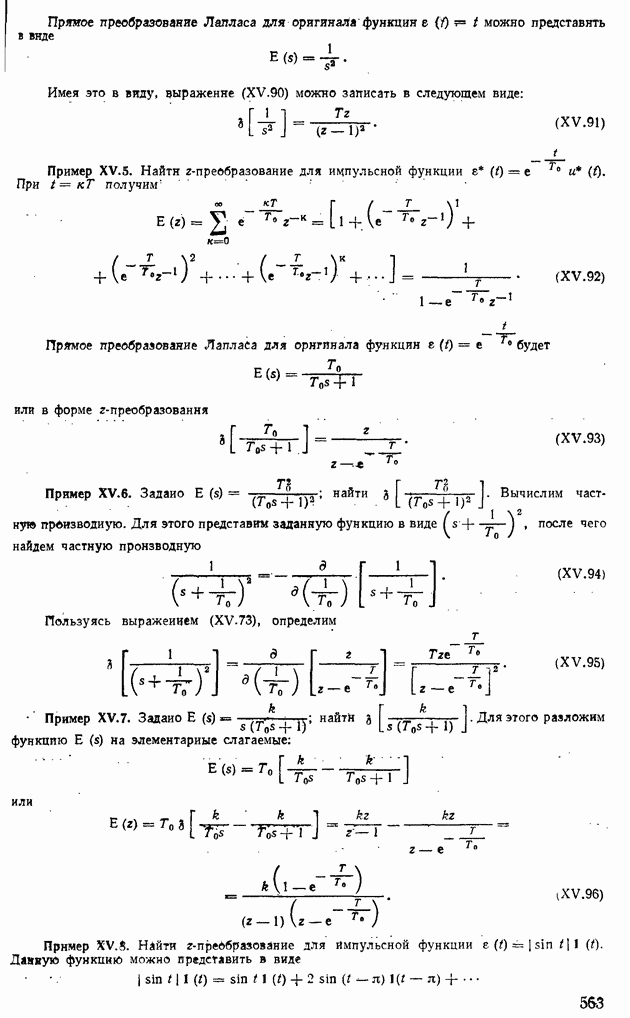
Рис. XVI.8. Процессы выхода регулятора в экстремум при различных методах поиска: а — по методу градиента; б — по методу нанскорейшего спуска
Имея в виду выражение (XVI.31), решение (XVI.28) можно записать в виде

Подставив в выражение (XVI.32) значения параметров системы и начальные условия, получим

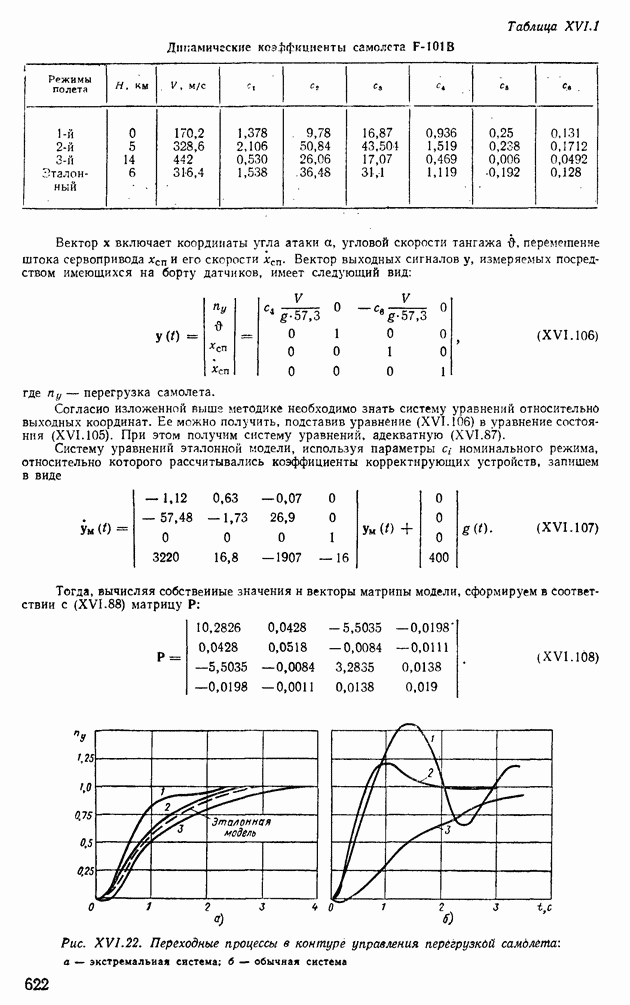
Подставляя в выражение (XVI.33) значения  от 0 до 120 с, получим переходной процесс выхода регулятора в зону экстремума (рис. XVI.8, а). Для определения времени выхода Треж регулятора на оптимальный режим необходимо найти зону
от 0 до 120 с, получим переходной процесс выхода регулятора в зону экстремума (рис. XVI.8, а). Для определения времени выхода Треж регулятора на оптимальный режим необходимо найти зону

Откладывая на рис. XVI.8, а  рад, получим
рад, получим

Пример XVI.2. Для примера XVI.1 определить процесс выхода регулятора к экстремуму, если поиск осуществляется по методу наискорейшего спуска.
Как известно, при поиске по методу наискорейшего спуска перемещение по координатам  осуществляется с постоянной скоростью, равной значению градиента в начальной точке,
осуществляется с постоянной скоростью, равной значению градиента в начальной точке, 

Скорости отработки исполнительных устройств определяем по уравнениям (XVI.34) в виде

откуда

Имея в виду формулы (XVI.35) и (XVI.36), уравнения (XVI.22) запишем в виде

Полученное уравнение можно переписать как

где

Решая уравнение (XVI.38), получим

При  имеем
имеем  тогда
тогда

Подставив соотношение (XVI.40) в выражение (XVI.39), найдем

где  определено выражением (XVI.31). Подставив в выражение (XVI.41) значение параметров системы и начальные условия, получим
определено выражением (XVI.31). Подставив в выражение (XVI.41) значение параметров системы и начальные условия, получим

Подставляя в выражение (XVI.42) значение от 0 до 20 с, определим переходный процесс выхода регулятора в зону экстремума (рис. XVI.8, б). Время выхода регулятора на оптимальный режим  . Сравнивая полученное значение Треж с соответствующим значением из примера XVI. 1, видим, что метод наискорейшего спуска приводит к более быстрому выходу регулятора на оптимальный режим.
. Сравнивая полученное значение Треж с соответствующим значением из примера XVI. 1, видим, что метод наискорейшего спуска приводит к более быстрому выходу регулятора на оптимальный режим.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 1. ПРИНЦИПЫ ДЕЙСТВИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
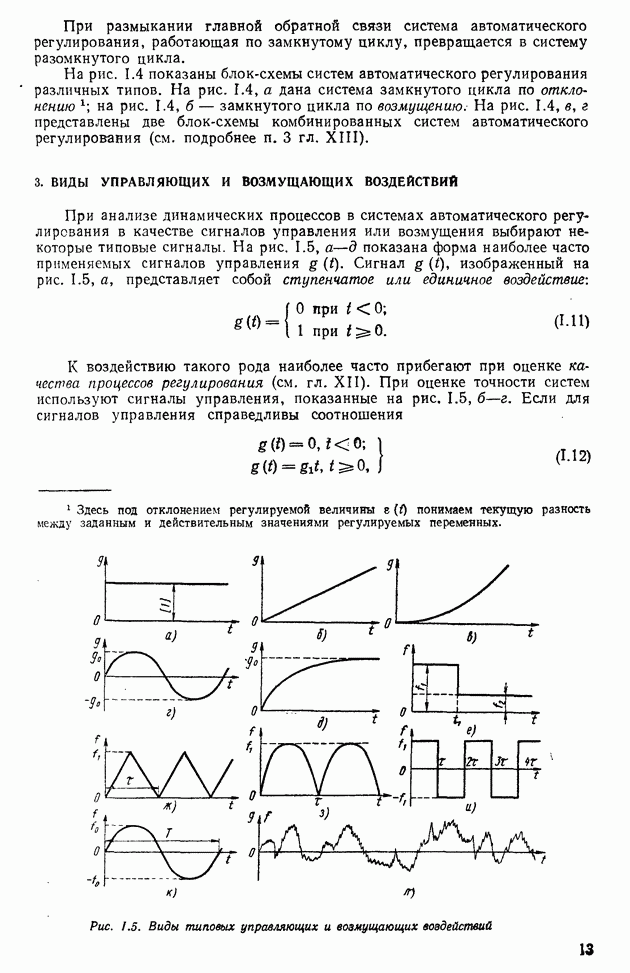
- 3. ВИДЫ УПРАВЛЯЮЩИХ И ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ
- 4. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Глава II. ВИДЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛТРОВАНИЯ
- 1. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
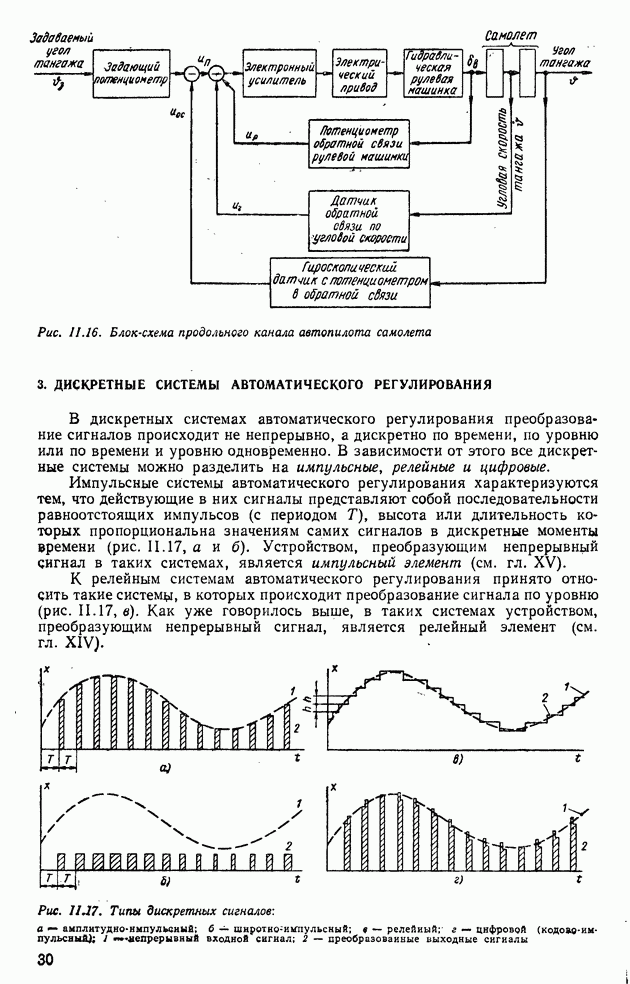
- 3. ДИСКРЕТНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ПРИМЕНЕНИЕ ЦВМ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. ПРИМЕНЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ДЛЯ УПРАВЛЕНИЯ СЛОЖНЫМИ ПРОИЗВОДСТВЕННЫМИ ПРОЦЕССАМИ. СИСТЕМЫ КОМПЛЕКСНОЙ АВТОМАТИЗАЦИИ ПРОИЗВОДСТВА
- Глава III. ОБЪЕКТЫ РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ СВОЙСТВА ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 2. ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 3. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ ДИНАМИКИ
- 4. УСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (ДИЗЕЛЬ, ГИДРОТУРБИНА, САМОЛЕТ)
- 5. НЕУСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (РЕСИВЕР, РАКЕТА-НОСИТЕЛЬ КОСМИЧЕСКИХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ)
- 6. АСТАТИЧЕСКИЕ ОБЪЕКТЫ (ТРЕХФАЗНЫЙ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ, ЯДЕРНЫЙ ЭНЕРГЕТИЧЕСКИЙ РЕАКТОР НА ТЕПЛОВЫХ НЕЙТРОНАХ, КОСМИЧЕСКИЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ)
- 7. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- Глава IV. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОПРЕДЕЛЕНИЕ ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ИЗМЕРИТЕЛЬНЫХ ПОДСИСТЕМ
- 2. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Индуктивные устройства.
- Емкостные устройства.
- Сельсины.
- Дифференциальный сельсин.
- Погрешность сельсинов.
- Устройства для замера угловых скоростей.
- Устройства замера угловых ускорений.
- 4. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И ТОКА
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕМПЕРАТУР И ИЗЛУЧЕНИЙ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЙ И РАСХОДОВ ЖИДКОСТИ И ГАЗА
- 7. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ ВЕЛИЧИН, УГЛОВЫХ СКОРОСТЕЙ И ЛИНЕЙНЫХ УСКОРЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ
- Устройства для измерения линейных ускорений подвижных объектов (акселерометры).
- 8. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- Глава V. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ
- 2. МАГНИТНЫЕ УСИЛИТЕЛИ
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 4. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 5. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ РАЗЛИЧНЫХ УСИЛИТЕЛЕЙ
- ГЛАВА VI. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА
- 1. УСИЛИТЕЛИ-ПРЕОБРАЗОВАТЕЛИ
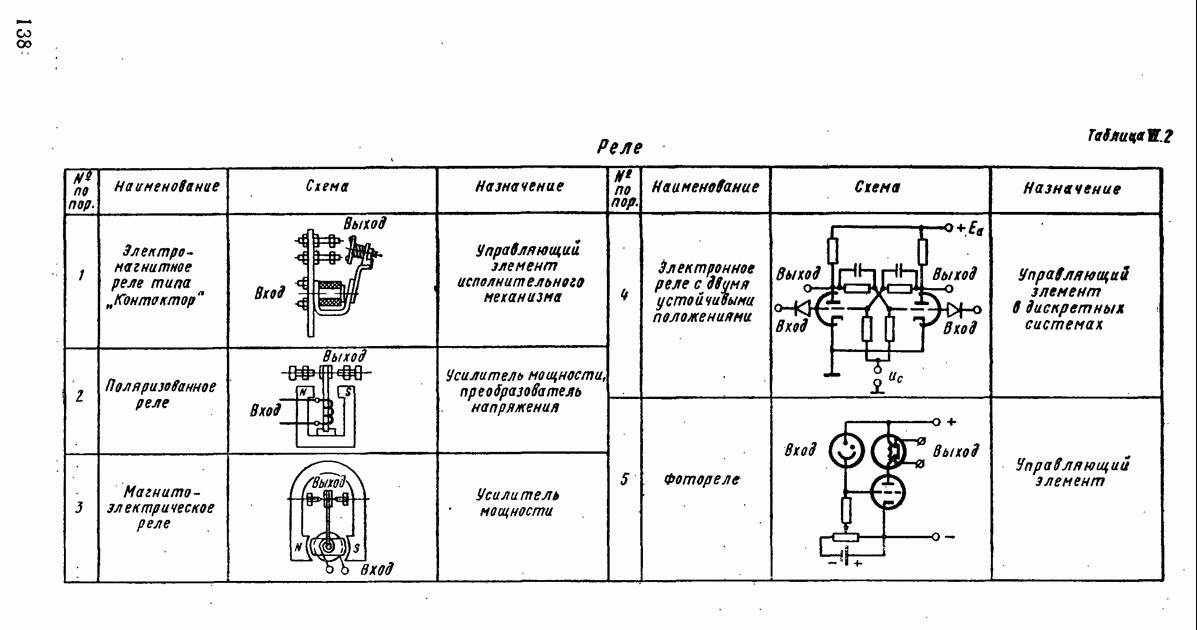
- 2. РЕЛЕ
- 3. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. ПРЕОБРАЗОВАТЕЛИ АНАЛОГ—КОД
- 5. ПРЕОБРАЗОВАТЕЛИ КОД—АНАЛОГ
- 6. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ УПРАВЛЯЮЩИЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
- 8. ПНЕВМАТИЧЕСКИЕ АНАЛОГОВЫЕ И ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 9. ТОЧНОСТЬ РАБОТЫ И БЫСТРОДЕЙСТВИЕ УПРАВЛЯЮЩИХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
- 10. СРАВНИТЕЛЬНАЯ ОЦЕНКА ПРЕОБРАЗУЮЩИХ УСТРОЙСТВ
- Глава VII. ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 1. ЭЛЕКТРИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 2. МЕХАНИЧЕСКИЕ ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. ГИДРАВЛИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 4. ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 5. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- 6. СРАВНИТЕЛЬНАЯ ОЦЕНКА ИСПОЛНИТЕЛЬНЫХ ЭЛЕМЕНТОВ
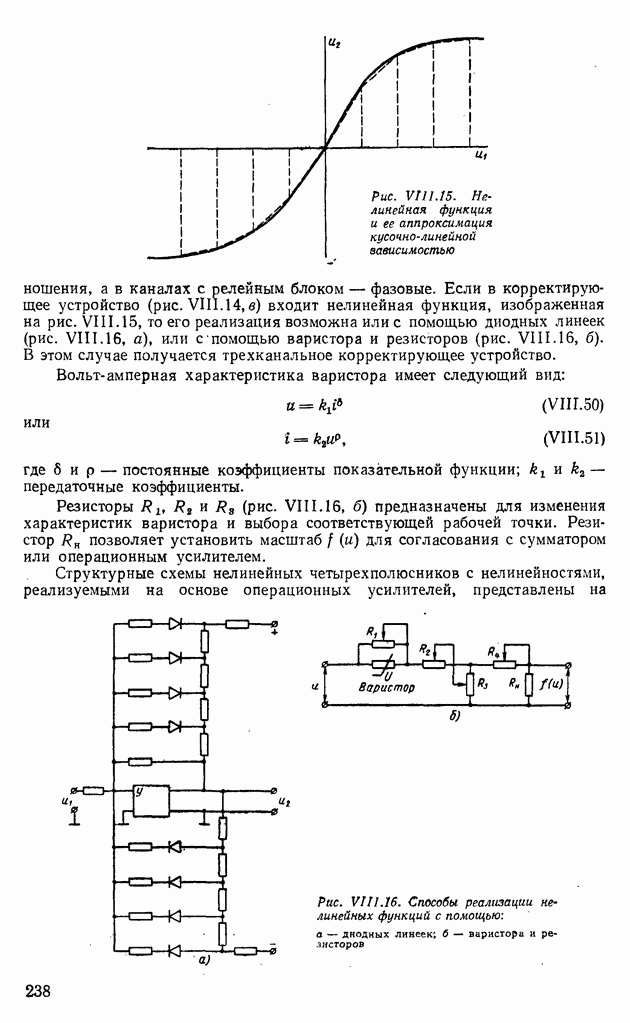
- Глава VIII. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. НЕЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 3. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 4. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ЛИНИЯХ ЗАДЕРЖЕК И ДИСКРЕТНЫХ ЭЛЕМЕНТАХ
- Глава IX. УРАВНЕНИЯ ДИНАМИКИ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- 1. ПРЕДСТАВЛЕНИЕ ОБЪЕКТОВ И УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С СОСРЕДОТОЧЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
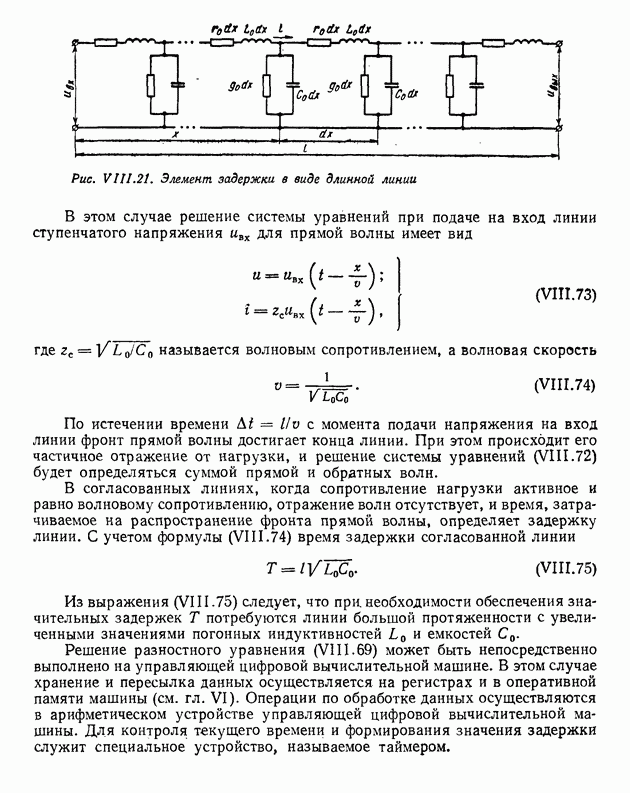
- 2. ПРЕДСТАВЛЕНИЕ УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С РАСПРЕДЕЛЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ТРАНСЦЕДЕНТНЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 3. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
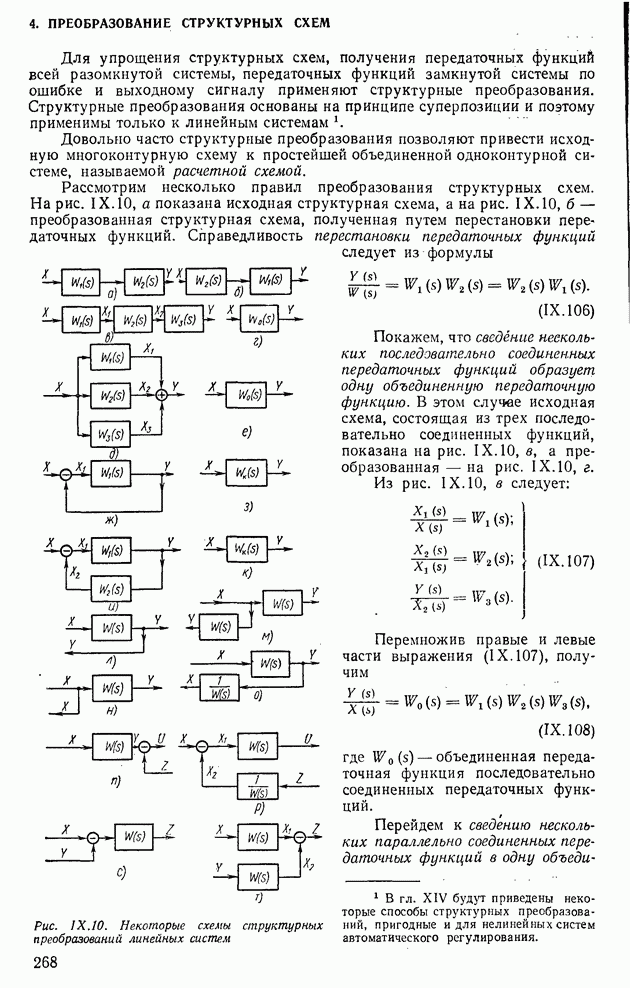
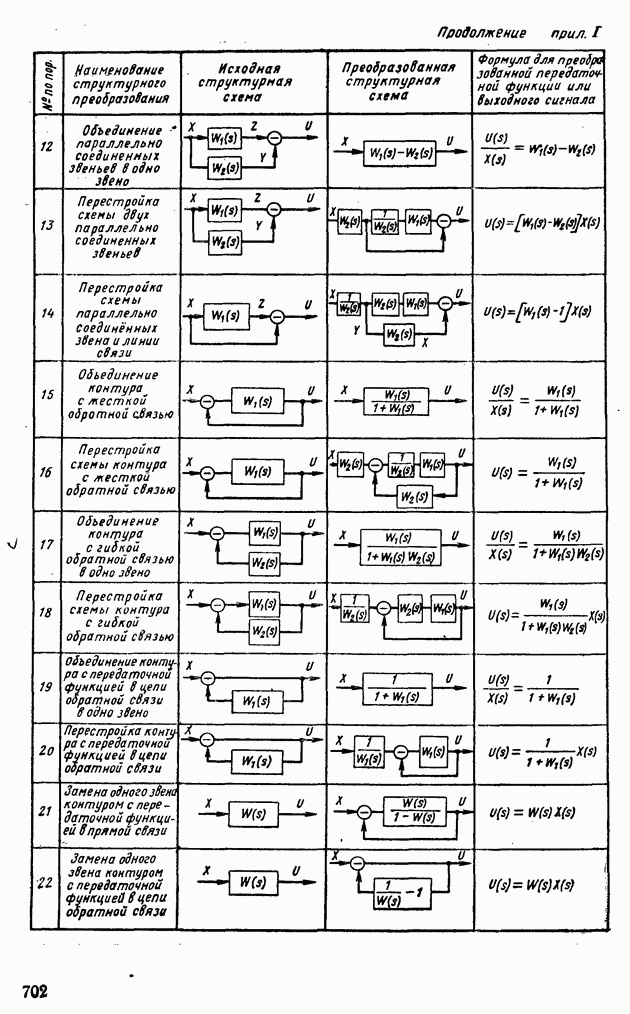
- 4. ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ
- 5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ОПИСАНИЕ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ РЕГУЛИРОВАНИЯ В ВЕКТОРНО-МАТРИЧНОЙ ФОРМЕ
- 7. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 8. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 9. РЕШЕНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ УРАВНЕНИЙ СОСТОЯНИЯ
- 10. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ МАТРИЦ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ ЛИНЕЙНЫХ СИСТЕМ
- 12. ПРЕДСТАВЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ИМПУЛЬСНЫМИ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ
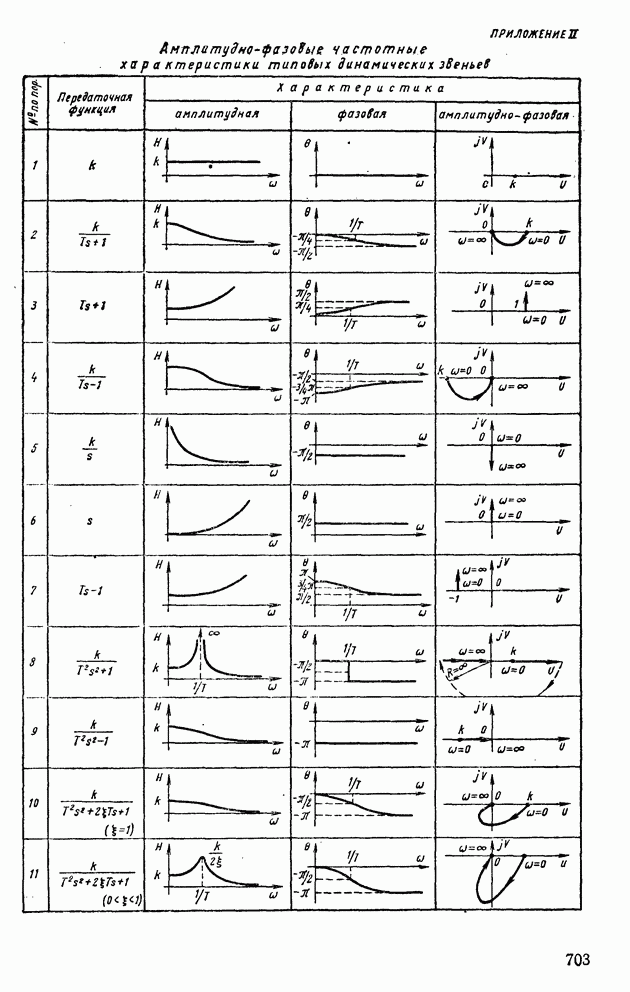
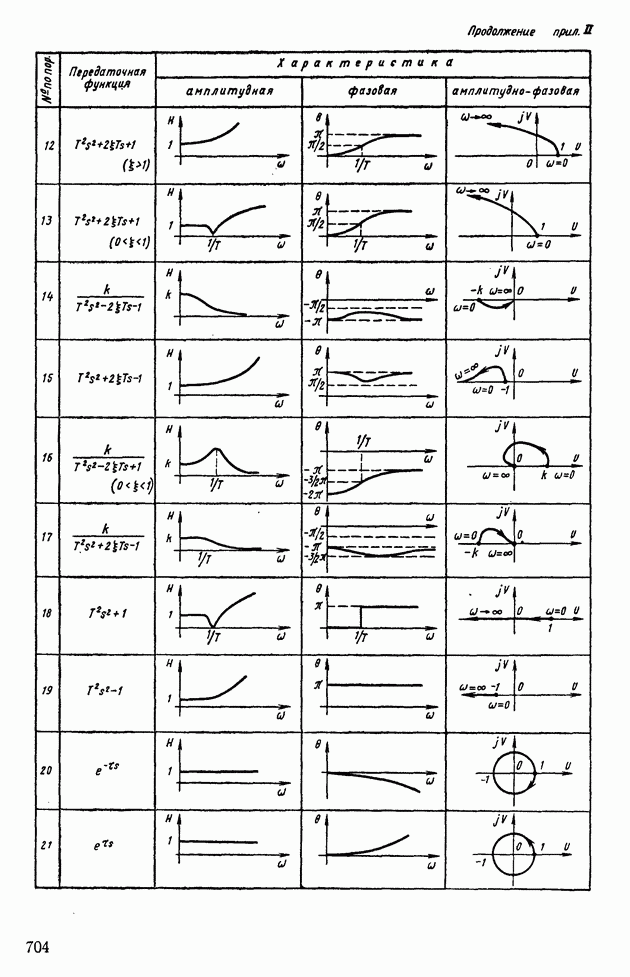
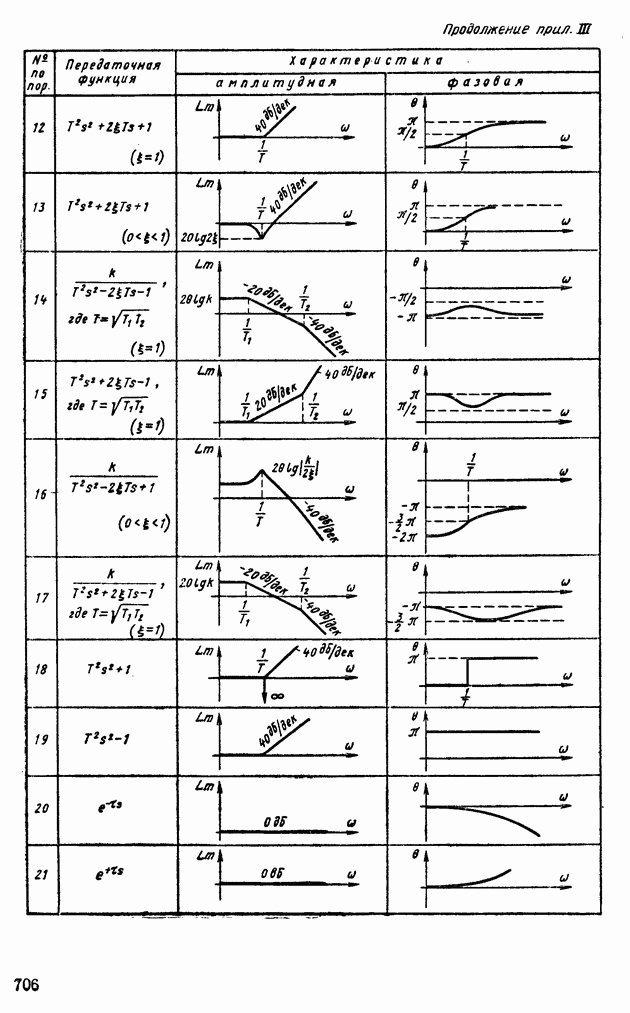
- Глава X. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ АМПЛИТУДНО-ФАЗОВЫЕ И ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 1. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- Логарифмические амплитудная и фазовая частотные характеристики апериодического звена.
- 2. АПЕРИОДИЧЕСКОЕ НЕУСТОЙЧИВОЕ ЗВЕНО
- 4. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 5. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ (УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ)
- 6. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО РОДА
- 7. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО РОДА
- 8. ТРАНСЦЕНДЕНТНЫЕ ЗВЕНЬЯ
- 9. ФАЗОВАЯ ЛИНЕЙКА
- 10. ПОСТРОЕНИЕ АМПЛИТУДНО-ФАЗОВЫХ И ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ ГРУПП ТИПОВЫХ ЗВЕНЬЕВ
- 11. ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ВИДА ПЕРЕДАТОЧНЫХ ФУНКЦИЙ И ПАРАМЕТРОВ ГРУПП ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
- ГЛАВА XI. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ
- 2. ОПРЕДЕЛЕНИЕ ФУНКЦИЙ ЛЯПУНОВА МЕТОДАМИ Г. СЕГЕ И Д. ШУЛЬЦА
- 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 5. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 6. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ТРАНСЦЕНДЕНТНЫМИ ЗВЕНЬЯМИ
- 9. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ С ПОМОЩЬЮ D-РАЗБИЕНИЯ
- Глава XII. ИССЛЕДОВАНИЕ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
- 2. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПО ЗАДАННЫМ ПЕРЕДАТОЧНЫМ ФУНКЦИЯМ ЗАМКНУТЫХ СИСТЕМ
- 3. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПО РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ ЛЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ
- 4. МЕТОД КОРНЕВОГО ГОДОГРАФА
- 5. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА
- 6. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ СИСТЕМ РЕГУЛИРОВАНИЯ И ИХ СВЯЗЬ С ХАРАКТЕРИСТИКАМИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 7. ОПРЕДЕЛЕНИЕ ВЕЩЕСТВЕННЫХ И МНИМЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СИСТЕМ ПО АМПЛИТУДНО-ФАЗОВЫМ И ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ РАЗОМКНУТЫХ СИСТЕМ
- 8. ЧАСТОТНЫЕ ОЦЕНКИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9. ЧАСТОТНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ТРАПЕЦЕИДАЛЬНЫХ ХАРАКТЕРИСТИК
- 10. УСТАНОВЛЕНИЕ НОРМ ЗАПАСОВ УСТОЙЧИВОСТИ ПО ФАЗЕ И МОДУЛЮ, ОБЕСПЕЧИВАЮЩИХ ТРЕБУЕМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМ РЕГУЛИРОВАНИЯ
- ГЛАВА XIII. ДИНАМИЧЕСКАЯ ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ОШИБОК В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ АМПЛИТУДНЫХ ХАРАКТЕРИСТИК
- 3. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПУТЕМ ПРИМЕНЕНИЯ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ
- 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 5. СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ СТАЦИОНАРНЫХ ПРОЦЕССОВ
- 6. СВОЙСТВА СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ
- 7. ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ
- 8. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЛИНЕЙНЫМИ СИСТЕМАМИ
- 9. РАСЧЕТ ОШИБОК В СИСТЕМЕ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ШУМОВ
- 10. ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ВОЗДЕЙСТВИИ СЛУЧАЙНЫХ СИГНАЛОВ И ШУМОВ
- ГЛАВА XIV. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ТИПОВЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ ПО ВТОРОМУ МЕТОДУ ЛЯПУНОВА
- 3. АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
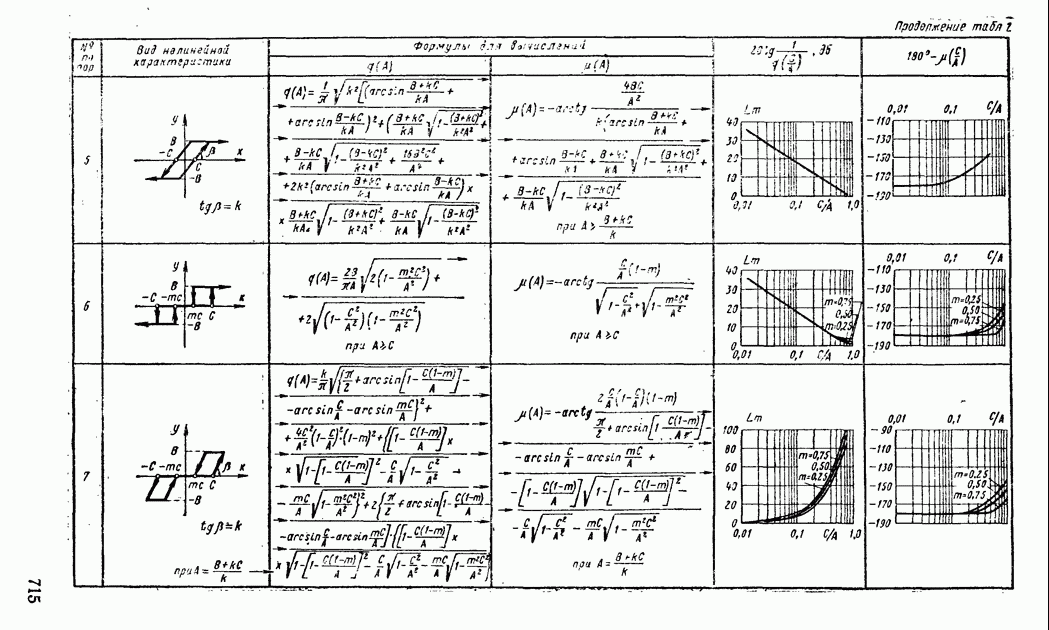
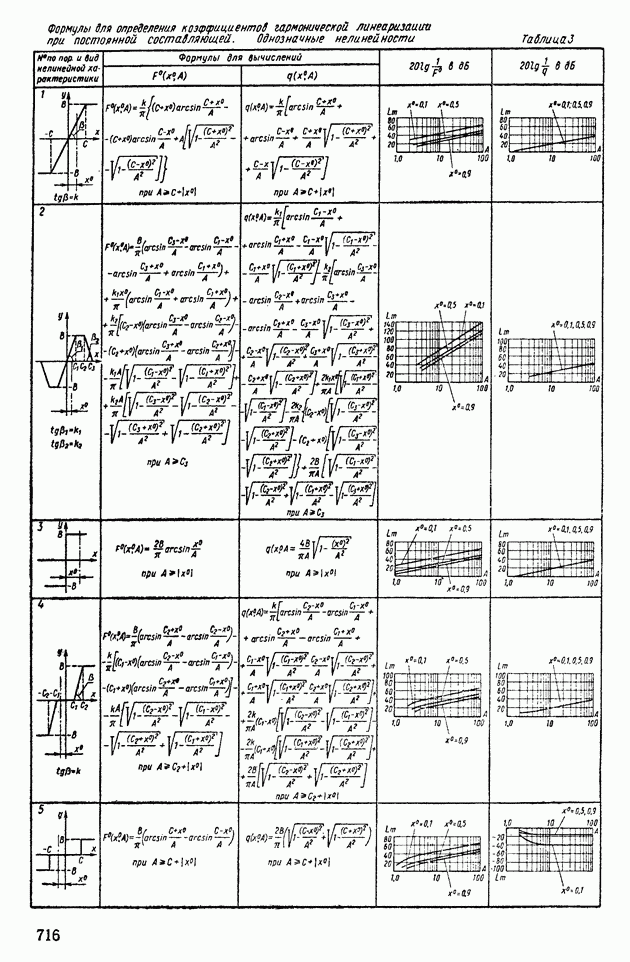
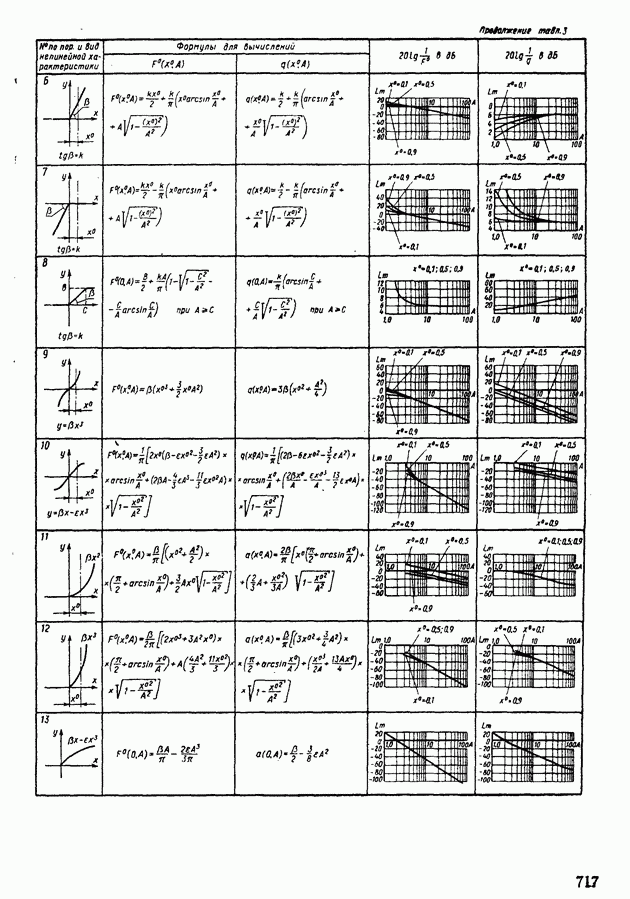
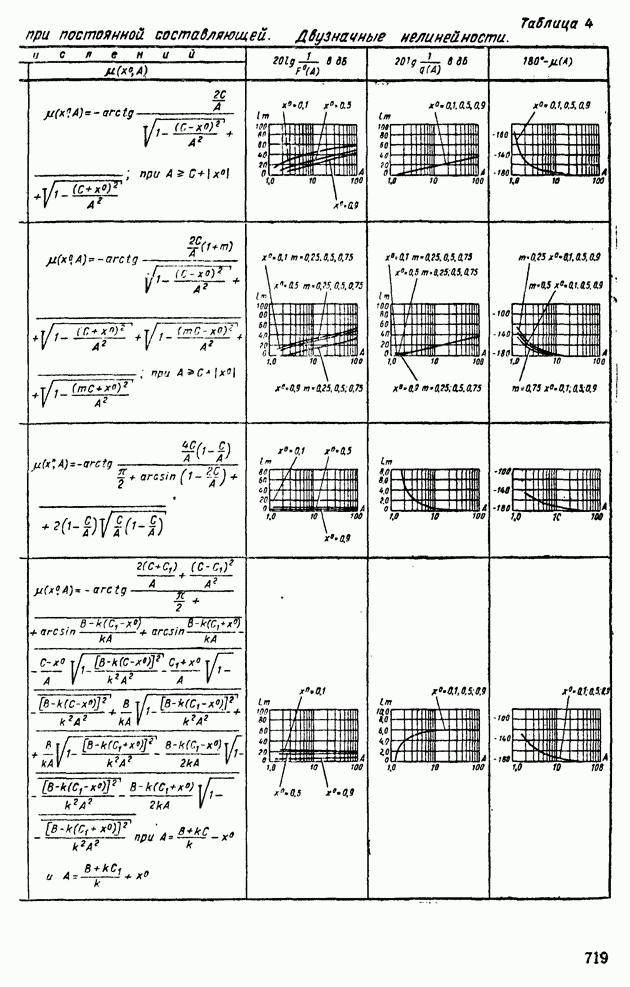
- 4. ПРИМЕНЕНИЕ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. АНАЛИЗ АВТОКОЛЕБАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДВУМЯ НЕЛИНЕЙНОСТЯМИ
- 7. ДВУХКОНТУРНЫЕ НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕДЛЕННО ИЗМЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
- 9. СПОСОБЫ ПОДАВЛЕНИЯ АВТОКОЛЕБАНИЙ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 10. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 11. КРИТЕРИЙ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
- 12. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- Глава XIV. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ИМПУЛЬСНЫХ УСТРОЙСТВ
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. АМПЛИТУДНО-ФАЗОВЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ СИСТЕМ
- 4. ПРИМЕНЕНИЕ ВЕКТОРНО-МАТРИЧНОГО АППАРАТА К ИМПУЛЬСНЫМ СИСТЕМАМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ОСНОВНЫЕ СВОЙСТВА z-ПРЕОБРАЗОВАНИЯ
- 6. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Критерий устойчивости для импульсных систем на плоскостях z и W(z).
- Критерий устойчивости Шур—Кона.
- Критерии устойчивости, основанные на применении билинейного преобразования.
- 7. МЕТОДЫ АНАЛИЗА КАЧЕСТВА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕТОДЫ АНАЛИЗА ТОЧНОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 9. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С УПРАВЛЯЮЩИМИ ЦВМ
- 10. СПОСОБЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ В УПРАВЛЯЮЩИХ ЦВМ И ОПРЕДЕЛЕНИЕ ИХ ОСНОВНЫХ ПАРАМЕТРОВ
- Глава XVI. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МЕТОДЫ ПОИСКА ЭКСТРЕМУМА
- 2. СПОСОБЫ ОРГАНИЗАЦИИ ДВИЖЕНИЯ К ЭКСТРЕМУМУ
- 3. МЕТОДЫ РАСЧЕТА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРОВ
- 4. ВЫБОР КОРРЕКТИРУЮЩИХ УСТРОЙСТВ В ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРАХ
- 5. ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ С ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ
- Глава XVII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ ВОЗДЕЙСТВИЯХ
- 2. ВЫБОР ПАРАМЕТРОВ УСТРОЙСТВ НЕИЗМЕНЯЕМОЙ ЧАСТИ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ПОСТРОЕНИЕ ЖЕЛАЕМОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 4. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. СИНТЕЗ ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 6. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
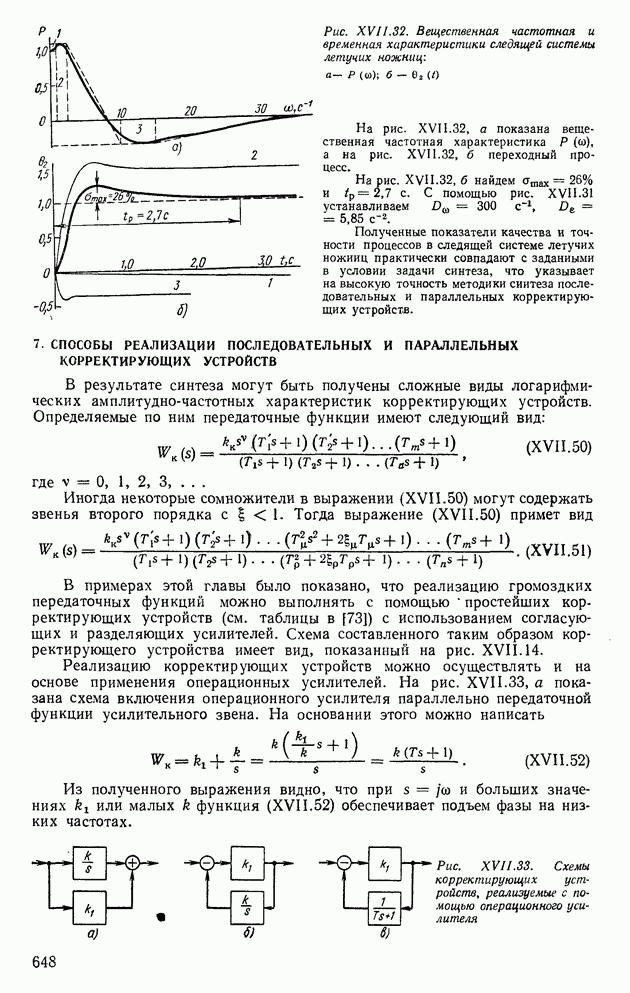
- 7. СПОСОБЫ РЕАЛИЗАЦИИ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Глава XVIII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 1. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА НА ОСНОВЕ КРИТЕРИЯ МИНИМУМА ИНТЕГРАЛЬНОЙ ОШИБКИ
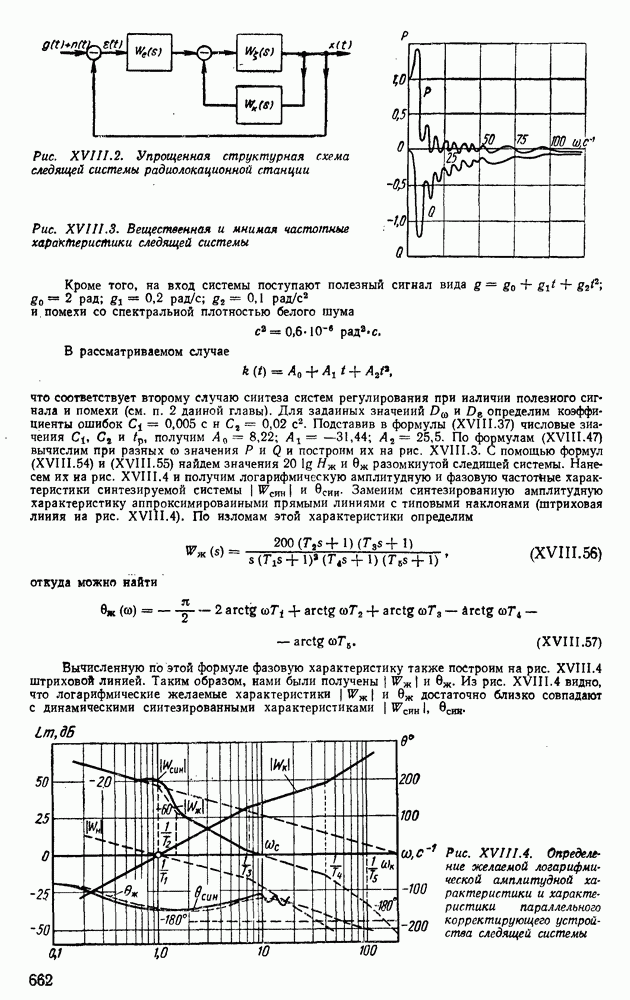
- 2. СИНТЕЗ СИСТЕМ РЕГУЛИРОВАНИЯ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЖЕЛАЕМОЙ СИСТЕМЫ
- 4. ПРИМЕР СИНТЕЗА КОРРЕКТИРУЮЩИХ УСТРОЙСТВ СИСТЕМЫ РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- ГЛАВА XIX. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИНТЕЗ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ, ОСНОВАННЫЙ НА ПРИМЕНЕНИИ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- 2. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. РЕАЛИЗАЦИЯ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ ПРИ ПОМОЩИ RC-ЦЕПЕЙ
- 4. РЕАЛИЗАЦИЯ ПРОГРАММ КОРРЕКЦИИ НА УПРАВЛЯЮЩЕЙ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- ГЛАВА XX. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ПРИНЦИП МАКСИМУМА
- 3. ТЕОРЕМА О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
- 4. ПРИМЕРЫ ПРИМЕНЕНИЯ ПРИНЦИПА МАКСИМУМА
- 5. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 6. СИНТЕЗ НЕПРЕРЫВНЫХ ОПТИМАЛЬНЫХ СИСТЕМ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ