| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
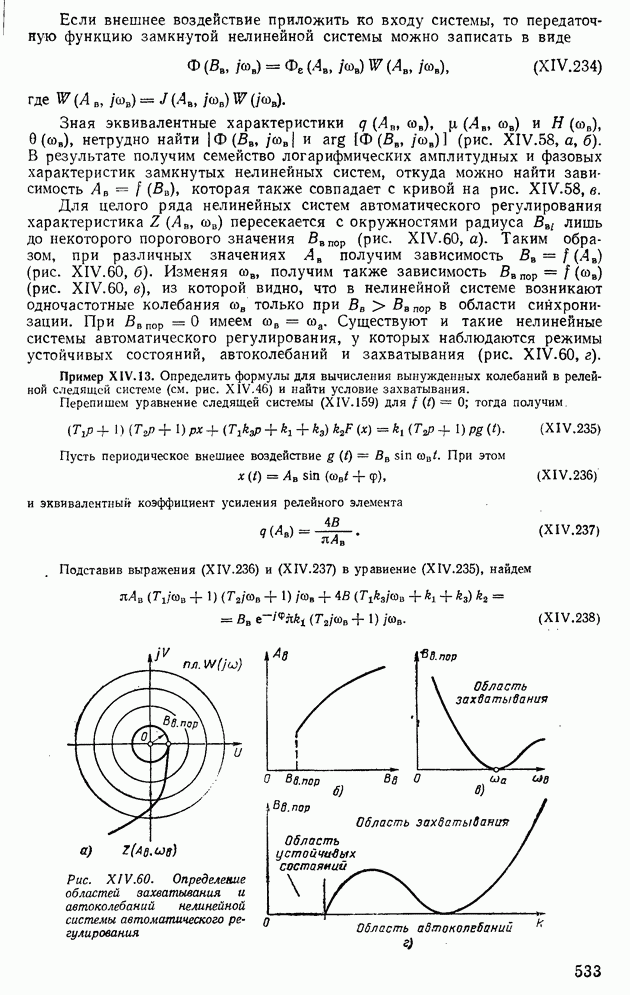
4. УСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (ДИЗЕЛЬ, ГИДРОТУРБИНА, САМОЛЕТ)
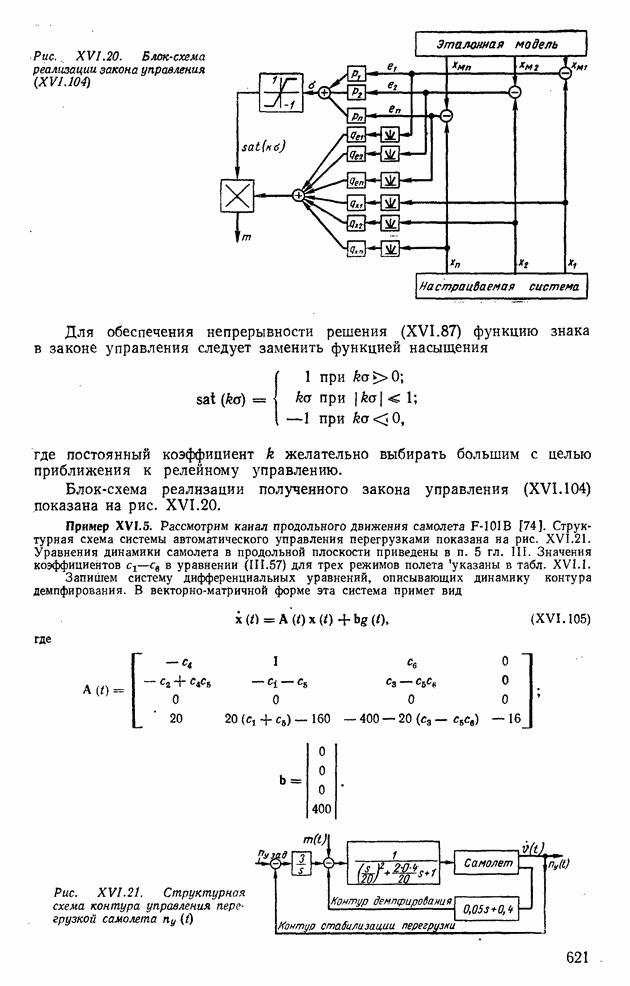
В качестве устойчивых статических объектов регулирования будем рассматривать дизель, гидротурбину и самолет. Уравнение динамики для дизеля будем составлять с помощью экспериментально снятых характеристик, для гидротурбины — аналитическим путем, а для самолета — аналитически с применением некоторых экспериментальных характеристик.
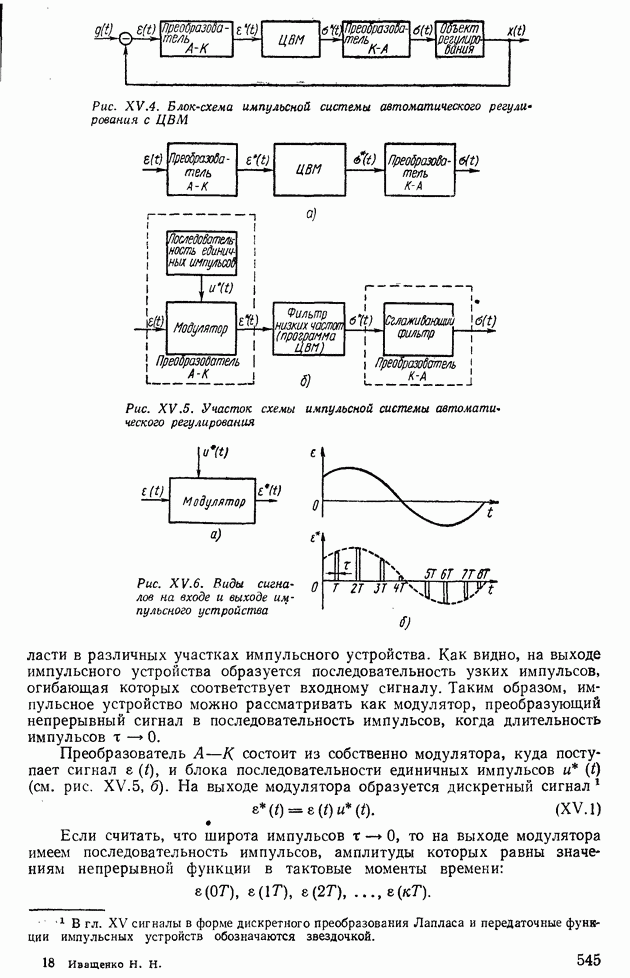
Дизель. В дизеле в зависимости от перемещения рейки топливного насоса (рис. II 1.3) происходит изменение движущего момента. На валу дизеля имеется момент сопротивления от нагрузки. Разность движущего момента и момента сопротивления расходуется только на ускорение (замедление)

Рис. 111.3. Схема дизеля

Рис. III.4. Экспериментальные характеристики дизеля: а — движущего момента при четырех различных положениях рейки топливного насоса; б — момента сопротивления
выходного вала дизеля. Приведенный к валу дизеля суммарный момент инерции всех масс можно считать постоянным. В этом случае уравнение вращающихся масс дизеля можно записать в виде

где  — момент инерции всех вращающихся масс, приведенный к выходному валу дизеля;
— момент инерции всех вращающихся масс, приведенный к выходному валу дизеля;  — угловая скорость вращения вала дизеля;
— угловая скорость вращения вала дизеля;  — движущий момент на валу дизеля;
— движущий момент на валу дизеля;  — момент сопротивления на валу дизеля.
— момент сопротивления на валу дизеля.
Экспериментальные характеристики движущего момента от угловой скорости вращения выходного вала со при различных положениях рейки I топливного насоса показаны на рис. II 1.4, а. Пользуясь этим рисунком, можно написать, что

Момент сопротивления изменяется в зависимости от угловой скорости вращения вала двигателя. Его характеристика показана на рис. III.4, б, т. е.

Из приведенных характеристик  видно, что они не имеют разрывов и плавно изменяются, поэтому допустима их линеаризация. Для линеаризации этих зависимостей нанесем характеристику момента сопротивления на двигательные характеристики, как это показано на рис. III.5. В точке пересечения характеристик
видно, что они не имеют разрывов и плавно изменяются, поэтому допустима их линеаризация. Для линеаризации этих зависимостей нанесем характеристику момента сопротивления на двигательные характеристики, как это показано на рис. III.5. В точке пересечения характеристик  при некотором значении I получим новое начало координат
при некотором значении I получим новое начало координат  Тогда новая ось абсцисс, пересекая старую ось ординат, отсечет на ней установившееся значение моментов; движущего
Тогда новая ось абсцисс, пересекая старую ось ординат, отсечет на ней установившееся значение моментов; движущего  и сопротивления
и сопротивления 
Новая ось ординат пересечет старую ось абсцисс и отсечет на ней установившееся значение угловой скорости вращения вала дизеля 
Рассматривая малые отклонения переменных от принятых установившихся значений, запишем


Рис. III.5. Характеристики  с наложенной на них характеристикой
с наложенной на них характеристикой 

Рис. III.6. Характеристики дизеля: а -  при четырех значениях
при четырех значениях  ; б - изменение угловой скорости вращения вала от времени относительно установившегося значения
; б - изменение угловой скорости вращения вала от времени относительно установившегося значения
Имея это в виду, разложим в ряд Тейлора правые части уравнений (III.25) и (III.26):

Для линеаризации нелинейных уравнений (II 1.25) и (III.26) воспользуемся лишь линейными членами в выражениях (III.28) и (III.29); тогда

где  — тангенс наклона касательной к кривой
— тангенс наклона касательной к кривой  построенной в зависимости от со, в точке
построенной в зависимости от со, в точке  установившегося режима дизеля (рис. III.5);
установившегося режима дизеля (рис. III.5);  — тангенс наклона касательной к кривой
— тангенс наклона касательной к кривой  построенной в зависимости от I, в точке установившегося режима работы дизеля (точка
построенной в зависимости от I, в точке установившегося режима работы дизеля (точка  на рис. III.6, a);
на рис. III.6, a);  — тангенс наклона касательной к кривой
— тангенс наклона касательной к кривой  в точке установившегося режима дизеля (см. рис. II
в точке установившегося режима дизеля (см. рис. II 
В процессе регулирования характеристики  используются при изменении нагрузки не на всем протяжении изменения со и
используются при изменении нагрузки не на всем протяжении изменения со и  а лишь в определенных пределах. Пределы изменения со выделены на рис. III.5 штрих-пунктирными линиями. Тогда можно считать, что в зависимости от времени угловая скорость вала изменяется относительно установившегося значения
а лишь в определенных пределах. Пределы изменения со выделены на рис. III.5 штрих-пунктирными линиями. Тогда можно считать, что в зависимости от времени угловая скорость вала изменяется относительно установившегося значения  на малую величину (рис. III.6, б), и реальные нелинейные характера
на малую величину (рис. III.6, б), и реальные нелинейные характера  стики в определенных пределах изменения переменных можно заменить линейными. Такая замена нелинейной характеристики называется линеаризацией характеристик. Подставим выражения (III.30) и (III.31) в уравнение (II 1.24); тогда получим
стики в определенных пределах изменения переменных можно заменить линейными. Такая замена нелинейной характеристики называется линеаризацией характеристик. Подставим выражения (III.30) и (III.31) в уравнение (II 1.24); тогда получим

Уравнение установившегося режима будет 

Учитывая Соотношение (III.33), уравнение (III.32) можно записать в виде

Выражение (III.34) представляет собой линеаризованное уравнение динамики дизеля в приращениях. Все коэффициенты данного уравнения имеют размерность. В теории автоматического регулирования уравнения динамики принято записывать с безразмерными коэффициентами (за исключением йостоянных времени). Для этого уравнение (III.34) представим в форме

где  — положение рейки топливного насоса, соответствующее
— положение рейки топливного насоса, соответствующее  . Преобразуем уравнение (III.35) к виду
. Преобразуем уравнение (III.35) к виду

Введем в уравнение (II 1.36) следующие обозначения:

Тогда получим окончательную форму уравнения динамики дизеля

где  — постоянная времени дизеля в секундах;
— постоянная времени дизеля в секундах;  — передаточный коэффициент дизеля (безразмерная величина).
— передаточный коэффициент дизеля (безразмерная величина).
Проанализируем коэффициенты уравнения (111.37). Коэффициент  всегда больше нуля (рис. III.6, а), Но
всегда больше нуля (рис. III.6, а), Но  может быть больше или меньше нуля в зависимости от соотношения наклонов характеристик.
может быть больше или меньше нуля в зависимости от соотношения наклонов характеристик.
При  уравнение (III.32) приводится к виду
уравнение (III.32) приводится к виду

Если  рассматриваемый режим работы дизеля является устойчивым, при
рассматриваемый режим работы дизеля является устойчивым, при  — неустойчивым, а при
— неустойчивым, а при  — нейтрально-устойчивым. В нормальных эксплуатационных режимах работы дизель как объект регулирования является устойчивым, т. е. обеспечивается условие
— нейтрально-устойчивым. В нормальных эксплуатационных режимах работы дизель как объект регулирования является устойчивым, т. е. обеспечивается условие 

Рис. 111.7. Схема гидротурбины
Гидротурбина. В ряде случаев для объекта регулирования не представляется возможным пользоваться экспериментальными характеристиками  и
и  Тогда можно получить линейные дифференциальные уравнения объекта регулирования, пользуясь аналитическими выражениями. Рассмотрим это на примере гидравлической турбины, схема которой показана на рис. III.7.
Тогда можно получить линейные дифференциальные уравнения объекта регулирования, пользуясь аналитическими выражениями. Рассмотрим это на примере гидравлической турбины, схема которой показана на рис. III.7.
Вода из водоема 1 через короткий 1 канал 2 поступает к колесу гидротурбины 4. Количество воды регулируется направляющим аппаратом 3, изображенным на рис. III.7 в виде заслонки. На валу гидротурбины установлен турбогенератор 5. Слив воды происходит через канал 6.
Уравнение движения ротора гидротурбины запишем в виде уравнения типа (III.24). Движущий момент зависит от скорости  течения воды в канале, величины z открытия направляющего аппарата 3 и угловой скорости
течения воды в канале, величины z открытия направляющего аппарата 3 и угловой скорости  вращения колеса гидротурбины, т. е.
вращения колеса гидротурбины, т. е.

где  — коэффициент, зависящий от конструкции гидротурбины.
— коэффициент, зависящий от конструкции гидротурбины.
Уравнение (III.39) является нелинейным. Линеаризуем его с помощью разложения в ряд Тейлора по степеням со,  и
и  отбрасывая члены разложения второго и более высоких порядков малости. При этом будем считать, что скорость течения воды в канале постоянна; тогда
отбрасывая члены разложения второго и более высоких порядков малости. При этом будем считать, что скорость течения воды в канале постоянна; тогда

где  .
.
Уравнение (II 1.40) приведем к виду

Момент сопротивления представим в виде

где  — установившийся момент сопротивления на валу гидротурбины;
— установившийся момент сопротивления на валу гидротурбины;  — момент от изменения нагрузки на гидротурбине за счет мгновенного подключения или отключения потребителей электроэнергии, т. е.
— момент от изменения нагрузки на гидротурбине за счет мгновенного подключения или отключения потребителей электроэнергии, т. е.

Для определенности будем считать, что часть нагрузки отключилась; тогда в уравнение (111.24) можно подставить зависимости (111.42) и (111.44):

В установившемся состоянии  тогда уравнение турбины в приращениях примет вид
тогда уравнение турбины в приращениях примет вид

Номинальными значениями для гидротурбины будем считать следующие:  Имея это в виду, перепишем уравнения (III.46):
Имея это в виду, перепишем уравнения (III.46):

Введем в уравнение (III.47) следующие обозначения:

после чего получим

Данное уравнение гидротурбины является линейным дифференциальным уравнением первого порядка.
Самолет. Движение самолета в вертикальной плоскости описывается двумя уравнениями сил и одним уравнением моментов. Все силы, действующие на самолет, приведем к центру масс (точка О на рис. II 1.8), а моменты — к моментам относительно поперечной оси самолета, проходящей через точку О. При составлении уравнений будем пользоваться следующими допущениями: влияние действия потока от крыла на оперение самолета незначительно и им можно пренебречь;
колебания угловой скорости поперечной оси на величину аэродинамической силы влияния не оказывают;
влиянием ошибок стабилизации по крену можно пренебречь; моменты, создаваемые силой тяги двигателя, можно не учитывать. Тогда уравнение проекции сил на касательную к траектории полета самолета (ось  ) будет иметь вид
) будет иметь вид

где  — масса самолета;
— масса самолета;  — сила тяги двигателя, направленная по оси
— сила тяги двигателя, направленная по оси  — площадь крыльев самолета;
— площадь крыльев самолета;  — коэффициент лобового сопротивления самолета, отнесенный к площади крыльев;
— коэффициент лобового сопротивления самолета, отнесенный к площади крыльев;  — соответственно углы вектора скорости и атаки;
— соответственно углы вектора скорости и атаки;  — плотность воздуха;
— плотность воздуха;  — ускорение свободного падения.
— ускорение свободного падения.
Составим уравнение сил, действующих на самолет по нормали к траектории его полета:

где  — коэффициент подъемной силы, отнесенный к площади крыльев.
— коэффициент подъемной силы, отнесенный к площади крыльев.

Рис. III.8. Схематический вид самолета

Рис. III.9. Типовые зависимости  для самолета от числа М
для самолета от числа М

Рис. III.10. Типовые зависимости изменения тяги турбореактивного двигателя от высоты полета Н и числа М
Уравнение моментов относительно поперечной оси  зэпищем в виде
зэпищем в виде

где  — момент инерции самолета относительно оси;
— момент инерции самолета относительно оси;  — средняя аэродинамическая хорда крыла;
— средняя аэродинамическая хорда крыла;  — угол тангажа;
— угол тангажа;  — коэффициент момента всех сил, действующих на самолет;
— коэффициент момента всех сил, действующих на самолет;  — угол отклонения руля высоты.
— угол отклонения руля высоты.
К уравнениям аэродинамики добавим зависимость, связывающую угловые параметры самолета:

Параметры  зависят от скорости полета самолета.
зависят от скорости полета самолета.
Типовые графики зависимостей  от числа М показаны на рис. III.9. В зависимости от условий полета (числа М и высоты полета Н) изменяются тяговые характеристики турбореактивного двигателя. На рис.
от числа М показаны на рис. III.9. В зависимости от условий полета (числа М и высоты полета Н) изменяются тяговые характеристики турбореактивного двигателя. На рис.  показаны кривые изменения тяги турбореактивного двигателя от М и Н. Зависимости
показаны кривые изменения тяги турбореактивного двигателя от М и Н. Зависимости  при учете графиков, приведенных на рис. III.9 и III.10, представляют собой нелинейные уравнения с переменными коэффициентами. Непосредственное их использование для анализа систем управления самолетом вызывает большие трудности. Для их преодоления применяют метод линеаризации, при котором уравнения динамики полета самолета рассматривают в отклонениях от некоторой «опорной» траектории полета (см. п. 3 гл. III).
при учете графиков, приведенных на рис. III.9 и III.10, представляют собой нелинейные уравнения с переменными коэффициентами. Непосредственное их использование для анализа систем управления самолетом вызывает большие трудности. Для их преодоления применяют метод линеаризации, при котором уравнения динамики полета самолета рассматривают в отклонениях от некоторой «опорной» траектории полета (см. п. 3 гл. III).
Опорную траекторию можно найти методом численного интегрирования следующей системы уравнений:

Решая эту систему уравнений, получаем опорные параметры полета самолета при  Последнее соотношение справедливо лишь на некотором участке полета (см. рис. III.10). Опорные параметры
Последнее соотношение справедливо лишь на некотором участке полета (см. рис. III.10). Опорные параметры  траектории будут
траектории будут  Имея это в виду, уравнения динамики
Имея это в виду, уравнения динамики
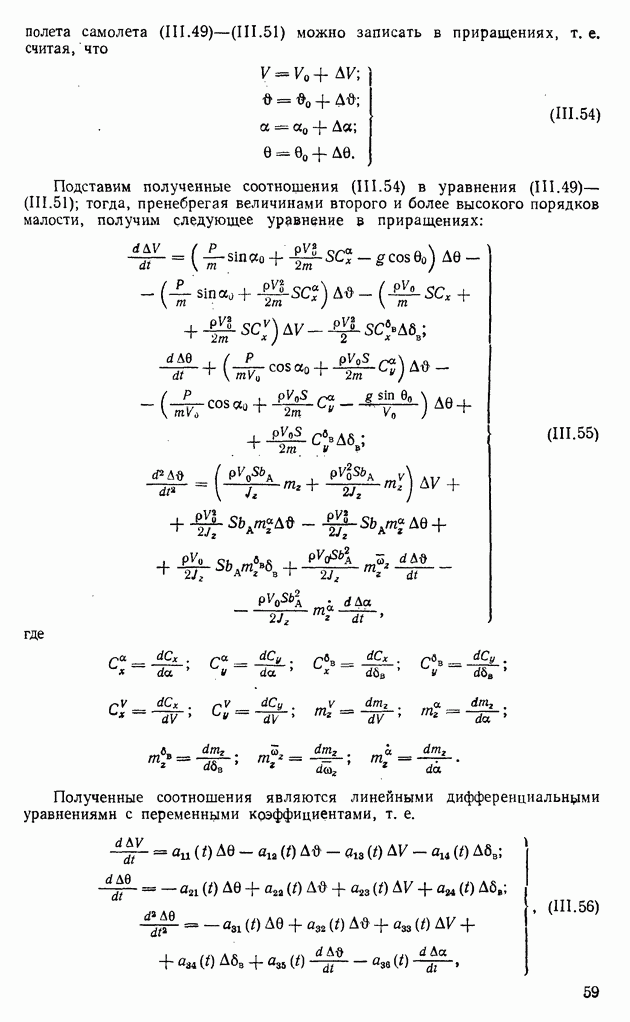
полета самолета (III.49)-(III.51) можно записать в приращениях, т. е. считая, что

Подставим полученные соотношения (III.54) в уравнения (III.49) - (III.51); тогда, пренебрегая величинами второго и более высокого порядков малости, получим следующее уравнение в приращениях:

где

Полученные соотношения являются линейными дифференциальными уравнениями с переменными коэффициентами, т. е.

где
(см. скан)
Характеристики самолета  показаны на рис. III.11, a и б [72].
показаны на рис. III.11, a и б [72].
Из динамики полета самолета известно [43], что движение его центра масс в направлении полета практически не зависит от движения относиг тельно центра масс. В этом случае можно пренебречь первым уравнением (III.56) и некоторыми членами уравнений, а также считать, что 

Рис. III.11. Типовые характеристики  для самолета
для самолета

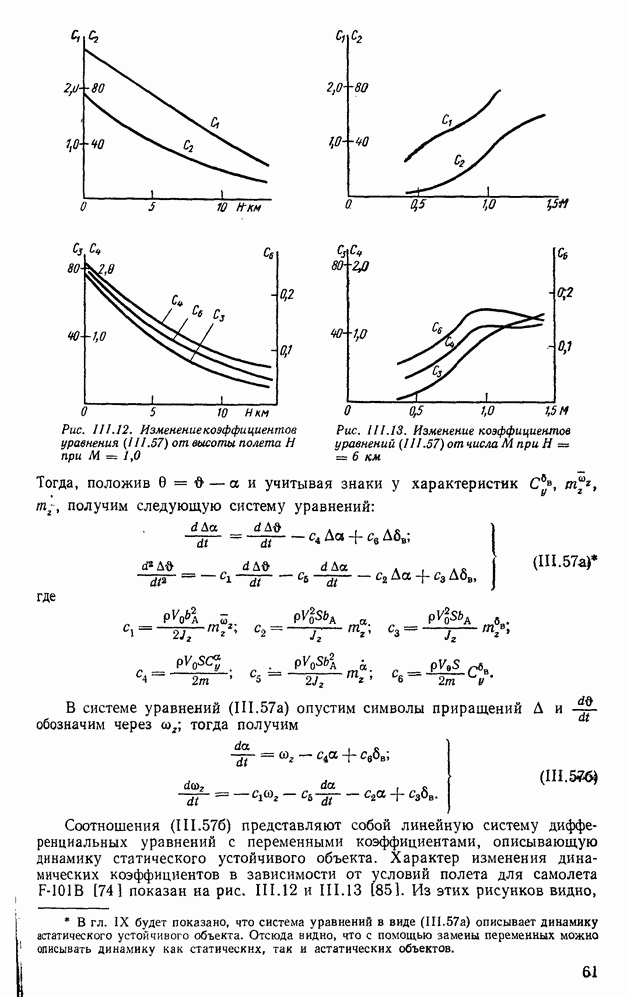
Рис. III.12. Изменение коэффициентов уравнения  от высоты, полета Н при
от высоты, полета Н при 

Рис. 111.13. Изменение коэффициентов уравнений (III.57) от чист М при  .
.
Тогда, положив  — а и учитывая знаки у характеристик
— а и учитывая знаки у характеристик  получим следующую систему уравнений:
получим следующую систему уравнений:

где

В системе уравнений (III.57а) опустим символы приращений  и обозначим через
и обозначим через  тогда получим
тогда получим

Соотношения (III.576) представляют собой линейную систему дифференциальных уравнений с переменными коэффициентами, описывающую динамику статического устойчивого объекта. Характер изменения динамических коэффициентов в зависимости от условий полета для самолета  показан на рис. III.12 и III.13 185]. Из этих рисунков видно,
показан на рис. III.12 и III.13 185]. Из этих рисунков видно,
что на некоторых достаточно малых участках полета самолета эти коэффициенты можно считать постоянными (не зависящими от времени) (см. гл. IX). Такой способ в теории регулирования принято называть методом «замораживания» коэффициентов [72]. Существуют такие режимы полета самолета, например набор высоты или снижение, при которых происходит быстрое изменение коэффициентов. В этих случаях метод «замораживания» коэффициентов неприменим, и анализ системы управления самолетом приходится выполнять на аналоговых или цифровых электронных вычислительных машинах.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 1. ПРИНЦИПЫ ДЕЙСТВИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
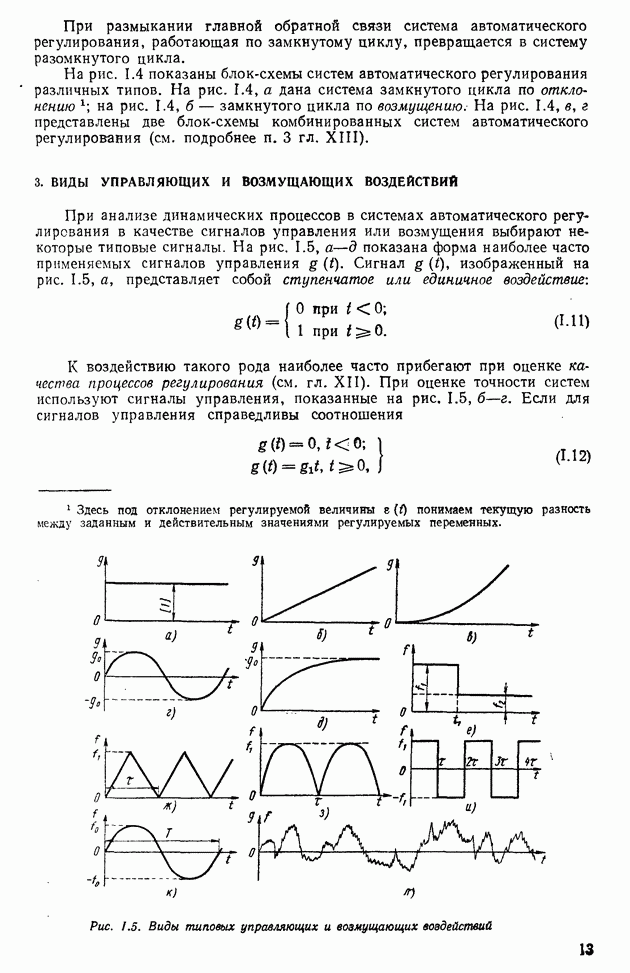
- 3. ВИДЫ УПРАВЛЯЮЩИХ И ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ
- 4. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Глава II. ВИДЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛТРОВАНИЯ
- 1. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
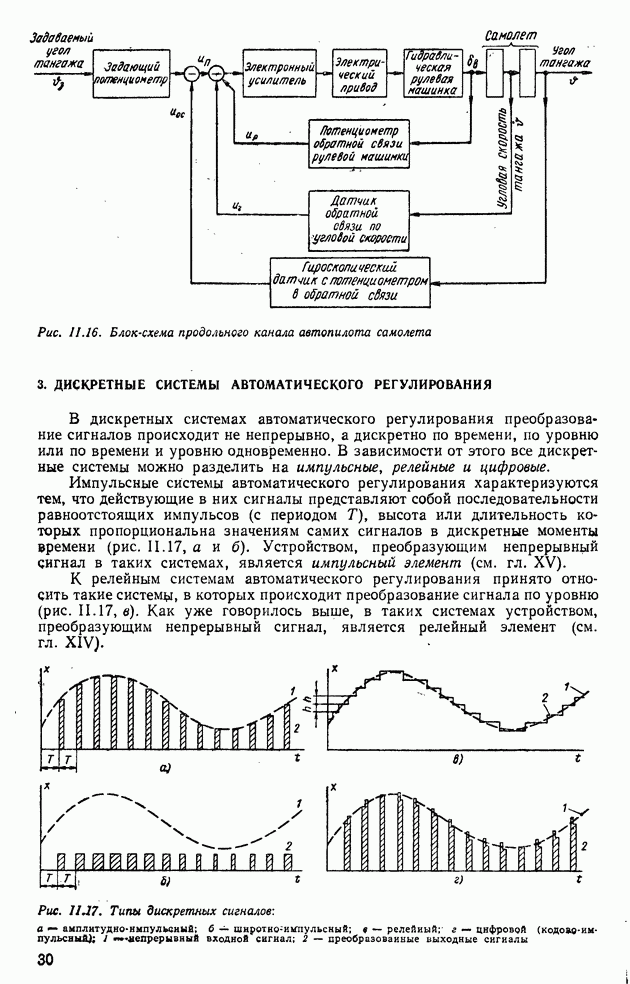
- 3. ДИСКРЕТНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ПРИМЕНЕНИЕ ЦВМ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
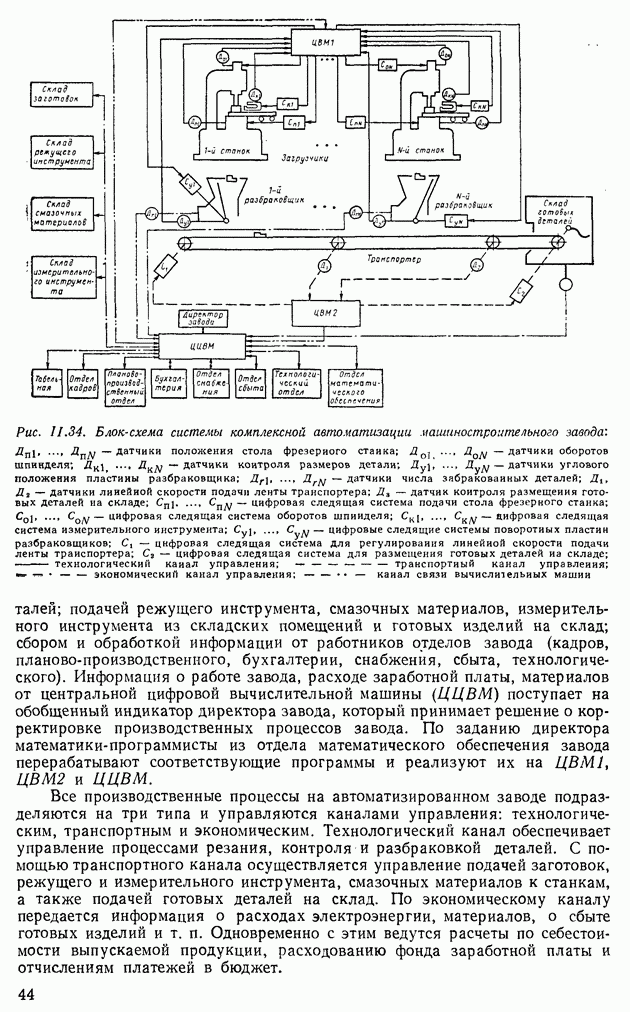
- 7. ПРИМЕНЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ДЛЯ УПРАВЛЕНИЯ СЛОЖНЫМИ ПРОИЗВОДСТВЕННЫМИ ПРОЦЕССАМИ. СИСТЕМЫ КОМПЛЕКСНОЙ АВТОМАТИЗАЦИИ ПРОИЗВОДСТВА
- Глава III. ОБЪЕКТЫ РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ СВОЙСТВА ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 2. ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 3. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ ДИНАМИКИ
- 4. УСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (ДИЗЕЛЬ, ГИДРОТУРБИНА, САМОЛЕТ)
- 5. НЕУСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (РЕСИВЕР, РАКЕТА-НОСИТЕЛЬ КОСМИЧЕСКИХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ)
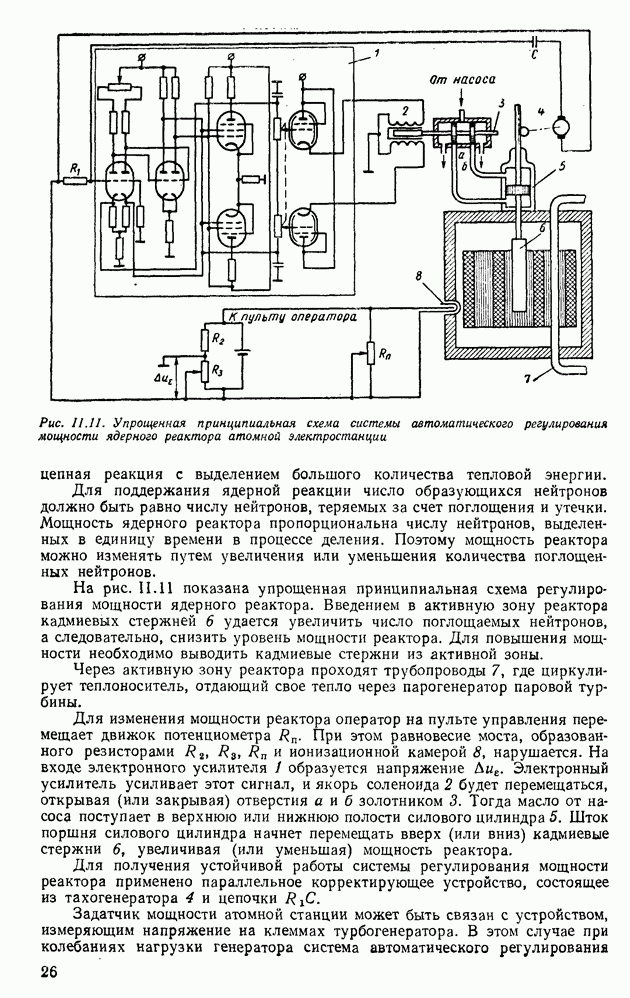
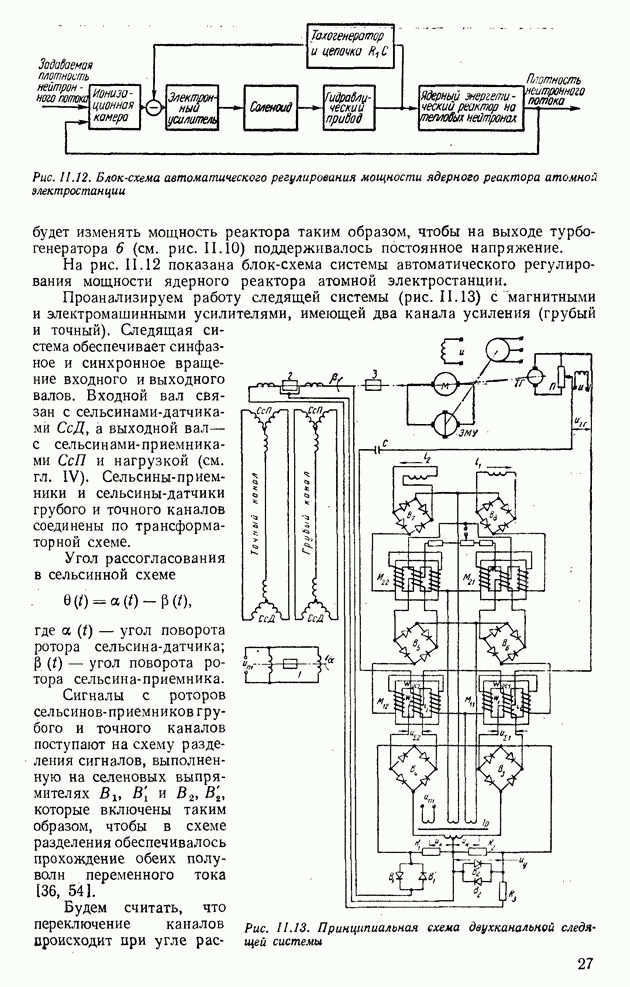
- 6. АСТАТИЧЕСКИЕ ОБЪЕКТЫ (ТРЕХФАЗНЫЙ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ, ЯДЕРНЫЙ ЭНЕРГЕТИЧЕСКИЙ РЕАКТОР НА ТЕПЛОВЫХ НЕЙТРОНАХ, КОСМИЧЕСКИЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ)
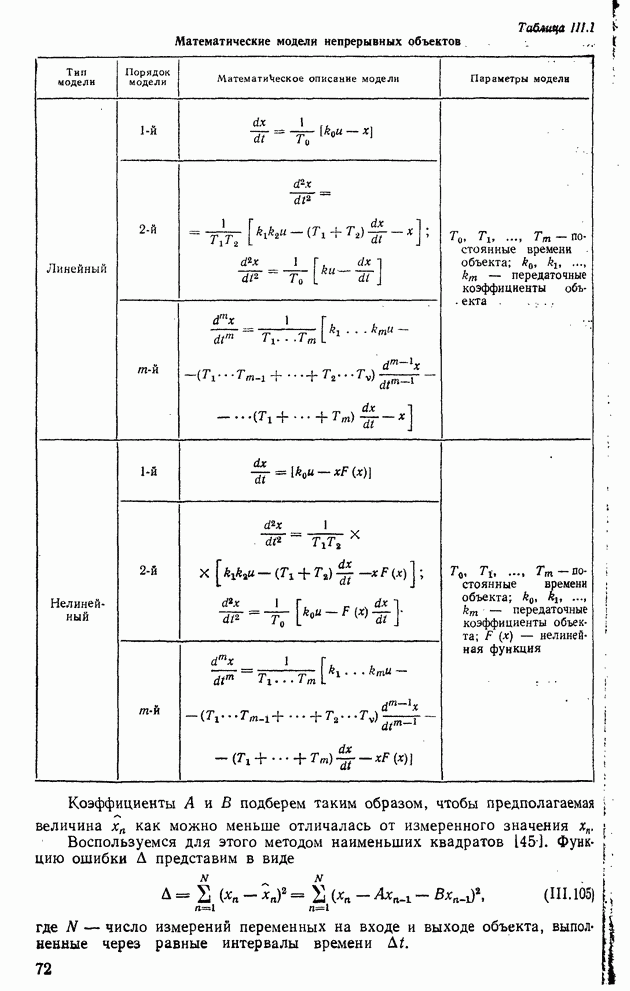
- 7. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- Глава IV. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОПРЕДЕЛЕНИЕ ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ИЗМЕРИТЕЛЬНЫХ ПОДСИСТЕМ
- 2. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Индуктивные устройства.
- Емкостные устройства.
- Сельсины.
- Дифференциальный сельсин.
- Погрешность сельсинов.
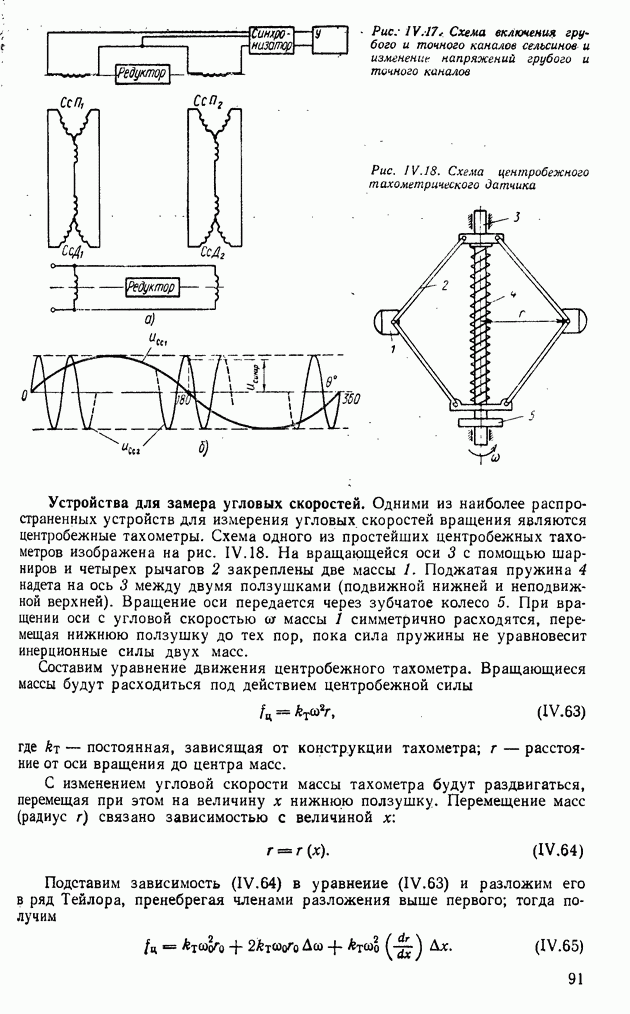
- Устройства для замера угловых скоростей.
- Устройства замера угловых ускорений.
- 4. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И ТОКА
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕМПЕРАТУР И ИЗЛУЧЕНИЙ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЙ И РАСХОДОВ ЖИДКОСТИ И ГАЗА
- 7. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ ВЕЛИЧИН, УГЛОВЫХ СКОРОСТЕЙ И ЛИНЕЙНЫХ УСКОРЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ
- Устройства для измерения линейных ускорений подвижных объектов (акселерометры).
- 8. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- Глава V. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ
- 2. МАГНИТНЫЕ УСИЛИТЕЛИ
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 4. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 5. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ РАЗЛИЧНЫХ УСИЛИТЕЛЕЙ
- ГЛАВА VI. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА
- 1. УСИЛИТЕЛИ-ПРЕОБРАЗОВАТЕЛИ
- 2. РЕЛЕ
- 3. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. ПРЕОБРАЗОВАТЕЛИ АНАЛОГ—КОД
- 5. ПРЕОБРАЗОВАТЕЛИ КОД—АНАЛОГ
- 6. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ УПРАВЛЯЮЩИЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
- 8. ПНЕВМАТИЧЕСКИЕ АНАЛОГОВЫЕ И ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 9. ТОЧНОСТЬ РАБОТЫ И БЫСТРОДЕЙСТВИЕ УПРАВЛЯЮЩИХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
- 10. СРАВНИТЕЛЬНАЯ ОЦЕНКА ПРЕОБРАЗУЮЩИХ УСТРОЙСТВ
- Глава VII. ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 1. ЭЛЕКТРИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 2. МЕХАНИЧЕСКИЕ ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. ГИДРАВЛИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 4. ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 5. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- 6. СРАВНИТЕЛЬНАЯ ОЦЕНКА ИСПОЛНИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- Глава VIII. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
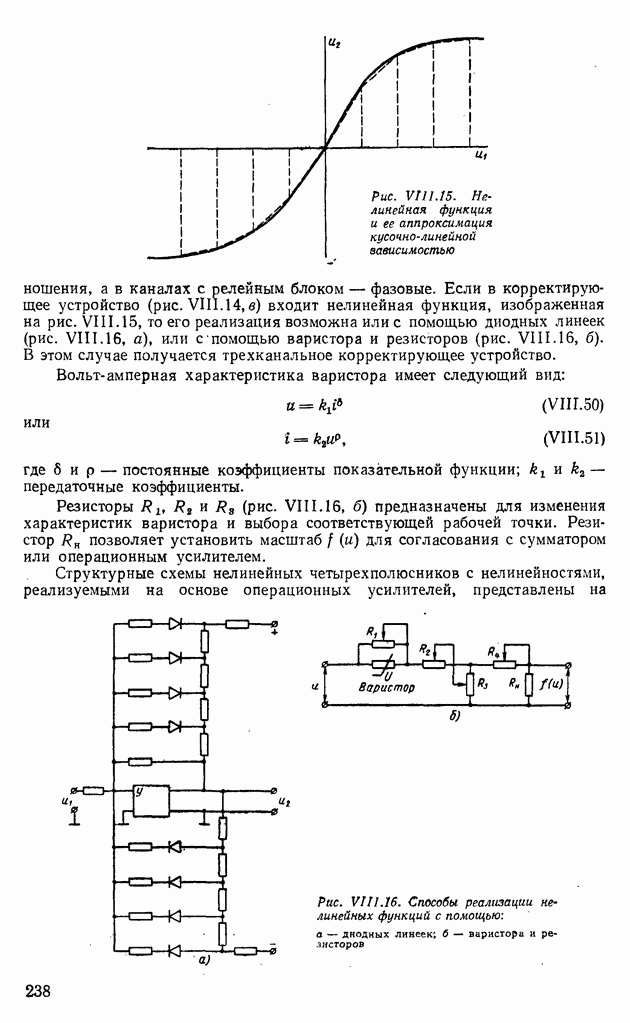
- 2. НЕЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 3. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
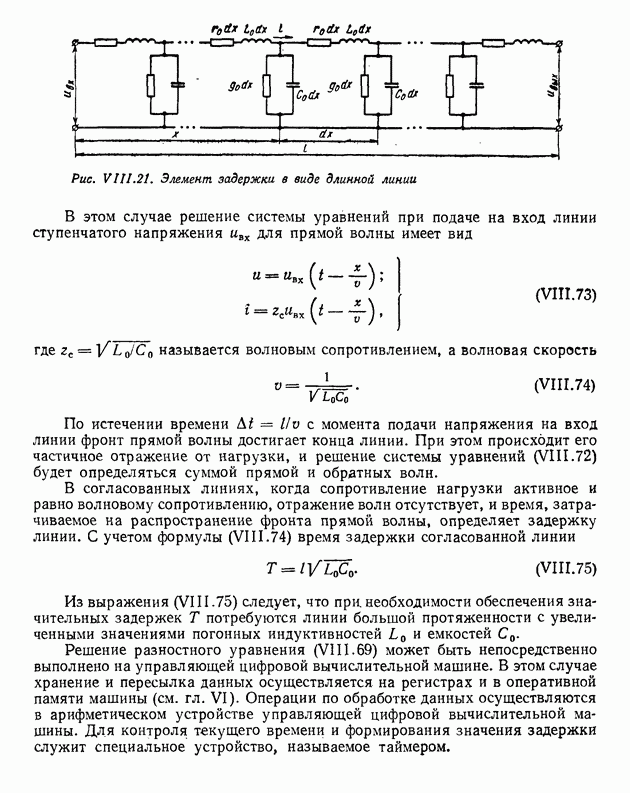
- 4. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ЛИНИЯХ ЗАДЕРЖЕК И ДИСКРЕТНЫХ ЭЛЕМЕНТАХ
- Глава IX. УРАВНЕНИЯ ДИНАМИКИ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- 1. ПРЕДСТАВЛЕНИЕ ОБЪЕКТОВ И УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С СОСРЕДОТОЧЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 2. ПРЕДСТАВЛЕНИЕ УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С РАСПРЕДЕЛЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ТРАНСЦЕДЕНТНЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 3. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
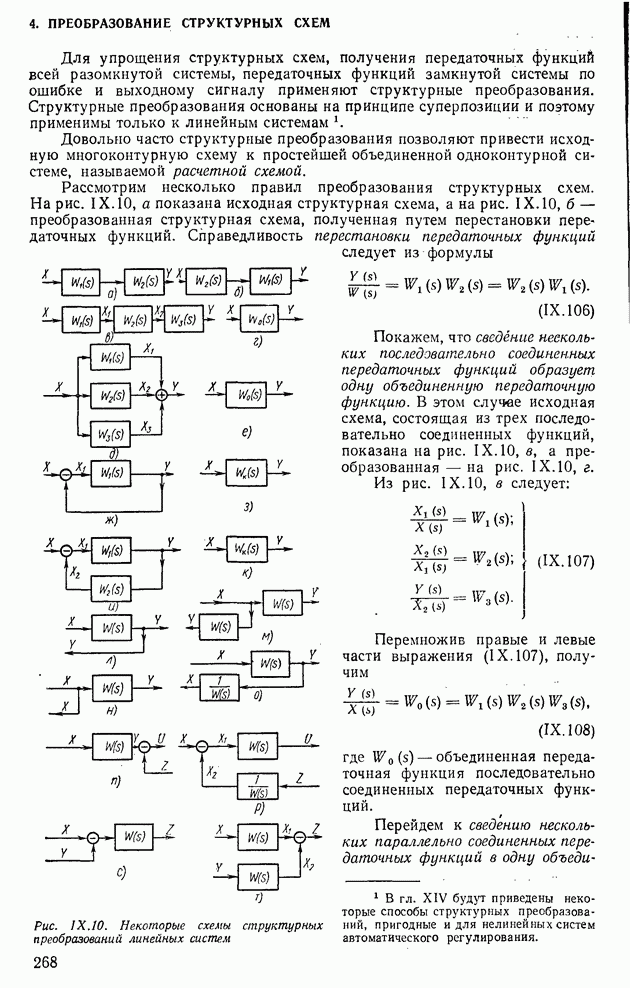
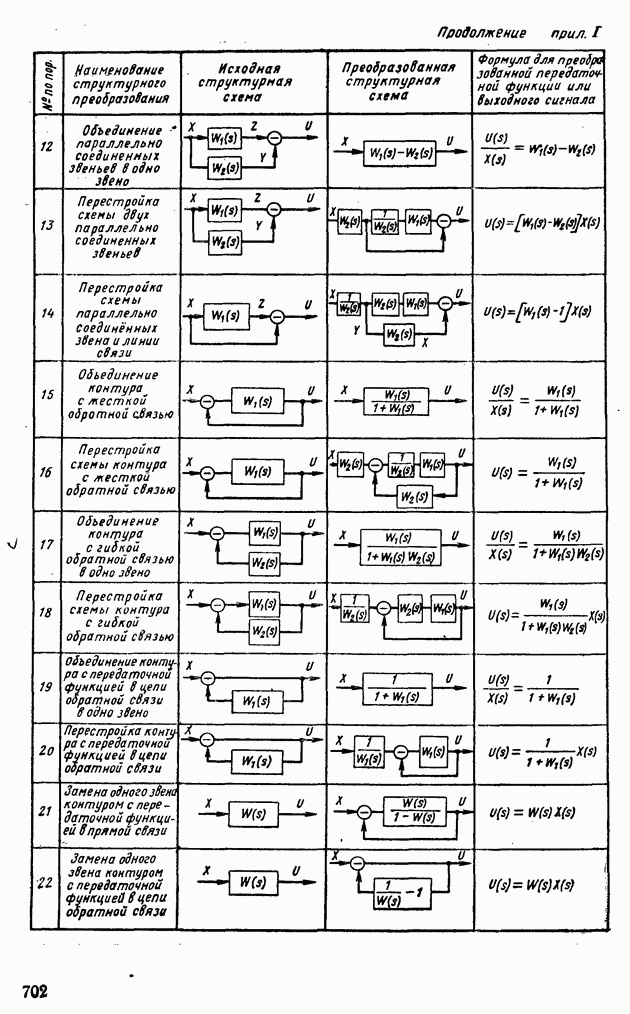
- 4. ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ
- 5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ОПИСАНИЕ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ РЕГУЛИРОВАНИЯ В ВЕКТОРНО-МАТРИЧНОЙ ФОРМЕ
- 7. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 8. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 9. РЕШЕНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ УРАВНЕНИЙ СОСТОЯНИЯ
- 10. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ МАТРИЦ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ ЛИНЕЙНЫХ СИСТЕМ
- 12. ПРЕДСТАВЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ИМПУЛЬСНЫМИ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ
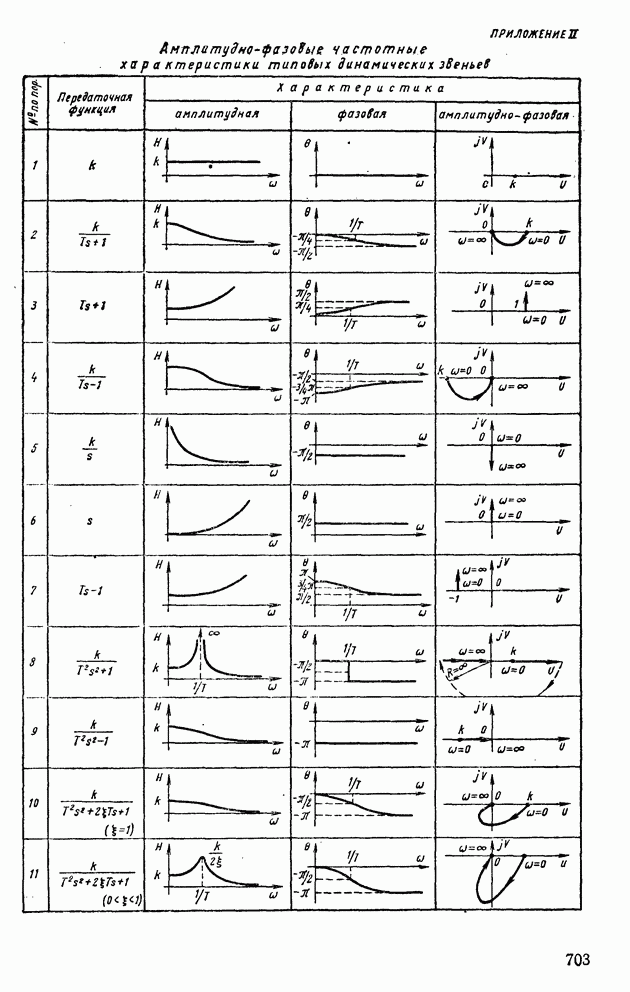
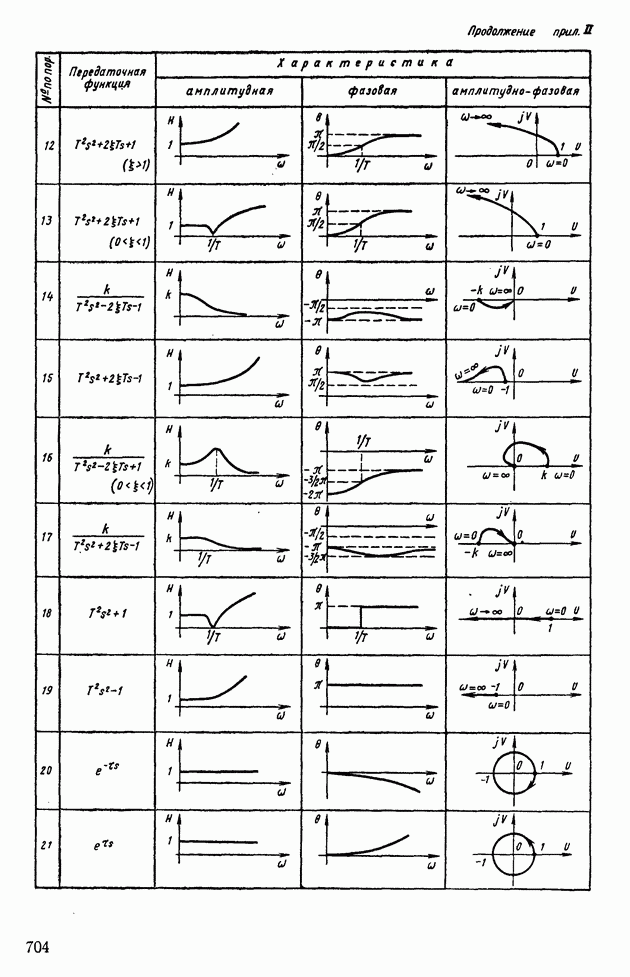
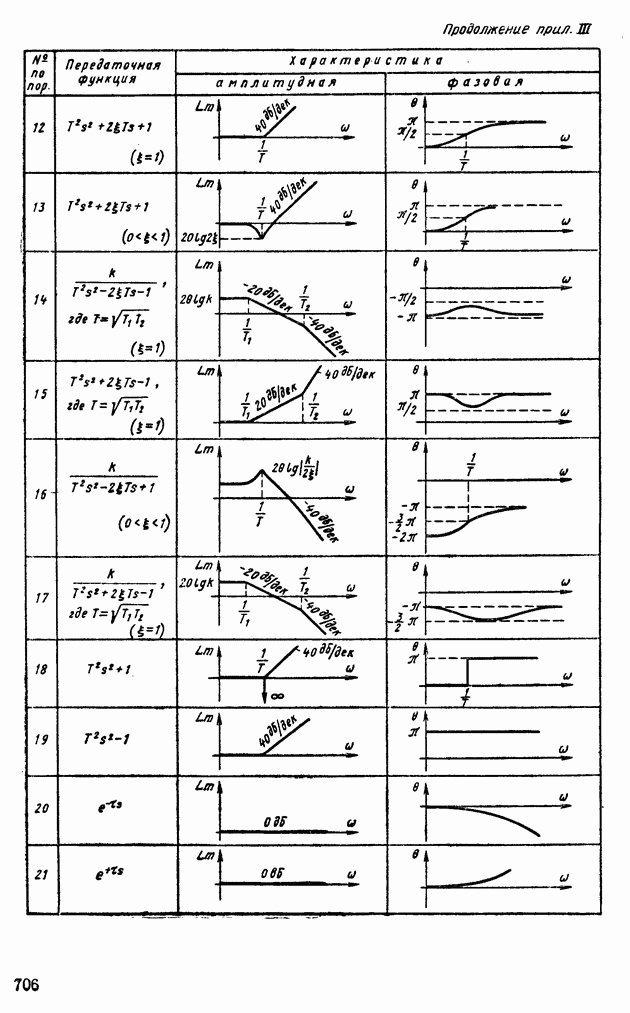
- Глава X. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ АМПЛИТУДНО-ФАЗОВЫЕ И ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 1. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- Логарифмические амплитудная и фазовая частотные характеристики апериодического звена.
- 2. АПЕРИОДИЧЕСКОЕ НЕУСТОЙЧИВОЕ ЗВЕНО
- 4. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 5. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ (УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ)
- 6. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО РОДА
- 7. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО РОДА
- 8. ТРАНСЦЕНДЕНТНЫЕ ЗВЕНЬЯ
- 9. ФАЗОВАЯ ЛИНЕЙКА
- 10. ПОСТРОЕНИЕ АМПЛИТУДНО-ФАЗОВЫХ И ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ ГРУПП ТИПОВЫХ ЗВЕНЬЕВ
- 11. ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ВИДА ПЕРЕДАТОЧНЫХ ФУНКЦИЙ И ПАРАМЕТРОВ ГРУПП ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
- ГЛАВА XI. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ
- 2. ОПРЕДЕЛЕНИЕ ФУНКЦИЙ ЛЯПУНОВА МЕТОДАМИ Г. СЕГЕ И Д. ШУЛЬЦА
- 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 5. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 6. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ТРАНСЦЕНДЕНТНЫМИ ЗВЕНЬЯМИ
- 9. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ С ПОМОЩЬЮ D-РАЗБИЕНИЯ
- Глава XII. ИССЛЕДОВАНИЕ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
- 2. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПО ЗАДАННЫМ ПЕРЕДАТОЧНЫМ ФУНКЦИЯМ ЗАМКНУТЫХ СИСТЕМ
- 3. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПО РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ ЛЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ
- 4. МЕТОД КОРНЕВОГО ГОДОГРАФА
- 5. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА
- 6. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ СИСТЕМ РЕГУЛИРОВАНИЯ И ИХ СВЯЗЬ С ХАРАКТЕРИСТИКАМИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 7. ОПРЕДЕЛЕНИЕ ВЕЩЕСТВЕННЫХ И МНИМЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СИСТЕМ ПО АМПЛИТУДНО-ФАЗОВЫМ И ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ РАЗОМКНУТЫХ СИСТЕМ
- 8. ЧАСТОТНЫЕ ОЦЕНКИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9. ЧАСТОТНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ТРАПЕЦЕИДАЛЬНЫХ ХАРАКТЕРИСТИК
- 10. УСТАНОВЛЕНИЕ НОРМ ЗАПАСОВ УСТОЙЧИВОСТИ ПО ФАЗЕ И МОДУЛЮ, ОБЕСПЕЧИВАЮЩИХ ТРЕБУЕМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМ РЕГУЛИРОВАНИЯ
- ГЛАВА XIII. ДИНАМИЧЕСКАЯ ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ОШИБОК В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ АМПЛИТУДНЫХ ХАРАКТЕРИСТИК
- 3. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПУТЕМ ПРИМЕНЕНИЯ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ
- 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 5. СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ СТАЦИОНАРНЫХ ПРОЦЕССОВ
- 6. СВОЙСТВА СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ
- 7. ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ
- 8. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЛИНЕЙНЫМИ СИСТЕМАМИ
- 9. РАСЧЕТ ОШИБОК В СИСТЕМЕ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ШУМОВ
- 10. ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ВОЗДЕЙСТВИИ СЛУЧАЙНЫХ СИГНАЛОВ И ШУМОВ
- ГЛАВА XIV. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ТИПОВЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ ПО ВТОРОМУ МЕТОДУ ЛЯПУНОВА
- 3. АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
- 4. ПРИМЕНЕНИЕ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. АНАЛИЗ АВТОКОЛЕБАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДВУМЯ НЕЛИНЕЙНОСТЯМИ
- 7. ДВУХКОНТУРНЫЕ НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕДЛЕННО ИЗМЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
- 9. СПОСОБЫ ПОДАВЛЕНИЯ АВТОКОЛЕБАНИЙ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 10. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 11. КРИТЕРИЙ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
- 12. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- Глава XIV. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ИМПУЛЬСНЫХ УСТРОЙСТВ
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. АМПЛИТУДНО-ФАЗОВЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ СИСТЕМ
- 4. ПРИМЕНЕНИЕ ВЕКТОРНО-МАТРИЧНОГО АППАРАТА К ИМПУЛЬСНЫМ СИСТЕМАМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ОСНОВНЫЕ СВОЙСТВА z-ПРЕОБРАЗОВАНИЯ
- 6. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Критерий устойчивости для импульсных систем на плоскостях z и W(z).
- Критерий устойчивости Шур—Кона.
- Критерии устойчивости, основанные на применении билинейного преобразования.
- 7. МЕТОДЫ АНАЛИЗА КАЧЕСТВА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕТОДЫ АНАЛИЗА ТОЧНОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 9. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С УПРАВЛЯЮЩИМИ ЦВМ
- 10. СПОСОБЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ В УПРАВЛЯЮЩИХ ЦВМ И ОПРЕДЕЛЕНИЕ ИХ ОСНОВНЫХ ПАРАМЕТРОВ
- Глава XVI. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МЕТОДЫ ПОИСКА ЭКСТРЕМУМА
- 2. СПОСОБЫ ОРГАНИЗАЦИИ ДВИЖЕНИЯ К ЭКСТРЕМУМУ
- 3. МЕТОДЫ РАСЧЕТА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРОВ
- 4. ВЫБОР КОРРЕКТИРУЮЩИХ УСТРОЙСТВ В ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРАХ
- 5. ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ С ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ
- Глава XVII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ ВОЗДЕЙСТВИЯХ
- 2. ВЫБОР ПАРАМЕТРОВ УСТРОЙСТВ НЕИЗМЕНЯЕМОЙ ЧАСТИ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ПОСТРОЕНИЕ ЖЕЛАЕМОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ РЕГУЛИРОВАНИЯ
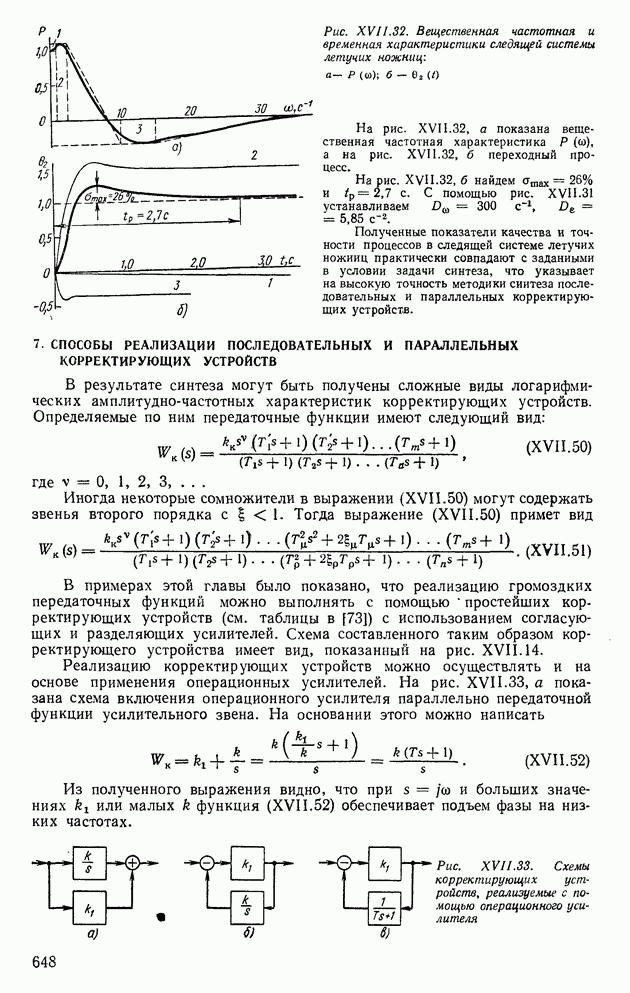
- 4. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. СИНТЕЗ ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 6. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 7. СПОСОБЫ РЕАЛИЗАЦИИ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Глава XVIII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 1. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА НА ОСНОВЕ КРИТЕРИЯ МИНИМУМА ИНТЕГРАЛЬНОЙ ОШИБКИ
- 2. СИНТЕЗ СИСТЕМ РЕГУЛИРОВАНИЯ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЖЕЛАЕМОЙ СИСТЕМЫ
- 4. ПРИМЕР СИНТЕЗА КОРРЕКТИРУЮЩИХ УСТРОЙСТВ СИСТЕМЫ РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- ГЛАВА XIX. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИНТЕЗ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ, ОСНОВАННЫЙ НА ПРИМЕНЕНИИ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- 2. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. РЕАЛИЗАЦИЯ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ ПРИ ПОМОЩИ RC-ЦЕПЕЙ
- 4. РЕАЛИЗАЦИЯ ПРОГРАММ КОРРЕКЦИИ НА УПРАВЛЯЮЩЕЙ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- ГЛАВА XX. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ПРИНЦИП МАКСИМУМА
- 3. ТЕОРЕМА О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
- 4. ПРИМЕРЫ ПРИМЕНЕНИЯ ПРИНЦИПА МАКСИМУМА
- 5. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 6. СИНТЕЗ НЕПРЕРЫВНЫХ ОПТИМАЛЬНЫХ СИСТЕМ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ