| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
7. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Логарифмический критерий устойчивости многоконтурных систем автоматического регулирования можно сформулировать в следующем виде. Для того чтобы многоконтурная система автоматического регулирования, имеющая  неустойчивых звеньев, была устойчивой в замкнутом состоянии, необходимо и достаточно для положительных значений логарифмической амплитудной характеристики иметь разность между числом положительных и отрицательных переходов прямой
неустойчивых звеньев, была устойчивой в замкнутом состоянии, необходимо и достаточно для положительных значений логарифмической амплитудной характеристики иметь разность между числом положительных и отрицательных переходов прямой  всеми фазовыми частотными характеристиками, получаемыми путем последовательного включения каждого из контуров обратной связи, равную
всеми фазовыми частотными характеристиками, получаемыми путем последовательного включения каждого из контуров обратной связи, равную 
Рассмотрим двухконтурную систему автоматического регулирования, структурная схема которой изображена на рис. XI.29, а. Будем считать, что в частотной характеристике  имеется одно неустойчивое звено
имеется одно неустойчивое звено  Для определения устойчивости системы разомкнем обратные связи. Затем построим логарифмические частотные характеристики
Для определения устойчивости системы разомкнем обратные связи. Затем построим логарифмические частотные характеристики  и определим разность между числом положительных и отрицательных переходов фазовой характеристики
и определим разность между числом положительных и отрицательных переходов фазовой характеристики  прямой
прямой  при
при  Допустим, что имеем только один отрицательный переход; тогда получим
Допустим, что имеем только один отрицательный переход; тогда получим 
Построим логарифмические амплитудную и фазовую частотные характеристики после замыкания  контура, имея в виду, что
контура, имея в виду, что

и фазовая характеристика

будет пересекать ось  раза в положительном направлении. Тогда согласно сформулированному выше критерию имеем
раза в положительном направлении. Тогда согласно сформулированному выше критерию имеем  что указывает на устойчивость замкнутой системы автоматического регулирования.
что указывает на устойчивость замкнутой системы автоматического регулирования.
Следствие. Еслн в системе автоматического регулирования отсутствуют неустойчивые звенья, то для ее устойчивости в замкнутом состоянии необходимо и достаточно, чтобы разность между числом положительных и отрицательных переходов оси  всеми логарифмическими фазовыми частотными характеристиками при последовательном включении всех обратных связей для положительных значений частотных характеристик
всеми логарифмическими фазовыми частотными характеристиками при последовательном включении всех обратных связей для положительных значений частотных характеристик  была равна нулю.
была равна нулю.

Рис. XI.29. Структурные схемы для двухконтурной системы автоматического регулирования: а — исходная; б - преобразованная
Как первая, так и вторая формулировка логарифмических критериев устойчивости многоконтурных систем требует определения логарифмических частотных характеристик замкнутых контуров. Например, для системы, изображенной на рис. XI.29, а, частотную характеристику внутреннего контура можно записать в виде

Преобразуем выражение (XI. 114); тогда получим

что соответствует преобразованной структурной схеме, изображенной на рис. XI.29, б. Введем следующее обозначение:

Найдем, что

Прологарифмируем выражение (XI. 116):

Введем новую переменную

связывающую частотную характеристику преобразованного замкнутого контура  с характеристикой разомкнутого контура
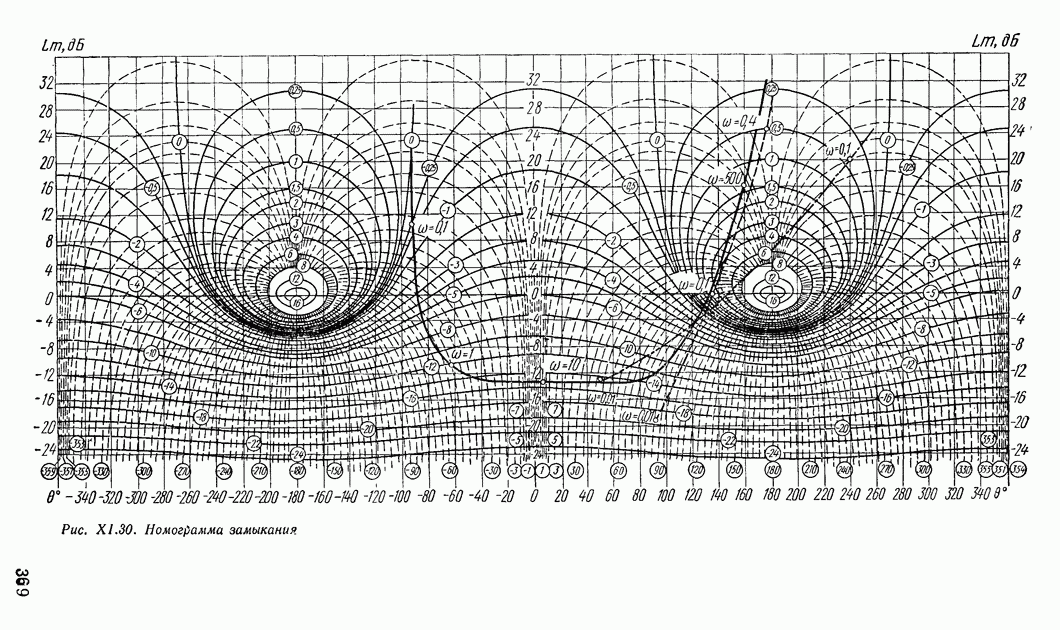
с характеристикой разомкнутого контура  Для определения логарифмических амплитудных и фазовых частотных характеристик разомкнутого контура служит номограмма замыкания (номограмма Никольса). Для ее получения воспользуемся следующими выражениями:
Для определения логарифмических амплитудных и фазовых частотных характеристик разомкнутого контура служит номограмма замыкания (номограмма Никольса). Для ее получения воспользуемся следующими выражениями:

здесь  — амплитудная характеристика разомкнутого контура;
— амплитудная характеристика разомкнутого контура;  — фазовая характеристика разомкнутого контура;
— фазовая характеристика разомкнутого контура;

где  — амплитудная характеристика преобразованного замкнутого контура;
— амплитудная характеристика преобразованного замкнутого контура;  — фазовая характеристика преобразованного замкнутого контура.
— фазовая характеристика преобразованного замкнутого контура.
Подставив выражения (XI.119) и (XI.120) в формулу (XI.118), получим

Воспользуемся формулой Эйлера; тогда соотношение (XI. 121) перепишем в виде

Выделяя в правой части формулы (XI. 122) действительную и мнимую части и приравнивая их соответствующим выражениям левой части, находим

и

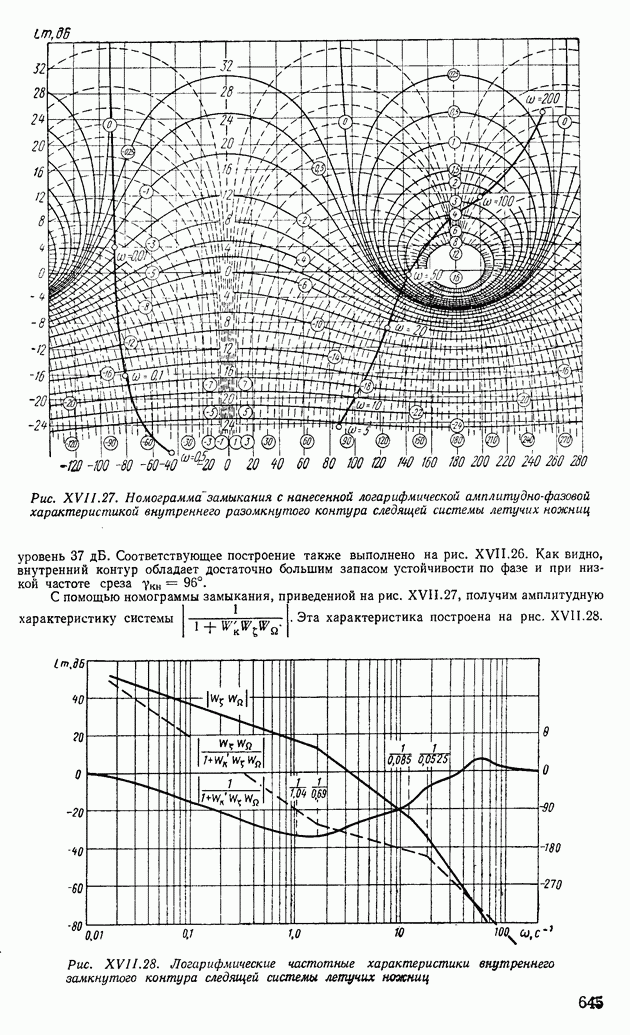
С помощью формул (XI. 123) и (XI. 124) получают номограмму Никольса. Откладывая по оси ординат  в децибелах, а по оси абсцисс
в децибелах, а по оси абсцисс  в градусах, строят кривые равных значений
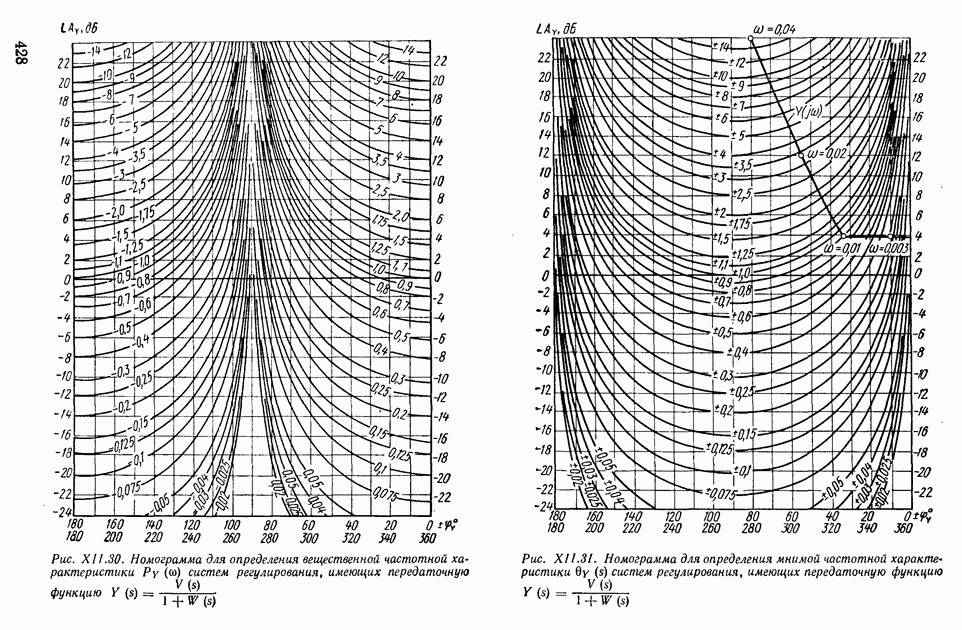
в градусах, строят кривые равных значений  в децибелах (сплошные линии номограммы на рис. XI.30). Штриховые линии номограммы получаются как линии равных значений
в децибелах (сплошные линии номограммы на рис. XI.30). Штриховые линии номограммы получаются как линии равных значений  в градусах. Числовые значения
в градусах. Числовые значения  в децибеллах приведены в кружочках для соответствующих сплошных линий номограммы. Числовые значения
в децибеллах приведены в кружочках для соответствующих сплошных линий номограммы. Числовые значения  в градусах приведены в кружочках внизу.
в градусах приведены в кружочках внизу.
Номограммой можно пользоваться следующим образом: 1) построенные логарифмические амплитудную  и фазовую
и фазовую  частотные характеристики перенесем на номограмму в виде кривой; 2) нанесем на эту кривую значения круговых частот
частотные характеристики перенесем на номограмму в виде кривой; 2) нанесем на эту кривую значения круговых частот  как параметр; 3) в точках пересечения сплошных кривых номограммы с логарифмической кривой
как параметр; 3) в точках пересечения сплошных кривых номограммы с логарифмической кривой  при некоторых значениях со находим числовые значения амплитуд приведенного замкнутого контура
при некоторых значениях со находим числовые значения амплитуд приведенного замкнутого контура  в точках же пересечения со штриховыми кривыми номограммы определяем фазовые значения приведенного замкнутого контура
в точках же пересечения со штриховыми кривыми номограммы определяем фазовые значения приведенного замкнутого контура  сложим полученные характеристики с логарифмическими амплитудой
сложим полученные характеристики с логарифмическими амплитудой  и фазовой
и фазовой  характеристиками; тогда получим исходные частотные характеристики замкнутого контура.
характеристиками; тогда получим исходные частотные характеристики замкнутого контура.
Можно пользоваться и другим способом построения логарифмических частотных характеристик замкнутого контура. Для этого выражение (XI. 114) перепишем в виде

В полученное выражение введем следующее обозначение:

тогда получим

По формуле (XI. 127) нетрудно проследить следующий способ построения логарифмических амплитудной и фазовой частотных характеристик замкнутого контура: 1) построим зеркальное отображение относительно оси частот для характеристик  и перенесем их на номограмму замыкания; 2) нанесем на полученную кривую значения круговых частот
и перенесем их на номограмму замыкания; 2) нанесем на полученную кривую значения круговых частот  ; 3) в точках пересечения кривой с линиями номограммы найдем значения амплитуд
; 3) в точках пересечения кривой с линиями номограммы найдем значения амплитуд  и фаз
и фаз  сложим полученные характеристики с логарифмической амплитудной
сложим полученные характеристики с логарифмической амплитудной  и фазовой
и фазовой  характеристиками; тогда получим исходные логарифмические частотные характеристики контура
характеристиками; тогда получим исходные логарифмические частотные характеристики контура 
Следует отметить, что при решении ряда практических задач второй способ часто оказывается более удобным, нежели первый.

(кликните для просмотра скана)
Указанная методика пригодна и для построения логарифмических амплитудных и фазовых частотных характеристик замкнутых систем автоматического регулирования. Передаточная функция замкнутой системы при 

по своей структуре аналогична формуле (XI.118). Поэтому, зная логарифмические амплитудные и фазовые частотные характеристики разомкнутой системы  с помощью номограммы замыкания можно получить амплитудную и фазовую частотные характеристики замкнутой системы.
с помощью номограммы замыкания можно получить амплитудную и фазовую частотные характеристики замкнутой системы.
Номограмму замыкания можно использовать и при построении логарифмических частотных характеристик замкнутой системы (или замкнутого контура) с положительной обратной связью. Покажем это следующим образом. Пусть передаточная функция замкнутой системы с положительной обратной связью при  определяется по формуле вида
определяется по формуле вида

Из формулы (XI. 128), которой соответствует номограмма на рис. XI.30, найдем частотную характеристику разомкнутой системы

Сравнивая формулы (XI.129) и (XI.130), можно установить, что по своему написанию они тождественны. Только в формуле (XI. 129) в левой части стоит функция замкнутой системы, а в правой части — функции разомкнутой системы. В формуле (XI. 130), наоборот, в левой части функция разомкнутой системы, а в правой части — функции замкнутой системы. Отсюда нетрудно сформулировать правило построения частотных характеристик систем с положительной обратной связью: значения амплитуд и фаз разомкнутой системы следует отмечать на кривых номограммы, а значения амплитуд и фаз замкнутой системы считывать по осям ординат и абсцисс номограммы.
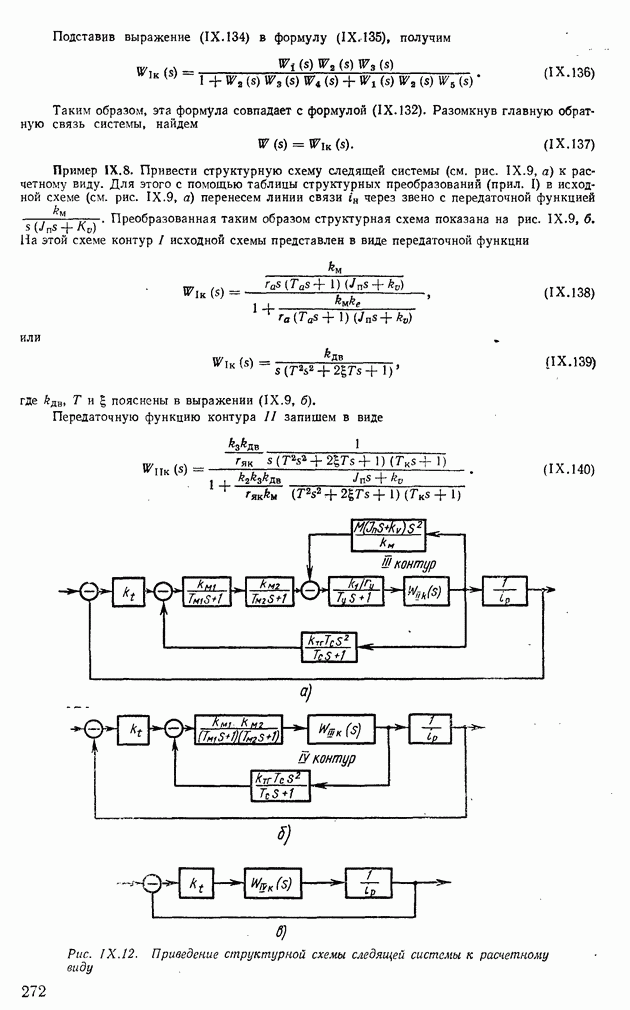
Пример XI.22. Передаточную функцию разомкнутой следящей системы (ем. рис. IX. 12) запишем в виде

где 
Для построения частотной характеристики по передаточной функции (X1.131) введем следующие обозначения:

Тогда получим

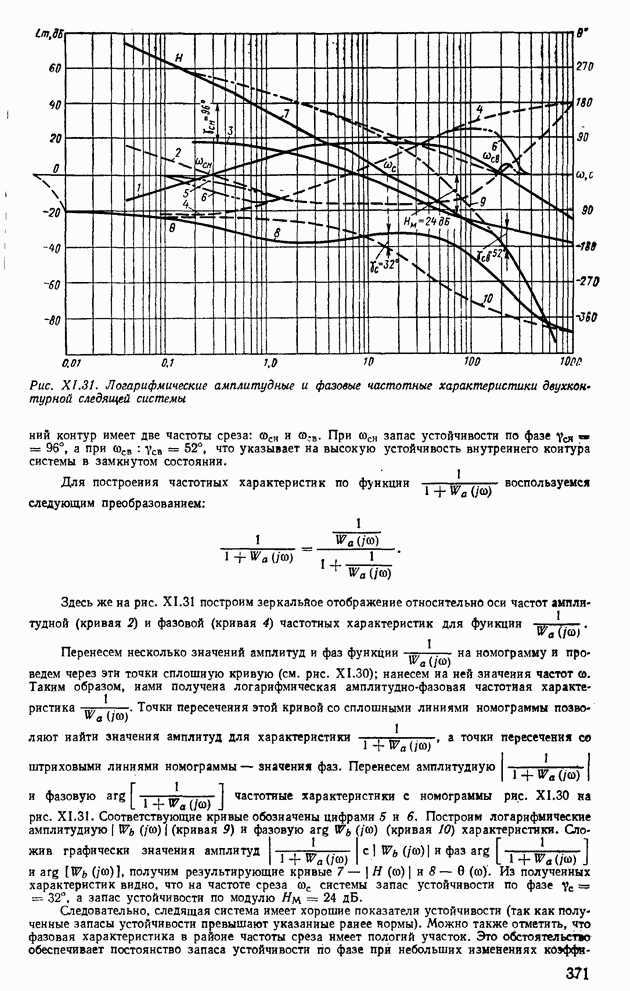
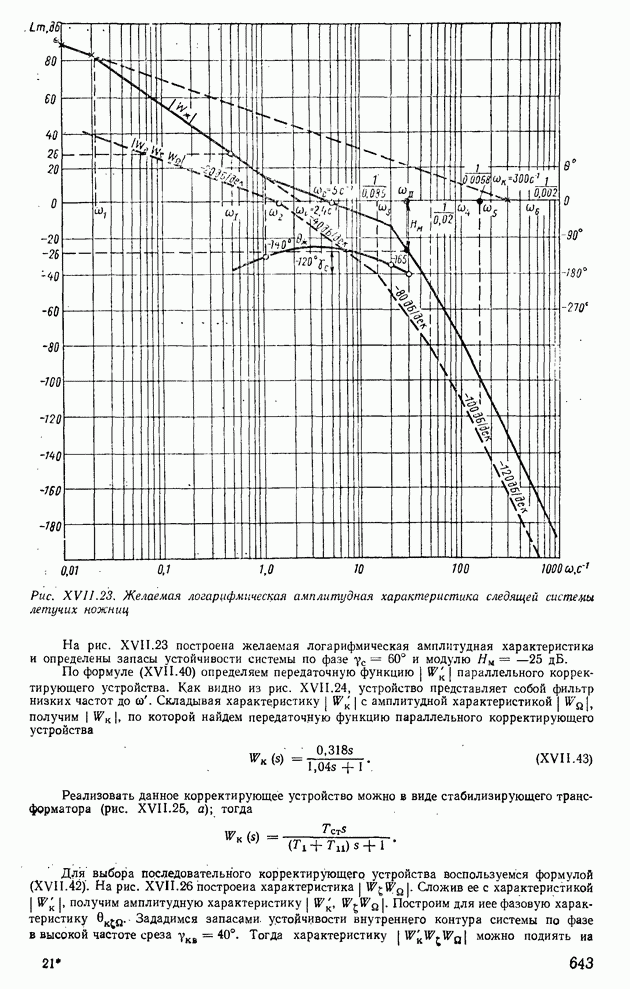
Пользуясь выражениями (XI. 132) и (XI. 133), построим логарифмические частотные характеристики. На рис. XI.31 построены логарифмическая амплитудная (кривая 1) и фазовая (кривая 3) частотйые характеристики по функции  Из рис. XI.31 видно, что
Из рис. XI.31 видно, что
Рис. XI.31. (см. скан) Логарифмические амплитудные и фазовые частотные характеристики двухконтурной следящей системы
внутренний контур имеет две частоты среза:  При сосн запас устойчивости по фазе
При сосн запас устойчивости по фазе  , а при сосв
, а при сосв  , что указывает на высокую устойчивость внутреннего контура системы в замкнутом состоянии.
, что указывает на высокую устойчивость внутреннего контура системы в замкнутом состоянии.
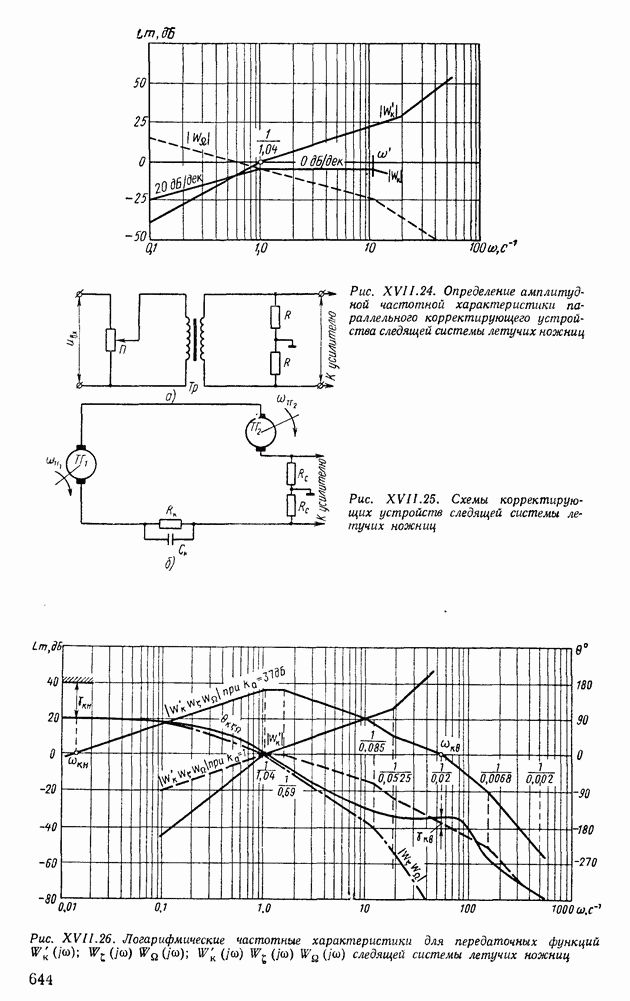
Для построения частотных характеристик по функции  воспользуемся следующим преобразованием:
воспользуемся следующим преобразованием:

Здесь же на рис. XI.31 построим зеркальйое отображение относительно оси частот амплитудной (кривая 2) и фазовой (кривая 4) частотных характеристик для функции 
Перенесем несколько значений амплитуд и фаз функции на номограмму и проведем через эти точки сплошную кривую (см. рис. XI.30); нанесем на ней значения частот  Таким образом, нами получена логарифмическая амплитудно-фазовая частотная характеристика Точки пересечения этой кривой со сплошными линиями номограммы позволяют найти значения амплитуд для характеристики
Таким образом, нами получена логарифмическая амплитудно-фазовая частотная характеристика Точки пересечения этой кривой со сплошными линиями номограммы позволяют найти значения амплитуд для характеристики  точки пересечения со штриховыми линиями номограммы — значения фаз. Перенесем амплитудную
точки пересечения со штриховыми линиями номограммы — значения фаз. Перенесем амплитудную  и фазовую
и фазовую  частотные характеристики с номограммы рис. XI.30 на рис. XI.31. Соответствующие кривые обозначены цифрами 5 и 6. Построим логарифмические амплитудную
частотные характеристики с номограммы рис. XI.30 на рис. XI.31. Соответствующие кривые обозначены цифрами 5 и 6. Построим логарифмические амплитудную  (кривая 9) и фазовую
(кривая 9) и фазовую  (кривая 10) характеристики. Сложив графически значения амплитуд
(кривая 10) характеристики. Сложив графически значения амплитуд  и фаз
и фаз  получим результирующие кривые
получим результирующие кривые  . Из полученных характеристик видно, что на частоте среза сос системы запас устойчивости по фазе
. Из полученных характеристик видно, что на частоте среза сос системы запас устойчивости по фазе  , а запас устойчивости по модулю
, а запас устойчивости по модулю  дБ.
дБ.
Следовательно, следящая система имеет хорошие показатели устойчивости (так как полученные запасы устойчивости превышают указанные ранее нормы). Можно также отметить, что фазовая характеристика в районе частоты среза имеет пологий участок. Это обстоятельство обеспечивает постоянство запаса устойчивости по фазе при небольших изменениях
коэффициентов усиления элементов системы. Иначе говоря, данная система является высокостабильной по отношению к колебанйям напряжения источников питания, износу электрических машии и агрегатов.
Пример XI.23. Исследовать устойчивость многоконтурной системы стабилизации (автопилот—самолет), структурная схема которой изображена на рис. IX.6. Преобразуем первый внутренний контур, заменив его передаточной функцией:

или

где

Заменив первый внутренний контур передаточной функцией (XI. 135), получим преобразованную структурную схему, изображенную на рис. XI.32.
Запишем частотную характеристику двухконтурной системы в виде

где

здесь 
Примем, что параметры системы стабилизации имеют следующие числовые значения:  .
.
При степени колебательности  колебательное звено
колебательное звено  распадается на два апериодических -
распадается на два апериодических - 
Проанализируем устойчивость внутреннего контура системы автоматической стабилизации по передаточной функции  Логарифмические амплитудная
Логарифмические амплитудная  и фазовая
и фазовая  частотные характеристики построены на рис. XI.33. Как видно из рисунка, запасы устойчивости внутреннего контура по фазе
частотные характеристики построены на рис. XI.33. Как видно из рисунка, запасы устойчивости внутреннего контура по фазе  , а по модулю
, а по модулю  дБ. На этом же рисунке показаны обратные логарифмические характеристики по функции
дБ. На этом же рисунке показаны обратные логарифмические характеристики по функции  Полученные значения обратных логарифмических частотных характеристик нанесены на номограмму замыкания (см. рис. XI.30, где логарифмическая обратная амплитудно-фазовая характеристика построена штрихпунктирной линией). Точки пересечения этой кривой со сплошными и штриховыми линиями номограммы определяют характеристики
Полученные значения обратных логарифмических частотных характеристик нанесены на номограмму замыкания (см. рис. XI.30, где логарифмическая обратная амплитудно-фазовая характеристика построена штрихпунктирной линией). Точки пересечения этой кривой со сплошными и штриховыми линиями номограммы определяют характеристики  — и
— и  Перенесем эти характеристики на рис. XI.33.
Перенесем эти характеристики на рис. XI.33.

Рис. XI.32. Преобразованная структурная схема системы автоматической стабилизации (автопилот—самолет)

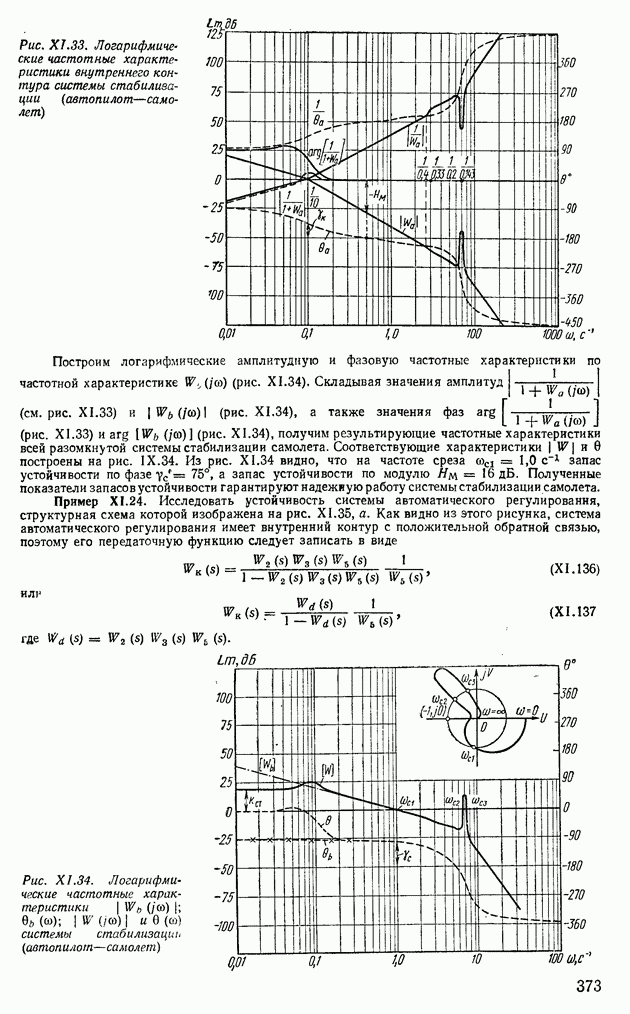
Рис.  Логарифмические частотные характеристики внутреннего контура системы стабилизации (автопилот—самолет)
Логарифмические частотные характеристики внутреннего контура системы стабилизации (автопилот—самолет)
Построим логарифмические амплитудную и фазовую частотные характеристики по частотной характеристике  (рис. XI.34). Складывая значения амплитуд
(рис. XI.34). Складывая значения амплитуд  (см. рис. XI.33) и
(см. рис. XI.33) и  (рис. XI.34), а также значения фаз
(рис. XI.34), а также значения фаз  (рис. XI.33) и
(рис. XI.33) и  (рис. XI.34), получим результирующие частотные характеристики всей разомкнутой системы стабилизации самолета. Соответствующие характеристики
(рис. XI.34), получим результирующие частотные характеристики всей разомкнутой системы стабилизации самолета. Соответствующие характеристики  и 0 построены на рис. IX.34. Из рис. XI.34 видно, что на частоте среза
и 0 построены на рис. IX.34. Из рис. XI.34 видно, что на частоте среза  запас устойчивости по фазе
запас устойчивости по фазе  , а запас устойчивости по модулю
, а запас устойчивости по модулю  дБ. Полученные показатели запасов устойчивости гарантируют надежную работу системы стабилизации самолета.
дБ. Полученные показатели запасов устойчивости гарантируют надежную работу системы стабилизации самолета.
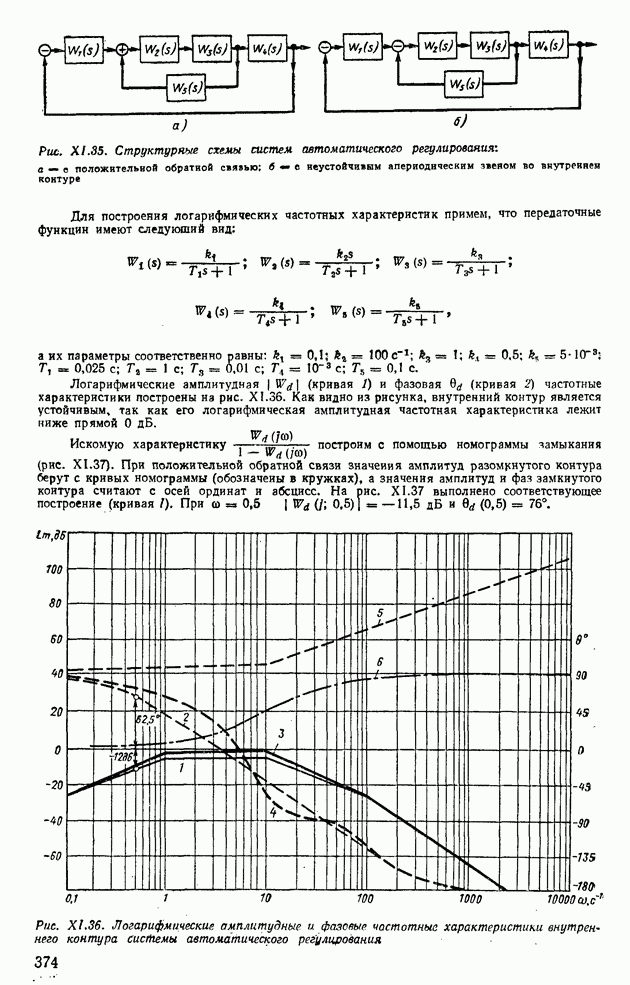
Пример XI.24. Исследовать устойчивость системы автоматического регулирования, структурная схема которой изображена на рис. XI.35, а. Как видно из этого рисунка, система автоматического регулирования имеет внутренний контур с положительной обратной связью, поэтому его передаточную функцию следует записать в виде

или

где

Рис. XI.34. Логарифмические частотные характеристики  системы стабилизации (автопилот—самолет)
системы стабилизации (автопилот—самолет)

Рис. XI.35. Стрдктдряые схемы систем автоматического регулировали: а — о положительной обратной связью; б — о неустойчивым апериодическим звеном во внутренней контуре
Для построения логарифмических частотных характеристик примем, что передаточные функции имеют следующий вид:

а их параметры соответственно равны: 
Логарифмические амплитудная  (кривая 1) и фазовая (кривая 2) частотные характеристики построены на рис. XI.36. Как видно из рисунка, внутренний контур является устойчивым, так как его логарифмическая амплитудная частотная характеристика лежит ниже прямой 0 дБ.
(кривая 1) и фазовая (кривая 2) частотные характеристики построены на рис. XI.36. Как видно из рисунка, внутренний контур является устойчивым, так как его логарифмическая амплитудная частотная характеристика лежит ниже прямой 0 дБ.
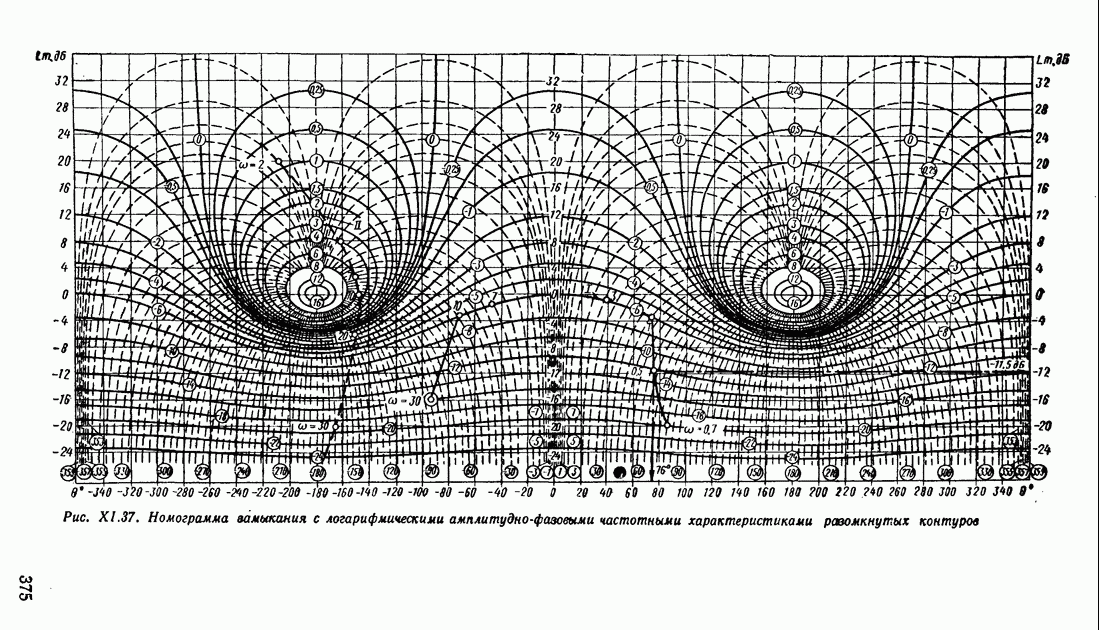
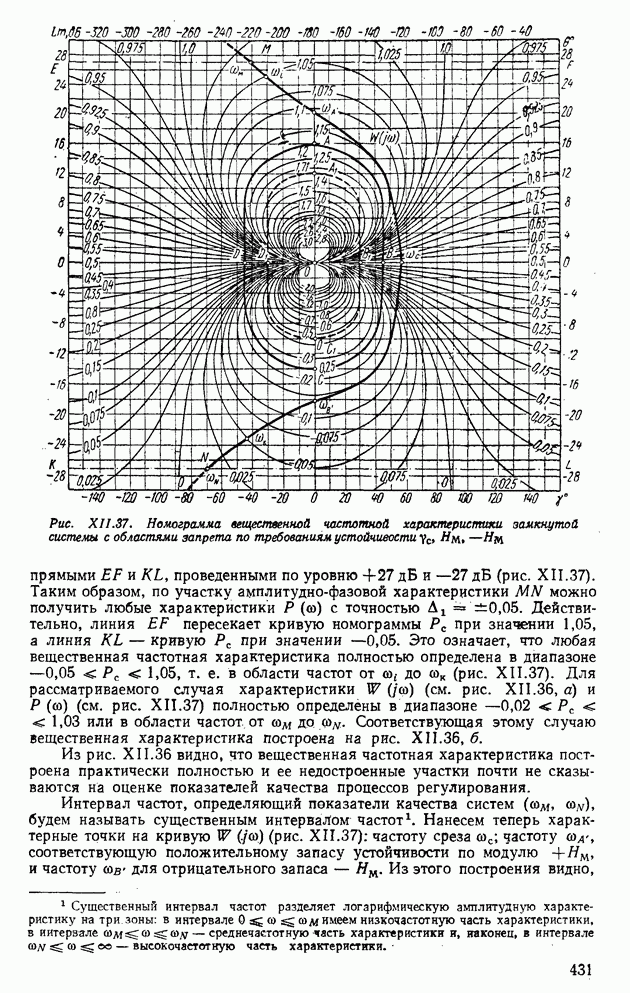
Искомую характеристику  построим о помощью номограммы замыкания (рис. XI.37). При положительной обратной связи значения амплитуд разомкнутого контура берут с кривых номограммы (обозначены в кружках), а значения амплитуд и фаз замкнутого контура считают с осей ординат и абсцисс. На рис.
построим о помощью номограммы замыкания (рис. XI.37). При положительной обратной связи значения амплитуд разомкнутого контура берут с кривых номограммы (обозначены в кружках), а значения амплитуд и фаз замкнутого контура считают с осей ординат и абсцисс. На рис.  выполнено соответствующее построение (кривая
выполнено соответствующее построение (кривая  При
При  .
.
Рис. XI.36. (см. скан) Логарифмические амплитудные и фазовые частотные характеристики внутреннего контура системы автоматического регулирования

(кликните для просмотра скана)
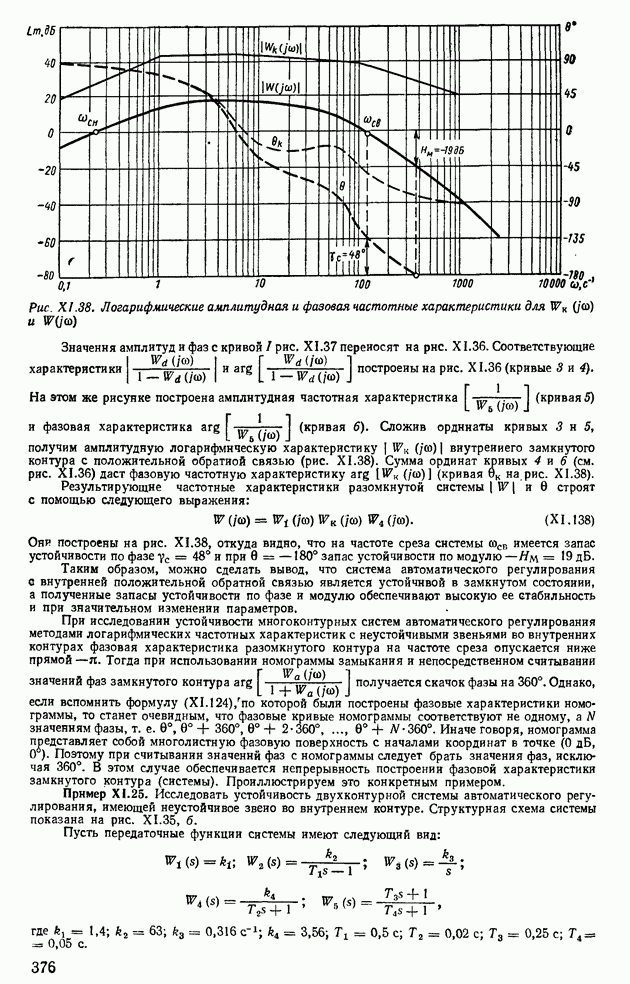
Рис. XI.38. (см. скан) Логарифмические амплитудная и фазовая частотные характеристики для 
Значения амплитуд и фаз с кривой I рис. XI.37 переносят на рис. XI.36. Соответствующие характеристики  построеиы на рис. X 1.36 (кривые 3 и 4).
построеиы на рис. X 1.36 (кривые 3 и 4).
На этом же рисунке построена амплитудная частотная характеристика  (кривая 5) и фазовая характеристика
(кривая 5) и фазовая характеристика  (кривая
(кривая  Сложив ординаты кривых 3 и 5, получим амплитудную логарифмическую характеристику
Сложив ординаты кривых 3 и 5, получим амплитудную логарифмическую характеристику  внутреннего замкнутого контура с положительной обратной связью (рис. XI.38). Сумма ординат кривых 4 и 6 (см. рис. XI.36) даст фазовую частотную характеристику
внутреннего замкнутого контура с положительной обратной связью (рис. XI.38). Сумма ординат кривых 4 и 6 (см. рис. XI.36) даст фазовую частотную характеристику  (кривая
(кривая  на рис. XI.38).
на рис. XI.38).
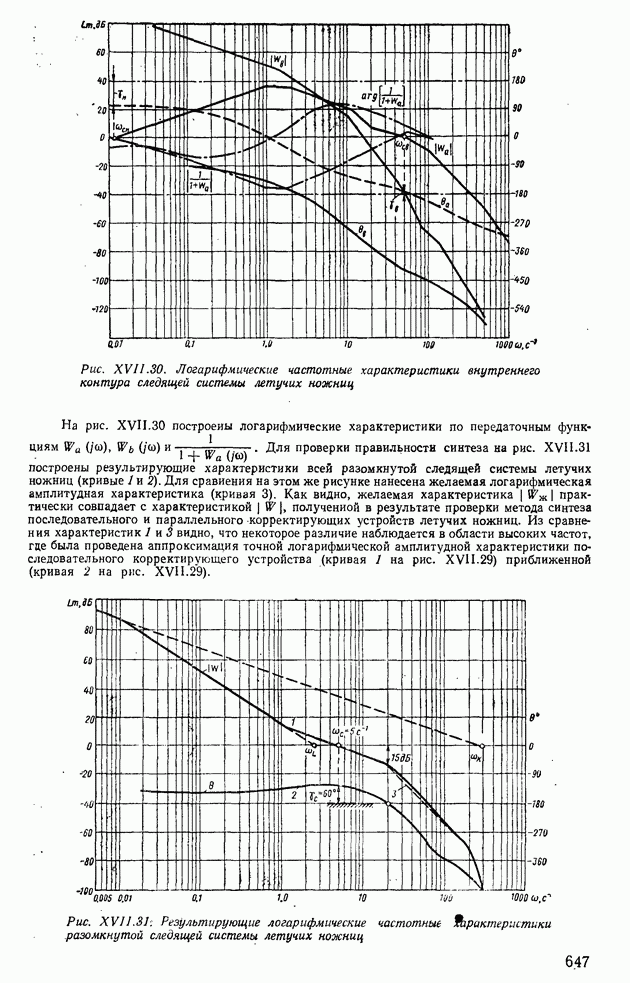
Результирующие частотные характеристики разомкнутой системы  и 0 строят с помощью следующего выражения:
и 0 строят с помощью следующего выражения:

Они построены на рис. XI.38, откуда видно, что на частоте среза системы сосв имеется запас устойчивости по фазе  и при
и при  запас устойчивости по модулю
запас устойчивости по модулю  .
.
Таким образом, можно сделать вывод, что система автоматического регулирования с внутренней положительной обратной связью является устойчивой в замкнутом состоянии, а полученные запасы устойчивости по фазе и модулю обеспечивают высокую ее стабильность и при значительном изменении параметров.
При исследовании устойчивости многоконтурных систем автоматического регулирования методами логарифмических частотных характеристик с неустойчивыми звеньями во внутренних контурах фазовая характеристика разомкнутого контура на частоте среза опускается ниже прямой —я. Тогда при использовании номограммы замыкания и непосредственном считывании значений фаз замкнутого контура  получается скачок фазы на 360°. Однако, если вспомнить формулу
получается скачок фазы на 360°. Однако, если вспомнить формулу  которой были построены фазовые характеристики номограммы, то станет очевидным, что фазовые кривые номограммы соответствуют не одному, а
которой были построены фазовые характеристики номограммы, то станет очевидным, что фазовые кривые номограммы соответствуют не одному, а  значениям фазы, т. е.
значениям фазы, т. е.  . Иначе говоря, номограмма представляет собой многолистную фазовую поверхность с началами координат в точке
. Иначе говоря, номограмма представляет собой многолистную фазовую поверхность с началами координат в точке  Поэтому при считывании значений фаз с номограммы следует брать значения фаз, исключая 360°. В этом случае обеспечивается непрерывность построении фазовой характеристики замкнутого контура (системы). Проиллюстрируем это конкретным примером.
Поэтому при считывании значений фаз с номограммы следует брать значения фаз, исключая 360°. В этом случае обеспечивается непрерывность построении фазовой характеристики замкнутого контура (системы). Проиллюстрируем это конкретным примером.
Пример XI.25. Исследовать устойчивость двухконтурной системы автоматического регулирования, имеющей неустойчивое звено во внутреннем контуре. Структурная схема системы показана на рис. XI.35, б.
Пусть передаточные функции системы имеют следующий вид:

где 
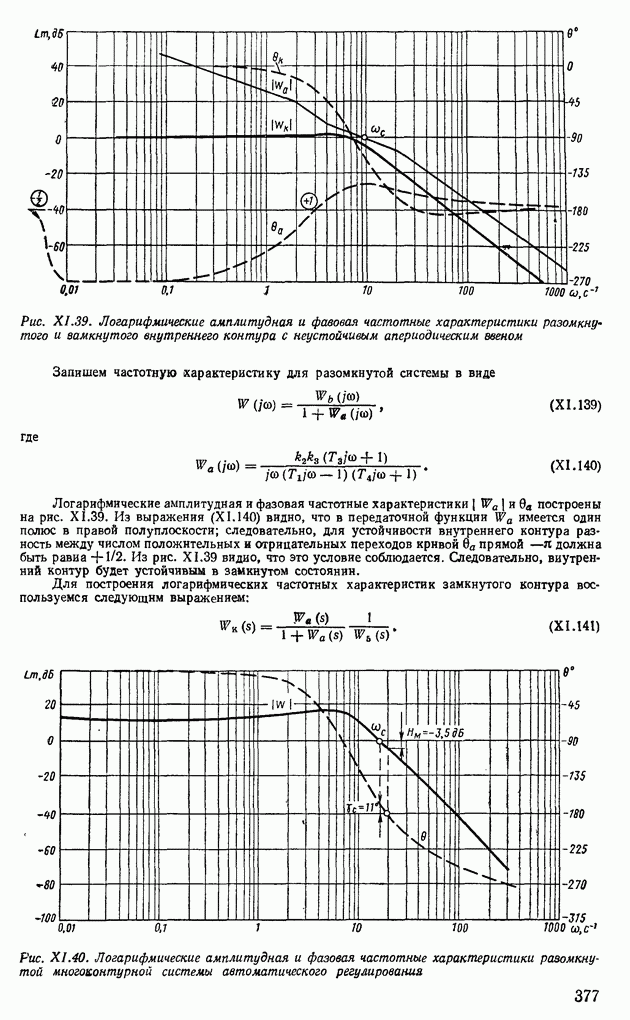
Рис. XI.39. (см. скан) Логарифмические амплитудная и фавовая частотные характеристики разомкнутого и замкнутого внутреннего контура с неустойчивым апериодическим звеном
Запишем частотную характеристику для разомкнутой системы в виде

где

Логарифмические амплитудная и фазовая частотные характеристики  и
и  построены на рис. XI.39. Из выражения (XI. 140) видно, что в передаточной функции
построены на рис. XI.39. Из выражения (XI. 140) видно, что в передаточной функции  имеется один полюс в правой полуплоскости; следовательно, для устойчивости внутреннего контура разность между числом положительных и отрицательных переходов кривой
имеется один полюс в правой полуплоскости; следовательно, для устойчивости внутреннего контура разность между числом положительных и отрицательных переходов кривой  прямой
прямой  должна быть равна
должна быть равна  Из рис. XI.39 видно, что это условие соблюдается. Следовательно, внутренний контур будет устойчивым в замкнутом состоянии.
Из рис. XI.39 видно, что это условие соблюдается. Следовательно, внутренний контур будет устойчивым в замкнутом состоянии.
Для построения логарифмических частотных характеристик замкнутого контура воспользуемся следующим выражением:

Рис. XI.40. (см. скан) Логарифмические амплитудная и фазовая частотные характеристики разомкнутой многоконтурной системы автоматического регулирования
Подставим в выражение  в построим характеристики
в построим характеристики  . Затем нанесем на номограмму рис. XI.37 логарифмическую амплитудно-фазовую частотную характеристику
. Затем нанесем на номограмму рис. XI.37 логарифмическую амплитудно-фазовую частотную характеристику  (кривая 11) Перенеся соответствующие ординаты и учитывая характеристики звена
(кривая 11) Перенеся соответствующие ординаты и учитывая характеристики звена  получим логарифмические амплитудную и фазовую частотные
получим логарифмические амплитудную и фазовую частотные  характеристики
характеристики 
Результирующие амплитудную и фазовую частотные характеристики всей системы находят о помощью выражения

Соответствующее построение выполнено на рис. XI.40 — кривые  и 0, Из рис. XI.40 видно, что данная система автоматического регулирования устойчива в замкнутом состоянии в
и 0, Из рис. XI.40 видно, что данная система автоматического регулирования устойчива в замкнутом состоянии в  .
.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 1. ПРИНЦИПЫ ДЕЙСТВИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
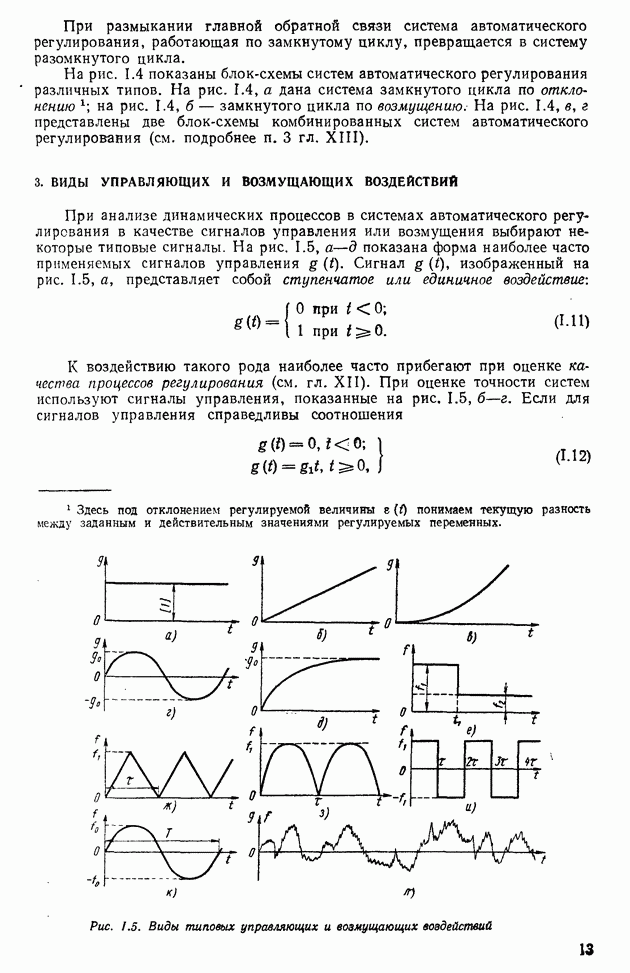
- 3. ВИДЫ УПРАВЛЯЮЩИХ И ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ
- 4. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Глава II. ВИДЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛТРОВАНИЯ
- 1. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
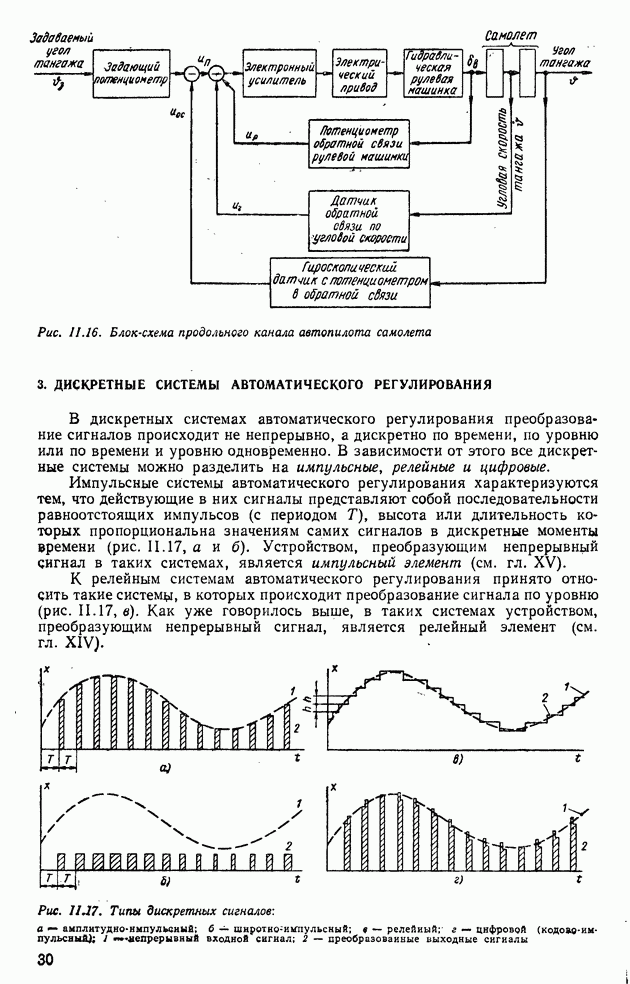
- 3. ДИСКРЕТНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ПРИМЕНЕНИЕ ЦВМ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
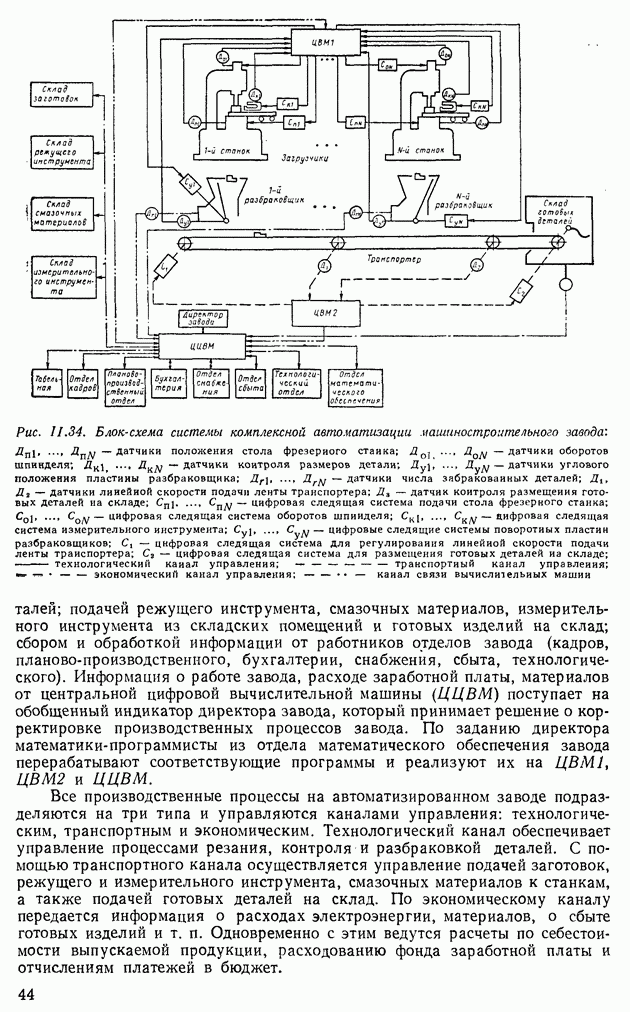
- 7. ПРИМЕНЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ДЛЯ УПРАВЛЕНИЯ СЛОЖНЫМИ ПРОИЗВОДСТВЕННЫМИ ПРОЦЕССАМИ. СИСТЕМЫ КОМПЛЕКСНОЙ АВТОМАТИЗАЦИИ ПРОИЗВОДСТВА
- Глава III. ОБЪЕКТЫ РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ СВОЙСТВА ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 2. ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 3. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ ДИНАМИКИ
- 4. УСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (ДИЗЕЛЬ, ГИДРОТУРБИНА, САМОЛЕТ)
- 5. НЕУСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (РЕСИВЕР, РАКЕТА-НОСИТЕЛЬ КОСМИЧЕСКИХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ)
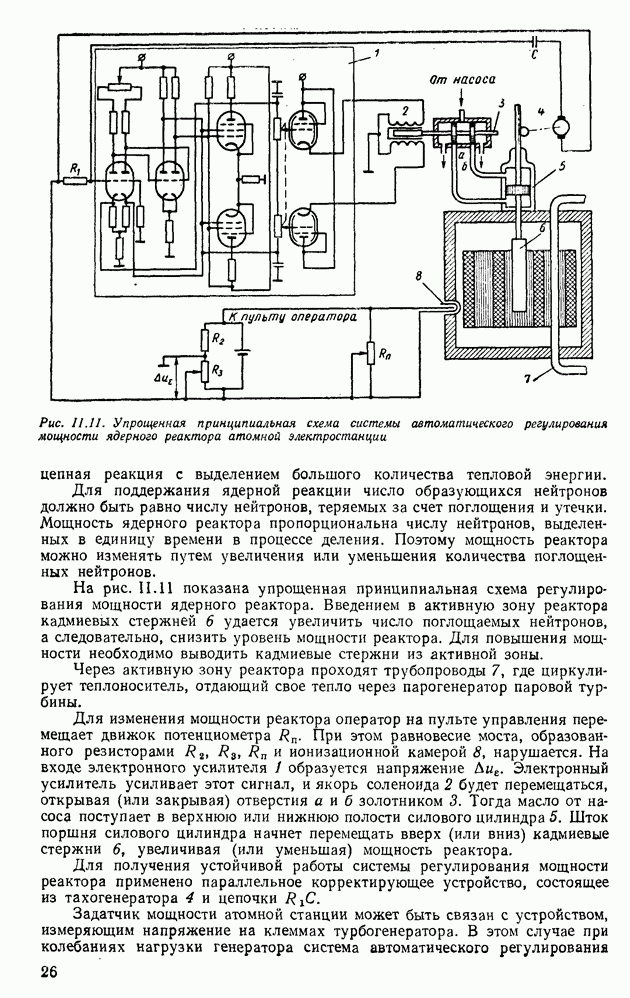
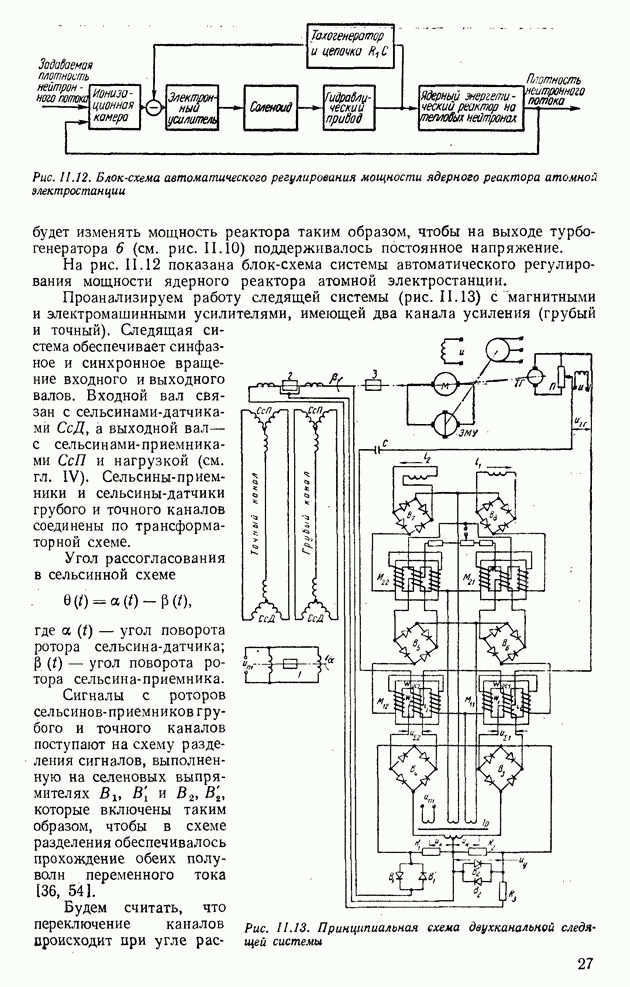
- 6. АСТАТИЧЕСКИЕ ОБЪЕКТЫ (ТРЕХФАЗНЫЙ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ, ЯДЕРНЫЙ ЭНЕРГЕТИЧЕСКИЙ РЕАКТОР НА ТЕПЛОВЫХ НЕЙТРОНАХ, КОСМИЧЕСКИЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ)
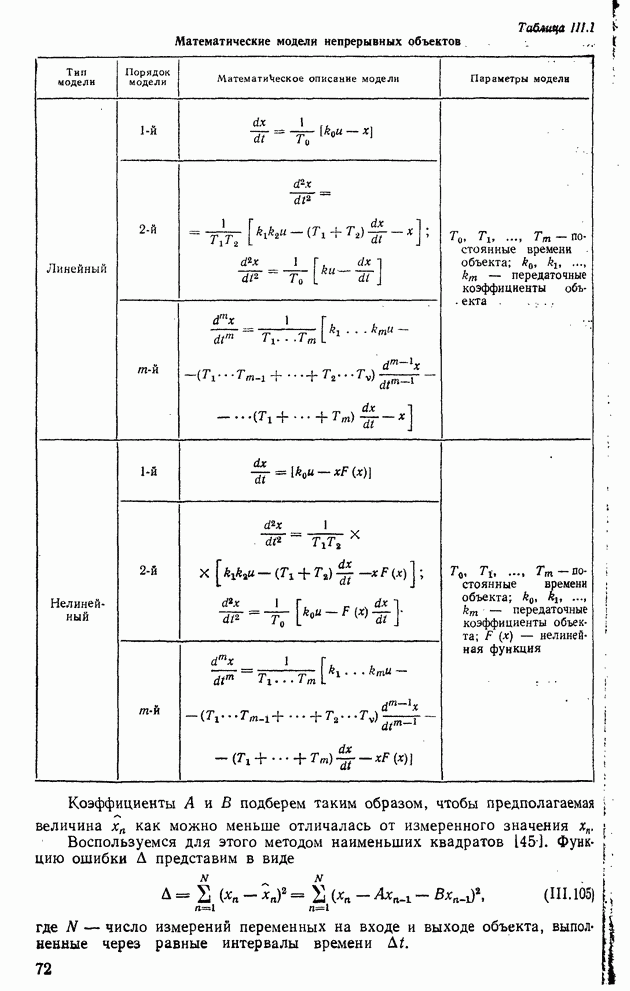
- 7. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- Глава IV. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОПРЕДЕЛЕНИЕ ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ИЗМЕРИТЕЛЬНЫХ ПОДСИСТЕМ
- 2. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Индуктивные устройства.
- Емкостные устройства.
- Сельсины.
- Дифференциальный сельсин.
- Погрешность сельсинов.
- Устройства для замера угловых скоростей.
- Устройства замера угловых ускорений.
- 4. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И ТОКА
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕМПЕРАТУР И ИЗЛУЧЕНИЙ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЙ И РАСХОДОВ ЖИДКОСТИ И ГАЗА
- 7. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ ВЕЛИЧИН, УГЛОВЫХ СКОРОСТЕЙ И ЛИНЕЙНЫХ УСКОРЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ
- Устройства для измерения линейных ускорений подвижных объектов (акселерометры).
- 8. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- Глава V. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ
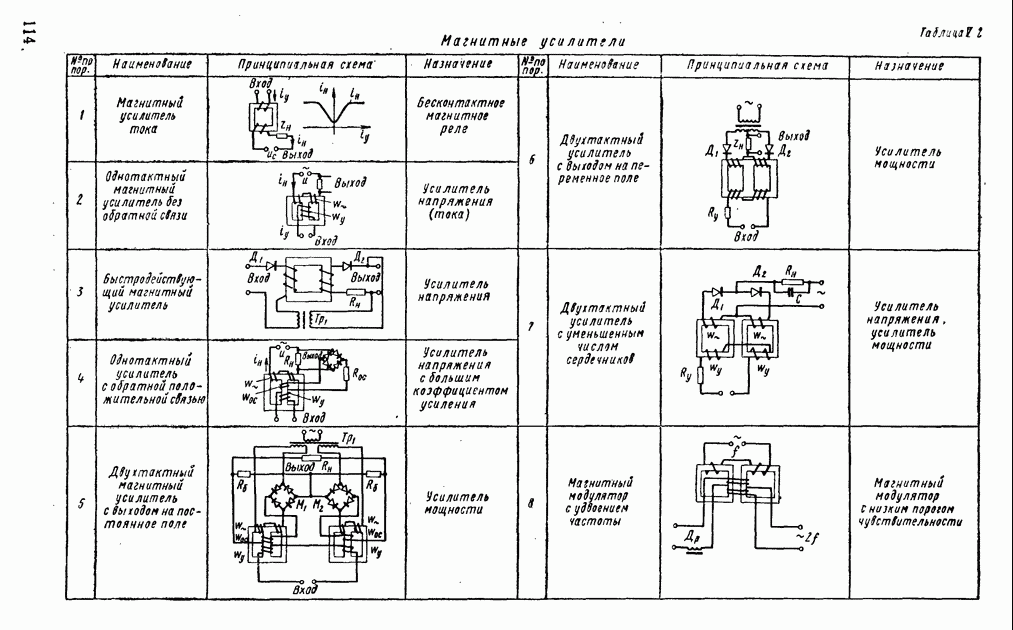
- 2. МАГНИТНЫЕ УСИЛИТЕЛИ
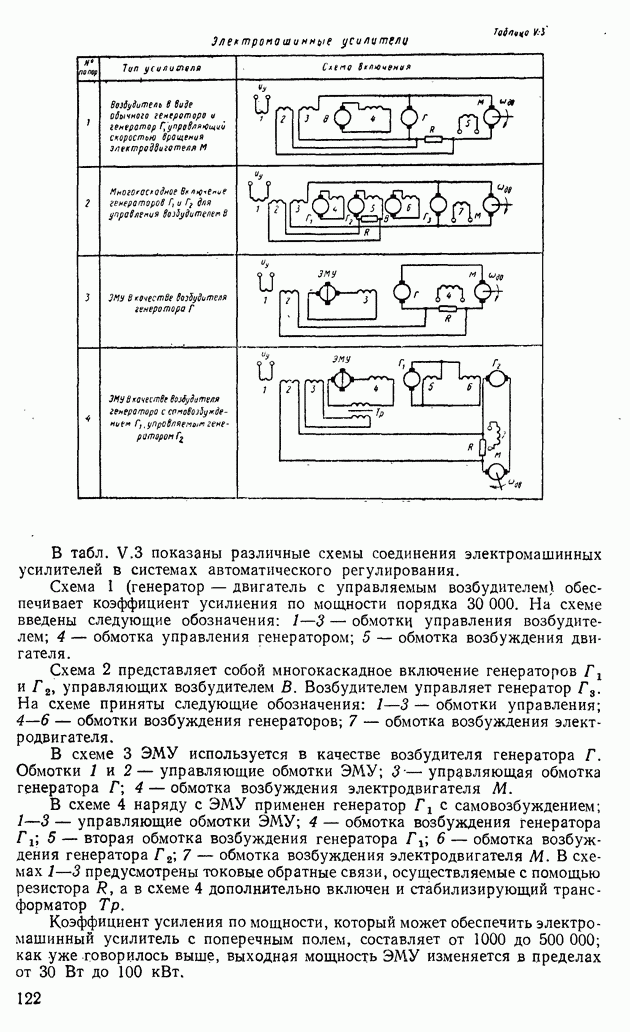
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
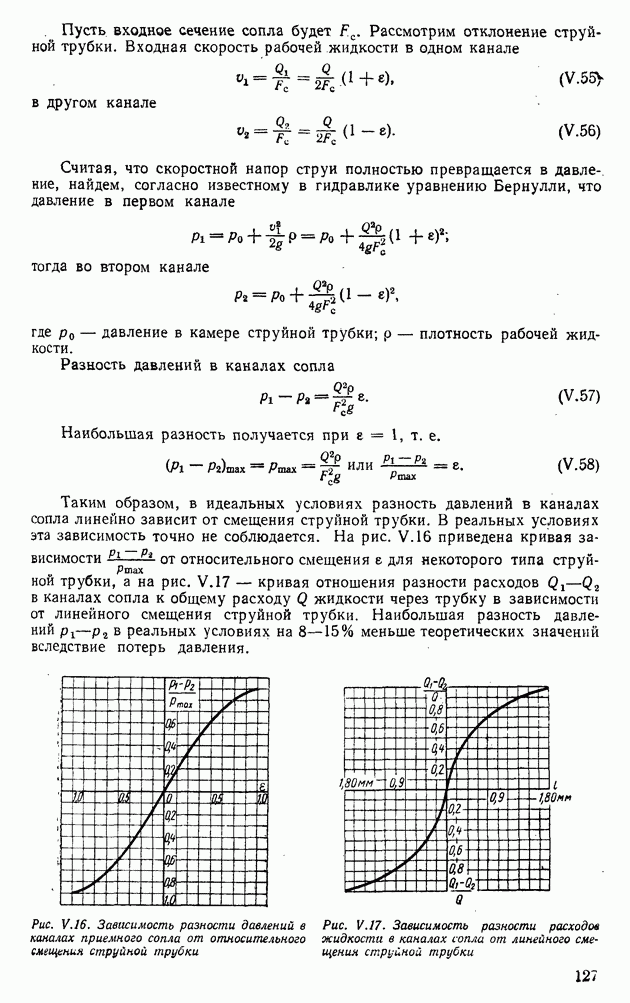
- 4. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 5. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ РАЗЛИЧНЫХ УСИЛИТЕЛЕЙ
- ГЛАВА VI. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА
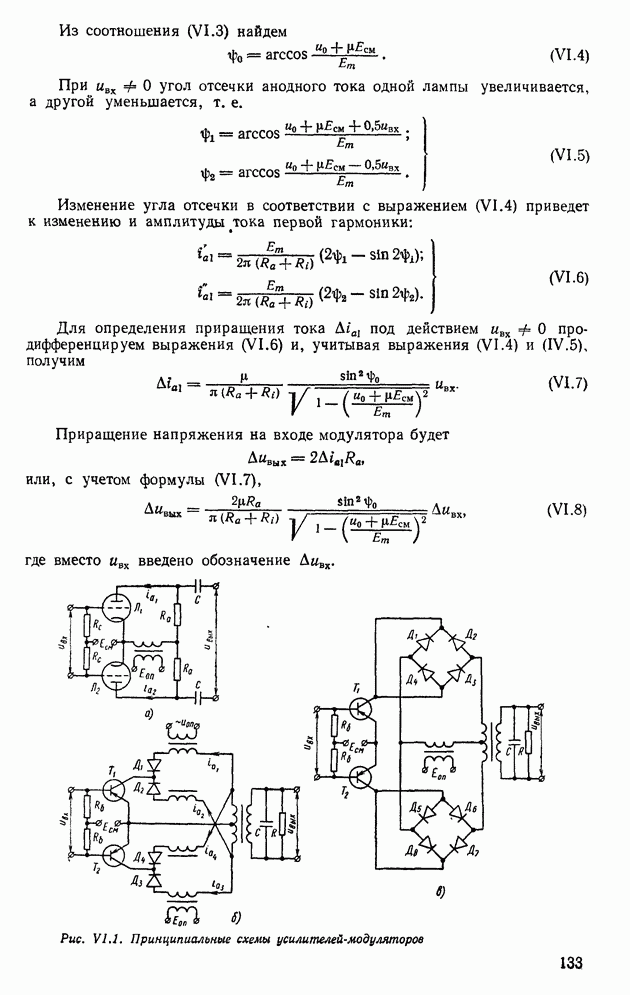
- 1. УСИЛИТЕЛИ-ПРЕОБРАЗОВАТЕЛИ
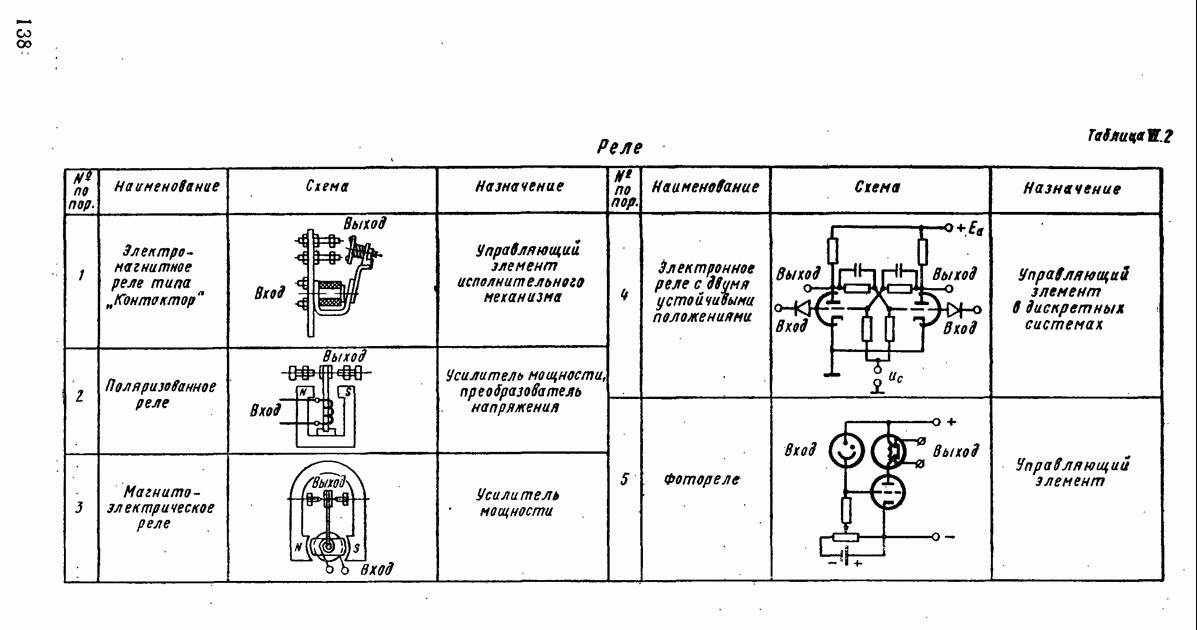
- 2. РЕЛЕ
- 3. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
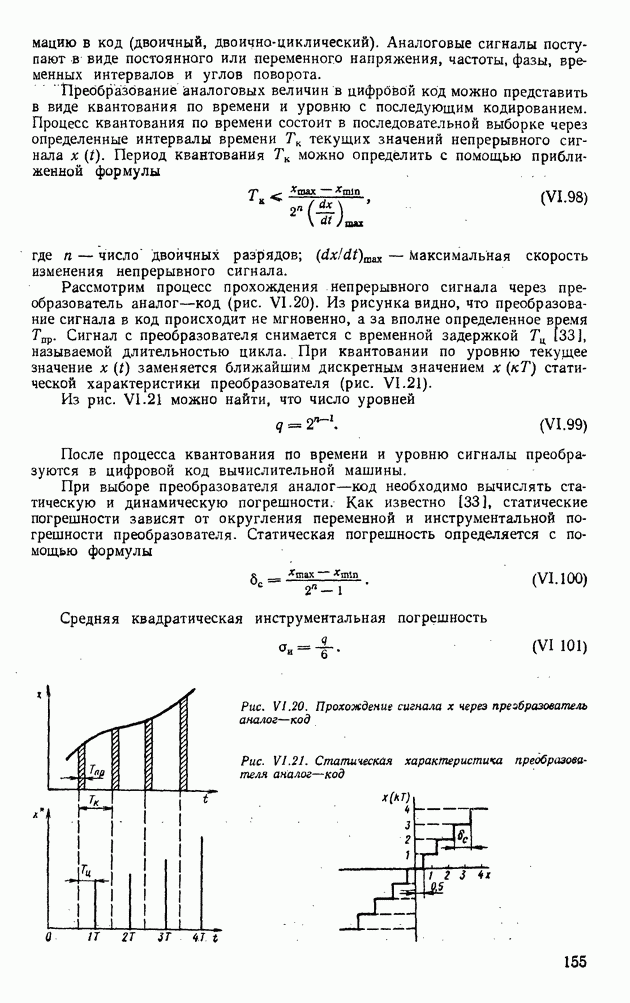
- 4. ПРЕОБРАЗОВАТЕЛИ АНАЛОГ—КОД
- 5. ПРЕОБРАЗОВАТЕЛИ КОД—АНАЛОГ
- 6. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ УПРАВЛЯЮЩИЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
- 8. ПНЕВМАТИЧЕСКИЕ АНАЛОГОВЫЕ И ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 9. ТОЧНОСТЬ РАБОТЫ И БЫСТРОДЕЙСТВИЕ УПРАВЛЯЮЩИХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
- 10. СРАВНИТЕЛЬНАЯ ОЦЕНКА ПРЕОБРАЗУЮЩИХ УСТРОЙСТВ
- Глава VII. ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 1. ЭЛЕКТРИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 2. МЕХАНИЧЕСКИЕ ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. ГИДРАВЛИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 4. ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 5. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- 6. СРАВНИТЕЛЬНАЯ ОЦЕНКА ИСПОЛНИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- Глава VIII. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
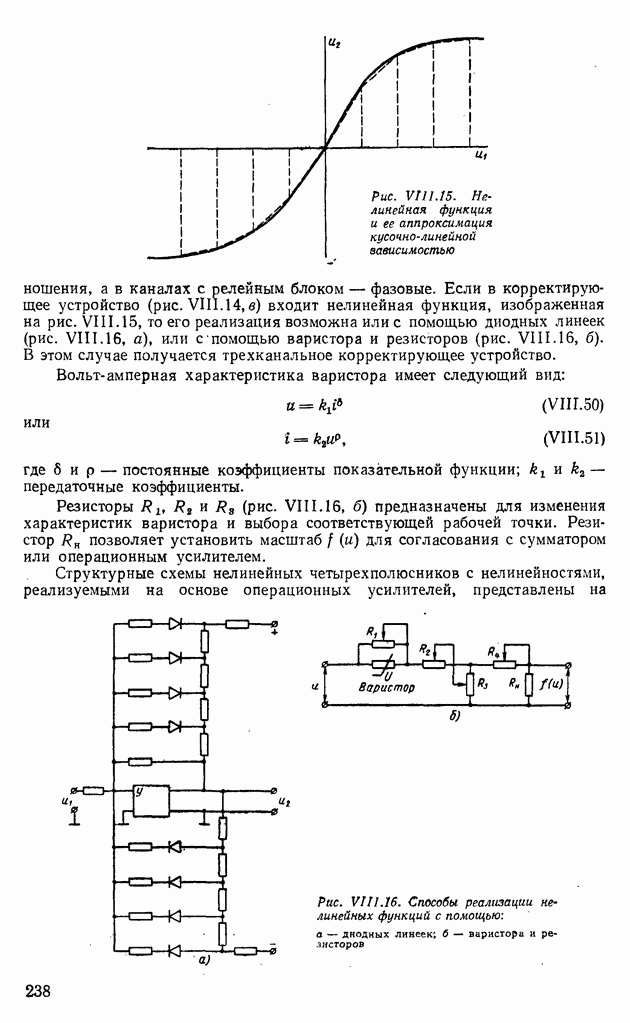
- 2. НЕЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 3. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 4. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ЛИНИЯХ ЗАДЕРЖЕК И ДИСКРЕТНЫХ ЭЛЕМЕНТАХ
- Глава IX. УРАВНЕНИЯ ДИНАМИКИ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- 1. ПРЕДСТАВЛЕНИЕ ОБЪЕКТОВ И УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С СОСРЕДОТОЧЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
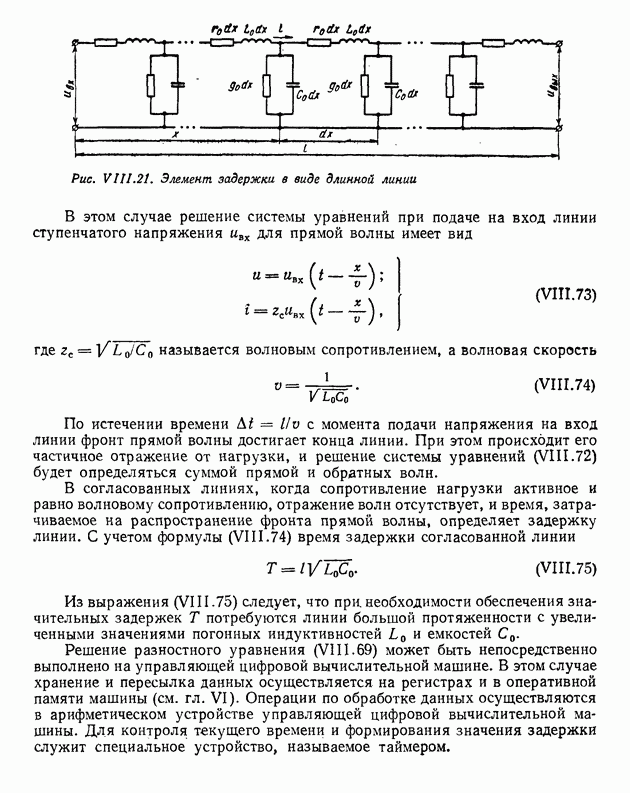
- 2. ПРЕДСТАВЛЕНИЕ УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С РАСПРЕДЕЛЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ТРАНСЦЕДЕНТНЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 3. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
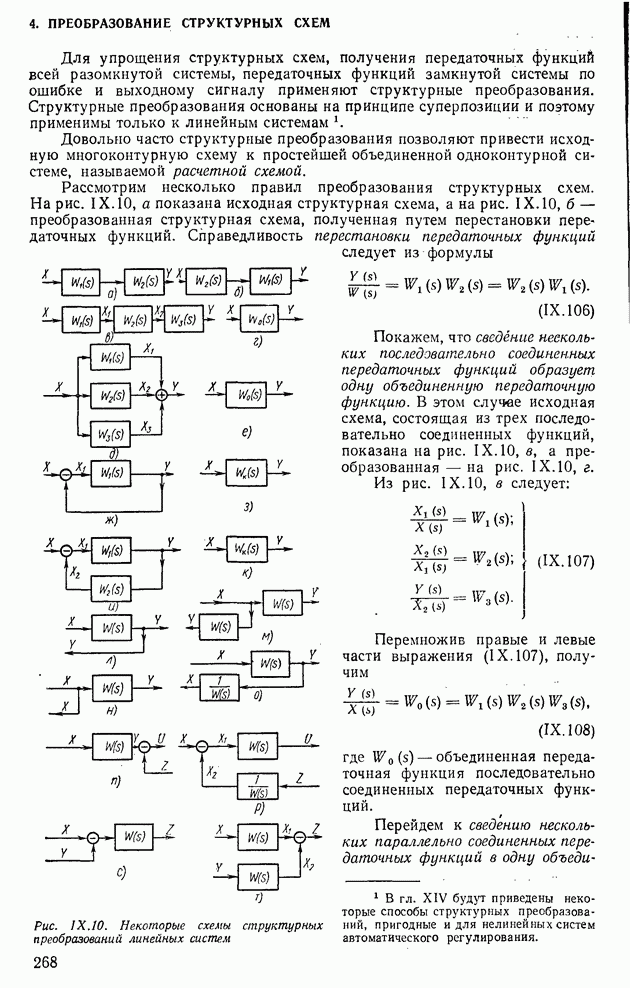
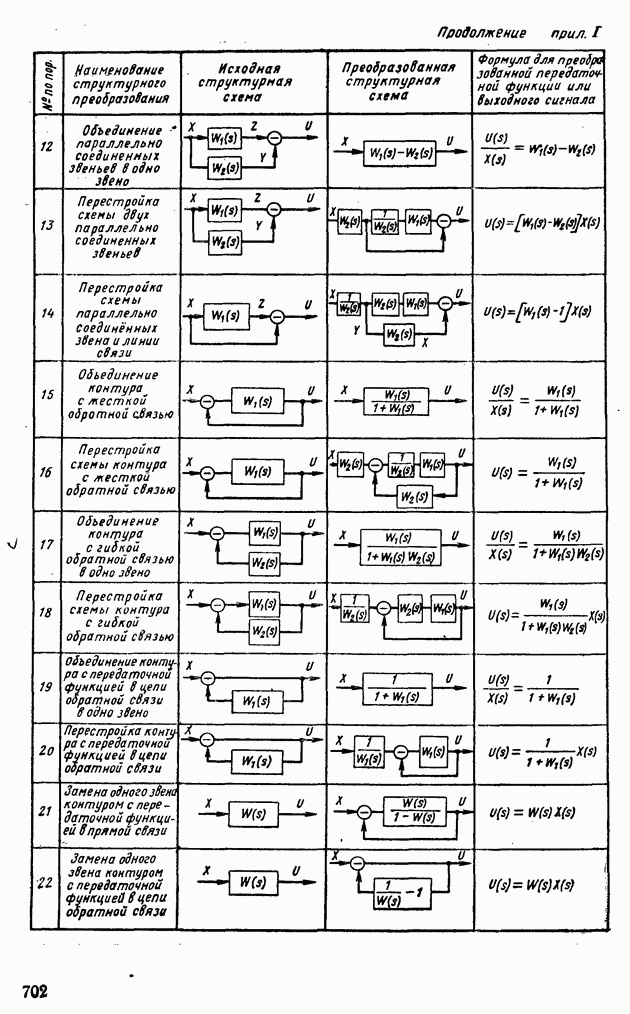
- 4. ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ
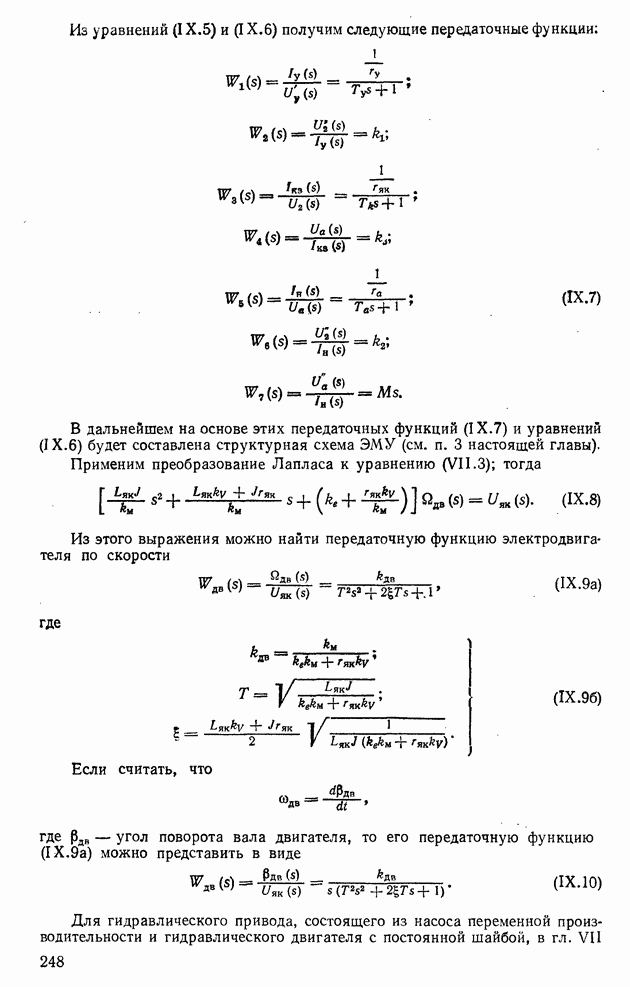
- 5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ОПИСАНИЕ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ РЕГУЛИРОВАНИЯ В ВЕКТОРНО-МАТРИЧНОЙ ФОРМЕ
- 7. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 8. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 9. РЕШЕНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ УРАВНЕНИЙ СОСТОЯНИЯ
- 10. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ МАТРИЦ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ ЛИНЕЙНЫХ СИСТЕМ
- 12. ПРЕДСТАВЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ИМПУЛЬСНЫМИ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ
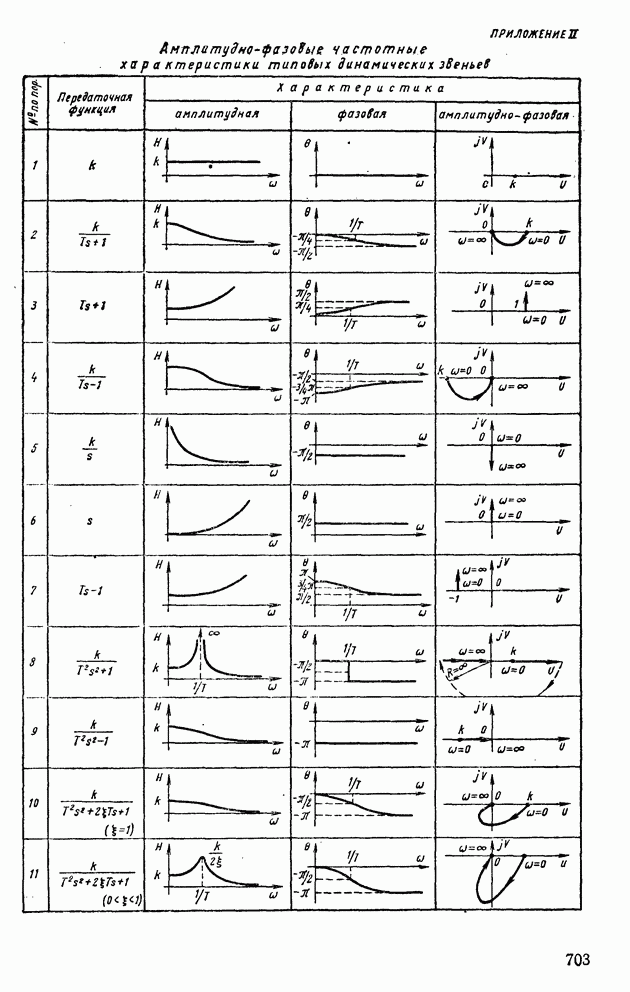
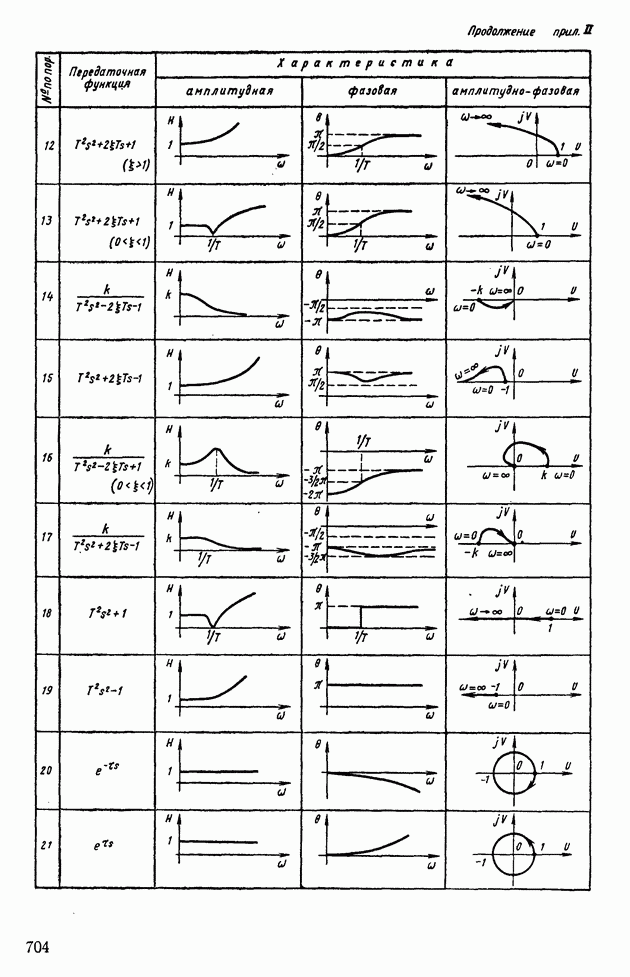
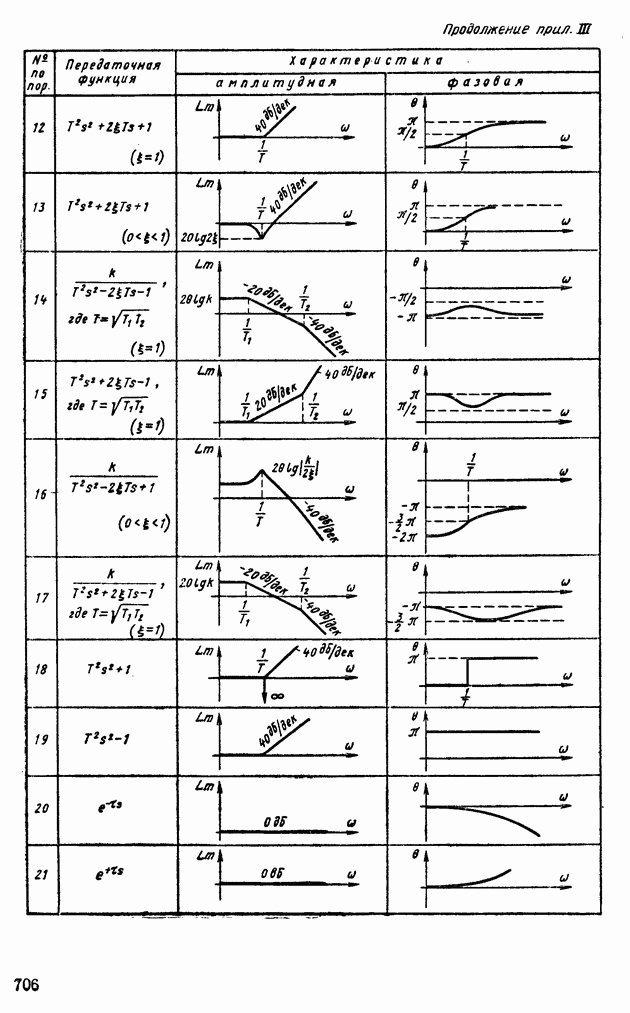
- Глава X. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ АМПЛИТУДНО-ФАЗОВЫЕ И ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 1. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- Логарифмические амплитудная и фазовая частотные характеристики апериодического звена.
- 2. АПЕРИОДИЧЕСКОЕ НЕУСТОЙЧИВОЕ ЗВЕНО
- 4. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 5. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ (УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ)
- 6. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО РОДА
- 7. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО РОДА
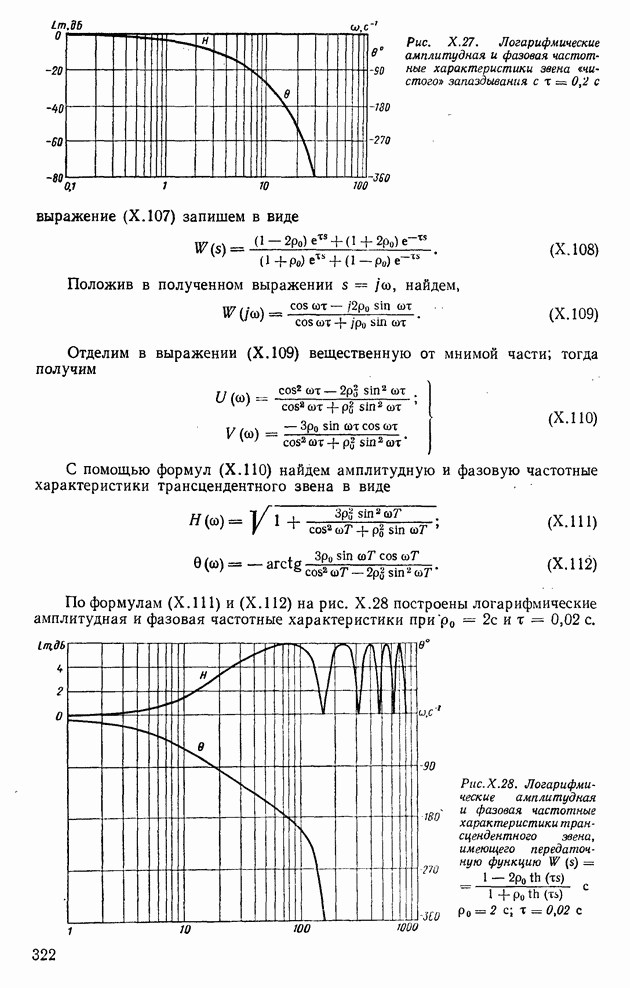
- 8. ТРАНСЦЕНДЕНТНЫЕ ЗВЕНЬЯ
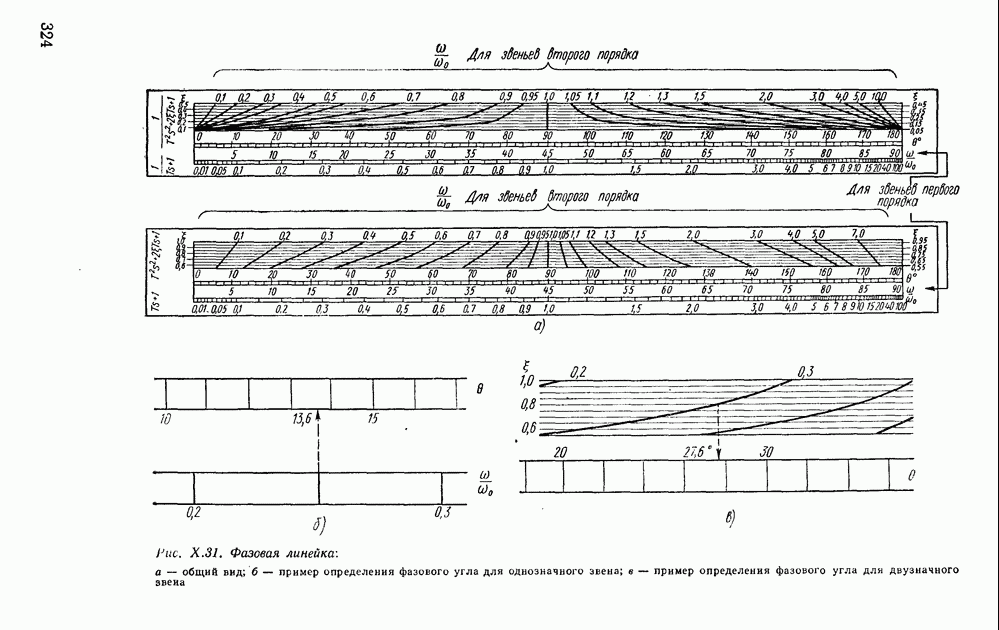
- 9. ФАЗОВАЯ ЛИНЕЙКА
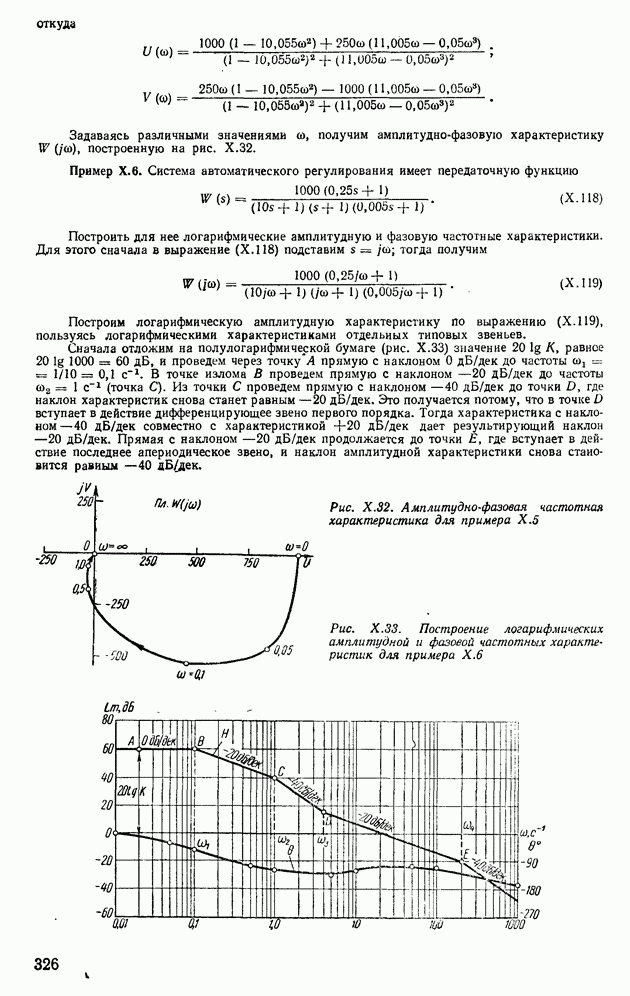
- 10. ПОСТРОЕНИЕ АМПЛИТУДНО-ФАЗОВЫХ И ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ ГРУПП ТИПОВЫХ ЗВЕНЬЕВ
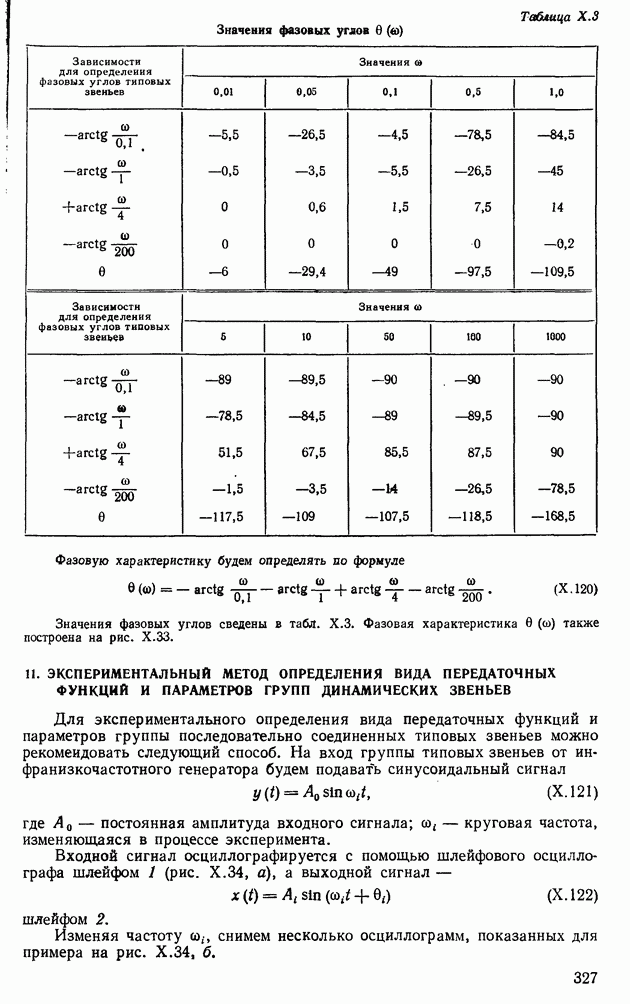
- 11. ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ВИДА ПЕРЕДАТОЧНЫХ ФУНКЦИЙ И ПАРАМЕТРОВ ГРУПП ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
- ГЛАВА XI. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ
- 2. ОПРЕДЕЛЕНИЕ ФУНКЦИЙ ЛЯПУНОВА МЕТОДАМИ Г. СЕГЕ И Д. ШУЛЬЦА
- 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 5. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 6. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
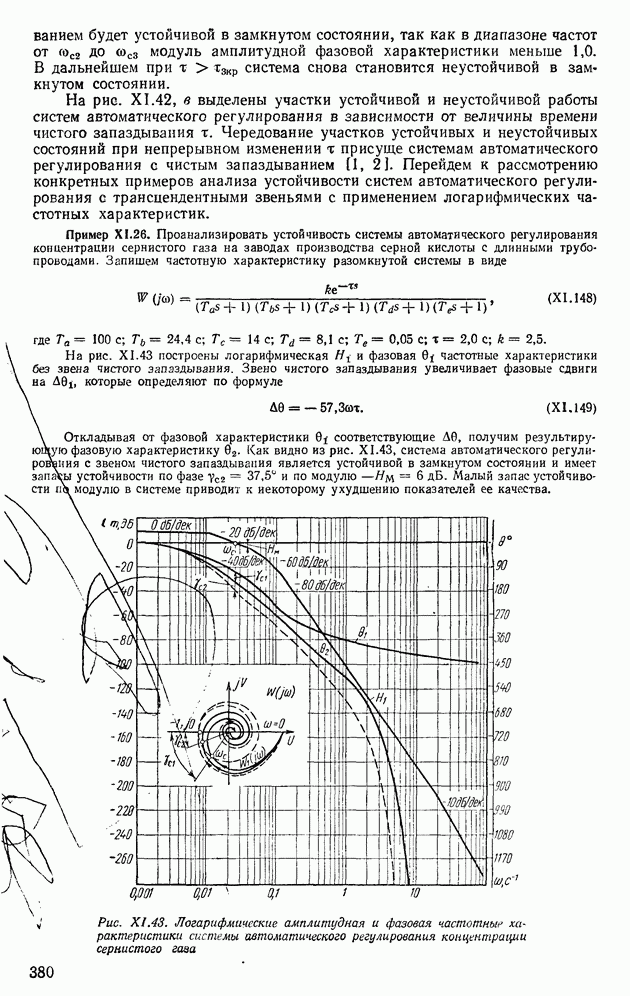
- 8. АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ТРАНСЦЕНДЕНТНЫМИ ЗВЕНЬЯМИ
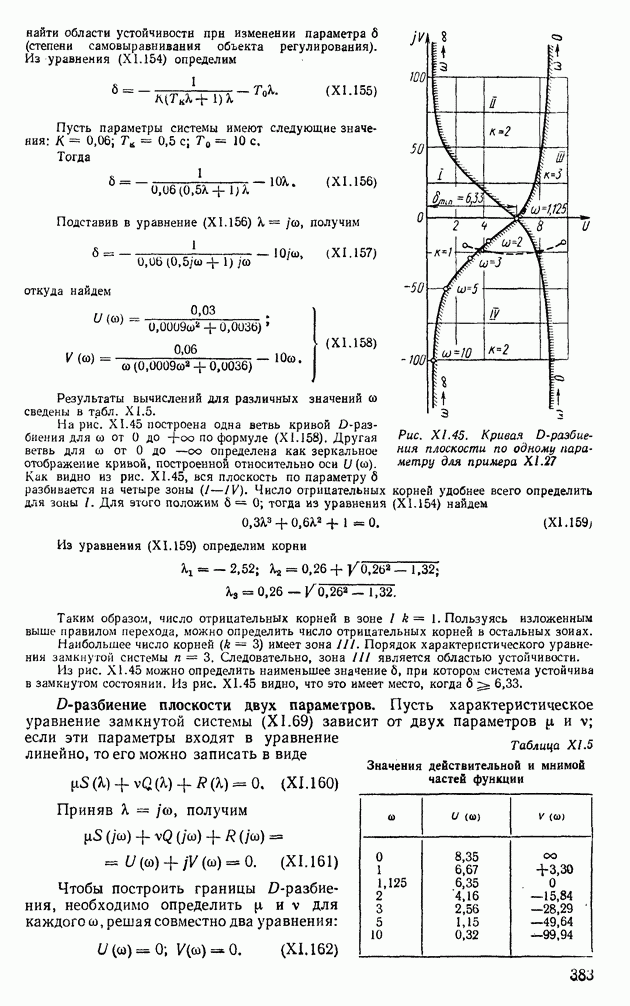
- 9. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ С ПОМОЩЬЮ D-РАЗБИЕНИЯ
- Глава XII. ИССЛЕДОВАНИЕ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
- 2. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПО ЗАДАННЫМ ПЕРЕДАТОЧНЫМ ФУНКЦИЯМ ЗАМКНУТЫХ СИСТЕМ
- 3. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПО РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ ЛЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ
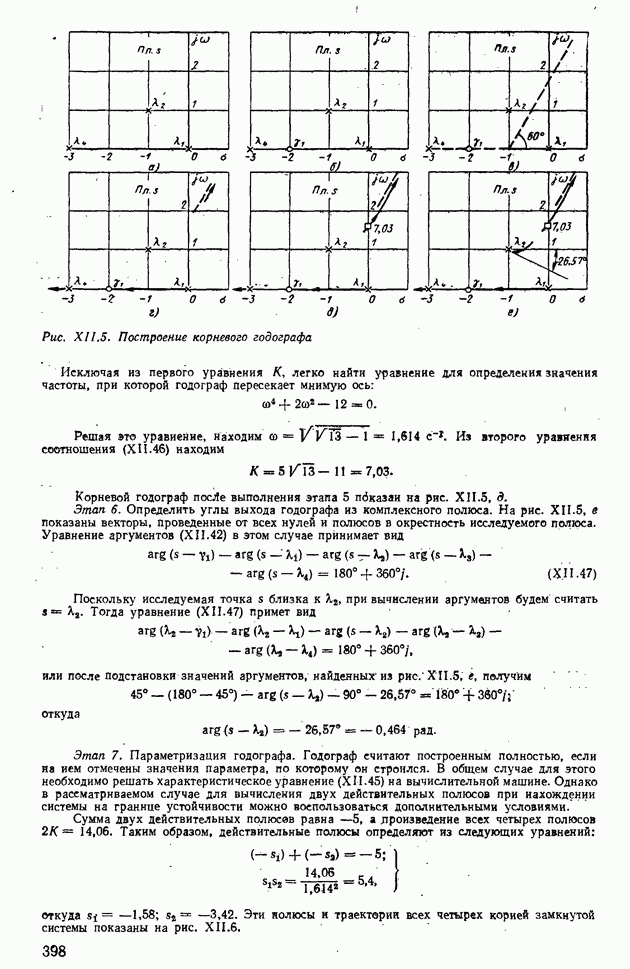
- 4. МЕТОД КОРНЕВОГО ГОДОГРАФА
- 5. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА
- 6. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ СИСТЕМ РЕГУЛИРОВАНИЯ И ИХ СВЯЗЬ С ХАРАКТЕРИСТИКАМИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 7. ОПРЕДЕЛЕНИЕ ВЕЩЕСТВЕННЫХ И МНИМЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СИСТЕМ ПО АМПЛИТУДНО-ФАЗОВЫМ И ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ РАЗОМКНУТЫХ СИСТЕМ
- 8. ЧАСТОТНЫЕ ОЦЕНКИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9. ЧАСТОТНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ТРАПЕЦЕИДАЛЬНЫХ ХАРАКТЕРИСТИК
- 10. УСТАНОВЛЕНИЕ НОРМ ЗАПАСОВ УСТОЙЧИВОСТИ ПО ФАЗЕ И МОДУЛЮ, ОБЕСПЕЧИВАЮЩИХ ТРЕБУЕМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМ РЕГУЛИРОВАНИЯ
- ГЛАВА XIII. ДИНАМИЧЕСКАЯ ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ОШИБОК В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ АМПЛИТУДНЫХ ХАРАКТЕРИСТИК
- 3. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПУТЕМ ПРИМЕНЕНИЯ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ
- 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 5. СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ СТАЦИОНАРНЫХ ПРОЦЕССОВ
- 6. СВОЙСТВА СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ
- 7. ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ
- 8. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЛИНЕЙНЫМИ СИСТЕМАМИ
- 9. РАСЧЕТ ОШИБОК В СИСТЕМЕ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ШУМОВ
- 10. ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ВОЗДЕЙСТВИИ СЛУЧАЙНЫХ СИГНАЛОВ И ШУМОВ
- ГЛАВА XIV. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ТИПОВЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ ПО ВТОРОМУ МЕТОДУ ЛЯПУНОВА
- 3. АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
- 4. ПРИМЕНЕНИЕ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. АНАЛИЗ АВТОКОЛЕБАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДВУМЯ НЕЛИНЕЙНОСТЯМИ
- 7. ДВУХКОНТУРНЫЕ НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕДЛЕННО ИЗМЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
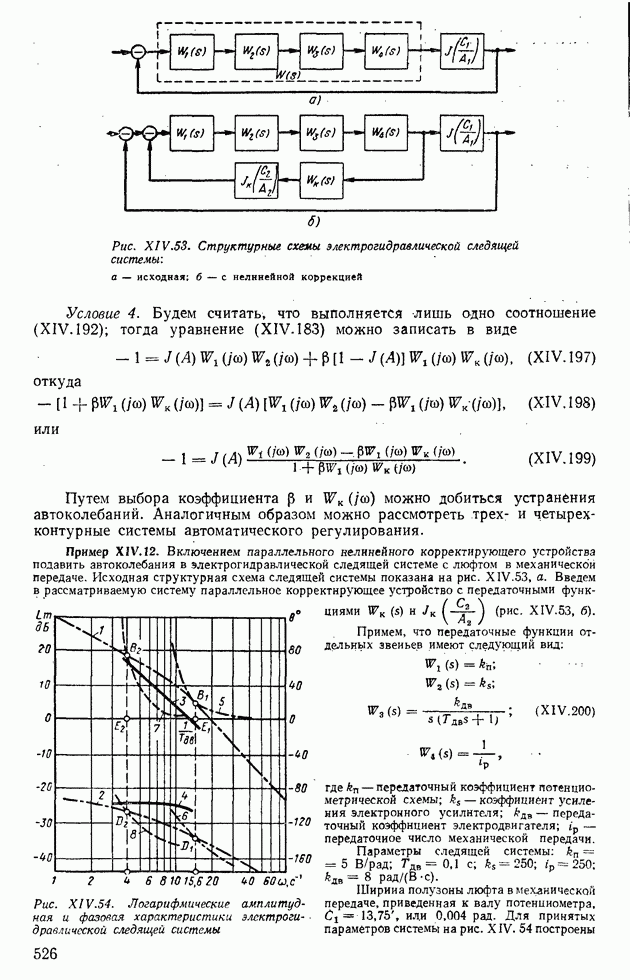
- 9. СПОСОБЫ ПОДАВЛЕНИЯ АВТОКОЛЕБАНИЙ В НЕЛИНЕЙНЫХ СИСТЕМАХ
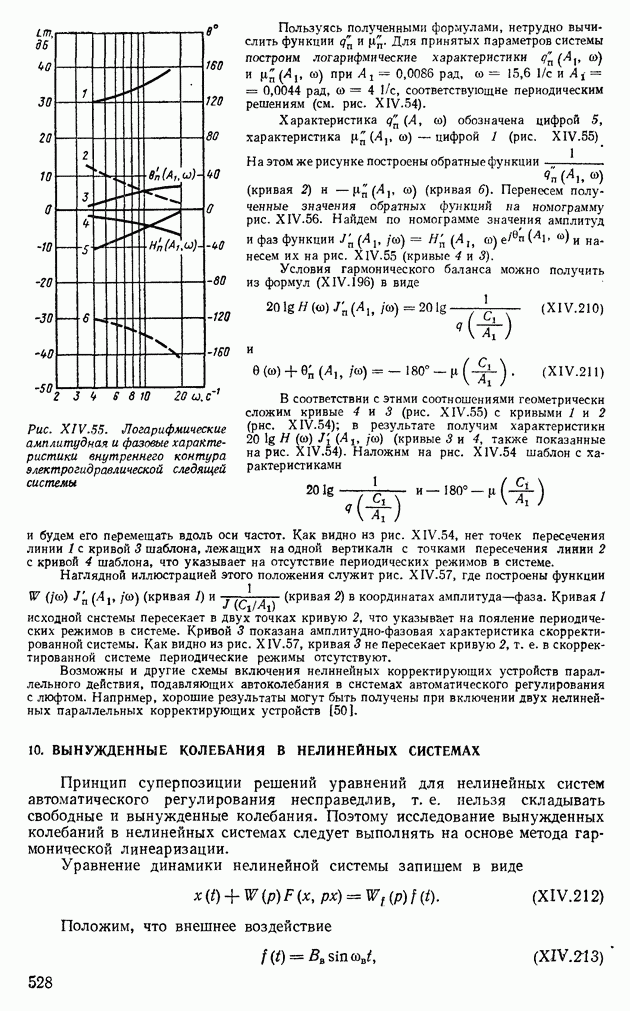
- 10. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 11. КРИТЕРИЙ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
- 12. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ
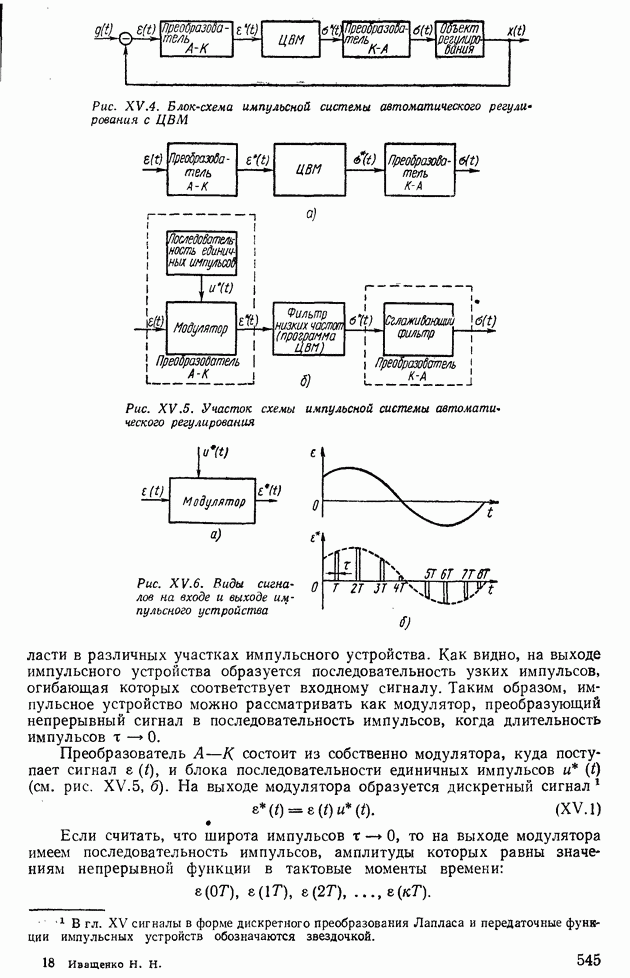
- Глава XIV. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ИМПУЛЬСНЫХ УСТРОЙСТВ
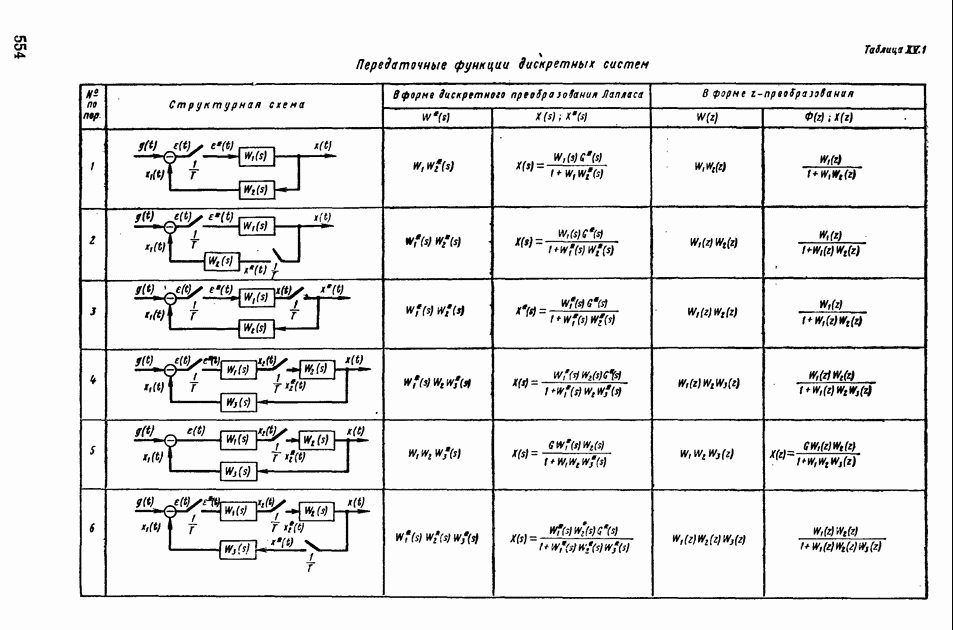
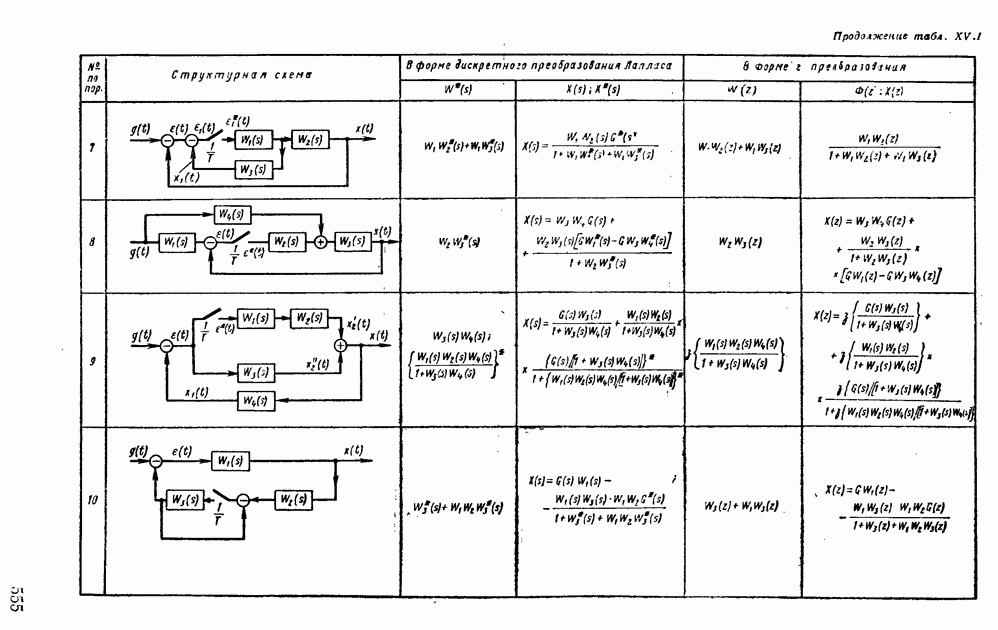
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. АМПЛИТУДНО-ФАЗОВЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ СИСТЕМ
- 4. ПРИМЕНЕНИЕ ВЕКТОРНО-МАТРИЧНОГО АППАРАТА К ИМПУЛЬСНЫМ СИСТЕМАМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
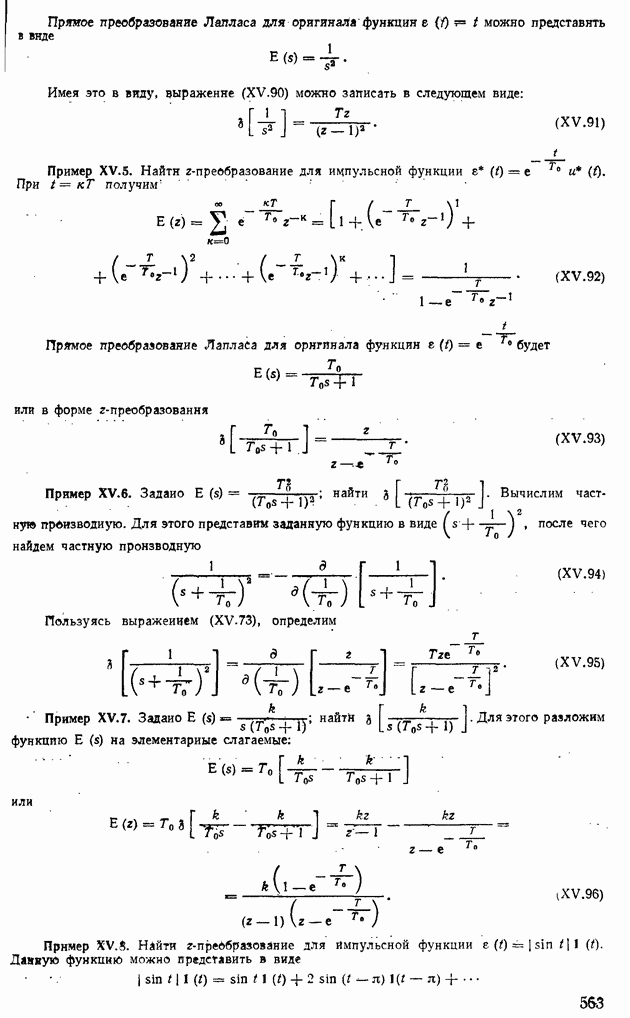
- 5. ОСНОВНЫЕ СВОЙСТВА z-ПРЕОБРАЗОВАНИЯ
- 6. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Критерий устойчивости для импульсных систем на плоскостях z и W(z).
- Критерий устойчивости Шур—Кона.
- Критерии устойчивости, основанные на применении билинейного преобразования.
- 7. МЕТОДЫ АНАЛИЗА КАЧЕСТВА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕТОДЫ АНАЛИЗА ТОЧНОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 9. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С УПРАВЛЯЮЩИМИ ЦВМ
- 10. СПОСОБЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ В УПРАВЛЯЮЩИХ ЦВМ И ОПРЕДЕЛЕНИЕ ИХ ОСНОВНЫХ ПАРАМЕТРОВ
- Глава XVI. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МЕТОДЫ ПОИСКА ЭКСТРЕМУМА
- 2. СПОСОБЫ ОРГАНИЗАЦИИ ДВИЖЕНИЯ К ЭКСТРЕМУМУ
- 3. МЕТОДЫ РАСЧЕТА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРОВ
- 4. ВЫБОР КОРРЕКТИРУЮЩИХ УСТРОЙСТВ В ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРАХ
- 5. ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ С ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ
- Глава XVII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ ВОЗДЕЙСТВИЯХ
- 2. ВЫБОР ПАРАМЕТРОВ УСТРОЙСТВ НЕИЗМЕНЯЕМОЙ ЧАСТИ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ПОСТРОЕНИЕ ЖЕЛАЕМОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 4. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. СИНТЕЗ ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 6. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 7. СПОСОБЫ РЕАЛИЗАЦИИ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Глава XVIII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 1. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА НА ОСНОВЕ КРИТЕРИЯ МИНИМУМА ИНТЕГРАЛЬНОЙ ОШИБКИ
- 2. СИНТЕЗ СИСТЕМ РЕГУЛИРОВАНИЯ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЖЕЛАЕМОЙ СИСТЕМЫ
- 4. ПРИМЕР СИНТЕЗА КОРРЕКТИРУЮЩИХ УСТРОЙСТВ СИСТЕМЫ РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- ГЛАВА XIX. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИНТЕЗ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ, ОСНОВАННЫЙ НА ПРИМЕНЕНИИ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- 2. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. РЕАЛИЗАЦИЯ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ ПРИ ПОМОЩИ RC-ЦЕПЕЙ
- 4. РЕАЛИЗАЦИЯ ПРОГРАММ КОРРЕКЦИИ НА УПРАВЛЯЮЩЕЙ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- ГЛАВА XX. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ПРИНЦИП МАКСИМУМА
- 3. ТЕОРЕМА О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
- 4. ПРИМЕРЫ ПРИМЕНЕНИЯ ПРИНЦИПА МАКСИМУМА
- 5. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 6. СИНТЕЗ НЕПРЕРЫВНЫХ ОПТИМАЛЬНЫХ СИСТЕМ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ