| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. ПРИМЕНЕНИЕ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
Сущность метода гармонической линеаризации заключается в отыскании периодического решения на входе нелинейного элемента, разложении сигнала на выходе нелинейного элемента в ряд Фурье и его замене первой гармоникой. Такая замена справедлива, если система автоматического регулирования является фильтром низких частот, хорошо Гасящим колебания высших гармоник [5,15,60].
Рассмотрим блок-схему релейной системы автоматического регулирования (рис. XIV.22), принципиальная схема которой изображена на рис. XIV.1, а. На входе релейного элемента имеется синусоидальный сигнал вида


Рис. XIV.22. Блок-схема релейной системы регулирования температуры печи
Сигнал на выходе трехпозиционного релейного элемента  с гистерезисом (или двузначной нелинейности) обозначим через
с гистерезисом (или двузначной нелинейности) обозначим через  а его приближенное значение через
а его приближенное значение через  . В этом случае имеем
. В этом случае имеем

где  — коэффициенты гармонической линеаризации.
— коэффициенты гармонической линеаризации.
Ошибку в выходном сигнале относительно его приближенного значения запишем в виде

Функция  является периодической с периодом
является периодической с периодом  а ее среднее квадратическое значение
а ее среднее квадратическое значение  удовлетворяет соотношению
удовлетворяет соотношению

Подставив в формулу (XIV.65) выражения (XIV.62) — (XIV.64), получим

Запишем условия минимума средней квадратической ошибки при замене точного значения выходного сигнала  приближенным:
приближенным:

С учетом выражения (XIV.66) найдем

откуда

или

Из выражений (XIV.70) имеем

откуда

Полученные выражения (XIV.72) и (XIV.73) для коэффициентов гармонической линеаризации обеспечивают минимум средней квадратической ошибки при замене точной функции  ее приближенным значением
ее приближенным значением  и являются формулами для определения первых коэффициентов ряда Фурье [49].
и являются формулами для определения первых коэффициентов ряда Фурье [49].
Для нелинейностей без гистерезиса (однозначных)  тогда имеем
тогда имеем

Линеаризуем однозначную нелинейность  Заменив ее выражением (XIV.74), получим
Заменив ее выражением (XIV.74), получим

Подставив в полученную формулу соотношение (XIV.61), найдем

или

Следовательно, коэффициент гармонической линеаризации представляет собой коэффициент усиления в виде отношения амплитуды первой гармоники выходного сигнала у к входному сигналу х, т. е.

На рис. XIV.23 показано графическое определение коэффициента гармонической линеаризации для однозначной нелинейности.
Как видно из рис. XIV.23, синусоидальный вход сигнал  с амплитудой А образует на выходе нелинейности сигнал
с амплитудой А образует на выходе нелинейности сигнал  Заменяя этот сигнал первой гармонической составляющей, получим
Заменяя этот сигнал первой гармонической составляющей, получим

где  амплитуда первой гармоники выходного сигнала.
амплитуда первой гармоники выходного сигнала.
В этом случае коэффициент гармонической линеаризации, определяемый по формуле (XIV.78), есть наклон прямой 1, равный а  При изменении амплитуды входного сигнала до А коэффициент гармонической линеаризации — наклон прямой 2 — уменьшается до
При изменении амплитуды входного сигнала до А коэффициент гармонической линеаризации — наклон прямой 2 — уменьшается до  Отсюда следует,
Отсюда следует,

Рис. XIV.23. Определение козфициента гармонической линеаризации идеальной релейной характеристики с воной нечувствительности
что при таком подходе свойства нелинейного элемента эквивалентно отображаются в изменении коэффициента гармонической линеаризации в зависимости от амплитуды входного сигнала.
В соответствии с формулой (XIV.78) нелинейность в дифференциальных уравнениях можно представить в виде следующего линеаризованного соотношения

Из соотношения (XIV.79) видно, что с изменением амплитуды входного сигнала изменяется коэффициент гармоничёскбй линеаризации, а следовательно, изменяется и значение 
Составим нелинейные дифференциальные уравнения для релейной системы автоматического регулирования температуры печи а виде

Пользуясь методом гармонической линеаризации, приведем данное нелинейное дифференциальное уравнение к гармонически линеаризованному. Вместо функции  подставим коэффициент а
подставим коэффициент а  тогда получим
тогда получим

Последнее уравнение, хотя и является линеаризованным, однако оно сохраняет основные свойства нелинейного уравнения, так как коэффициент а  изменяется в зависимости от амплитуды А. В этом и заключается основное отличие гармонической линеаризации нелинейных уравнений от обычной, линеаризации, рассмотреннной в гл. III.
изменяется в зависимости от амплитуды А. В этом и заключается основное отличие гармонической линеаризации нелинейных уравнений от обычной, линеаризации, рассмотреннной в гл. III.
Перейдем к замене двузначной нелинейной функции  линеаризованным выражением. Для этого представим зависимость
линеаризованным выражением. Для этого представим зависимость  в виде
в виде

где

Из уравнения (XIV.61) найдем

откуда

Кроме того, из выражения (XIV.61) следует, что

Подставим выражения (XIV.84) и  в уравнение (XIV.82); в результате получим следующее линеаризованное соотношение:
в уравнение (XIV.82); в результате получим следующее линеаризованное соотношение:

Первый член соотношения (XIV.86) имеет тот же смысл, что и в уравнении (XIV.79), а второй член определяет запаздывание, зависящее от производной входного сигнала.
Соотношение (XIV.86) можно переписать и в следующем виде:

Пйльзуясь Соотношением (XIV.87), гармонически линеаризуем нелинейное уравнение (XIV.80):

Дифференциальное уравнение (XIV.88) является гармонически линеаризованным.
По аналогии с передаточными функциями линейных звеньев введем понятие эквивалентной передаточной функции нелинейного двузначного звена

бднозначного нелинейного звена

Соотношение (XIV.89) можно переписать и в виде

где  — эквивалентная амплитудная характеристика нелинейного звена;
— эквивалентная амплитудная характеристика нелинейного звена;  — эквивалентная фазовая характеристика нелинейного звена.
— эквивалентная фазовая характеристика нелинейного звена.
Функции  связаны с коэффициентами гармонической линеаризации следующими зависимостями:
связаны с коэффициентами гармонической линеаризации следующими зависимостями:

Полученные зависимости (XIV.92) и (XIV.93) справедливы для двузначных нелинейностей. Для однозначных нелинейностей при  имеем
имеем

и

Графический способ определения частот и амплитуд автоколебаний в нелинейных системах (метод шаблонов) [49]. В основу метода шаблонов графического определения амплитуд и частот колебаний положено условие гармонического баланса. Для его нахождения воспользуемся характеристическим уравнением нелинейной системы, структурная схема которой изображена на рис. XIV.24, а:

где  — передаточная функция линейной части системы;
— передаточная функция линейной части системы;  — эквивалентная передаточная функция нелинейной части системы.
— эквивалентная передаточная функция нелинейной части системы.

Рис. XIV.24. Структурные схемы релейных (нелинейных) систем автоматического регулирования: а — с линейной и нелинейной частями в прямой цепи; б — с нелинейной частью в прямой цепи и линейной частью в цепи главной обратной связи; в — с линейной частью в прямой цепи и нелинейной частью в цепи главной обратной связи
Передаточную функцию  представим в виде
представим в виде

где  — амплитудная частотная характеристика линейной части системы;
— амплитудная частотная характеристика линейной части системы;  — фазовая частотная характеристика линейной части разомкнутой системы.
— фазовая частотная характеристика линейной части разомкнутой системы.
Подставим выражения (XIV.91) и (XIV.97) в уравнение (XIV.96); тогда получим

откуда нетрудно найти, что

или

Из уравнения (XIV. 100) получим следующие условия гармонического баланса:

или

Из соотношений (XIV. 102) видно, что при одновременном выполнении условий баланса для амплитуд и фаз в системе автоматического регулирования возникают автоколебания.
Одновременность выполнения условий (XIV. 102) графически выражается в том, что точки пересечения амплитудных характеристик  и фазовых характеристик
и фазовых характеристик  лежат на одной вертикали. Таким образом с помощью графического решения уравнений (XIV. 102) можно определить частоту
лежат на одной вертикали. Таким образом с помощью графического решения уравнений (XIV. 102) можно определить частоту  и амплитуду А автоколебаний в системе с двузначной нелинейностью.
и амплитуду А автоколебаний в системе с двузначной нелинейностью.
В системе с однозначной нелинейностью имеем

Условие (XIV. 103) возникновения периодического режима для такой системы заключается в одновременном пересечении амплитудных характеристик  и фазовой характеристики
и фазовой характеристики  с линией
с линией  .
.

Рис. XIV.25. Шаблоны для нелинейных элементов: а — идеального реле; б - реле с зоной нечувствительности; в — реле с гистерезисом; г - реле с гистерезисом и зоной нечувствительности
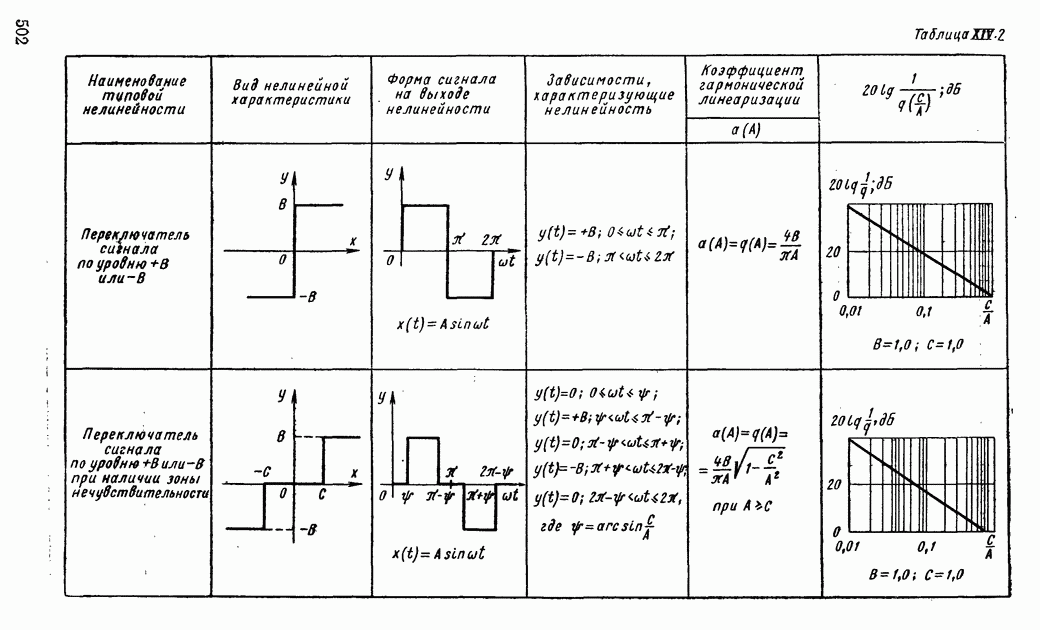
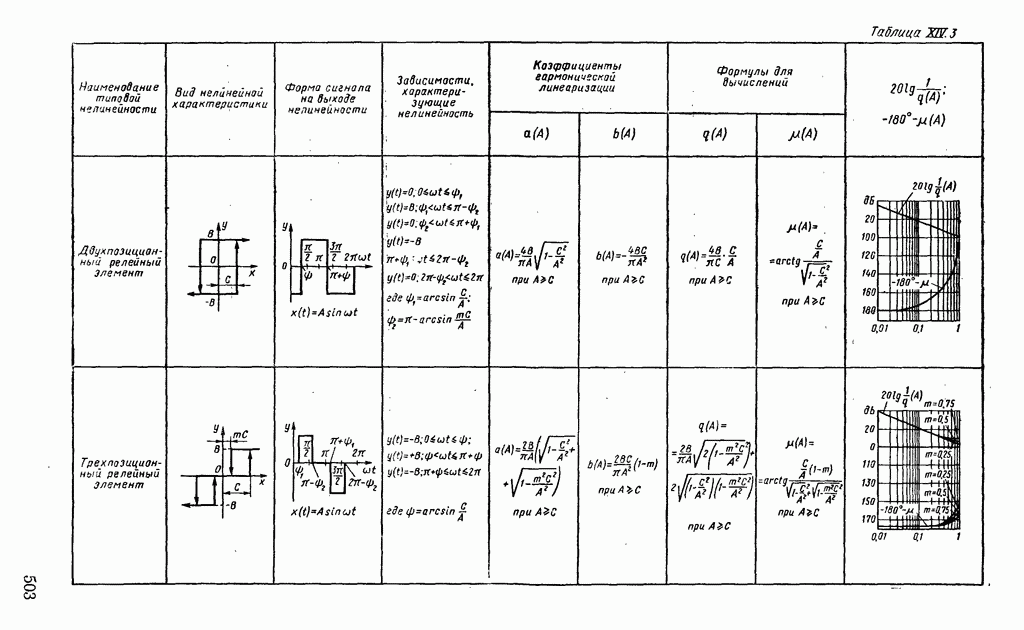
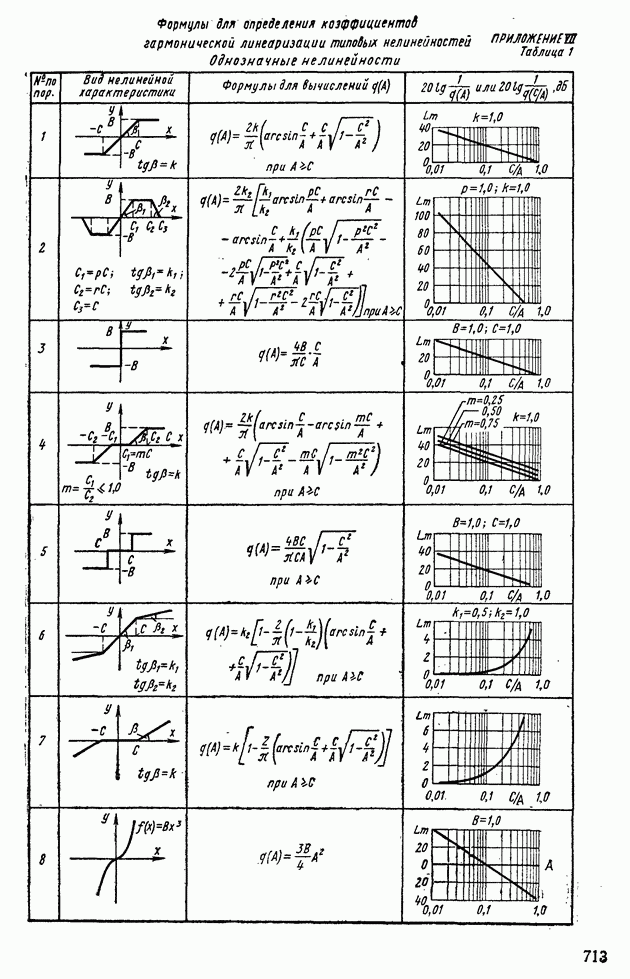
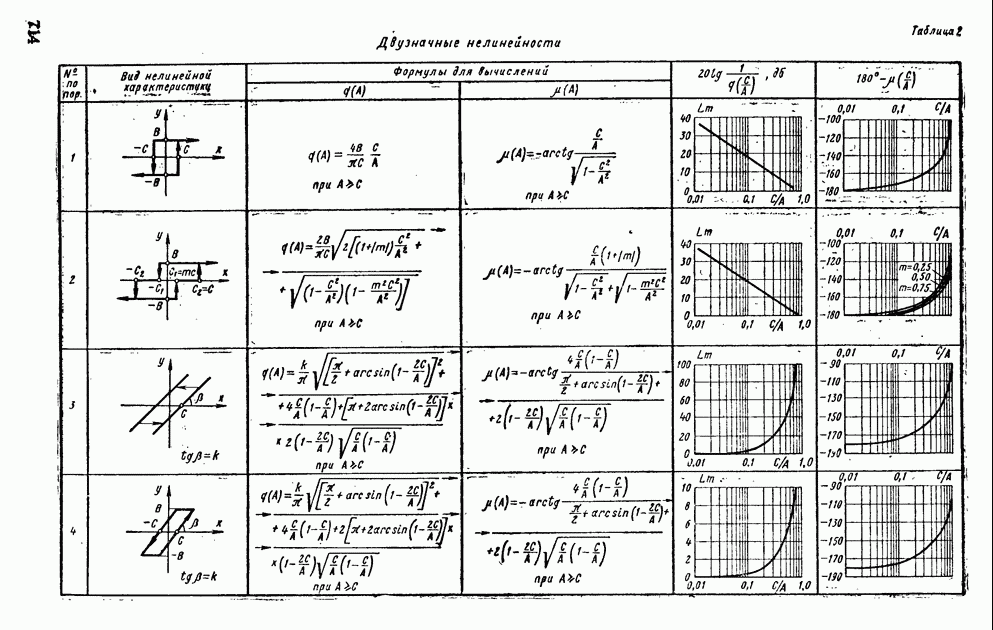
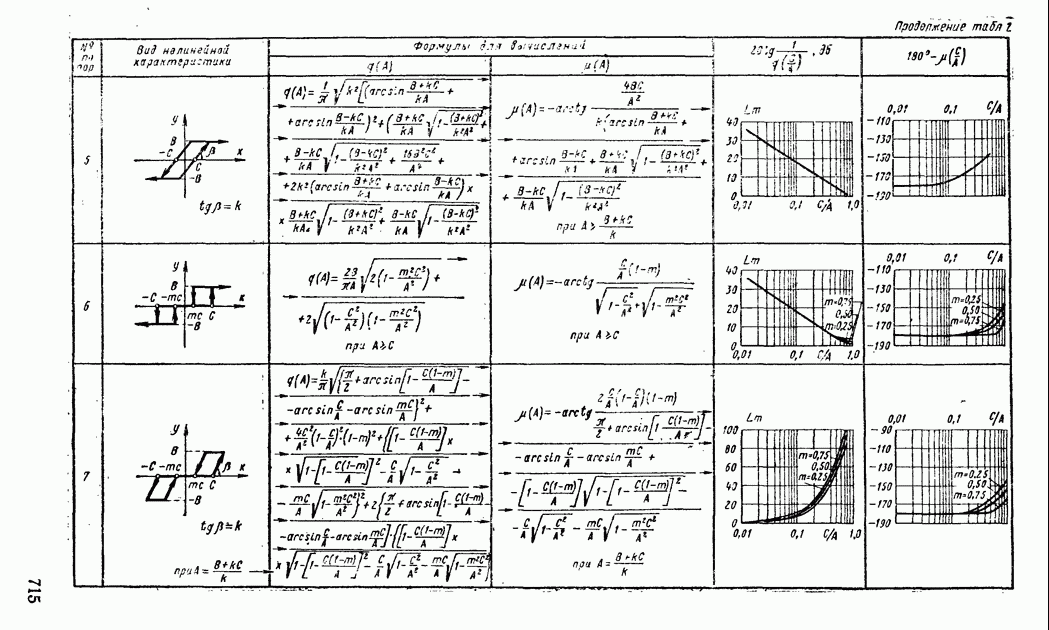
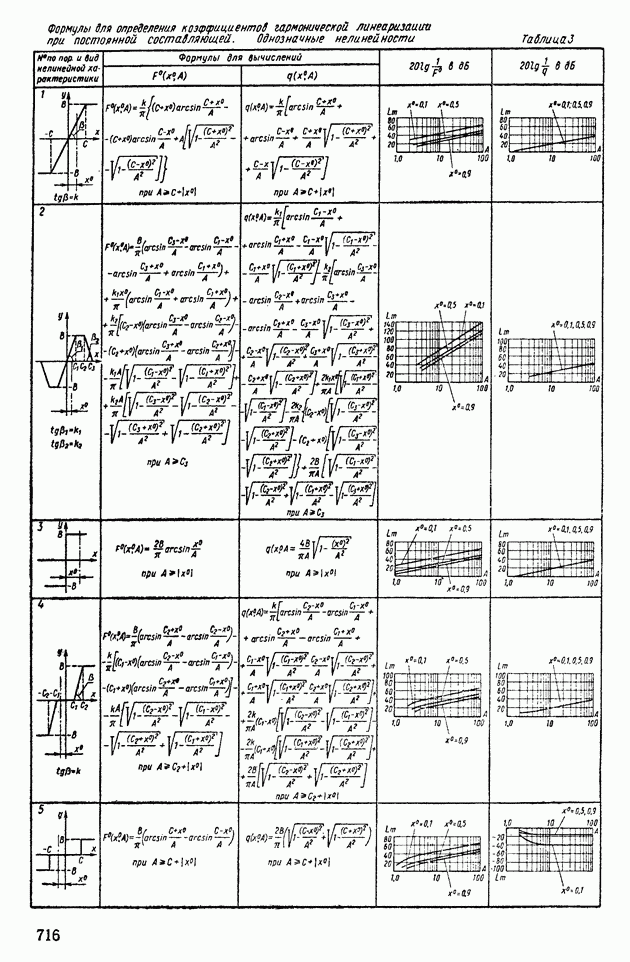
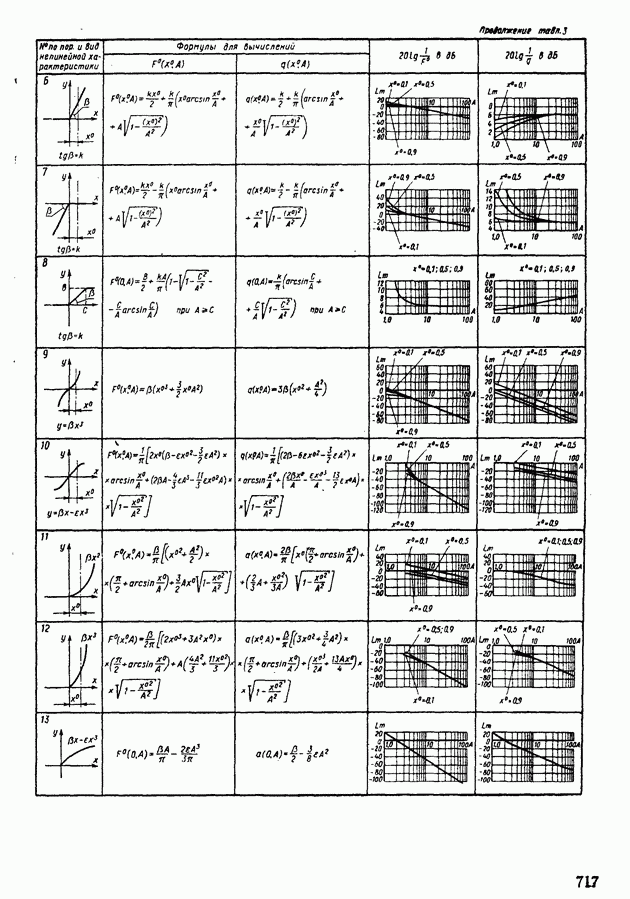
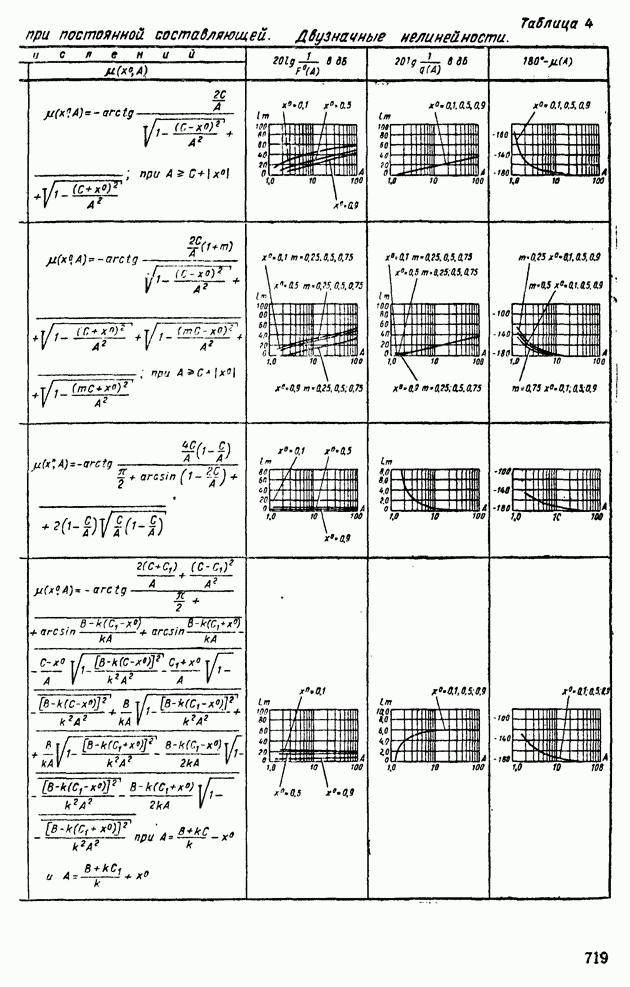
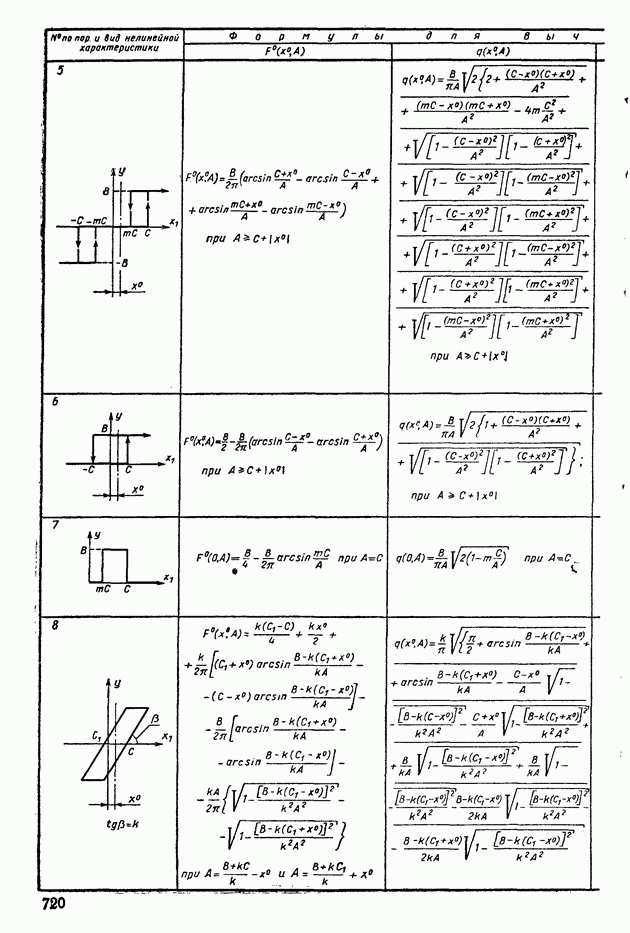
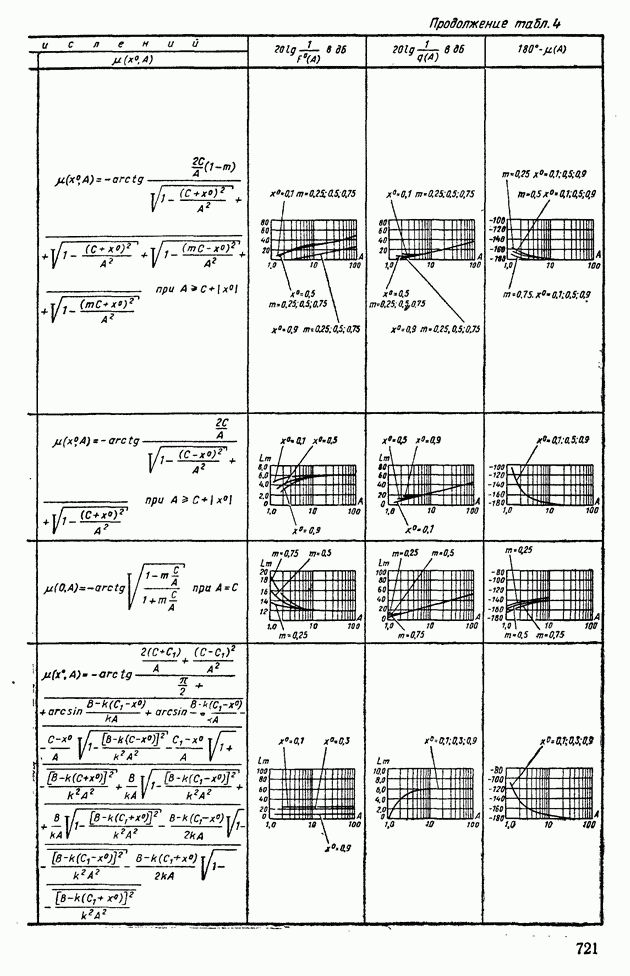
В табл. XIV.2 и XIV.3 даны формулы для определения характеристик  и
и  и приведены шаблоны
и приведены шаблоны  Пользуясь этими шаблонами и логарифмическими амплитудной и фазовой частотными характеристиками линейной части системы регулирования, определяют периодические решения. Для этого шаблон с характеристиками
Пользуясь этими шаблонами и логарифмическими амплитудной и фазовой частотными характеристиками линейной части системы регулирования, определяют периодические решения. Для этого шаблон с характеристиками  построенными на полулогарифмической бумаге (рис. XIV.25), накладывают на. частотные характеристики
построенными на полулогарифмической бумаге (рис. XIV.25), накладывают на. частотные характеристики  совмещая ось частот с осью относительных амплитуд
совмещая ось частот с осью относительных амплитуд  Перемещая шаблон вдоль оси частот, определяют точки пересечения кривых
Перемещая шаблон вдоль оси частот, определяют точки пересечения кривых  Если точки пересечения амплитудных и фазовых характеристик находятся на одной вертикали, то в системе наблюдаются периодические режимы.
Если точки пересечения амплитудных и фазовых характеристик находятся на одной вертикали, то в системе наблюдаются периодические режимы.
На рис. XIV.26 показаны различные положения шаблонов относительно частотных характеристик линейной части системы. При положении шаблона, показанном на рис. XIV.26, а, отсутствуют точки пересечения амплитудных и фазовых характеристик, следовательно, в такой системе регулирования не могут существовать периодические колебания. Перемещаем шаблон влево до тех пор, пока точки пересечения  не окажутся на одной вертикали (рис. XIV.26, б). При этом в релейной системе возникают периодические колебания с частотой
не окажутся на одной вертикали (рис. XIV.26, б). При этом в релейной системе возникают периодические колебания с частотой  При дальнейшем перемещении шаблона влево снова находятся две точки пересечения
При дальнейшем перемещении шаблона влево снова находятся две точки пересечения  (рис. XIV.26, в), соответствующие периодическому колебанию с частотой
(рис. XIV.26, в), соответствующие периодическому колебанию с частотой  , наконец, при положении шаблона, показанном на рис. XIV.26, г, точки пересечения
, наконец, при положении шаблона, показанном на рис. XIV.26, г, точки пересечения  амплитудных и фазовых характеристик не лежат на одной вертикали, что означает отсутствие автоколебаний в системе.
амплитудных и фазовых характеристик не лежат на одной вертикали, что означает отсутствие автоколебаний в системе.

(кликните для просмотра скана)

(кликните для просмотра скана)
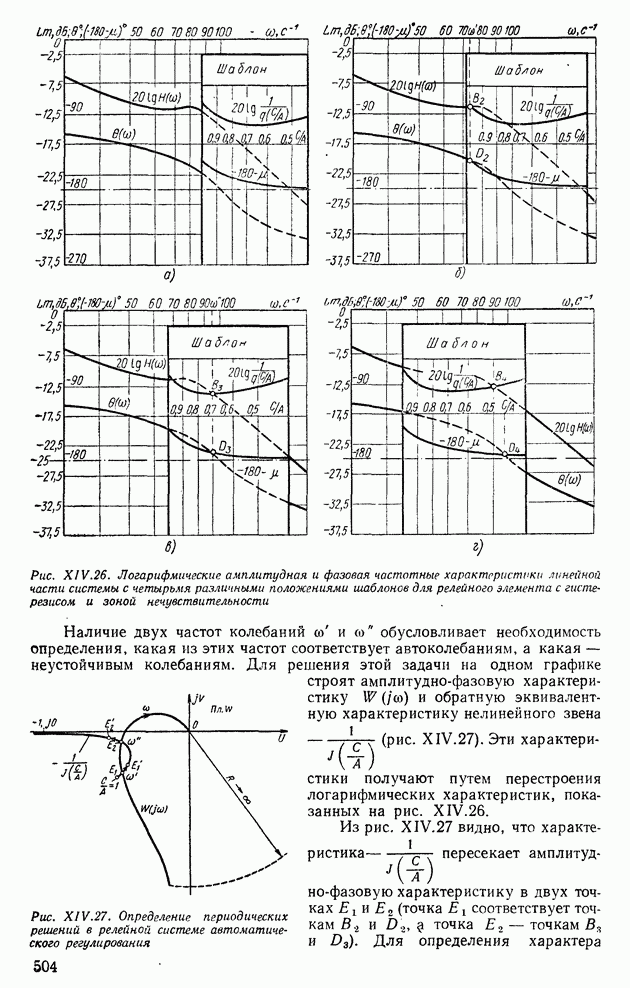
Рис. XIV.26. (см. скан) Логарифмические амплитудная и фазовая частотные характеристики линейной части системы с четырьмя различными положениями шаблонов для релейного элемента с гистерезисом и зоной нечувствительности
Наличие двух частот колебаний  обусловливает необходимость определения, какая из этих частот соответствует автоколебаниям, а какая — неустойчивым колебаниям. Для решения этой задачи на одном графике строят амплитудно-фазовую характеристику
обусловливает необходимость определения, какая из этих частот соответствует автоколебаниям, а какая — неустойчивым колебаниям. Для решения этой задачи на одном графике строят амплитудно-фазовую характеристику  и обратную эквивалентную характеристику нелинейного звена
и обратную эквивалентную характеристику нелинейного звена  (рис. XIV.27). Эти характеристики получают путем перестроения логарифмических характеристик, показанных на рис. XIV.26.
(рис. XIV.27). Эти характеристики получают путем перестроения логарифмических характеристик, показанных на рис. XIV.26.
Из рис. XIV.27 видно, что характеристика  пересекает амплитудно-фазовую характеристику в двух точках
пересекает амплитудно-фазовую характеристику в двух точках  (точка
(точка  соответствует точкам
соответствует точкам  точка
точка  — точкам
— точкам  Для определения характера
Для определения характера

Рис. XIV.27. Определение периодических решений в релейной системе автоматического регулирования
колебаний воспользуемся критерием предложенным Е. П. Поповым [60]. В релейной (нелинейной) системе автоматического регулирования возникают автоколебания (устойчивые периодические решения), когда годограф  не охватывает точку, расположенную на обратной эквивалентной характеристике нелинейного звена, если эта точка получена путем малого увеличения амплитуды на А А (на рис. XIV.27 эти точки обозначены как
не охватывает точку, расположенную на обратной эквивалентной характеристике нелинейного звена, если эта точка получена путем малого увеличения амплитуды на А А (на рис. XIV.27 эти точки обозначены как  Иначе говоря, если с ростом амплитуды характеристика в точке пересечения кривых выходит за годограф
Иначе говоря, если с ростом амплитуды характеристика в точке пересечения кривых выходит за годограф  то в системе наблюдаются автоколебания. На рис. XIV.27 эта частота обозначена
то в системе наблюдаются автоколебания. На рис. XIV.27 эта частота обозначена  Если с ростом амплитуды точка охватывается годографом
Если с ростом амплитуды точка охватывается годографом  то в системе возникают неустойчивые колебания. На рис. XIV.27 эта частота обозначена
то в системе возникают неустойчивые колебания. На рис. XIV.27 эта частота обозначена  .
.
Для установления характера колебаний можно пользоваться следующим критерием, предложенным для систем с двузначными нелинейностями [40]. В нелинейной системе автоматического регулирования с двузначными нелинейностями возникают автоколебания, если с ростом амплитуды А точка пересечения характеристик  лежащая на одной вертикали с точкой пересечения характеристик —
лежащая на одной вертикали с точкой пересечения характеристик —  находится вне области, образованной линиями
находится вне области, образованной линиями  и осью частот
и осью частот  и, наоборот, в нелинейной системе колебания будут неустойчивыми, если с ростом амплитуды указанная точка пересечения будет входить внутрь указанной области.
и, наоборот, в нелинейной системе колебания будут неустойчивыми, если с ростом амплитуды указанная точка пересечения будет входить внутрь указанной области.
На рис. XIV.26, б точка, соответствующая увеличенному значению амплитуды, будет находиться в области между амплитудной частотной характеристикой системы и осью частот; следовательно, колебания с частотой со будут неустойчивыми.
Рассмотрим колебания с частотой  (см. рис. XIV.26, в). При увеличении амплитуды А точка
(см. рис. XIV.26, в). При увеличении амплитуды А точка  выйдет из области, ограниченной амплитудной частотной характеристикой и осью частот, и, следовательно, колебания с частотой
выйдет из области, ограниченной амплитудной частотной характеристикой и осью частот, и, следовательно, колебания с частотой  соответствуют автоколебаниям в релейной системе.
соответствуют автоколебаниям в релейной системе.
При анализе устойчивости нелинейных систем регулирования с нелинейностью типа насыщения можно пользоваться следующим критерием для определения типа колебаний. В системе регулирования наблюдаются автоколебания, если в точке пересечения логарифмической фазовой характеристики с линией  производная
производная  и, наоборот, если в точке пересечения
и, наоборот, если в точке пересечения  то в системе наблюдаются неустойчивые колебания.
то в системе наблюдаются неустойчивые колебания.
Построение областей устойчивых и неустойчивых состояний в релейных системах. Для построения областей устойчивых и неустойчивых состояний релейной системы будем изменять параметры ее линейной и нелинейной частей. Накладывая соответствующие шаблоны на логарифмические характеристики системы, находим значения частот  и амплитуд А и
и амплитуд А и  Откладывая по оси абсцисс требуемые значения параметров К системы, а по оси ординат частоту (рис. XIV.28, а) или амплитуду (рис. XIV.28, б) колебаний, строим зависимости частот и амплитуд колебаний от параметров системы. Частоты и амплитуды устойчивых колебаний (автоколебаний) обозначим стрелками, направленными к линии, а неустойчивых колебаний — стрелками, направленными от линии.
Откладывая по оси абсцисс требуемые значения параметров К системы, а по оси ординат частоту (рис. XIV.28, а) или амплитуду (рис. XIV.28, б) колебаний, строим зависимости частот и амплитуд колебаний от параметров системы. Частоты и амплитуды устойчивых колебаний (автоколебаний) обозначим стрелками, направленными к линии, а неустойчивых колебаний — стрелками, направленными от линии.
Проведем вертикальную прямую  через точку А и прямую I—II через точку
через точку А и прямую I—II через точку  тогда получим две области: первая — между осью ординат и прямой
тогда получим две области: первая — между осью ординат и прямой  (II—II) образует область устойчивых состояний; вторая — от прямой I—I (II—II) вправо до бесконечности образует область неустойчивых состояний и автоколебаний (рис. XIV.28).
(II—II) образует область устойчивых состояний; вторая — от прямой I—I (II—II) вправо до бесконечности образует область неустойчивых состояний и автоколебаний (рис. XIV.28).

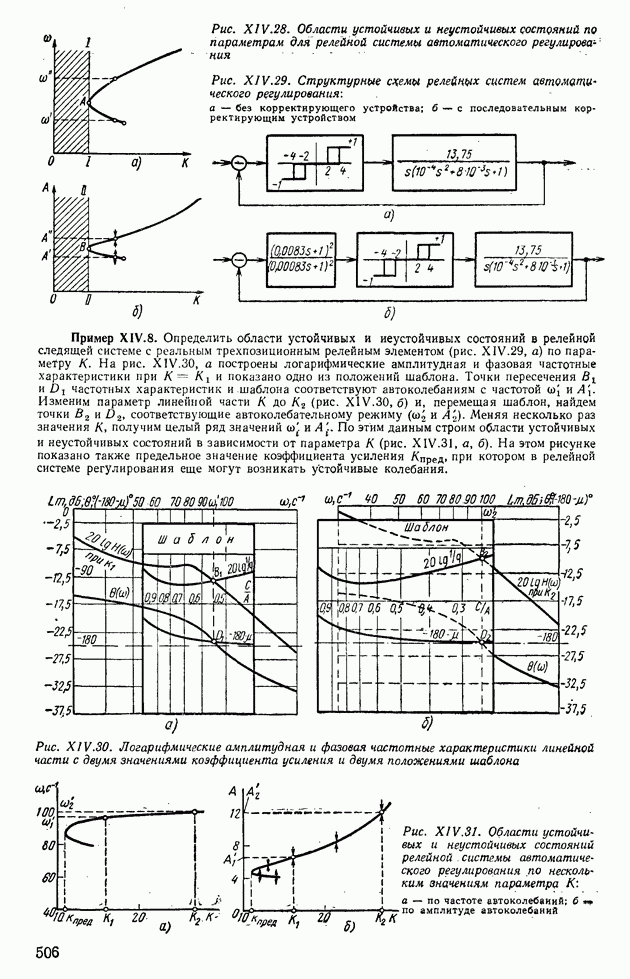
Рис. XIV.28. Области устойчивых и неустойчивых состояний по параметрам для релейной системы автоматического регулирования

Рис. XIV.29. Структурные схемы релейных систем автоматического регулирования: а — без корректирующего устройства; б — с последовательным корректирующим устройством
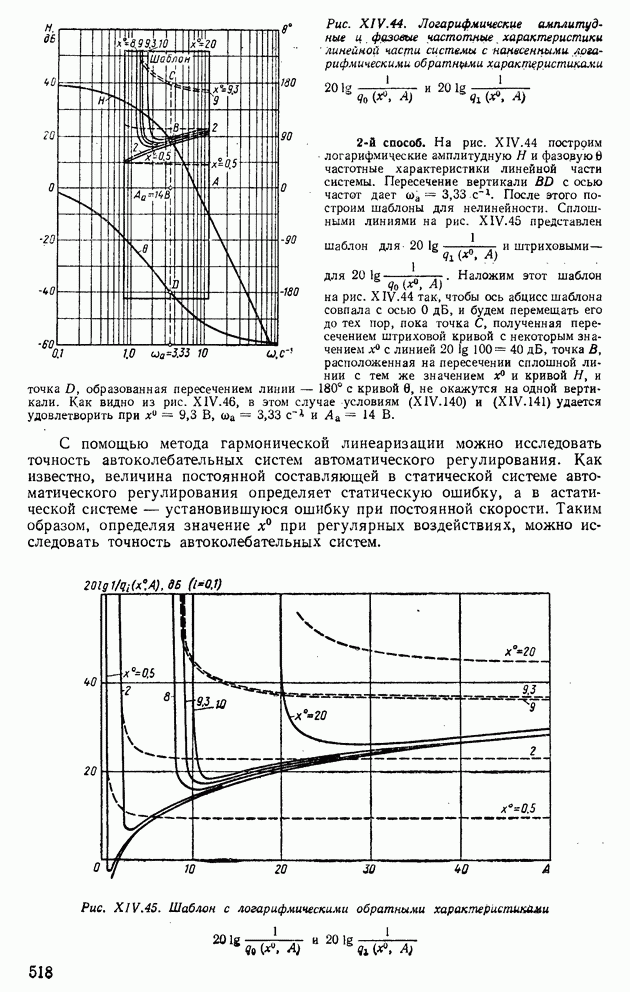
Пример XIV.8. Определить области устойчивых и неустойчивых состояний в релейной следящей системе с реальным трехпозиционным релейным элементом (рис. XIV.29, а) по параметру К. На рис. XIV.30, а построены логарифмические амплитудная и фазовая частотные характеристики при  и показано одно из положений шаблона. Точки пересечения
и показано одно из положений шаблона. Точки пересечения  частотных характеристик и шаблона соответствуют автоколебаниям с частотой
частотных характеристик и шаблона соответствуют автоколебаниям с частотой  Изменим параметр линейной части К до
Изменим параметр линейной части К до  (рис. XIV.30, б) и, перемещая шаблон, найдем точки
(рис. XIV.30, б) и, перемещая шаблон, найдем точки  соответствующие автоколебательному режиму и
соответствующие автоколебательному режиму и  Меняя несколько раз значения
Меняя несколько раз значения  получим целый ряд значений
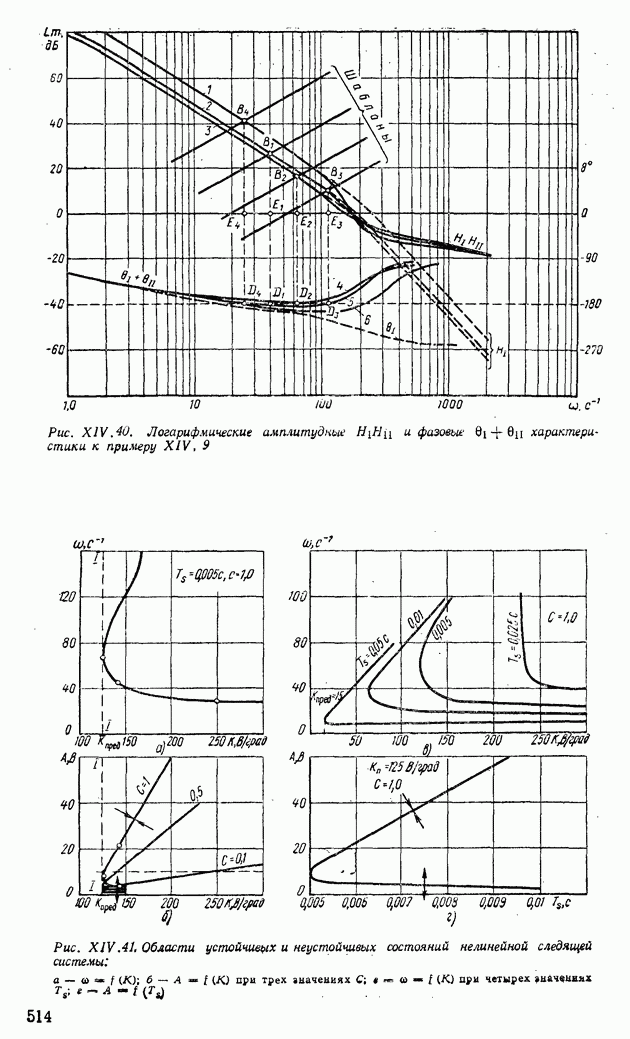
получим целый ряд значений  .. По этим данным строим области устойчивых и неустойчивых состояний в зависимости от параметра К (рис. XIV.31, а, б). На этом рисунке показано также предельное значение коэффициента усиления
.. По этим данным строим области устойчивых и неустойчивых состояний в зависимости от параметра К (рис. XIV.31, а, б). На этом рисунке показано также предельное значение коэффициента усиления  котором в релейной системе регулирования еще могут возникать устойчивые колебания.
котором в релейной системе регулирования еще могут возникать устойчивые колебания.

Рис. XIV.30. Логарифмические амплитудная и фазовая частотные характеристики линейной части с двумя значениями коэффициента усиления и двумя положениями шаблона

Рис. XIV.31. Области устойчивых и неустойчивых состояний релейной - системы автоматического регулирования по нескольким значениям параметра К: а — по частоте автоколебаний; б - по амплитуде автоколебаний

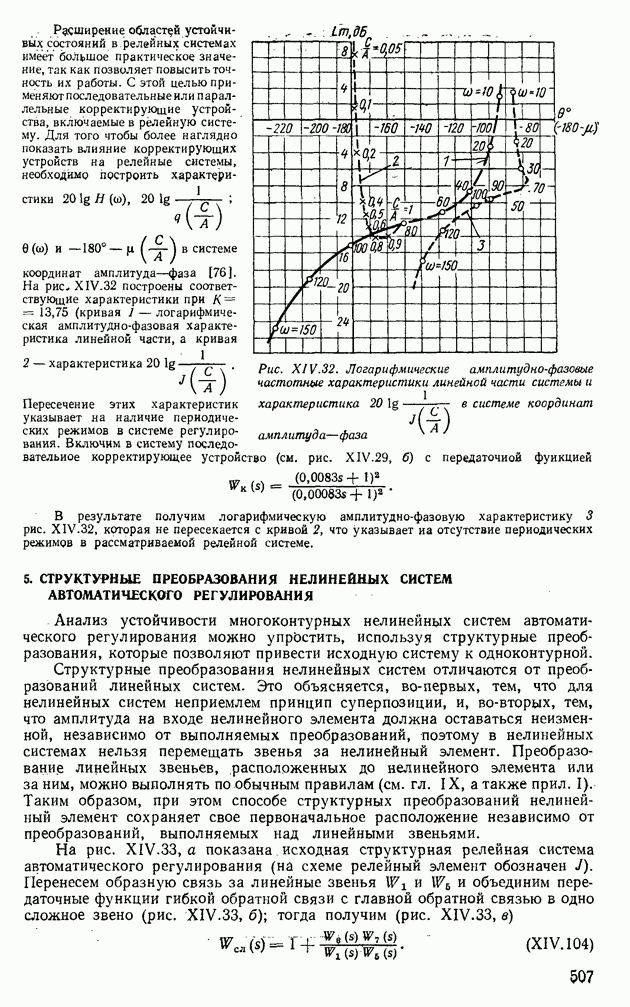
Рис. XIV.32. Логарифмические амплитудно-фазовые частотные характеристики линейной части системы и характеристика  в системе координат амплитуда—фаза
в системе координат амплитуда—фаза
Расширение областей устойчивых состояний в релейных системах имеет большое практическое значение, так как позволяет повысить точность их работы. С этой целью применяют последовательные или параллельные корректирующие устройства, включаемые в релейную систему. Для того чтобы более наглядно показать влияние корректирующих устройств на релейные системы, необходимо построить характеристики  в системе координат амплитуда—фаза [76].
в системе координат амплитуда—фаза [76].
На рис. XIV.32 построены соответствующие характеристики при  (кривая 1 — логарифмическая амплитудно-фазовая характеристика линейной части, а кривая 2 — характеристика
(кривая 1 — логарифмическая амплитудно-фазовая характеристика линейной части, а кривая 2 — характеристика 
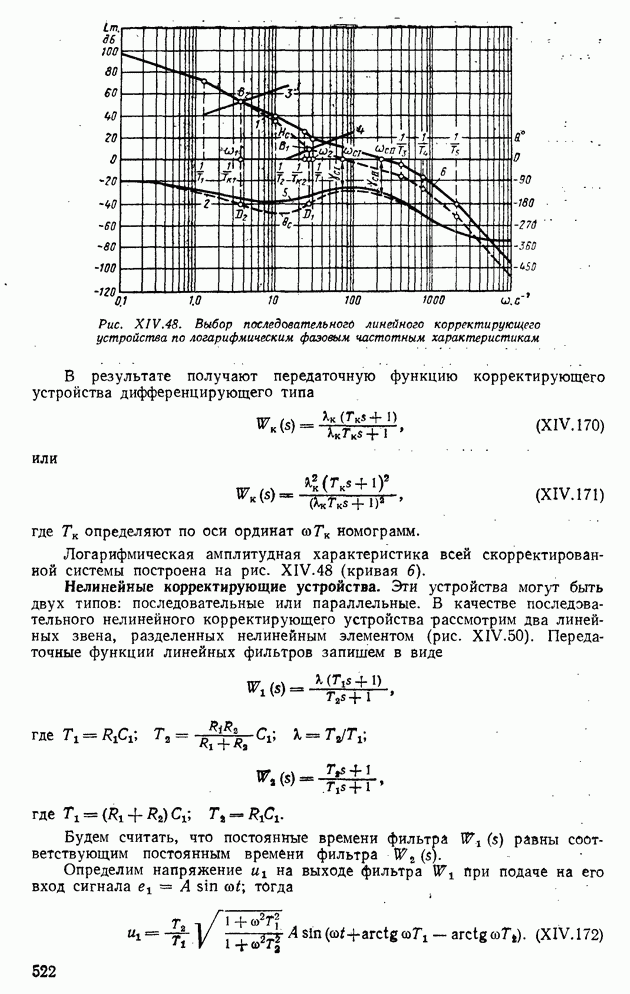
Пересечение этих характеристик указывает на наличие периодических режимов в системе регулирования. Включим в систему последовательное корректирующее устройство (см. рис. XIV.29, б) с передаточной функцией

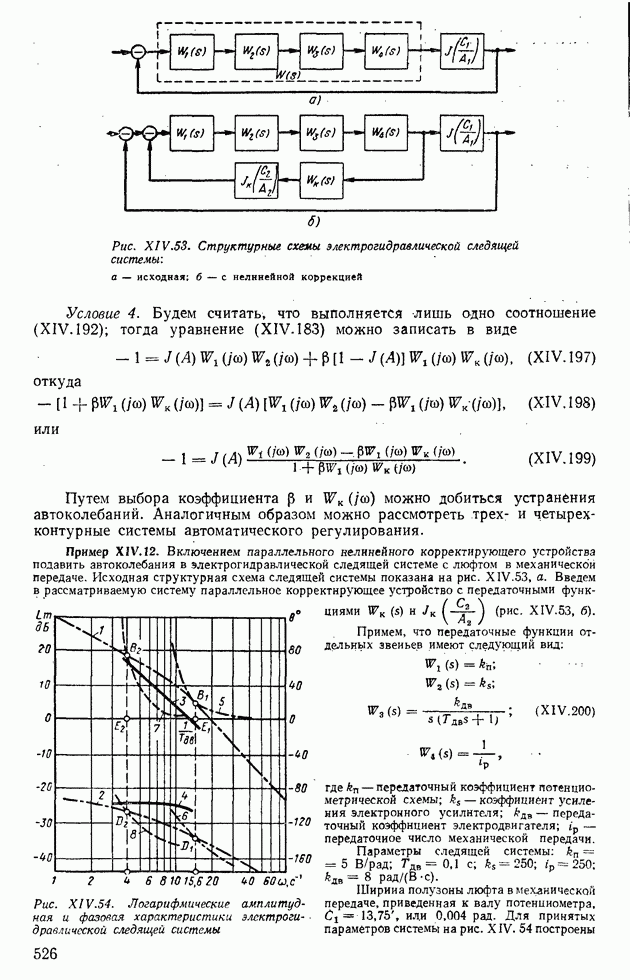
В результате получим логарифмическую амплитудно-фазовую характеристику 3 рис. XIV.32, которая не пересекается с кривой 2, что указывает на отсутствие периодических режимов в рассматриваемой релейной системе.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 1. ПРИНЦИПЫ ДЕЙСТВИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
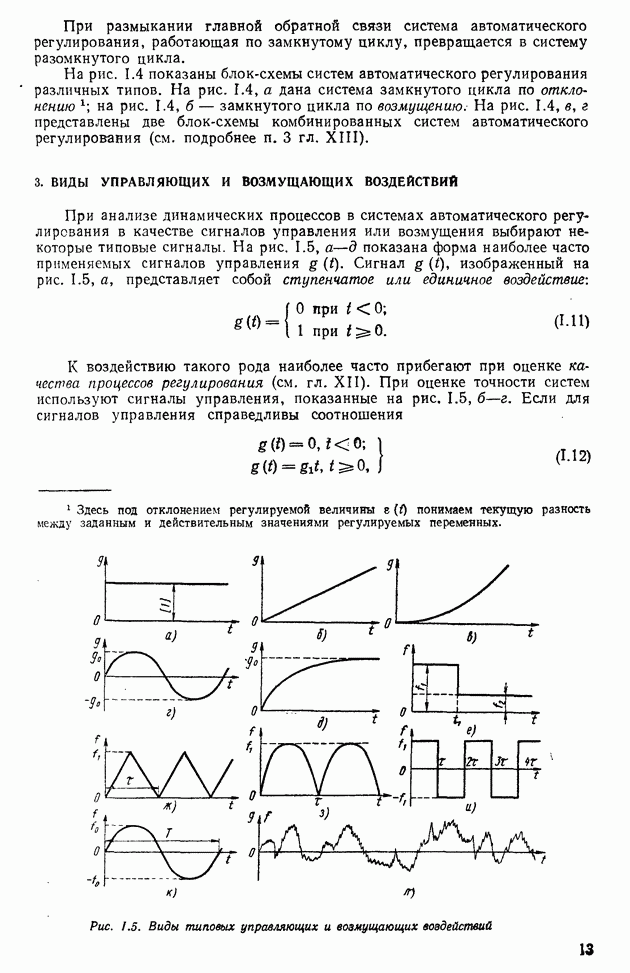
- 3. ВИДЫ УПРАВЛЯЮЩИХ И ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ
- 4. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Глава II. ВИДЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛТРОВАНИЯ
- 1. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
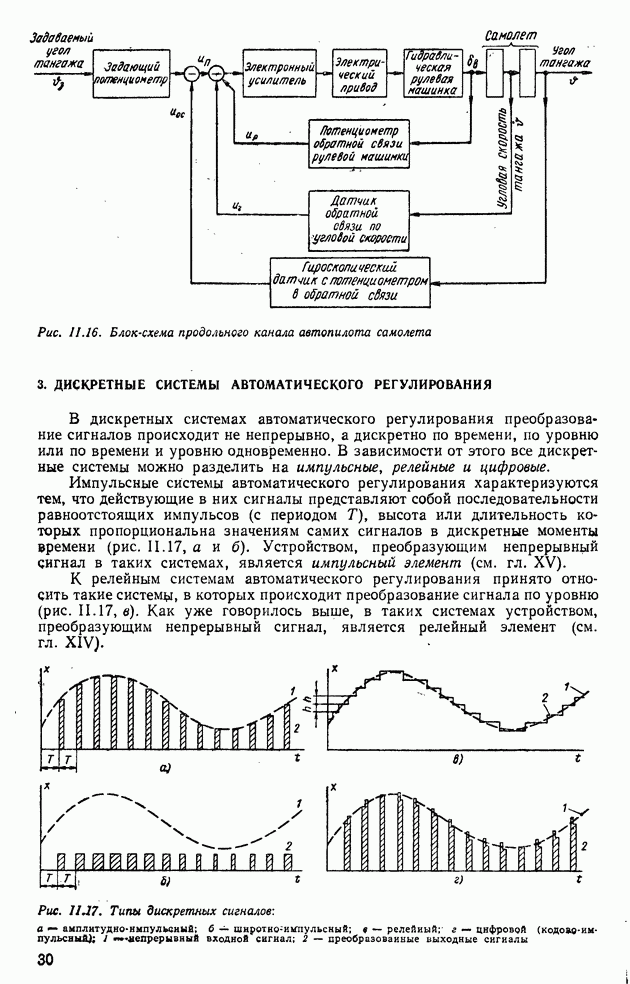
- 3. ДИСКРЕТНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ПРИМЕНЕНИЕ ЦВМ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
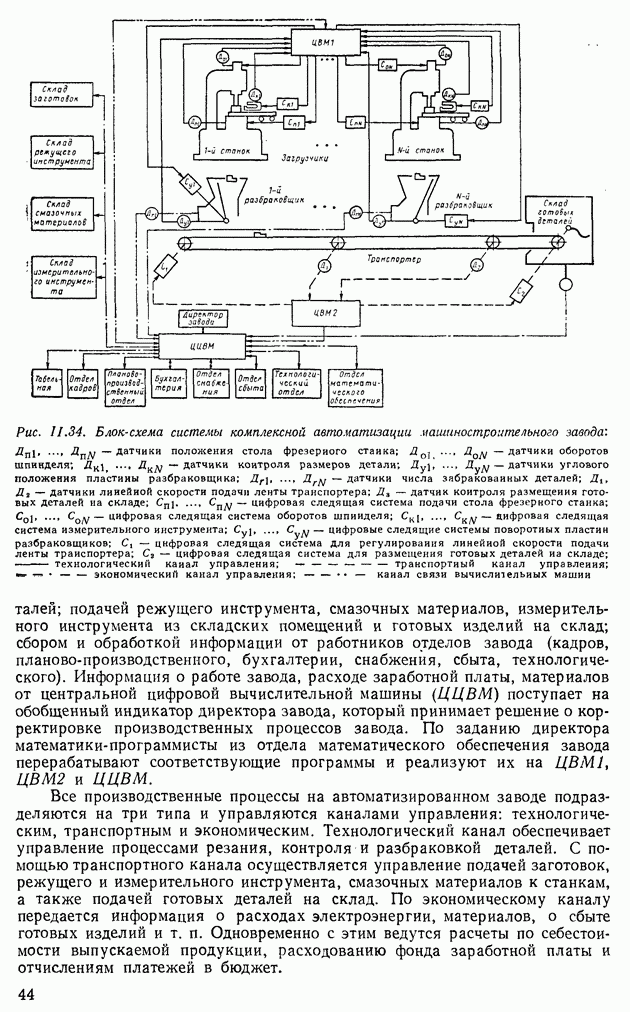
- 7. ПРИМЕНЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ДЛЯ УПРАВЛЕНИЯ СЛОЖНЫМИ ПРОИЗВОДСТВЕННЫМИ ПРОЦЕССАМИ. СИСТЕМЫ КОМПЛЕКСНОЙ АВТОМАТИЗАЦИИ ПРОИЗВОДСТВА
- Глава III. ОБЪЕКТЫ РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ СВОЙСТВА ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 2. ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 3. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ ДИНАМИКИ
- 4. УСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (ДИЗЕЛЬ, ГИДРОТУРБИНА, САМОЛЕТ)
- 5. НЕУСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (РЕСИВЕР, РАКЕТА-НОСИТЕЛЬ КОСМИЧЕСКИХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ)
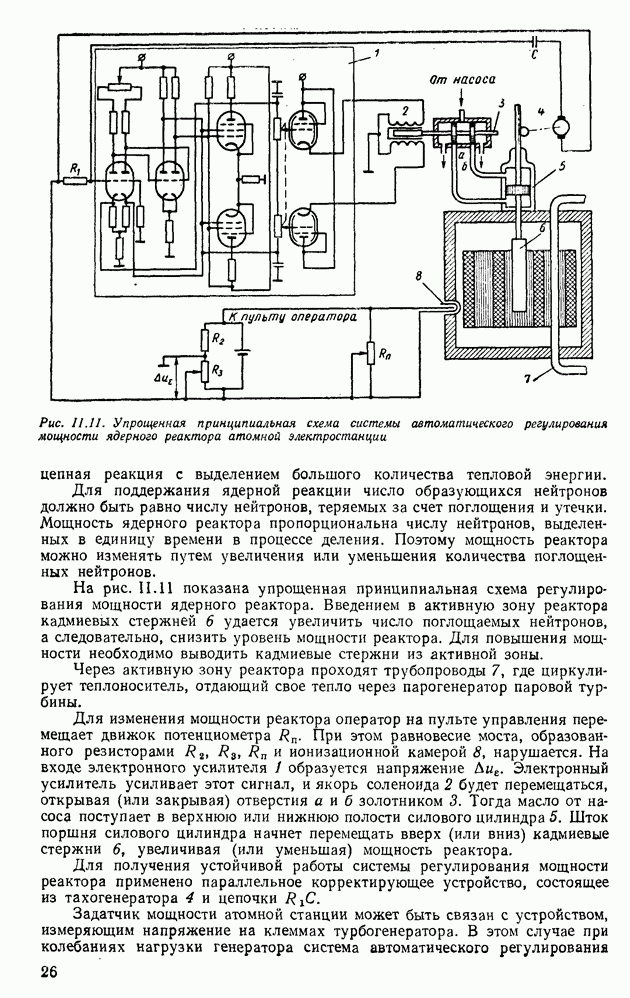
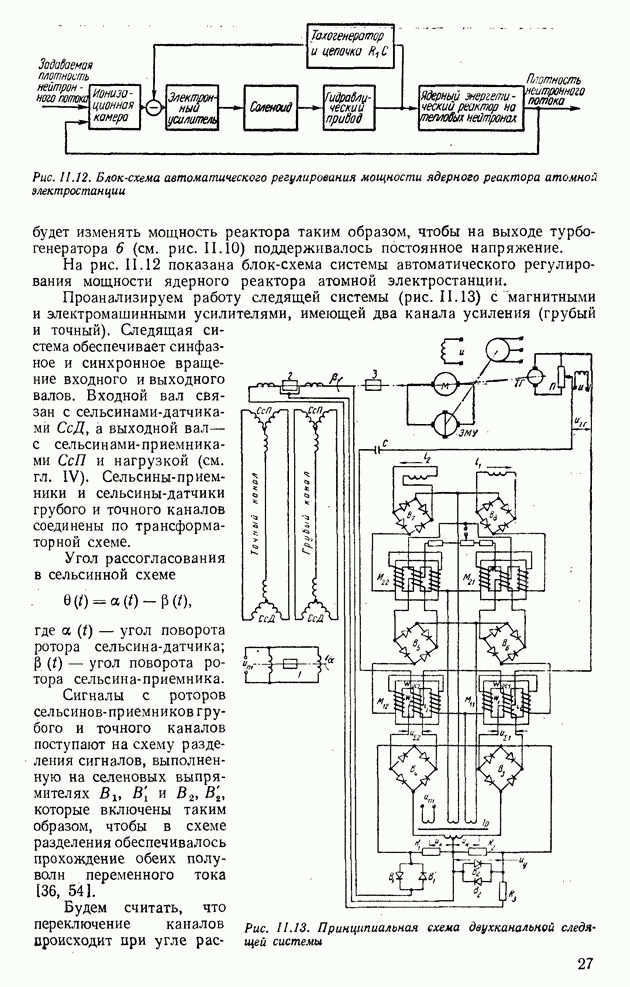
- 6. АСТАТИЧЕСКИЕ ОБЪЕКТЫ (ТРЕХФАЗНЫЙ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ, ЯДЕРНЫЙ ЭНЕРГЕТИЧЕСКИЙ РЕАКТОР НА ТЕПЛОВЫХ НЕЙТРОНАХ, КОСМИЧЕСКИЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ)
- 7. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- Глава IV. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОПРЕДЕЛЕНИЕ ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ИЗМЕРИТЕЛЬНЫХ ПОДСИСТЕМ
- 2. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Индуктивные устройства.
- Емкостные устройства.
- Сельсины.
- Дифференциальный сельсин.
- Погрешность сельсинов.
- Устройства для замера угловых скоростей.
- Устройства замера угловых ускорений.
- 4. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И ТОКА
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕМПЕРАТУР И ИЗЛУЧЕНИЙ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЙ И РАСХОДОВ ЖИДКОСТИ И ГАЗА
- 7. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ ВЕЛИЧИН, УГЛОВЫХ СКОРОСТЕЙ И ЛИНЕЙНЫХ УСКОРЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ
- Устройства для измерения линейных ускорений подвижных объектов (акселерометры).
- 8. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- Глава V. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ
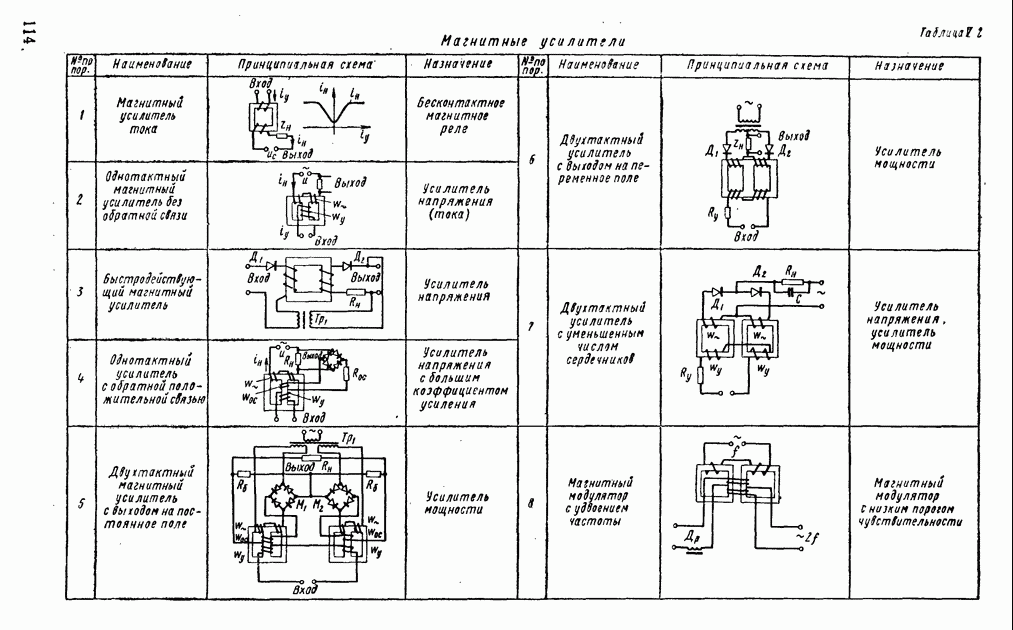
- 2. МАГНИТНЫЕ УСИЛИТЕЛИ
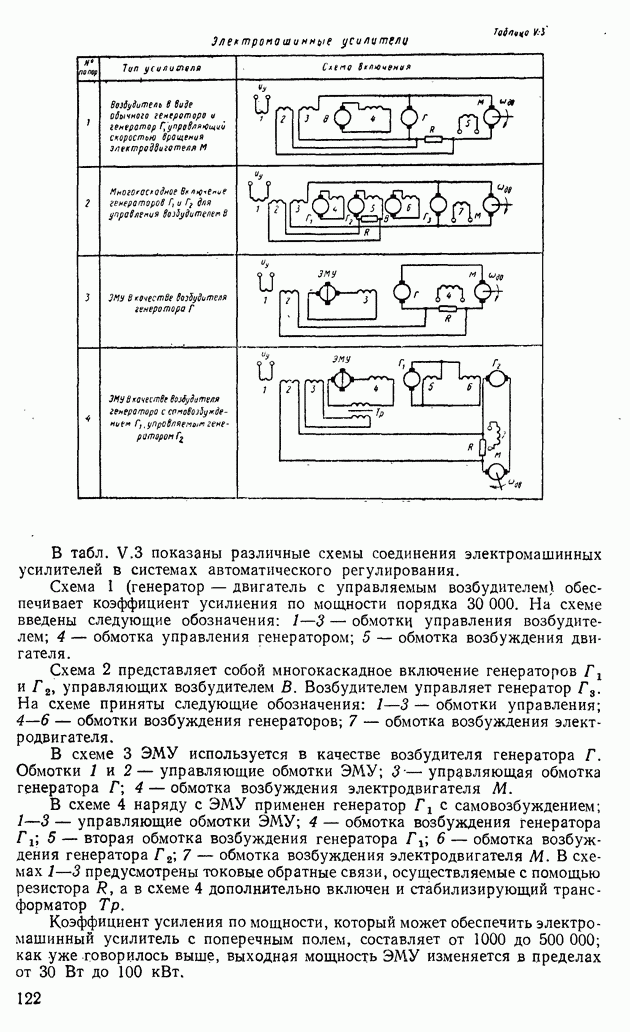
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 4. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 5. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ РАЗЛИЧНЫХ УСИЛИТЕЛЕЙ
- ГЛАВА VI. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА
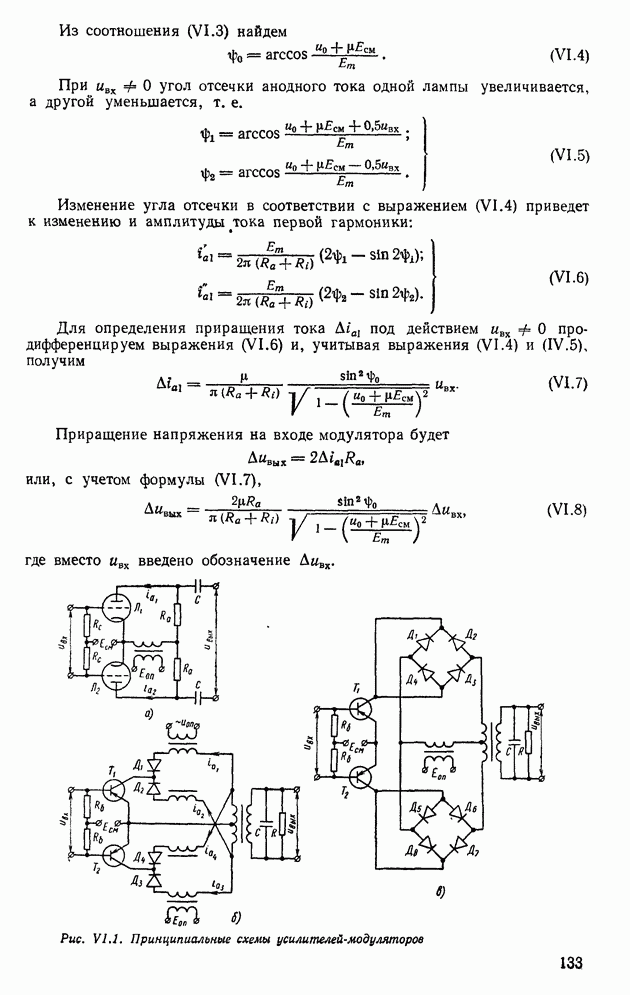
- 1. УСИЛИТЕЛИ-ПРЕОБРАЗОВАТЕЛИ
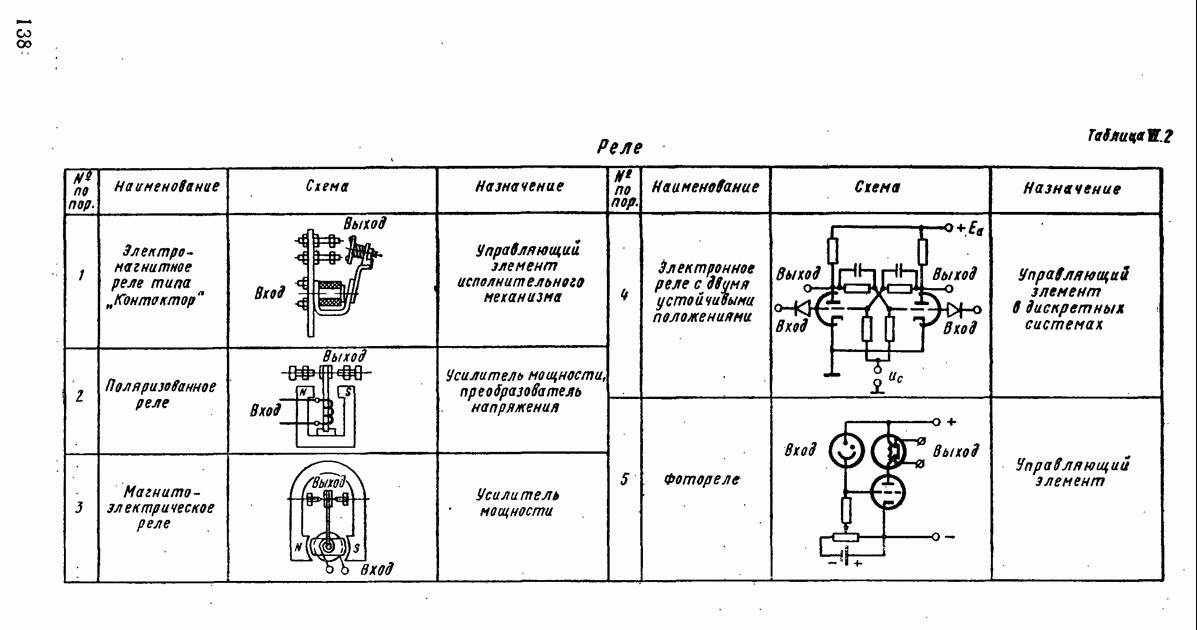
- 2. РЕЛЕ
- 3. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. ПРЕОБРАЗОВАТЕЛИ АНАЛОГ—КОД
- 5. ПРЕОБРАЗОВАТЕЛИ КОД—АНАЛОГ
- 6. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ УПРАВЛЯЮЩИЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
- 8. ПНЕВМАТИЧЕСКИЕ АНАЛОГОВЫЕ И ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 9. ТОЧНОСТЬ РАБОТЫ И БЫСТРОДЕЙСТВИЕ УПРАВЛЯЮЩИХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
- 10. СРАВНИТЕЛЬНАЯ ОЦЕНКА ПРЕОБРАЗУЮЩИХ УСТРОЙСТВ
- Глава VII. ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 1. ЭЛЕКТРИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 2. МЕХАНИЧЕСКИЕ ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. ГИДРАВЛИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 4. ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 5. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- 6. СРАВНИТЕЛЬНАЯ ОЦЕНКА ИСПОЛНИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- Глава VIII. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. НЕЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 3. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 4. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ЛИНИЯХ ЗАДЕРЖЕК И ДИСКРЕТНЫХ ЭЛЕМЕНТАХ
- Глава IX. УРАВНЕНИЯ ДИНАМИКИ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- 1. ПРЕДСТАВЛЕНИЕ ОБЪЕКТОВ И УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С СОСРЕДОТОЧЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 2. ПРЕДСТАВЛЕНИЕ УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С РАСПРЕДЕЛЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ТРАНСЦЕДЕНТНЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 3. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
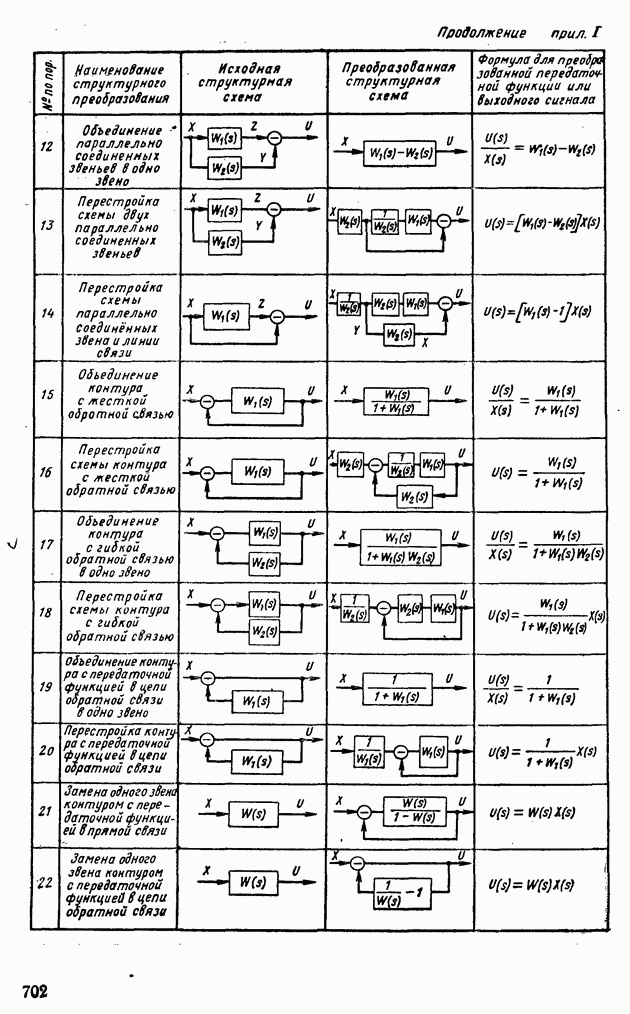
- 4. ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ
- 5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ОПИСАНИЕ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ РЕГУЛИРОВАНИЯ В ВЕКТОРНО-МАТРИЧНОЙ ФОРМЕ
- 7. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 8. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 9. РЕШЕНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ УРАВНЕНИЙ СОСТОЯНИЯ
- 10. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ МАТРИЦ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ ЛИНЕЙНЫХ СИСТЕМ
- 12. ПРЕДСТАВЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ИМПУЛЬСНЫМИ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ
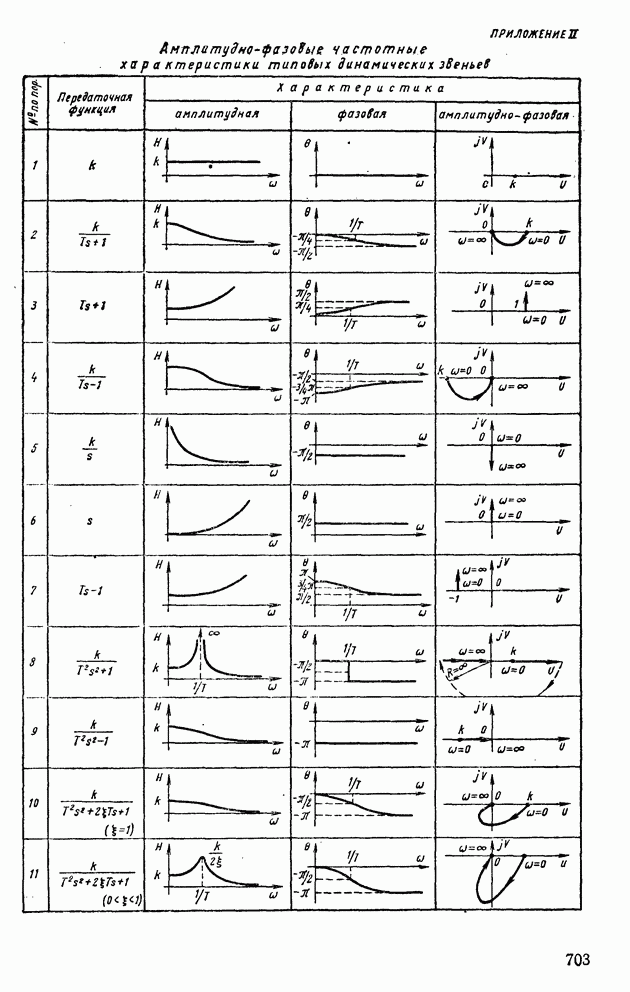
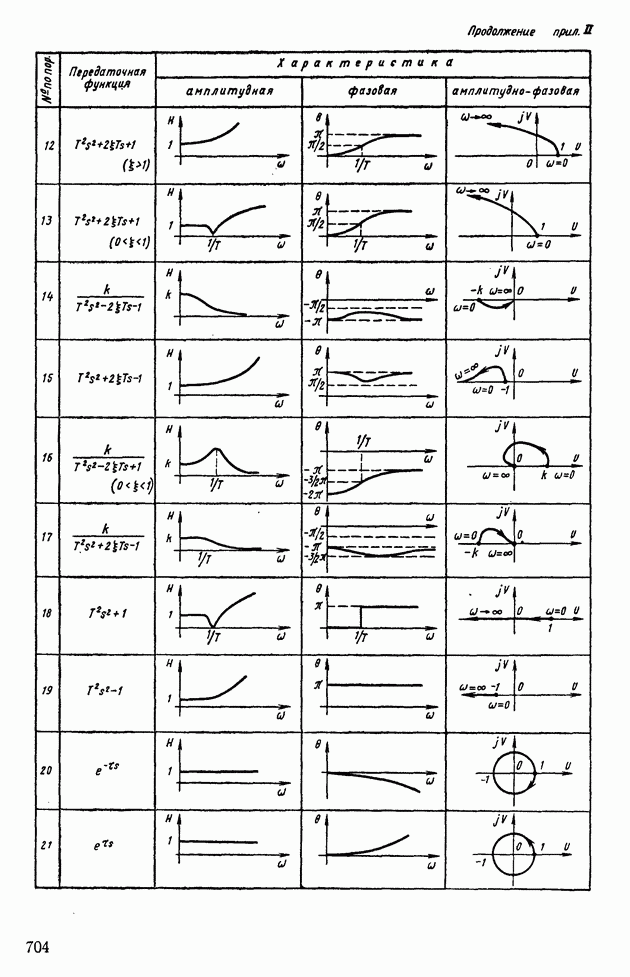
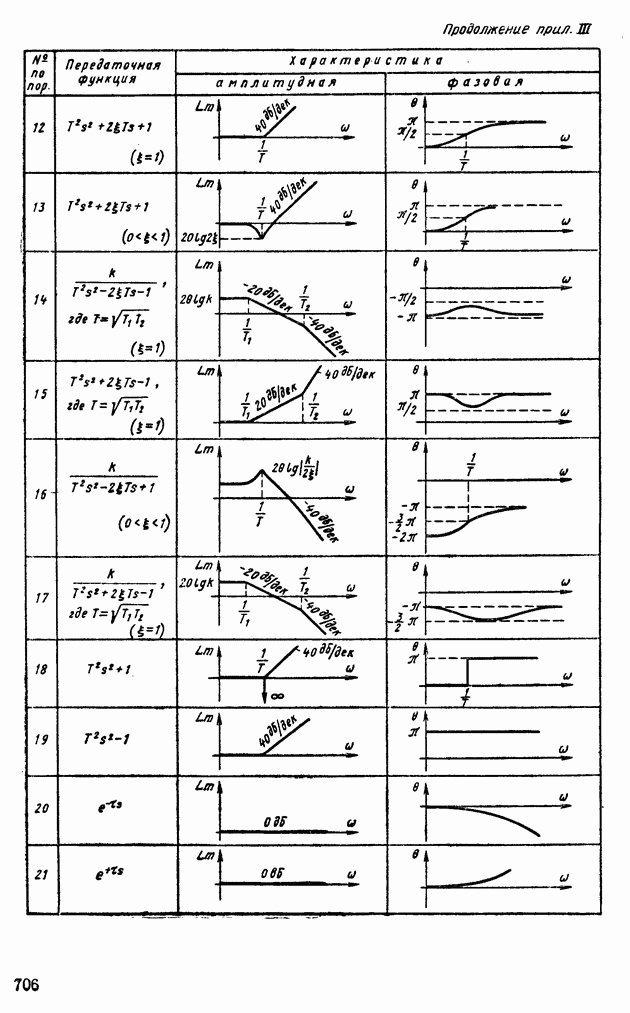
- Глава X. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ АМПЛИТУДНО-ФАЗОВЫЕ И ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 1. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- Логарифмические амплитудная и фазовая частотные характеристики апериодического звена.
- 2. АПЕРИОДИЧЕСКОЕ НЕУСТОЙЧИВОЕ ЗВЕНО
- 4. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 5. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ (УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ)
- 6. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО РОДА
- 7. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО РОДА
- 8. ТРАНСЦЕНДЕНТНЫЕ ЗВЕНЬЯ
- 9. ФАЗОВАЯ ЛИНЕЙКА
- 10. ПОСТРОЕНИЕ АМПЛИТУДНО-ФАЗОВЫХ И ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ ГРУПП ТИПОВЫХ ЗВЕНЬЕВ
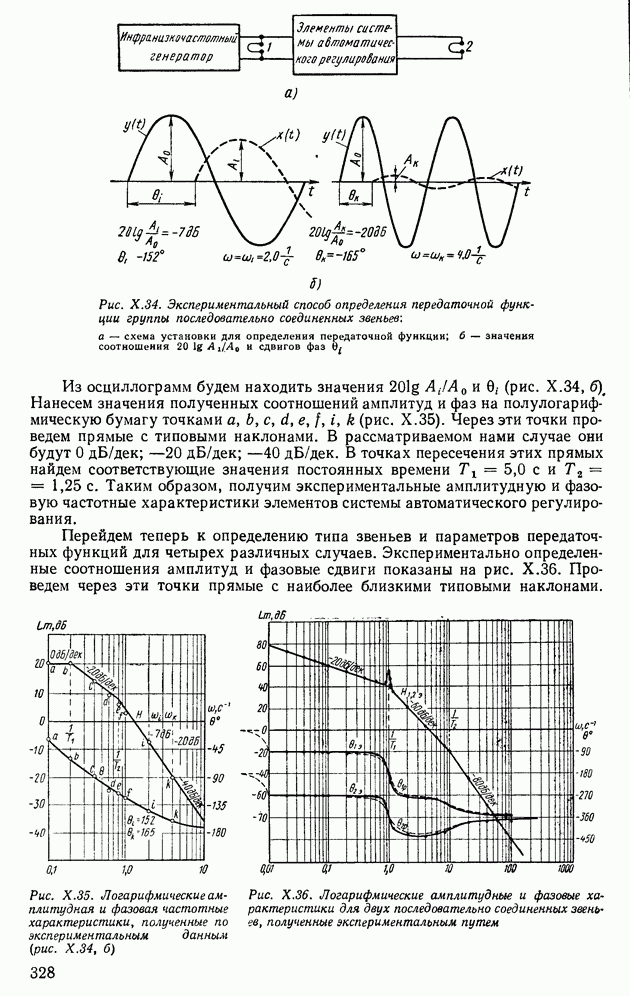
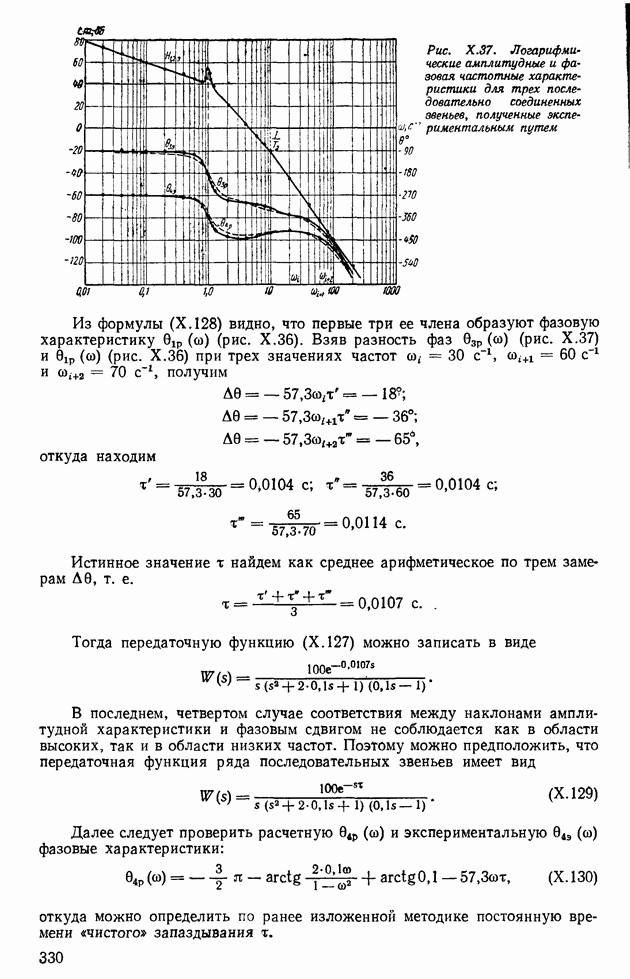
- 11. ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ВИДА ПЕРЕДАТОЧНЫХ ФУНКЦИЙ И ПАРАМЕТРОВ ГРУПП ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
- ГЛАВА XI. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
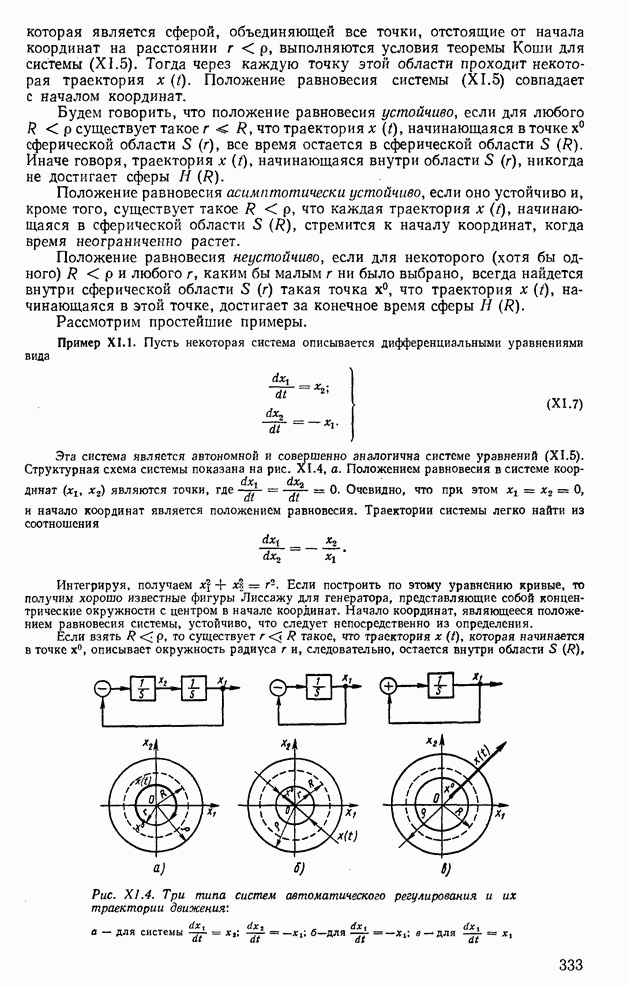
- 1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ
- 2. ОПРЕДЕЛЕНИЕ ФУНКЦИЙ ЛЯПУНОВА МЕТОДАМИ Г. СЕГЕ И Д. ШУЛЬЦА
- 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
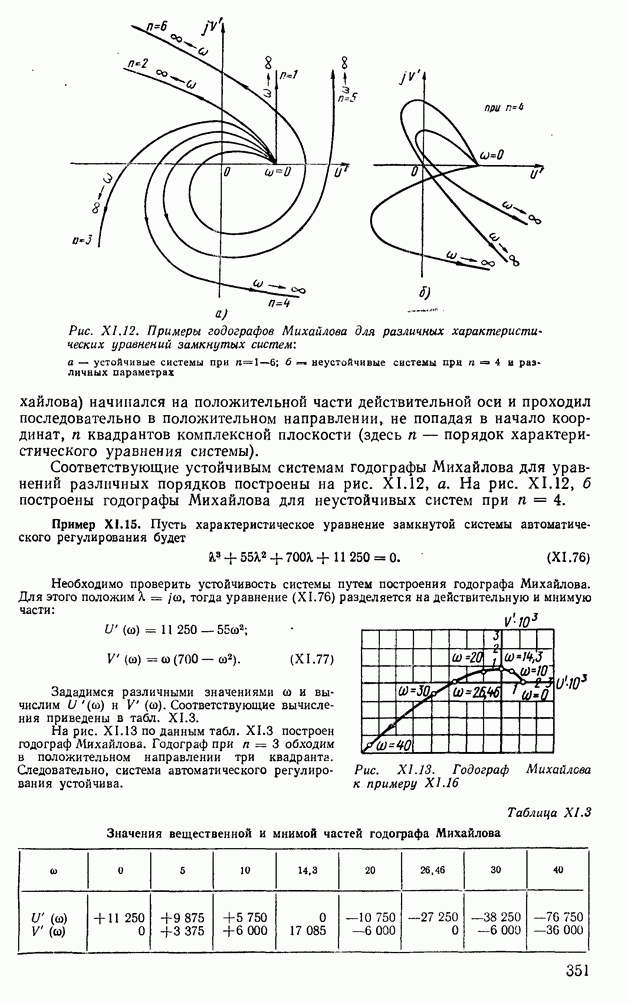
- 5. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 6. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ТРАНСЦЕНДЕНТНЫМИ ЗВЕНЬЯМИ
- 9. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ С ПОМОЩЬЮ D-РАЗБИЕНИЯ
- Глава XII. ИССЛЕДОВАНИЕ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
- 2. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПО ЗАДАННЫМ ПЕРЕДАТОЧНЫМ ФУНКЦИЯМ ЗАМКНУТЫХ СИСТЕМ
- 3. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПО РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ ЛЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ
- 4. МЕТОД КОРНЕВОГО ГОДОГРАФА
- 5. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА
- 6. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ СИСТЕМ РЕГУЛИРОВАНИЯ И ИХ СВЯЗЬ С ХАРАКТЕРИСТИКАМИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
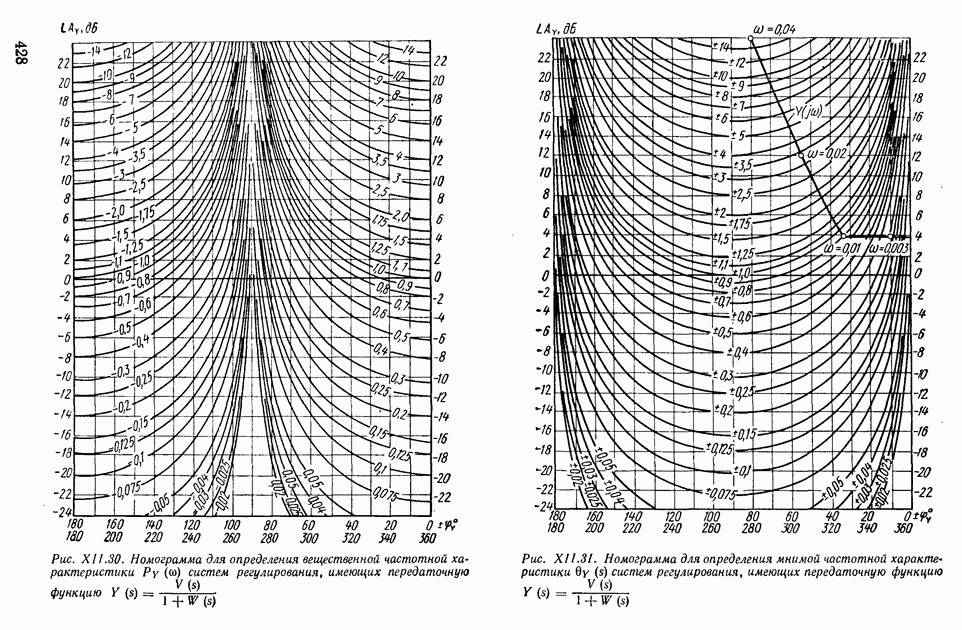
- 7. ОПРЕДЕЛЕНИЕ ВЕЩЕСТВЕННЫХ И МНИМЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СИСТЕМ ПО АМПЛИТУДНО-ФАЗОВЫМ И ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ РАЗОМКНУТЫХ СИСТЕМ
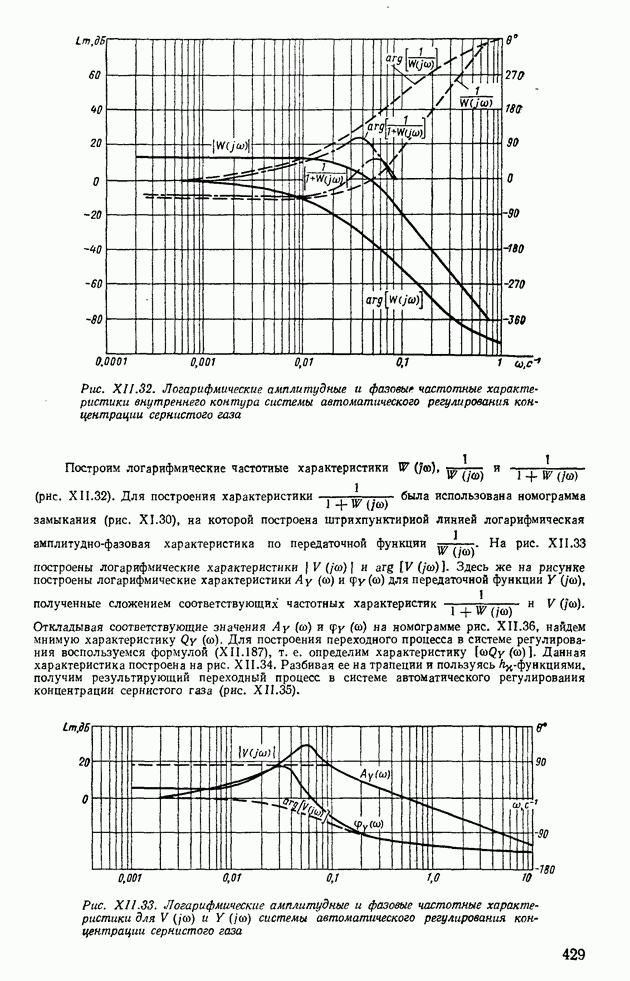
- 8. ЧАСТОТНЫЕ ОЦЕНКИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
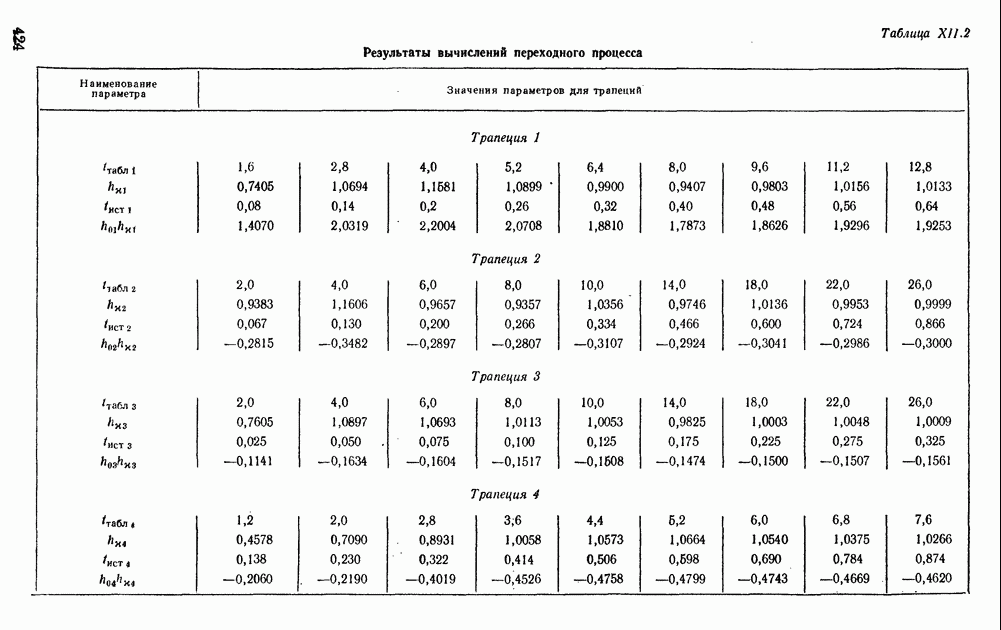
- 9. ЧАСТОТНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ТРАПЕЦЕИДАЛЬНЫХ ХАРАКТЕРИСТИК
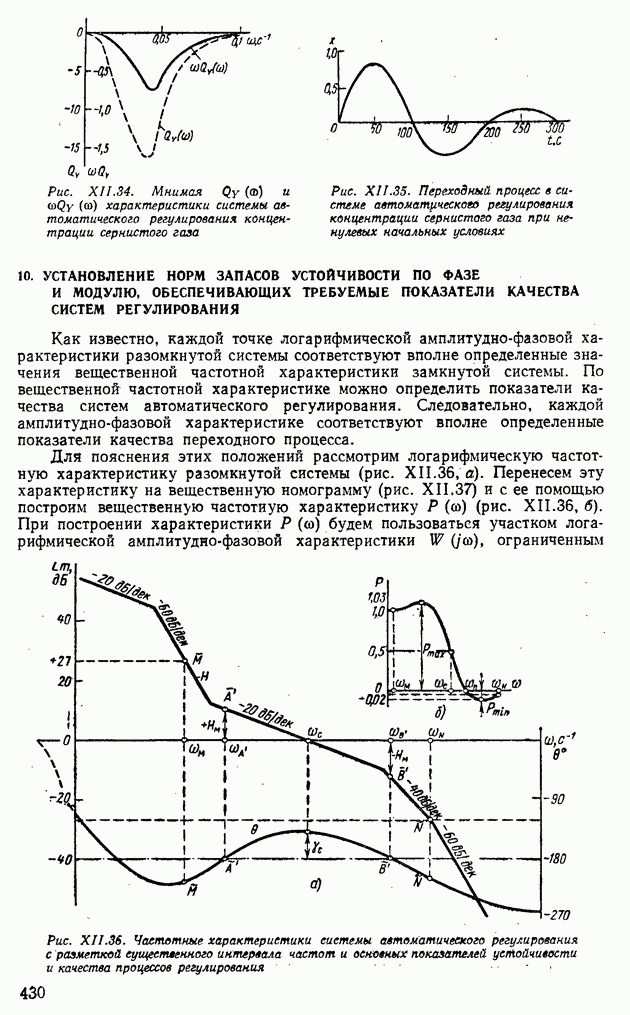
- 10. УСТАНОВЛЕНИЕ НОРМ ЗАПАСОВ УСТОЙЧИВОСТИ ПО ФАЗЕ И МОДУЛЮ, ОБЕСПЕЧИВАЮЩИХ ТРЕБУЕМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМ РЕГУЛИРОВАНИЯ
- ГЛАВА XIII. ДИНАМИЧЕСКАЯ ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ОШИБОК В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ АМПЛИТУДНЫХ ХАРАКТЕРИСТИК
- 3. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПУТЕМ ПРИМЕНЕНИЯ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ
- 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 5. СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ СТАЦИОНАРНЫХ ПРОЦЕССОВ
- 6. СВОЙСТВА СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ
- 7. ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ
- 8. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЛИНЕЙНЫМИ СИСТЕМАМИ
- 9. РАСЧЕТ ОШИБОК В СИСТЕМЕ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ШУМОВ
- 10. ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ВОЗДЕЙСТВИИ СЛУЧАЙНЫХ СИГНАЛОВ И ШУМОВ
- ГЛАВА XIV. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ТИПОВЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ ПО ВТОРОМУ МЕТОДУ ЛЯПУНОВА
- 3. АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
- 4. ПРИМЕНЕНИЕ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
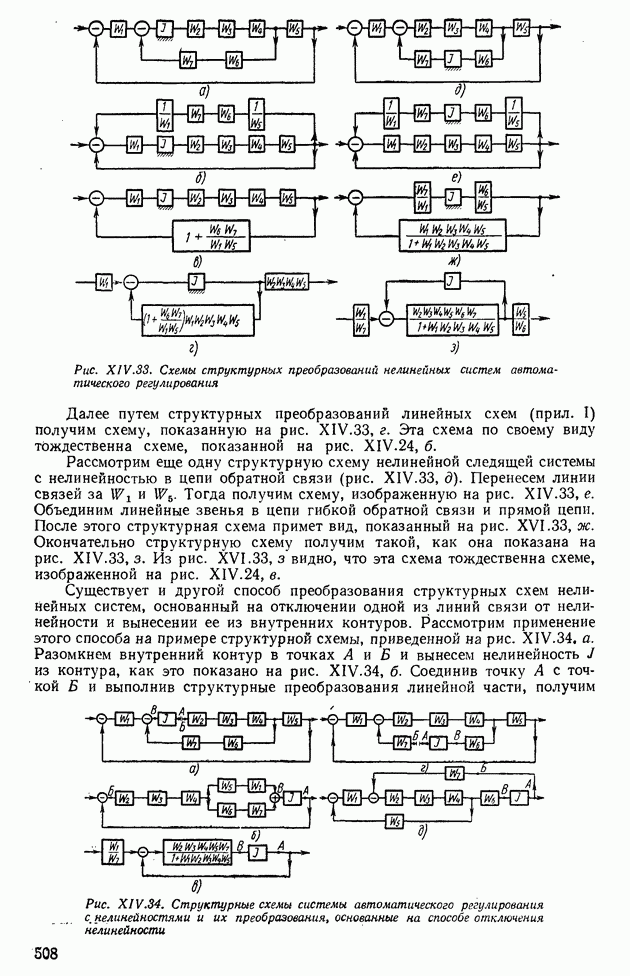
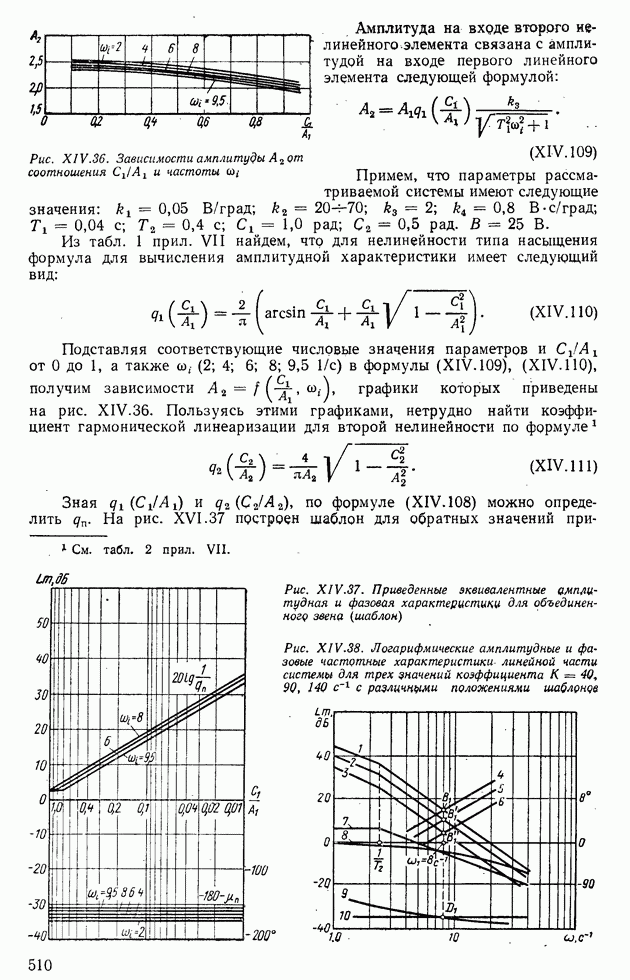
- 5. СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. АНАЛИЗ АВТОКОЛЕБАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДВУМЯ НЕЛИНЕЙНОСТЯМИ
- 7. ДВУХКОНТУРНЫЕ НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕДЛЕННО ИЗМЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
- 9. СПОСОБЫ ПОДАВЛЕНИЯ АВТОКОЛЕБАНИЙ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 10. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 11. КРИТЕРИЙ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
- 12. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- Глава XIV. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ИМПУЛЬСНЫХ УСТРОЙСТВ
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. АМПЛИТУДНО-ФАЗОВЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ СИСТЕМ
- 4. ПРИМЕНЕНИЕ ВЕКТОРНО-МАТРИЧНОГО АППАРАТА К ИМПУЛЬСНЫМ СИСТЕМАМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ОСНОВНЫЕ СВОЙСТВА z-ПРЕОБРАЗОВАНИЯ
- 6. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Критерий устойчивости для импульсных систем на плоскостях z и W(z).
- Критерий устойчивости Шур—Кона.
- Критерии устойчивости, основанные на применении билинейного преобразования.
- 7. МЕТОДЫ АНАЛИЗА КАЧЕСТВА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕТОДЫ АНАЛИЗА ТОЧНОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 9. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С УПРАВЛЯЮЩИМИ ЦВМ
- 10. СПОСОБЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ В УПРАВЛЯЮЩИХ ЦВМ И ОПРЕДЕЛЕНИЕ ИХ ОСНОВНЫХ ПАРАМЕТРОВ
- Глава XVI. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МЕТОДЫ ПОИСКА ЭКСТРЕМУМА
- 2. СПОСОБЫ ОРГАНИЗАЦИИ ДВИЖЕНИЯ К ЭКСТРЕМУМУ
- 3. МЕТОДЫ РАСЧЕТА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРОВ
- 4. ВЫБОР КОРРЕКТИРУЮЩИХ УСТРОЙСТВ В ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРАХ
- 5. ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ С ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ
- Глава XVII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ ВОЗДЕЙСТВИЯХ
- 2. ВЫБОР ПАРАМЕТРОВ УСТРОЙСТВ НЕИЗМЕНЯЕМОЙ ЧАСТИ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ПОСТРОЕНИЕ ЖЕЛАЕМОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 4. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. СИНТЕЗ ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 6. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 7. СПОСОБЫ РЕАЛИЗАЦИИ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Глава XVIII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 1. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА НА ОСНОВЕ КРИТЕРИЯ МИНИМУМА ИНТЕГРАЛЬНОЙ ОШИБКИ
- 2. СИНТЕЗ СИСТЕМ РЕГУЛИРОВАНИЯ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЖЕЛАЕМОЙ СИСТЕМЫ
- 4. ПРИМЕР СИНТЕЗА КОРРЕКТИРУЮЩИХ УСТРОЙСТВ СИСТЕМЫ РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- ГЛАВА XIX. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИНТЕЗ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ, ОСНОВАННЫЙ НА ПРИМЕНЕНИИ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- 2. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. РЕАЛИЗАЦИЯ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ ПРИ ПОМОЩИ RC-ЦЕПЕЙ
- 4. РЕАЛИЗАЦИЯ ПРОГРАММ КОРРЕКЦИИ НА УПРАВЛЯЮЩЕЙ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- ГЛАВА XX. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ПРИНЦИП МАКСИМУМА
- 3. ТЕОРЕМА О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
- 4. ПРИМЕРЫ ПРИМЕНЕНИЯ ПРИНЦИПА МАКСИМУМА
- 5. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 6. СИНТЕЗ НЕПРЕРЫВНЫХ ОПТИМАЛЬНЫХ СИСТЕМ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ