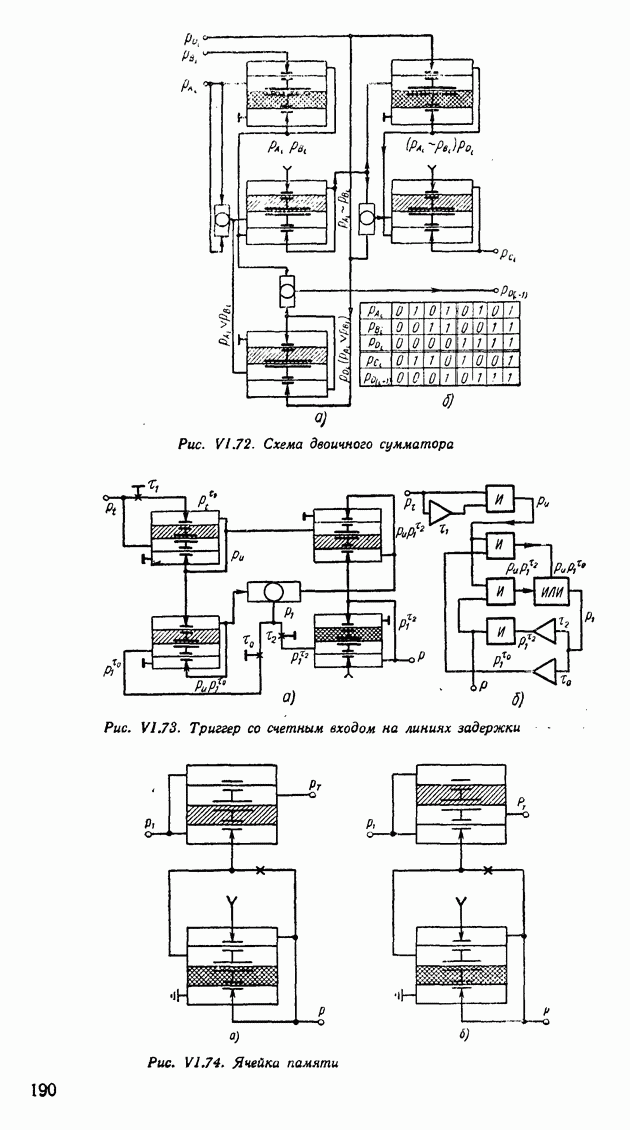
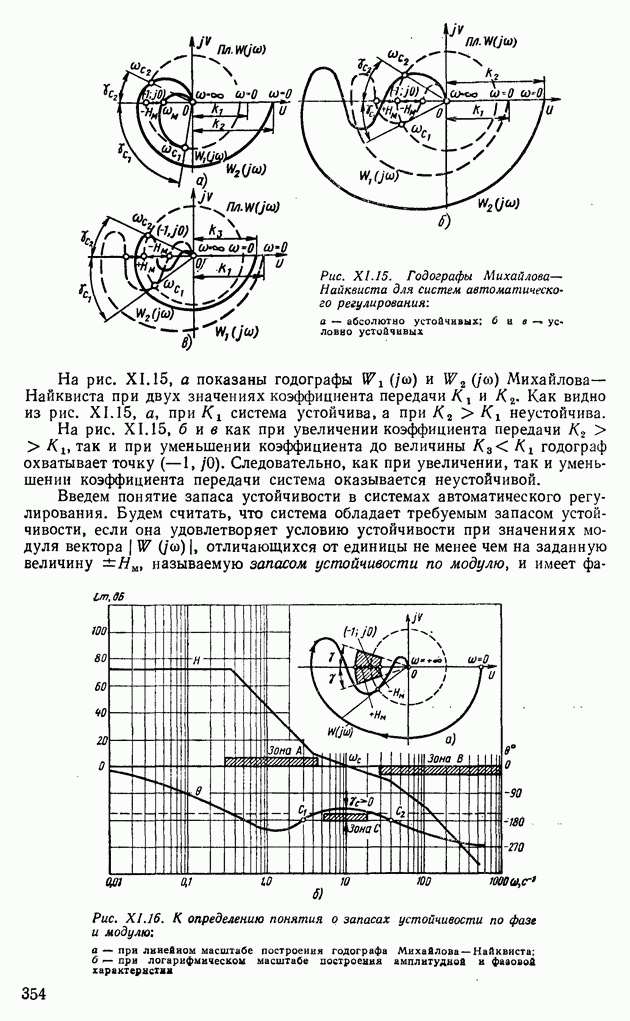
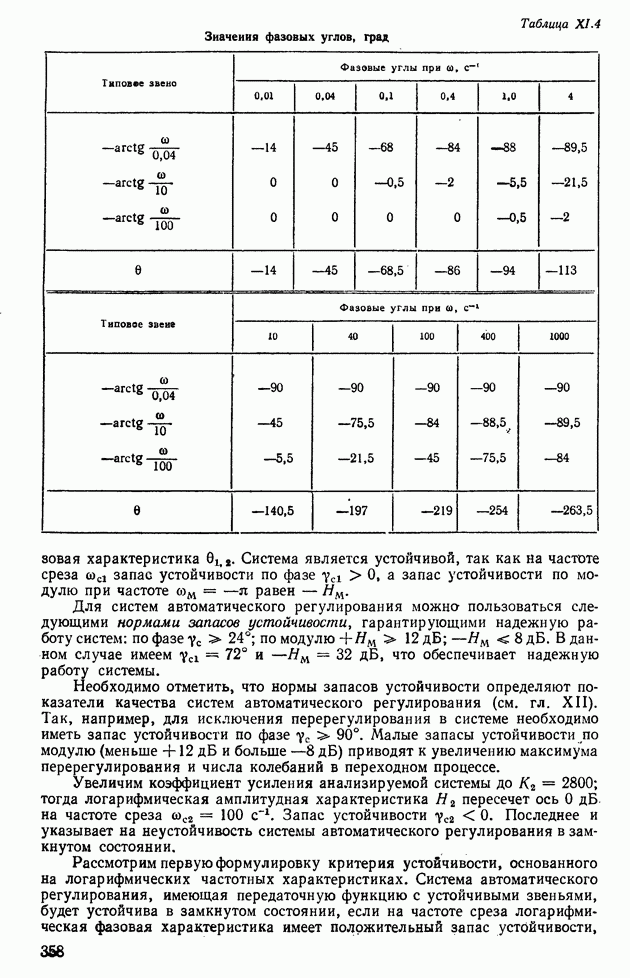
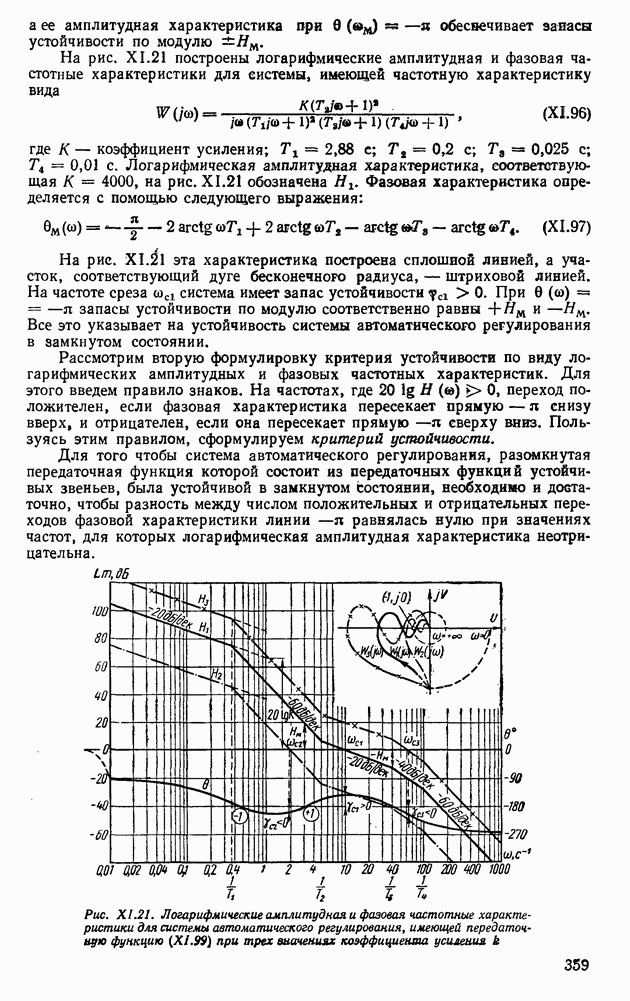
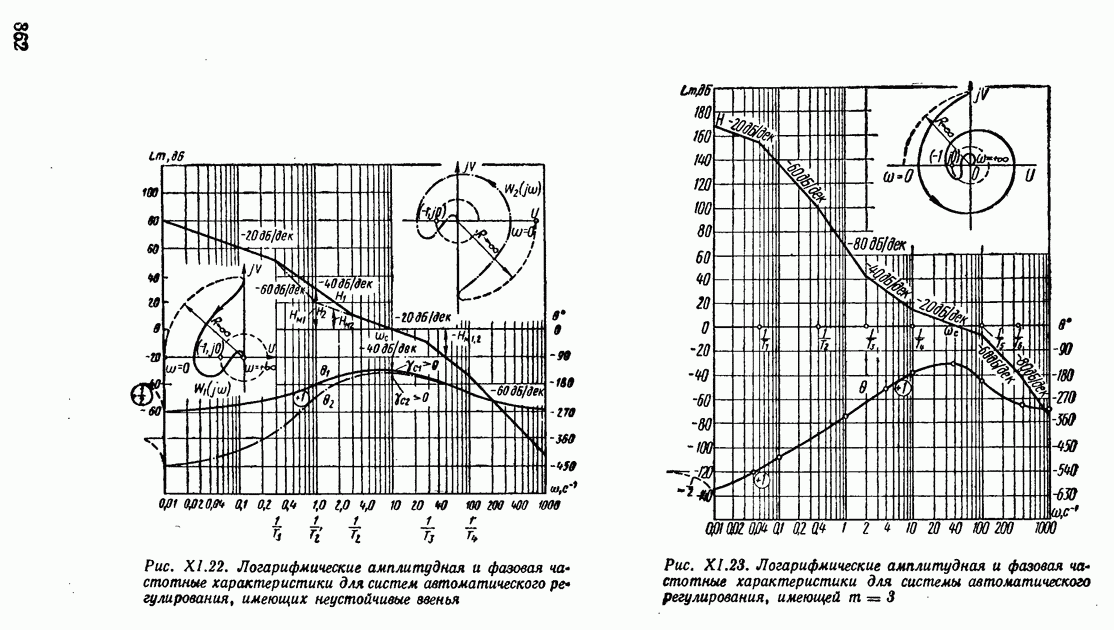
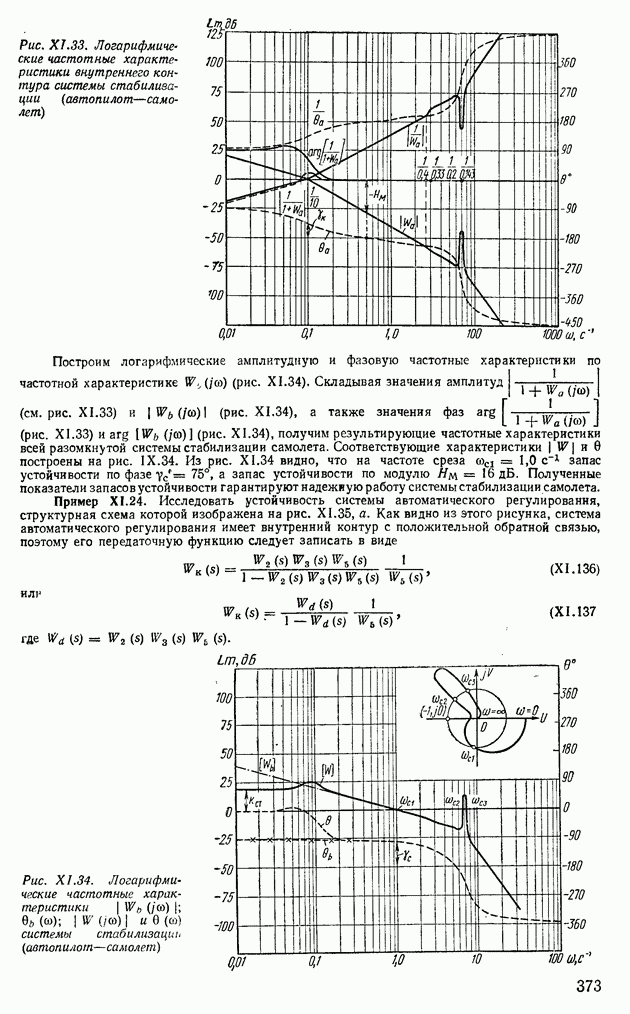
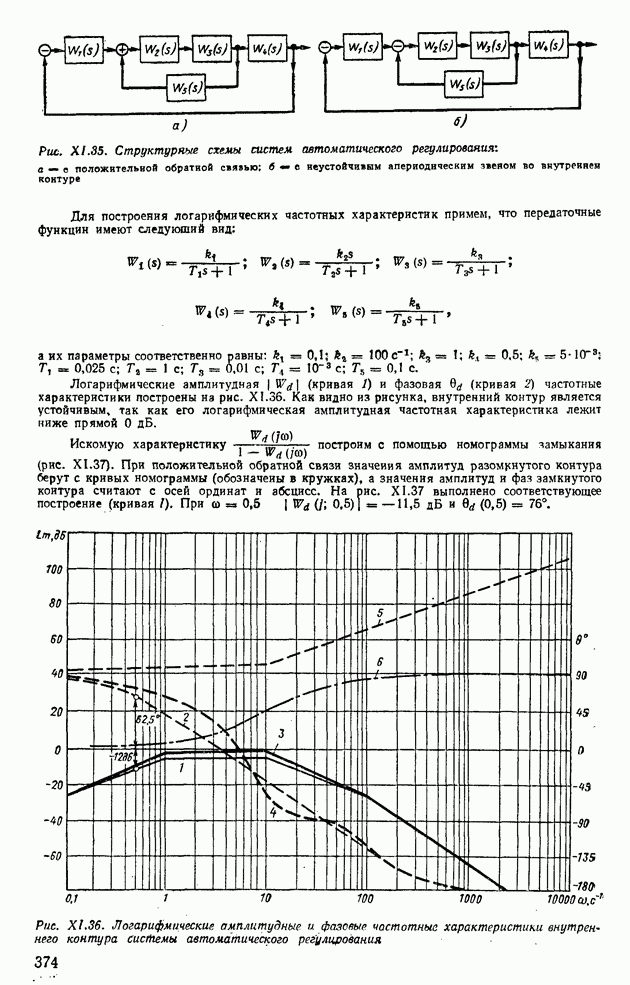
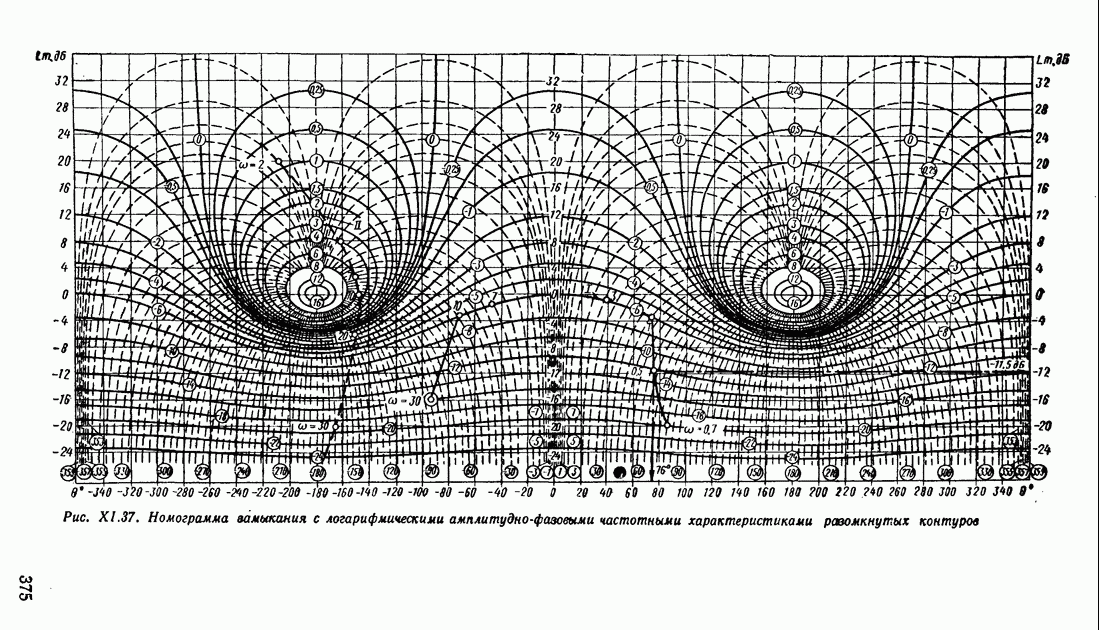
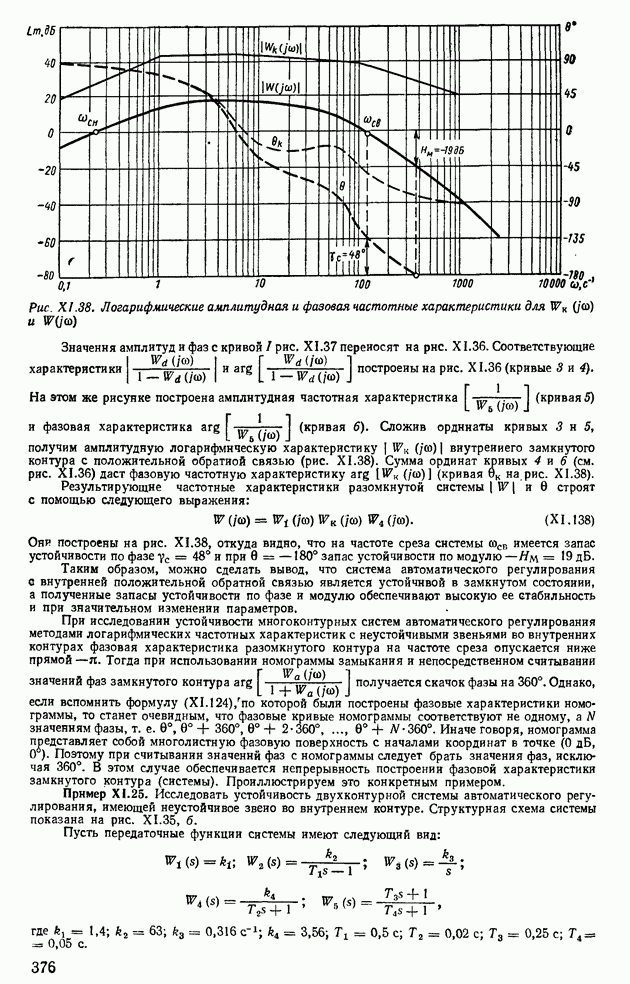
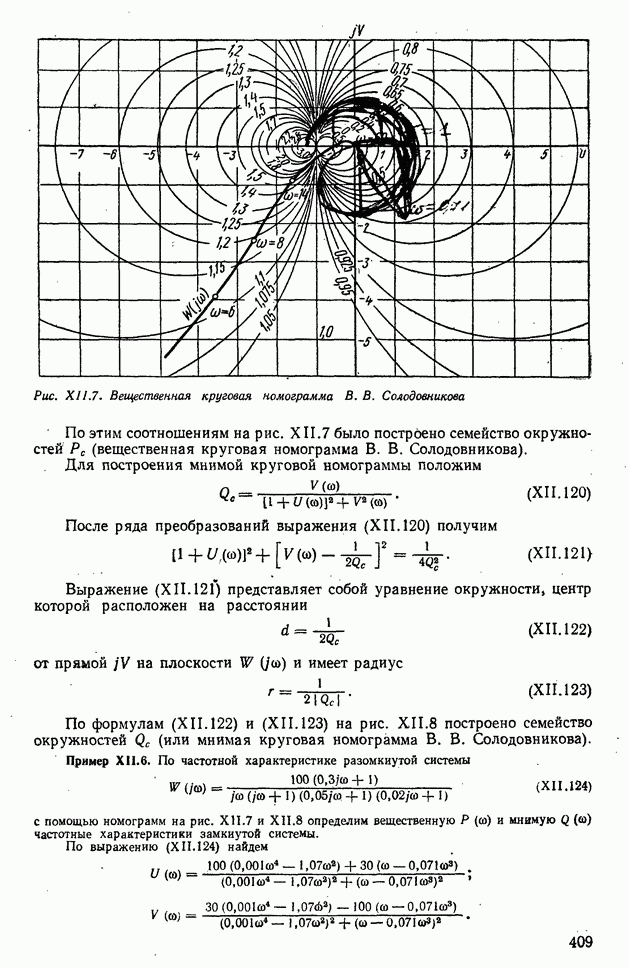
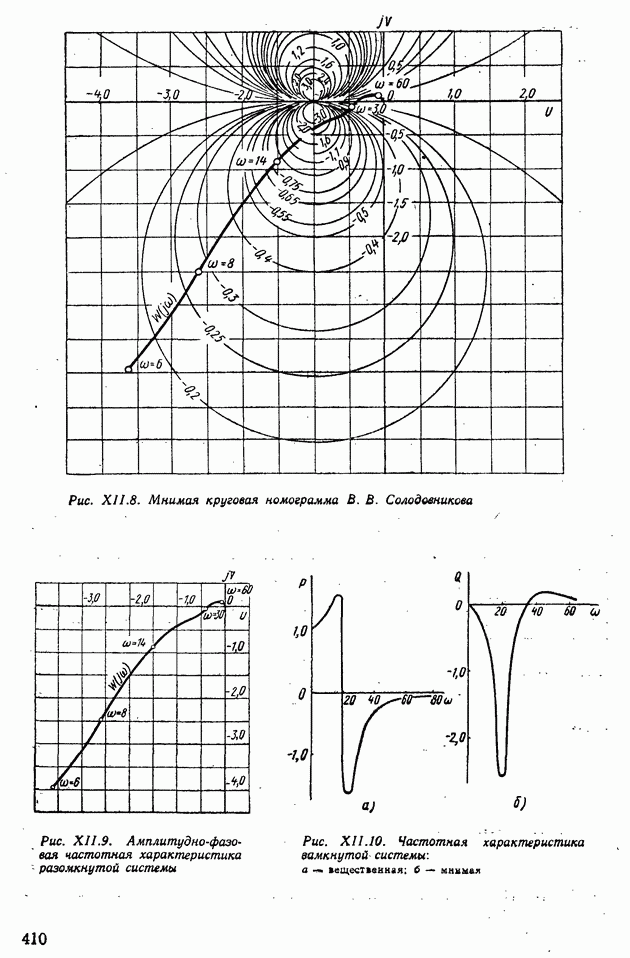
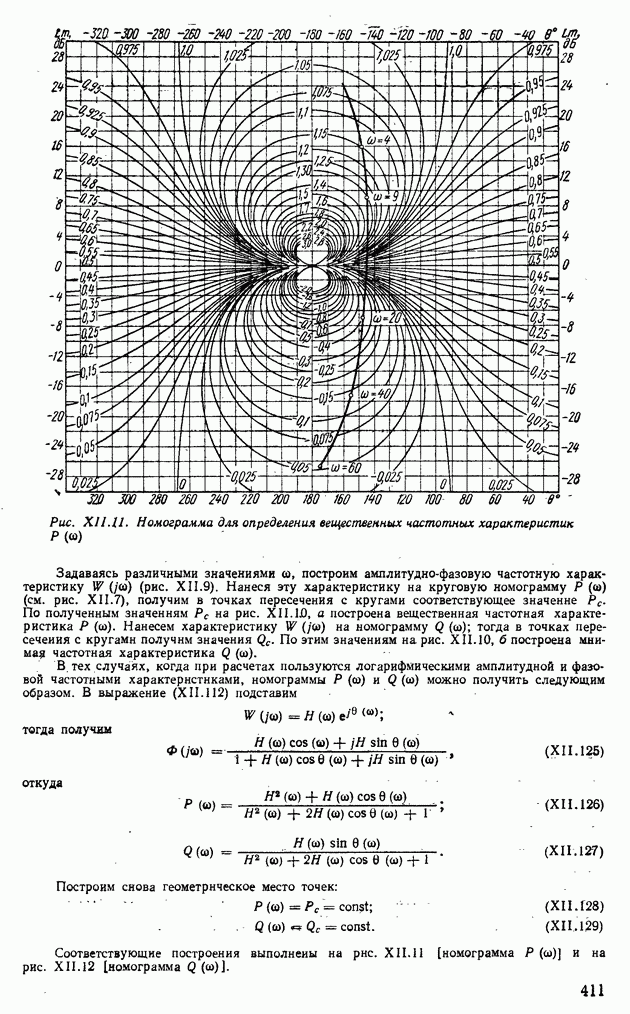
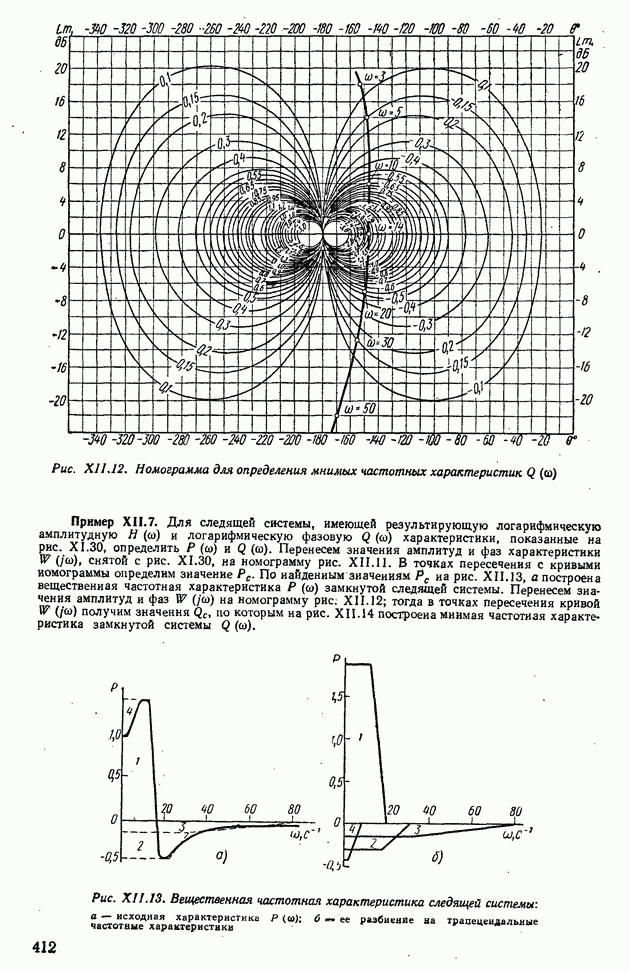
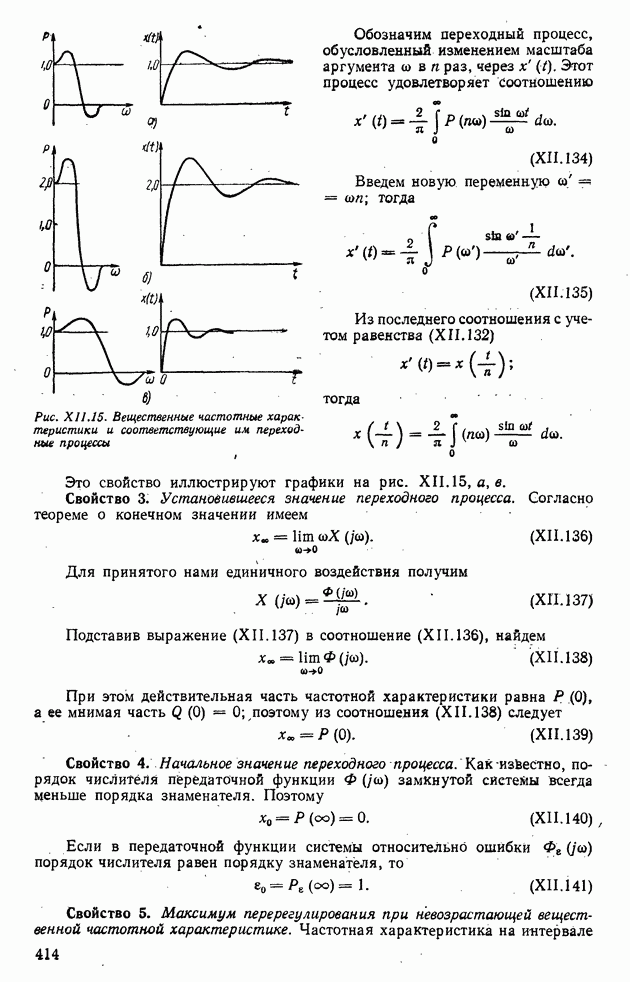
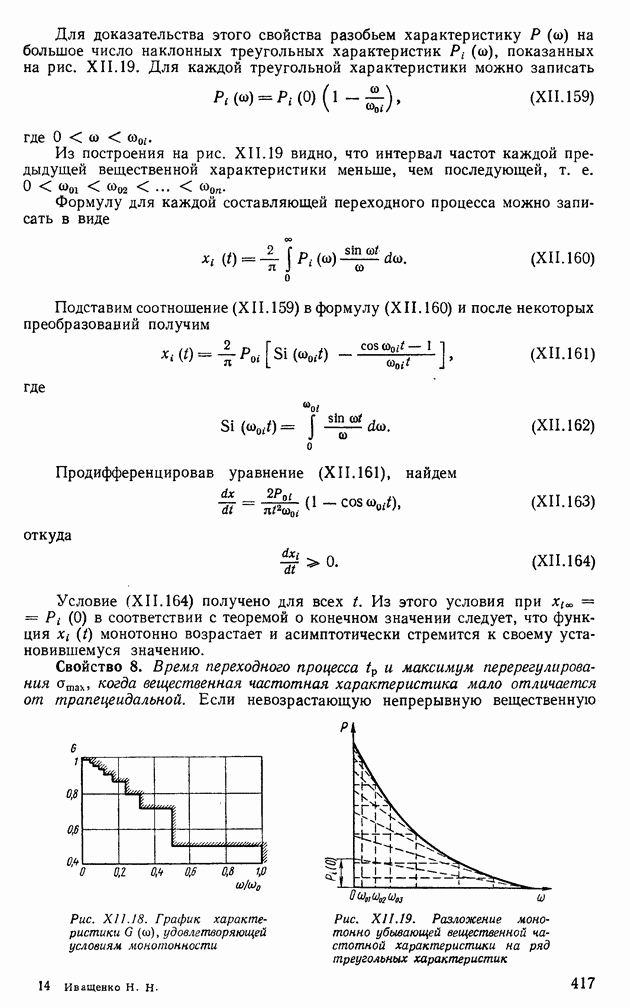
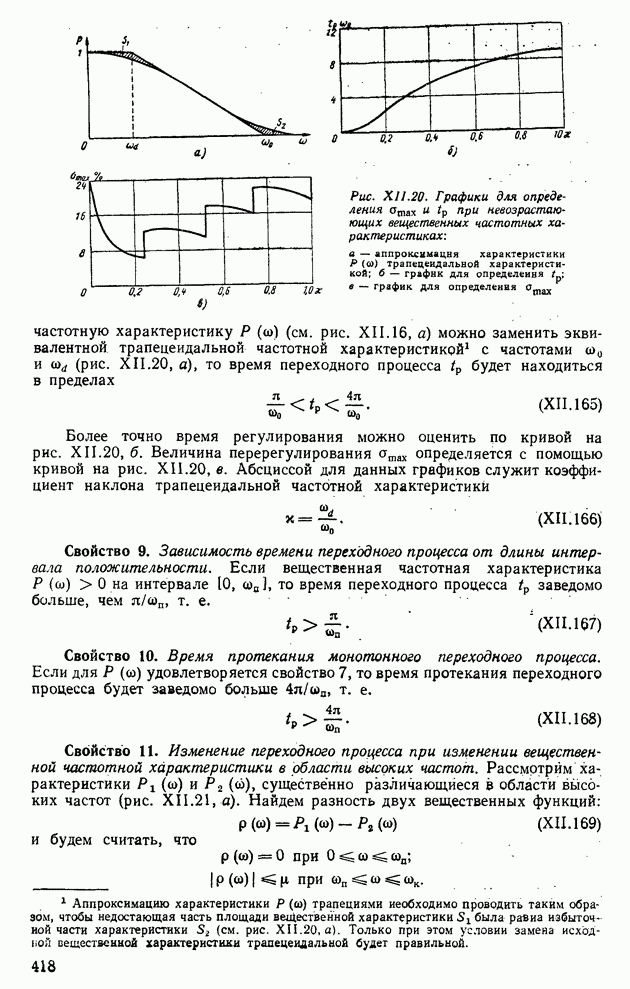
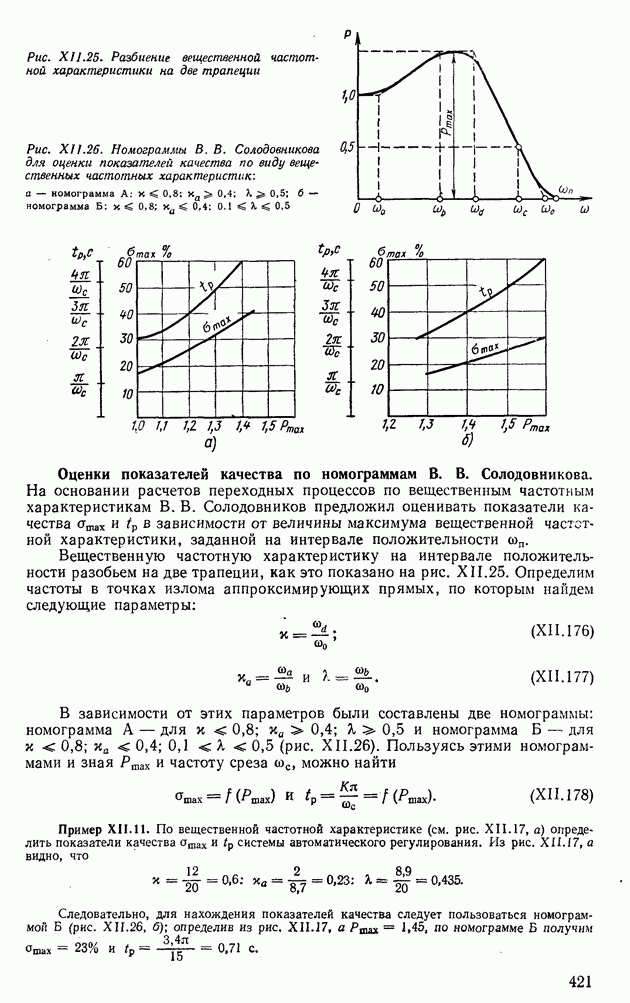
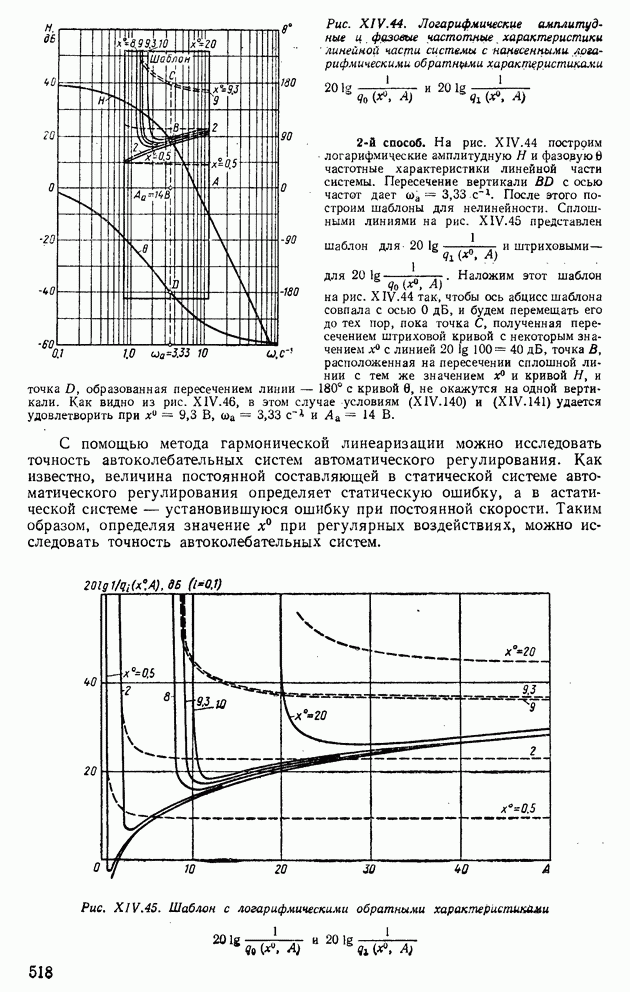
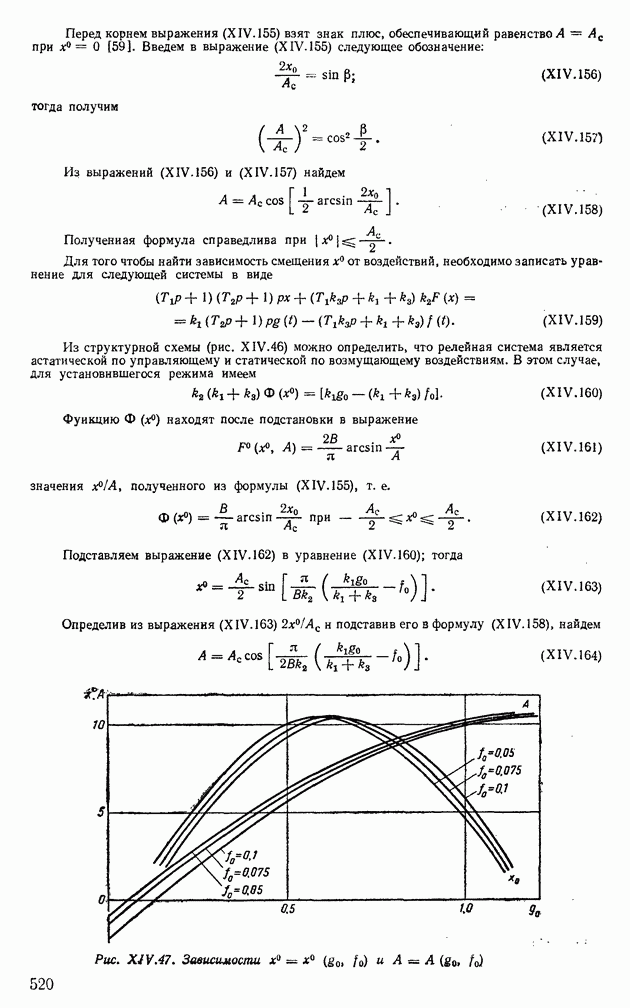
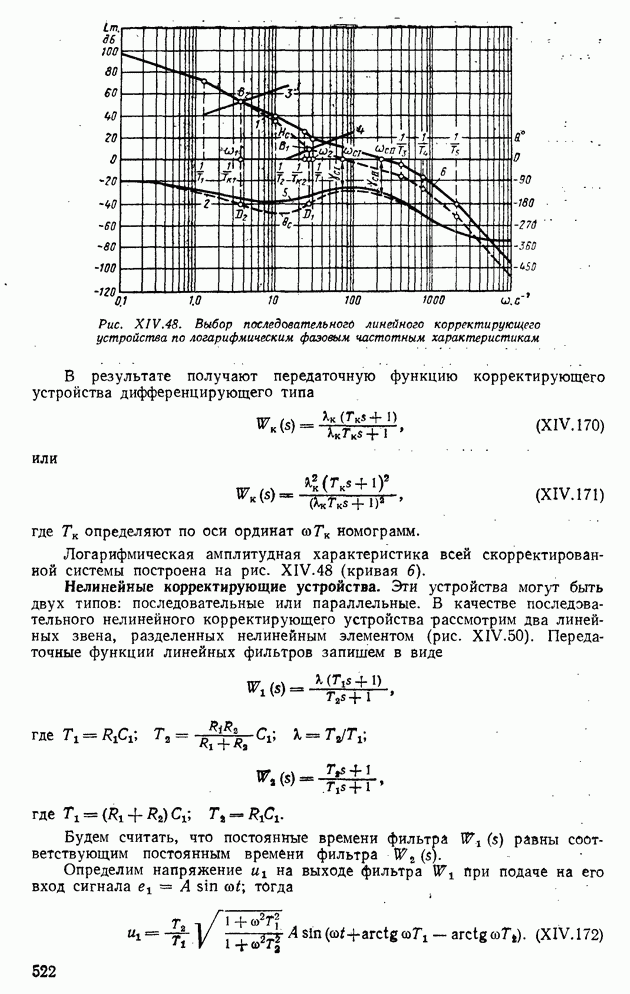
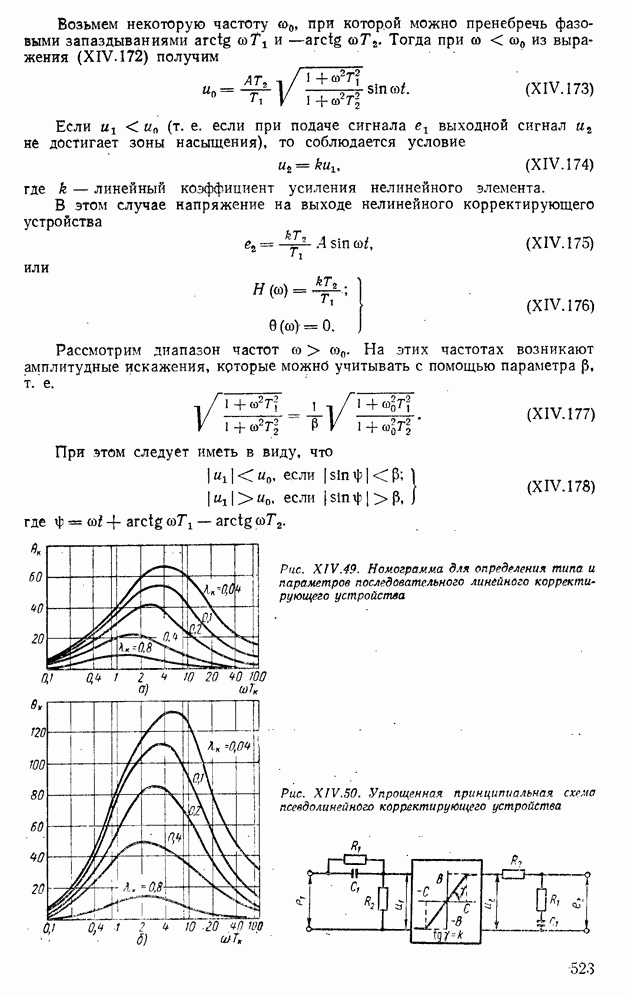
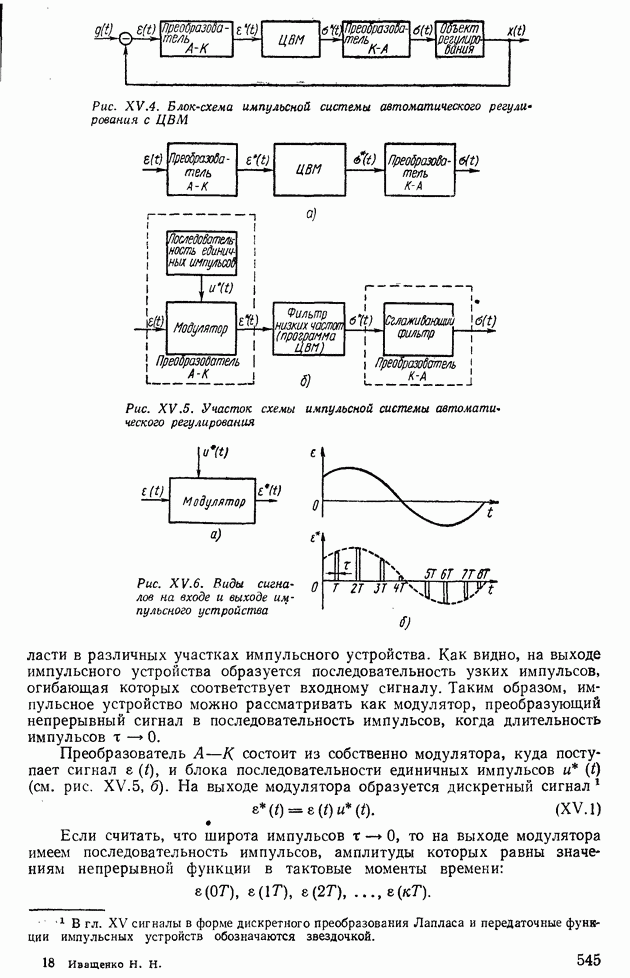
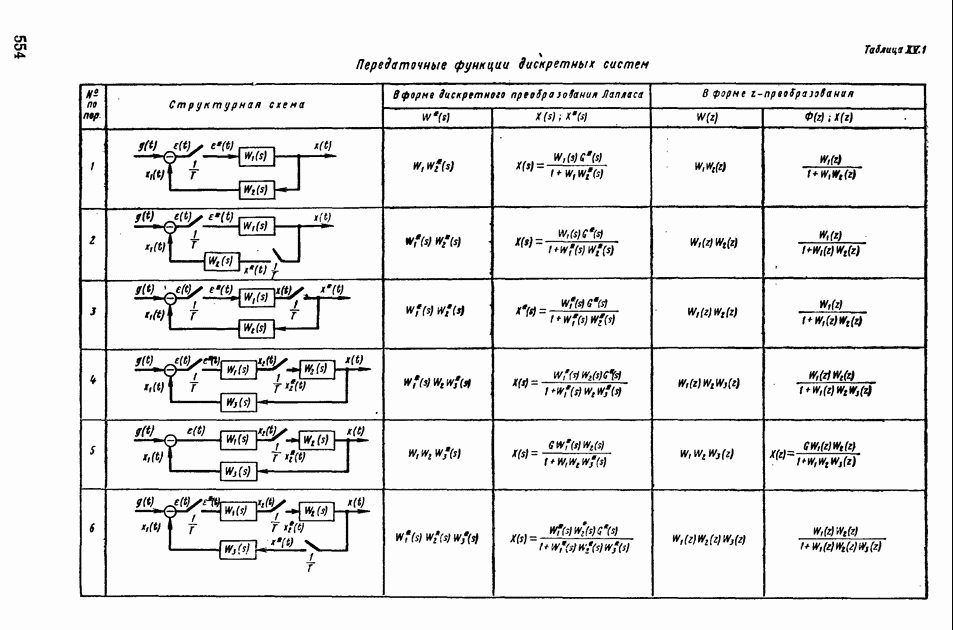
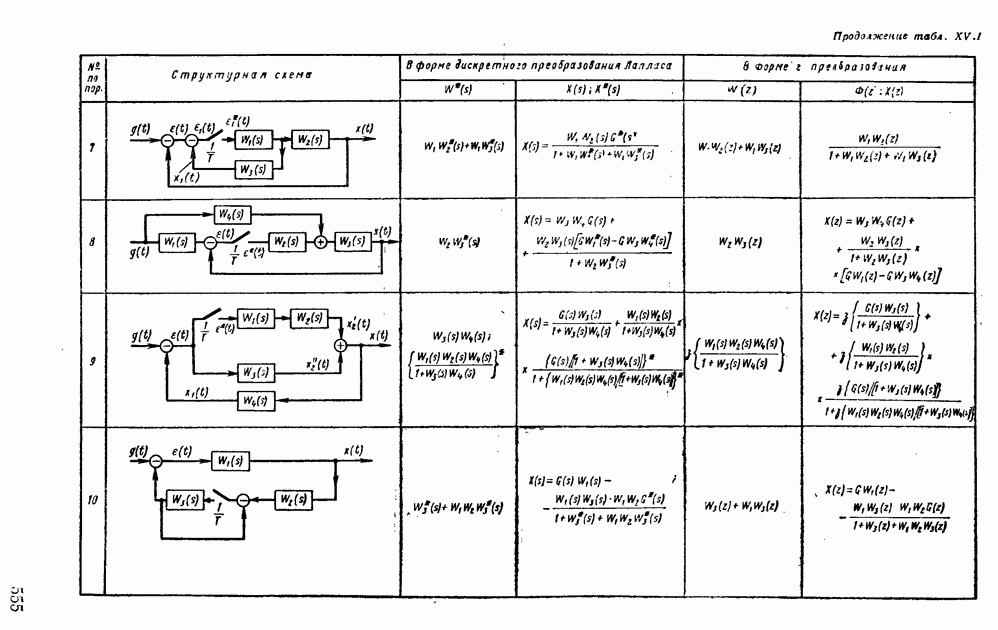
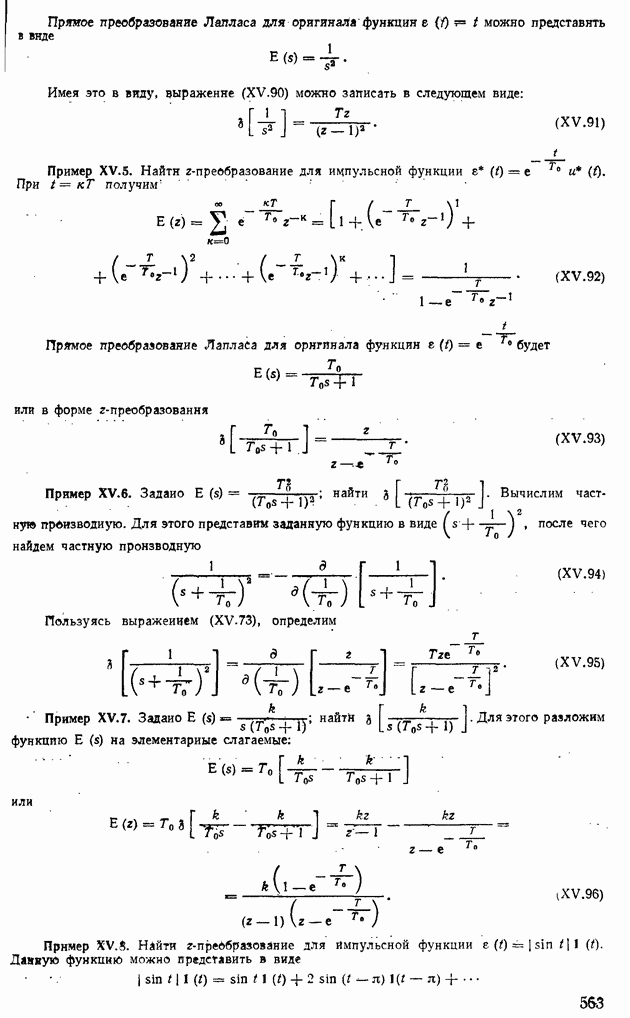
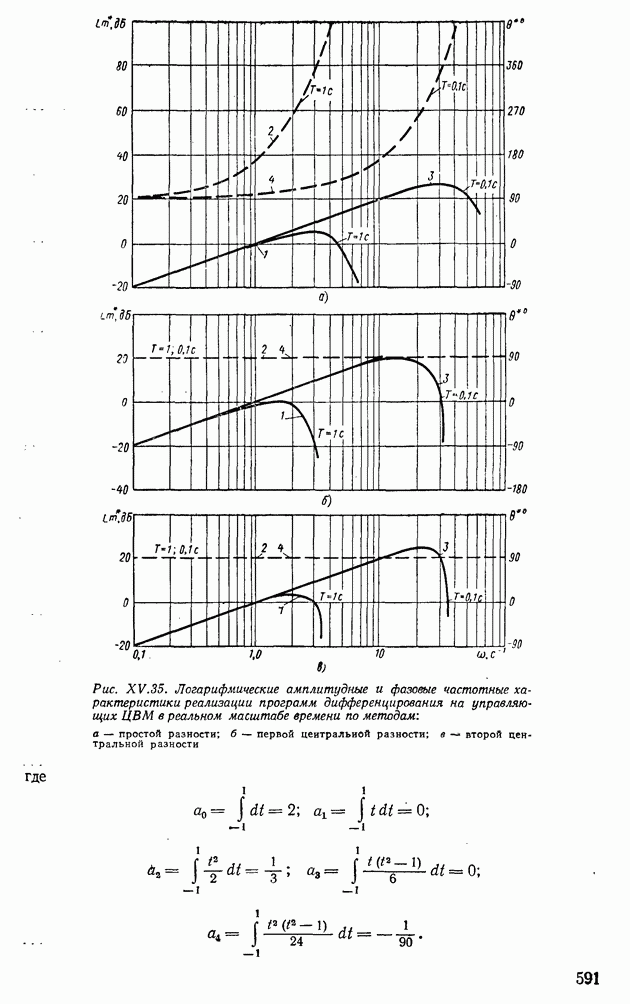
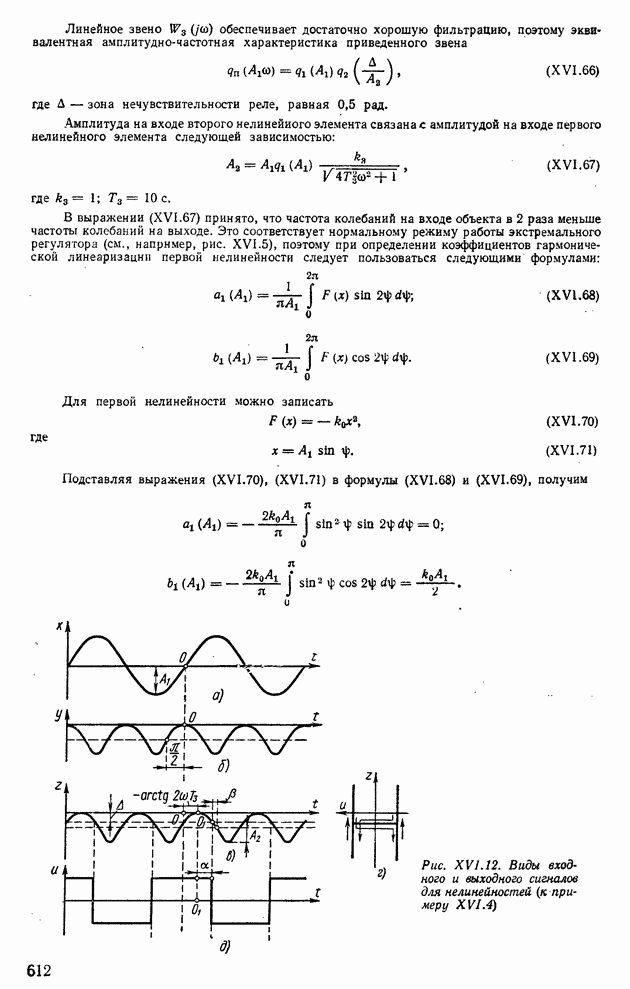
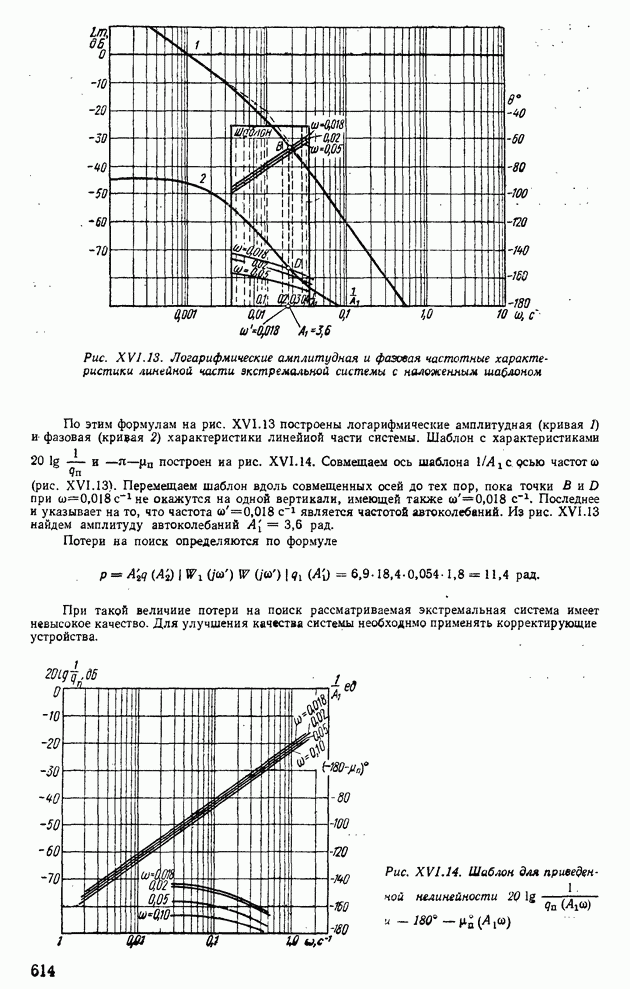
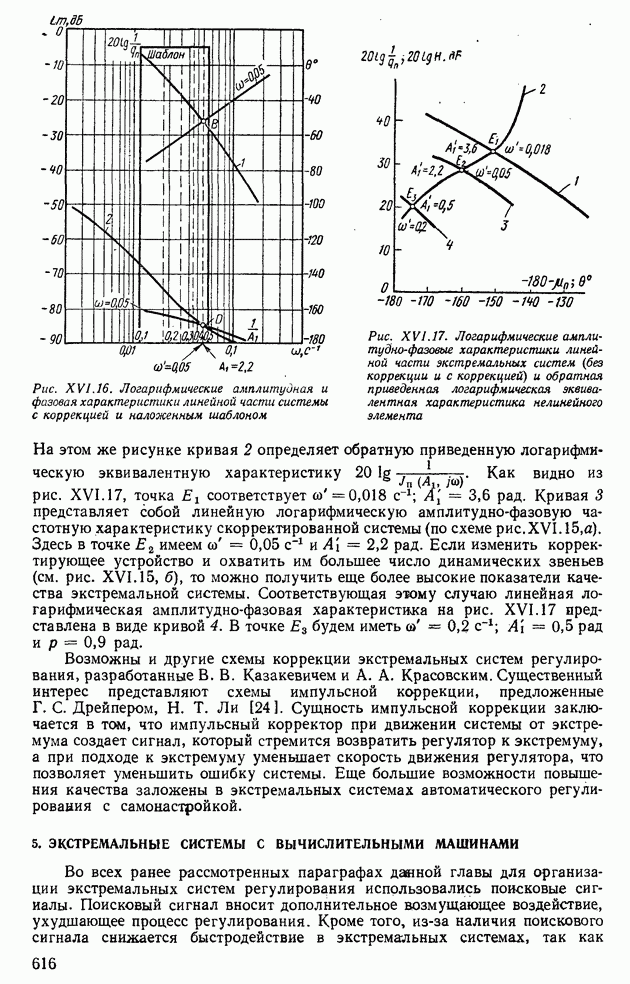
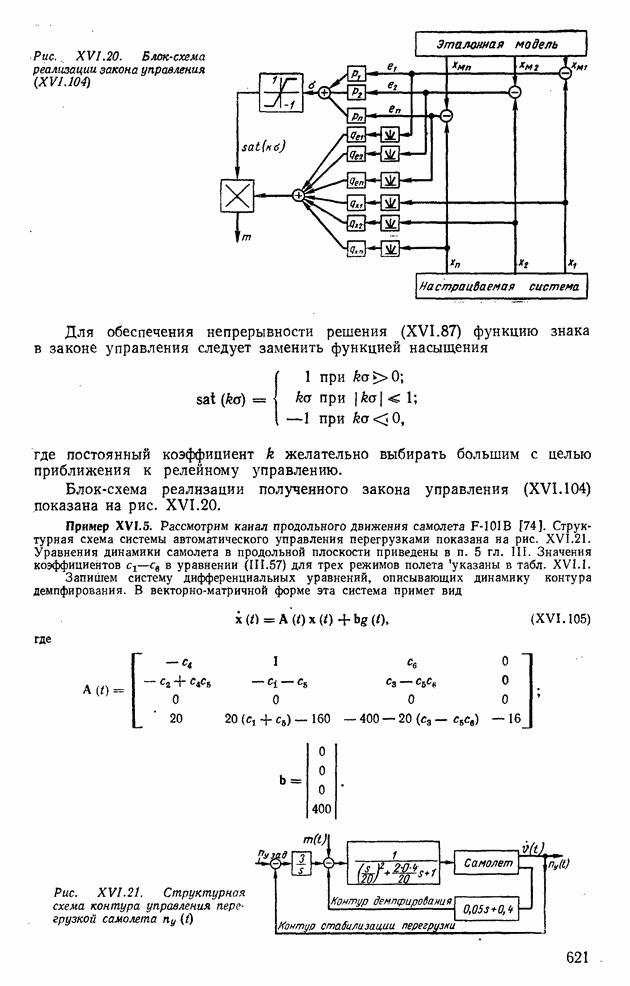
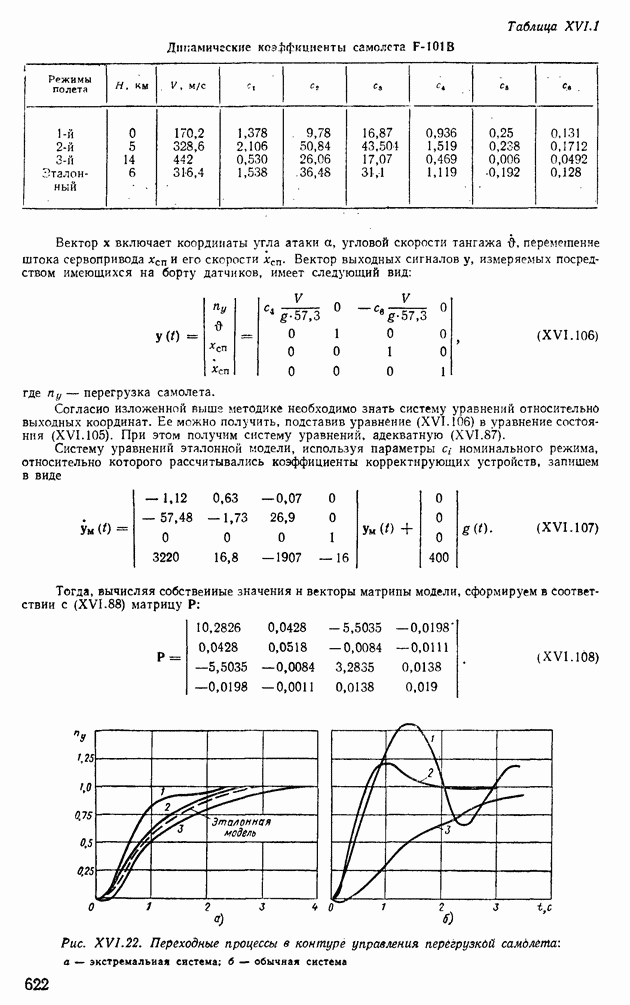
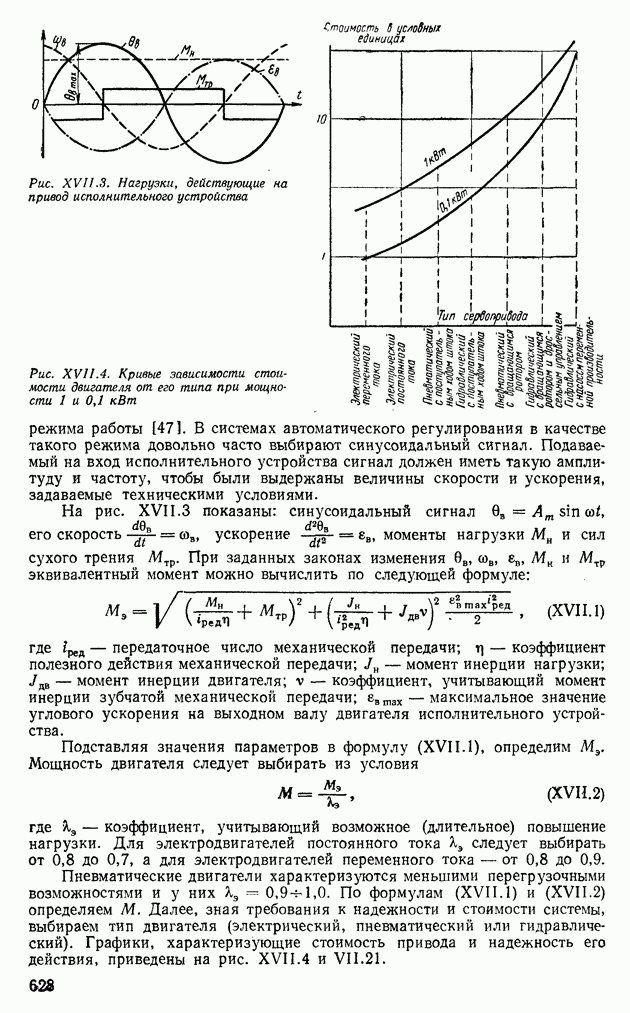
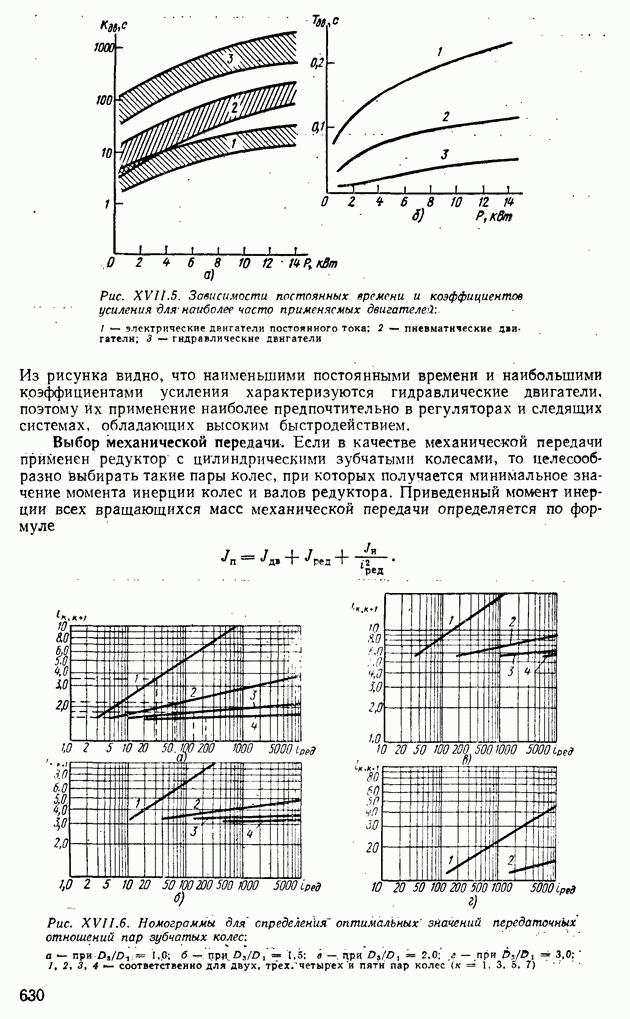
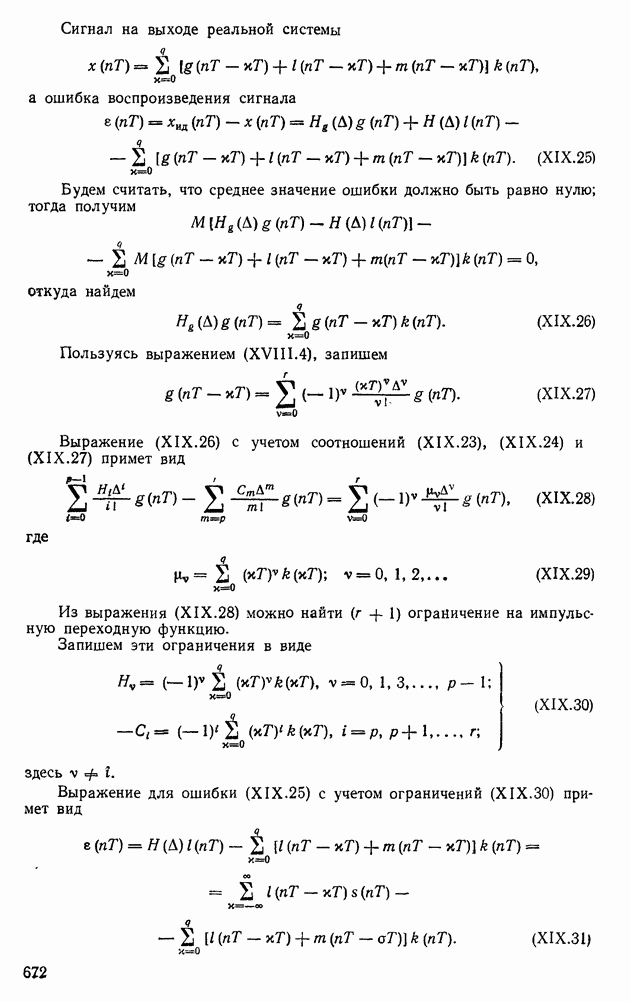| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
4. ПРЕОБРАЗОВАТЕЛИ АНАЛОГ—КОД
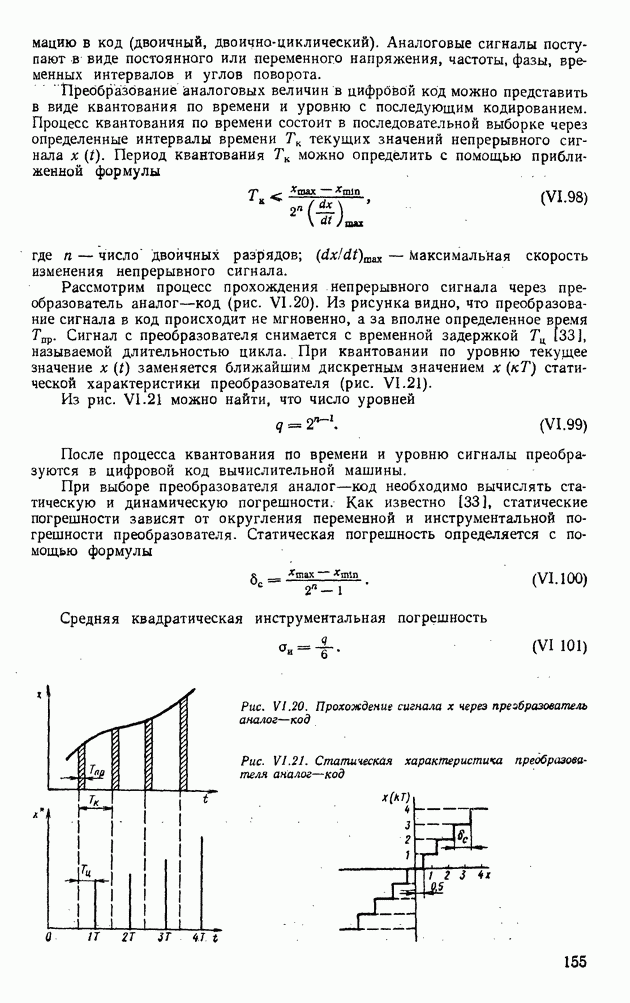
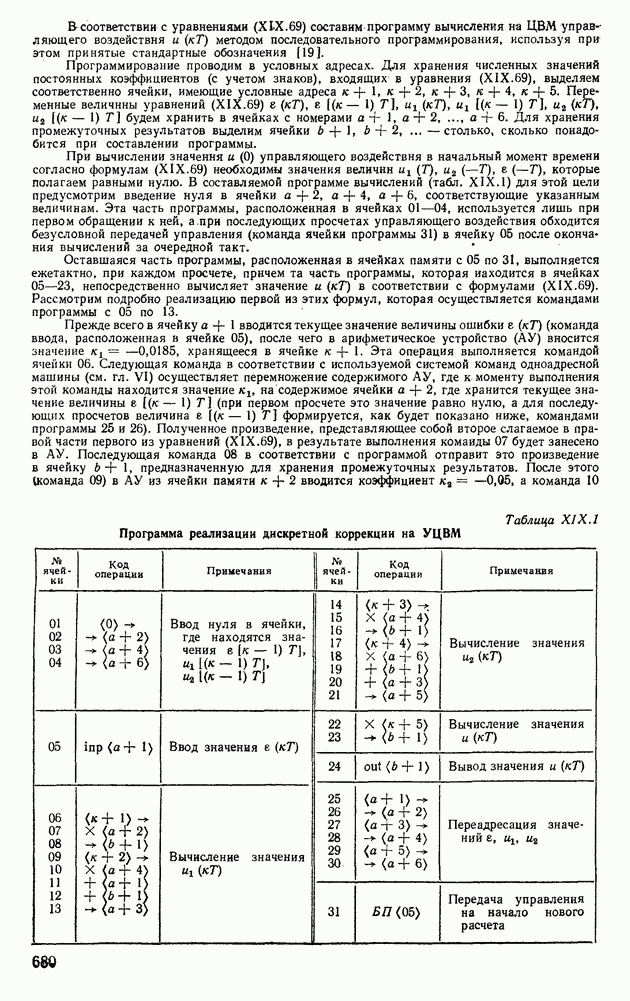
Измерительные устройства непрерывного действия, применяемые в системах автоматического регулирования с управляющими цифровыми вычислительными машинами, могут присоединяться к ЦВМ лишь через преобразователи аналог—код, преобразующие исходную аналоговую инфор.
мацию в код (двоичный, двоично-циклический). Аналоговые сигналы поступают в виде постоянного или переменного напряжения, частоты, фазы, временных интервалов и углов поворота.
Преобразование аналоговых величин в цифровой код можно представить в виде квантования по времени и уровню с последующим кодированием. Процесс квантования по времени состоит в последовательной выборке через определенные интервалы времени Т текущих значений непрерывного сигнала  Период квантования Тк можно определить с помощью приближенной формулы
Период квантования Тк можно определить с помощью приближенной формулы

где  — число двоичных разрядов;
— число двоичных разрядов;  — Максимальная скорость изменения непрерывного сигнала.
— Максимальная скорость изменения непрерывного сигнала.
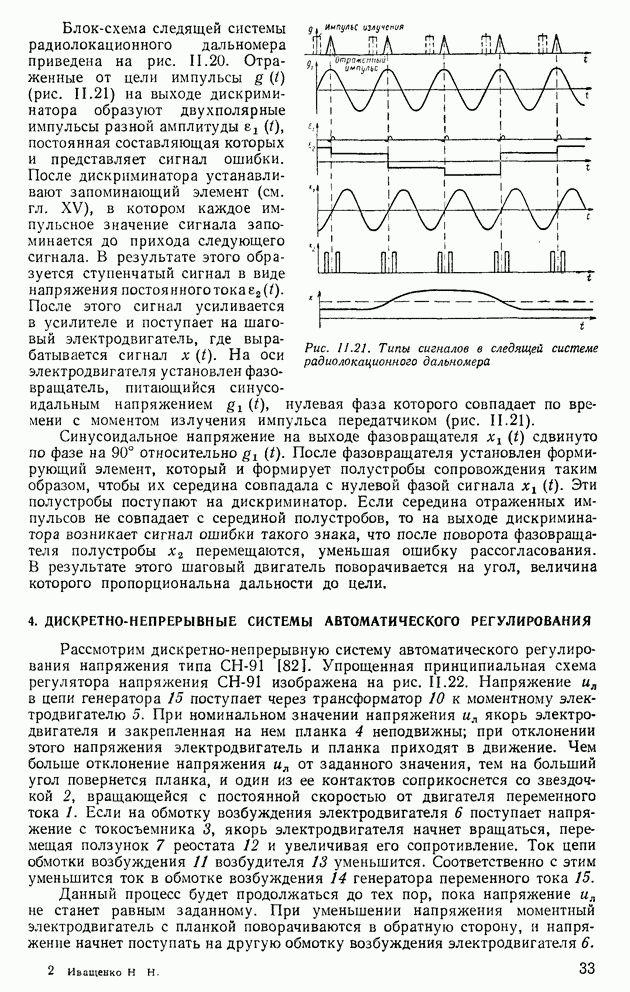
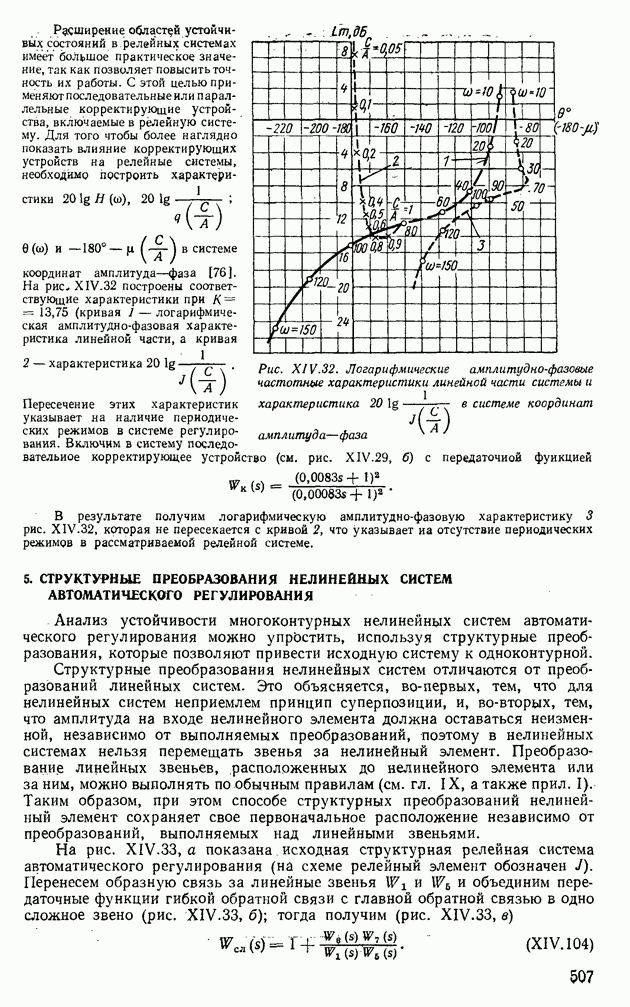
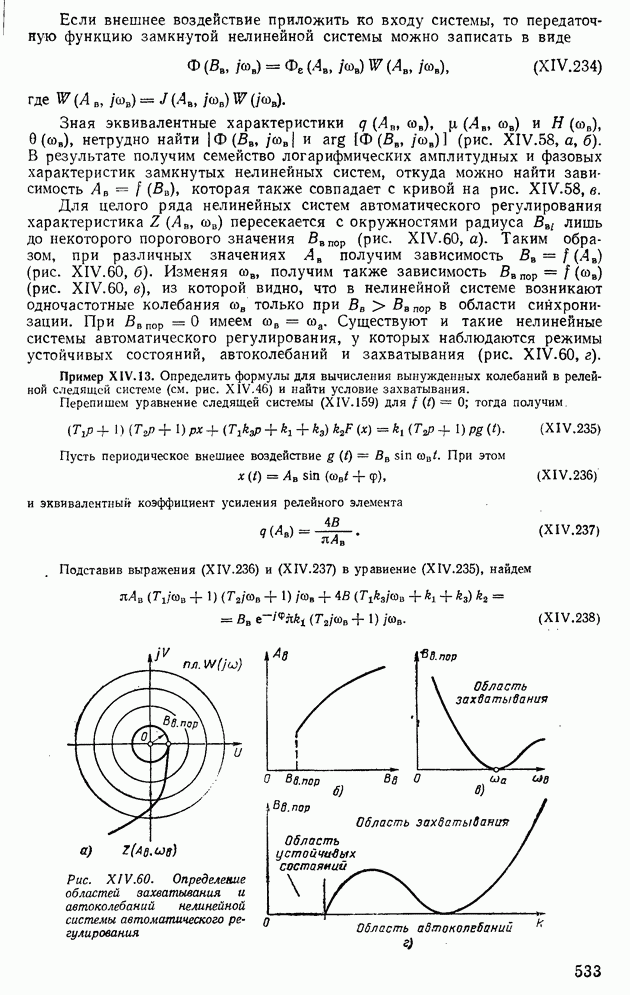
Рассмотрим процесс прохождения непрерывного сигнала через преобразователь аналог—код (рис. VI.20). Из рисунка видно, что преобразование сигнала в код происходит не мгновенно, а за вполне определенное время  . Сигнал с преобразователя снимается с временной задержкой Гц [331, называемой длительностью цикла. При квантовании по уровню текущее значение
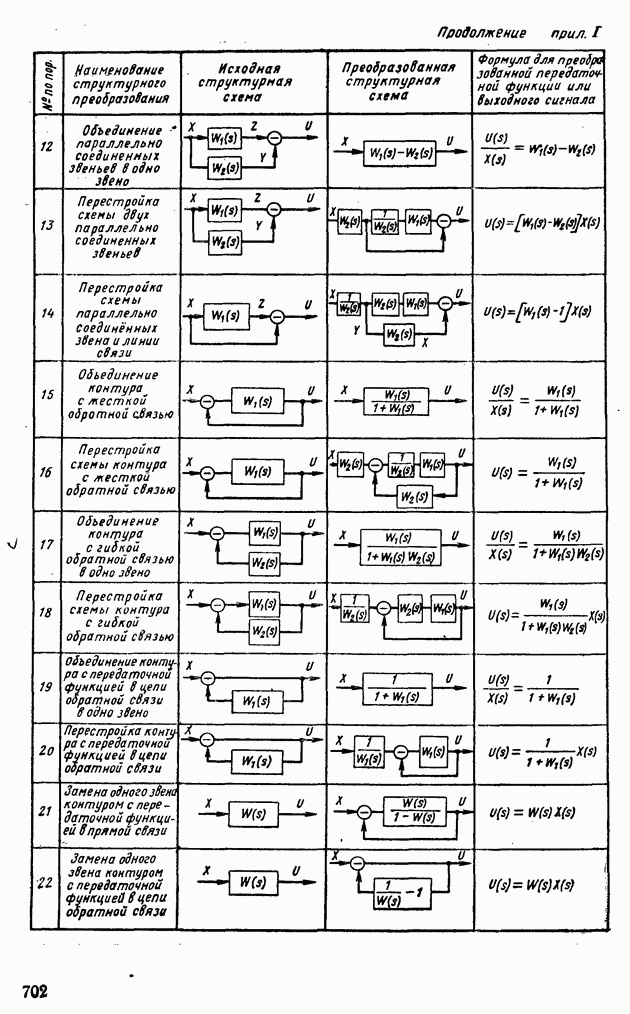
. Сигнал с преобразователя снимается с временной задержкой Гц [331, называемой длительностью цикла. При квантовании по уровню текущее значение  заменяется ближайшим дискретным значением
заменяется ближайшим дискретным значением  статической характеристики преобразователя (рис. VI.21).
статической характеристики преобразователя (рис. VI.21).
Из рис. VI.21 можно найти, что число уровней

После процесса квантования по времени и уровню сигналы преобразуются в цифровой код вычислительной машины.
При выборе преобразователя аналог—код необходимо вычислять статическую и динамическую погрешности. Как известно [33], статические погрешности зависят от округления переменной и инструментальной погрешности преобразователя. Статическая погрешность определяется с помощью формулы

Средняя квадратическая инструментальная погрешность


Рис. VI.20. Прохождение сигнала х через презбразоеатель аналог—код

Рис. VI.21. Статическая характеристика преобразователя аналог—код
Дисперсия погрешности квантования по уровню при  будет
будет

откуда средняя квадратическая ошибка

Среднюю квадратическую ошибку преобразователя можно найти, пользуясь формулами (VI.101) и VI-102), т. е.

Значение случайной погрешности

зависит от коэффициента  величина которого определяется характером закона распределения. Для большинства преобразователей
величина которого определяется характером закона распределения. Для большинства преобразователей 
Динамическую погрешность преобразователя в момент времени  можно записать в виде
можно записать в виде

или

Максимальная величина динамической погрешности преобразователя аналог—код с постоянной длительностью такта определяется максимальной величиной переходного процесса на первом такте преобразования:

где  — коэффициент, определяющий максимальную относительную величину переходного процесса;
— коэффициент, определяющий максимальную относительную величину переходного процесса;  — показатель степени переходного процесса;
— показатель степени переходного процесса;  — время, затрачиваемое преобразователем для выполнения всех операций. Более точные значения динамических погрешностей преобразователей можно получить экспериментальным путем или методом моделирования на ЦВМ [32].
— время, затрачиваемое преобразователем для выполнения всех операций. Более точные значения динамических погрешностей преобразователей можно получить экспериментальным путем или методом моделирования на ЦВМ [32].
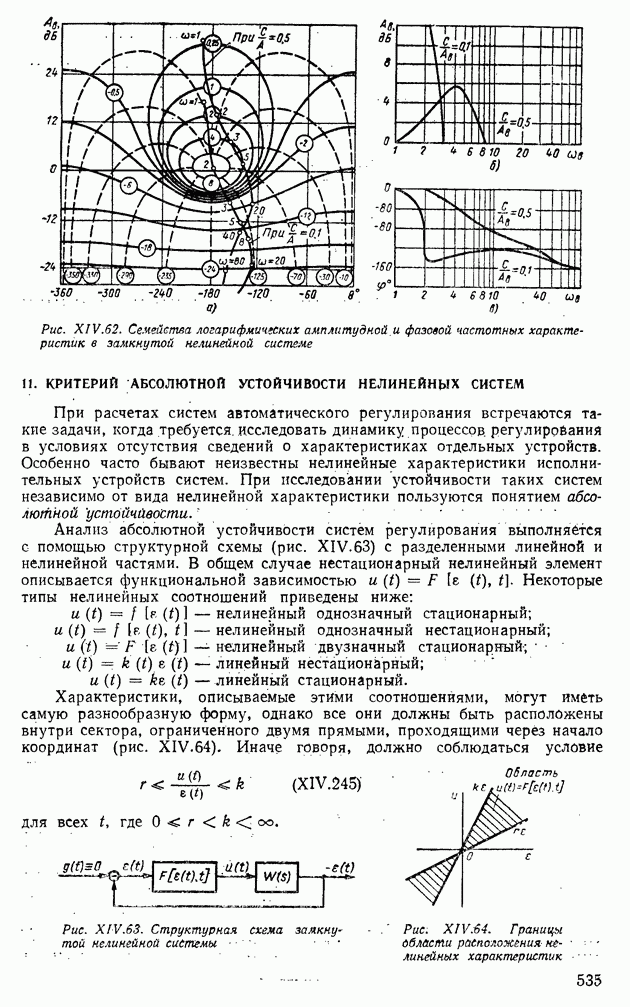
Рассмотрим преобразователи аналог—код различных типов. Наибольшее применение получили преобразователи напряжения и угла поворота в коды.
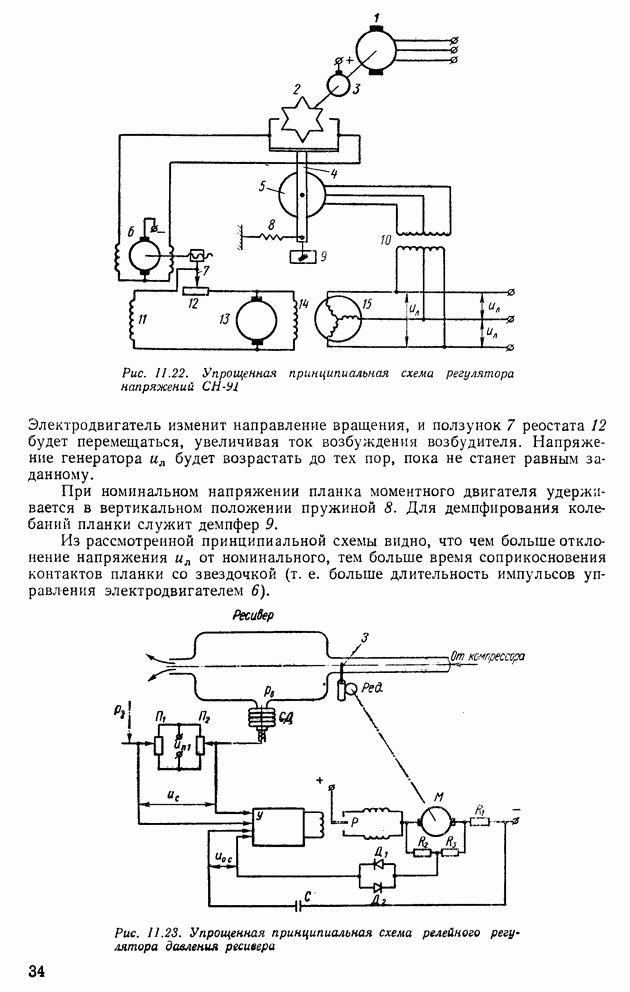
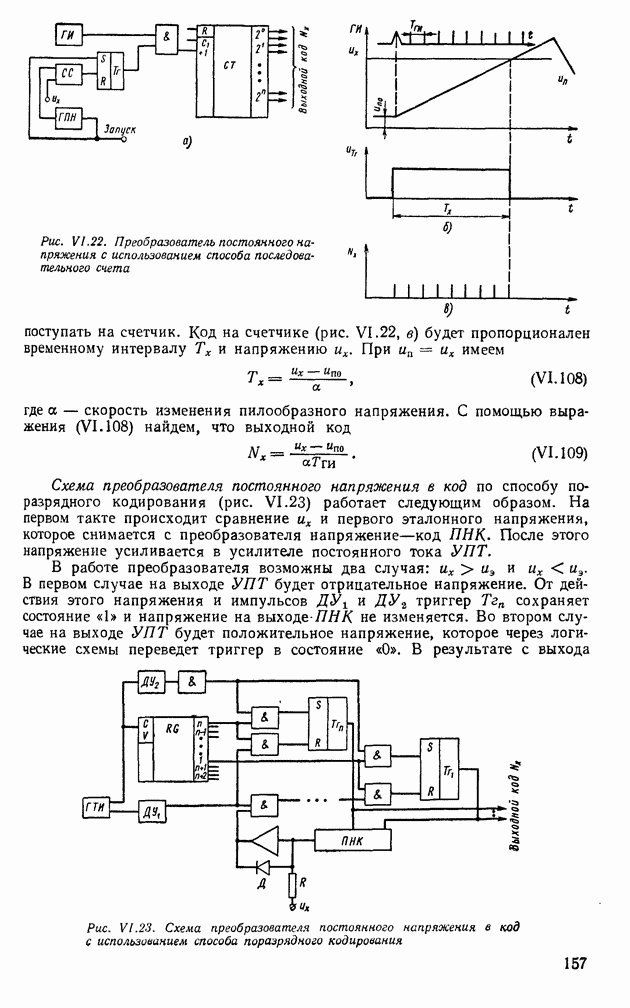
Преобразователи, постоянного и переменного напряжения в код. Существует три способа преобразования непрерывного постоянного напряжения в код: последовательного счета, поразрядного кодирования, считывания. Схема преобразователя аналог—код, работающего по способу последовательного счета, приведена на рис. VI.22, а.
Входное напряжение их преобразуется сначала в пропорциональный временной интервал  (рис. VI.22, б), а затем в код (рис. VI.22, в). Из схемы видно, что импульсы запуска поступают на генератор пилообразного напряжения
(рис. VI.22, б), а затем в код (рис. VI.22, в). Из схемы видно, что импульсы запуска поступают на генератор пилообразного напряжения  который вырабатывает напряжение
который вырабатывает напряжение  Триггер
Триггер  открывает схему совпадения, и импульсы
открывает схему совпадения, и импульсы  поступают на счетчик
поступают на счетчик  . В момент равенства
. В момент равенства  и их срабатывает схема сравнения (рис. VI.22, б), которая ставит триггер
и их срабатывает схема сравнения (рис. VI.22, б), которая ставит триггер  в нулевое состояние, а импульсы
в нулевое состояние, а импульсы  перестают
перестают
Рис. VI.22. (см. скан) Преобразователь постоянного напряжения с использованием способа последовательного счета
поступать на счетчик. Код на счетчике (рис. VI.22, в) будет пропорционален временному интервалу  и напряжению их. При
и напряжению их. При  имеем
имеем

где а — скорость изменения пилообразного напряжения. С помощью выражения (VI. 108) найдем, что выходной код

Схема преобразователя постоянного напряжения в код по способу поразрядного кодирования (рис. VI.23) работает следующим образом. На первом такте происходит сравнение их и первого эталонного напряжения, которое снимается с преобразователя напряжение—код ПНК. После этого напряжение усиливается в усилителе постоянного тока УПТ.
В работе преобразователя возможны два случая:  и
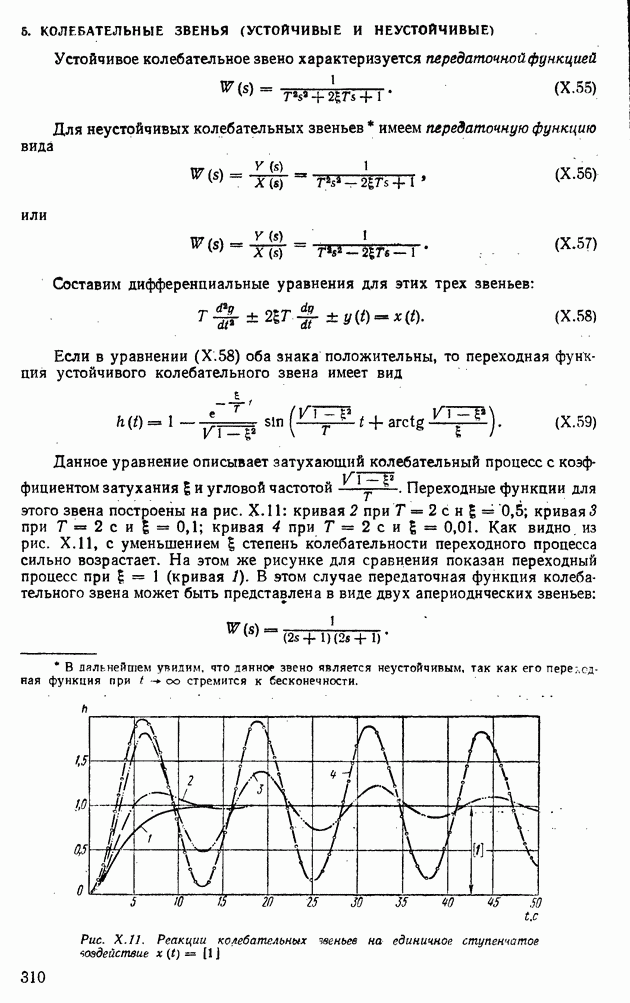
и  . В первом случае на выходе УПТ будет отрицательное напряжение. От действия этого напряжения и импульсов
. В первом случае на выходе УПТ будет отрицательное напряжение. От действия этого напряжения и импульсов  и
и  триггер
триггер  сохраняет состояние «1» и напряжение на выходе
сохраняет состояние «1» и напряжение на выходе  не изменяется. Во втором случае на выходе УПТ будет положительное напряжение, которое через логические схемы переведет триггер в состояние «0». В результате с выхода
не изменяется. Во втором случае на выходе УПТ будет положительное напряжение, которое через логические схемы переведет триггер в состояние «0». В результате с выхода

Рис. VI.23. Схема преобразователя постоянного напряжения в код с использованием способа поразрядного кодирования

Рис. VI.24. Схема преобразователя постоянного напряжения в код с использованием способа считывания
ПНК снимается напряжение  Такие же преобразования выполняются и на последующих тактах (т. е. в каждом из тактов происходит сравнение их с суммой эталонных напряжений
Такие же преобразования выполняются и на последующих тактах (т. е. в каждом из тактов происходит сравнение их с суммой эталонных напряжений  После окончания
После окончания  рабочих тактов поступает
рабочих тактов поступает  тактовый импульс, приводящий к считыванию параллельного кода
тактовый импульс, приводящий к считыванию параллельного кода  Преобразователь приходит в нулевое состояние после подсчета
Преобразователь приходит в нулевое состояние после подсчета  импульса.
импульса.
Преобразователь напряжения, построенный по способу считывания (рис. VI.24), имеет  опорных напряжений, снимаемых с делителей. Каждое из этих напряжений поступает на схемы сравнения
опорных напряжений, снимаемых с делителей. Каждое из этих напряжений поступает на схемы сравнения  куда подается напряжение их. В зависимости от результатов сравнения получается параллельный код
куда подается напряжение их. В зависимости от результатов сравнения получается параллельный код  Для исключения неоднозначности считывания применяются фиксирующие триггеры
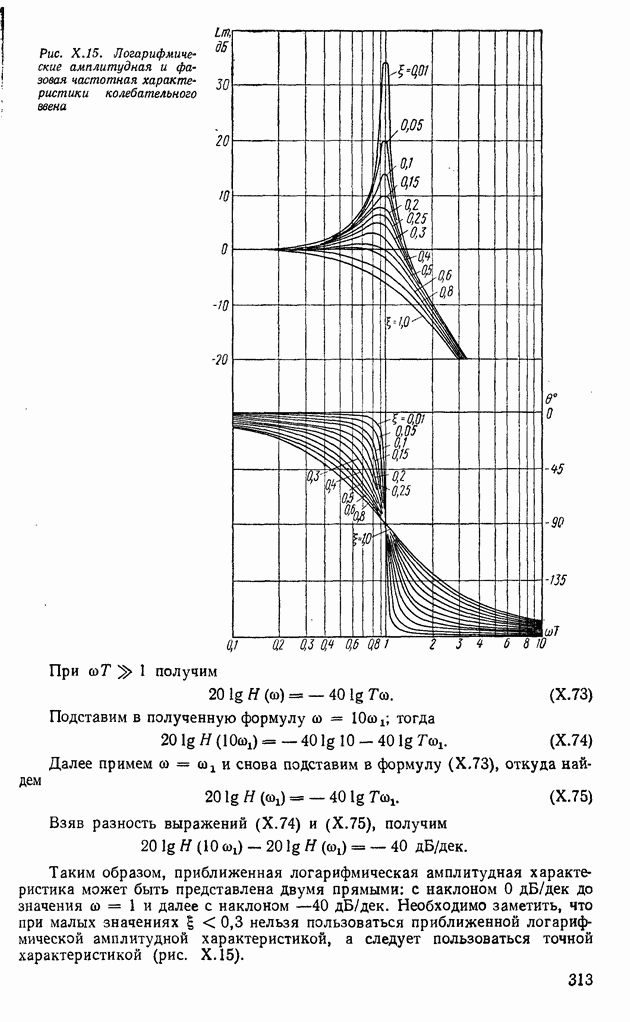
Для исключения неоднозначности считывания применяются фиксирующие триггеры  Выходной сигнал снимается со счетчика
Выходной сигнал снимается со счетчика  Преобразователи этого типа нашли самое широкое распространение из-за высокого быстродействия.
Преобразователи этого типа нашли самое широкое распространение из-за высокого быстродействия.
В преобразователях переменного напряжения в код используется принцип формирования опорных напряжений (рис. VI.25), когда входной сигнал переменного тока их поступает через блок масштабного преобразования БМП на схему сравнения  Одновременно с этим сигнал их через блок
Одновременно с этим сигнал их через блок  попадает на вспомогательный блок масштабного преобразования ВБМП, представляющий собой делитель напряжений.
попадает на вспомогательный блок масштабного преобразования ВБМП, представляющий собой делитель напряжений.
Напряжение их сравнивается с постоянным эталонным напряжением  на блоке
на блоке  . В зависимости от сигнала разности этих напряжений цепи уравновешивания
. В зависимости от сигнала разности этих напряжений цепи уравновешивания  .н БМП устанавливают такой передаточный коэффициент
.н БМП устанавливают такой передаточный коэффициент  при котором имеет место равенство
при котором имеет место равенство

На выходе БМП получается напряжение  поступающее на ВБМП. В результате этого с блока ВБМП снимается напряжение их, управляющее схемой сравнения
поступающее на ВБМП. В результате этого с блока ВБМП снимается напряжение их, управляющее схемой сравнения  . С выхода
. С выхода  снимается сигнал для изменения передаточного коэффициента
снимается сигнал для изменения передаточного коэффициента  Когда разность
Когда разность  становится малой, коэффициент
становится малой, коэффициент  находят с помощью соотношения
находят с помощью соотношения

С учетом соотношения (VI. 111) выражение  примет вид
примет вид

поэтому код выхода  будет однозначно соответствовать положению ключей в делителе опорного напряжения ВБМП.
будет однозначно соответствовать положению ключей в делителе опорного напряжения ВБМП.

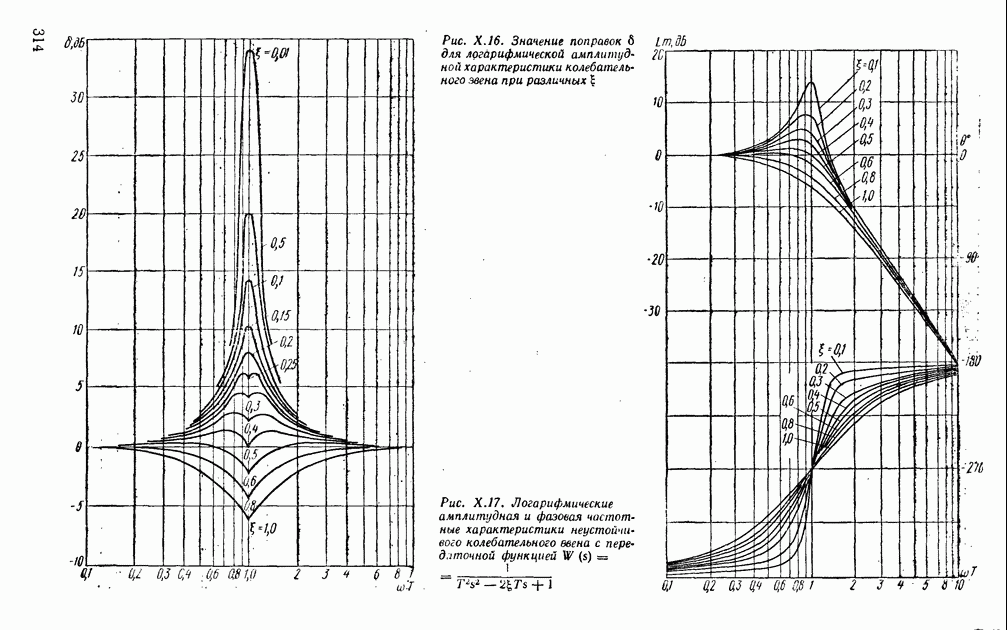
Рис. VI.25. Схема преобразователя переменного тока в код с использованием метода опорных напряжений

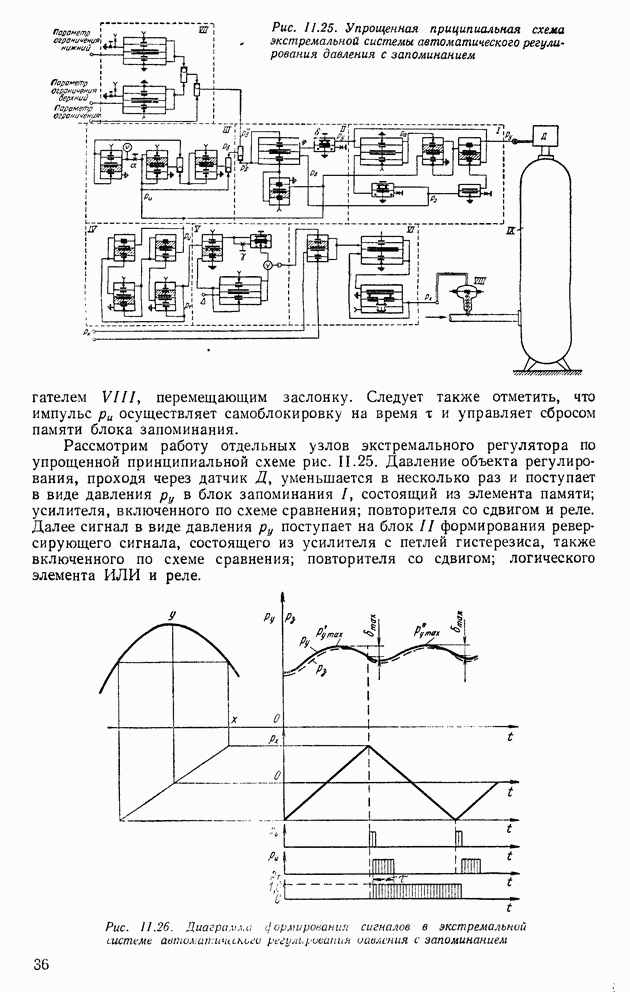
Рис. VI.26. Схема преобразователя временного интервала в код с линией задержки
Преобразователи временного интервала в код создают на основе схемы, работающей по методу последовательного счета. Однако для повышения точности в таких преобразователях применяют линии задержки (рис. VI.26). Линия задержки смещает на  импульсы
импульсы  в результате чего создаются две цепочки импульсов, поступающих на счетчики
в результате чего создаются две цепочки импульсов, поступающих на счетчики 
Если положение импульса останова, воздействующего на логические элементы запрета  и 32, будет определяться относительно этих двух цепочек импульсов, то максимальная ошибка временного интервала
и 32, будет определяться относительно этих двух цепочек импульсов, то максимальная ошибка временного интервала  уменьшится в 2 раза.
уменьшится в 2 раза.
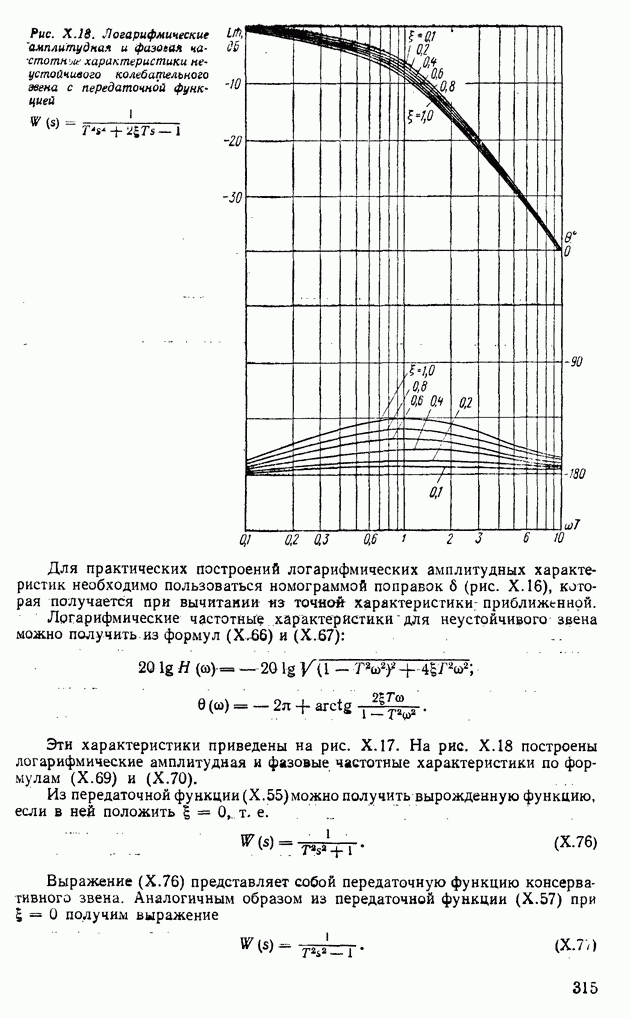
В преобразователях напряжения в частоту (рис. VI.27) после запуска напряжение их поступает на ключ К, при замыкании которого включается интегратор. Одновременно с этим схема совпадения начинает пропускать импульсы  на счетчик. Напряжение на выходе интегратора линейно возрастает до опорного
на счетчик. Напряжение на выходе интегратора линейно возрастает до опорного  . При
. При  схема сравнения
схема сравнения  срабатывает, и импульс
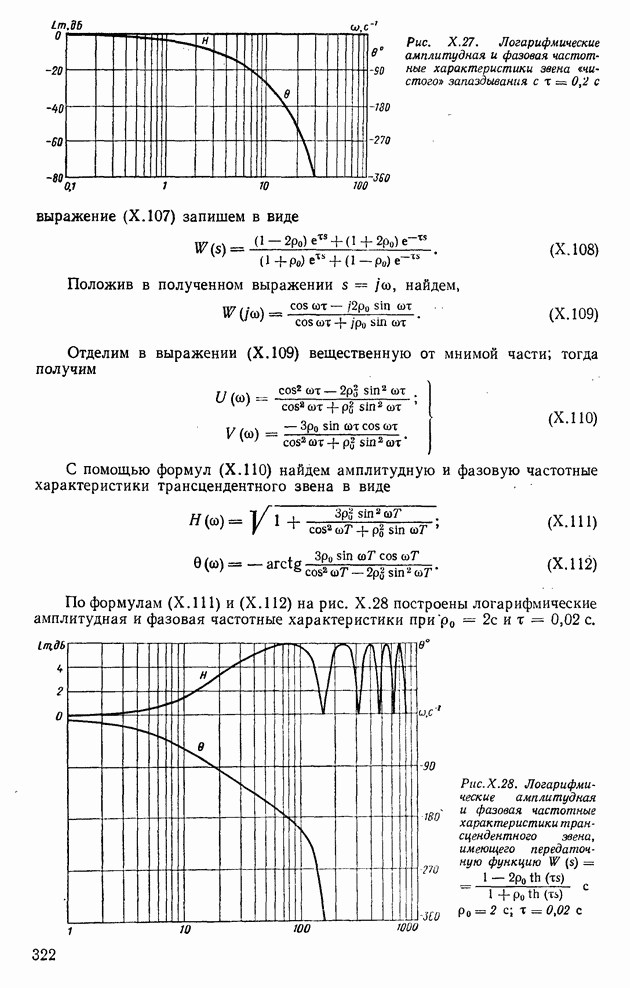
срабатывает, и импульс  поступает на второй вход интегратора. Амплитуда импульса
поступает на второй вход интегратора. Амплитуда импульса  имеет обратную полярность к
имеет обратную полярность к  а длительность равна т. В результате напряжение ни упадет. Итак, после действия импульса
а длительность равна т. В результате напряжение ни упадет. Итак, после действия импульса  напряжение
напряжение  снова начинает увеличиваться и цикл интегрирования повторяется.
снова начинает увеличиваться и цикл интегрирования повторяется.
Если считать, что приращение напряжения на выходе интегратора равно  то можно записать следующую зависимость
то можно записать следующую зависимость

При  в интервале от 0 до
в интервале от 0 до  из зависимости (VI. 113) найдем
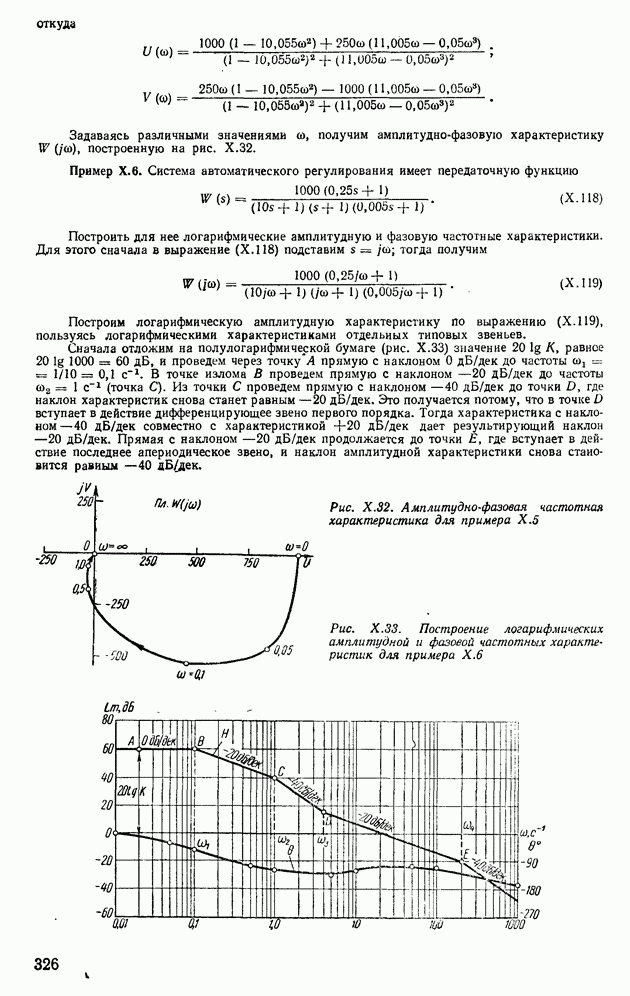
из зависимости (VI. 113) найдем

Если частота следования импульсов ГИ

а

где

то число импульсов, прошедшее через счетчик  за время Т, будет
за время Т, будет

Таким образом, показания счетчика  пропорциойальны входному напряжению.
пропорциойальны входному напряжению.

Рис. VI.27. Схема преобразователя напряжения в частоту

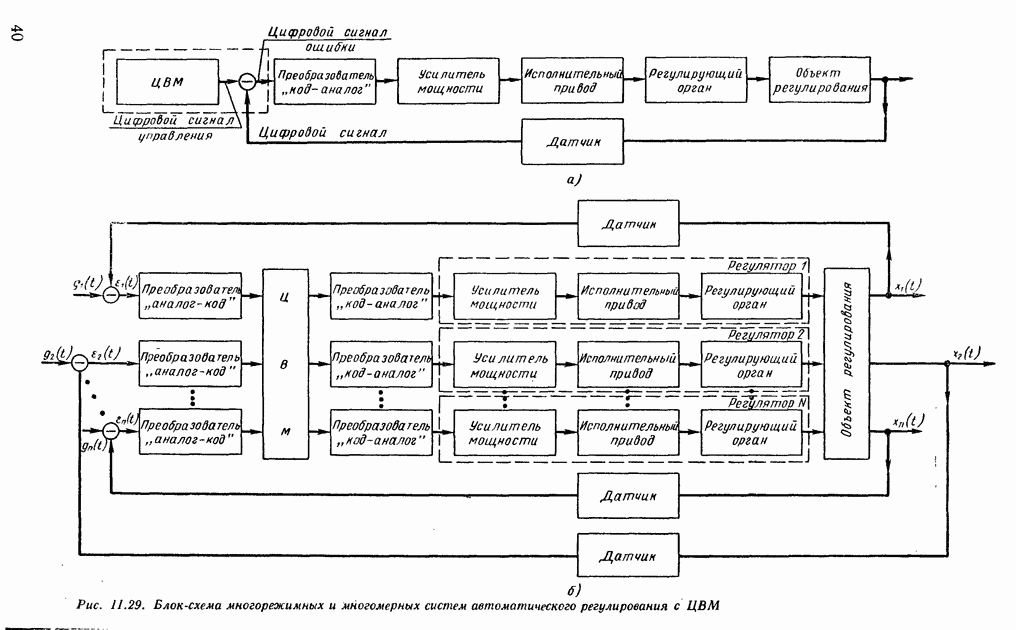
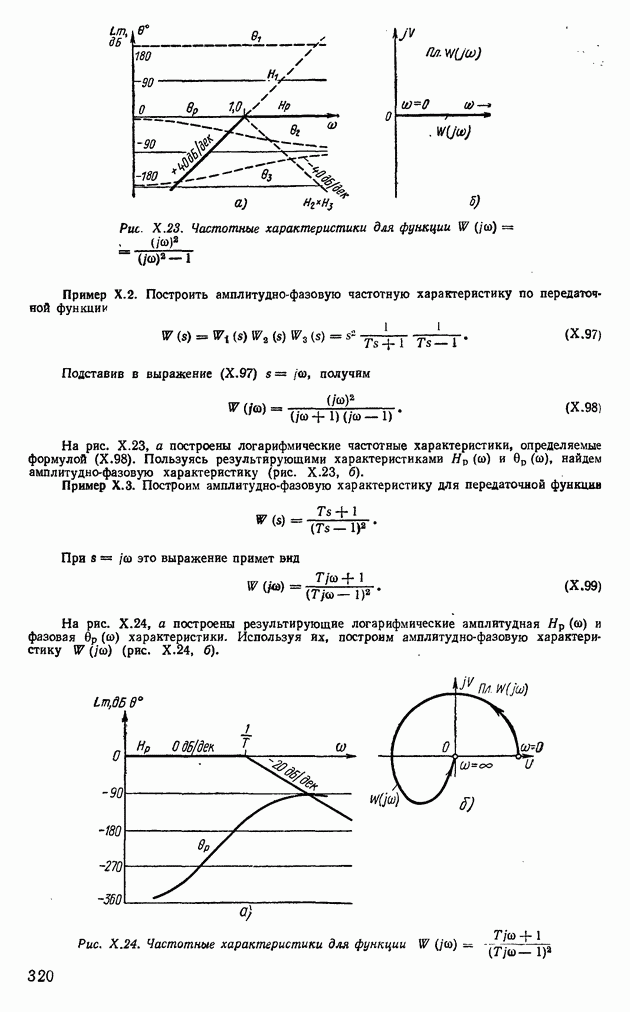
Рис. VI.28. Кодовые шкалы: а — двоичная; б - циклическая
Преобразователи углов поворота в коды имеют кодовые шкалы, считанный сигнал с которых образует двоичный или циклический код. В качестве устройств считывания применяются щетки, магнитные головки и фотодиодные датчики [78]. Если используется двоичная кодовая шкала 1 (рис. VI.28, а), то весь диапазон углового перемещения разбивают на равные интервалы  каждому интервалу соответствует вполне определенное двоичное число. Соотношение между числом разрядов
каждому интервалу соответствует вполне определенное двоичное число. Соотношение между числом разрядов  двоичного числа, интервалом
двоичного числа, интервалом  и диапазоном изменения переменных хшах —
и диапазоном изменения переменных хшах —  можно представить в виде
можно представить в виде

Младшему разряду двоичных чисел круговой кодовой шкалы соответствует внешнее кольцо, а старшему — внутреннее кольцо кодовых участков. В этом случае

где  — порядковый номер кольца.
— порядковый номер кольца.
Преимущество двоичной кодовой шкалы заключается в том, что считанный сигнал представляет собой код двоичного числа. Однако считывание сигналов, например, щетками 2 (рис. VI.28, а) может происходить со значительными ошибками. Так, в пятиразрядной двоичной кодовой шкале на границе между 15-м и 16-м секторами вместо двоичных чисел 01111 и 1000 может быть считано любое пятиразрядное число от 00000 до 11111.
Во избежание ошибок считывания применяют циклические кодовые шкалы (рис. VI.28, б). Циклические коды приводятся к двоичному коду путем сложения сдвинутого двоичного числа по модулю 2 (без переноса), т. е.

Пример VI. 1. Сложить двоичное число 10001 по модулю 2 (mod 2) и получить циклический код данного числа. Сдвинем число 10001 вправо на один разряд и сложим его с заданным числом (без переноса), т. е.

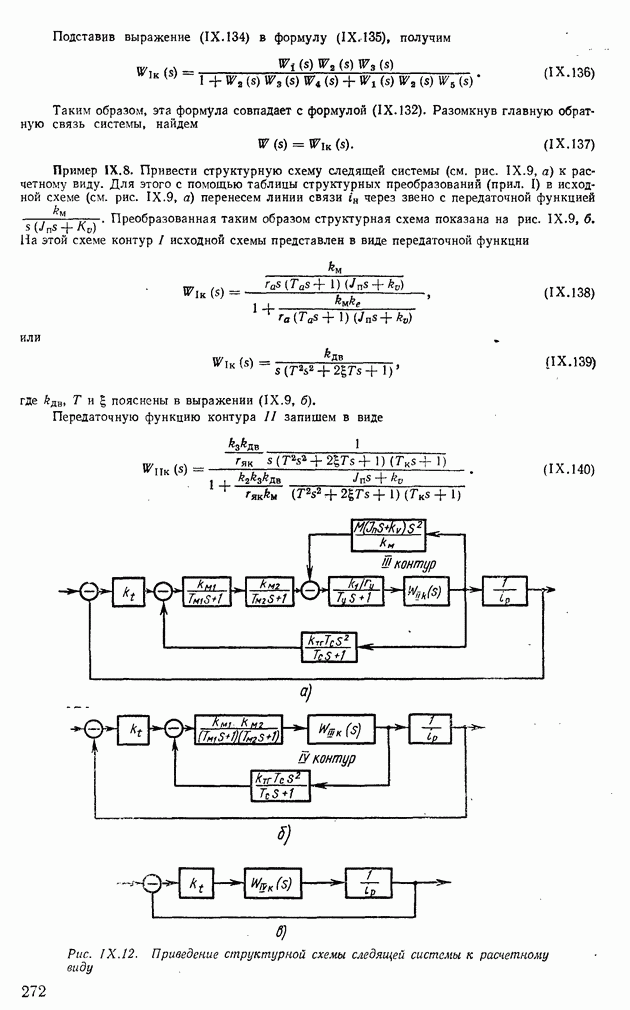
В результате получим циклический код 11001.
Обратный переход от изображения числа в циклическом коде в двоичный код осуществляется в виде

Из выражения (VI. 122) следует, что значение разрядов двоичного числа получается из его циклического кода последовательно, начиная со старшего разряда. Схема такого преобразования изображена на рис. VI.29, а.

Рис. V1.29. Устройство для преобразования последовательного циклического кода, начиная со старшего разряда, в последовательный двоичный код
Триггер  со счетным входом выполняет функции сумматора по
со счетным входом выполняет функции сумматора по  последовательного действия, на вход которого поступают импульсы циклического кода, начиная со старшего разряда. Триггер изменяет состояние с приходом каждого импульса, соответствующего «1» в циклическом коде. Выход триггера связан с одним из входов схемы совпадения. На второй вход этой схемы поступают импульсы ГИ.
последовательного действия, на вход которого поступают импульсы циклического кода, начиная со старшего разряда. Триггер изменяет состояние с приходом каждого импульса, соответствующего «1» в циклическом коде. Выход триггера связан с одним из входов схемы совпадения. На второй вход этой схемы поступают импульсы ГИ.
Импульсы циклического кода сдвинуты на полпериода относительно импульсов ГИ. Если триггер находится в положении «1», то сигнал с его входа отпирает схему совпадения для пропускания синхронизирующих импульсов, а если он находится в положении  то схема заперта. На выходе схемы совпадения образуется двоичный код. Временная диаграмма работы такого устройства показана на рис. VI.29, б.
то схема заперта. На выходе схемы совпадения образуется двоичный код. Временная диаграмма работы такого устройства показана на рис. VI.29, б.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
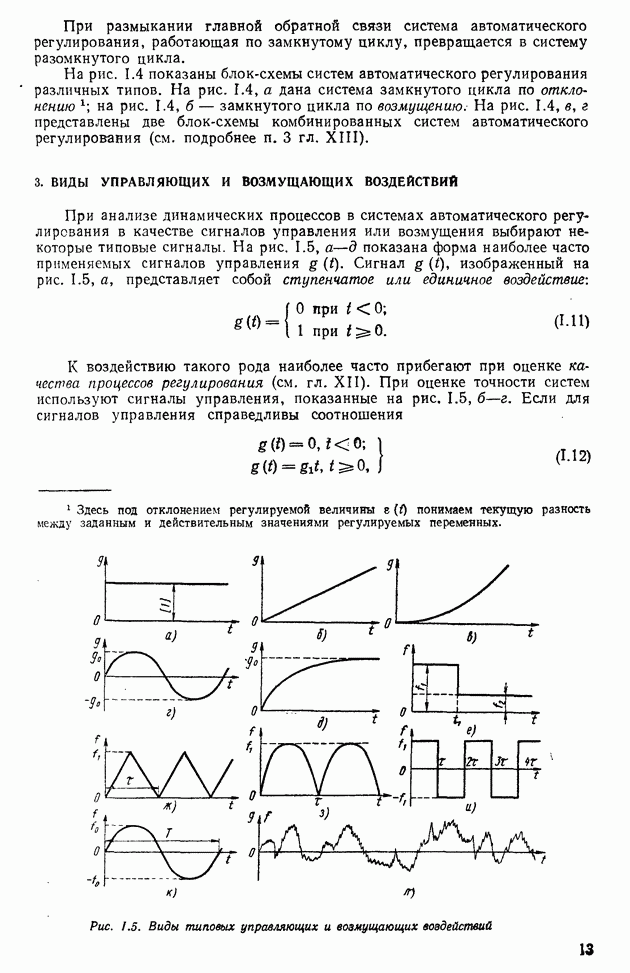
- 1. ПРИНЦИПЫ ДЕЙСТВИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ВИДЫ УПРАВЛЯЮЩИХ И ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ
- 4. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
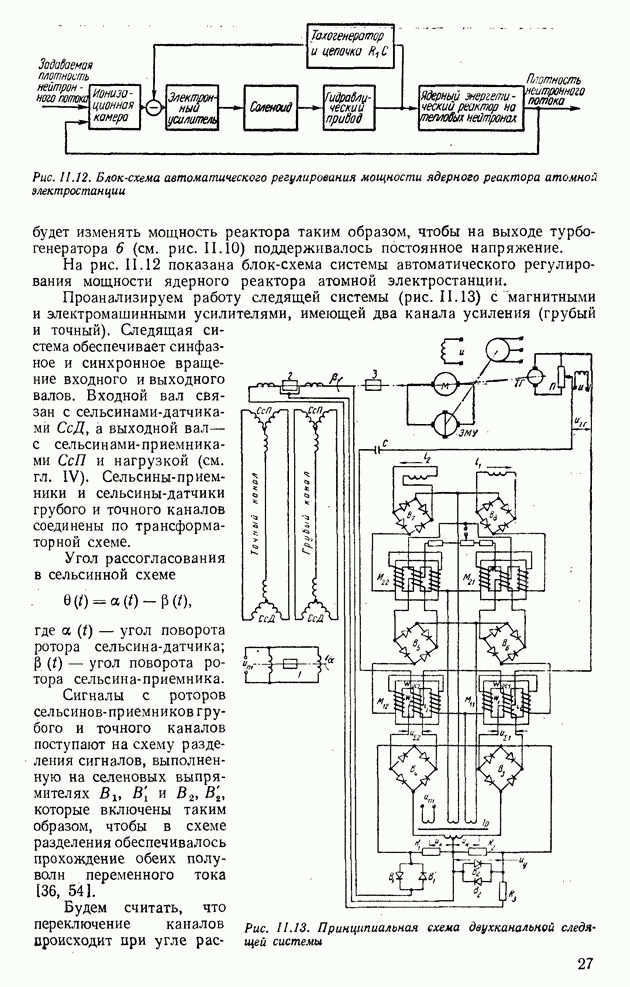
- Глава II. ВИДЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛТРОВАНИЯ
- 1. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
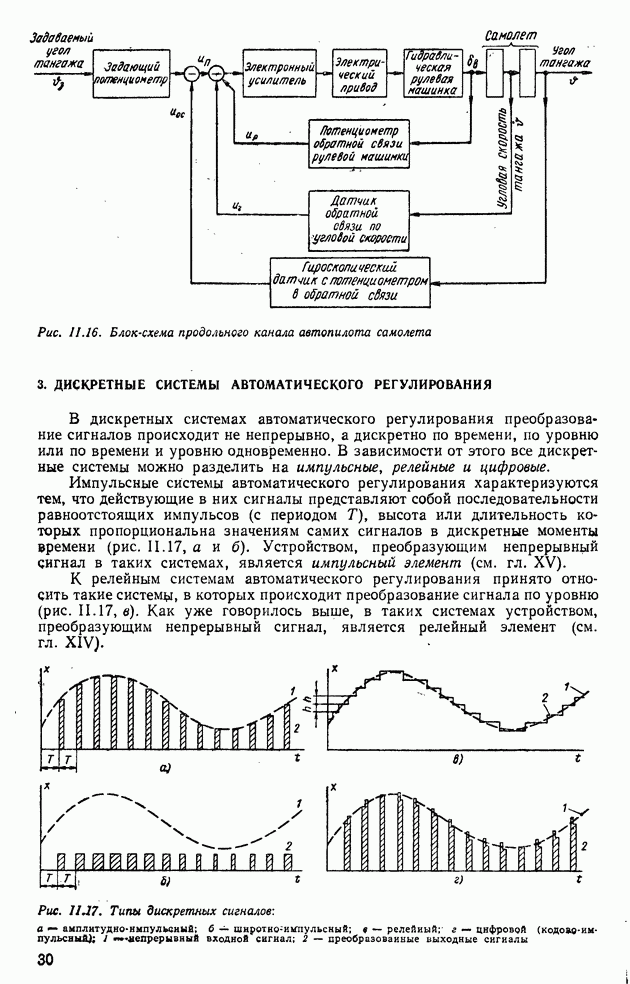
- 3. ДИСКРЕТНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ПРИМЕНЕНИЕ ЦВМ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
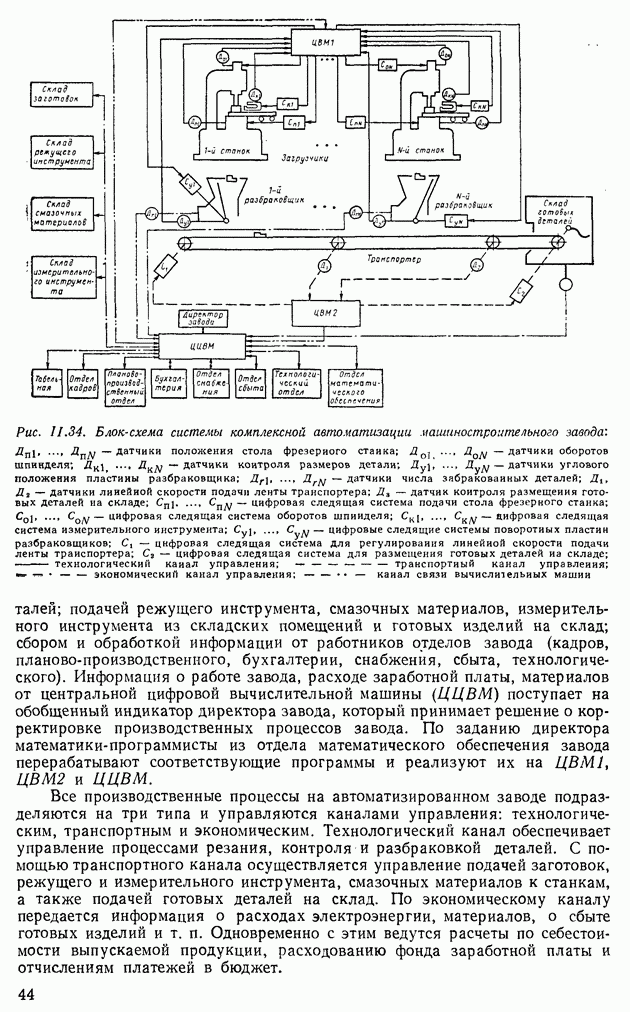
- 7. ПРИМЕНЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ДЛЯ УПРАВЛЕНИЯ СЛОЖНЫМИ ПРОИЗВОДСТВЕННЫМИ ПРОЦЕССАМИ. СИСТЕМЫ КОМПЛЕКСНОЙ АВТОМАТИЗАЦИИ ПРОИЗВОДСТВА
- Глава III. ОБЪЕКТЫ РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ СВОЙСТВА ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 2. ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 3. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ ДИНАМИКИ
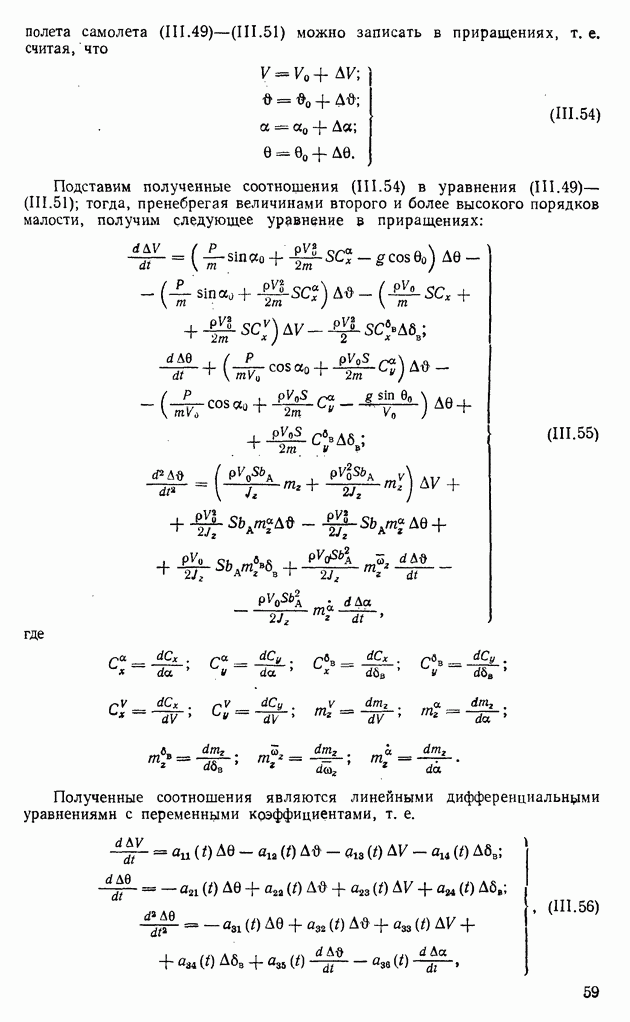
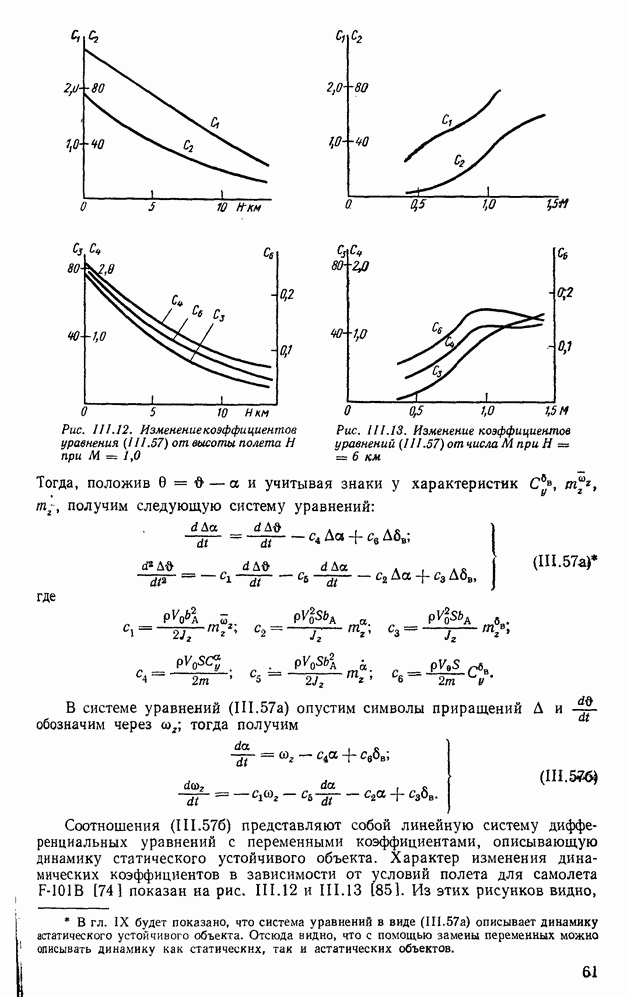
- 4. УСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (ДИЗЕЛЬ, ГИДРОТУРБИНА, САМОЛЕТ)
- 5. НЕУСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (РЕСИВЕР, РАКЕТА-НОСИТЕЛЬ КОСМИЧЕСКИХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ)
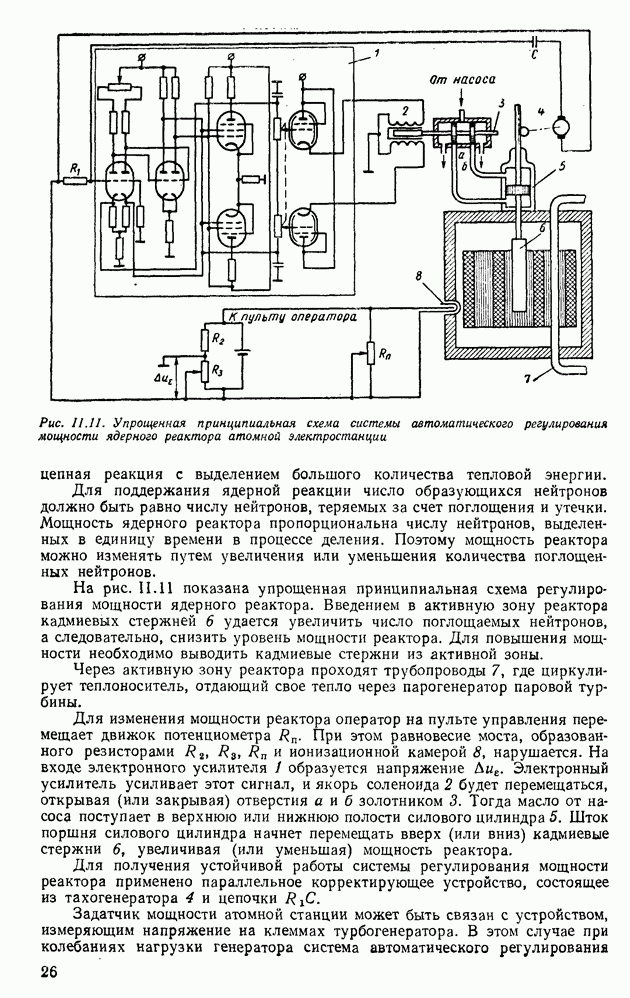
- 6. АСТАТИЧЕСКИЕ ОБЪЕКТЫ (ТРЕХФАЗНЫЙ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ, ЯДЕРНЫЙ ЭНЕРГЕТИЧЕСКИЙ РЕАКТОР НА ТЕПЛОВЫХ НЕЙТРОНАХ, КОСМИЧЕСКИЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ)
- 7. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- Глава IV. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОПРЕДЕЛЕНИЕ ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ИЗМЕРИТЕЛЬНЫХ ПОДСИСТЕМ
- 2. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Индуктивные устройства.
- Емкостные устройства.
- Сельсины.
- Дифференциальный сельсин.
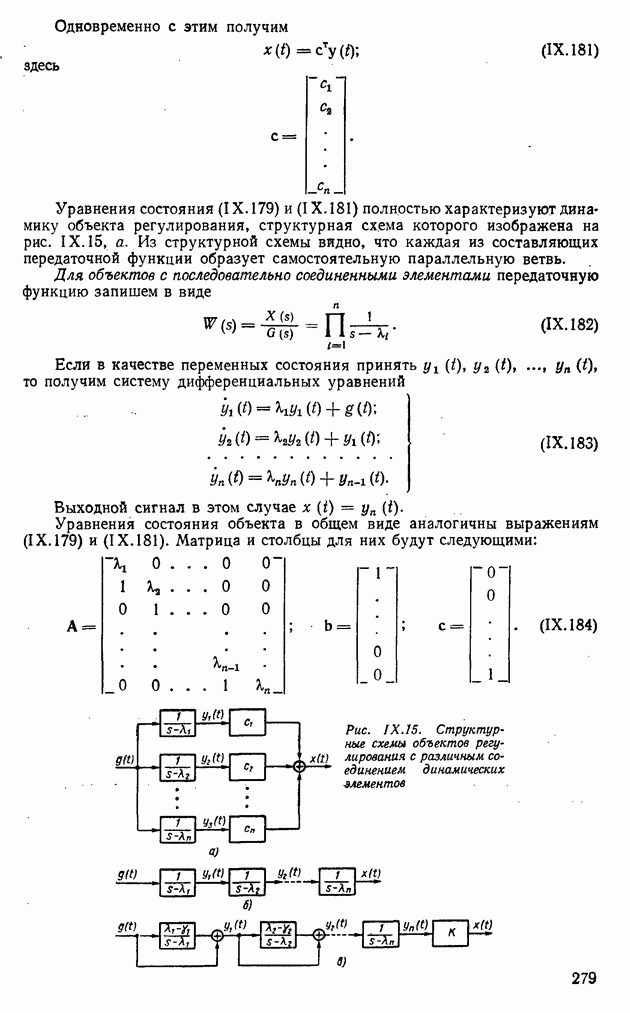
- Погрешность сельсинов.
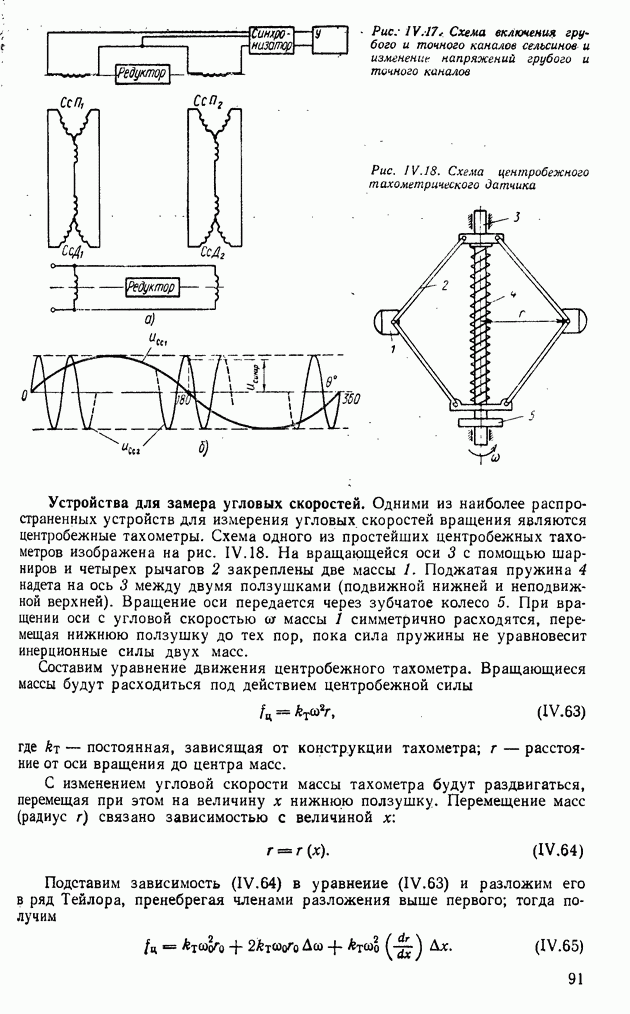
- Устройства для замера угловых скоростей.
- Устройства замера угловых ускорений.
- 4. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И ТОКА
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕМПЕРАТУР И ИЗЛУЧЕНИЙ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЙ И РАСХОДОВ ЖИДКОСТИ И ГАЗА
- 7. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ ВЕЛИЧИН, УГЛОВЫХ СКОРОСТЕЙ И ЛИНЕЙНЫХ УСКОРЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ
- Устройства для измерения линейных ускорений подвижных объектов (акселерометры).
- 8. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- Глава V. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ
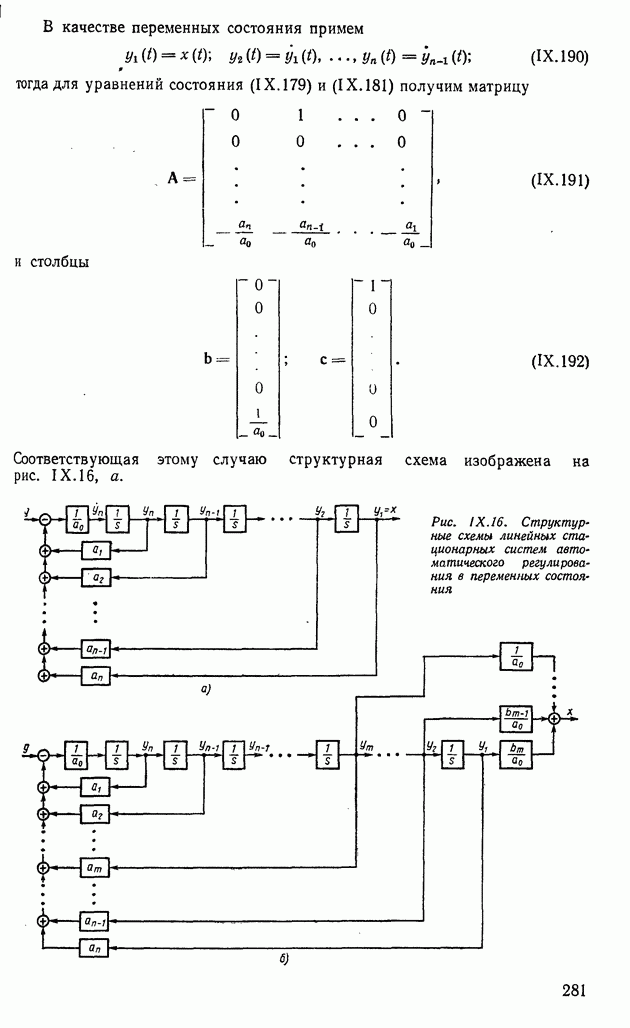
- 2. МАГНИТНЫЕ УСИЛИТЕЛИ
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 4. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 5. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ РАЗЛИЧНЫХ УСИЛИТЕЛЕЙ
- ГЛАВА VI. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА
- 1. УСИЛИТЕЛИ-ПРЕОБРАЗОВАТЕЛИ
- 2. РЕЛЕ
- 3. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. ПРЕОБРАЗОВАТЕЛИ АНАЛОГ—КОД
- 5. ПРЕОБРАЗОВАТЕЛИ КОД—АНАЛОГ
- 6. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ УПРАВЛЯЮЩИЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
- 8. ПНЕВМАТИЧЕСКИЕ АНАЛОГОВЫЕ И ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 9. ТОЧНОСТЬ РАБОТЫ И БЫСТРОДЕЙСТВИЕ УПРАВЛЯЮЩИХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
- 10. СРАВНИТЕЛЬНАЯ ОЦЕНКА ПРЕОБРАЗУЮЩИХ УСТРОЙСТВ
- Глава VII. ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 1. ЭЛЕКТРИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 2. МЕХАНИЧЕСКИЕ ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. ГИДРАВЛИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 4. ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 5. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- 6. СРАВНИТЕЛЬНАЯ ОЦЕНКА ИСПОЛНИТЕЛЬНЫХ ЭЛЕМЕНТОВ
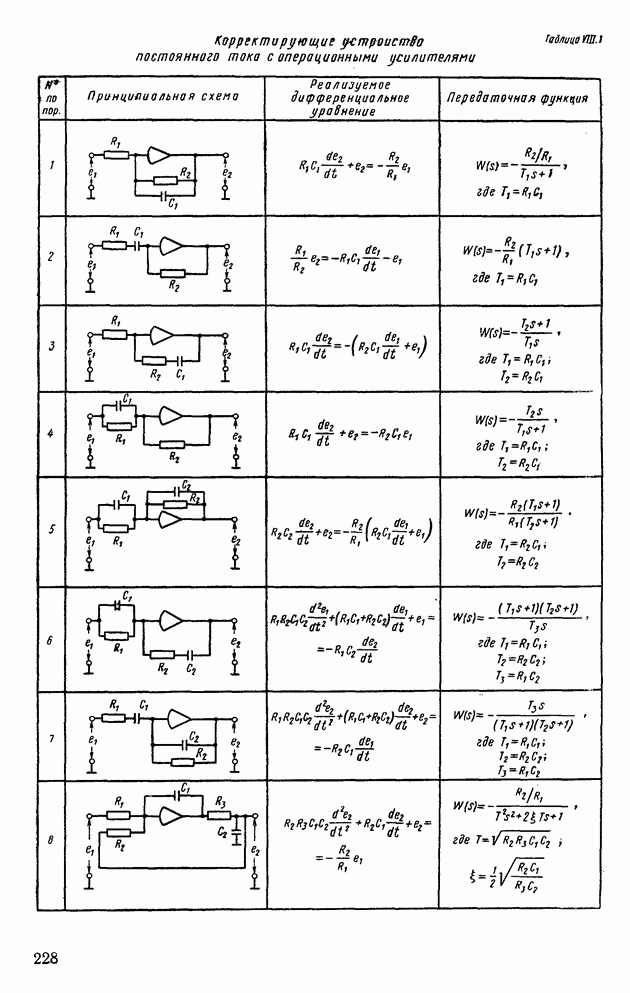
- Глава VIII. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
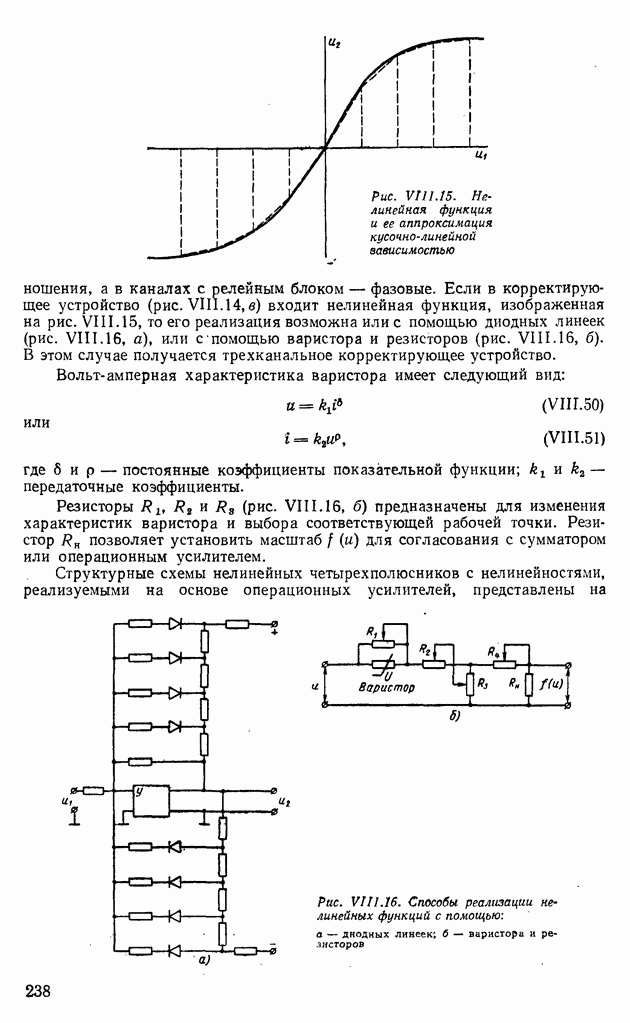
- 2. НЕЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 3. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
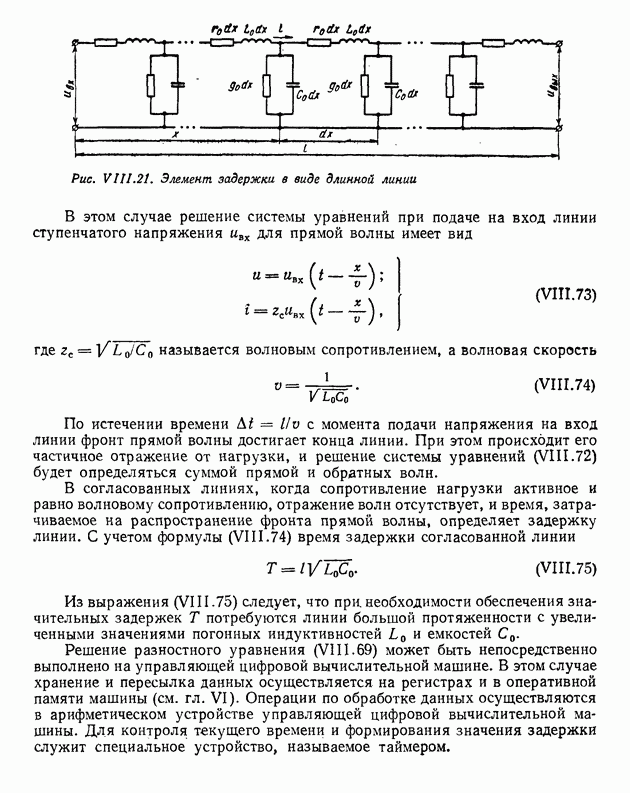
- 4. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ЛИНИЯХ ЗАДЕРЖЕК И ДИСКРЕТНЫХ ЭЛЕМЕНТАХ
- Глава IX. УРАВНЕНИЯ ДИНАМИКИ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- 1. ПРЕДСТАВЛЕНИЕ ОБЪЕКТОВ И УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С СОСРЕДОТОЧЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
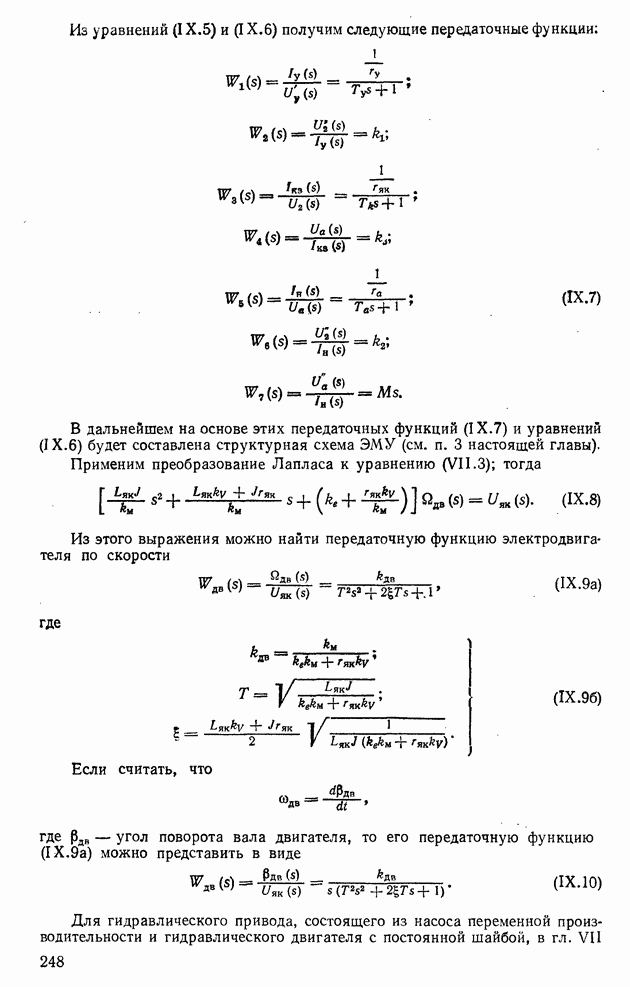
- 2. ПРЕДСТАВЛЕНИЕ УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С РАСПРЕДЕЛЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ТРАНСЦЕДЕНТНЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 3. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
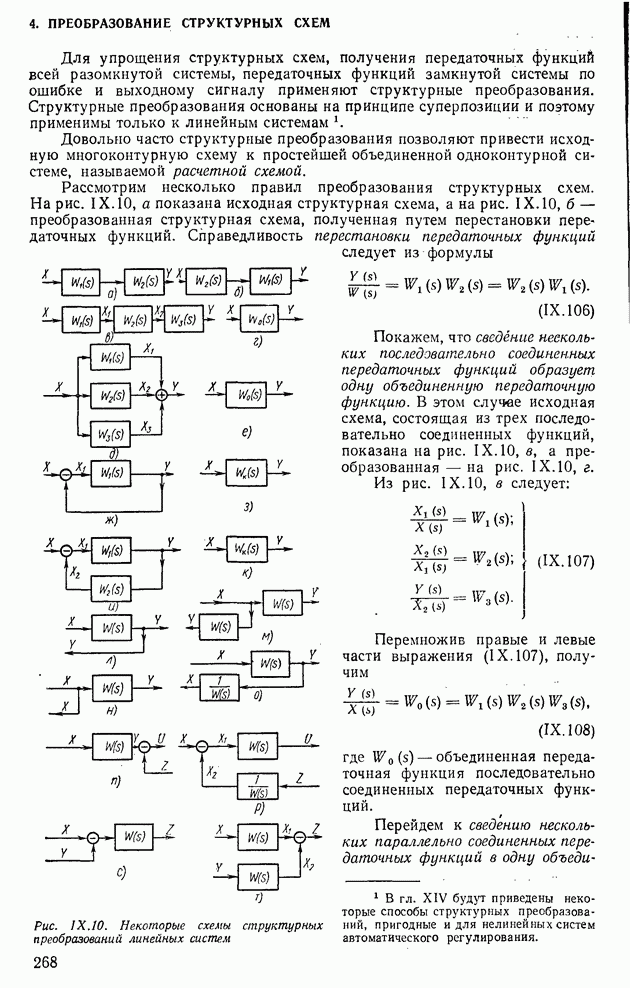
- 4. ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ
- 5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ОПИСАНИЕ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ РЕГУЛИРОВАНИЯ В ВЕКТОРНО-МАТРИЧНОЙ ФОРМЕ
- 7. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 8. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 9. РЕШЕНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ УРАВНЕНИЙ СОСТОЯНИЯ
- 10. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ МАТРИЦ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ ЛИНЕЙНЫХ СИСТЕМ
- 12. ПРЕДСТАВЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ИМПУЛЬСНЫМИ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ
- Глава X. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ АМПЛИТУДНО-ФАЗОВЫЕ И ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 1. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- Логарифмические амплитудная и фазовая частотные характеристики апериодического звена.
- 2. АПЕРИОДИЧЕСКОЕ НЕУСТОЙЧИВОЕ ЗВЕНО
- 4. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 5. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ (УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ)
- 6. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО РОДА
- 7. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО РОДА
- 8. ТРАНСЦЕНДЕНТНЫЕ ЗВЕНЬЯ
- 9. ФАЗОВАЯ ЛИНЕЙКА
- 10. ПОСТРОЕНИЕ АМПЛИТУДНО-ФАЗОВЫХ И ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ ГРУПП ТИПОВЫХ ЗВЕНЬЕВ
- 11. ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ВИДА ПЕРЕДАТОЧНЫХ ФУНКЦИЙ И ПАРАМЕТРОВ ГРУПП ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
- ГЛАВА XI. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ
- 2. ОПРЕДЕЛЕНИЕ ФУНКЦИЙ ЛЯПУНОВА МЕТОДАМИ Г. СЕГЕ И Д. ШУЛЬЦА
- 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 5. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 6. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ТРАНСЦЕНДЕНТНЫМИ ЗВЕНЬЯМИ
- 9. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ С ПОМОЩЬЮ D-РАЗБИЕНИЯ
- Глава XII. ИССЛЕДОВАНИЕ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
- 2. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПО ЗАДАННЫМ ПЕРЕДАТОЧНЫМ ФУНКЦИЯМ ЗАМКНУТЫХ СИСТЕМ
- 3. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПО РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ ЛЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ
- 4. МЕТОД КОРНЕВОГО ГОДОГРАФА
- 5. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА
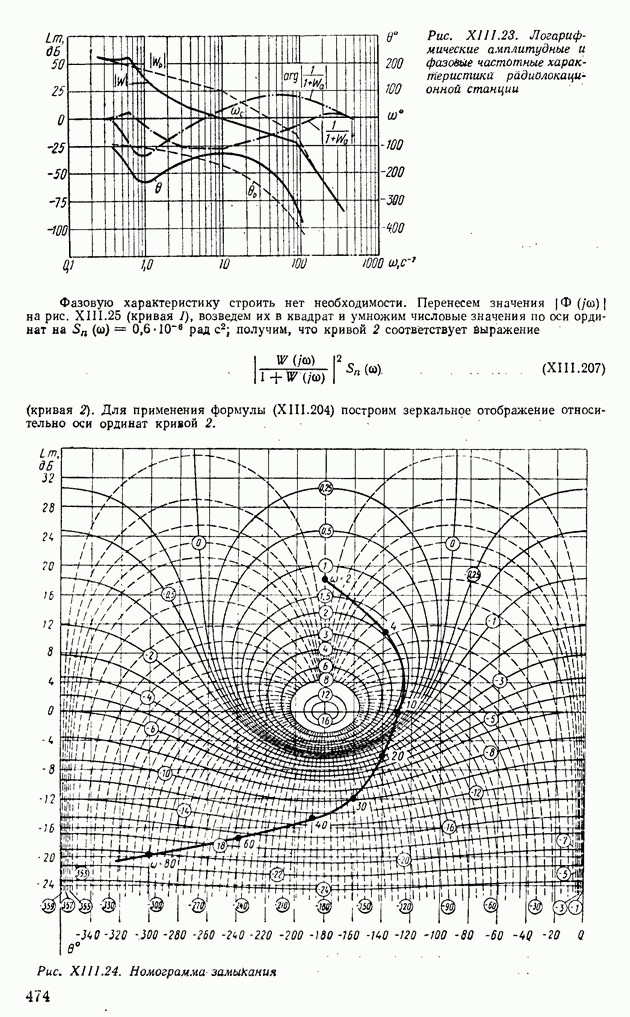
- 6. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ СИСТЕМ РЕГУЛИРОВАНИЯ И ИХ СВЯЗЬ С ХАРАКТЕРИСТИКАМИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
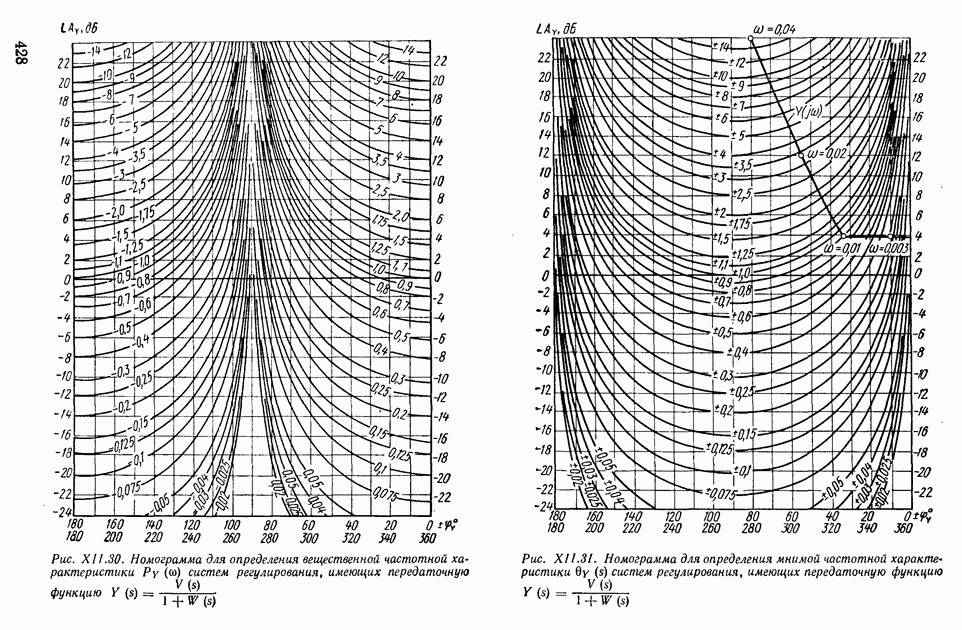
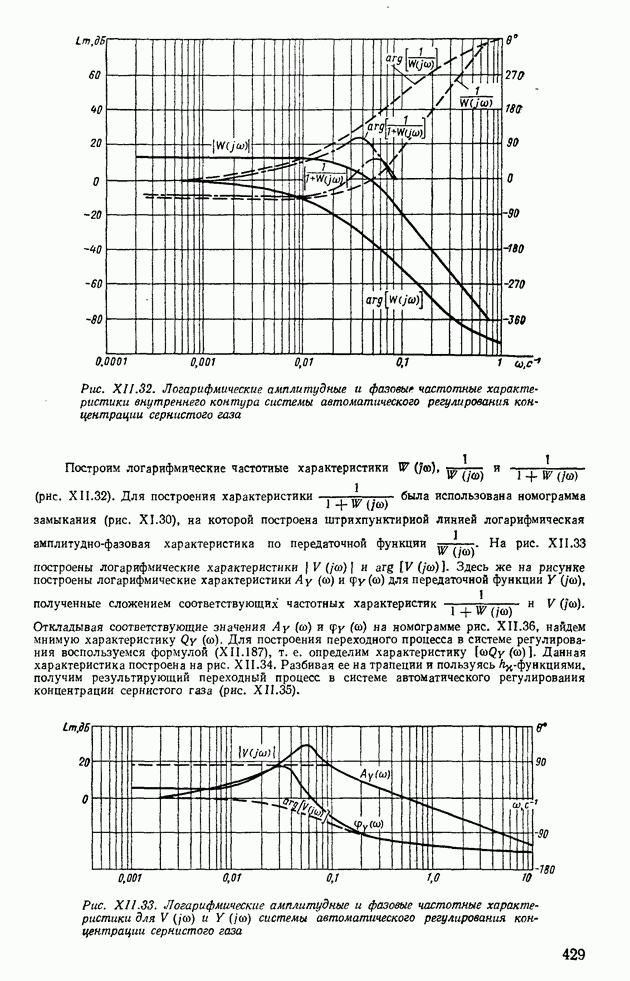
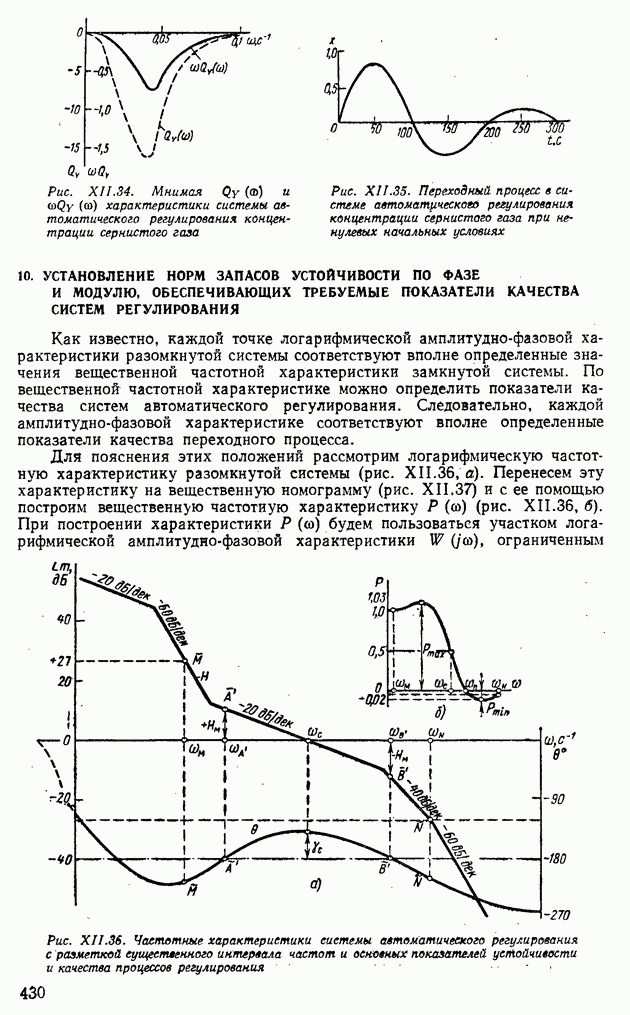
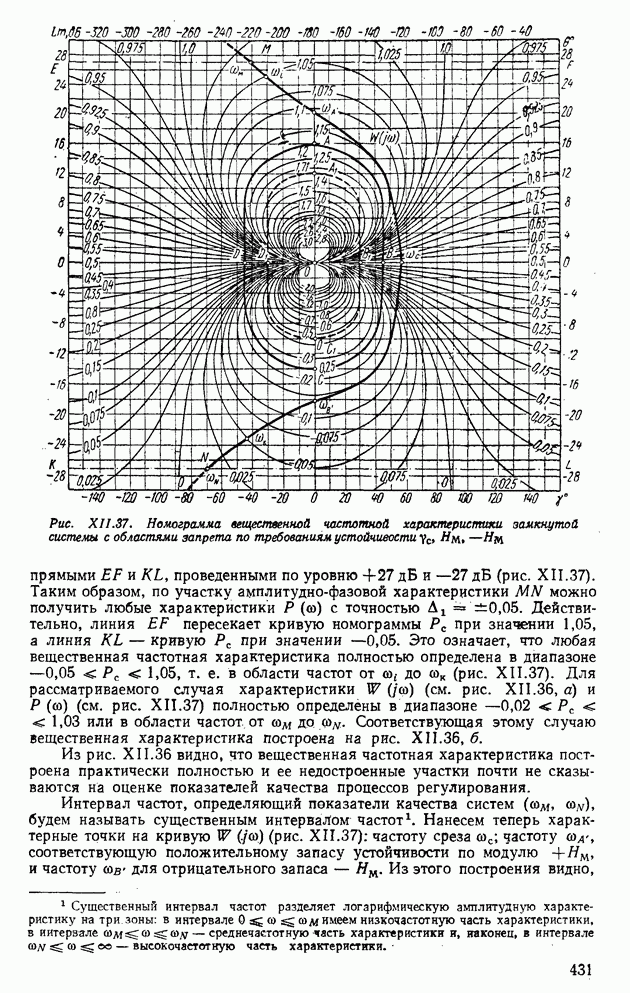
- 7. ОПРЕДЕЛЕНИЕ ВЕЩЕСТВЕННЫХ И МНИМЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СИСТЕМ ПО АМПЛИТУДНО-ФАЗОВЫМ И ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ РАЗОМКНУТЫХ СИСТЕМ
- 8. ЧАСТОТНЫЕ ОЦЕНКИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
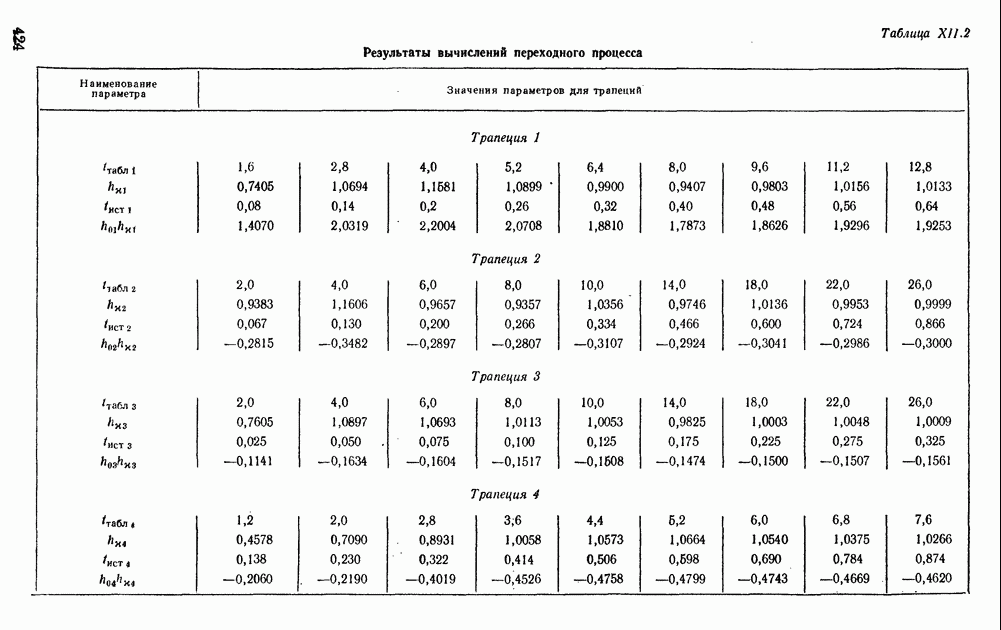
- 9. ЧАСТОТНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ТРАПЕЦЕИДАЛЬНЫХ ХАРАКТЕРИСТИК
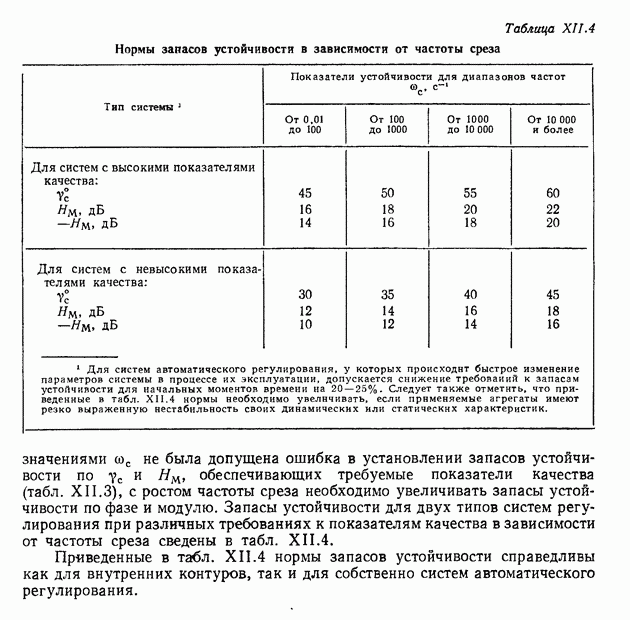
- 10. УСТАНОВЛЕНИЕ НОРМ ЗАПАСОВ УСТОЙЧИВОСТИ ПО ФАЗЕ И МОДУЛЮ, ОБЕСПЕЧИВАЮЩИХ ТРЕБУЕМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМ РЕГУЛИРОВАНИЯ
- ГЛАВА XIII. ДИНАМИЧЕСКАЯ ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
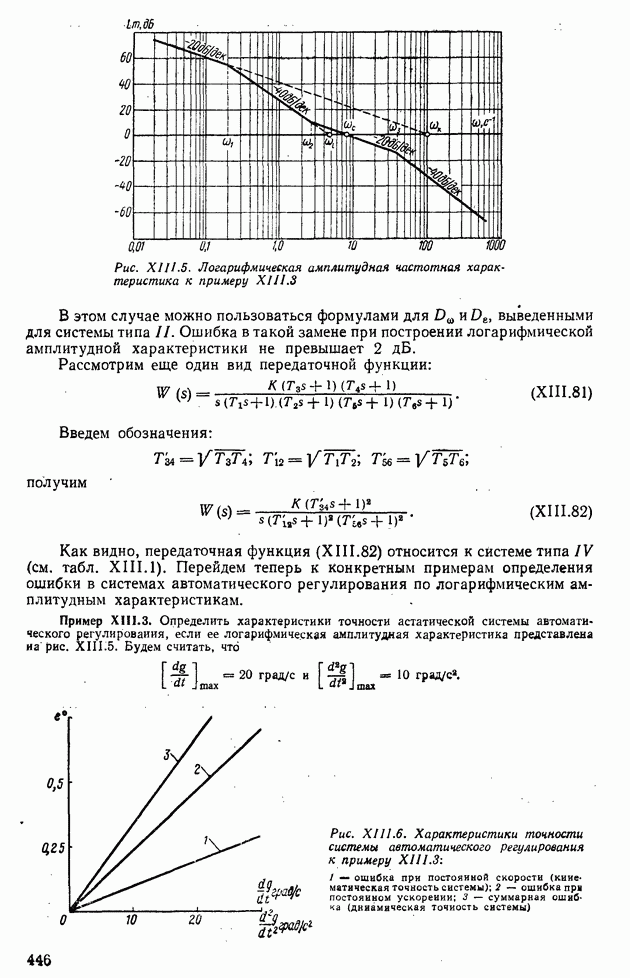
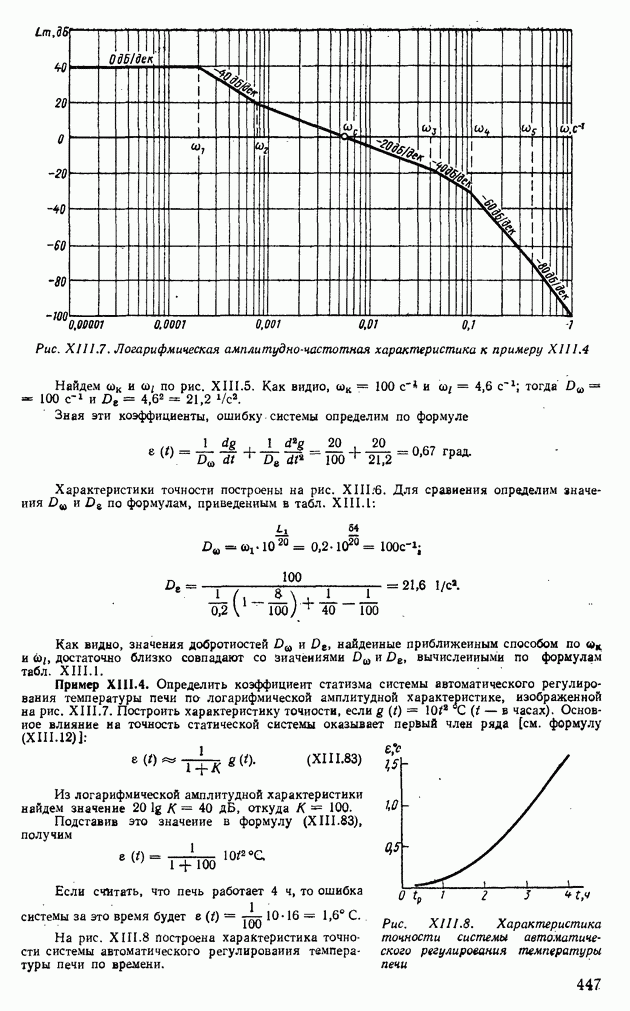
- 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ОШИБОК В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ АМПЛИТУДНЫХ ХАРАКТЕРИСТИК
- 3. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПУТЕМ ПРИМЕНЕНИЯ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ
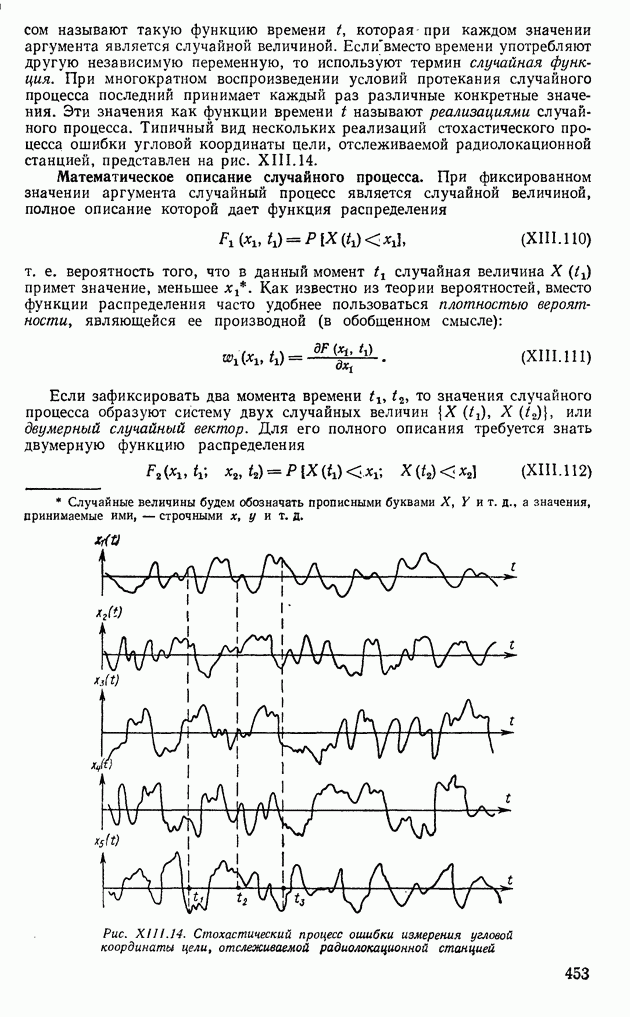
- 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 5. СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ СТАЦИОНАРНЫХ ПРОЦЕССОВ
- 6. СВОЙСТВА СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ
- 7. ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ
- 8. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЛИНЕЙНЫМИ СИСТЕМАМИ
- 9. РАСЧЕТ ОШИБОК В СИСТЕМЕ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ШУМОВ
- 10. ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ВОЗДЕЙСТВИИ СЛУЧАЙНЫХ СИГНАЛОВ И ШУМОВ
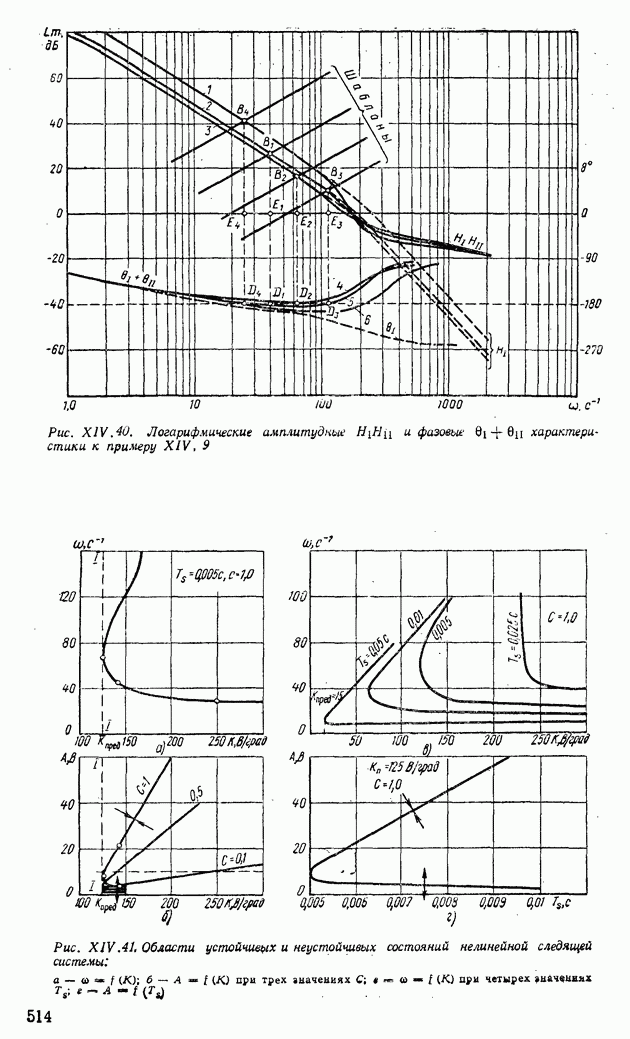
- ГЛАВА XIV. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
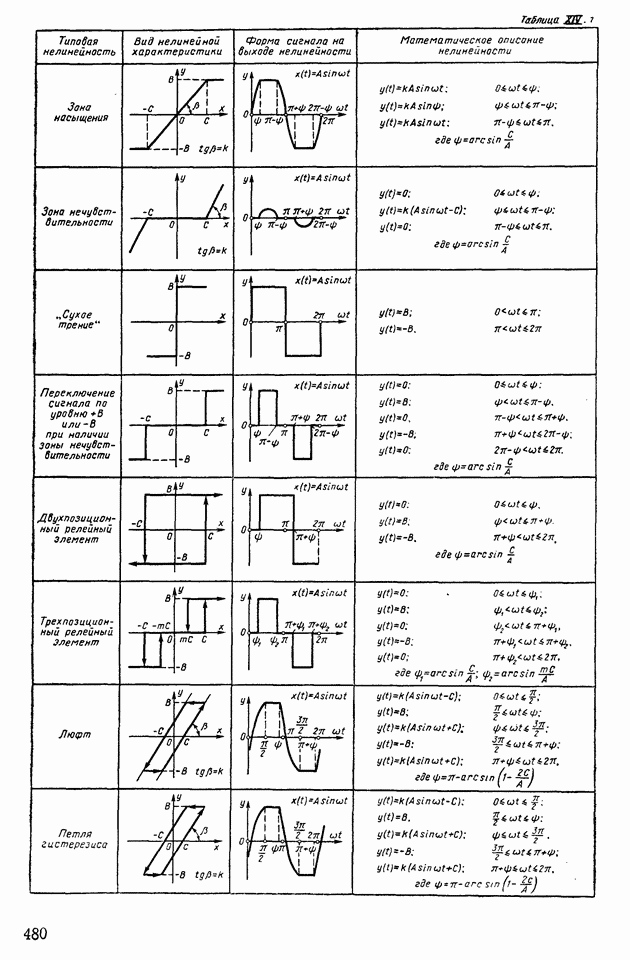
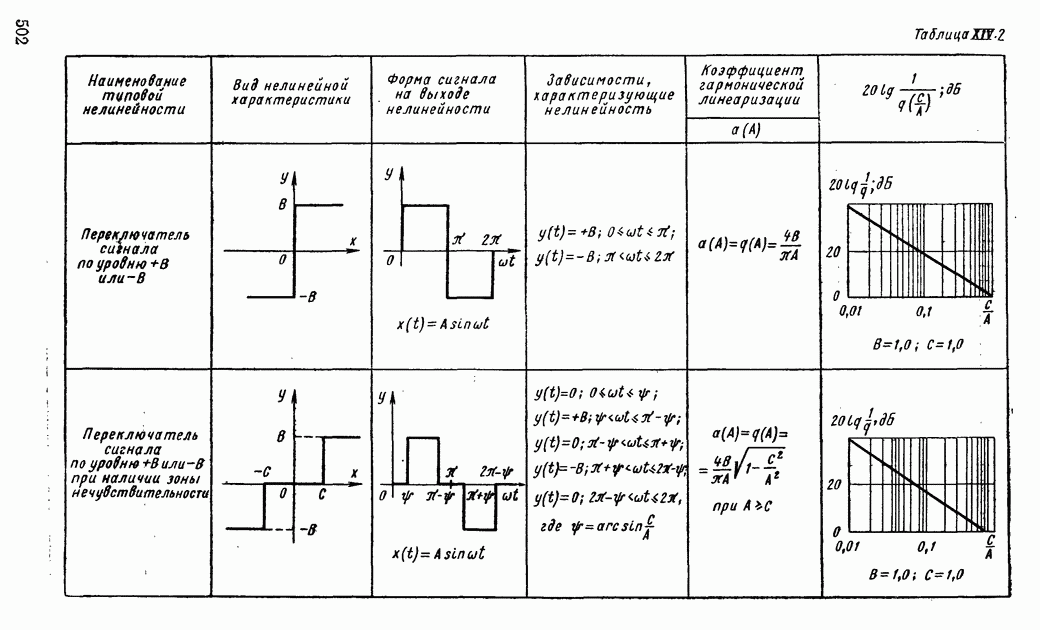
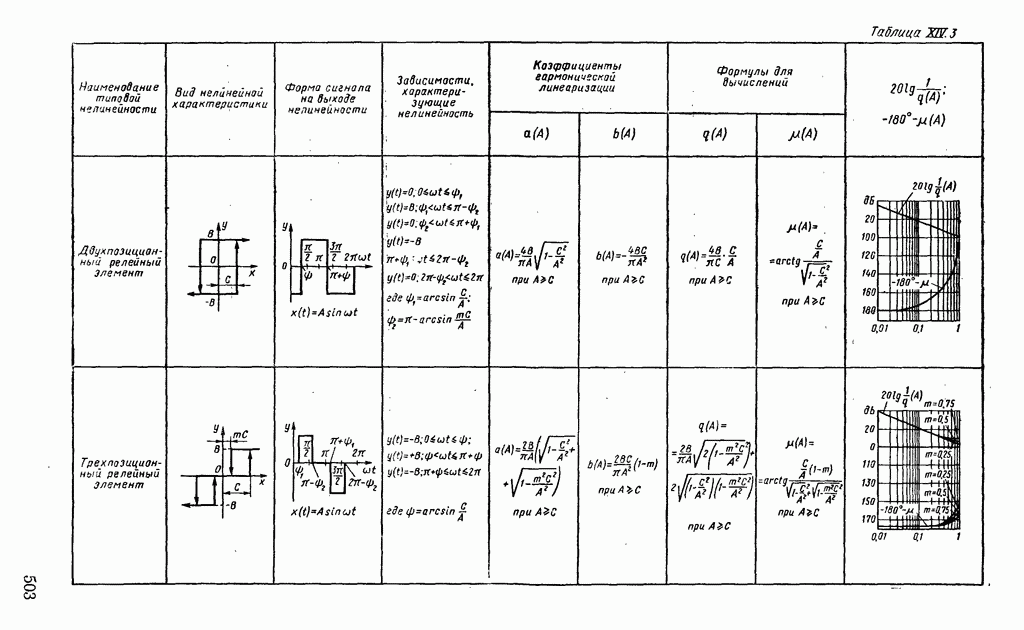
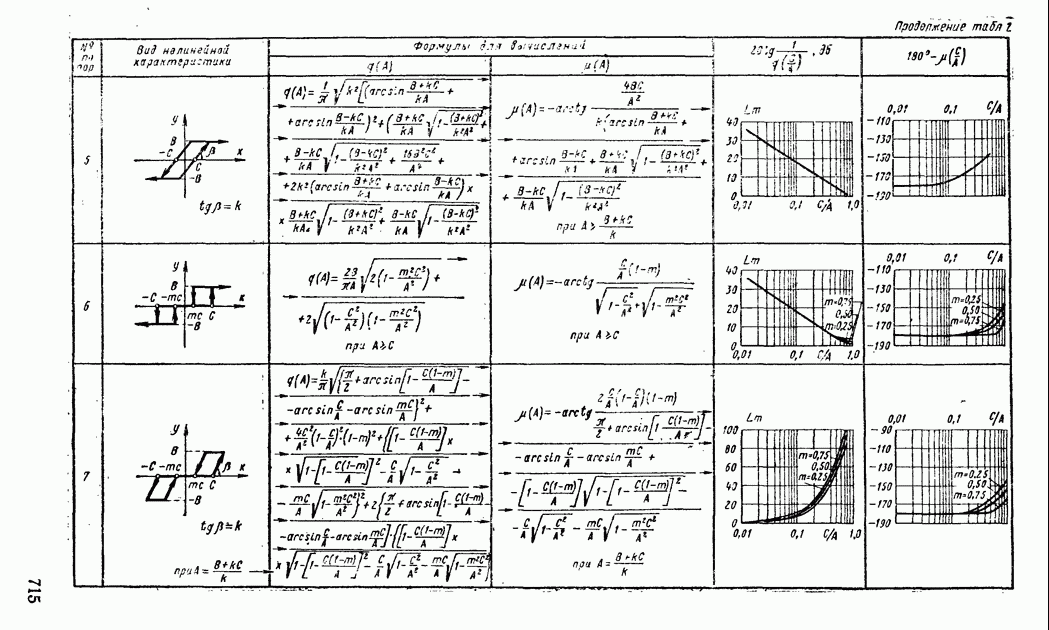
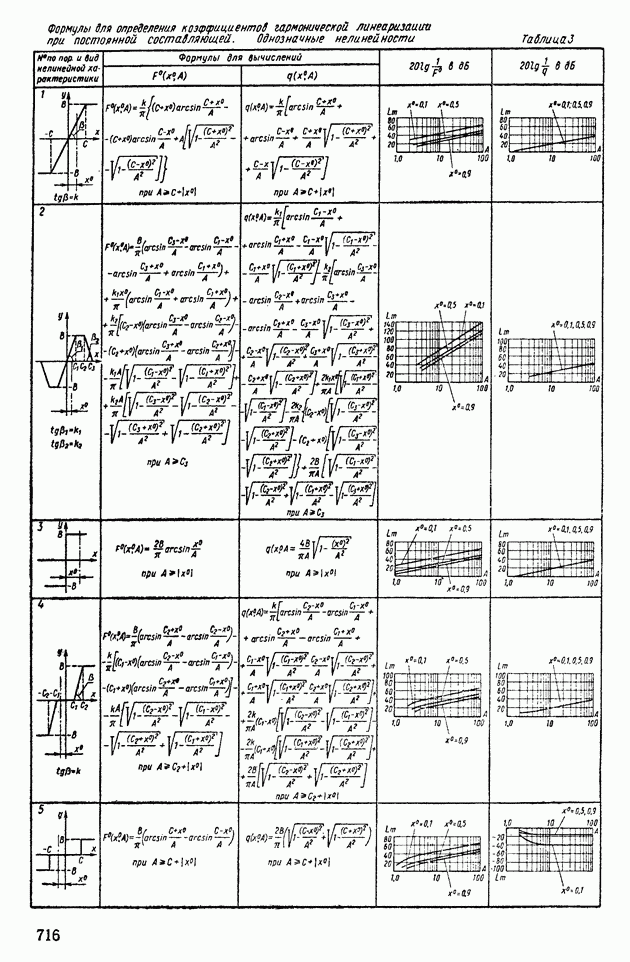
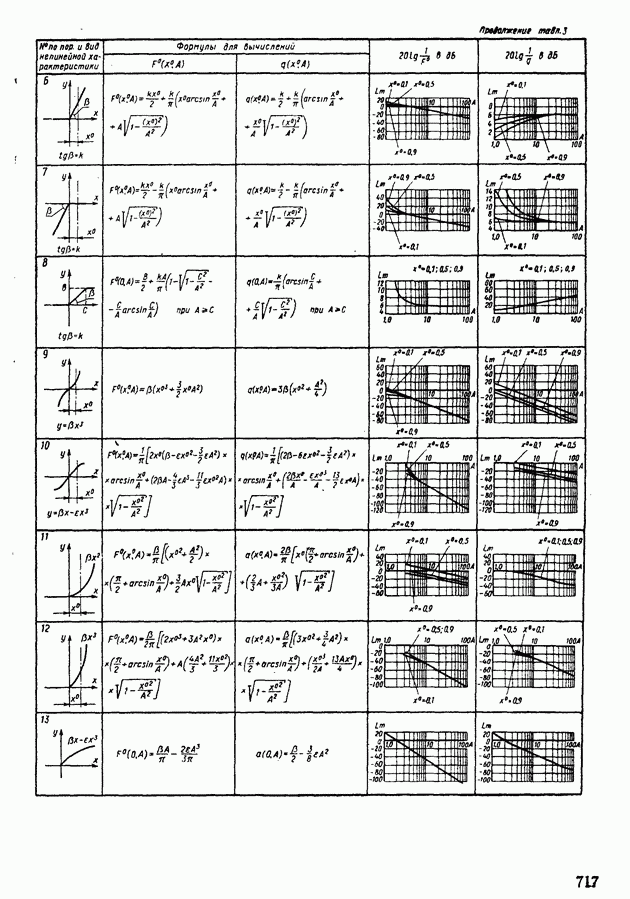
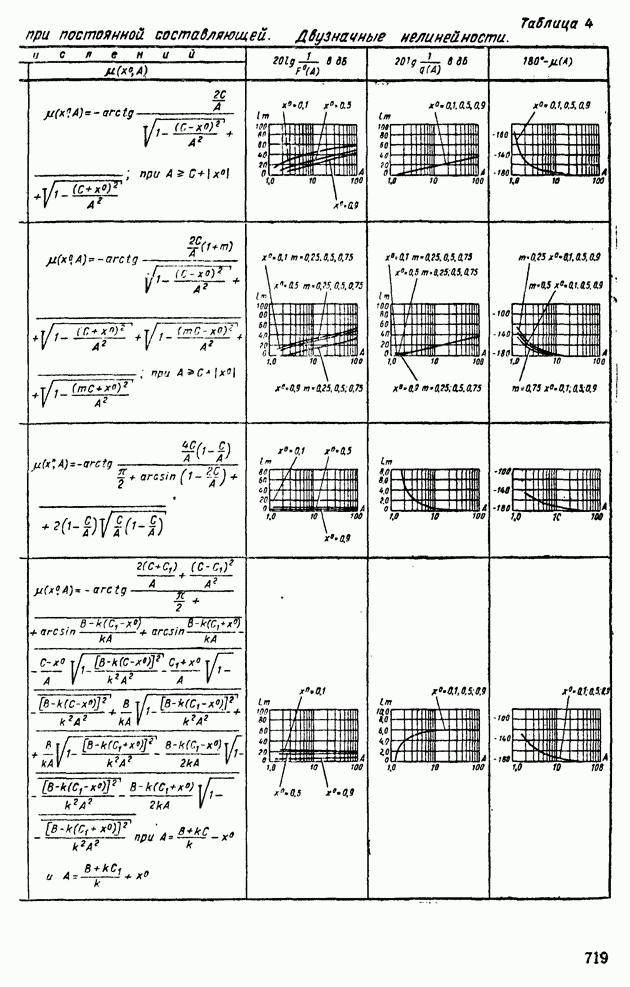
- 1. ТИПОВЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ ПО ВТОРОМУ МЕТОДУ ЛЯПУНОВА
- 3. АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
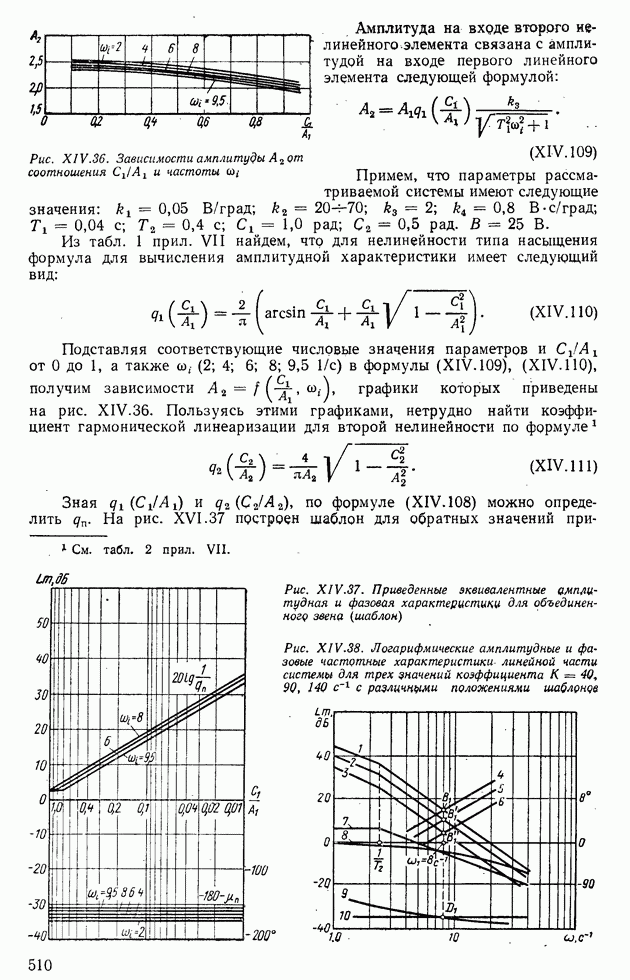
- 4. ПРИМЕНЕНИЕ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
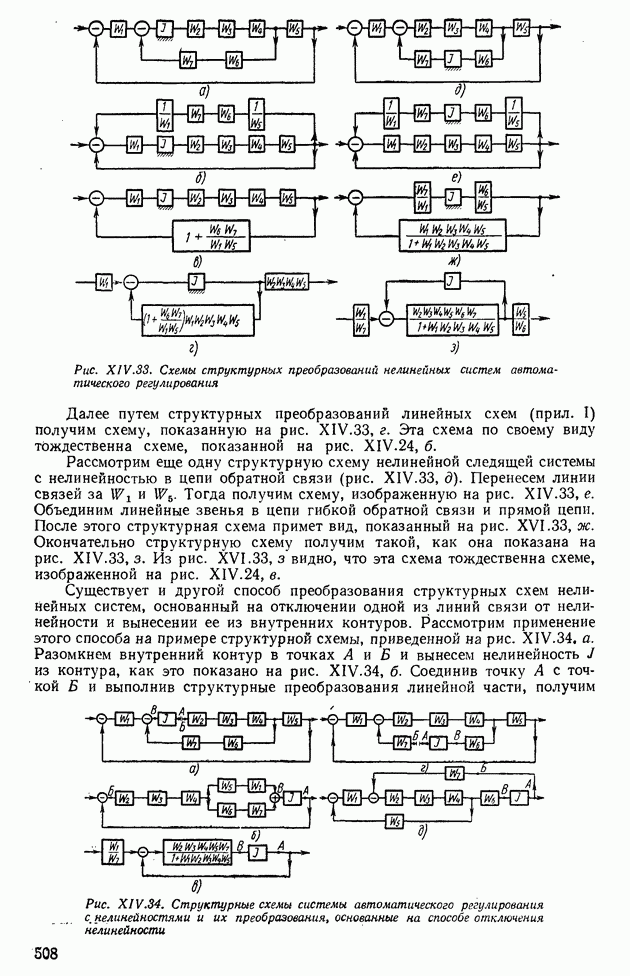
- 5. СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
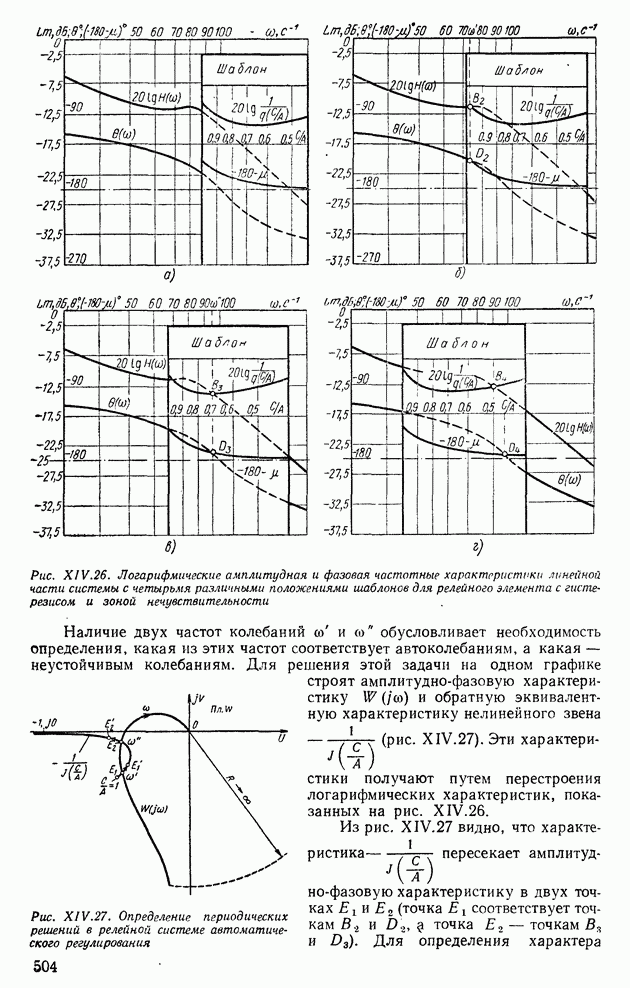
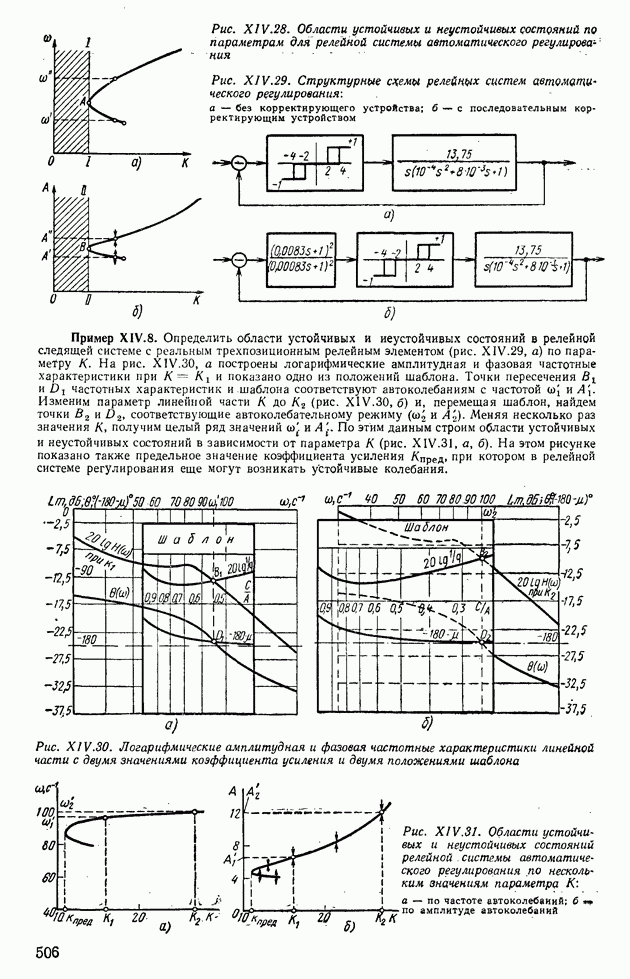
- 6. АНАЛИЗ АВТОКОЛЕБАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДВУМЯ НЕЛИНЕЙНОСТЯМИ
- 7. ДВУХКОНТУРНЫЕ НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕДЛЕННО ИЗМЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
- 9. СПОСОБЫ ПОДАВЛЕНИЯ АВТОКОЛЕБАНИЙ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 10. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 11. КРИТЕРИЙ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
- 12. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- Глава XIV. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ИМПУЛЬСНЫХ УСТРОЙСТВ
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. АМПЛИТУДНО-ФАЗОВЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ СИСТЕМ
- 4. ПРИМЕНЕНИЕ ВЕКТОРНО-МАТРИЧНОГО АППАРАТА К ИМПУЛЬСНЫМ СИСТЕМАМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ОСНОВНЫЕ СВОЙСТВА z-ПРЕОБРАЗОВАНИЯ
- 6. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Критерий устойчивости для импульсных систем на плоскостях z и W(z).
- Критерий устойчивости Шур—Кона.
- Критерии устойчивости, основанные на применении билинейного преобразования.
- 7. МЕТОДЫ АНАЛИЗА КАЧЕСТВА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕТОДЫ АНАЛИЗА ТОЧНОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 9. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С УПРАВЛЯЮЩИМИ ЦВМ
- 10. СПОСОБЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ В УПРАВЛЯЮЩИХ ЦВМ И ОПРЕДЕЛЕНИЕ ИХ ОСНОВНЫХ ПАРАМЕТРОВ
- Глава XVI. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МЕТОДЫ ПОИСКА ЭКСТРЕМУМА
- 2. СПОСОБЫ ОРГАНИЗАЦИИ ДВИЖЕНИЯ К ЭКСТРЕМУМУ
- 3. МЕТОДЫ РАСЧЕТА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРОВ
- 4. ВЫБОР КОРРЕКТИРУЮЩИХ УСТРОЙСТВ В ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРАХ
- 5. ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ С ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ
- Глава XVII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ ВОЗДЕЙСТВИЯХ
- 2. ВЫБОР ПАРАМЕТРОВ УСТРОЙСТВ НЕИЗМЕНЯЕМОЙ ЧАСТИ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ПОСТРОЕНИЕ ЖЕЛАЕМОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 4. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. СИНТЕЗ ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 6. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 7. СПОСОБЫ РЕАЛИЗАЦИИ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Глава XVIII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 1. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА НА ОСНОВЕ КРИТЕРИЯ МИНИМУМА ИНТЕГРАЛЬНОЙ ОШИБКИ
- 2. СИНТЕЗ СИСТЕМ РЕГУЛИРОВАНИЯ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЖЕЛАЕМОЙ СИСТЕМЫ
- 4. ПРИМЕР СИНТЕЗА КОРРЕКТИРУЮЩИХ УСТРОЙСТВ СИСТЕМЫ РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- ГЛАВА XIX. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИНТЕЗ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ, ОСНОВАННЫЙ НА ПРИМЕНЕНИИ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- 2. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. РЕАЛИЗАЦИЯ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ ПРИ ПОМОЩИ RC-ЦЕПЕЙ
- 4. РЕАЛИЗАЦИЯ ПРОГРАММ КОРРЕКЦИИ НА УПРАВЛЯЮЩЕЙ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- ГЛАВА XX. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ПРИНЦИП МАКСИМУМА
- 3. ТЕОРЕМА О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
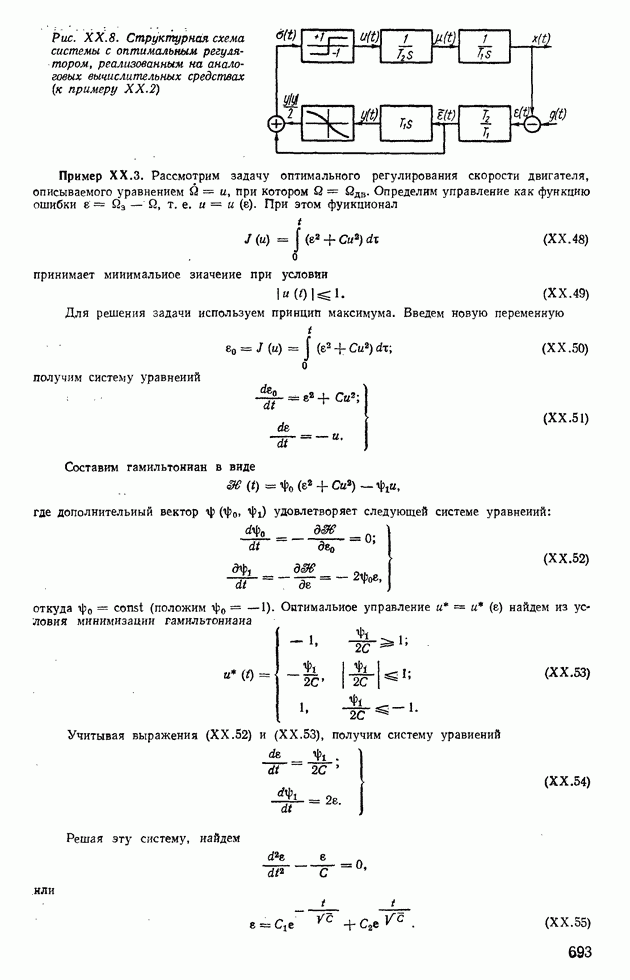
- 4. ПРИМЕРЫ ПРИМЕНЕНИЯ ПРИНЦИПА МАКСИМУМА
- 5. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 6. СИНТЕЗ НЕПРЕРЫВНЫХ ОПТИМАЛЬНЫХ СИСТЕМ
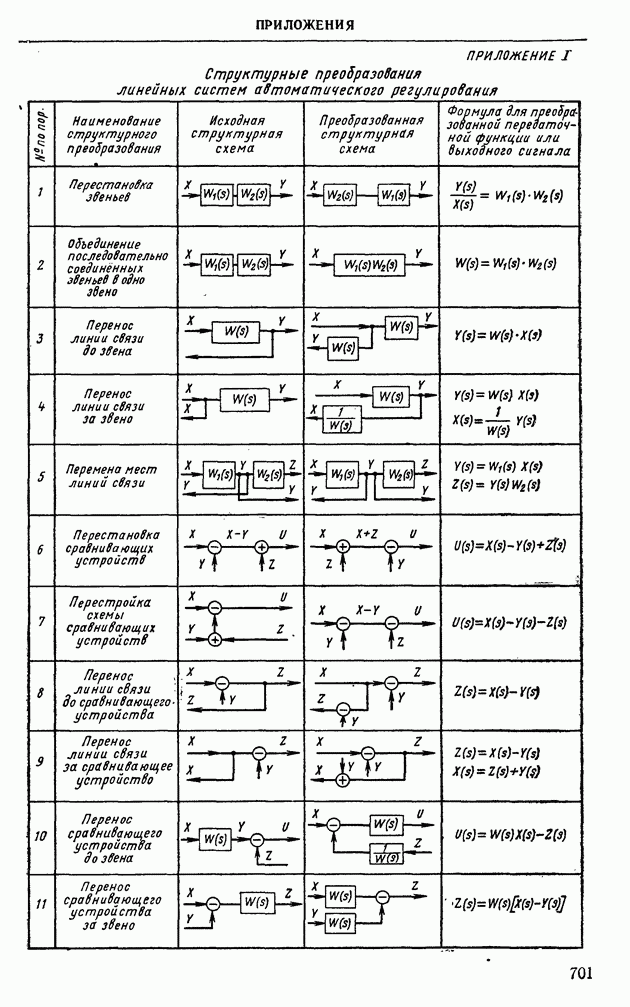
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ