| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ С ПОМОЩЬЮ D-РАЗБИЕНИЯ
Вернемся к рассмотрению характеристического уравнения замкнутой системы

Будем считать, что при некотором фиксированном значении  данное уравнение имеет
данное уравнение имеет  корней в левой полуплоскости (от мнимой оси) и
корней в левой полуплоскости (от мнимой оси) и  корней в правой полуплоскости. Изменение в определенных границах коэффициента
корней в правой полуплоскости. Изменение в определенных границах коэффициента  не будет менять числа корней в полуплоскостях. Поэтому на плоскости
не будет менять числа корней в полуплоскостях. Поэтому на плоскости  можно построить кривую, отображающую мнимую ось плоскости корней, и найти область
можно построить кривую, отображающую мнимую ось плоскости корней, и найти область  -устойчивости на числовой прямой по параметру
-устойчивости на числовой прямой по параметру  Эту кривую обычно называют кривой D-разбиения по параметру
Эту кривую обычно называют кривой D-разбиения по параметру  [1]. Если D-разбиение требуется выполнить по двум параметрам
[1]. Если D-разбиение требуется выполнить по двум параметрам  то строят D-разбиение плоскости по двум параметрам. В этом случае по оси ординат откладывают значения параметра
то строят D-разбиение плоскости по двум параметрам. В этом случае по оси ординат откладывают значения параметра  а по оси абсцисс — значения параметра
а по оси абсцисс — значения параметра  Здесь также определяются области устойчивости в плоскости двух коэффициентов.
Здесь также определяются области устойчивости в плоскости двух коэффициентов.
Если в характеристическом уравнении не определены три коэффициента  то необходимо рассматривать трехмерное пространство, откладывая по осям
то необходимо рассматривать трехмерное пространство, откладывая по осям  Область D-разбиения в пространстве в этом случае будет представлять собой некоторую поверхность.
Область D-разбиения в пространстве в этом случае будет представлять собой некоторую поверхность.
Можно увеличить число изменяемых параметров характеристического уравнения до  но тогда придется рассматривать многомерное пространство коэффициентов, и область D-разбиения будет определяться гиперповерхностью. Как и в первом случае, граница D-разбиения по двум, трем и т. д. параметрам представляет собой отображения мнимой оси плоскости корней на пространство коэффициентов характеристического уравнения. В создании и развитии этого метода анализа устойчивости систем автоматического регулирования важную роль сыграли работы М. А. Айзермана [1, 2] и Ю. И. Неймарка.
но тогда придется рассматривать многомерное пространство коэффициентов, и область D-разбиения будет определяться гиперповерхностью. Как и в первом случае, граница D-разбиения по двум, трем и т. д. параметрам представляет собой отображения мнимой оси плоскости корней на пространство коэффициентов характеристического уравнения. В создании и развитии этого метода анализа устойчивости систем автоматического регулирования важную роль сыграли работы М. А. Айзермана [1, 2] и Ю. И. Неймарка.
D-разбиение плоскости по одному комплексному параметру. Рассмотрим влияние параметра  характеристического уравнения (XI.69). Разрешив это уравнение относительно
характеристического уравнения (XI.69). Разрешив это уравнение относительно  получим
получим

или

Положим, что  — комплексное число. Отобразим мнимую ось плоскости корней X на плоскость
— комплексное число. Отобразим мнимую ось плоскости корней X на плоскость  Затем подставим в выражение (XI.151)
Затем подставим в выражение (XI.151) 

или


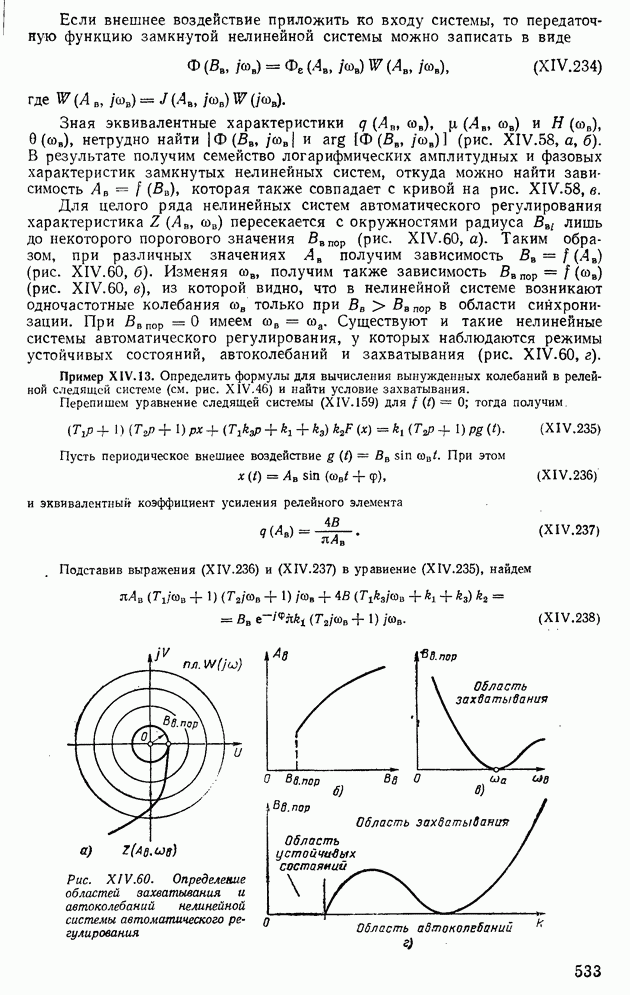
Рис.  Правила штриховки мнимой оси плоскости К и кривой D-раабиения плоскости
Правила штриховки мнимой оси плоскости К и кривой D-раабиения плоскости 
Изменяя значения о от  до
до  построим в плоскости
построим в плоскости  (или
(или  ) кривую, отображающую мнимую ось
) кривую, отображающую мнимую ось  плоскости
плоскости  на плоскость
на плоскость  Полученная кривая является кривой D-разбиения. Кривая D-разбиения симметрична относительно действительной оси, поэтому можно строить лишь ее участок, соответствующий изменению частот 0 <з
Полученная кривая является кривой D-разбиения. Кривая D-разбиения симметрична относительно действительной оси, поэтому можно строить лишь ее участок, соответствующий изменению частот 0 <з  и дополнить кривую зеркальным отображением относительно действительной оси. На рис. XI.44 построены плоскость корней К (рис. 44, а) и кривая D-разбиения (рис. 44, б).
и дополнить кривую зеркальным отображением относительно действительной оси. На рис. XI.44 построены плоскость корней К (рис. 44, а) и кривая D-разбиения (рис. 44, б).
Построение кривой D-разбиения еще не решает вопроса о выделении области устойчивости. Последняя должна представлять собой совокупность точек плоскости, в которых все корни характеристического уравнения замкнутой системы имеют отрицательные вещественные части. В то же время кривая D-разбиения представляет собой только совокупность точек, в которых характеристическое уравнение имеет, по крайней мере, хотя бы один чисто мнимый корень  Для того чтобы решить вопрос о выделении области устойчивости, необходимо по определенным правилам заштриховать D-кривую.
Для того чтобы решить вопрос о выделении области устойчивости, необходимо по определенным правилам заштриховать D-кривую.
Правила штриховки D-кривой и выделение областей устойчивости.
При перемещении в плоскости корней  вдоль мнимой оси от
вдоль мнимой оси от  до
до  (рис. XI.44, а), область, в которой корни имеют отрицательные вещественные части, будет находиться все время слева. Заштрихуем мнимую ось плоскости
(рис. XI.44, а), область, в которой корни имеют отрицательные вещественные части, будет находиться все время слева. Заштрихуем мнимую ось плоскости  слева. Имея это в виду, будем теперь перемещаться вдоль линии D-разбиения от точки
слева. Имея это в виду, будем теперь перемещаться вдоль линии D-разбиения от точки  к точке, соответствующей
к точке, соответствующей  Выполним штриховку этой кривой также слева (рис. XI.44, б). Таким образом получим четыре зоны
Выполним штриховку этой кривой также слева (рис. XI.44, б). Таким образом получим четыре зоны  II, III и IV.
II, III и IV.
Допустим, что каким-либо способом удалось установить, что в зоне III имеется  отрицательных корней слева от мнимой оси. Если при переходе в другую зону кривые D-разбиения пересекаются с незаштрихованной стороны на заштрихованную, то этой зоне соответствует полином с
отрицательных корней слева от мнимой оси. Если при переходе в другую зону кривые D-разбиения пересекаются с незаштрихованной стороны на заштрихованную, то этой зоне соответствует полином с  корнем в левой полуплоскости К (рис. XI.44, б). При переходе через кривую с заштрихованной стороны на незаштрихованную число отрицательных корней уменьшается на единицу. Если штриховка двойная (что соответствует точке пересечения D-кривых), то число корней увеличивается на 2, т. е. в этой зоне имеем
корнем в левой полуплоскости К (рис. XI.44, б). При переходе через кривую с заштрихованной стороны на незаштрихованную число отрицательных корней уменьшается на единицу. Если штриховка двойная (что соответствует точке пересечения D-кривых), то число корней увеличивается на 2, т. е. в этой зоне имеем  корня.
корня.
Практически представляет интерес рассмотрение только действительных значений параметра  Поэтому, построив кривые D-разбиения и определив число корней в каждой зоне, необходимо найти тот отрезок действительной оси на плоскости
Поэтому, построив кривые D-разбиения и определив число корней в каждой зоне, необходимо найти тот отрезок действительной оси на плоскости  который принадлежит области устойчивости. Далее устанавливают соответствие между числом отрицательных корней и степенью характеристического уравнения. При таком соответствии зона с наибольшим числом отрицательных корней будет областью устойчивости. Если этого соответствия нет, то области устойчивости не существует.
который принадлежит области устойчивости. Далее устанавливают соответствие между числом отрицательных корней и степенью характеристического уравнения. При таком соответствии зона с наибольшим числом отрицательных корней будет областью устойчивости. Если этого соответствия нет, то области устойчивости не существует.
Пример XI.27. Для системы автоматического регулирования, имеющей характеристическое уравнение замкнутой системы в виде

найти области устойчивости при изменении параметра  (степени самовыравнивания объекта регулирования).
(степени самовыравнивания объекта регулирования).
Из уравнения (XI. 154) определим

Пусть параметры системы имеют следующие значения:  с.
с.
Тогда

Подставив в уравнение (XI.156)  получим
получим

откуда найдем

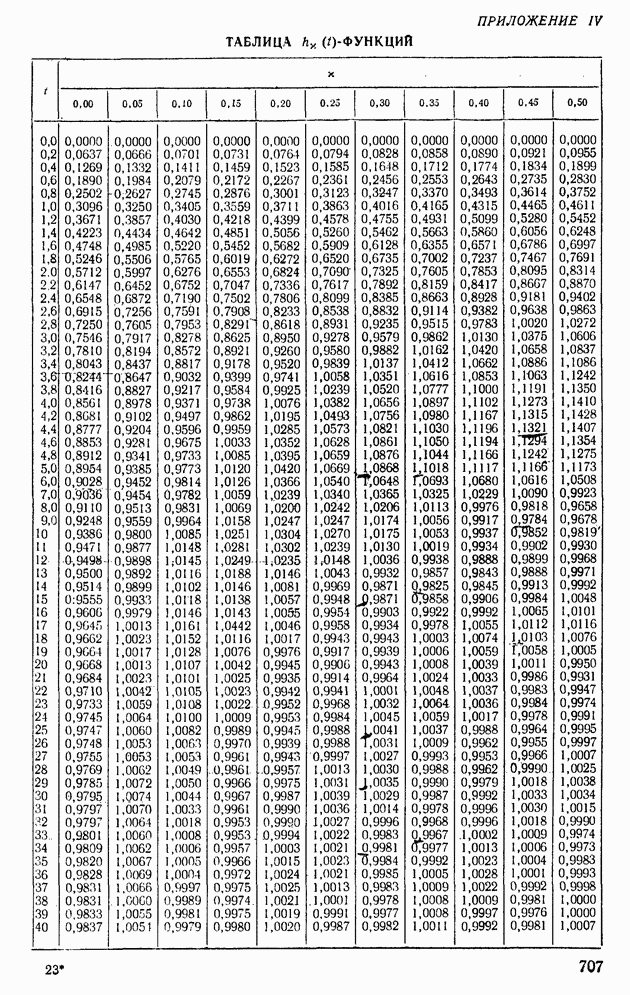
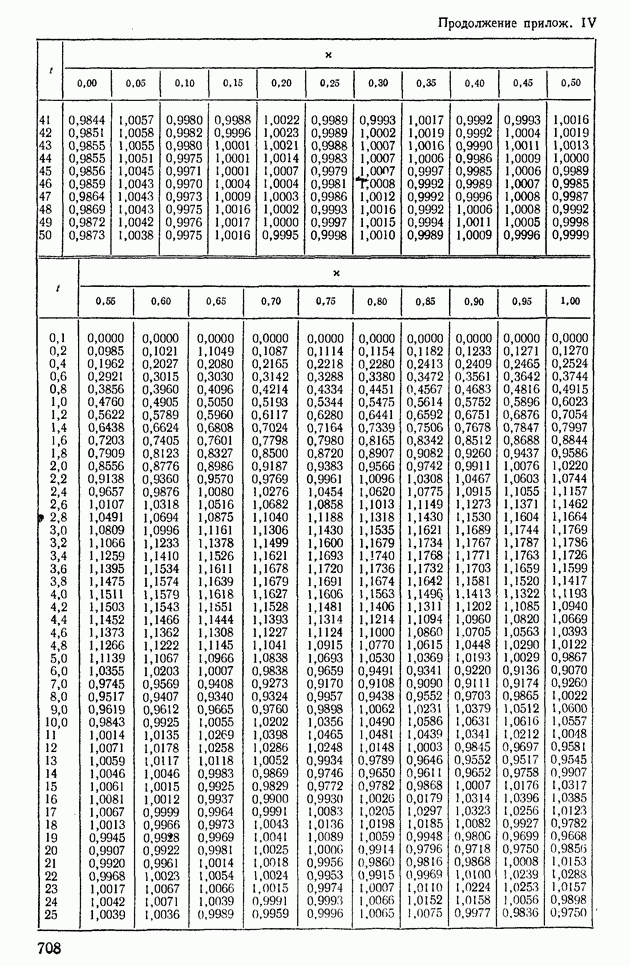
Результаты вычислений для различных значений со сведены в табл. XI.5.
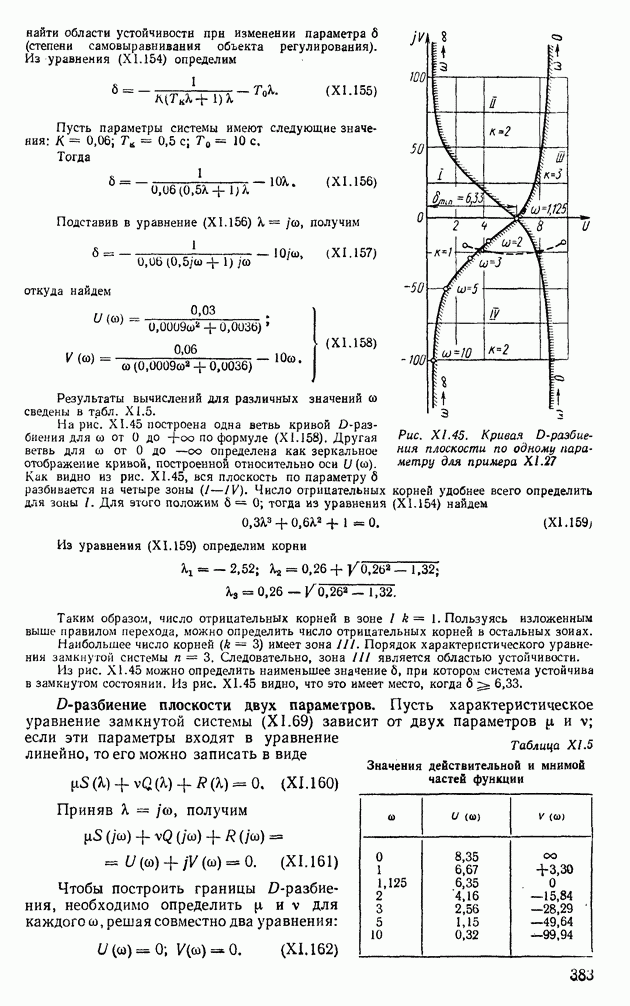
На рис. XI.45 построена одна ветвь кривой  -разбиения для и от 0 до
-разбиения для и от 0 до  по формуле (ХI.158). Другая ветвь для
по формуле (ХI.158). Другая ветвь для  от 0 до
от 0 до  определена как зеркальное отображение кривой, построенной относительно оси
определена как зеркальное отображение кривой, построенной относительно оси  .
.
Как видно из рис. XI.45, вся плоскость по параметру  разбивается на четыре зоны
разбивается на четыре зоны  Число отрицательных корней удобнее всего определить для зоны I. Для этого положим
Число отрицательных корней удобнее всего определить для зоны I. Для этого положим  тогда из уравнения (XI.154) найдем
тогда из уравнения (XI.154) найдем

Из уравнения (XI. 159) определим корни

Таким образом, число отрицательных корней в зоне  Пользуясь изложенным выше правилом перехода, можно определить число отрицательных корней в остальных зоиах.
Пользуясь изложенным выше правилом перехода, можно определить число отрицательных корней в остальных зоиах.
Наибольшее число корней  имеет зона III. Порядок характеристического уравнения замкнутой системы
имеет зона III. Порядок характеристического уравнения замкнутой системы  Следовательно, зона III является областью устойчивости.
Следовательно, зона III является областью устойчивости.
Из рис. XI.45 можно определить наименьшее значение  при котором система устойчива в замкнутом состоянии. Из рис. XI.45 видно, что это имеет место, когда
при котором система устойчива в замкнутом состоянии. Из рис. XI.45 видно, что это имеет место, когда 
D-разбиение плоскости двух параметров. Пусть характеристическое уравнение замкнутой системы (XI.69) зависит от двух параметров  и
и  если эти параметры входят в уравнение линейно, то его можно записать в виде
если эти параметры входят в уравнение линейно, то его можно записать в виде

Приняв  получим
получим

Чтобы построить границы D-разбиения, необходимо определить  и
и  для каждого со, решая совместно два уравнения:
для каждого со, решая совместно два уравнения:


Рис. XI.45. Кривая D-раэбиения плоскости по одному параметру для примера XI.27
Таблица XI.5. Значения действительной и мнимой частей функции


Рис. XI.46. Правила штриховки кривых D-разбиения в плоскости двух параметров
Если в каждом из этих уравнений выделить члены, содержащие и  то получим систему двух уравнений:
то получим систему двух уравнений:

Решив эту систему уравнений, получим

Уравнения (XI. 164) представляют собой параметрические зависимости, определяющие границы области D-разбиения в плоскости параметров и 
При перемещении точки по мнимой оси в плоскости К снизу вверх точка в плоскости параметров  при изменении
при изменении  от
от  до
до  будет перемещаться по границе области D-разбиения.
будет перемещаться по границе области D-разбиения.
Сформулируем правило штриховки. При перемещении по границе D-разбиения ее штрихуют слева в тех точках, для которых  и справа — при
и справа — при  Точка по кривой перемещается 2 раза: первый раз от
Точка по кривой перемещается 2 раза: первый раз от  до
до  и второй раз от
и второй раз от  до
до  (рис. XI.46). При переходе точкой границы с двойной штриховкой из заштрихованной зоны в незаштрихованную два корня характеристического уравнения переходят из левой полуплоскости в правую. И, наоборот, при переходе точки в заштрихованную область имеем переход двух комплексно-сопряженных корней в левую полуплоскость.
(рис. XI.46). При переходе точкой границы с двойной штриховкой из заштрихованной зоны в незаштрихованную два корня характеристического уравнения переходят из левой полуплоскости в правую. И, наоборот, при переходе точки в заштрихованную область имеем переход двух комплексно-сопряженных корней в левую полуплоскость.

Рис. XI.47. Правила штриховки особых прямых кривых D-разбиения в плоскости двух параметров
Для определения области устойчивости необходимо в какой-то зоне с помощью любого из рассмотренных ранее критериев оценить устойчивость, а далее, пользуясь правилами штриховки, установив число корней в остальных зонах. При построении границ D-разбиения необходимо учитывать,

Рис. К 1.48. Кривая D-разбиения плоскости по двум параметрам для примера XI.28
что при некоторой частоте  урабнения (XI. 164) становятся линейно зависимыми, а определители равными нулю, т. е.
урабнения (XI. 164) становятся линейно зависимыми, а определители равными нулю, т. е.  . В этом случае образуется уравнение особой прямой. Если знак
. В этом случае образуется уравнение особой прямой. Если знак  при о
при о  или о
или о  не изменяется, то эти прямые не штрихуют (рис. XI.47, а); если же при этом изменяется знак
не изменяется, то эти прямые не штрихуют (рис. XI.47, а); если же при этом изменяется знак  то прямые штрихуют двойной штриховкой, как это показано на рис. XI.47, б [1].
то прямые штрихуют двойной штриховкой, как это показано на рис. XI.47, б [1].
Часто определители  равны нулю. В этом случае
равны нулю. В этом случае  зависит от параметра
зависит от параметра  При этом также получается уравнение особой прямой. Соответствующее расположение этих прямых показано на рис. XI.47, в и г. Как видно из рис. XI.47,е и г, такие особые прямые штрихуют с одной стороны.
При этом также получается уравнение особой прямой. Соответствующее расположение этих прямых показано на рис. XI.47, в и г. Как видно из рис. XI.47,е и г, такие особые прямые штрихуют с одной стороны.
Пример XI.28. По заданному характеристическому уравнению замкнутой системы

построить D-разбиение по двум параметрам  Остальные параметры системы примем равными
Остальные параметры системы примем равными 
Подставив эти значения в уравнение (XI. 165) и заменив  получим
получим

Отделяя действительную и мнимую части, найдем

откуда

Задаваясь различными значениями  от 0 до
от 0 до  получим кривые D-разбиений показанные на рис. XI.48, а. Двигаясь вдоль кривой от точки
получим кривые D-разбиений показанные на рис. XI.48, а. Двигаясь вдоль кривой от точки  к точке
к точке  наносим двойную штриховку справа, так как
наносим двойную штриховку справа, так как  При
При  определитель
определитель  ; тогда наносим двойную штриховку слева. Приравнивая нулю свободный член и коэффициент при старшем члене характеристического уравнения, получим уравнения двух прямых:
; тогда наносим двойную штриховку слева. Приравнивая нулю свободный член и коэффициент при старшем члене характеристического уравнения, получим уравнения двух прямых:  для
для  для
для  На рис. XI.48, а
На рис. XI.48, а  прямые показаны одинарной штриховкой. Здесь же в зонах указано чнсло корней. Для определения области устойчивости можно положить
прямые показаны одинарной штриховкой. Здесь же в зонах указано чнсло корней. Для определения области устойчивости можно положить  ; тогда характеристическое уравнение (XI. 166) примет вид
; тогда характеристическое уравнение (XI. 166) примет вид  где
где 
При смещении от точки  вправо (рис. Х 1.48, б) число корней с отрицательной действительной частью увеличивается на единицу.
вправо (рис. Х 1.48, б) число корней с отрицательной действительной частью увеличивается на единицу.
Следовательно, для системы (X 1.165) третьего порядка эта область является областью устойчивости.
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 1. ПРИНЦИПЫ ДЕЙСТВИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
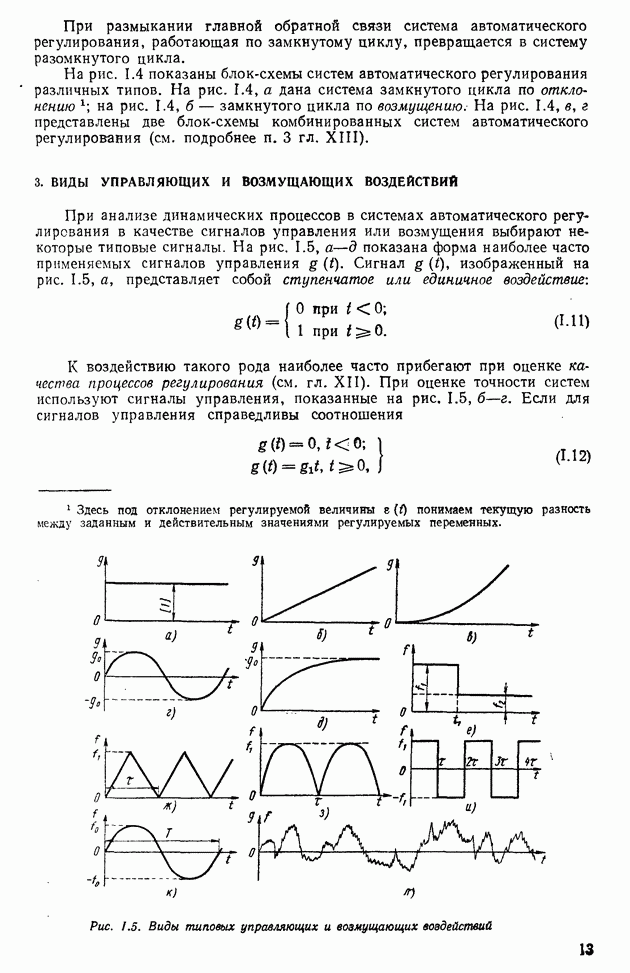
- 3. ВИДЫ УПРАВЛЯЮЩИХ И ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ
- 4. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Глава II. ВИДЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛТРОВАНИЯ
- 1. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
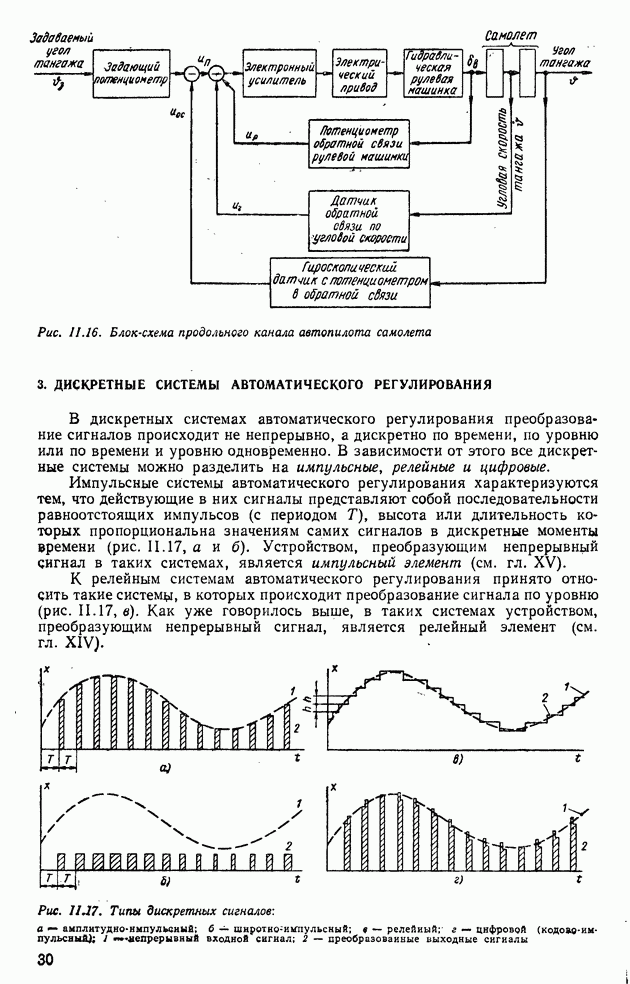
- 3. ДИСКРЕТНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ПРИМЕНЕНИЕ ЦВМ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. ПРИМЕНЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ДЛЯ УПРАВЛЕНИЯ СЛОЖНЫМИ ПРОИЗВОДСТВЕННЫМИ ПРОЦЕССАМИ. СИСТЕМЫ КОМПЛЕКСНОЙ АВТОМАТИЗАЦИИ ПРОИЗВОДСТВА
- Глава III. ОБЪЕКТЫ РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ СВОЙСТВА ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 2. ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 3. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ ДИНАМИКИ
- 4. УСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (ДИЗЕЛЬ, ГИДРОТУРБИНА, САМОЛЕТ)
- 5. НЕУСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (РЕСИВЕР, РАКЕТА-НОСИТЕЛЬ КОСМИЧЕСКИХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ)
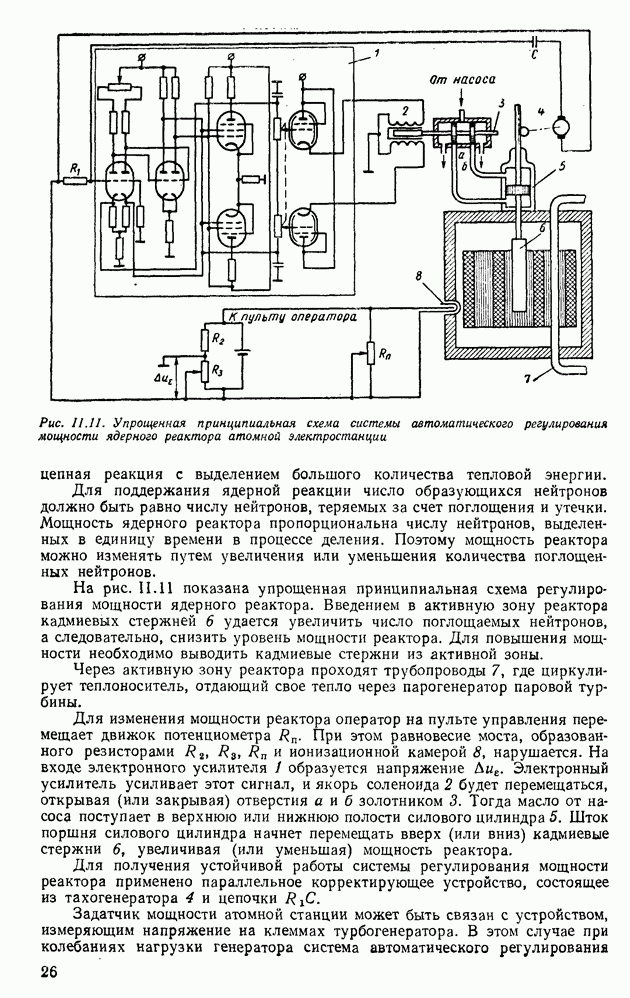
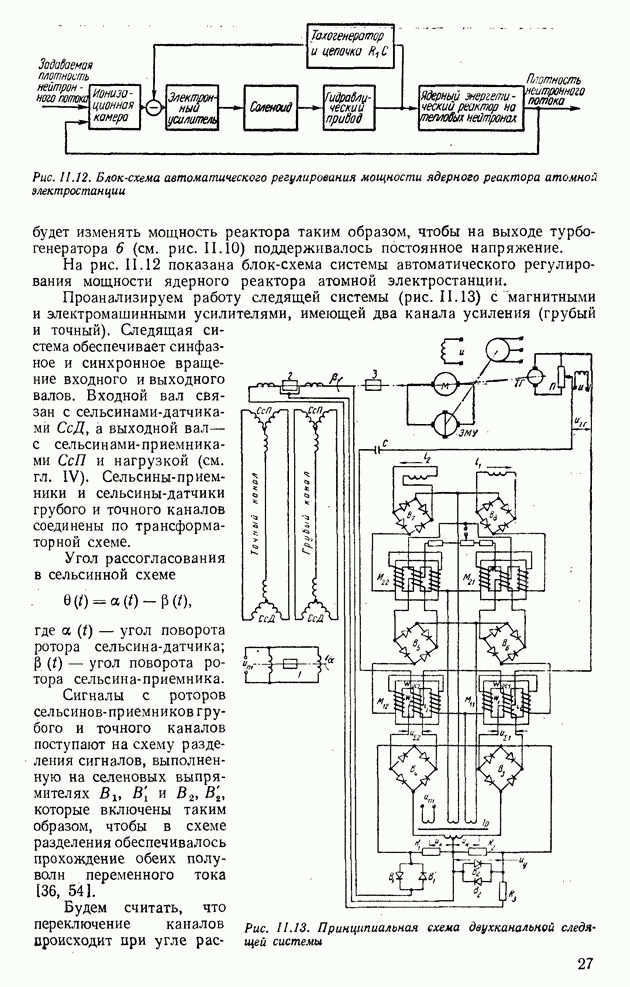
- 6. АСТАТИЧЕСКИЕ ОБЪЕКТЫ (ТРЕХФАЗНЫЙ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ, ЯДЕРНЫЙ ЭНЕРГЕТИЧЕСКИЙ РЕАКТОР НА ТЕПЛОВЫХ НЕЙТРОНАХ, КОСМИЧЕСКИЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ)
- 7. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- Глава IV. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОПРЕДЕЛЕНИЕ ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ИЗМЕРИТЕЛЬНЫХ ПОДСИСТЕМ
- 2. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Индуктивные устройства.
- Емкостные устройства.
- Сельсины.
- Дифференциальный сельсин.
- Погрешность сельсинов.
- Устройства для замера угловых скоростей.
- Устройства замера угловых ускорений.
- 4. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И ТОКА
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕМПЕРАТУР И ИЗЛУЧЕНИЙ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЙ И РАСХОДОВ ЖИДКОСТИ И ГАЗА
- 7. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ ВЕЛИЧИН, УГЛОВЫХ СКОРОСТЕЙ И ЛИНЕЙНЫХ УСКОРЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ
- Устройства для измерения линейных ускорений подвижных объектов (акселерометры).
- 8. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- Глава V. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ
- 2. МАГНИТНЫЕ УСИЛИТЕЛИ
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 4. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 5. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ РАЗЛИЧНЫХ УСИЛИТЕЛЕЙ
- ГЛАВА VI. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА
- 1. УСИЛИТЕЛИ-ПРЕОБРАЗОВАТЕЛИ
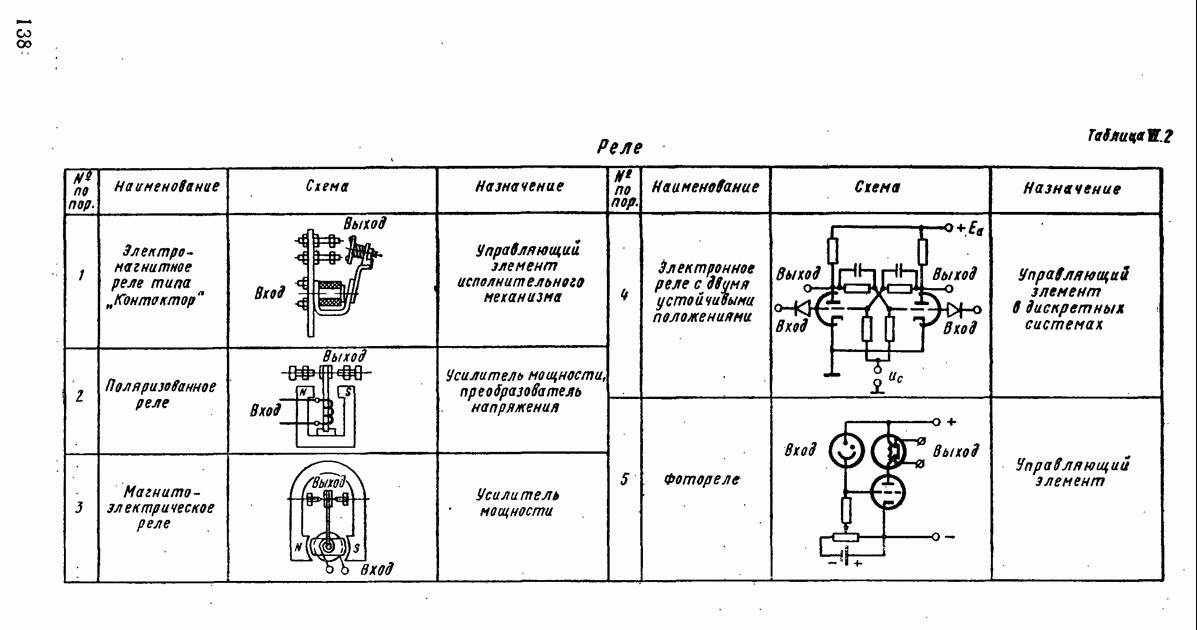
- 2. РЕЛЕ
- 3. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. ПРЕОБРАЗОВАТЕЛИ АНАЛОГ—КОД
- 5. ПРЕОБРАЗОВАТЕЛИ КОД—АНАЛОГ
- 6. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ УПРАВЛЯЮЩИЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
- 8. ПНЕВМАТИЧЕСКИЕ АНАЛОГОВЫЕ И ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 9. ТОЧНОСТЬ РАБОТЫ И БЫСТРОДЕЙСТВИЕ УПРАВЛЯЮЩИХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
- 10. СРАВНИТЕЛЬНАЯ ОЦЕНКА ПРЕОБРАЗУЮЩИХ УСТРОЙСТВ
- Глава VII. ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 1. ЭЛЕКТРИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 2. МЕХАНИЧЕСКИЕ ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. ГИДРАВЛИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 4. ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 5. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- 6. СРАВНИТЕЛЬНАЯ ОЦЕНКА ИСПОЛНИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- Глава VIII. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. НЕЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 3. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 4. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ЛИНИЯХ ЗАДЕРЖЕК И ДИСКРЕТНЫХ ЭЛЕМЕНТАХ
- Глава IX. УРАВНЕНИЯ ДИНАМИКИ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- 1. ПРЕДСТАВЛЕНИЕ ОБЪЕКТОВ И УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С СОСРЕДОТОЧЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 2. ПРЕДСТАВЛЕНИЕ УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С РАСПРЕДЕЛЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ТРАНСЦЕДЕНТНЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 3. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
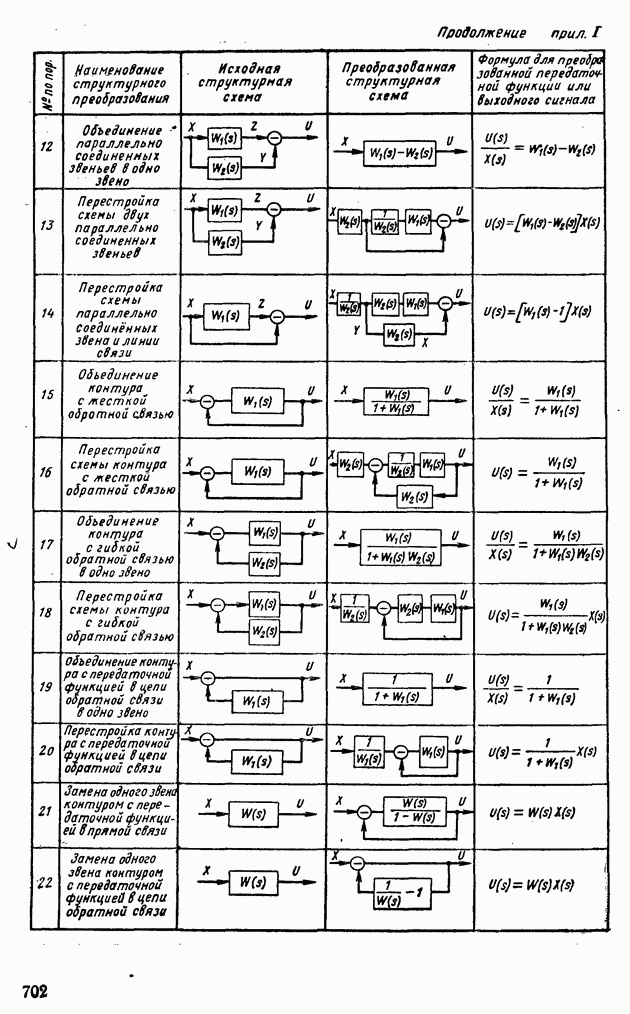
- 4. ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ
- 5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ОПИСАНИЕ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ РЕГУЛИРОВАНИЯ В ВЕКТОРНО-МАТРИЧНОЙ ФОРМЕ
- 7. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 8. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 9. РЕШЕНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ УРАВНЕНИЙ СОСТОЯНИЯ
- 10. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ МАТРИЦ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ ЛИНЕЙНЫХ СИСТЕМ
- 12. ПРЕДСТАВЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ИМПУЛЬСНЫМИ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ
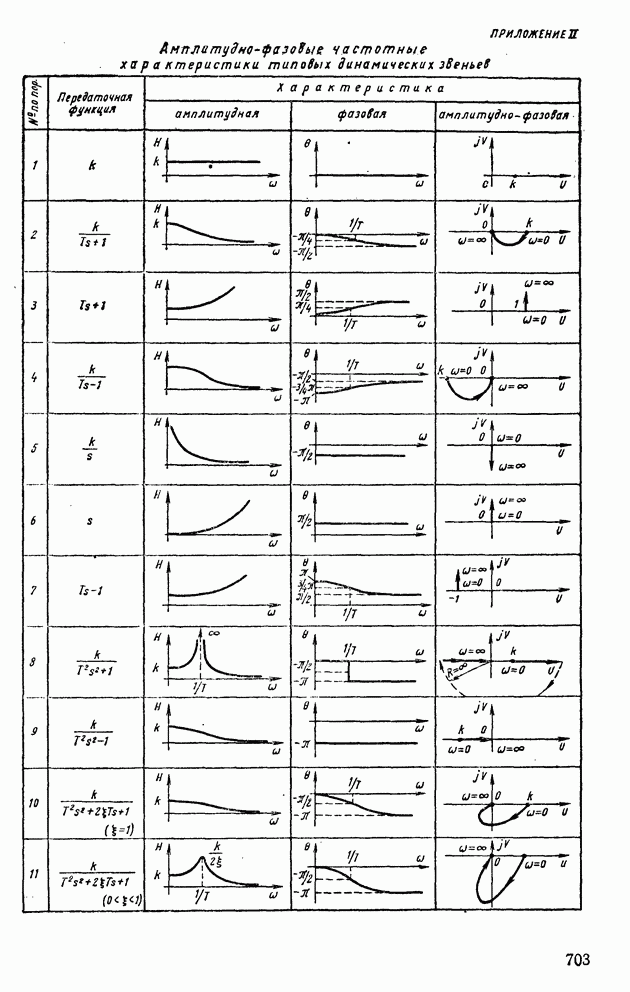
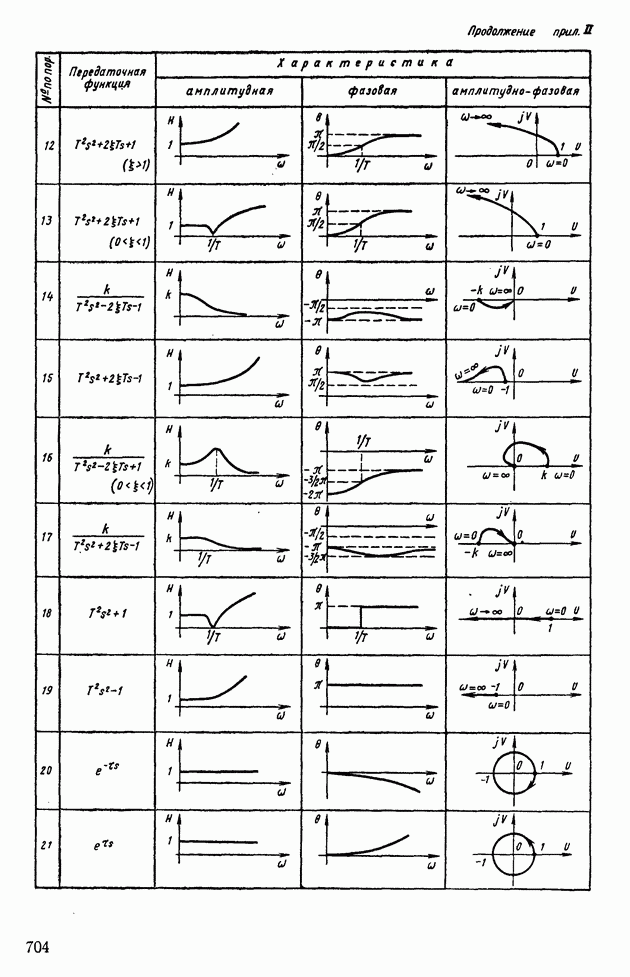
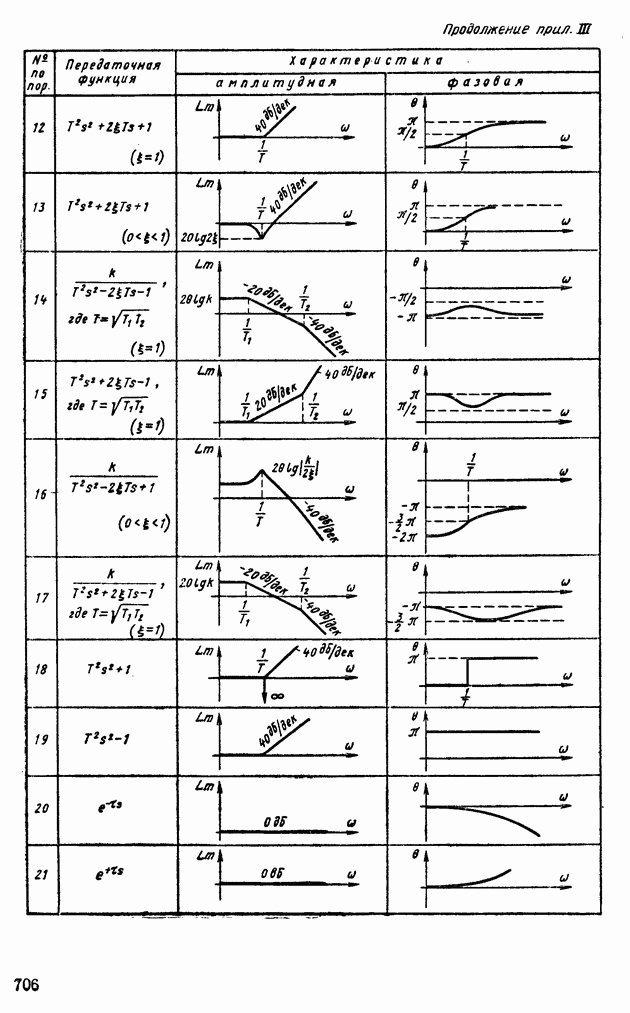
- Глава X. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ АМПЛИТУДНО-ФАЗОВЫЕ И ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 1. АПЕРИОДИЧЕСКОЕ ЗВЕНО
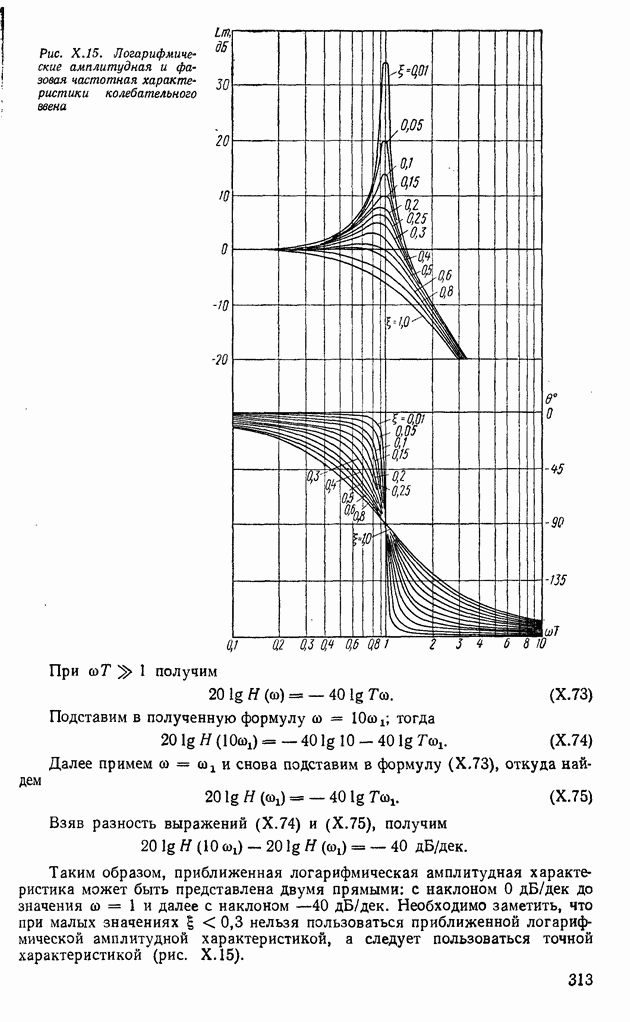
- Логарифмические амплитудная и фазовая частотные характеристики апериодического звена.
- 2. АПЕРИОДИЧЕСКОЕ НЕУСТОЙЧИВОЕ ЗВЕНО
- 4. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 5. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ (УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ)
- 6. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО РОДА
- 7. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО РОДА
- 8. ТРАНСЦЕНДЕНТНЫЕ ЗВЕНЬЯ
- 9. ФАЗОВАЯ ЛИНЕЙКА
- 10. ПОСТРОЕНИЕ АМПЛИТУДНО-ФАЗОВЫХ И ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ ГРУПП ТИПОВЫХ ЗВЕНЬЕВ
- 11. ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ВИДА ПЕРЕДАТОЧНЫХ ФУНКЦИЙ И ПАРАМЕТРОВ ГРУПП ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
- ГЛАВА XI. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ
- 2. ОПРЕДЕЛЕНИЕ ФУНКЦИЙ ЛЯПУНОВА МЕТОДАМИ Г. СЕГЕ И Д. ШУЛЬЦА
- 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 5. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 6. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ТРАНСЦЕНДЕНТНЫМИ ЗВЕНЬЯМИ
- 9. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ С ПОМОЩЬЮ D-РАЗБИЕНИЯ
- Глава XII. ИССЛЕДОВАНИЕ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
- 2. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПО ЗАДАННЫМ ПЕРЕДАТОЧНЫМ ФУНКЦИЯМ ЗАМКНУТЫХ СИСТЕМ
- 3. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПО РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ ЛЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ
- 4. МЕТОД КОРНЕВОГО ГОДОГРАФА
- 5. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА
- 6. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ СИСТЕМ РЕГУЛИРОВАНИЯ И ИХ СВЯЗЬ С ХАРАКТЕРИСТИКАМИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 7. ОПРЕДЕЛЕНИЕ ВЕЩЕСТВЕННЫХ И МНИМЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СИСТЕМ ПО АМПЛИТУДНО-ФАЗОВЫМ И ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ РАЗОМКНУТЫХ СИСТЕМ
- 8. ЧАСТОТНЫЕ ОЦЕНКИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9. ЧАСТОТНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ТРАПЕЦЕИДАЛЬНЫХ ХАРАКТЕРИСТИК
- 10. УСТАНОВЛЕНИЕ НОРМ ЗАПАСОВ УСТОЙЧИВОСТИ ПО ФАЗЕ И МОДУЛЮ, ОБЕСПЕЧИВАЮЩИХ ТРЕБУЕМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМ РЕГУЛИРОВАНИЯ
- ГЛАВА XIII. ДИНАМИЧЕСКАЯ ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ОШИБОК В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ АМПЛИТУДНЫХ ХАРАКТЕРИСТИК
- 3. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПУТЕМ ПРИМЕНЕНИЯ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ
- 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 5. СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ СТАЦИОНАРНЫХ ПРОЦЕССОВ
- 6. СВОЙСТВА СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ
- 7. ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ
- 8. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЛИНЕЙНЫМИ СИСТЕМАМИ
- 9. РАСЧЕТ ОШИБОК В СИСТЕМЕ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ШУМОВ
- 10. ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ВОЗДЕЙСТВИИ СЛУЧАЙНЫХ СИГНАЛОВ И ШУМОВ
- ГЛАВА XIV. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ТИПОВЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ ПО ВТОРОМУ МЕТОДУ ЛЯПУНОВА
- 3. АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
- 4. ПРИМЕНЕНИЕ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. АНАЛИЗ АВТОКОЛЕБАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДВУМЯ НЕЛИНЕЙНОСТЯМИ
- 7. ДВУХКОНТУРНЫЕ НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕДЛЕННО ИЗМЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
- 9. СПОСОБЫ ПОДАВЛЕНИЯ АВТОКОЛЕБАНИЙ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 10. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 11. КРИТЕРИЙ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
- 12. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- Глава XIV. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ИМПУЛЬСНЫХ УСТРОЙСТВ
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. АМПЛИТУДНО-ФАЗОВЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ СИСТЕМ
- 4. ПРИМЕНЕНИЕ ВЕКТОРНО-МАТРИЧНОГО АППАРАТА К ИМПУЛЬСНЫМ СИСТЕМАМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ОСНОВНЫЕ СВОЙСТВА z-ПРЕОБРАЗОВАНИЯ
- 6. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Критерий устойчивости для импульсных систем на плоскостях z и W(z).
- Критерий устойчивости Шур—Кона.
- Критерии устойчивости, основанные на применении билинейного преобразования.
- 7. МЕТОДЫ АНАЛИЗА КАЧЕСТВА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕТОДЫ АНАЛИЗА ТОЧНОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 9. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С УПРАВЛЯЮЩИМИ ЦВМ
- 10. СПОСОБЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ В УПРАВЛЯЮЩИХ ЦВМ И ОПРЕДЕЛЕНИЕ ИХ ОСНОВНЫХ ПАРАМЕТРОВ
- Глава XVI. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МЕТОДЫ ПОИСКА ЭКСТРЕМУМА
- 2. СПОСОБЫ ОРГАНИЗАЦИИ ДВИЖЕНИЯ К ЭКСТРЕМУМУ
- 3. МЕТОДЫ РАСЧЕТА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРОВ
- 4. ВЫБОР КОРРЕКТИРУЮЩИХ УСТРОЙСТВ В ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРАХ
- 5. ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ С ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ
- Глава XVII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ ВОЗДЕЙСТВИЯХ
- 2. ВЫБОР ПАРАМЕТРОВ УСТРОЙСТВ НЕИЗМЕНЯЕМОЙ ЧАСТИ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ПОСТРОЕНИЕ ЖЕЛАЕМОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 4. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. СИНТЕЗ ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 6. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 7. СПОСОБЫ РЕАЛИЗАЦИИ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Глава XVIII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 1. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА НА ОСНОВЕ КРИТЕРИЯ МИНИМУМА ИНТЕГРАЛЬНОЙ ОШИБКИ
- 2. СИНТЕЗ СИСТЕМ РЕГУЛИРОВАНИЯ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЖЕЛАЕМОЙ СИСТЕМЫ
- 4. ПРИМЕР СИНТЕЗА КОРРЕКТИРУЮЩИХ УСТРОЙСТВ СИСТЕМЫ РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- ГЛАВА XIX. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИНТЕЗ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ, ОСНОВАННЫЙ НА ПРИМЕНЕНИИ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- 2. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. РЕАЛИЗАЦИЯ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ ПРИ ПОМОЩИ RC-ЦЕПЕЙ
- 4. РЕАЛИЗАЦИЯ ПРОГРАММ КОРРЕКЦИИ НА УПРАВЛЯЮЩЕЙ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- ГЛАВА XX. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ПРИНЦИП МАКСИМУМА
- 3. ТЕОРЕМА О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
- 4. ПРИМЕРЫ ПРИМЕНЕНИЯ ПРИНЦИПА МАКСИМУМА
- 5. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 6. СИНТЕЗ НЕПРЕРЫВНЫХ ОПТИМАЛЬНЫХ СИСТЕМ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ