| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
9. СПОСОБЫ ПОДАВЛЕНИЯ АВТОКОЛЕБАНИЙ В НЕЛИНЕЙНЫХ СИСТЕМАХ
Как было показано ранее, нелинейности различного рода в одноконтурных и двухконтурных системах автоматического регулирования являются причиной возникновения автоколебаний. Автоколебания для систем регулирования некоторых видов совершенно недопустимы, так как приводят к снижению точности системы или нарушению режима нормальной эксплуатации. Так, например, в следящих системах режим автоколебаний вызывает колебания объекта регулирования, что нарушает плавность режима слежения и недопустимо по требованиям эксплуатации. В высококачественных системах автоматического регулирования автоколебания недопустимы по требованиям точности и т. д. Для устранения режимов автоколебаний в системах регулирования применяют линейные или нелинейные корректирующие устройства.
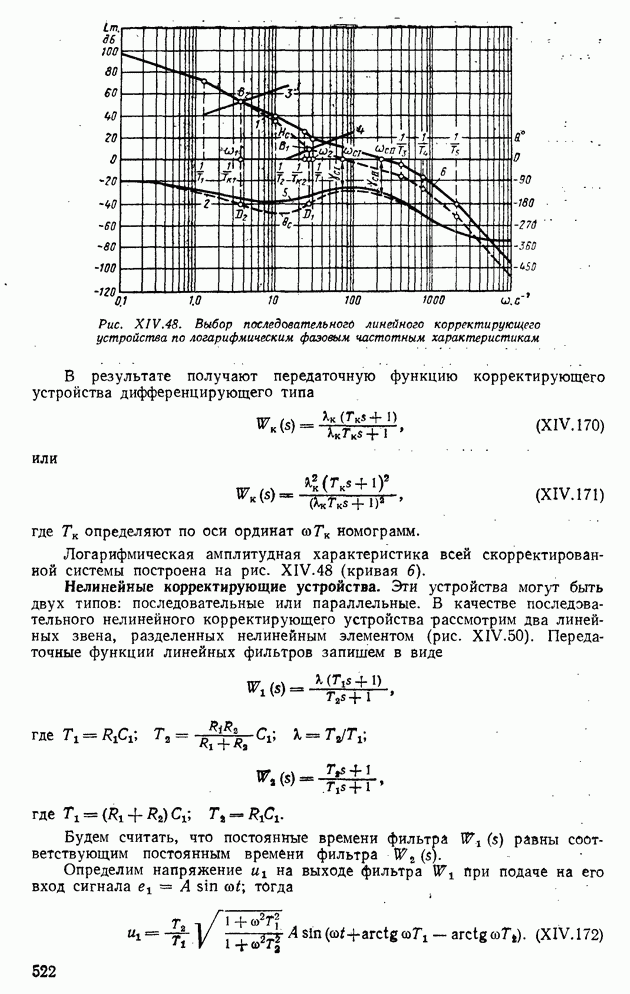
Линейные корректирующие устройства. С целью подавления автоколебаний в системе параметры линейных корректирующих устройств выбирают таким образом, чтобы условие баланса амплитуд и фаз не выполнялось. Рассмотрим логарифмические амплитудную 1 и фазовую 2 частотные характеристики линейной части системы. Они изображены на рис. XIV.48 штриховыми линиями. Как видно из этого рисунка, кривая 2 пересекает линию  в двух точках
в двух точках  где
где  дБ. Соответствующие этим точкам положения шаблонов нелинейного звена показаны кривыми 3 к 4. Точки
дБ. Соответствующие этим точкам положения шаблонов нелинейного звена показаны кривыми 3 к 4. Точки  и В 2 пересечения шаблонов с кривой 1 лежат на одной вертикали с точками
и В 2 пересечения шаблонов с кривой 1 лежат на одной вертикали с точками  и
и  Следовательно, в этих точках могут наблюдаться колебания.
Следовательно, в этих точках могут наблюдаться колебания.
В точке  производная
производная  что указывает на автоколебательный режим в системе, а в точке
что указывает на автоколебательный режим в системе, а в точке  производная
производная  и система находится в неустойчивом режиме колебаний. Для устранения периодических режимов необходимо поднять фазовую характеристику выше оси
и система находится в неустойчивом режиме колебаний. Для устранения периодических режимов необходимо поднять фазовую характеристику выше оси  На рис. XIV.48 такая фазовая характеристика (желаемая) показана сплошной линией (кривая 5). Требуемое корректирующее устройство можно выбрать по наибольшей разности фазовых углов, т. е.
На рис. XIV.48 такая фазовая характеристика (желаемая) показана сплошной линией (кривая 5). Требуемое корректирующее устройство можно выбрать по наибольшей разности фазовых углов, т. е.

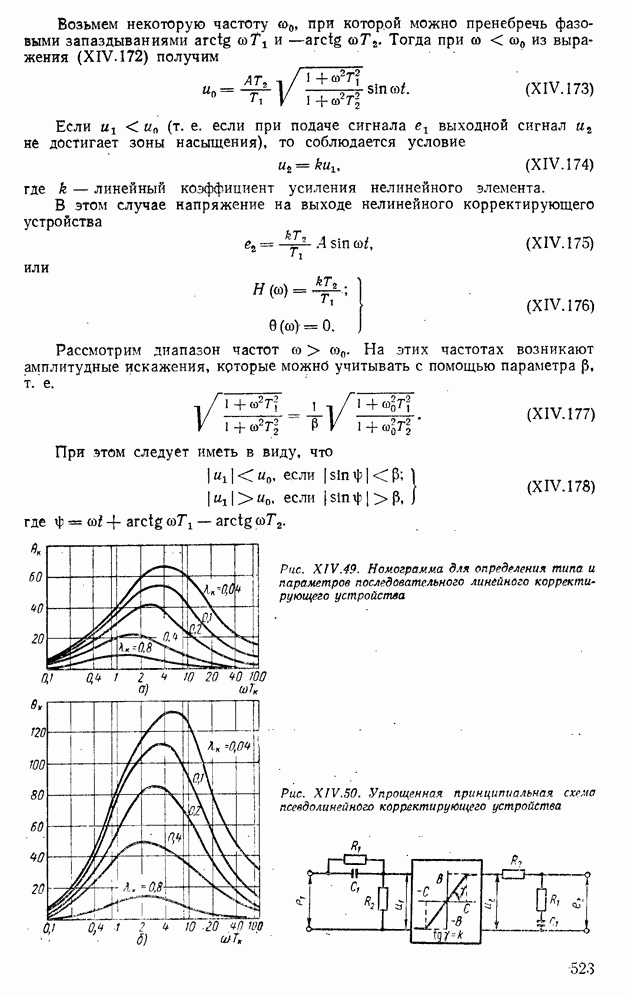
По  с помощью специальных номограмм (рис. XIV.49) можно выбрать тип корректирующего устройства, а также его параметр
с помощью специальных номограмм (рис. XIV.49) можно выбрать тип корректирующего устройства, а также его параметр 
Рис. XIV.48. (см. скан) Выбор последовательного линейного корректирующего устройства по логарифмическим фазовым частотным характеристикам
В результате получают передаточную функцию корректирующего устройства дифференцирующего типа

или

где  определяют по оси ординат
определяют по оси ординат  номограмм.
номограмм.
Логарифмическая амплитудная характеристика всей скорректированной системы построена на рис. XIV.48 (кривая 6).
Нелинейные корректирующие устройства. Эти устройства могут быть двух типов: последовательные или параллельные. В качестве последовательного нелинейного корректирующего устройства рассмотрим два линейных звена, разделенных нелинейным элементом (рис. XIV.50). Передаточные функции линейных фильтров запишем в виде

где 

Будем считать, что постоянные времени фильтра  равны соответствующим постоянным времени фильтра
равны соответствующим постоянным времени фильтра 
Определим напряжение  на выходе фильтра при подаче на его вход сигнала
на выходе фильтра при подаче на его вход сигнала  тогда
тогда

Возьмем некоторую частоту  при которой можно пренебречь фазовыми запаздываниями
при которой можно пренебречь фазовыми запаздываниями  Тогда при
Тогда при  из выражения (XIV. 172) получим
из выражения (XIV. 172) получим

Если  (т. е. если при подаче сигнала
(т. е. если при подаче сигнала  выходной сигнал
выходной сигнал  не достигает зоны насыщения), то соблюдается условие
не достигает зоны насыщения), то соблюдается условие

где  — линейный коэффициент усиления нелинейного элемента.
— линейный коэффициент усиления нелинейного элемента.
В этом случае напряжение на выходе нелинейного корректирующего устройства

или

Рассмотрим диапазон частот  На этих частотах возникают амплитудные искажения, которые можнб учитывать с помощью параметра
На этих частотах возникают амплитудные искажения, которые можнб учитывать с помощью параметра 

При этом следует иметь в виду, что

где 
Рис. XIV.49. (см. скан) Номограмма для определения типа, и параметров последовательного линейного корректирующего устройства
Рис. XIV.50. (см. скан) Упрощенная принципиальная схема псевдолинейного корректирующего устройства
Коэффициенты гармонической линеаризации для данного нелинейного корректирующего устройства при симметричности сигнала на входе нелинейности определяют с помощью следующего выражения:

где  откуда
откуда

Пользуясь этой формулой, найдем выражение для сигнала на выходе нелинейного корректирующего устройства:

Из выражения (XIV. 181) определим

где 
По формуле (XIV. 182) на рис. XIV.51 построены логарифмические эквивалентные амплитудные характеристики рассматриваемого нелинейного корректирующего устройства при  Как видно из рисунка, корректирующее устройство изменяет только эквивалентную амплитудную характеристику системы и является псевдолинейным, что упрощает анализ устойчивости систем автоматического регулирования.
Как видно из рисунка, корректирующее устройство изменяет только эквивалентную амплитудную характеристику системы и является псевдолинейным, что упрощает анализ устойчивости систем автоматического регулирования.
Еще большие возможности по диапазону изменения амплитуд на входе нелинейности имеют параллельные нелинейные корректирующие устройства. Выбор корректирующего устройства такого рода рассмотрим на примере системы автоматического регулирования (рис. XIV.52, а). Введем в исходную систему, как это предложил Д. Шулкинд [76], параллельное корректирующее устройство, состоящее из линейной  и нелинейной
и нелинейной  частей (рис. XIV-52, б). Условие устойчивости для этой системы запишем в виде
частей (рис. XIV-52, б). Условие устойчивости для этой системы запишем в виде

Для выбора передаточных функций корректирующих устройств  и
и  введем ряд дополнительных условий.
введем ряд дополнительных условий.
Условие 1. Будем считать, что нелинейное корректирующее устройство  и основная нелинейность
и основная нелинейность  одинаковы, т. е.
одинаковы, т. е.

При выполнении равенства (XIV. 184) условие устойчивости системы

можно представить в виде

или


Рис. XIV.51. Логарифмические приведенные эквивалентные амплитудные характеристики псевдолинейного корректирующего устройства

Рис. XIV.52. Структурная схема системы автоматического регулирования с нелинейностью: а — исходная; б — включением нелинейного параллельного корректирующего устройства
Из выражений (XIV. 187) и (XIV. 188) следует, что  нужно выбирать таким образом, чтобы при
нужно выбирать таким образом, чтобы при  результирующая фазовая характеристика
результирующая фазовая характеристика  не пересекала линию
не пересекала линию  .
.
Условие 2. Пусть  тогда уравнение (XIV. 183) примет следующий вид:
тогда уравнение (XIV. 183) примет следующий вид:

или, после объединения обеих нелинейностей в одну,

где  .
.
Из уравнения (XIV. 190) получим соотношения, обеспечивающие условия гармонического баланса:

Путем соответствующего выбора характеристики  в передаточной функции
в передаточной функции  можно получить значительное расширение областей устойчивых состояний системы по ее параметрам.
можно получить значительное расширение областей устойчивых состояний системы по ее параметрам.
Условие 3. Примем, что

где  — постоянный коэффициент, изменяющийся в пределах от 0 до 1, и
— постоянный коэффициент, изменяющийся в пределах от 0 до 1, и

Имея в виду соотношения (XIV. 192) и (XIV. 193), перепишем уравнение (XIV. 183):

Соответствующим выбором  уравнение (XIV. 194) можно привести к виду
уравнение (XIV. 194) можно привести к виду

или

т. е. при  кривая
кривая  должна быть выше линии
должна быть выше линии 

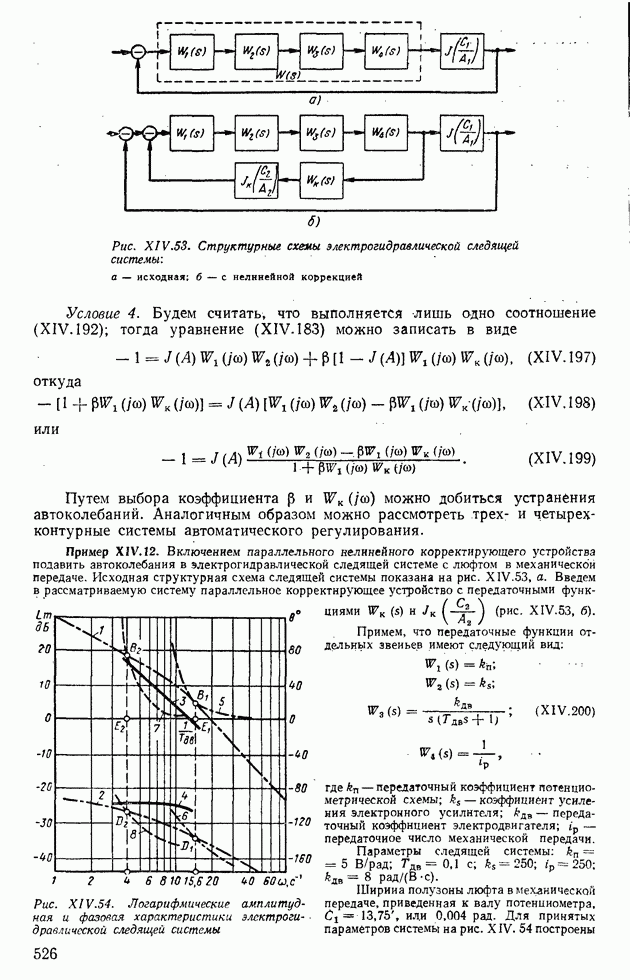
Рис. XI V.53. Структурные схемы электрогидравлической следящей системы: а — исходная; б - с нелинейной коррекцией
Условие 4. Будем считать, что выполняется лишь одно соотношение (XIV. 192); тогда уравнение (XIV. 183) можно записать в виде

откуда

или

Путем выбора коэффициента  можно добиться устранения автоколебаний. Аналогичным образом можно рассмотреть трех- и четырехконтурные системы автоматического регулирования.
можно добиться устранения автоколебаний. Аналогичным образом можно рассмотреть трех- и четырехконтурные системы автоматического регулирования.
Пример  Включением параллельного нелинейного корректирующего устройства подавить автоколебания в электрогидравлической следящей системе с люфтом в механической передаче. Исходная структурная схема следящей системы показана на рис. XIV.53, а. Введем в рассматриваемую систему параллельное корректирующее устройство с передаточными функциями
Включением параллельного нелинейного корректирующего устройства подавить автоколебания в электрогидравлической следящей системе с люфтом в механической передаче. Исходная структурная схема следящей системы показана на рис. XIV.53, а. Введем в рассматриваемую систему параллельное корректирующее устройство с передаточными функциями  и
и  -
-  (рис. XIV.53, б).
(рис. XIV.53, б).
Примем, что передаточные функции отдельных звеньев имеют следующий вид:

где  — передаточный коэффициент потенциометрической схемы;
— передаточный коэффициент потенциометрической схемы;  — коэффициент усиления электронного усилителя;
— коэффициент усиления электронного усилителя;  — передаточный коэффициент электродвигателя;
— передаточный коэффициент электродвигателя;  — передаточное число механической передачи.
— передаточное число механической передачи.
Параметры следящей системы:  .
.
Ширина полузоны люфта в механической передаче, приведенная к валу потенциометра,  иди 0,004 рад. Для принятых параметров системы на рис. XIV. 54 построены
иди 0,004 рад. Для принятых параметров системы на рис. XIV. 54 построены

Рис. XIV.54. Логарифмические амплитудная и фазовая характеристики электрогидравлической следящей системы
логарифмические амплитудная (кривая 1) и фазовая (кривая 2) частные характеристики линейной части системы. На этом же рисунке показаны положения шаблонов (кривые 5, 6 и 7, 8), соответствующие периодическим режимам в системе. С ростом амплитуды точка  шаблона
шаблона  выходит из области, ограниченной линиями
выходит из области, ограниченной линиями  , т. е. при частоте, соответствующей точке
, т. е. при частоте, соответствующей точке  имеются автоколебания с частотой
имеются автоколебания с частотой  и амплитудой
и амплитудой  рад. Точка
рад. Точка  кривой 7 с ростом амплитуды входнт внутрь указанной области, т. е. при частоте, соответствующей точке
кривой 7 с ростом амплитуды входнт внутрь указанной области, т. е. при частоте, соответствующей точке  возникают неустойчивые колебания с частотой
возникают неустойчивые колебания с частотой  и амплитудой
и амплитудой  рад.
рад.
Для устранения автоколебаний и неустойчивых колебаний в следящей системе выберем в качестве параллельного нелинейного корректирующего устройства тахогенератор с цепочкой RC и нелинейность типа насыщения (с зоной  т. е.
т. е.

и

где  Примем, что ширина участка насыщения нелинейности
Примем, что ширина участка насыщения нелинейности  Запишем характеристическое уравнение системы
Запишем характеристическое уравнение системы

где 
Из уравнения (XIV.203) найдем

Введем в уравнение (XIV.204) следующие обозначения:

где

Для использования логарифмических частотных характеристик выражение (XIV.205) перепишем в виде

Амплитудная характеристика

где

и фазовая


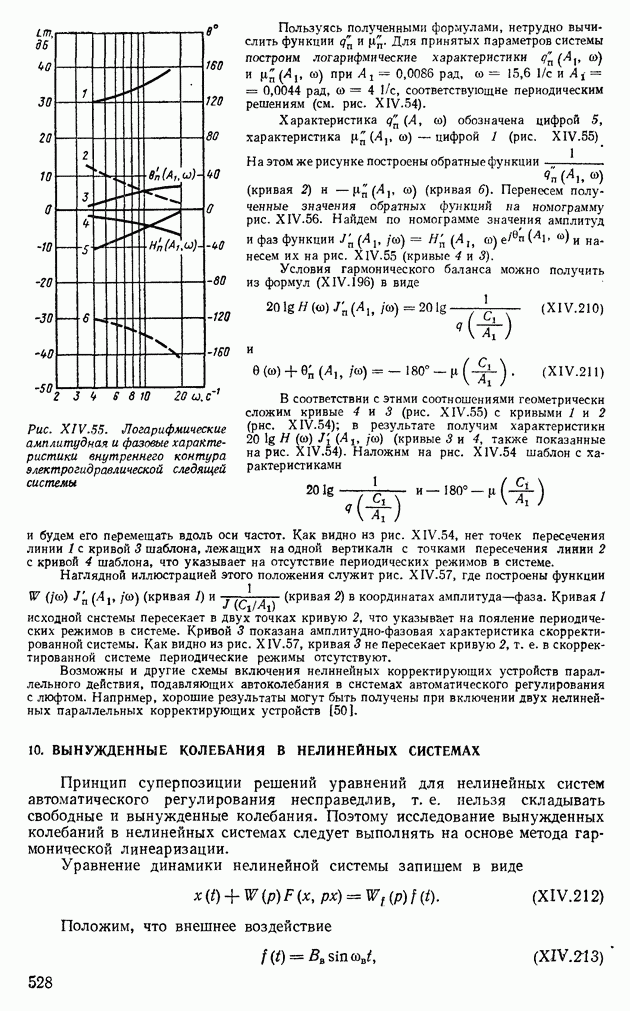
Рис. XIV.55. Логарифмические амплитудная и фазовые характеристики внутреннего контура электрогидравлической следящей системы
Пользуясь полученными формулами, нетрудно вычислить функции  Для принятых параметров системы построим логарифмические характеристики
Для принятых параметров системы построим логарифмические характеристики  при
при  рад,
рад,  , соответствующие периодическим решениям (см. рис. XIV.54).
, соответствующие периодическим решениям (см. рис. XIV.54).
Характеристика  обозначена цифрой 5, характеристика
обозначена цифрой 5, характеристика  — цифрой 1 (рис. XIV.55)
— цифрой 1 (рис. XIV.55)
На этом же рисунке построены обратные функции  (кривая 2) и
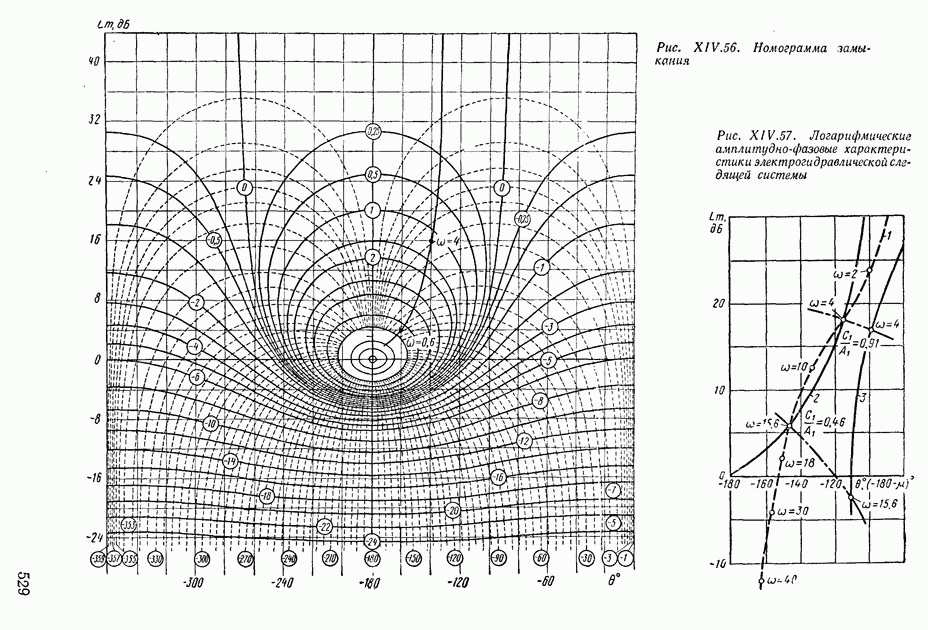
(кривая 2) и  (кривая 6). Перенесем полученные значения обратных функций на номограмму рис. XIV.56. Найдем по номограмме значения амплитуд и фаз функции
(кривая 6). Перенесем полученные значения обратных функций на номограмму рис. XIV.56. Найдем по номограмме значения амплитуд и фаз функции  и нанесем их на рис. XIV.55 (кривые 4 и 3).
и нанесем их на рис. XIV.55 (кривые 4 и 3).
Условия гармонического баланса можно получить из формул (XIV. 196) в виде

и

В соответствии с этими соотношениями геометрически сложим кривые 4 и 3 (рис. XIV.55) с кривыми 1 и 2 (рис. XIV.54); в результате получим характеристики  (кривые 3 и 4, также показанные на рис. XIV.54). Наложим на рис. XIV.54 шаблон с характеристиками
(кривые 3 и 4, также показанные на рис. XIV.54). Наложим на рис. XIV.54 шаблон с характеристиками

и будем его перемещать вдоль оси частот. Как видно из рис. XIV.54, нет точек пересечения линии 1 с кривой 3 шаблона, лежащих на одной вертикали с точками пересечения линии 2 с кривой 4 шаблона, что указывает на отсутствие периодических режимов в системе.
Наглядной иллюстрацией этого положения служит рис. XIV.57, где построены функции  (кривая 1) и
(кривая 1) и  (кривая в координатах амплитуда—фаза. Кривая 1 исходной системы пересекает в двух точках кривую 2, что указывает на пояление периодических режимов в системе. Кривой 3 показана амплитудно-фазовая характеристика скорректированной системы. Как видно из рис. XIV.57, кривая 3 не пересекает кривую 2, т. е. в скорректированной системе периодические режимы отсутствуют.
(кривая в координатах амплитуда—фаза. Кривая 1 исходной системы пересекает в двух точках кривую 2, что указывает на пояление периодических режимов в системе. Кривой 3 показана амплитудно-фазовая характеристика скорректированной системы. Как видно из рис. XIV.57, кривая 3 не пересекает кривую 2, т. е. в скорректированной системе периодические режимы отсутствуют.
Возможны и другие схемы включения нелинейных корректирующих устройств параллельного действия, подавляющих автоколебания в системах автоматического регулирования с люфтом. Например, хорошие результаты могут быть получены при включении двух нелинейных параллельных корректирующих устройств [50].
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 1. ПРИНЦИПЫ ДЕЙСТВИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ВИДЫ УПРАВЛЯЮЩИХ И ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ
- 4. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Глава II. ВИДЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛТРОВАНИЯ
- 1. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ДИСКРЕТНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ПРИМЕНЕНИЕ ЦВМ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. ПРИМЕНЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ДЛЯ УПРАВЛЕНИЯ СЛОЖНЫМИ ПРОИЗВОДСТВЕННЫМИ ПРОЦЕССАМИ. СИСТЕМЫ КОМПЛЕКСНОЙ АВТОМАТИЗАЦИИ ПРОИЗВОДСТВА
- Глава III. ОБЪЕКТЫ РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ СВОЙСТВА ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 2. ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 3. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ ДИНАМИКИ
- 4. УСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (ДИЗЕЛЬ, ГИДРОТУРБИНА, САМОЛЕТ)
- 5. НЕУСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (РЕСИВЕР, РАКЕТА-НОСИТЕЛЬ КОСМИЧЕСКИХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ)
- 6. АСТАТИЧЕСКИЕ ОБЪЕКТЫ (ТРЕХФАЗНЫЙ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ, ЯДЕРНЫЙ ЭНЕРГЕТИЧЕСКИЙ РЕАКТОР НА ТЕПЛОВЫХ НЕЙТРОНАХ, КОСМИЧЕСКИЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ)
- 7. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- Глава IV. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОПРЕДЕЛЕНИЕ ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ИЗМЕРИТЕЛЬНЫХ ПОДСИСТЕМ
- 2. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Индуктивные устройства.
- Емкостные устройства.
- Сельсины.
- Дифференциальный сельсин.
- Погрешность сельсинов.
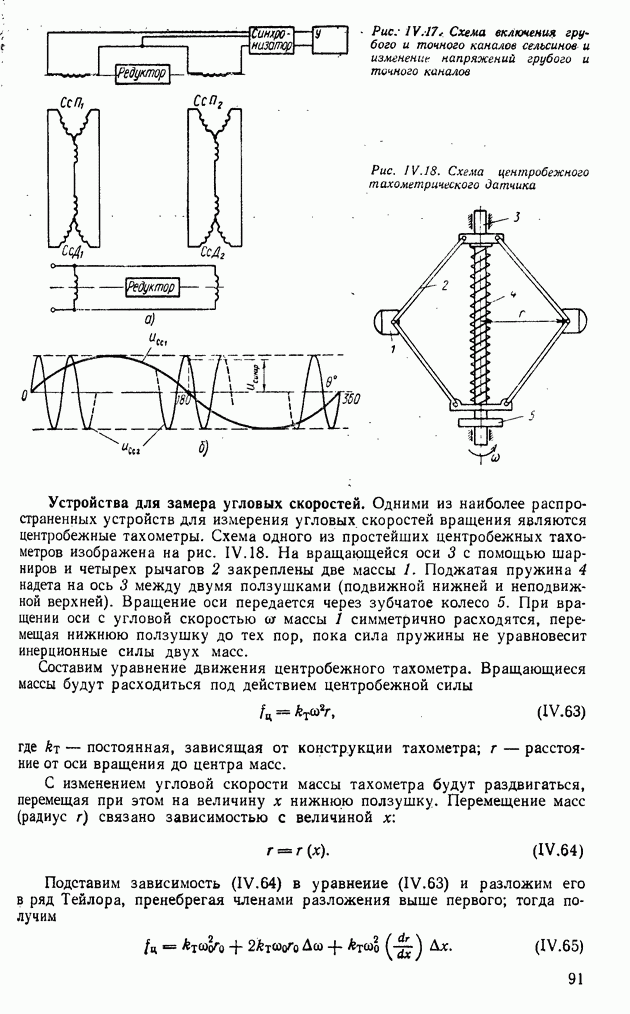
- Устройства для замера угловых скоростей.
- Устройства замера угловых ускорений.
- 4. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И ТОКА
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕМПЕРАТУР И ИЗЛУЧЕНИЙ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЙ И РАСХОДОВ ЖИДКОСТИ И ГАЗА
- 7. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ ВЕЛИЧИН, УГЛОВЫХ СКОРОСТЕЙ И ЛИНЕЙНЫХ УСКОРЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ
- Устройства для измерения линейных ускорений подвижных объектов (акселерометры).
- 8. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- Глава V. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ
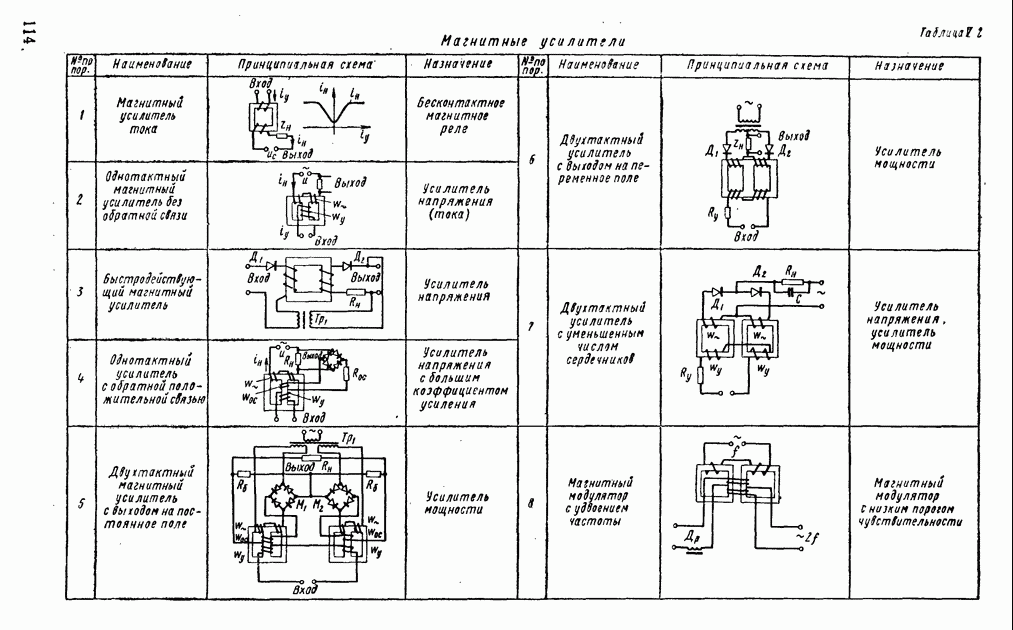
- 2. МАГНИТНЫЕ УСИЛИТЕЛИ
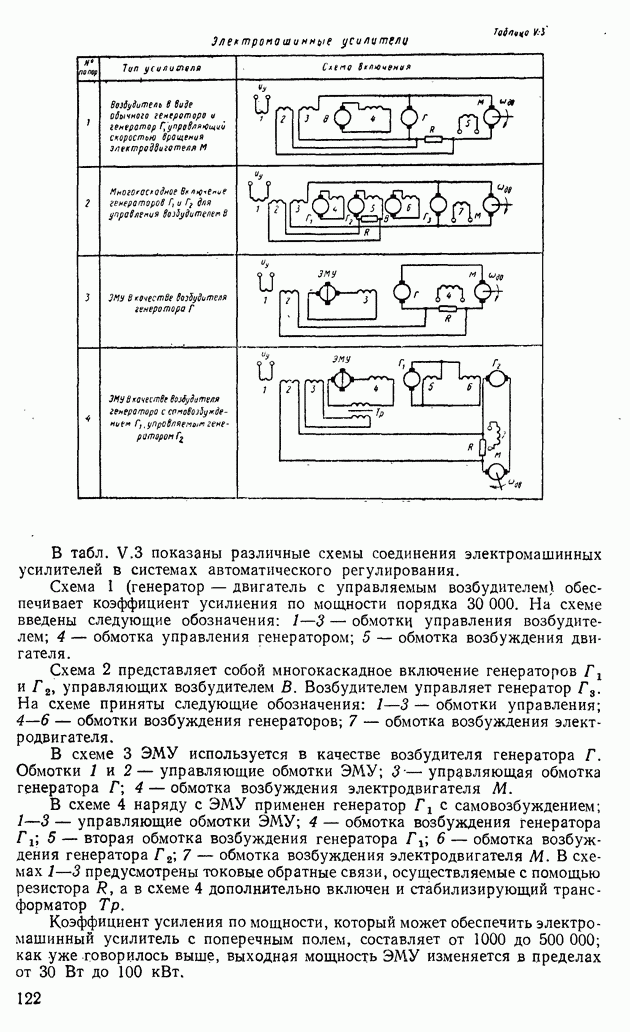
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
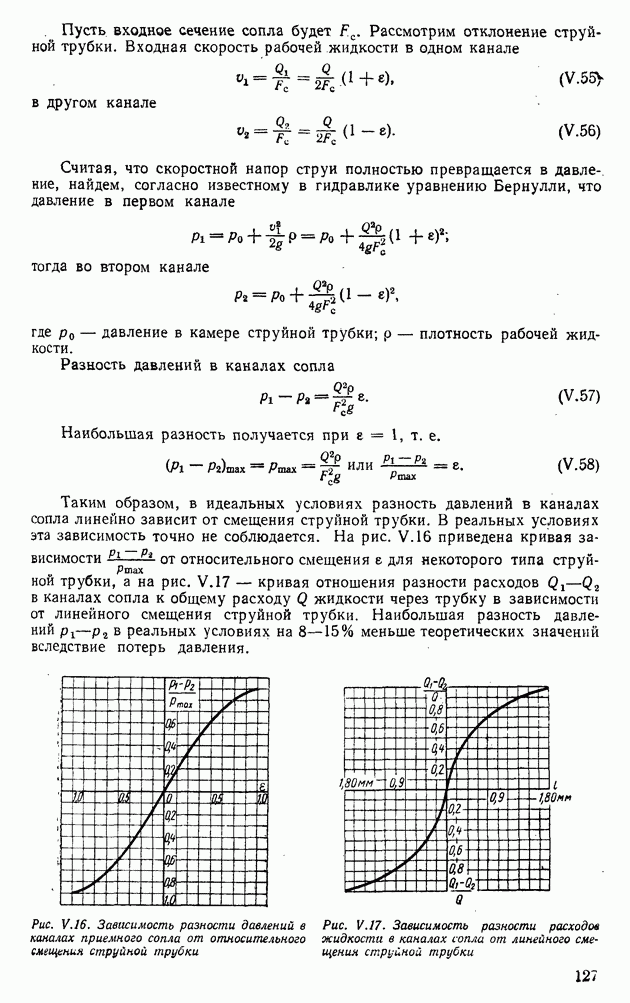
- 4. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 5. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ РАЗЛИЧНЫХ УСИЛИТЕЛЕЙ
- ГЛАВА VI. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА
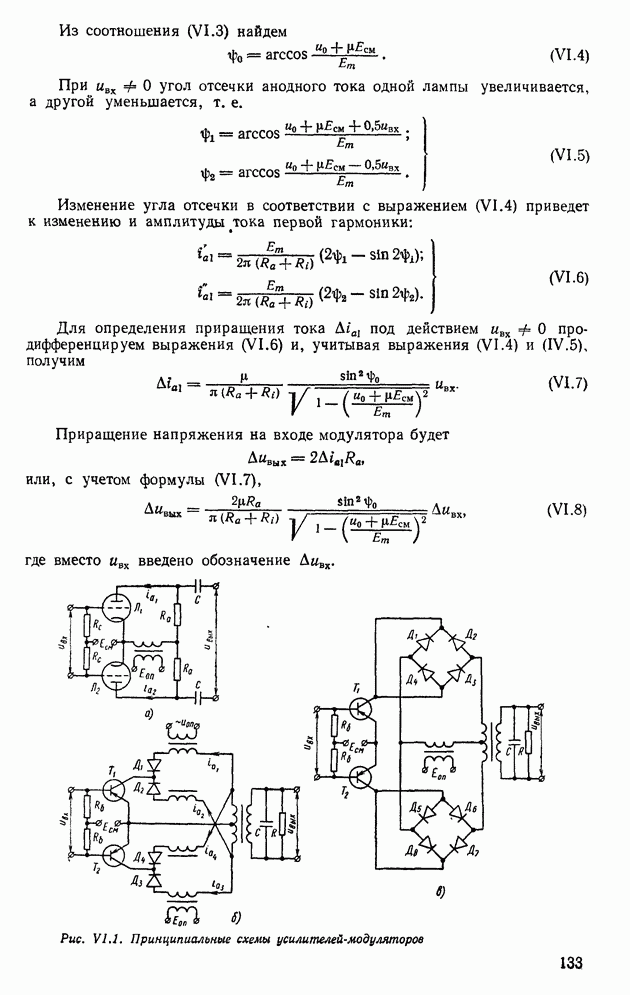
- 1. УСИЛИТЕЛИ-ПРЕОБРАЗОВАТЕЛИ
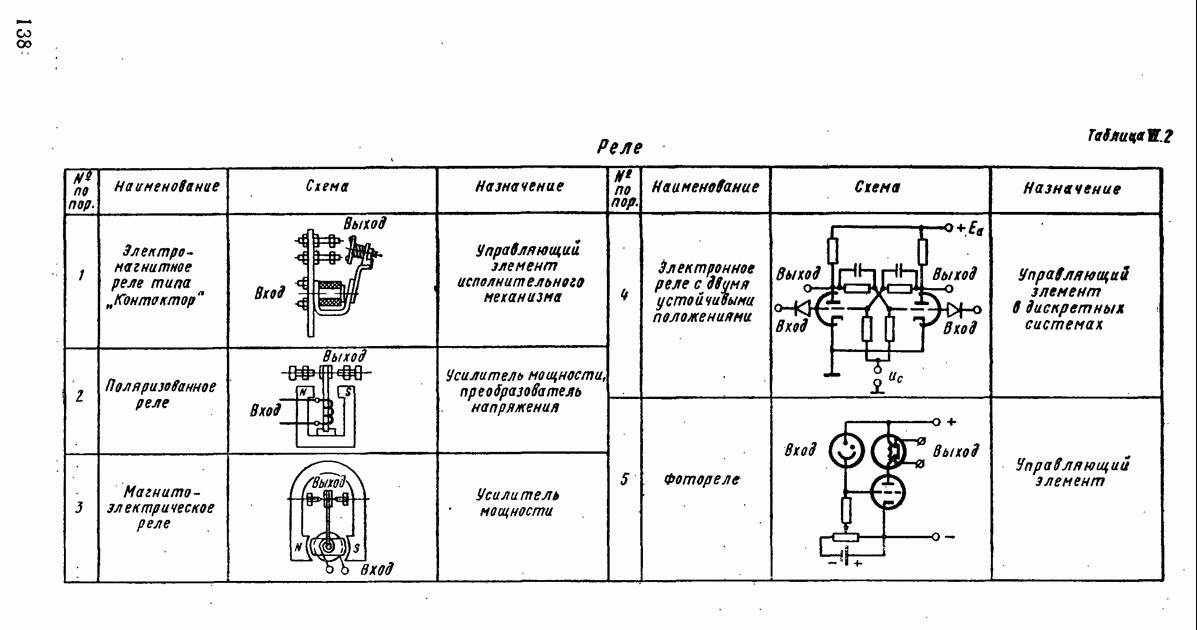
- 2. РЕЛЕ
- 3. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. ПРЕОБРАЗОВАТЕЛИ АНАЛОГ—КОД
- 5. ПРЕОБРАЗОВАТЕЛИ КОД—АНАЛОГ
- 6. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ УПРАВЛЯЮЩИЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
- 8. ПНЕВМАТИЧЕСКИЕ АНАЛОГОВЫЕ И ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 9. ТОЧНОСТЬ РАБОТЫ И БЫСТРОДЕЙСТВИЕ УПРАВЛЯЮЩИХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
- 10. СРАВНИТЕЛЬНАЯ ОЦЕНКА ПРЕОБРАЗУЮЩИХ УСТРОЙСТВ
- Глава VII. ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 1. ЭЛЕКТРИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 2. МЕХАНИЧЕСКИЕ ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. ГИДРАВЛИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 4. ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 5. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- 6. СРАВНИТЕЛЬНАЯ ОЦЕНКА ИСПОЛНИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- Глава VIII. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. НЕЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 3. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 4. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ЛИНИЯХ ЗАДЕРЖЕК И ДИСКРЕТНЫХ ЭЛЕМЕНТАХ
- Глава IX. УРАВНЕНИЯ ДИНАМИКИ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- 1. ПРЕДСТАВЛЕНИЕ ОБЪЕКТОВ И УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С СОСРЕДОТОЧЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 2. ПРЕДСТАВЛЕНИЕ УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С РАСПРЕДЕЛЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ТРАНСЦЕДЕНТНЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 3. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ
- 5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ОПИСАНИЕ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ РЕГУЛИРОВАНИЯ В ВЕКТОРНО-МАТРИЧНОЙ ФОРМЕ
- 7. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 8. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 9. РЕШЕНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ УРАВНЕНИЙ СОСТОЯНИЯ
- 10. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ МАТРИЦ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ ЛИНЕЙНЫХ СИСТЕМ
- 12. ПРЕДСТАВЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ИМПУЛЬСНЫМИ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ
- Глава X. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ АМПЛИТУДНО-ФАЗОВЫЕ И ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 1. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- Логарифмические амплитудная и фазовая частотные характеристики апериодического звена.
- 2. АПЕРИОДИЧЕСКОЕ НЕУСТОЙЧИВОЕ ЗВЕНО
- 4. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 5. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ (УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ)
- 6. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО РОДА
- 7. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО РОДА
- 8. ТРАНСЦЕНДЕНТНЫЕ ЗВЕНЬЯ
- 9. ФАЗОВАЯ ЛИНЕЙКА
- 10. ПОСТРОЕНИЕ АМПЛИТУДНО-ФАЗОВЫХ И ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ ГРУПП ТИПОВЫХ ЗВЕНЬЕВ
- 11. ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ВИДА ПЕРЕДАТОЧНЫХ ФУНКЦИЙ И ПАРАМЕТРОВ ГРУПП ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
- ГЛАВА XI. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ
- 2. ОПРЕДЕЛЕНИЕ ФУНКЦИЙ ЛЯПУНОВА МЕТОДАМИ Г. СЕГЕ И Д. ШУЛЬЦА
- 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 5. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 6. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ТРАНСЦЕНДЕНТНЫМИ ЗВЕНЬЯМИ
- 9. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ С ПОМОЩЬЮ D-РАЗБИЕНИЯ
- Глава XII. ИССЛЕДОВАНИЕ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
- 2. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПО ЗАДАННЫМ ПЕРЕДАТОЧНЫМ ФУНКЦИЯМ ЗАМКНУТЫХ СИСТЕМ
- 3. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПО РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ ЛЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ
- 4. МЕТОД КОРНЕВОГО ГОДОГРАФА
- 5. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА
- 6. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ СИСТЕМ РЕГУЛИРОВАНИЯ И ИХ СВЯЗЬ С ХАРАКТЕРИСТИКАМИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 7. ОПРЕДЕЛЕНИЕ ВЕЩЕСТВЕННЫХ И МНИМЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СИСТЕМ ПО АМПЛИТУДНО-ФАЗОВЫМ И ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ РАЗОМКНУТЫХ СИСТЕМ
- 8. ЧАСТОТНЫЕ ОЦЕНКИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 9. ЧАСТОТНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ТРАПЕЦЕИДАЛЬНЫХ ХАРАКТЕРИСТИК
- 10. УСТАНОВЛЕНИЕ НОРМ ЗАПАСОВ УСТОЙЧИВОСТИ ПО ФАЗЕ И МОДУЛЮ, ОБЕСПЕЧИВАЮЩИХ ТРЕБУЕМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМ РЕГУЛИРОВАНИЯ
- ГЛАВА XIII. ДИНАМИЧЕСКАЯ ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ОШИБОК В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ АМПЛИТУДНЫХ ХАРАКТЕРИСТИК
- 3. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПУТЕМ ПРИМЕНЕНИЯ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ
- 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 5. СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ СТАЦИОНАРНЫХ ПРОЦЕССОВ
- 6. СВОЙСТВА СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ
- 7. ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ
- 8. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЛИНЕЙНЫМИ СИСТЕМАМИ
- 9. РАСЧЕТ ОШИБОК В СИСТЕМЕ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ШУМОВ
- 10. ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ВОЗДЕЙСТВИИ СЛУЧАЙНЫХ СИГНАЛОВ И ШУМОВ
- ГЛАВА XIV. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ТИПОВЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ ПО ВТОРОМУ МЕТОДУ ЛЯПУНОВА
- 3. АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
- 4. ПРИМЕНЕНИЕ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
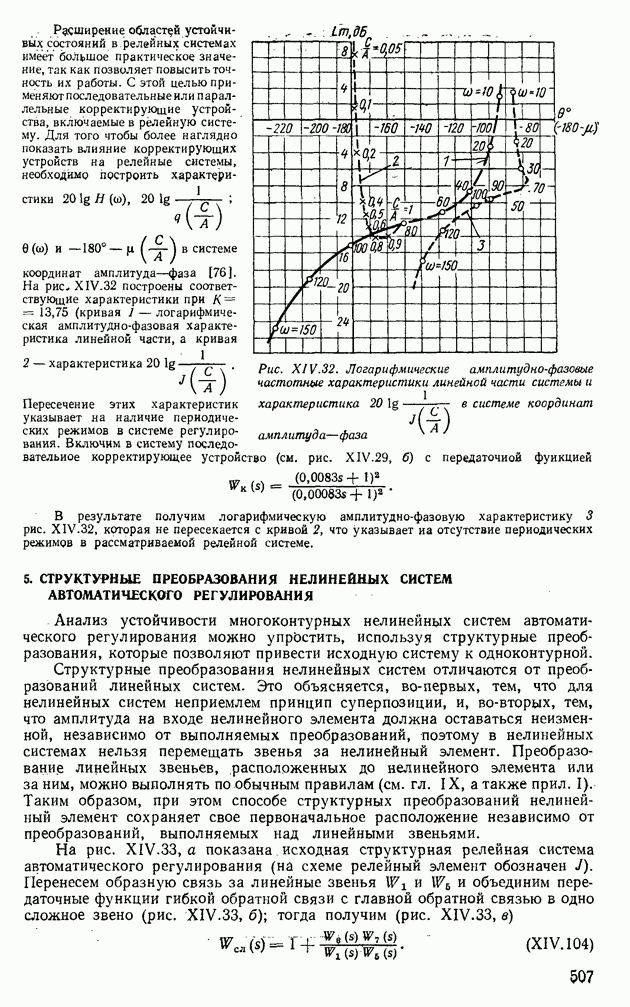
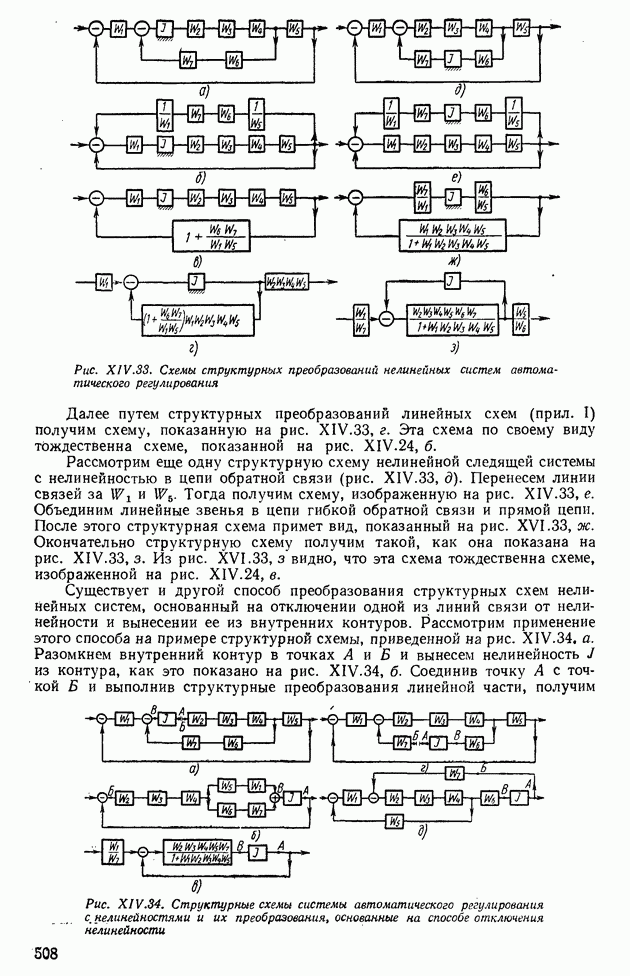
- 5. СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. АНАЛИЗ АВТОКОЛЕБАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДВУМЯ НЕЛИНЕЙНОСТЯМИ
- 7. ДВУХКОНТУРНЫЕ НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕДЛЕННО ИЗМЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
- 9. СПОСОБЫ ПОДАВЛЕНИЯ АВТОКОЛЕБАНИЙ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 10. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 11. КРИТЕРИЙ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
- 12. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- Глава XIV. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ИМПУЛЬСНЫХ УСТРОЙСТВ
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. АМПЛИТУДНО-ФАЗОВЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ СИСТЕМ
- 4. ПРИМЕНЕНИЕ ВЕКТОРНО-МАТРИЧНОГО АППАРАТА К ИМПУЛЬСНЫМ СИСТЕМАМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ОСНОВНЫЕ СВОЙСТВА z-ПРЕОБРАЗОВАНИЯ
- 6. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Критерий устойчивости для импульсных систем на плоскостях z и W(z).
- Критерий устойчивости Шур—Кона.
- Критерии устойчивости, основанные на применении билинейного преобразования.
- 7. МЕТОДЫ АНАЛИЗА КАЧЕСТВА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕТОДЫ АНАЛИЗА ТОЧНОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 9. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С УПРАВЛЯЮЩИМИ ЦВМ
- 10. СПОСОБЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ В УПРАВЛЯЮЩИХ ЦВМ И ОПРЕДЕЛЕНИЕ ИХ ОСНОВНЫХ ПАРАМЕТРОВ
- Глава XVI. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МЕТОДЫ ПОИСКА ЭКСТРЕМУМА
- 2. СПОСОБЫ ОРГАНИЗАЦИИ ДВИЖЕНИЯ К ЭКСТРЕМУМУ
- 3. МЕТОДЫ РАСЧЕТА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРОВ
- 4. ВЫБОР КОРРЕКТИРУЮЩИХ УСТРОЙСТВ В ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРАХ
- 5. ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ С ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ
- Глава XVII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ ВОЗДЕЙСТВИЯХ
- 2. ВЫБОР ПАРАМЕТРОВ УСТРОЙСТВ НЕИЗМЕНЯЕМОЙ ЧАСТИ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ПОСТРОЕНИЕ ЖЕЛАЕМОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 4. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. СИНТЕЗ ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 6. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 7. СПОСОБЫ РЕАЛИЗАЦИИ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Глава XVIII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 1. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА НА ОСНОВЕ КРИТЕРИЯ МИНИМУМА ИНТЕГРАЛЬНОЙ ОШИБКИ
- 2. СИНТЕЗ СИСТЕМ РЕГУЛИРОВАНИЯ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЖЕЛАЕМОЙ СИСТЕМЫ
- 4. ПРИМЕР СИНТЕЗА КОРРЕКТИРУЮЩИХ УСТРОЙСТВ СИСТЕМЫ РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- ГЛАВА XIX. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИНТЕЗ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ, ОСНОВАННЫЙ НА ПРИМЕНЕНИИ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- 2. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. РЕАЛИЗАЦИЯ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ ПРИ ПОМОЩИ RC-ЦЕПЕЙ
- 4. РЕАЛИЗАЦИЯ ПРОГРАММ КОРРЕКЦИИ НА УПРАВЛЯЮЩЕЙ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- ГЛАВА XX. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ПРИНЦИП МАКСИМУМА
- 3. ТЕОРЕМА О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
- 4. ПРИМЕРЫ ПРИМЕНЕНИЯ ПРИНЦИПА МАКСИМУМА
- 5. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 6. СИНТЕЗ НЕПРЕРЫВНЫХ ОПТИМАЛЬНЫХ СИСТЕМ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ