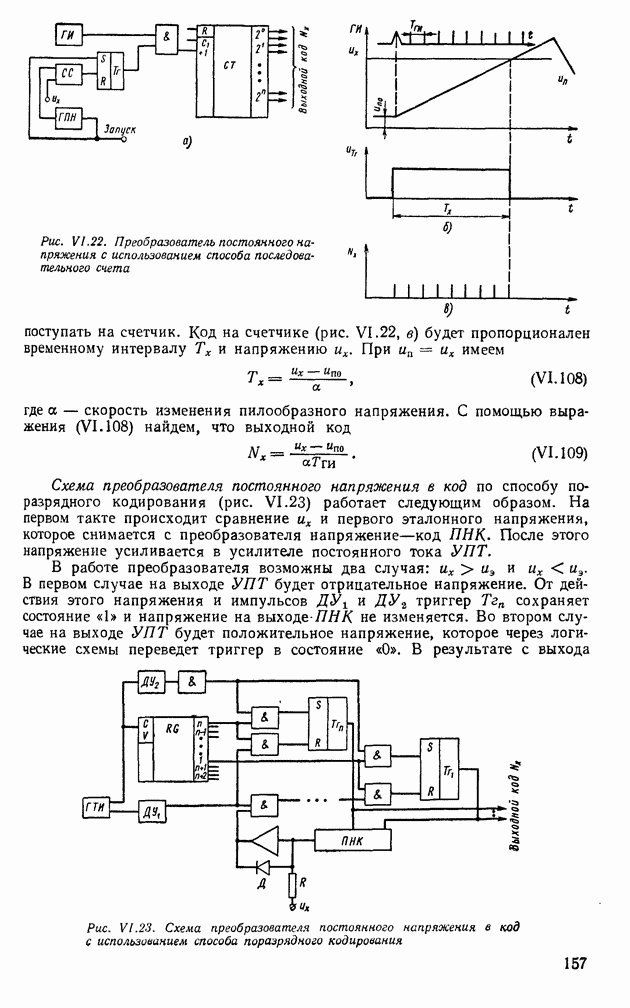
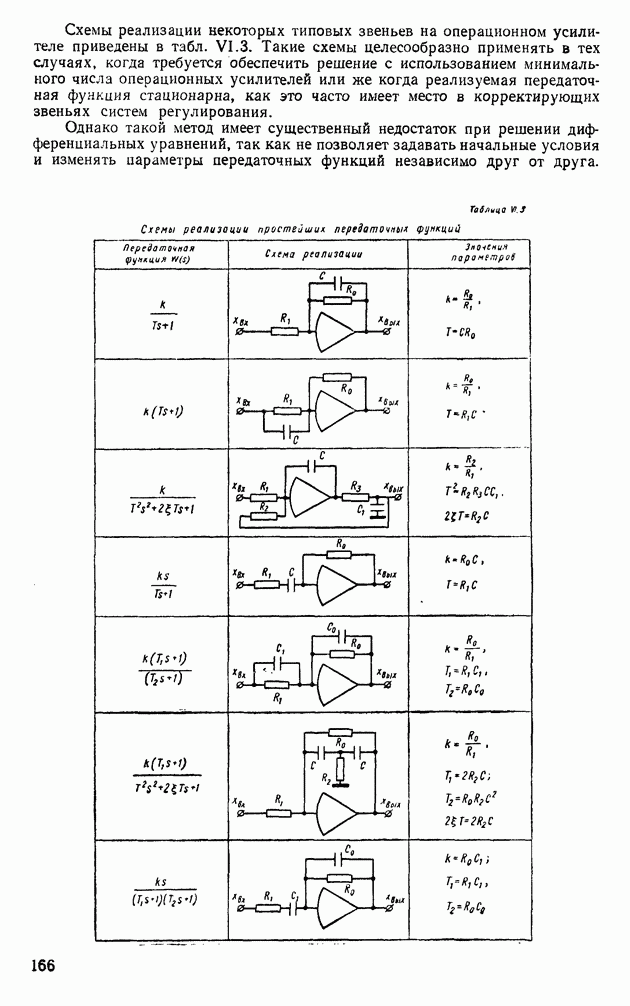
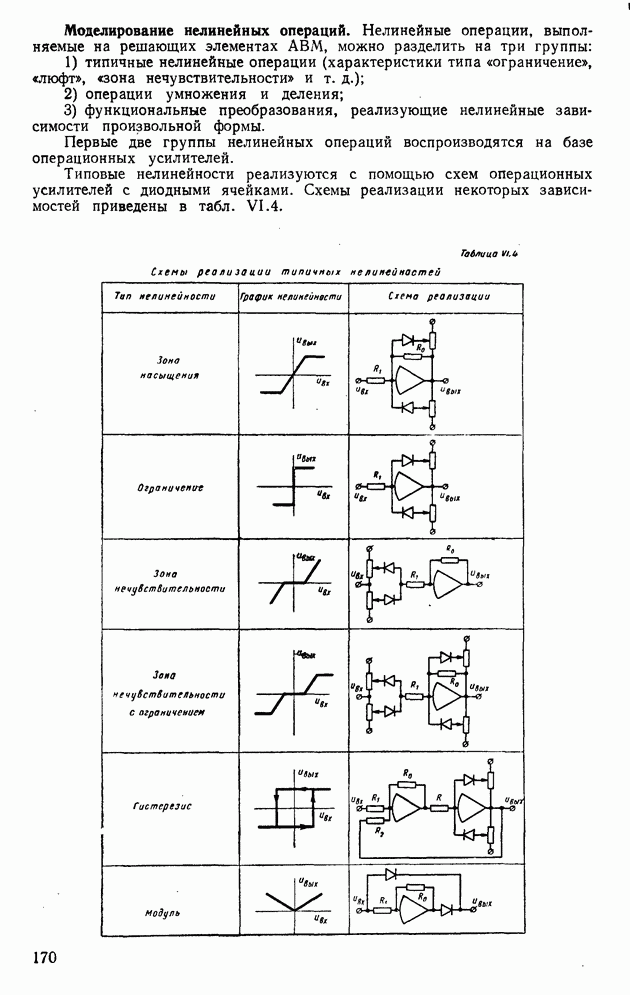
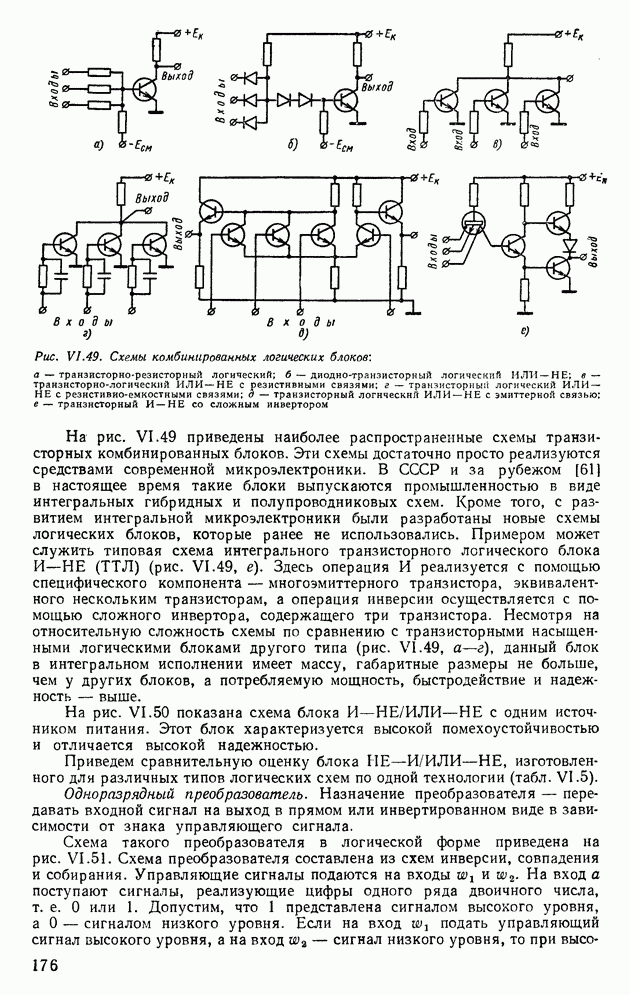
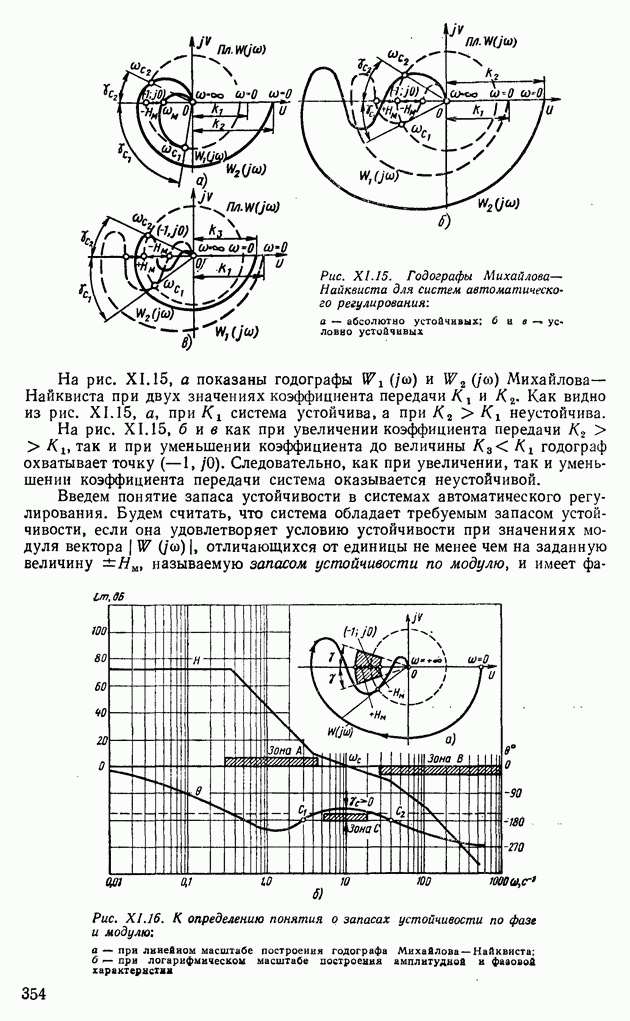
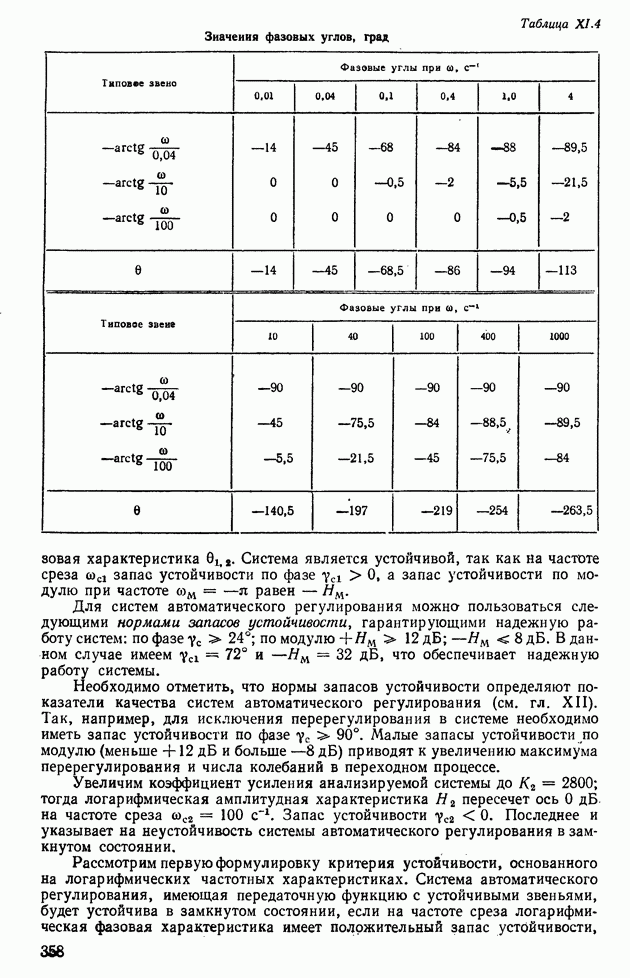
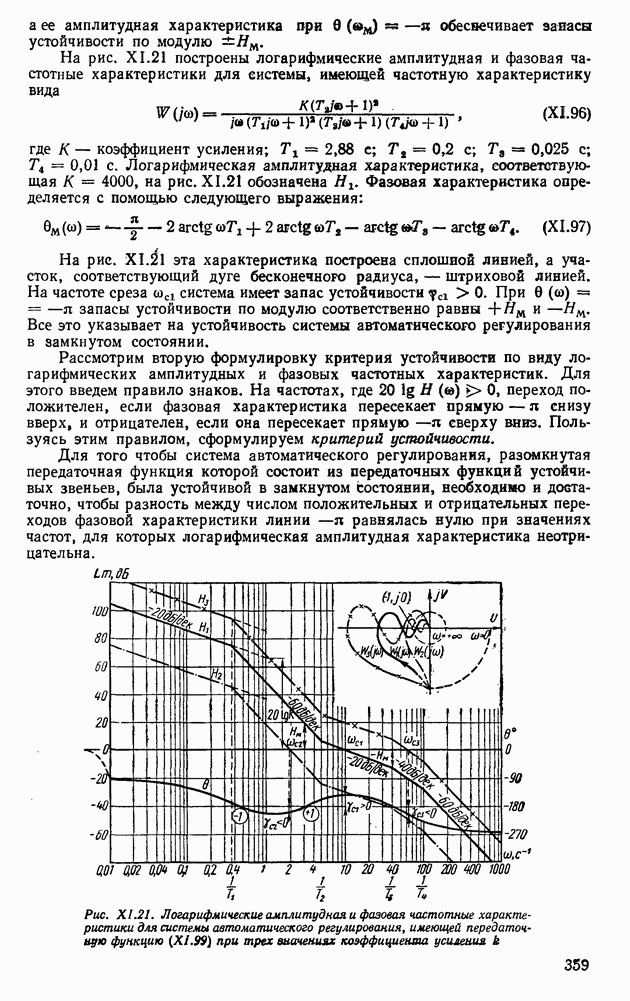
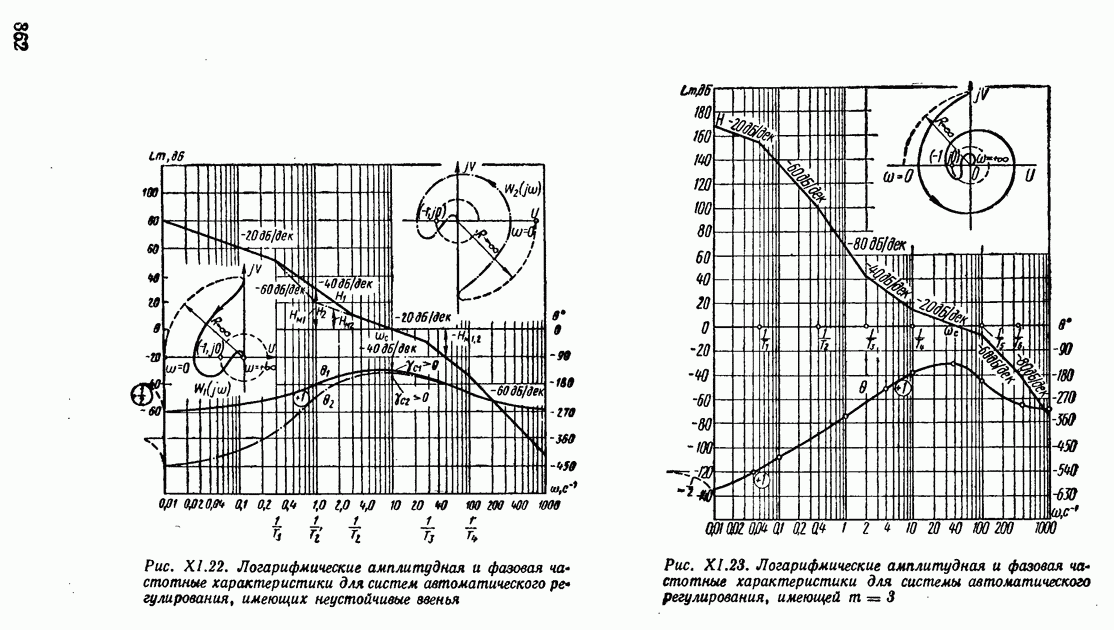
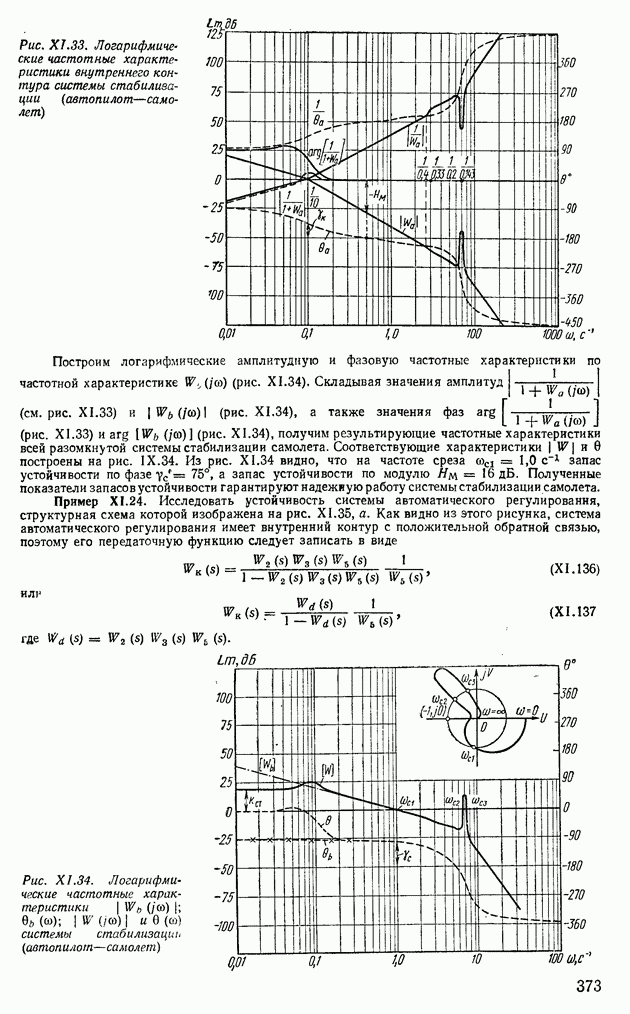
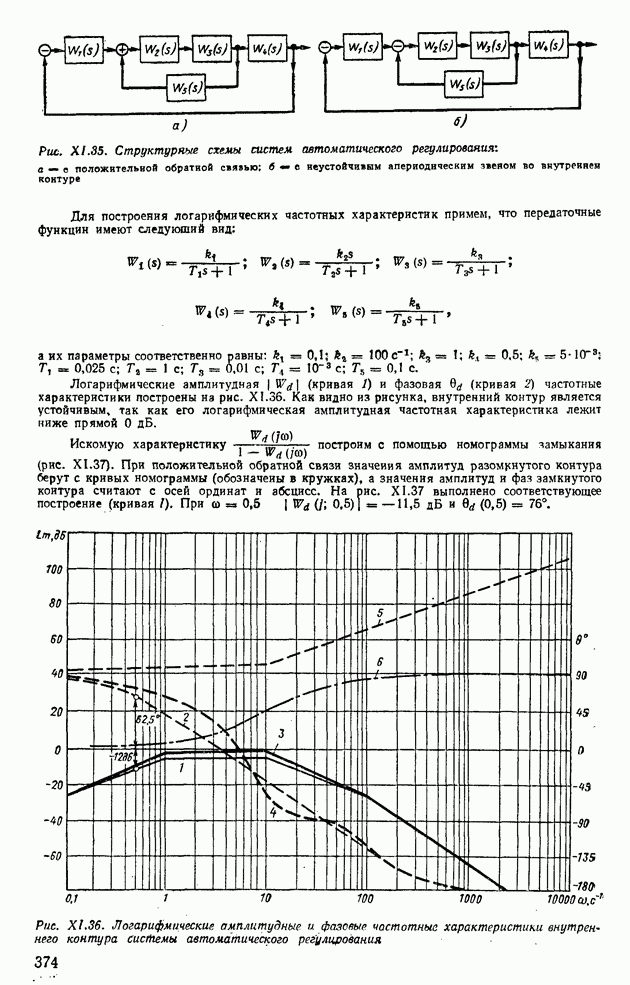
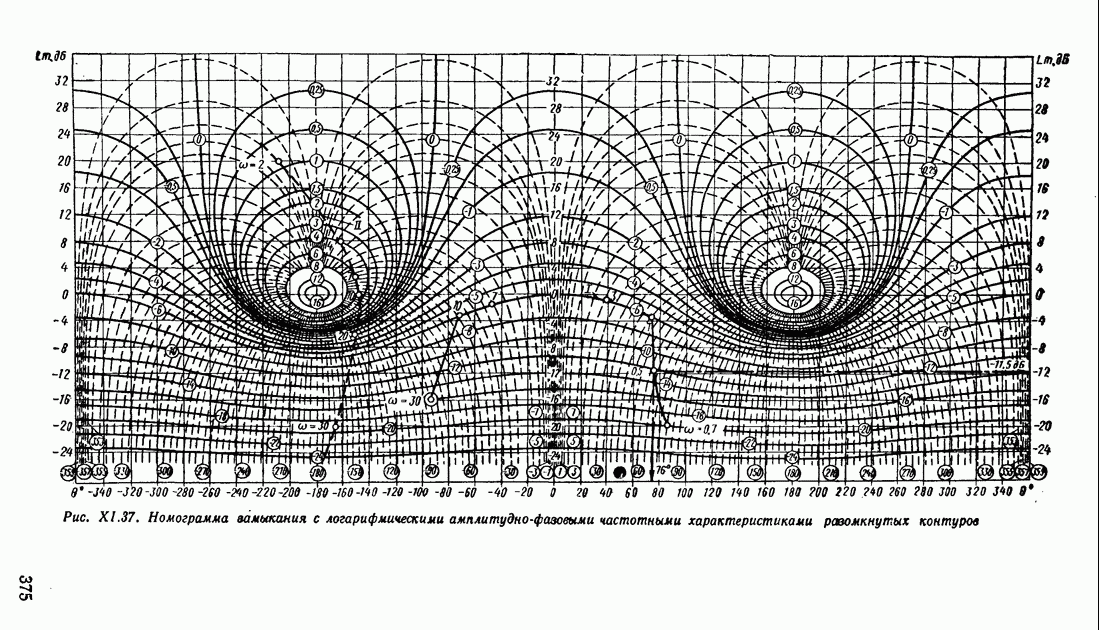
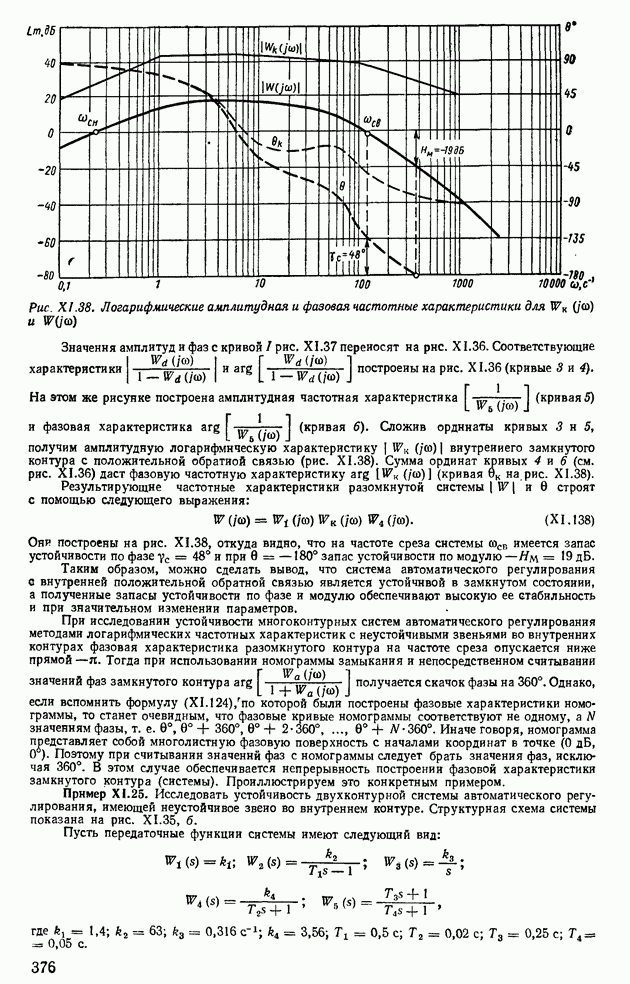
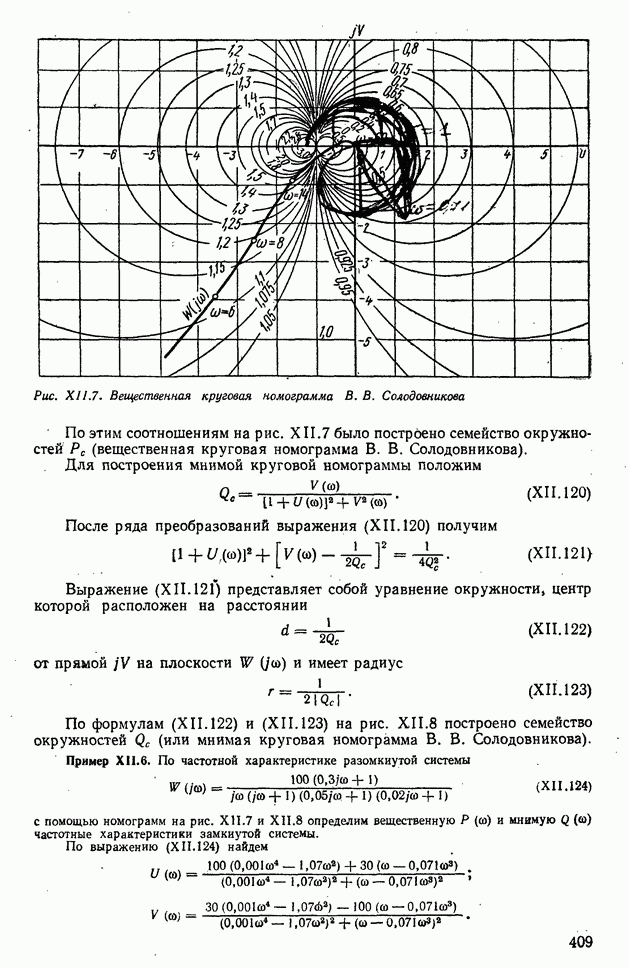
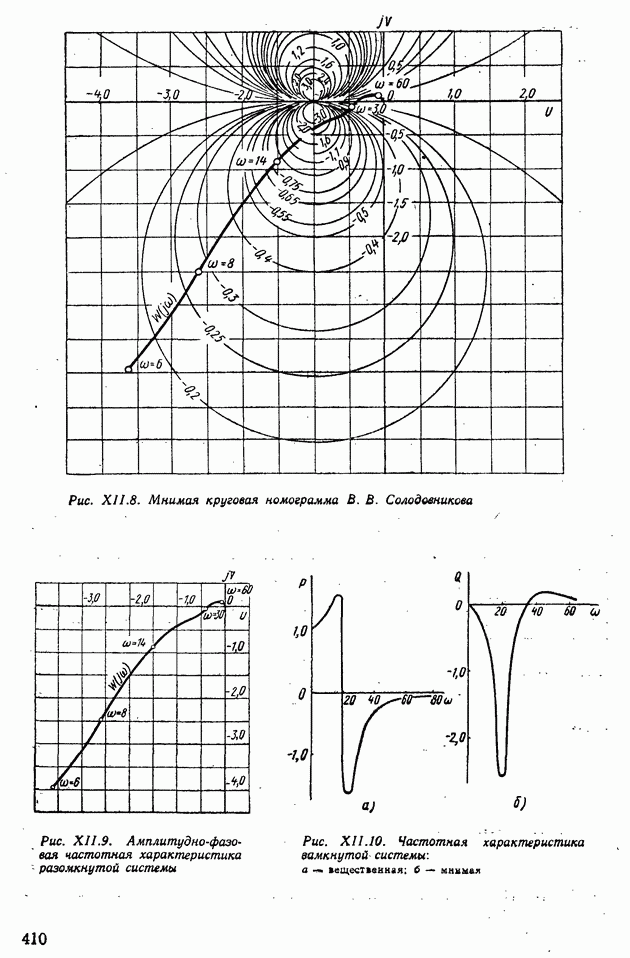
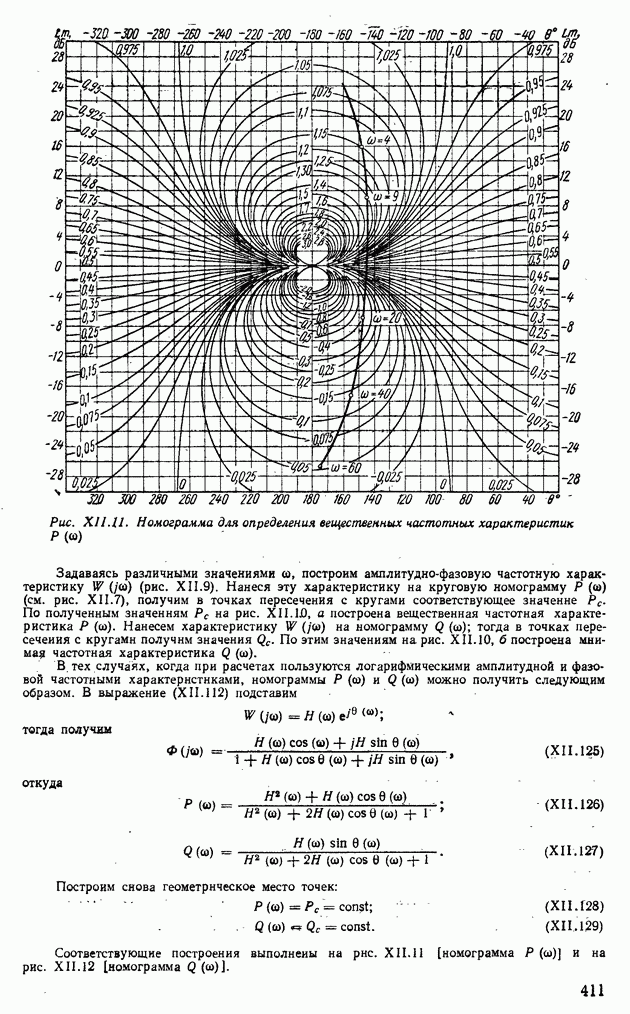
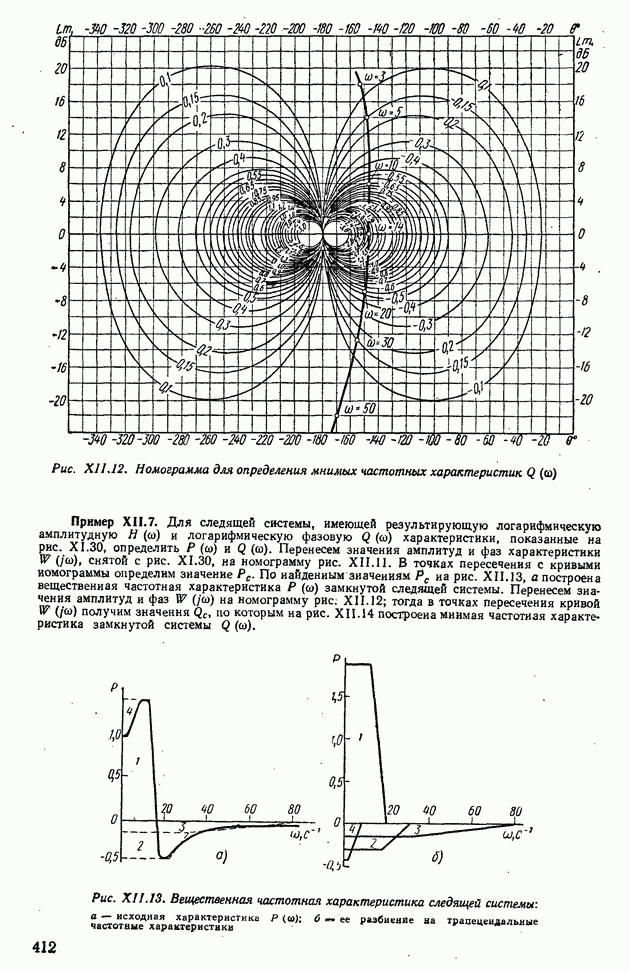
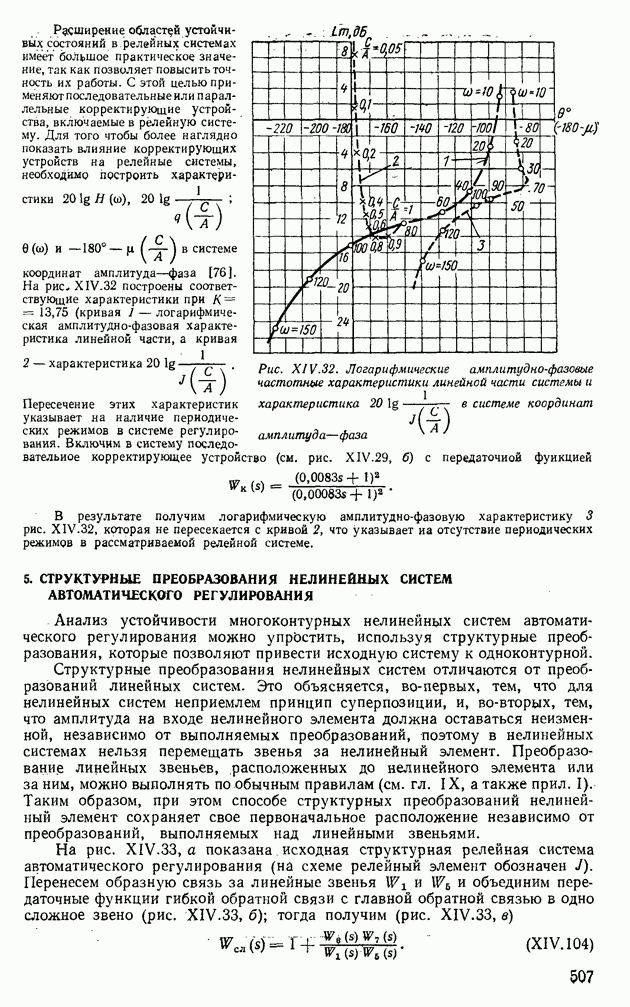
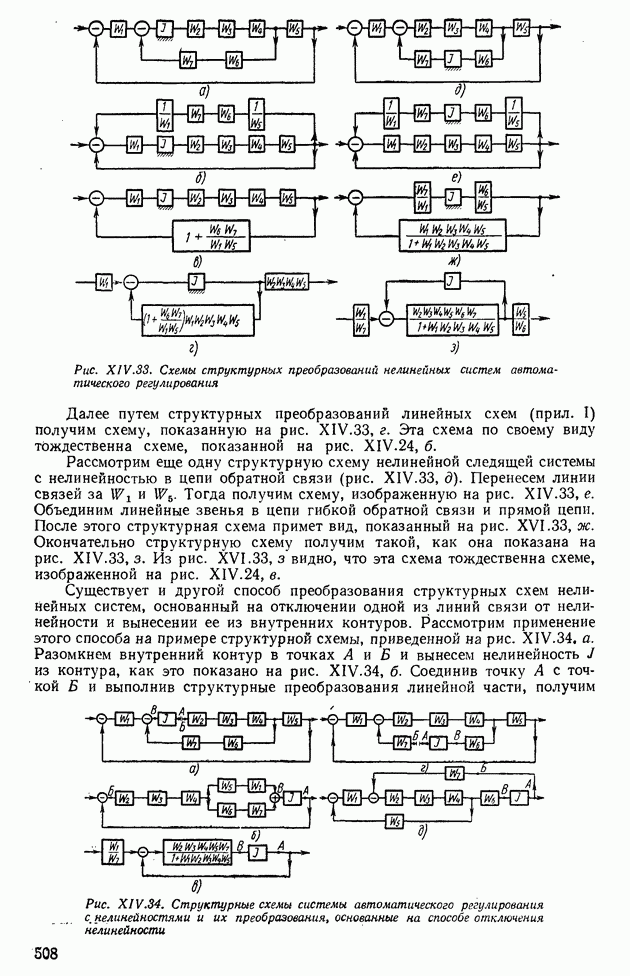
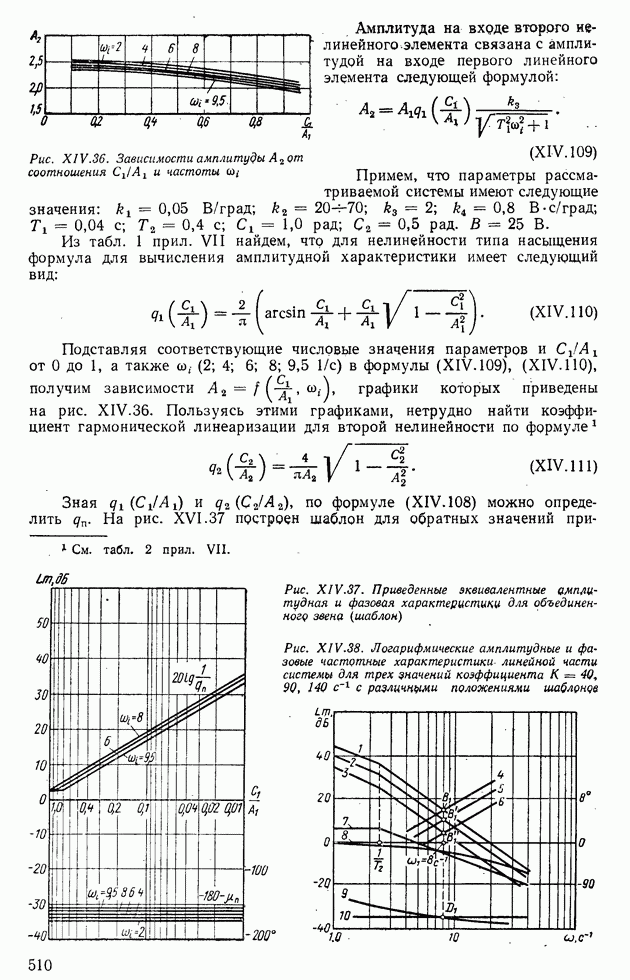
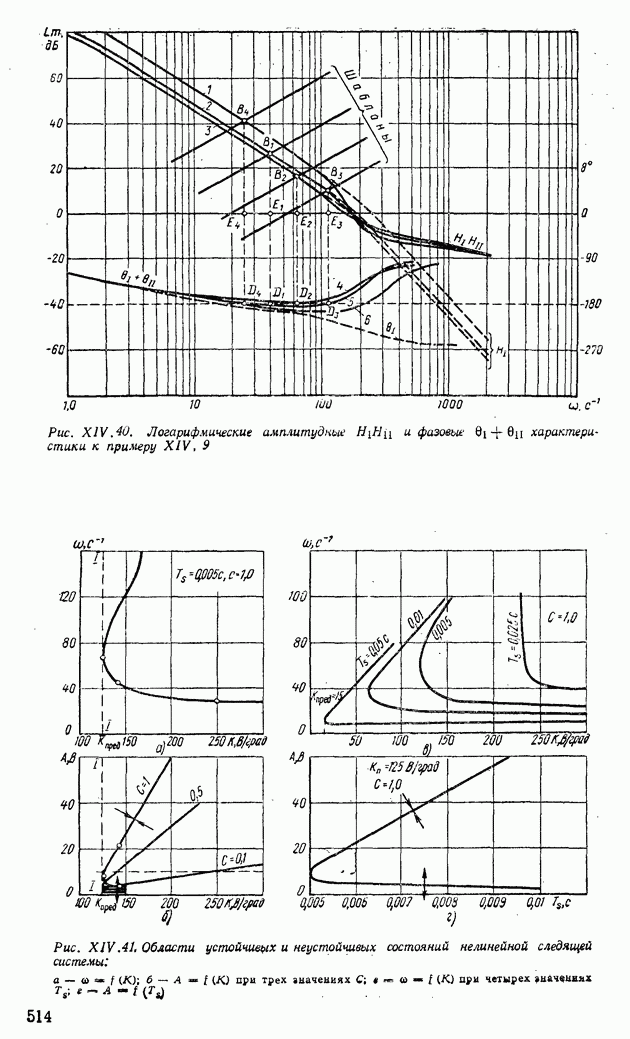
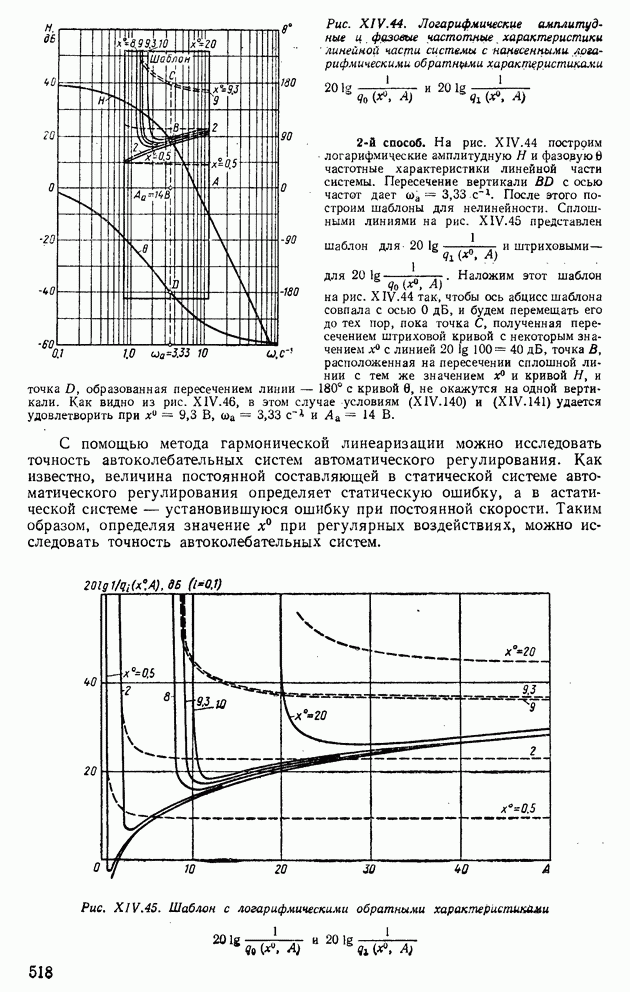
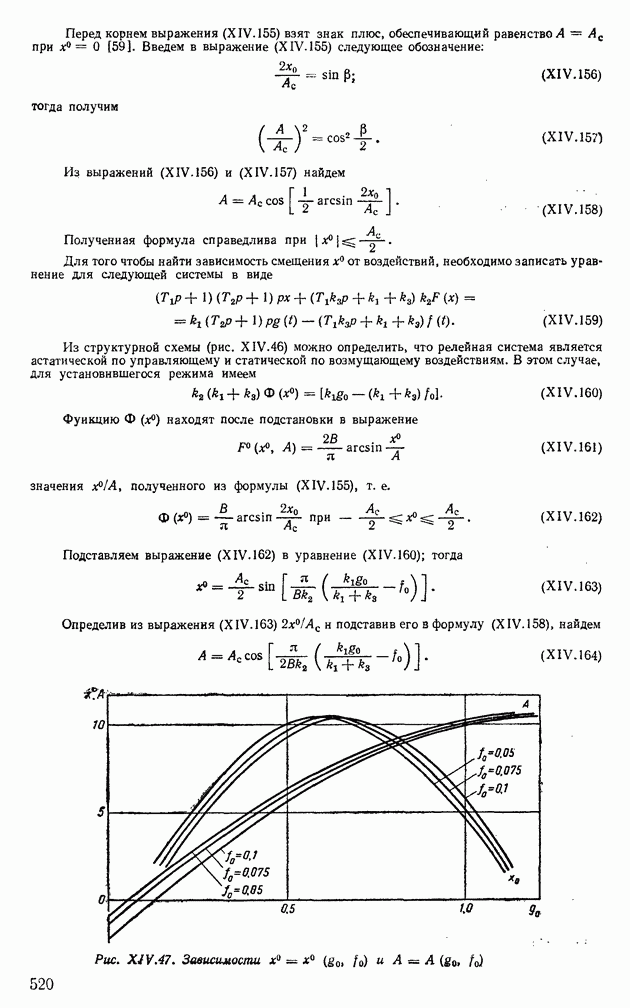
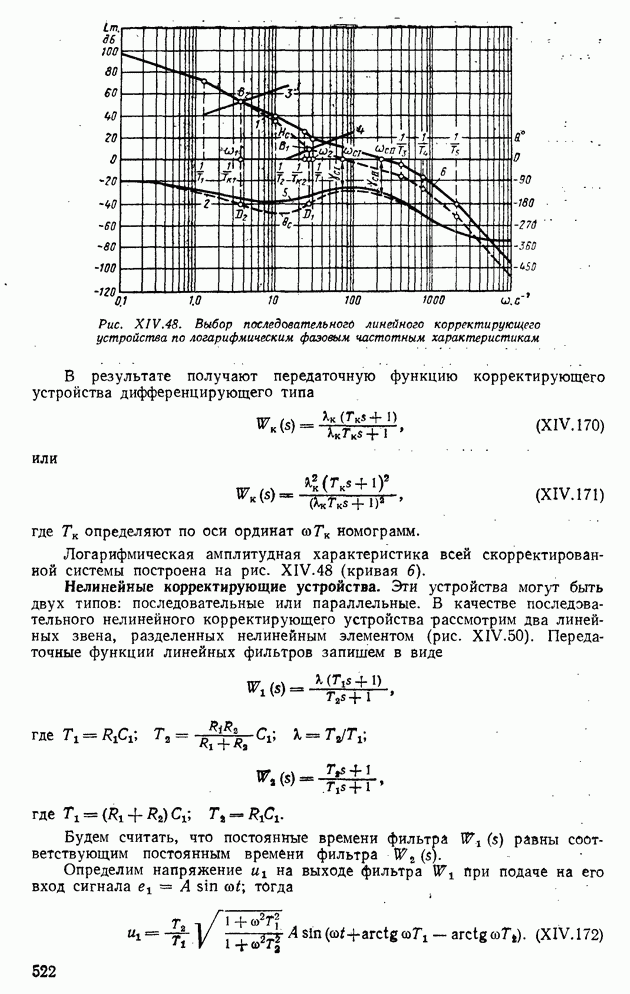
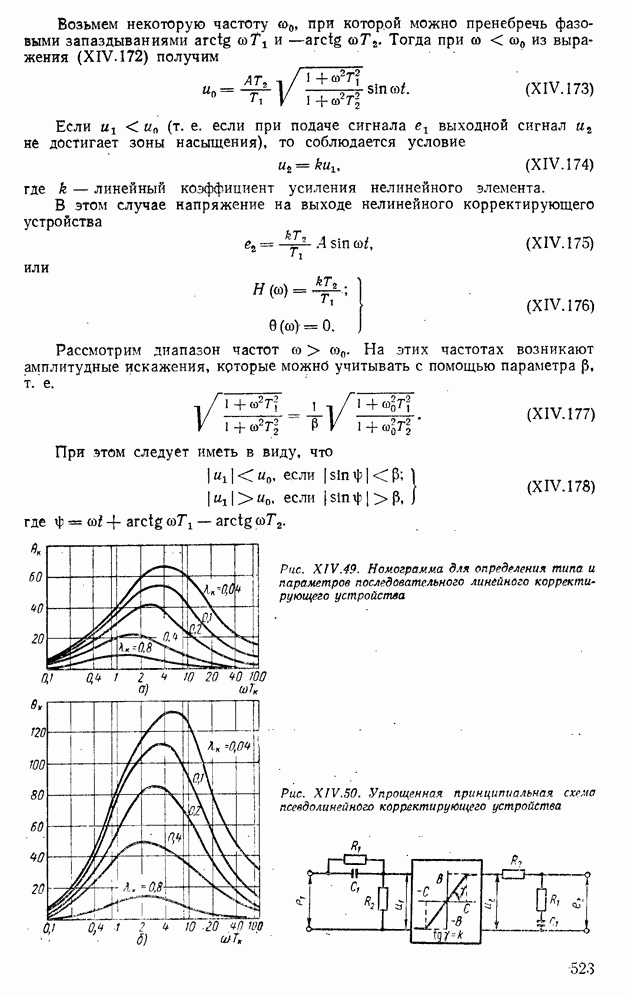
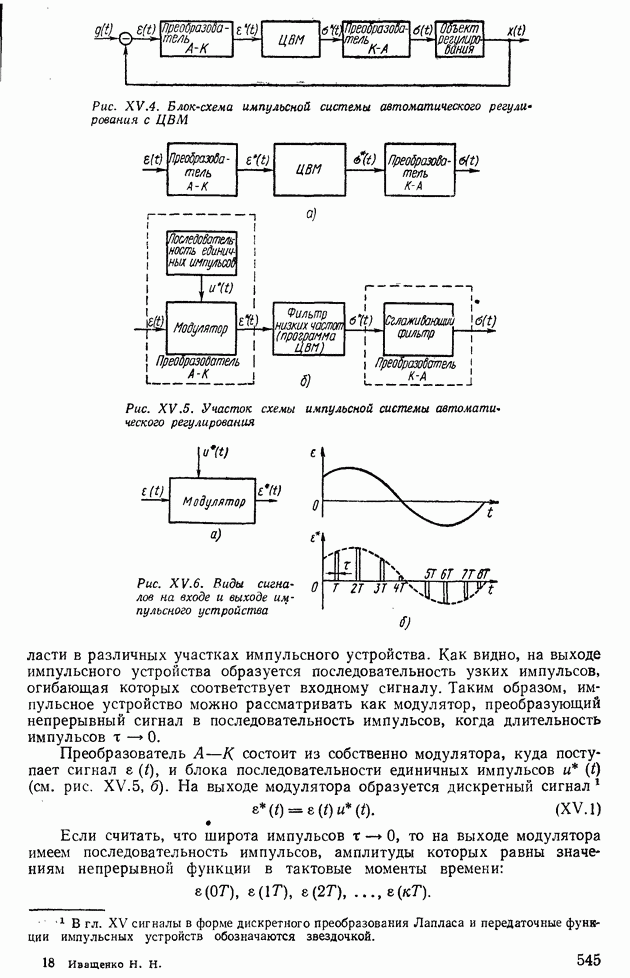
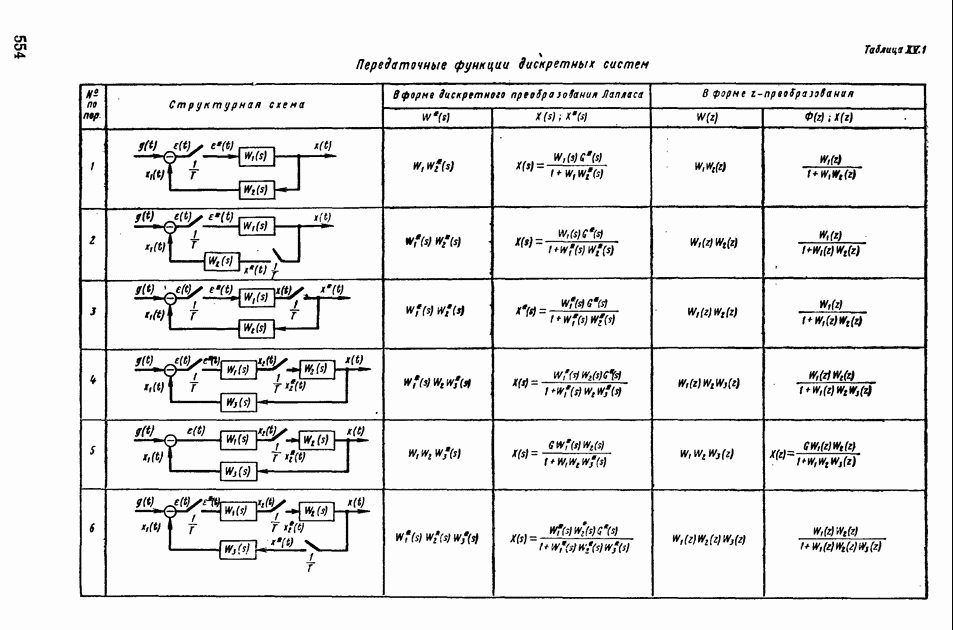
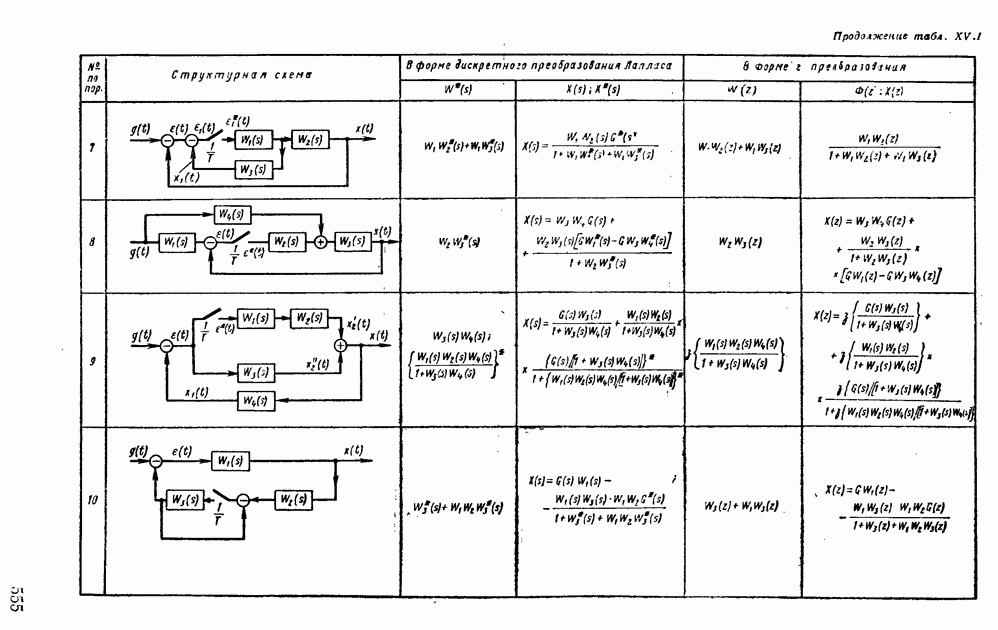
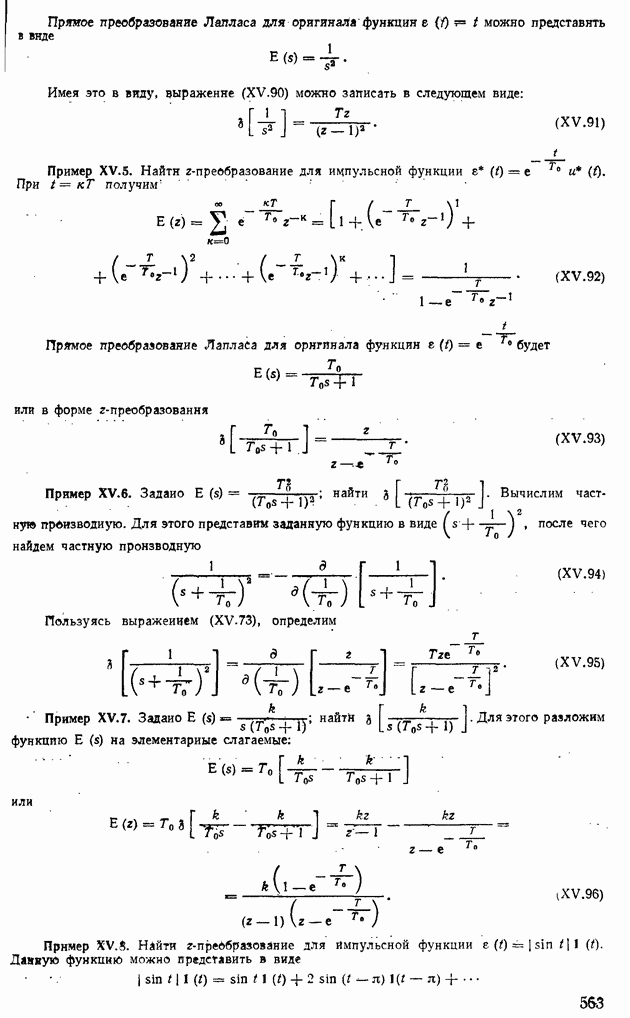
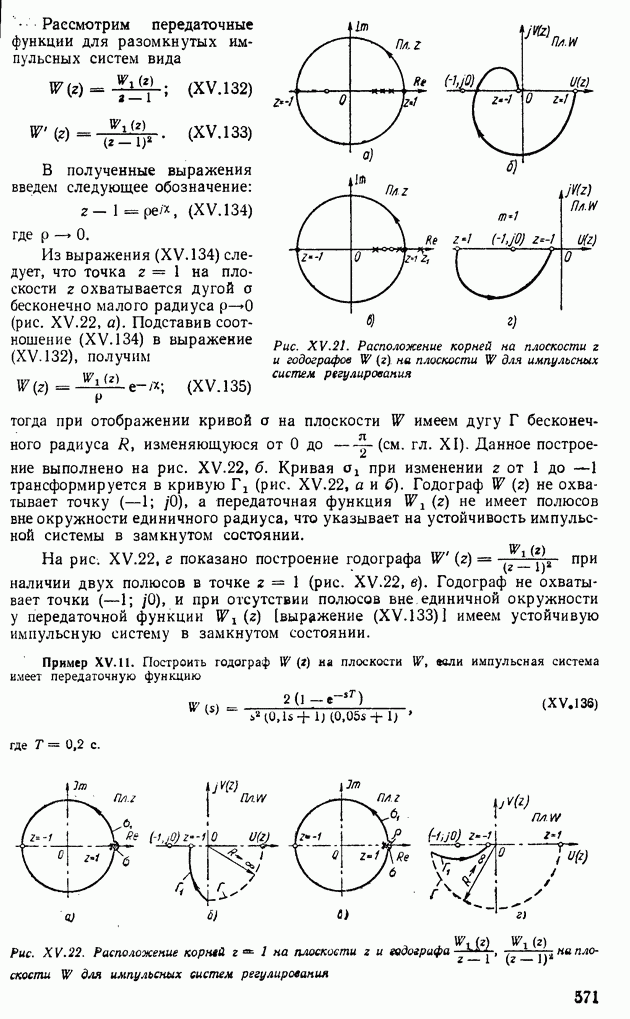
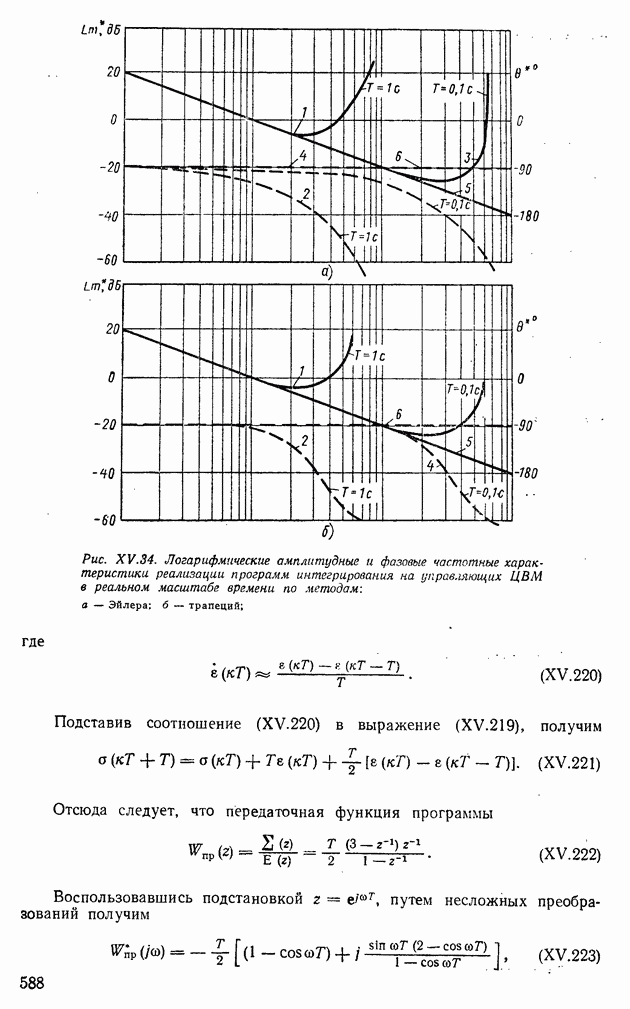
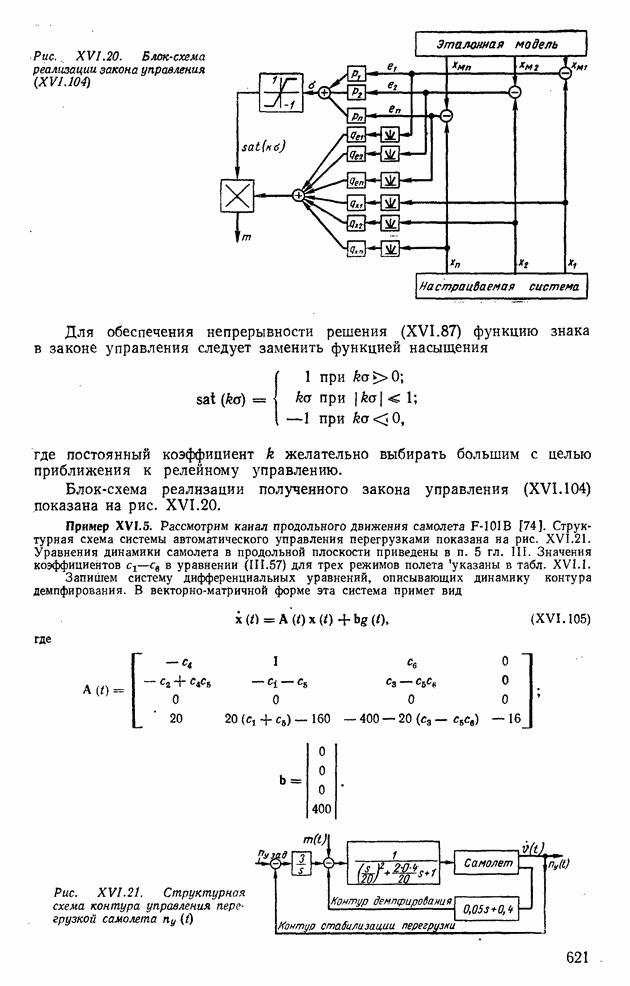
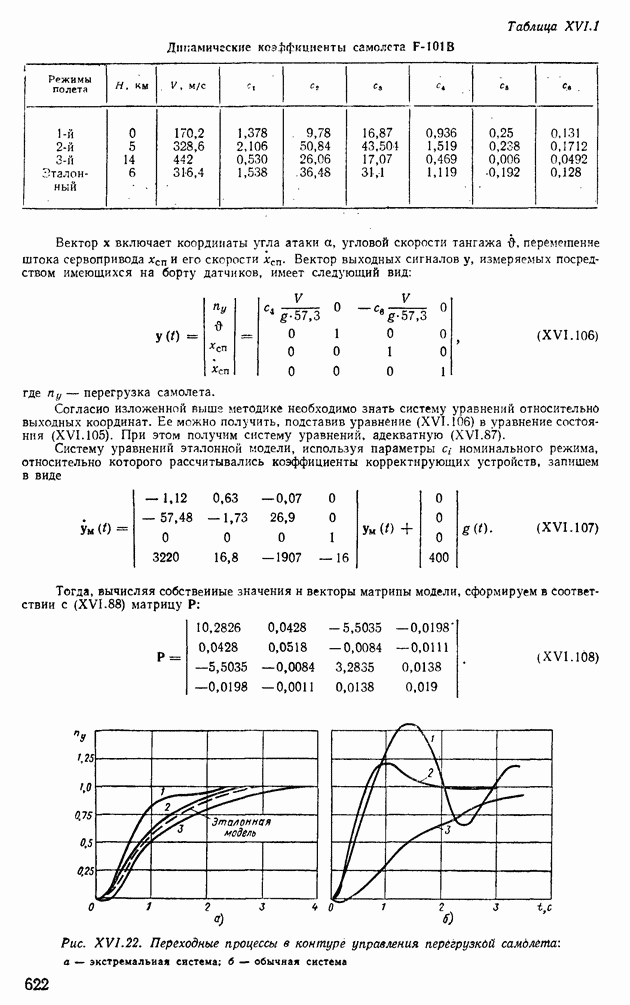
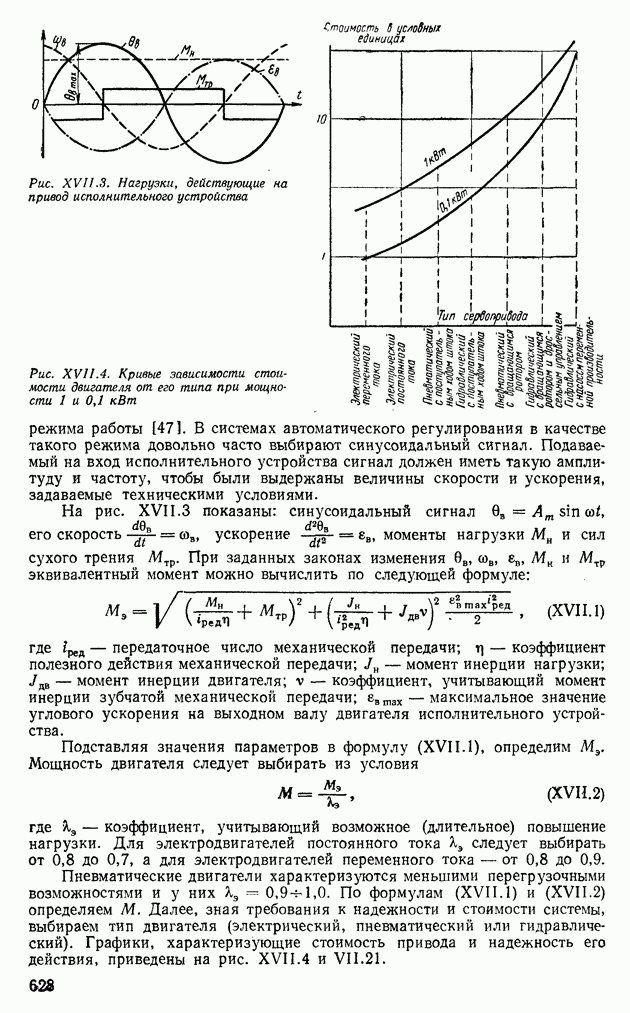
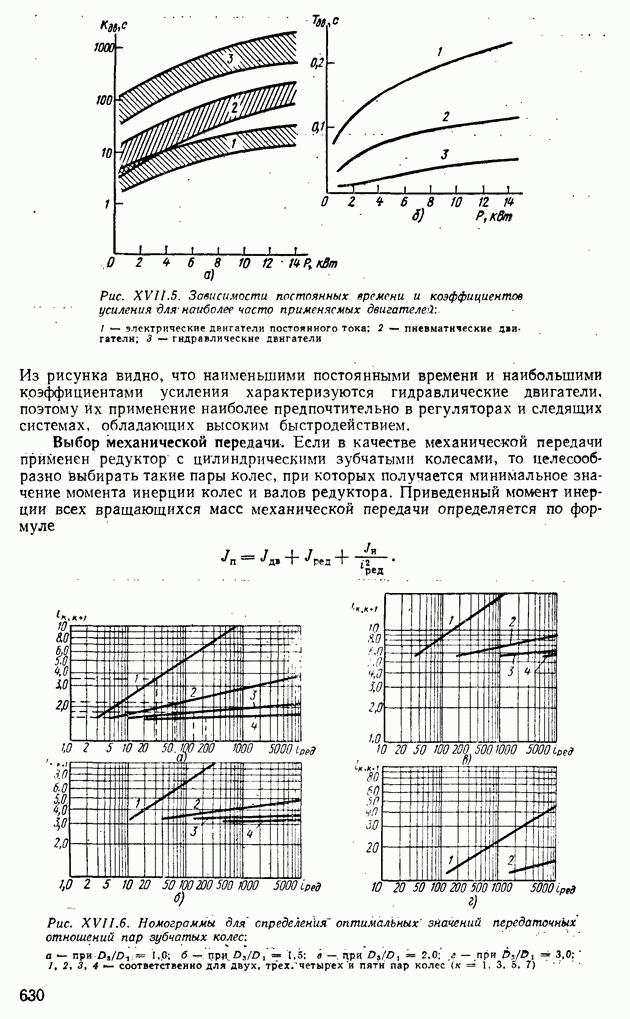
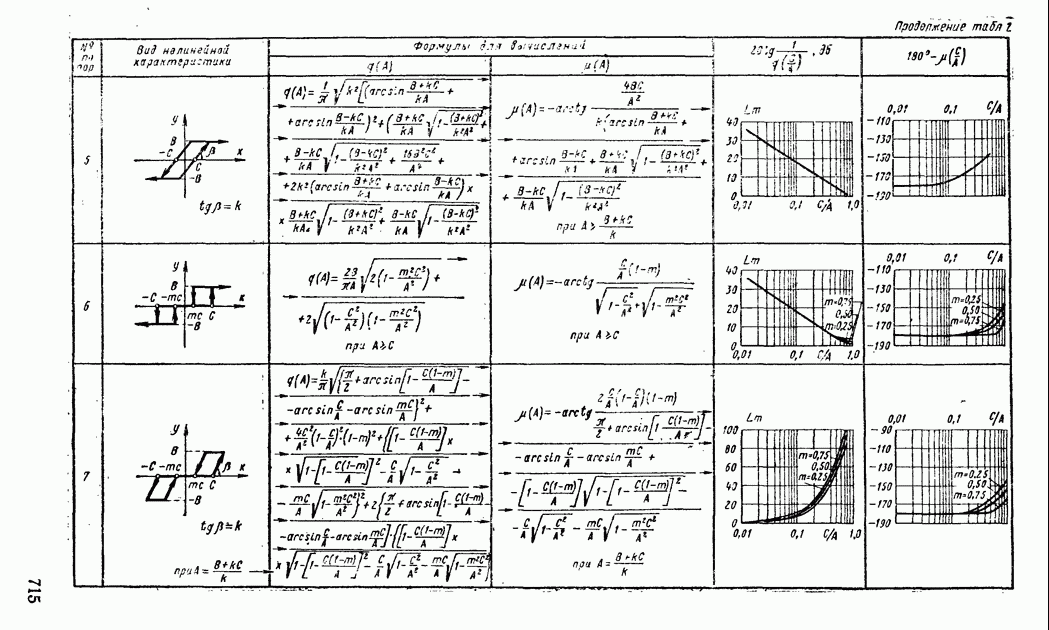
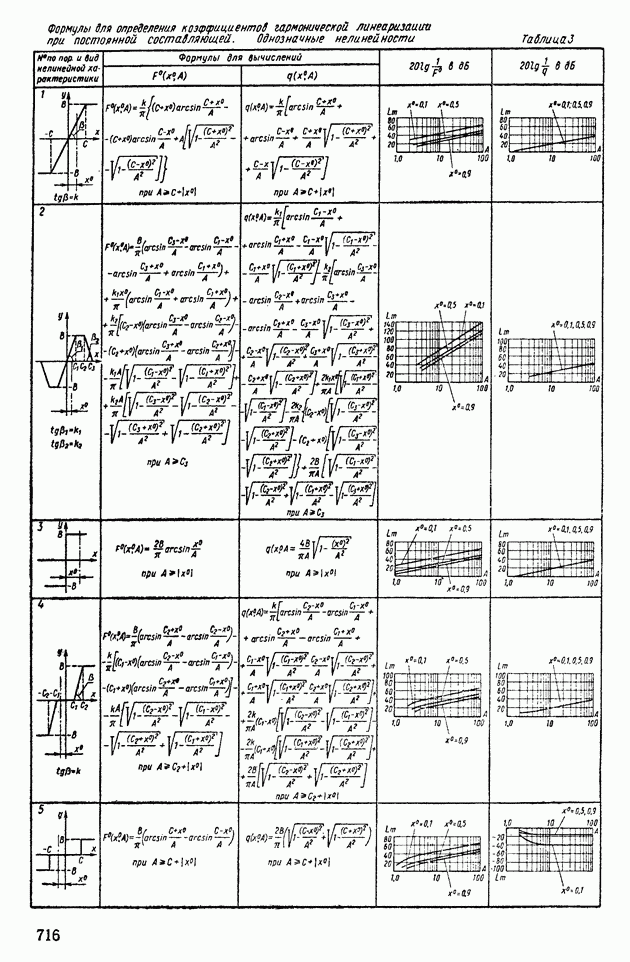
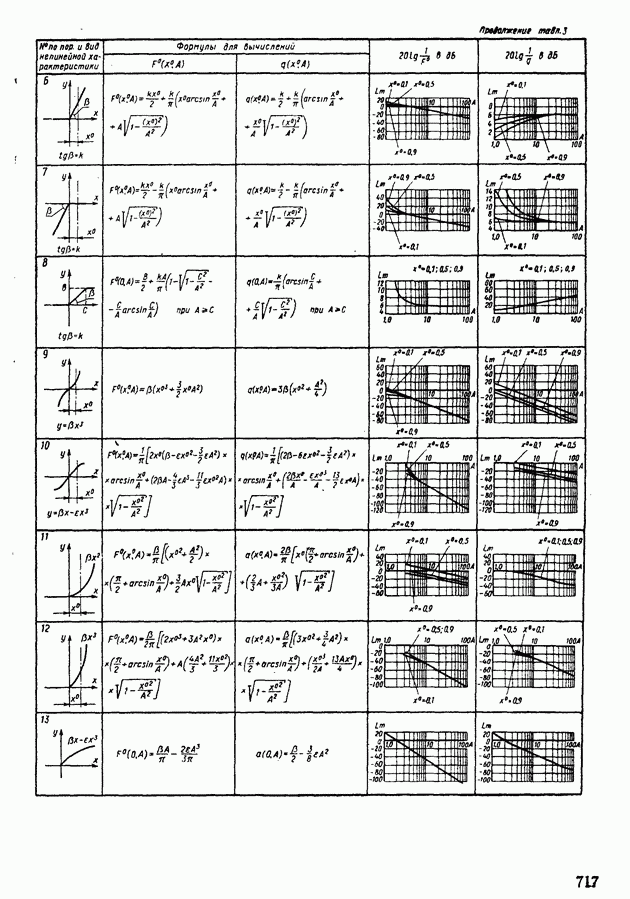
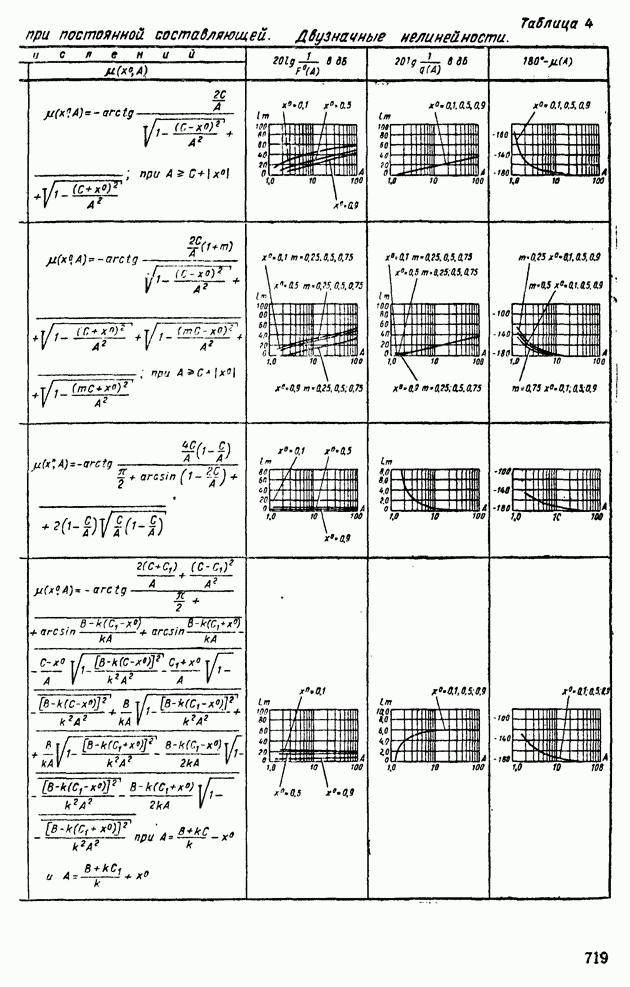
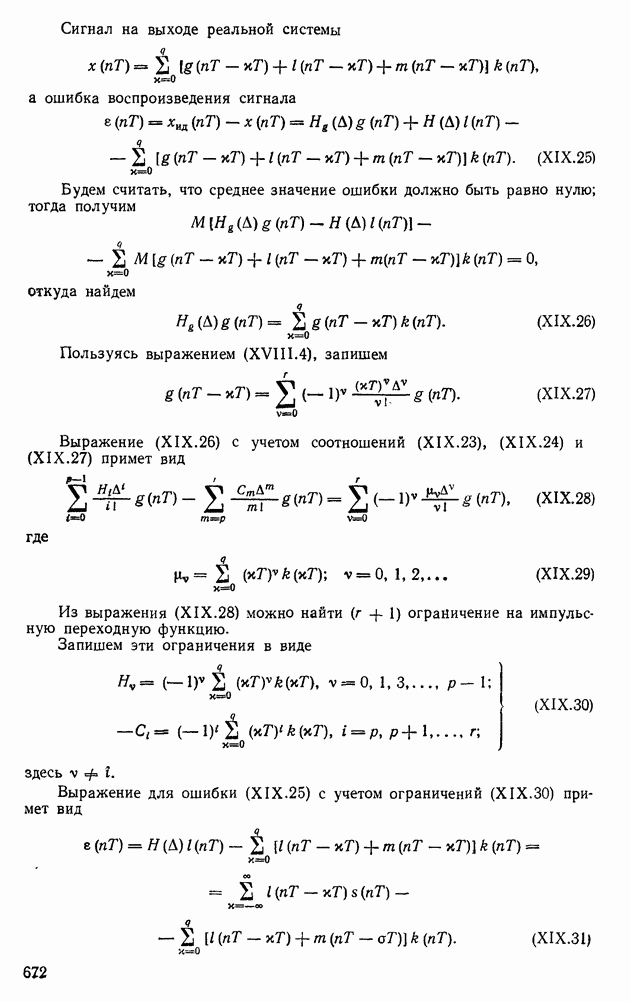| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
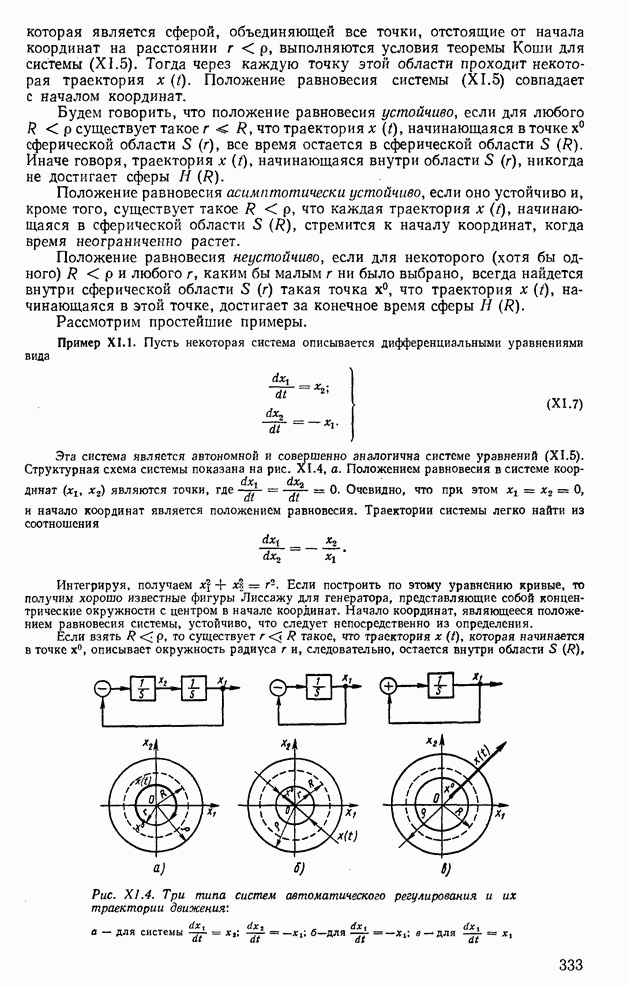
Рассмотрим частный случай автономной системы (XI.5), а именно линейную систему, которая описывается уравнениями

или в матричной форме записи

где

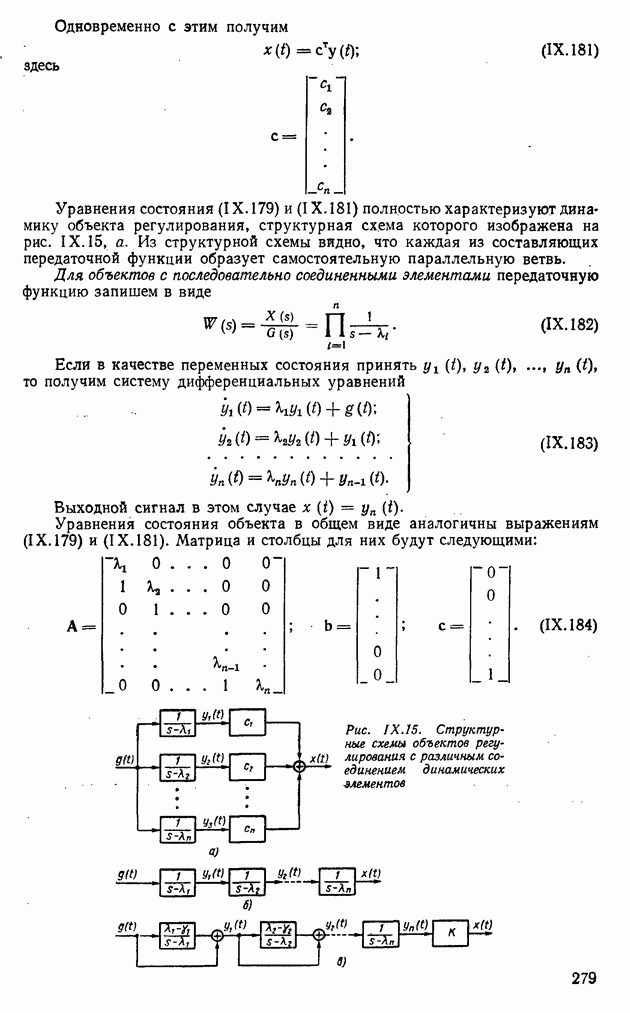
Для того чтобы проанализировать устойчивость, введем функцию Ляпунова в виде положительно определенной квадратичной формы  [см. формулу (XI.14)]. Найдем производную этой функции с учетом уравнений (XI.49):
[см. формулу (XI.14)]. Найдем производную этой функции с учетом уравнений (XI.49):

Введем обозначение

Если матрица  положительно определенная,
положительно определенная,  когда
когда  т. е. происходит убывание функции V, а следовательно, траектории системы стремятся к началу координат. Итак, если одновременно выполняются неравенства
т. е. происходит убывание функции V, а следовательно, траектории системы стремятся к началу координат. Итак, если одновременно выполняются неравенства  в некоторой области пространства переменных
в некоторой области пространства переменных  включающей начало координат, то положение равновесия в начале координат асимптотически устойчиво.
включающей начало координат, то положение равновесия в начале координат асимптотически устойчиво.
Теорема Ляпунова об асимптотической устойчивости. Для того чтобы нулевое решение автономной линейной системы (XI.49) было асимптотически устойчиво, необходимо и достаточно, чтобы для произвольной положительно определенной матрицы  существовала положительно определенная матрица Р, удовлетворяющая уравнению (XI.51). Отметим, что обе матрицы Р и
существовала положительно определенная матрица Р, удовлетворяющая уравнению (XI.51). Отметим, что обе матрицы Р и  являются симметрическими. Действительно, если матрица Р симметрическая, т. е.
являются симметрическими. Действительно, если матрица Р симметрическая, т. е.  то
то

и, следовательно, матрица  симметрическая. Справедливо и обратное.
симметрическая. Справедливо и обратное.
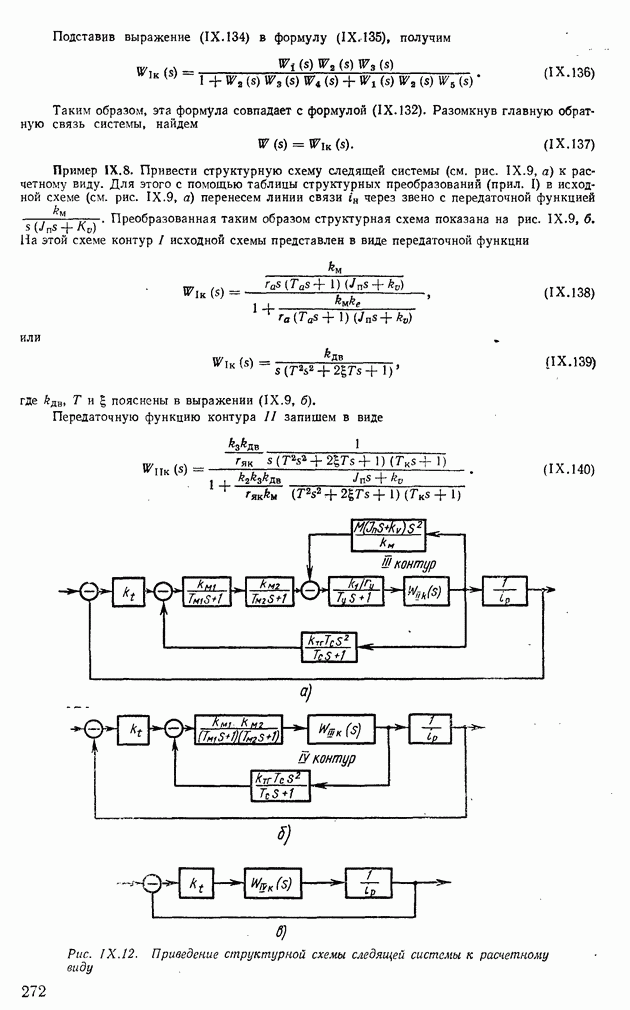
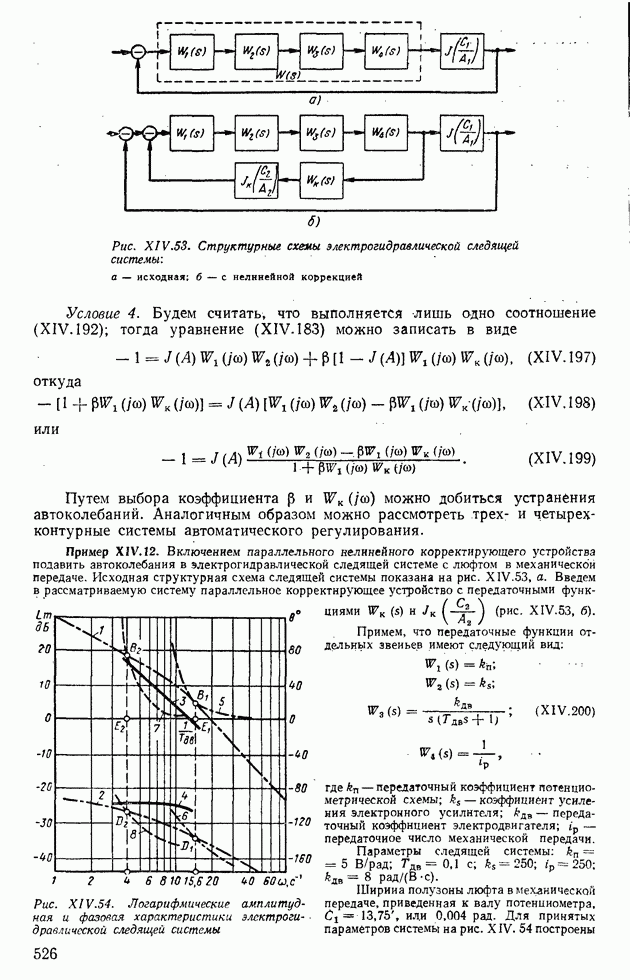
Пример XI.9. Используя теорему Ляпунова, проанализируем устойчивость системы, структурная схема которой показана на рис. XI.7, б. Ей соответствует система уравнений

В теореме фигурирует произвольная положительно определенная матрица  выберем в качестве последней единичную матрицу. Тогда уравнение (XI.60) принимает вид
выберем в качестве последней единичную матрицу. Тогда уравнение (XI.60) принимает вид

Поскольку матрица  симметрическая, то матрица Р также симметрическая, т. е.
симметрическая, то матрица Р также симметрическая, т. е.  Составим из матричного уравнения (XI.51) три уравнения с тремя неизвестными для определения элементов
Составим из матричного уравнения (XI.51) три уравнения с тремя неизвестными для определения элементов 

или

Решая последнюю систему, находим 
Полученная матрица  является положительно определенной. Следовательно, рассматриваемая линейная автономная система асимптотически устойчива.
является положительно определенной. Следовательно, рассматриваемая линейная автономная система асимптотически устойчива.
Наряду с изложенным подходом к анализу устойчивости линейных автономных систем используется и другой способ, связанный с анализом корней характеристического уравнения матрицы А (XI.49). Характеристическое уравнение для матрицы записывается так:

где Е — единичная матрица.
Раскрывая этот определитель, получим уравнение  порядка
порядка

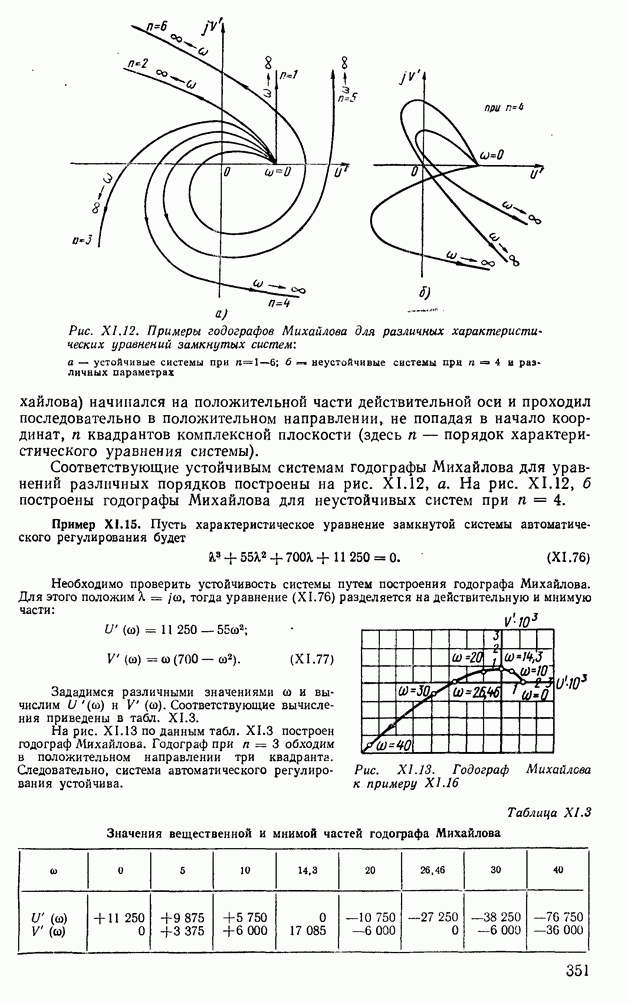
Если все корни уравнения (XI.54) имеют отрицательные вещественные части (рис. XI.8), то нулевое решение системы (XI.49) асимптотически устойчиво.
Если среди корней уравнения (XI.54) есть хотя бы один с положительной вещественной частью, то нулевое решение системы (XI.49) неустойчиво.
Если уравнение (XI.54) не имеет корней с положительной вещественной частью, но имеется часть корней с нулевой вещественной частью, то положение равновесия системы (XI.49) будет устойчивым (неасимптотическим).
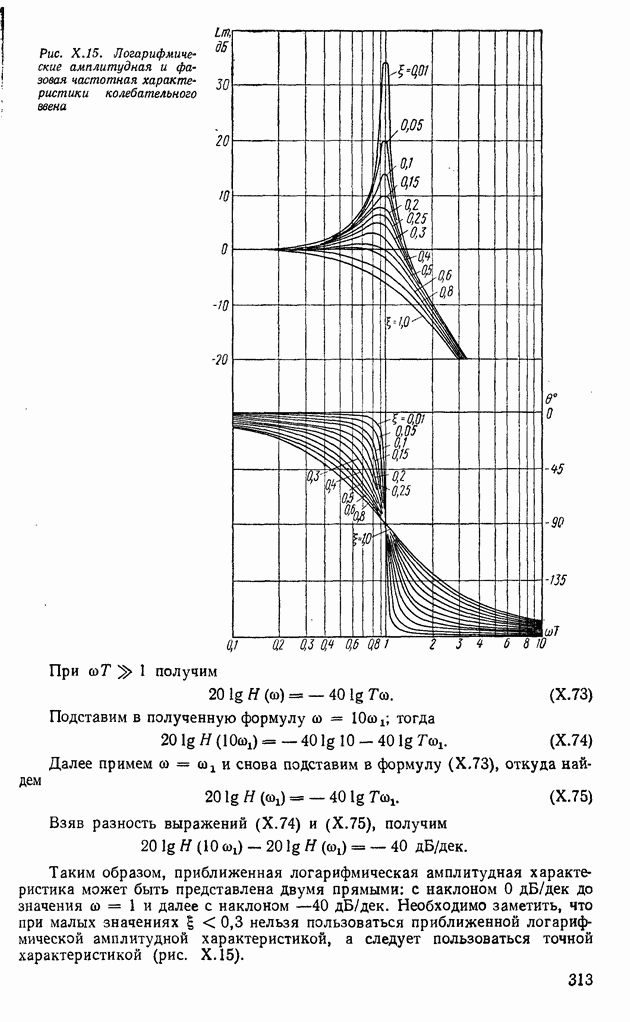
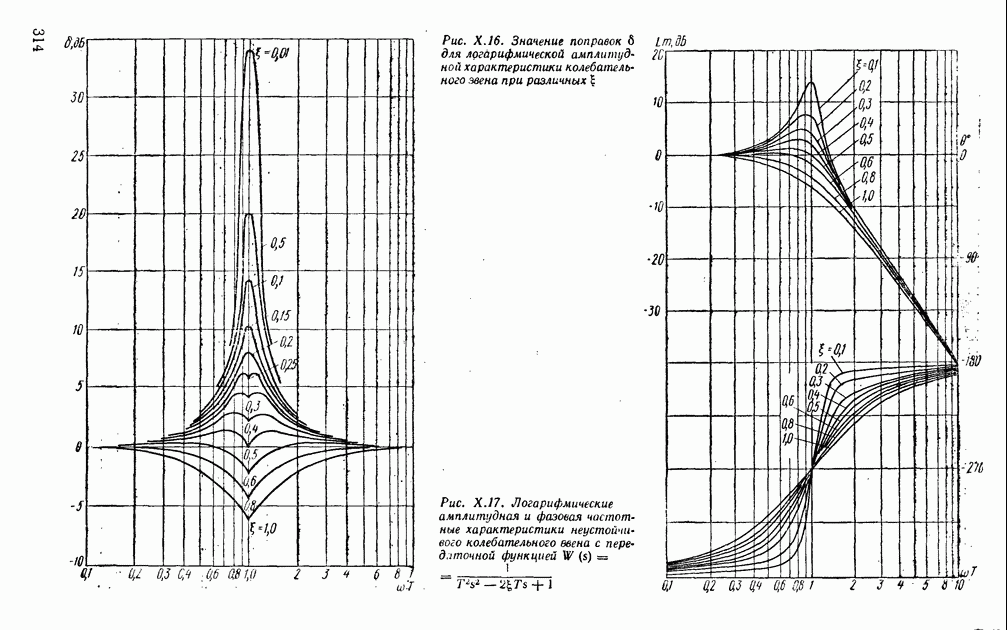
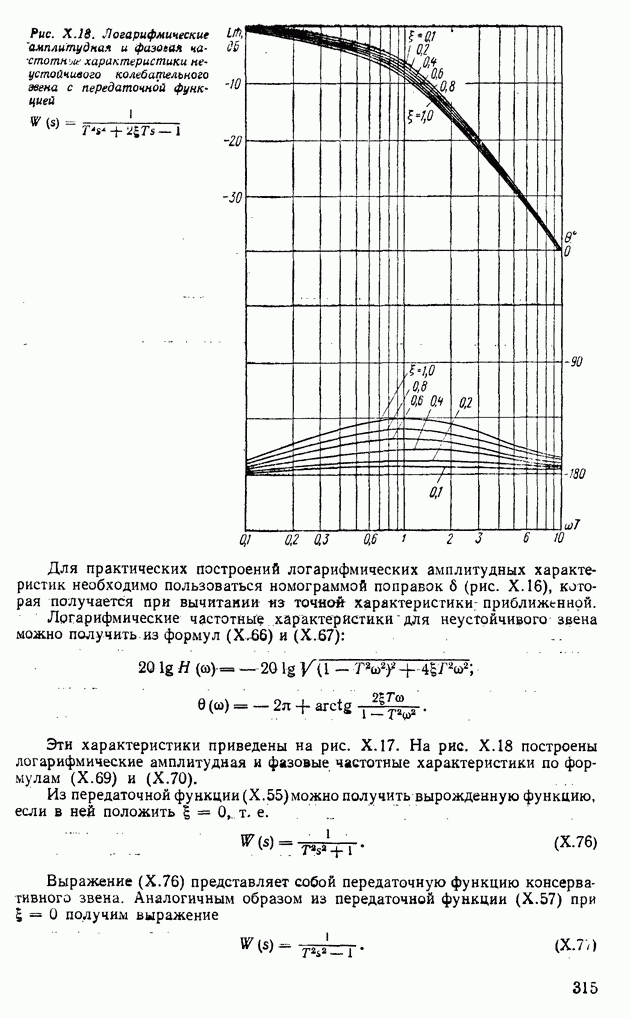
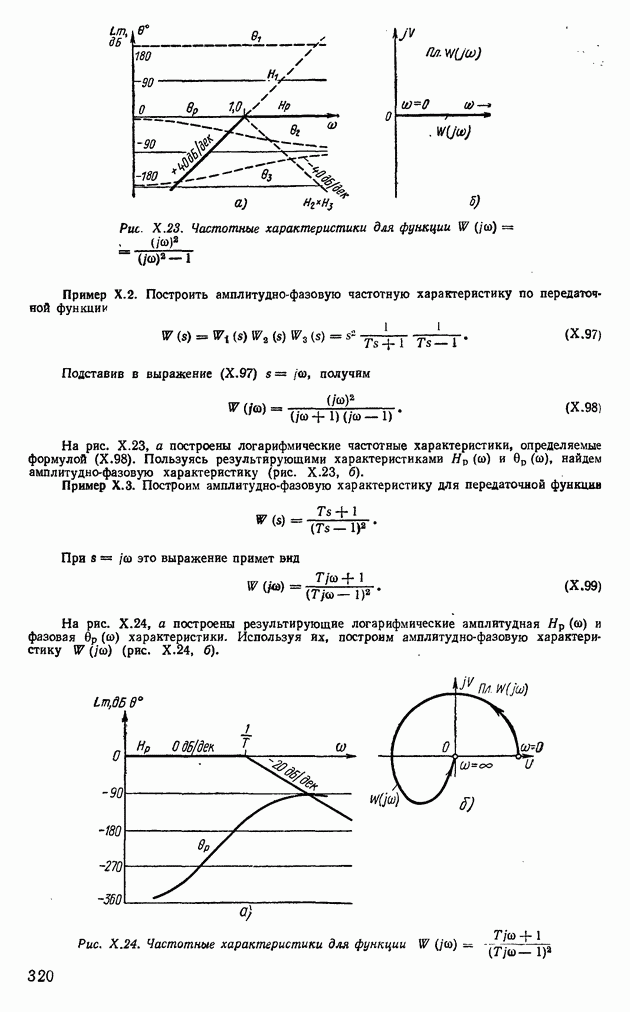
Таким образом, вопрос об устойчивости нулевого решения системы (XI.49) сводится к исследованию корней характеристического уравнения (XI.54). Однако определение корней характеристических уравнений высоких порядков представляет значительные трудности, так как корни уравнений выше четвертого порядка не выражаются аналитически через коэффициенты уравнений.
Теоремы об устойчивости линейных систем практически были бы бесполезны, если бы в природе не существовало нелинейных систем, близких в некотором смысле к линейным. Функции  в уравнениях (XI. 1) могут быть разложены в степенные ряды, которые сходятся в некоторой окрестности
в уравнениях (XI. 1) могут быть разложены в степенные ряды, которые сходятся в некоторой окрестности

Рис. XI.8. Расположение корней характеристического уравнения для асимтотически устойчивой системы
начала координат. Тогда в этой окрестности наряду  исходной системой можно рассматривать и систему первого приближения, которая в этой области линейна, т. е. исходная система (XI. 1) представляется в виде
исходной системой можно рассматривать и систему первого приближения, которая в этой области линейна, т. е. исходная система (XI. 1) представляется в виде

где  — остаточные члены.
— остаточные члены.
Система уравнений

называется системой первого приближения. Эта система совершенно аналогична системе уравнений (XI.48), (XI.49).
Во многих случаях по устойчивости системы (XI.56) оказывается возможным судить и об устойчивости нелинейной системы (XI.55).
А. М. Ляпунов доказал следующие теоремы.
Если вещественные части всех корней характеристического уравнения системы первого приближения (XI.56) отрицательны, то нулевое решение системы (XI.55) асимптотически устойчиво независимо от членов разложения выше первого порядка.
Если среди корней характеристического уравнения системы первого приближения имеется хотя бы один с положительной вещественной частью, то нулевое решение системы (XI.55) неустойчиво независимо от членов разложения выше первого порядка.
Если среди корней характеристического уравнения первого приближения есть нулевые, то в этом случае для суждения об устойчивости нулевого решения системы (XI.55) необходимо учитывать члены выше первого порядка.
Рассмотрим применение этих теорем на конкретном примере.
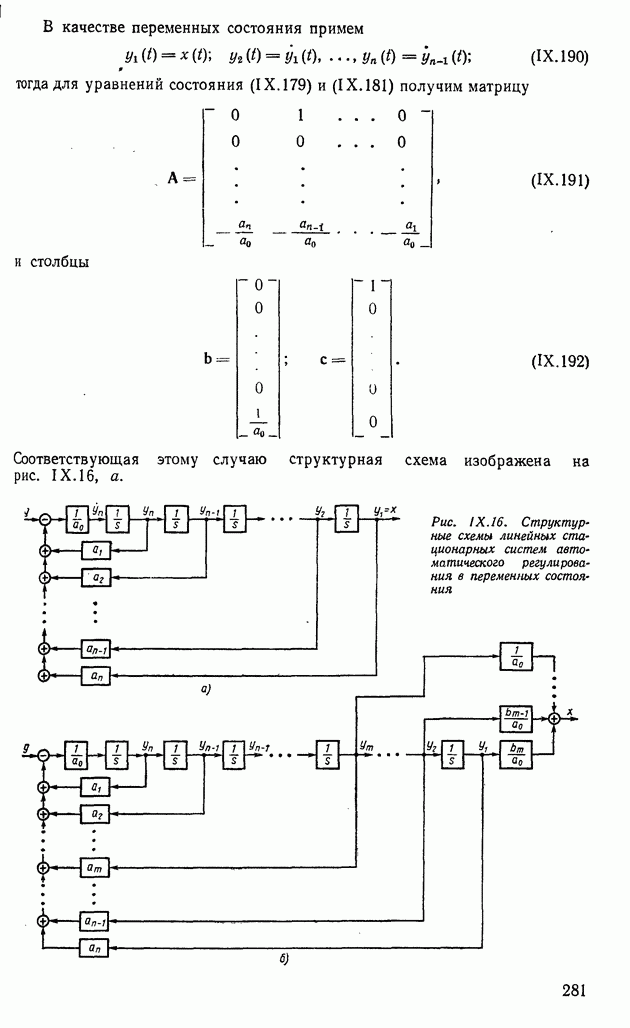
Пример XI.10. Систему, соответствующую структурной схеме на рис. XI.9, можно описать в виде

Положение равновесия соответствует началу координат. Система первого приближения будет

Характеристическое уравнение

имеет корни 

Рис. XI.9. Структурная схема динамической системы
В данном случае об устойчивости системы (XI.57), исследуя первое приближение, ничего сказать нельзя; необходимо учитывать члены разложения выше первого порядка.
Отметим, что в данном случае нулевое решение системы первого приближения неустойчиво, так как

но в то же время нелинейная система (XI.57) устойчива асимптотически.
Действительно, введем функцию Ляпунова

Производная этой функции, взятая с учетом системы (XI.57),

является знакоотрицательной. Однако, еслн  то в силу уравнений (XI.57)
то в силу уравнений (XI.57)  и наоборот; следовательно, всюду, где проходят траектории системы (XI.57), производная
и наоборот; следовательно, всюду, где проходят траектории системы (XI.57), производная  отрицательно определена, а
отрицательно определена, а  положительно определенна. Отсюда следует, что начало координат системы (XI.57) асимптотически устойчиво.
положительно определенна. Отсюда следует, что начало координат системы (XI.57) асимптотически устойчиво.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ВВЕДЕНИЕ
- Глава 1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
- 1. ПРИНЦИПЫ ДЕЙСТВИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ОСНОВНЫЕ УСТРОЙСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
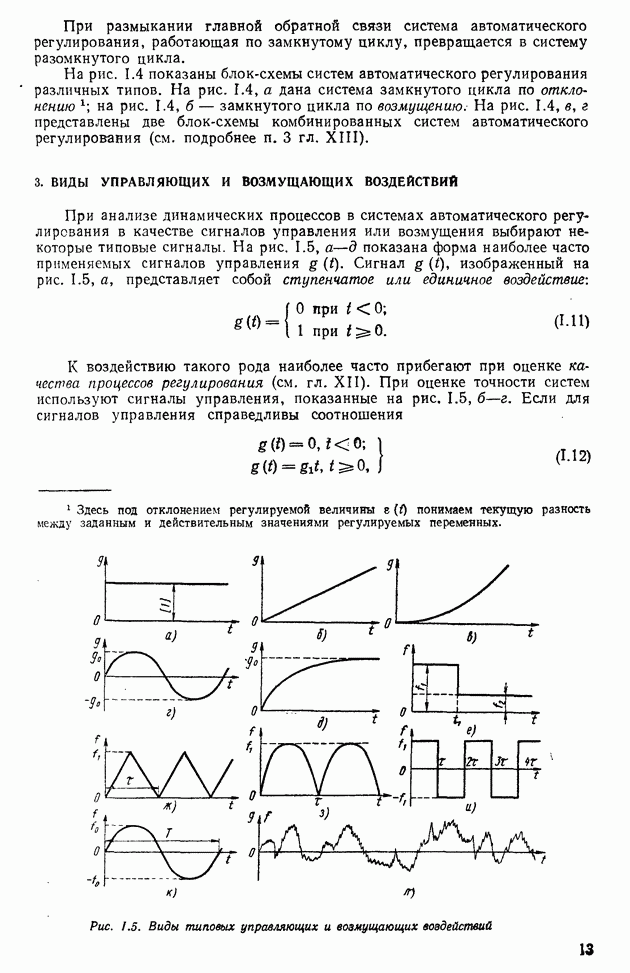
- 3. ВИДЫ УПРАВЛЯЮЩИХ И ВОЗМУЩАЮЩИХ ВОЗДЕЙСТВИЙ
- 4. СТАТИЧЕСКИЕ И АСТАТИЧЕСКИЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Глава II. ВИДЫ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛТРОВАНИЯ
- 1. КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
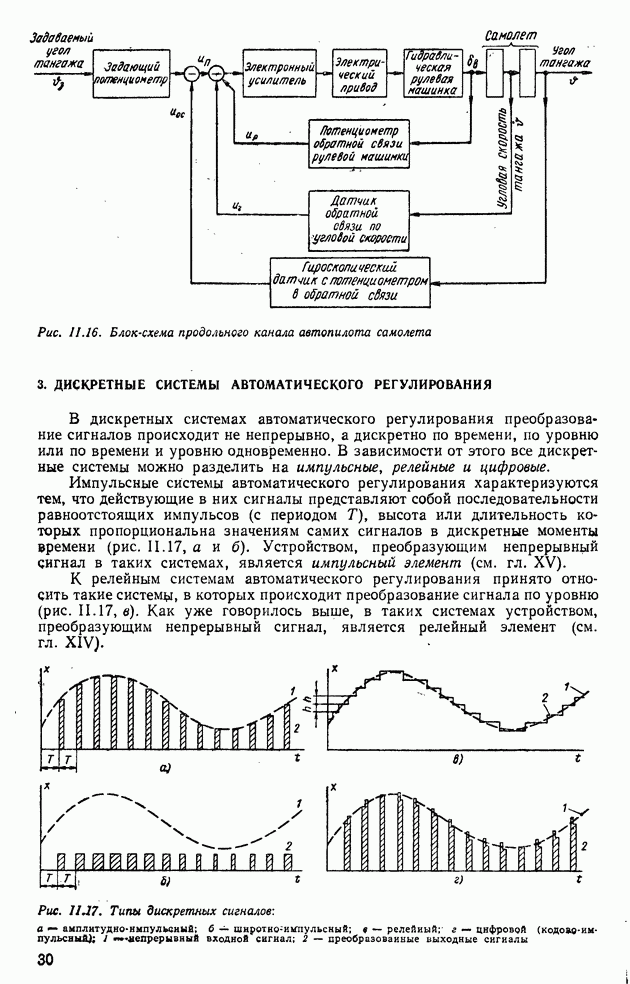
- 3. ДИСКРЕТНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ДИСКРЕТНО-НЕПРЕРЫВНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ПРИМЕНЕНИЕ ЦВМ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
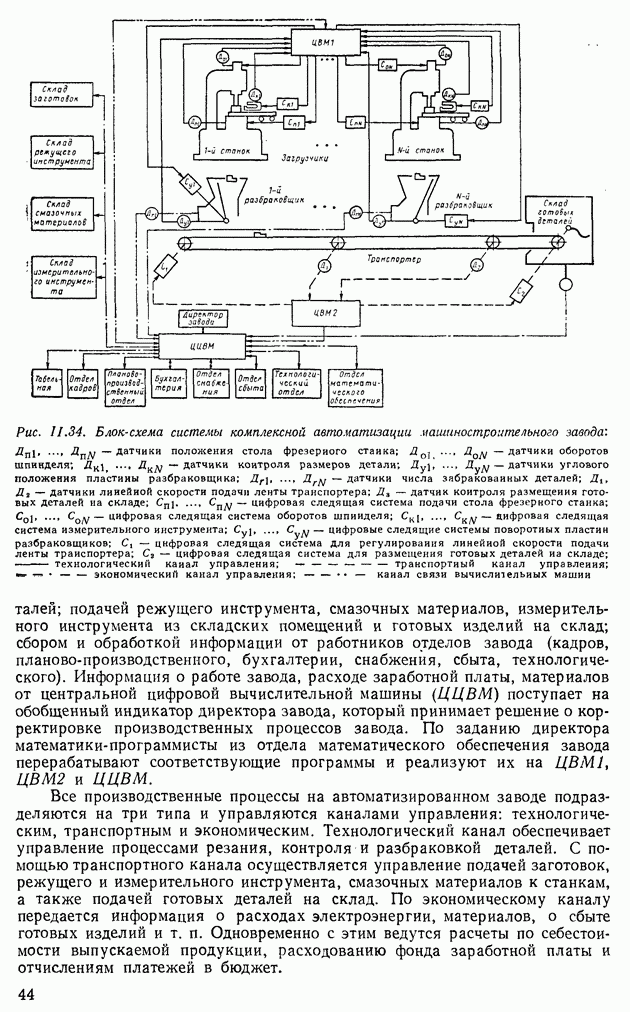
- 7. ПРИМЕНЕНИЕ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ДЛЯ УПРАВЛЕНИЯ СЛОЖНЫМИ ПРОИЗВОДСТВЕННЫМИ ПРОЦЕССАМИ. СИСТЕМЫ КОМПЛЕКСНОЙ АВТОМАТИЗАЦИИ ПРОИЗВОДСТВА
- Глава III. ОБЪЕКТЫ РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ СВОЙСТВА ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 2. ОСОБЕННОСТИ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- 3. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЙ ДИНАМИКИ
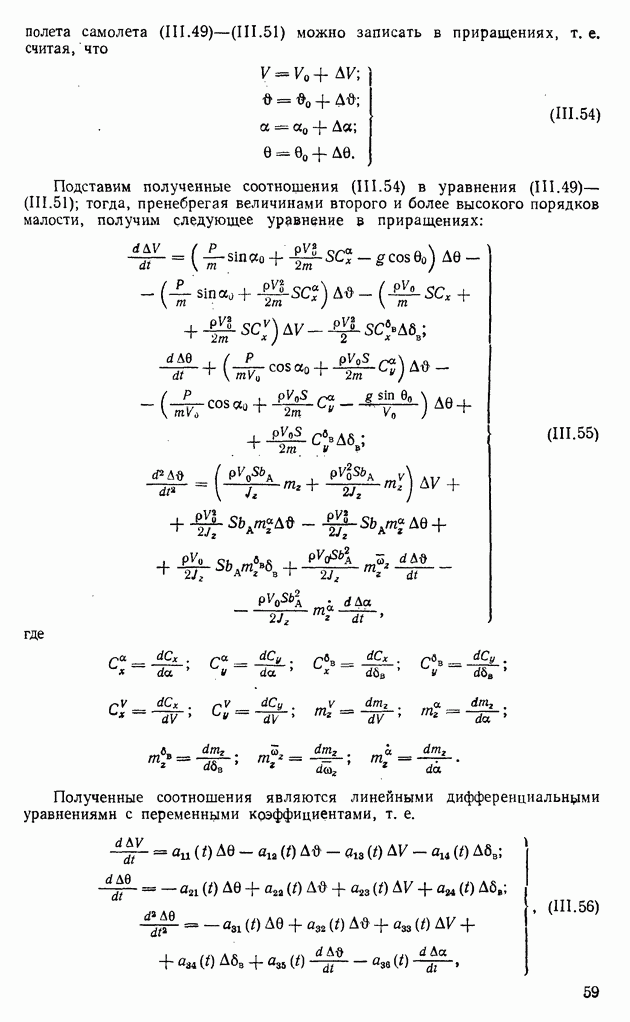
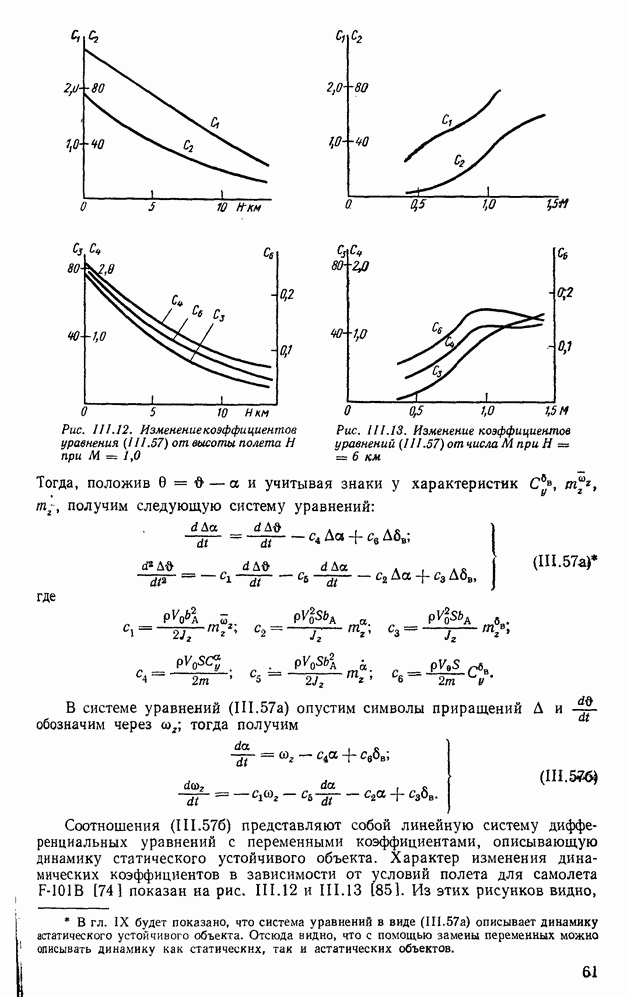
- 4. УСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (ДИЗЕЛЬ, ГИДРОТУРБИНА, САМОЛЕТ)
- 5. НЕУСТОЙЧИВЫЕ СТАТИЧЕСКИЕ ОБЪЕКТЫ (РЕСИВЕР, РАКЕТА-НОСИТЕЛЬ КОСМИЧЕСКИХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ)
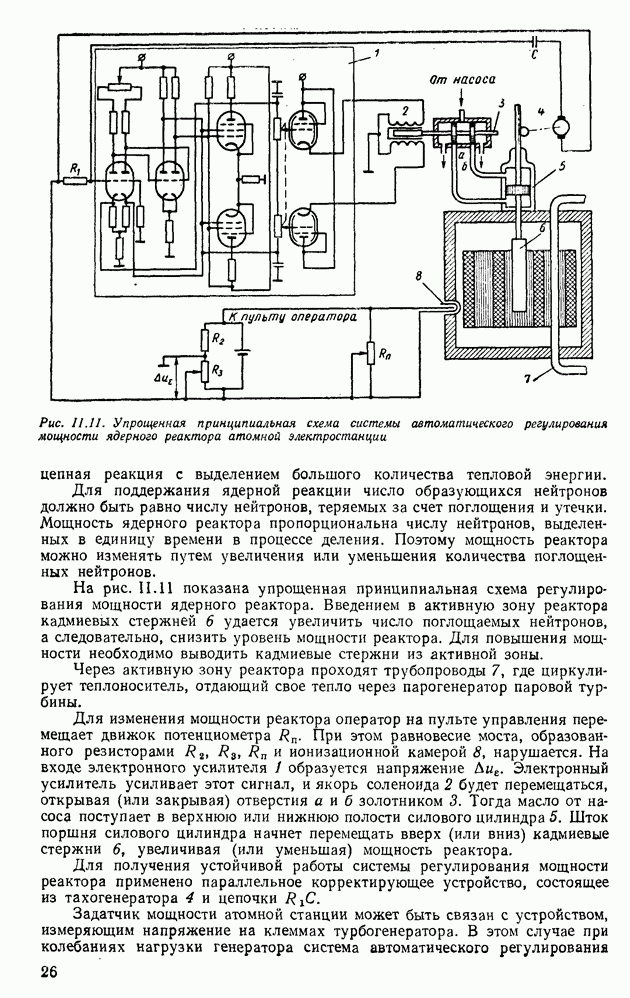
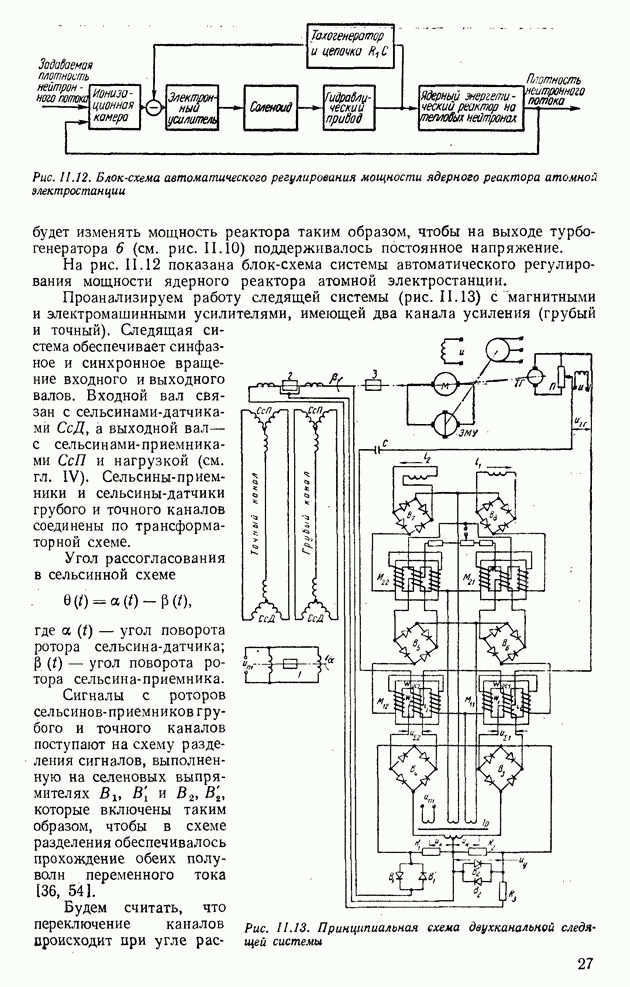
- 6. АСТАТИЧЕСКИЕ ОБЪЕКТЫ (ТРЕХФАЗНЫЙ ЭЛЕКТРИЧЕСКИЙ ДВИГАТЕЛЬ, ЯДЕРНЫЙ ЭНЕРГЕТИЧЕСКИЙ РЕАКТОР НА ТЕПЛОВЫХ НЕЙТРОНАХ, КОСМИЧЕСКИЙ ЛЕТАТЕЛЬНЫЙ АППАРАТ)
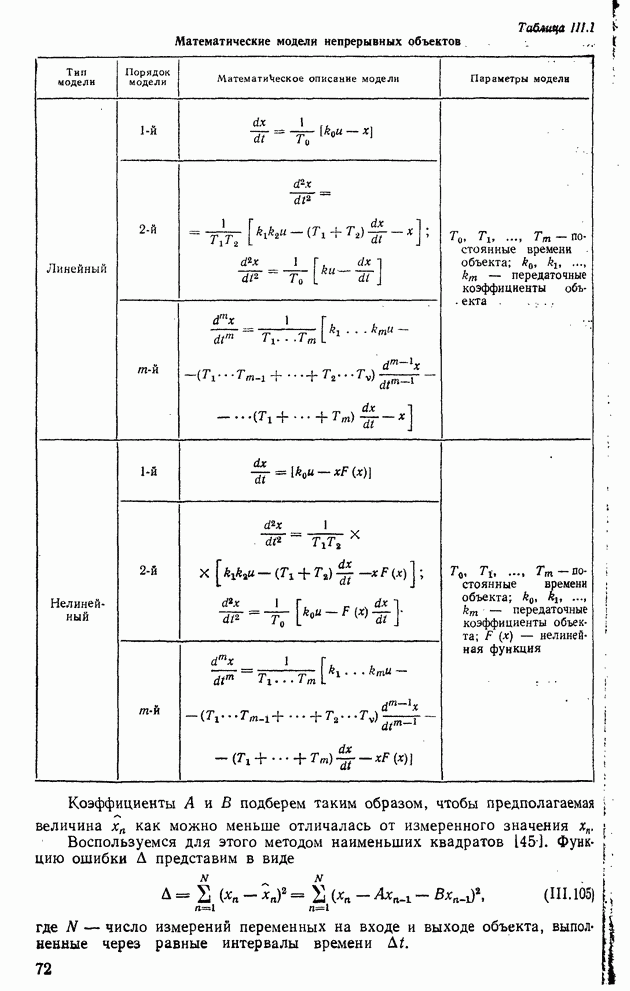
- 7. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ОБЪЕКТОВ РЕГУЛИРОВАНИЯ
- Глава IV. ИЗМЕРИТЕЛЬНЫЕ УСТРОЙСТВА
- 1. ОПРЕДЕЛЕНИЕ ИНФОРМАТИВНОСТИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ И ИЗМЕРИТЕЛЬНЫХ ПОДСИСТЕМ
- 2. КЛАССИФИКАЦИЯ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- 3. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ПЕРЕМЕЩЕНИЙ, СКОРОСТЕЙ И УСКОРЕНИЙ
- Индуктивные устройства.
- Емкостные устройства.
- Сельсины.
- Дифференциальный сельсин.
- Погрешность сельсинов.
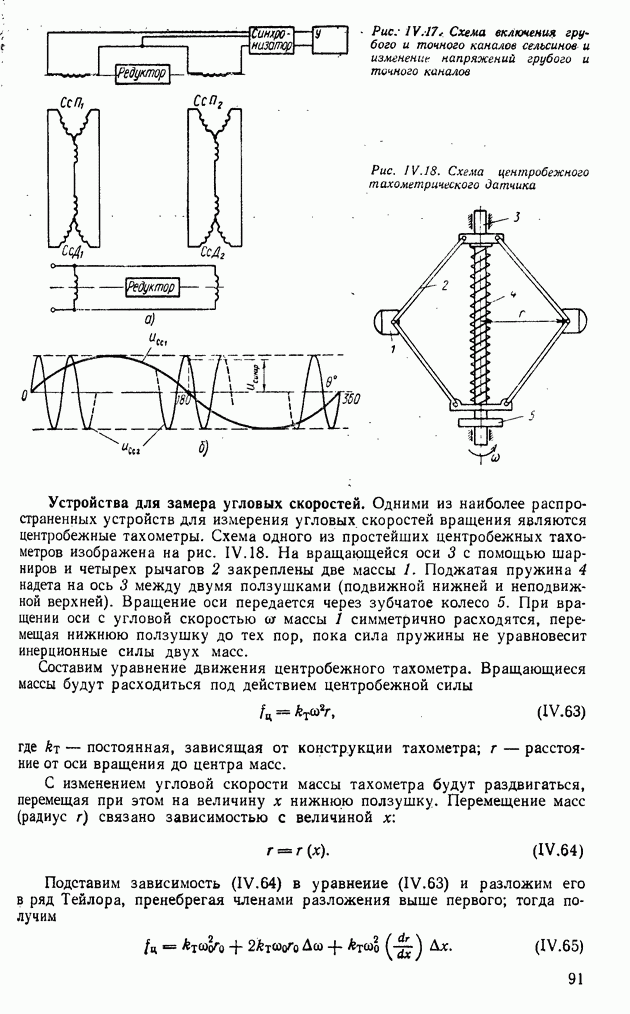
- Устройства для замера угловых скоростей.
- Устройства замера угловых ускорений.
- 4. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ И ТОКА
- 5. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ТЕМПЕРАТУР И ИЗЛУЧЕНИЙ
- 6. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ ДАВЛЕНИЙ И РАСХОДОВ ЖИДКОСТИ И ГАЗА
- 7. УСТРОЙСТВА ДЛЯ ИЗМЕРЕНИЯ УГЛОВЫХ ВЕЛИЧИН, УГЛОВЫХ СКОРОСТЕЙ И ЛИНЕЙНЫХ УСКОРЕНИЙ ПОДВИЖНЫХ ОБЪЕКТОВ
- Устройства для измерения линейных ускорений подвижных объектов (акселерометры).
- 8. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ
- Глава V. УСИЛИТЕЛЬНЫЕ УСТРОЙСТВА
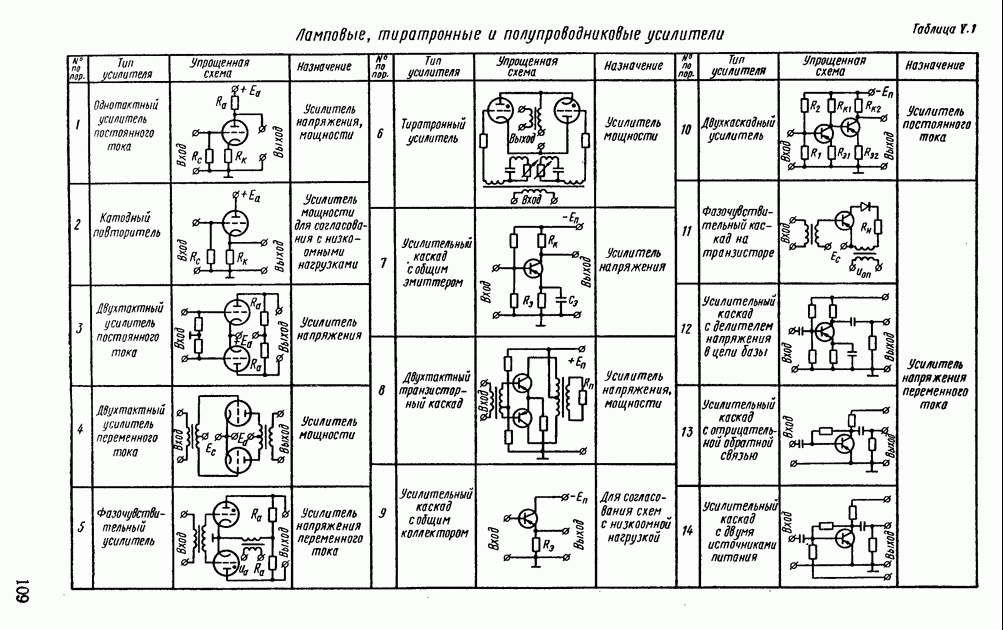
- 1. ЭЛЕКТРОННЫЕ УСИЛИТЕЛИ
- 2. МАГНИТНЫЕ УСИЛИТЕЛИ
- 3. ЭЛЕКТРОМАШИННЫЕ УСИЛИТЕЛИ
- 4. ГИДРАВЛИЧЕСКИЕ УСИЛИТЕЛИ
- 5. ПНЕВМАТИЧЕСКИЕ УСИЛИТЕЛИ
- 6. СРАВНИТЕЛЬНЫЕ ХАРАКТЕРИСТИКИ РАЗЛИЧНЫХ УСИЛИТЕЛЕЙ
- ГЛАВА VI. ПРЕОБРАЗУЮЩИЕ УСТРОЙСТВА
- 1. УСИЛИТЕЛИ-ПРЕОБРАЗОВАТЕЛИ
- 2. РЕЛЕ
- 3. ФУНКЦИОНАЛЬНЫЕ ПРЕОБРАЗОВАТЕЛИ
- 4. ПРЕОБРАЗОВАТЕЛИ АНАЛОГ—КОД
- 5. ПРЕОБРАЗОВАТЕЛИ КОД—АНАЛОГ
- 6. ЭЛЕКТРОННЫЕ АНАЛОГОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 7. ЭЛЕКТРОННЫЕ ЦИФРОВЫЕ УПРАВЛЯЮЩИЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
- 8. ПНЕВМАТИЧЕСКИЕ АНАЛОГОВЫЕ И ЦИФРОВЫЕ ВЫЧИСЛИТЕЛЬНЫЕ УСТРОЙСТВА
- 9. ТОЧНОСТЬ РАБОТЫ И БЫСТРОДЕЙСТВИЕ УПРАВЛЯЮЩИХ ЦИФРОВЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
- 10. СРАВНИТЕЛЬНАЯ ОЦЕНКА ПРЕОБРАЗУЮЩИХ УСТРОЙСТВ
- Глава VII. ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 1. ЭЛЕКТРИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 2. МЕХАНИЧЕСКИЕ ИСПОЛНИТЕЛЬНЫЕ ЭЛЕМЕНТЫ
- 3. ГИДРАВЛИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 4. ПНЕВМАТИЧЕСКИЕ СЕРВОДВИГАТЕЛИ
- 5. МЕХАНИЧЕСКИЕ ПЕРЕДАЧИ
- 6. СРАВНИТЕЛЬНАЯ ОЦЕНКА ИСПОЛНИТЕЛЬНЫХ ЭЛЕМЕНТОВ
- Глава VIII. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 1. ЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 2. НЕЛИНЕЙНЫЕ ПАССИВНЫЕ И АКТИВНЫЕ ЭЛЕКТРИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 3. ГИДРАВЛИЧЕСКИЕ И ПНЕВМАТИЧЕСКИЕ КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА
- 4. КОРРЕКТИРУЮЩИЕ УСТРОЙСТВА НА ЛИНИЯХ ЗАДЕРЖЕК И ДИСКРЕТНЫХ ЭЛЕМЕНТАХ
- Глава IX. УРАВНЕНИЯ ДИНАМИКИ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ И ИХ СТРУКТУРНЫЕ СХЕМЫ
- 1. ПРЕДСТАВЛЕНИЕ ОБЪЕКТОВ И УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С СОСРЕДОТОЧЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 2. ПРЕДСТАВЛЕНИЕ УСТРОЙСТВ СИСТЕМ РЕГУЛИРОВАНИЯ С РАСПРЕДЕЛЕННЫМИ ЭЛЕМЕНТАМИ В ВИДЕ ТРАНСЦЕДЕНТНЫХ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ
- 3. СОСТАВЛЕНИЕ СТРУКТУРНЫХ СХЕМ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. ПРЕОБРАЗОВАНИЕ СТРУКТУРНЫХ СХЕМ
- 5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 6. ОПИСАНИЕ ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ РЕГУЛИРОВАНИЯ В ВЕКТОРНО-МАТРИЧНОЙ ФОРМЕ
- 7. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 8. УРАВНЕНИЯ СОСТОЯНИЯ ЛИНЕЙНЫХ НЕСТАЦИОНАРНЫХ СИСТЕМ РЕГУЛИРОВАНИЯ
- 9. РЕШЕНИЕ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ УРАВНЕНИЙ СОСТОЯНИЯ
- 10. ОПРЕДЕЛЕНИЕ ПЕРЕХОДНЫХ МАТРИЦ ЛИНЕЙНЫХ СТАЦИОНАРНЫХ И НЕСТАЦИОНАРНЫХ СИСТЕМ
- 11. УПРАВЛЯЕМОСТЬ И НАБЛЮДАЕМОСТЬ ЛИНЕЙНЫХ СИСТЕМ
- 12. ПРЕДСТАВЛЕНИЕ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ОБЪЕКТОВ, УСТРОЙСТВ И СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ИМПУЛЬСНЫМИ ПЕРЕХОДНЫМИ ФУНКЦИЯМИ
- Глава X. ДИНАМИЧЕСКИЕ ЗВЕНЬЯ, ИХ АМПЛИТУДНО-ФАЗОВЫЕ И ЛОГАРИФМИЧЕСКИЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
- 1. АПЕРИОДИЧЕСКОЕ ЗВЕНО
- Логарифмические амплитудная и фазовая частотные характеристики апериодического звена.
- 2. АПЕРИОДИЧЕСКОЕ НЕУСТОЙЧИВОЕ ЗВЕНО
- 4. ИНТЕГРИРУЮЩЕЕ ЗВЕНО
- 5. КОЛЕБАТЕЛЬНЫЕ ЗВЕНЬЯ (УСТОЙЧИВЫЕ И НЕУСТОЙЧИВЫЕ)
- 6. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ПЕРВОГО РОДА
- 7. ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО ВТОРОГО РОДА
- 8. ТРАНСЦЕНДЕНТНЫЕ ЗВЕНЬЯ
- 9. ФАЗОВАЯ ЛИНЕЙКА
- 10. ПОСТРОЕНИЕ АМПЛИТУДНО-ФАЗОВЫХ И ЛОГАРИФМИЧЕСКИХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНО СОЕДИНЕННЫХ ГРУПП ТИПОВЫХ ЗВЕНЬЕВ
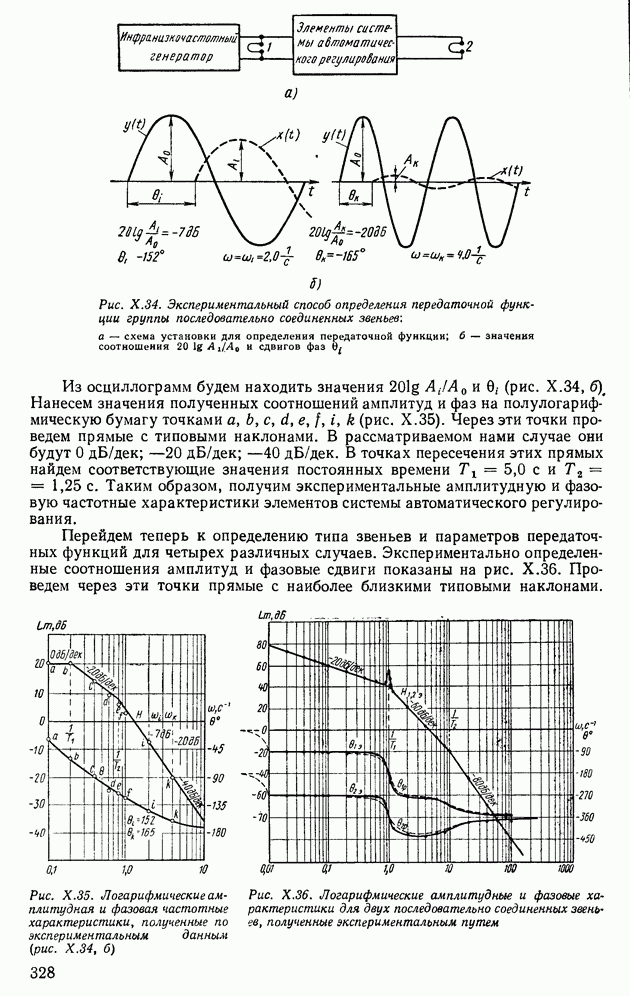
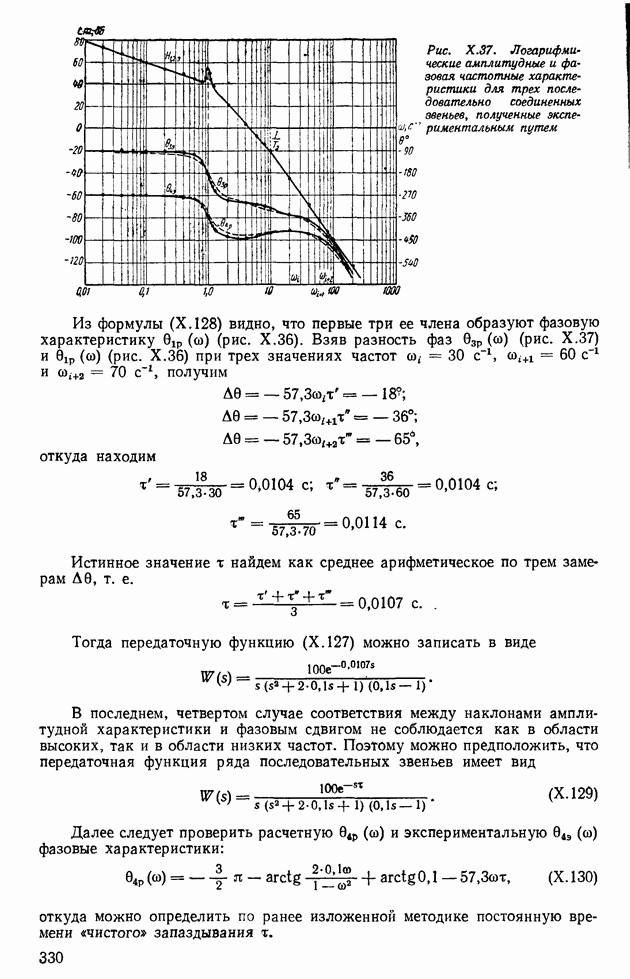
- 11. ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ВИДА ПЕРЕДАТОЧНЫХ ФУНКЦИЙ И ПАРАМЕТРОВ ГРУПП ДИНАМИЧЕСКИХ ЗВЕНЬЕВ
- ГЛАВА XI. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ УСТОЙЧИВОСТИ ПО ЛЯПУНОВУ
- 2. ОПРЕДЕЛЕНИЕ ФУНКЦИЙ ЛЯПУНОВА МЕТОДАМИ Г. СЕГЕ И Д. ШУЛЬЦА
- 3. УСТОЙЧИВОСТЬ ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 4. АЛГЕБРАИЧЕСКИЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 5. ЧАСТОТНЫЕ КРИТЕРИИ УСТОЙЧИВОСТИ
- 6. АНАЛИЗ УСТОЙЧИВОСТИ ОДНОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 7. АНАЛИЗ УСТОЙЧИВОСТИ МНОГОКОНТУРНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
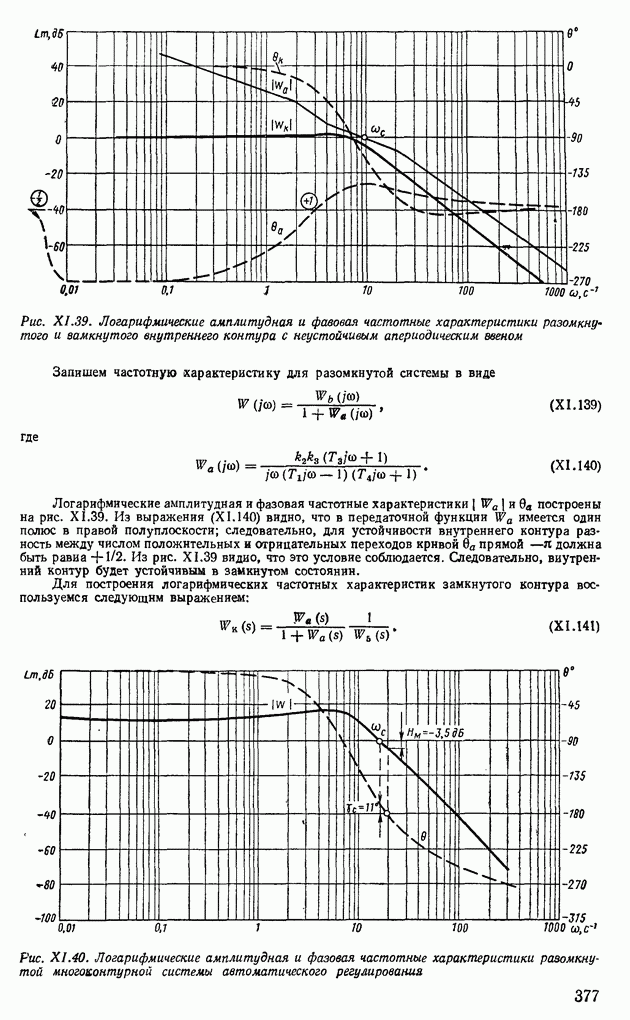
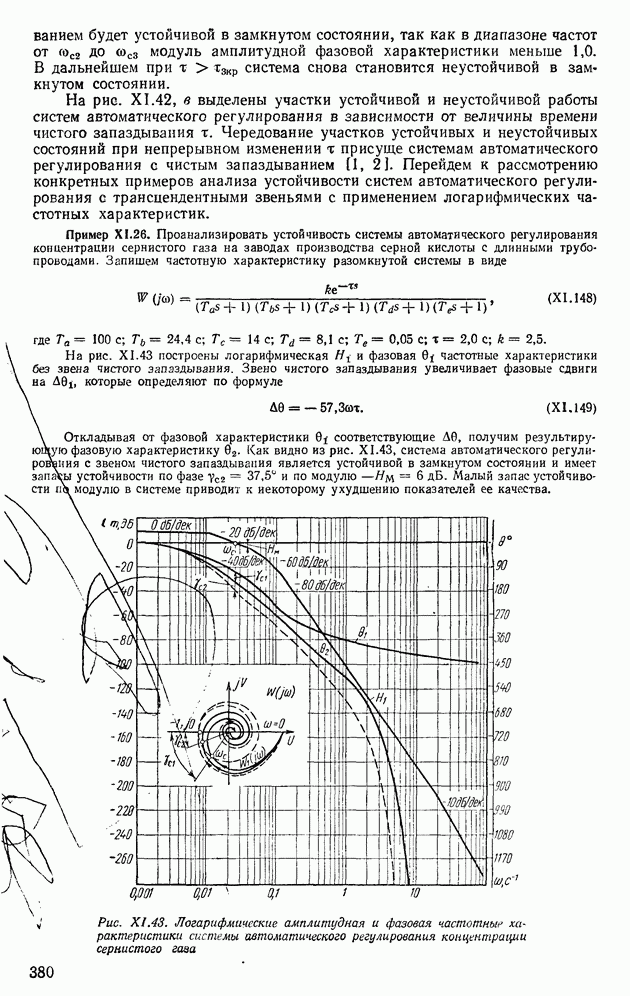
- 8. АНАЛИЗ УСТОЙЧИВОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ТРАНСЦЕНДЕНТНЫМИ ЗВЕНЬЯМИ
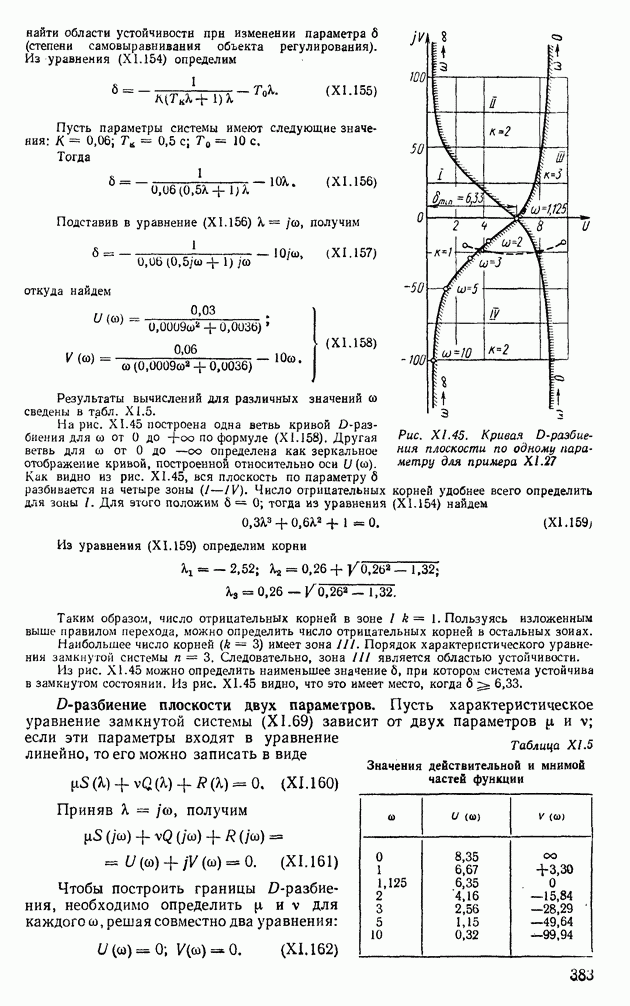
- 9. ВЫДЕЛЕНИЕ ОБЛАСТЕЙ УСТОЙЧИВОСТИ С ПОМОЩЬЮ D-РАЗБИЕНИЯ
- Глава XII. ИССЛЕДОВАНИЕ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. ОСНОВНЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА ПРОЦЕССОВ РЕГУЛИРОВАНИЯ
- 2. ПОСТРОЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПО ЗАДАННЫМ ПЕРЕДАТОЧНЫМ ФУНКЦИЯМ ЗАМКНУТЫХ СИСТЕМ
- 3. ОПРЕДЕЛЕНИЕ ПОКАЗАТЕЛЕЙ КАЧЕСТВА ПО РАСПОЛОЖЕНИЮ НУЛЕЙ И ПОЛЮСОВ ЛЕРЕДАТОЧНОЙ ФУНКЦИИ ЗАМКНУТОЙ СИСТЕМЫ
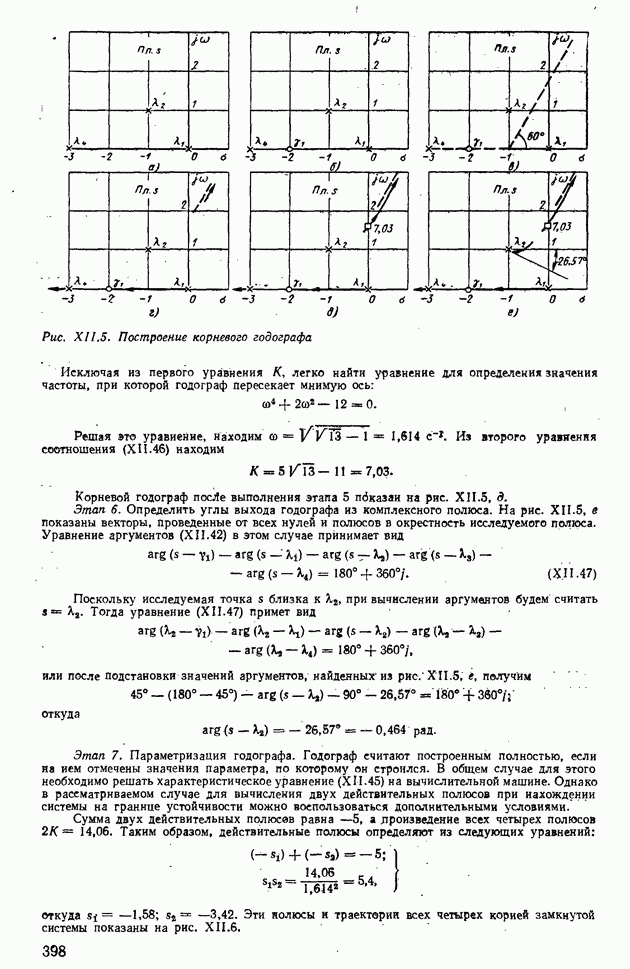
- 4. МЕТОД КОРНЕВОГО ГОДОГРАФА
- 5. ИНТЕГРАЛЬНЫЕ ОЦЕНКИ КАЧЕСТВА
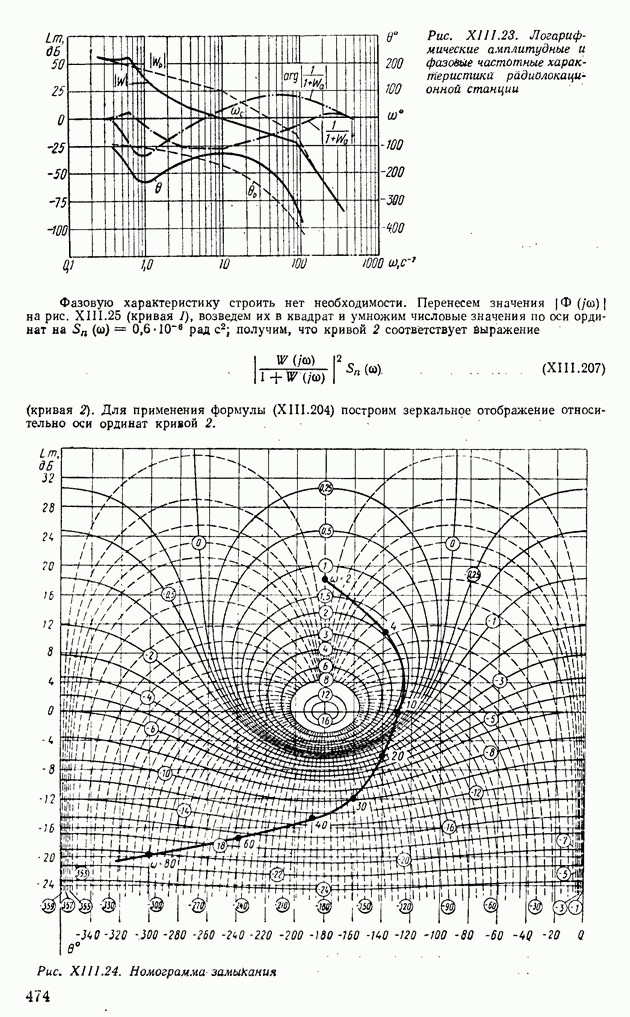
- 6. ОБОБЩЕННЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ СИСТЕМ РЕГУЛИРОВАНИЯ И ИХ СВЯЗЬ С ХАРАКТЕРИСТИКАМИ ПЕРЕХОДНЫХ ПРОЦЕССОВ
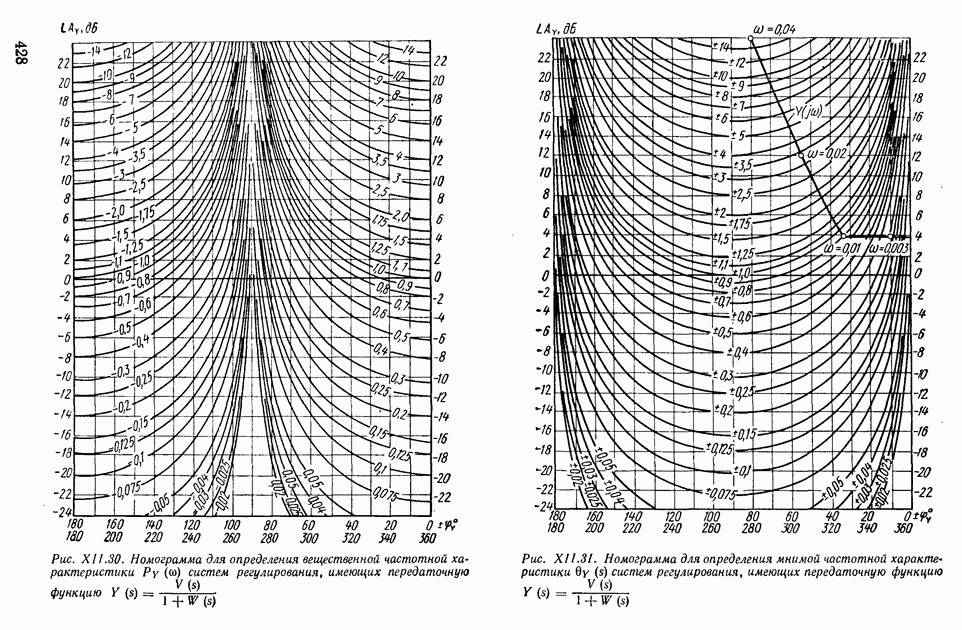
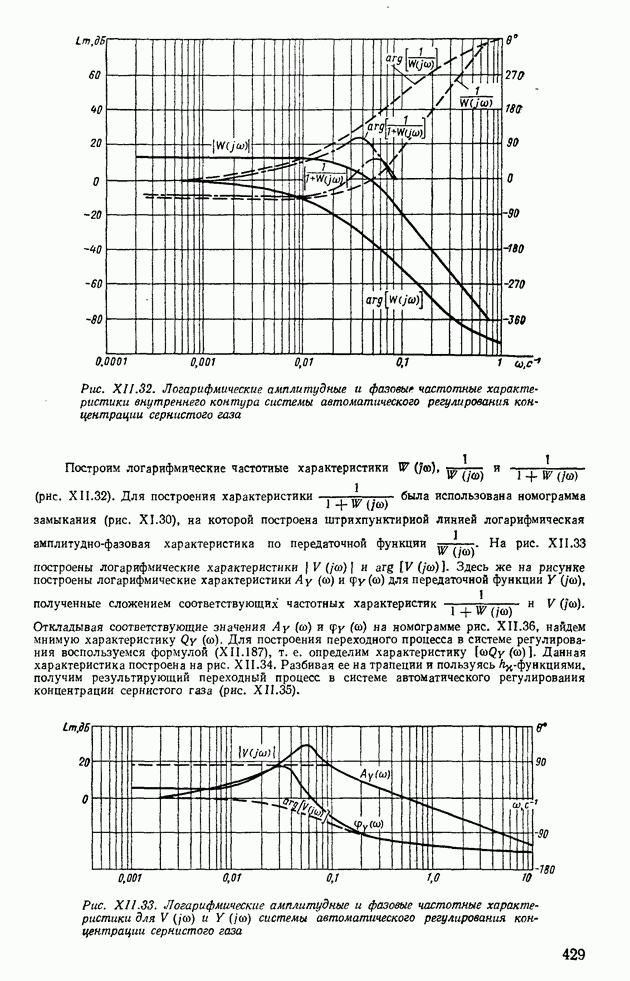
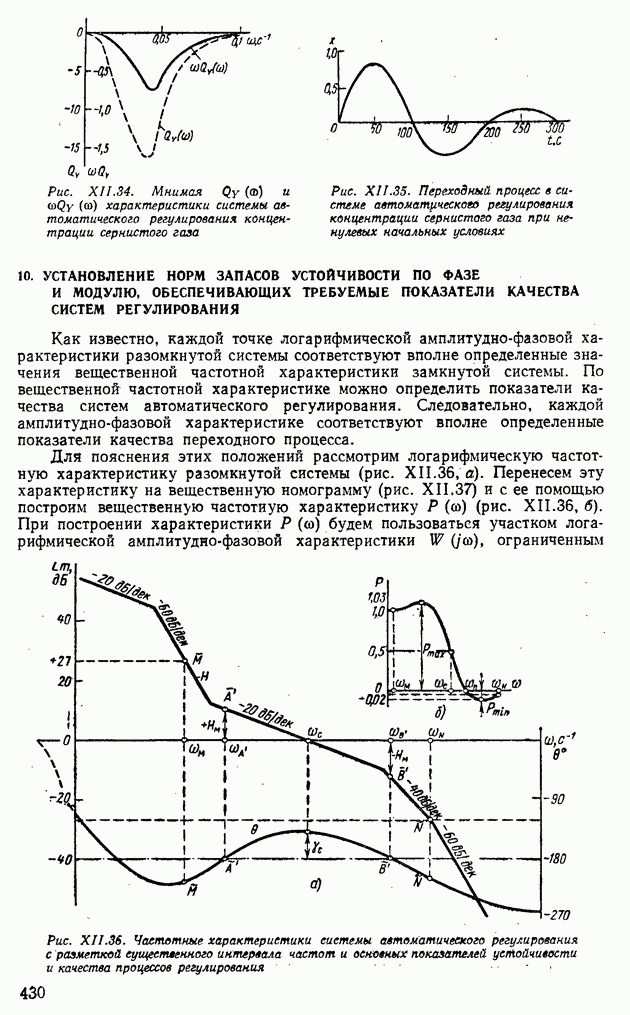
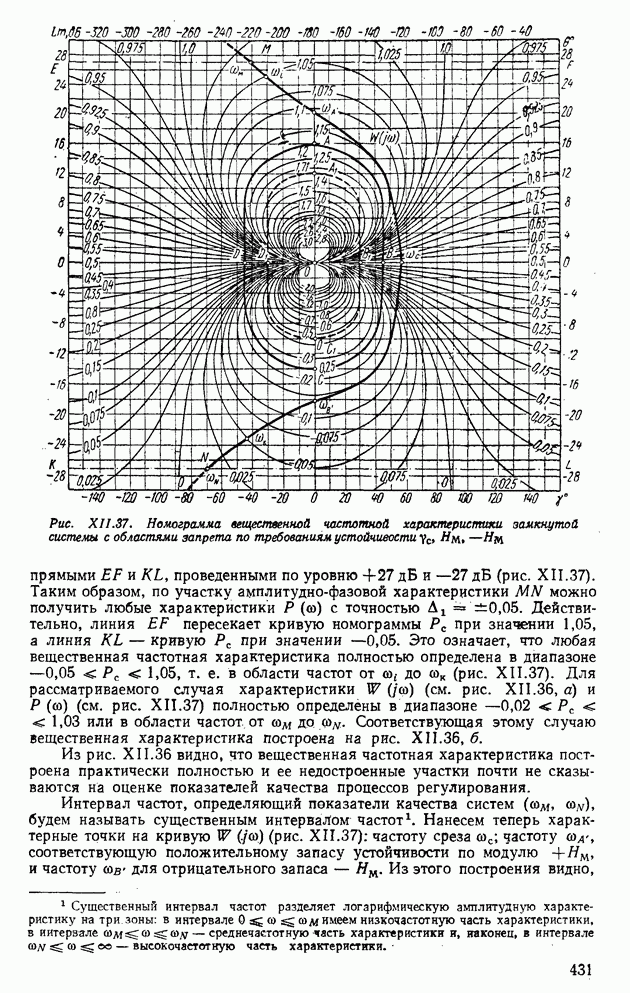
- 7. ОПРЕДЕЛЕНИЕ ВЕЩЕСТВЕННЫХ И МНИМЫХ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ЗАМКНУТЫХ СИСТЕМ ПО АМПЛИТУДНО-ФАЗОВЫМ И ЛОГАРИФМИЧЕСКИМ ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ РАЗОМКНУТЫХ СИСТЕМ
- 8. ЧАСТОТНЫЕ ОЦЕНКИ КАЧЕСТВА СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
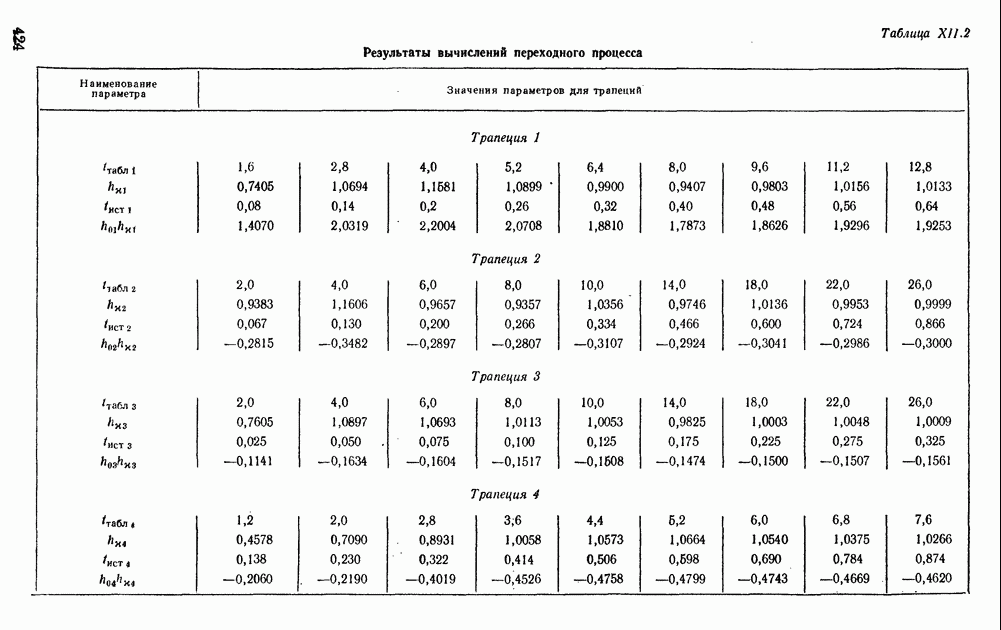
- 9. ЧАСТОТНЫЕ МЕТОДЫ ПОСТРОЕНИЯ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ТРАПЕЦЕИДАЛЬНЫХ ХАРАКТЕРИСТИК
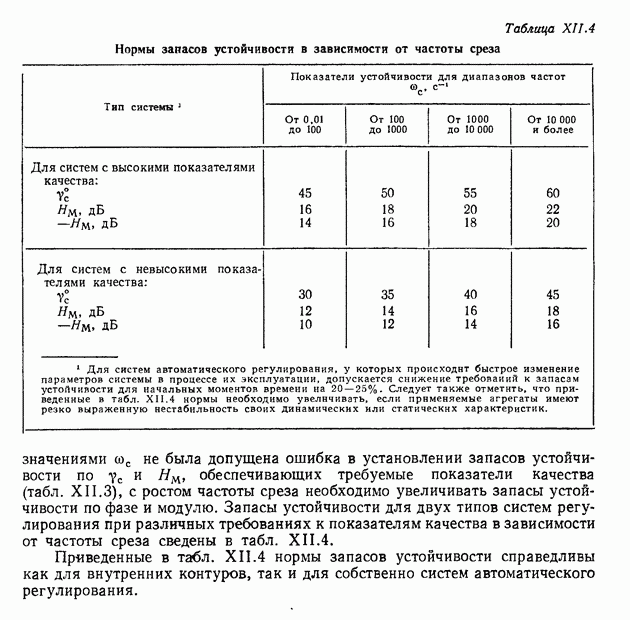
- 10. УСТАНОВЛЕНИЕ НОРМ ЗАПАСОВ УСТОЙЧИВОСТИ ПО ФАЗЕ И МОДУЛЮ, ОБЕСПЕЧИВАЮЩИХ ТРЕБУЕМЫЕ ПОКАЗАТЕЛИ КАЧЕСТВА СИСТЕМ РЕГУЛИРОВАНИЯ
- ГЛАВА XIII. ДИНАМИЧЕСКАЯ ТОЧНОСТЬ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
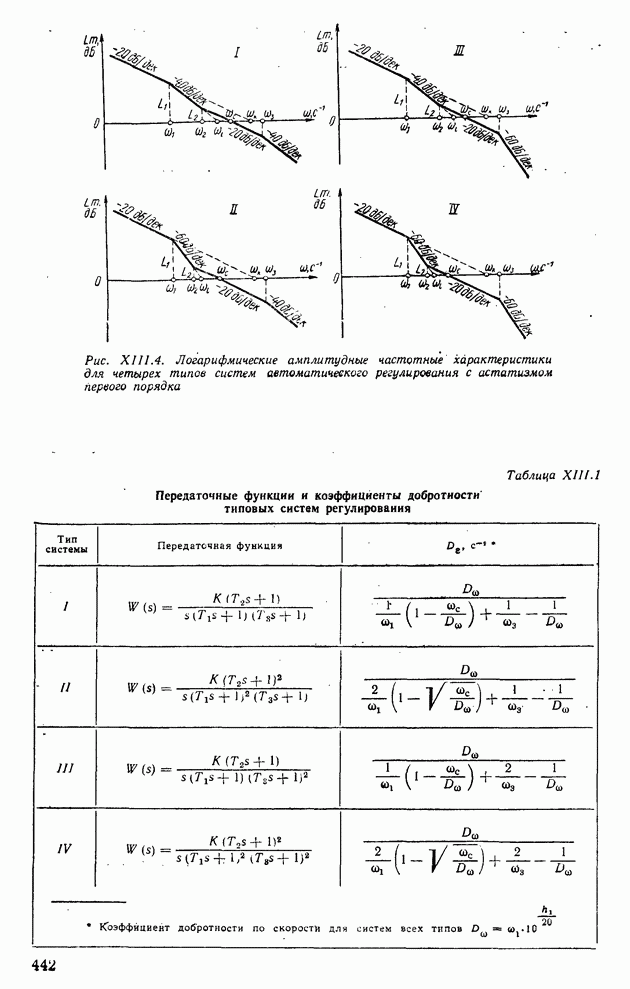
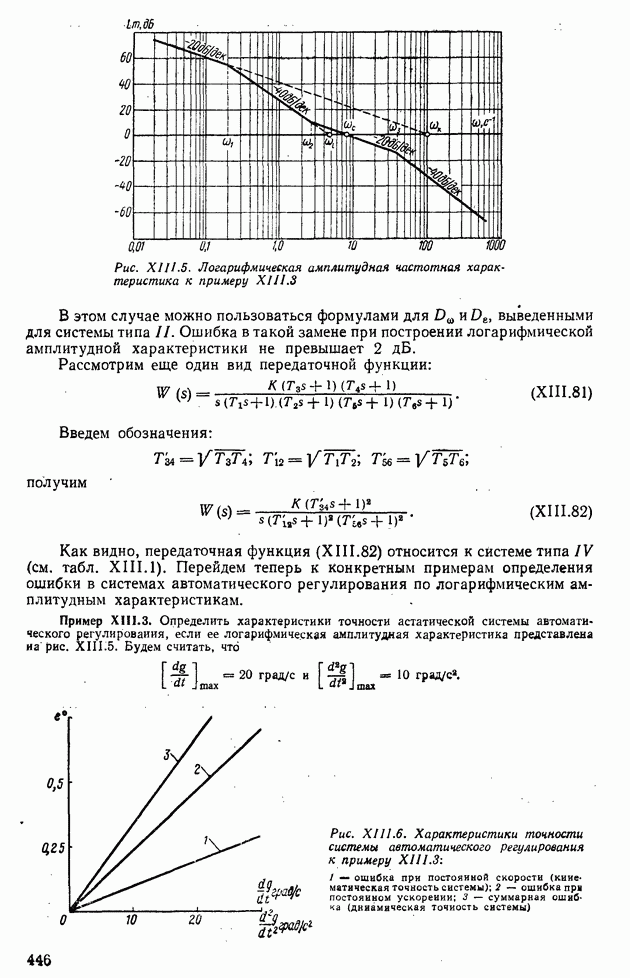
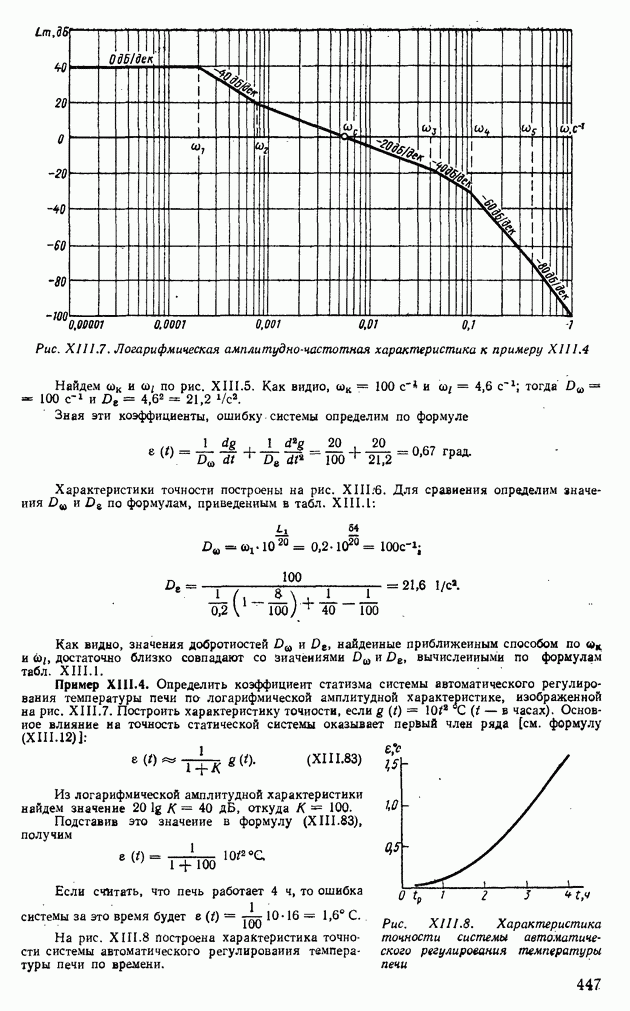
- 2. ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ОШИБОК В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ПОМОЩЬЮ ЛОГАРИФМИЧЕСКИХ АМПЛИТУДНЫХ ХАРАКТЕРИСТИК
- 3. ПОВЫШЕНИЕ ТОЧНОСТИ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПУТЕМ ПРИМЕНЕНИЯ КОМБИНИРОВАННОГО УПРАВЛЕНИЯ
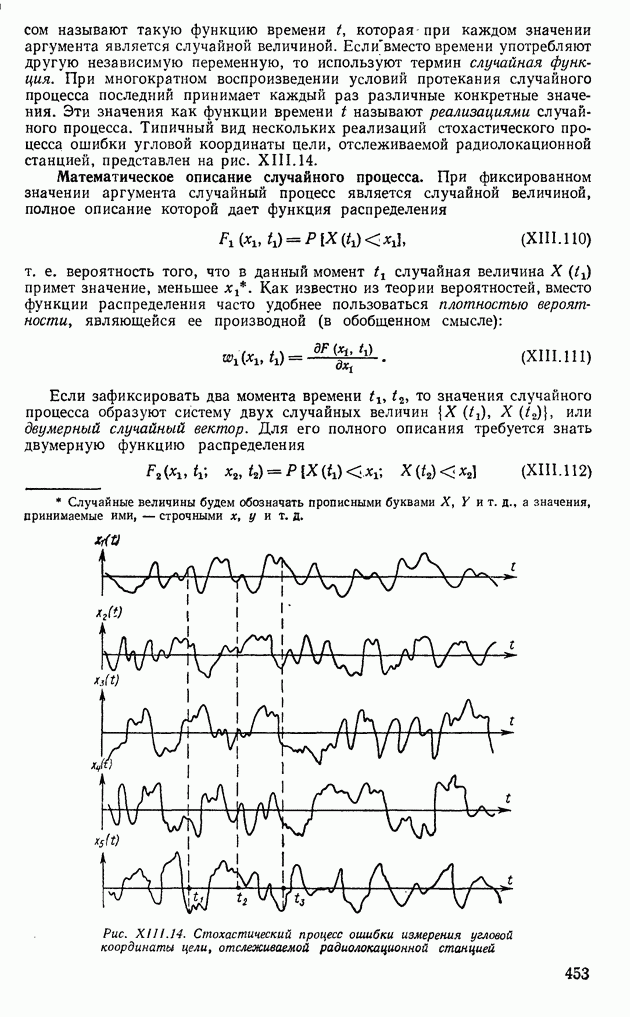
- 4. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ПРОЦЕССОВ
- 5. СВОЙСТВА КОРРЕЛЯЦИОННЫХ ФУНКЦИЙ СТАЦИОНАРНЫХ ПРОЦЕССОВ
- 6. СВОЙСТВА СПЕКТРАЛЬНОЙ ПЛОТНОСТИ МОЩНОСТИ
- 7. ОПЕРАЦИИ НАД СЛУЧАЙНЫМИ ПРОЦЕССАМИ
- 8. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ СИГНАЛОВ ЛИНЕЙНЫМИ СИСТЕМАМИ
- 9. РАСЧЕТ ОШИБОК В СИСТЕМЕ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ШУМОВ
- 10. ОПТИМИЗАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ ВОЗДЕЙСТВИИ СЛУЧАЙНЫХ СИГНАЛОВ И ШУМОВ
- ГЛАВА XIV. НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
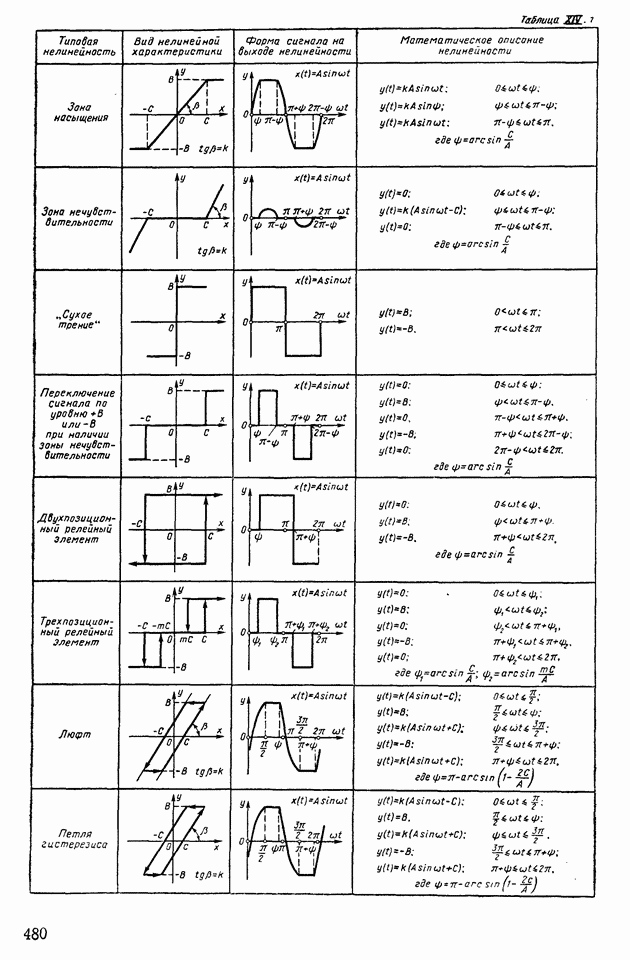
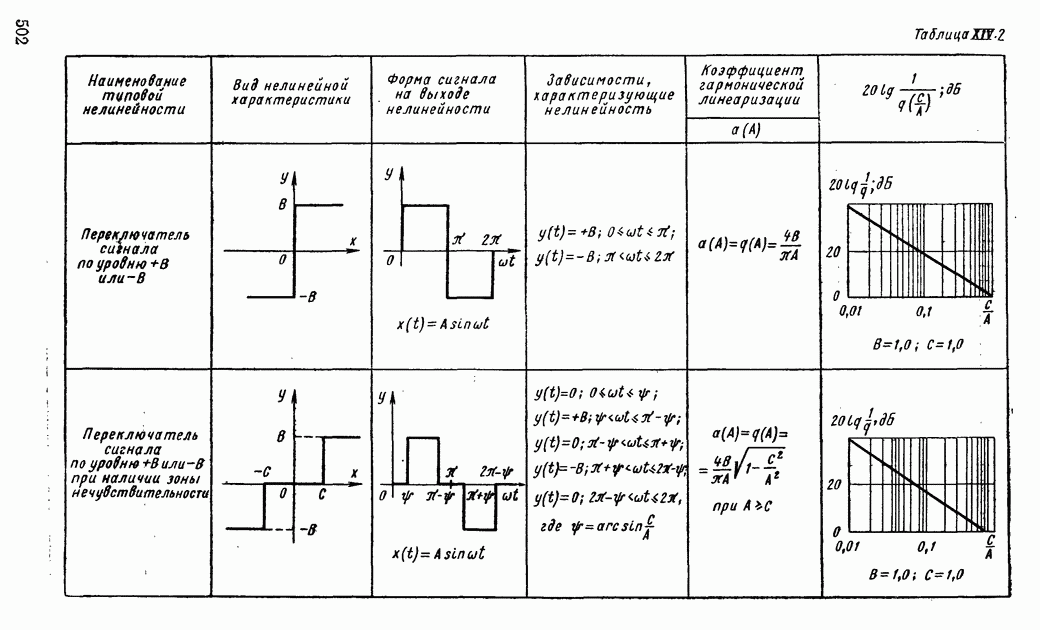
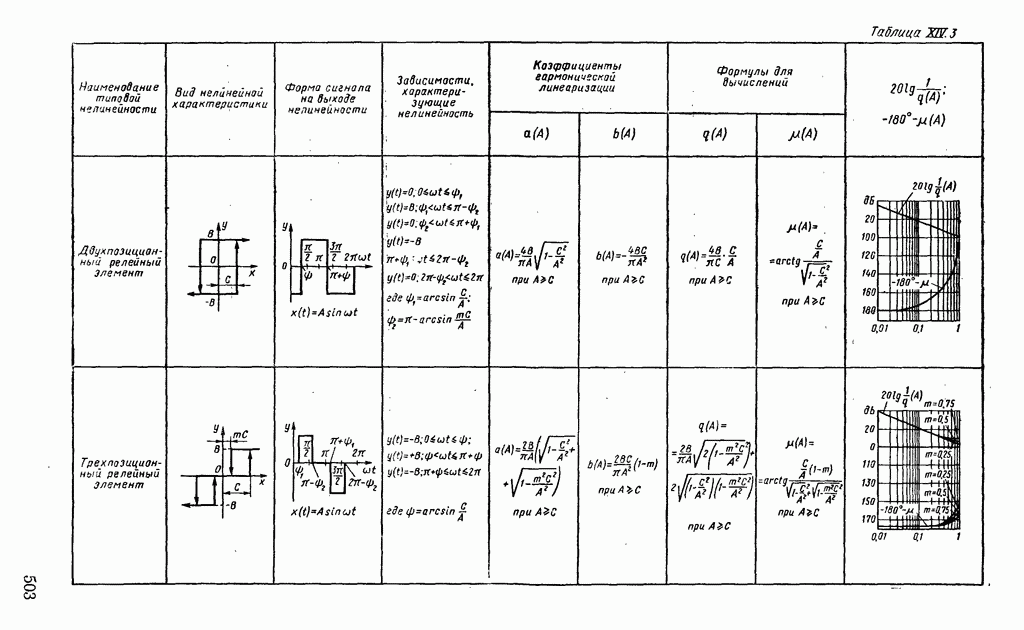
- 1. ТИПОВЫЕ НЕЛИНЕЙНЫЕ ЭЛЕМЕНТЫ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ ПО ВТОРОМУ МЕТОДУ ЛЯПУНОВА
- 3. АНАЛИЗ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ МЕТОДОМ ФАЗОВОЙ ПЛОСКОСТИ
- 4. ПРИМЕНЕНИЕ МЕТОДА ГАРМОНИЧЕСКОЙ ЛИНЕАРИЗАЦИИ ДЛЯ АНАЛИЗА УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. СТРУКТУРНЫЕ ПРЕОБРАЗОВАНИЯ НЕЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
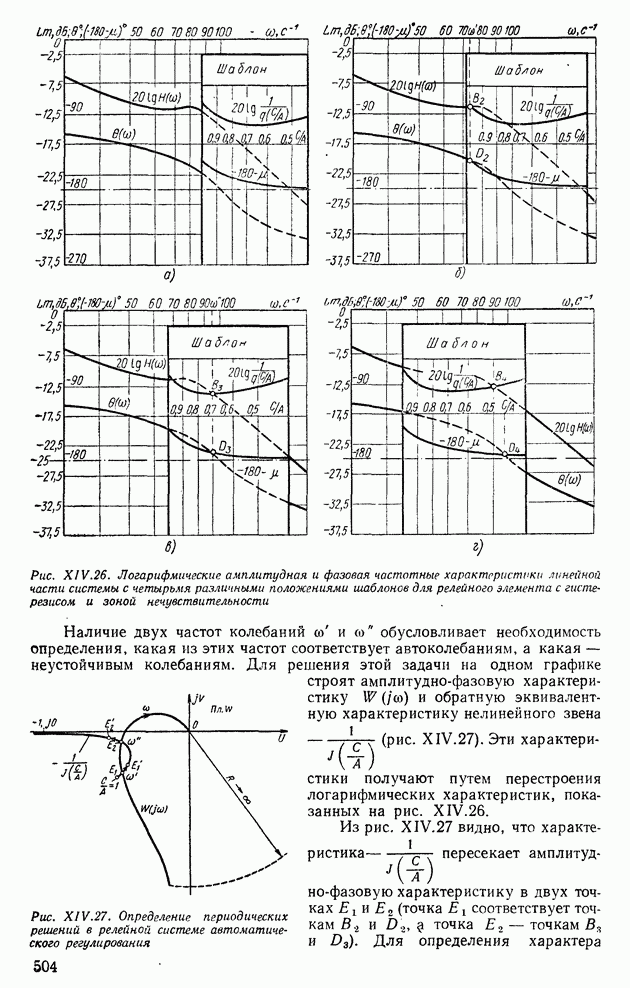
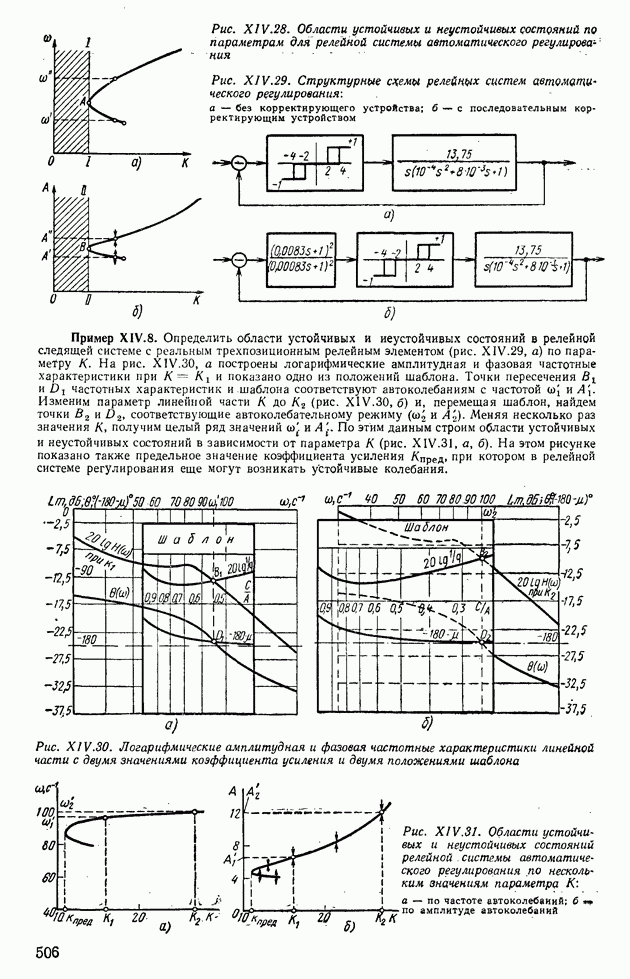
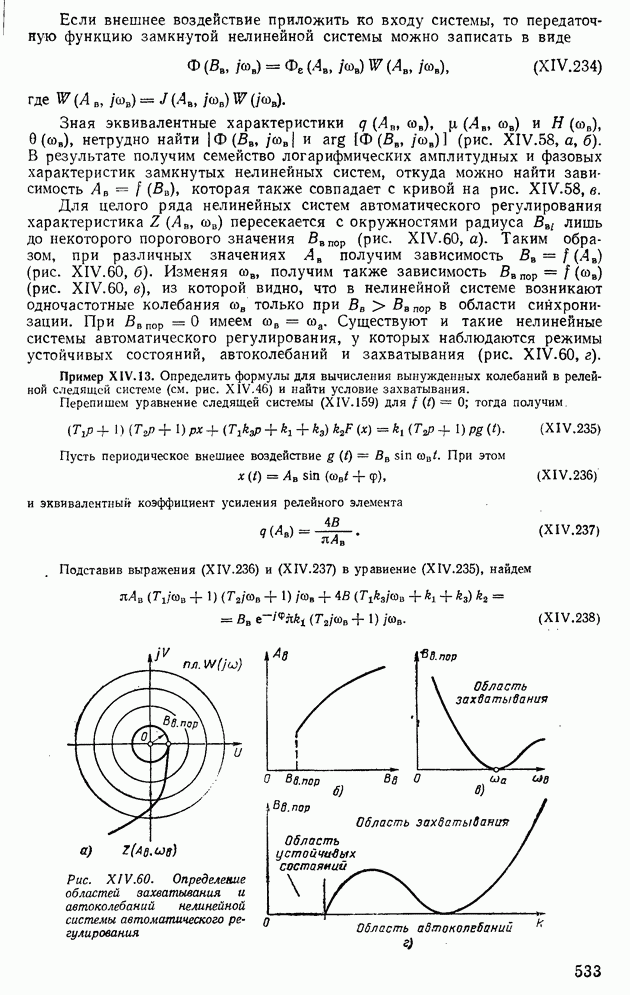
- 6. АНАЛИЗ АВТОКОЛЕБАНИЙ В СИСТЕМАХ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С ДВУМЯ НЕЛИНЕЙНОСТЯМИ
- 7. ДВУХКОНТУРНЫЕ НЕЛИНЕЙНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕДЛЕННО ИЗМЕНЯЮЩИЕСЯ ПРОЦЕССЫ В АВТОКОЛЕБАТЕЛЬНЫХ СИСТЕМАХ
- 9. СПОСОБЫ ПОДАВЛЕНИЯ АВТОКОЛЕБАНИЙ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- 10. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ В НЕЛИНЕЙНЫХ СИСТЕМАХ
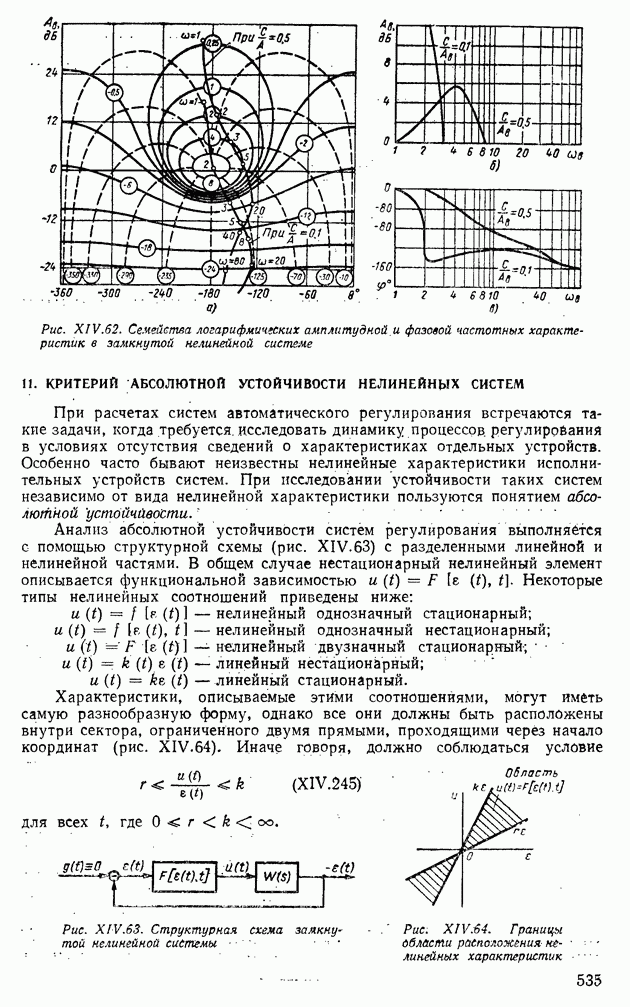
- 11. КРИТЕРИЙ АБСОЛЮТНОЙ УСТОЙЧИВОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
- 12. СЛУЧАЙНЫЕ ПРОЦЕССЫ В НЕЛИНЕЙНЫХ СИСТЕМАХ
- Глава XIV. ИМПУЛЬСНЫЕ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
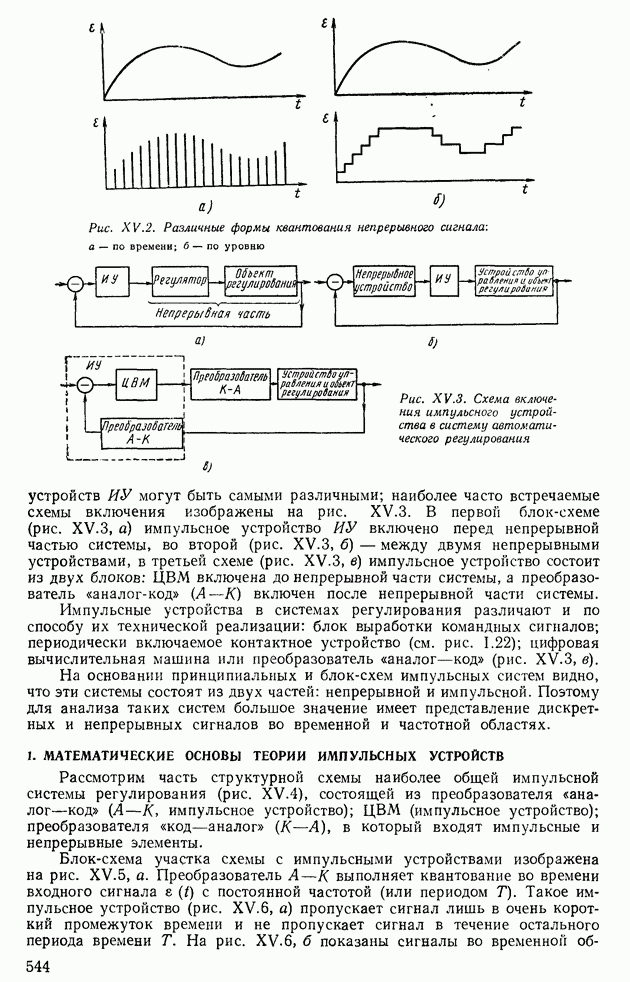
- 1. МАТЕМАТИЧЕСКИЕ ОСНОВЫ ТЕОРИИ ИМПУЛЬСНЫХ УСТРОЙСТВ
- 2. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. АМПЛИТУДНО-ФАЗОВЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ИМПУЛЬСНЫХ СИСТЕМ
- 4. ПРИМЕНЕНИЕ ВЕКТОРНО-МАТРИЧНОГО АППАРАТА К ИМПУЛЬСНЫМ СИСТЕМАМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 5. ОСНОВНЫЕ СВОЙСТВА z-ПРЕОБРАЗОВАНИЯ
- 6. МЕТОДЫ АНАЛИЗА УСТОЙЧИВОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- Критерий устойчивости для импульсных систем на плоскостях z и W(z).
- Критерий устойчивости Шур—Кона.
- Критерии устойчивости, основанные на применении билинейного преобразования.
- 7. МЕТОДЫ АНАЛИЗА КАЧЕСТВА ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 8. МЕТОДЫ АНАЛИЗА ТОЧНОСТИ ИМПУЛЬСНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ И СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 9. СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С УПРАВЛЯЮЩИМИ ЦВМ
- 10. СПОСОБЫ РЕАЛИЗАЦИИ АЛГОРИТМОВ В УПРАВЛЯЮЩИХ ЦВМ И ОПРЕДЕЛЕНИЕ ИХ ОСНОВНЫХ ПАРАМЕТРОВ
- Глава XVI. ЭКСТРЕМАЛЬНЫЕ И САМОНАСТРАИВАЮЩИЕСЯ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. МЕТОДЫ ПОИСКА ЭКСТРЕМУМА
- 2. СПОСОБЫ ОРГАНИЗАЦИИ ДВИЖЕНИЯ К ЭКСТРЕМУМУ
- 3. МЕТОДЫ РАСЧЕТА ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРОВ
- 4. ВЫБОР КОРРЕКТИРУЮЩИХ УСТРОЙСТВ В ЭКСТРЕМАЛЬНЫХ РЕГУЛЯТОРАХ
- 5. ЭКСТРЕМАЛЬНЫЕ СИСТЕМЫ С ВЫЧИСЛИТЕЛЬНЫМИ МАШИНАМИ
- Глава XVII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ РЕГУЛЯРНЫХ ВОЗДЕЙСТВИЯХ
- 2. ВЫБОР ПАРАМЕТРОВ УСТРОЙСТВ НЕИЗМЕНЯЕМОЙ ЧАСТИ СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 3. ПОСТРОЕНИЕ ЖЕЛАЕМОЙ АМПЛИТУДНОЙ ХАРАКТЕРИСТИКИ СИСТЕМЫ РЕГУЛИРОВАНИЯ
- 4. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 5. СИНТЕЗ ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 6. СИНТЕЗ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- 7. СПОСОБЫ РЕАЛИЗАЦИИ ПОСЛЕДОВАТЕЛЬНЫХ И ПАРАЛЛЕЛЬНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ
- Глава XVIII. СИНТЕЗ НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ ПРИ СЛУЧАЙНЫХ ВОЗДЕЙСТВИЯХ
- 1. ПОСТАНОВКА ЗАДАЧИ СИНТЕЗА НА ОСНОВЕ КРИТЕРИЯ МИНИМУМА ИНТЕГРАЛЬНОЙ ОШИБКИ
- 2. СИНТЕЗ СИСТЕМ РЕГУЛИРОВАНИЯ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. ФОРМУЛЫ ДЛЯ ОПРЕДЕЛЕНИЯ ПЕРЕДАТОЧНОЙ ФУНКЦИИ ЖЕЛАЕМОЙ СИСТЕМЫ
- 4. ПРИМЕР СИНТЕЗА КОРРЕКТИРУЮЩИХ УСТРОЙСТВ СИСТЕМЫ РЕГУЛИРОВАНИЯ ПРИ ДЕЙСТВИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- ГЛАВА XIX. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 1. СИНТЕЗ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ, ОСНОВАННЫЙ НА ПРИМЕНЕНИИ БИЛИНЕЙНОГО ПРЕОБРАЗОВАНИЯ
- 2. СИНТЕЗ ДИСКРЕТНО-НЕПРЕРЫВНЫХ СИСТЕМ ПРИ НАЛИЧИИ ПОЛЕЗНОГО СИГНАЛА И ПОМЕХИ
- 3. РЕАЛИЗАЦИЯ ДИСКРЕТНЫХ КОРРЕКТИРУЮЩИХ УСТРОЙСТВ ПРИ ПОМОЩИ RC-ЦЕПЕЙ
- 4. РЕАЛИЗАЦИЯ ПРОГРАММ КОРРЕКЦИИ НА УПРАВЛЯЮЩЕЙ ЦИФРОВОЙ ВЫЧИСЛИТЕЛЬНОЙ МАШИНЕ
- ГЛАВА XX. СИНТЕЗ ОПТИМАЛЬНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ
- 2. ПРИНЦИП МАКСИМУМА
- 3. ТЕОРЕМА О ЧИСЛЕ ПЕРЕКЛЮЧЕНИЙ
- 4. ПРИМЕРЫ ПРИМЕНЕНИЯ ПРИНЦИПА МАКСИМУМА
- 5. МЕТОД ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
- 6. СИНТЕЗ НЕПРЕРЫВНЫХ ОПТИМАЛЬНЫХ СИСТЕМ
- ПРИЛОЖЕНИЯ
- СПИСОК ЛИТЕРАТУРЫ