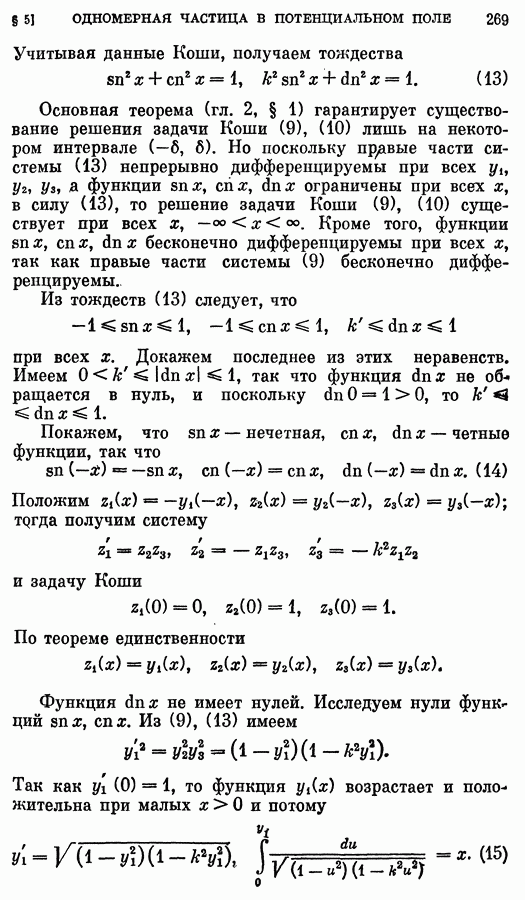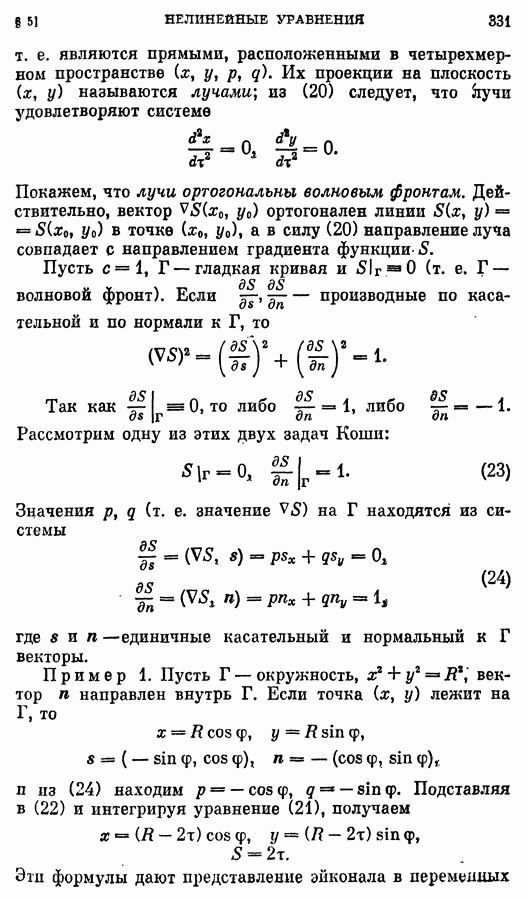| << Предыдущий параграф | Следующий параграф >> |
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
2. Задача Коши.
Постановка этой задачи для нелинейного уравнения (1) отличается от постановки задачи Коши для линейных и квазилинейных уравнений с частными производными. С такого рода различием мы уже встречались для обыкновенных дифференциальных уравнений. Именно, для уравнения, разрешенного относительно производной:  в качестве начальных данных задается значение функции в некоторой точке:
в качестве начальных данных задается значение функции в некоторой точке:  . Для уравнения, не разрешенного относительно производной:
. Для уравнения, не разрешенного относительно производной:  задаются значения функции и производной в некоторой точке:
задаются значения функции и производной в некоторой точке:  Эти значения должны быть согласованы, т. е. должно выполняться соотношение
Эти значения должны быть согласованы, т. е. должно выполняться соотношение  Аналогично, для нелинейного уравнения (1) в качестве данных Коши следует вадать значения функции и всех ее частных производных (т. е. вадать градиент этой функции) на некоторой гиперповерхности
Аналогично, для нелинейного уравнения (1) в качестве данных Коши следует вадать значения функции и всех ее частных производных (т. е. вадать градиент этой функции) на некоторой гиперповерхности  Эти значения функции
Эти значения функции  и ее градиента должны быть согласованы с уравнением (1).
и ее градиента должны быть согласованы с уравнением (1).
Рассмотрим вначале случай, когда  есть гиперплоскость
есть гиперплоскость  и пусть
и пусть  Введем обозначения
Введем обозначения

Зададим на  значения функции
значения функции  Тогда значения
Тогда значения  известных
известных  Для определения
Для определения  получаем уравнение
получаем уравнение

т. е.  определяется как неявная функция. Уравнение (8) может определять не одну, а несколько функций, его решение может не быть гладким и т. д. Пусть при
определяется как неявная функция. Уравнение (8) может определять не одну, а несколько функций, его решение может не быть гладким и т. д. Пусть при  это уравнение имеет корень
это уравнение имеет корень  Если выполнено условие
Если выполнено условие

то по теореме о неявной функции (гл. 2, § 8) уравнение (8) определяет единственную гладкую в окрестности точки  функцию
функцию  такую, что
такую, что  Данные Коши в этом случае таковы:
Данные Коши в этом случае таковы:

Здесь  — указанный выше корень уравнения (8).
— указанный выше корень уравнения (8).
Перейдем к общему случаю. Пусть  задается уравнениями
задается уравнениями

где  лежит в некоторой области
лежит в некоторой области  Пусть, для определенности,
Пусть, для определенности,  Гиперповерхность
Гиперповерхность  предполагается гладкой, т. е. ранг матрицы Якоби
предполагается гладкой, т. е. ранг матрицы Якоби  тождественно равен
тождественно равен  Задача Коши для уравнения (1) ставится так: найти решение уравнения такое, что
Задача Коши для уравнения (1) ставится так: найти решение уравнения такое, что

где  — заданные гладкие функция и вектор-функция. Для данных Коши (12) должны выполняться два условия согласования.
— заданные гладкие функция и вектор-функция. Для данных Коши (12) должны выполняться два условия согласования.

Это следует из того, что значения функции  и ее градиента на
и ее градиента на  должны быть согласованы с уравнением (1),
должны быть согласованы с уравнением (1),

Это следует из тождества  инвариантности первого дифференциала. Такую задачу Коши
инвариантности первого дифференциала. Такую задачу Коши
не всегда можно поставить: для этого требуется чтобы выполнялся аналог условия (9). Соответствующее условие имеет вид

где значения производных функции Я взяты в точке 
Теорема. Пусть условия (13)-(15) выполнены. Тогда в малой окрестности точки  задача Коши (1), (12) имеет решение и притом единственное.
задача Коши (1), (12) имеет решение и притом единственное.
Доказательство. Мы ограничимся случаем, когда  есть гиперплоскость
есть гиперплоскость  Рассмотрим семейство задач Коши
Рассмотрим семейство задач Коши

для характеристической системы (6). Здесь  и У меняется в малой окрестности точки
и У меняется в малой окрестности точки  Решение задачи Коши (16) обозначим
Решение задачи Коши (16) обозначим  Это решение дважды непрерывно дифференцируемо по совокупности переменных
Это решение дважды непрерывно дифференцируемо по совокупности переменных  в некоторой окрестности
в некоторой окрестности  точки
точки  (гл. 2, § 7).
(гл. 2, § 7).
Фиксируем у и рассмотрим уравнение (7) вдоль соответствующей характеристики, т. е.

Данные Коши для функции  определяются из (10);
определяются из (10);  . Решение этой задачи Коши обозначим
. Решение этой задачи Коши обозначим  ); оно имеет вид
); оно имеет вид

и потому дважды непрерывно дифференцируемо в области 
Чтобы завершить доказательство теоремы, проверим следующие факты;
1. Переменные  являются гладкими функциями от переменных
являются гладкими функциями от переменных 
Напомним, что все наши рассмотрения носят локальный характер: х лежит в малой окрестности точки 
Тогда  — гладкая функция
— гладкая функция  — гладкая вектор-функция х.
— гладкая вектор-функция х.
2. Справедливо тождество 
3. Функция  удовлетворяет уравнению (1). Рассмотрим систему из
удовлетворяет уравнению (1). Рассмотрим систему из  уравнений
уравнений

относительно неизвестных  Из данных Коши (16) имеем
Из данных Коши (16) имеем

так что

в точке  . В этой же точке
. В этой же точке  в силу условия (9). Следовательно,
в силу условия (9). Следовательно,  в указанной точке и утверждение 1 следует из теоремы об обратной функции (гл. 2, § 8). Докажем, что
в указанной точке и утверждение 1 следует из теоремы об обратной функции (гл. 2, § 8). Докажем, что

Это следует из того, что функция  первый интеграл гамильтоновой системы (6) (гл. 4, § 4). Остается доказать утверждение 2; его можно записать в виде
первый интеграл гамильтоновой системы (6) (гл. 4, § 4). Остается доказать утверждение 2; его можно записать в виде

Эти тождества эквивалентны следующим:

где  Первое из них следует из (7). Дифференцируя по
Первое из них следует из (7). Дифференцируя по  первое из соотношений (18) и
первое из соотношений (18) и
дифференцируя по  остальиые, получаем
остальиые, получаем

Следовательно,

в силу (17). Так как

в силу определения функций  то
то  и (18) доказано. Тем самым существование решения задачи Коши доказано; его единственность следует из единственности решения задачи Коши для системы (6), (7).
и (18) доказано. Тем самым существование решения задачи Коши доказано; его единственность следует из единственности решения задачи Коши для системы (6), (7).
В качестве примера рассмотрим уравнение эйконала

описывающее распространение световых лучей в однородной и изотропной среде. Здесь  — постоянная (скорость света). Поверхности
— постоянная (скорость света). Поверхности  называются волновыми фронтами. Само слово «эйконал» означает «изображение» (сравните «икона»). Ограничимся случаем
называются волновыми фронтами. Само слово «эйконал» означает «изображение» (сравните «икона»). Ограничимся случаем  т. е.
т. е.

 и положим
и положим  тогда уравнение (19) примет вид
тогда уравнение (19) примет вид  Характеристическая система (6) имеет вид
Характеристическая система (6) имеет вид  а из (7) находим
а из (7) находим

Характеристики имеют вид

т. е. являются прямыми, расположенными в четырехмерном пространстве  Их проекции на плоскость
Их проекции на плоскость  называются лучами; из (20) следует, что Згучи удовлетворяют системе
называются лучами; из (20) следует, что Згучи удовлетворяют системе

Покажем, что лучи ортогональны волновым фронтам. Действительно, вектор  ортогонален линии
ортогонален линии  в точке
в точке  а в силу (20) направление луча совпадает с направлением градиента функции
а в силу (20) направление луча совпадает с направлением градиента функции 
Пусть  — гладкая кривая и
— гладкая кривая и  (т. е. Г — волновой фронт). Если
(т. е. Г — волновой фронт). Если  — производные по касательной и по нормали к Г, то
— производные по касательной и по нормали к Г, то

Так как  то либо
то либо  либо
либо  Рассмотрим одну из этих двух задач Коши:
Рассмотрим одну из этих двух задач Коши:

Значения  (т. е. значение
(т. е. значение  на Г находятся из системы
на Г находятся из системы

где  — единичные касательный и нормальный к Г векторы.
— единичные касательный и нормальный к Г векторы.
Пример 1. Пусть Г — окружность,  вектор
вектор  направлен внутрь Г. Если точка
направлен внутрь Г. Если точка  лежит на Г, то
лежит на Г, то

и из (24) находим  Подставляя в (22) и интегрируя уравнение (21), получаем
Подставляя в (22) и интегрируя уравнение (21), получаем

Эти формулы дают представление эйконала в перемешдах
 Исключая
Исключая  получаем
получаем

Таким образом, эйконал оказывается неоднозначной и, более того, негладкой (в начале координат) функцией. Проанализйруем картину лучей. Если  меняется от 0 до то лучи уходят на бесконечность и не пересекаются. При
меняется от 0 до то лучи уходят на бесконечность и не пересекаются. При  лучи также не пересекаются, а волновые фронты — окружности радиуса
лучи также не пересекаются, а волновые фронты — окружности радиуса  при
при  При
При  все лучи сходятся в точку
все лучи сходятся в точку  . Это явление называется фокусировкой лучей, а точка
. Это явление называется фокусировкой лучей, а точка  называется фокусом.
называется фокусом.
Исключив  уравнение семейства лучей можно записать в виде
уравнение семейства лучей можно записать в виде

т. е. лучи образуют однопараметрическое семейство кривых. Найдем его огибающую (гл. 2, § 11), исключив  из
из  системы
системы  Тогда получим одну точку
Тогда получим одну точку  ;
;
в данном случае огибающая вырождается в точку.
Пример 2. Пусть Г — парабола  Точки на Г можно представить как функции одного параметра
Точки на Г можно представить как функции одного параметра  . В данном примере
. В данном примере

и из системы (20) находим

Далее,  Функция S не может быть однозначной на всей плоскости, так как лучи могут пересекаться. Неоднозначность может возникнуть в тех точках, в которых нельзя выразить
Функция S не может быть однозначной на всей плоскости, так как лучи могут пересекаться. Неоднозначность может возникнуть в тех точках, в которых нельзя выразить  через
через  однозначно; в этих точках должны нарушаться условия теоремы об обратной функции, т. е. должен обращаться в пуль якобиан:
однозначно; в этих точках должны нарушаться условия теоремы об обратной функции, т. е. должен обращаться в пуль якобиан:

Это приводит к следующему соотношению между

и из (25) находим, что искомые точки расположены на полу кубической параболе (рис. 41)


Рис. 41.
Эта кривая — эволюта исходной параболы Г.
Последний факт носит общий характер. Именно, если кривая Г — волновой фронт (т. е.  то точки, в которых нарушается гладкость функции
то точки, в которых нарушается гладкость функции  , расположены на эволюте кривой Г.
, расположены на эволюте кривой Г.
Уравнение (1) не содержит явно неизвестной функции. Рассмотрим уравнение первого порядка с частными производными самого общего вида:

В этом случае характеристическая система имеет вид

а  по-прежнему удовлетворяет уравнению (7). Постановка задачи Коши и теорема существования и единственности формулируются точно так же, как и для уравнения (1).
по-прежнему удовлетворяет уравнению (7). Постановка задачи Коши и теорема существования и единственности формулируются точно так же, как и для уравнения (1).
| << Предыдущий параграф | Следующий параграф >> |
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Дифференциальные уравнения первого порядка
- 2. Уравнения с разделяющимися переменными.
- 3. Однородные уравнения.
- 4. Линейные уравнения.
- 5. Уравнения в полных дифференциалах.
- 6. Интегрирующий множитель.
- 7. Уравнение Бернулли.
- 8. Уравнение Риккати.
- § 3. Линейные дифференциальные уравнения. Принцип суперпозиции
- 2. Принцип суперпозиции.
- § 4. Линейное уравнепие первого порядка с постоянными коэффициентами
- 2. Комплексные функции вещественного аргумента. Комплексная экспонента.
- § 5. Линейные однородные дифференциалыше уравнения с постоянными коэффициентами
- 2. Случай простых корней.
- 3. Случай кратных корней.
- 4. Уравнение Эйлера.
- 5. Выделение вещественных решений.
- § 6. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- 2. Ангармонические колебания.
- § 7. Линейные уравнения с правой частью — квазимногочленом
- § 8. Линейные системы с постоянными коэффициентами. Случай простых корней
- § 9. Фазовая плоскость линейной системы
- 2. Комплексные корни.
- 3. Уравнение второго порядка.
- § 10. Линейные системы с постоянными коэффициентами. Случай кратных корней
- § 11. Операционное исчисление
- § 12. Линейные разностные уравнения
- ГЛАВА 2. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Доказательство основной теоремы при n = 1.
- 3. Теорема Коши.
- § 2. Линейные нормированные пространства
- § 3. Принцип сжатых отображений
- § 4. Лемма Адамара
- § 5. Доказательство основной теоремы. Теорема существования и единственности для уравнений n-го порядка
- 2. Дифференциальные уравнения n-го порядка.
- 3. Комментарии к основной теореме.
- 4. Продолжение решений.
- § 6. Гладкость решений
- § 7. Зависимость решений от параметров и начальных условий
- § 8. Обратные и неявные функции
- 2. Теорема о неявной функции.
- 3. Дифференцирование сложных функций.
- § 9. Зависимые и независимые функции. Криволинейные координаты
- 2. Кривые и поверхности.
- 3. Криволинейные координаты.
- § 10. Уравнения первого порядка, не разрешенные относительно производной
- 2. Особые решения. Огибающая.
- 3. Интегрирование уравнений вида (1).
- ГЛАВА 3. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
- 2. Доказательство теоремы.
- 3. Линейное уравнение n-го порядка.
- § 2. Функции от матриц и однородные линейные системы с постоянными коэффициентами
- 2. Вычисление матричной экспоненты.
- 3. Функции от матриц.
- 4. Малые колебания механических систем.
- § 3. Линейная зависимость и независимость функций и вектор-функций. Определитель Вронского
- 2. Определитель Вронского.
- § 4. Формула Лиувилля
- § 5. Фундаментальные системы решений
- § 6. Неоднородные линейные системы с переменными коэффициентами
- § 7. Линейные дифференциальные уравнения n-го порядка
- 2. Уравнения второго порядка.
- § 8. Понижение порядка линейных и нелинейных дифференциальных уравнений
- § 9. Нули решений однородных линейных уравнений второго порядка
- 2. Теорема сравнения.
- § 10. Элементы аналитической теории дифференциальных уравнений. Уравнение Бесселя
- 2. Регулярные особые точки.
- 3. Уравнение Бесселя.
- § 11. Уравнения с периодическими коэффициентами
- 2. Зоны устойчивости и неустойчивости.
- § 12. Дельта-функция и ее применения
- 2. Толчки. Принцип Дюамеля.
- 3. Периодические толчки в системах с трением.
- ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ И ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Векторные поля. Механическая интерпретация фазовых траекторий.
- § 2. Структура решений автономной системы в окрестности неособой точки
- § 3. Изменение фазового объема
- 2. Замечания о системах в трехмерном пространстве.
- § 4. Производная в силу системы. Первые интегралы
- 2. Первые интегралы.
- § 5. Одномерное движение частицы в потенциальном поле
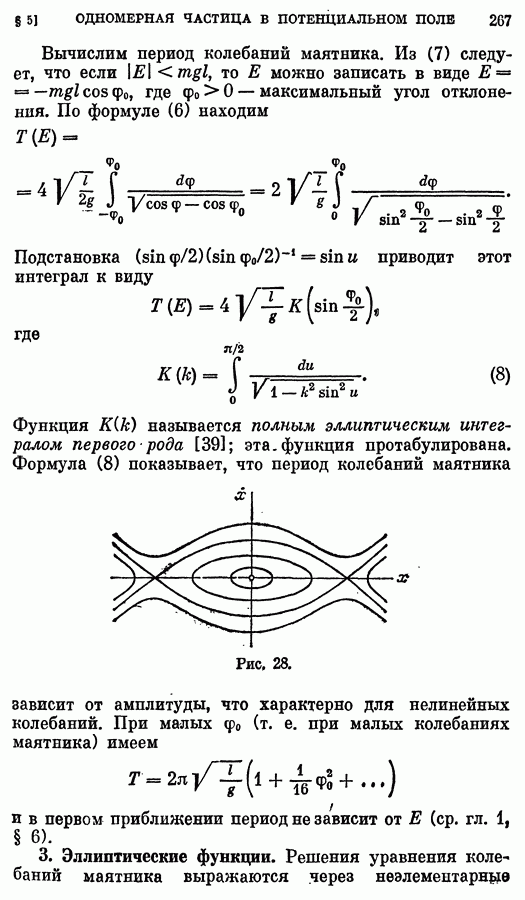
- 2. Колебания маятника.
- 3. Эллиптические функции.
- 4. Движение частицы в поле с кубическим потенциалом.
- § 6. Устойчивость. Функция Ляпунова
- § 7. Устойчивость положения равновесия линейной системы
- § 8. Устойчивость по линейному приближению
- 2. Устойчивость по линейному приближению.
- 3. Неустойчивость по линейному приближению.
- 4. Устойчивость неавтономных систем.
- 5. Устойчивые многообразия решений (условная устойчивость).
- § 9. Двумерные автономные системы (элементы качественной теории)
- 2. Предельное поведение траекторий.
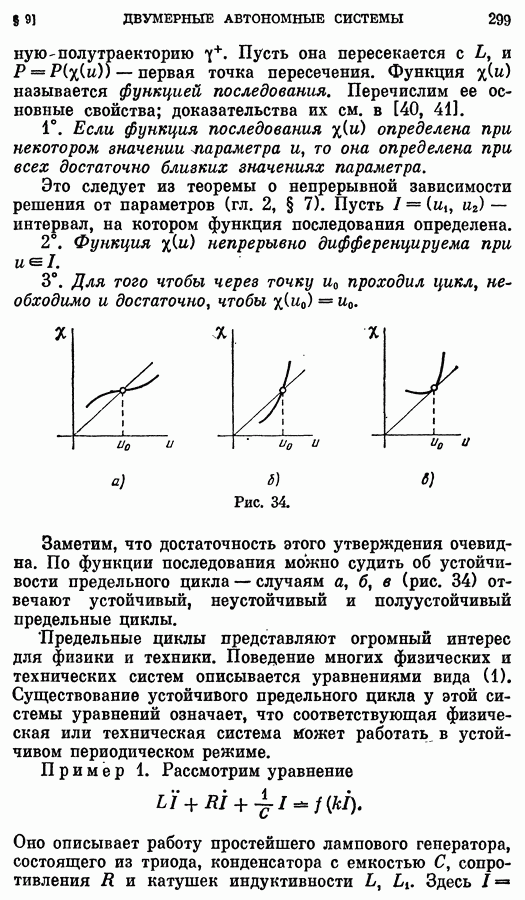
- 3. Функция последования. Автоколебания.
- ГЛАВА 5. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
- 2. Другие примеры.
- 3. Классификация уравнений с частными производными 1-го порядка.
- § 2. Интегрирование линейных и квазилинейных уравнений
- 2. Квазилинейные уравнения.
- 3. Характеристики и интегральные поверхности.
- § 3. Задача Коши для линейных и квазилинейных уравнений
- 2. Область зависимости от начальных данных.
- 3. Линейные уравнения со многими переменными.
- 4. Квазилинейные уравнения.
- § 4. Линейные и нелинейные волны
- § 5. Нелинейные уравнения
- 2. Задача Коши.
- ГЛАВА 6. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- § 2. Функционалы в линейных нормированных пространствах
- 2. Линейные функционалы.
- 3. Первая вариация.
- 4. Необходимое условие экстремума.
- § 3. Простейшие задачи вариационного исчисления
- 2. Задача с одним закрепленным и с одним подвижным концом.
- 3. Примеры.
- § 4. Функционалы, зависящие от высших производных
- § 5. Функционалы, зависящие от вектор-функций. Принцип наименьшего действия в механике
- 2. Принцип наименьшего действия.
- § 6. Условный экстремум
- § 7. Задача Лагранжа
- § 8. Функционалы от функций многих переменных
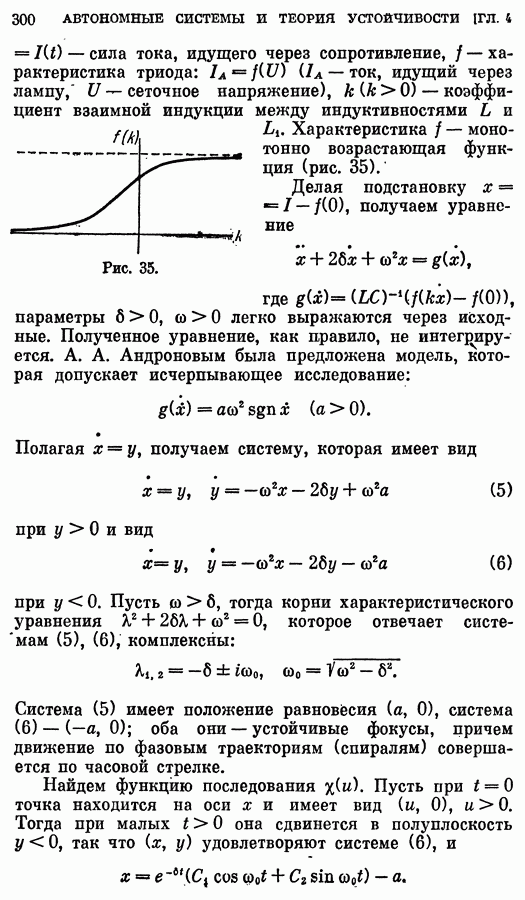
- 2. Уравнение колебаний мембраны.
- § 9. Достаточные условия слабого экстремума
- 2. Квадратичные функционалы.
- 3. Достаточные условия слабого экстремума.
- § 10. Дополнительные сведения из вариационного исчисления
- 2. Гамильтонова форма уравнений механики.
- 3. Задача с подвижными концами.
- § 11. Принцип максимума Понтрягина
- 2. Необходимые условия экстремума.
- ГЛАВА 7. АСИМПТОТИКА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Основные оценки
- 2. Оценка решений.
- § 3. Асимптотика решений при больших значениях аргумента
- 2. Неосциллирующие решения.
- 3. Уравнения с комплексными коэффициентами.
- § 4. Асимптотика решений при больших значениях параметра
- 2. Неосциллирующие решения.
- 3. Двойные асимптотики.
- 4. Асимптотические разложения решений.
- § 5. Элементы теории возмущений
- 2. Метод Линдштедта — Пуанкаре.
- 3. Метод Крылова — Боголюбова.
- 4. Метдд осреднения.
- 5. Пограничный слой и метод сращивания асимптотических разложений.
- 6. Метод ВКБ для нелинейных уравнений.
- СПИСОК ЛИТЕРАТУРЫ