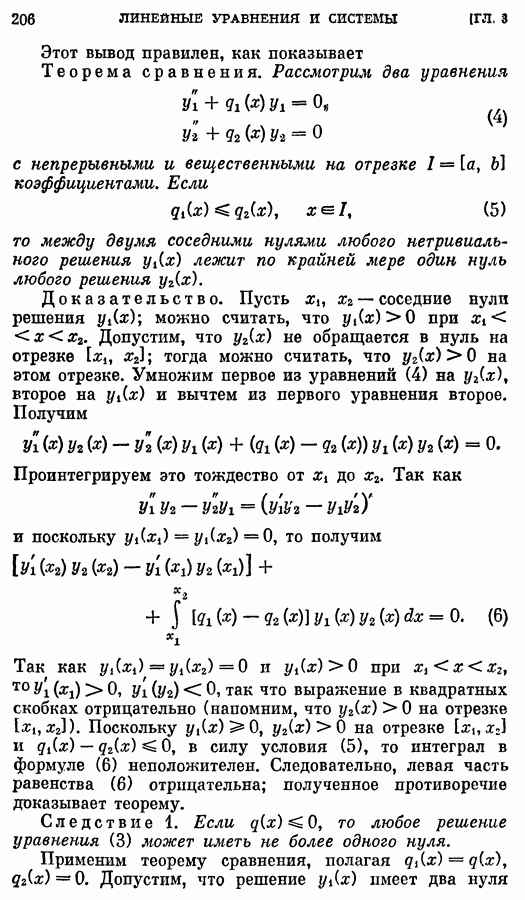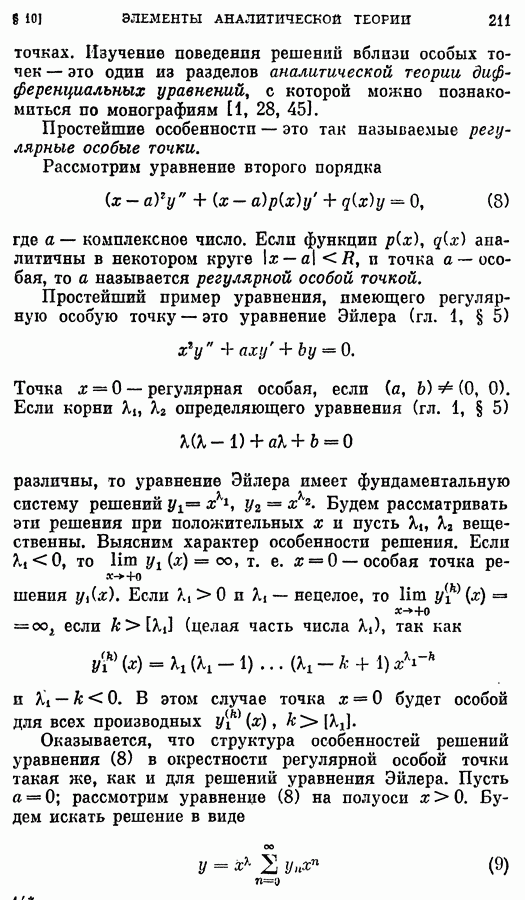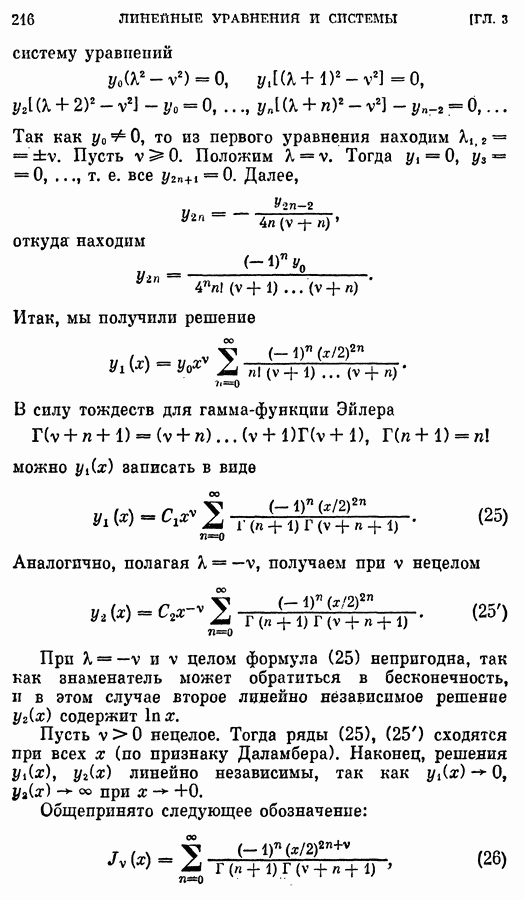| << Предыдущий параграф | Следующий параграф >> |
Пред.
След.
Макеты страниц
Распознанный текст, спецсимволы и формулы могут содержать ошибки, поэтому с корректным вариантом рекомендуем ознакомиться на отсканированных изображениях учебника выше
Также, советуем воспользоваться поиском по сайту, мы уверены, что вы сможете найти больше информации по нужной Вам тематике
ДЛЯ СТУДЕНТОВ И ШКОЛЬНИКОВ ЕСТЬ
ZADANIA.TO
2. Толчки. Принцип Дюамеля.
Рассмотрим уравнение

где  постоянная, функции
постоянная, функции  непрерывны на всей оси, для простоты. При
непрерывны на всей оси, для простоты. При  функция
функция  удовлетворяет однородному уравнению
удовлетворяет однородному уравнению

Покажем, что если  — решение уравнения (10), то
— решение уравнения (10), то  удовлетворяет уравнению (11) при
удовлетворяет уравнению (11) при  и следующим краевым условиям:
и следующим краевым условиям:

Здесь обозначено 
Действительно, решение  непрерывно на полуосях
непрерывно на полуосях  Далее, эта функция должна быть непрерывна при
Далее, эта функция должна быть непрерывна при  в противном случае производная была бы суммой обычной функции и функции
в противном случае производная была бы суммой обычной функции и функции  (см. 3°), а функция содержала бы слагаемое
(см. 3°), а функция содержала бы слагаемое  и потому левая часть уравнения (10) не совпала бы с правой. Итак,
и потому левая часть уравнения (10) не совпала бы с правой. Итак,  но производная
но производная  может иметь конечный скачок в точке
может иметь конечный скачок в точке  Проинтегрируем обе части уравнения (10) по интервалу
Проинтегрируем обе части уравнения (10) по интервалу  тогда получим
тогда получим

Перейдем в этом равенстве к пределу при  , тогда интеграл обратится в нуль (подынтегральная функция ограничена) и мы получим
, тогда интеграл обратится в нуль (подынтегральная функция ограничена) и мы получим

Тем самым условие (12) получено.
Если рассматривать  как координату точки, движущейся по оси х, то соотношения (12) означают, что в момент времени
как координату точки, движущейся по оси х, то соотношения (12) означают, что в момент времени  координата точки не меняется, а скорость получает конечное приращение V. Такое воздействие на точку называется в механике и физике толчком (или мгновенным удйром); например, это резкий удар кием по биллиардному шару).
координата точки не меняется, а скорость получает конечное приращение V. Такое воздействие на точку называется в механике и физике толчком (или мгновенным удйром); например, это резкий удар кием по биллиардному шару).
Толчок можно получить как результат предельного Перехода. Рассмотрим уравнение

где  при
при  Правая часть есть большая постоянная сила
Правая часть есть большая постоянная сила  действующая малое время, причем так, что интеграл
действующая малое время, причем так, что интеграл  (импульс конечен). Решив это уравнение и перейдя к пределу при
(импульс конечен). Решив это уравнение и перейдя к пределу при  получим, что предельная функция
получим, что предельная функция  будет решением уравнения (10). Но ценность дельта-функции в том и состоит, что ее
будет решением уравнения (10). Но ценность дельта-функции в том и состоит, что ее
применение позволяет избежать необходимости каждый раз совершать предельный переход — этот предельный переход содержится в самом определении дельта-функции (см. (7)).
Найдем результат воздействия толчка. Рассмотрим задачу Коши

для уравнения (11), и пусть  — решение этой задачи, определенное при —
— решение этой задачи, определенное при —  Положим
Положим

где  — решение уравнения (10) с данными Коши (13). Тогда для функции
— решение уравнения (10) с данными Коши (13). Тогда для функции  получим задачу Коши
получим задачу Коши

Кроме того,

Функция  — это результат воздействия единичного толчка (т. е.
— это результат воздействия единичного толчка (т. е.  ) на систему. Заметим, что
) на систему. Заметим, что  не зависит от данных Коши (13) (т. е. не зависит от того, как двигалась точка при
не зависит от данных Коши (13) (т. е. не зависит от того, как двигалась точка при  ).
).
Функция  называется функцией Грина уравнения (10) и может быть найдена, если известна фундаментальная система решений
называется функцией Грина уравнения (10) и может быть найдена, если известна фундаментальная система решений  однородного уравнения
однородного уравнения  Так как
Так как  удовлетворяет этому уравнению при
удовлетворяет этому уравнению при  то
то

где  — постоянные. Данные Коши (15) приводят к системе уравнений
— постоянные. Данные Коши (15) приводят к системе уравнений

откуда находятся  и мы получаем
и мы получаем

Здесь  — вронскиан решений
— вронскиан решений  При
При  имеем
имеем 
Отметим также, что  есть решение уравнения
есть решение уравнения

равное нулю при 
Если функция Грина известна, то можно найти решение неодйородного уравнения

с любой (непрерывной) правой частью 
Теорема. Функция 

удовлетворяет уравнению (19) при  и нулевым данным Коши при
и нулевым данным Коши при 

Прежде чем привести строгое доказательство, приведем формальное. Так как  при
при  то
то

Формально дифференцируя под знаком интеграла, получаем

так что  — решение уравнения (19).
— решение уравнения (19).
Теперь строгое доказательство. Имеем  Далее,
Далее,

Так как  , то
, то

так что

поскольку подынтегральное выражение равно нулю (см. (15)).
Правая часть формулы (20) — это континуальная (т. е. непрерывная) сумма толчков. Они совершаются в момент ты времени  с плотностями
с плотностями  где
где  пробегает интервал
пробегает интервал  Итак, результат воздействия на частицу непрерывно действующей силы
Итак, результат воздействия на частицу непрерывно действующей силы  эквивалентен воздействию континуальной суммы последовательных толчков. Этот факт (а точнее, формула
эквивалентен воздействию континуальной суммы последовательных толчков. Этот факт (а точнее, формула  называется принципом Дюамеля.
называется принципом Дюамеля.
Замечание 1. Формулы (20), (17), дающие частное решение уравнения (19), совпадают с полученными в § 7 формулами (16) для частного решения неоднородного уравнения второго порядка.
Замечание 2. Рассмотрим нелинейное уравнение с дельта-функцией в правой части:

Тем же способом, что и выше, можно показать, что  удовлетворяет уравнению
удовлетворяет уравнению

при  условиям (12) при
условиям (12) при 
Приведем аналогичные результаты для линейного уравнения  -го порядка
-го порядка

где  коэффициенты
коэффициенты  непрерывны на всей прямой, для простоты. Тогда функция
непрерывны на всей прямой, для простоты. Тогда функция  удовлетворяет однородному уравнению
удовлетворяет однородному уравнению

при  условиям
условиям

В данном случае функция Грина  есть решение задачи Коши
есть решение задачи Коши

равное нулю при  Функция
Функция

при  удовлетворяет неоднородному уравнению
удовлетворяет неоднородному уравнению

и данным Коши

Замечание 3. Рассмотрим систему из  уравнений
уравнений

Здесь  непрерывные
непрерывные  -матрицы и V — постоянный
-матрицы и V — постоянный  -вектор. Тогда решение
-вектор. Тогда решение  удовлетворяет однородной системе
удовлетворяет однородной системе  при
при  и соотношениям (12). Роль функции Грина играет
и соотношениям (12). Роль функции Грина играет  -матрица
-матрица  — матрица Грина, которая при
— матрица Грина, которая при  есть решение задачи Коши
есть решение задачи Коши

и равна нулю при  Здесь
Здесь  — нулевая и единичная
— нулевая и единичная  -матрицы. Теорема 1 остается в силе (в формуле (20),
-матрицы. Теорема 1 остается в силе (в формуле (20),  есть
есть  -вектор), но формула (17) уже не имеет песта.
-вектор), но формула (17) уже не имеет песта.
| << Предыдущий параграф | Следующий параграф >> |
Оглавление
- ПРЕДИСЛОВИЕ
- ГЛАВА 1. МЕТОДЫ ИНТЕГРИРОВАНИЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Дифференциальные уравнения первого порядка
- 2. Уравнения с разделяющимися переменными.
- 3. Однородные уравнения.
- 4. Линейные уравнения.
- 5. Уравнения в полных дифференциалах.
- 6. Интегрирующий множитель.
- 7. Уравнение Бернулли.
- 8. Уравнение Риккати.
- § 3. Линейные дифференциальные уравнения. Принцип суперпозиции
- 2. Принцип суперпозиции.
- § 4. Линейное уравнепие первого порядка с постоянными коэффициентами
- 2. Комплексные функции вещественного аргумента. Комплексная экспонента.
- § 5. Линейные однородные дифференциалыше уравнения с постоянными коэффициентами
- 2. Случай простых корней.
- 3. Случай кратных корней.
- 4. Уравнение Эйлера.
- 5. Выделение вещественных решений.
- § 6. Линейные однородные уравнения второго порядка с постоянными коэффициентами
- 2. Ангармонические колебания.
- § 7. Линейные уравнения с правой частью — квазимногочленом
- § 8. Линейные системы с постоянными коэффициентами. Случай простых корней
- § 9. Фазовая плоскость линейной системы
- 2. Комплексные корни.
- 3. Уравнение второго порядка.
- § 10. Линейные системы с постоянными коэффициентами. Случай кратных корней
- § 11. Операционное исчисление
- § 12. Линейные разностные уравнения
- ГЛАВА 2. ОСНОВНЫЕ СВОЙСТВА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- 2. Доказательство основной теоремы при n = 1.
- 3. Теорема Коши.
- § 2. Линейные нормированные пространства
- § 3. Принцип сжатых отображений
- § 4. Лемма Адамара
- § 5. Доказательство основной теоремы. Теорема существования и единственности для уравнений n-го порядка
- 2. Дифференциальные уравнения n-го порядка.
- 3. Комментарии к основной теореме.
- 4. Продолжение решений.
- § 6. Гладкость решений
- § 7. Зависимость решений от параметров и начальных условий
- § 8. Обратные и неявные функции
- 2. Теорема о неявной функции.
- 3. Дифференцирование сложных функций.
- § 9. Зависимые и независимые функции. Криволинейные координаты
- 2. Кривые и поверхности.
- 3. Криволинейные координаты.
- § 10. Уравнения первого порядка, не разрешенные относительно производной
- 2. Особые решения. Огибающая.
- 3. Интегрирование уравнений вида (1).
- ГЛАВА 3. ЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ
- 2. Доказательство теоремы.
- 3. Линейное уравнение n-го порядка.
- § 2. Функции от матриц и однородные линейные системы с постоянными коэффициентами
- 2. Вычисление матричной экспоненты.
- 3. Функции от матриц.
- 4. Малые колебания механических систем.
- § 3. Линейная зависимость и независимость функций и вектор-функций. Определитель Вронского
- 2. Определитель Вронского.
- § 4. Формула Лиувилля
- § 5. Фундаментальные системы решений
- § 6. Неоднородные линейные системы с переменными коэффициентами
- § 7. Линейные дифференциальные уравнения n-го порядка
- 2. Уравнения второго порядка.
- § 8. Понижение порядка линейных и нелинейных дифференциальных уравнений
- § 9. Нули решений однородных линейных уравнений второго порядка
- 2. Теорема сравнения.
- § 10. Элементы аналитической теории дифференциальных уравнений. Уравнение Бесселя
- 2. Регулярные особые точки.
- 3. Уравнение Бесселя.
- § 11. Уравнения с периодическими коэффициентами
- 2. Зоны устойчивости и неустойчивости.
- § 12. Дельта-функция и ее применения
- 2. Толчки. Принцип Дюамеля.
- 3. Периодические толчки в системах с трением.
- ГЛАВА 4. АВТОНОМНЫЕ СИСТЕМЫ И ТЕОРИЯ УСТОЙЧИВОСТИ
- 2. Векторные поля. Механическая интерпретация фазовых траекторий.
- § 2. Структура решений автономной системы в окрестности неособой точки
- § 3. Изменение фазового объема
- 2. Замечания о системах в трехмерном пространстве.
- § 4. Производная в силу системы. Первые интегралы
- 2. Первые интегралы.
- § 5. Одномерное движение частицы в потенциальном поле
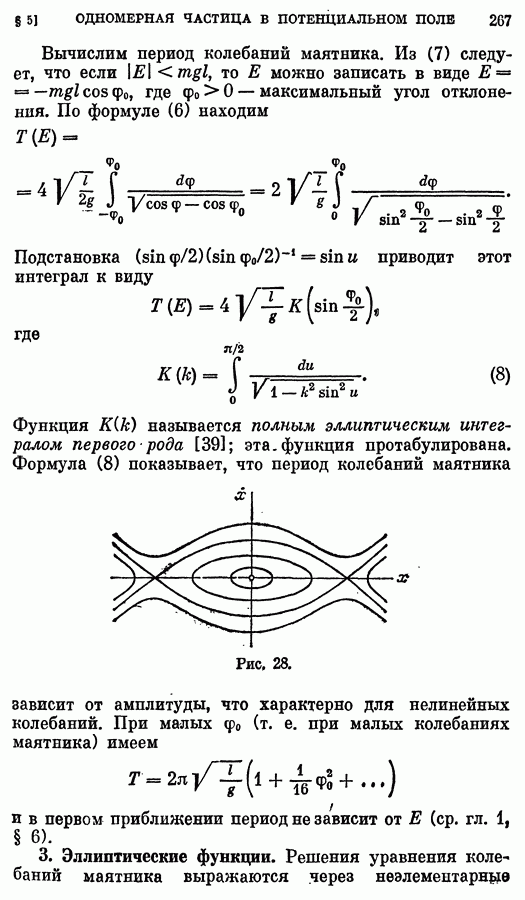
- 2. Колебания маятника.
- 3. Эллиптические функции.
- 4. Движение частицы в поле с кубическим потенциалом.
- § 6. Устойчивость. Функция Ляпунова
- § 7. Устойчивость положения равновесия линейной системы
- § 8. Устойчивость по линейному приближению
- 2. Устойчивость по линейному приближению.
- 3. Неустойчивость по линейному приближению.
- 4. Устойчивость неавтономных систем.
- 5. Устойчивые многообразия решений (условная устойчивость).
- § 9. Двумерные автономные системы (элементы качественной теории)
- 2. Предельное поведение траекторий.
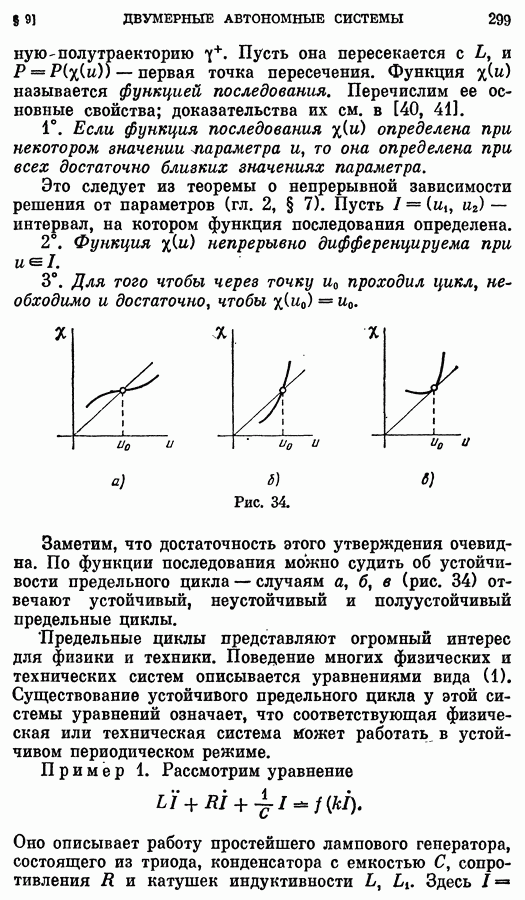
- 3. Функция последования. Автоколебания.
- ГЛАВА 5. УРАВНЕНИЯ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА
- 2. Другие примеры.
- 3. Классификация уравнений с частными производными 1-го порядка.
- § 2. Интегрирование линейных и квазилинейных уравнений
- 2. Квазилинейные уравнения.
- 3. Характеристики и интегральные поверхности.
- § 3. Задача Коши для линейных и квазилинейных уравнений
- 2. Область зависимости от начальных данных.
- 3. Линейные уравнения со многими переменными.
- 4. Квазилинейные уравнения.
- § 4. Линейные и нелинейные волны
- § 5. Нелинейные уравнения
- 2. Задача Коши.
- ГЛАВА 6. ЭЛЕМЕНТЫ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ
- § 2. Функционалы в линейных нормированных пространствах
- 2. Линейные функционалы.
- 3. Первая вариация.
- 4. Необходимое условие экстремума.
- § 3. Простейшие задачи вариационного исчисления
- 2. Задача с одним закрепленным и с одним подвижным концом.
- 3. Примеры.
- § 4. Функционалы, зависящие от высших производных
- § 5. Функционалы, зависящие от вектор-функций. Принцип наименьшего действия в механике
- 2. Принцип наименьшего действия.
- § 6. Условный экстремум
- § 7. Задача Лагранжа
- § 8. Функционалы от функций многих переменных
- 2. Уравнение колебаний мембраны.
- § 9. Достаточные условия слабого экстремума
- 2. Квадратичные функционалы.
- 3. Достаточные условия слабого экстремума.
- § 10. Дополнительные сведения из вариационного исчисления
- 2. Гамильтонова форма уравнений механики.
- 3. Задача с подвижными концами.
- § 11. Принцип максимума Понтрягина
- 2. Необходимые условия экстремума.
- ГЛАВА 7. АСИМПТОТИКА РЕШЕНИЙ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
- § 2. Основные оценки
- 2. Оценка решений.
- § 3. Асимптотика решений при больших значениях аргумента
- 2. Неосциллирующие решения.
- 3. Уравнения с комплексными коэффициентами.
- § 4. Асимптотика решений при больших значениях параметра
- 2. Неосциллирующие решения.
- 3. Двойные асимптотики.
- 4. Асимптотические разложения решений.
- § 5. Элементы теории возмущений
- 2. Метод Линдштедта — Пуанкаре.
- 3. Метод Крылова — Боголюбова.
- 4. Метдд осреднения.
- 5. Пограничный слой и метод сращивания асимптотических разложений.
- 6. Метод ВКБ для нелинейных уравнений.
- СПИСОК ЛИТЕРАТУРЫ